The stability evaluation of clay tunnels via the non-linear deterioration of physical and mechanical properties of surrounding rocks

Simple, fast, and reliable methods for the stability evaluation of tunnels can facilitate the construction and development of tunneling projects. The problems related to tunnel stability at this stage can be well analyzed via theoretical analysis method, model test method, or numerical analysis method. On the other hand, those methods are hard to be effectively analyzed these projects with higher importance, shorter decision and design period, and more urgent construction period. This paper proposed research works on the stability evaluation of clay tunnels. Firstly, a state function with the variables of stress and strain state is presented to predict the stress and strain states of surrounding rocks caused by tunnel excavation, which characterize the physical-mechanical state of surrounding rocks (also called stability state). Secondly, the non-linear deterioration of the physical and mechanical properties of surrounding rocks will be simulated, and the expressions and calculation methods of the tunnel stability reserve factor will be yielded. Finally, the results of the proposed method were compared with the strength reduction method and the limit equilibrium method with a clay tunnel example. The comparison between the three feature points of the arch crown, sidewall, and arch bottom showed that the stability reserve factor of the clay tunnel was smaller than those of the strength reduction method and the limit equilibrium method. The values of limit displacement obtained by the proposed method were closer to the field monitoring data than that of the strength reduction method. Therefore, this study could be better applied to the stability evaluation of clay tunnels.

1 Introduction

Research in tunnel stability evaluation is very important for the safe construction and operation of tunnel projects. Modern subway tunnels have short construction cycles and high construction and operation safety requirements. Thus, tunnel engineers need to process the project more rapidly, and more efficiently, and make stability analysis decisions accurately. Therefore, tunnel stability evaluation is facing challenges i.e., rapid response, decision-making judgment, prevention and disposal, and the need for further in-depth optimization.

At present, the research methods of tunnel stability can be summarized as the empirical, theoretical, experimental, and numerical analysis methods (Song et al., 2001; Osman et al., 2006; Son and Cording, 2008; Yang and Yang, 2009; Fraldi and Guarracino, 2010; Yang and Huang, 2013; Shiau and Al-Asadi, 2020; Song and Marshall, 2020; Tan et al., 2020; Tyagi et al., 2020; Yertutanol et al., 2020; Li L. P. et al., 2021; Pandit and Sivakumar, 2021; Liu et al., 2022a; Zhang et al., 2022a; Zhang Z. et al., 2022; Hao et al., 2022; Lu et al., 2022; Qin et al., 2022; Li et al., 2023; Xue et al., 2023). The primary purpose of these methods is to obtain more effective and accurate stability analysis results and provide a more reliable basis for the actual tunnel construction and operation decisions. Early researchers (Broms and Bennermark, 1967; Davis et al., 1979; Mair, 1979; Rowe and Kack, 1983; Assadi and Sloan, 1991a; Assadi and Sloan, 1991b; Leca and Dormieux, 1991; Sloan and Assadi, 1991; Mair et al., 1993) usually relied on the experience to evaluate the stability of tunnels due to the lack of theoretical basis. The experience of tunnel construction is accumulated with the development of geotechnical theory and technology. The researchers (Lee and Park, 2000; Lyamin et al., 2001; Wang et al., 2001; Lee et al., 2006; Fraldi and Guarracino, 2009; Wilson et al., 2011; Yang and Huang, 2011; Fan et al., 2013; Rojat et al., 2015) considering more influencing factors to evaluate the stability of tunnels and formed the corresponding stability evaluation methods and techniques. The tunnel stability evaluation methods have been developed by the emergence of more adverse factors and complex environmental conditions with the continuous development of tunnel construction. Since the researchers of tunnel stability evaluation focus on the response of surrounding rocks’ stress field and deformation field caused by tunnel excavation, tunnel model tests (Marshall et al., 2012; Shiau and Al-Asadi, 2020; Song and Marshall, 2020; Yertutanol et al., 2020; Lu et al., 2022; Sun et al., 2022; Qin et al., 2023a; Qin et al., 2023b) is used to reveal the rule of the stress field and deformation field of surrounding rocks by excavation. The model’s test of tunnel experimental (Franza, 2019; Huang et al., 2019; Zhang et al., 2020), in-situ, and centrifugal, can be well revealed the failure pattern. The stress distribution and deformation characteristics of surrounding rocks will help to understand tunnel stability research. Researchers (Liu et al., 2020; Antão et al., 2021; Fernández et al., 2021; Han et al., 2021; Nguyen and Nguyen-Son, 2022; Pelech et al., 2022; Zhuo et al., 2022; Qin et al., 2023c) established numerical models based on the numerical method, e.g., finite element method or discrete element method with the continuous improvement of computer performance and the development of computing technology. Numerical modeling is closer to the accurate geometric scale, surrounding rock materials, loading effects, boundary conditions, etc., and visualizes the process of surrounding rock loading evolution. Numerical methods can solve the construction problems faced by large tunnel projects effectively, and promote tunnel engineering development. Currently, the methods of tunnel stability are not limited to a narrow field. These methods (Sukkarak et al., 2019; Shiau and Al-Asadi, 2020; Kumar and Jain, 2021; Li T. Z. et al., 2021; Liu et al., 2022b; Zhang et al., 2022b; Man et al., 2022; Xue et al., 2022; Xue et al., 2023) are not only applied to but also inspired by other fields of research. The researchers of tunnel stability problems still have the power of sustainable development.

Researchers are still trying to find more operational, more straightforward physically meaningful, and applicable methods for tunnel stability evaluation problems. In this paper, a clay tunnel project is used as the case study, and the deterioration characteristics of the physical and mechanical properties of surrounding rocks are taken into account. The development of surrounding rocks from the stable to the limit state until the failure. This paper introduced a strategy for the deterioration of the strength and deformation resistance of surrounding rocks for tunnel stability evaluation.

2 State function of clay tunnel surrounding rocks

The general failure of tunnel loading can be summarized into two cases. The first one is the redistribution of stresses in surrounding rocks and destabilization is yield due to the stress is exceeded the limit value (the accumulated deformation before stress failure may not exceed the limit). The second type of instability is due to the cumulative deformation caused by excavation-induced restraint relaxation exceeding the limit (the stress state may not exceed the limit at this time). The basic idea of the strength reduction method is to allow the material strength to deteriorate until the material reaches its ultimate state. In general, the failure of clay tunnels has been corresponding to both cases described. The deterioration of the strength and deformation resistance in surrounding rocks should take into account to evaluate stability reserves.

According to the basic knowledge of solid mechanics, elastic mechanics, and material mechanics, it is known that stress redistribution occurs in clay strata due to tunnel excavation, which leads to the change of stress-strain state in surrounding rocks. The stress state at a point in surrounding rocks can be characterized by the stress and strain of this point at this moment. So it assumed the existence of a state function F_s, which was a function of the stress state and strain state at a point in surrounding rocks. It was that the state function could reflect the stress state characteristics of surrounding rocks. The expression of the state function F_S was as follows.

$F_S=f\left(\sigma ,\epsilon \right)(1)$

Where $\sigma$ refers to the stress state at a point in surrounding rocks, and $\epsilon$ refers to the strain state at a point in surrounding rocks.

According to the definition of the state function, when the stress state or strain state of any point in surrounding rocks reaches the limit state, it can be considered that the state function at that point reaches the limit state at this time. There should be three limit states at a point in surrounding rocks.

1) A point of surrounding rocks stress state and strain state have reached the limit state: $F_{SL}=f\left({\sigma }_L,{\epsilon }_L\right)$;

2) Only the stress state at a point of surrounding rocks reaches the limit state: $F_{SL}=f\left({\sigma }_L,\epsilon \right)$;

3) Only the deformation at a point of surrounding rocks reaches the limit state: $F_{SL}=f\left(\sigma ,{\epsilon }_L\right)$.

$F_{SL}$ is the limit state function. The stability of the point can be determined via the limit state function at a point of surrounding rocks,

1) if $F_S=F_{SL}$, it is in the limit state;

2) if $F_S<F_{SL}$, it is in a steady state;

3) if $F_S>F_{SL}$, it is in the failure state.

These can be used as guidelines to distinguish the stability state of tunnel surrounding rocks. Then, these guidelines can play an important role when the engineer needs to evaluate the tunnel stability quantitatively. According to strength theory, the limit state of surrounding rocks at a point can be considered as the limit stress or strain state, which depends on the strength or deformation resistance of surrounding rocks. Then, since the physical and mechanical properties of surrounding rocks deteriorate during the redistribution of stress due to excavation, the objective of quantitative evaluation of the stability of surrounding rocks can be achieved by characterizing the evolution of their deterioration.

3 Method of characterizing the deterioration of surrounding rocks

The stability state evolution of the tunnel surrounding rocks can be described as follows: stable to the limit state, and reach the failure. In the whole state of the evolution process, the physical and mechanical state of surrounding rocks is constantly changed, while the quantitative evaluation of the stability reserve of the tunnel surrounding rocks only needs to measure the “distance” between the physical and mechanical state of the surrounding rocks at the stable and the limit state. “Large distance” indicates that the surrounding rocks are more stable. According to the strength theory, the limit state of a point of surrounding rocks depends on its strength or deformation resistance, while the failure state indicates that the physical and mechanical state at that point exceeds the limit state. Therefore, the deterioration of the physical and mechanical properties of the surrounding rock can be used to bring it closer to the actual state of stress at that point. The quantitative parameters which reflect the deterioration can be used to measure the stability reserve of the tunnel surrounding rocks at that point. This method considering the deterioration of the physical and mechanical properties of surrounding rocks is called the strength-deformation parameter deterioration method.

3.1 Principle of strength-deformation parameter deterioration method

The stability reserve of a tunnel can be estimated via the strength-deformation parameter deterioration method, and simulating the deterioration of the physical and mechanical properties of surrounding rocks reach the limit state. The failure mechanism of the clay tunnel failure mechanism can be divided into tensile and shear failure. Tensile failure also can be regarded as a generalized shear failure. Therefore, at a point of surrounding rocks, the stress state can be determined by its shear stress, and strength parameters can characterize the shear strength. The strain state can be determined by the deformation of that point, and the strength parameters and deformation parameters can characterize the deformation resistance at that point. A function (Eq. 2) that takes the shear stress and strain state into account can represent the state of the point.

$F_S=f\left(\tau ,\epsilon \right)(2)$

Where $\tau$ represents the shear stress state at this point of surrounding rocks; $\epsilon$ represents the generalized strain state at this point of surrounding rocks.

If the shear stress state or strain state of any point in surrounding rocks reaches the ultimate stress state or ultimate strain state, the state function at that point will reach the limit state. This paper established a method taking the coupled deterioration of strength and deformation resistance into account. To distinguish from the previous method, which only considers the strength deterioration of surrounding rocks, this paper assumed the limit state for the state function, as shown below.

$F_{SL}=f\left({\sigma }_L,{\epsilon }_L\right)(3)$

The strength and deformation resistance deterioration process is described as a form of strength and deformation resistance reduction, such as the strength reduction method. Based on the above analysis and the core idea of the strength-deformation parameter deterioration method, the basic idea of this method was expressed as follows when exploring the stability of clay tunnels by changing the limit state of surrounding rocks at a certain point ($F_{SL}$) and bringing it to the actual state ($F_{S0}$).

$F_{S0}=\frac{F_{SL}}{D}(4)$

Where D is the deterioration coefficient, which can measure the quantitative parameter of the deterioration of physical and mechanical properties at a point in surrounding rocks, and the value is constantly greater than zero.

Then, combining Eqs. 2, 3, the strength-deformation parameter deterioration method was expressed as that,

$F_{S0}=\frac{F_{SL}}{D}=f\left(\frac{{\tau }_L}{D_s},\frac{{\epsilon }_L}{D_d}\right)(5)$

Where $F_{S0}$ denotes the actual state function at a certain point of the tunnel surrounding rocks, and, $D_s$, $D_d$ are the strength deterioration coefficient and the deformation resistance deterioration coefficient respectively, and their values are not less than zero.

The strength-deformation parameter deterioration method is applied by first reducing the shear strength and the deformation resistance simultaneously, stopping the iterative calculation once the tunnel is in the limit state. The shear strength corresponds to a strength deterioration coefficient and deformation resistance deterioration coefficient (which $D_s$ may be different from the value of $D_d$). The stability reserve factor of tunnel surrounding rocks can be defined as the ratio of the maximum shear strength and the maximum deformation resistance of the tunnel surrounding rocks to the actual shear stress or deformation by the external load, without taking into account the influence of water and dynamic factors.

$S_f=D=\frac{F_{SL}}{F_{S0}}(6)$

According to Eqs. 4, 5, the stability reserve factor of the tunnel surrounding rocks $S_f$ is equal to the deterioration coefficient D. When considering the non-linear characteristics of the overall physical and mechanical property deterioration, the values of the strength deterioration coefficient $D_s$ and the deformation resistance deterioration coefficient $D_d$ may be different. According to the definition of the limit state, the stability reserve factor at a point of the tunnel surrounding rocks could be obtained according to the minimum principle.

$S_f=\min \left(D_s,D_d\right)(7)$

The parameters affecting the shear strength of the clay are cohesion c and the internal friction angle φaccording to Coulomb’s law. The parameters of the deformation resistance of clay are as follows: the cohesion c and the internal friction angle φ, Young’s modulus E, and Poisson’s ratio ν. Eq 5 can be expressed as

$F_{S0}=\frac{F_{SL}}{D}=f\left[\frac{\left(c+\sigma \tan \phi \right)}{D_s},\frac{\epsilon \left(c,\phi ,E,\nu \right)}{D_d}\right](8)$

Eq 8 can be expressed as

$F_{S0}=f\left({\tau }_0,u_0\right)=\frac{f\left({\tau }_L,{\epsilon }_L\right)}{D}=f\left(\frac{c}{D_c},\frac{\phi }{D_{\phi }},\frac{E}{D_E},\frac{\nu }{D_{\nu }}\right)(9)$

$D_c$, $D_{\phi }$, $D_E$ and $D_{\nu }$ are the deterioration coefficients of cohesion, the internal friction angle, Young’s modulus, and Poisson’s ratio, respectively.

Then, according to Eqs. 6, 8, the stability reserve factor of surrounding rocks can be further calculated.

$S_f=\min \left(D_c,D_{\phi },D_E,D_{\nu }\right)(10)$

3.2 Calculation of the deterioration coefficients

Coulomb’s law can also be expressed by the shear strength of clay as

${\tau }_L=c_0+\sigma \tan {\phi }_0(11)$

The strength deterioration coefficient of clay can be obtained by referring to the principle of the strength reduction method. For example, $c_0$ and $\tan {\phi }_0$ are reduced by $D_s$, respectively.

$\tau =\frac{c_0}{D_s}+\sigma \frac{\tan {\phi }_0}{D_s}(12)$

Where $c_0$ and ${\phi }_0$ are the actual cohesion and the actual internal friction angle of surrounding rocks at this moment, respectively. Previous researchers (Duncan and Chang, 1970; Lade and Duncan, 1975) proposed to fit the triaxial stress-strain relationship of clay with a hyperbolic curve, in which Young’s modulus can be expressed as the tangential modulus. Then, Young’s modulus of the clay can be calculated by the following equation.

$E_i={\left(1-R_{f}s\right)}^2{E}_0(13)$

Where E₀ is the initial Young’s modulus of clay, $E_i$ is Young’s modulus (also tangential modulus) of the clay in the ith state via the parameter reduction; the deviatoric stress ratio of the clay is expressed as $s=\frac{\left({\sigma }_1-{\sigma }_3\right)}{{\left({\sigma }_1-{\sigma }_3\right)}_f}$; the clay failure ratio is expressed as $R_f=\frac{{\left({\sigma }_1-{\sigma }_3\right)}_f}{{\left({\sigma }_1-{\sigma }_3\right)}_{ult}}$. $\left({\sigma }_1-{\sigma }_3\right)$ is the deviatoric stress; ${\left({\sigma }_1-{\sigma }_3\right)}_f$ is the yield strength. ${\left({\sigma }_1-{\sigma }_3\right)}_{ult}$ refers to the ultimate value of deviatoric stress corresponding to the horizontal asymptote of the hyperbola, and can be determined by laboratory tests.

From Eq. 13, the deterioration coefficient of Young’s modulus can be calculated by the following equation.

$D_E=\frac{E_0}{E_i}=\frac{1}{{\left(1-R_{f}s\right)}^2}(14)$

According to Eq. 14, we will obtain the following expressions.

${\sigma }_1-{\sigma }_3=\left[1-{\left(D_E\right)}^{-0.5}\right]{\left({\sigma }_1-{\sigma }_3\right)}_{ult}(15)$

If let ${\left({\sigma }_1-{\sigma }_3\right)}_{ult}={\left({\sigma }_1-{\sigma }_3\right)}_f$

${\sigma }_1-{\sigma }_3=\left[1-{\left(D_E\right)}^{-0.5}\right]{\left({\sigma }_1-{\sigma }_3\right)}_f(16)$

According to the Mohr-Coulomb theory, the yield strength can be expressed as the following equation.

${\left({\sigma }_1-{\sigma }_3\right)}_f=\frac{2c\cos \phi +2{\sigma }_3\phi }{1-\sin \phi }(17)$

${\sigma }_1-{\sigma }_3=\left[1-{\left(D_E\right)}^{-0.5}\right]\left(\frac{2c\cos \phi +2{\sigma }_3\phi }{1-\sin \phi }\right)(18)$

Therefore, when c₀ and φ₀ are reduced by the strength deterioration coefficient D_s, the new cohesion and internal friction angle can be substituted into Eq. 18. It also indicates the effect of the deterioration coefficient of Young’s modulus $D_E$ on the stress state. It could also characterize the non-linear deterioration of the physical and mechanical properties of the clay tunnel surrounding rocks.

It was found that Poisson’s ratio change on stress, strain, and displacement could be far less than the impact of other parameters, so Poisson’s ratio deterioration was not considered here.

3.3 The physical meaning of the strength-deformation parameter deterioration method

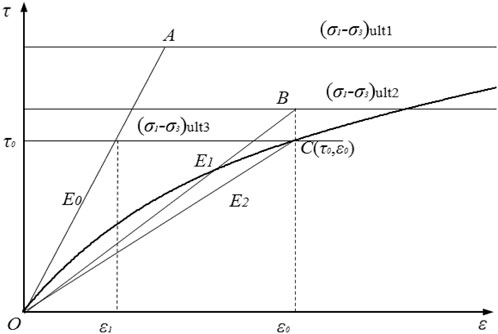
The specific physical meaning of the strength-deformation parameter deterioration method was given in Figure 1. The coordinate of a point on the constitutive curve is $\left({\tau }_0,{\epsilon }_0\right)$, which means the actual stress and strain state of surrounding rocks. The horizontal line in Figure 1 is the asymptote of the hyperbola, which is mainly controlled by c and φ, reflecting the strength of the clay, ${\left({\sigma }_1-{\sigma }_3\right)}_{ult}$; Reducing the value of cohesion c and internal friction angle φ, the horizontal asymptote keeps moving downward. However, this process is consistent with the strength reduction method. If only change the strength parameters of surrounding rocks are changed and the initial Young’s modulus E₀ is kept constant (the line OA as shown in Figure 1), the strength changes from ${\left({\sigma }_1-{\sigma }_3\right)}_{ult1}$ to ${\left({\sigma }_1-{\sigma }_3\right)}_{ult3}$ and close to the actual stress state ${\tau }_0$, the strain state at this time is not close to or consistent with the initial strain state. However, at the same time, Young’s modulus E₀ degrades to E₂ in the process of strength deterioration, as shown in line OC, then the stress state at the yield point at this moment is closer to the stress state and strain states are closer to the actual stability states $\left({\tau }_0,{\epsilon }_0\right)$.

FIGURE 1

FIGURE 1. Non-linear stress-strain relationship in hardening soil.

In summary, the actual state changes of surrounding rocks deterioration during tunnel excavation and the stability evaluation of clay tunnels with non-linear behavior can be better simulated by the strength-deformation parameter deterioration method (simultaneous reducing of the cohesive force c, the internal friction angle φ, and Young’s modulus E). Both the strength and deformation parameters can be reduced by the same scale factor when simulating the deterioration process of the physical and mechanical properties of surrounding rocks, and the different contributions of these parameters to the limit state can also be reflected. At the same time, when the strength and deformation resistance of surrounding rocks is weakened, the displacement of surrounding rocks at a point will increase, making the surrounding rocks more prone to instability. The cohesion, internal friction angle, Young’s modulus, Poisson’s ratio of the deterioration coefficients and the scale factor $\beta$ satisfy the following relationship equation.

$D_c=D_{\phi }=D_E=D_{\mu }=\beta (19)$

Generally, if the strength and deformation parameters are all known, the stress, strain, and displacement of a point of surrounding rocks can be calculated according to the relevant theory of geotechnics. The strength or deformation parameters are variables in these formulas and have different relationships with the dependent variables (stress, strain, displacement), which also reflects the different influences of these parameters. Therefore, in the numerical analysis of clay tunnels using the strength-deformation parameter deterioration method, the process of non-linear deterioration of the physical and mechanical properties of surrounding rocks can be better simulated, although the strength and deformation parameters are reduced by the same scale factor. If the clay’s physical-mechanical properties make surrounding rocks reach the limit state at a point during the process, the tunnel stability reserve factor is equal to the scale factor.

$S_f={\beta }_L(20)$

${\beta }_L$ refers to the scale factor corresponding to the limit state at a point of the surrounding rock.

To sum up, the key point of the strength-deformation parameter deterioration method (referred to as “the proposed method”) is that the strength and deformation parameters are continuously reduced with the scale factor until the limit state. The specific calculation step is shown in Figure 2.

FIGURE 2

FIGURE 2. Calculation step of strength-deformation parameter deterioration method.

3.4 Limit state conditions of tunnel numerical model

Many researchers have proposed a variety of limit state criteria for tunnel numerical model, among which the more widely used are 1) the connectivity of the plastic zone, 2) the abrupt and accelerated increase in strain or displacement at the feature points of surrounding rocks, and 3) the non-convergence of numerical calculation. This paper used a hyperbolic model to fit the stress-strain relationship of clay, there was no plastic strain and plastic zone. Then the above criterion 1) could not apply to this proposed method, but it could still be used for the strength reduction method.

The field monitoring data indicates that surrounding rocks may have great deformation before the abrupt stress, strain, or displacement change. Furthermore, adopting the hyperbolic principal model, which is closer to the actual mechanical behavior of the clay, also makes the numerical analysis of the tunnel deformation field closer to reality. Finally, the displacement (or strain) at a point of surrounding rocks is itself a comprehensive response to the physical and mechanical properties of surrounding rocks under the external load. Therefore, this paper adopted the allowable relative convergence value between two measurement points as a further criterion for identifying the tunnel stability state, which can be described as follows: when the displacement (or strain) changes abruptly and the calculation does not converge, if the relative convergence value between two feature points in surrounding rocks does not exceed the limit value, the tunnel surrounding rocks is identified to be in the limit state.

For a clay tunnel, if the defined state function is a one-point displacement function of the surrounding rock, then its limit state corresponds to the displacement limit state. Table 1 shows the allowable values of relative convergence ω of tunnels which can be calculated by linear interpolation of the tunnel burial depth. The allowable limit displacement $u_L$ at the feature point of the tunnel can be calculated using the following equation.

$u_L=\frac{\omega d}{2}(21)$

Where d is the diameter of the tunnel. The parameter depth is the burial depth of the tunnel in Table 1.

TABLE 1

TABLE 1. Allowable values of relative convergence around tunnels and caverns (from GB50086-2015 in China).

4 Limit equilibrium method for clay tunnel stability evaluation

4.1 The wedge-shaped failure mechanism of surrounding rocks

This paper derived the analytical formula of the stability reserve factor of the tunnel surrounding rocks via the limit equilibrium analysis theory and took the more ideal clay tunnel surrounding rocks loading mechanics model into account, analogous to the slope safety factor idea. The limit equilibrium method takes the failure mechanism of the wedge-shaped block as an example according to Terzaghi’s theoretical soil mechanics.

4.2 Mechanics of wedge-shaped collapsing block in clay surrounding rocks

It assumed that the collapsing block is wedge-shaped in the circular clay tunnel, and the stability reserve factor can be calculated by the limit equilibrium method. The mechanics of the wedge-shaped collapsing block (the block is rigid) is shown in Figure 3, and clay conforms to rigid plastic constitutive relation.

FIGURE 3

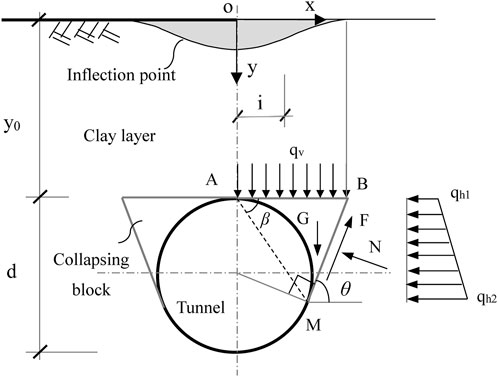
FIGURE 3. Two-dimensional mechanical model of the wedge-shaped collapsing block in a circular tunnel.

y₀ is the tunnel burial depth and d is the tunnel diameter. According to symmetry, the right-hand part ABM of the wedge-shaped collapsing block is chosen as the calculation object. The angles between the wedge failure lines BM and the horizontal plane are $\theta$, and point M is the intersection point between the failure surface and the tunnel boundary.

The stability reserve factor for the collapsing block can be defined as:

$S_f=\frac{P_R}{P_1}(22)$

$S_f$ is the stability reserve factor of the tunnel surrounding rocks; $P_R$ and $P_1$ are the anti-slip force, and the slip force, respectively.

4.3 Limit equilibrium analysis based on the mechanical model of wedge-shaped failure

The static equilibrium equation of the wedge can be listed according to Figure 3. The main loads in this model are as follows: G is the self-weight of the right-hand collapsing block ABM, $q_v$ is the vertical loosening pressure generated by the overlying soil and $P_v$ is the combined vertical pressure on the right-hand collapsing block ABM, $q_{h1}$ and ${q_h}_2$ are the upper and lower pressure of the horizontal pressure trapezoid acting on the collapsing block ABM, $P_h$ is the combined horizontal pressure force acting on the collapsing block ABM, T is the shear resistance acting on the collapsing block ABM, N is the normal force acting on the side BM.

$P_1=\left(G+P_v\right)\sin \theta +P_h\cos \theta (23)$

$P_R=F(24)$

$F=\left(c+q_h\tan \phi \right)L_{BM}(25)$

Where,

$N=\left(G+P_v\right)\cos \theta +P_h\sin \theta$

$G=\gamma ·S_{ABM},\theta =\frac{\pi }{4}+\frac{\phi }{2},q_h=\frac{1}{2}\left(q_{h1}+q_{h2}\right)$

Where $S_{ABM}$ is the area of the collapsing block ABM. $\gamma$, $c$ and $\varphi$ are the bulk unit weight, cohesion, and internal friction angle of the clay, respectively. According to the geometry relationship, the side length L_BM can be calculated via the equation as follows.

$\frac{L_{AB}}{\sin \theta }=\frac{L_{BM}}{\sin \beta }(26)$

Where $\alpha$ and $\beta$ are the angles between side AB and side BM and the horizontal line, respectively, and satisfy $\beta =\frac{\pi -\alpha }{2}$.

The formula for calculating the vertical soil stress acting on the collapsing block ABM is expressed as follows.

$q_v=\frac{L_{AB}\left(L_{AB}\gamma -c\right)}{2K_0\tan \phi }\left(1-e^{-2K_0\frac{y_0}{L_{AB}}\tan \phi }\right)(27)$

According to the Gaussian curve of ground settlement (the shadow area in Figure 3),

$L_{AB}=2.5i,i=k\left(y_0+d/2\right)$

Where $i$ is the horizontal distance from the inflection point of the ground settlement curve to the axis; $k$ is the scale constant, generally taken as $k=0.5$.

The combined vertical pressure can be calculated by the following equation for the collapsing block ABM.

$P_v=\frac{L_{AB}^2\left(L_{AB}\gamma -c\right)}{2K_0\tan \phi }\left(1-e^{-2K_0\frac{y_0}{L_{AB}}\tan \phi }\right)(28)$

Where $L_{AB}$ and $L_{BM}$ are the lengths of the sides AB and BM, respectively; $K_0$ is the lateral pressure coefficient.

The horizontal pressure acting on the sliding surface BM of the collapsing block ABM can be calculated according to the following equation.

$P_h=q_h{L}_{BM}\sin \theta =\left(\frac{1}{2}\gamma L_{BM}^2{\sin }^2\theta +{\sigma }_v{L}_{BM}\sin \theta \right)K_a(29)$

where the parameter $q_{h1}$ satisfies $q_{h1}=q_v{K}_a$, and the parameter $q_{h2}$ satisfies the relation of $q_{h2}=\left(q_v+\gamma L_{BM}\sin \theta \right)K_a$. Where $K_a$ is the active earth pressure coefficient, a dimensionless parameter.

$K_a={\tan }^2\left(\frac{\pi }{4}-\frac{\phi }{2}\right)(30)$

Finally, we can obtain the stability reserve factor for the clay tunnel surrounding rocks by substituting the anti-slip force and slip force on the sliding surface calculated from the wedge failure mechanics model into Eq. 22.

5 An example application of stability analysis of clay tunnels

5.1 Engineering overview and cross-sectional geometry of a clay tunnel

The Yinchuan-Xi’an high-speed railway tunnel was used as a study case in this paper. The tunnel mainly traverses across the loess plateau area, and most of the strata powder clay layer. The tunnel section at DK267+457.1 was selected for the study. The burial depth of the tunnel at this location is 170.5 m, the span D is about 12.75 m, and the height H is about 11.50 m. The radii of these arcs are R=10.50 m, R₁=8.78 m, R₂=7.10 m, and R₃=1.50 m, and the angle α is ${62.03}^{\circ }$. The location of the feature points of the tunnel and the simplified model was shown in Figure 4 (the feature points at the tunnel perimeter are located at the arch crown, left and right sidewalls, and arch bottom respectively). The above-mentioned feature points were arranged with displacement monitoring devices, which mainly monitor their vertical displacements and horizontal displacements.

FIGURE 4

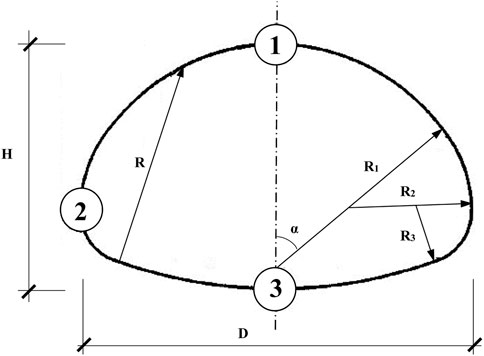
FIGURE 4. Schematic diagram of the shape, dimensions, and feature points of the clay tunnel cross-section.

To facilitate the validation of the proposed method, it was assumed that the stratum is a single isotropic and homogeneous clay layer, and the physical and mechanical parameters of the clay can be given in Table 2. It was also assumed that the constitutive model of the clay is hyperbolic and satisfies the Mohr-Coulomb yield criterion of non-associated flow. To apply the strength reduction method, it assumed the clay is an ideal elastic-plastic material, while all other conditions are consistent. The length of the left and right boundaries of the numerical model of the clay tunnel is more than 3 times the span from the center axis of the tunnel. The left and right boundaries are respectively constrained horizontally, the bottom boundary is fixed, and the upper boundary is free. This tunnel stability evaluation could be considered a plane strain problem.

TABLE 2

TABLE 2. Physical and mechanical parameters of clay.

5.2 Analysis of the results of different methods

A numerical model for tunnel stability evaluation was developed based on a tunnel section of the Yinchuan-Xi’an high-speed railway. Firstly, the strength reduction method and the proposed method were used to analyze the stability of the same tunnel finite element model; secondly, based on the geometry and material parameters of this tunnel, it was assumed that a wedge-shaped failure mechanism also occurs in this tunnel, so that the limit equilibrium analysis method could be used to calculate the tunnel stability reserve factor; finally, the results of the three stability analyses were compared.

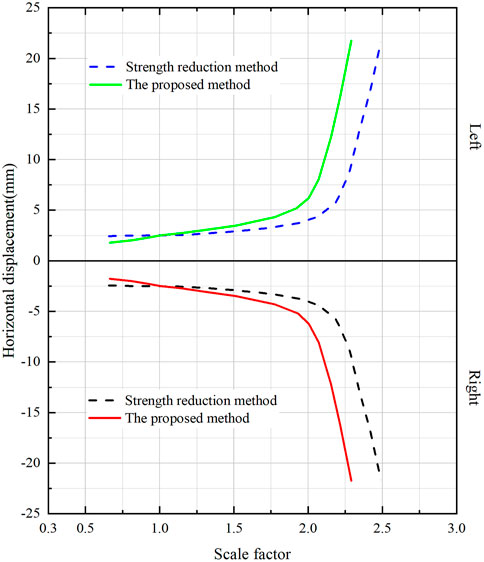
First of all, the key point of both the strength reduction method and the method is to simulate the deterioration of the physical and mechanical properties of surrounding rocks as realistically as possible, and the scale factor is a quantitative description of the deterioration mechanism of surrounding rocks so that the displacement of the feature point of surrounding rocks will change with the change of the scale factor. When the scale factor increases to a certain level, the actual rock condition is at the limit, and the scale factor can be regarded as the stability reserve factor of the tunnel, which is given by the abrupt change of the displacement-scale factor curve at the point of the scale factor (Figures 5–6). Although the scale factors of the intensity reduction method and the proposed method are close in the range of values, the results of these two methods are not only different in value but also the physical meaning. The proposed method not only simulates the deterioration process of the strength parameters but also couples the deterioration process of the deformation parameters of surrounding rocks, which is closer to reality. Moreover, the strength reduction method only considers strength deterioration in the analysis process, and can not represent the realistic representation of the actual change in the deformation field of surrounding rocks during the deterioration process for clay. The constitutive relationship is consistent with either the elastic or elastoplastic model.

FIGURE 5

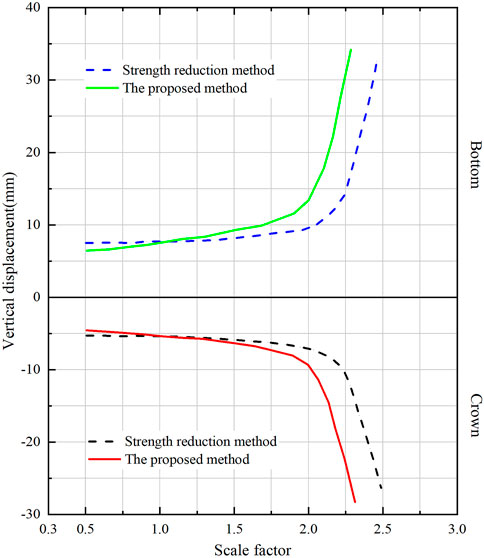
FIGURE 5. Scale factor versus vertical displacement of two feature points in the crown and bottom of the arc.

The three feature points of the tunnel correspond to three key locations, such as the arc crown, the sidewall, and the arc bottom. The displacements of each feature point are different, and the direction of displacement of the arc crown is vertical (settlement), the direction of displacements of two feature points in the left and right sidewall are horizontal, and these values are equal due to the symmetry. The direction of displacement of the arch bottom is vertical displacement (uplift). The displacement values of the feature points based on the strength reduction method are generally smaller than those based on this paper’s method when the scale factor is less than one. However, the relationship between the two magnitudes is reversed (Figures 5, 6; Table 3) when the scale factor is greater than one. Meanwhile, the allowable limit displacement of feature points (also as the recommended limit displacement) can be calculated by Eq. 30, according to the classification of surrounding rocks, the tunnel depth, tunnel diameter, and the allowable values of relative convergence specified in Table 4. The limit displacements of feature points (the displacement value corresponding to the abrupt curve change in Figures 5, 6 calculated by the proposed method are closer compared with the recommended limit displacement values. The actual deformation field in the tunnel stability evaluation will be predicted via the proposed method. It also reflects the variation of the displacement with the physical and mechanical properties of the clay with a small scale factor corresponding to the abrupt change in displacement. The analysis results indicate that the actual stability reserve of the tunnel is smaller than the evaluation results of the strength-deformation method (Table 5). This paper took the strength-deformation property deterioration of surrounding rocks into account to reflect the actual stress or deformation fields and achieve the goal of better evaluation of the tunnel stability reserve.

FIGURE 6

FIGURE 6. Scale factor versus horizontal displacement of two feature points in the sidewall.

TABLE 3

TABLE 3. Displacement of each feature point with different scale factors (Unit: mm).

TABLE 4

TABLE 4. Limit displacement at feature points in surrounding rocks obtained by different methods (Unit: mm)

TABLE 5

TABLE 5. Stability reserve factors of the tunnel calculated by different methods.

The stability reserve factor calculated by the limit equilibrium method based on the wedge-shaped collapsing block (θ=π/4+φ/2) is significantly larger than the other two results significantly. The limit equilibrium method can not reflect the actual state, because the tunnel cross section is circular instead of the one shown in Figure 4. More assumptions will be used in the calculation process of the limit equilibrium method. The tunnel stability reserve factors obtained from the displacement-scale factor curves of the different feature points are relatively close, despite the different types and directions of displacement at the different feature points. This analysis shows that the overall tunnel stability can also be reflected by the stability reserve factor of a single point, and this method is recommended in preference.

6 Conclusion

The method suggested in this paper provides a practical and efficient way to evaluate the stability reserve of clay tunnels. The following conclusions can be drawn based on theoretical analysis and example calculation results.

1) The stress and deformation fields in the surrounding rock will be redistributed by tunnel excavation. The state function F_S is defined with the stress state and strain state of a point as variables, which can comprehensively characterize the stability state of the point at this moment.

2) The formula for calculating the tunnel stability reserve factor S_f from the actual state F_S0 at a point of the surrounding rock and its limit state F_SL at a point of the surrounding rock is established with the definition of the state function. Then, taking the non-linear relationship between this limit state and the physical and mechanical properties of the surrounding rock into account, the non-linear deterioration of the physical and mechanical properties of the surrounding rock is simulated to calculate the tunnel stability reserve factor. The strength and deformation parameters that characterize the clay properties are discounted by a scaling factor until the limit state is close to or equal to the actual state.

3) An analytical formula for the calculation of the tunnel stability reserve factor by the limit equilibrium method is established based on the physical model of wedge-shaped failure of the surrounding rock.

4) The analysis results of a clay tunnel project example show that the non-linear deterioration process of physical and mechanical properties of the surrounding rock will be better predicted by the proposed method in this paper. Compared with the strength reduction and the limit equilibrium methods, could the proposed method in this paper have more reliable quantitative evaluation results of tunnel stability.

5) The analysis results in this paper could provide broader and more valuable references in the study of clay tunnel stability problems and also support the engineering practice. However, tunnel stability is also closely related to construction factors for the actual tunnel construction. Therefore, construction factors such as construction methods and support forms should be introduced into tunnel stability evaluation as variables as well and guided the construction of tunnel projects.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

JH was in charge of conceptualization, funding acquisition, writing of the original draft, and editing. XL was in charge of data resources and analysis. ZM was in charge of the development of the mathematical model of the research and overall supervision of the whole research investigation. GL was in charge of the numerical simulations. KD was in charge of the post-processing data.

Funding

This work was supported by the Science and technology innovation fund project of Hanjiang-to-Weihe river valley water diversion project construction Co. LTD. (Grant No. 2020302), Open Research Fund Program of State Key Laboratory of Eco-hydraulics in Northwest Arid Region (Grant No. 2018KFKT-16), Shaanxi Provincial Urban and Rural Construction Science and Technology Research and Development ProgramProject (2020-K41), National Natural Science Foundation of China (51806173).

Acknowledgments

The authors would like to thank Shaanxi Key Lab of Petroleum Accumulation Geology for providing high-performance computing devices.

Conflict of interest

XL was employed by PowerChina Northwest Engineering Corporation Limited: KD was employed by Hanjiang-to-Weihe River Valley Water Diversion Project Construction Co.LTD.

The authors declare that this study received funding from Hanjiang-to-Weihe river valley water diversion project construction Co. LTD. The funder had the following involvement in the study: the funder participated in the data processing.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Antão, A. N., Vicente da Silva, M., Monteiro, N., and Deusdado, N. (2021). Upper and lower bounds for three-dimensional undrained stability of shallow tunnels. Transp. Geotech. 27, 100491. doi:10.1016/j.trgeo.2020.100491

CrossRef Full Text | Google Scholar

Assadi, A., and Sloan, S. (1991b). “Stability of a shallow circular tunnel in cohesive-frictional soil,” in International Conference on Finite Element Methods.

Google Scholar

Assadi, A., and Sloan, S. (1991a). Undrained stability of shallow square tunnel. J. Geotechnical Eng. 117117 (8), 11528–21173. doi:10.1061/(asce)0733-9410(1991)117:8(1152)

CrossRef Full Text | Google Scholar

Broms, B. B., and Bennermark, H. J. (1967). Stability of clay at vertical opening. Soil Mech. Found. Div. J. 193 (1), 71–94. doi:10.1061/JSFEAQ.0000946

CrossRef Full Text | Google Scholar

Davis, E. H., Gunn, M. J., Mair, R. J., and Seneviratne, H. N. (1979). The stability of shallow tunnels and underground openings in cohesive material. Géotechnique 30, 397–416. doi:10.1680/geot.1980.30.4.397

CrossRef Full Text | Google Scholar

Duncan, J. M., and Chang, C. Y. (1970). Nonlinear analysis of stress and strain in soils. J. Soil Mech. Found. Div. ASCE 96 (5), 1629–1653. doi:10.1061/JSFEAQ.0001458

CrossRef Full Text | Google Scholar

Fan, W., Yu, M., Deng, L., Peng, X., and Chen, L. (2013). New strength formulae for rock surrounding a circular opening. Can. Geotechnical J. 50 (7), 735–743. doi:10.1139/cgj-2012-0001

CrossRef Full Text | Google Scholar

Fernández, F., Rojas, J. E. G., Vargas, E. A., Velloso, R. Q., and Dias, D. (2021). Three-dimensional face stability analysis of shallow tunnels using numerical limit analysis and material point method. Tunn. Undergr. Space Technol. 112, 103904. doi:10.1016/j.tust.2021.103904

CrossRef Full Text | Google Scholar

Fraldi, M., and Guarracino, F. (2010). Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections. Int. J. Solids Struct. 47 (2), 216–223. doi:10.1016/j.ijsolstr.2009.09.028

CrossRef Full Text | Google Scholar

Fraldi, M., and Guarracino, F. (2009). Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. 46 (4), 665–673. doi:10.1016/j.ijrmms.2008.09.014

CrossRef Full Text | Google Scholar

Franza, A., Marshall, A. M., and Zhou, B. (2019). Greenfield tunnelling in sands: The effects of soil density and relative depth. Géotechnique 69 (4), 297–307. doi:10.1680/jgeot.17.P.091

CrossRef Full Text | Google Scholar

Han, K., Wang, L., Su, D., Hong, C., Chen, X., and Lin, X. (2021). An analytical model for face stability of tunnels traversing the fault fracture zone with high hydraulic pressure. Comput. Geotechnics 140, 104467. doi:10.1016/j.compgeo.2021.104467

CrossRef Full Text | Google Scholar

Hao, X., Yuan, L., Sun, Z., Zhao, Y., Ren, B., Zhao, D., et al. (2022). An integrated study of physical and numerical modelling on the stability of underground tunnel influenced by unloading rate. Tunn. Undergr. Space Technol. 129, 104602. doi:10.1016/j.tust.2022.104602

CrossRef Full Text | Google Scholar

Huang, M., Wang, H., Yu, J., and Tang, Z. (2019). Undrained stability analysis of a plane strain circular tunnel using streamline velocity fields. Int. J. Geomechanics 19 (5), 06019006. doi:10.1061/(ASCE)GM.1943-5622.0001395

CrossRef Full Text | Google Scholar

Kumar, J., and Jain, H. (2021). Elasto-plastic ground settlement response and stability of single and twin circular unsupported and supported tunnels. Transp. Geotech. 30, 100620. doi:10.1016/j.trgeo.2021.100620

CrossRef Full Text | Google Scholar

Lade, P. V., and Duncan, J. M. (1975). Elasto-plastic stress-strain theory for cohesionless soil with curved yield surfaces. J. Geotechnical Eng. Div. 101 (10), 1019–1035. doi:10.1016/0020-7683(77)90073-7

CrossRef Full Text | Google Scholar

Leca, E., and Dormieux, L. (1991). Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Géotechnique 40 (4), 581–606. doi:10.1680/geot.1990.40.4.581

CrossRef Full Text | Google Scholar

Lee, C. J., Wu, B. R., Chen, H. T., and Chiang, K. H. (2006). Tunnel stability and arching effects during tunneling in soft clayey soil. Tunn. Undergr. Space Technol. 21 (2), 119–132. doi:10.1016/j.tust.2005.06.003

CrossRef Full Text | Google Scholar

Lee, I. M., and Park, J. K. (2000). Stability analysis of tunnel keyblock: A case study. Tunn. Undergr. Space Technol. 15 (4), 453–462. doi:10.1016/S0886-7798(01)00014-1

CrossRef Full Text | Google Scholar

Li, L. P., Shang, C. S., Chu, K. W., Zhou, Z. Q., Song, S. G., Liu, Z. H., et al. (2021). Large-scale geo-mechanical model tests for stability assessment of super-large cross-section tunnel. Tunn. Undergr. Space Technol. 109, 103756. doi:10.1016/j.tust.2020.103756

CrossRef Full Text | Google Scholar

Li, T. Z., Gong, W. P., and Tang, H. M. (2021). Three-dimensional stochastic geological modeling for probabilistic stability analysis of a circular tunnel face. Tunn. Undergr. Space Technol. 118, 104190. doi:10.1016/j.tust.2021.104190

CrossRef Full Text | Google Scholar

Li, Z., Lai, J., Ren, Z., Shi, Y., and Kong, X. (2023). Failure mechanical behaviors and prevention methods of shaft lining in China. Eng. Fail. Anal. 143, 106904. doi:10.1016/j.engfailanal.2022.106904

CrossRef Full Text | Google Scholar

Liu, N. F., Li, N., Li, G. F., Song, Z. P., and Wang, S. J. (2022a). Method for evaluating the equivalent thermal conductivity of a freezing rock mass containing systematic fractures. Rock Mech. Rock Eng. 55 (12), 7333–7355. doi:10.1007/s00603-022-03038-9

CrossRef Full Text | Google Scholar

Liu, N. F., Li, N., Wang, S. J., Li, G. F., and Song, Z. P. (2022b). A fully coupled thermo-hydro-mechanical model for fractured rock masses in cold regions. Cold Regions Sci. Technol. 205, 103707. doi:10.1016/j.coldregions.2022.103707

CrossRef Full Text | Google Scholar

Liu, N. F., Li, N., Xu, C. B., Li, G. F., Song, Z. P., and Yang, M. (2020). Mechanism of secondary lining cracking and its simulation for the dugongling tunnel. Rock Mech. Rock Eng. 53 (9), 4539–4558. doi:10.1007/s00603-020-02183-3

CrossRef Full Text | Google Scholar

Lu, H., Gutierrez, M., and Kim, E. (2022). Empirical approach for reliability evaluation of tunnel excavation stability using the Q rock mass classification system. Undergr. Space 7 (5), 862–881. doi:10.1016/j.undsp.2022.01.001

CrossRef Full Text | Google Scholar

Lyamin, A. V., Jack, D. L., and Sloan, S. W. (2001). “Collapse analysis of square tunnels in cohesive–frictional soils,” in Computational mechanics–new Frontiers for the new millennium. Editors S. Valliappan, and N. Khalili (Elsevier), 405–414. doi:10.1016/B978-0-08-043981-5.50063-8

CrossRef Full Text | Google Scholar

Mair, R. J. (1979). Centrifuge modelling of tunnel construction in soft clay. Phd Thesis. Cambridge University.

Google Scholar

Mair, R. J., Taylor, R. N., and Bracegirdle, A. (1993). Subsurface settlement profiles above tunnels in clays. Géotechnique 43 (2), 315–320. doi:10.1680/geot.1993.43.2.315

CrossRef Full Text | Google Scholar

Man, J., Zhou, M., Zhang, D., Huang, H., and Chen, J. (2022). Face stability analysis of circular tunnels in layered rock masses using the upper bound theorem. J. Rock Mech. Geotechnical Eng. 14, 1836–1848. doi:10.1016/j.jrmge.2021.12.023

CrossRef Full Text | Google Scholar

Marshall, A. M., Farrell, R., Klar, A., and Mair, R. (2012). Tunnels in sands: The effect of size, depth and volume loss on greenfield displacements. Géotechnique 62 (5), 385–399. doi:10.1680/geot.10.P.047

CrossRef Full Text | Google Scholar

Nguyen, H. C., and Nguyen-Son, L. (2022). A stable CS-FEM for the static and seismic stability of a single square tunnel in the soil where the shear strength increases linearly with depth. J. Rock Mech. Geotechnical Eng. 14 (4), 1253–1265. doi:10.1016/j.jrmge.2022.01.006

CrossRef Full Text | Google Scholar

Osman, A. S., Mair, R. J., and Bolton, M. D. (2006). On the kinematics of 2D tunnel collapse in undrained clay. Géotechnique 56 (9), 585–595. doi:10.1680/geot.2006.56.9.585

CrossRef Full Text | Google Scholar

Pandit, B., and Sivakumar, B. G. (2021). Probabilistic stability assessment of tunnel-support system considering spatial variability in weak rock mass. Comput. Geotechnics 137, 104242. doi:10.1016/j.compgeo.2021.104242

CrossRef Full Text | Google Scholar

Pelech, T., Barnett, N., Dello-Iacovo, M., Oh, J., and Saydam, S. (2022). Analysis of the stability of micro-tunnels in lunar regolith with the Discrete Element Method. Acta Astronaut. 196, 1–12. doi:10.1016/j.actaastro.2022.03.037

CrossRef Full Text | Google Scholar

Qin, Y., Lai, J., Gao, G., Yang, T., Zan, W., Feng, Z., et al. (2022). Failure analysis and countermeasures of a tunnel constructed in loose granular stratum by shallow tunnelling method. Eng. Fail. Anal. 141, 106667. doi:10.1016/j.engfailanal.2022.106667

CrossRef Full Text | Google Scholar

Qin, Y. W., Chen, Y. H., Lai, J. X., Qiu, J. L., Yang, T., and Liu, T. (2023a). Loess landslide-tunnel system: A systematic review of its failure characteristics, interaction mechanism and countermeasures. Engineering Geology. inpress.

Google Scholar

Qin, Y. W., Lai, J. X., Cao, X. Y., Zan, W. B., and Feng, Z. H. (2023b). Experimental study on the collapse evolution law of unlined tunnel in boulder-cobble mixed formation. Tunnelling and Underground Space Technology. inpress.

Google Scholar

Qin, Y. W., Lai, J. X., Li, C., Fan, F. F., and Liu, T. (2023c). Negative pressure testing standard for welded scar tightness of waterproofing sheet for tunnels: Experimental and Numerical Investigation. Tunnelling and Underground Space Technology. inpress.

Google Scholar

Rojat, F., Labiouse, V., and Mestat, P. (2015). Improved analytical solutions for the response of underground excavations in rock masses satisfying the generalized Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. 79, 193–204. doi:10.1016/j.ijrmms.2015.08.002

CrossRef Full Text | Google Scholar

Rowe, R. K., and Kack, G. J. (1983). A theoretical examination of the settlements induced by tunnelling: Four case histories. Can. Geotechnical J. 20 (2), 299–314. doi:10.1139/t83-033

CrossRef Full Text | Google Scholar

Shiau, J., and Al-Asadi, F. (2020). Determination of critical tunnel heading pressures using stability factors. Comput. Geotechnics 119, 103345. doi:10.1016/j.compgeo.2019.103345

CrossRef Full Text | Google Scholar

Sloan, S., and Assadi, A. (1991). Undrained stability of a square tunnel in a soil whose strength increases linearly with depth. Comput. Geotechnics 12 (4), 321–346. doi:10.1016/0266-352X(91)90028-E

CrossRef Full Text | Google Scholar

Son, M., and Cording, E. J. (2008). Numerical model tests of building response to excavation-induced ground movements. Can. Geotechnical J. 45 (11), 1611–1621. doi:10.1139/t08-074

CrossRef Full Text | Google Scholar

Song, G., and Marshall, A. M. (2020). Centrifuge modelling of tunnelling induced ground displacements: Pressure and displacement control tunnels. Tunn. Undergr. Space Technol. 103, 103461. doi:10.1016/j.tust.2020.103461

CrossRef Full Text | Google Scholar

Song, J., Lee, C., and Seto, M. (2001). Stability analysis of rock blocks around a tunnel using a statistical joint modeling technique. Tunn. Undergr. Space Technol. 16 (4), 341–351. doi:10.1016/S0886-7798(01)00063-3

CrossRef Full Text | Google Scholar

Sukkarak, R., Jongpradist, P., and Pramthawee, P. (2019). A modified valley shape factor for the estimation of rockfill dam settlement. Comput. Geotechnics 108, 244–256. doi:10.1016/j.compgeo.2019.01.001

CrossRef Full Text | Google Scholar

Sun, M., Liang, H., Zhu, Y., Gao, X., Liu, H., and Zhu, Z. (2022). Deformation and failure mode analysis of the tunnel structure based on the tunnel-related landslides cases. Front. Earth Sci. 10. doi:10.3389/feart.2022.906884

CrossRef Full Text | Google Scholar

Tan, X., Chen, W., Wang, L., Tan, X., and Yang, J. (2020). Integrated approach for structural stability evaluation using real-time monitoring and statistical analysis: Underwater shield tunnel case study. J. Perform. Constr. Facil. 34 (2), 04019118. doi:10.1061/(ASCE)CF.1943-5509.0001391

CrossRef Full Text | Google Scholar

Tyagi, A., Liu, Y., Pan, Y.-T., and Lee, F.-H. (2020). Equivalent strength for tunnels in cement-admixed soil columns with spatial variability and positioning error. J. geotechnical geoenvironmental Eng. 146 (10), 04020101. doi:10.1061/(ASCE)GT.1943-5606.0002351

CrossRef Full Text | Google Scholar

Wang, W. L., Wang, T. T., Su, J. J., Lin, C. H., Seng, C. R., and Huang, T. H. (2001). Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 16 (3), 133–150. doi:10.1016/S0886-7798(01)00047-5

CrossRef Full Text | Google Scholar

Wilson, D. W., Abbo, A. J., Sloan, S. W., and Lyamin, A. V. (2011). Undrained stability of a circular tunnel where the shear strength increases linearly with depth. Can. Geotechnical J. 48 (9), 1328–1342. doi:10.1139/t11-041

CrossRef Full Text | Google Scholar

Xue, Y., Liu, J., Ranjith, P. G., Gao, F., Xie, H., and Wang, J. (2022). Changes in microstructure and mechanical properties of low-permeability coal induced by pulsating nitrogen fatigue fracturing tests. Rock Mech. Rock Eng. 55, 7469–7488. doi:10.1007/s00603-022-03031-2

CrossRef Full Text | Google Scholar

Xue, Y., Ranjith, P. G., Chen, Y., Cai, C., Gao, F., and Liu, X. (2023). Nonlinear mechanical characteristics and damage constitutive model of coal under CO2 adsorption during geological sequestration. Fuel 331, 125690. doi:10.1016/j.fuel.2022.125690

CrossRef Full Text | Google Scholar

Yang, F., and Yang, J. S. (2009). “Rigid blocks failure mechanism for stability of shallow tunnel using upper bound solution,” in Recent advancement in soil behavior, in situ test methods, pile foundations, and tunneling, 249–255. doi:10.1061/41044(351)39

CrossRef Full Text | Google Scholar

Yang, X. L., and Huang, F. (2011). Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 26 (6), 686–691. doi:10.1016/j.tust.2011.05.008

CrossRef Full Text | Google Scholar

Yang, X. L., and Huang, F. (2013). Three-dimensional failure mechanism of a rectangular cavity in a Hoek–Brown rock medium. Int. J. Rock Mech. Min. Sci. 61, 189–195. doi:10.1016/j.ijrmms.2013.02.014

CrossRef Full Text | Google Scholar

Yertutanol, K., Akgün, H., and Sopacı, E. (2020). Displacement monitoring, displacement verification and stability assessment of the critical sections of the Konak tunnel, İzmir, TTurkey Tunn. Undergr. Space Technol. 101, 103357. doi:10.1016/j.tust.2020.103357

CrossRef Full Text | Google Scholar

Zhang, X., Wang, M., Wang, Z., Li, J., Zhao, S., Tong, J., et al. (2020). Stability analysis model for a tunnel face reinforced with bolts and an umbrella arch in cohesive-frictional soils. Comput. Geotechnics 124, 103635. doi:10.1016/j.compgeo.2020.103635

CrossRef Full Text | Google Scholar

Zhang, Y., Fan, S., Yang, D., and Zhou, F. (2022a). Investigation about variation law of frost heave force of seasonal cold region tunnels: A case study. Front. Earth Sci. 9, 806843. doi:10.3389/feart.2021.806843

CrossRef Full Text | Google Scholar

Zhang, Y., Song, Z., and Weng, X. (2022b). A constitutive model for loess considering the characteristics of structurality and anisotropy. Soil Mech. Found. Eng. 59 (1), 32–43. doi:10.1007/s11204-022-09781-z

CrossRef Full Text | Google Scholar

Zhang, Z., Zhao, C., Peng, L., Zhang, X., and Lei, M. (2022). Research on the stability of shallow-buried large cross-section tunnel by construction method conversion. Front. Earth Sci. 10. doi:10.3389/feart.2022.831169

CrossRef Full Text | Google Scholar

Zhuo, H., Xie, D., Sun, J., and Shi, X. (2022). Mining hazards to the safety of segment lining for tunnel boring machine inclined tunnels. Front. Earth Sci. 9. doi:10.3389/feart.2021.814672

CrossRef Full Text | Google Scholar