Effect of pre-confining pressure on unloading-induced coalburst: Insights from distinct element modelling

Coalburst is a violent dynamic failure of coal during underground mining. It is of significance to study failure pattern as well as energy evolution and transition during coalbursts and how they are influenced by pre-confinement. This paper presents unloading-induced coalburst simulations using the distinct element method via a combined static–dynamic loading–unloading strategy. The numerical model is calibrated and validated by comparison with the failure process observed in laboratory tests. The influence of pre-confining pressure on unloading-induced coalburst was numerically investigated from the perspective of crack propagation, fracturing process, failure pattern, and energy evolution. In addition, failure mechanism and energy conversion during coalbursts under different pre-confining pressures are discussed. The results show that the stress change caused by sudden unloading of the pre-confining results in the initiation and development of cracks. Crack density and crack propagation velocity increase with increasing pre-confining pressure. As the pre-confining pressure increases, the coalburst becomes more intense and takes less time to be completed, and the main failure pattern in coalburst transforms from a tensile type to a shear type. In addition, the conversion ratio of kinetic energy and frictional energy during coalbursts increase non-linearly with increasing pre-confining pressure.

1 Introduction

Coalburst is a dynamic failure phenomenon, characterized by an instantaneous release of a large amount of energy and ejection of coal pieces (Dou and He, 2001; Jiang et al., 2017; Zhang et al., 2017). According to its occurrence mechanism, coal burst can be classified into unloading-induced and remote mining induced seismicity triggered (Vardar et al., 2018; Mottahedi and Ataei, 2019). Unloading-induced coalbursts, which frequently occur in high stressed mining areas without remote seismic events during roadway development, also cause many casualties and severe damages (Dou and He, 2001). It is important to investigate failure mechanism as well as evolution and transition of energy during unloading-induced coalbursts.

Dynamic cracking behaviour is quite different from those under static loading conditions (Bažant et al., 1993; Zhao et al., 1999; Li et al., 2004; Zhang et al., 2021). To reproduce rock or coal bursts in the laboratory, He et al. (2010) developed a true triaxial test machine with the capacity to rapidly unload stress at one loading face and to observe the rock burst process of limestone in the laboratory. He studied the crack fractal dimensions during rockbursts using this testing device, and results showed that the values of fractal dimension become larger after dynamic failure (He et al., 2014). Su et al. (2017) investigated the evolution of acoustic emissions (AE) using a rockburst testing machine and found that the main frequency of the AE decreased before rockburst. However, it is difficult to conduct coalburst tests using true triaxial unloading test machines. The Split Hopkinson Pressure Bar (SHPB) system was employed to study the dynamic response of coal samples, including dynamic mechanical characteristics (Kong et al., 2020; Li et al., 2022), crack propagation (Hao et al., 2020; Ju et al., 2020; Li et al., 2021), as well as the influence of bedding structure (Zhao et al., 2014; Ai et al., 2020). The above results have enriched our understanding of rock or coal bursts. However, the knowledge of the cracking mechanisms of dynamic failures at the micro-scale still needs to be further studied.

Numerical simulation can provide insights into the complicated process of rock and coal failures at the micro-scale. In past decades, many numerical methods have been applied to study crack development, including the finite element method (FEM) (Zubelewicz and Mroz, 1983; Wang and Park, 2001; Manouchehrian and Cai, 2016; Hauquin et al., 2018), discontinuous deformation analysis (DDA) method (He et al., 2016; Hatzor et al., 2017; Chen et al., 2018), and the distinct element method (DEM) (Cundall and Strack, 1979; Potyondy and Cundall, 2004; Hu et al., 2020). In particular, the DEM has become a promising method for investigating the dynamic fracturing process of rocks (Zhang and Wong, 2018). Hu et al. (2018) applied a 3D bonded block DEM model to simulate dynamic disturbance triggered rockbursts and investigated the crack evolution during rockbursts. Compared to 3D DEM simulations, 2D DEM simulations have great advantages in computational efficiency. Unstable shear and compressive failure of rock related to rockbursts were reproduced by using the 2D DEM model based on the universal Distinct Element Code (UDEC) (Gu and Ozbay, 2015). He et al. (2018) performed abruptly unloading induced strainburst simulations through the Particle Flow Code (PFC), and found that the system stiffness has a significant effect on dynamic failure. Duan et al. (2019) employed a 2D DEM model to simulate unloading-induced strainbursts, and showed that a sudden reduction in confining pressure caused non-uniform deformation in the sample. A UDEC-Trigon numerical model was employed to capture unloading-induced strainbursts including analysis of crack patterns (Gao et al., 2019a). The development of rock dynamic failure is related to the release and transition of elastic energy (Cook, 1965; Tarasov and Stacey, 2017; Gao and Yang, 2021). Therefore, particular attention should also be paid to study the energy release and transition during coalbursts.

In this study, we focus on analysis of unloading-induced coalbursts. 2D DEM simulations of unloading-induced coalbursts under different pre-confining pressures are performed. This paper is organized as follows. First, modelling method and procedure are introduced. Then, model calibration and validation are documented by comparison with typical experimental results. Subsequently, micro-cracking mechanisms and energy evolution during unloading-induced coalbursts are investigated considering different aspects, including crack propagation, failure mode and energy evolution. Finally, the influence of the pre-confining pressure on failure mechanism and energy conversion during coalbursts is discussed.

2 Model description and calibration

2.1 Modelling method

UDEC, a 2D numerical program based on the DEM, has been widely applied to investigate rock mechanical and mining engineering problems (e.g. Kazerani et al., 2011; Huang et al., 2019; Cao et al., 2020). The UDEC-Trigon model proposed by Gao and Stead (2014) has an excellent ability to capture the brittle cracking of hard rock, and has also been applied to study rockbursts or coalbursts (Gao et al., 2019a; b; Gao and Yang, 2021). Thus, for this study, a UDEC-Trigon model and a static–dynamic coupled loading strategy are adopted to simulate unloading-induced coalbursts.

2.1.1 Failure criterion

In the UDEC-Trigon method, a coal sample is composed of many blocks of different size and contacts between blocks. Each block is deformable based on a finite-difference mesh. There are two possible failure patterns of a contact: shear cracking along the shear direction and tensile cracking along the normal direction (ICG, 2014). Failures of contacts are controlled by the stresses acting at the contacts and the Coulomb friction law with tension cut-off.

2.1.2 Calculation of energy components

Energy analysis is an important aspect in studying dynamic failure. The UDEC-internal program language FISH was used to acquire the distribution of the three energy types: elastic energy, kinetic energy and frictional energy. The formulas (ICG, 2014) are shown below.

The total elastic energy stored in the coal sample $W_C$ is calculated as:

$W_C=\sum E_b(1)$

where $\sum E_b$ is the total amount of elastic energy stored in all of the individual blocks in the numerical coal sample. The elastic energy of a block $E_b$ is calculated as:

$E_b=\sum E_z(2)$

where $\sum E_z$ is the sum of elastic energy stored in all individual zones in a block. For a given zone, the elastic energy $E_z$ is determined by:

$E_z=\frac{A}{2E}\left[{\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2-2\upsilon \left({\sigma }_1{\sigma }_2+{\sigma }_1{\sigma }_3+{\sigma }_2{\sigma }_3\right)\right](3)$

where $E$ is Young’s modulus. $\upsilon$ is Poisson’s ratio. $A$ is the area of the zone and ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ are the three principal stresses.

The total amount of kinetic energy $W_K$ is calculated as:

$W_K=\sum E_{gk}(4)$

where $\sum E_{gk}$ is the total amount of the kinetic energy of all individual gridpoints in the numerical coal sample at a given timestep. For a given gridpoint g, the kinetic energy can be calculated as:

$E_{gk}=\frac{1}{2}{m}_g{u}_x^2+\frac{1}{2}{m}_g{u}_y^2(5)$

where $m_g$ is the mass of the gridpoint and $u_x$ and $u_y$ are the corresponding velocities in the $x$- and $y$-direction at a given timestep, respectively.

The total frictional energy $W_F$ of the coal sample is calculated as:

$W_F=\sum E_{cf}(6)$

where $\sum E_{cf}$ is the sum of frictional energy of all contacts in the numerical coal sample at a given timestep. For a given contact, the frictional energy $E_{cf}$ at that timestep is calculated as:

$E_{cf}=\frac{1}{2}\left(f_s+f_s^{\prime }\right)△u_s(7)$

where $△u_s$ is the increment in the shear displacement of the contact and $f_s$ and $f_s^{\prime }$ are the current and previous shear forces (considering the current time step) at the contact, respectively.

2.2 Model configuration and modelling procedure

The numerical model considers a rectangular sample with width of 50 mm and height of 100 mm, as shown in the Figure 1. The triangular blocks have an average edge length of 2 mm. This meshing is sufficiently fine to study both the static and dynamic cracking behaviour of rocks at that scale (Gao and Stead, 2014; Gao and Yang, 2021). The block size in the model varies in a range considering the heterogeneity of the coal. However, the non-uniformity coefficients of block size are identical in all models. Several monitoring points are placed at the bottom plate and the coal sample to monitor stresses and velocities, respectively.

FIGURE 1

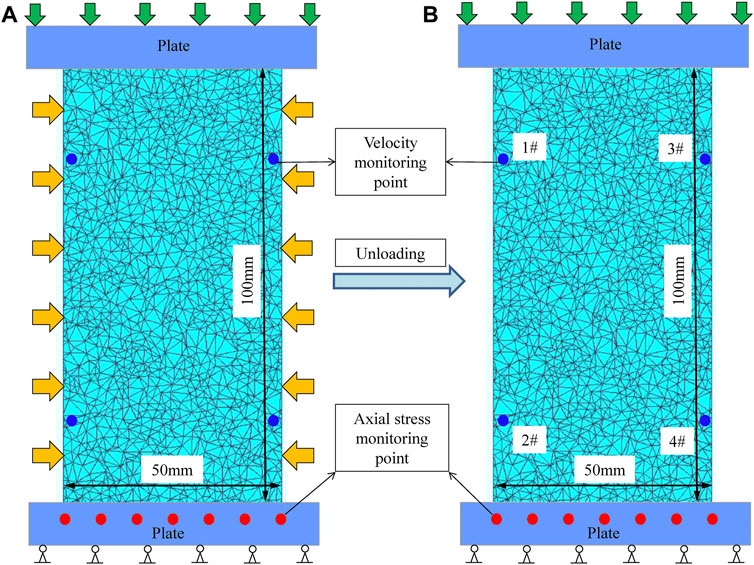
FIGURE 1. UDEC-Trigon model of coal sample incl. Location of monitoring points: (A) before unloading, (B) after unloading.

The modelling procedure comprises four steps. First, top and bottom plate are fixed. After that, pre-confining pressure is applied on the two lateral sides, as shown in Figure 1A. Then, the coal samples are loaded to the peak strength under the corresponding confining pressure. The loading velocity of the top plate is set to .01 m/s, while the bottom plate is fixed. The time step of a cycle is 10–8 s in the static mode. Therefore, a loading velocity of .01 m/s implies that the model uses 10,000,000 calculation steps for 1 mm of plate movement, which is sufficient for static analysis (Gao and Yang, 2021). Finally, the dynamic calculation mode is activated. Top and bottom boundaries of the model obtain absorbing boundary conditions, and the two lateral sides of the model obtain reflecting boundary conditions. The confining pressures are unloaded abruptly (see Figure 1B). The bottom plate remains fixed. Meanwhile, the dynamic mode is adopted. Rayleigh damping of .5% is used in the dynamic analyses, similar to the method adopted by Gao et al. (2019a) and Zhu et al. (2020).

The axial stress is the average stress of all monitoring points inside the loading plate in vertical direction. Mechanical parameters of the coal are calibrated by conducting a series of numerical uniaxial compression (UCS) and Brazilian tension (BT) tests, as seen in Figure 2. This calibration method has been demonstrated to be effective for UDEC-Trigon modelling (Gao and Yang, 2021). The calibrated mechanical parameters adopted in the Trigon model are listed in Table 1. The maximum deviation between target values and numerical simulation results do not exceed 3%, which is acceptable.

FIGURE 2

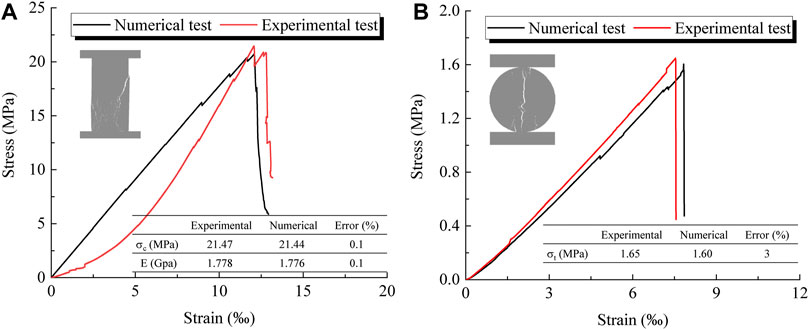
FIGURE 2. Calibration of mechanical parameters in the UDEC-Trigon model: (A) uniaxial compression tests, (B) Brazilian tension tests.

TABLE 1

TABLE 1. Mechanical parameters for UDEC-Trigon numerical model.

2.3 Model validation

2.3.1 Stress–strain behaviour

Figure 3 displays the stress–strain curves of the numerical coal samples during static loading. The pre-confining pressures are instantly unloaded after loading to the peak strength. All the other model parameters are identical except for the pre-confining pressure. It can be seen that the starting points of the stress–strain curves are different, which is caused by the loading sequence of the simulation. First, before the confining pressures are applied, upper and lower plates are in contact with the coal sample, the force at the contact surface is 0 MPa, and then a pre-determined pre-confining pressure is applied to the sample. At this time, upper and lower pressure plates are fixed. Under the influence of Poisson’s ratio, compression occurs along the vertical direction when the coal sample is compressed in the lateral direction. Therefore, vertical stresses with different magnitude appear after different pre-confining pressures are applied. When pre-confining pressures of .1 MPa, 1.0 MPa, 2.5 MPa, and 5.0 MPa are applied, the peak strength of the coal samples are 20.7 MPa, 24.1 MPa, 31.0 MPa, and 39.5 MPa, respectively, indicating that the pre-confining pressure significantly influences the peak strength. It is widely recognized that peak strength increases with confining pressure (Haimson and Chang, 2000; Liu et al., 2004; Hokka et al., 2016; Yao et al., 2016). Since the pre-confining pressure is immediately unloaded and the calculation mode becomes dynamic, the coal sample does not change from brittle to ductile.

FIGURE 3

FIGURE 3. Stress-strain curves of numerical samples under different pre-confining pressures.

2.3.2 Coalburst process

The failure characteristics observed in the simulations are compared with dynamic failure modes of coal samples as observed in experiments (Figure 4). First, after the sudden unloading of pre-confining pressure, the trigger of coalburst is marked by the ejection of localized coal fragments close to the unloading surface. Then, the area of the coal block ejection area continues to expand, and completely penetrating cracks form inside the sample with increasing tangential stress. As a result, coal plates are thrown out. Finally, coal fragments and plates are ejected in large quantities with maximum ejection velocity exceeding 10 m/s. In addition, some coalburst pits are formed on the surface of the coal sample when these ejected blocks are removed. These results show that the method adopted in this study can reproduce the unloading-induced coalbursts properly.

FIGURE 4

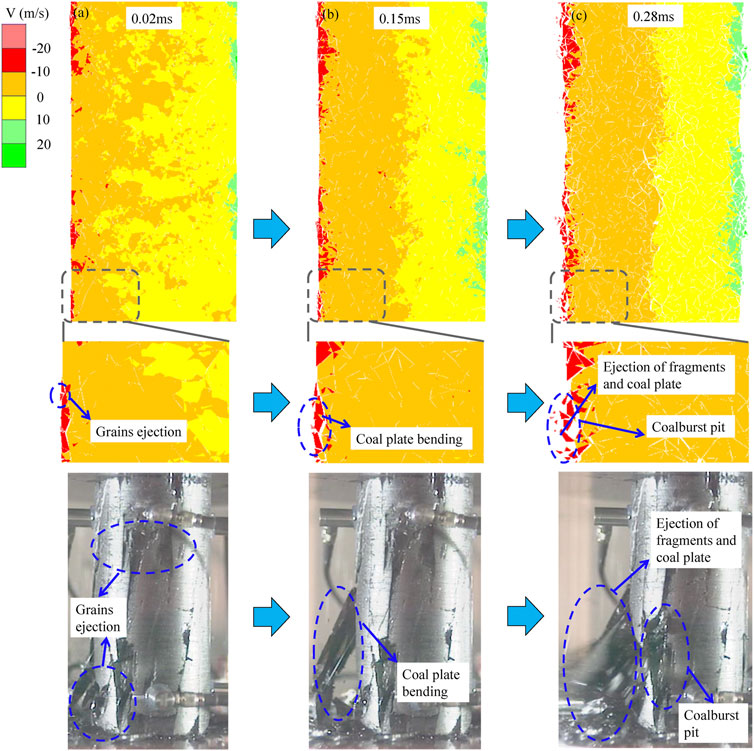
FIGURE 4. Coalburst process: numerical and experimental results: (A) grain ejection in local zones; (B) coal plate bending; (C) coal fragmentation, plate ejection and V-shaped coalburst pit formation.

3 Numerical results and analysis

3.1 Fracturing process of coalbursts

Figure 5 shows the crack development process and the eventual velocity cloud during coalburst induced by unloading of different pre-confining pressures. The blue and red lines represent tensile and shear cracks, respectively. Tensile failure is dominant in the area close to the unloading face, while most shear cracks are distributed in the region away from the unloading face, regardless of the value of the pre-confining pressure. The abrupt unloading results in a sudden change of the stress state in the blocks near the unloading surface. The stress change formed at the moment of unloading induces a considerable horizontal deformation near to the surfaces. A great number of mainly tensile cracks form near the unloading surface and ultimately result in the ejection of fragments and coal plates. These observations are in agreement with previous study on rockbursts (Duan et al., 2019). A comparison of Figure 5A and Figure 5D shows that the pre-confining pressure has an important influence on the development of cracks during a coalburst. Cracks initiate more intensively in coal samples under higher stress, resulting in the formation of a denser fracture network after sudden release of high pre-confining pressure. In addition, different pre-confining pressures result in significant differences in the crack propagation of coalbursts, as demonstrated in Figure 5A. When the pre-confining pressure is low, at first, few shear cracks are initiated in the interior of the coal sample after unloading. Then, the number of tensile fractures near the unloading surface increases rapidly with increasing dynamic calculation time, which results in the ejection of fragments. However, when the coal sample is under a high pre-confining pressure, a large number of cracks with different failure modes (shear and tensile cracks), appear instantaneously in almost the entire area near the unloading surface, as demonstrated in Figure 5D. Fewer shear cracks form and the distribution is more dispersed under a lower pre-confining pressure. However, the number of shear cracks in the coal sample is greater under higher pre-confining pressure. As shown in Figure 5, with increasing pre-confining pressure, the coalburst intensity increases significantly. When the pre-confining pressure is .1 MPa or 1.0 MPa, the coalburst only occurs in a local area of the unloading surface. However, under the condition that the pre-confining pressure is 2.5 MPa or 5.0 MPa, the range of the coalburst covers almost the entire area on both sides of the coal sample, and many coal fragments and plates are ejected from the entire unloading surface. The ejection is more powerful when the pre-confining pressure is higher. The graph indicates that the fracturing process during the coalburst is affected by the pre-confining pressure. A coalburst under a higher pre-confining pressure has a wider fracturing range and a higher ejection velocity.

FIGURE 5

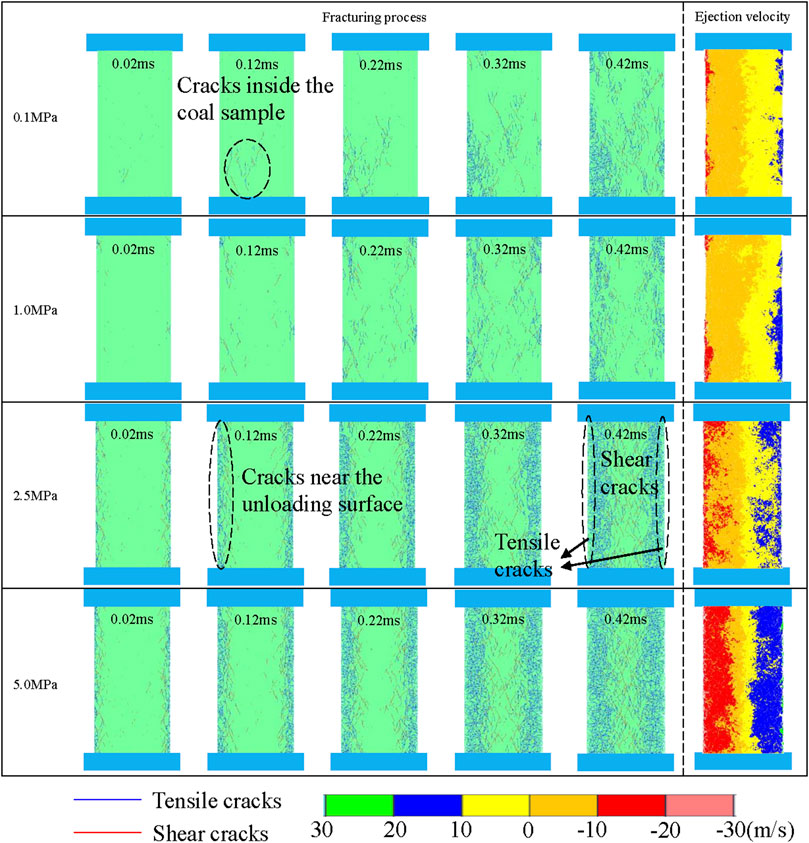
FIGURE 5. Crack development process of coalburst under different pre-confining pressures: (A) .1 MPa; (B) 1 MPa; (C) 2.5 MPa and (D) 5 MPa. Note: blue lines indicate tensile cracks, and red lines indicate shear.

To further study the ejection of coal fragments during coalbursts, four monitoring points are set-up on both sides of the numerical model to monitor the horizontal velocities of fragments, as shown in Figure 1. The horizontal velocities of the fragments are shown in Figure 6. Positive values indicate movement towards the right and vice versa. Numerous studies imply that the velocities of fragments that form during coalbursts are more than 10 m/s (Frith et al., 2020; Yang et al., 2020; Gao et al., 2021). As shown in Figure 6, most of the recorded velocities exceed 10 m/s, and the magnitude of the velocities increases with increasing pre-confining pressure. The maximum velocities of the coal fragments are 16.76 m/s, 17.76 m/s, 20.60 m/s and 30.00 m/s during coalbursts when the pre-confining pressures are .1 MPa, 1.0 MPa, 2.5 MPa and 5.0 MPa, respectively. The velocity is zero for a period of time after the pre-confining pressure of .1 MPa is released, indicating that a coalburst does not occur immediately after the low pre-confining pressure is released. However, the ejection velocity of the fragments grows rapidly with time when the pre-confining pressure becomes 5.0 MPa, indicating that a violent coalburst occurs at the moment of unloading in this situation. The rise in pre-confining pressure leads to an increase in stress and elastic energy in the coal sample, which is more prone to coalburst. The simulations suggest that a critical stress level or a critical energy level may exist for coalbursts. This result provides direct evidence of the mechanism of rock dynamic failure proposed in previous research (Dou and He, 2001; Su et al., 2017).

FIGURE 6

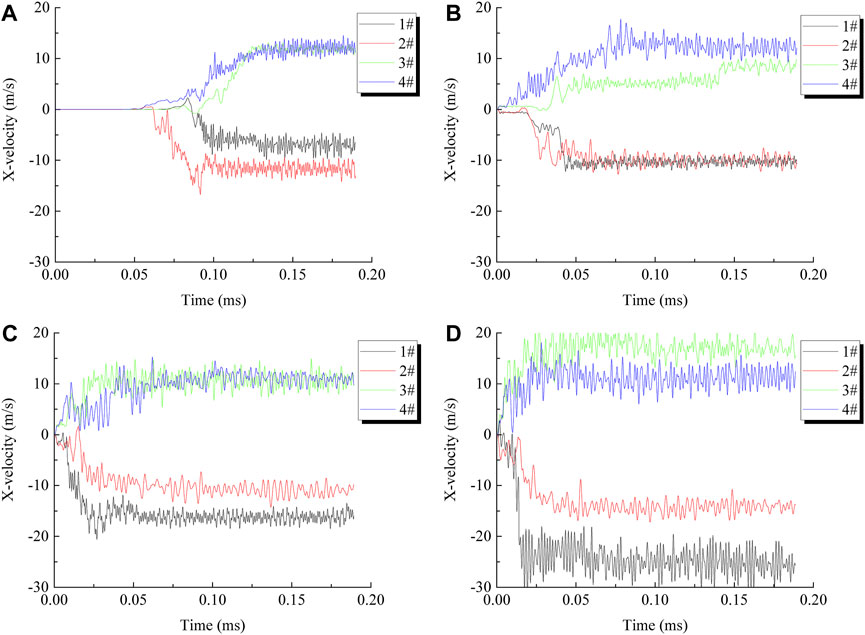
FIGURE 6. Magnitudes of horizontal velocities of fragments under different pre-confining pressures: (A) .1 MPa; (B) 1.0 MPa; (C) 2.5 MPa and (D) 5.0 MPa.

3.2 Energy evolution of coalbursts

3.2.1 Elastic energy

Figure 7 illustrates how the elastic energy changes during the coalburst process. The initial elastic energy is 519 J when the pre-confining pressure is .1 MPa and increases to 1777 J when the pre-confining pressure is 5.0 MPa. After a coal sample is completely destroyed via coalburst, the elastic energy is close to 0 J. No coalburst occurs under the pre-confining pressure of .1 MPa during the dynamic calculation time of .00–.05 m, and only a small number of micro-cracks are generated inside the coal sample, so the dissipation of elastic energy is not obvious at this stage. When the dynamic calculation time is greater than .05 m, the elastic energy of the sample gradually decreases with the occurrence of a small burst near the unloading surface. For coal samples with initial confining pressures of 1.0 MPa, 2.5 MPa and 5.0 MPa, various degrees of coalburst occur after the confining pressure is released, and the elastic energy decreases immediately. The initiation and coalescence of cracks as well as the ejection of fragments cause the dissipation of elastic energy. The elastic energy release rate increases with increasing pre-confining pressure. Therefore, the rate of reduction in elastic energy can be used to characterize the coalburst.

FIGURE 7

FIGURE 7. Change in elastic energy vs time for different pre-confining pressures.

The dissipation process of elastic energy during the coalburst is fully captured by the simulations. The distribution of the elastic energy is given in Figure 8. Figure 8 reveals that the stored elastic energy increases with rising pre-confining pressure. Higher pre-confining pressures lead to a stronger inhomogeneity of elastic energy distribution in coal. High pre-confining pressure causes high local stresses inside the coal sample. Obviously, the higher the inhomogeneity of stress or energy distribution in the coal, the higher the possibility of coalburst. The dissipation process of elastic energy basically corresponds to the crack evolution process. The dissipation of elastic energy is obvious in the areas with densely distributed cracks, and the remaining elastic energy in these areas is small. In other words, development and growth of the fractures are the main reasons for the elastic energy dissipation. In the numerical simulation, the coal sample is loaded in the vertical direction and unloaded in the horizontal direction, and the coal burst also occurs mainly in the horizontal direction, so that a large amount of elastic energy is dissipated along the horizontal direction. It can be seen that strain energy is released at different rates for different pre-confining pressure s, and there is still a large amount of strain energy in the coal sample when the dynamic time is .09 m for a pre-confining pressure of .1 MPa. As the pre-confining pressure increases, the strain energy release rate is greater when the dynamic time is the same, indicating that the coal burst more violent.

FIGURE 8

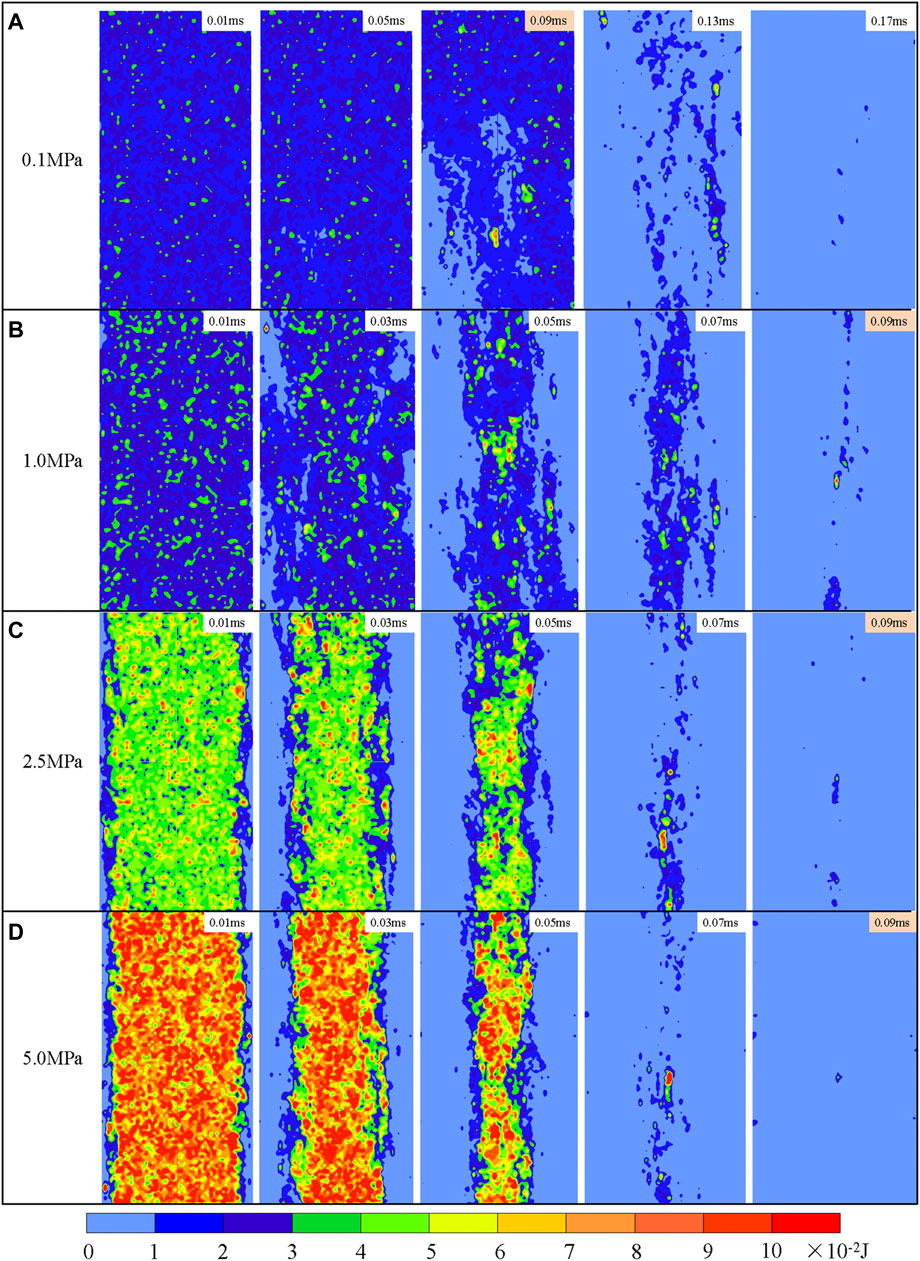
FIGURE 8. Distribution of elastic energy under different pre-confining pressures: (A) .1 MPa; (B) 1 MPa; (C) 2.5 MPa and (D) 5 MPa for different points in time.

3.2.2 Kinetic energy

Figure 9 illustrates the kinetic energy evolution for different pre-confining pressures. The cumulative kinetic energy is zero within .0–.05 m when the pre-confining pressure is .1 MPa, indicating that a coalburst does not occur. A coalburst will end when the kinetic energy does no longer change (coal sample is completely destroyed or has reached a certain final damage state). The kinetic energy during the coalburst is larger under higher pre-confining pressure. The kinetic energy increases more rapidly and reaches the peak earlier when the pre-confining pressure increases. This indicates that a higher pre-confining pressure causes a shorter coalburst triggering time and more violent fragment ejection, resulting in a more harmful coalburst.

FIGURE 9

FIGURE 9. Change in kinetic energy vs time for different pre-confining pressures.

Figure 10 shows the distribution of the kinetic energy during the coalburst process. There is a clear difference in the kinetic energy near and far from the unloading surface, which leads to the separation of coal fragments and plates as shown in Figure 5. The evolution of kinetic energy under different pre-confining pressures shows that the cracks gradually expand from the boundaries to the centre of the coal samples, which is in good agreement with field and experimental observations (He et al., 2012; Zhang et al., 2012; Jiang et al., 2020). The evolution process of kinetic energy shows that the ejection of fragments during coalbursts starts at some areas on the unloading surface of the sample, and new areas of coalburst are continuously formed and expand, eventually leading to a violent coalburst. As shown in Figures 8, 10, the transformation between elastic energy and kinetic energy during coalbursts is captured by the numerical simulations. Notably, the distribution of kinetic energy in the sample is not uniform. On the one hand, there are many “kinetic energy accumulation areas” near the unloading surface, which lead to the occurrence of “coalburst pits” with different depths and locations on the unloading surface of the coal samples, as can be seen in Figure 10C. There is another interesting phenomenon: some independent “kinetic energy concentration areas” form inside the coal sample under high pre-confining pressure, as shown in Figures 10C, D. These regions have a higher kinetic energy value than their surroundings, which indicates that some violent “internal burst” occur inside the coal sample, promoting the ejection of fragments and coal plates. This is because there is higher stress within the coal sample under high pre-surrounding pressure, and the internal stress and energy distribution are not uniform. When the pre-surrounding pressure was suddenly unloaded, the dynamic failure occurred inside the coal sample.

FIGURE 10

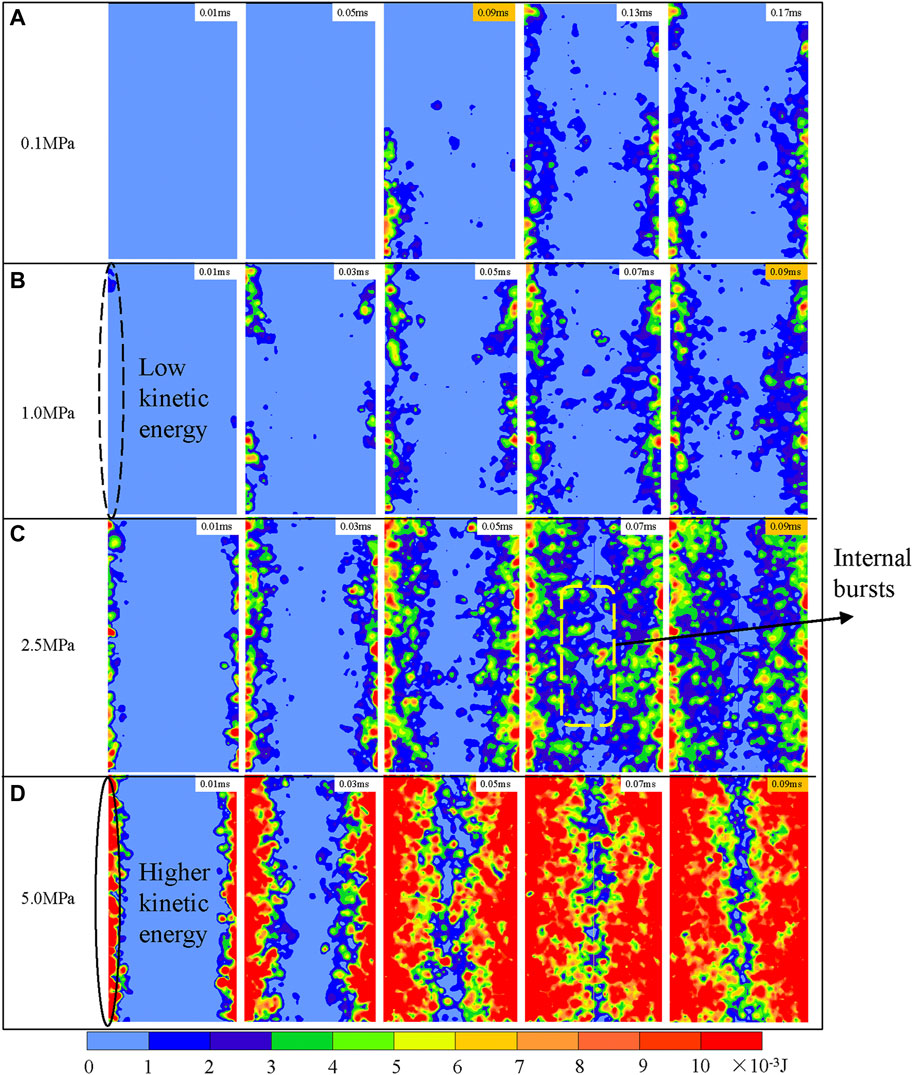
FIGURE 10. Distribution of kinetic energy under different pre-confining pressures of (A) .1 MPa; (B) 1 MPa; (C) 2.5 MPa and (D) 5 MPa for different points in time.

3.2.3 Frictional energy

Shear failure is an important element in the coalburst process. When shear failure occurs, dislocation (frictional sliding) along the blocks is triggered, so a certain amount of elastic energy is converted into work to overcome frictional resistance. This part of the energy dissipated due to the shear slip during a coalburst is called frictional energy. Figure 11 illustrates how the frictional energy changes during a coalburst. The increase in accumulated frictional energy is an indication of shear failure in the coal sample. As shown in Figure 11, the peak of the frictional energy during the coalburst increases with rising pre-confining pressure. This demonstrates that more shear cracks occur during the coalburst under high pre-confining pressure.

FIGURE 11

FIGURE 11. Change of frictional energy vs time for different pre-confining pressures.

Figure 12 shows the distribution of the frictional energy at different stages during the coalburst. Figure 12 documents, those regions where the frictional energy is concentrated develop from areas near the unloading surface towards the centre of the sample. This is consistent with the gradual expansion of shear cracks. The pre-confining pressure has an important influence on the distribution of frictional energy. Compared with a low pre-confining pressure, the frictional energy is higher and more concentrated in the centre of the sample under higher pre-confining pressure. This shows that more shear cracks are formed in the core of the sample during the coalburst induced by release of a higher pre-confining pressure, resulting in predominant shear failure of the sample.

FIGURE 12

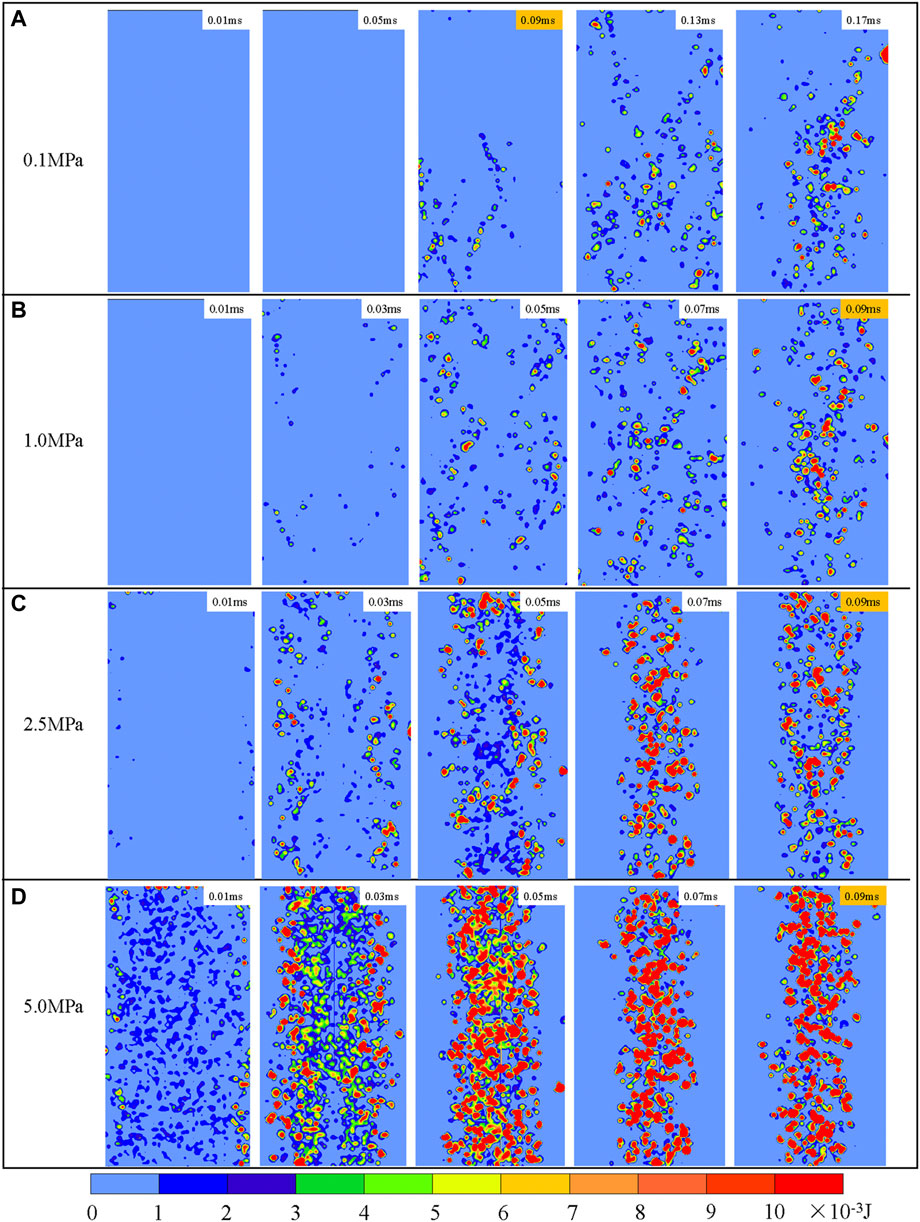
FIGURE 12. Distribution of frictional energy under different pre-confining pressures of (A) .1 MPa; (B) 1 MPa; (C) 2.5 MPa and (D) 5 MPa for different points in time.

4 Discussion

4.1 Influence of pre-confining pressure on failure mechanism during coalburst

Strainbursts of rock are divided into tensile strainbursts (Diederichs, 2007; Hu et al., 2018) and shear strainbursts (Ortlepp, 2001; Zhang et al., 2012; Feng et al., 2016). In this study, under different pre-confining pressures different failure modes occur like analysed in Section 3.1 and illustrated in Figure 13. The coalburst induced by release of a low pre-confining pressure is dominated by tensile failure, which is referred to as tensile coalburst. During a tensile coalburst, the failure is characterized by coal fragment ejection caused by tensile failure in certain areas near the unloading surface, small failure areas, and limited ejection intensity. Apart from tensile failure on both sides, there is no complete penetrating shear fracturing in the centre of the specimen. However, shear failure is the dominant during coalbursts under high pre-confining pressure, which is referred to as shear coalburst. There are two types of micro-cracks in shear coalbursts. On the one hand: splitting and throwing out of a large number of coal fragments and plates are caused by the coalescence of tensile cracks near the unloading surface. Fragments are ejected at a fairly high velocity, such as 10–30 m/s. On the other hand, many shear cracks form in the central region of the coal sample, which is the major cause of coal failure during coalburst. Notice, that the pre-confining pressure applied to the two lateral sides are both released in the numerical simulation. Therefore, significant lateral deformation and failure occur on both sides of the coal samples in the numerical simulation.

FIGURE 13

FIGURE 13. Two failure modes of coalburst under different pre-confining pressures.

As discussed above, the failure modes of coal during a unloading-induced coalburst are complex. As shown in Figure 13, the failure during coalbursts as presented by numerical simulations, are different from single failure under static or quasi-static loads as presented for instance by (Haimson and Chang, 2000; Chang and Lee, 2004; Yang et al., 2012). The numerical results in this study show that tensile failures mainly occur near the unloading surface, while shear cracks are mainly distributed in the core region of the coal samples. This is in good agreement with earlier studies (Feng et al., 2018; Su et al., 2018). The density of tensile cracks rises and they expand deeper below the unloaded surface with increasing pre-confining pressure. Moreover, the number of shear cracks that appears far from the unloaded surface also increase significantly, and these cracks interpenetrate. It is possible to explain this failure phenomenon in the following way. On the one hand, the stress change caused by the sudden unloading of the pre-confining pressure causes the deformation (extension) of the coal sample near the unloading surface, and this lateral deformation is causing the tensile cracks. On the other hand, the instantaneous unloading of the pre-confining pressure causes an increase in the vertical stress in the remaining more or less intact part of the coal sample. The higher the pre-confining pressure, the greater the vertical stress of the sample after unloading. It promotes the initiation and development of shear failure in the centre of the coal sample. The failure mechanism of unloading-induced coalburst gradually transforms from tensile mode to shear mode as the pre-confining pressure increases.

4.2 Influence of pre-confining pressure on energy conversion of coalbursts

Figure 14 presents peak elastic energy, peak kinetic energy and peak frictional energy of the coal samples under different pre-confining pressures during unloading-induced coalbursts. The graph shows that when the pre-confining pressure rises, the three energies rise as well. The higher the pre-confining stress, the higher the peak strength of the rock. Therefore, the ultimate energy-storage capacity of the coal increases with the peak strength. Compared with low pre-confining pressures, at high pre-confining pressures a higher stress change occur at the moment of unloading, resulting in more tensile cracks appearing near the unloading surface. Tensile failure is the main source of kinetic energy increase. The frictional energy is mainly caused by the shear slip between blocks. Severe shear failure occurs during coalburst due to the increase in vertical stress induced by unloading of the high pre-confining pressure, which causes an increase in frictional energy. The relationship between the above mentioned three energy types and the pre-confining pressure is not linear.

FIGURE 14

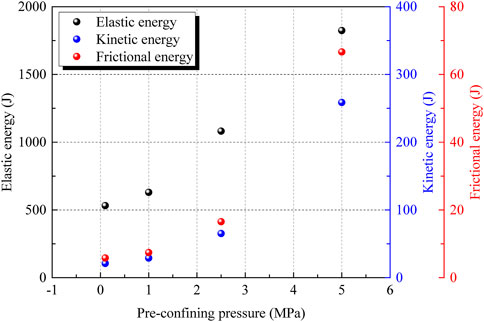
FIGURE 14. Peak elastic energy, peak kinetic energy and peak frictional energy of the coal samples under different pre-confining pressures.

The elastic energy displayed in Figure 7 is only the elastic energy stored in the coal sample. It is well known that the elastic energy released during coalbursts includes the elastic energy stored in the sample and the elastic energy stored in the loading system (Manouchehrian and Cai, 2016; Tarasov and Stacey, 2017; Gao and Yang, 2021). The elastic energy in the loading plate $W_L$ should be calculated as:

$W_L=\frac{{\sigma }_{\max }^2{A}_{L}l}{2E_{\mathrm{L}}}(8)$

where ${\sigma }_{\max }$ is the maximum vertical stress monitored at the loading plate, and the properties of the loading plate are l = .1 m, E_L = 17 GPa, and A_L = π × .1 m².

Consequently, the conversion ratio of kinetic energy $\alpha$ and the conversion ratio of frictional energy $\beta$ are calculated by:

$\alpha =\frac{W_K}{W_C+W_L}(9)$

$\beta =\frac{W_F}{W_C+W_L}(10)$

where $W_K$ and $W_F$ are the kinetic energy and the frictional energy during the coalburst, respectively. $W_C$ and $W_L$ are the elastic energy stored in the coal and the plate, respectively.

Figure 15 shows the conversion ratios of elastic energy into kinetic and frictional energy during unloading-induced coalbursts under different pre-confining pressures. As illustrated in Figure 15, the pre-confining pressure has an important influence on the energy transformation during a coalburst. In this study, the conversion ratio of kinetic energy is between 2% and 4% when the pre-confining pressure is less than 5 MPa, which means only a small percentage of elastic energy is transformed into kinetic energy, which is consistent with previous findings (Gu and Ozbay, 2015; Hu et al., 2020). However, the conversion ratio of kinetic energy increases significantly as the pre-confining pressure continues to rise, suggesting that more coal fragments and plates are thrown out at a higher velocity during a severe coalburst. In addition, as the pre-confining pressure rises, the conversion ratio of frictional energy increases as well, indicating that the shear failure in coal samples intensifies and that a shear coalburst occurs under a higher pre-confining pressure.

FIGURE 15

FIGURE 15. Energy conversion ratio during coalbursts under different pre-confining pressures.

4.3 Recommendations to prevent coalbursts

Violent coalbursts can occur in roadway developments as a result of the unloading of high pre-confining pressure according to simulation findings. Based on the above research results, three measures presented below are recommended to prevent the occurrence of coalbursts. First, a sudden unloading of a coal pillar with high pre-confining pressure should be avoided, and a slower excavation speed should be adopted to reduce the unloading rate in the coal pillar. Second, some measures should be taken to reduce the elastic energy stored in the coal pillar, such as cutting the rock layer above the coal pillar to reduce the vertical load or performing large-diameter drilling in the coal to reduce the energy storage capacity. Third, it is necessary to provide timely support to the free surface formed by the excavation, which will inhibit the formation of tensile failures and the expansion of cracks away from the unloading surface.

5 Conclusion

This paper presents a numerical study of unloading-induced coalbursts failure analysis using DEM and a static–dynamic loading strategy. This method, well calibrated and validated, is effective in capturing the typical phenomena of coalbursts. The main conclusions in respect to the influence of pre-confining pressure on crack propagation, failure mechanism, energy evolution and energy conversion during unloading-induced coalbursts are as follows.

1) The pre-confining pressure has a significant effect on crack development and failure mode of unloading-induced coalbursts. Localized failure patterns are observed in coalbursts. Regions near the unloading surface are more prone to tensile failure, while shear cracks are the main failure type in the centre of the body. With increasing pre-confining pressure, the failure mechanism of coal transforms from a tensile coalburst towards a shear coalburst.

2) The numerical simulations provide direct evidence for the conversion of stored elastic energy into kinetic energy and frictional energy during unloading-induced coalbursts. The evolution of energy is consistent with the development of cracks. During coalbursts, the higher the pre-confining pressure, the greater the rate at which the elastic energy decreases and the greater the rate at which kinetic and frictional energy increase. Some independent “kinetic energy concentration areas” are observed during unloading-induced coalbursts, indicating that violent “internal bursts” occur inside the coal, providing new insights into the mechanism of coalbursts.

3) The pre-confining pressure obviously affects the energy transition during unloading-induced coalbursts. The conversion ratio of kinetic energy increases non-linearly with increasing pre-confining pressure, indicating that coalbursts under high pre-confining pressure are more dangerous. The conversion ratio of frictional energy is approximately one-quarter of the conversion ratio of kinetic energy. With increasing pre-confining pressure, the conversion ratio of frictional energy also increases non-linearly, indicating that the coalburst becomes dominated by shear failure under high pre-confining pressure.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. Conceptualization: JC, LD, and KZ; Methodology: JC and KZ; Software: LD; Validation: JC and YC; Formal Analysis: JC, JL, and JK; Investigation: JC, KZ, and JK; Data curation: JC, LD and YC; Writing-Original Draft Preparation: JC; Writing-Review & Editing: JC and YC; Supervision: JC, LD, and JL; Project Administration: LD and JL; Funding Acquisition: LD and JL. All authors have read and agreed to the published version of the manuscript.

Funding

This work was conducted with support from the National Natural Science Foundation of China (Grant No. 51874292, 51934007 and 52004004) and the Major Project of Natural Science Research in Higher Education Institutions in Anhui Province (Grant No. KJ2021ZD0051).

Acknowledgments

The authors thank for financial support from the National Natural Science Foundation of China (Grant Nos. 51874292, 51934007 and 52004004) and the Major Project of Natural Science Research in Higher Education Institutions in Anhui Province (Grant Nos. KJ2021ZD0051). The first author JC would like to express his sincere thanks to the China Scholarship Council (CSC) for the financial support for his study at TU Bergakademie Freiberg, Germany.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ai, D., Zhao, Y., Wang, Q., and Li, C. (2020). Crack propagation and dynamic properties of coal under SHPB impact loading: Experimental investigation and numerical simulation. Theor. Appl. Fract. Mech. 105, 102393. doi:10.1016/j.tafmec.2019.102393

CrossRef Full Text | Google Scholar

Bažant, Z. P., Shang-Ping, B., and Ravindra, G. (1993). Fracture of rock: Effect of loading rate. Eng. Fract. Mech. 45 (3), 393–398. doi:10.1016/0013-7944(93)90024-m

CrossRef Full Text | Google Scholar

Cao, J., Dou, L., Zhu, G., He, J., Wang, S., and Zhou, K. (2020). Mechanisms of rock burst in horizontal section mining of a steeply inclined extra-thick coal seam and prevention Technology. Energies 13 (22), 6043. doi:10.3390/en13226043

CrossRef Full Text | Google Scholar

Chang, S-H., and Lee, C-I. (2004). Estimation of cracking and damage mechanisms in rock under triaxial compression by moment tensor analysis of acoustic emission. Int. J. Rock Mech. Min. Sci. 41 (7), 1069–1086. doi:10.1016/j.ijrmms.2004.04.006

CrossRef Full Text | Google Scholar

Chen, G., He, M., and Fan, F. (2018). Rock burst analysis using DDA numerical simulation. Int. J. Geomechanics 18 (3). doi:10.1061/(asce)gm.1943-5622.0001055

CrossRef Full Text | Google Scholar

Cook, N. G. W. (1965). A note on rockbursts considered as a problem of stability. J. South. Afr. Inst. Min. Metallurgy 65 (8), 437–446. doi:10.10520/AJA0038223X_4914

CrossRef Full Text | Google Scholar

Cundall, P. A., and Strack, O. D. L. (1979). A discrete numerical model for granular assemblies. Géotechnique. 29 (1), 47–65. doi:10.1680/geot.1979.29.1.47

CrossRef Full Text | Google Scholar

Diederichs, M. S. (2007). The 2003 Canadian Geotechnical Colloquium: Mechanistic interpretation and practical application of damage and spalling prediction criteria for deep tunnelling. Can. Geotechnical J. 44 (9), 1082–1116. doi:10.1139/t07-033

CrossRef Full Text | Google Scholar

Dou, L., and He, X. (2001). Theory and technology of rock burst prevention. Xuzhou: China University of Mining and Technology Press.

Google Scholar

Duan, K., Ji, Y., Wu, W., and Kwok, C. Y. (2019). Unloading-induced failure of brittle rock and implications for excavation-induced strain burst. Tunn. Undergr. Space Technol. 84, 495–506. doi:10.1016/j.tust.2018.11.012

CrossRef Full Text | Google Scholar

Feng, X-T., Xu, H., Qiu, S-L., Li, S-J., Yang, C-X., Guo, H-S., et al. (2018). Situ Observation of Rock Spalling in the Deep Tunnels of the, 51, 1193–1213. doi:10.1007/s00603-017-1387-8China jinping underground laboratory (2400 m depth)Rock Mech. Rock Eng.

CrossRef Full Text | Google Scholar

Feng, X-T., Yu, Y., Feng, G-L., Xiao, Y-X., Chen, B., and Jiang, Q. (2016). Fractal behaviour of the microseismic energy associated with immediate rockbursts in deep, hard rock tunnels. Tunn. Undergr. Space Technol. 51, 98–107. doi:10.1016/j.tust.2015.10.002

CrossRef Full Text | Google Scholar

Frith, R., Reed, G., and Jones, A. (2020). A causation mechanism for coal bursts during roadway development based on the major horizontal stress in coal: Very specific structural geology causing a localised loss of effective coal confinement and Newton’s second law. Int. J. Min. Sci. Technol. 30 (1), 39–47. doi:10.1016/j.ijmst.2019.12.018

CrossRef Full Text | Google Scholar

Gao, F., Kaiser, P. K., Stead, D., Eberhardt, E., and Elmo, D. (2019b). Numerical simulation of strainbursts using a novel initiation method. Comput. Geotechnics 106, 117–127. doi:10.1016/j.compgeo.2018.10.018

CrossRef Full Text | Google Scholar

Gao, F., Kaiser, P. K., Stead, D., Eberhardt, E., and Elmo, D. (2019a). Strainburst phenomena and numerical simulation of self-initiated brittle rock failure. Int. J. Rock Mech. Min. Sci. 116, 52–63. doi:10.1016/j.ijrmms.2019.03.021

CrossRef Full Text | Google Scholar

Gao, F., Kang, H., and Li, J. (2021). Numerical simulation of fault-slip rockbursts using the distinct element method. Tunn. Undergr. Space Technol. 110, 103805. doi:10.1016/j.tust.2020.103805

CrossRef Full Text | Google Scholar

Gao, F., and Yang, L. (2021). Experimental and numerical investigation on the role of energy transition in strainbursts. Rock Mech. Rock Eng. 54 (9), 5057–5070. doi:10.1007/s00603-021-02550-8

CrossRef Full Text | Google Scholar

Gao, F. Q., and Stead, D. (2014). The application of a modified Voronoi logic to brittle fracture modelling at the laboratory and field scale. Int. J. Rock Mech. Min. Sci. 68, 1–14. doi:10.1016/j.ijrmms.2014.02.003

CrossRef Full Text | Google Scholar

Gu, R., and Ozbay, U. (2015). Numerical investigation of unstable rock failure in underground mining condition. Comput. Geotechnics 63, 171–182. doi:10.1016/j.compgeo.2014.08.013

CrossRef Full Text | Google Scholar

Haimson, B., and Chang, C. (2000). A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite. Int. J. Rock Mech. Min. Sci. 37 (1-2), 285–296. doi:10.1016/s1365-1609(99)00106-9

CrossRef Full Text | Google Scholar

Hao, X., Du, W., Zhao, Y., Sun, Z., Zhang, Q., Wang, S., et al. (2020). Dynamic tensile behaviour and crack propagation of coal under coupled static-dynamic loading. Int. J. Min. Sci. Technol. 30 (5), 659–668. doi:10.1016/j.ijmst.2020.06.007

CrossRef Full Text | Google Scholar

Hatzor, Y. H., He, B-G., and Feng, X-T. (2017). Scaling rockburst hazard using the DDA and GSI methods. Tunn. Undergr. Space Technol. 70, 343–362. doi:10.1016/j.tust.2017.09.010

CrossRef Full Text | Google Scholar

Hauquin, T., Gunzburger, Y., and Deck, O. (2018). Predicting pillar burst by an explicit modelling of kinetic energy. Int. J. Rock Mech. Min. Sci. 107, 159–171. doi:10.1016/j.ijrmms.2018.05.004

CrossRef Full Text | Google Scholar

He, B-G., Zelig, R., Hatzor, Y. H., and Feng, X-T. (2016). Rockburst generation in discontinuous rock masses. Rock Mech. Rock Eng. 49 (10), 4103–4124. doi:10.1007/s00603-015-0906-8

CrossRef Full Text | Google Scholar

He, M., Ren, F., and Cheng, C. (2018). Mechanism of strain burst by laboratory and numerical analysis. Shock Vib. 2018, 1–15. doi:10.1155/2018/8940798

CrossRef Full Text | Google Scholar

He, M. C., Miao, J. L., and Feng, J. L. (2010). Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions. Int. J. Rock Mech. Min. Sci. 47 (2), 286–298. doi:10.1016/j.ijrmms.2009.09.003

CrossRef Full Text | Google Scholar

He, M. C., Nie, W., Zhao, Z. Y., and Guo, W. (2012). Experimental investigation of bedding plane orientation on the rockburst behavior of sandstone. Rock Mech. Rock Eng. 45 (3), 311–326. doi:10.1007/s00603-011-0213-y

CrossRef Full Text | Google Scholar

He, M. C., Zhao, F., Cai, M., and Du, S. (2014). A novel experimental technique to simulate pillar burst in laboratory. Rock Mech. Rock Eng. 48 (5), 1833–1848. doi:10.1007/s00603-014-0687-5

CrossRef Full Text | Google Scholar

Hokka, M., Black, J., Tkalich, D., Fourmeau, M., Kane, A., Hoang, N-H ., et al. (2016). Effects of strain rate and confining pressure on the compressive behavior of Kuru granite. Int. J. Impact Eng. 91, 183–193. doi:10.1016/j.ijimpeng.2016.01.010

CrossRef Full Text | Google Scholar

Hu, L., Ma, K., Liang, X., Tang, C., Wang, Z., and Yan, L. (2018). Experimental and numerical study on rockburst triggered by tangential weak cyclic dynamic disturbance under true triaxial conditions. Tunn. Undergr. Space Technol. 81, 602–618. doi:10.1016/j.tust.2018.08.014

CrossRef Full Text | Google Scholar

Hu, L., Su, G., Liang, X., Li, Y., and Yan, L. (2020). A distinct element based two-stage-structural model for investigation of the development process and failure mechanism of strainburst. Comput. Geotechnics 118, 103333. doi:10.1016/j.compgeo.2019.103333

CrossRef Full Text | Google Scholar

Huang, F., Shen, J., Cai, M., and Xu, C. (2019). An empirical UCS model for anisotropic blocky rock masses. Rock Mech. Rock Eng. 52 (9), 3119–3131. doi:10.1007/s00603-019-01771-2

CrossRef Full Text | Google Scholar

Itasca Consulting Group Inc (2014). UDEC manual. Minneapolis.Version 6.0.

Google Scholar

Jiang, J., Su, G., Zhang, X., and Feng, X-T. (2020). Effect of initial damage on remotely triggered rockburst in granite: An experimental study. Bull. Eng. Geol. Environ. 79 (6), 3175–3194. doi:10.1007/s10064-020-01760-8

CrossRef Full Text | Google Scholar

Jiang, Y., Zhao, Y., Wang, H., and Zhu, J. (2017). A review of mechanism and prevention technologies of coal bumps in China. J. Rock Mech. Geotechnical Eng. 9 (1), 180–194. doi:10.1016/j.jrmge.2016.05.008

CrossRef Full Text | Google Scholar

Ju, M., Li, J., Li, J., and Zhao, J. (2020). Loading rate effects on anisotropy and crack propagation of weak bedding plane-rich rocks. Eng. Fract. Mech. 230, 106983. doi:10.1016/j.engfracmech.2020.106983

CrossRef Full Text | Google Scholar

Kazerani, T., Yang, Z. Y., and Zhao, J. (2011). A discrete element model for predicting shear strength and degradation of rock joint by using compressive and tensile test Data. Rock Mech. Rock Eng. 45 (5), 695–709. doi:10.1007/s00603-011-0153-6

CrossRef Full Text | Google Scholar

Kong, X., Wang, E., Li, S., Lin, H., Zhang, Z., and Ju, Y. (2020). Dynamic mechanical characteristics and fracture mechanism of gas-bearing coal based on SHPB experiments. Theor. Appl. Fract. Mech. 105, 102395. doi:10.1016/j.tafmec.2019.102395

CrossRef Full Text | Google Scholar

Li, X., Gu, H., Tao, M., Peng, K., Cao, W., and Li, Q. (2021). Failure characteristics and meso-deterioration mechanism of pre-stressed coal subjected to different dynamic loads. Theor. Appl. Fract. Mech. 115, 103061. doi:10.1016/j.tafmec.2021.103061

CrossRef Full Text | Google Scholar

Li, X. B., Lok, T. S., and Zhao, J. (2004). Dynamic characteristics of granite subjected to intermediate loading rate. Rock Mech. Rock Eng. 38 (1), 21–39. doi:10.1007/s00603-004-0030-7

CrossRef Full Text | Google Scholar

Li, Y., Yang, S-Q., Liu, Z-L., Sun, B-W., Yang, J., and Xu, J. (2022). Study on mechanical properties and deformation of coal specimens under different confining pressure and strain rate. Theor. Appl. Fract. Mech. 118, 103287. doi:10.1016/j.tafmec.2022.103287

CrossRef Full Text | Google Scholar

Liu, H. Y., Kou, S. Q., Lindqvist, P-A ., and Tang, C. A. (2004). Numerical studies on the failure process and associated microseismicity in rock under triaxial compression. Tectonophysics 384 (1-4), 149–174. doi:10.1016/j.tecto.2004.03.012

CrossRef Full Text | Google Scholar

Manouchehrian, A., and Cai, M. (2016). Simulation of unstable rock failure under unloading conditions. Can. Geotechnical J. 53 (1), 22–34. doi:10.1139/cgj-2015-0126

CrossRef Full Text | Google Scholar

Mottahedi, A., and Ataei, M. (2019). Fuzzy fault tree analysis for coal burst occurrence probability in underground coal mining. Tunn. Undergr. Space Technol. 83, 165–174. doi:10.1016/j.tust.2018.09.029

CrossRef Full Text | Google Scholar

Ortlepp, W. D. (2001). The behaviour of tunnels at great depth under large static and dynamic pressures. Tunn. Undergr. Space Technol. 16 (1), 41–48. doi:10.1016/s0886-7798(01)00029-3

CrossRef Full Text | Google Scholar

Potyondy, D. O., and Cundall, P. A. (2004). A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 41 (8), 1329–1364. doi:10.1016/j.ijrmms.2004.09.011

CrossRef Full Text | Google Scholar

Su, G., Hu, L., Feng, X., Yan, L., Zhang, G., Yan, S., et al. (2018). True triaxial experimental study of rockbursts induced by ramp and cyclic dynamic disturbances. Rock Mech. Rock Eng. 51 (4), 1027–1045. doi:10.1007/s00603-017-1384-y

CrossRef Full Text | Google Scholar

Su, G., Shi, Y., Feng, X., Jiang, J., Zhang, J., and Jiang, Q. (2017). True-triaxial experimental study of the evolutionary features of the acoustic emissions and sounds of rockburst processes. Rock Mech. Rock Eng. 51 (2), 375–389. doi:10.1007/s00603-017-1344-6

CrossRef Full Text | Google Scholar

Tarasov, B. G., and Stacey, T. R. (2017). Features of the energy balance and fragmentation mechanisms at spontaneous failure of class I and class II rocks. Rock Mech. Rock Eng. 50 (10), 2563–2584. doi:10.1007/s00603-017-1251-x

CrossRef Full Text | Google Scholar

Vardar, O., Zhang, C., Canbulat, I., and Hebblewhite, B. (2018). A semi-quantitative coal burst risk classification system. Int. J. Min. Sci. Technol. 28 (5), 721–727. doi:10.1016/j.ijmst.2018.08.001

CrossRef Full Text | Google Scholar

Wang, J-A ., and Park, H. D. (2001). Comprehensive prediction of rockburst based on analysis of strain energy in rocks. Tunn. Undergr. Space Technol. 16 (1), 49–57. doi:10.1016/s0886-7798(01)00030-x

CrossRef Full Text | Google Scholar

Yang, S-Q., Jing, H-W., and Wang, S-Y. (2012). Experimental investigation on the strength, deformability, failure behavior and acoustic emission locations of red sandstone under triaxial compression. Rock Mech. Rock Eng. 45 (4), 583–606. doi:10.1007/s00603-011-0208-8

CrossRef Full Text | Google Scholar

Yang, X., Ren, T., and Tan, L. (2020). Estimation of average ejection velocity generated by rib burst under compression load. Int. J. Rock Mech. Min. Sci. 128, 104277. doi:10.1016/j.ijrmms.2020.104277

CrossRef Full Text | Google Scholar

Yao, M., Rong, G., Zhou, C., and Peng, J. (2016). Effects of thermal damage and confining pressure on the mechanical properties of coarse marble. Rock Mech. Rock Eng. 49 (6), 2043–2054. doi:10.1007/s00603-016-0916-1

CrossRef Full Text | Google Scholar

Zhang, C., Canbulat, I., Hebblewhite, B., and Ward, C. R. (2017). Assessing coal burst phenomena in mining and insights into directions for future research. Int. J. Coal Geol. 179, 28–44. doi:10.1016/j.coal.2017.05.011

CrossRef Full Text | Google Scholar

Zhang, C., Feng, X-T., Zhou, H., Qiu, S., and Wu, W. (2012). Case histories of four extremely intense rockbursts in deep tunnels. Rock Mech. Rock Eng. 45 (3), 275–288. doi:10.1007/s00603-011-0218-6

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, X., Zhang, Y., Qin, X., and Khan, M. (2021). Comparative study on fracture characteristics of coal and rock samples based on acoustic emission technology. Theor. Appl. Fract. Mech. 111, 102851. doi:10.1016/j.tafmec.2020.102851

CrossRef Full Text | Google Scholar

Zhang, Y., and Wong, L. N. Y. (2018). A review of numerical techniques approaching microstructures of crystalline rocks. Comput. Geosciences 115, 167–187. doi:10.1016/j.cageo.2018.03.012

CrossRef Full Text | Google Scholar

Zhao, J., Zhou, Y. X., Hefny, A. M., Cai, J. G., Chen, S. G., Li, H. B., et al. (1999). Rock dynamics research related to cavern development for Ammunition storage. Tunn. Undergr. Space Technol. 14 (4), 513–526. doi:10.1016/s0886-7798(00)00013-4

CrossRef Full Text | Google Scholar

Zhao, Y., Zhao, G-F., Jiang, Y., Elsworth, D., and Huang, Y. (2014). Effects of bedding on the dynamic indirect tensile strength of coal: Laboratory experiments and numerical simulation. Int. J. Coal Geol. 132, 81–93. doi:10.1016/j.coal.2014.08.007

CrossRef Full Text | Google Scholar

Zhu, J., Li, Y., Peng, Q., Deng, X., Gao, M., and Zhang, J. (2020). Stress wave propagation across jointed rock mass under dynamic extension and its effect on dynamic response and supporting of underground opening. Tunn. Undergr. Space Technol. 108, 103648. doi:10.1016/j.tust.2020.103648

CrossRef Full Text | Google Scholar

Zubelewicz, A., and Mroz, Z. (1983). Numerical simulation of rock burst processes treated as problems of dynamic instability. Rock Mech. Rock Eng. 16 (4), 253–274. doi:10.1007/bf01042360

CrossRef Full Text | Google Scholar