Seismic response of a mid-story-isolated structure considering soil–Structure interaction in sloping ground under three-dimensional earthquakes

A mid-story-isolated structure is developed from a base-isolated structure. Mid-story-isolated structures located in sloping ground have become a research hotspot in recent years. It is important to consider the soil–structure interaction (SSI) effects and multi-dimensional earthquakes on these structures. This paper established a model of the mid-story-isolated structure considering SSI in sloping ground. An elastic–plastic time history analysis was carried out under the one-dimensional (1D), two-dimensional (2D), and three-dimensional (3D) earthquakes. Under 3D earthquakes, the traditional 2D isolated bearing has limited damping capacity. Therefore, two kinds of 3D isolated bearings were designed. Results show that the seismic response of the mid-story-isolated structure considering SSI in sloping ground can be amplified compared with that of the mid-story-isolated structure without considering SSI. The seismic response of the structure under 3D earthquakes is more significant than that under 2D earthquakes and 1D earthquakes. For the two kinds of 3D isolated bearings, the minimum reduction rate of tensile and compressive stress is about 46% compared with that of the traditional 2D isolated bearings. When the 3D isolated bearings are used, the stress of the soil foundation decreases, which is more conducive to the stability of the soil foundation.

1 Introduction

There are many sloping ground areas in the world, some of which are also vulnerable to earthquakes. Factors affecting structures can include unstable soil foundations, deep buried bedrock, and even inclined soil foundations and earthquakes can cause significant harm to soil structures when they occur (Zhu, 2016; Xu et al., 2021). Research on energy dissipation and earthquake resistance in sloping ground is therefore significant. Yoshida et al. (2018) proposed a real-time hybrid simulation method for semi-active control using a vibration table to simulate a mid-story-isolated building. Wang et al. (2011) and Wang et al. (2013) studied the simplified three-particle model and the substructure modal of the mid-story-isolated structure. Zhang et al. (2022), Liu et al. (2022), and Gharad and Sonparote (2021) analyzed the damage to the new staggered isolated structure and found that the structure had good shock absorption performance, and the damage was slight. Chang et al. (2012) put forward the concept of BMD (building mass damper) by integrating the TMD principle into the mid-story-isolated structure. The results show that the BMD system with optimal parameters can effectively control the upper and lower reactions of the structure.

The anisotropy, complexity, and uncertainty of soil in the natural environment need to be considered when exploring soil–structure interaction theory (Li C et al., 2013). Huynh et al. (2021) proposed a simplified modeling strategy to simulate soil–foundation–structure interaction under earthquake loads. The results were verified through shaking-table tests and numerical simulation, and the numerical simulation results were in good agreement with the experimental results. Pérez-Rocha et al. (2021) studied the effect of SSI on the dynamic response of a high-rise building with the base isolated. Based on the Timoshenko theory, Gharad and Sonparote (2021) considered 3D bridge finite element analysis under three different soil foundation conditions to determine their impact factor (IF) values. This proves the importance of SSI analysis. Zhuang et al. (2014) and Zhang et al. (2019) showed that the isolated efficiency of the isolated layer will be severely weakened by the SSI effect. The property of foundation soil was from hard to soft, and its damping effect was from significant to poor. Askouni and Karabalis (2021) carried out non-linear dynamic analysis of asymmetric small low-rise 3D reinforced concrete buildings to study the effect of SSI on seismic response through structural characteristics and detailed parameters. Yang et al. (2021) studied the influence of near-fault earthquake characteristics on the seismic response of structures, including SSI energy dissipation devices. Forcellini (2021) studied a probabilistic-based approach to assessing the impact of SSI effects on buildings. Sarcheshmehpour et al. (2021) and Galal and Naimi (2008) and Nie et al. (2022) analyzed SSI effects on the seismic performance of structures with steel shear wall lateral resisting systems. Galal and Naimi (2008) studied the seismic response of frames with different layers on different soil foundations through dynamic time-history analysis. The results show that the influence of soil foundation for the frame increased with the increase in structure layers.

Actual earthquakes have multi-dimensional characteristics. To prevent and limit the effects of multi-dimensional earthquakes it is important to consider factors beyond horizontal earthquake action. Nie et al. (2022) developed a novel 3D isolated bearing that can reduce horizontal and vertical seismic responses of space double-layer cylindrical reticulated shells (SDLCRS). Zhu et al. (2021) proposed a new 3D composite isolated bearing (3D-CIB), which consists of a laminated rubber bearing and composite coil spring bearing. The results show that 3D-CIB can effectively reduce the seismic response of the superstructure in horizontal and vertical directions. Jeon et al. (2015) analyzed this through the study of the vertical seismic response and the brittleness of typical old highway bridges. The probability of severe damage caused by vertical earthquakes has increased by about 10%. Han et al. (2021) proposed a novel air spring-friction pendulum system (FPS) 3D isolated bearing. The results show that a 3D isolated bearing can effectively reduce the impact of long-period earthquakes. Shimada et al. (2005) and Tetsuya et al. (2012) developed a 3D isolated system with laminated rubber bearings as horizontal isolators and air springs as vertical isolators. Li X et al. (2013) combined the horizontal isolated bearing and vertical isolated disc spring to form a three-dimensional isolated bearing.

Few studies to date have examined the seismic response of mid-story-isolated structures, considering SSI in sloping ground. To explore this further, the present study constructed a model of a mid-story-isolated structure by considering SSI in sloping. Elastic–plastic time history analysis under 1D, 2D, and 3D earthquakes was udnertaken, and the seismic response of the mid-story-isolated structure, considering and without considering SSI were compared. To solve the problem that the tensile and compression stress of isolated bearings exceed the limit value under 3D earthquakes, two kinds of 3D isolated bearings are proposed and compared with the traditional 2D isolated bearings. The effect of the soil foundation on the structure, the working mechanism, and the mid-isolated effect of the structural system are also discussed.

2 Methods and materials

2.1 Theoretical analysis of the soil–structure interaction

In traditional seismic response analysis, the soil foundation is usually regarded as rigid, and the influence of the soil foundation on the dynamic response of structures is not considered (Galal and Naimi, 2008; Karabork et al., 2014; Abdel et al., 2015). The soil foundation material is not absolutely rigid. There is not only interaction of force but also mutual restriction of deformation between the structure and the soil foundation, which leads to mutual propagation and exchange of vibration energy, meaning the dynamic response of the actual structure is quite different from that calculated under the assumption of a rigid soil foundation. In sloping ground, the SSI effect has particularities and the height and properties of the soil foundation on both sides of the structure may be different. The SSI effect on sloping ground is different from that in flat ground.

The 3D soil–structure system equation of structural dynamics is shown in Formula 1 (Tabatabaiefar and Massumi, 2010; Yang et al., 2022):

$M\ddot{X}\left(\mathrm{t}\right)+C\dot{X}\left(\mathrm{t}\right)+KX\left(\mathrm{t}\right)=-m_x{\ddot{v}}_x\left(\mathrm{t}\right)-m_y{\ddot{v}}_y\left(\mathrm{t}\right)-m_z{\ddot{v}}_z\left(\mathrm{t}\right),(1)$

where $M$ is the mass matrix; $C$ is the damping matrix; $K$ is the stiffness matrix; and $X\left(t\right)$, $\dot{X}\left(t\right)$, and $\ddot{X}\left(t\right)$ are displacement, velocity, and acceleration vectors, respectively. $m_x$, $m_y$, and $m_z$ are mass in X, Y, and Z directions, respectively. ${\ddot{v}}_x\left(\mathrm{t}\right)$, ${\ddot{v}}_y\left(\mathrm{t}\right)$, and ${\ddot{v}}_z\left(\mathrm{t}\right)$ are free-field components of the acceleration in X, Y, and Z directions, respectively.

2.2 Engineering situations

The total height of the nine-story frame structure was 34.9 m with a rectangular plane of 24 m×18 m. The bottom story's height was 4.5 m, and the height of the other stories was 3.6 m. The designed earthquake acceleration was .20 g, and the isolated layer was set at the bottom of the second floor. The beams, columns, and plates were C40, and the foundation was C40. The steel reinforcement of the structure was HRB400, and the reinforced steel stirrup was HPB300.

2.3 Model establishment

Finite element software SAP2000 was used to establish a mid-story-isolated structure considering SSI in sloping ground (Gu et al., 1999; Pala et al., 2008; Institute CBSD, 2012; Shang et al., 2012; Karabork et al., 2014; Jiang et al., 2018; Huang et al., 2020a). Solid elements were used to simulate the soil foundation, and the Mohr–Coulomb model was adopted. The plane size of the soil foundation element was 240 m×180 m, which was ten times the structure size. The soil foundation was connected with rigid bedrock at the bottom and simulated by fixed hinge bearings. Table 1 shows the parameters of the soil foundation. The frame and soil were connected by a raft foundation. A non-linear linking damper element was used to simulate the artificial viscoelastic boundary at the soil foundation edge (Wolf, 1986; Liu and Lv, 1998; Givoli, 2004; Liu et al., 2005; Liu et al., 2006; Kouroussis et al., 2011; Haider et al., 2019). The artificial boundary parameters are shown in Table 2.

TABLE 1

TABLE 1. Parameters of the soil foundation layer.

TABLE 2

TABLE 2. Damping parameter of the artificial boundary.

The beam element was used to simulate the frame structure, and the shell element was used to simulate the floor. Rayleigh damping was applied to the structure with a damping coefficient of 5%. The calculation formula is shown as follows (Jiménez and Dias, 2022):

$C=\alpha \left[M\right]+\beta \left[K\right],(2)$

where $C$ is the damping matrix; $M$ and $K$ are the mass and stiffness matrices; and $\alpha$ and $\beta$ are the mass-proportional and stiffness-proportional damping constants, respectively.

The elevation of the frame structure is shown in Figure 1. The detailed parameters of the structure are shown in Table 3 and Table 4. The size and type of isolated bearings are estimated based on the vertical reaction of 2%. Detailed information on the isolated bearings is shown in Table 5. The layout and the simplified mechanical model of isolated bearings are shown in Figure 2.

FIGURE 1

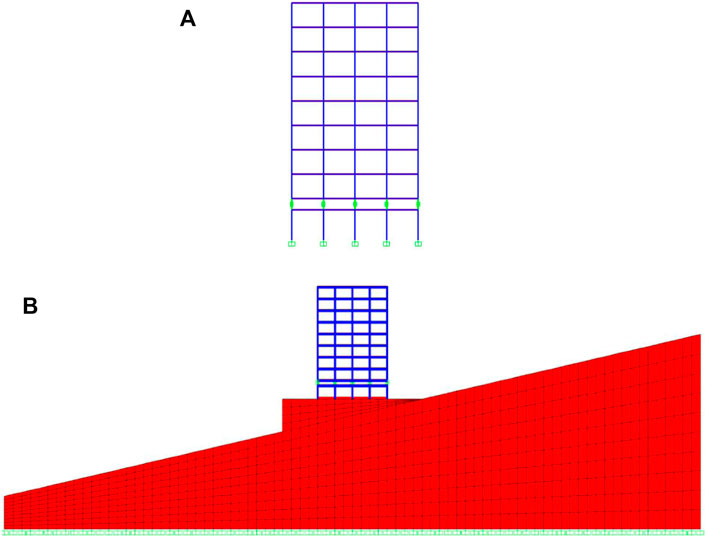
FIGURE 1. Model elevation. (A) Vertical plane of the mid-story-isolated structure. (B) Vertical plane of the mid-story-isolated structure considering the soil–structure interaction (SSI) in sloping ground.

TABLE 3

TABLE 3. Information of the frame.

TABLE 4

TABLE 4. Parameters of the material.

TABLE 5

TABLE 5. Design parameters of isolated bearings.

FIGURE 2

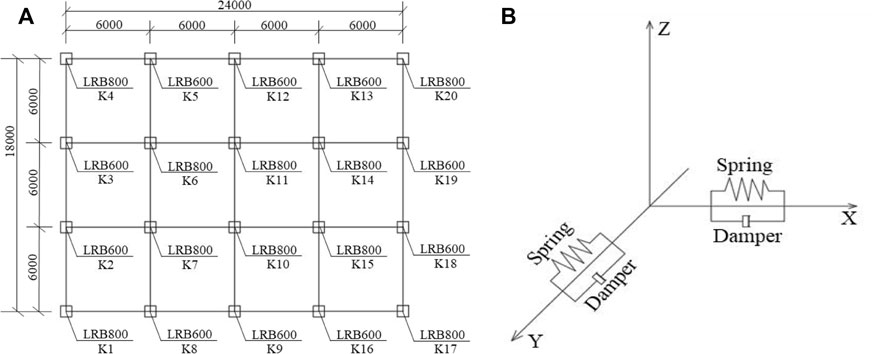
FIGURE 2. Isolated bearings. (A) Layout of isolated bearings. (B) Simplified mechanical model of the isolated bearing.

2.4 Selection of earthquakes

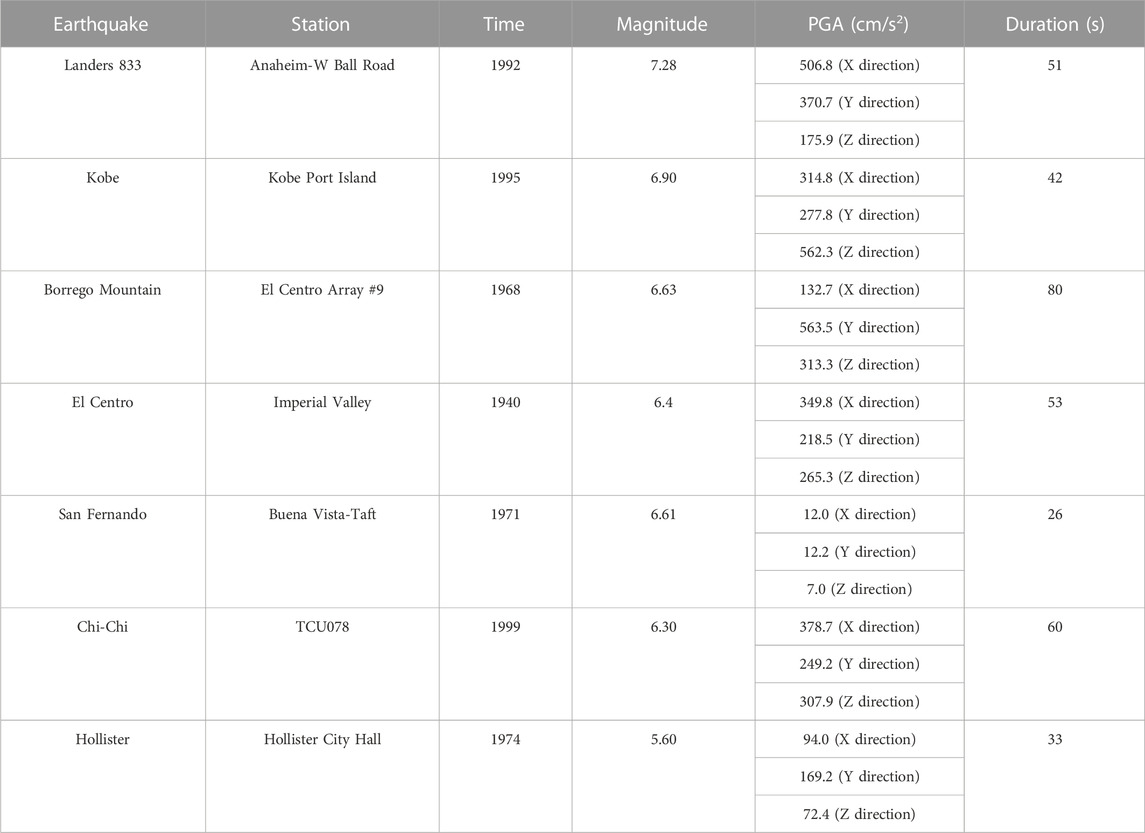
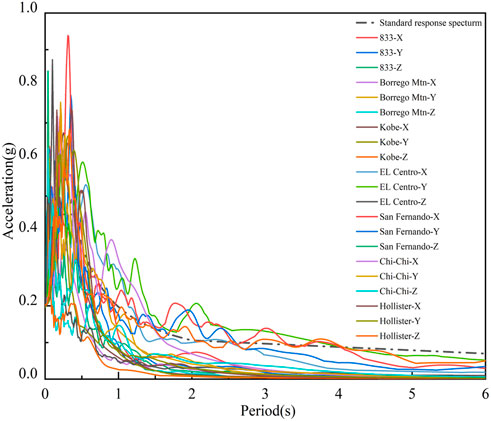
In this paper, the Borrego Mountain wave, Landers 833 wave, Kobe wave, El Centro wave, San Fernando wave, Chi-Chi wave, and Hollister wave were selected from the PEER website. The earthquakes are input in 1D, 2D, and 3D directions, and the proportional coefficients of the three directions are adjusted as X: Y: Z=1: .85: .65. According to the Code for Seismic Design of Buildings (GB 50011-2016) (Standard, 2010), the peak ground acceleration (PGA) was adjusted to 400 cm/s². Figure 3 shows the acceleration response spectrum of the earthquakes. Details of earthquakes are shown in Table 6.

TABLE 6

TABLE 6. Parameters of earthquakes.

FIGURE 3

FIGURE 3. Earthquake response spectrum.

3 Results of traditional 2D mid-story-isolated structural analysis

The seismic response of the structure was analyzed under the Landers 833 wave, Borrego Mountain wave, Kobe wave, El Centro wave, San Fernando wave, Chi-Chi wave, and Hollister wave. The envelope values of the seven earthquakes are used in the subsequent analysis.

3.1 Horizontal seismic response analysis of the structure under multi-dimensional earthquakes

3.1.1 Horizontal seismic response of the global structure

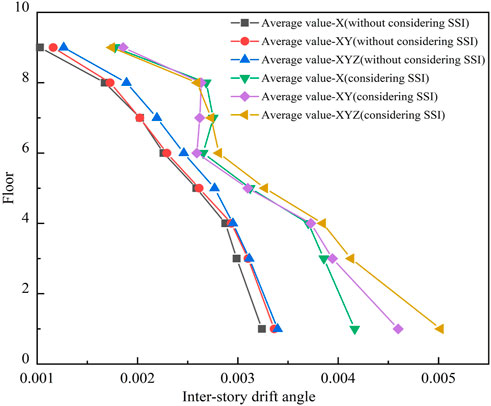
The inter-story drift angle of the structure is shown in Figure 4. It can be seen from the figure that the inter-story drift angle of the mid-story-isolated structure considering SSI in sloping ground can be amplified compared with that of the mid-story-isolated structure without considering SSI. The order of the inter-story drift angle under multi-dimensional earthquakes is 3D > 2D > 1D.

FIGURE 4

FIGURE 4. Inter-story drift angle of the structure.

One reason for this is that earthquakes reflect in the mountain in the process of transmission. Therefore, earthquakes converge and overlap locally on the mountain, resulting in an increased seismic response of buildings in sloping ground. Another reason is that the wavelength component of the earthquake is coupled with the size of the terrain. Therefore, the dynamic effect of the earthquake is amplified in sloping ground, which can cause serious damage to the structure. At the same time, the Code for Seismic Design of Buildings (GB 50011-2016) and Assimaki and Kausel (2007) also mentioned that the seismic response in mountainous and sloping areas needs to be multiplied by the corresponding amplification.

3.1.2 Horizontal seismic response of the isolated bearings

Table 7 shows the displacement of the isolated bearings. According to the “Code for Seismic Design of Buildings” (GB 50011-2016), the maximum horizontal displacement of the isolated bearings under earthquakes should not exceed the smaller value of .55 times the diameter of the isolated bearings and three times the total thickness of the rubber layer.

$u_{\max }=600\times 0.55=330\mathrm{m}\mathrm{m}.(3)$

TABLE 7

TABLE 7. Maximum displacement of isolated bearings.

It can be seen from Table 7 that the displacement of the isolated bearings does not exceed the limit value of 330 mm. The displacement of the isolated bearings of the mid-story-isolated structure without considering SSI is smaller than that of the mid-story-isolated structure considering SSI in sloping ground. The displacement of the isolated bearings in the X direction is smaller than that in the XY direction and more minor than that in the XYZ direction.

3.2 Vertical seismic response analysis of the structure under multi-dimensional earthquakes

The tensile and compressive stress values of the isolated bearing of the two structures under multi-dimensional earthquakes were extracted and are shown in Figure 5. The number of isolated bearings is shown in Figure 2A.

FIGURE 5

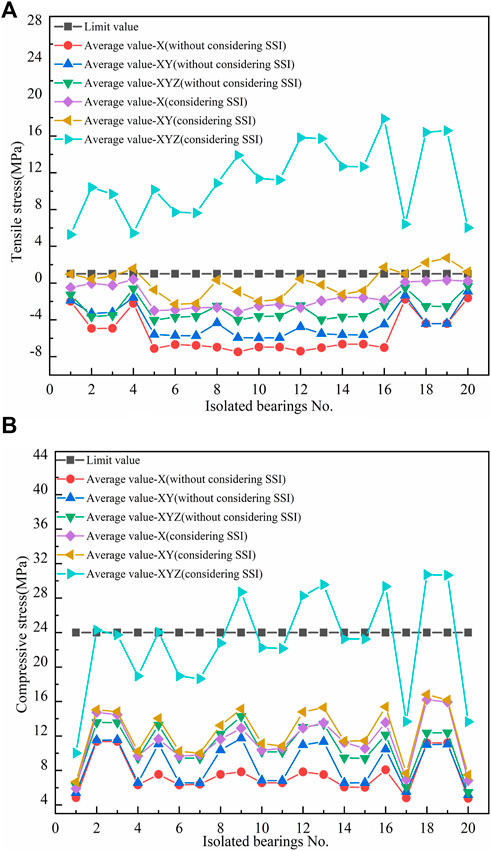
FIGURE 5. Stress of isolated bearings. (A) Tensile stress of isolated bearings. (B) Compressive stress of isolated bearings.

The tensile stress of the isolated bearings of the mid-story-isolated structure is shown in Figure 5A, and the tensile stress limit value is 1 MPa. As can be seen from Figure 5A, the tensile stress of the isolated bearings of the mid-story-isolated structures considering SSI in sloping ground is greater than that of the mid-story-isolated structures without considering SSI. The order of the tensile stress of the isolated bearings under multi-dimensional earthquakes is 3D > 2D > 1D. The tensile stress of the isolated bearings of the mid-story-isolated structure considering SSI in sloping ground all exceeds the limit value under 3D earthquakes. The tensile stress of some isolated bearings exceeds the limit value under 2D earthquakes. The maximum tensile stress of the isolated bearing of the mid-story-isolated structure without considering SSI is -.331 MPa, which is still in the range of compressive stress.

The compressive stress of the isolated bearings of the mid-story-isolated structure is shown in Figure 5B, and the compressive stress limit value is 24 MPa. It can be seen from Figure 5B that the compressive stress of the isolated bearings of the mid-story-isolated structure considering SSI in sloping ground is greater than that of the mid-story-isolated structure without considering SSI. The order of compressive stress of isolated bearings under multi-dimensional earthquakes is 3D > 2D > 1D. The compressive stress of some isolated bearings of mid-story-isolated structure considering SSI in sloping ground under 3D earthquakes is beyond the limit value. The compressive stress of the isolated bearings of the mid-story-isolated structure without considering SSI is smaller than 24 MPa under 1D, 2D, and 3D earthquakes.

In conclusion, the seismic response of a mid-story-isolated structure considering SSI in sloping ground can be amplified compared to that of a mid-story-isolated structure without considering SSI. Three-dimensional earthquakes will increase the tensile and compressive stresses of the isolated bearings, which has a negative effect. Therefore, the influence of 3D earthquakes should be considered in structural design.

4 Results of the 3D mid-story-isolated structural analysis

4.1 Theoretical basis of 3D isolated bearings

In order to solve the problem that the traditional 2D isolated bearing cannot meet the requirements under 3D earthquakes, two kinds of 3D isolated bearings are proposed: vertical and horizontal isolated devices. The 3D isolated device must have good vertical bearing capacity and self-recovery capacity. The vertical device must meet the assumption of small deformation, and the device should work in the elastic range as far as possible and should be able to self-recover after the earthquakes.

At present, 3D isolated bearings are mainly divided into three categories: rubber 3D isolated bearing, metal spring 3D isolated bearing, and combined 3D isolated bearing. In this paper, two different 3D isolated bearings are used. The first one is the 3D lead–rubber isolated bearings (3D LRBs), which adjust the vertical stiffness to reduce the vertical earthquake. The second is the tensile and compressive friction pendulum bearings (T/C FPBs). The vertical stiffness of the 3D isolated bearing is calculated by the vertical force of the earthquake. It is assumed that the stiffness of the 3D isolated bearing is uncoupled in the horizontal and vertical directions (Li C et al., 2013; Liang et al., 2022).

The design parameters of two 3D isolated bearings are shown in Table 8 and Table 9. Figure 6A shows the simplified mechanical model of a 3D isolated bearing. Figure 6B and Figure 6C show the layout of the two 3D isolated bearings.

TABLE 8

TABLE 8. Design parameters of 3D LRB isolated bearing.

TABLE 9

TABLE 9. Design parameters of the 3D T/C FPB isolated bearing.

FIGURE 6

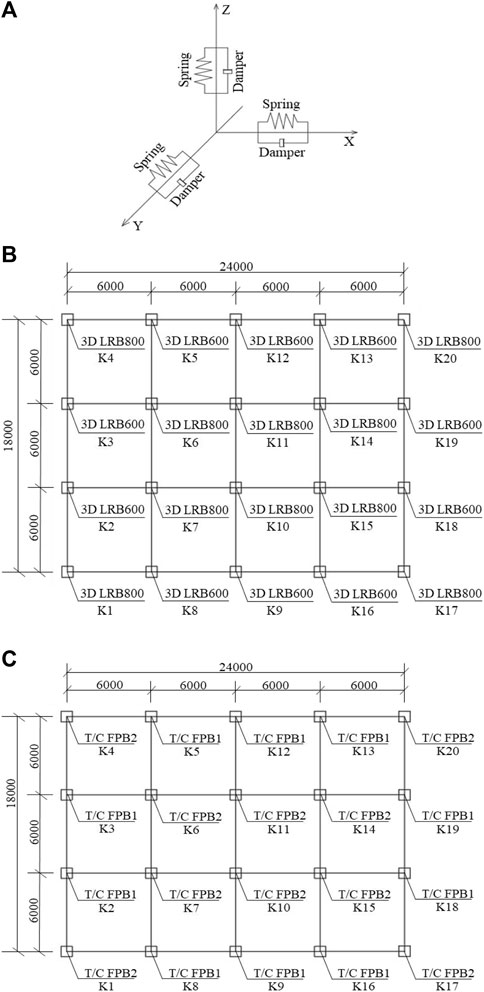
FIGURE 6. Layout of 3D isolated bearings. (A) Simplified mechanical model of the 3D isolated bearing. (B) Layout of the 3D LRB isolated bearings. (C) Layout of the 3D T/C FPB isolated bearings.

4.2 Structural modal periods comparison

Modal analysis was carried out on the two 3D mid-story-isolated structures considering SSI in sloping ground and the traditional 2D mid-story-isolated structure considering SSI in sloping ground. The first three modal periods are shown in Table 10. It can be seen from the table that the modal periods of the mid-story-isolated structure with 3D isolated bearings are more significant than those of the mid-story-isolated structure with traditional 2D isolated bearings. The results show that the 3D mid-story-isolated structure considering SSI in sloping ground is more flexible than the traditional 2D mid-story-isolated structure considering SSI in sloping ground, and the modal periods of the structure are further prolonged.

TABLE 10

TABLE 10. First three modal periods of structures.

4.3 Horizontal seismic response analysis of the structure under 3D earthquakes

4.3.1 Horizontal seismic response of the global structure

When 3D isolated bearings are used, not only the vertical damping effect of the structure should be paid attention to, but also the horizontal damping effect of the structure cannot be ignored. The elastic limit value ${\theta }_w=1/550$ and elastic–plastic limit value ${\theta }_d=1/50$ of the maximum inter-story drift angle, as specified in the Code for Seismic Design of Buildings (GB 50011-2016), is used as the limit value of the inter-story drift angle under the condition of without damage and destruction. At the same time, the limit values of inter-story drift angle 2 ${\theta }_w$ and 4 ${\theta }_w$ are defined as medium damage and severe damage. The five failure modes of the structure are divided according to the limit values of four inter-story drift angles, as shown in Table 11. Figure 7 shows the inter-story drift angle of the structure with three different isolated bearings.

FIGURE 7

FIGURE 7. Inter-story drift angle of the structure.

TABLE 11

TABLE 11. Limit of the inter-story drift angle ratio.

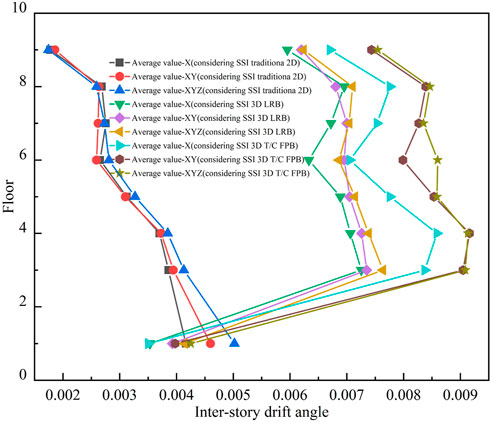
Figure 7shows that the inter-story drift angle of the bottom story using 3D isolated bearings is smaller than that of the traditional 2D isolated structure under 1D, 2D, or 3D earthquakes. From the isolated layer and above, the inter-story drift angle of the 3D mid-story-isolated structure is more significant than that of the 2D mid-story-isolated structure. The traditional 2D maximum inter-story drift angle is within the medium damage range. Only one point of the maximum inter-story drift angle of 3D LRB exceeds the medium damage range. Most of the inter-story drift angles of 3D T/C FPB are within the severe damage range. The inter-story drift angle of the three structures is less than .02, which has not reached the destruction stage. The inter-story drift angle of 3D LRB is smaller than that of 3D T/C FPB. This is due to the different types of 3D isolated bearings produced using different materials.

4.3.2 Horizontal seismic response of the isolated bearings

It can be seen from Table 12 that the displacement of the isolated bearings does not exceed the limit value of 330 mm. The displacement of the isolated bearings of the 3D mid-story-isolated structure considering SSI in sloping ground is smaller than that of the traditional 2D mid-story-isolated structure considering SSI in sloping ground. The displacement of the isolated bearings of the 3D LRB mid-story-isolated structure considering SSI in sloping ground is smaller than that of the 3D T/C FPB mid-story-isolated structure considering SSI in sloping ground. The displacement of the isolated bearings of the three structures in the X direction is smaller than that in the XY direction and more minor than that in the XYZ direction.

TABLE 12

TABLE 12. Maximum displacement of isolated bearings.

4.4 Vertical seismic response analysis of the structure under 3D earthquakes

4.4.1 Stress comparison of isolated bearings

Based on the previous analysis, the tensile and compressive stress of the traditional 2D isolated bearings will exceed the limit value under 3D earthquakes. This paper extracts the maximum tensile and compressive stress of two kinds of 3D isolated bearings, as shown in Figure 8. The tensile stress limit value is 1 MPa, and the compressive stress limit value is 24 MPa.

FIGURE 8

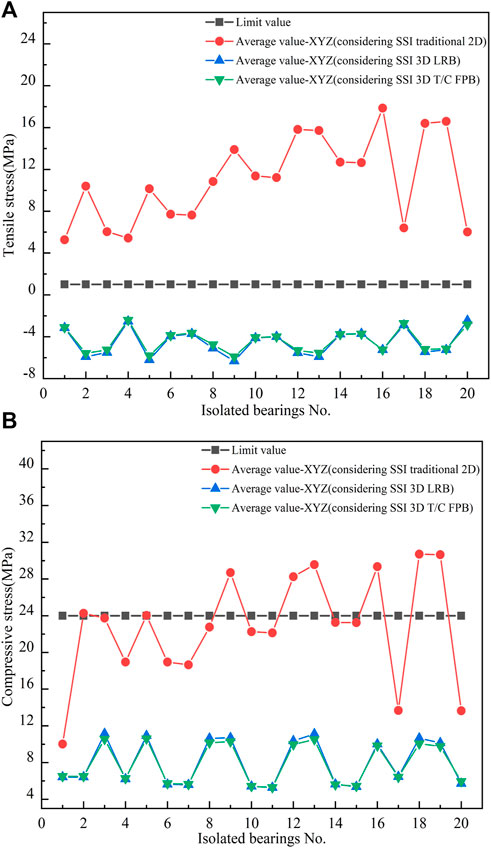
FIGURE 8. Stress of isolated bearings. (A) Tensile stress of isolated bearings. (B) Compressive stress of isolated bearings.

It can be seen from Figure 8 that the maximum tensile stress of the isolated bearings in traditional 2D mid-story-isolated structures considering SSI in sloping ground is far beyond the limit value. The maximum tensile stress of the isolated bearing of the 3D mid-story-isolated structure considering SSI in sloping ground is -2.45 MPa, which is less than the limit value and standard requirements. The maximum compressive stress of the isolated bearing of the 3D mid-story-isolated structure considering SSI in sloping ground is 11.15 MPa, which is lower than the limit value.

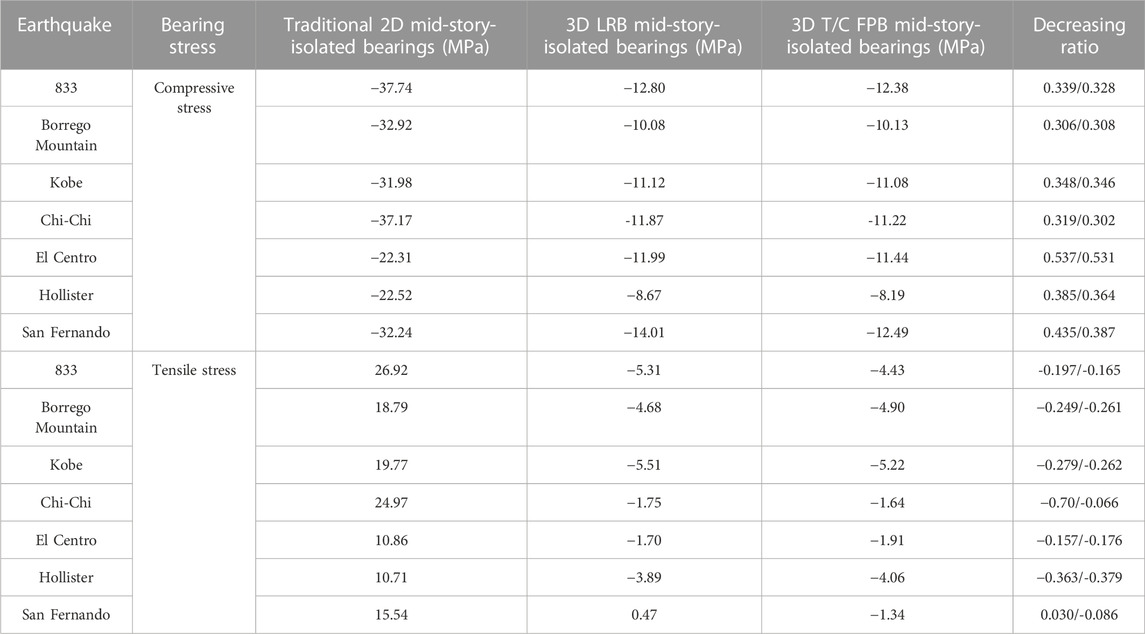
Table 13 shows the maximum stress reduction rate of the two kinds of 3D isolated bearings. It can be seen from Table 13 that the 3D mid-story-isolated bearings can effectively solve the stress overload problem of the traditional 2D isolated bearing and achieve the expected effect of structural shock absorption. For the two kinds of 3D isolated bearings, the minimum reduction rate of tensile and compressive stress is about 46%.

TABLE 13

TABLE 13. Decreasing rate of 3D isolated bearings.

4.4.2 Comparison of vertical acceleration

Figure 9 shows the comparison of story accelerations in the vertical direction. It can be seen from Figure 9 that the 3D mid-story-isolated structure considering SSI in sloping ground can significantly reduce the vertical story accelerations except for the isolated layer. The performance of 3D LRB is better.

FIGURE 9

FIGURE 9. Vertical acceleration comparison of structural floors.

4.5 Torsion effect of structure

The soil foundation is asymmetric and irregular in the transverse slope direction, which is easy to cause a structural torsion effect. The current standards have not put forward a suitable limit value for the torsion angle, so the research work from this aspect needs to be further studied. In order to ensure the safety of the structure, the torsion effect of the structure should not be too larger under earthquakes.

The calculation diagram of the structural torsion angle is shown in Figure 10A. The torsion angle of the traditional 2D mid-story-isolated structure considering SSI in sloping ground and the 3D mid-story-isolated structure considering SSI in sloping ground is shown in Figure 10B. The structural torsion angle is calculated as shown in Formula 4 (Jia et al., 2016; Wang et al., 2020; Xu et al., 2022).

${\theta }_{\mathrm{i}}=\frac{{△}_1-{△}_2}{l},(4)$

where ${△}_1$, ${△}_2$ are the displacement of the corner column relative to the initial structure and $l$ is the distance between the corresponding corner columns of the structure, which is taken as 18 m in this paper.

FIGURE 10

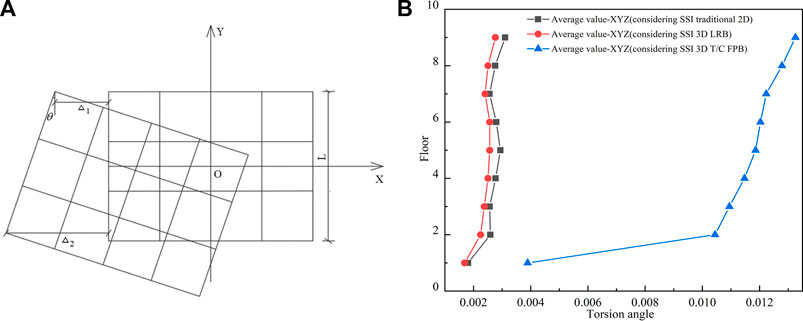
FIGURE 10. Torsion angle of the structure. (A) Calculation schematic diagram of the structural torsion angle. (B) Torsion angle.

As can be seen from Figure 10B, the torsion angle of the 3D LRB mid-story-isolated structure considering SSI in sloping ground is smaller than that of the traditional 2D mid-story-isolated structure considering SSI in sloping ground. The torsion angle of the 3D T/C FPB mid-story-isolated structure considering SSI in sloping ground is more significant than that of the traditional 2D mid-story-isolated structure considering SSI in sloping ground. The torsion angle of the two kinds of the 3D isolated bearing is different, and the performance of 3D LRB is better.

4.6 Structure stress analysis

Figure 11 shows the stress of a 3D mid-story-isolated structure considering SSI in sloping ground and the traditional 2D mid-story-isolated structure considering SSI in sloping ground. It can be seen from the figure that the stress of 3D mid-story-isolated structures considering SSI in sloping ground is significantly reduced compared with that of the traditional 2D mid-story-isolated structure considering SSI in sloping ground. The structural stress of the two 3D mid-story-isolated structures considering SSI in sloping ground is similar.

FIGURE 11

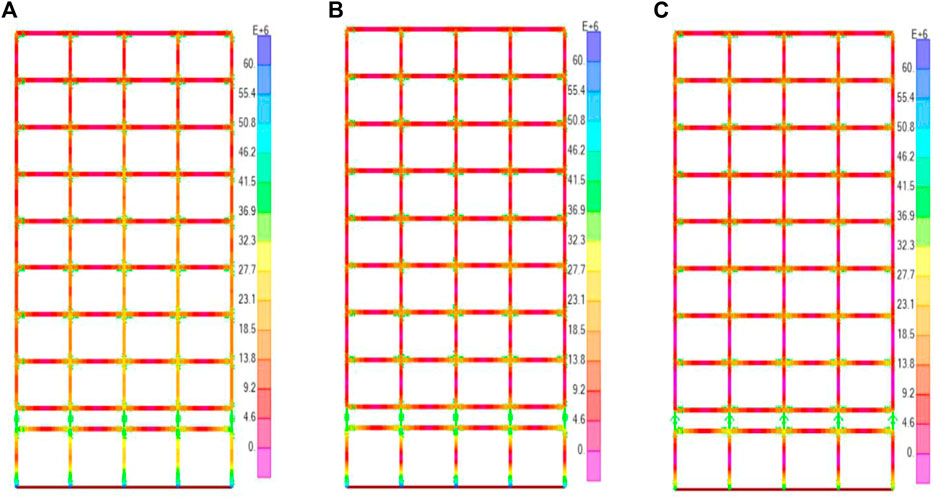
FIGURE 11. Stress of the structure (N/m²). (A) Traditional 2D isolated structure. (B) 3D LRB mid-story-isolated structure. (C) 3D T/C FPB mid-story-isolated structure.

4.7 Soil foundation stress comparison

The stress of the soil foundation is a critical evaluation index. Figure 12 shows the maximum stress of the soil foundation of the mid-story-isolated structure considering SSI in sloping ground under 3D earthquakes. It can be seen from Figure 12 that the stress near the soil foundation of the structure with 3D isolated bearings is smaller than that with the traditional 2D isolated bearing. This is because the vertical spring of the 3D isolated bearings can effectively reduce the vertical earthquake.

FIGURE 12

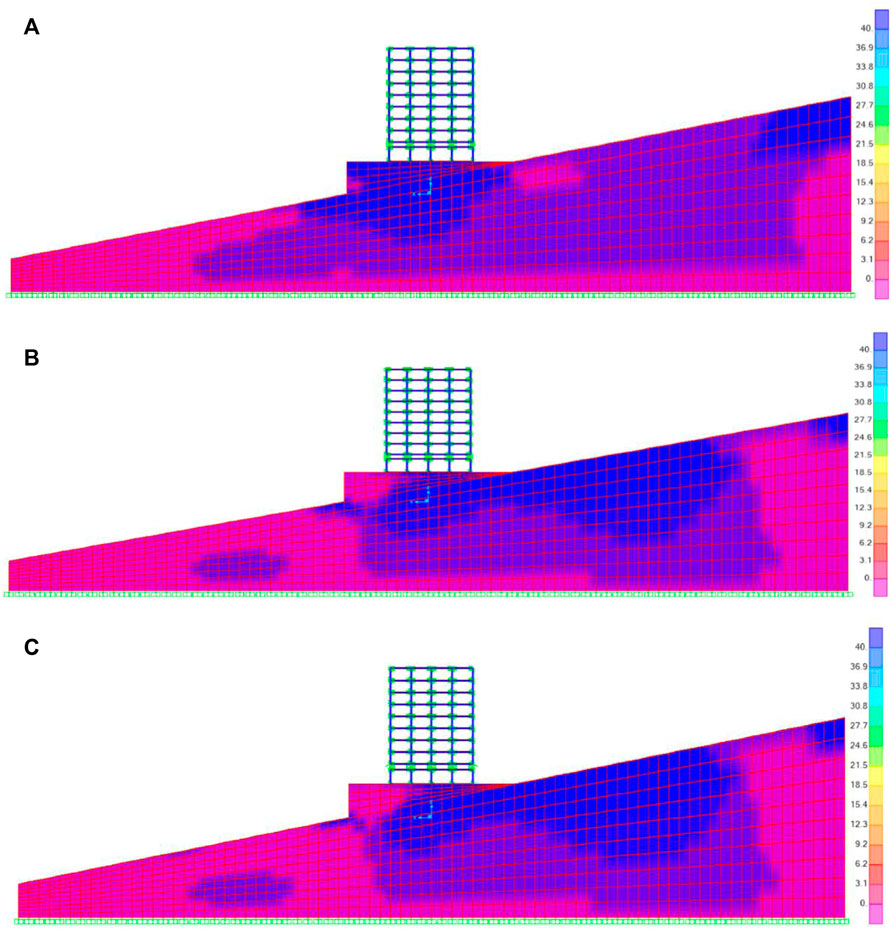
FIGURE 12. Stress of the soil foundation (N/m²). (A) Traditional 2D mid-story-isolated structure. (B) 3D LRB mid-story-isolated structure. (C) 3D T/C FPB mid-story-isolated structure.

5 Discussion

In this paper, the seismic responses of a mid-story-isolated structure without considering SSI and a mid-story-isolated structure considering SSI in sloping ground are studied under 3D earthquakes. However, this paper mainly focuses on a numerical analysis of two kinds of mid-story-isolated structures (Loh et al., 2013; Nakamizo and Koitabashi, 2018). The finite element verification results exhibit some deviation in various parameter settings. Shaking table tests should be added to verify the results of this study (Benavent-Climent et al., 2018; Choi et al., 2022).

The results show that the mid-story-isolated structure considering SSI in sloping ground further amplifies seismic responses. One reason is that earthquakes will reflect in the mountain in the process of transmission. Therefore, earthquakes converge and overlap locally on the mountain, resulting in an increased seismic response of buildings in sloping ground. Another reason is that the wavelength component of the earthquake is coupled with the size of the terrain. Therefore, the dynamic effect of the earthquake is amplified in sloping ground, which can cause serious damage to the structure. (Xiao et al., 2018).

The SSI effect is complicated due to the massive difference in mechanical properties. The research on the mechanism, theory, and method of the static and dynamic SSI effect has a big gap with the practical engineering application (Mylonakis and Gazetas, 2000; Kausel, 2010; Lou et al., 2011; Anand and Kumar, 2018; Huang, et al., 2020b; Chang et al., 2020). In the finite element simulation of the SSI effect, parameters such as water content, porosity, and liquefaction of the soil foundation should be further considered to reflect the more real impact of the SSI effect (Oñate et al., 2011; von Estorff and Kausel, 1989; Huang et al., 2020c). Permafrost exists in nature and should be further considered in finite element simulation. The mechanism of the torsional effect of the soil foundation should be further explored (Nazarimofrad and Zahrai, 2016; Vicencio and Alexander, 2019; Terzi and Athanatopoulou, 2023).

In order to reduce the impact of the 3D earthquake on the building structure, two different isolated bearings are used in the research. The effects of two kinds of isolated bearings on the structure and the soil foundation are analyzed. The energy dissipation capacity of the vertical earthquake set on the 3D isolated bearing can be further enhanced compared with that on the traditional 2D isolated bearings. At the same time, the influence of different parameters of the vertical damper on the 3D isolated bearing should be further analyzed (Li et al., 2021; Yip et al., 2022). The coupling behavior of 3D isolated bearing stiffness in horizontal and vertical directions should be further considered.

In this study, many numerical analysis results are obtained, and the numerical analysis results are discussed. The structure’s damage index (Park and Ang, 1985) and the isolated bearing damage index (Du et al., 2016) need to be further discussed in the following research.

6 Conclusion

In this paper, finite element software was used to establish the mid-story-isolated structure considering the SSI effect in sloping ground. An elastic–plastic time history analysis under earthquakes was carried out to obtain the seismic response. In order to reduce the damage caused by multi-dimensional earthquakes, the finite element modeling of two kinds of 3D isolated bearings is proposed. The conclusions are listed as follows:

1) The seismic response of the mid-story-isolated structure considering SSI in sloping ground can be amplified compared with that of the mid-story-isolated structure without considering SSI. The seismic response of the structure under 3D earthquakes is more significant than that under 2D and 1D earthquakes. Under 3D earthquakes, the tensile and compressive stress of the isolated bearings exceeds the limit value, which leads to the failure of the isolated bearings and the instability and overturning of the structure.

2) The 3D isolated bearings can effectively reduce the tensile and compression stress of the isolated bearings, and the structure has good vertical and horizontal earthquake absorption performance. The performance of 3D LRB is better than that of the 3D T/C FPB. For the two kinds of 3D isolated bearings, the minimum reduction rate of tensile and compressive stress is about 46% compared with that of the traditional 2D isolated bearings. However, the 3D T/C FPB has some defects in controlling the torsional effect of the structure.

3) The soil stress of the 3D isolated bearings is reduced compared with that of the 2D isolated bearings. This study provides a basis for the reinforcement and reconstruction of structures under multi-dimensional earthquakes.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

FW, DL, CL, and SY contributed to the conception and design of the study. FW wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel, R. S. E., Ahmed, M. M., and Alazrak, T. M. (2015). Evaluation of soil-foundation-structure interaction effects on seismic response demands of multi-story MRF buildings on raft foundations. Sci. Inf. Database 11, 11–30. doi:10.1007/s40091-014-0078-x

CrossRef Full Text | Google Scholar

Anand, V., and Kumar, S. S. (2018). Seismic soil-structure interaction: A state-of-the-art review. Structures 16, 317–326. doi:10.1016/j.istruc.2018.10.009

CrossRef Full Text | Google Scholar

Askouni, P. K., and Karabalis, D. L. (2021). SSI influence on the seismic response of asymmetrical small, low-rise R/C buildings. Structures 32, 1355–1373. doi:10.1016/j.istruc.2021.03.073

CrossRef Full Text | Google Scholar

Assimaki, D., and Kausel, E. (2007). Modified topographic amplification factors for a single-faced slope due to kinematic soil-structure interaction. J. Geotechnical Geoenvironmental Eng. 133, 1414–1431. doi:10.1061/(asce)1090-0241(2007)133:11(1414)

CrossRef Full Text | Google Scholar

Benavent-Climent, A., Ramírez-Márquez, A., and Pujol, S. (2018). Seismic strengthening of low-rise reinforced concrete frame structures with masonry infill walls: Shaking-table test. Eng. Struct. 165, 142–151. doi:10.1016/j.engstruct.2018.03.026

CrossRef Full Text | Google Scholar

Chang, K., Hwang, J., and Wang, S. (2012). “Seismic behavior of structures with building mass damper design,” in Proceedings of the 15th World Conference on Earthquake Engineering, International Convention Center, Lisbon, Portugal, September 24–28.

Google Scholar

Chang, Z., Du, Z., Zhang, F., Huang, F., Chen, J., Li, W., et al. (2020). Landslide susceptibility prediction based on remote sensing images and GIS: Comparisons of supervised and unsupervised machine learning models. Remote Sens. 12, 502. doi:10.3390/rs12030502

CrossRef Full Text | Google Scholar

Choi, Y., Park, D., Kim, S., and Hong, J. W. (2022). Seismic performance of crack-damaged masonry wall structures via shaking table tests. Structures 45, 2272–2291. doi:10.1016/j.istruc.2022.09.120

CrossRef Full Text | Google Scholar

Du, D., Wang, S., and Liu, W. (2016). Reliability-based damage performance of base-isolated structures. J. Vib. Shock 35, 222–227. doi:10.13465/j.cnki.jvs.2016.01.035

CrossRef Full Text | Google Scholar

Forcellini, D. (2021). Analytical fragility curves of shallow-founded structures subjected to Soil-Structure Interaction (SSI) effects. Soil Dyn. Earthq. Eng. 141, 106487. doi:10.1016/j.soildyn.2020.106487

CrossRef Full Text | Google Scholar

Galal, K., and Naimi, M. (2008). Effect of soil conditions on the response of reinforced concrete tall structures to near-fault earthquakes. Struct. Des. Tall Special Build. 17, 541–562. doi:10.1002/tal.365

CrossRef Full Text | Google Scholar

Gharad, A. M., and Sonparote, R. S. (2021). Evaluation of vertical impact factor coefficients for continuous and integral railway bridges under high-speed moving loads. Earthq. Eng. Eng. Vib. 20, 495–504. doi:10.1007/s11803-021-2034-7

CrossRef Full Text | Google Scholar

Givoli, D. (2004). High-order local non-reflecting boundary conditions: A review. Wave Motion 39, 319–326. doi:10.1016/j.wavemoti.2003.12.004

CrossRef Full Text | Google Scholar

Gu, Y., Zhang, H., Guan, Z., Kang, Z., Li, Y., and Zhong, W. (1999). New generation software of structural analysis and design optimization-JIFEX. Struct. Eng. Mech. Int. J. 7, 589–599. doi:10.12989/sem.1999.7.6.589

CrossRef Full Text | Google Scholar

Haider, A., Song, E., and Li, P. (2019). Numerical simulation and absorbing boundary conditions for wave propagation in a semi-infinite media with a linear isotropic hardening plastic model. Soil Dyn. Earthq. Eng. 125, 105627. doi:10.1016/j.soildyn.2019.04.001

CrossRef Full Text | Google Scholar

Han, Q., Jing, M., Lu, Y., and Liu, M. (2021). Mechanical behaviors of air spring-FPS three-dimensional isolation bearing and isolation performance analysis. Soil Dyn. Earthq. Eng. 149, 106872. doi:10.1016/j.soildyn.2021.106872

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Guo, J., and Jiang, S. H. (2020a). Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 191, 104580. doi:10.1016/j.catena.2020.104580

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Jiang, S., Zhou, C., Huang, J., and Guo, Z. (2020b). Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 17, 2919–2930. doi:10.1007/s10346-020-01473-9

CrossRef Full Text | Google Scholar

Huang, F., Zhang, J., Zhou, C., Wang, Y., Huang, J., and Zhu, L. (2020c). A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 17, 217–229. doi:10.1007/s10346-019-01274-9

CrossRef Full Text | Google Scholar

Huynh, V. Q., Nguyen, T. K., and Nguyen, X. H. (2021). Seismic analysis of soil-structure interaction: Experimentation and modeling. Geomechanics Eng. 27, 115–121.

Google Scholar

Institute CBSD (2012). SAP2000 Chinese version usage guide. Beijing, China: China Communications Press.

Google Scholar

Jeon, J., Shafieezadeh, A., Lee, D. H., Choi, E., and DesRoches, R. (2015). Damage assessment of older highway bridges subjected to three-dimensional ground motions: Characterization of shear-axial force interaction on seismic fragilities. Eng. Struct. 87, 47–57. doi:10.1016/j.engstruct.2015.01.015

CrossRef Full Text | Google Scholar

Jia, Y. G., Wu, G. Y., Liu, L., and Yang, Z. J. (2016). Nonlinear simulation analysis on resistant-lateral stiffness and structure torsion effect of asymmetric arrangement RC frame-shear structure. Rev. Téc. Ing. Univ. Zulia 39, 365–377. doi:10.21311/001.39.5.47

CrossRef Full Text | Google Scholar

Jiang, S., Huang, J., Huang, F., Yang, J., Yao, C., and Zhou, C. B. (2018). Modelling of spatial variability of soil undrained shear strength by conditional random fields for slope reliability analysis. Appl. Math. Model. 63, 374–389. doi:10.1016/j.apm.2018.06.030

CrossRef Full Text | Google Scholar

Jiménez, G. A. L., and Dias, D. (2022). Dynamic soil-structure interaction effects in buildings founded on vertical reinforcement elements. CivilEng 3, 573–593. doi:10.3390/civileng3030034

CrossRef Full Text | Google Scholar

Karabork, T., Deneme, I. O., and Bilgehan, R. P. (2014). A comparison of the effect of SSI on base isolation systems and fixed-base structures for soft soil. Geomechanics Eng. 7, 87–103. doi:10.12989/gae.2014.7.1.087

CrossRef Full Text | Google Scholar

Kausel, E. (2010). Early history of soil-structure interaction. Soil Dyn. Earthq. Eng. 30, 822–832. doi:10.1016/j.soildyn.2009.11.001

CrossRef Full Text | Google Scholar

Kouroussis, G., Verlinden, O., and Conti, C. (2011). Finite-dynamic model for infinite media: Corrected solution of viscous boundary efficiency. J. Eng. Mech. 137, 509–511. doi:10.1061/(asce)em.1943-7889.0000250

CrossRef Full Text | Google Scholar

Li, C., Liu, W., and Wang, S. (2013). Shaking table test on high-rise isolated structure on soft soil foundation. J. Build. Struct. 34, 72. doi:10.14006/j.jzjgxb.2013.07.011

CrossRef Full Text | Google Scholar

Li, S., Xiang, P., Wei, B., Zuo, C., Jiang, L., and He, W. (2021). Interface friction effects on scaling a vertical spring-viscous damper isolation system in a shaking table test. Structures 33, 1878–1891. doi:10.1016/j.istruc.2021.05.046

CrossRef Full Text | Google Scholar

Li, X., Xue, S., and Cai, Y. (2013). Three-dimensional seismic isolation bearing and its application in long span hangars. Earthq. Eng. Eng. Vib. 12, 55–65. doi:10.1007/s11803-013-0151-7

CrossRef Full Text | Google Scholar

Liang, Q., Luo, W., Zhou, Y., Ke, X., and Li, J. (2022). Seismic performance of a novel three-dimensional isolation bearing. J. Build. Eng. 57, 104818. doi:10.1016/j.jobe.2022.104818

CrossRef Full Text | Google Scholar

Liu, D., Li, L., Zhang, Y., Chen, L., Wan, F., and Yang, F. (2022). Study on seismic response of a new staggered story isolated structure considering SSI effect. J. Civ. Eng. Manag. 28, 397–407. doi:10.3846/jcem.2022.16825

CrossRef Full Text | Google Scholar

Liu, J., Gu, Y., Du, Y., Wang, Z., and Wu, J. (2006). 3D viscous-spring artificial boundary in time domain. Chin. J. Geotechnical Eng. 1075, 93–102. doi:10.1007/s11803-006-0585-2

CrossRef Full Text | Google Scholar

Liu, J., and Lv, Y. (1998). A direct method for analysis of dynamic soil-structural interaction. China Civ. Eng. J. 64, 55.

Google Scholar

Liu, J., Wang, Z., and Du, X. (2005). Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems. Eng. Mech. 51, 46.

Google Scholar

Loh, C. H., Weng, J. H., Chen, C. H., and Lu, K. C. (2013). System identification of mid-story isolation building using both ambient and earthquake response data. Struct. Control Health Monit. 20, 139–155. doi:10.1002/stc.479

CrossRef Full Text | Google Scholar

Lou, M., Wang, H., Chen, X., and Zhai, Y. (2011). Structure-soil-structure interaction: Literature review. Soil Dyn. Earthq. Eng. 31, 1724–1731. doi:10.1016/j.soildyn.2011.07.008

CrossRef Full Text | Google Scholar

Mylonakis, G., and Gazetas, G. (2000). Seismic soil-structure interaction: Beneficial or detrimental? J. Earthq. Eng. 4, 277–301. doi:10.1080/13632460009350372

CrossRef Full Text | Google Scholar

Nakamizo, D., and Koitabashi, Y. (2018). Structural design of mid-story isolated high-rise building-Roppongi Grand Tower. Int. J. High-Rise Build. 7, 233–242. doi:10.21022/IJHRB.2018.7.3.233

CrossRef Full Text | Google Scholar

Nazarimofrad, E., and Zahrai, S. M. (2016). Seismic control of irregular multistory buildings using active tendons considering soil–structure interaction effect. Soil Dyn. Earthq. Eng. 89, 100–115. doi:10.1016/j.soildyn.2016.07.005

CrossRef Full Text | Google Scholar

Nie, G., Zhang, C., Wang, Z., Xu, W. d., and Shi, Y. j. (2022). Shaking table test of space double-layer cylindrical reticulated shell with three-dimensional isolation bearing. J. Constr. Steel Res. 189, 107107. doi:10.1016/j.jcsr.2021.107107

CrossRef Full Text | Google Scholar

Oñate, E., Celigueta, M. A., Idelsohn, S. R., Salazar, F., and Suarez, B. (2011). Possibilities of the particle finite element method for fluid–soil–structure interaction problems. Comput. Mech. 48, 307–318. doi:10.1007/s00466-011-0617-2

CrossRef Full Text | Google Scholar

Pala, M., Caglar, N., Elmas, M., Cevik, A., and Saribiyik, M. (2008). Dynamic soil-structure interaction analysis of buildings by neural networks. Constr. Build. Mater. 22, 330–342. doi:10.1016/j.conbuildmat.2006.08.015

CrossRef Full Text | Google Scholar

Park, Y., and Ang, A. H. (1985). Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 111, 722–739. doi:10.1061/(asce)0733-9445(1985)111:4(722)

CrossRef Full Text | Google Scholar

Pérez-Rocha, L. E., Avilés-López, J., and Tena-Colunga, A. (2021). Base isolation for mid-rise buildings in presence of soil-structure interaction. Soil Dyn. Earthq. Eng. 151, 106980. doi:10.1016/j.soildyn.2021.106980

CrossRef Full Text | Google Scholar

Sarcheshmehpour, M., Shabanlou, M., Meghdadi, Z., Estekanchi, H., and Mofid, M. (2021). Seismic evaluation of steel plate shear wall systems considering soil-structure interaction. Soil Dyn. Earthq. Eng. 145, 106738. doi:10.1016/j.soildyn.2021.106738

CrossRef Full Text | Google Scholar

Shang, S., Chen, W., and Xi, L. (2012). The effect to structure due to SSI. Appl. Mech. Mater. 188, 112–118. doi:10.4028/www.scientific.net/amm.188.112

CrossRef Full Text | Google Scholar

Shimada, T., Suhara, J., and Inoue, K. (2005). “Three dimensional seismic isolation system for next-generation nuclear power plant with rolling seal type air spring and hydraulic rocking suppression system,” in ASME Pressure Vessels and Piping Conference, 183–190.

CrossRef Full Text | Google Scholar

Standard (2010). Code for seismic design of buildings: GB 50011-2016. Beijing, China: China Architecture and Building Press.

Google Scholar

Tabatabaiefar, H. R., and Massumi, A. (2010). A simplified method to determine seismic responses of reinforced concrete moment resisting building frames under influence of soil–structure interaction. Soil Dyn. Earthq. Eng. 30, 1259–1267. doi:10.1016/j.soildyn.2010.05.008

CrossRef Full Text | Google Scholar

Terzi, V. G., and Athanatopoulou, A. (2023). Dynamic optimum torsion axis under soil-structure interaction effects. Eng. Struct. 274, 115150. doi:10.1016/j.engstruct.2022.115150

CrossRef Full Text | Google Scholar

Tetsuya, T., Osamu, T., Suhara, J., Okada, K., Tsuyuki, Y., and Fujita, T. (2012). Earthquake observation record in the building using three-dimensional seismic base isolation system. J. Struct. Constr. Eng. Trans. AIJ) 77, 1393–1402. doi:10.3130/aijs.77.1393

CrossRef Full Text | Google Scholar

Vicencio, F., and Alexander, N. A. (2019). Dynamic Structure-Soil-Structure Interaction in unsymmetrical plan buildings due to seismic excitation. Soil Dyn. Earthq. Eng. 127, 105817. doi:10.1016/j.soildyn.2019.105817

CrossRef Full Text | Google Scholar

von Estorff, O., and Kausel, E. (1989). Coupling of boundary and finite elements for soil-structure interaction problems. Earthq. Eng. Struct. Dyn. 18, 1065–1075. doi:10.1002/eqe.4290180711

CrossRef Full Text | Google Scholar

Wang, B., Li, C., and Jin, T. (2020). Research on torsional effect of friction pendulum isolation structure based on nonlinear time history analysis. IOP Conf. Ser. Earth Environ. Sci. 560, 12097. doi:10.1088/1755-1315/560/1/012097

CrossRef Full Text | Google Scholar

Wang, S. J., Chang, K. C., Hwang, J. S., and Lee, B. H. (2011). Simplified analysis of mid-story seismically isolated buildings. Earthq. Eng. Struct. Dyn. 40, 119–133. doi:10.1002/eqe.1004

CrossRef Full Text | Google Scholar

Wang, S. J., Hwang, J. S., Chang, K. C., Lin, M. H., and Lee, B. H. (2013). Analytical and experimental studies on midstory isolated buildings with modal coupling effect. Earthq. Eng. Struct. Dyn. 42, 201–219. doi:10.1002/eqe.2203

CrossRef Full Text | Google Scholar

Wolf, J. P. (1986). A comparison of time-domain transmitting boundaries. Earthq. Eng. Struct. Dyn. 14, 655–673. doi:10.1002/eqe.4290140412

CrossRef Full Text | Google Scholar

Xiao, W., Liao, J., and Zhang, L. (2018). Shaking table test on seismic dynamic responses of isolated mountains. China Earthq. Eng. J. 40, 582–590. doi:10.3969/j.issn.1000-0844.2018.03.582

CrossRef Full Text | Google Scholar

Xu, L., Sui, X., and Zhang, W. (2021). Stability analysis of building foundation in complex mountainous area. Build. Struct. 51, 122–129. doi:10.19701/j.jzjg.2021.24.019

CrossRef Full Text | Google Scholar

Xu, L., Wu, Y., and Tian, H. (2022). Shaking table test of eccentric base-isolated structure on soft soil foundation under long-period ground motion. J. Build. Struct. 43, 1. doi:10.14006/j.jzjgxb.2021.0097

CrossRef Full Text | Google Scholar

Yang, J., Li, P., Jing, H., and Gao, M. (2021). near-fault ground motion influence on the seismic responses of a structure with viscous dampers considering SSI effect. Adv. Civ. Eng. 2021, 1–20. doi:10.1155/2021/6649124

CrossRef Full Text | Google Scholar

Yang, K., Tan, P., and Chen, H. (2022). Complex mode superposition response spectrum approach for isolated structure analysis. J. Vib. Shock 41, 97–105. doi:10.13465/j.cnki.jvs.2022.06.013

CrossRef Full Text | Google Scholar

Yip, C., Wong, J., Amran, M., Fediuk, R., and Vatin, N. I. (2022). Reliability analysis of reinforced concrete structure with shock absorber damper under pseudo-dynamic loads. Materials 15, 2688. doi:10.3390/ma15072688

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoshida, S., Fujitani, H., Mukai, Y., and Ito, M. (2018). Real-time hybrid simulation of semi-active control using shaking table: Proposal and verification of a testing method for mid-story isolated buildings. Jpn. Archit. Rev. 1, 221–234. doi:10.1002/2475-8876.12034

CrossRef Full Text | Google Scholar

Zhang, H., Fu, J., Yu, X., Chen, S., and Cai, X. (2019). Earthquake responses of a base-isolated structure on a multi-layered soft soil foundation by using shaking table tests. Eng. Struct. 179, 79–91. doi:10.1016/j.engstruct.2018.10.060

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, D., Fang, S., Lei, M., Zhu, Z., and Liao, W. (2022). Study on shock absorption performance and damage of a new staggered story isolated system. Adv. Struct. Eng. 25, 1136–1147. doi:10.1177/13694332211056113

CrossRef Full Text | Google Scholar

Zhu, B. (2016). Issues about the structural design of mountainous building. Build. Struct. 46, 122–125. doi:10.19701/j.jzjg.2016.s2.025

CrossRef Full Text | Google Scholar

Zhu, X., Pan, R., Li, J., and Lin, G. (2021). Study of isolation effectiveness of nuclear reactor building with three-dimensional seismic base isolation. Eng. Comput. 39, 1209–1233. doi:10.1108/ec-11-2020-0637

CrossRef Full Text | Google Scholar

Zhuang, H., Xu, Y., Chao, Z., and Dandan, J. (2014). Shaking table tests for the seismic response of a base-isolated structure with the SSI effect. Soil Dyn. Earthq. Eng. 67, 208–218. doi:10.1016/j.soildyn.2014.09.013

CrossRef Full Text | Google Scholar