Experimental and numerical analysis of strengthening prestressed concrete cylinder pipes using a post-tensioning method

Prestress loss caused by broken wires can lead to a decline in the carrying capacity of prestressed concrete cylinder pipes (PCCPs). The strengthening of PCCPs using a post-tensioning method is becoming more and more widely utilized to restore strengthened pipes to the needed design capacity and to withstand combined loads. There is no need to drain the pipe during strengthening construction, and this strengthening actively replenishes the prestress loss caused by wire breakage at a cost-effective price. To verify the strengthening effect of this method, a full-scale test and its corresponding three-dimensional finite-element model were established. A three-dimensional numerical model of three continuous prototype pipes was established and accounted for the particularity of the bell and spigot. The numerical model of prestressing wires was optimized in two aspects, which was more in line with the actual situation. The spiral winding method instead of single winding was adopted to apply prestress, and the prestressing wires with a broken point were partitioned into two separate areas due to the bond quality between the mortar coating and the wires. The simulation and the full-scale test both contain the five processes of strengthening with external prestressed strands as follows: pressurized to working pressure→breaking the prestressing wires until visible cracks propagate→gradual depressurization to artesian pressure→the tensioning operation of strands→and pressurized to design pressure. A sensitivity analysis of the related factors of strengthening was performed through finite-element simulation to provide a better understanding of the design. The simulation results were consistent with the data on the full-scale test and indicated the rationality of this process. The strengthening of PCCP with a post-tensioning method can meet the design demand and is a feasible strengthening method. The working pressure and control coefficient of tensioning have the most significant impact on the strengthening effect. Technical recommendations and a better understanding of the application of the post-tensioning method on PCCP are provided in this study.

Introduction

Prestressed concrete cylinder pipes (PCCPs) are playing an increasingly remarkable role in water conveyance projects in municipal, industrial, and agricultural systems due to their structural merits such as high bearing capacity, strong permeability resistance, and cost-effectiveness. The fractures of prestressing wires can be a consequence of external corrosion, hydrogen embrittlement, or manufacturing defects (Amaechi et al., 2022a). The composites differ from standard materials such as steel (Amaechi et al., 2022b), and the ruptures of PCCP may cause a significant loss to society and make the strengthening of pipes with broken wires essential.

Recent developments of strengthening methods have attracted great attention. To strengthen deteriorating pipes, comprehensive strengthening methods have been proposed such as the replacement (Zhang et al., 2017), internal strengthening methods (such as relining (Smith and Bruny, 2004; Ambroziak et al., 2010; Matthews et al., 2013), slip-lining (Rahman et al., 2012), and carbon fiber-reinforced polymer (CFRP) (Dou et al., 2017a; Dou et al., 2017b; Dou et al., 2018)), and external strengthening methods (Elnakhat and Raymond, 2006). Strengthening with external prestressed strands is prominent, given that draining the pipeline is non-essential for construction. This method is capable of actively replenishing the prestress loss caused by wire breakage (Rahman et al., 2012). Ge and Sunil (2012) presented a literature review of the most commonly used condition assessment technologies and performance prediction methods for PCCP by listing their capabilities and limitations. They also (Ge and Sunil, 2015; Ge, 2016) optimized the finite-element model by considering the prestress residue after wire breakage. Zarghamee M. S. conducted a series of studies on the limit state of PCCP under multiple load conditions (Zarghamee et al., 1988; Heger et al., 1990; Zarghamee et al., 1990; Zarghamee et al., 1993) and failure mechanisms (Zarghamee and Fok, 1990; Zarghamee et al., 2002; Erbay et al., 2007) through experiments and finite-element analysis. Najafi et al. (2011) and Hajali M. [(Hajali et al., 2015), (Hajali et al., 2016)] studied the influence of PCCPs’ carrying capacity by using finite elements for different breaking locations and different numbers of broken wires. Results suggest that the location of broken wires has a pivotal effect on the PCCP carrying capacity. Merrin et al. (2014) utilized finite-element simulation to analyze the interaction between the pipe and soil under external traffic and internal pressure loads. A sensitivity analysis was performed to determine the degree of pipeline characteristics, soil characteristics, and multiple loads on the structural performance of the pipeline. Zhao L.J (Zhao et al., 2019a; Zhao et al., 2019b) developed a theoretical study and a prototype test to confirm the strengthening effect of the post-tensioning method on PCCP.

To verify the strengthening effect of this method, a full-scale test and a three-dimensional numerical model of three continuous prototype pipes were established in this study. The external strengthening method aims at mitigates multi-hazard risks for PCCP.

The numerical model of prestressing wires was optimized, and the concrete damaged plasticity (CDP) was utilized as the constitutive model of the concrete core and the mortar coating considering the decrease in stiffness. The whole process of strengthening with external prestressed strands was simulated in both the finite-element simulation and the full-scale test as follows: pressurized to working pressure →breaking the prestressing wires until visible cracks propagate→gradual depressurization to artesian pressure→the tensioning operation of strands→and pressurized to design pressure. Furthermore, a sensitivity analysis of the related factors of strengthening was performed through finite-element simulation to provide a better understanding of the design.

Numerical simulation model

Model description

Geometric and material properties

The three-dimensional finite-element model was conducted with a 2.0-m diameter embedded PCCP (ECP). All components of the pipe and surrounding soil were separately considered in this model. The total length of an ECP with a bell and spigot (GB/T, 2017) is 5.135 m. There was one complete pipe and two parts of a pipe modeled to account for the effect of the bell and spigot (Figure 1). Pipe #1 and Pipe #3 were original and were not processed, while the prestressing wires were cut in Pipe #2 and the pipe was reinforced. In the simulation model, the contact between the bell and spigot was fully considered. The structures of the bell and spigot are appropriately simplified due to their complexity, as shown in Figure 2.

FIGURE 1

FIGURE 1. Schematic diagram of the modeled pipes.

FIGURE 2

FIGURE 2. Schematic diagram of the simplified socket and spigot.

The concrete core, mortar coating, and surrounding soil were meshed into a solid using a three-dimensional eight-node brick element with reduced integration (C3D8R). A three-dimensional truss element (T3D2) was utilized to simulate the prestressing wires and steel strands. To simulate the real form of the prestressing wires as much as possible, the prestressing wires in this finite-element model were spirally wound around the outside of the concrete core at a pitch of 22.1 mm (Figure 3). Considering that the thickness of the cylinder can be ignored compared to the total length of the pipe, the steel cylinder was modeled with a four-node quadrilateral shell element with reduced integration (S4R). The geometric and material properties of the pipe analyzed in this paper are displayed in Table 1. The tensile stress of the strand simulated in this model was 1860 $\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, and the diameter of the strand was 15.2 mm. The key parameters of the strands utilized in the numerical model and the full-scale test are illustrated in Table 2.

FIGURE 3

FIGURE 3. Finite-element mesh model of the prestressing wires.

TABLE 1

TABLE 1. Major parameters of the pipe.

TABLE 2

TABLE 2. Major parameters of the strand.

The overall size of the surrounding soil was $12\mathrm{m}\times 9.75\mathrm{m}\times 7.025\mathrm{m}$. The disturbed soil at each end of pipe #2 (PART B) extends 1.0 m along the direction of the axis to Pipe #1 and Pipe #3 (PART A and PART C) and considers the influence of the bell and spigot (Figure 4). During the strengthening process, the soil surrounding Pipe #2 needs to be excavated and back-filled, which leads to the disturbance of the surrounding soil and is shown in Figure 4. Therefore, the surrounding soil of PART B was divided into eight parts based on the actual disturbance (Figure 5). The corresponding material properties of each part are provided in Table 3.

FIGURE 4

FIGURE 4. Axial division of the surrounding soil (Dimension: m).

FIGURE 5

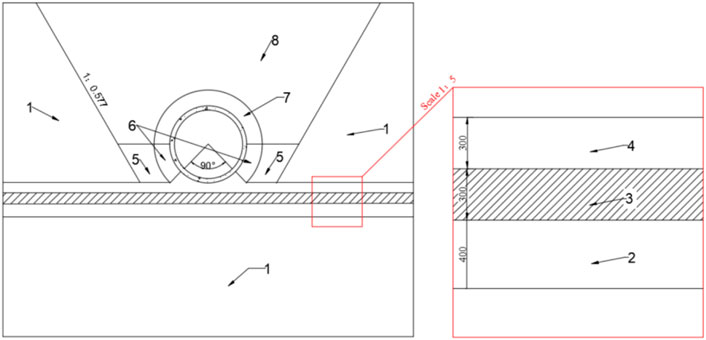
FIGURE 5. Partition of the surrounding soil of PART B: (1) stereogram of the soil; (2) front view of part B as follows: 1—undisturbed section; 2—light disturbed section; 3—moderately disturbed section; 4—severely disturbed section; 5—bottom fill-back; 6—cradle section; 7—buffer section; and 8—upper fill-back (Dimension: mm).

TABLE 3

TABLE 3. Material properties of the surrounding soil.

The concrete damaged plasticity (CDP) model (GB, 2010; Hu et al., 2019) was applied to the concrete core and mortar coating. For the steel cylinder, prestressing wires and strands and the elastoplastic stress–strain relationship in tension and compression were utilized in this model, and the Mohr–Coulomb model was suitable for the surrounding soil.

Load and boundary conditions

Combined loads acting on the pipe mainly included internal water pressure and the gravity acting on the pipe and the surrounding soil. The bottom of the soil was totally fixed. The top surface of the model was free, and the other four sides of this model were fixed in the normal direction of their surfaces. The working value of the water pressure was $0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, and the design pressure was $0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2+0.2\mathrm{N}/{\mathrm{m}\mathrm{m}}^2=0.876\mathrm{N}/{\mathrm{m}\mathrm{m}}^2\approx 0.9\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$. The gravity of the soil and pipe was also considered.

Interaction

For the interaction between each component, the concrete was completely tied with the mortar coating. The prestressing wires were embedded in the mortar coating, and the cylinder was embedded in the concrete core. The slide between the other materials was ignored in this paper. The friction relationship was applied between the bell and spigot with a coefficient of 0.2, and the same relationship was applied between the pipe and the surrounding soil with a coefficient of 0.35.

Special treatment of prestressing wires

The prestress of the wires and strands was applied using the equivalent temperature cooling method. In previous models, the prestress of the wires was considered zero once the break occurred. However, in the majority of the ruptures, pipes fail at the four or eight o′clock orientation (Ge and Sunil, 2015). The bond between the prestressing wires and the mortar coating attributes to the remaining prestress beyond a certain length from the broken point (AWWA, 2015). The corresponding angle of this length was assumed to be $90°$ (Hu et al., 2019). The stress of prestressed wires was assumed as zero within this length. Additionally, the prestress over the length of the wires was not affected by the wire breakage, that is, ${\sigma }_s=f_{sg}$. The prestress of the broken wires was considered, as shown in Figure 6.

FIGURE 6

FIGURE 6. Stress distribution of the broken prestressing wires.

There are various methods for applying prestress, such as the initial strain method, equivalent temperature cooling method, and initial stress method. The second method was adopted to apply prestress in this simulation. The temperature difference is calculated as $∆\mathrm{T}=\raisebox{1ex}{$\sigma $}\!\left/ \!\raisebox{-1ex}{$\left(E\bullet \alpha \right)$}\right.$, wherein $\sigma$ is the target prestress and $\alpha$ is the expansion coefficient of strands. The temperature difference of prestressing the wires was calculated as 474°C, and the temperature difference of the steel strands was 523°C.

Analysis procedure

The entire analysis process (Figure 7) involves five procedures: (I) pressurizing to the working pressure ($0\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$ → $0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$), (II) breaking the prestressing wires until the visible cracks propagate ($0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$), (III) de-pressurizing to the artesian pressure ($0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$ → $0.2\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$), (IV) laying and tensioning operation of strands ($0.2\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$), and (V) pressurizing to the design value ($0.2\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$ → $0.9\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$).

FIGURE 7

FIGURE 7. Analysis steps.

Full-scale test

A full-scale test was conducted (Figure 8), and the geometric and material properties of the two pipes were the same as the simulated models.

FIGURE 8

FIGURE 8. Details of the test apparatus.

The monitoring objects include the strains of each component of the pipe and the prestressed strands. Resistance strain gauges were utilized due to their high reliability and strong anti-interference abilities.

Figure 9 presents the layout of monitoring points along the axial direction. Section 1 (S1, 2.5 m) is located in the middle of the zone where all prestressing wires break. Section 2 (S2, 3.0 m) is the zone affected by the broken wires. Section 3 (S3, 4.0 m) is the zone that is sufficiently far from the broken wires. The orientations of the resistance strain gauges are arranged on the concrete core, and the wires were 90°, 180°, 270°, and 360°, respectively. The strain gauges that were chosen were 50 × 3 mm and 10 × 2 mm for the concrete and wires, respectively.

FIGURE 9

FIGURE 9. Layout of measuring sections (Dimension: mm).

The strain gauges were located on strands at 90°, 180°, 270°, and 360° orientations of S1, as shown in Figure 10. There were a total of nine measuring points. The choice of the strain gauge was 2 × 1 mm for the strands.

FIGURE 10

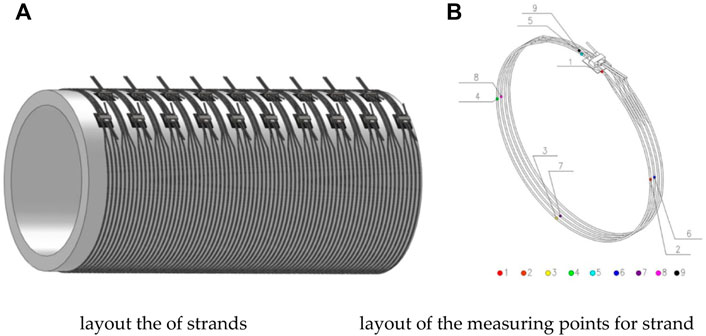
FIGURE 10. Details of the strands. (A) Layout of the strands and (B) layout of the measuring points for the strand.

The prestress of the wires contributed to the initial compressive strains of the concrete core. The pre-strains of the concrete core and the wires were included in the strains obtained by the resistance strain gauges. The real strain of the concrete core and prestressing wires should be revised as follows:

${\epsilon }_r={\epsilon }_i+{\epsilon }_m,(1)$

where ${\epsilon }_r$ is the real strain, ${\epsilon }_i$ is the prestrain caused by the prestress of wires, and ${\epsilon }_m$ is the strain measured by the resistance strain gauges. The calculated prestrain of the concrete core and prestressing wires is −227 $\times {10}^{-6}$ (compressive strain) and $4492\times {10}^{-6}$ (tensile strain) according to ANSI/AWWA C304-2014 (Feng, 2008), respectively. Therefore, the results illustrated in this study were all revised.

Results and analysis

Deformation of components

The process of the full-scale test and the finite-element simulation both contain the following five stages. The stress response of each component and prestressed strands in each process were analyzed. Once the real strain of the concrete core (Feng, 2008; GB, 2015) reaches $207\times {10}^{-6}$, micro-cracks begin to occur. The strain of $1522\times {10}^{-6}$ in the concrete core indicates the onset of macro-cracks.

Load stage I) Pressurizing to a working pressure of ($0\mathrm{N}/{\mathrm{m}\mathrm{m}}^2\to 0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$)

The hoop strains of the concrete core and prestressing wires of Section 2 with the increase of the internal water pressure are illustrated in Figures 11A, B, respectively. The FEM and test in Figures 11A, B correspond to the simulated results and full-scale test results.

FIGURE 11

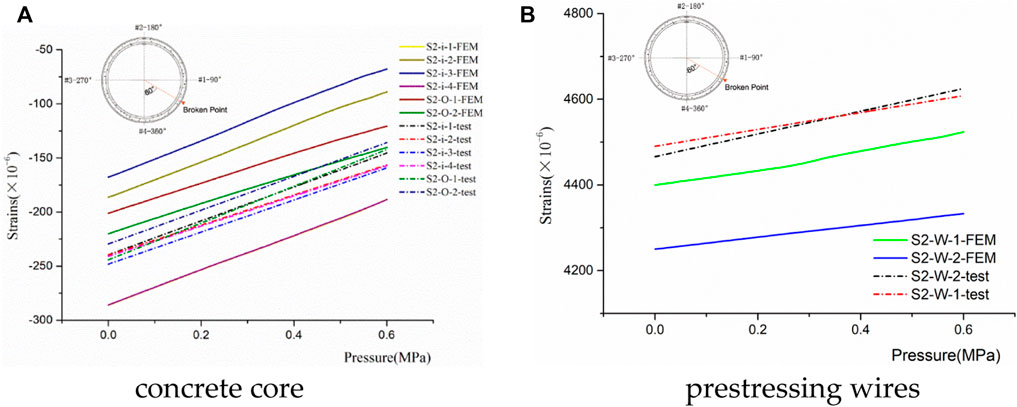
FIGURE 11. Comparison of FEM and test results of the concrete core at load stage I. (A) Concrete core and (B) prestressing wires.

A rise in the water pressure resulted in a linear growth of the strains in the concrete core and prestressing wires. The concrete core and the prestressing wires were primarily responsible for withstanding the internal water pressure, and the concrete core was still under compression. The strains at $90°$, $180°$, $270°$, and $360°$ orientations of the concrete core were basically equal, and the stress in the prestressing wires was uniform, which indicated that the pipe was uniformly forced.

There was no crack initiation in the concrete core. The structural integrity condition was good. Figure 11 shows that the simulation results were in agreement with the full-scale test data.

Figure 12 illustrates the stress and strain of the concrete core at a pressure of $0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$. The strain of the concrete core reached a maximum value of 874.6 $\mu \epsilon$ (Figure 12(b)). The element with the maximum strain was located at a position near the spigot at the spring-line, which indicated that the spigot bell is the weakness of the whole pipe (Figure 12).

FIGURE 12

FIGURE 12. Nephogram of the concrete core at load stage I (LE/m)

Load stage (II) Breaking the prestressing wires until visible cracks propagate ($0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$)

Figure 13A presents corresponding strains in the prestressing wires with the rate of broken wires measured in the prototype test. Compared to measuring point #2 of Section 1 and Section 2, the strains at measuring point #1 of Section 1 and Section 2 sharply dropped. The bonding between the mortar coating and wires was in a benign state. The wire strains at measuring point 1 decreased to some extent, while the prestress of the broken wires at measuring point 2 remained. The wire breakage has little impact on the prestressing wires of Section 3, which is also due to the bonding.

FIGURE 13

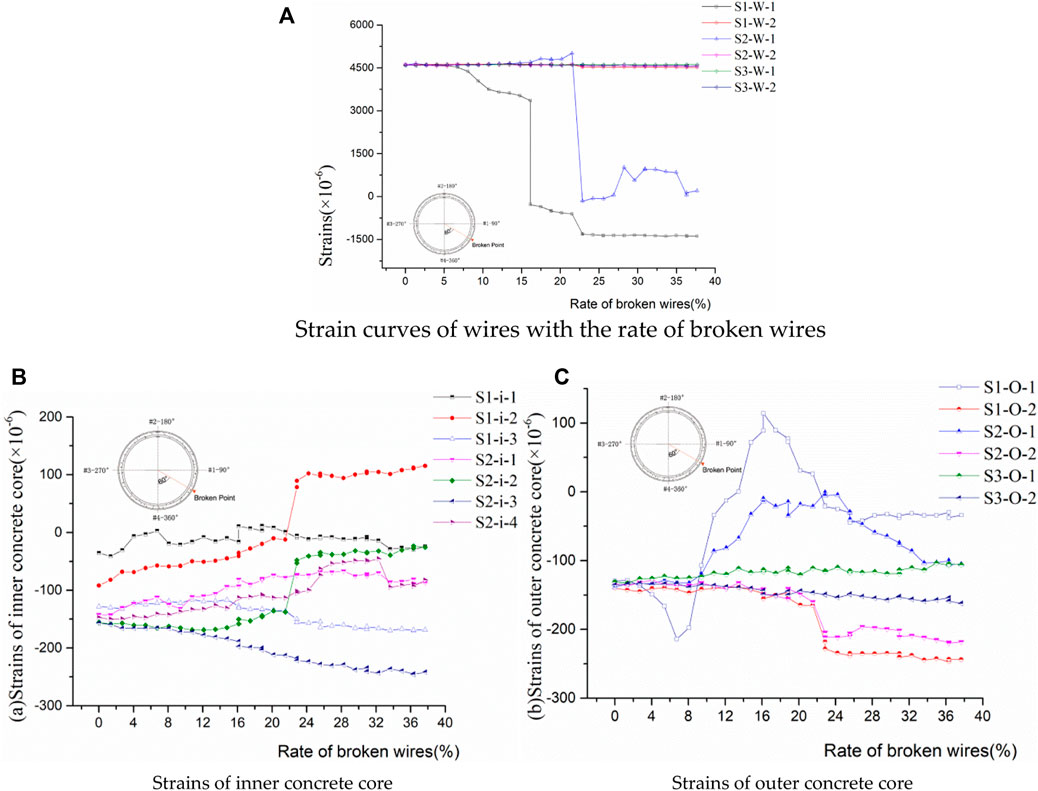
FIGURE 13. Strain curves of wires with the rate of broken wires. (A) Strain curves of wires with the rate of broken wires, (B) strains of the inner concrete core, and (C) strains of the outer concrete core.

Figures 13B, C exhibit the hoop strain in the inner concrete core and the outer concrete core. The strain in the concrete core fluctuated non-linearly with the increase in the rate of broken wires. The strains in the concrete core of S1 and S2 fluctuated. Similar to the situation of prestressed wires, the strains in the concrete core area sufficiently far from the broken wires (Section 3) were less affected by breaking wires. Figure 14 depicts the visible cracks that occurred in the outer concrete core near measuring point #1. The longitudinal cracks rapidly propagated with the growth rate of broken wires. Several narrow branches were induced piecemeal and extra longitudinal cracks simultaneously appeared. The maximum width of the macro-cracks in the outer concrete core at a $90°$ orientation reached 2.2 mm.

FIGURE 14

FIGURE 14. Distribution of cracks in the outer concrete core.

The operation of breaking wires was terminated when the rate of broken wires reached 37.7%. Then, the strain of the concrete core was $1958\times {10}^{-6}$ through finite-element simulation, which exceeded $1522\times {10}^{-6}$. In particular, the existence and propagation of the visible cracks increased damage to the pipe’s integrity. The element with the maximum strain was also located at the position near the spigot at the spring-line, which is the weakest point of the entire pipe (Figure 15).

FIGURE 15

FIGURE 15. Nephogram of the concrete core of load stage II (LE/m).

Load stage (III) De-pressurizing to the artesian pressure of ($0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2\to 0.2\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$)

Figure 16 illustrates the hoop strains in the concrete core with a decrease of internal water pressure. A decrease in the water pressure decreased the corresponding strains of the concrete core. The stress redistribution of the pipe was induced by dynamic fluctuation. The width of macro-cracks in the outer concrete core at $90°$ orientation remained at a maximum of 1.2 mm.

FIGURE 16

FIGURE 16. Strain curves of the concrete core with the rate of broken wires.

Load stage (IV) The laying and tensioning operation of the strands as ($0.2\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$)

The tensioning operation of the strands was performed after depressurization. The strains in the concrete core all exhibited an obvious decrease after the tensioning operation of strains (Figure 17). The width of macro-cracks at the $90°$ orientation decreased to 0.1 mm. The majority of macro-cracks closed and were difficult to find with the naked eye.

FIGURE 17

FIGURE 17. Strain comparison of the concrete core before and after the tensioning operation.

Load stage (V) Pressurizing to the design value ($0.2\mathrm{N}/{\mathrm{m}\mathrm{m}}^2\to 0.9\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$).

A step-by-step pressurization was adopted to increase the water pressure to the design value of $0.9\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$. The continuing growth in water pressure made a moderate increase in the strain of the concrete core (Figure 18). The strain simulation values of the concrete core are greater than the test results, which indicates that the simulation results have a certain degree of safety.

FIGURE 18

FIGURE 18. Comparison of FEM and test results of the concrete core at stage V.

Figure 18 illustrates the strain comparison of each measuring point in the concrete core before and after strengthening of the water pressure at $0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$. Overall, the strain after strengthening was far less than the level before. The concrete core was again at a compressive condition. The width of the macro-cracks in the concrete core at the $90°$ orientation remained unchanged when the pressure continued to increase, which indicates that the maximum value of the macro-cracks was still 0.1 mm. The reinforced pipe was able to withstand the design loads and did not leak when the internal water pressure reached $0.9\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$ (Figure 19).

FIGURE 19

FIGURE 19. Strain of the concrete core at the working pressure before and after strengthening.

Stress situation of the steel strands

The stress of the prestressed strands was 1026 N/mm² through finite-element analysis at a pressure of 0.9 N/mm² (Figure 20). This is slightly less than the target tensile strength of the prestressed strands and can meet the strengthening requirements.

FIGURE 20

FIGURE 20. Nephogram of the prestressed strands at design pressures.

Sensibility analysis of influencing factors

To investigate the sensitivity of the relating factors and optimize the design of the external strengthening, a series of parametric studies were conducted. In each case, the effect of changing a single parameter by numerical analysis was examined.

Parameters of the test pipe

The working pressure and depth of the soil above the top of the pipe are the main internal and external load, respectively. These parameters both play an important role in the carrying capacity of the pipe.

The first parameter to examine is the working pressure of the test pipe. The working pressure was $0.4\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $0.5\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $0.6\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $0.7\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $0.8\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, and $0.9\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$ for each case; the corresponding value of the design pressure was 0.676 N/mm², 0.776 N/mm², 0.876 N/mm², 0.98 N/mm², 1.12 N/mm², 1.26 N/mm², respectively. The other parameters remained constant. The maximum strain of the concrete core at the design pressure is considered the final judgment standard (as shown in Figure 21A).

FIGURE 21

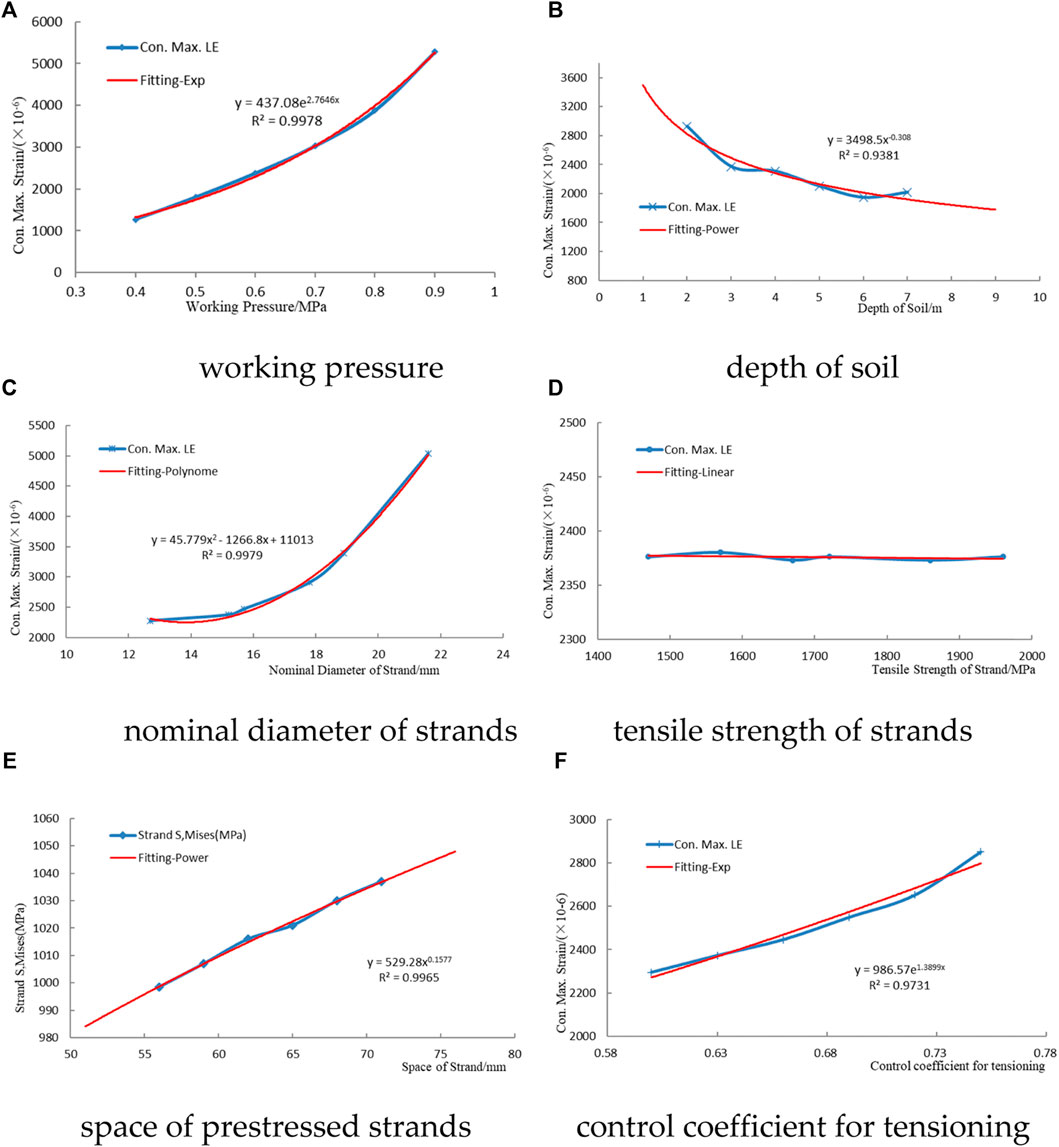
FIGURE 21. Sensitivity analysis of the working pressure. (A) Working pressure, (B) soil depth, (C) nominal diameter of the strands, (D) tensile strength of the strands, (E) space of prestressed strands, and (F) control coefficient for tensioning.

The maximum strain in the concrete core increased exponentially with an increase of the working pressure. The change of the internal water pressure significantly influenced the bearing capacity of the PCCP. The determination coefficient was $R^2=0.9967$, while $R^2$ is the critical index used to evaluate the fitting degree of the trend line.

The effects of strengthening under different soil depths were analyzed using finite-element analysis. The depth of the soil above the top of the pipe was 2 m, 3 m, 4 m, 5 m, 6 m, and 7 m, while the other parameters remained constant. The maximum strain of the concrete core at the design pressure is considered the final judgment standard (as depicted in Figure 21B).

The maximum strain in the concrete core decreased with an increase of soil depth. The element with the maximum strain was always located at the spigot ring. The trend line is a power function, and the determination coefficient is ${\mathrm{R}}^2=0.9313$. The rate of change of the higher-order polynomial is less than any exponential function with a base greater than 1. The change of the pressure influenced the bearing capacity of the PCCP.

Parameters of the prestressed strands

The pivotal factors that influence the selection of strands include its nominal diameter and tensile strength. The structural performance of the pipe under different nominal diameters and tensile strengths of the strands was analyzed.

The nominal diameter of the strands was 12.7 mm, 15.2 mm, 15.7 mm, 17.8 mm, 18.9 mm, and 21.6 mm for each case. The corresponding section area at unit length [34] is 98.7 ${mm}^2$, 140 ${mm}^2$, 150 ${mm}^2$, 191 ${mm}^2$, 220 ${mm}^2$, and 285 ${mm}^2$, while the other parameters remained constant. The maximum strain of the concrete core at the design pressure is considered the final judgment standard (as given in Figure 21C).

The maximum strain in the concrete core increased as the nominal diameter of the strands increased. The trend line was a second-order polynomial, and the determination coefficient was $R^2=0.9979$.

The effects of strengthening with different strand tensile strengths were analyzed. The tensile strength of the strands was the only factor that was changed, which was $1470\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $1570\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $1670\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $1720\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, $1860\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$, and $1960\mathrm{N}/{\mathrm{m}\mathrm{m}}^2$ for each situation, while the other parameters remained constant. The maximum strain of the concrete core at the design pressure was considered the final judgment standard (as illustrated in Figure 21D).

The maximum value of the strain in the concrete core was nearly unchanged. The variety of tensile strengths had little effect on the carrying capacity of the PCCP. In addition, exorbitant tensile strength does not play a significant role in improving the safety and carrying capacity of the pipe.

The spacing of prestressed strands directly determines the cross-sectional area within the unit length. The effects of strengthening with different spacing of strands were analyzed. The strand space was 56 mm, 59 mm, 62 mm, 65 mm, 68 mm, and 71 mm, while the other parameters remained constant. The maximum stress of the prestressed strands at the design pressure is considered the final judgment standard (as displayed in Figure 21E).

The maximum stress value in the prestressed strands increases with an increase in the strand spacing. The trend line is a power function, and the determination coefficient is ${\mathrm{R}}^2=0.9965$ .

The control coefficient for tensioning is another critical parameter for strengthening. The effects of strengthening with different control coefficients for tensioning were analyzed. The control coefficients for tensioning were 0.60, 0.63, 0.66, 0.69, 0.72, and 0.75, while the other parameters remained constant. The maximum strain of the concrete core at the design pressure is considered the final judgment standard (as described in Figure 21F).

The maximum strain in the concrete core increased exponentially with an increase of the control coefficient for tensioning, and the determination coefficient was ${\mathrm{R}}^2=0.9748$. The change in the control coefficient for tensioning significantly influenced the bearing capacity of the PCCP.

Conclusions

A full-scale test and numerical analysis were conducted to determine the strengthening effect of the post-tensioning method on PCCP. The main discussion points are as follows:

1) The simulation results agreed with the full-scale test data, which indicated the rationality of the simulation and the full-scale test. The reinforced pipe was capable of withstanding the design loads and did not leak after strengthening. The cracks in the outer concrete core at the $90°$ orientation significantly closed, and the crack propagation was simultaneously constrained by the strands. The strengthening of PCCP with the post-tensioning method was able to meet the design demand and is a feasible strengthening method. Furthermore, this method is able to mitigate multi-hazard risks for PCCP.

2) The spigot ring has the largest strain value during the entire procedure and is the weakest point of the whole pipe. Breaking wires attribute to the apparent loss of prestress within a certain length. The wire prestress resumes to the original state when moving away from the broken point due to the bonding between the mortar coating and the prestress wires.

3) The working pressure and control coefficient for tensioning have the most significant impact on the strengthening effect, followed by the effects of the soil depth above the top of the pipe, the nominal diameter, and the strand spacing. The tensile strength of the strands has little effect on the strengthening of the PCCP with the post-tensioning method. This study presents the comprehensive work needed for strengthening of PCCP with the post-tensioning method.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, TD and LZ; methodology, TD; software, CL; writing—original draft preparation, LZ; writing—review and editing, ML.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amaechi, C. V., Reda, A., and Kgosiemang, I. M. (2022). Guidelines on asset management of offshore facilities for monitoring, sustainable maintenance, and safety practices. Sensors 22 (19), 7270.

PubMed Abstract | CrossRef Full Text | Google Scholar

Amaechi, C. V., Chesterton, C., Butler, H. O., Gillet, N., Wang, C., Ja’e, I. A., et al. (2022). Review of composite marine risers for deep-water applications: Design, development and mechanics. J. Compos. Sci. 6 (3), 96.

CrossRef Full Text | Google Scholar

Ambroziak, M., Kelso, P. E. B., and Sinclair, J. (2010)“Development and construction of the nation’s largest water main rehab project,” in Proceedings of the Pipelines 2010: Climbing New Peaks to Infrastructure Reliability: Renew, Rehab, and Reinvest, held in Keystone, Colorado, August 28-September 1, 2010, 51–60.

Google Scholar

AWWA (2015). AWWA C304 standard for design of prestressed concrete cylinder pipe. Denver, CO, USA: American Water Works Association.

Google Scholar

Dou, T. S., Cheng, B. Q., Hu, H., Xia, S. F., Yang, J. X., and Zhang, Q. (2018). The prototype test study of prestressed concrete cylinder pipe structure deformation law.The external pressure. J. Hydraul. Eng. 49 (2), 207–215.

Google Scholar

Dou, T. S., Cheng, B. Q., Hu, H., Xia, S. F., Yang, J. X., and Zhang, Q. (2017a). The prototype test study of prestressed concrete cylinder pipe structure deformation law.The internal pressure. J. Hydraul. Eng. 48 (12), 1438–1446.

Google Scholar

Dou, T. S., Cheng, B. Q., Hu, H., Xia, S. F., and Zhao, L. J. (2017b). The experimental study on CFRP renewal of PCCP with broken wires. China Concr. Cem. Prod. 12, 35–40.

Google Scholar

Elnakhat, H., and Raymond, R. (2006). “Repair of PCCP by post tensioning,” in Pipeline Division Speciality Conference 2006, Chicago, Illinois, 12 July 2006, 1–5.

CrossRef Full Text | Google Scholar

Erbay, O. O., Zarghamee, M. S., and Ojdrovic, R. P. (2007). “Failure risk analysis of lined cylinder pipes with broken wires and corroded cylinder,” in Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects, Boston, Massachusetts, 8-11 July 2007, 1–10.

CrossRef Full Text | Google Scholar

Feng, X. Z. (2008). Comparison of ASTM concrete compressive strength and China’s concrete strength grade. Northwest Hydropower 3, 65–67.

Google Scholar

GB (2010). GB 50010-2010 Code for design of concrete structures. Beijing: National Standard of the people’s Republic of China.

Google Scholar

GB (2015). GB 5224-2014 Steel strand for prestressed concrete. Beijing: National Standard of the people’s Republic of China.

Google Scholar

GB/T (2017). Prestressed concrete cylinder pipe. Beijing: National Standard of the people’s Republic of China.

Google Scholar

Ge, S. Q. (2016). “PCCP condition assessment are current numerical models too conservative,” in Pipelines 2016, Canada, Calgary, 26-30 September 2016, 527–537.

Google Scholar

Ge, S. Q., and Sunil, S. (2015). Effect of mortar coating’s bond quality on the structural integrity of prestressed concrete cylinder pipe with broken wires. J. Mat. Sci. Res. 4, 59–75. doi:10.5539/jmsr.v4n3p59

CrossRef Full Text | Google Scholar

Ge, S. Q., and Sunil, S. (2012). Failure analysis, condition assessment technologies, and performance prediction of prestressed concrete cylinder pipe (PCCP): A state-of-the-art literature review. J. Perform Constr. Fac. 3, 618–628.

Google Scholar

Hajali, M., Alavinasab, A., and Abi Shdid, C. (2016). Structural performance of buried prestressed concrete cylinder pipes with harnessed joints interaction using numerical modeling. Tunn. Undergr. Sp. Tech. 51, 11–19. doi:10.1016/j.tust.2015.10.016

CrossRef Full Text | Google Scholar

Hajali, M., Alavinasab, A., and Shdid, C. A. (2015). Effect of the location of broken wire wraps on the failure pressure of prestressed concrete cylinder pipes. Struct. Concr. 16 (2), 297–303. doi:10.1002/suco.201400070

CrossRef Full Text | Google Scholar

Heger, F. J., Zarghamee, M. S., and Dana, W. R. (1990). Limit-States design of prestressed concrete pipe. I: Criteria. J. Struct. Eng. 116 (8), 2083–2104. doi:10.1061/(asce)0733-9445(1990)116:8(2083)

CrossRef Full Text | Google Scholar

Hu, B., Fang, H., Wang, F., and Zhai, K. (2019). Full-scale test and numerical simulation study on load-carrying capacity of prestressed concrete cylinder pipe (PCCP) with broken wires under internal water pressure. Eng. Fail. Anal. 104, 513–530. doi:10.1016/j.engfailanal.2019.06.049

CrossRef Full Text | Google Scholar

Matthews, J. C., Selvakumar, A., and Condit, W. (2013). Current and emerging water main renewal technologies. J. Infrastruct. Syst. 19 (2), 231–241. doi:10.1061/(asce)is.1943-555x.0000121

CrossRef Full Text | Google Scholar

Merrin, J., Hung, H. P., Rajeev, P., Robert, D. J., and Kodikara, J. (2014). “Stress analysis of buried pipes,” in 8th Australasian Congress on Applied Mechanics, ACAM 8, Melbourne, Australia, 23-26 November 2014, 1–10.

Google Scholar

Najafi, M., Mielke, R., and Ramirez, G. (2011). “Analysis and testing of a prototype jointing system for bar,” in Pipelines: A Sound Conduit for Sharing Solutions - Proceedings of the Pipelines 2011 Conference, Beijing, China, 26-29 October 2011, 864–871.

Google Scholar

Rahman, S., Smith, G., Mielke, R., and Keil, B. (2012). “Rehabilitation of large diameter PCCP: Relining and sliplining with steel pipe,” in Proceedings of the Pipelines 2012: Innovations in Design, Construction, Operations, and Maintenance -Doing More with Less, Miami, Florida, USA, 19-22 August 2012, 494–504.

CrossRef Full Text | Google Scholar

Smith, G., and Bruny, J. (2004). “Relining prestressed concrete cylinder pipe, A manufacturers perspective,” in Pipelines 2004: Pipeline Engineering and Construction - What's on the Horizon?, San Diego California, United States, 01-04 August 2004 (American Society of Civil Engineers), 1–6.

CrossRef Full Text | Google Scholar

Zarghamee, M. S., Egger, D. W., and Ojdrovic, R. P. (2002). “Finite-element modeling of failure of PCCP with broken wires subjected to combined loads,” in Pipelines 2002 Beneath Our Feet: Challengers and Solutions - Proceedings of the Pipeline Division Specialty Conference, Cleveland, Ohio, 4-7 August 2002, 1–17.

CrossRef Full Text | Google Scholar

Zarghamee, M. S., and Fok, K. (1990). Analysis of prestressed concrete pipe under combined loads. J. Struct. Eng. 116 (7), 2022–2039. doi:10.1061/(asce)0733-9445(1990)116:7(2022)

CrossRef Full Text | Google Scholar

Zarghamee, M. S., Fok, K., and Sikiotis, E. S. (1990). Limit states design of prestressed concrete pipe II: Procedure. J. Struct. Eng. 116 (8), 2105–2126. doi:10.1061/(asce)0733-9445(1990)116:8(2105)

CrossRef Full Text | Google Scholar

Zarghamee, M. S., Heger, F. J., and Dana, W. R. (1988). Experimental evaluation of design methods for prestressed concrete plpe. J. Transp. Eng. 114 (6), 635–655. doi:10.1061/(asce)0733-947x(1988)114:6(635)

CrossRef Full Text | Google Scholar

Zarghamee, M. S., Ojdrovic, R. P., and Dana, W. R. (1993). Coating delamination by radial tension in prestressed concrete pipe. I experiments. J. Struct. Eng. 119 (9), 2701–2719. doi:10.1061/(asce)0733-9445(1993)119:9(2701)

CrossRef Full Text | Google Scholar

Zhang, H., Dong, S., and Zhou, W. (2017). Introduction of the technology for repairing and updating the prestressed concrete cylinder pipe (PCCP) structure. Water $ Wastewater Eng. 53 (8), 104–108.

Google Scholar

Zhao, L. J., Dou, T. S., Cheng, B. Q., Xia, S. F., Yang, J. X., Zhang, Q., et al. (2019). Experimental study on the reinforcement of prestressed concrete cylinder pipes with external prestressed steel strands. Appl. Sci.-Base 9 (1), 149. doi:10.3390/app9010149

CrossRef Full Text | Google Scholar

Zhao, L. J., Dou, T. S., Cheng, B. Q., Xia, S. F., Yang, J. X., Zhang, Q., et al. (2019). Theoretical study and application of the reinforcement of prestressed concrete cylinder pipes with external prestressed steel strands. Appl. Sci.-Base 9 (24), 5532. doi:10.3390/app9245532

CrossRef Full Text | Google Scholar