Impacts of train-induced dynamic loads on goaf foundation of Qinshui coalfield

For the high-speed railway built in the goaf sites, if the influence depth of the additional loads reaches the collapse fault zone of the goaf foundation, the overburden rock mass above the mined area will move again, causing the surface to deform again, which seriously threatens the construction, operation, and maintenance of the high-speed railway lines. Therefore, in order to improve the safety and stability of operation of high-speed railway in goaf sites, it is essential to determine the activation deformation of the goaf foundation. In this paper, based on the additional stress method, the newly added embankment materials are taken as uniformly distributed strip static loads, and the high-speed railway in operation is regarded as the fluctuation-concentrated dynamic loads. The 1/4 vehicle vibration model with two degrees of freedom is introduced, and the influence depth of the additional loads of the goaf foundation is calculated. The criterion of activation is proposed based on the relationship between the influence depth of additional loads and the height of the collapse zone and fault zone. Conclusions drawn are as follows: i) the activation judgment criterion for the goaf foundation under the influence of high-speed railway vibration loads is recommended; ii) case study shows that the rail surface vibration model applicable to quantify the influence depth of high-speed railway mentioned previously mined-out regions; iii) the influence of rail surface irregularity on influence depth cannot be ignored; iv) the research conclusion can provide reference for site selection of high-speed railway and embankment deformation analysis.

1 Introduction

In China, the mineral resources are rich and widely distributed. After the underground minerals are extracted, mined areas will be formed. Under the influence of mined-out areas, the overlying strata and the surface will produce continuous movement, deformation and damage, and geological disasters, such as ground subsidence and surface cracks. According to incomplete statistics, the subsidence area of goaf sites in China has exceeded 8000 km² and is still expanding at the speed of 200 km²/a. For the key coal mines, the average subsidence area accounts for almost 1/10 of the total mining area (Li, 2004). The surface cracks will provide sufficient oxygen for the underground coal seams, and coal fire in the underground will aggravate the caving of overburden in mined-out areas, widen and lengthen the surface subsidence, and finally form a vicious cycle of “ground fissures–fire areas–surface subsidence”. It not only threatens the safety of human life and property but also breaks the original ecological balance.

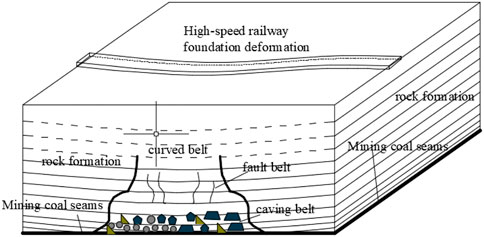
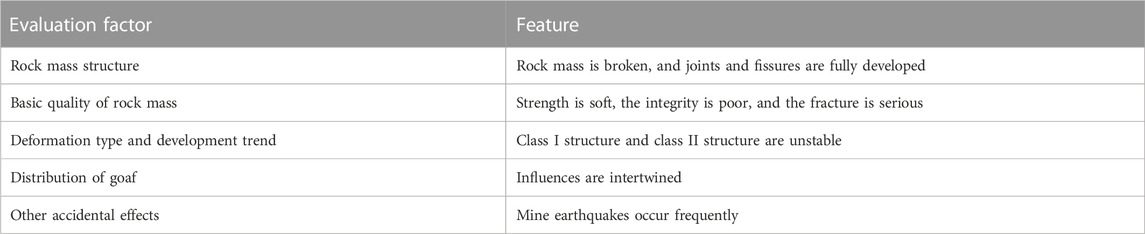
When these goaf sites are used to construct, the original stress state of the rock and soil of the stratum will be changed due to the disturbance of the new building loads. When the influence depth, which is generated by the building loads and anthropogenic activities, is enough to reach the collapse zone and fracture zone, the balanced state of the mined-out area will be broken and the roof of the mined-out area will move again. This will lead to re-deformation of the stable surface. The residual deformation of goaf sites and activation deformation of the goaf foundation will cause chain disasters in the geological environment, underground structure engineering, ground building facilities, and ground traffic engineering. In particular, under the cyclic loads of high-speed railway, its disaster type has the characteristics of coupling chain disaster, as shown in Figure 1, which poses a severe challenge to the construction, operation, and maintenance of high-speed railway. Many experts and scholars at home and abroad have carried out a lot of research on environmental disasters in mined-out areas, the calculation model of train dynamic loads, and the activation deformation of the goaf foundation, and some research results have been achieved.

FIGURE 1

FIGURE 1. Schematic diagram of the coupling chain disaster in goaf sites.

In terms of the calculation model of cyclic dynamic loads, Yang et al. (2015) and Fu et al. (2021) used the excitation force function to simulate the dynamic loads of the train, Zhang et al. (2011) and Sun et al. (2019) analyzed the dynamic loads of the vehicle based on the road surface roughness, Yao et al. (2009) assumed that the road surface roughness obeyed the sinusoidal function and simplified the 1/4 vehicle body structure into a two-degree-of-freedom vibration system to determine the dynamic loads, and Li et al. (2021) carried out dynamic triaxial tests of continuous loading and intermittent loading and put forward the prediction model of the cumulative plastic strain.

In the aspect of the activation deformation mechanism, some scholars summarized and prospected the subgrade deformation of the high-speed railway in the goaf sites. Buodhu and Adiyaman (2010), Ren et al. (2010), and Ren et al. (2018) analyzed the disturbance of the cyclic traffic dynamic loads on the rock mass structure in the goaf sites through numerical simulation. Liu et al. (2019) attributed the key factors of goaf activation to water filling and building loads. Du et al. (2015) used field monitoring, numerical simulation, and orthogonal tests to study the impacts of the underlying goaf on the expressway. Li et al. (2012) used the similar material model to study the influence of key strata and mining on the disturbance depth. Zhou et al. (2015), Feng et al. (2021), and Cheng et al. (2022) conducted an experimental study on the deformation and settlement characteristics of the mining surface and overburden under the thick overburden strata.

On the field of goaf activation under dynamic loads, prior studies defined the critical mining depth of activation deformation of broken rock and soil mass, which is the sum of the maximum disturbance depth generated by the additional building loads and the height of fault zone in goaf sites. Guo et al. (2004), Tong et al. (2013) and Gao et al. (2014) summarized the activation deformation of the goaf foundation under dynamic loads and pointed out that the calculation of goaf deformation under dynamic loads is almost blank. Xu et al. (2014), Wang et al. (2019) and Guo et al. (2021) calculated the influence depth of additional building loads through numerical simulation. Wang (2013) used the mechanical balance analysis method to obtain the calculation formula of the critical depth. Zhang et al. (2015) calculated the disturbance depth by considering the newly added subgrade materials above the goaf foundation as the static loads and operational trains as the dynamic loads moving along the sinusoidal curve.

Most of the aforementioned research results are based on new buildings or highways, and there is a lack of research on the safety evaluation of the goaf foundation under high-speed railway vibration. Compared with highways, high-speed railway has higher speed, greater influence depth of vibration loads, greater possibility of activation of the underlying goaf foundation, and can cause greater harm to the fragile ecological environment. This paper studies the interaction among the overburden rock mass, high-speed railway subgrade, and the engineering environment under the cyclic dynamic loads of the high-speed railway, establishes the criteria and evaluation system for evaluating activation deformation of the goaf foundation, and makes a strategic analysis on the ecological environment restoration of construction of the high-speed railway.

2 Dynamic response of subgrade caused by high-speed railway operation

The vibration generated by the railway operation is transmitted to the subgrade and surrounding soil through the steel rail and sleeper rail. Two aspects are mainly considered when analyzing the dynamic stress response: intensity and attenuation of dynamic stress.

For the intensity of the dynamic stress, the formula for calculating the dynamic stress amplitude is given in <Code for Design on Subgrade of Railway>: ${\sigma }_{dl}=0.26\times P\times \left(1+\alpha v\right)$; for the attenuation of dynamic stress, Chen and Bian (2018) showed that the dynamic stress decreases with the increase of the depth, and the attenuation coefficient decreases with the increase of the vehicle speed. It shows that the higher the vehicle speed, the greater is the influence depth of the dynamic loads. In addition, with the increase of vehicle speed, simple models such as the single axle and double axle cannot take into account the actual situation of the railway, and it is necessary to consider the superposition and dispersion effects of the dynamic loads of the high-speed railway.

2.1 Superposition effect of the train dynamic load

At present, the single-point excitation model is mainly used to calculate the dynamic loads of the high-speed railway, and the superposition effect of the dynamic loads between adjacent carriages, adjacent bogies, and different wheel sets cannot be considered, which is quite different from the real dynamic loads and cannot accurately reflect the main dynamic response characteristics of the real railway subgrade. The train is composed of a series of vehicles with almost the same length. As a whole, its wheel loads are non-periodically distributed along the line (Li and Li, 1995). For this reason, suppose that the train is infinitely long and the wheel loads are divided into four combinations, as shown in Figure 2, each group of wheel loads is a periodic moving load and its period is the length L of the vehicle. Since it is assumed that the materials of a roadbed and subgrade are viscoelastic and their properties remain unchanged along the line, the responses generated by the four groups of wheel loads can be combined and superposed in the line, that is, they are equivalent to the dynamic responses generated by the original whole train load, and only one group of wheel loads needs to be calculated for the generated dynamic responses, and the effects of the other three groups can be gained by superposing. When superposing, it is required to be multiplied by a superposition coefficient k₁ which is more than 1 (this coefficient mainly reflects the superposition effect between adjacent wheels and rails, especially related to wheel spacing, number of wheels, and wheel weight.) (Liang et al., 2006).

FIGURE 2

FIGURE 2. Diagram of separation and combination of vehicle loads.

2.2 Transmission and dispersion of rails and sleepers to the train dynamic load

In Section 2.1, the superposition effect of dynamic loads from the high-speed railway is considered and the wheel load is regarded as a concentrated load acting directly on the subgrade surface. Each set of the wheel load must pass through the transfer and dispersion of rails and sleepers before it reaches the surface of the roadbed, which must be considered in the establishment of the theoretical model.

According to the relevant data (Ren et al., 2021), the single wheel load P is considered to be shared by five sleepers. For simplicity, it is assumed that the top surface of the subgrade bears the uniformly distributed pressure distributed within the effective length of the sleeper end, a single wheel load P acts on a certain sleeper, and each wheel load is shared by five sleepers. Therefore, in the cross-sectional analysis, the load must be multiplied by a dispersion coefficient which is less than 1 to reflect the actual situation.

2.3 Establishment of a dynamic model

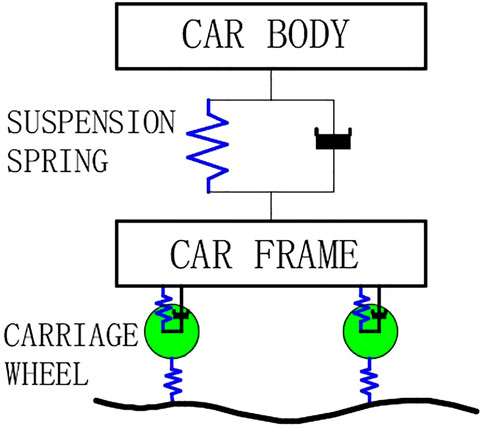
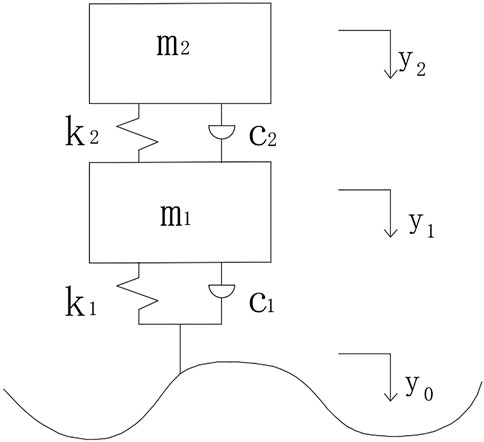
The train load is a very complex problem, and the establishment of the dynamic model needs to involve the axle load of the train, suspension system, running speed, track composition, line smoothness, and other factors at the same time. The more comprehensive the problem is considered, the closer the research result is to the truth, but the more complicated the calculation process is. In order to simplify the calculation process, this paper only considers the vertical vibration caused by the rail surface irregularity, which is the main reason for the vibration and establishes the function of rail surface flatness. Sato (1973) proposed the Sato lumped-parameter model of “half car track,” as shown in Figure 3. It is simplified to the 1/4 vehicle vibration model with the two-degree-of-freedom system, as shown in Figure 4. The dynamic loads acting on the rail surface by the vehicle flow are calculated by using the dynamic load coefficient, that is, the product of the static load and the dynamic load coefficient of the vehicle flow is regarded as the vehicle flow load so as to analyze the influence of vehicle flow load on embankment.

FIGURE 3

FIGURE 3. “Half-car-track” lumped parameter model.

FIGURE 4

FIGURE 4. Vehicle vibration model.

As shown in Figure 4, m₁(kg) is the mass of the frame, k₁(kN/m) is the axle stiffness, c₁(kN s/m) is the axle damping, y₁(m) is the vertical displacement of the frame, m₂(kg) is the mass of the train body, k₂(kN/m) is the suspension stiffness, c₂(kN s/m) is the suspension damping, y₂(m) is the vertical displacement of the train body, and y₀ is the smoothness function of the rail surface.

2.4 Solution of the dynamic model

The basic governing equation of dynamic calculation is

$\mathrm{f}\left(\mathrm{t}\right)=\mathrm{M}\ddot{Y}+C\dot{Y}+KY,(1)$

where

M is the mass matrix

C is the damping matrix

K is the stiffness matrix

Y is the displacement matrix

$\mathrm{f}\left(\mathrm{t}\right)$ is the load matrix.

The specific expression is

$\left\{\begin{array}{l}\left[M\right]=\left[\begin{array}{cc}{m}_2& 0\\ 0& m_1\end{array}\right],\\ \left[C\right]=\left[\begin{array}{cc}{c}_2& -c_2\\ -c_2& c_2+c_1\end{array}\right],\\ \left[K\right]=\left[\begin{array}{cc}{k}_2& -k_2\\ -k_2& k_2+k_1\end{array}\right],\\ \left[Y\right]=\left[\begin{array}{c}{y}_2\\ y_1\end{array}\right],\\ \left[F\right]=\left[\begin{array}{c}0\\ c_1{y}_0\cdot +k_1{y}_0\end{array}\right].\end{array}\right.(2)$

According to Eqs 1, 2, the result is as follows:

$\{\begin{array}{l}{m}_2{\ddot{y}}_2+c_2\left({\dot{y}}_2-{\dot{y}}_1\right)+k_2\left(y_2-y_1\right)=0,\hfill \\ m_1{\ddot{y}}_1+c_1\left({\dot{y}}_1-{\dot{y}}_0\right)+k_1\left(y_1-y_0\right)\hfill \\ -c_2\left({\dot{y}}_2-{\dot{y}}_1\right)-k_2\left(y_2-y_1\right)=0.\hfill \end{array}(3)$

Let $z_1=y_1-y_0,z_2=y_2-y_1,f_1=\frac{c_1}{m_1},f_2=\frac{c_2}{m_2},\mu =\frac{m_2}{m_1},g_1=\frac{k_1}{m_1},g_2=\frac{k_2}{m_2},$ by sorting out Eq. 3, the result is as follows:

$\{\begin{array}{c}\ddot{z_1}+\ddot{z_2}+f_2\dot{z_2}+g_2{z}_2=-\ddot{y_0,}\\ \ddot{z_1}+f_1\dot{z_1}-f_2\mu \dot{z_2}+g_1{z}_1-\mu g_2\dot{z_2}=-\ddot{y_0.}\end{array}(4)$

According to the undetermined coefficient method, set

$\left\{\begin{array}{c}{z}_1=A_1\cos \left(\omega t\right)+A_2\sin \left(\omega t\right),\\ z_2=A_3\cos \left(\omega t\right)+A_4\sin \left(\omega t\right).\end{array}\right.(5)$

Written in matrix form,

$\left[\begin{array}{cccc}-{\omega }^2& 0& g_2-{\omega }^2& f_2\omega \\ 0& -{\omega }^2& -f_2\omega & g_2-{\omega }^2\\ g_1-{\omega }^2& f_1\omega & -\mu g_2& -\mu f_2\omega \\ -f_1\omega & g_1-{\omega }^2& \mu f_2\omega & -\mu g_2\end{array}\right]\left[\begin{array}{c}{A}_1\\ A_2\\ A_3\\ A_4\end{array}\right]=\left[\begin{array}{c}0\\ Q{\omega }^2\\ 0\\ Q{\omega }^2\end{array}\right].(6)$

According to the MATLAB program, A₁ and A₂ can be obtained.

When the high-speed railway runs on the track, the wheels actually jump on the track with a certain frequency and amplitude and the dynamic loads are sometimes greater than the static loads, sometimes less than the static loads, showing a state of fluctuation. The additional dynamic load is a function of the amplitude, wavelength, and vehicle speed of the unevenness, as shown in Eq. 7.

$y_0=f\left(t\right)=Qsin\left(\omega t\right),(7)$

where Q is the unevenness of the track surface, m; ω is the frequency, ω=2πν/λ; ν is the speed of the vehicle, km/h; and λ is the wavelength, m.

Substituting z₁, z₂, and y₀ in Eq. 6, the additional dynamic load of the wheel to the track is obtained as

$P_d=\sqrt{\left(k_1^2+c_1^2{\omega }^2\right)\left(A_1^2+A_2^2\right)}\sin \left(\omega t+\phi \right).(8)$

Therefore,

$P_{d,\mathit{max}}=\sqrt{\left(k_1^2+c_1^2{\omega }^2\right)\left(A_1^2+A_2^2\right).}(9)$

Among it,

$\mathrm{\phi }=\theta +co{s}^{-1}(\frac{k_1}{\sqrt{k_1^2+{\left(c_1\omega \right)}^2}},\theta =ta{n}^{-1}\left(A_1/A_2\right).$

Therefore, the dynamic load coefficient is

$\mathrm{D}=1+P_{d,\mathit{max}}/P_{wheel},(10)$

where $P_{wheel}$ is the static axle load of the train, kN, and $P_{wheel}$ = (m₁+m₂)g, g=9.8N/kg.

The total uniaxial vertical vibration load of vehicle is

$P={\mathit{P}}_{\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{e}\mathrm{l}}+P_{d,\max }.(11)$

Considering the superposition and combination of the wheelset force on the line and the dispersed transmission factors of rails and sleepers, Eq. 11 is modified, and the following can be obtained:

${\mathrm{P}}^{\prime }={\mathrm{P}}_{\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{e}\mathrm{l}}+{\mathrm{\rho }}_1{\mathrm{\rho }}_2{\mathrm{P}}_{\mathrm{d},\max },(12)$

where ${\rho }_1$ is the superposition coefficient and ${\rho }_2$ is the dispersion coefficient. ${\rho }_1$ and ${\rho }_2$ can be calculated according to the vehicle type and track structure, including the axle load, length, train speed, rail and sleeper type, and other conditions. Generally, ${\rho }_1$ is in the range of 1.2–1.7, and ${\rho }_2$ is in the range of 0.6–0.9.

3 Activation judgment of the goaf foundation in the high-speed railway

3.1 Influence depth of new loads

For the high-speed railway with the underlying mined-out area, the new embankment and vehicles in operation will form loads, which will be continuously transmitted downward in a certain form. When reaching a certain depth, the rock mass in equilibrium at the lower part will be disturbed and destabilized, resulting in the decline of embankment stability and re-deformation, which will make it impossible for vehicles to be driven normally and safely. In this paper, the new embankment materials above the goaf foundation are taken as the static load and the train in operation as the dynamic load, and the influence depth of the newly added loads on the goaf foundation is analyzed.

3.1.1 Additional stress caused by the static load

Since the length–width ratio of the embankment for the high-speed railway is very large (l/b $\gg$ 10), it can be simplified as the vertical uniform strip load of the plane problem. According to the Boussinesq equation, the expression of vertical stress at any point M under the action of the vertical concentrated force P in the elastic body of semi-infinite space is deduced as follows:

${\sigma }_z=\frac{3P{z}^3}{2\pi R^5}(13)$

where R is the distance between point M and the action point O of the concentrated force P, m; σ_z is the vertical stress with the distance R from the depth z to the concentrated force P in the foundation, kPa. By integrating Eq. 13, it can be deduced that the vertical stress of any point M in the foundation under the action of the strip uniformly distributed load P₀ is

${\sigma }_z=\frac{2}{\pi }\left[\frac{2n}{1+4n^2}+\arctan \frac{1}{2n}\right]\cdot P_0.(14)$

where n=z/b, and b is the width of the strip embankment, m.

3.1.2 Additional stress caused by the dynamic load

According to the aforementioned analysis, considering the superposition of the wheelset force of the train on the line and the dispersion of the rails and sleepers, the additional stress generated by the vertical vibration load of the vehicle is

${\mathrm{\sigma }}_{\mathrm{d},\max }^{\prime }=\frac{3{\mathrm{P}}^{\prime }{\mathrm{Z}}^3}{2{\pi \mathrm{R}}^5}(15)$

3.1.3 Calculation of the disturbance depth

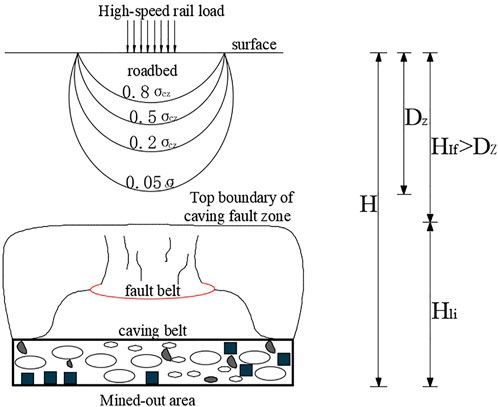
According to Zhou (2017), for the safety of the traffic operation, under the dynamic load of the high-speed railway, the additional stress in the foundation should be 5% of the gravity stress to determine the influence depth of the high-speed railway above the goaf foundation.

${\sigma }_{cz}=\gamma z(16)$

where σ_cz is the gravity stress (kPa) of the rock mass with a weight unit of γ (kN/m³) and a depth of z (m).

${\sigma }_z=0.05\gamma D_z(17)$

Considering the static load of the newly added embankment as a strip uniform load, according to the Flanant elastic theory, the influence depth ($D_{z1}$) of the static load of the embankment is calculated as

$D_{z1}=2\sqrt{\frac{10P_0}{\pi \gamma }}(18)$

The train wheel load is regarded as the moving concentrated force acting on the continuous steel rails, and the steel rails transmit the load to the fasteners and then act on the uniformly distributed sleepers. Considering the superposition of the wheelset force on the line and the dispersion effect of steel rails and sleepers, refer to Eqs 12, 15, 17; the influence depth ($D_{z2}$) of the dynamic load of the high-speed railway is obtained as follows:

$D_{z2}=\sqrt[3]{\frac{30P^{\prime }}{\pi \gamma }}.(19)$

In Eq. 18, the calculation starting point of the influence depth of static load is the ground surface, and in Eq. 19, the calculation starting point of the influence depth of the dynamic load is the top surface of embankment.

3.2 Criteria for activation of the goaf foundation

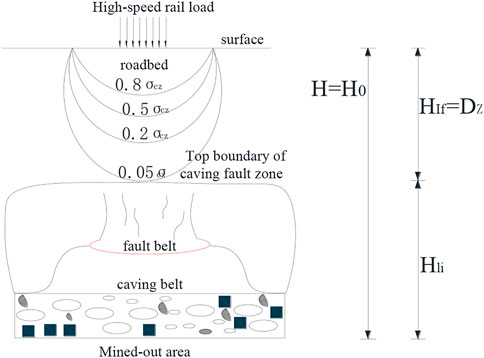
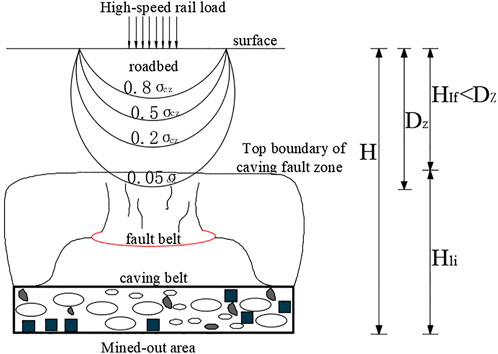
The activation deformation of the goaf foundation is the main influencing factor of safety evaluation. The position relationship between the influence depth of the load and the height of the collapsing fault zone in the goaf foundation is typically used to determine whether the goaf foundation is activated. This position relationship includes three cases: i) there is a certain distance between the influence depth of the loads and the height of the collapse fault zone, that is, separation, as shown in Figure 5, and the goaf foundation does not produce activation deformation; ii) the influence depth of the load is in contact with the height of the collapse fault zone, that is, the tangent, as shown in Figure 6, and the activation deformation of the goaf foundation is in a critical state; iii) the influence depth of the load enters into the height of collapse fault zone, that is, intersection, as shown in Figure 7, and the goaf foundation produces activation deformation.

FIGURE 5

FIGURE 5. Positional relationship: Separation.

FIGURE 6

FIGURE 6. Positional relationship: Tangent.

FIGURE 7

FIGURE 7. Positional relationship: Secant.

The depth ${\mathrm{H}}_{lf}$ of the caving fault zone is calculated as follows:

$H_{lf}=H-H_{li}.(20)$

where ${\mathrm{H}}_{li}$ is the height of the collapse fault zone, m; $\mathrm{H}$ is the mining depth of goaf, m.

According to the National Standard of the People’s Republic of China (2017), the critical depth H₀ of activation of the goaf foundation meets the following conditions:

$H_0=D_z+H_{li}.(21)$

where D_z is the influence depth of the high-speed railway (including the dynamic load and static load), m.

Since the influence of external factors, such as mining, groundwater, and earthquake in the adjacent areas, is not considered in this paper, according to the conventional critical instability conditions, it is too dangerous. Although the influence depth of the loads is separated from the height of the collapse fault zone, the goaf foundation is still affected by the additional stress, resulting in instability. Therefore, in order to ensure accuracy and improve safety, other factors affecting the stability of the goaf foundation should be considered and the activation condition of the goaf foundation is modified.

$H_0=D_z+H_{li}+H_s.(22)$

In Eq. 22, H_s (m) is the height of the protective belt between D_z and H_li, taking D_z × 20%.

The activation deformation of the goaf foundation shall meet one of the following conditions:

$H_0\ge H\mathrm{o}\mathrm{r}{D}_z\le H_{lf}.(23)$

4 Example and analysis

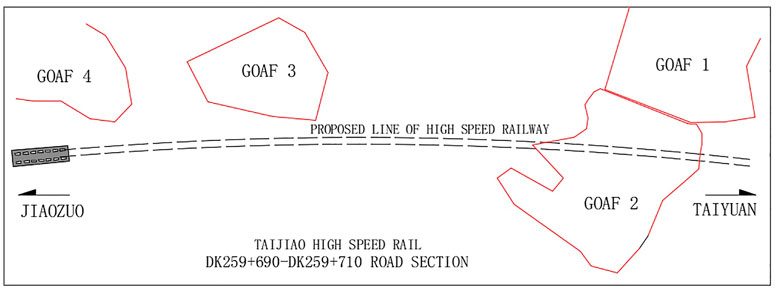
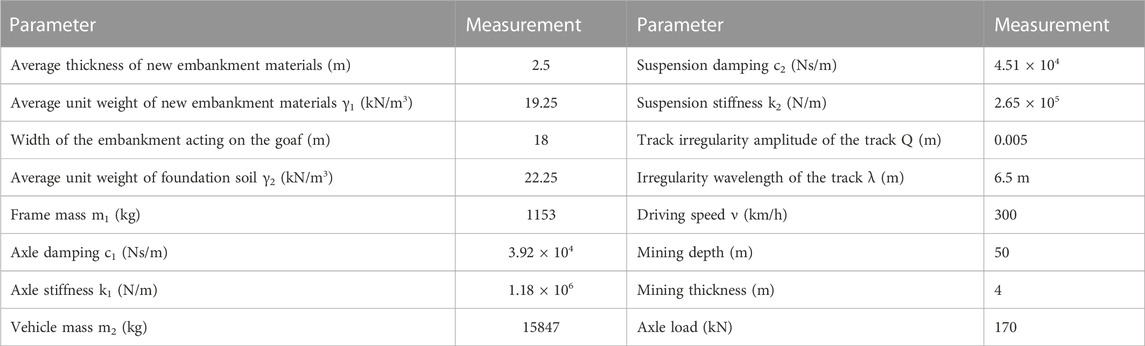
In 2020, the project team conducted field investigation on the goaf foundation of Qinshui coalfield under the DK259+690-DK259+710.00 section of the Taiyuan–Jiaozuo high-speed railway and obtained basic information, such as the embankment design and the overlying strata of the mined-out area. The distribution of mined-out area is shown in Figure 8. The high speed railway and topography of goaf sites are shown in Figure 9. Taking the No.2 goaf crossed by the proposed high-speed railway line as an example, the buried depth is 45.2–60.3 m, it follows shallow mining, and the mining thickness is 1.2–6.5 m. Taking the high-speed railway in operation above the goaf foundation as the analysis object, the dynamic load coefficient is determined and the influence depth of the newly added loads is calculated. According to the raw data on field measurement and the design of <grouting treatment of the foundation of Taiyuan–Jiaozuo high-speed railway crossing mined-out regions>, the relevant data on goaf and subgrade are given, as shown in Table 1. The parameters of the high-speed railway are taken from Gao (2011).

FIGURE 8

FIGURE 8. Distribution of goafs.

FIGURE 9

FIGURE 9. High-speed railway and topography of goaf sites. (A) Cutting segment of high-speed railway lines. (B) Bridge, embankment, and the river of high-speed railway lines.

TABLE 1

TABLE 1. Calculation parameters.

4.1 Disturbance depth of additional loads

The waveform function of the rail surface is

y₀(t)=Qsin(ωt)=.005sin(80.51t).

Here, ω = 80.51, μ = 13.74, f₁ = 34, f₂ = 2.85, g₁ = 1023.42, g₂ = 16.72, and Q = 0.005 are substituted into Eq. 6, and the superposition coefficient and dispersion coefficient are taken into account. According to the calculation conditions in the Research Report on Dynamic Simulation (Southwest Jiaotong University, 2000), ${\rho }_1$ is 1.538 and ${\rho }_2$ is 0.7.

The maximum dynamic load of the wheel on the rail surface is ${\mathrm{P}}^{\prime }$ =182795.22N.

Therefore, D_z2 = 4.28 m, where the depth of influence caused by an additional dynamic load is 1.91 m.

Considering

$Dz1=2\sqrt{\frac{10P_0}{\pi \gamma }}=22.27m,$

we obtain

$D_Z=D_{Z2}-2.5+D_{Z1}=24.05m.$

4.2 Height of the collapse fault zone in the goaf foundation

According to the National Standard of the People’s Republic of China (2017), the maximum height of the collapse fault zone H_li can be obtained

$H_{li}=10\sqrt{\sum M}+5=25m.$

According to Eqs 22, 23, the following can be obtained: D_z+H_li+H_s=53.86 m> H. Therefore, it is judged that the goaf foundation is more likely to be activated and destabilized, and the goaf foundation needs to be treated by grouting. The stability evaluation of the goaf foundation has been conducted in the previous survey, and most of the goaf foundation is unstable. The information about the goaf foundation in the investigation report is shown in Table 2. The evaluation results are consistent with the actual field results.

TABLE 2

TABLE 2. Features of the goaf foundation.

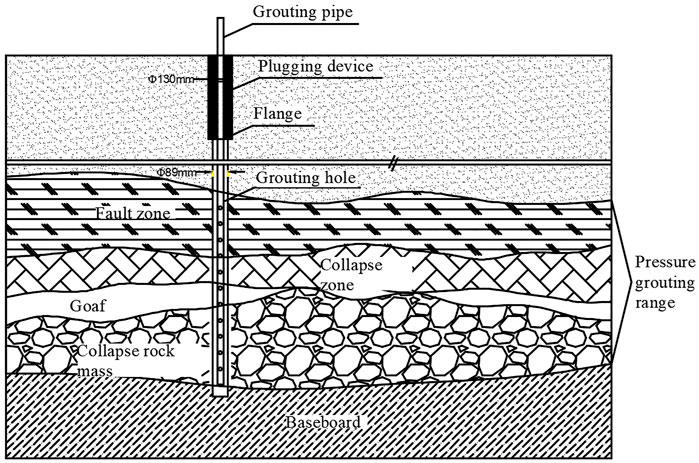
The solution of this section adopts grouting with full filling pressure to reinforce the goaf foundation. When applying this method, holes are drilled into the surface and the grouting pipelines penetrate through the collapse zone and fault zone to 1∼2 m below the floor of the goaf. The main functions of grouting are to fill the empty holes, voids, and cracks and reinforce the fractured and broken rock mass. The aim is to reduce or eliminate the residual deformation of the goaf site and the activated deformation of the goaf foundation, as shown in Figure 10. The distribution of grouting holes in the goaf foundation of the Taiyuan–Jiaozuo high-speed railway is shown in Figure 11.

FIGURE 10

FIGURE 10. Schematic diagram of foundation grouting treatment in goaf.

FIGURE 11

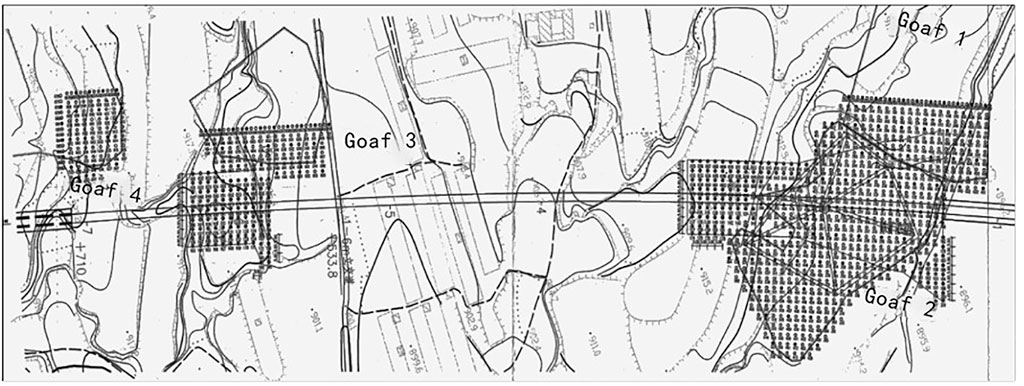
FIGURE 11. Location distribution of grouting holes in the goaf foundation of the Taiyuan–Jiaozuo high-speed railway.

4.3 Strategic analysis of the ecological environment in mining areas

The average buried depth of goaf 2 is 45.2–60.3 m, and the mining thickness is 1.2–6.5 m. The dip angle of the coal seam is smaller, which belongs to moderately inclined coal seams. The overburden rock mass of coal seams belongs to medium hardness. These geological conditions and characteristics result in the typical distribution of the caving zone, fault zone, and bending zone in the goaf foundation. According to the previous calculation results, the height of the collapse fault zone is 25 m, which is 2.8 times the maximum mining thickness. When the subsidence of mined-out areas affects the surface, it will cause geological disasters, such as ground subsidence and surface cracks. In addition, the faults in the mined-out area of the Qinshui coalfield are relatively developed, and coal mining promotes the activation of the faults, connecting the aquifer with the mined-out area. This has caused the groundwater level in the mined-out area of the Qinshui coalfield to drop and the water environment to deteriorate, which has become a key problem restricting the urban economic transformation and sustainable development. In order to solve the impact of the aforementioned artificial mining activities on the environment, the construction of the high-speed railway on goaf sites can provide a good ecological restoration. At the same time of high-speed railway construction, the goaf foundation shall be treated to effectively control disasters of goaf. In addition, the land reclamation and greening work along the high-speed railway lines can repair the ecological environment disasters caused by coal mining.

5 Discussion

1) The analysis of the interaction between the train and track, which is a complex process, is the key to calculate the additional stress caused by the train-induced dynamic loads. Not only the dispersion effect of the roadbed and embankment but also the superposition effect of the dynamic loads should be considered. At present, the 1/4 vehicle vibration model is mainly used to calculate the vibration stress of vehicles on highways and expressways. Compared with automobiles and high-speed tracks, high-speed trains have their own characteristics. When using the same model to calculate objects with different working conditions, it is necessary to consider the differences of working conditions.

2) The flatness requirement of the high-speed railway track is higher. In order to simplify the calculation, most literature seldom consider the influence of track surface irregularity on vibration, and the calculated results are quite different from the actual results.

3) In order to simplify the calculation, this paper only considers the vertical vibration caused by rail surface irregularity and establishes the flatness function of the rail surface, which is the main cause of vibration. The calculation results are not compared with other calculation methods (such as the excitation force function). The contribution of transverse vibration to additional stress is not discussed here.

4) This paper puts forward a relatively simple theoretical analytical formula, which has a great guiding significance for engineering practice. However, the selection of parameters is very important, which directly affects the reliability of the calculation results. When using the theoretical formula, designers should pay attention to the selection of parameters, such as the irregularity wavelength and irregularity amplitude.

5) In future, spatio-temporal evolution patterns of the overburdened structure, groundwater, and ecological environment in the coal mine area will be revealed, and the information system of coal mining, overburdened structure, hydrogeology, and ecological environment evolution, including the evaluation method of environment and ecological security will be established. From coal mining to overburdened structure, then to groundwater, finally to mining subsidence and surface ecology, some research must be carried out, including realizing reconstruction and repair of the whole cycle and combining the source control with end treatment to achieve high-quality development of coal mining areas.

6 Conclusion

In this paper, based on the additional stress method, a vehicle vibration model is established by considering the superimposition and combination of the wheelset force on the line and the dispersed transmission factors of rails and sleepers. Taking the section DK259+690-DK259+710.00 of the Taiyuan–Jiaozuo high-speed railway as the research background, the activation deformation of the goaf foundation under the operation of the Taiyuan–Jiaozuo high-speed railway is calculated. The research results are as follows:

1) The deformation evolution law of the overlying rock and soil mass of the goaf foundation and the deformation characteristics of buildings and structures in the goaf sites are revealed. The method of additional stress influence depth for determining the activation of the goaf foundation is proposed, which provides a theoretical basis for establishing the method system to calculate the foundation deformation of buildings and structures in the goaf sites.

2) Based on the standard high-speed railway axle load of 170 kN and running speed of 300 km/h, combined with the information on the overlying rock layer in shallow goaf sites of the Qinshui coalfield, MATLAB mathematical calculation software was used to obtain the influence depth of the additional dynamic load of 1.91 m by using the established vehicle vibration model.

3) During the operation of the high-speed railway, the additional load of track irregularity on the foundation is the result of the interaction between the high-speed railway and the embankment. The influence depth calculated by considering the dynamic load and not considering the dynamic load is quite different. It shows that the influence of the additional dynamic load on the operation of the high-speed railway above the goaf foundation cannot be ignored, which is one of the main cause of activation deformation.

4) When the high-speed railway is built in the goaf sites, it is usually necessary to treat the goaf foundation of the high-speed railway, which can effectively control disasters so as to achieve coordinated development of ecological environment protection and coal development and utilization.

This paper only considers the impact of the high-speed railway cyclic dynamic load on the underlying goaf and does not consider the effects of mining, groundwater, and earthquake in the adjacent area. The coupling effect should be studied subsequently.

Data availability statement

The original contribution presented in the study is included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

HW was responsible for reviewing and editing of the article, JZ was responsible for original draft preparation of the article, and JC was responsible for the investigation and data sorting of the cases. ZlD was responsible for funding acquisition. ZyD was responsible for data curation. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant number U1810203, and the General Research Project of Humanities and Social Sciences in Colleges and Universities of Henan Province, grant number 2023-ZDJH-145.

Acknowledgments

The authors wish to acknowledge the financial support given to this research by the National Fund Committee. They also thank for the kind assistance and valuable contributions of the staff of the School of Civil Engineering, Henan Polytechnic University, who provided field investigation and field testing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Buodhu, M., and Adiyaman, I. B. (2010). Mechanics of land subsidence due to groundwater pumping. Int. J. Numer. Anal. Methods Geomechanics 34 (14), 1459–1478. doi:10.1002/nag.863

CrossRef Full Text | Google Scholar

Chen, Y., and Bian, X. (2018). The review of high-speed railway track foundation Dynamics. China Civ. Eng. J. 51 (6), 1–13.

Google Scholar

Cheng, J. H., Guo, L. L., Wang, H., and Dun, Z. L. (2022). Time-varying analysis of retaining structures enhanced with soil nails and prestressed anchors. Buildings 12 (4), 458. doi:10.3390/buildings12040458

CrossRef Full Text | Google Scholar

Du, D., Zhang, X., Zhang, S., and Yang, Y. (2015). Influence of goaf on highway deformation. J. Guangxi Univ. (Nat Sci Ed). 40 (4), 984–988.

Google Scholar

Feng, G., Bai, J., Shi, X., Qi, T., Wang, P., Guo, J., et al. (2021). Key pillar theory in the chain failure of residual coal pillars and its application prospect. J. China Coal Soc. 46 (1), 164–179.

Google Scholar

Fu, Z., Zhou, W., Zhu, Y., Pan, H., Luo, X., and Luo, X. (2021). Analysis on deformation of deep foundation pit and vibration isolation effect under the influence of train dynamic load. J. Fuzhou Univ. Natl. Sci. Ed. 49, 537–543.

Google Scholar

Gao, G., Nie, C., and Zhou, T. (2014). Review of surface deformation in the area under dynamic load. J. Undergr. Space Eng. 10 (S2), 1963–1969.

Google Scholar

Gao, X. J. (2011). Seismic response analysis of long-span bridge considering earthquake and vertical trainloads. Beijing: Beijing Jiaotong University.

Google Scholar

Guo, G., Zhang, G., and Liu, B. (2004). Influence of ground load on critical disturbance depth of underground goaf. Ground Press. Strata Control (1), 72–73. 77.

Google Scholar

Guo, Q., Guo, G., Lv, X., and Zhang, Y. (2021). Study on numerical simulation of safety depth of goaf under expressway. Coal Sci. Technol. 49 (10), 193–200.

Google Scholar

Li, J. S., and Li, K. C. (1995). The finite element analysis about dynamic response of subgrade of high speed railway. J. China Railw. Soc. 17 (1), 66–75.

Google Scholar

Li, L., Hao, G., Wu, K., and Li, R. (2012). New viewpoint of foundation stability of newly building upon goaf. Energy Procedia 17, 1717–1723. doi:10.1016/j.egypro.2012.02.303

CrossRef Full Text | Google Scholar

Li, L. J. (2004). Research on collapse disaster of goaf sites and prevention countermeasures in coal cities in China. Taiyuan: Shanxi Academy of Social Sciences.

Google Scholar

Li, Y., Nie, R., Li, Y., Leng, W., and Ruan, B. (2021). Cumulative plastic deformation of subgrade fine-grained soil under intermittent cyclic loading and its prediction model. Rock Soil Mech. 42 (4), 1065–1077.

Google Scholar

Liang, B., Luo, H., and Sun, C. X. (2006). Simulated study on vibration load of high speed railway. J. China Railw. Soc. 28 (4), 89–94.

Google Scholar

Liu, Z., Wang, C., Yang, R., Sun, Q., and Jiang, N. (2019). Simulation analysis of key factors of activation instability in tope area. Coal Mine Saf. 50 (06), 240–244.

Google Scholar

National standard of the people's Republic of China (2017). GB 51044-2014 Code for investigation of geotechnical engineering in the coal mine goaf. Beijing: China Planning Press.

Google Scholar

Ren, L., Ning, H., Zou, Y., Dun, Z., and Guo, W. (2021). Research status and prospect on deformation control of high-speed railway subgrade in goaf site. J. China coal Soc. 46 (08), 2534–2547.

Google Scholar

Ren, L., Zhou, G., Dun, Z., He, T., Yang, Q., and Zhang, M. (2018). Case study on suitability and settlement of foundation in goaf site. Rock Soil Mech. 39 (8), 2922–29322940.

Google Scholar

Ren, W., Guo, C., Peng, Z., and Wang, Y. (2010). Model experimental research on deformation and subsidence characteristics of ground and wall rock due to mining under thick overlying terrane. J. Rock Mech. Min. Sci. 47, 614–624. doi:10.1016/j.ijrmms.2009.12.012

CrossRef Full Text | Google Scholar

Sato, Y. (1973). Abnormal wheel load of test train. Perm. Way (Tokyo) 14 (53), 1–8.

Google Scholar

Southwest Jiaotong University (2000). Lanzhou railway college research report on dynamic simulation of speed-up reconstruction project of beijing qinhuangdao passenger transport corridor. Chengdu: Southwest Jiaotong University; Lanzhou: Lanzhou Railway College.

Google Scholar

Sun, J., Li, M., and Tian, H. (2019). Dynamic load response analysis of heavy vehicle on unevenness pavement. J. Chongqing Jiaot. Univ. Natl. Sci. Ed. 38 (7), 48–53.

Google Scholar

Tong, L., Liu, L., Yu, Q., and Liu, S. (2013). Tunneling in abandoned coal mine areas:Problems, impacts and protection measures. Tunn. Undergr. Space Technol. 38, 409–422. doi:10.1016/j.tust.2013.07.020

CrossRef Full Text | Google Scholar

Wang, S., Shi, K., He, Y., and Wang, X. (2019). Dynamic response analysis of middle pillar for ultra-small spacing tunnels under train vibration loads. J. Eng. Sci. Technol. Rev. 12 (3), 30–37.

Google Scholar

Wang, Y. (2013). Deformation and instability-evolution analysis of high embankment caused by waste area activation in faultage geological structure condition. Chin. J. Rock Mech. Eng. 32 (S2), 3784–3789.

Google Scholar

Xu, P., Mao, X., Zhang, M., Zhou, Y., and Yu, B. (2014). Safety analysis of building foundations over old goaf under additional stress from building load and seismic actions. Int. J. Min. Sci. Technol. 4 (5), 713–718. doi:10.1016/j.ijmst.2014.03.030

CrossRef Full Text | Google Scholar

Yang, C., Xie, S., and Sun, J. (2015). Vehicle dynamic load coefficient analysis based on pavement roughness. J. Chongqing Jiaot. Univ. Natl. Sci. Ed. 34 (4), 77–80.

Google Scholar

Yao, H., Lu, Z., Luo, H., and Yang, Y. (2009). Dynamic response of rough pavement on Kelvin foundation subjected to traffic loads. Rock Soil Mech. 30 (4), 890–896.

Google Scholar

Zhang, G., Kang, H., and Zheng, Y. (2011). Establishment of vehicle vibration model and calculation of vehicle dynamic load. J. Wuhan Univ. Technol. Transp. Sci. Eng. 35 (4), 771–775.

Google Scholar

Zhang, Z., Wang, Y., Zhang, Z., and Feng, T. (2015). Analysis on disturbance to subsidence area by dynamic load of highway. J. Saf. Sci. Technol. 11 (01), 104–109.

Google Scholar

Zhou, D., Wu, K., Cheng, G., and Li, L. (2015). Mechanism of mining subsidence in coal mining area with thick alluvium soil in China. Arabian J. Geosciences 8 (4), 1855–1867. doi:10.1007/s12517-014-1382-2

CrossRef Full Text | Google Scholar

Zhou, T. (2017). Analysis of the subgrade settlement above the goaf under traffic loading. Zhengzhou: Zhengzhou University.

Google Scholar