- Department of Biological and Agricultural Engineering, Zachry Department of Civil and Environmental Engineering, Texas A and M University, College Station, TX, United States
Multispecies pollutant migration often occurs in polluted groundwater systems. Most of the multispecies problems that have been dealt in the literature assume constant transport parameters, primarily because analytical solutions for varying parameters become a challenge. The present study analytically solves a two-species convection-dispersion transport equation, considering spatially varying dispersion coefficient and seepage velocity, which corresponds to the steady migration in a steady flow domain. Indeed, the methodology can be adopted for other cases, such as the transient migration in a steady flow domain and transient migration in an unsteady flow domain, without any difficulty. Three kinds of homotopy-based methods, namely the homotopy perturbation method (HPM), homotopy analysis method (HAM), and optimal homotopy asymptotic method (OHAM), are used to derive approximate analytical solutions in the form of truncated series. In homotopy analysis method, the convergence-control parameter ℏ plays a key role in the convergence of the series solution. It is observed that for a specific case of this parameter, namely ℏ=−1, the HAM-based solution recovers the HPM-based solution. For the verification of homotopy-based solutions, we utilize the MATLAB routine pdepe, which efficiently solves a class of parabolic PDEs (single/system). An excellent agreement is found between the derived analytical solutions and the numerical solutions for all three methods. Further, a quantitative assessment is carried out for the derived solutions. Also, convergence theorems are proposed for the series solutions obtained using HAM and OHAM.
1 Introduction
Pollution is caused by a number of sources, such as agricultural fertilizers, erosion, industries, energy generation, waste disposal, hospital wastage, vehicular transport, nuclear waste, and domestic waste. A significant portion of pollution generated by these sources finds its way either directly or indirectly into ground water (Sposito et al., 1979; Domenico 1987; Bear 1988; Clement et al., 1998; Batu 2005). Often pollutants are different species, and their chemical characteristics are different. In general, pollutant transport in groundwater is modeled using the conservation of mass of water, flux law for flow of water, conservation of mass of pollutant, and flux law for pollutant transport. Depending on the type, a pollutant can be physical, chemical, or biological. A chemical pollutant can be conservative or non-conservative for which production and decay functions need to be specified. When these equations are combined, the resulting equation is the convection-dispersion equation. This equation is for a specific species. This paper discusses the case of two species pollutant transport.
There are several works done for the analysis of multispecies pollutant transport problems. These works adopted either analytical or numerical methods. The analytical solutions were obtained using Fourier transforms, Laplace transform, general integral transforms, decomposition methods, series solutions, etc. (Lunn et al., 1996; Van Genuchten 1985; Fujikawa and Fukui 1990; Sun and Clement 1999; Sun et al., 1999; Chamkha 2005; Slodička and Balážová, 2008; Slodička and Balážová, 2010; Natarajan and Kumar 2010; Chen et al., 2012; Simpson and Ellery 2014). Numerical methods basically adopted the finite difference method (Arnold et al., 2017; Natarajan and Kumar 2018). However, the afore-mentioned works used constant transport parameter—a consideration that makes it easier to deal it mathematically. In reality, it is necessary to model the system using variable parameters in order to fully understand the pollutant dispersion behaviour. There are a few works available for the variable transport parameters; however, some are for single species or restricted formulation. Chaudhary and Singh (2020) used the homotopy analysis method (HAM) for two-species convection-dispersion transport equation, considering spatial-temporal varying dispersion coefficient and seepage velocity. They used the standard HAM to deal with the system of PDEs governing the phenomenon. However, since the inception of HAM, there have been several modifications done. The most popular variants of the method are homotopy perturbation method (HPM) and optimal homotopy asymptotic method (OHAM). On the other hand, it is worth mentioning that the transport of heavy metals in groundwater and the interactions between them and the soil medium are key concepts in environmental engineering. Such transport processes are useful for studying the damage to the environment caused by the smelting of metallic materials, the seepage of landfill leachates, the use of pesticides and chemical fertilizers, the treatment of municipal wastewater, etc. Furthermore, the solid particles (bacteria, silicon powders, etc.) present in the soil interact with the transport mechanism of the heavy metals by accelerating the migration rate of those. Thus, in order to choose a suspended matter of particular for removing the heavy metals from soils, it is crucial to understand the coupling mechanism. In fact, because of the suspended particles adsorb the heavy metals, they show an influence on the migration process of the metals in soil under seepage conditions. There are several factors affecting the coupling mechanism of heavy metals and suspended particles, such as the size and concentration of the particles, seepage velocity, types of heavy metals, porous media, coupling mechanism (solid-solid, solid-liquid, gas-liquid, etc.). The detail discussion can be found in Bai et al. (2021a), Bai et al. (2021b).
The core idea of homotopy-based methods is based on the concept of homotopy from topology. It creates a continuous mapping that deforms continuously to obtain one function from another. Liao (1992) used this concept to develop an analytical method for the solution of non-linear problems in terms of a series solution. Since then, it has been used extensively in different areas of science and engineering (Liao, 2003; Liao, 2012). On the other hand, He (1999) presented an analytical methodology named HPM. Recently, Marinca and Herişanu (2008) extended the concept of HAM using an approximation method to derive the so-called OHAM. These methods have their own advantages/disadvantages in terms of their applicability. Therefore, the present work presents three kinds of approximate series solutions using HAM, HPM, and OHAM. This paper considers the case of spatially varying transport parameters. Indeed, the methodologies can be adopted for other cases such as the ones provided in Chaudhary and Singh (2020).
2 Brief overview of homotopy-based methods
Here, first we describe the homotopy-based methods in a general framework considering a system of PDEs. Before doing so, it is pertinent to mention that all these methods are based on the mathematical concept called ‘homotopy’ from topology (Liao 1992). Two objects (mathematical) are homotopic if one can be continuously deformed into the other. Mathematically, a homotopy
2.1 Homotopy analysis method
Let a system of PDEs be written as:
where
subject to the initial and boundary conditions:
where
where
and
where
One can truncate the series Eq. 7 to obtain an approximate solution to a non-linear system. It can be seen that the method involves several operators and functions, which should be adequately chosen in order to have a convergent series. For that purpose, Liao (2003) proposed three generalized rules, namely rule of solution expressions, rule of coefficient ergodicity, and rule of solution existence. These rules will be discussed in a later section in relation to the problem under consideration.
2.2 Homotopy perturbation method
Here, we rewrite a system of PDEs as follows:
Now, we can construct a homotopy that satisfies (He 1999):
where the symbols denote the same variables as mentioned in the previous section. Also, similar to HAM, Eq. 9 shows that at
where
In this method, similar to the classical perturbation approach, one can substitute the series (10) in Eq. 9 and then equate the like powers of
2.3 Optimal homotopy asymptotic method
In order to obtain an accurate approximate solution with just a few terms of the series, Marinca and Herişanu (2008) proposed a variant of homotopy-based method, known as the optimal homotopy asymptotic method (OHAM), using asymptotic expansions of the functions and operators. We consider a non-linear system of PDEs as:
subject to the initial and boundary conditions:
where symbols denote the same variables as discussed in the previous section. Following HAM, one can construct a family of equations as follows:
where symbols have their usual meaning and
It is easy to verify that when
subject to the boundary conditions:
In OHAM, expanding the auxiliary function with respect to the embedding parameter is the key step. The auxiliary function
where
Substituting Eq. 19 into Eq. 14, and equating the like powers of
For
subject to the initial and boundary conditions:
where the term
It can be observed from Eq. 22 that like HAM and HPM, OHAM also converts the original non-linear equation into an infinite set of linear sub-equations. Further, the method does not depend on the presence of a small parameter in the governing equation. The convergence of the series Eq. 19 depends on the choice of
Finally, the approximate solution can be obtained by considering a finite number of terms of the series Eq. 25. The unknown parameters
3 Governing equation and solution methodologies
In a one-dimensional flow field, the general form for a reactive transport system which describes the phenomenon of multi-species migration having spatially and temporally varying parameters can be modelled as follows (Chaudhary and Singh 2020):
Here,
The present work considers two-species system (i.e.,
where
The initial and boundary conditions for the model can be given as follows:
where
Eqs 29, 30, 31 show that spatially dependent pollution exists initially for the parent species. However, for the daughter species, the initial concentration is zero.
Based on the forms of
where
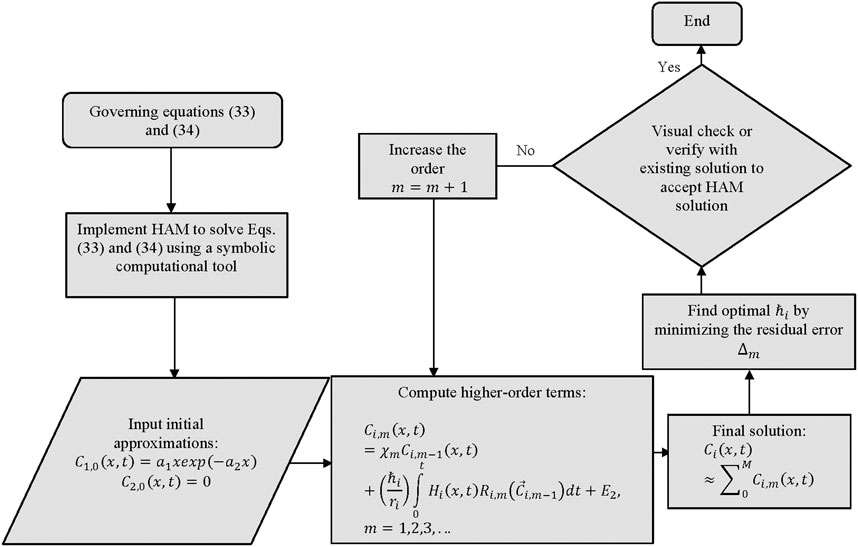
3.1 HAM-based solution
As discussed in Section 2.1, one can apply the HAM to the system of Eqs 33, 34 by constructing some operators and functions that are given below. The non-linear operators for the problem are selected as:
The above equations are the original operators of the equations, which is always an easy and convenient consideration for the non-linear operators in the framework of HAM. Therefore, using Eqs 35, 36, terms
Now, as discussed earlier, we need to follow three fundamental rules provided by Liao (2003) to have a convergent series solution. First, we consider the following set of base functions to represent the solutions
so that
where
where
where
Now, the auxiliary functions
where
For the convenience of readers, a flowchart containing the steps of the method is provided in Figure 1.
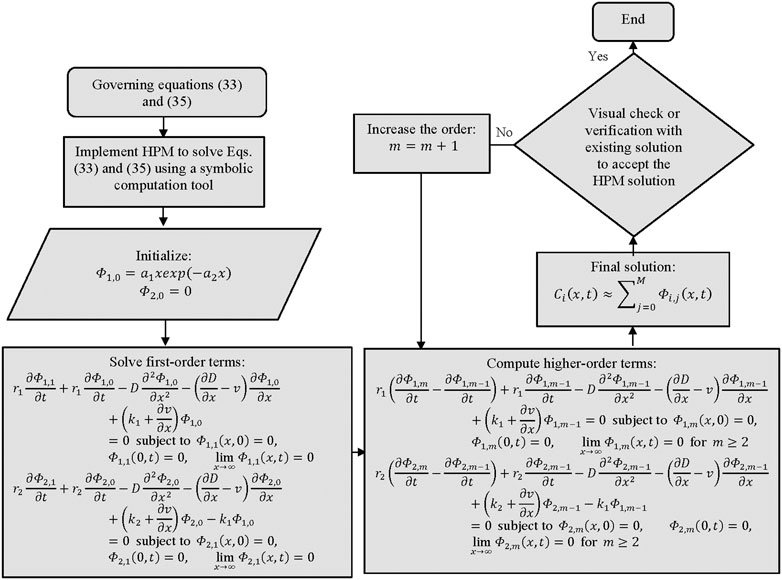
3.2 HPM-based solution
In relation to the discussion in Section 2.2, for simplicity, we consider the linear operator as follows:
The non-linear operators are selected as Eqs 35, 36. In the framework of HPM also, the selection of these operators is not unique; indeed, one can choose any other forms to check for a better solution. Using these expressions in Eq. 9 and then substituting the series Eq. 10, we obtain the following systems of differential equations after equating the like powers of
Proceeding in a like manner, one can arrive at the following recurrence relation:
The initial approximation can be chosen as
A flowchart containing the steps of the method is given in Figure 2.
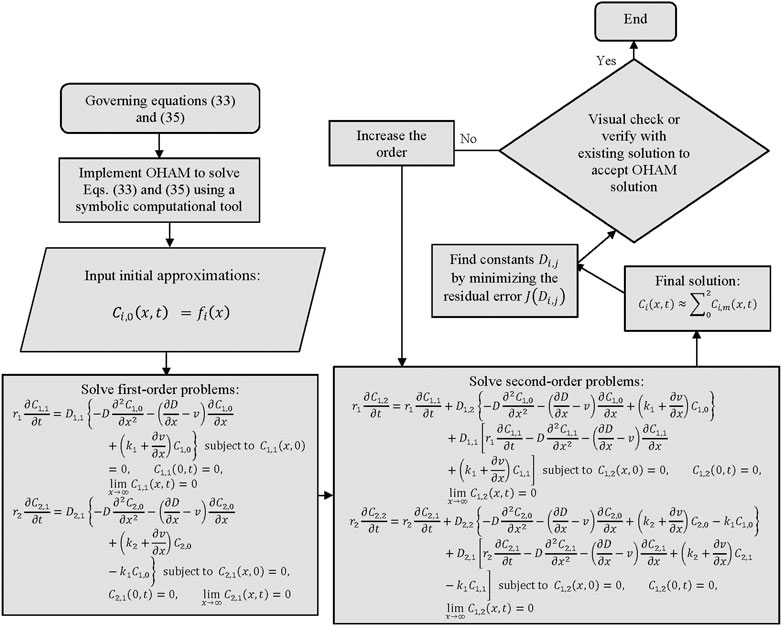
3.3 OHAM-based solution
In relation to the discussion given in Section 2.3, we choose the following operators:
and
With these considerations, we can solve the zeroth-order Eq. 16 to have the following solution:
Now to have the higher-order equations, we need the expressions
The auxiliary functions can be chosen in many ways. Here, we select
Here, we choose
where the terms are given by Eqs. 60, 61, 62, 63, 64. A flowchart containing the steps of the method is provided in Figure 3.
In Section 2, we discussed the homotopy-based methods from a general framework of system of PDEs. Indeed, the methodologies are equally applicable to single equations, integral equations, etc. Then, in Section 3, the methodologies were applied to a system of equations describing two-species pollutant transport. It can be seen from the application of these methods that they are different from the construction of different functions, operators, and parameters, and therefore may have advantages or disadvantages while dealing with a particular problem. From a theoretical perspective, the convergence theorems for HAM- and OHAM-based solutions are provided in Appendix A.
4 Results and discussion
First, we discuss the expressions and the values of parameters needed for the assessment of the developed solutions. Then, the numerical convergence of the HAM-based analytical solution is established for a specific test case, and then the solution is validated over a numerical solution. Finally, the HPM- and OHAM-based analytical solutions are validated by comparing them with the numerical solution.
4.1 Selection of expressions and parameters
For the assessment of solutions, it can be seen that the dispersion coefficient
For the validation of solutions, space and time domains are considered as
4.2 Numerical convergence and validation of the HAM solution
There are two ways to handle the convergence of HAM: one is based on the
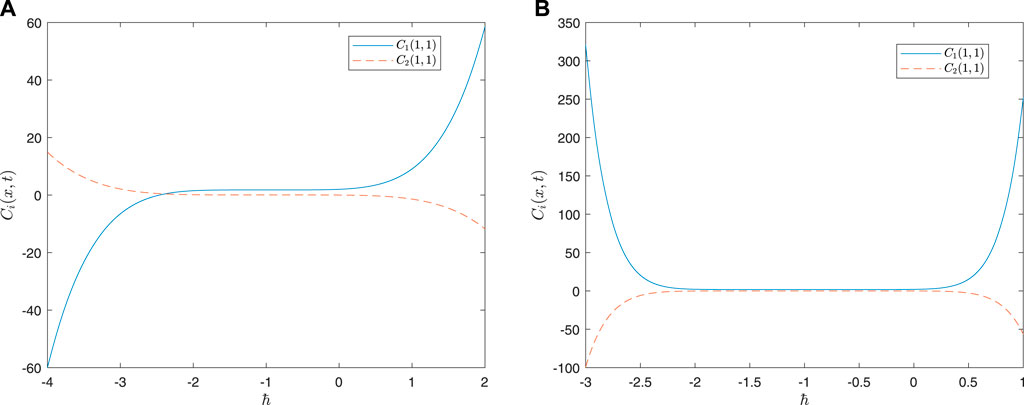
FIGURE 4.
Here, we test the performance of the HAM-based analytical solutions for the present problem by comparing them with a numerical solution. The numerical solution is obtained using an efficient MATLAB tool, namely ‘pdepe’. This MATLAB routine uses the method of lines by discretizing a parabolic PDE (single or system) in one space direction (Skeel and Berzins 1990). For the parameters described in the previous section, the pollutant concentrations are computed using pdepde for
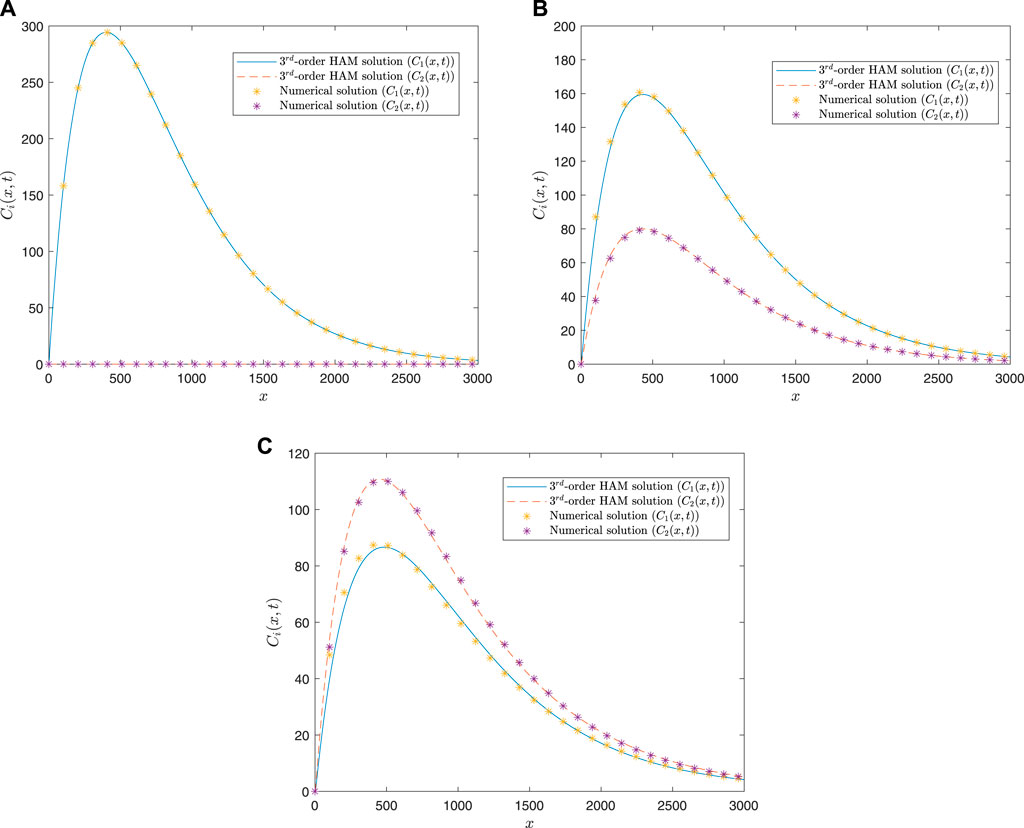
FIGURE 5. HAM-based pollutant concentrations versus distance for both species at: (A)
4.3 Validation of HPM-based solution
The HPM-based analytical solutions for the selected test case are validated over the numerical solution obtained using pdepe of MATLAB. It is seen that the five-term HPM series produces accurate results over the selected domain. Figure 6 compares the numerical solutions and the HPM-based approximations.
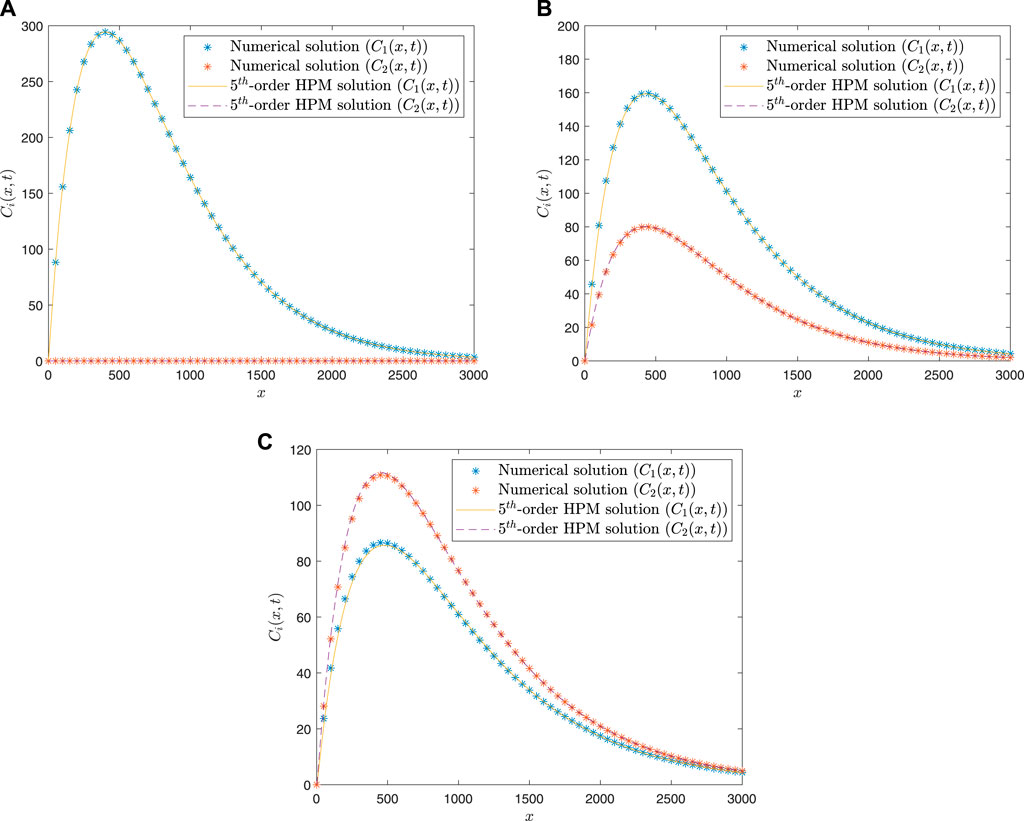
FIGURE 6. HPM-based pollutant concentrations versus distance for both species at: (A)
4.4 Validation of OHAM-based solution
For the assessment of the OHAM-based analytical solution, one needs to calculate the constants
where
where
Solving this system, one can obtain the optimal values of the parameters. We obtain the optimal values using the MATLAB routine fminsearch, which minimizes an unconstrained multivariate function. Three-term OHAM solution is computed and compared in Figure 7 with the numerical solution obtained using pdepe to see the effectiveness of the proposed approach. It can be seen that the OHAM-based approximation agrees well with the numerical solution for all cases.
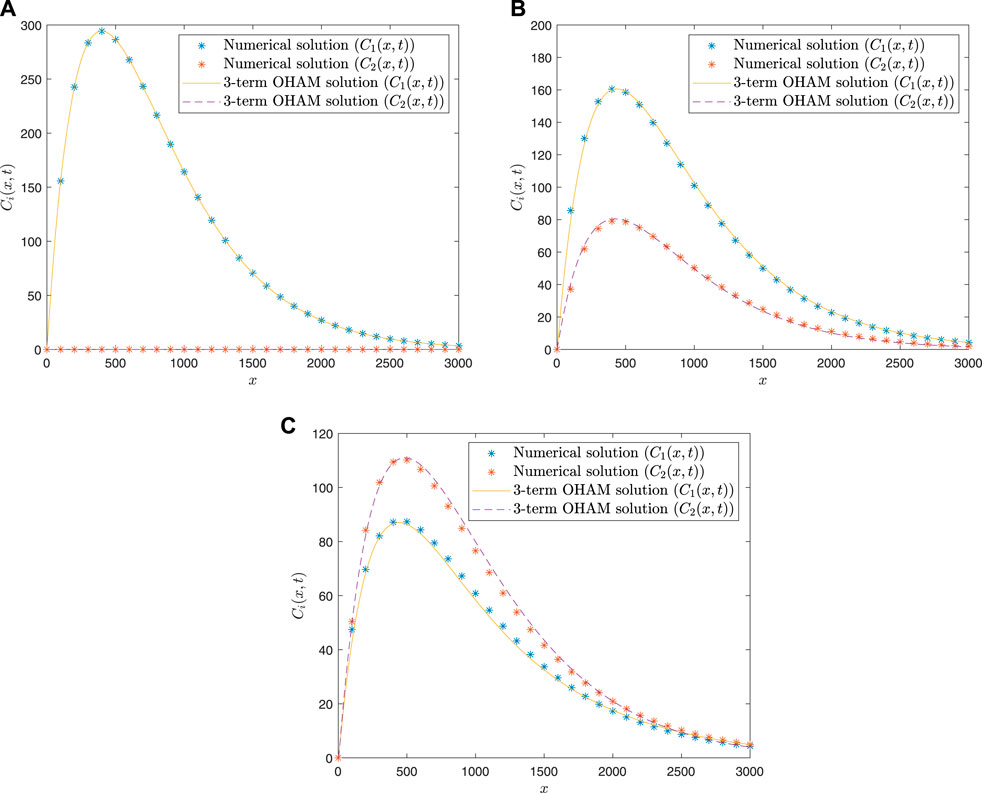
FIGURE 7. OHAM-based pollutant concentrations versus distance for both species at: (A)
4.5 Comparison between different solutions
This work develops three kinds of analytical solutions for two-species pollutant transport equation using the homotopy-based methods. In this section, we validated the performances of different solutions. It is shown that all of them agree well with the corresponding numerical solutions to the non-linear problem. However, the methods have their own advantages or disadvantages. Specifically, the HAM provides a great freedom in choosing linear, non-linear operators, and auxiliary functions subject to the choice of base functions. Further, the convergence-control parameter present in HAM greatly enhances the radius of convergence of the series and monitors the rate of convergence. On the other hand, the OHAM solution is an improved version of homotopy-based method with the aim of obtaining an accurate approximation with just two-three terms of the series. For a quantitative assessment, the performances of different solutions are compared numerically in Tables 1, 2, 3.
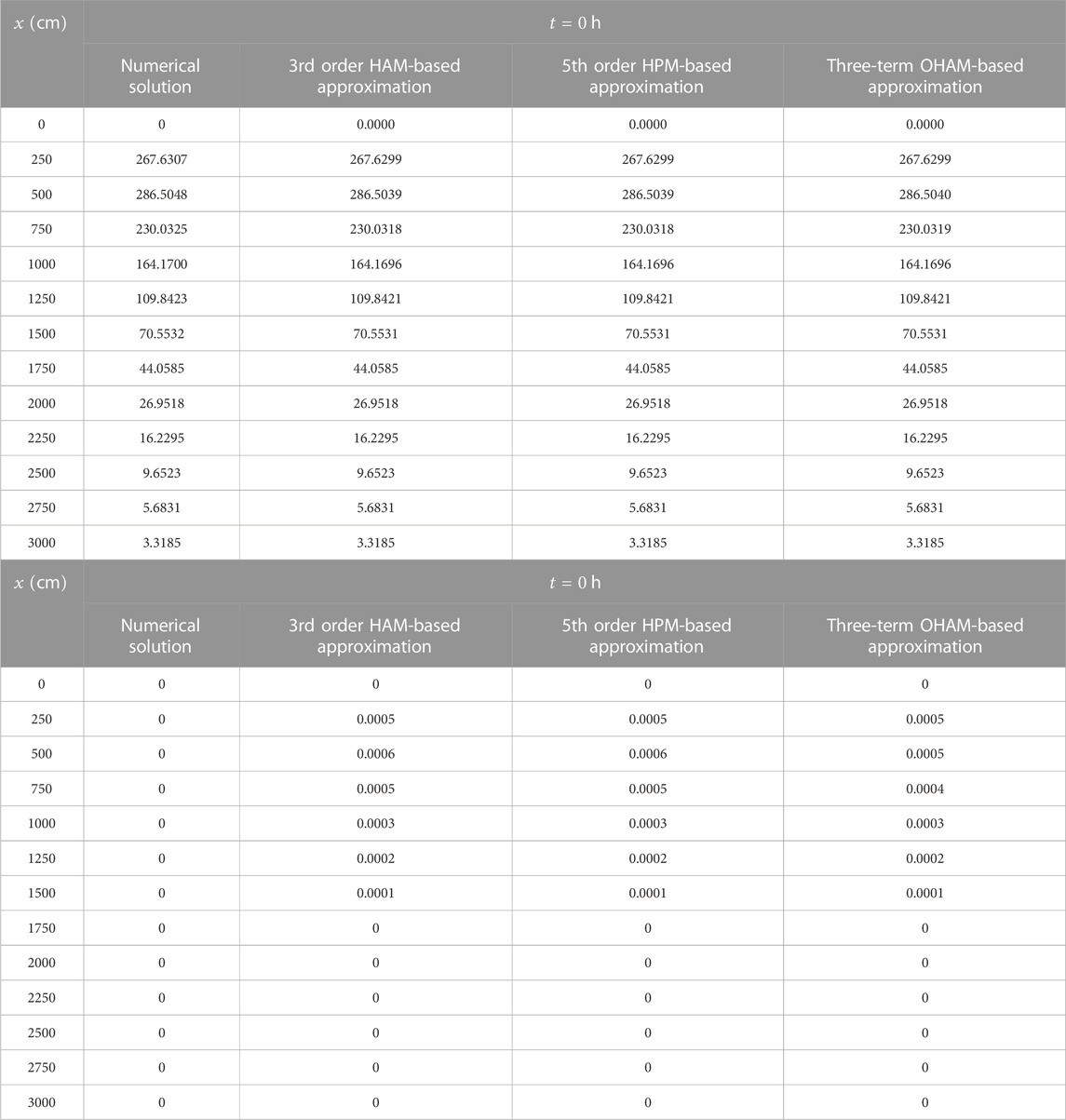
TABLE 1. Comparison between HAM-, HPM-, and OHAM-based approximations and numerical solution for the selected case for
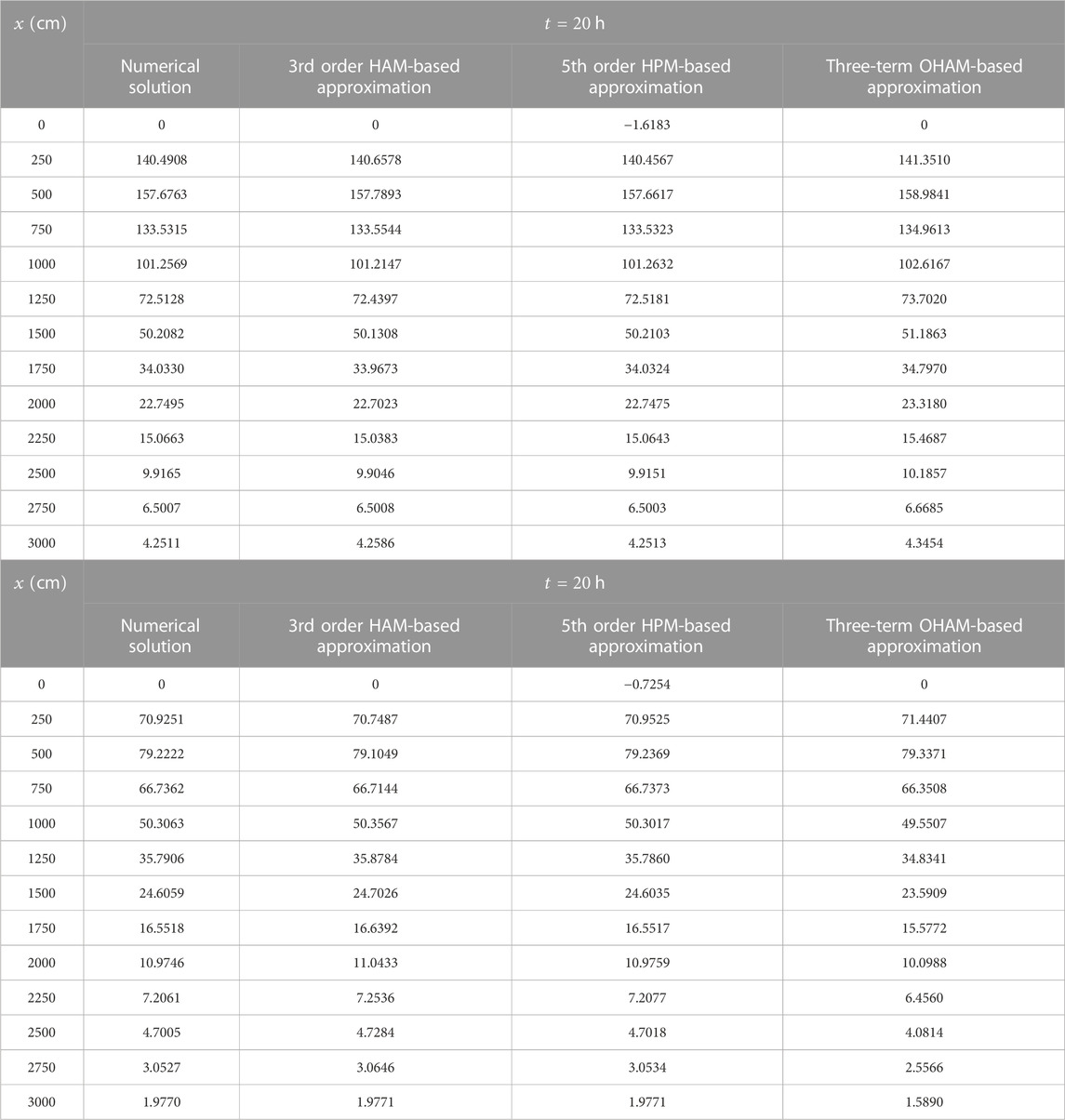
TABLE 2. Comparison between HAM-, HPM-, and OHAM-based approximations and numerical solution for the selected case for
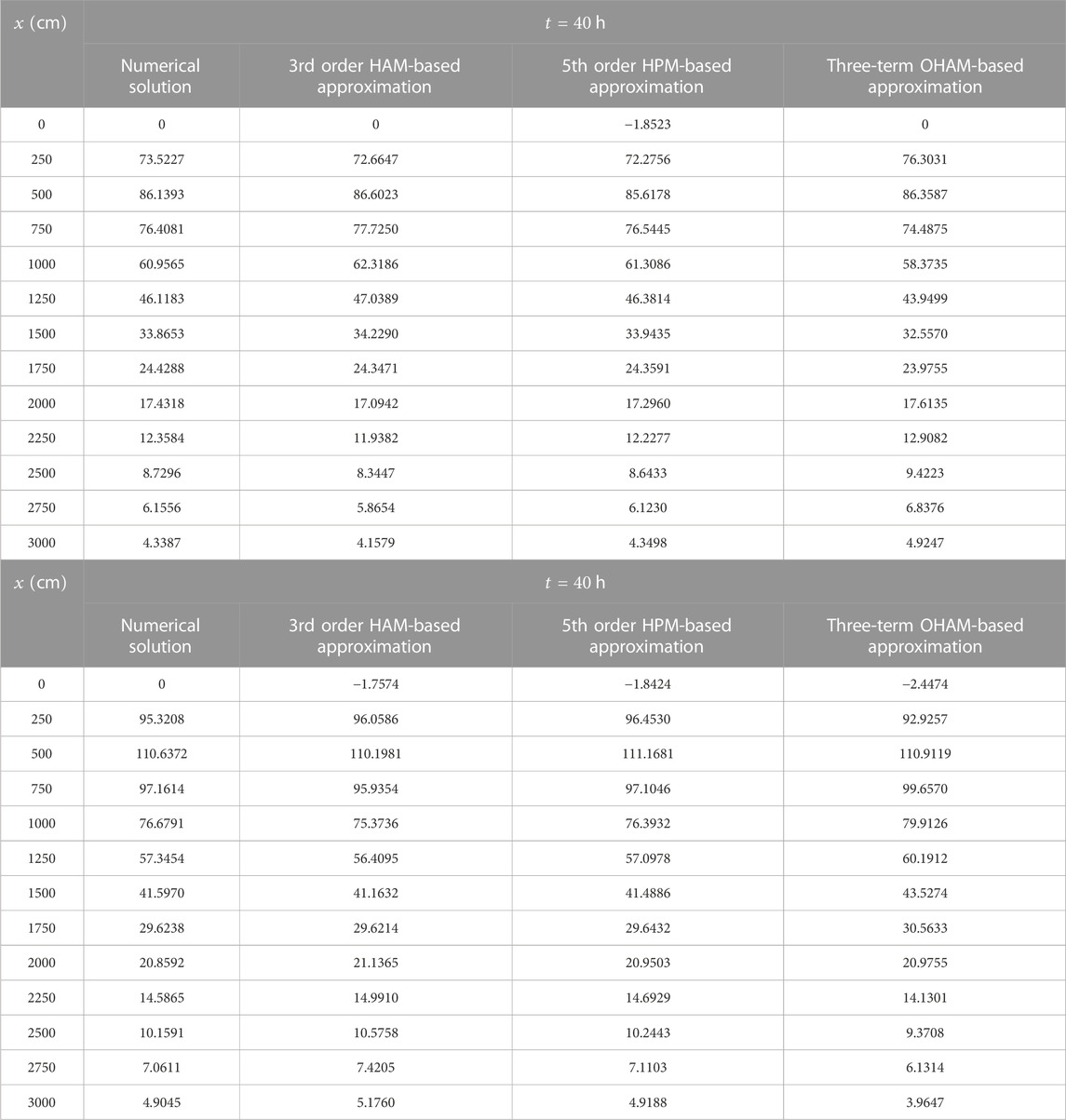
TABLE 3. Comparison between HAM-, HPM-, and OHAM-based approximations and numerical solution for the selected case for
5 Concluding remarks
Here, we derive the HAM-, HPM-, and OHAM-based analytical solutions for two-species transport equations with spatially varying dispersion coefficient and seepage velocity. The same equations were studied analytically using HAM by Chaudhary and Singh (2020). A numerical solution is also developed using the MATLAB routine pdepe. The proposed methods produce accurate solutions for all the cases. This work shows the potential of HAM, HPM, and OHAM in the context of obtaining a series solution for a system of parabolic PDEs. The theoretical as well as numerical convergence of the series solutions are provided.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MK: conceptualization, methodology, writing—original draft. VS: conceptualization, supervision, writing—review and editing, project administration.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbasbandy, S., Shivanian, E., and Vajravelu, K. (2011). Mathematical properties of h-curve in the framework of the homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 16 (11), 4268–4275. doi:10.1016/j.cnsns.2011.03.031
Arnold, J., Duddu, R., Brown, K., and Kosson, D. S. (2017). Influence of multi-species solute transport on modeling of hydrated Portland cement leaching in strong nitrate solutions. Cem. Concr. Res. 100, 227–244. doi:10.1016/j.cemconres.2017.06.002
Bai, B., Jiang, S., Liu, L., Li, X., and Wu, H. (2021b). The transport of silica powders and lead ions under unsteady flow and variable injection concentrations. Powder Technol. 387, 22–30. doi:10.1016/j.powtec.2021.04.014
Bai, B., Nie, Q., Zhang, Y., Wang, X., and Hu, W. (2021a). Cotransport of heavy metals and SiO2 particles at different temperatures by seepage. J. Hydrology 597, 125771. doi:10.1016/j.jhydrol.2020.125771
Batu, V. (2005). Applied flow and solute transport modeling in aquifers: Fundamental principles and analytical and numerical methods. Florida, United States: CRC Press.
Chamkha, A. J. (2005). Modeling of multi-species contaminant transport with spatially-dependent dispersion and coupled linear/non-linear reactions. Int. J. Fluid Mech. Res. 32 (1), 1–20. doi:10.1615/interjfluidmechres.v32.i1.10
Chaudhary, M., and Singh, M. K. (2020). Study of multispecies convection-dispersion transport equation with variable parameters. J. Hydrology 591, 125562. doi:10.1016/j.jhydrol.2020.125562
Chen, J. S., Lai, K. H., Liu, C. W., and Ni, C. F. (2012). A novel method for analytically solving multi-species advective–dispersive transport equations sequentially coupled with first-order decay reactions. J. Hydrology 420, 191–204. doi:10.1016/j.jhydrol.2011.12.001
Clement, T. P., Sun, Y., Hooker, B. S., and Petersen, J. N. (1998). Modeling multispecies reactive transport in ground water. Groundw. Monit. Remediat. 18 (2), 79–92. doi:10.1111/j.1745-6592.1998.tb00618.x
Domenico, P. A. (1987). An analytical model for multidimensional transport of a decaying contaminant species. J. Hydrology 91 (1-2), 49–58. doi:10.1016/0022-1694(87)90127-2
Fujikawa, Y., and Fukui, M. (1990). Adsorptive solute transport in fractured rock: Analytical solutions for delta-type source conditions. J. Contam. Hydrology 6 (1), 85–102. doi:10.1016/0169-7722(90)90013-7
He, J. H. (1999). Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 178 (3-4), 257–262. doi:10.1016/s0045-7825(99)00018-3
Liao, S. (2003). Beyond perturbation: Introduction to the homotopy analysis method. Boca Raton: Chapman and Hall/CRC.
Liao, S. (2012). Homotopy analysis method in nonlinear differential equations. Beijing: Higher education press, 153–165.
Liao, S. J. (1992). The proposed homotopy analysis technique for the solution of nonlinear problems. Doctoral dissertation, PhD thesis. Shanghai: Shanghai Jiao Tong University.
Lunn, M., Lunn, R. J., and Mackayb, R. (1996). Determining analytic solutions of multiple species contaminant transport, with sorption and decay. J. Hydrology 180 (1-4), 195–210. doi:10.1016/0022-1694(95)02891-9
Marinca, V., and Herişanu, N. (2008). Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. Int. Commun. Heat Mass Transf. 35 (6), 710–715. doi:10.1016/j.icheatmasstransfer.2008.02.010
Natarajan, N., and Kumar, G. S. (2010). Finite difference approach for modeling multispecies transport in porous media. Int. J. Eng. Sci. Technol. 2, 3344–3350.
Natarajan, N., and Kumar, G. S. (2018). Spatial moment analysis of multispecies contaminant transport in porous media. Environ. Eng. Res. 23 (1), 76–83. doi:10.4491/eer.2016.147
Simpson, M. J., and Ellery, A. J. (2014). Exact series solutions of reactive transport models with general initial conditions. J. Hydrology 513, 7–12. doi:10.1016/j.jhydrol.2014.03.035
Skeel, R. D., and Berzins, M. (1990). A method for the spatial discretization of parabolic equations in one space variable. SIAM J. Sci. Stat. Comput. 11 (1), 1–32. doi:10.1137/0911001
Slodička, M., and Balážová, A. (2010). Decomposition method for solving multi-species reactive transport problems coupled with first-order kinetics applicable to a chain with identical reaction rates. J. Comput. Appl. Math. 234 (4), 1069–1077. doi:10.1016/j.cam.2009.04.021
Slodička, M., and Balážová, A. (2008). Singular value decomposition method for multi-species first-order reactive transport with identical decay rates. Transp. Porous Media 73 (2), 161–172. doi:10.1007/s11242-007-9175-7
Sposito, G., Gupta, V. K., and Bhattacharya, R. N. (1979). Foundation theories of solute transport in porous media: A critical review. Adv. Water Resour. 2, 59–68. doi:10.1016/0309-1708(79)90012-5
Sun, Y., and Clement, T. P. (1999). A decomposition method for solving coupled multi–species reactive transport problems. Transp. Porous Media 37 (3), 327–346. doi:10.1023/a:1006507514019
Sun, Y., Petersen, J. N., and Clement, T. P. (1999). Analytical solutions for multiple species reactive transport in multiple dimensions. J. Contam. Hydrology 35 (4), 429–440. doi:10.1016/s0169-7722(98)00105-3
Vajravelu, K., and Van Gorder, R. (2013). Nonlinear flow phenomena and homotopy analysis. Berlin: Springer.
Appendix A. Convergence theorems
The convergence of the HAM- and OHAM-based solutions are proved theoretically using the following theorems.
A.1 Convergene Theorem of HAM-Based Solution.
The convergence theorem for the HAM-based solutions given by Eq. 45 can be proved using the following theorems.
Theorem A.1: If the homotopy series
Proof: The auxiliary linear operators was defined as follows:
According to Eq. 4, we obtain:
Adding all the above terms, we get:
As the series
Theorem A.2: If
which is basically the original governing Eqs 33, 34. Furthermore, subject to the initial and boundary conditions
One can write:
Using Eq. A11, one can obtain from Eq. A10:
Eq. A12 can be rearranged as:
Using the property of the linear operator, i.e.,
Now, since
which shows that
Keywords: pollutant transport, multispecies, homotopy, analytical solution, series solution
Citation: Kumbhakar M and Singh VP (2023) Approximate analytical solutions for multispecies convection-dispersion transport equation with variable parameters. Front. Earth Sci. 10:1064110. doi: 10.3389/feart.2022.1064110
Received: 07 October 2022; Accepted: 28 December 2022;
Published: 01 February 2023.
Edited by:
Yingfang Zhou, University of Aberdeen, United KingdomCopyright © 2023 Kumbhakar and Singh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Manotosh Kumbhakar, bWFub3Rvc2gua3VtYmhha2FyQGdtYWlsLmNvbQ==
†Present address: Department of Civil Engineering, National Taiwan University, Taipei, Taiwan
 Manotosh Kumbhakar
Manotosh Kumbhakar Vijay P. Singh
Vijay P. Singh