Seismic effects of loess slopes using physical modeling and numerical simulation

A large shaking-table test of a loess slope with a geometric similarity ratio of 1:25 was established as a prototype model of the loess landslide in Yongguang Village, which occurred during the 2013 Minxian–Zhangxian M6.6 earthquake. Combined with finite-element–numerical-simulation software, the dynamic response characteristics of the loess slope were compared and analyzed under the action of the same Minxian horizontal seismic wave characteristics. The results show that the seismic waves observed in the model test and numerical simulation clearly exhibit non-linear amplification effects along the slope surface and in the loess vertical direction, reaching a maximum value at the top of the slope. The ground-motion acceleration waveforms observed in the model test and numerical simulation at each observation point of the slope were similar, and the horizontal peak ground acceleration (PGA) obtained from the numerical simulation at these locations was larger than that of the slope top. The horizontal a_{Simulated-max}/a_Model-max values ranged from 1.5 to 2.2 and the vertical a_{Simulated-max}/a_Model-max values were more discrete in the range of 0.5–2.7, while the horizontal and vertical-PGA-amplification factors at the slope surface were similar. The Fourier amplitude and main horizontal frequencies were mainly distributed between 0.1 and 12 Hz. The Fourier spectrum observed in the model test was approximately 0.5 Hz, while the main frequency of the vertical Fourier spectrum was approximately 4 Hz. Additionally, the main frequency of the horizontal and vertical Fourier spectra observed in the numerical simulation was approximately 2 and 1.2 Hz, respectively.

1 Introduction

The Loess Plateau is located in China’s northeast edge of the Qinghai–Tibet Plateau seismic belt and the north–south seismic belt. Its geological structure is complex, and it experiences strong neotectonic movement, which contributes to the frequent mega-geological disasters experienced in China, mainly in the form of strong earthquakes. The Loess Plateau area has a large number of slopes, loess, beams, mountings, and other special topographic features. Compared with other soil types, loess is a special Quaternary deposition of porous and weakly cemented material, with strong water sensitivity and very high dynamic vulnerability (Liu et al., 1985). Geological hazards, such as loess landslides and liquefaction, can be induced under the action of moderate-to-strong earthquakes (Wang, 2003). A previous study showed that the amplification effects of ground motion caused by thick loess deposits were the main cause of intensity anomalies (Wang and Xie, 2010; Wang et al., 2013). On September 6, 2018, a 6.7-magnitude earthquake that occurred in Hokkaido, Japan, triggered more than 4,000 landslides, and 44 casualties were reported as predominantly caused by these landslides (Wang L. et al., 2019). Most of the landslides formed at an angle of 15–30°, with very few forming between 30 and 39°. The same situation occurred in China, where an M6.6-magnitude earthquake occurred on July 22, 2013, at the border of Min and Zhang counties, which triggered more than 2,330 landslides that resulted in 95 deaths. Most of these landslides have slopes ranging between 10 and 20° (Wang et al., 2017a, Wang et al., 2017b, Wang et al., 2017c). A massive mudslide with a slope angle of 18° in Yongguang Village, Minxian County, formed a part of these landslides.

With the “Belt and Road” initiative and the rapid development of China’s social and economic development, the center of gravity of national infrastructure construction is gradually shifting to the west, along with an increasing scale of cities and human engineering activities, leaving more people increasingly vulnerable to sudden earthquakes owing to the loess slopes. To prevent and better mitigate disasters, it is necessary to study deformation, damage mechanisms, and response laws of loess slopes under the action of earthquakes. Current analysis methods for slope dynamic responses are divided into three types: analytical methods, numerical calculations, and physical models. Owing to the discontinuity and inhomogeneity of the soil medium, as well as the complexity of slope dynamics, it is very difficult to solve slope dynamic problems using theoretical derivations. The theory of geotechnical slope dynamic response is far from mature, and its accuracy is to be tested yet (Bouckovalas and Papadimitriou, 2005). Wu et al. (2015) used shaking table model tests to study the destabilization damage process and acceleration response characteristics of pure loess slopes with low moisture contents and slope angles under earthquake excitation. Wang et al. (2018) conducted shaking-table model tests on loess slopes and studied the dynamic response law under the coupled action of earthquakes and rainfall. Song et al. (2021a) studied the seismic cumulative failure effects on a reservoir-bank slope with a complex geological structure, considering its plastic-deformation characteristics using shaking-table tests. Zhang et al. (2018) analyzed the damage characteristics and dynamic response law of loess-mudstone slopes under different amplitudes using centrifuge shaking-table tests and numerical simulations. To investigate the seismic response of pile systems in multi-tilted and layered soils under earthquake and rainfall conditions, two models were built and tested using a large 1-g shaking table (Jian Zhang et al., 2022). The shaking-table test by Wang and Wang (1987) indicated that the peak acceleration response at the crest of a slope was amplified more than that at the foot. Studies have also demonstrated that surficial soil and rock-mass structures have a pronounced effect on the seismic response of slopes (He et al., 2020; He et al., 2021; Song et al., 2021b; Song et al., 2021c; Song et al., 2021d). Murphy (2006) conducted a study based on the landslide data from the 1970 Peru and 1999 Taiwan Jiji earthquakes to investigate the amplification effect of mountains and found that the amplification effect of ground shaking was the most obvious at ridge locations. By studying the distribution maps of earthquake landslides near the Northridge region in California, United States, the Chiji region in Taiwan, and the Finisterre Mountains in Papua New Guinea, Meunier et al. (2008) found that earthquake-induced landslides were clustered near ridges, the peak ground acceleration (PGA) occurred at the top of the ridges, and the sudden change in the slope on both sides of the ridges was significantly amplified. Wang et al. (2010) conducted a study on the amplification effect of site conditions and soil structure on ground shaking based on the time course of mainshock acceleration recorded by the Zigong topographic table array during the Wenchuan earthquake. Chen and Wu (2012) conducted a dynamic response analysis of the Loess Plateau with different cover thicknesses and slopes under earthquake loads by deploying a strong ground-motion observation array and using a two-dimensional equivalent linear time-response–dynamic-analysis method. The results showed that the amplification effects of peak seismic acceleration, loess cover thickness, and angle of the loess slope were related. Mitani et al. (2013) investigated the amplification effect of ground motion on homogeneous slopes with different heights and slopes using a finite-element–numerical-analysis method. Wang et al. (2018) numerically analyzed the amplification effect of earthquake ground motion in terms of the loess-layer thickness and slope. The results show that the amplification effect is more evident as the thickness of the loess layer and slope increase. However, under the action of dynamic loads, the loess microstructure is gradually damaged and deformed, such that the macroscopic properties of the soil are continuously degraded. Finite-element–numerical-simulation software cannot simulate this degradation–evolution process, and the laws summarized by its numerical analysis need to be mutually verified by actual earthquake or model tests (Jiang, 2019). Qi et al. (2003) and Qi (2006) investigated the topographic effect of a single surface slope on an entire slope section using numerical simulations and reported two types of slope dynamic responses. Bouckovalas and Papadimitriou (2005) stated that this type of topography may lead to intense amplification or deamplification variability at neighboring points (within a few tens of meters) behind the crest of the slope, particularly during high-frequency motion. He et al. (2020) demonstrated that the combined effect of superficial soil and topography resulted in a complex seismic response on the Lengzhuguan slope.

To study the ground-motion response characteristics of a low-angle loess slope, we combined shaking-table model tests with simulation calculations. We adopted this approach because shaking-table model tests are more complex, costly, and reliable than numerical simulations. However, although numerical simulations are simple and less costly, they lack validation. A comparative study between shaking-table model tests and numerical simulations of the same loess-slope model can be conducted to verify the reliability of both methods and establish a relationship between the two seismic parameters, thus establishing reliable samples for future numerical calculations. By selecting a low-angle (approximately 20°) loess slope as the prototype, the dimensions and materials of the low-angle slope model were determined according to the law of similarity. Additionally, the dynamic response characteristics of the low-angle loess slope under the strong motion load of the Minxian Station during the M6.6 earthquake in Minxian, Zhangxian County, were observed using seismic acceleration sensors. Additionally, a two-dimensional soil model was constructed using the geo-mechanical and physical–mechanical parameters obtained from an indoor test of the in situ loess of the prototype slope. Simultaneously, this model was simulated using the finite-element method, and the same seismic wave used in the model test was incorporated in the numerical simulation of the ground-motion amplification effect of the prototype loess slope. Based on the model test and simulation calculation results, the acceleration, amplification factor, displacement, and other dynamic response laws of a low-angle loess slope under earthquake conditions were compared and analyzed to reveal the characteristics of the ground-motion amplification effect.

2 Ground-motion response of the shaking-table test on loess slopes

2.1 Test setup

The test was conducted on a large electric-servo shaking table at the Key Laboratory of Loess Earthquake Engineering, China Earthquake Administration (Figure 1). The shaking table size is 4 × 6 m, driven by 28 servo motors, which can realize horizontal (x), vertical (z), and horizontal–vertical coupling vibrations. Maximum load capacity: F_x = 250 kN and F_z = 150 kN; frequency range in x and z directions: f_x = 0.1–70.0 Hz and f_z = 0.1–50.0 Hz; maximum displacement in x and z directions: u_x = ±250 mm and u_z = ±100 mm; maximum acceleration: a_x = 1.7 g and a_z = 1.2 g for x and z directions independently; a_x = 1.2 g for x and z directions combined; and maximum acceleration: a_x = 1.7 g and a_z = 1.2 g for x- and z-directional vibration independently; a_x = 1.2 g and a_z = 1.0 g for combined x- and z-directional vibration.

FIGURE 1

FIGURE 1. Shaking table and model box.

2.2 Slope prototype

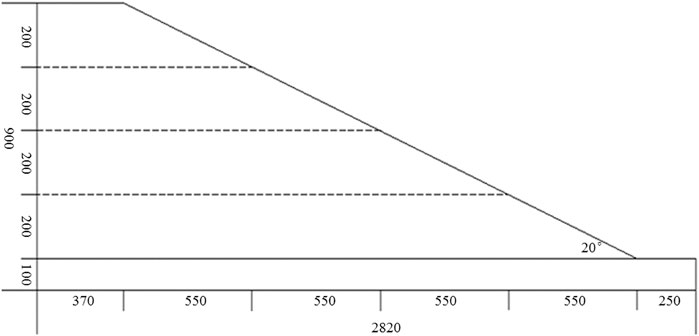
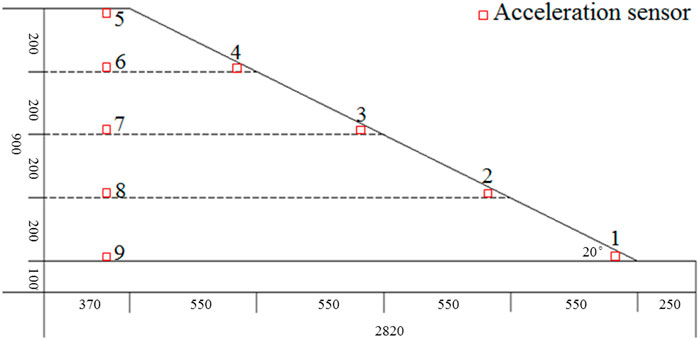
The landslide of the loess slope from Min County to Zhang County was triggered by an M6.6 earthquake in the west of Yongguang Village and was selected as a prototype for this study (Figure 2). The parameters measured on site include the prototype slope height of 20.00 m, slope bottom length of 70.50 m, slope top length of 9.25 m, slope width of 35.00 m, slope body leading edge of 6.25 m, leading edge thickness of 2.5 m, and average slope of 20°. The prototype slope-soil body was used for Q₃ loess.

FIGURE 2

FIGURE 2. Prototype slope. (A) Distant view of the landslide in Yongguang Village; (B) close-range view of the landslide in Yongguang Village.

2.3 Boundary conditions and shaking-table similar design

Broadly speaking, a slope is a semi-infinite geological body with a slope that has at least one side exposed to air and possesses no theoretical boundary. However, the model soil is placed in a model box of finite size during the test, which results in wave reflection at the boundary, producing the “model-box effect” and changing the motion pattern of the entire system, as well as causing secondary damage to the model slope (Lu et al., 2000). Therefore, measures must be taken to mitigate these effects at the boundaries. The general approach is to add a liner inside the model box or to change the box structure and material. In this experiment, a 5-cm-thick polystyrene foam sponge was attached to each side of the box to absorb the energy at the boundary.

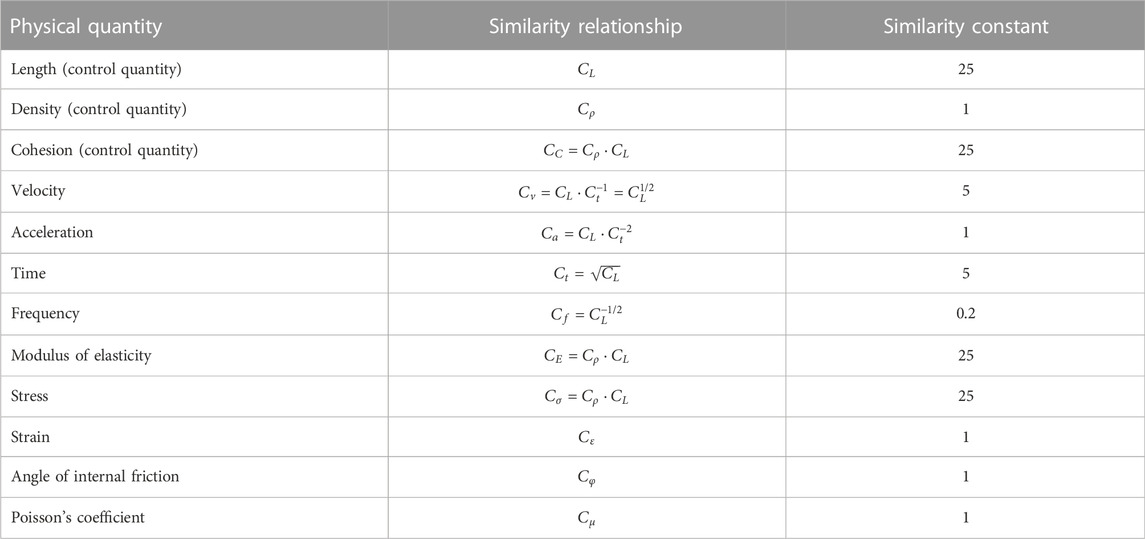
The biggest challenge in the model design is to accurately reflect the properties of the prototype slope; therefore, it is necessary to use a similarity theory design to guide the test. Model tests include geometric, kinematic, and kinetic similarities. If two physical quantities are similar in terms of geometry and kinematics, their dynamics are also similar. However, owing to the complexity of the model and limitations of the objective conditions, it is difficult to satisfy the similarity of all parameters. Thus, it was necessary to select the primary control parameters and ignore the secondary control parameters according to the purpose of the test. In this test, geometry, material density, and gravitational acceleration were used as the basic magnitudes, and their similarity constants were taken as C_L = 25, C_ρ = 1, and C_a = 1, respectively. The remaining physical quantities were derived according to Buckingham’s theory (π theorem) and magnitude analysis (Yuan, 1998; Gao et al., 2000). The final similarity constants are listed in Table 1.

TABLE 1

TABLE 1. Similarity constants for the shaking model test.

2.4 Model design and sensor arrangement

The geometric similarity ratio between the model and prototype slope was 1:25. The slope model has a slope height of 0.8 m, slope bottom length of 2.82 m, slope top length of 0.37 m, slope width of 1.4 m, and slope gradient of 20°. The loess-slope model is illustrated in Figure 3. This test used a rigid closed model box with an inner size of L × W × H = 2.8 × 1.4 × 1 m, with Plexiglas plates installed in the length direction to facilitate the observation of macroscopic phenomena during the experiment and organic carbon steel plates in the width direction to increase the strength of the model box.

FIGURE 3

FIGURE 3. Loess-slope model (unit: mm).

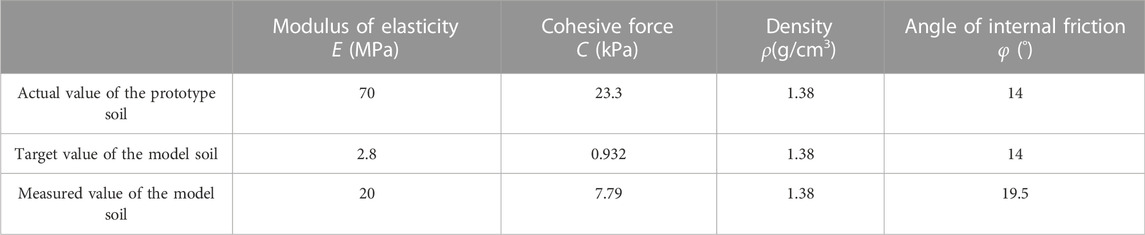
Remodeled loess was used as the primary material in the model tests because the prototype slope was a pure loess slope. The internal friction angle and cohesion parameters of the material were controlled by restricting the water content and density of the remodeled soil to achieve physical properties that were similar to those of the prototype material. Loess, fly ash, light foam soil, heavy gold stone powder, and water were used as the test materials. Through several material proportioning tests, it was determined that the ratio of loess: fly ash: light foam soil: heavy gold stone powder: water was 10:3:3:3:1. The physical and mechanical parameters of the prototype and model materials measured by multiple sets of static triaxial and direct shear tests are listed in Table 2, which shows that the internal friction angle and density satisfy a similar theory and the modulus of elasticity and cohesion decrease significantly and converge to the target value of the model soil.

TABLE 2

TABLE 2. Soil parameters.

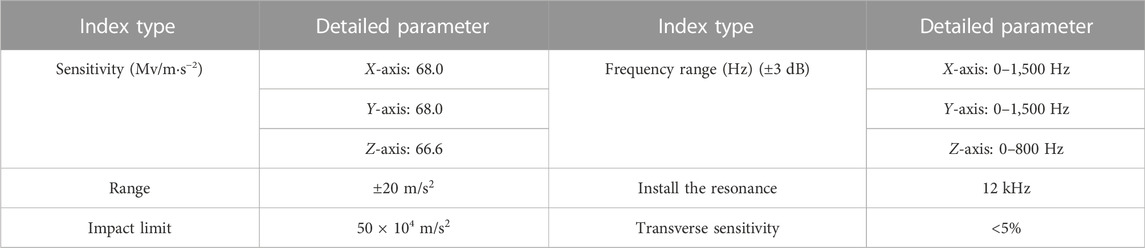
The test used a three-phase capacitive DH301-type acceleration sensor, and the detailed parameters are listed in Table 3. Only two horizontal and vertical channels of the sensor were selected for the test because only horizontal and vertical two-directional seismic loadings were tested. The arrangement of the acceleration sensors used in the test is shown in Figure 4.

TABLE 3

TABLE 3. Main technical specifications of a DH301 series three-way capacitive acceleration sensor.

FIGURE 4

FIGURE 4. Layout scheme of the acceleration sensor (unit: mm).

2.5 Loaded waveform and spectral characteristics

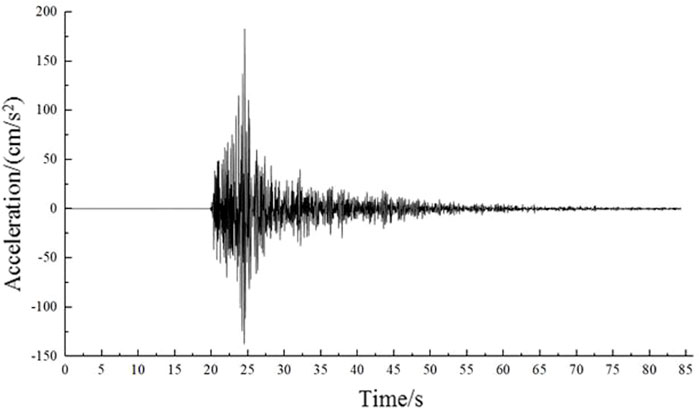
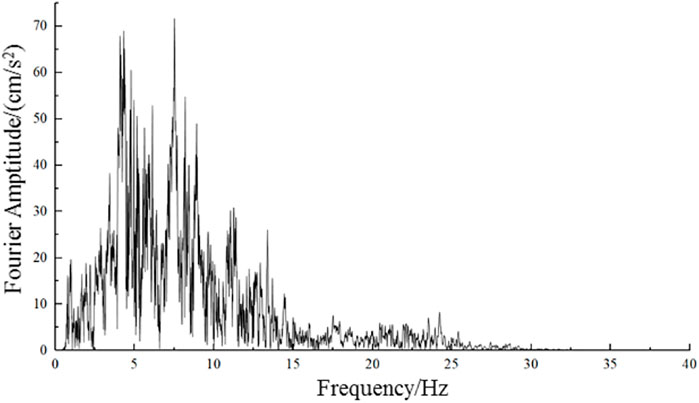
According to a similar design and the dimensional analysis method used to simulate the original site conditions, only the dimensional and material similarities are considered in this study because dynamic similarity is difficult to achieve. To study the dynamic response characteristics of low-angle pure loess slopes under the effect of strong earthquakes, shaking-table physical model tests and numerical simulations were used for comparison and analysis. The loading waveforms and Minxian seismic wave (NS direction, horizontal component) were used, and the specific parameters are listed in Table 4. The Minxian seismic wave was the mainshock acceleration time course recorded by the Minxian strong seismic station of the 2013 Minxian–Zhangxian M6.6 earthquake. The waveform of the horizontal component of the Minxian seismic wave is shown in Figure 5 with a time interval of 0.005 s and waveform holding time of 84.23 s, and the maximum acceleration amplitude is 183.2 gal, which occurs near 24.56 s. Figure 6 shows the spectrum of the horizontal component of the Minxian seismic wave, from which it can be observed that its frequency is concentrated at approximately 5 Hz. The waveform of the vertical component of the Minxian seismic wave is shown in Figure 7, with a time interval of 0.005 s, a waveform holding time of 84.32 s, and a maximum acceleration amplitude of 86.8 gal, which occurs near 24.92 s.

TABLE 4

TABLE 4. Waveform input parameters of ground-motion loading.

FIGURE 5

FIGURE 5. Seismic waveform of the horizontal component of the Minxian seismic wave.

FIGURE 6

FIGURE 6. Seismic spectrum of the horizontal component of the Minxian seismic wave.

FIGURE 7

FIGURE 7. Schematic diagram of the finite-element calculation model of the soil layer.

3 Ground-motion response of the loess slope by numerical simulation

3.1 Numerical simulation principle of dynamic response

3.1.1 Basic equation for the analysis of soil-layer earthquake response

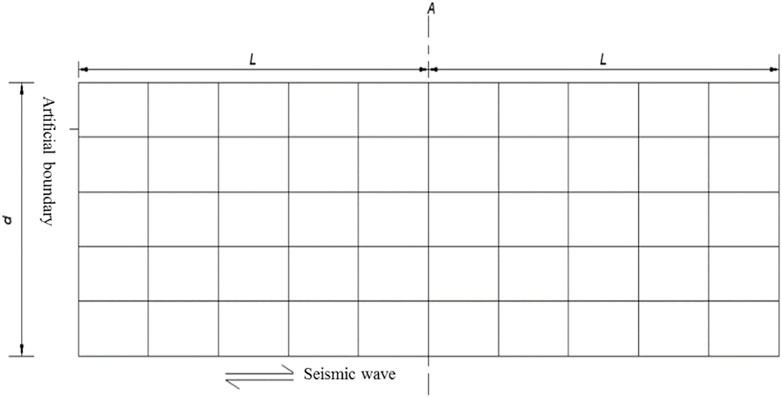
When analyzing loess soil using the finite-element method, a limited range of soil layers must be intercepted for the calculation because the real soil has a semi-infinite space. After intercepting a reasonable soil-layer range, the analysis of the soil-layer seismic reaction is equivalent to solving the dynamic reaction of a discrete system with “n” supports under the earthquake action. We performed a transformation from the soil-layer fluctuation analysis problem under external excitation in the semi-infinite domain to the soil-layer motion analysis problem of the finite domain under basic excitation. Figure 7 shows a schematic of the finite-element model of this finite soil layer, where seismic wave excitation occurred in the bedrock surface at the bottom of the soil layer. The basic equations of the seismic response analysis in the soil layer are divided into two categories: equations of motion under consistent and multi-point seismic excitation. The following is a brief introduction to the equations of motion under consistent seismic excitation (Bai, 2010).

The structural dynamics method can be used to establish the equations of motion when the soil layer is discretized into a motion system with finite elements. The discrete soil-layer system is a structural system with finite degrees of freedom, and the bedrock surface is a structural foundation surface. The equation of motion of the structural time domain under a consistent seismic input is:

$\left[M\right]\left\{{\ddot{u}}_d\left(t\right)\right\}+\left[C\right]\left\{{\dot{u}}_d\left(t\right)\right\}+\left[K\right]\left\{u_d\left(t\right)\right\}+\left[M\right]\left\{I\right\}{\ddot{u}}_g\left(t\right)=0.(1)$

In this equation, [C], [K], and [M] are the damping, stiffness, and mass matrices after the discrete structure finite-element structure, respectively; {I} is a unit array, whose elements are 0 and 1, indicating whether the dynamic action–reaction of seismic motion in all degrees of freedom is present; ${\ddot{u}}_g\left(t\right)$ is the seismic-wave acceleration time course input; and {$u_d$} is the displacement component of each node relative to the structural substrate and caused by seismic motion. The absolute acceleration {$\ddot{u}$} of the nodes in the structure can be expressed as

$\left\{\ddot{u}\right\}=\left\{{\ddot{u}}_d\right\}+\left\{I\right\}{\ddot{u}}_g\left(t\right).(2)$

Because the order of the finite-element model is higher in practical problems, two types of solutions are generally adopted to solve the equation of motion for the aforementioned system: motion-type superposition and direct integration methods. The motion-type superposition method regards the dynamic reaction of the soil as a reaction (motion-type) produced by the soil under a series of motions at different frequencies. The motion-type superposition method is theoretically concise; however, it is complicated and unsuitable for non-linear dynamic analyses. The direct integration method can solve the internal force and displacement of each moment without the self-motion frequency of the system. The common direct integration methods include Newmark, Wilson-θ, linear acceleration, and central difference methods.

3.1.2 Newmark method

Assuming a finite-element discrete system with n degrees of freedom, n differential equations of motion can be established and expressed in the form of a matrix:

$\left[M\right]\left\{\ddot{u}\right\}+\left[I\right]-\left[P\right]=0,(3)$

where [M] is the mass matrix, [I] is the viscous damping matrix, [P] is the external load, and {u ̈} is the acceleration of the unit node.

The differential equations of motion at moments t and t + Δt are expressed as follows:

$\left[M\right]{\left\{\ddot{u}\right\}}_t+{\left[I\right]}_t-{\left[P\right]}_t=0,(4)$

$\left[M\right]{\left\{\ddot{u}\right\}}_{t+∆t}+{\left[I\right]}_{t+∆t}-{\left[P\right]}_{t+∆t}=0.(5)$

To facilitate this solution, Eqs 4, 5 can be rewritten as follows:

$\left[M\right]{\left\{\ddot{u}\right\}}_{t+∆t}+\left[C\right]{\left\{\dot{u}\right\}}_{t+∆t}+K{\left\{u\right\}}_{t+∆t}={\left[P\right]}_{t+∆t}.(6)$

The displacement and velocity at moment t + Δt can be obtained using the Newmark-β method, which can be expressed as

${\left\{u\right\}}_{t+∆t}={\left\{u\right\}}_t+{\left\{\dot{u}\right\}}_t∆t+\left[\left(\frac{1}{2}-\beta \right){\left\{\ddot{u}\right\}}_t+\beta {\left\{\ddot{u}\right\}}_{t+∆t}\right]\Delta t^2,(7)$

${\left\{\dot{u}\right\}}_{t+∆t}={\left\{\dot{u}\right\}}_t+\left[\left(1-\gamma \right){\left\{\ddot{u}\right\}}_t+\gamma {\left\{\ddot{u}\right\}}_{t+∆t}\right]\Delta t,(8)$

where $\beta \in \left(0,\frac{1}{2}\right)$ and $\gamma \in \left(0\right.,\left.1\right]$ are the weighting factors.

The accuracy of the Newmark-β method and its convergence and stability are influenced by the values of β and γ. Many researchers have developed kinetic equations that consider different values.

When β = 1/6 and γ = 1/2, this is termed the linear acceleration method. When β = 1/4 and γ = 1/2, Eqs 7, 8 can be rewritten as

${\left\{u\right\}}_{t+∆t}={\left\{u\right\}}_t+{\left\{\dot{u}\right\}}_t∆t+\frac{\Delta t^2}{4}\left[{\left\{\ddot{u}\right\}}_t+{\left\{\ddot{u}\right\}}_{t+∆t}\right],(9)$

${\left\{\dot{u}\right\}}_{t+∆t}={\left\{\dot{u}\right\}}_t+\frac{∆t}{2}\left[{\left\{\ddot{u}\right\}}_t+{\left\{\ddot{u}\right\}}_{t+∆t}\right].(10)$

Eqs 9, 10, that is, when β = 1/4 and γ = 1/2, can be termed the inertia table shape rule.

A transformation of the Newmark-β method using the displacement at moment t + Δt and the acceleration, velocity, and displacement at moment t can be used to calculate the acceleration and velocity at moment t + Δt in the following form:

${\left\{\ddot{u}\right\}}_{t+∆t}=\frac{1}{\beta ∆t^2}\left({\left\{u\right\}}_{t+∆t}-{\left\{u\right\}}_t\right)-\frac{1}{\beta ∆t}{\left\{\dot{u}\right\}}_t-\left(\frac{1}{2\beta }-1\right){\left\{\ddot{u}\right\}}_t,(11)$

$\begin{array}{l}\{\dot{u}{\}}_{t+∆t}=\{\dot{u}{\}}_t+\left\{\left(1-\gamma \right)\right\{\ddot{u}{\}}_t+\gamma [\frac{1}{\beta ∆t^2}\left(\left\{u{\}}_{t+∆t}-\{u{\}}_t\right.\right)-\frac{1}{\beta ∆t}\{\dot{u}{\}}_t\\ -\left(\frac{1}{2\beta }-1\right)\left\{\left.\ddot{u}{\}}_t\right]\right\}∆t\\ =\{\dot{u}{\}}_t+∆t\left(1-\gamma \right)\{\ddot{u}{\}}_t+\frac{\gamma }{\beta ∆t}\left(\left\{u{\}}_{t+∆t}-\{u{\}}_t\right.\right)-\frac{\gamma }{\beta }\{\dot{u}{\}}_t-\gamma \left(\frac{∆t}{2\beta }-∆t\right)\{\ddot{u}{\}}_t\\ =\frac{\gamma }{\beta \Delta t}\left(\left\{u{\}}_{t+∆t}-\{u{\}}_t\right.\right)+\left(1-\frac{\gamma }{\beta }\right)\{\dot{u}{\}}_t+∆t\left(1-\frac{\gamma }{2\beta }\right)\{\ddot{u}{\}}_{t.}\end{array}(12)$

To solve the linear problem using the stiffness matrix [K], the internal force $Q_{t+∆t}$ can be expressed as

${\left\{Q\right\}}_{t+∆t}=\left[K\right]{\left\{u\right\}}_{t+∆t}.(13)$

Thus, the Newmark-β method was implemented using the following equation:

$\begin{array}{l}\left(\frac{1}{\beta ∆t^2}\left[M\right]+\frac{\gamma }{\beta ∆t}\left[C\right]+\left[K\right]\right){\left\{u\right\}}_{t+∆t}\\ ={\left\{Q\right\}}_{t+∆t}+\left[M\right]\left(\frac{1}{\beta ∆t^2}{\left\{u\right\}}_t+\frac{1}{\beta ∆t}{\left\{\dot{u}\right\}}_t+\left(\frac{1}{2\beta }-1\right){\left\{\ddot{u}\right\}}_t\right)\\ +\left[C\right]\left(\frac{\gamma }{\beta ∆t}{\left\{u\right\}}_t+\left(\frac{\gamma }{\beta }-1\right){\left\{\dot{u}\right\}}_t+\left(\frac{1}{2\beta }-1\right)∆t{\left\{\ddot{u}\right\}}_t\right).\end{array}(14)$

A linear program can be used when the stiffness matrix [K] is substituted with $\left(\frac{1}{\beta ∆t^2}\left[M\right]+\frac{\gamma }{\beta ∆t}\left[C\right]+\left[K\right]\right)$. When solving linear problems, the solutions of the dynamic equations are not affected by the value of Δt, when β = 1/4 and γ = 1/2, and they are all satisfied. In addition, when β = 1/6 and γ = 1/2, the solution is stable when Δt is less than a certain value, resulting in a conditional stable solution. However, when γ > 1/2, the solution exhibits a numerical decay.

3.2 Dynamic analysis model of the loess slope

3.2.1 Overview of the model

This numerical analysis of the dynamic response of a loess slope under seismic loading used a typical loess-slope model as the research object and established a two-dimensional simplified numerical calculation model, as shown in Figure 8. The model stratification was based on Kun (2020) for the stratification of the borehole data of the landslide. The distribution of the model soil layers from the top to bottom was Malan loess, Lishi loess, and bedrock. The thickness of the Malan loess layer is 15 m, Lishi loess layer is 7.5 m, and bedrock layer is 13.5 m. A finite-element two-dimensional slope model with a slope of 20° was established, and in order to compare it with the ground motion of the shaking-table model test, a total of nine observation points for the ground-motion parameter were arranged at the corresponding locations, including five slope locations (points 1–5) and four vertical slope top locations (points 6–9), as shown in Figure 9. An infinite-element boundary was used for the left and right boundaries of the model, and a fixed boundary was used at the bottom of the model. The finite-element cell size of the model was 2.5 × 2.5 m, and the infinite-element cell size was 2.5 × 10 m. Before the dynamic calculation, the model must be equilibrated for ground stresses because the soil material is used in an elastoplastic instantaneous model. Numerical calculations were first performed for the gravity analysis of the model (Bai, 2010), and predefined fields were created in the ground stress analysis step. The stresses obtained in the gravity analysis step were used as the initial stress conditions for ground stress analysis to achieve ground stress equilibrium. Finally, the model was dynamically analyzed.

FIGURE 8

FIGURE 8. Structure of the finite-element 2D model of the prototype loess slope.

FIGURE 9

FIGURE 9. Grid division and observation point arrangement of the ground motion parameters of the prototype loess slope.

3.2.2 Numerical calculation parameters and loadings of the loess slope

The kinetic parameters for the numerical calculation were adopted from the results of dynamic triaxial tests conducted by Zhijian et al. (2020) on in situ soil samples, and the soil material was selected as an elastoplastic material, satisfying the Moore–Coulomb yield criterion. The mechanical parameters of the model are listed in Table 5. The loading waveform had the same ground-motion acceleration time course as that of the shaking-table model test, as shown in Figure 5.

TABLE 5

TABLE 5. Slope model mechanical parameters of soil layers.

3.2.3 Numerical simulation acceleration and displacement clouds of the loess slope

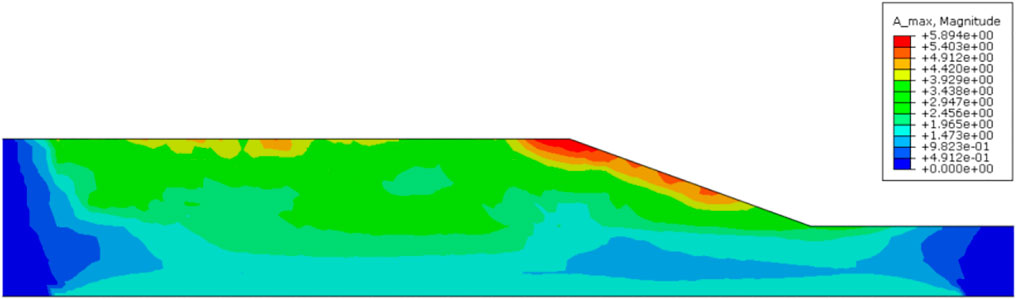
The horizontal seismic acceleration distribution characteristics of the Minxian–Zhangxian M6.6 earthquake prototype loess slope were obtained using finite-element calculations (Figure 10). It can be observed from the figure that the acceleration response had an amplification effect with an increase in the slope height, and the maximum value appeared at the top loess and the leading edge of the slope. The seismic displacement value showed a decreasing trend as the distance from the top loess edge of the slope increased.

FIGURE 10

FIGURE 10. Seismic acceleration cloud of the loess slope by numerical simulation.

The horizontal seismic displacement distribution characteristics of the Minxian–Zhangxian M6.6 earthquake prototype loess slope were obtained using finite-element calculations (Figure 11). It can be observed from the figure that the seismic displacement and acceleration response changes show a similar trend, and the seismic displacement response has an amplification effect with an increase in the slope height. The maximum value appeared at the top loess and leading edge of the slope, and the seismic acceleration value showed a decreasing trend as the distance from the top loess edge of the slope increased.

FIGURE 11

FIGURE 11. Seismic displacement cloud of the loess slope by numerical simulation.

4 Comparative analysis of the shaker-model test and numerical simulation calculation results

4.1 Acceleration time range

Owing to the acquisition process, seismic acceleration waveforms are subjected to sensor drift and high-frequency noise interference from the surrounding environment, such as those originating from the model-box resonance. To eliminate these effects, all PGA data were baseline-corrected using SeismoSignal software during the post-processing stage of the experiment, and the corrected seismic acceleration waveforms were band-pass-filtered from 0.1 to 40 Hz. Figure 12 shows the time course of horizontal ground-shaking acceleration at each observation point when the shaking table and numerical simulation were subjected to a horizontal seismic wave with a PGA of 183.2 gal, in accordance with the Minxian–Zhangxian M6.6 earthquake. The ground-motion acceleration waveforms at these slope observation points were similar to the clear amplification effect, and the peak horizontal ground-motion acceleration observed in the numerical simulation was larger than that observed in the shaking-table test.

FIGURE 12

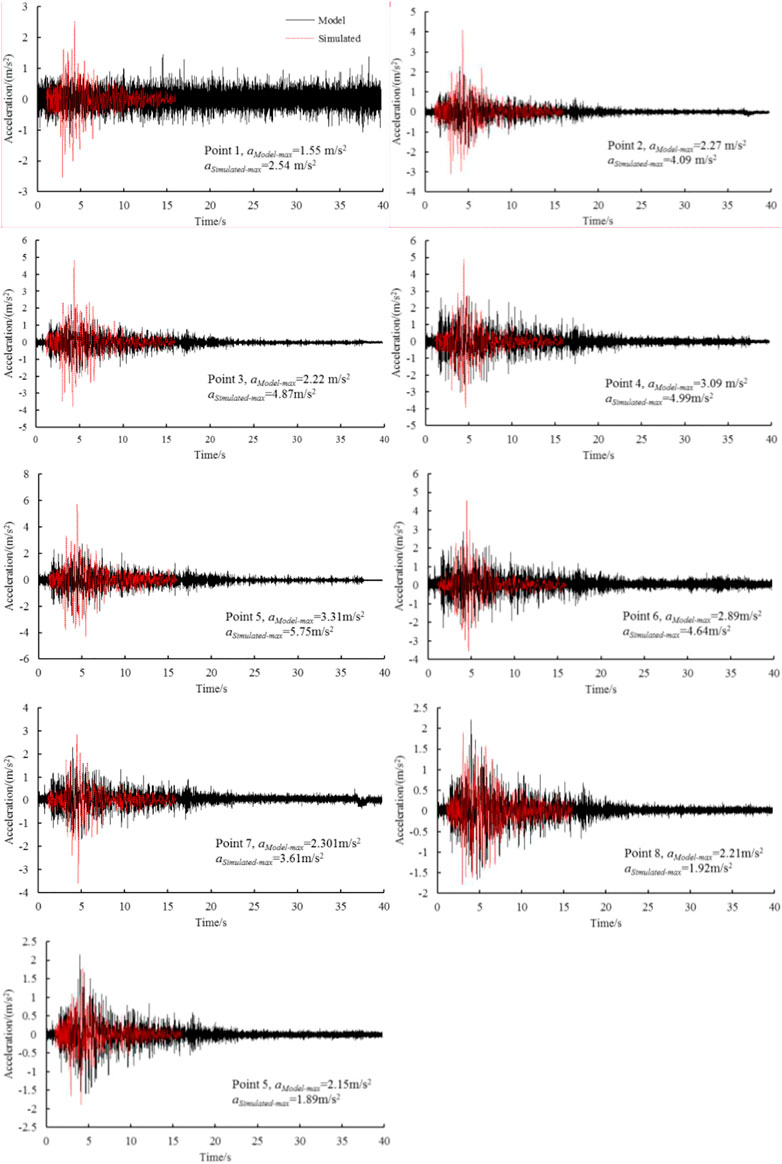
FIGURE 12. Time course of horizontal ground-motion acceleration at each measuring point of the slope under seismic wave excitation with a peak ground acceleration (PGA) of 183.2 gal used in the model test and numerical simulation.

This study explored the dynamic response law of loess slopes by considering the variation characteristics of the slope surface seismic acceleration and internal vertical direction. For comparison, the dimensionless acceleration amplification factor (M_PGA) was introduced, and the ratio of the PGA at each measuring point of the slope surface and vertical section to that at measuring point 1 of the table surface, and measuring point 9 of the vertical section, was defined as the PGA amplification factor. The distribution law of the amplification factor represents that of seismic acceleration.

4.2 Comparative analysis of seismic acceleration response between the slope-model test and numerical simulation

Figures 13, 14 show the horizontal and vertical PGA and amplification factor curves for the model test and numerical simulation at each slope-measuring point under seismic-wave excitation, with a PGA of 183.2 gal, respectively. Figure 15 shows the PGA ratio of each measuring point in the model test and numerical simulation of the loess slope.

FIGURE 13

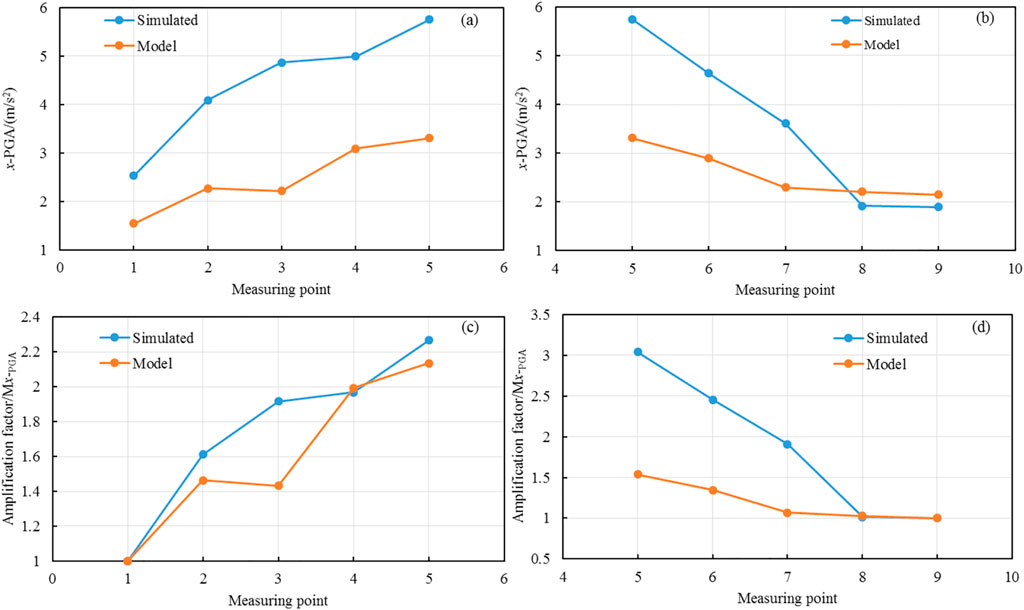
FIGURE 13. Horizontal PGA and amplification factors of each measurement point of the slope. (a) x-PGA of the loess-slope surface; (b) x-PGA of vertical section; (c) Amplification factor of x-PGA of the loess-slope surface; (d) Amplification factor of x-PGA of vertical section.

FIGURE 14

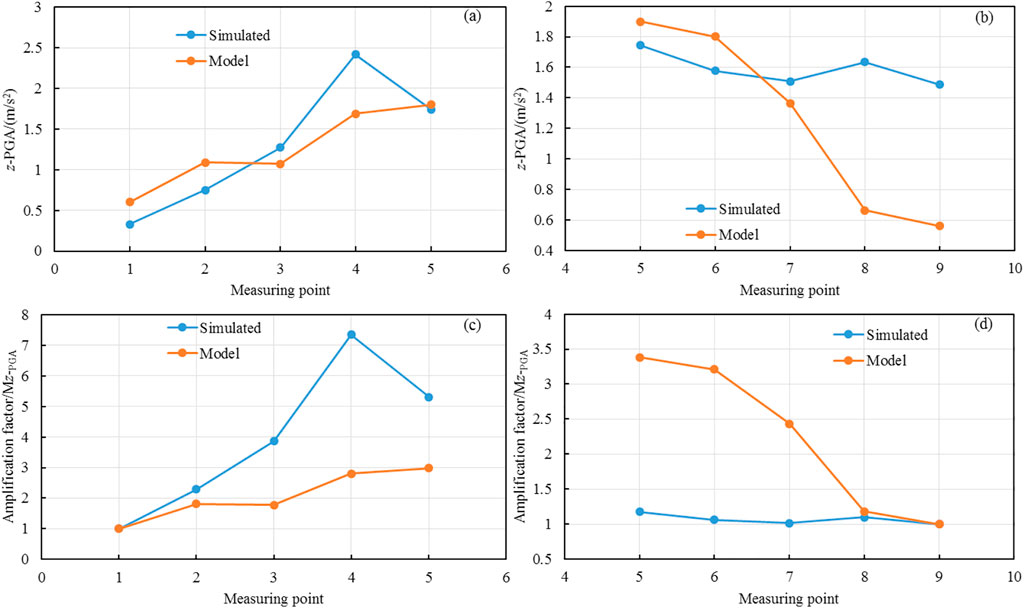
FIGURE 14. Vertical PGA and amplification factors of each measurement point of the slope. (a) z-PGA of the loess-slope surface; (b) z-PGA of vertical section; (c) Amplification factor of z-PGA of the loess-slope surface; (d) Amplification factor of z-PGA of vertical section.

FIGURE 15

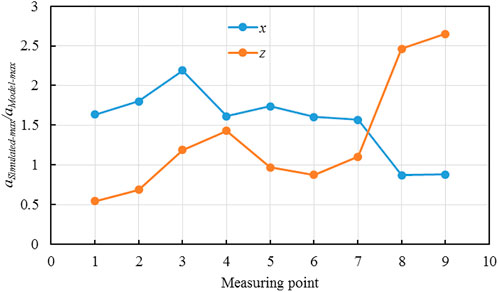
FIGURE 15. Ratio of the PGA at each measuring point using the model test and numerical simulation of the loess slope.

As shown in Figure 13, the horizontal PGA and amplification factors of the loess-slope surface and vertical section measured during the model test and numerical simulation under the same seismic wave excitation showed a clear linearity in elevation with great similarity, and the PGA measured by the model test was lower than that of the corresponding numerical simulation. The distribution of acceleration in the slope surface and vertical section showed regularity; that is, the PGA and amplification factors showed a linearly increasing trend with increasing elevation, and the amplification factors were similar at the same slope-measuring point.

From Figures 13A, C, it can be seen that under seismic wave excitation with a PGA of 183.2 gal, the horizontal PGAs of slope-measuring points 1, 2, 3, 4, and 5 of the model test were 1.55 m/s², 2.27 m/s², 2.22 m/s², 3.09 m/s², and 3.31 m/s², respectively, and the amplification factors of measuring points 2, 3, 4, and 5 were 1.46, 1.43, 1.99, and 2.14, respectively. The horizontal PGAs of slope-measuring points 1, 2, 3, 4, and 5 of the numerical simulation were 2.54 m/s², 4.09 m/s², 4.86 m/s², 4.99 m/s², and 5.75 m/s², respectively, and the amplification factors of measuring points 2, 3, 4, and 5 were 1.61, 1.92, 1.96, and 2.27, respectively, whereas the PGA amplification factors of both were extremely close to each other (Figure 13C). From Figures 13B, D, it can be observed that the horizontal PGAs of measuring points 9, 8, 7, 6, and 5 of the vertical section of the slope tested under seismic wave excitation with a PGA of 183.2 gal were 2.15 m/s², 2.21 m/s², 2.30 m/s², 2.89 m/s², and 3.31 m/s², respectively, and the amplification factors of measuring points 8, 7, 6, and 5 were 1.03, 1.07, 1.34, and 1.54, respectively. The horizontal PGA of the vertical section of the slope corresponding to its height was much lower than the value of the measuring point at the same height of the slope, and the amplification factor of the PGA was also lower than that at the same height of the slope (Figure 13B). The horizontal PGAs of measuring points 9, 8, 7, 6, and 5 of the numerical simulation of the slope were 1.89 m/s², 1.92 m/s², 3.61 m/s², 4.64 m/s², and 5.75 m/s², respectively, and the amplification factors of measuring points 8, 7, 6, and 5 were 1.02, 1.91, 2.45, and 3.04, respectively, whereas the amplification factors of both were similar to those of the horizontal direction with the change in elevation. However, the values differ greatly; that is, the amplification factors increased overall with increasing section elevation, but the amplification factors of the same measuring point in the numerical simulation were much larger than those of the shaking-table model test (Figure 13D).

From Figures 14A, C, it is observed that under seismic wave excitation with a PGA of 183.2 gal, the vertical PGAs of slope-measuring points 1, 2, 3, 4, and 5 of the model test were 0.60 m/s², 1.09 m/s², 1.07 m/s², 1.69 m/s², and 1.90 m/s², respectively, and the amplification factors of measuring points 2, 3, 4, and 5 were 1.81, 1.77, 2.80, and 2.99, respectively. The vertical PGAs of measuring points 1, 2, 3, 4, and 5 on the slope surface of numerical simulation were 0.33 m/s², 0.75 m/s², 1.27 m/s², 2.42, and 1.74 m/s², respectively, and the amplification factors of measuring points 2, 3, 4, and 5 were 2.29, 3.87, 7.35, and 5.31, respectively. However, the vertical PGA of the two were closer (Figure 14A), while the difference in amplification factors was larger (Figure 14C). Compared with the horizontal PGA values and amplification factors on the loess slope, the vertical PGA values were significantly smaller, but the amplification factors of the vertical PGA were larger. From Figures 14B, D, it can be observed that the vertical PGAs of the vertical section of the slope at measuring points 9, 8, 7, 6, and 5 of the model test under seismic wave excitation with a PGA of 183.2 gal were 0.56 m/s², 0.66 m/s², 1.37 m/s², 1.80 m/s², and 1.90 m/s², respectively, and the amplification factors of measuring points 8, 7, 6, and 5 were 1.18, 2.43, 3.21, and 3.39, respectively. The amplification factors of both were similar to the amplification factors of the vertical PGA with elevation, but the values were different; that is, the overall amplification factors increase with an increasing section elevation, but the amplification factors of the same measuring point in the numerical simulation were much smaller than those of the shaking-table model test (Figure 14D) and the horizontal PGA.

As shown in Figures 13, 14, both the model tests and numerical simulations under the same seismic wave excitation conditions indicate that the loess slope exhibits a significant amplification effect along the elevation, and that there is a linear amplification of ground motion with a consistent trend on the slope surface. The results from both the model tests and numerical simulations verify that horizontal seismic forces under the natural earthquake action may be the main cause of loess slope damage.

It can be observed from Figure 15 that there is a similarity between the PGA ratios of measuring points 1–7 at the same elevation for the slope surface and vertical sections. The values of the horizontal PGA a_{Simulated-max}/a_Model-max range from 1.5 to 2.2 and the values of the vertical PGA a_{Simulated-max}/a_Model-max range from 0.5 to 1.5, indicating that the horizontal PGA measured by the numerical simulation is much larger than that measured by the model test for the slope surface and vertical section at the same elevation. However, the ratio of the vertical PGA was closer to 1.0, and the horizontal PGA measured by the numerical simulation was smaller than that measured by the model test. At measuring points 8–9 of the vertical section of the slope, the values of the horizontal PGA a_{Simulated-max}/a_Model-max range from 0.86 to 0.88 and the values of the vertical PGA a_{Simulated-max}/a_Model-max range from 2.45 to 2.65, which are different from the corresponding PGA ratios at measuring points 1–7. This large difference indicates that for the same elevation of the loess slope with a lower vertical section elevation, the position of the PGA inside the slope body is influenced by the physical model conditions and numerical simulation parameter settings, resulting in a large dispersion. This means that the numerical simulation is closer to the real measured ground-motion characteristics, whereas the model test displayed differences in the ground motion and curves owing to factors such as reshaping the soil and parameter settings. There are some differences between the main ground motions and the curves.

4.3 Spectrum analysis

4.3.1 Spectrum analysis method of strong ground motion

The spectral analysis of data from strong ground-motion observations is a process of Fourier transform and Fourier inverse transform. The value of N (even) of the time function at equal time interval points $x_m\left(m=\mathrm{0,1,2},...,N-1\right)$ is

$\begin{array}{c}{A}_k=\frac{2}{N}{\displaystyle \sum }_{m=0}^{N-1}{x}_m\cos \frac{2\pi km}{N}k=\mathrm{0,1,2},...,N/2-1,N/2,\\ B_k=\frac{2}{N}{\displaystyle \sum }_{m=0}^{N-1}{x}_m\sin \frac{2\pi km}{N}k=\mathrm{1,2},...,N/2-1,\end{array}(15)$

where $x_m$ is denoted as a finite trigonometric function with $A_k$ and $B_k$ as coefficients.

$x_m=\frac{A_0}{2}+{\displaystyle \sum }_{k=1}^{N/2-1}\left[A_k\cos \frac{2\pi km}{N}+B_k\sin \frac{2\pi km}{N}\right]+\frac{A_{N/2}}{2}\cos \frac{2\pi \left(N/2\right)m}{N}.(16)$

Considering that this function is nothing but an approximation of the metric function $x_t$, we get

$\stackrel{\sim }{x}\left(t\right)=\frac{A_0}{2}+{\displaystyle \sum }_{k=1}^{N/2-1}\left[A_k\cos \frac{2\pi kt}{N\Delta t}+B_k\sin \frac{2\pi kt}{N\Delta t}\right]+\frac{A_{N/2}}{2}\cos \frac{2\pi \left(N/2\right)t}{N\Delta t}.(17)$

Eq. 17 is a finite Fourier approximation of function xt. The coefficients Ak and Bk in Eq. 15 are を finite Fourier coefficients. The calculation of Eq. 15 is called the Fourier transform of the discrete value xm, and Eq. 16 is called the inverse Fourier transform.

Here, the introduction of the complex Fourier coefficient C_k implies

$x_m={\displaystyle \sum }_{k=0}^{N-1}{C}_k{e}^{i\left(2\pi km\right)}m=\mathrm{0,1,2},...,N-1.(18)$

More concisely, it can be expressed by the following equation, called the finite complex Fourier series:

$C_k=\frac{1}{N}{\displaystyle \sum }_{m=0}^{N-1}{x}_m{e}^{-i\left(2\pi km/N\right)}k=\mathrm{0,1,2},...,N-1.(19)$

Eq. 19 is the Fourier transform, and Eq. 18 is the inverse Fourier transform. Using this calculation method, the observed data can be subjected to spectral analysis.

4.3.2 Comparative analysis between the model test and numerical simulation of the Fourier spectrum of each loess slope-measuring point

The Fourier spectrum characteristics of each measuring point of the slope surface and vertical section from model tests and numerical simulations were compared and analyzed by the Fourier transform. This was performed from the perspective of variations in seismic wave frequencies to explore the possible causes of differences in the seismic acceleration response of the slope due to model conditions and numerical simulation parameters.

The Fourier spectra of the horizontal and vertical seismic accelerations at each measuring point on the slope surface and vertical section of the loess slope for the model test and numerical simulation under the same ground motion are shown in Figure 16. The magnitude of the amplitude in the Fourier spectrum represents the amount of energy contained at the measuring point, and the difference in amplitude between the spectral lines represents the change in energy between the measuring points as the seismic wave passes through various parts of the soil. It can be observed from this figure that with an increase in the elevation, the spectral-line shapes of the different measuring points of the slope from both the model tests and numerical simulations were similar. From Figures 16A–I, it can be observed that under seismic wave excitation with a PGA of 183.2 gal, the horizontal first-principal frequency of the slope surface and vertical section of the model test was mainly concentrated at approximately 0.5 Hz at low frequency, the Fourier amplitude frequencies were mainly distributed between 0.1 and 12 Hz, and the amplitude value was between 2.83 and 3.81 m/s². The amplitude value was positively correlated with the overall slope height, and the spectral-line shapes of different measuring points showed similarities at different measuring points. The first main frequency in the horizontal direction of each measuring point in the numerical simulation of the slope surface and vertical section was concentrated around 2.0 Hz at low frequencies. The Fourier amplitude frequencies were distributed between 0.1 and 12 Hz, with an amplitude value ranging from 2.08 to 6.57 m/s². The amplitude was positively correlated with the overall slope height, and the spectral-line shapes of the different measuring points showed similarities. Figures 16A–I show seismic wave excitation with a PGA of 183.2 gal.

FIGURE 16

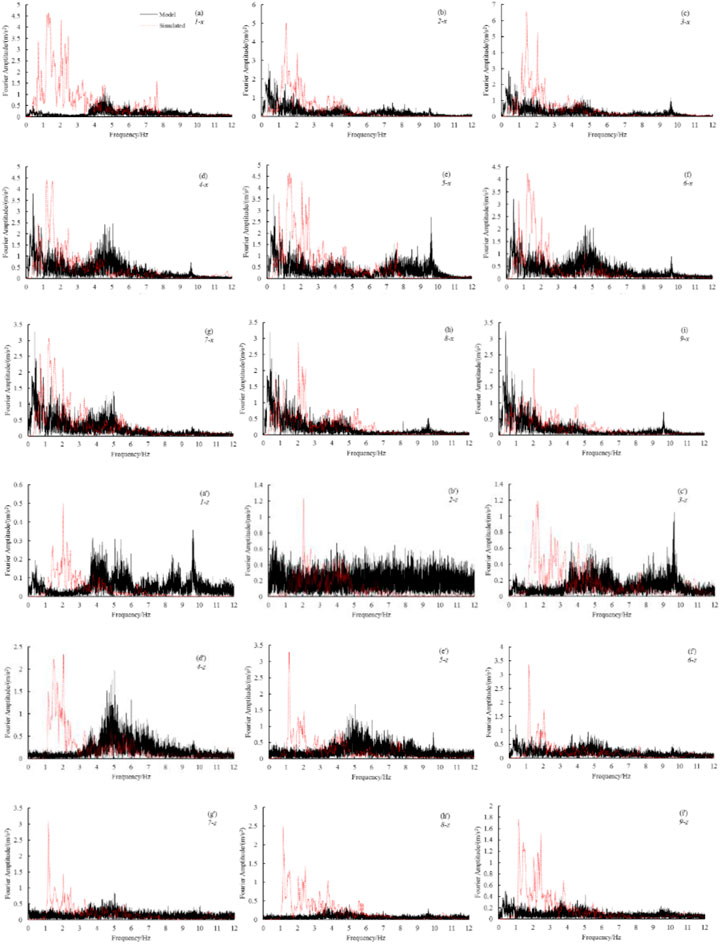
FIGURE 16. Fourier spectrum of each measuring point of the slope in the model test and numerical simulation.

The first main frequency in the vertical direction at each measuring point of the slope surface and vertical section of the model test was similar to that in the horizontal direction, mainly concentrated at approximately 0.5 Â Hz, with low frequencies. The amplitudes were between 0.50 and 1.96 m/s², which are positively correlated with the overall slope height, and the spectral-line shapes of the different measuring points showed similarities. The first main frequency of the vertical direction of each measuring point in the numerical simulation of the slope surface and vertical section was mainly concentrated around 2.0 Hz, with a low frequency, and the amplitude was between 1.19 and 3.36 m/s². The amplitude was positively correlated with the overall slope height, and the spectral-line shapes of the different observation points showed similarities. From the aforementioned details, although the same seismic wave input was used, the main frequencies of the Fourier spectrum of the model test and numerical simulation were different, and the latter was approximately four times that of the former. However, the main frequency of the Fourier spectrum of each measuring point of the model test and numerical simulation is different from that of the seismic wave input; however, the numerical simulation is closer and the curve is more similar, which means that the numerical simulation is closer to the real observed ground-motion spectrum characteristics, while the model test showed differences between the main frequency of the Fourier spectrum and the curve owing to the non-primary loess, the similarity ratio, and other possible factors.

It can be observed from Figure 17 that the Fourier spectrum amplitudes of measuring points 2–9 of the slope surface and vertical section, taking into account both the model test and numerical simulation of the slope at the same elevation measuring points, increased with the increasing elevation, and the trend was similar; however, the Fourier spectrum amplitudes of the numerical simulation were higher than those of the model test, and there were significant similarities between them and the corresponding PGA. The inconsistencies between the Fourier spectrum amplitude at individual points and the overall trend in the figure are due to the presence of data errors caused by the discrete-model test-measuring data.

FIGURE 17

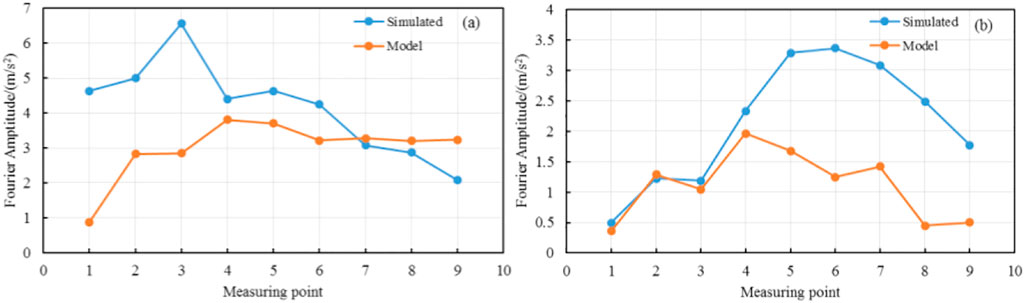
FIGURE 17. Comparison of Fourier spectrum amplitude at each measuring point of the slope between the model test and numerical simulation: (A) horizontal direction; (B) vertical direction.

5 Conclusion

The dynamic response characteristics of a low-angle loess slope under the input of the same horizontal seismic wave load were studied through a combination of shaking-table model test and simulation calculations. The response law of seismic waves on the slope surface and body of the loess slope was explored, and the seismic acceleration Fourier spectra of the slope surface and section were analyzed. The following conclusions were drawn:

1) The PGA and peak ground displacement on the slope surface and internal vertical section of the loess slope both exhibited elevation amplification effects; that is, the closer to the top of the slope, the more evident the amplification effects. Under the same seismic load, the seismic acceleration waveforms of each loess slope-measuring point in the model test and numerical simulation were similar.

2) Under the same seismic load, the PGA and amplification factors of the slope and loess-slope vertical sections measured by the model test and numerical simulation showed clear linearity in elevation with great similarity, and the PGAs measured by the model test were lower than those of the corresponding numerical simulation. The Fourier spectrum amplitude for the same elevation measuring point of the slope in both the model test and numerical simulation increased with an increasing elevation, and there was a similar trend. However, the overall Fourier spectrum amplitude of the numerical simulation was higher than that of the model test, and there was a significant similarity between amplitude and the corresponding PGA.

3) There was a similarity between the ratios of the measuring points at the same elevation, with the values of the horizontal PGA a_{Simulated-max}/a_Model-max ranging from 1.5 to 2.2 and the vertical PGA a_{Simulated-max}/a_Model-max ranging from 0.5 to 1.5, indicating that for the loess slope at the same elevation and vertical section. However, for the vertical PGA, the ratio of the two was predominantly close to 1.0, and the horizontal peak acceleration measured by the numerical simulation was smaller than that measured by the model test.

4) Under the same seismic load, the first predominant frequency of the slope surface Fourier spectrum and the vertical section of the model test was concentrated at approximately 0.5 Hz (low frequency) and the amplitude was positively correlated with the overall slope height, whereas the spectral-line shapes at different measuring points exhibited similarities. The first predominant frequency of the Fourier spectra at the slope and vertical section of the numerical simulation was approximately 2.0 Hz, and the amplitude was positively correlated with the slope height.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, Further inquiries can be directed to the corresponding author.

Author contributions

YW: writing—original draft, visualization, formal analysis, and writing—review and editing. TX: numerical simulation. WZ: conceptualization, methodology, formal analysis, and writing—review and editing. WP: writing—review and editing. KL: physical modeling test.

Funding

Financial support for this project was provided by the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (Grant No. 2020EEEVL0304), the Second Tibetan Plateau Scientific Expedition and Research Program (STEP) (Grant no. 2019QZKK0905), the Scientific Research Fund of Institute of Earthquake Forecasting, China Earthquake Administration (Grant no. 2014IESLZ01), the National Natural Science Foundation of China (Grant nos. 51678545, 41472297, and U1939209), and the Topics of Gansu Province Key R&D Program (Grant no. 18YF1FA101).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, Jianfang (2010). Introduction to site seismic response analysis. Beijing, China: China Railway Press.

Google Scholar

Bouckovalas, G. D., and Papadimitriou, A. G. (2005). Numerical evaluation of slope topography effects on seismic ground motion. Soil Dyn. Earthq. Eng. 25 (7-10), 547–558. doi:10.1016/j.soildyn.2004.11.008

CrossRef Full Text | Google Scholar

Chen, T., Wu, Z. J., Ma, W, Wang, L. M, and Zeng, L. F. (2012). Study on the influence of site conditions on ground vibration amplification effect in loess areas. J. Undergr. Space Eng. 8 (05), 969–974.

Google Scholar

Gao, Lin, Zhu, Tong, and Lin, Bei (2000). Similarity technique for dynamic structural model test. J. Dalian Univ. Technol. 40 (1), 1–8.

Google Scholar

Jiang, Ming-jing (2019). New paradigm for modern soil mechanics: Geomechanics from micro to macro. Chin. J. Geotechnical Eng. 41 (2), 195–254. doi:10.11779/CJGE201902001

CrossRef Full Text | Google Scholar

Liu, Kung (2020). “Earthquake-induced failure mechanism and stability evaluation of loess slope under rainfall effects,” (Lanzhou, China: Lanzhou University). PhD Thesis.

Google Scholar

Liu, T. S. (1985). Loess and the environment. Beijing, china: Ocean Press.

Google Scholar

Lu, Xi-lin, Yue-qing, C. H. E. N., Chen, Bo, Huang, W., and Zhao, L. (2000). Shaking table test of dynamic soil-structure interaction system. Seismic Eng. Eng. Vib. 20 (4), 20–29.

Google Scholar

Meunier, P., Hovius, N., and Haines, J. A. (2008). Topographic site effects and the location of earthquake induced landslides. Earth Planet. Sci. Lett. 275 (3-4), 221–232. doi:10.1016/j.epsl.2008.07.020

CrossRef Full Text | Google Scholar

Murphy, W. (2006). “The role of topographic amplification on the initiation of rock slopes failures during earthquake,” in Landslides from massive rock slope failure. Editors S. G. Evans, G. S. Mugnozza, A. Strom, and R. L. Hermanns (Springer), 49, 139–154.Celano, Italy2

Google Scholar

Wang, H. Y., and Xie, L. L. (2010). Influence of topography on ground shaking in xishan park, Zigong. J. Geophys. 53 (7), 1631–1638.

Google Scholar

Wang, Lanmin (2003). Loess dynamics. San Diego, CA: Seismic Press.

Google Scholar

Wang, Lanmin, Pu, Xiaowu, Wu, Zhi-jian, Xu, X., and Liu, K. (2018). Shaking table tests of dynamic response of loess slopes under the coupling effects of earthquake and rainfalls. Chin. J. Geotechnical Eng. 40 (7), 1287–1293.

Google Scholar

Wang, L. M., Che, A. L., and Wang, L. (2019). Characteristics and enlightenment of Hokkaido Ms6.7 earthquake disaster in Japan. City Disaster Reduct. 1, 1–8.

Google Scholar

Wang, L. M., Pu, X. W., Chai, S., Wang, P., and Wang, Q. (2017c). “A performance-based design method of loess slopes under the coupling effects of earthquakes and rainfalls,” in PBD III VANCOUVER Earthquake Geotechnical Engineering, Vancouver, Canada, July 16-19, 2017.

Google Scholar

Wang, L. M., Wang, Q., Wu, Z. J., and Che., A. L. (2017a). “Loessial landslides induced by the minxian–zhangxian Ms6.6 earthquake of China in 2013,” in Geotechnical hazards from large earthquakes and heavy rainfalls (Tokyo, Japan: Springer).

Google Scholar

Wang, L., Sun, J., Wang, Q., Pu, X., and Wang, N. (2017b). “Physical mechanism and prevention method of loess slope failure induced by the coupling effect of earthquake and rainfall,” in 16th World Conference on Earthquake, Santiago, Chile, January 09-13 2017.

Google Scholar

Wang, L., Wua, Zhijian, Xia, Kun, Liu, K., Wang, P., Pu, X., et al. (2019). Amplification of thickness and topography of loess deposit on seismic ground motion and its seismic design methods. Soil Dyn. Earthq. Eng. 126, 105090–105112, 1–12. doi:10.1016/j.soildyn.2018.02.021

CrossRef Full Text | Google Scholar

Wu, Zhi-jian, Wang, Lan-min, Wang, Ping, Chen, T., Shi, H., and Yang, X. p. (2013). Influence of site conditions on ground motion at far field loess sites during strong earthquake. J. Cent. South Univ. 20, 2333–2341. doi:10.1007/s11771-013-1741-2

CrossRef Full Text | Google Scholar

Wu, Zhijian, Tian, Lei, Chen, Yujin, Wang, Ping., and Chai, Shao-feng. (2015). Deformation and instability characteristics of loess slope base on shaking table model. J. Shanghai Jiaot. Univ. 49 (7), 940–945.

Google Scholar

Yasuhiro, Mitani, Wang, Fawu, Okeke, Austin Chukwueloka, and Qi, W. (2013). “Dynamic analysis of earthquake amplification effect of slopes in different topographic and geological conditions by using ABAQUS,” in Environmental science and engineering (Berlin, Heidelberg: Springer).

Google Scholar

Yuan, Wen-zhong (1998). Similar theoretical and static model test. Chengdu, China: Southwest Jiaotong University Press.

Google Scholar

Zhang, Zelin, Wu, Shuren, and Wang, Tao (2018). Influence of seismic wave amplitude on dynamic response of loess-mudstone slope. Rock Soil Mech. 39 (7), 2403–2412.

Google Scholar