Energy analysis of intact granite based on test while drilling under different confining stresses and drilling parameters

The rock properties are related to the stress environment and dynamic disturbance during construction, and the testing-while-drilling-technique was used for evaluation of rock properties. However, the related research ignored the influences of stress environment and drilling parameters. In this study, triaxial compression tests and laboratory drilling tests under different confining stresses and drilling parameters were conducted for intact granite, and the numerical changes of drilling parameters were recorded. Then the static elastic energy and drilling specific energy (dynamic energy) of rock were calculated by using linear energy storage theory and rock breaking energy theory, respectively. According to the characteristics of energy variation, an energy analysis method based on drilling process was proposed, and the sum of static elastic energy and dynamic elastic energy was defined as the total energy. The results showed that: 1) the static elastic energy increased with the increase of confining stress, while the drilling specific energy was opposite. 2) For the same rock, the total energy was constant under the same drilling parameters. 3) The influence of drilling parameters on total energy was quantified by dynamic load influence factor. Finally, the potential application of energy analysis method in stress estimation was discussed through drilling tests.

1 Introduction

An engineering rock mass is generally in a state of combined action of static stress and dynamic load. Self-weight and tectonic stress constitute the static environment of the rock. Explosive blasting, mechanical drilling, and other construction-related factors can cause dynamic disturbances to the rock mass. Drilling plays a vital role in engineering construction and monitoring, energy exploration and development. In recent years, test-while-drilling (TWD) technology has fully exploited the advantages of in-situ testing.

TWD is a typical field test method (Xia et al., 2022) to evaluate rock properties by collecting and analyzing drilling parameters (drilling rate, drilling force, bit rotation speed, and bit torque). Many studies have proved that differences in rock properties can lead to changes in drilling parameters, and the hardness, rock integrity and spatial distribution of faults and holes can be determined by drilling rate (Yang et al., 2012; Chen and Yue, 2015), bit torque (Gui et al., 2002; Van Wyk et al., 2014; Wang et al., 2018a), and specific energy (Yasar et al., 2011). Determination of rock grade by drilling energy analysis is a commonly used method (Tan et al., 2007; Oparin et al., 2018; Sakiz et al., 2021), and current TWD theory assumes the energy required to break the same rock is a constant value, and this energy is only related to the grade and type of rock (Kahraman, 1999; Karasawa et al., 2002; Mostofi et al., 2011; Wang et al., 2018b; Wang et al., 2019). However, in engineering practice, drilling parameters vary greatly in the same stress environment. The strength and stiffness of rock vary with confining stresses and loading rates (Yang et al., 2006; Liu S. H. et al., 2014). Compared with other types of rocks, the confining stress and loading rate have more significant effects on intact, hard and brittle rocks, implying that the confining stress and drilling parameters have a greater impact on the drilling specific energy of intact rock. The drilling specific energy is the energy required to excavate unit volume of rock by the bit. In the process of rock failure, it is not only necessary to absorb energy from the outside, but also to dissipate energy in the form of plastic properties or kinetic energy (Bai et al., 2019; Bai et al., 2021; Bai et al., 2022). However, current TWD energy analysis methods ignore the stress environment, drilling parameters (Zhang and Gao, 2015; Su et al., 2022; Zhao et al., 2022), and energy dissipation which leads to limited applicability of energy analysis results.

In the drilling tests, the authors have found that for the same rock, the drilling specific energy varies under different confining stresses and drilling parameters. The tests results cannot be reasonably explained by the current TWD energy theory, which indicates that the TWD energy theory needs to be improved.

In the analysis of rockburst energy in hard rock, considering the influence of confining stress and construction disturbance, a coupled static-dynamic loading theory was proposed (Li and Gu, 2002). This theory assumes that rock failure is the result of the combined action of confining static stress and construction disturbance, the initial stress condition determines the intensity and quantity of energy released during failure, and the dynamic disturbance is only the induced condition (Gong et al., 2010; Gong et al., 2010, 2014; Gong et al., 2020), this theory is currently applied to rockburst prediction in tunnel excavation and underground mining (Liu Q. S. et al., 2014; Luo et al., 2015; Wang et al., 2015; He et al., 2018; Li et al., 2019). Studies have shown that when the confining stress is constant, different dynamic load conditions will affect the absorption and release of energy by rocks, resulting in changes in its mechanical properties (Li et al., 2011a). The stronger the dynamic disturbance, the less energy released during rock failure (Gong et al., 2011). These findings are consistent with the drilling tests results performed by the authors.

Therefore, in order to reasonably explain the impact of confining stress and drilling parameters on rock drilling energy and better evaluate rock properties through TWD, triaxial compression tests under different confining stresses and drilling tests under different confining stresses and drilling parameters were conducted on intact granite. The influence of stress conditions and drilling parameters on drilling specific energy was analyzed. Referring to the coupled static-dynamic loading theory for rockburst, a new energy analysis method based on drilling process was proposed to evaluate rock properties.

2 Energy of intact granite under static load

2.1 Linear energy storage theory

The confining stress can be regarded as static load, and the energy generated is referred to as static load energy $U_{\mathrm{s}}$. Rock loading and unloading tests are conducted on a mechanical testing machine. During the loading process, the testing machine continues to work on the rock; during the unloading process, the energy stored in the rock is gradually released. The loading and unloading test results show that when the rock is compressed, the internal energy can be stored. Typical stress-strain curves of rock are shown in Figure 1. $U_{\mathrm{s}}$ can be divided into static elastic energy $U_{\mathrm{s}}^{\mathrm{e}}$ and static plastic energy $U_{\mathrm{s}}^{\mathrm{p}}$. The area between the unloading curve and the x-axis is the static elastic energy per unit volume of rock $u_{\mathrm{s}}^{\mathrm{e}}$. $u_{\mathrm{s}}^{\mathrm{e}}$ can be completely released during the unloading process, and the elastic deformation is restored. The area between the unloading process curve and loading curve is the static plastic energy per unit volume of rock $u_{\mathrm{s}}^{\mathrm{p}}$. During loading, $u_{\mathrm{s}}^{\mathrm{p}}$ dissipates in the form of plastic deformation and microcracks and is not stored in the rock. Herein, the elastic energy is taken as the static load energy storage index affected by confining stress ${\sigma }_{\mathrm{c}}$ (Gong et al., 2018). The sum of $u_{\mathrm{s}}^{\mathrm{e}}$ and $u_{\mathrm{s}}^{\mathrm{p}}$ is the static energy per unit volume of rock $u_{\mathrm{s}}$. $u_{\mathrm{s}}$, $u_{\mathrm{s}}^{\mathrm{e}}$, and $u_{\mathrm{s}}^{\mathrm{p}}$ can be calculated by graphical integration (Figure 1):

$\left\{\begin{array}{l}{u}_{\mathrm{s}}=u_{\mathrm{s}}^{\mathrm{e}}+u_{\mathrm{s}}^{\mathrm{p}}\\ u_{\mathrm{s}}=\underset{0}{\overset{{\epsilon }_p}{{\displaystyle \int }}}\sigma \mathrm{d}\epsilon \\ u_{\mathrm{s}}^{\mathrm{e}}=\underset{{\epsilon }_0}{\overset{{\epsilon }_p}{{\displaystyle \int }}}\sigma \mathrm{d}\epsilon \end{array}\right.(1)$

where ${\epsilon }_0$ is the plastic strain value after unloading; ${\epsilon }_{\mathrm{p}}$ is the peak strain; ${\sigma }_{\mathrm{p}}$ is the peak stress. Gong et al. (2018) conducted uniaxial compression single loading unloading tests on various rocks under different stress levels, and found that the proportion of $u_{\mathrm{s}}^{\mathrm{e}}$ in $u_{\mathrm{s}}$ under different stress levels is a constant value. It is called linear energy storage theory which assumed that $u_{\mathrm{s}}$ and $u_{\mathrm{s}}^{\mathrm{e}}$ were linearly related. Many loading and unloading tests suggest that the linear energy storage is as given by Eq. 2 (Gong et al., 2018):

$u_{\mathrm{s}}^{\mathrm{e}}=A{u}_{\mathrm{s}}+B(2)$

where $A$ is the static load energy storage coefficient, which is the slope of the linear fitting formula of $u_{\mathrm{s}}$ and $u_{\mathrm{s}}^{\mathrm{e}}$, representing the proportion of $u_{\mathrm{s}}^{\mathrm{e}}$ in $u_{\mathrm{s}}$. $A$ can be obtained through the laws summarized by the linear energy storage theory. Brittle rock can store a large amount of energy, so $A$ is close to 1. For intact granite, $A$ is .8542 (Gong et al., 2018). $B$ represents the intercept of the linear fitting formula for $u_{\mathrm{s}}$ and $u_{\mathrm{s}}^{\mathrm{e}}$, which has little influence on the result and can be ignored. The static elastic energy in rock can be calculated by using linear energy storage theory with triaxial compression results. The $u_{\mathrm{s}}$ can be calculated through the graphical integration of the stress-strain curve of the triaxial compression test, and the static elastic energy $u_{\mathrm{s}}^{\mathrm{e}}$ are finally obtained.

FIGURE 1

FIGURE 1. Stress-strain whole-process curves.

2.2 Rock compression tests

Granite is a common engineering rock mass. Many hydropower stations and pumped storage dam foundations are based on intact granite, and some underground power plants are built in intact granite rock mass. The natural intact granite from Changtai County, Quanzhou, Fujian, China, was sampled. The average compressive strength obtained by the uniaxial compression test is 251 MPa, the tensile strength is 13.57 MPa, the cohesion is 39.49 MPa, and the internal friction angle is 56.95°. The granite was processed into a standard triaxial sample with a diameter of 50 mm and a height of 100 mm. Since the depth of most underground power plants is usually less than 1 km, and the confining stress at this depth is about 25 MPa. The confining stresses in the compression test were set to 0, 5, 10, 15, 20 and 25 MPa. According to “DZ/T 0276.19-2015 Rock Physical and Mechanical Property Test Specification Part 19: Rock Uniaxial Compression Deformation Test”, China, “DZ/T 0276.20-2015 Rock Physical and Mechanical Property Test Specification Part 20: Rock Triaxial Compression Strength Test,” China, confining and axial stresses were applied at a rate of .05 MPa/s. When the confining stress was increased to a predetermined value, the variation therein should not exceed 2%. The axial load was controlled by displacement, and the cross-head displacement rate was .001 mm/s until the sample breaks. The compression test under each confining stress is repeated five times (error less than 1 MPa). The average value of five tests is taken as the compressive strength of rock under this confining stress. Figures 2, 3 show the rock failure mode and stress-strain curve of only one of the five tests. Axial and confining stress were recorded during the compression process, and the stress-strain curve of rock was plotted. Test design and stress-strain data are displayed in Table 1.

FIGURE 2

FIGURE 2. Typical failure modes of samples. (A) 0 MPa (B) 5 MPa (C) 10 MPa (D) 15 MPa (E) 20 MPa (F) 25 MPa.

FIGURE 3

FIGURE 3. Stress-strain curves of rock under different confining stresses.

TABLE 1

TABLE 1. Results of rock compression testing.

According to Table 1, the peak stress and peak strain increase with the increase of confining stress. The failure mode of intact granite is a typical brittle failure; especially in unconfined compression tests, rock failure is accompanied by a tremendous release of energy, a loud sound, and ejection of debris. This finding indicates that granite is an elastic brittle rock that stores a significant amount of energy before failure. Typical failure modes are shown in Figure 2. The stress-strain curves are depicted in Figure 3, and each curve only truncates before the peak stress.

The stress-strain curves of each group accord with the typical characteristics of elastic materials. Upon initiation of loading, the pores and micro-cracks in the granite are gradually closed, and the stress-strain curve is slightly concave. Then it enters the elastic stage, and the stress-strain relationship is linear. When failure is imminent, the curve is concave, and the micro-cracks in the granite are in the state of branching and expansion. At peak stress, the fissures are connected to form a failure surface, and the granite breaks. The linear part accounts for a large proportion of the whole stress-strain curve, which indicates that the mechanical properties of granite are elastic when the confining stress is within 25 MPa.

2.3 Static elastic energy

The values of $u_{\mathrm{s}}$ under different confining stresses can be obtained by graphical integration of the stress-strain curve (Figure 3). We then substitute $u_{\mathrm{s}}$ into Eq. 2 to calculate the $u_{\mathrm{s}}^{\mathrm{e}}$ of intact granite, as shown in Table 2. It can be observed that the greater the confining stress, the greater the $u_{\mathrm{s}}^{\mathrm{e}}$ within the rock (Figure 4). Using linear fitting, the relationship between $u_{\mathrm{s}}^{\mathrm{e}}$ and confining stress is shown in Eq. 3:

$u_{\mathrm{s}}^{\mathrm{e}}=0.082{\sigma }_{\mathrm{c}}+0.65(3)$

TABLE 2

TABLE 2. Static load energy and static elastic energy under different confining stresses.

FIGURE 4

FIGURE 4. Diagram of static elastic energy and confining stress.

In the elastic stage, $u_{\mathrm{s}}^{\mathrm{e}}$ increases by about .082 $\text{mJ}/{\text{mm}}^3$ when the confining stress increases by 1 MPa. The higher the confining stress in the elastic stage, the more energy is stored in the rock. When rock energy reaches its energy storage limit under the action of axial load, the energy released increases accordingly.

3 Energy of intact granite under dynamic load

3.1 Laboratory drilling test design

According to the working characteristics of a drilling rig in engineering practice, a laboratory drilling test platform that can simulate the stress environment of surrounding rock was developed. The test platform comprises a servo-motor control system, drilling acquisition system, propulsion acquisition system, and confining stress system. The four systems control and collect drilling parameters, including drilling rate, drilling force, bit rotation speed, bit torque, and confining stress. The platform allows controllable drilling under different confining stresses. The internal structure of the confining stress system is shown in Figure 5. The main technical parameters of the test platform are listed in Table 3.

FIGURE 5

FIGURE 5. Internal structure of confining stress system.

TABLE 3

TABLE 3. Main technical parameters of the test platform.

Three-edge, three-water way flat-tooth diamond-impregnated core bits were used in drilling tests. The outer diameter of the bit is 32 mm, the inner diameter is 24 mm, and the water way spacing is 6 mm (Figure 6). The granite sample used in the drilling test is the same as that used in the compression test. The sample size is 100 mm × 100 mm ×100 mm.

FIGURE 6

FIGURE 6. Diamond impregnated bit.

The granite sample is put into the confining stress system, and the hydraulic servo-motor controlled jack exerts and maintains the confining stress in two directions. The bit rotates from the free face, as shown in Figure 7. The test adopts the working mode of adjusting drilling rate and bit rotation speed, monitoring drilling depth, drilling force, and bit torque. According to “DZ/T 0227-2010 geological core drilling regulations,” China, in the rotary core drilling mode, the recommended drilling rate of 32 mm diameter-impregnated bit in granite is 13.33–35.00 mm/min, and the recommended bit rotation speed is about 800 rpm. Drilling test parameters are designed as follows: the drilling rate is 15 mm/min, the bit speed is 600 rpm, and the confining stresses are 0, 5, 10, 15, 20, and 25 MPa, respectively, corresponding depth 0–1,000 m from the ground. To study the influences of different drilling parameter combinations and confining stress conditions on the test results, the drilling test design is as follows: the bit rotation speed is 800 rpm, drilling velocities are 15 mm/min and 25 mm/min, and the confining stresses are 0, 5, 15, 25, and 35 MPa, corresponding depth 0–1,400 m from the ground. To ensure the reliability of the test data, the drilling test was repeated three times under the same conditions. The results show that the corresponding characteristics of the three tests are consistent. For illustrative purposes, only one test result is shown for each test condition.

FIGURE 7

FIGURE 7. Schematic diagram of drilling test.

Results are summarized in Table 4. Drilling tests are numbered from A to P. There are three combinations of drilling parameters: 15 mm/min-600 rpm (drilling parameter combination 1); 15 mm/min-800 rpm (drilling parameter combination 2); 25 mm/min-800 rpm (drilling parameter combination 3), as listed in Table 4. The sample after drilling test is shown in Figure 8.

TABLE 4

TABLE 4. Drilling test parameters.

FIGURE 8

FIGURE 8. Post-test view of the granite block.

3.2 Drilling specific energy analysis

Rapid loading rate is deemed to be dynamic, and the energy generated is called dynamic load energy $U_{\mathrm{d}}$. In the drilling process, $U_{\mathrm{d}}$ mainly comes from the work done by the drilling tool. Teale proposed the concept of specific energy in rock drilling (Teale, 1965; Lu et al., 2007; Niu et al., 2009), which can be used to determine the energy required for drilling. The drilling specific energy is the energy required to excavate unit volume rock based on the energy conservation theorem and the working characteristics of the drilling rig. The drilling specific energy $u_{\mathrm{m}}$ can be calculated by Eq. 4 (Teale, 1965):

$u_{\mathrm{m}}=\frac{Fv+120\pi MN}{Sv}(4)$

Where $F$ is the drilling force; $v$ is the drilling rate; $M$ is the bit torque; $N$ is the bit rotation speed; $S$ is the bit area. Equation 4 can be divided into two parts, the drilling force energy per unit volume of rock $u_{\mathrm{s}}^{\mathrm{f}}$ and the bit torque energy per unit volume of rock $u_{\mathrm{d}}^{\mathrm{t}}$.

$u_{\mathrm{s}}^{\mathrm{f}}=\frac{F}{S}(5)$

$u_{\mathrm{d}}^{\mathrm{t}}=\frac{120\pi MN}{Sv}(6)$

The curves of drilling force and bit torque for 16 groups of tests are as shown in Figures 9, 10. To better display the data, the drilling force and bit torque results for each drilling parameter combination are divided into two parts. The results of A, C, and E are shown in Figures 9A, 10A and results of B, D, and F are shown in Figures 9B, 10B. The drilling force and bit torque results for drilling parameter combination 2 (tests G–K) are shown in Figures 9C, 10C, respectively. The drilling force and bit torque for drilling parameter combination 3 (tests L–P) are shown in Figures 9D, 10D, respectively. As shown in Figures 9, 10, the drilling force and bit torque fluctuate throughout the drilling process, but the fluctuation range is small. Although there are some overlaps between the data among different test groups, there are significant differences in the distribution domains. The higher the confining stress, the lower the drilling force and bit torque.

FIGURE 9

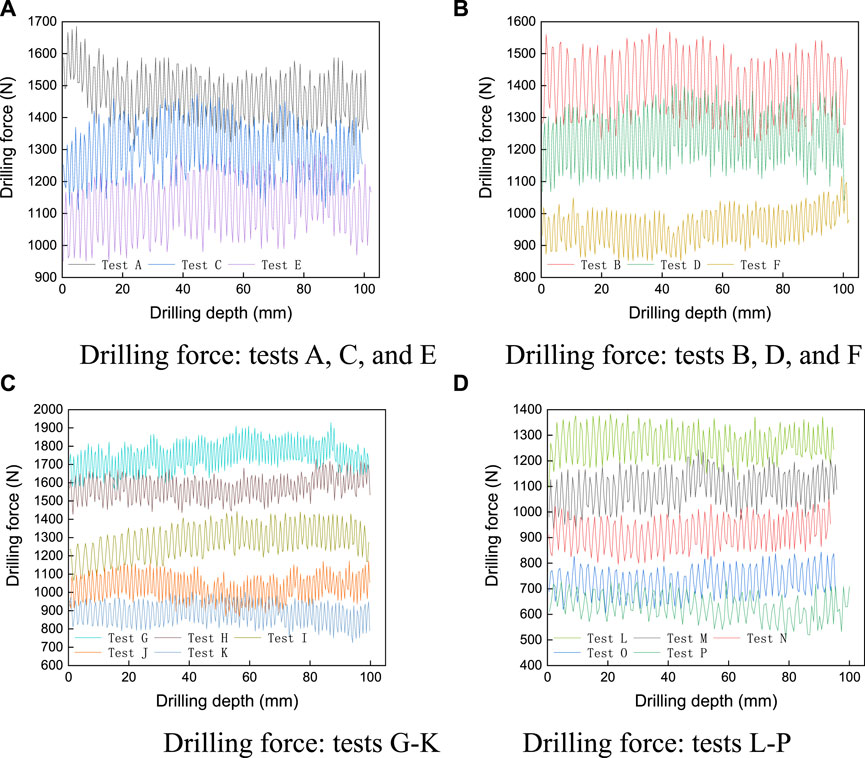
FIGURE 9. Drilling force v. drilling depth. (A) Drilling force: tests A, C, and E (B) Drilling force: tests B, D, and F. (C) Drilling force: tests G–K (D) Drilling force: tests L–P.

FIGURE 10

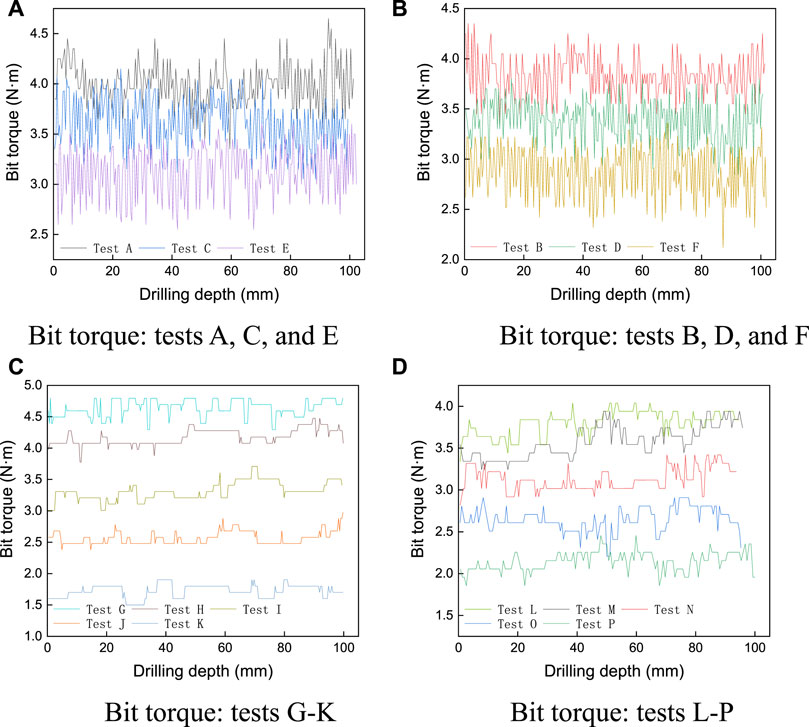
FIGURE 10. Torque v. drilling depth. (A) Bit torque: tests A, C, and E (B) Bit torque: tests B, D, and F (C) Bit torque: tests G–K (D) Bit torque: tests L–P.

The average (AVG) and standard deviation (STD) of drilling force and bit torque in each test were calculated as shown in Table 5. With the increase of confining stress, the AVG of drilling force and bit torque decrease, and the STDs of each group are similar, suggesting that the drilling force and bit torque fluctuate regularly around the average. The fluctuation range of each test is consistent. $u_{\mathrm{s}}^{\mathrm{f}}$ and $u_{\mathrm{d}}^{\mathrm{t}}$ were calculated by substituting the drilling test data into Eqs 5, 6. As the confining stress increases, both $u_{\mathrm{s}}^{\mathrm{f}}$ and $u_{\mathrm{d}}^{\mathrm{t}}$ decrease. $u_{\mathrm{d}}^{\mathrm{t}}$ is much larger than $u_{\mathrm{s}}^{\mathrm{f}}$, so $u_{\mathrm{m}}=u_{\mathrm{d}}^{\mathrm{t}}$.

TABLE 5

TABLE 5. Statistical parameters.

The results of the drilling test are shown in Figure 11. The theory of specific energy in rock drilling assumes that the drilling specific energy of the same rock is similar, and the rock properties can be inferred based thereon. He (2017) found that the drilling specific energy of the same kind of rock remains near a constant value under different drilling parameters. Based on the research results and the classification of rock hardness in “GB/T 50,218-2014 Engineering Rock Mass Classification Standard,” China, they established a rock hardness evaluation criterion as shown in Table 6; however, their drilling tests did not take into account confining stress. The drilling test results undertaken in the present work show that the confining stress condition and the drilling parameter combinations greatly influences the drilling specific energy. E.g., in drilling parameter combination 1, the drilling specific energy is 2,783.78 $\text{mJ}/{\text{mm}}^3$ when the confining stress is 0 MPa, and the drilling specific energy is 2,011.32 $\text{mJ}/{\text{mm}}^3$ when the confining stress is 25 MPa. In drilling parameter combination 2, the drilling specific energy is 5,410.00 $\text{mJ}/{\text{mm}}^3$ when the confining stress is 0 MPa, and the drilling specific energy is 2016.40 $\text{mJ}/{\text{mm}}^3$ when the confining stress is 35 MPa. In drilling parameter combination 3, the drilling specific energy is 2,664.54 $\text{mJ}/{\text{mm}}^3$ when the confining stress is 0 MPa, and the drilling specific energy is 1,508.41 $\text{mJ}/{\text{mm}}^3$ when the confining stress is 35 MPa. Under the same confining stress, the drilling specific energy of drilling parameter combination 1 is less than that of drilling parameter combination 2, and the drilling specific energy of drilling parameter combination 2 is greater than that of drilling parameter combination 3. The drilling specific energy decreases with the acceleration of drilling rate and increases with the acceleration of bit rotation speed. The drilling specific energy is related to the confining stress conditions and the drilling parameter combinations. The drilling specific energy is inversely proportional to the confining stress, showing a linear relationship therewith. This is contrary to popular perception. The drilling specific energy is directly proportional to the bit rotation speed and inversely proportional to the drilling rate.

FIGURE 11

FIGURE 11. Relationship between drilling specific energy and confining stress.

TABLE 6

TABLE 6. Drilling specific energy - rock hardness evaluation criteria ^[3.^3].

According to “GB/T 50,218-2014 Engineering Rock Mass Classification Standard,” China, the intact granite used in these tests is a hard rock. In this paper, the drilling specific energy range of intact granite under different confining stresses is 1,508.41–5,410.00$\text{mJ}/{\text{mm}}^3$. If the rock hardness is predicted according to Table 6, the results are as listed in Table 7.

TABLE 7

TABLE 7. Prediction of rock hardness.

Except for tests G and H, the other prediction results are inconsistent with the actual situation, and the misjudgement rate is as high as 87.5%. This shows that although the evaluation criteria has certain applicability under low confining stress, it is easy to misjudge the rock properties by the drilling specific energy without considering the confining stress conditions. In drilling parameter combination 1, when the confining stress is 0 MPa, hard rock can be predicted only when the drilling specific energy reaches 2,783.78$\text{mJ}/{\text{mm}}^3$. When the confining stress is 25 MPa, hard rock can be predicted when the drilling specific energy reaches 2,011.32$\text{mJ}/{\text{mm}}^3$. The drilling specific energy difference between the two confining stresses is 38.45%. This difference is even more significant in drilling parameter combination 2, and the drilling specific energy under a 35-MPa confining stress is only 50% of that with no confining stress. As shown in Table 7, according to the evaluation criteria in Table 6, the rock properties cannot be accurately predicted by the drilling specific energy. This indicates that it is unreliable to predict the rock properties by the drilling specific energy, ignoring the confining stress conditions and the drilling parameter combinations.

For a particular site, the confining stress conditions are similar, and it is feasible to use the drilling specific energy to predict the rock properties, however, such conclusions have significant limitations when applied to different confining stress and drilling conditions. The results of the test in this paper confirm this.

4 Energy analysis of intact granite under different confining stresses and drilling parameters

The test results of intact granite under different confining stresses and drilling parameters cannot be explained by the existing drilling specific energy theory. Based on the characteristics of the drilling process and the coupled static-dynamic loading theory, a rock energy analysis method based on drilling process is proposed.

Both the original rock mass and the engineering rock mass exchange energy with the external environment (Li et al., 2011b). The energy in the rock mainly comes from the self-weight stress and tectonic stress. According to the coupled static-dynamic loading theory, the engineering rock mass is generally in the combined stress state of “static and dynamic load” (Li et al., 2019). The totale energy required for rock failure remains unchanged and is mainly controlled by the initial static stress.

In the drilling tests, the static load energy $U_{\mathrm{s}}$ of rock comes from the work done by the confining stress, while the dynamic load energy $U_{\mathrm{d}}$ comes from the work done by the drilling tool, called drilling specific energy $u_{\mathrm{m}}$. The dynamic load energy $U_{\mathrm{d}}$ can be divided into dynamic load dissipation energy $U_{\mathrm{d}}^{\mathrm{p}}$ and dynamic elastic energy $U_{\mathrm{d}}^{\mathrm{e}}$. The dynamic load energy releases to the outside in the form of surface energy, acoustic emissions, and heat during the loading process, and this part of dynamic load energy per unit volume of rock is called $u_{\mathrm{d}}^{\mathrm{p}}$. Another part of the dynamic load energy accumulated in the rock in the form of elastic energy is defined as $u_{\mathrm{d}}^{\mathrm{e}}$ (Zhao et al., 2022).

The energy in a unit volume of rock consists of two parts: that generated by the stress environment $u_{\mathrm{s}}^{\mathrm{e}}$, the other generated by drilling $u_{\mathrm{d}}^{\mathrm{e}}$. For a rotary drilling rig, the rock breaking process of the drill bit includes two actions: bit-advance is related to drilling rate and force; bit-rotation is related to bit torque and rotation speed. The elastic energy of rock under static and dynamic loads are plotted in Figure 12. When the confining stress and drilling rate are the same, the faster the bit rotation speed is, the greater the drilling specific energy is; When the confining stress and bit rotation speed are the same, the faster the drilling rate is, the smaller the drilling specific energy is. As the confining stress increases, $u_{\mathrm{s}}^{\mathrm{e}}$ linearly increases, and $u_{\mathrm{m}}$ linearly decreases. According to the coupled static-dynamic loading theory, the energy in the rock mass is constant. A new energy analysis method based on drilling is proposed. It is assumed that total energy in the rock consists of static elastic energy $u_{\mathrm{s}}^{\mathrm{e}}$ formed by confining stress and dynamic elastic energy $u_{\mathrm{d}}^{\mathrm{e}}$ created by the drilling process. Under the same dynamic load conditions, the sum of $u_{\mathrm{s}}^{\mathrm{e}}$ and $u_{\mathrm{d}}^{\mathrm{e}}$ is constant, this limits how much energy the rock can store. When the energy storage limit is reached, the rock breaks down. As the confining stress increases, $u_{\mathrm{s}}^{\mathrm{e}}$ increases, and the $u_{\mathrm{d}}^{\mathrm{e}}$ required for rock failure decreases, and vice versa. The total rock energy for failure is a constant value called the energy storage limit. The formula giving the energy analysis based on drilling process is as follows:

$u_{\mathrm{d}}^{\mathrm{e}}+u_{\mathrm{s}}^{\mathrm{e}}=\delta u_{\mathrm{m}}+u_{\mathrm{s}}^{\mathrm{e}}=u^{\mathrm{e}}(7)$

where $\delta$ is the dynamic load influence factor; $u^{\mathrm{e}}$ is the total energy in the rock.

FIGURE 12

FIGURE 12. Static elastic energy and drilling specific energy under different confining stresses.

The influences of dynamic load conditions such as drilling rate must be considered when quantizing $u_{\mathrm{d}}^{\mathrm{e}}$, and $\delta$ is used to represent the influence of dynamic load conditions on $u_{\mathrm{d}}^{\mathrm{e}}.$ Using Eq. 7, $u_{\mathrm{m}}$ can be calculated:

$u_{\mathrm{m}}=\frac{-u_{\mathrm{s}}^{\mathrm{e}}+u^{\mathrm{e}}}{\delta }(8)$

According to Eq. 3, when the confining stress is 35 MPa, $u_{\mathrm{s}}^{\mathrm{e}}$ is 3.52 $\text{mJ}/{\text{mm}}^3$. The relationship between $u_{\mathrm{m}}$ and $u_{\mathrm{s}}^{\mathrm{e}}$ in these drilling tests is shown in Figure 13. By linear fitting, it can be obtained that $\delta$ is 1/381 and $u^{\mathrm{e}}$ is about 8.05 $\text{mJ}/{\text{mm}}^3$ under drilling parameter combination 1. Under drilling parameter combination 2, $\delta$ is 1/1,179, and $u^{\mathrm{e}}$ is about 5.21$\text{mJ}/{\text{mm}}^3$. Under drilling parameter combination 3, $\delta$ is 1/404, and $u^{\mathrm{e}}$ is about 7.27$\text{mJ}/{\text{mm}}^3$. Substituting $\delta$ into Eq. 7, $u^{\mathrm{e}}$ was calculated for each test (Table 8; Figure 14). The value of $u^{\mathrm{e}}$ under different confining stresses is approximately constant, which is independent of confining stress. However, the total energy in the rock varies under different drilling parameter combinations. The maximum difference of $u^{\mathrm{e}}$ among these tests is 36.9%. This indicates that dynamic load conditions have a great influence on the total energy of rock, and the test results herein show that the total energy that rock can bear varies with drilling conditions.

FIGURE 13

FIGURE 13. Drilling specific energy and static elastic energy.

TABLE 8

TABLE 8. Rock energy parameters.

FIGURE 14

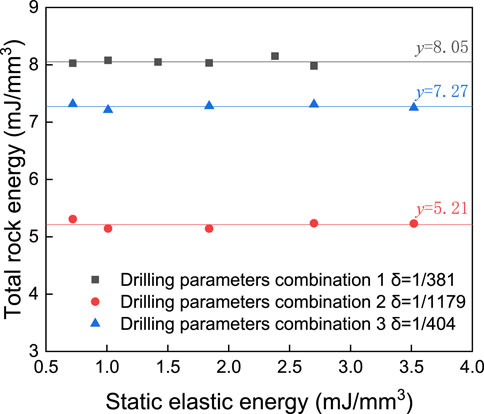
FIGURE 14. Relationship between confining stress and total energy under different drilling parameter combinations.

The drilling parameters controlled herein are drilling rate and bit rotation speed. Therefore, the relationship between $\delta$, drilling rate and bit rotation speed should be considered. When the drilling rate is the same, $\delta$ decreases significantly and $u^{\mathrm{e}}$ decreases, with the increase of bit rotation speed. When the bit rotation speed is the same, $\delta$ increases and $u^{\mathrm{e}}$ increases, with the increase of drilling rate. The relationship between drilling rate, bit rotation speed, and $\delta$ is shown in Figure 15. Equation 9 is used to express the relationship between drilling rate, bit rotation speed and $\delta$:

$\alpha v+\beta N+\gamma =\delta (9)$

where $\alpha$ is the influence factor of drilling force; $\beta$ is the influence factor of bit rotation speed; $\gamma$ is the dynamic load compensation factor.

FIGURE 15

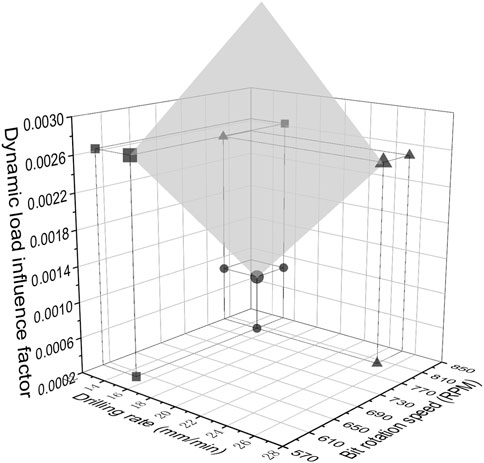
FIGURE 15. Relationship between dynamic load influence factors and drilling rate and bit rotation speed.

The results show that $\alpha$ = 1.63 × 10⁻⁴, $\beta$ = −8.88 × 10⁻⁶, and $\gamma$ = 5.51 × 10⁻³, which implies that $\delta$ increases with increasing drilling rate and $\delta$ decreases with rising bit rotation speed. The influence of drilling rate and bit rotation speed on rock dynamic load energy is just the opposite.

The larger value of $u^{\mathrm{e}}$ indicates that more energy is required to break the rock. The value of $u^{\mathrm{e}}$ is about 5.21 $\text{mJ}/{\text{mm}}^3$ under drilling parameter combination 2, but $u_{\mathrm{m}}$ is much larger than that under drilling parameter combinations 1 or 3 under the same confining stress. The reason is that $\delta$ in the 15 mm/min-800 rpm drilling parameter combination is very small, and the ratio of $u_{\mathrm{m}}$ to $u_{\mathrm{d}}^{\mathrm{e}}$ is small, and more energy is needed to break the rock. Since it is hard to make a theoretical derivation for the relationship between δ and $u^{\mathrm{e}}$, Linear fitting, polynomial fitting and exponential fitting were used to explore the relationship between $\delta$ and $u^{\mathrm{e}}$, as shown in Figure 16. The $R^2$ of exponential fitting is closer to 1. Therefore, among the three common fitting functions, it is believed that the relationship between $\delta$ and $u^{\mathrm{e}}$ is the exponential type according to the drilling test results. With the increase of $\delta$, $u^{\mathrm{e}}$ increases exponentially.

FIGURE 16

FIGURE 16. Relationship between the total energy in the rock and dynamic load influence factor.

When the drilling parameters are the same, the total energy of intact granite equals a certain value. When the drilling parameters change, the total energy changes accordingly. The total energy is an energy index considering confining stress and drilling parameters, which provides a basis for evaluating rock properties. Through further drilling tests, the relationship between drilling parameters, dynamic load influence factor and total energy can be established, and the total energy can be calculated using drilling parameters and dynamic load influence factor to evaluate rock properties.

The total energy can also be used to estimate the in-situ stress of rocks. Taking drilling parameter combination 3 as an example, the dynamic elastic energy is calculated by using the drilling parameters of test L, test M, and test N, and the static elastic energy is calculated by using the compression tests results, and the total energy is obtained to be about 7.23 $\text{mJ}/{\text{mm}}^3$. Taking the confining stresses in tests O and P as unknown quantities, the static elastic energy is calculated by substituting the total energy and dynamic elastic energy into Eq. 7. The confining stresses is calculated by substituting the static elastic energy into Eq. 3, and the corresponding confining stresses in tests O and P are 24.39 and 35.03 MPa, respectively. These are very close to the actual confining stresses of 25 and 35 MPa (the error is less than 3%).

5 Discussion

According to the tests results herein, when the drilling parameters are the same, the total energy of intact granite is constant and independent of the confining stress, when the drilling parameters change, the total energy varies significantly. The dynamic load influence factor was proposed to characterize the influence of drilling parameters on the energy of intact granite. The tests results show that the total energy of intact granite increases exponentially with the increase of the dynamic load influence factor. The dynamic load influence factor depends on the drilling parameters. Since only 3 drilling parameter combinations were considered in the tests, more drilling tests are needed to ascertain a more accurate relationship between the total energy and the dynamic load influence factor for intact granite.

With the increase of confining stress, the plastic characteristics of rock become more apparent, and rock gradually transforms from brittle to ductile behavior (Yang, 2012). The value of confining stress that causes brittle rocks to become ductile is generally .33–1.0 times the uniaxial compressive strength (Yang et al., 2008). For the intact granite tested in this paper, this stress is not less than 82 MPa. The maximum confining stress in the drilling test of intact granite in this paper is 35 MPa, and the granite is in a brittle state. Therefore, the conclusions drawn herein are based on the premise that the granite is in a brittle state. Since the energy is closely related to the type and state of rock, it is helpful to improve the energy analysis method based on the drilling process through experimental research on more types of rocks. In addition, for simplicity, the confining stress conditions of the drilling tests in this paper are biaxial, and the stresses are equal. The energy analysis method of rock under unequal biaxial and triaxial stress is also worthy of further study.

6 Conclusion

Triaxial compression tests and laboratory drilling tests under different confining stresses and drilling parameters are conducted on intact granite specimens. According to the test results, it is found that the drilling specific energy for same rock is not a constant value but varies with confining stress and drilling parameters. Subsequently, an energy analysis method based on drilling process was proposed, and the main conclusions are drawn as follows:

(1) Based on linear energy storage theory, the static elastic energy in the rock is calculated according to the triaxial compression test results. The static elastic energy increases with the increase of confining stress.

(2) Drilling test results show that when the confining stress is within the range of 0–35 MPa, the drilling specific energy decreases with the increase of confining stress, showing a linear relationship and it varies significantly with drilling parameters, differing from the current understanding. When the rotation speed is within the range of 600–800 and the drilling speed is within the range of 15–25 mm/min as recommended by “DZ/T 0227-2010 geological core drilling regulations, China,” the drilling specific energy increases with the increase of bit rotation speed and decreases with the increase of drilling rate. The limitation of using drilling specific energy to evaluate rock properties without considering confining stress conditions and drilling parameter combinations was highlighted. In terms of the test results herein, the rate of misjudgement of rock properties using drilling specific energy reaches 87.5%.

(3) An energy analysis method based on drilling process was proposed. A total energy index was defined as the sum of static elastic energy and dynamic elastic energy, which varies with drilling parameters and is constant under the same drilling parameters. The total energy considers the confining stresses and drilling parameters and provides a new energy index for evaluating rock properties. A dynamic load influence factor was proposed to characterize the influence of drilling parameters on the total energy of intact granite.

(4) The potential application of the energy analysis method in rock stress estimation was explored, and the error in rock stress estimation is less than 3% in drilling test.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HT: Write papers and analyze experiments D-CL: Conduct and analyze experiments Z-JW: Theory analysis XC: Experimental design.

Funding

The study is financially supported by Traffic Science and Technology Project of Yunnan Province, China [Grant No. (2020)-74].

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer (KX) declared a shared affiliation with the authors to the handling editor at time of review.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, B., Wang, Y., Rao, D. Y., and Bai, F. (2022). The effective thermal conductivity of unsaturated porous media deduced by pore-scale SPH simulation. Front. Earth Sci. (Lausanne). 10 (10), 943853. doi:10.3389/feart.2022.943853

CrossRef Full Text | Google Scholar

Bai, B., Yang, G. C., Li, T., and Yang, G. S. (2019). A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials. Mech. Mater. 139, 103180. doi:10.1016/j.mechmat.2019.103180

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G. Q., Hu, W., and Yang, G. C. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotechnics 137, 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Chen, J., and Yue, Z. Q. (2015). Ground characterization using breaking-action-based zoning analysis of rotary-percussive instrumented drilling. Int. J. Rock Mech. Min. Sci. 75, 33–43. doi:10.1016/j.ijrmms.2014.11.008

CrossRef Full Text | Google Scholar

Gong, F. Q., Li, X. B., and Liu, X. L. (2011). Preliminary experimental study of characteristics of rock subjected to 3d coupled static and dynamic loads. Chin. J. Rock Mech. Eng. 30 (06), 1179–1190.

Google Scholar

Gong, F. Q., Li, X. B., Liu, X. L., and Zhao, J. (2010). Experimental study of dynamic characteristics of sandstone under one-dimensional coupled static and dynamic loads. Chin. J. Rock Mech. Eng. 29 (10), 2076–2085.

Google Scholar

Gong, F. Q., Lu, D. H., Li, X. B., Rao, Q. H., and Fu, Z. T. (2014). Toughness increasing or decreasing effect of hard rock failure with pre-static loading under dynamic disturbance. Chin. J. Rock Mech. Eng. 33 (9), 1905–1915. doi:10.13722/j.cnki.jrme.2014.09.022

CrossRef Full Text | Google Scholar

Gong, F. Q., Wu, W. X., and Zhang, L. (2020). Brazilian disc test study on tensile strength-weakening effect of high pre-loaded red sandstone under dynamic disturbance. J. Cent. South Univ. 27 (10), 2899–2913. doi:10.1007/s11771-020-4517-5

CrossRef Full Text | Google Scholar

Gong, F. Q., Yan, J. Y., and Li, X. B. (2018). A new criterion of rock burst proneness based on the linear energy storage law and the residual elastic energy index. Chin. J. Rock Mech. Eng. 37 (09), 1993–2014. doi:10.13722/j.cnki.jrme.2018.0232

CrossRef Full Text | Google Scholar

Gui, M. W., Soga, K., Bolton, M. D., and Hamelin, J. P. (2002). Instrumented borehole drilling for subsurface investigation. J. Geotech. Geoenviron. Eng. 128 (4), 283–291. doi:10.1061/(asce)1090-0241(2002)128:4(283)

CrossRef Full Text | Google Scholar

He, M. C., Wang, Y., Su, J. S., and Liu, D. Q. (2018). Analysis of fractal characteristics of fragment of sandstone impact rock burst under static and dynamic coupled loads. J. China Univ. Min. Technol. 47 (04), 699–705. doi:10.13247/j.cnki.jcumt.000876

CrossRef Full Text | Google Scholar

He, M. M. (2017). “Research on the prediction of rock mass mechanics characteristics based on the rotary penetration technology,”. PhD Thesis (Xi'an, Shaanxi, China: Xi'an University of Technology).

Google Scholar

Kahraman, S. (1999). Rotary and percussive drilling prediction using regression analysis. Int. J. Rock Mech. Min. Sci. 36 (7), 981–989. doi:10.1016/S0148-9062(99)00050-9

CrossRef Full Text | Google Scholar

Karasawa, H., Ohno, T., Kosugi, M., and Rowley, J. C. (2002). Methods to estimate the rock strength and tooth wear while drilling with roller-bits—Part 1: Milled-tooth bits. J. Energy Resour. Technol. 124 (3), 125–132. doi:10.1115/1.1482405

CrossRef Full Text | Google Scholar

Li, X. B., Gong, F. Q., Wang, S. F., Li, D. Y., Tao, M., Zhou, J., et al. (2019). Coupled static-dynamic loading mechanical mechanism and dynamic criterion of rockburst in deep hard rock mines. Chin. J. Rock Mech. Eng. 38 (04), 708–723. doi:10.13722/j.cnki.jrme.2018.1496

CrossRef Full Text | Google Scholar

Li, X. B., and Gu, D. S. (2002). “The hazard control and cataclastic muta-genesis induced by high stress in hard rock mining at depth,” in Proceedings of the 175th Xiangshan Science Congress, Beijing, China, April 28.

Google Scholar

Li, X. B., Tao, M., Gong, F. Q., Yin, Z. Q., and Du, K. (2011a). Theoretical and experimental study of hard rock spalling fracture under impact dynamic loading. Chin. J. Rock Mech. Eng. 30 (06), 1081–1088.

Google Scholar

Li, X. B., Yao, J. R., and Gong, F. Q. (2011b). Dynamic problems in deep exploitation of hard rock metal mines. Chin. J. Nonferrous Metals 10, 2551–2563. doi:10.19476/j.ysxb.1004.0609.2011.10.022

CrossRef Full Text | Google Scholar

Liu, Q. S., Liu, K. D., Lu, X. L., and Zhu, J. B. (2014a). Study of mechanical properties of raw coal under high stress with triaxial compression. Chin. J. Rock Mech. Eng. 36 (01), 24–34. doi:10.13722/j.cnki.jrme.2014.s2.006

CrossRef Full Text | Google Scholar

Liu, S. H., Mao, D. B., Qi, Q. X., and Li, F. M. (2014b). Under static loading stress wave propagation mechanism and energy dissipation in compound coal-rock. J. China Coal Soc. 16 (S1), 15–22. doi:10.13225/j.cnki.jccs.2013.0411

CrossRef Full Text | Google Scholar

Lu, X. S., Wang, Y. Z., and Lei, M. (2007). Using mathematical statistics to optimize bits and comment on the effects of use. Fault-Block Oil Gas Field 30 (06), 63–65+93.

Google Scholar

Luo, Y., Li, X. P., Dong, Q., Huang, J. H., and Guo, Y. H. (2015). Damage cause study for static and dynamic combination of excavation and unloading in deep underground tunnels. Chin. J. Rock Mech. Eng. 34 (S1), 3365–3371. doi:10.13722/j.cnki.jrme.2014.0839

CrossRef Full Text | Google Scholar

Mostofi, M., Rasouli, V., and Mawuli, E. (2011). An estimation of rock strength using a drilling performance model: A case study in blacktip field, Australia. Rock Mech. Rock Eng. 44 (3), 305–316. doi:10.1007/s00603-011-0142-9

CrossRef Full Text | Google Scholar

Niu, T., Liang, H. W., and Xu, Y. J. (2009). Study on the pressure loss laws in micro hole circulatory system. Drill. Prod. Technol. 32 (04), 31–33.

Google Scholar

Oparin, V. N., Timonin, V. V., Karpov, V. N., and Smolyanitsky, B. N. (2018). Energy-based volumetric rock destruction criterion in the rotary-percussion drilling technology improvement. J. Min. Sci. 53 (6), 1043–1064. doi:10.1134/S1062739117063114

CrossRef Full Text | Google Scholar

Sakiz, U., Aydin, H., and Yarali, O. (2021). Investigation of the rock drilling performance of rotary core drilling. Bull. Eng. Geol. Environ. 81, 24. doi:10.1007/s10064-021-02534-6

CrossRef Full Text | Google Scholar

Su, Y. Q., Gong, F. Q., Luo, S., and Liu, Z. X. (2022). Experimental study on energy storage and dissipation characteristics of granite under two-dimensional compression with constant confining pressure. J. Cent. South Univ. 28 (03), 848–865. doi:10.1007/s11771-021-4649-2

CrossRef Full Text | Google Scholar

Tan, Z. Y., Yue, Z. Q., and Cai, M. F. (2007). Analysis of energy for rotary drilling in weathered granite formation. Chin. J. Rock Mech. Eng. 26 (3), 478–483.

Google Scholar

Teale, R. (1965). The concept of specific energy in rock drilling. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 2 (1), 245–273. doi:10.1016/0148-9062(65)90016-1

CrossRef Full Text | Google Scholar

Van Wyk, G., Els, D. N. J., Akdogan, G., Bradshaw, S. M., and Sacks, N. (2014). Discrete element simulation of tribological interactions in rock cutting. Int. J. Rock Mech. Min. Sci. 65, 8–19. doi:10.1016/j.ijrmms.2013.10.003

CrossRef Full Text | Google Scholar

Wang, Q., Gao, H. K., Yu, H. C., Jiang, B., and Liu, B. H. (2019). Method for measuring rock mass characteristics and evaluating the grouting-reinforced effect based on digital drilling. Rock Mech. Rock Eng. 52 (3), 841–851. doi:10.1007/s00603-018-1624-9

CrossRef Full Text | Google Scholar

Wang, Q., Gao, S., Jiang, B., Li, S. C., He, M. C., Gao, H. K., et al. (2018a). Rock-cutting mechanics model and its application based on slip-line theory. Int. J. Geomech. 18 (5), 1–10. doi:10.1061/(ASCE)GM.1943-5622.0001136

CrossRef Full Text | Google Scholar

Wang, Q., Gao, S., Li, S. C., He, M. C., GaoHK, , Jiang, B., et al. (2018b). Upper bound analytic mechanics model for rock cutting and its application in field testing. Tunn. Undergr. Space Technol. 73, 287–294. doi:10.1016/j.tust.2017.12.023

CrossRef Full Text | Google Scholar

Wang, W., Li, H. M., Gu, H. L., and Wang, C. (2015). Feature analysis of energy dissipation of water-saturated coal samples under coupled static-dynamic loads. Chin. J. Rock Mech. Eng. 34 (S2), 3965–3971. doi:10.13722/j.cnki.jrme.2015.0546

CrossRef Full Text | Google Scholar

Xia, K. Z., Chen, C. X., Wang, T. L., Zheng, Y., and Wang, Y. (2022). Estimating the geological strength index and disturbance factor in the Hoek–Brown criterion using the acoustic wave velocity in the rock mass. Eng. Geol. 306 (306), 106745. doi:10.1016/j.enggeo.2022.106745

CrossRef Full Text | Google Scholar

Yang, D. H. (2012). “Preliminary research of rock breaking methods and impregnated diamond core bit in scientific ultra-deep drilling process,”. PhD Thesis (Wuhan, China: China University of Geosciences).

Google Scholar

Yang, G. L., Huang, R. Q., Cai, G. J., Fu, X. M., Lin, F., and Xu, D. M. (2008). Conventional triaxial compression test I of altered rock:study of classification of strain-stress curve before and after destruction and brittle-ductile diversion confining pressure. Rock Soil Mech. 30 (10), 2759–2763. doi:10.16285/j.rsm.2008.10.044

CrossRef Full Text | Google Scholar

Yang, W. W., Yue, Z. Q., and Tham, L. G. (2012). Automatic monitoring of inserting or retrieving SPT sampler in drillhole. Geotech. Test. J. 35 (3), 420–436. doi:10.1520/gtj103450

CrossRef Full Text | Google Scholar

Yang, Y. J., Song, Y., and Chen, S. J. (2006). Test study of coal's strength and deformation characteristics under triaxial compression. Min. Eng. 31 (02), 150–153.

Google Scholar

Yasar, E., Ranjith, P. G., and Viete, D. R. (2011). An experimental investigation into the drilling and physico-mechanical properties of a rock-like brittle material. J. Petroleum Sci. Eng. 76 (3), 185–193. doi:10.1016/j.petrol.2011.01.011

CrossRef Full Text | Google Scholar

Zhang, Z. Z., and Gao, F. (2015). Confining pressure effect on rock energy. Chin. J. Rock Mech. Eng. 34 (01), 1–11. doi:10.13722/j.cnki.jrme.2015.01.001

CrossRef Full Text | Google Scholar

Zhao, G. M., Liu, Z. X., Meng, X. R., Zhang, R. F., Kao, S. M., and Qi, M. J. (2022). Energy accumulation and dissipation test and analysis method of height-diameter ratio sandstone. J. China Coal Soc. 47 (03), 1110–1121. doi:10.13225/j.cnki.jccs.xr21.1606

CrossRef Full Text | Google Scholar

Glossary

The following abbreviations are used in this document:

${\mathit{U}}_{\mathbf{s}}$ Static load energy

${\mathit{U}}_{\mathbf{s}}^{\mathbf{e}}$ Static elastic energy

${\mathit{U}}_{\mathbf{s}}^{\mathbf{p}}$ Static plastic energy

${\mathit{u}}_{\mathbf{s}}$ Static load energy per unit volume of rock

${\mathit{u}}_{\mathbf{s}}^{\mathbf{e}}$ Static elastic energy per unit volume of rock

${\mathit{u}}_{\mathbf{s}}^{\mathbf{p}}$ Static plastic energy per unit volume of rock

${\mathit{U}}_{\mathbf{d}}$ Dynamic load energy

${\mathit{U}}_{\mathbf{d}}^{\mathbf{e}}$ Dynamic elastic energy

${\mathit{U}}_{\mathbf{d}}^{\mathbf{p}}$ Dynamic plastic energy

${\mathit{u}}_{\mathbf{d}}$ Dynamic load energy per unit volume of rock

${\mathit{u}}_{\mathbf{d}}^{\mathbf{e}}$ Dynamic elastic energy per unit volume of rock

${\mathit{u}}_{\mathbf{d}}^{\mathbf{p}}$ Dynamic plastic energy per unit volume of rock

${\mathit{u}}_{\mathbf{m}}$ Drilling specific energy (energy per unit volume of rock broken by the bit)

${\mathit{u}}_{\mathbf{s}}^{\mathbf{f}}$ Drilling force energy per unit volume of rock

${\mathit{u}}_{\mathbf{d}}^{\mathbf{t}}$ Bit torque energy per unit volume of rock

${\mathit{u}}^{\mathbf{e}}$ Total rock energy per unit volume of rock

$\mathit{F}$ Drilling force

$\mathit{v}$ Drilling rate

$\mathit{M}$ Bit torque

$\mathit{N}$ Bit rotation speed (number of revolutions per unit time)

$\mathit{S}$ Bit area

L Drilling depth

${\mathit{\epsilon }}_{\mathbf{0}}$ Plastic strain value after unloading

${\mathit{\epsilon }}_{\mathbf{p}}$ Peak strain

${\mathit{\sigma }}_{\mathbf{c}}$ Confining stress

${\mathit{\sigma }}_{\mathbf{p}}$ Peak stress

$\mathit{A}$ Static load energy storage coefficient

$\mathit{B}$ The intercept of the linear fitting formula for $u_{\mathrm{s}}$ and $u_{\mathrm{s}}^{\mathrm{e}}$

$\mathit{\delta }$ Dynamic load influence factor

$\mathit{\alpha }$ Drilling force influence factor

$\mathit{\beta }$ Bit rotation speed influence factor

$\mathit{\gamma }$ Dynamic load compensation factor