System reliability analysis of landslides involving sliding surfaces using intelligent multiple response surfaces

The shear strength reduction method provides an effective tool of numerical analysis for landslides reliability analysis. However, it ignores the failure probability of the secondary failure surfaces and requires huge computational cost. To avoid these common criticisms, an intelligent multiple response surfaces method for system reliability using multiple response-surface method (MRSM) and least-squares support vector machine (LSSVM) is presented to evaluate the stability of complex multistage historic landslides with multiple sliding surfaces. Deterministic analysis of each sliding surface is first performed using the finite element method of sliding surface stress analysis, which is applied to obtain the safety factors of different sliding surfaces from the stress fields generated by finite element simulations. The LSSVM model with excellent nonlinear fitting ability is then employed to construct the multiple response-surface method (MRSM) of the sliding surfaces and a genetic algorithm (GA) is adopted to optimize the LSSVM. This proposed methodology is finally applied to investigate the probability of system failure of the Zhenggang landslide in southwestern China. The results indicate that the proposed approach can reduce the computational cost of finite element analysis in direct Monte Carlo simulation (MCS) by proper training using a limited of samples, and the calculation accuracy meets the engineering requirements of complex multistage historic landslides.

1 Introduction

Evaluation of landslide stability is an important topic in geotechnical engineering and disaster prevention. However, large uncertainties of landslide stability are commonly associated with rock and soil properties and measurement errors (Su et al., 2011; Hong et al., 2016; Li et al., 2019). Reliability analysis is an effective approach to account for the uncertainties associated with the underlying landslide stability parameters (Griffiths and Fenton 2004; Ji et al., 2012). For example, Wu et al. (2014) used Monte Carlo simulations (MCS) to study the random-fuzzy reliability of the Liangshuijing landslide, and Dadashzadeh et al. (2017) employed an integrated response surface method to investigate the reliability of rock slopes. However, a complex historic landslide may have experienced several sliding episodes and formed multiple sliding surfaces (i.e., potential failure modes). Considering the single most critical failure mode (i.e., the most critical surface) may not give a complete picture of the overall reliability of the landslide. System reliability, which considers all significant failure modes and their correlations, should therefore be employed to study landslide stability.

Due to the stochastic characteristic of probability analysis, it is necessary to implement a large number of deterministic analyses to obtain the safety factors of the landslide stability probabilistically. The deterministic analysis for landslide system reliability is almost based on rigid limit equilibrium methods in literatures (Liu and Cheng 2016; Wang et al., 2020). This is because the strength reduction method cannot simultaneously estimate the safety factors of landslide with multiple potential sliding surfaces, and it requires the long solution time in the iterative process of shear strength reduction, which has dramatically increase because of the large number of deterministic analyses. Finite element method of sliding surface stress analysis (Zou et al., 1995; Kim and Lee 1997), the hybrid of limit element method (LEM) and finite element method (FEM), can calculate directly the safety factor of multiple potential sliding surfaces based on stress field generated by a FEM simulation, and thus expands greatly the application of numerical simulation in landslide system reliability.

Currently, the system reliability methods for landslide mainly include Monte Carlo simulation (MCS) (Wang and Goh 2021; Pei et al., 2022), bounds method (Ditlevsen 1979; Low et al., 1997, 2011), mvncdf method (Liu and Low 2017) and multiple response-surface method (MRSM) (Li et al., 2015). The Monte Carlo simulation (MCS) is one of the most popular methods for analyzing the system reliability without closed-form solutions. However, the MCS requires extensive computational efforts due to a large number of sampling needed to ensure a sufficiently accurate estimation of the failure probability (Dong and Lu 2021). The bounds method and mvncdf method are based on the situation where an explicit mathematical function exists (Fu et al., 2019), but it is often difficult to obtain the explicit relationship function between the safety factor of landslide and the shear strength parameters. The MRSM is a metamodel-based method for replacing a complex model by approximating the actual limit state functions (Li et al., 2015). It can thus effectively alleviate the cost of functions evaluation in the response surfaces of all failure modes, and provides efficient strategies for system reliability analysis.

Generally, traditional MRSM employs multiple polynomial functions to model low-order problems, and corresponding computational efficiency of response surface models can satisfy the requirements of probabilistic numerical models. Low-order polynomial response surfaces, however, are difficult to approximate the actual response state function (RSF) with obvious nonlinear characteristics of landslide. Thus, several researchers proposed the intelligent algorithms to construct more accurate RSF in the literatures. For example, Li et al. (2013) employed a support vector machine (SVM) to approach the RSF of landslide stability because of its excellent fitting ability with a limited number of samples. Sung (2008) developed artificial neural network (ANN) as an approximate RSF to express the relationship function of landslide between the safety factor and the shear strength parameters. Tan et al. (2011) studied the similarities and differences between these RSFs using ANN and SVM. Applying the similar method, intelligent multiple response surfaces method can be used for probabilistic numerical modeling of landslide stability considering multiple sliding surfaces.

In this study, a system reliability method is proposed for probabilistic numerical study of landslide stability based on LSSVM and MRSM. The safety factors of multiple sliding surfaces, which form the basis of system reliability analysis, are obtained from results of finite element method of sliding surface stress analysis. The MRSM, which integrates LSSVM and genetic algorithm (GA) is then applied to generate the explicit relationship function between the safety factor and random variables of landslide. Next, the system failure probability of a landslide with multiple sliding surfaces can be obtained by the MCS approach. As a case study, the system failure probability method is finally applied to the Zhenggang landslide in southwestern China to illustrate the proposed approach.

2 Methodology

2.1 Finite element method of sliding surface stress analysis

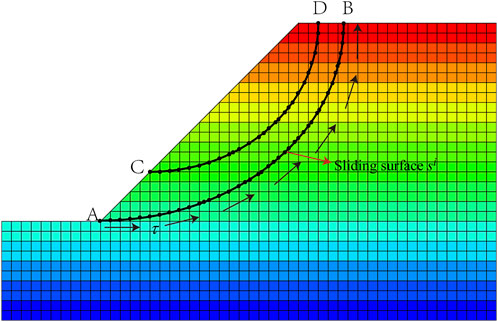
The deterministic analysis of landslide is determined using finite element method of sliding surface stress analysis in this paper, which is a numerical technique based on the limit equilibrium method (LEM) and finite element method (FEM). The finite element method of sliding surface stress analysis can be applied to evaluate the safety factors of multiple potentially active sliding surfaces using a finite element simulation (Farias and Naylor 1998). The nodal stress components (σ_x, σ_y, τ_xy) on a sliding surface can be obtained from the FEM analysis. The two-dimensional curve of a sliding surface is discretized into several segments. The stresses of the two end-points of a segment are used to approximate the stress components in the segment by interpolation. The normal stress ${\sigma }_n$ and shear stress $\tau$ of each segment are expressed as (Yang et al., 2015):

${\sigma }_n=\frac{\left[\left({\sigma }_x+{\sigma }_y\right)+\left({\sigma }_y-{\sigma }_x\right)\cos 2\alpha \right]}{2}+{\tau }_{xy}\sin 2\alpha ,(1)$

$\tau =\frac{\left({\sigma }_y-{\sigma }_x\right)\sin 2\alpha }{2}+{\tau }_{xy}\cos 2\alpha ,(2)$

where α is the angle between the sliding surface and horizontal plane. For a discrete ith sliding surface $s^i$ of landslide (Figure 1), the safety factor $F{s}_i$ can be defined as:

$F{s}_i=\frac{{\sum }_{j=1}^n{\tau }_{fj}{s}_j^i}{{\sum }_{j=1}^n{\tau }_j{s}_j^i}=\frac{{\displaystyle \int }{\tau }_{f}d{s}^i}{{\displaystyle \int }\tau d{s}^i}.(3)$

where $s_j^i$ is the length of segment j in ith sliding surface $s^i$; n is the number of discrete segments, and ${\tau }_{fj}$ and ${\tau }_j$ are, respectively, the shear strength and shear stress on the plane of the jth segment of the sliding surface. According to the Mohr-Coulomb strength criterion, the safety factor $F{s}_i$ along sliding surface $s^i$ can be expressed as:

$F{s}_i=\frac{{\displaystyle \int }\left(c+{\sigma }_n\tan \varphi \right)d{s}^i}{{\displaystyle \int }\tau d{s}^i},(4)$

where c and $\varphi$ are respectively cohesion and friction angle.

FIGURE 1

FIGURE 1. Schematic diagram for the ith sliding surface of a discrete slope.

2.2 Least-squares support vector machine

The LSSVM is introduced by Suykens (1999) as a modified form of the support vector machine (SVM), which can transform the quadratic optimization problem of the SVM into a linear system of equations based on linear least squares criteria. For a given data set ${\left({\mathit{x}}_k,y_k\right)}_{k=1}^m\in R^m\times R$ with input data ${\mathit{x}}_k$ and output data $y_k$. The LSSVM regression model can be described as (Tan et al., 2016):

$f\left(\mathit{x}\right)={\displaystyle \sum }_{k=1}^m{a}_{k}K\left(\mathit{x},{\mathit{x}}_k\right)+b,(5)$

where $K\left(\mathit{x},{\mathit{x}}_k\right)$ is a symmetric kernel function, and the Gaussian radial basic function (RBF) $K\left(\mathit{x},{\mathit{x}}_k\right)=\exp \left(-{\left(\mathit{x}-{\mathit{x}}_k\right)}^2/\left(2{\sigma }^2\right)\right)$ is adopted as the kernel function in this paper. Where $\sigma$ is the kernel parameter; m is the sample number; $a_k$ is the Lagrange multiplier; b is a bias term; and a linear equation can be obtained (Cai et al., 2016):

$\left[\begin{array}{cc}0& 1_v^T\\ 1_v& \mathrm{\Omega }+\frac{1}{\gamma }\mathrm{{\rm I}}\end{array}\right]\left[\begin{array}{c}b\\ \mathit{a}\end{array}\right]=\left[\begin{array}{c}0\\ \mathit{y}\end{array}\right],(6)$

where $\gamma$ is a e tolerance error; $\mathit{y}={\left[y_1,y_2,\cdots ,y_m\right]}^T$; $1_v={\left[\mathrm{1,1},\cdots ,1\right]}^T$; $\mathit{a}={\left[a_1,a_2,\cdots ,a_m\right]}^T$; $\Omega$ is a symmetric matrix, $\Omega =\varphi {\left(x\right)}^T\varphi \left(x_m\right)=K\left(x,x_m\right)$. The analytical of $\mathit{a}$ and b can be obtained by:

$\left[\begin{array}{c}b\\ \mathit{a}\end{array}\right]={\mathrm{\Phi }}^{-1}\left[\begin{array}{c}0\\ \mathit{y}\end{array}\right],(7)$

Where

$\mathrm{\Phi }=\left[\begin{array}{cc}0& 1_v^T\\ 1_v& \mathrm{\Omega }+\frac{1}{\gamma }\mathrm{{\rm I}}\end{array}\right].(8)$

Note that there are two user-determined parameters (kernel parameter $\sigma$ and tolerance error $\gamma$) in the LSSVM model. Generally, the kernel parameter $\sigma$ determines the local properties of RBF function, and the tolerance error $\gamma$ balances the training error and model complexity (Roy et al., 2019). Therefore, the optimal selection of parameters is crucial to improve the accuracy of LSSVM model.

2.3 Parameters optimization of least-squares support vector machine using genetic algorithm

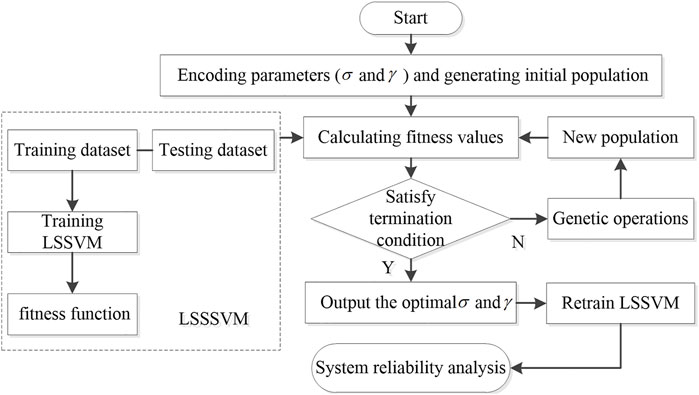
Genetic algorithm (GA) is a global searching method for handling optimization problems (Li et al., 2018). Actually, GA is an evolutionary algorithm inspired from the evolution theory of genetics and natural selection based on the implementation of natural genetic mechanisms such as selective reproduction, crossover and mutation. Compared with other optimization algorithms, GA requires fewer adjustment parameters to obtain the globally optimal solution and is easy to implement. Hence, GA is applied to seek the optimum parameters of LSSVM considering its excellent global search abilities in this paper. The GA optimization strategy starts by initializing a randomly generated population. Next, a population with new individuals can be formed by genetic operations, and the process is repeated in computational iterations of the evolving population. Subsequently, each individual is evaluated by the statistical fitness function until the best individual (the optimal parameters) are attained. The calculating process of optimal LSSVM parameters using GA for system reliability analysis of landslide is described in Figure 2.

FIGURE 2

FIGURE 2. Calculation diagram of GA optimized LSSVM in system reliability analysis of landslide.

In this paper, the root mean square error (RMSE) is used as the fitness function to evaluate the fitting performance of LSSVM. It can be defined as:

$\mathit{R}MSE=\sqrt{\frac{1}{m}{\displaystyle \sum }_{i=1}^m{\left(y_i-{\stackrel{\sim }{y}}_i\right)}^2,}(9)$

where m is the number of sample points, $y_i$ and ${\stackrel{\sim }{y}}_i$ are the actual values and fitting values by the LSSVM model, respectively.

2.4 least-squares support vector machine-based multiple response-surface method for system reliability of landslide

For a complex multistage historic landslide with several failure modes, i.e., sliding surfaces, the limit state function for ith failure mode $g_i\left(\mathit{X}\right)$ can be written as:

$g_i\left(\mathit{X}\right)=F{s}_i\left(\mathit{X}\right)-1.(10)$

Note that an explicit equation $F{s}_i\left(\mathit{x}\right)$ for ith sliding surface of landslide is difficult to obtain by the FEM simulation. The GA-LSSVM model is adopted to construct the RSF ${\stackrel{\sim }{g}}_i\left(\mathit{X}\right)$ to approximate the implicit relationship function of landslide between the safety factor and the shear strength parameters. Applying the similar method, a multiple RSFs with all sliding surfaces can be established for the system reliability analysis. According to Eq. 5, the ith LSSVM-based RSF ${\stackrel{\sim }{g}}_i\left(\mathit{X}\right)$ can be expressed as:

${\stackrel{\sim }{g}}_i\left(\mathit{X}\right)={\displaystyle \sum }_{k=1}^m{a}_{i,k}K\left(\mathit{X},{\mathit{X}}_k\right)+b_i.(11)$

After a LSSVM-based MRSM is constructed, a direct Monte-Carlo simulation (MCS) approach (Liu and Low 2017) can be applied to obtain the failure probability of ith sliding surface $p_{f_i}$ and system failure probability $p_f^{\text{sys}}$ as follows:

$p_{fi}=\frac{1}{N_p}{\displaystyle \sum }_{k=1}^{N_p}I\left[{\stackrel{\sim }{g}}_i\left(\mathit{X}\right)<0\right],(12)$

$p_f^{\text{sys}}=\frac{1}{N_p}{\displaystyle \sum }_{k=1}^{N_p}I\left[\underset{i=\mathrm{1,2},\cdots N_m}{\min }{\stackrel{\sim }{g}}_i\left(\mathit{X}\right)<0\right],(13)$

where $N_p$ and $N_m$ are the number of MCS simulations and sliding surfaces of landslide, respectively; $I\left(\cdot \right)$ is an indicator function.

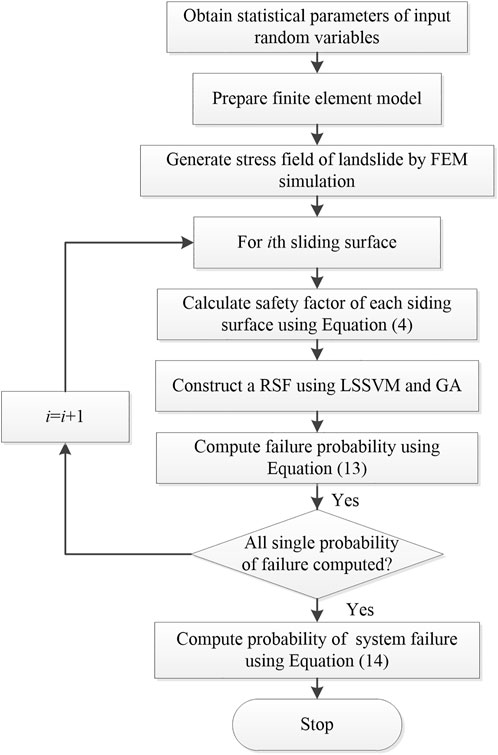
Once the LSSVM-based MRSM is generated, the evaluation of the safety factors can be obtained directly by the evaluation of the algebraic expression without deterministic analysis of landslide stability. This means that the computational cost of the MCS is greatly reduced, especially for the deterministic analysis of finite element simulations. In addition, for deterministic multiple sliding surfaces of multistage landslides, the hybridization of the limit equilibrium method (LEM) and finite element method (FEM) only needs one finite element simulation to calculate the safety factors of all potentially sliding surfaces from the stress fields generated, which will further reduce the computation of FEM. The flow chart of this proposed approach for system reliability of landslide can be shown in Figure 3.

FIGURE 3

FIGURE 3. The flowchart of the system reliability analysis for landslide.

3 Case study

3.1 Characterization and geology features of landslide

To illustrate the proposed methodology, the Zhenggang landslide, which is located on the right bank of the Gushui hydroelectric power station along the Lancang River near the village of Zhenggang in Yunnan Province, China, is considered. The landslide volume is approximately 47.5 million m³ with an elevation of 2180–3220 m, and its external boundary is indicated by the yellow line in Figure 4A. The landslide, which has formed three dynamic sliding stages, lies mainly between the right No. 7 gully on the right bank and the Yagong gully. Because intensive erosion of the Zhenggang gully has generated the deepest terrain incision depth, the landslide can be divided into two geomorphological zones (I and II).

FIGURE 4

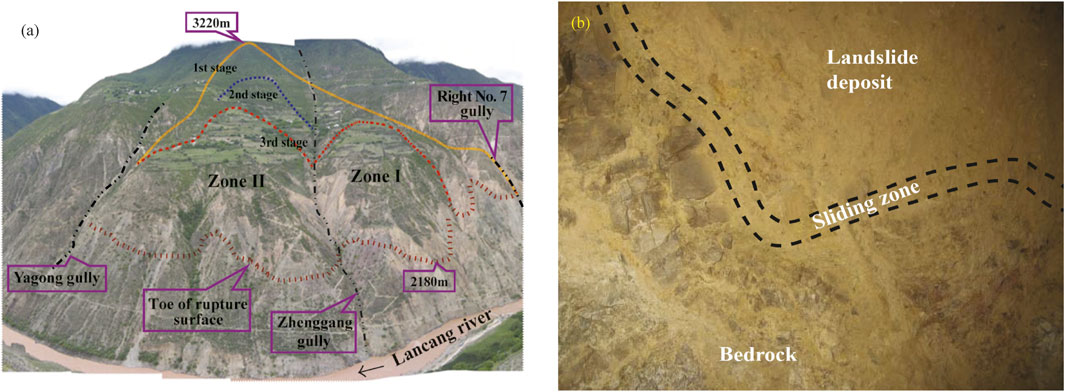
FIGURE 4. Aerial view and geomorphic features of the Zhenggang landslide (Xu 2010).p

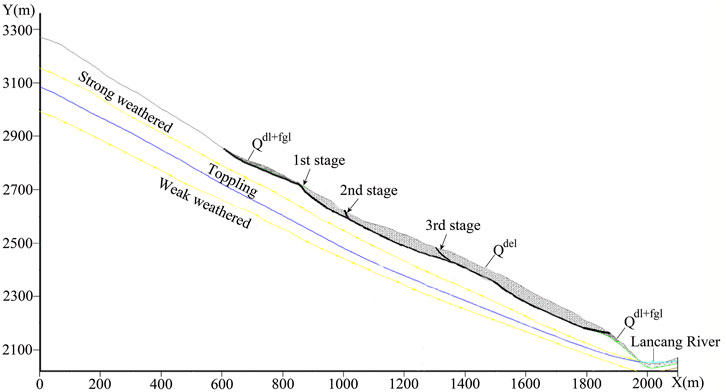
According to a geological reconnaissance survey, the Zhenggang landslide has undergone three episodes of large-scale sliding in the past and formed three potential sliding surfaces, as evidenced by its long-term deformation evolution and the destructive features in the surrounding environment (Wang et al., 2017). The largest bedrock landslide formed in the first stage and was caused by fracturing, i.e., shear failure of layered rock, which was subjected to large bending and/or toppling forces. A transfixion surface gradually formed with the continuous development of the shear plane and tensile cracking at the trailing edge, which led to rapid offsets along Lancang River and formation of the first stage of the landslide mass. The second- and third-stage landslides occurred inside the first stage of the landslide body. Their formation mechanisms are essentially the same: all slides deformed locally in the late reformation of the oldest landslide. Heavy rainfall, snowfall, groundwater flow, earthquakes, long-term erosion by melting glaciers, and weathering are factors that led to the two subsequent large-scale sliding events, forming the current second and third landslides. Figure 4B shows it can be clearly seen that the sliding zone of the Zhenggang landslide is between the landslide deposit and bedrock in the site.

Figure 5 shows that the landslide deposit formed three potential sliding surfaces. The same transfixion surface observed in all stages indicates high correlation between the three surfaces. The landslide deposit is mainly composed of diluvium (Q^dl), glacial and fluvial deposits (Q^fgl), and landslide deposits (Q^del). A typical profile of the Zhenggang landslide, as shown in Figure 5, is chosen for the case study.

FIGURE 5

FIGURE 5. A typical profile of the Zhenggang landslide with three sliding surfaces.

3.2 Statistical parameters

The values of some material properties, such as unit weights γ, Young’s modulus E, and Poisson’s ratio μ, typically have a limited rate of change and have little influence on the reliability analysis (Tan et al., 2011). They can therefore be considered as deterministic variables in this case. Furthermore, the slide mass of the Zhenggang landslide is mainly in landslide deposit and sliding zone; as a result, it is acceptable to ignore the randomness of bedrock parameters. The randomness of shear strength parameters c and $\phi$ for deposit and sliding zone is considered in this paper.

To determine statistical characteristics of shear strength parameters of the Zhenggang landslide, a certain number of shear tests are conducted for 22 deposit samples and 3 samples of sliding zone. The laboratory tests result shows the cohesion c_d and friction angle ${\phi }_d$ of deposits can be modelled as normally distributed random variables (Xu 2010), and the corresponding histograms are shown in Figure 6. However, we could not make definite conclusions regarding the statistical distribution types of shear strength parameters for the sliding zone because of the small number of acquisition trials. Combined with the parameter inversion analysis and statistical results of similar engineering, the cohesion c_s and friction angle ${\phi }_s$ of sliding zone can be considered as standard normally distribution of random variables. Descriptive statistical parameters for the Zhenggang landslide are listed in Table 1.

FIGURE 6

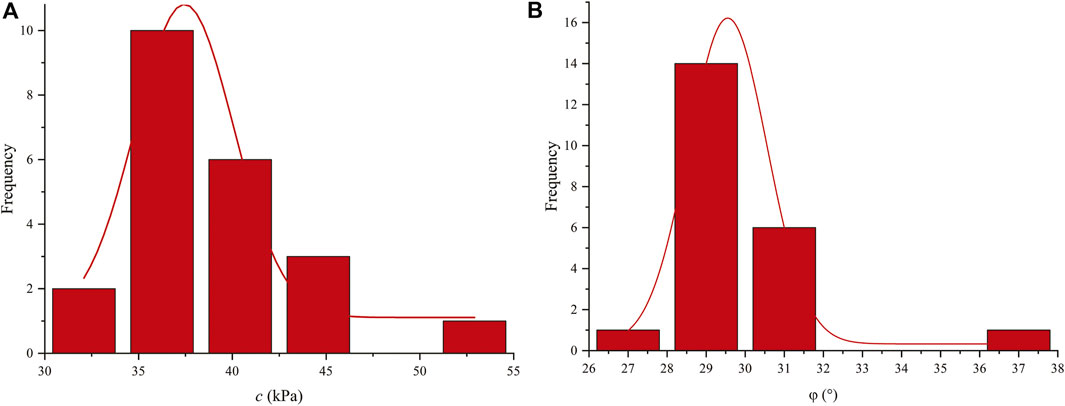
FIGURE 6. Histograms of material properties of landslide deposit (A) cohesion and (B) friction angle.

TABLE 1

TABLE 1. Descriptive statistics parameters for the Zhenggang landslide.

4 Results

4.1 Validation of the finite element model

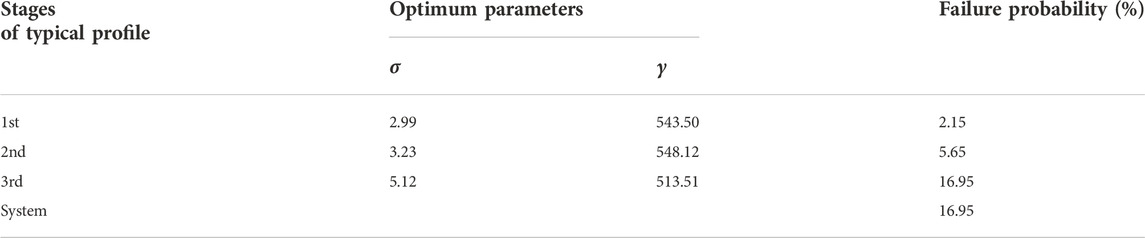
Deterministic methods, i.e., finite element model and simplified Bishop method, are employed to analyze the Zhenggang landslide stability using the mean parameter values listed in Table 1. The FEM analysis on Zhenggang landslide is built based on the lastic-plastic constitutive model and Mohr-Coulomb criterion. The vertical borders of the landslide model are horizontally constrained, and the bottom is completely fixed. The calculation results of the three sliding surfaces are respectively 1.119, 1.090 and 1.052, which is in good agreement with that (i.e., 1.140, 1.069 and 1.059) calculated from the simplified Bishop. This verifies the accuracy and feasibility of the sliding surface stress as the deterministic method of landslide numerical modeling. All safety factors are greater than 1.05, which demonstrates that the Zhenggang landslide remains in an essentially stable state. The third stage (i.e., front area) of the landslide has the lowest safety factor value, indicating that it is most likely to destabilize; the first failure is expected to occur in the front area of the landslide. When not supported by the third sliding body, the landslide gradually disintegrates and moves towards the Lancang River.

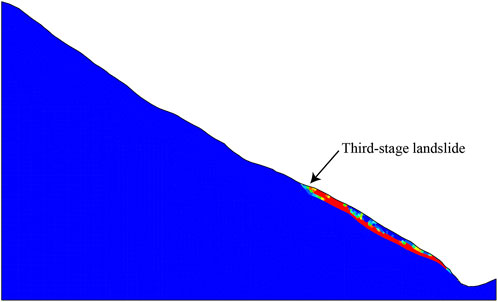
Moreover, for system reliability analysis of landslides involving deterministic multiple sliding surfaces, the sliding surface stress analysis has an incomparable advantage than shear strength reduction. The shear strain colour plot of Figure 7 indicates that finite element strength reduction technique can only obtain the most dangerous failure plane (Third-stage landslide) but cannot reflect the effects of the secondary failure surfaces on the system stability of landslide. In contrast, the sliding surface stress analysis can calculate the safety factors of multiple potentially active sliding surfaces from the stress fields generated by a finite element simulation, which will effectively expand the application of FEM analysis in landslide system reliability analysis.

FIGURE 7

FIGURE 7. Landslide failure plane deduced from finite element simulation.

4.2 Validation of least-squares support vector machine-based multiple response-surface method

The key to system reliability analysis is to construct the MRSM of $Fs$ for all sliding surfaces using the random variables of landslide. In this paper, a total of 400 samples with four random variables, i.e., c_d and ${\phi }_d$ of deposit, c_s and ${\phi }_s$ of sliding zone, are first randomly generated as training samples based on normal distribution characters of random variables. These training samples are generated using the Latin hypercube sampling method (Huang et al., 2020). The safety factors of the three sliding surfaces from the 400 training samples are subsequently used to determine the multiple response-surface functions. That means that perform 400 runs of FEM analyses to obtain the corresponding safety factors of the three sliding surfaces.

The LSSVM models for the three sliding surfaces are then used to construct the MRSM based on the 400 training samples, and GA is used to search for optimum parameters of LSSVM ($\sigma$ and $\gamma$). During the build process, three different and independent suites of LSSVM models are trained simultaneously, each of which corresponds to a response surface of sliding surface. The population size of GA is set to 50 and the maximum generation number is set to 50, the crossover probability and mutation probability are set to 0.8 and 0.08 respectively. The results of optimum parameters $\sigma$ and $\gamma$ of multiple LSSVM models with the three sliding surfaces are presented in Table 2.

TABLE 2

TABLE 2. Calculation results of intelligent multiple response surfaces for the Zhenggang landslide.

After the LSSVM-based MRSM is constructed, an additional dataset of 2000 samples are generated using the Latin hypercube sampling. The trained LSSVM models are then adopted to predict the safety factors of the three sliding surfaces associated with the 2000 random samples. A MCS method is applied to obtain the failure probability of ith sliding surface $p_{f_i}$ and system failure probability $p_f^{\text{sys}}$ from the 2000 LSSVM-predicted values of safety factors, and the results of calculation are presented in Table 2.

The failure probabilities of the three sliding surfaces are respectively 2.15%, 5.65%, 16.95%, which is consistent with the evaluation of landslide safety factor, that is, system failure of the Zhengang landslide is mainly contributed by the third sliding. Although the safety factors of the Zhenggang landslide with the three sliding surfaces are all greater than 1.05, the failure probability of the third stage landslide is as high as 16.95%. It is suggested that accurate evaluation of landslide stability based on deterministic analysis of the landslide alone is insufficient and system reliability analysis is essential to have a complete picture of the risk of land sliding. The system failure probability (16.95%) demonstrates that engineering measures be taken to reinforce the Zhenggang landslide because of low landslide stability.

For comparison, a direct finite element MCS with 2000 samples is used to estimate the system failure probability of the Zhenggang with the three sliding surfaces. This means that the FEM of the sliding surface stress analyses are conducted with 2000 simulations. The calculation result of the three sliding surfaces are respectively 2.20%, 5.60% and 16.70%, which is in good agreement with that (i.e., 2.15%, 5.65% and 16.95%) calculated from the LSSVM-based MRSM. The good agreement signifies the promising performance of LSSVM-based MRSM as metamodel of the FEM models.

4.2.1 Nonlinear characteristics of multiple response surfaces

To study the nonlinear characteristics of multiple response surfaces of the Zhenggang landslide, four different training sample sizes, 100, 200, 300 and 400, are used to construct the multiple response surfaces with the three sliding surfaces in this paper. Figures 8–11 show the safety factors of three sliding surfaces with different training sample sizes. Each subplot contains different number of scatter points that correspond to the training samples. Label of X-axis, Y-axis and Z-axis represents respectively the c_d and ${\phi }_d$ of deposit and c_s of sliding zone, and the size of scatters is ${\phi }_d$ of sliding zone. According to the calculation results of the FEM method, the safety factors are marked in different colors on the scatters, where yellow and blue are safety factors less than 1 and greater than 1 respectively. As shown in Figures 8–11, failure points (Fs < 1) of each failure sliding surface increase obviously as the increase of training sample size. There are the most failure points and the largest failure zone in the third sliding surface, indicating that the third stage is most likely to destabilize, which is consistent with the evaluation of landslide safety factor. What’s more, the shape of response surfaces (red surfaces) with safety factor of 1 is complex and changeable under the condition of multi-dimensional parameters. It is obvious that the traditional polynomial-based RSMs are difficult to fit the red response surfaces with highly nonlinear characteristics. Therefore, the LSSVM model with excellent nonlinear fitting ability is used to build the MRSM of Zhenggang landslide in this paper.

FIGURE 8

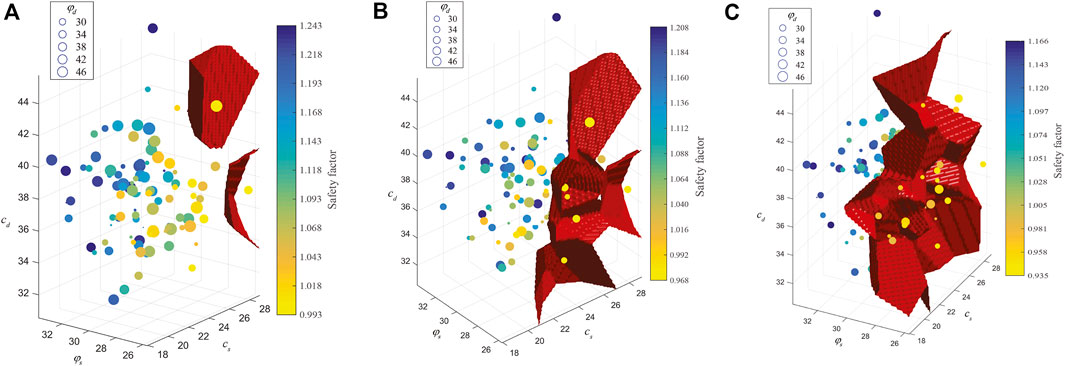
FIGURE 8. Safety factors of three sliding surfaces with 100 training samples. (A) 1st sliding surface (B) 2nd sliding surface (C) 3rd sliding surface.

FIGURE 9

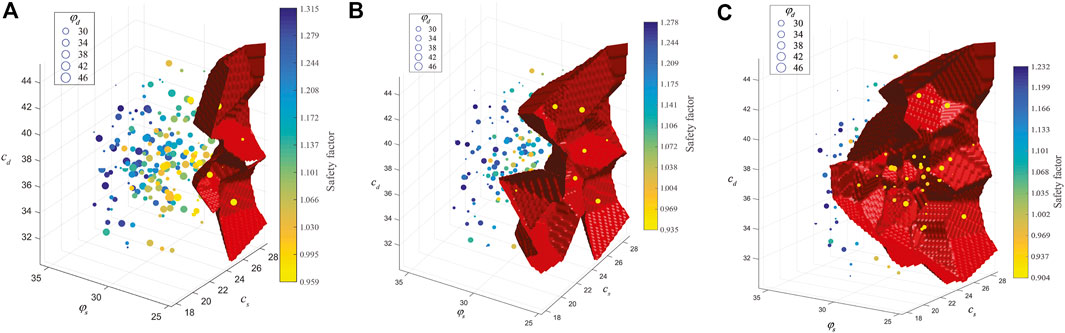
FIGURE 9. Safety factors of three sliding surfaces with 200 training samples. (A) 1st sliding surface (B) 2nd sliding surface (C) 3rd sliding surface.p

FIGURE 10

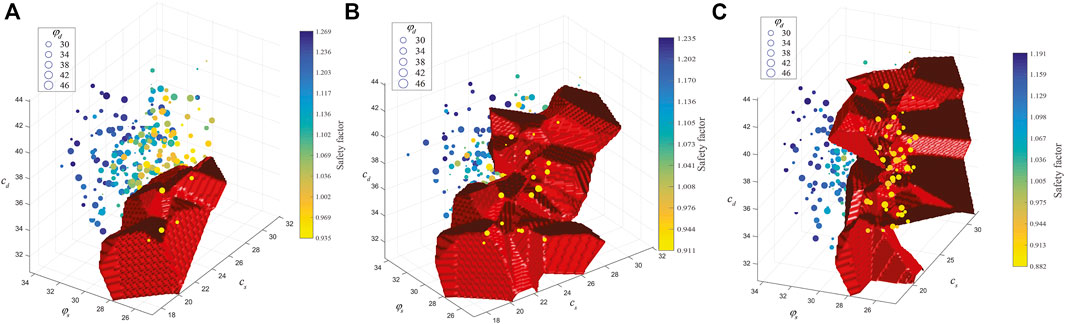
FIGURE 10. Safety factors of three sliding surfaces with 300 training samples. (A) 1st sliding surface (B) 2nd sliding surface (C) 3rd sliding surface.

FIGURE 11

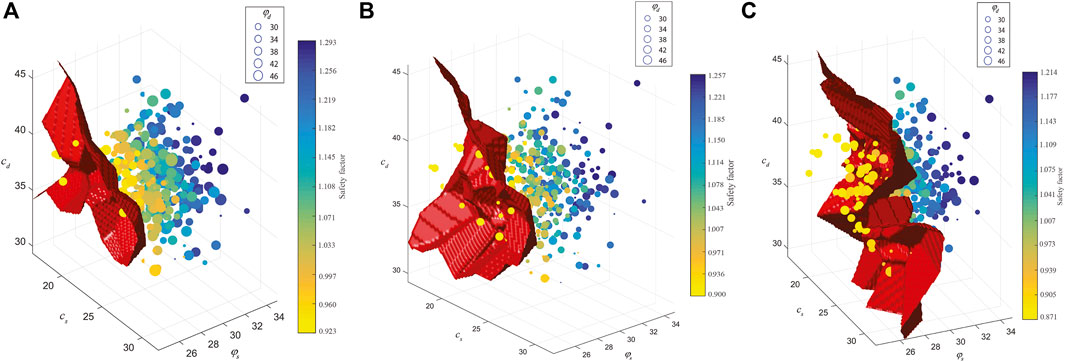
FIGURE 11. Safety factors of three sliding surfaces with 400 training samples. (A) 1st sliding surface (B) 2nd sliding surface (C) 3rd sliding surface.

4.2.2 Performance of least-squares support vector machine-based multiple response-surface method

Figure 12 shows the predicted safety factors of LSSVM are compared with the FEM of the sliding surface stress analysis calculated values under the four different training samples (100, 200, 300 and 400). The 2000 safety factors results from the direct finite element MCS are taken as the “exact” solutions to examine the accuracy of the trained LSSVM with the four training sample sizes. The calculation results show the training sample size directly affects the prediction performance of the proposed method. As expected, more training samples means that the GA optimized LSSVM model can learn more nonlinear features to describe the mapping relationships between the safety factor and random variables, resulting in decrease RMSE values. Moreover, the RMSE values are all smaller than 0.04, which indicates the safety factors predicted by LSSVM agree reasonably well with the FEM calculated values in all three subplots. However, a bias in the trends is also easily observed when the safety factor is greater than 1.15 or less than 0.97. The convergence of the bias is generally attained within 300 training samples, which implies that 400 training samples performed for this study are sufficient.

FIGURE 12

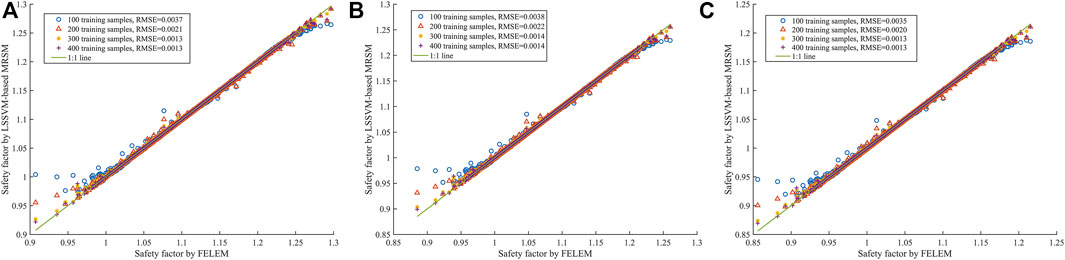
FIGURE 12. Comparison of safety factor predicted by LSSVM-based MRSM with the four training sample sizes. (A) 1st sliding surface (B) 2nd sliding surface (C) 3rd sliding surface.

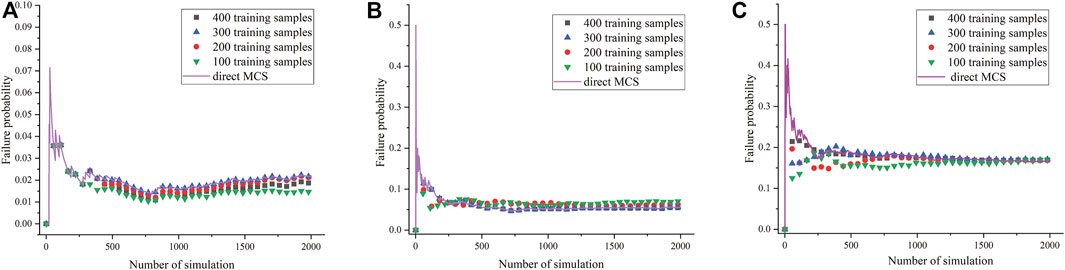
Figure 13A–C show the failure probability of the three sliding surfaces with different number of simulations, for both the LSSVM-based MRSM and direct MCS results. As the number of simulations increases, failure probability gradually decreases and converges within 1500 MCS simulations, indicating that the 2000 simulations are suitable. Some discrepancies between the safety factors predicted by LSSVM and calculated by finite element are observed, and the discrepancies gradually reduce by using more training samples. The good agreement of the three sliding surfaces further demonstrates 400 training samples are the appropriate sample size, and the LSSVM model shows good prediction performance for the nonlinear response surface.

FIGURE 13

FIGURE 13. Comparison of failure probability for different number of simulation.p

In summary, from the perspective of both accuracy and efficiency, it can be seen that the use of LSSVM-based MRSM provides a highly promising method for probabilistic numerical modeling of landslide stability considering multiple sliding surfaces.

5 Discussion

The promising performance of system reliability analysis heavily depends on the computational cost of deterministic landslide analysis and the number of samplings. Considering the deterministic analysis adopted by the proposed method, sliding surface stress analysis can effectively avoid the iterative calculation in the process of shear strength reduction. The computational cost associated with the construction of probabilistic numerical modeling can be quite high should the other shear strength reduction is applied.

Besides, the accuracy and time costs of system reliability increase linearly with the number of samplings, and more samples means more deterministic analyses are performed. Compared the directly MCS, the MRSM adopts metamodels with a small number of samples to replace the deterministic analysis procedure, which greatly improves the computational efficiency. However, the traditional MRSM method is limited to the design of sample number and ranges, and quadratic polynomial functions are difficult to approximate true RSFs nonlinearities for this case are presented in Figure 8–11.

The proposed intelligent multiple response surfaces method employs the robust generality of the LSSVM to approximate the values of implicit RSFs, which combines the advantages of the LSSVM and traditional MRSM approach. As shown in Figure 12, the proposed method is quite capable of representing the RSFs by using only 400 training samples that system reliability analysis can be implemented with acceptable accuracy. Therefore, it is applicable to a wide range of system reliability problems in engineering geology, including the complex system reliability analysis of multistage landslide involving sliding surfaces.

There are some shortcomings associated with the present study. The minimum failure probability of the three sliding surfaces is approximately 2% in this case, and the landslide reliability problem with low levels of failure probability has not yet been considered. It is well known that reliability calculation could be very time consuming especially when the failure probability is less than 10^–4 (Jiang and Huang 2016). Additional studies of geotechnical problems involving the inherent spatial variability of soil properties will be implemented to further illustrate the promising performance of the proposed method in future work.

6 Conclusion

An intelligent multiple response surfaces method is proposed to study the probability of system failure of a landslide by using the MRSM combined with GA optimized LSSVM. The method is applied to investigate the system reliability of the Zhenggang landslide, in Yunnan Province, China, involving sliding surfaces. The following conclusions can be drawn:

1 The sliding surface stress analysis can calculate simultaneously the safety factors of multiple sliding surfaces for system reliability analysis, which is not possible using shear strength reduction method. This effectively expands the application of FEM analysis in system reliability analysis of landslides involving deterministic multiple sliding surfaces.

2 The GA optimized LSSVM can effectively improve the fitting accuracy of the multiple response-surface method with a limited number of samples, from which they obtain substantially obtain the ability to make high-quality FEM predictions.

3 By comparing the LSSVM-based MRSM against direct MCS method, the accuracy and validity of the proposed intelligent multiple response surfaces method are verified using the Zhenggang landslide case study involving sliding surfaces. Wong, 1985.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZC: Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing—Original Draft; SS: Data Curation, Writing—Original Draft; JZ: Writing—Review andamp; Editing; BT: Investigation, Software; BX: Resources, Supervision; YM: Conceptualization, Funding Acquisition, Resources, Supervision, Writing—Review and Editing.

Funding

The work presented in this paper is financially supported by the National Natural Science Foundation of China (U2240221 and 51939004).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, Z. L., Xu, W. Y., Meng, Y. D., Shi, C., and Wang, R. (2016). Prediction of landslide displacement based on GA-LSSVM with multiple factors. Bull. Eng. Geol. Environ. 75 (2), 637–646. doi:10.1007/s10064-015-0804-z

CrossRef Full Text | Google Scholar

Dadashzadeh, N., Duzgun, H. S. B., and Yesiloglu-Gultekin, N. (2017). Reliability-based Stability Analysis of rock slopes using numerical analysis and response surface method. Rock Mech. Rock Eng. 50 (8), 2119–2133. doi:10.1007/s00603-017-1206-2

CrossRef Full Text | Google Scholar

Ditlevsen, O. (1979). Narrow reliability bounds for structural systems. J. Struct. Mech. 7 (4), 453–472. doi:10.1080/03601217908905329

CrossRef Full Text | Google Scholar

Dong, B., and Lu, Z. Z. (2022). Efficient adaptive Kriging for system reliability analysis with multiple failure modes under random and interval hybrid uncertainty. Chin. J. Aeronautics 35, 333–346. doi:10.1016/j.cja.2021.08.017

CrossRef Full Text | Google Scholar

Farias, M. M., and Naylor, D. J. (1998). Safety analysis using finite elements. Comput. Geotechnics 22 (2), 165–181. doi:10.1016/s0266-352x(98)00005-6

CrossRef Full Text | Google Scholar

Fu, X. Q., Zhang, X. R., Qiao, Z., and Li, G. (2019). Estimating the failure probability in an integrated energy system considering correlations among failure patterns. Energy 178, 656–666. doi:10.1016/j.energy.2019.04.176

CrossRef Full Text | Google Scholar

Griffiths, D. V., and Fenton, G. A. (2004). Probabilistic slope stability analysis by finite elements. J. Geotech. Geoenviron. Eng. 130 (5), 507–518. doi:10.1061/(asce)1090-0241(2004)130:5(507)

CrossRef Full Text | Google Scholar

Hong, Y., Yu, G. M., and He, K. Q. (2016). Probabilistic landslide risk assessment of a historic and cultural site on the north slope of Lishan Mountain, Xian, China. Environ. Earth Sci. 75, 646. doi:10.1007/s12665-016-5434-7

CrossRef Full Text | Google Scholar

Huang, Y., Chen, S., Chen, Z., Hu, W., and Huang, Q. (2020). Improved probabilistic load flow method based on D-vine copulas and Latin hypercube sampling in distribution network with multiple wind generators. IET Gener. Transm. &amp. Distrib. 14 (5), 893–899. doi:10.1049/iet-gtd.2019.1126

CrossRef Full Text | Google Scholar

Ji, J., Liao, H. J., and Low, B. K. (2012). Modeling 2-D spatial variation in slope reliability analysis using interpolated autocorrelations. Comput. Geotech. 40, 135–146. doi:10.1016/j.compgeo.2011.11.002

CrossRef Full Text | Google Scholar

Jiang, S. H., and Huang, J. S. (2016). Efficient slope reliability analysis at low-probability levels in spatially variable soils. Comput. Geotechnics 75, 18–27. doi:10.1016/j.compgeo.2016.01.016

CrossRef Full Text | Google Scholar

Kim, J. Y., and Lee, S. R. (1997). An improved search strategy for the critical slip surface using finite element stress fields. Comput. Geotechnics 21 (4), 295–313. doi:10.1016/s0266-352x(97)00027-x

CrossRef Full Text | Google Scholar

Li, D. Q., Jiang, S. H., Cao, Z. J., Zhou, W., Zhou, C. B., and Zhang, L. M. (2015). A multiple response-surface method for slope reliability analysis considering spatial variability of soil properties. Eng. Geol. 187, 60–72. doi:10.1016/j.enggeo.2014.12.003

CrossRef Full Text | Google Scholar

Li, K., Wang, L. Y., Wu, J. J., Zhang, Q. J., Liao, G., and Su, L. (2018). Using GA-SVM for defect inspection of flip chips based on vibration signals. Microelectron. Reliab. 81, 159–166. doi:10.1016/j.microrel.2017.12.032

CrossRef Full Text | Google Scholar

Li, S. J., Zhao, H. B., and Ru, Z. L. (2013). Slope reliability analysis by updated support vector machine and Monte Carlo simulation. Nat. Hazards (Dordr). 65 (1), 707–722. doi:10.1007/s11069-012-0396-x

CrossRef Full Text | Google Scholar

Li, Z., Hu, Z., Zhang, X. Y., Du, S., Guo, Y., and Wang, J. (2019). Reliability analysis of a rock slope based on plastic limit analysis theory with multiple failure modes. Comput. Geotechnics 110, 132–147. doi:10.1016/j.compgeo.2019.02.021

CrossRef Full Text | Google Scholar

Liu, H. X., and Low, B. K. (2017). System reliability analysis of tunnels reinforced by rockbolts. Tunn. Undergr. Space Technol. 65, 155–166. doi:10.1016/j.tust.2017.03.003

CrossRef Full Text | Google Scholar

Liu, L. L., and Cheng, Y. M. (2016). Efficient system reliability analysis of soil slopes using multivariate adaptive regression splines-based Monte Carlo simulation. Comput. Geotechnics 79, 41–54. doi:10.1016/j.compgeo.2016.05.001

CrossRef Full Text | Google Scholar

Low, B. K. (1997). Reliability analysis of rock wedges. J. Geotech. Geoenviron. Eng. 123 (6), 498–505. doi:10.1061/(asce)1090-0241(1997)123:6(498)

CrossRef Full Text | Google Scholar

Low, B. K., Zhang, J., and Tang, W. H. (2011). Efficient system reliability analysis illustrated for a retaining wall and a soil slope. Comput. Geotechnics 38, 196–204. doi:10.1016/j.compgeo.2010.11.005

CrossRef Full Text | Google Scholar

Pei, L., Chen, C., He, K., and Lu, X. (2022). System reliability of a gravity dam-foundation system using Bayesian networks. Reliab. Eng. Syst. Saf. 218, 108178. doi:10.1016/j.ress.2021.108178

CrossRef Full Text | Google Scholar

Roy, A., Manna, R., and Chakraborty, S. (2019). Support vector regression based metamodeling for structural reliability analysis. Probabilistic Eng. Mech. 55, 78–89. doi:10.1016/j.probengmech.2018.11.001

CrossRef Full Text | Google Scholar

Su, Y. H., Li, X., and Xie, Z. Y. (2011). Probabilistic evaluation for the implicit limit-state function of stability of a highway tunnel in China. Tunn. Undergr. Space Technol. 26, 422–434. doi:10.1016/j.tust.2010.11.009

CrossRef Full Text | Google Scholar

Sung, E. C. (2009). Probabilistic stability analyses of slopes using the ANN-based response surface. Comput. Geotechnics 36 (5), 787–797. doi:10.1016/j.compgeo.2009.01.003

CrossRef Full Text | Google Scholar

Suykens, J. A. K., and Vandewalle, J. (1999). Least squares support vector machines classifiers. Neural Process Lett. 9 (3), 293–300.

Google Scholar

Tan, X. H., Bi, W. H., Hou, X. L., and Wang, W. (2011). Reliability analysis using radial basis function networks and support vector machines. Comput. Geotechnics 38, 178–186. doi:10.1016/j.compgeo.2010.11.002

CrossRef Full Text | Google Scholar

Wang, B., Liu, L. L., Li, Y. H., and Jiang, Q. (2020). Reliability analysis of slopes considering spatial variability of soil properties based on efficiently identified representative slip surfaces. J. Rock Mech. Geotechnical Eng. 12 (3), 642–655. doi:10.1016/j.jrmge.2019.12.003

CrossRef Full Text | Google Scholar

Wang, S. N., Xu, W. Y., Shi, C., and Chen, H. J. (2017). Run-out prediction and failure mechanism analysis of the Zhenggang deposit in southwestern China. Landslides 14 (2), 719–726. doi:10.1007/s10346-016-0770-y

CrossRef Full Text | Google Scholar

Wang, Z. Z., and Goh, H. S. (2021). Novel approach to efficient slope reliability analysis in spatially variable soils. Eng. Geol. 281, 105989. doi:10.1016/j.enggeo.2020.105989

CrossRef Full Text | Google Scholar

Wong, F. S. (1985). Slope reliability and response surface method. J. Geotech. Engrg. 111 (1), 32–53. doi:10.1061/(asce)0733-9410(1985)111:1(32)

CrossRef Full Text | Google Scholar

Wu, Y. P., Cheng, C., He, G. F., and Qiuxia, Z. (2014). Landslide stability analysis based on random-fuzzy reliability: Taking liangshuijing landslide as a case. Stoch. Environ. Res. Risk Assess. 28 (7), 1723–1732. doi:10.1007/s00477-013-0831-x

CrossRef Full Text | Google Scholar

Xu, W. Y. (2010). Further research report on the Zhenggang landslide deposits of Gushui hydropower station project in Lancang river. Nan Jing: Hohai University. (in Chinese).

Google Scholar

Yang, Y. C., Xing, H. G., Yang, , Huang, K. x., and Zhou, J. w. (2015). Two-dimensional stability analysis of a soil slope using the finite element method and the limit equilibrium principlenite element method and the limit equilibrium principle. fiThe IES J. Part A Civ. Struct. Eng. 8 (4), 251–264. doi:10.1080/19373260.2015.1072299(

CrossRef Full Text | Google Scholar

Zou, J. Z., Willians, D. J., and Xiong, W. L. (1995). Search for critical slip surfaces based on finite element method. Can. Geotech. J. 32 (2), 233–246. doi:10.1139/t95-026

CrossRef Full Text | Google Scholar