Hydrothermal formation of fibrous mineral structures: The role on strength and mode of failure

Studying the mechanisms that control the rheology of rocks and geomaterials is crucial as much for predicting geological processes as for functionalizing geomaterials. That requires the understanding of how structural arrangements at the micro and nano scale control the physical and mechanical properties at the macroscopic scale. This is an area of rock physics still in its infancy. In this paper, we focus the attention on the formation of cementitious phases made of micro- and nano-scale fibrous structures, and the controls of the arrangement of these phases on mechanical properties. We use hydrothermal synthesis, and the properties of hydrothermal water, to promote the growth of fibrous mineral phases having nano-size diameter and length of a few microns, creating disordered and entangled mats of fibrous bundles as those found in natural samples. We draw inferences from structural microscopy to inform a statistical model that establishes an interdependence between structural parameters of fibrous structures and bulk mechanical response. Structural parameters include number and length of fibers, spatial orientation, and fraction of fibrous threads bearing the load. Mechanical properties include strength and mode of failure. Results show that as the fibrous microstructure evolves from ordered and aligned to disordered and entangled, the mechanical response of the fibrous composite transitions from a brittle to ductile behavior. Furthermore, the disordered and entangled microstructure exhibits lower strength at failure though strength increases as the number of fibers within the microstructure increases. Finally, the longer the entangled fiber, the larger the strain that the matrix can accommodate. The value of this study lies in further understanding fault healing through hydrothermal fluids and how the physical properties of fibrous microstructures resulting from it control brittle-ductile transitions, and possibly, slow slip events along subduction zones.

1 Introduction

For decades the focus of geophysicists has been to study how rocks possibly respond to stress—from elastic to plastic deformation, to failure. This type of knowledge has been foundational to deciphering the geologic structures of regions and the geological activity at plate boundaries that suddenly lurch forward causing earthquakes. But how do rocks self-heal through cementation? And how does the micro- and nano-structural arrangement of cementitious matrices affect strength and mode of failure? Answering these questions is as much crucial as elusive for the geosciences. Whether the focus is diagenesis leading to lithification, weakening and crack-healing and sealing mechanisms occurring over the seismic cycle, mechanisms of heat transfer during metamorphism, the scavenging of rare elements and their concentration ranges, in every of these cases the germane question to be asked concerns the nature of crustal fluids and their transport characteristics. Since the seminal paper by Ramsay (1980) and the topical volumes on fluids in the Earth’s crust (Fyfe et al., 1978; National Research Council, 1990) the literature on crack-seal mechanism of rock deformation has grown considerably. So far, much of the work has concerned structural geology and tectonics, whether it is observational field work (Urai et al., 1991; Menzel et al., 2022) or modeling (Späth et al., 2022; Virgo et al., 2014) addressing the formation of veins. However, how these processes impact rock physical properties and, in turn, the geophysical observables remain elusive in rock physics.

Cement is an important element of lithification. Despite its small volumetric fraction, cement provides cohesion and support to the rock frame as much as hinges provide strength and stability to a scaffolding structure. Observations and models for cementation processes, fracture growth and sealing have been widely studied in the literature (Laubach et al., 2019 and references therein; Lander and Laubach, 2015) but there is a disconnect between processes and rock physics properties. So far, in describing the macroscopic properties of rock composites, rock physics models have primarily relied on the knowledge of the volume fractions of the primary phases constituting the rock, namely the solid grains and pore fluids, along with the properties of these phases (Mavko et al., 2009). Some of the models for granular media have more specifically addressed the effect of stress transmission between deformable grains through deformable interparticle cement bonds (Dvorkin, 1997), which included the role of quantity and type of cement in controlling elastic and mechanical properties (Lade and Overton, 1989; Dvorkin et al., 1994; Yin and Dvorkin, 1994). However, all these mixing schemes have traditionally neglected the arrangements of minerals forming the microstructure (Mavko et al., 2009). Little or no attention has been devoted in rock physics to how the heterogeneity of the structural properties of the cementitious phase, and specifically the arrangements at the micro and nano scale, control the effective physical and mechanical properties at the macroscopic scale—a tenet that is central to materials science. The effect of interparticle cement on rock physics and mechanics properties might appear inconspicuous at first glance, but cementitious matrices may control the mechanical response of rocks as much as a small fraction of glue controls strength and toughness of any material composite. The most familiar example of glue that supports this thinking is the collagen protein. Collagen is a long-chain (polymeric) biomolecule providing cohesion and support in animal connective tissues, so named in reference to its ability to produce a glue, or κóλλα in ancient Greek and colla in Italian. Although collagen makes up only 30% of the body proteins, this bio-glue consists of nano-scale bundles of fibers (i.e., natural long-chain structures) interspersed within a gel-like substance, altogether strengthening the connective tissues from the micro to the macro scale. Making the same connection in rock physics across scales of observations is an area of research still in its infancy due to three main challenges. First, until one or 2 decades ago, there was simply not enough spatial and temporal resolution to image the structure of nano mineral phases or even characterize the chemistry and the growth of these phases (Hochella et al., 2008; Barnard and Guo, 2012; Caraballo et al., 2015). Thanks to the improved resolution of imaging techniques, apparently unstructured rock matrices appear now as a meshwork of intertwined fibers that look tangled when imaged at the micro and nanoscale (Shervais et al., 2011; Verbene et al., 2013; Verberne et al., 2014; Vanorio and Kanitpanyacharoen, 2015; Rossi et al., 2016; Viti et al., 2018). Nanogeoscience observations provide us with another perspective from which to view rock chemical, physical, and mechanical properties (Hochella et al., 2008). As emphasized in the recent review by Laubach et al. (2019), a major challenge is to understand how, and to what extent, microscopic (grain-scale and subgrain to nanoscale) fracture growth processes are linked to the observed macroscale mechanical behavior of rock. Secondly, connecting structure to bulk properties represents a substantial challenge for rock physicists since Earth materials are the result of the engineering capability of Earth. Not only does such a capability need to be reversed, from processes to design, but it also encompasses a range of conditions that are only indirectly known and often yet-to-be diagnosed. Such limitations lead to the third challenge. The knowledge required to understand cementation and its structure designs is cross-disciplinary in nature, comprising both chemistry and engineering. It is worth mentioning that the most capable method used in chemistry and engineering to fabricate nano- and micro-phases with high crystallinity and well-defined morphology (Barhoum et al. 2019; Altaf et al., 2020) is hydrothermal synthesis, involving vapor-transport reactions (Binnewies et al., 2012; Binnewies et al., 2013; Schmidt et al., 2013) akin to those carried out by hydrothermal fluids that circulate through faults and volcanic systems (Bunsen et al., 1852). In that respect, much can be learned from engineering in which process controllers like fluid temperature and composition, are routinely used in the laboratory to functionalize properties of cementitious phases, including flexibility and stiffness (Barhoum et al. 2019).

From a rock physics perspective, understanding the cementation and the fine structure of the mineral phases forming from the healing process of faults is foundational to studying the seismic cycle, which to first order includes alternating phases of interseismic strain accumulation and coseismic strain release. Hidden in the concepts of strain accumulation and release, there is the fundamental notion of contact aging as a key mechanism of frictional healing—a concept involving the strengthening of fault gouge sediments during the interseismic phase. Several mechanisms and weakening processes have been proposed to potentially operate during earthquakes (Tullis, 2015). So far, the study of healing and frictional aging has mostly focused on physical parameters that are both extrinsic and intrinsic to the formation of rock cement and its properties, including the effect of time and shear displacement (Marone, 1998a and Marone, 1998b), temperature and hydrothermal fluid conditions at depths (Karner et al., 1997; Olsen et al., 1998; Niemeijer et al., 2002; Muhuri et al., 2003; Tenthorey et al., 2003), thin aqueous films at grain contacts (Spiers et al., 2004), shear stress and micromechanical processes such as compaction and packing density (Ryan et al., 2018). There remains a gap in how healing happens, and specifically, how subsurface water produces the very fine structure of cement under hydrothermal conditions, and how the spatial arrangement of the building blocks in the form of phases and defects give rise to its properties. It is worth emphasizing that in the geosciences the term “hydrothermal conditions” generally relates to or denotes the action of heated water rising in the earth’s crust from a cooling magma body and forming minerals. In chemistry and engineering, the term hydrothermal or solvothermal refers to a method for crystallizing substances at high vapor pressure and temperature range of 100°C–250°C (Byrappa and Yoshimura, 2001; O’Hare, 2001). Crystal growth and synthesis are performed in an apparatus consisting of a steel pressure vessel called an autoclave in which powder (i.e., a nutrient solute) is supplied along with water. The method takes advantage of the PT state diagram of water. As such, the pressure developed in a working autoclave is autogenous (i.e., autonomously generated due to the thermal expansion of water within a confined volume), and very sensitive to both temperature and the amount of water present in the volume (i.e., degree of fill). At the hotter end of the vessel (the bottom) the nutrient solute dissolves because of the physicochemical properties of hydrothermal water (Franck (1978), while at the cooler end (the top) the dissolved solute is transported by vapor and deposited on a seed crystal, growing the desired crystalline phase. Understanding these basic aspects of mineral growth and the condition of growth is important because the arrangements of mineral phases at the micro- and nanoscale may affect as much the stress-strain response as the dependence of friction on the “rate” of sliding and on the continually accrued slip—that is, the pace of the evolution of the “state” of the interface in response to changes in lip rate (Dieterich, 1979). Current friction laws are approximate, and damage and healing rates are poorly constrained (Richardson and Marone, 1999; Morgan, 2004)

Our approach to this problem is to analyze natural designs through the lens of engineering design practices. Active faults in the Earth’s crust can be viewed to function as large-scale kiln factories—they mechanically pulverize aluminosilicate rocks to the micron or finer scale, and internally channel heat that primes the fault gouge for fluid-mediated chemical reactions, eventually leading to cementation. Observations from geophysical data show that fault healing, which entails strength recovery from repeated failures of the Earth’s crust, is a relatively fast process (Vidale and Li, 2003; Li et al., 2006; Peng, and Ben-Zion, 2006; Sawazaki et al., 2009; Nakata and Snieder, 2011; Pei et al., 2019) but we are missing how fault healing works and how to predict the friction force from fundamental physics principles. Recently, Liu and Szlufarska (2012) discovered molecular mechanisms that can lead to a logarithmic increase of friction based on interfacial chemistry. Generalization of these mechanisms requires the time scales of reactions and imaging the arrangements of mineral matrices across scales of observation, soliciting the need for experiments that replicate the growth of cementitious phases in the laboratory.

This study advances knowledge on the natural cementation processes by studying the formation of micro- and nano-scale structures of cementitious phases via hydrothermal synthesis along with the mechanical properties of possible arrangements of these phases. We focus the attention on how hydrothermal synthesis leads to the formation of fibrous arrangements of mineral phases. Then, we draw inferences from structural microscopy of micro- and nano-structures of fibrous phases created in nature and the laboratory to inform a statistical model that establishes a structure–mechanics interdependence between structural parameters of fibrous structures and bulk mechanical response. Structural parameters include number and length of fibers, spatial orientation, and fraction of fibrous threads bearing the load. Mechanical properties include strength, mode of failure, and the transition of the load-deformation relationship from brittle to ductile regimes.

2 Materials and methods

2.1 Sample characterization and hydrothermal synthesis

For most, fibrous phases form naturally as a diagenetic product of the hydrothermal alteration of highly reactive sediments such as basaltic glass, volcanic ash, or carbonates. Aluminosilicate fibrous minerals consist of long-chain structures forming complex frameworks of silicon-oxygen tetrahedra (T) and aluminum-oxygen octahedra(O) hosting cations within their structure (Bergaya et al., 2013; Brigattia et al., 2013; Wang and Wang, 2019; ). At the structural level, these units are described in the geosciences as long tetrahedral silicate sheets in which the oxygen is binding to ribbons of Al-Mg-Fe octahedra, which elongates in one preferential direction while bonding to alkaline cations and water molecules. In the laboratory, high-crystallinity phases of nano- and micro-fibers are routinely synthesized via hydrothermal processes, which involves vapor-transport reactions (Schmidt et al., 2013; Barhoum et al. 2019; Altaf et al., 2020).

Structural observations via scanning electron microscope (SEM) imaging of mats of micro- and nano-structures of fibrous phases constitutes the basis for modeling the interdependence between structural parameters of fibrous structures and bulk mechanical response. We relied both on rock samples exposed to faulting and hydrothermal circulation, as well as samples created in the laboratory through hydrothermal synthesis. The natural samples come from a well-preserved, carbonate fault mirror being part of the Nazareth normal fault system, northern Israel. This fault segment is dipping 70°/140° and cut through the dolomite units of Late Cretaceous.

Regarding the fibrous structures created in the laboratory, we used two types of hydrothermal reactors with the difference mainly consisting in the type of sample used (unconsolidated vs consolidated) and the boundary conditions applied during the experiments. The first reactor is a Teflon-lined, stainless steel laboratory autoclave vessel (model 4760) manufactured by the Parr Instrument Company (Figure 1, top left). The autoclave is a closed vessel with an internal cup and lid made of Teflon. The vessel is charged with reagents, namely water and unconsolidated rock sediment placed at the bottom (the dissolution zone) and closed. Sediment is also placed in an hourglass-shaped sample holder that is partially submerged in water, which is characterized by a filter diaphragm allowing the passage of water vapor through the sediment. Under external heating, the autoclave is specifically designed for harsh chemical environments (i.e., alkaline) while exposing the sediment slurry to hydrothermal temperatures (150–250°C) and vapor pressures. The second reactor is an in-house built HPHT reactor (Figure 1, top right) that allows for reactive-fluid flow through a porous rock sample. This design allows for experiments where the sample withstands a confining pressure, exerted by argon gas, and pore fluid pressure, which is supplied by injecting water through a system of pumps. During the experiment, the sample is jacketed into a core-holder consisting of a thin-walled, annealed copper tube that separates the pore and confining pressure media. The copper tube is flared and sealed onto stainless steel end caps that are connected to the downstream and upstream pore pressure lines. A set of four thermocouples is arranged such that one controls the temperature near the top, one at the bottom, and two in the middle of the sample. The core-holder is then wrapped by a heater, composed of an iron-chrome-aluminum wire helically wound and cemented into a grooved ceramic refractory holder. The HTHP reactor vessel is rated for a maximum temperature of 510°C, a maximum P_c=34.5 MPa, and a maximum P_f=13.8 MPa. A schematic of the interior of the reactor with the core holder is shown in Figure 1B, and further details about the apparatus can be found in Head et al. (2018), Suwannasri et al. (2018), and Allan et al. (2016).

FIGURE 1

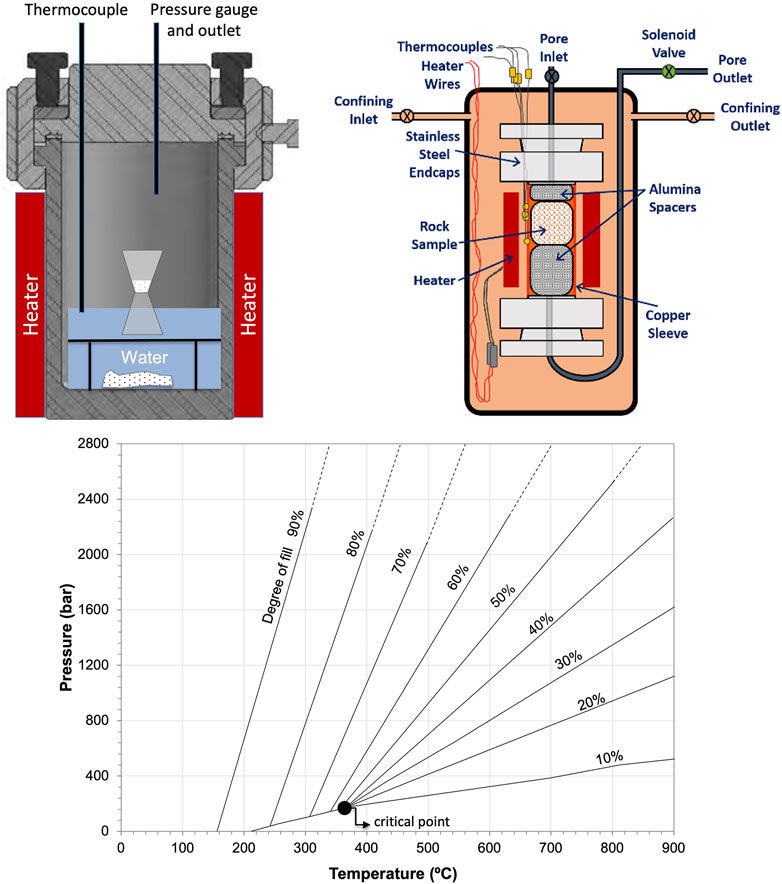
FIGURE 1. Schematics of laboratory autoclave vessel (top left) and the in-house built HPHT reactor (top right). In the autoclave vessel, the sediment is placed in water at the bottom of the vessel representing the dissolution zone as well as in an hourglass-shaped sample holder that is partially submerged in water. In the HPHT reactor, the sample is jacketed into a core-holder consisting of a thin-walled, annealed copper tube wrapped by a heater, separating the pore and confining pressure media. (Bottom) PT diagram of water showing the filling factor (degree of fill) of the autoclave as a parameter. The autogenerated pressure depends on temperature and it is very sensitive to the amount of water present in the volume (i.e., degree of fill).

Regardless of the reactor vessel used, the PT diagram of water (Figure 1, bottom) is extremely important for experimental hydrothermal synthesis as the process takes advantage of the changes in the properties of water as temperature increases. Under hydrothermal conditions, water provides heat with autogenous pressure and vapor-transport reactions (Barhoum et al. 2019). The pressure prevailing under working conditions is determined by the degree of fill of the vessel, i.e., by the volume of the reaction vessel that was originally filled with the aqueous solvent (Figure 1, bottom). These conditions promote vapor-transport reactions (Binnewies et al., 2012; Binnewies et al., 2013) that are key to the formation of crystalline solids since crystal growth proceeds via a gas phase. Vapor-transport reactions consists of a condensed phase, typically a solid phase with an insufficient pressure for its own volatilization, which can be volatilized in the presence of a gaseous reactant serving as the transport agent, and then deposited elsewhere in the form of crystals. Reactions are initiated by hydrothermal water since its properties undergo profound changes due to the breaking of the hydrogen bonds network (Unterlass, 2017). As temperature increases, both density and viscosity of the water decrease while mass diffusion coefficient and thermal diffusivity increase. Hence, the mobility of molecules and ions of hydrothermal fluids is much higher than water under normal condition. Furthermore, upon reaching hydrothermal temperatures (i.e., 200°C), water transforms into a powerful solvent. Its ionic product (Kw) shows a maximum between 150°C and 250°C and its dielectric constant (DC), which essentially controls fluid polarity (Hladký et al., 1966), reaches values that mimic those of common organic solvents, namely acetone, hexane, methanol, ethanol (Unterlass, 2017).

2.2 Modeling

We use a statistical model developed in bioscience for micro/nanofibrous materials (Rizvi et al., 2012) to establish a structure–mechanics interdependence between structural parameters of arrangements of fibrous minerals and the bulk mechanical response. Specifically, the model allows us to interpret the tensile response of fibrous matrices as a function of geometrical parameters describing an assemblage of fibrous micro- and nano-structures that draw insights from observations done via microscopy imaging.

We analyzed the stress-strain response of microstructural arrangements of fiber, from disorderly entangled to orderly straight. The conceptual model (Figure 2) proceeds from the approximation that the single fibers in the matrix are initially curved until mechanically loaded. Since mineral fibers are generally characterized by limited flexural strength, each single fiber has little load-bearing capacity until it straightens and begins to resist longitudinal elongation. The microstructure of a fibrous composite is described in according to input parameters that characterize both the properties of the single fibers and the arrangement within the matrix. These parameters describe the fibrous arrangement of the matrix and include length (l) of the fiber, diameter (a), and width (w). The width is the end-to-end lateral separation of the fiber. The diameter (a) is approximated to be constant over the length of a fiber. Within the matrix, the distribution of the fibers according to these specified parameters is described by a probability density function (PDF). Eq. 1 describes the probability of finding a fiber that has length between l and l + dl, diameter between a and a + da, and end-to-end width separation between w and w + dw,

$\underset{l_{\mathit{min}}}{\overset{l_{\mathit{max}}}{{\displaystyle \int }}}\underset{w_{\mathit{min}}}{\overset{w_{\mathit{max}}}{{\displaystyle \int }}}PDF\left(l,w\right)dwdl=1(1)$

FIGURE 2

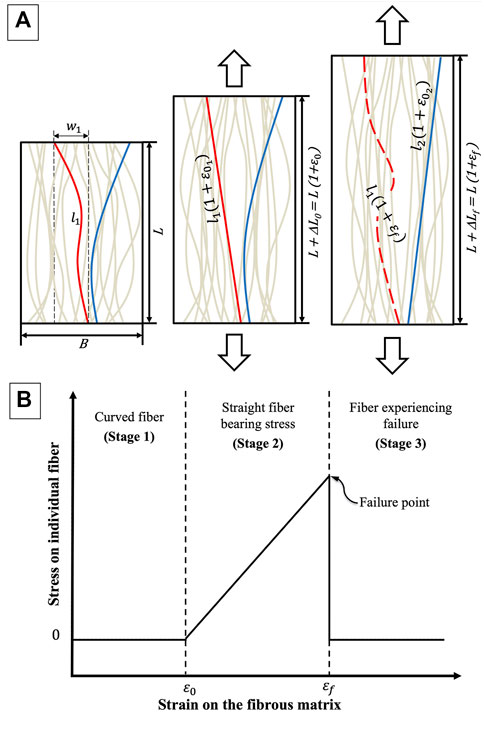
FIGURE 2. Schematic showing tensile load applied on a fibrous material (A) and load–displacement characteristic of a single fiber (B). (A, left panel) The fibrous matrix is shown at the beginning of longitudinal stretching when all fibers are curved, and the material exhibits no mechanical resistance (B, Stage 1). Upon loading (A, central panel), a fiber (red, solid line) becomes straight and begins to resist deformation, thereby providing mechanical strength to the matrix (B, Stage 2). As the fibrous matrix is stretched to length L + ΔL_f, the fiber breaks (red, dashed line), stress drops (B, Stage 3) but a new fiber (solid blue line) straightens to start resisting the deformation.

In a fibrous matrix, the shortest load-bearing fiber would be straight and parallel with the respect to the longitudinal dimension (L) of the fibrous sample, satisfying the conditions that l_min is ≥ L and w_min is ≥0. Similarly, the length and end-to-end width separation must satisfy the condition that length of the fiber along the longitudinal direction of sample must be greater than or equal to the length of the sample (L), i.e., l²—w² ≥ L². In such a design, the parameter l/L represents the curvature of the fiber while w/L describes the alignment of the fiber within the matrix. Therefore, the length and the curvature of the fiber are linked to each other, with highly curved fibers being longer. This set of parameters (l, w) along with the PDF p(l, w) are used to describe the structural properties of a fibrous cementitious matrix.

The model assumes that each individual fiber contributes to the overall resistance of the fibrous matrix to stress. Upon longitudinal loading each single fiber of the assemblage undergoes three deformation stages (Figure 2), which are function of the geometrical parameters characterizing the fibers. In the first stage (Figure 2A, left panel) the fibers are under an undeformed state, they are curved and entangled before being loaded. Therefore, they do not provide any mechanical resistance, bearing negligible stress (Figure 2A). The second stage starts as the fiber (l₁) within the matrix (Figure 2B, central panel, red color) straightens up. During this stage, the fiber accumulates strain that is function of the fiber’s elastic constants, and stress increases while resisting deformation (Figure 2A). Upon reaching the third stage, the fiber attains a deformation equal to its failure strain (${\epsilon }_f)$ (Figure 2B, right panel), thus leading the stress to drop. Once the failure stage is reached another fiber (l₂) within the matrix takes over (Figure 2B, right panel, blue color), thus supporting the load.

Because of the heterogeneity that connotes rocks, in this study we utilize a gamma distribution function in addition to a gaussian distribution to describe the arrangement of the fibrous minerals within the microstructure of cementitious matrix. Both distribution scenarios enable to capture the heterogeneous nature of microstructural arrangements that characterize natural composites such as rocks. In particular, the gamma distribution is used as a statistical function that physically conveys a skewed distribution of the arrangement of mineral fibers in terms of both length and width. In practice this means that, when this distribution is used in the model, we have a control on the fraction of mineral fibers bears the load. The gamma and the normal distributions are presented in Eqs. 2, 3, respectively,

$PDF\left(l,w\right)=\frac{1}{{\mathrm{C}\bullet \left(\mathrm{\Gamma }\left(k\right)\right)}^2}{\left[\left(l-{\mu }_l\right)\left(w-{\mu }_w\right)\right]}^2\bullet \exp \left[-\left(\left(l-{\mu }_l\right)+\left(w-{\mu }_w\right)\right)\right](2)$

$PDF\left(l,w\right)=\frac{1}{C}\exp \left[-\left(\frac{{\left(l-{\mu }_l\right)}^2}{{\sigma }_l^2}+\frac{{\left(w-{\mu }_w\right)}^2}{{\sigma }_w^2}\right)\right](3)$

where C is a constant that enforce the normalization condition (1), μ_l and μ_w are the mean length and end-to-end width separation, σ_l and σ_w represents the standard deviation of the length and end-to-end width separation, Γ(k) is the gamma function, and k is the shape factor of the skewed function distribution. In this study, a value of 1.3 for k was assumed for a left-skewed distribution.

The total resistance offered by the fibrous matrix that results from the deformation ΔL is expressed by (4). It is given by the sum of the single components of resisting forces of all load-bearing fibers along the direction of stretching:

${\sigma }_{total}\left(∆L\right)=\frac{N}{A}{\int }_{l_{\mathit{min}}}^{l_{\mathit{max}}}{\int }_{w_{\mathit{min}}}^{w_{\mathit{max}}}\frac{{\sigma }_{single}\bullet \left(L+∆L\right)}{\sqrt{{\left(L+∆L\right)}^2+w^2}}PDF\left(l,w\right)dwdl(4)$

In Eq. 4 N is the total number of fibers that can bear tensile load when stretched, A is the cross-sectional area of the fiber (A= ½ a²π), and σ_single is the contribution of the individual fibers to stress. To calculate the total stress (σ_total) for a specific longitudinal stretch ΔL and the PDFs simulating different fiber arrangements in the matrix, Eq. 4 was integrated numerically using the trapezoidal rule (Chapra and Canale, 2007). The current model neglects the interfacial frictions between fibers since the normal stress is negligible compared to the tensile stress (Rizvi et al., 2012).

3 Results

3.1 SEM imaging of fibrous matrices

Figure 3 shows SEM images of cementitious matrices both formed in fault gouges and created in the laboratory through hydrothermal synthesis. SEM imaging across scales of observation shows the cementitious matrix to have a muscle-like, fibrous texture being characterized by the presence of bundles of fibrous phases. Fibers are interspersed within the matrix and form a grain lining cement that coats carbonate grains. As singly considered, the fibrous phases are made of nanowires having a nano-size diameter and length of a few microns, altogether creating disordered and entangled mats. The disordered and entangled nature of the fibril structures is observed both in the natural samples (Figure 3, top) and the samples fabricated in the laboratory (Figure 3 bottom left panel). The hydrothermal synthesis performed in the laboratory allows us to image the products of the vapor-transport reactions in a time-lapse fashion, capturing the distribution of the fibrous structures at various stages of the mineral growth. These observations at the nano- and micro-scale constitutes the basis for drawing inference on the structural parameters of the fibrous bundles and informing the statistical model.

FIGURE 3

FIGURE 3. Scanning Electron Microscope images of the fibrous matrix of natural samples from carbonate fault mirrors (top) and fibrous mats forming through hydrothermal processes (bottom, Head et al., 2018 and this study). Fibrous minerals have nano-size diameter and length of a few microns, altogether creating disordered and entangled structures; (bottom central) growth of mineral fibers through vapor-transport reactions induced via hydrothermal processes.

3.2 Modeling the stress-strain response of fibrous matrices

We modeled the role of structural parameters of fibrous matrices in controlling strength, mode of failure, and the transition of the load-deformation relationship from brittle to ductile regimes. In particular, we modeled the role of the number and length of fibrous minerals, their spatial orientation and arrangement, and the fraction of fibrous threads bearing the load. In these modeling realizations, we used the properties of fibrous minerals commonly forming cementitious matrices of man-made cement (Speziale et al., 2008) and fault gouges (Sanchez-Roa et al., 2017). The Young’s modulus, the diameter and the strain at fracture of the single fiber used for the modeling are respectively, 25 GPa, 1.12 nm, and .004. To calculate the load–displacement data, we used both a Gaussian and Gamma PDFs that are given, respectively, by Eqs. 2, 3. The different fiber arrangements and corresponding PDFs are calculated as functions of fiber length l and end-to-end separation w, while keeping the fiber diameter constant.

In Figure 3 we modeled the response of three structural arrangements of mineral fibers, from disordered and entangled (blue curve), to moderately disordered (green curve), to ordered and aligned (red curve). In modeling the role of the fiber arrangement alone, both the number of fibers in the volume unit and the properties of the single fibers are kept the same. The plot of Figure 4 shows the stress-strain relationship of a mix of randomly oriented curved fibers having a PDF with relatively wider spread along both l and w. Result show that when the microstructure is made of disordered and entangled fibers, the mode of failure appears to be ductile (blue curve). Instead, the red curve in Figure 4 describes the stress-strain response of a fibrous microstructure consisting of straight fibers aligned long the vertical direction of the sample, which is the loading direction. This arrangement has thus a spike-like PDF centered around l = L and w = 0. The stress-strain response shows that strength increases as the alignment of the fiber arrangement within the microstructure increases (from the blue to the red curve), but the microstructure of aligned fibers shows a more brittle failure (red curve). At the root of this behavior there is the alignment of the fibers, which collectively resist deformation while loaded, and then reaching failure all at the same time. The maximum (tensile) stress is sustained along to direction of elongation of the fibers.

FIGURE 4

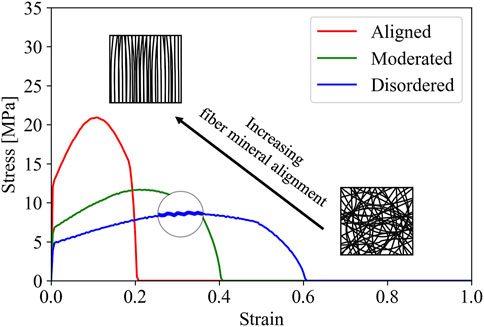
FIGURE 4. The role of the microstructural arrangement of fiber in modifying the stress-strain behavior of a fibrous microstructure that consists of fibrous minerals characterized by Young’s modulus, diameter, and strain at fracture equal to 25 GPa, 1.12 nm, and .004, respectively. The stress-strain response transitions from brittle (red curve) to ductile (blue curve) as the arrangement of fibers within the microstructure evolves from ordered and aligned to disordered and entangled. The ductile response (blue curve) exhibits a saw-tooth pattern (magnified insert), which results from the contribution to the bulk response of the load–displacement characteristic of a single fiber described in Figure 2B.

Figure 5 describes the effect of the number of fibers on the stress-strain response while keeping the microstructural arrangement of fibrous matrix constant. Just as an example the figure refers to a model of a microstructure characterized by a moderately disordered arrangement of the fibers. This modeling realization addresses the question of how to maintain the magnitude of strain (pertaining to a specific arrangement) while increasing strength at failure. The stress-strain response in Figure 5 shows that the number of fibers does not affect the strain magnitude but rather the strength of the matrix. That is, the greater the number of fibers, the higher the bearable stress.

FIGURE 5

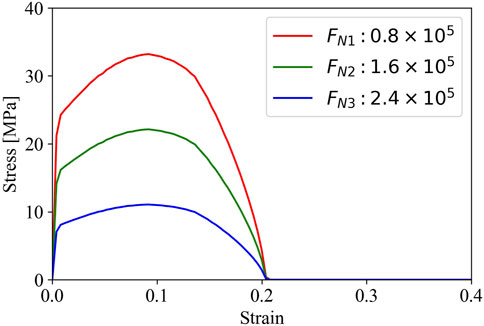
FIGURE 5. The role of the number of fibers in modifying the stress-strain behavior of a fibrous microstructure. The greater the number of fibrous minerals within the microstructure, the higher is the stress at failure. The modeling realization refers to a microstructure characterized by a moderately disordered arrangement of the fibers. The properties of the fibrous minerals used for modeling the role of the fiber number are as those used for the modeling of Figure 4.

Figure 6 shows the role of the length of fibers in controlling the stress-strain response. In these modeling realizations both type of microstructural arrangement and number of fibers is maintained constant. The model shows that the longer the fibers, the greater the resisting stress and the larger is the allowable strain. Thus, the greater is the toughness of the composite. Finally, we also used a Gamma distribution of the mineral fibers to explore the effect of the heterogeneity of arrangements of fiber minerals within the microstructure. Specifically, we explored a left-skewed distribution, entailing that the fraction of mineral fibers that bears the load are characterized by shorter length l and greater end-to-end lateral separation w. In the plot of Figure 7, the continuous lines show the stress-strain response of a fibrous matrix whose physical descriptors (l and w) follows a Gaussian distribution; conversely, the dashed lines correspond to the stress-strain response of the fiber physical descriptors that follows a Gamma distribution. Stress-strain responses are calculated for the three arrangements, from aligned to disordered, while keeping the number of fibers within the matrix constant. The results show that matrices characterized by fibrous minerals whose physical descriptors follow a left-skewed gamma exhibit greater stress at failure as well as an earlier failure compared to the normal distribution. A right-skewed distribution, characterized by longer length l and smaller end-to-end lateral separation w, would give an opposite (specular) behavior.

FIGURE 6

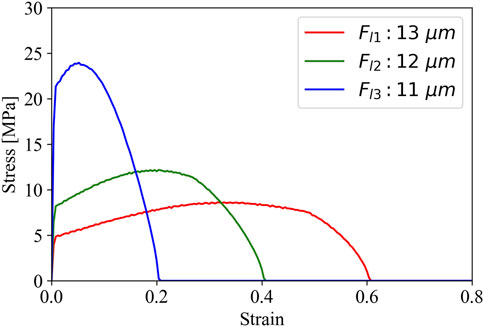
FIGURE 6. The role of the length of fibers in modifying the stress-strain behavior of a fibrous microstructure. The longer the fibers, the greater is the ability of the microstructure to accommodate strain (red curve) with the respect to microstructures characterized by shorter fibers (blue curve).

FIGURE 7

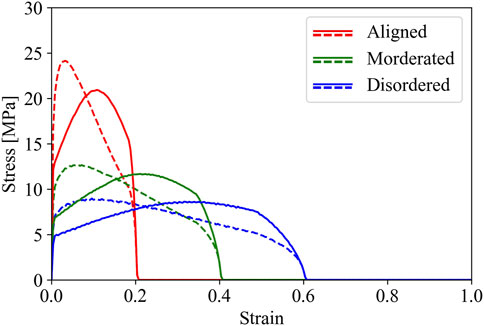
FIGURE 7. The effect of the heterogeneity of arrangements of fiber minerals within the microstructure. The plot shows the comparison between a Gaussian distribution of the arrangement of the fibrous minerals within the microstructure of cementitious matrix and the Gamma distribution. This latter refers to a left-skewed distribution, entailing that the fraction of mineral fibers that bears the load are characterized by shorter length l and greater end-to-end lateral separation w. Matrices characterized by fibrous minerals whose l and w follow a left-skewed gamma exhibit greater stress at failure as well as an earlier failure compared to matrices whose arrangement of fibers follow a normal (Gaussian) distribution.

4 Discussion

The physiochemistry of cementation is a concept crucial to rock physics. Its study is fundamental as much for predicting the influence of cement properties on the effective elastic properties of rocks as for studying the workings of the interseismic fault healing—an essential process in the seismic cycle. Traditionally, geophysicists have primarily focused the attention on how rocks respond to stress to study the mechanisms that control deformation. Nevertheless, the physics of rock deformation and failure cannot be separated from understanding the processes and designs that Earth uses to form rock cement as it provides cohesion between the grains and, as such, support to the whole rock frame. Such an understanding involves studying the authigenic growth of cementitious phases and how their arrangement at the micro- and nanoscale control the bulk stress-strain response at the macroscale.

Over the last decade, high-resolution microscopy had made great strides in revealing the textures of rock cementitious matrices, which often appear as a meshwork of fibers looking aligned, knotted, or tangled when imaged at the micron and nanoscale (Verberne et al., 2013; Verberne et al., 2014; Vanorio and Kanitpanyacharoen, 2015; Rossi et al., 2016; Viti et al., 2018). Fibrous minerals from the serpentine group, for example, are reported in the literature to form a variety of microstructures (Khilyas et al., 2019; Viti et al., 2018), from interconnected networks of ribbon-like or mesh textures to strongly aligned long fibers with preferred orientation. Even in very small percentages, short and straight fibers have been known in engineering to reduce crack propagation, and hence thave significant impacts on the strength and fracture mechanics of materials. This relates to the way load is transferred from the matrix into a fiber, which has laid the basis for fiber-reinforced materials (Banthia and Sheng, 1996; Matthews and Rawlings, 1999). SEM images reported in this study show that the matrix of rocks from fault mirrors may form mats of interwoven fibers of a calcium-magnesium aluminium phyllosilicate such as palygorskyte, coating rhombs of dolomite grains (Figure 3, top panel). Fibrous minerals can be viewed as long chain polymers being characterized by highly crystalline lattice. Palygorskyte is a 2:1 type phyllosilicate (Jones and Galan, 1988) with a structure that derives from talc-like T-O-T ribbons expanding along the axis of the fibers. Mats of these fibrous minerals form as a diagenetic product of the hydrothermal alteration of alkaline host rocks, from basaltic glass to carbonates, growing either on the outer surfaces of partially dissolved grains or within the hollow space formed by dissolution of the grain cores (Murray et al., 2011). These mineral phases are generally found in fault gouges, volcanic areas, and subduction systems that are characterized by hydrothermal circulation of fluids with an alkaline and hyper-alkaline chemistry. Alkaline earth metals and alkali metals (Na⁺, K⁺, Li⁺, Ca⁺⁺, Ba⁺⁺, NH4⁺, H3O⁺) are small, positive ions, which by balancing the negative charge of Al³⁺⁺ in IV-fold coordination act as crosslinking agents forming long chain of molecules in the lattice (Wang and Wang, 2019). In chemistry and engineering, long chains of aluminosilicates are commonly referred as geopolymers because of their polymeric structures as well as the resemblance with rock-forming phyllosilicate minerals of geological origin (Davidovits, 1991). The recent increase in spatial and temporal resolution of imaging is allowing us to study the structure of nanomineral phases and characterize their chemistry (Hochella et al., 2008; Caraballo et al., 2015). Nanograins are reported by Siman-Tov et al. (2013) to deform through bulk ductility, and hypothesized to be critical in controlling the frictional behavior of faults. More recently, laboratory friction experiments from velocity-step tests (Sánchez-Roa et al., 2017) showed that the friction coefficients of fibrous silicates, such as palygorskyte and sepiolite, are greater than their planar, or sheet-like equivalents, namely talc and saponite (Moore and Lockner, 2011; Sánchez-Roa et al., 2017). No explanation has been produced as to why fibrous minerals exhibit higher friction coefficient. Similarly, the mechanisms for the formation of nanograins are poorly understood, sometimes being ascribed to reactions triggered by frictional heating (Han et al., 2007; Han et al., 2010; De Paola et al., 2011) or shock waves (Sammis and Ben-Zion, 2008) resulting from the fast sliding of faults during an earthquake.

Fluids in the crust (National Research Council, 1990) have traditionally been thought to trigger reactions in the subsurface and serve as natural cementation agents. Hydrothermal water (HTW)—that is, water at 100°C < T < 250°C, holds interesting properties (Uematsu and Frank, 1980; Marshall and Franck, 1981; Sengers and Watson, 1986; Cengel and Boles, 2002), especially when operating as a mixture of high-temperature liquid and vapor. These conditions are attained at PT of hydrothermal environments operating exactly in the liquid–vapor coexistence area. The coexistence ensures that H₂O(l) constantly evaporates, and H₂O(g) constantly condenses, allowing the pore fluid pressure of a closed porous system to be generated autogenously.

In terms of physicochemical properties, the liquid–vapor coexistence of water within the subsurface makes HTW a highly interesting reaction medium that takes advantage of both the properties of liquid water and water vapor. The properties of liquid water undergo critical changes with temperature, which are a direct consequence of the breaking down the hydrogen bonds network of water (Figure 8). The ionic product, K_w, increases exhibiting its maximum between 150°C and 250°C—that is, the maximum concentrations of H+ and OH- ions in water. Within the same temperature range, the dielectric constant, ε, reaches values typical of organic solvents (Franck, 1978; Unterlass, 2017). Thus, hydrothermal water functions as a unique solvent capable of breaking the chemical bonds of silicate chains through hydrolysis (dissolution phase)—a process that if occurring in a fractured rock may lead to weakening and stress corrosion (Atkinson, 1980). At the same time, the co-presence in the system of the vapor phase triggers vapor-transport reactions. Bunsen was the first who observed and described the process (Bunsen et al., 1852), noticing the natural formation of crystalline Fe₂O₃ in presence of volcanic gases containing water vapor and gaseous hydrogen chloride. A pressurized gaseous phase functions as a transport agent, carrying the products of the hydrolysis while promoting reactions that repeatedly combine unit-base molecules to form chains of new silicate minerals (polycondensation phase). The polycondensation reactions are thus expected to follow the phase of the hydrolysis of silicates to first transport, and then deposit, the solute elsewhere in the form of crystalline phases (Unterlass, 2017). Not surprisingly, hydrothermal synthesis is the most widely used solid-liquid technique for fabricating nanomaterials with high crystallinity and well-defined morphology from an aqueous solution at or above the boiling point of water (Byrappa and Yoshimura, 2001; Brunner, 2014), and proposed mechanism for crystal growth (Hartman, 1973; Laudise, 1973 p. 162-165). In turn, crystal growth requires a substrate (i.e., crystal seeds) for nucleation, which is influenced by the crystallographic orientation of the substrate grain with respect to the fracture wall (Lander and Laubach, 2015; Fisher and Brantley, 1992).

FIGURE 8

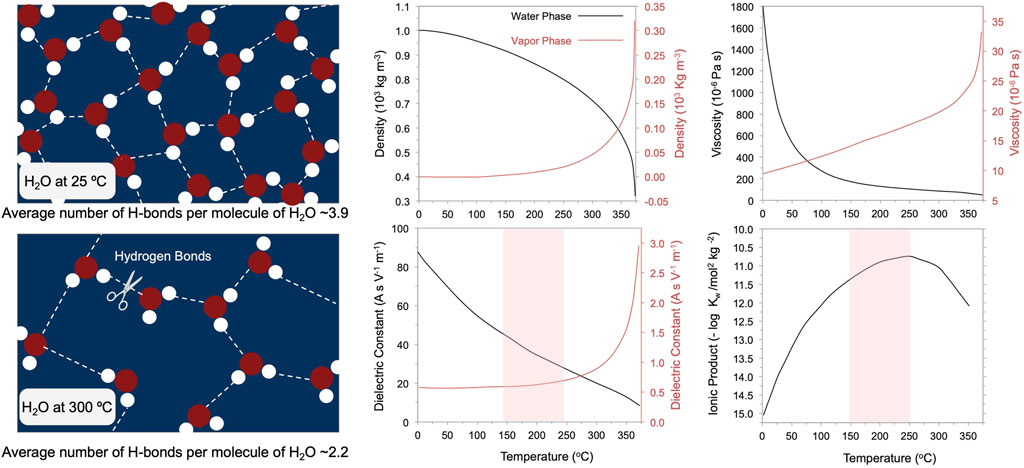
FIGURE 8. The change of the physicochemical properties of liquid water (black curve) and water vapor (red curve) as a function of temperature. Density and viscosity of liquid water decrease with temperature as the number of hydrogen bonds per molecule of water decreases from 3.9 at 25°C to 2.2 at 300°C. The ionic product, K_w, reaches its maximum between 150°C and 250°C (light red zone) when the dielectric constant, ε, reaches values that are typical of organic solvents, namely methanol and ethanol (from Unterlass, 2017 modified). Data are from Sengers and Watson (1986) and Uematsu and Frank (1980).

In that regard, it is interesting to note that just as fibrous bundles of collagen are produced to heal scratched skin through the activity of a vascular system that transports nutrients, oxygen, carbon dioxide and blood cells, so fibrous cementitious microstructures can be autonomously created by the activity of hydrothermal fluids healing aluminosilicates that are mechanically pulverized by active faults.

The laboratory experiments reported in this study made use of hydrothermal water to promote the growth of fibrous mineral phases. These phases are characterized by nano-size diameter and length of a few microns, altogether creating disordered and entangled mats of fibrous bundles as those found in natural samples. It is unclear at this stage of research as to whether turbulence of the superheated flow within the pore scale is responsible for the growth of spaghetti-like structures, forming eventually disordered and entangled structures. Similarly, the amorphous (gel-like) material between the fibrous bundles (Caraballo et al., 2015; Sánchez-Roa et al., 2017) requires structural and chemical characterization. We are only at the beginning of nanogeoscience characterization, and further research is needed in this area. So far, high-resolution imaging of the micro- and nano-geometries of these mineral phases allowed us to establish a structure–mechanics interdependence between structural parameters of the fibrous structures and the bulk mechanical response. As the fibrous microstructure evolves from ordered and aligned (Figure 4, red curve) to disordered and entangled (Figure 4, blue curve), the mechanical response of the fibrous composite experiences a transition from brittle to ductile behavior. This result shows that the microstructural arrangement of fibers strongly controls the mechanical behavior of the whole. Compared to the ordered and aligned arrangement, the disordered and entangled microstructure also exhibits lower strength at failure (Figure 4). Nevertheless, strength increases in magnitude as the number of fibers within the microstructure increases (Figure 5). Conversely, the longer the fibers the larger strain that the matrix can accommodate (Figure 6).

Overall, these results show that the mechanical response of a fibrous matrix depends not only on the elastic modulus of the individual mineral fibers and its fraction quantity as traditionally portrayed in the literature (Mavko et al., 2009), but also on the arrangement of the fibers within the matrix. Specifically, the deformation of an entangled arrangement of fibers involves three stages (Figures 2A, B). The first stage is characterized by fibers resting in an undeformed state; they are curved and intertwined before being loaded. As such, they do not provide any mechanical resistance (Stage 1). When a load is applied, each single fiber straightens first before beginning to bear the load (Figure 2A, central panel, red fiber). At this stage (Stage 2, Figure 2B), the fiber begins to resist the deformation, ε₀ < ε < ε_f, leading the stress on the individual fiber to increase. Upon reaching the failure point (Figure 2B), ε > ε_f, the fiber breaks, leading the stress to drop (Stage 3). Only when failure is reached, a new fiber (or bundle of fibers) straightens up, thus bearing the load. Such stress-strain behavior suggests that, collectively, entangled fibers undergoing loading behave as they participated in a team relay race—that is, each fiber (or bundle of fibers) bears stress until reaching failure, when it then passes on the baton to a different group of fibers that take over to continue resisting the deformation. In such a scenario, the strands of an entangled fibrous matrix go through the three deformation stages gradually and sequentially (Figure 2), which comprise discrete and yet continuous trends of small stress resistances and stress drops (Figure 4, magnified insert). The envelope of these single resistance-stress drops provides a ductile behavior capable of accommodating a larger strain. Conversely, arrangements of orderly aligned fibrous structures bear the load simultaneously. The fibrous strands resist deformation all at the same time, thus failing all at once. That leads to higher strength but brittle deformation. Just as an example, wood is an orthotropic material exhibiting this type of behavior.

The results of this study have both a fundamental and applied value. The study represents a first attempt to quantitatively describe the microstructure-property relations of grain-coating fibrous phases on the mechanics of rocks having a fibrous microstructure. This is an aspect traditionally neglected by most of the mixing schemes used to compute the elastic and mechanical properties of rocks. Because the presence of fibrous minerals in the matrix of rocks from tectonic and volcanic margins (Louderback, 1942; Schleicher, et al., 2006; Verberne et al., 2014; Vanorio and Kanitpanyacharoen, 2015; Viti et al., 2018; Harris, 2017; Moore et al., 2018), the characterization of their structural parameters at the micro- and nano-scale is also fundamental to the understanding of the resistance of healed caprocks or faut gouges, including the dependence of friction on the “rate” of sliding and on the continually accrued slip—that is, the pace of the evolution of the ‘state’ of the interface in response to changes in slip rate (Dieterich, 1979). Rate-and-state friction (RSF) (Dieterich, 1979) has been commonly used to provide an empirical relation between the measured coefficient of friction (μ), the rate of deformation (V), and state (θ). The relation is characterized by two proportionality constants—the parameters a and b—representing, respectively, the magnitudes of the instantaneous and time-dependent evolution effects. While these coefficients are thought to represent the material properties, their intrinsic nature is hidden to us. The RSF framework is in fact recognized to provide little physical basis for the extrapolation of laboratory results to the scales and conditions of natural fault systems. While it is acknowledged that friction on the contact surface between sliding bodies depends on the ratio between the applied normal (F_n) and tangential shear (F_s) forces, the adhesion theory (Amontons, 1699) portrays that friction depends on a real contact area, being described as made of a population of microcontacts or asperities (Bowden and Tabor, 1950). Thus, microphysics-based models have been proposed as an alternative to classical RSF for interpreting laboratory and field observations (Van den Ende et al., 2018), which require knowledge of the micro- and nanogeometry of structural-rock samples to calculate the resistance of an interface to sliding. The applied value of this study lies in the possibility to further understand the physical properties of the brittle-ductile transitions—from large earthquakes occurring as sudden slip events expressing a catastrophic (brittle) failure to slow-slip or clusters of many small earthquakes characterizing regions of the crust that benignly creep for long periods of time (Obara K., 2002; Rogers and Dragert, 2003; Brenguier, et al., 2008; Chen and Bürgmann, 2017; Harris, 2017). There are in fact segments of active margins worldwide, from the Cascadia subduction zone, to the San Andreas strike-slip system, being traditionally associated with fibrous mineral phases (Louderback, 1942; Schleicher, et al., 2006; Kirby et al., 2014; Harris, 2017; Moore et al., 2018) so this study advances new knowledge of understanding the role of fibrous microstructures in controlling brittle-to-ductile rheological behaviors, and possibly, slow slip events (Voss et al., 2018; Nuyen and Schmidt, 2021). To that end, we are currently using the in-house built acoustic emissions setup to perform experiments on the deformation of controlled fibrous arrangements at the micro and nanoscale to study their macroscopic deformation behavior and how failure of such microstructure translates into slip modes. Such integrated knowledge is functional to enhance our understanding of the mechanical response of materials absorbing strain energy, which is fundamental as much for studying rocks along subduction zones and devising durable geomaterials for engineering purposes.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

TV conceived and supervised the research project. JC performed the modeling for application to Earth materials. TV and SS-T acquired the microscopic images. TV wrote the manuscript, and JC SS-T, and AN contributed to discussion and revision.

Funding

This work was supported by the Stanford Rock Physics Affiliates Program; the School of Earth, Energy, and Environmental Sciences, and National Science Foundation NSF Award # 2149529.

Acknowledgments

Part of the work was performed at the Stanford Mineral and Microchemical Analysis Facility Stanford Nano Shared Facilities as supported by the National Science Foundation under the award ECCS-1542152. We thank Dale H. Burns for his valuable assistance during the acquisition of the images through Scanning Electron Microscopy and the chemical characterization and elemental analysis of the samples through Energy Dispersive Spectroscopy. We also thank the center for nanoscience and nanotechnology in the Hebrew University of Jerusalem, for generous electron microscopy assistance.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allan, A., Clark, A., Vanorio, T., Kanitpanyacharoen, W., and Wenk, H. (2016). On the evolution of the elastic properties of organic-rich shale upon pyrolysis-induced thermal maturation. Geophysics 81 (3). doi:10.1190/geo2015-0514.1

CrossRef Full Text | Google Scholar

Altaf, A. A., Ahmed, M., Hamayun, M., Kausar, S., Waqar, M., and Badshah, A. (2020). Titania nano-fibers: A review on synthesis and utilities. Inorganica Chim. Acta 501, 119268. ISSN 0020-1693. doi:10.1016/j.ica.2019.119268

CrossRef Full Text | Google Scholar

Atkinson, B. K. (1979). A fracture mechanics study of subcritical tensile cracking of quartz in wet environments. Pure Appl. Geophys. 117, 1011–1024. doi:10.1007/bf00876082

CrossRef Full Text | Google Scholar

Atkinson, B. K. (1980). Stress corrosion and the rate-dependent tensile failure of a fine-grained quartz rock. Tectonophysics 65, 281–290. doi:10.1016/0040-1951(80)90078-5

CrossRef Full Text | Google Scholar

Banthia, N., and Sheng, J. (1996). Fracture toughness of micro-fiber reinforced cement composites. Cem. Concr. Compos. 18 (4), 251–269. doi:10.1016/0958-9465(95)00030-5

CrossRef Full Text | Google Scholar

Barhoum, A., Bechelany, M., Salam, A., and Makhlouf, H. (2019). Handbook of Nanofibers, doi:10.1007/978-3-319-53655-2

CrossRef Full Text | Google Scholar

Barnard, A. S., and Guo, H. (2012). Nature’s nanostructures. Singapore: Pan Stanford Publishing.

Google Scholar

Bergaya, F., Detellier, C., and Lambert, J.-F. (2013). “Lagaly introduction to clay–polymer nanocomposites (CPN),” in Handbook of clay science. Editors F Bergaya, and G Lagaly, 5, 1.

CrossRef Full Text | Google Scholar

Binnewies, M., Glaum, R., Schmidt, M., and Schmidt, P. (2012). Chemical vapor transport reactions. Berlin: De Gruyter.

Google Scholar

Binnewies, M., Glaum, R., Schmidt, M., and Schmidt, P. (2013). Chemical vapor transport reactions – a historical review. Z. Anorg. Allg. Chem. 639, 219–229. doi:10.1002/zaac.201300048

CrossRef Full Text | Google Scholar

Bowden, F. P., and Tabor, D. (1950). The friction and lubrication of solids. Oxford: Clarendon Press.

Google Scholar

Brenguier, F., Campillo, M., Hadziioannou, C., Shapiro, N. M., Nadeau, R. M., and Larose, E. (2008). Postseismic relaxation along the San Andreas fault at Parkfield from continuous seismological observations. Science 321, 1478–1481. doi:10.1126/science.1160943

PubMed Abstract | CrossRef Full Text | Google Scholar

Brigattia, M. F., Galan, E., and Theng, B. K. G. (2013). “Structure and mineralogyof clay minerals,” in Handbook of clay science. Editors F Bergaya, and G Lagaly (Elsevier), 5, 1.

CrossRef Full Text | Google Scholar

Brunner, G. (2014). Hydrothermal and supercritical water processes, 5. United Kingdom: Elsevier Science & Technology

Google Scholar

Bunsen, R., Boutron-Charlard, , Henry, O., Barreswil, , Rilliet, , and Pohl, J. J. (1852). Volcanic exhalations, 1852. J. Prakt. Chem. 56, 53–64. doi:10.1002/prac.18520560106

CrossRef Full Text | Google Scholar

Byrappa, K., and Yoshimura, M. (2001). A Technology for Crystal Growth and Materials Processing. Handbook of hydrothermal technology. William Andrew.

Google Scholar

Caraballo, M., Michel, F., and Hochella, M. (2015). The rapid expansion of environmental mineralogy in unconventional ways: Beyond the accepted definition of a mineral, the latest technology, and using nature as our guide. Am. Mineralogist 100 (1), 14–25. doi:10.2138/am-2015-4749

CrossRef Full Text | Google Scholar

Çengel, Y. A., and Boles, M. A. (2002). Thermodynamics: An engineering approach. 4th edn. Boston: McGraw-Hill.

Google Scholar

Chapra, S. C., and Canale, R. P. (2007). Numerical methods for engineers. 5th Edition. New York: McGraw-Hill.

Google Scholar

Chen, K. H., and Bürgmann, R. (2017). Creeping faults: Good news, bad news? Rev. Geophys. 55, 282–286. doi:10.1002/2017RG000565

CrossRef Full Text | Google Scholar

Davidovits, J. (1991). Geopolymers: Inorganic polymeric new materials. J. Therm. Analysis 37, 1633–1656. doi:10.1007/bf01912193

CrossRef Full Text | Google Scholar

De Paola, N., Hirose, T., Mitchell, T., Di Toro, G., Viti, C., and Shimamoto, T. (2011). Fault lubrication and earthquake propagation in thermally unstable rocks. Geology 39 (1), 35–38. doi:10.1130/g31398.1

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1979). Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. 84 (B5), 2161–2168. doi:10.1029/JB084iB05p02161

CrossRef Full Text | Google Scholar

Dvorkin, J. (1997). “Cement among grains in rocks,” in IUTAM symposium on mechanics of granular and porous materials. Solid mechanics and its applications. Editors N. A. Fleck, and A. C. F. Cocks (Dordrecht: Springer), 53. doi:10.1007/978-94-011-5520-5_17

CrossRef Full Text | Google Scholar

Dvorkin, J., Nur, A., and Yin, H. (1994). Effective properties of cemented granular materials. Mech. Mater. 18 (4), 351–366. ISSN 0167-6636. doi:10.1016/0167-6636(94)90044-2

CrossRef Full Text | Google Scholar

Fisher, D. M., and Brantley, S. L. (1992). Models of quartz overgrowth and vein formation: Deformation and episodic fluid flow in an ancient subduction zone. J. Geophys. Res. 97 (B13), 20043–20061. doi:10.1029/92JB01582

CrossRef Full Text | Google Scholar

Franck, E. U. (1978). “Experimental investigations of fluids of high pressures and elevated temperatures,” in High pressure chemistry H. Kelm (Dordrecht, The Netherlands: Reidel), 221.

CrossRef Full Text | Google Scholar

Fyfe, W. S., Price, N. J., and Thompson, A. B. (1978). Fluids in the earth's crust. Amsterdam: North Holland.

Google Scholar

Han, R., Hirose, T., and Shimamoto, T. (2010). Strong velocity weakening and powder lubrication of simulated carbonate faults at seismic slip rates. J. Geophys. Res. 115, B03412. doi:10.1029/2008JB006136

CrossRef Full Text | Google Scholar

Han, R., Shimamoto, T., Hirose, T., Ree, J.-H., and Ando, J.-i. (2007). Ultralow friction of carbonate faults caused by thermal decomposition. Science 316 (5826), 878–881. doi:10.1126/science.1139763

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, R. A. (2017). Large earthquakes and creeping faults. Rev. Geophys. 55, 169–198. doi:10.1002/2016RG000539

CrossRef Full Text | Google Scholar

Hartman, P. (1973). “Crystal growth: An introduction,” in North-Holland series in crystal growth (Amsterdam-London: North-Holland Publishing Company), 1.

Google Scholar

Head, D., Vanorio, T., and Clark, A. (2018). Elastic softening of limestone upon decarbonation with episodic CO2 release. J. Geophys. Res. Solid Earth 123 (9), 7404–7420. doi:10.1029/2018JB015733

CrossRef Full Text | Google Scholar

Hladký, E., Kuc̆era, M., and Majerová, K. (1966). Influence of the dielectric constant on the rate of solution polymerization of trioxan. Polymer 7 (12), 587–594. ISSN 0032-3861. doi:10.1016/0032-3861(66)90015-2

CrossRef Full Text | Google Scholar

Hochella, M. F., Lower, S. K., Maurice, P. A., Penn, R. L., Sahai, N., Sparks, D. L., et al. (2008). Nanominerals, mineral nanoparticles, and Earth systems. Science 319 (5870), 1631–1635. doi:10.1126/science.1141134

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, B. F., and Galán, E. (1988). “Sepiolite and palygorskite,” in Reviews in mineralogy. Hydrous phyllosilicates. Editor S. W. Bailey (Michigan: Mineralogical Society of America), 19, 631.

CrossRef Full Text | Google Scholar

Karner, S. L., Marone, C., and Evans, B. (1997). Laboratory study of fault healing and lithification in simulated fault gouge under hydrothermal conditions. Tectonophysics 277 (1–3), 41–55. ISSN 0040-1951. doi:10.1016/S0040-1951(97)00077-2

CrossRef Full Text | Google Scholar

Khilyas, I. V., Sorokina, A. V., Elistratova, A. A., Markelova, M. I., Siniagina, M. N., Sharipova, M. R., et al. (2019). Microbial diversity and mineral composition of weathered serpentine rock of the Khalilovsky massif. PLOS ONE 14, 02259299–e226014. doi:10.1371/journal.pone.0225929

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirby, S. H., Wang, K., and Brocher, T. M. (2014). A large mantle water source for the northern san Andreas fault system: A ghost of subduction past. Earth Planet Sp. 66, 67. doi:10.1186/1880-5981-66-67

CrossRef Full Text | Google Scholar

Lade, P. V., and Overton, D. D. (1989). Cementation effects in frictional materials. J. Geotechnical Eng. 115115 (10), 137310–141387. doi:10.1061/(asce)0733-9410(1989)115:10(1373)

CrossRef Full Text | Google Scholar

Lander, R. H., and Laubach, S. E. (2015). Insights into rates of fracture growth and sealing from a model for quartz cementation in fractured sandstones. Geol. Soc. Am. Bull. 127 (3-4), 516–538. doi:10.1130/B31092.1

CrossRef Full Text | Google Scholar

Laubach, S. E., Lander, R. H., Criscenti, L. J., Anovitz, L. M., Urai, J. L., Pollyea, R. M., et al. (2019). The role of chemistry in fracture pattern development and opportunities to advance interpretations of geological materials. Rev. Geophys. 57, 1065–1111. doi:10.1029/2019RG000671

CrossRef Full Text | Google Scholar

Laudise, R. A. (1973). in Hydrothermal growth in crystal growth; an introduction. Editor P. Hartman (New York: NorthHolland/Elsevier), 210.

Google Scholar

Li, Y. G., Chen, P., Cochran, E. S., Vidale, J. E., and Burdette, T. (2006). Seismic velocity variations on the San Andreas fault caused by the 2004 M6 Parkfield Earthquake and their implications. BSSA 96 (4B), S349–S363. doi:10.1785/0120050803, No.

CrossRef Full Text | Google Scholar

Liu, Y., and Szlufarska, I. (2012). Chemical origins of frictional aging. Phys. Rev. Lett. 109, 186102. doi:10.1103/PhysRevLett.109.186102

PubMed Abstract | CrossRef Full Text | Google Scholar

Louderback, G.D. (1942). Faults and earthquakes, Bull. Seismol. Soc. Am., 32 (4), 305–330.

Google Scholar

Marone, C. (1998a). Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 26 (1), 643–696. doi:10.1146/annurev.earth.26.1.643

CrossRef Full Text | Google Scholar

Marone, C. (1998b). The effect of loading rate on static friction and the rate of fault healing during the earthquake cycle. Nature 391, 69–72. doi:10.1038/34157

CrossRef Full Text | Google Scholar

Marshall, W. L., and Franck, E. (1981). Ion product of water substance, 0–1000 C, 1–10, 000 bars new international formulation and its background. J. Phys. Chem. Ref. Data 10, 295–304. doi:10.1063/1.555643

CrossRef Full Text | Google Scholar

Matthews, F. L., and Rawlings, R. D. (1999). Composite materials: Engineering and science. Cambridge, England: Woodhead Publishing.

Google Scholar

Mavko, G., Mukerji, T., and Dvorkin, J. (2009). Rock physics handbook: Tools for seismic analysis in porous media. Cambridge: Cambridge University Press.

Menzel, M. D., Urai, J. L., Ukar, E., Hirth, G., Schwedt, A., Kovacs, A., et al. (2022). Ductile deformation during carbonation of serpentinized peridotite. Nat. Commun. 13, 3478. doi:10.1038/s41467-022-31049-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, D. E., and Lockner, D. A. (2011). Frictional strengths of talc-serpentine and talc-quartz mixtures. J. Geophys. Res. 116, B01403. doi:10.1029/2010JB007881

CrossRef Full Text | Google Scholar

Moore, D. E., McLaughlin, R. J., and Lienkaemper, J. J. (2018). Serpentinite-rich gouge in a creeping segment of the Bartlett Springs Fault, northern California: Comparison with SAFOD and implications for seismic hazard. Tectonics 37, 4515–4534. doi:10.1029/2018TC005307

CrossRef Full Text | Google Scholar

Morgan, J. K. (2004). Particle dynamics simulations of rate- and state-dependent frictional sliding of granular gouge. Pure Appl. Geophys. 161, 1877–1891. doi:10.1007/s00024-004-2537-y

CrossRef Full Text | Google Scholar

Muhuri, S., Dewers, T., Thurman, S., and Ze’ev, R. (2003). Interseismic fault strengthening and earthquake-slip instability: Friction or cohesion? Geology 31, 881. doi:10.1130/G19601.1

CrossRef Full Text | Google Scholar

Murray, H. H., Pozo, M., and Galan, E. (2011). An introduction to palygorskite and sepiolite deposits. Develop. Clay. Science 3. doi:10.1016/B978-0-444-53607-5.00004-9

CrossRef Full Text | Google Scholar

Nakata, N., and Snieder, R. (2011). Near-surface weakening in Japan after the 2011 Tohoku-Oki earthquake. Geophys. Res. Lett. 38, L17302. doi:10.1029/2011gl048800

CrossRef Full Text | Google Scholar

National Research Council (1990). The role of fluids in crustal processes. Washington, DC: The National Academies Press. doi:10.17226/1346

CrossRef Full Text | Google Scholar

Niemeijer, A. R., Spiers, C. J., and Bos, B. (2002). Compaction creep of quartz sand at 400 – 600°C: Experimental evidence for dissolution-controlled pressure solution. Earth Planet. Sci. Lett. 195, 261–275. doi:10.1016/s0012-821x(01)00593-3

CrossRef Full Text | Google Scholar

Nuyen, C. P., and Schmidt, D. A. (2021). Filling the gap in Cascadia: The emergence of low-amplitude long-term slow slip. Geochem. Geophys. Geosystems 22, e2020GC009477. doi:10.1029/2020GC009477

CrossRef Full Text | Google Scholar

Obara, K. (2002). Nonvolcanic Deep Tremor Associated with Subduction in Southwest Japan. Science 296 (5573), 1679–1681. doi:10.1126/science.1070378

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Hare, D. (2001). “Hydrothermal synthesis,” in Subhash mahajan, patrick veyssière, encyclopedia of materials: Science and technology. Editors K. H. Jürgen Buschow, R. W. Cahn, M. C. Flemings, B Ilschner, and E. J. Kramer (Elsevier), 3989. doi:10.1016/B0-08-043152-6/00701-4

CrossRef Full Text | Google Scholar

Olsen, M. P., Scholz, C. H., and Léger, A. (1998). Healing and sealing of a simulated fault gouge under hydrothermal conditions: Implications for fault healing. J. Geophys. Res. 103 (B4), 7421–7430. doi:10.1029/97JB03402

CrossRef Full Text | Google Scholar

Pei, S., Niu, F., Ben-Zion, Y., Sun, Q., Liu, Y., Xue, X., et al. (2019). Seismic velocity reduction and accelerated recovery due to earthquakes on the Longmenshan fault. Nat. Geosci. 12, 387–392. doi:10.1038/s41561-019-0347-1

CrossRef Full Text | Google Scholar

Peng, Z., and Ben-Zion, Y. (2006). Temporal changes of shallow seismic velocity around the Karadere–Duzce branch of the North Anatolian fault and strong ground motion. Pure Appl. Geophys. 163, 567–600. doi:10.1007/s00024-005-0034-6

CrossRef Full Text | Google Scholar

Ramsay, J. (1980). The crack–seal mechanism of rock deformation. Nature 284, 135–139. doi:10.1038/284135a0

CrossRef Full Text | Google Scholar

Richardson, E., and Marone, C. (1999). Effects of normal stress vibrations on frictional healing. J. Geophys. Res. 104 (28859–28), 28859–28878. doi:10.1029/1999jb900320

CrossRef Full Text | Google Scholar

Rizvi, M. S., Kumar, P., Katti, D. S., and Pal, A. (2012). Mathematical model of mechanical behavior of micro/nanofibrous materials designed for extracellular matrix substitutes. Acta Biomater. 8 (11), 4111–4122. doi:10.1016/j.actbio.2012.07.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, G., and Dragert, H. (2003). Episodic tremor and slip on the Cascadia subduction zone: The chatter of silent slip. Science 300, 1942–1943. doi:10.1126/science.1084783

PubMed Abstract | CrossRef Full Text | Google Scholar

Rossi, M., Nestola, F., Ghiara, M. R., and Capitelli, F. (2016). Fibrous minerals from Somma-Vesuvius volcanic complex. Min. Pet. 110, 471–489. doi:10.1007/s00710-015-0422-2

CrossRef Full Text | Google Scholar

Ryan, K. L., Rivière, J., and Marone, C. (2018). The role of shear stress in fault healing and frictional aging. J. Geophys. Res. Solid Earth 123 (10), 10 479–510, 495. 479– 10. doi:10.1029/2018JB016296

CrossRef Full Text | Google Scholar

Sammis, C. G., and Ben-Zion, Y. (2008). Mechanics of grain-size reduction in fault zones. J. Geophys. Res. 113, B02306. doi:10.1029/2006JB004892

CrossRef Full Text | Google Scholar

Sánchez-Roa, C., Faulkner, D. R., Boulton, C., Jimenez-Millan, J., and Nieto, F. (2017). How phyllosilicate mineral structure affects fault strength in Mg-rich fault systems. Geophys. Res. Lett. 44, 5457–5467. doi:10.1002/2017GL073055

CrossRef Full Text | Google Scholar

Sawazaki, K., Sato, H., Nakahara, H., and Nishimura, T. (2009). Time-lapse changes of seismic velocity in the shallow ground caused by strong ground motion shock of the 2000 Western Tottori earthquake, Japan, as revealed from coda deconvolution analysis. Bull. Seismol. Soc. Am. 99, 352–366. doi:10.1785/0120080058

CrossRef Full Text | Google Scholar

Schleicher, A. M., van der Pluijm, B. A., Solum, J. G., and Warr, L. N. (2006). Origin and significance of clay-coated fractures in mudrock fragments of the SAFOD borehole (Parkfield, California). Geophys. Res. Lett. 33, L16313. doi:10.1029/2006GL026505

CrossRef Full Text | Google Scholar

Schmidt, P., Binnewies, M., Glaum, R., and Schmidt, M. (2013). “Chemical vapor transport reactions–methods, materials, modeling,” in Advanced topics on crystal growth, London. Editor S. O. Ferreira (London: IntechOpen). doi:10.5772/55547

CrossRef Full Text | Google Scholar

Sengers, J., and Watson, J. T. R. (1986). Improved international formulations for the viscosity and thermal conductivity of water substance. J. Phys. Chem. Ref. Data 15, 1291–1314. doi:10.1063/1.555763

CrossRef Full Text | Google Scholar

Shervais, J. W., Choi, S. H., Sharp, W. D., Ross, J., Zoglman-Schuman, M., and Mukasa, S. B. (2011). Serpentinite matrix mélange: Implications of mixed provenance for mélange formation: Special Paper of the Geological Society of America. Geol. Soc. Am. doi:10.1130/2011.2480(01

CrossRef Full Text | Google Scholar

Siman-Tov, S., Aharonov, E., Sagy, A., and Emmanuel, S. (2013). Nanograins form carbonate fault mirrors. Geology 41 (6), 703–706. doi:10.1130/G34087.1

CrossRef Full Text | Google Scholar

Späth, M., Urai, J. L., and Nestler, B. (2022). Incomplete crack sealing causes localization of fracturing in hydrothermal quartz veins. Geophys. Res. Lett. 49, e2022GL098643. doi:10.1029/2022GL098643

CrossRef Full Text | Google Scholar

Speziale, S., Jiang, F., Mao, Z., Monteiro, P. J. M., Wenk, H-R., Duffy, T. S., et al. (2008). Single-crystal elastic constants of natural ettringite. Cem. Concr. Res. 38, 885–889. doi:10.1016/j.cemconres.2008.02.004

CrossRef Full Text | Google Scholar

Spiers, C. J., De Meer, S., Niemeijer, A. R., and Zhang, X. (2004). “Kinetics of rock deformation by pressure solution and the role of thin aqueous films,” in Physicochemistry of water in geological and Biological systems. Editor S. Nakashima (Tokyo: Univ. Acad. Press), 129.

Google Scholar

Suwannasri, K., Vanorio, T., and Clark, A. (2018). Monitoring the changes in the microstructure and the elastic and transport properties of Eagle Ford marl during maturation. Geophysics 83 (5), MR263–MR281. doi:10.1190/geo2017-0797.1

CrossRef Full Text | Google Scholar

Tenthorey, E., Cox, S. F., and Todd, H. F. (2003). Evolution of strength recovery and permeability during fluid-rock reaction in experimental fault zones. Earth Planet. Sci. Lett. 206 (1–2), 161–172. doi:10.1016/s0012-821x(02)01082-8

CrossRef Full Text | Google Scholar

Tullis, T. E. (2015). “Mechanisms for friction of rock at earthquake slip rates,” in Treatise on geophysics. Editor G. Schubert 2nd ed. (Oxford: Elsevier), 139.

CrossRef Full Text | Google Scholar

Uematsu, M., and Frank, (1980). Static dielectric constant of water and steam. J. Phys. Chem. Ref. Data 9, 1291–1306. doi:10.1063/1.555632

CrossRef Full Text | Google Scholar

Unterlass, M. M. (2017). Geomimetics and extreme biomimetics inspired by hydrothermal systems—what can we learn from nature for materials synthesis? Biomimetics 2, 8. doi:10.3390/biomimetics2020008

PubMed Abstract | CrossRef Full Text | Google Scholar

Urai, J. L., Williams, P. F., and van Roermund, H. L. M. (1991). Kinematics of crystal growth in syntectonic fibrous veins. J. Struct. Geol. 13 (7), 823–836. doi:10.1016/0191-8141(91)90007-6

CrossRef Full Text | Google Scholar

Van den Ende, M. P. A., Chen, J., Ampuero, J.-P., and Niemeijer, A. R. (2018). A comparison between rate-and-state friction and microphysical models, based on numerical simulations of fault slip. Tectonophysics 733, 273–295. ISSN 0040-1951. doi:10.1016/j.tecto.2017.11.040

CrossRef Full Text | Google Scholar

Vanorio, T., and Kanitpanyacharoen, W. (2015). Rock physics of fibrous rocks akin to Roman concrete explains uplifts at Campi Flegrei Caldera. Science 349 (6248), 617–621. doi:10.1126/science.aab1292

PubMed Abstract | CrossRef Full Text | Google Scholar

Verberne, B. A., de Bresser, J. H. P., Niemeijer, A. R., Spiers, C. J., de Winter, D. A. M., and Plümper, O. (2013). Nanocrystalline slip zones in calcite fault gouge show intense crystallographic preferred orientation: Crystal plasticity at sub-seismic slip rates at 18–150 °C. Geology 41 (8), 863–866. doi:10.1130/G34279.1

CrossRef Full Text | Google Scholar

Verberne, B. A., Plümper, O., de Winter, D. A. M., and Spiers, C. J. (2014). Superplastic nanofibrous slip zones control seismogenic fault friction. SCIENCE 346 (6215), 1342–1344. doi:10.1126/science.1259003

PubMed Abstract | CrossRef Full Text | Google Scholar

Vidale, J. E., and Li, Y. G. (2003). Damage to the shallow Landers fault from the nearby Hector Mine earthquake. Nature 421, 524–526. doi:10.1038/nature01354

PubMed Abstract | CrossRef Full Text | Google Scholar

Virgo, S., Abe, S., and Urai, J. L. (2014). The evolution of crack seal vein and fracture networks in an evolving stress field: Insights from discrete element models of fracture sealing. J. Geophys. Res. Solid Earth 119, 8708–8727. doi:10.1002/2014JB011520

CrossRef Full Text | Google Scholar

Viti, C., Collettini, C., Tesei, T., Tarling, M. S., and Smith, S. A. F. (2018). Deformation processes, textural evolution and weakening in retrograde SerpentinitesTextural evolution and weakening in retrograde serpentinites. MineralsMinerals 8 (6), 241. doi:10.3390/min8060241

CrossRef Full Text | Google Scholar

Voss, N., Dixon, T. H., Liu, Z., Malservisi, R., and Schwartz, M. P. S. (2018). Do slow slip events trigger large and great megathrust earthquakes? Sci. Adv. 4, eaat8472. doi:10.1126/sciadv.aat8472

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, A., and Wang, W. (2019). Nanomaterials from clay minerals. Cambridge, MA: Elsevier.

Google Scholar

Yin, H., and Dvorkin, J. (1994). Strength of cemented grains. Geophys. Res. 21 (10), 903–906. doi:10.1029/93gl03535

CrossRef Full Text | Google Scholar