Spatio-temporal evolution of ground motion intensity caused by reservoir-induced seismicity at the Pertusillo artificial lake (southern Italy)

We investigate the spatiotemporal evolution of ground motion caused by reservoir-induced seismicity at the Pertusillo artificial lake in southern Italy. The area has a strong seismogenic potential, having been affected in the past by the 1857, Mw 7.0 Basilicata earthquake. We consider ∼1,000 microearthquakes that occurred from 2001 to 2018 and were recorded by a local network of nine seismic stations. The ground motion intensity associated with microseismicity allows us to identify two periods, each lasting approximately 2 years. They are characterized by a high rate of events but exhibit different source properties and spatial distributions. In the first period, the seismicity is spatially clustered close to the lake, on faults with different orientations and kinematics. In the second period, the seismicity is distributed along the Monti della Maddalena faults. Comparing the ground motion intensities of the two periods, we observe that events that occurred in the first period are associated with higher stress levels than others, in agreement with the b-values of the respective frequency-magnitude distributions. We compare the temporal evolution of the ground motion intensity with the rainfall and water levels measured at the artificial lake, as well as with the discharge of a ∼80 km distant spring, which is strictly controlled by climate trends. The results provide information about the regional processes acting on the southern Apennines. Our results show that the microseismicity is clearly associated with the Pertusillo artificial lake in the first period, whereas in the second period is a result of a combination of local effects due to water table oscillations of the lake itself, regional tectonics, and the poroelastic and elastic phenomena associated with carbonate rocks hosting aquifers.

Key points

• Ground motion intensity is computed for ∼1,000 microearthquakes that occurred close to an artificial lake in Italy between 2001 and 2018.

• Temporal and spatial variation of the ground motion intensity highlights seismic swarms producing earthquakes with different rupture properties.

• Seismicity is due to a combination of tectonics, water level modulation, and hydrological forces triggering critically stressed faults.

Introduction

Reservoir-induced seismicity (RIS) related to water-level changes in artificial lakes is a well-documented phenomenon. The best known RIS example is certainly the 6.3 Mw 1967 Koyna-Warna earthquake (Gupta and Rastogi, 1976). However, it must be considered that small-to-moderate magnitude RIS occurs very often, both in relation to water load changes and poroelastic stress perturbation in pre-existing faults. Therefore, there is a real demand for monitoring of seismic hazards using dedicated, local, and dense seismic networks (Do Nascimento et al., 2004; Shashidhar et al., 2011; Stabile et al., 2020; Büyükakpınar et al., 2021).

This is especially important when artificial lakes are located in areas characterized by a high seismic hazard. Indeed, where the crust is affected by the presence of faults with a stress level close to failure, even static stress changes of a few tens of kPa associated with RIS might promote the worst-case scenario of large earthquakes (King et al., 1994; Harris, 1998; Shapiro et al., 2013).

Whereas in some cases RIS is observed only for a limited period following initial reservoir impoundment, in other cases it occurs almost every year (e.g., Carder, 1945; Simpson and Negmatullaev, 1981; Durá-Gómez and Talwani, 2010), often as swarms (El Hariri et al., 2010), and is called continuous or protracted RIS. This is the case for the RIS recorded near the Pertusillo artificial lake area in the High Agri Valley, southern Italy. This area is characterized by the complex Monti della Maddalena normal fault system (MMFS) which some authors (e.g., Burrato and Valensise, 2008) suggest was involved in the 1857 Mw 7.0 Basilicata earthquake.

RIS at the Pertusillo artificial lake has been previously studied by, among others, Valoroso et al. (2009) and Stabile et al. (2014). The latter study, in particular, concluded the following: 1) a cyclic annual pressure perturbation in the order of 0.10–0.15 MPa at the lake floor due to water column fluctuation, 2) the existence of two spatially distinct clusters of seismicity (i.e., one located northeast and the other southwest of the lake), with only the latter highly correlated to water level fluctuations, and finally, 3) a rather high b-value (i.e., b = 1.4) of the considered seismicity with respect to that estimated for this sector of the Apennine chain (b ∼ 1; Gulia and Meletti, 2007; Stabile et al., 2013).

Stabile et al. (2014) suggested a 1D pore-fluid pressure-diffusion mechanism acting from the reservoir toward the MMFS as the main physical driving mechanism of RIS in the Pertusillo artificial lake, with an average hydraulic diffusivity of ∼7.8 m²/s. Recently, Rinaldi et al. (2020) presented a first attempt to model RIS at the Pertusillo lake, considering both the static Coulomb failure stress changes and a rate-and-state model for investigating the temporal evolution correlation. Their work confirmed that the MMFS is favorably oriented with respect to the water loading to receive a positive stress change to trigger seismicity. We will return to the modelling results obtained by Rinaldi et al. (2020) later in this work.

Understanding of the physical processes that generate and characterize natural and induced earthquakes, including RIS, is often improved by studying the spatiotemporal evolution of the source parameters obtained through inversion of the seismic data (Allmann and Shearer 2007), or by studying the mechanical properties of rocks through seismic velocities (Brenguier et al., 2008). Nevertheless, the source parameters for small magnitude earthquakes such as stress-drop and seismic energy are difficult to estimate, are model-dependent, and, above all, are affected by large uncertainties (Cotton et al., 2013).

Recently, Picozzi et al. (2021a) studied the ground motion intensity of faults where the 1980 Ms 6.9 Irpinia earthquake enucleated (southern Apennines, Italy) in order to capture the temporal dependency affecting the fault behavior. The proposed approach was based on a well-established spectral decomposition of ground motion residuals into source, path, and site terms (Al Atik et al., 2010; Baltay et al., 2017), and has become standard for the development of Ground Motion Prediction Equations (GMPEs) in seismic hazard studies (e.g., Douglas and Edwards, 2016; Kotha et al., 2020).

In this work, we study the ground motion intensity variation in time and space of RIS associated with the Pertusillo artificial lake over 18 years (2001–2018). In the following, we first describe the main tectonic characteristics of the area, the dataset, and the methods. Then, we describe the temporal and spatial variation of the ground motion intensity for events occurring on the MMFS. Finally, we discuss the results and the interpretive scheme of continuous RIS at the Pertusillo artificial lake proposed by previous studies.

Plain Language Summary

The generation of earthquakes associated with water-level changes in artificial or natural lakes is named ‘reservoir-induced seismicity’ (RIS). Monitoring the temporal and spatial evolution of reservoir-induced seismicity is very important for assessing the mechanical state of faults, especially in areas prone to high levels of seismic hazards. The Pertusillo artificial lake is located in the High Agri Valley, which was affected by the 1857, 7.0 Mw Basilicata earthquake. Herein, we study how the ground motion intensity caused by ∼1,000 microearthquakes that occurred on the western side of the Pertusillo lake changes over time and space. We identify two periods with a high rate of seismicity characterized by events with distinct ground motion intensities and spatial distributions. Our analyses confirm that the events of the first swarms are strongly related to water level changes in the Pertusillo lake. Furthermore, we highlight that the spatially broader seismic swarm is likely related to hydrological forces triggering critically stressed faults. The ground motion intensity results are easily computable and free from assumptions in seismic source models. Therefore, ground motion intensity could become a useful parameter for monitoring RIS in near real-time.

Tectonic setting

The High Agri Valley is an intermontane Quaternary basin, WNW–ESE oriented, that developed in the axial zone of the southern Apennines NE–verging thrust and fold belt (Figure 1). The strong seismogenic potential of the area, as testified by the aforementioned 1857 Mw 7.0 Basilicata earthquake, is strictly related to the brittle tectonics affecting this region, which in turn depends on the region’s tectonic evolution. Indeed, three distinct phases may be distinguished, thus explaining the stratigraphic successions and the complexities of geological structures characterizing the area:

1) From the Mesozoic to very early Cenozoic era, an extensional phase was accommodated by a series of normal faults, causing separation of the western Apennine and the eastern Apulian carbonate platforms, and allowing the deposition of deep-water pelagic successions (Lagonegro Units) (Cello and Mazzoli, 1998).

2) Subsequently, a two-distinct-tectonic-styles shortening phase developed, which was responsible for the present configuration of the crustal structure and landscape of the High Agri Valley. First, since the upper Miocene, thin-skinned, low-angle thrust tectonics led the stacking of rootless nappes of Lagonegro Units, of foredeep flysch deposits, and of western platform carbonates on the Inner Apulian platform. The latter was then characterized by further thrusting in the final late Pliocene/early Pleistocene thick-skinned shortening phase (Patacca and Scandone, 2001; Mazzoli et al., 2008). The described compressional regime produced an imbricate system of reverse faults as well as wide anticlines striking from north-south to northwest-southeast. These folds developed in the Apulian carbonates, thus providing the main structural traps for the Agri Valley oilfield (Mazzoli et al., 2001; Shiner et al., 2004).

3) Since the Pliocene era, crustal shortening affecting the southern Apennines was gradually replaced by a transtensional tectonic phase, resulting from back-arc extension (Patacca and Scandone, 2007) related to the roll-back of the African Plate under the Eurasian plate (e.g. Cinque et al., 1993). Chronologically, the western portion of the orogen was first fragmented by a Pliocene NE–SW extension, accommodated by low-angle normal faults (Ferranti et al., 1996; Ferranti and Oldow, 1999) and later by normal to left-oblique transtensional faults (Cinque et al., 1993; Catalano et al., 2004). Finally, an extensional phase involving the fold-thrust belt and occurring since the Upper Pliocene/Early Pleistocene through NW–SE striking of high-angle normal faults (Vittori et al., 1997), which in some cases generated throws greater than 1,000 m (Brozzetti, 2011; Roda-Boluda and Whittaker, 2018). This tectonic regime is still active, as witnessed by stress indicators (Cello et al., 2003; Montone et al., 2004; Bello et al., 2022) as well as geodetic (Ferranti et al., 2014; Silverii et al., 2016; Devoti et al., 2018) and strain rate field data (D’Agostino, 2014), revealing an extension rate from 1 mm yr⁻¹ up to 5 mm yr⁻¹ in the axial part of the Apennines. In this extensional context, an important role is played by the Campania-Lucania Extensional Fault System (CLEFS; Papanikolaou and Roberts, 2007; Brozzetti, 2011), which is a regional, NW trending, east-dipping, normal fault system, developing as three main faults with alignments extending from northern Campania to northern Calabria. Its tectonic activity has led to the opening, widening, subsidence, and filling of several intramountain, hanging-wall quaternary basins, among which the High Agri Valley (HAV) basin is located. The HAV is bordered by two distinct arrays of separated normal fault segments: the Eastern Agri Fault System (EAFS) and the Monti della Maddalena Fault System (MMFS). The EAFS bounds the basin to the NE and develops along 30 km steep SW–dipping mature fault line scarps. This is the oldest system of faults bordering the valley, as extension was initially concentrated along master faults to the east of the basin. Nonetheless, geomorphic evidence of Quaternary offsets has been observed, suggesting that the EAFS is still tectonically active (Maschio et al., 2005; Ferranti et al., 2007). The MMFS bounds the valley to the SW, runs for approximately 25–30 km, and does not show any evident morphotectonic expression. Its immature morphology, and the displacement of ca. 0.75 Ma surfaces suggest a more recent fault initiation age (ca 0.18–0.75 Ma ago) (Maschio et al., 2005). It consists of a set of discontinuous, steep, tectonically active normal faults which dip to NE. The Pertusillo Lake is located to the south of the HAV. In particular, the lake develops along the strike of the southern portion of the Grumento Fault, which belongs to the southernmost sector of the MMFS and which Hager et al. (2021) called the Pertusillo Fault. Indeed, it seems that the valley delimiting the lake constitutes a structural lineament parallel to this fault, whose protraction underlays the lake itself. The southern part of the valley is also characterized by the presence of geological structures which constrain current physical models that try to explain RIS at Pertusillo Lake (e.g., Rinaldi et al., 2020): a set of northeast-striking tear faults extend from the lake to the southwest, as imaged by Stabile et al. (2014) using earthquake locations.

FIGURE 1

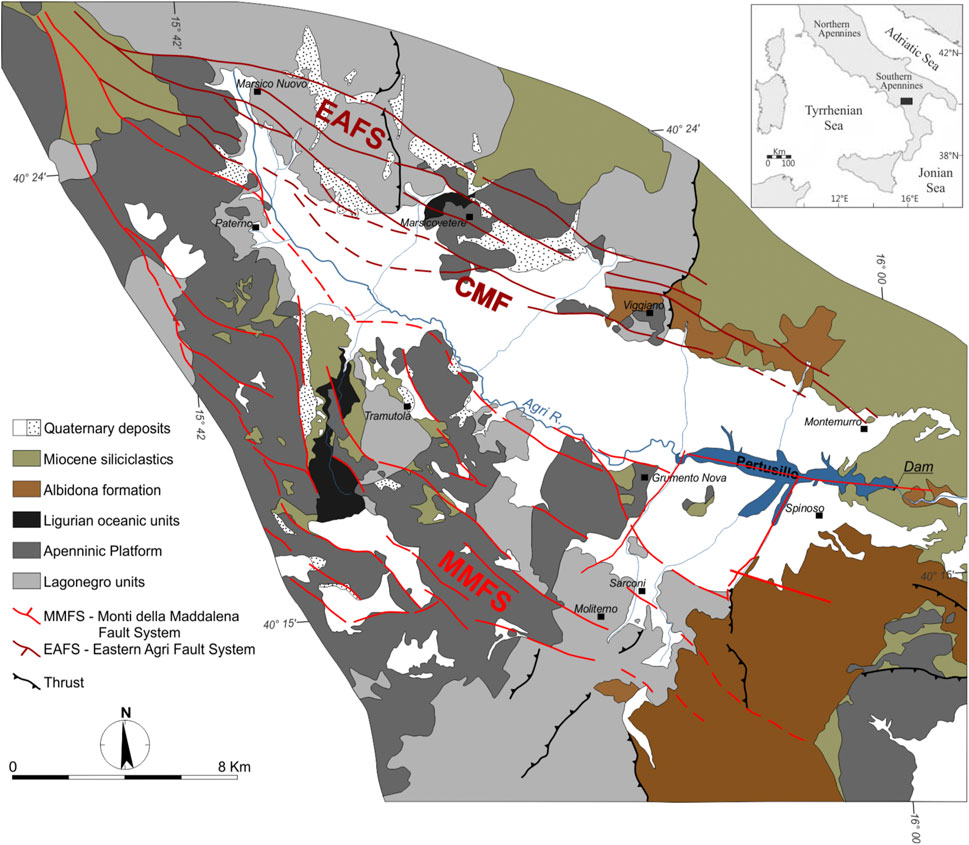
FIGURE 1. (A) Geological map of the High Agri Valley. The location of the Pertusillo reservoir with respect to the eastern Agri fault system (EAFS) to the Caggiano-Montemurro Fault (CMF), and to the Monti della Maddalena fault system (MMFS), is shown in the figure [modified from Giocoli et al. (2015), after Hager et al. (2021) and Bello et al. (2022)].

Dataset

This study considers 1,089 earthquakes that occurred during the period 2001 to 2018 and that were recorded by nine seismic stations in a local seismic network, managed by Eni since 2001. All stations are equipped with MARS-88/MC Lennartz digital data loggers and tri-axial Lennartz LE-3D 1 Hz velocimetric sensors. Data were sampled from 2001 to 2012 at 62.5 Hz and later at 125 Hz.

Earthquake locations were determined, including the P- and S-wave arrival times retrieved from the continuous data streams that were recorded by the Italian National Seismic network stations installed in the area (IV, https://doi.org/10.13127/SD/X0FXnH7QfY), obtaining a total of 9886 P-wave and 9054 S-wave manual picks. The probabilistic, absolute earthquake location algorithm NonLinLoc (Lomax et al., 2000) was applied, and 3D V_P and V_P/V_S models have been obtained by merging information from Serlenga and Stabile (2019) and Balasco et al. (2021). The distributions of the events and the Eni stations are shown in Figure 2A, from which we can see that the seismicity is distributed along the main strike of the MMFS (i.e., from south-east to north-west), with most of the seismicity concentrated south-west of the Pertusillo artificial lake.

FIGURE 2

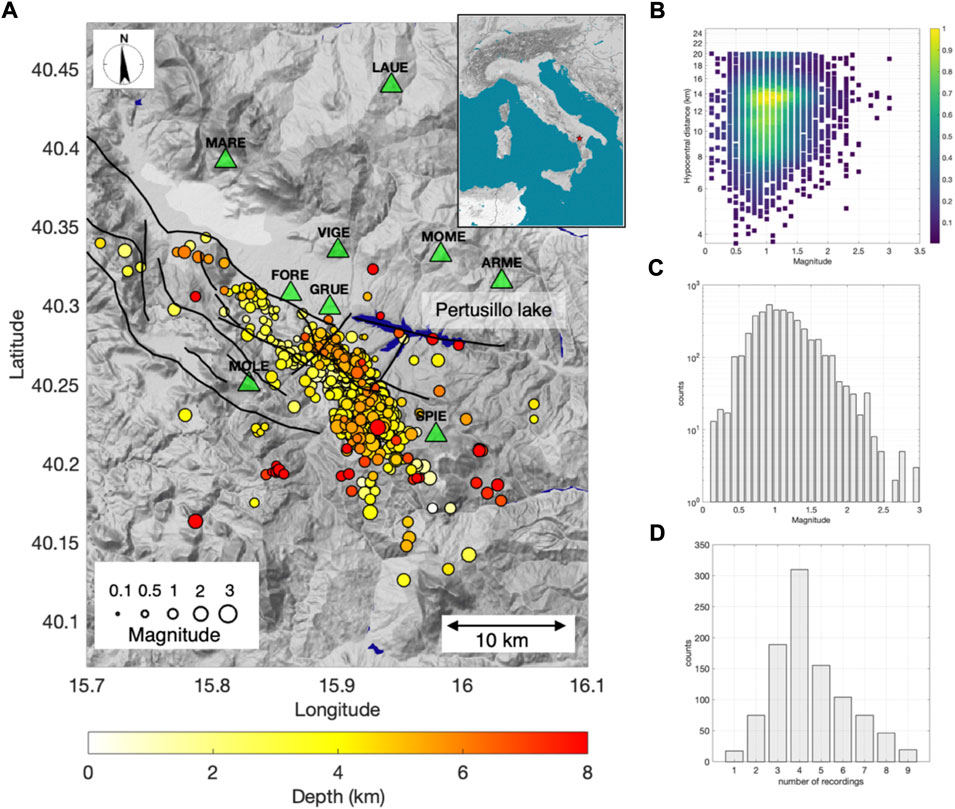
FIGURE 2. (A) Map showing the distribution of earthquakes (dots with dimensions according to the magnitude, and color according to the hypocentral depth) and the locations of seismic stations (green triangle). Monti della Maddalena fault system (MMFS; black lines). (B) Density plot, normalized between 0 and 1, of the magnitude versus hypocentral distance (i.e., the latter plotted on a logarithmic scale) for the recordings analyzed in this study. (C) Histogram showing the distribution of magnitudes for the considered events. (D) Histogram showing the number of recordings per event (i.e., the number of stations that recorded an event).

The moment magnitude, Mw, of earthquakes was derived by considering the local magnitude, M_L, from the Eni catalog, using the empirical relationship developed by Munafò et al. (2016) for Italian earthquakes with small magnitudes (up to Mw ∼ 4); Mw = 0.67 ML + 1.15.

Our dataset consists of 6,574 recordings. The data are distributed over a range of moment magnitudes between Mw 0.1 and Mw 3.0, while the hypocentral distances range from 3.7 km to 20 km (Figure 2B). The magnitude versus the hypocentral distance scatter plot (Figure 2B) shows that the dataset is dominated by earthquakes with magnitudes between Mw 0.6 and Mw 1.5, and hypocentral distances between 7 km and 15 km. The distribution of the magnitude of events shown in Figure 2C indicates that the completeness magnitude of our catalog is Mw ∼1. Figure 2D shows the number of recordings per event, with most of the earthquakes recorded by between three and six stations. Since our aim is to estimate the average ground motion intensity from estimates at multiple stations, we consider only events that have been recorded by at least three stations. After this selection procedure, the dataset consisted of 990 earthquakes and 4,441 recordings.

Velocimetric raw data were converted to a physical quantity (m/s) considering the instrumental sensitivity. Then, we applied a detrend and a cos-tapering (5%) to avoid anomalous trends in the conversion from velocity to acceleration (by differentiation).

For the sake of uniformity, a high-frequency cut-off at 25 Hz was selected for all data since, up to September 2012, data were recorded at a sampling frequency of 62.5 Hz, whereas, after September 2012, data were sampled at 125 Hz. Hence, a selected frequency of 25 Hz represents 80% of the Nyquist frequency for the sampling of older data. Data are thus filtered using a Butterworth filter (fourth order) in the band 1–25 Hz. The lowest frequency of the filter was selected considering the characteristics of the sensors used (Lennartz Le-3Dlite with a lower cut-off frequency of 1 Hz).

Methods

To estimate the ground motion intensities of the selected RIS events, we developed Ground Motion Prediction Equations, GMPEs, by applying a random effect strategy (Bates et al., 2015; Bindi et al., 2018).

Following Picozzi et al. (2021a), we considered the model:

$\log \left(y\right)=e1+e2\cdot \left(M-M\mathrm{r}\mathrm{e}\mathrm{f}\right)+e3\cdot {\left(M-M\mathrm{r}\mathrm{e}\mathrm{f}\right)}^2+e4\cdot \log R\mathrm{h}\mathrm{y}\mathrm{p}\mathrm{o}+e5\cdot R\mathrm{h}\mathrm{y}\mathrm{p}\mathrm{o}+\mathrm{\delta }\mathrm{B}\mathrm{e}+\mathrm{\delta }\mathrm{S}2\mathrm{S}+\in (1)$

where Y is the root mean square (RMS) of the PGA (m/s²) measured on two horizontal components, while Mref is the reference magnitude, which was set to 1.

The calibrated GMPE model 1) consists of five model coefficients (i.e., e1, e2, e3, e4 and e5) and three random effects (i.e., δBe, δS2S, and ε).

Following Al Atik et al. (2010), the first random effect is defined as a between-event distribution (δBe); it measures the systematic deviation from the median of each group of recordings for the same event: we define this as ‘ground motion intensity’.

The second random effect is the between-station residual distribution (δS2S), which measures the systematic deviation of Y from the median of the recordings relevant to the same station. In other words, we can consider δS2S as a relative measure of the site effects of the stations for the examined parameter. δS2S for each station is provided in the Supplementary Material (Supplementary Figure S1).

Finally, the last random effect is the single-station within-event residual (ε), which provides a measure of the left-over variability. For the sake of simplicity, Al Atik et al. (2010) provide a comprehensive review of the glossary of terms describing the components of ground motion variability in the context of probabilistic seismic hazard assessment. The results of the regression analysis for model 1) are provided in the Supplementary Material.

Of the random effects retrieved from model (1), the main parameter of interest in this work is δBe. δBe is, in simple terms, defined as the difference between the observation and the model prediction for each event. Therefore, δBe provides information about the importance of event-specific deviations from the median prediction, determined by the assumed magnitude and distance scaling in model (1).

An important issue related to the ground motion intensity, δBe, is that it can provide information on differences in the source parameters of the considered earthquakes (e.g., stress drop Δσ and rupture velocity, V_R); these impact the intensity measurements (PGA in our case) but are not included as independent parameters in the model (1). We save this discussion for the end.

In the following, we study the temporal and spatial variability of the ground motion intensity (δBe) to investigate the variability of RIS source processes occurring in the MMFS.

Results

The results of the parameterization of model 1) are summarized in Figure 3. The single-station within-event residuals, ε, for the recordings are shown, with respect to the hypocentral distance, in Figure 3A. Furthermore, to highlight the possible existence of trends in these residuals, we divided the range of hypocentral distances into bins of 2.5 km; for each bin we estimate the median and standard deviation of the residuals. Considering the single and median values of ε, we do not observe any significant trend, confirming that the model was correctly calibrated.

FIGURE 3

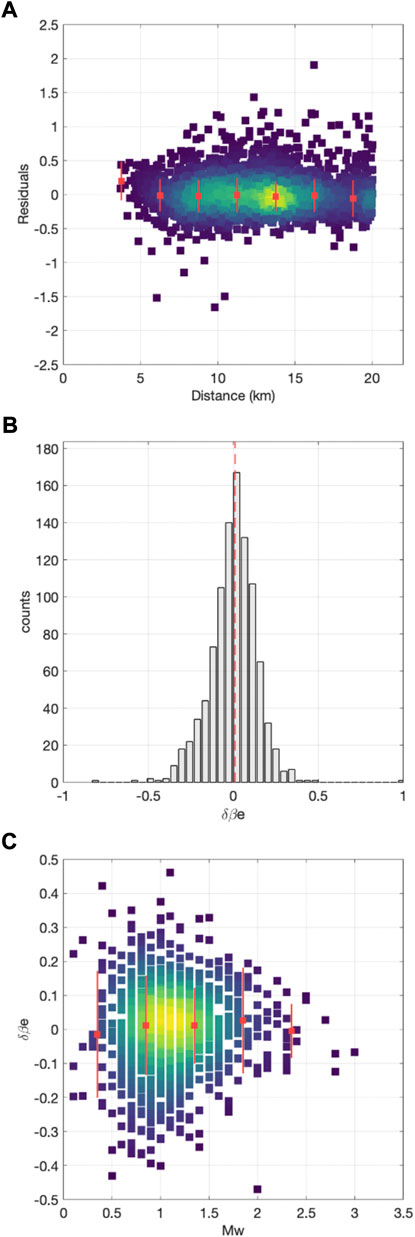
FIGURE 3. (A) Density plot, normalized between 0 and 1, for the within-event residuals (ε) versus the hypocentral distance; median (red squares) and standard deviation (red lines) of ε, computed for bins of the residuals in hypocentral distance (viridis color scale with yellow indicating higher density of data, as in Figure 1). (B) Between-event residuals (δBe) distribution and median values (red dashed line). (C) δBe versus Mw; median (red squares) and standard deviation (red lines) of (δBe), computed for bins of the values of hypocentral distance.

Figure 3B shows that the obtained δBe values well approximate a zero-mean normal distribution, as expected from the theory. Moreover, we checked the existence of trends in δBe values with respect to the magnitude. Hence, we divided the magnitude range into bins of 0.5 units and computed the median and standard deviations. Figure 3C shows that δBe has a rather large variability, but no trend with the magnitude. The variability of δBe is therefore not given by incorrect model calibration. Therefore, we proceed with investigating the δBe time and space variations.

Before discussing the temporal evolution of the ground motion intensity, we began by observing the distribution in time of the magnitude and depth. Figure 4A shows that the seismicity was not constant throughout the timescale studied, but occurred in swarms that were rather clustered from 2003 to 2005 (hereinafter referred to as period ^#1). Subsequently, we observe that the period between 2007 and 2012 was characterized by a small seismicity rate. Beginning in 2013 and lasting until 2015, seismicity occurred again as swarms (hereinafter referred to as period ^#2). Finally, from 2016, the seismicity rate decreased. The cyclical occurrence of seismicity was previously studied by Telesca et al. (2015), who found that a periodicity of 12 months was the most significant feature of the temporal evolution of the rate of seismicity associated with the Pertusillo artificial lake.

FIGURE 4

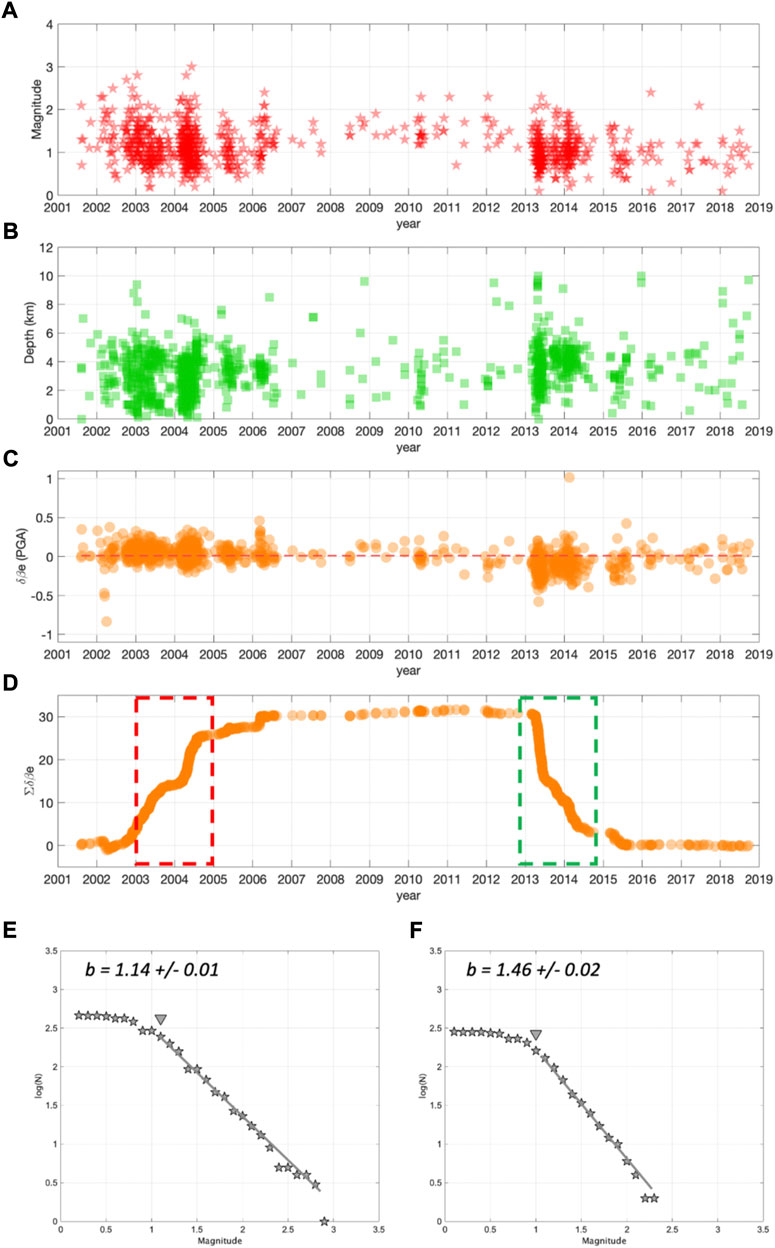
FIGURE 4. (A) Distribution of event magnitudes in time. (B) Distribution of hypocentral depths. (C) Distribution of δBe. (D) Cumulative of δBe in time. Period ^#1 (2003–2005, highlighted by the red dashed line) and period ^#2 (2013–2015, highlighted by the green dashed line). (E) Frequency-magnitude distribution of events for period ^#1; GR-model (gray line) and completeness magnitude (gray triangle). (F) The same as (E), but for period ^#2.

The magnitude and the hypocentral depth of the earthquakes for the considered period range between Mw 0.1 and Mw 3.0 and between 0 km and 10 km (Figure 4B), respectively. However, 95^th percentile of the magnitude and hypocentral depth distributions were Mw 1.8 and 5.8 km, respectively, which provide a clear indication of a small magnitude and shallow RIS seismicity associated with the Pertusillo lake.

Figure 4C shows the temporal evolution of δBe. Here, we observe that δBe clearly followed the earthquake occurrence rate in time, but interestingly, presented values that were not randomly distributed around zero, as expected. Despite the δBe distribution presenting a zero mean (Figure 3B), upon inspecting its temporal distribution we observe that for period ^#1 (i.e., from 2003 to 2005), the average δBe values were above zero, whereas for period ^#2 (i.e., from 2013 to 2015), they were below zero.

Following Picozzi et al. (2019a), we computed the cumulative of δBe to highlight how the ground motion intensity clusters in time (Figure 4D). The cumulative of δBe initially increased during period ^#1 (i.e., the dashed red area in Figure 4D, from 2003 to 2005) in line with the two main swarms, and then significantly decreased in period ^#2 (i.e., the dashed green area in Figure 4D, from 2013 to 2015). We will later discuss a possible interpretation of these trends in the cumulative of δBe. However, before continuing with the discussion, we analyzed the b-values of the two considered periods (Gutenberg and Richter, 1942). The interest in characterizing the b-value associated with seismicity occurring in the two selected periods is owing to the relationship between this parameter and stress (Scholz, 2019).

Amitrano (2003) showed the existence of an inverse linear relationship between the b-value and differential stress; Picozzi et al. (2019b) highlighted a similar relationship with the apparent stress. Therefore, we computed the b-value for periods ^#1 and ^#2, employing ZMAP software (Wiemer, 2001), and estimated its uncertainty using a bootstrap approach (Efron, 1979) considering 2000 iterations. Figures 4E,F show that the two frequency-magnitude distributions exhibited similar magnitudes of completeness (Mc ∼1) but different b-values. For period ^#1, the b-value was 1.14 (standard error ± 0.02), whereas for period ^#2 it was 1.46 (standard error ± 0.02). In the following, we interpret the difference in the b-values observed for periods ^#1 and ^#2 with relation to the independent information provided by δBe. These two pieces of information were therefore combined to attempt a first interpretation of the mechanism generating RIS in the two periods.

It is worth comparing the δBe temporal variability with the seasonal water level fluctuations in the Pertusillo lake. Stabile et al. (2014) showed that the cyclic annual pressure perturbation (0.10–0.15 MPa) at the lake floor, due to water column fluctuation, was able to drive RIS occurrence. In Figure 5A, we compare the cumulative of δBe with the Pertusillo lake’s water level. For period ^#1 (2003–2005), we observe a good correlation between the long-term trend of increased water levels, albeit with typical annual fluctuations, and the increased cumulative of ground motion intensity. On the contrary, for period ^#2 (2013–2015), we observe that the water level seemed on average stable, while the cumulative of δBe decreased. These results suggest a correlation between the water level fluctuations and δBe, in agreement with Stabile et al. (2014), but also that the interaction between RIS and external forces such as water level fluctuations can be rather complex. In Figure 5B, we compare the cumulative of δBe with 1) the normalized rainfall recorded at the Pertusillo lake and 2) the normalized discharge of the Caposele spring, located ∼80 km north of the Pertusillo lake. The Caposele spring is considered an important source of information concerning the underlying aquifer in fractured Mesozoic limestone, since it is not affected by anthropogenic modifications in its catchment (D’Agostino et al., 2018). As matter of fact, the Caposele spring is strictly controlled by climate trends thus providing information about regional processes acting on the southern Apennines (Allocca et al., 2014). For this reason, a comparison of the Caposele discharge and rainfall near the Pertusillo lake can allow us to call into question the dynamics of aquifers as RIS generators. For period ^#1, the increased Caposele discharge and rainfall (Figure 5A) is compatible with earlier observations (Figure 5B), and the correlation with δBe confirmed. On the other hand, focusing on period ^#2, we observe that both the Caposele discharge and rainfall decreased during the previous year (i.e., 2012), followed by a rather large increase at the beginning of 2013, when the cumulative of δBe began to decrease (Figure 5B). Therefore, although during period ^#2 the average Pertusillo lake water level remained stable, the rainfall levels suggest that the local aquifer suffered significant variations. Furthermore, the excellent correlation between the rainfall level and Caposele discharge suggests that the behavior of the local aquifers was influenced by large-scale, regional dynamic processes (D’Agostino et al., 2018). It is however worth noting that during 2008–2009, we observed changes in the levels of the Pertusillo lake, rainfall, and even the Caposele spring discharge, without any apparent effect on either the RIS rate and/or δBe.

FIGURE 5

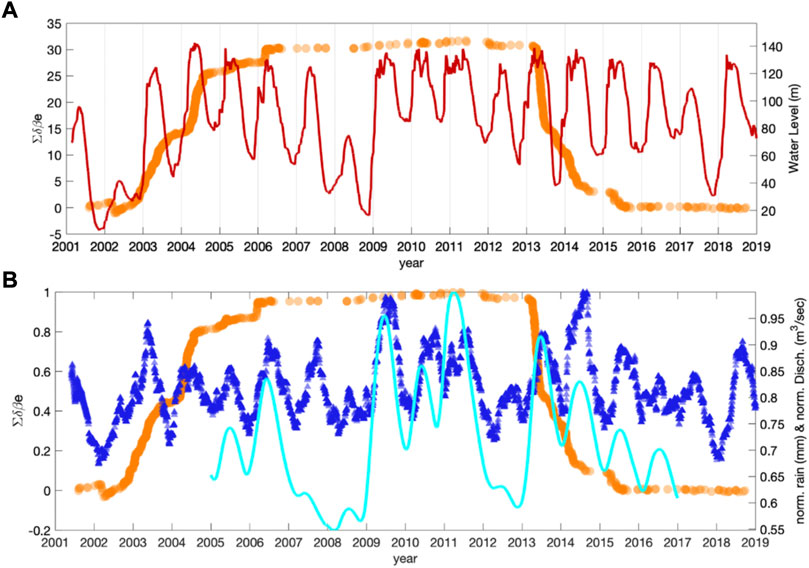
FIGURE 5. (A) Cumulative in time of δBe (orange), Pertusillo lake water level (red). (B) the same as (A), but also including the normalized rain level at the Pertusillo lake (blue), and the normalized water level discharge at the Caposele spring (cyan data; digitized by D’Agostino et al., 2018).

Discussion and conclusion

We showed that the δBe evolution of ∼1,000 earthquakes that occurred on the west side of the High Agri Valley highlights temporal variability in the seismicity characteristics. Previous authors (e.g., Bindi et al., 2007, 2017; Cotton et al., 2013; Causse and Song, 2015; Courboulex et al., 2016; Oth et al., 2017; Picozzi et al., 2021a) suggested that the ground motion intensity, δBe, is related to the stress drop, Δσ, and to the rupture velocity, V_R, variability. The advantage in using δBe for monitoring purposes comes from the fact that it provides information on relative differences in Δσ for earthquakes of interest, without the difficulties of directly measuring Δσ. Stress drop measures are, in fact, typically associated with large uncertainties, part of which are epistemic and part model-dependent (Cotton et al., 2013). Therefore, despite the fact that knowledge of Δσ is essential for defining scenarios in applications such as seismic hazard studies, we find that for real-time seismicity monitoring, where it is important to rapidly recognize variations in seismicity characteristics, δBe can be a very useful parameter, as suggested by Picozzi et al. (2021a).

Temporal evolution of the 2001–2018 seismicity occurred on the west side of the High Agri Valley basin, indicates variability of the seismicity rate during the timeframe considered: indeed, two periods characterized by swarm-type distributions of seismicity and high seismicity rates were observed (2003–2005, period ^#1, dashed red area in Figure 4D; 2013–2015, period ^#2, dashed green area in Figure 4D) and were followed by periods of low seismicity (2006–2012 and 2015–2018, Figure 4). It is worth noting that no change in the Eni network configuration used for estimating δBe occurred during the periods of lower seismicity.

Ground motion intensity (δBe) has allowed us to highlight temporal differences in RIS at the Pertusillo lake that correlate not only with the water level of the lake (which is inevitably influenced by anthropogenic modifications), but also with the rainfall amount (which we can consider a proxy for the mechanical behavior of karst aquifers). The two investigated periods, characterized by higher rates of seismicity, present distinct δBe values. In period ^#1, δBe is higher compared with the second period (i.e., ^#2). This result suggests that RIS in period ^#1 is associated with higher stress drop (Δσ) values (or higher rupture velocities) than in period ^#2. The variations in δBe are echoed by a change in the slope of the Gutenberg–Richter frequency-magnitude relationship (Gutenberg and Richter, 1942; b-value). Since period ^#1 exhibits a smaller b-value than period ^#2, it is straightforward to imagine a higher stress level in the former period with respect to the latter, which agrees with the information provided by δBe and thus Δσ.

δBe allows us to depict an interesting picture of the RIS temporal evolution at the Pertusillo lake. Even though 12-month periodicity represents the most significant feature of the temporal evolution of seismicity (Telesca et al., 2015), we show that δBe can capture the long-term seismicity behavior. During period ^#1, the link between the Pertusillo lake water fluctuation and the δBe increase is rather straightforward. For period ^#2, this link seems absent, but we show that RIS might be associated with the long-term regional dynamic of aquifers. Previous studies have investigated the role of crustal deformation, due to karst aquifers recharge and discharge, in modulating seismicity in Italy (e.g., D’Agostino et al., 2018 for the Irpinia region and Barajas et al., 2021 for the Pollino area, both in southern Italy; Silverii et al., 2019 provided a more general overview of this phenomenon for a wide region of Italy, including the central and southern Apennines). The High Agri Valley area investigated in this study is located between the Irpinia (to the North) and the Pollino (to the South) areas. The geologic structures in these three regions share identical features: the presence of shallow carbonate rocks, diffusely fractured by extensional tectonics, thus hosting karst aquifers. The role of hydrological forces in triggering critically stressed faults is a well-documented phenomenon (e.g., Hainzl et al., 2013; D’Agostino et al., 2018; Hsu et al., 2011). Concerning this issue, it is worth noting that, as observed for the central sector of the Apennine chain (Devoti et al., 2018), karst aquifers can follow annual and multiyear cycles, related to El-Niño oscillation (varying between 3 and 7 years; Brönnimann 2007). Recently, Picozzi et al. (2021b) and De Landro et al. (2022) found a positive correlation between the seismic source characteristics and V_P/V_S changes, with regard to groundwater recharge and geodetic displacement in the Irpinia area (southern Italy).

Based on our evidence from δBe, and the overall framework characterizing the hydrological forces in the Apennines, we can hypothesize that seismicity near the Pertusillo lake can be imagined as a complex combination of: 1) local effects due to water level modulation in the lake itself, 2) regional tectonics, and 3) poroelastic and elastic phenomena associated with carbonate rocks hosting aquifers. This hypothesis agrees with the observations of Stabile et al. (2015).

Thus far, we have not discussed the spatial distributions of seismicity for the two time periods. Figures 6A,B show the RIS spatial distributions for periods ^#1 and ^#2, respectively. It is immediately evident that the two swarms occurred on distinct faults of the same system. Furthermore, Figure 7 shows the relative distance versus the relative time of occurrence between the first event and all others in the same swarm for each period.

FIGURE 6

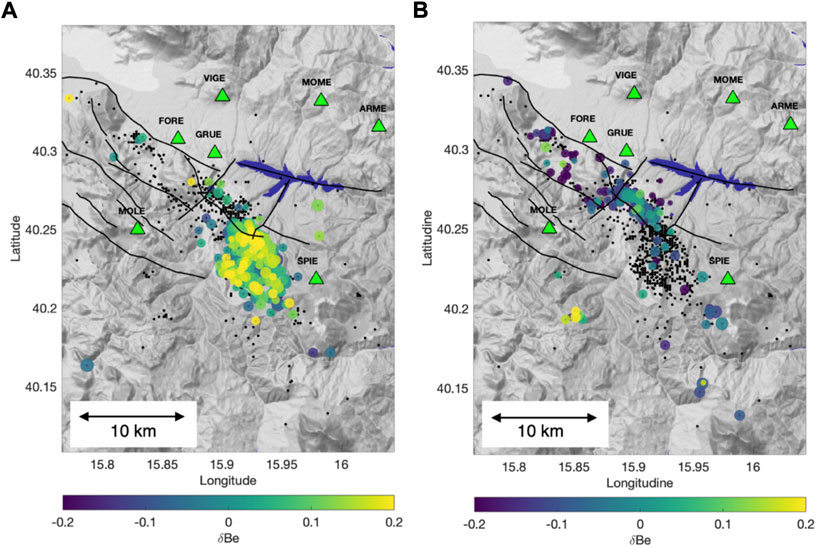
FIGURE 6. (A) Distribution of events for period ^#1 (2003–2005), colored as per δBe. (B) The same as (A), but for period ^#2 (2013–2015).

FIGURE 7

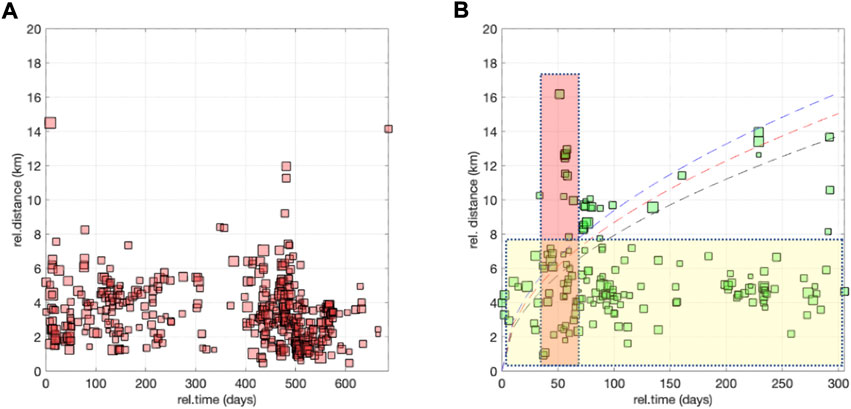
FIGURE 7. (A) Distribution of period ^#1 events; relative distance vs. relative time from the first event. (B) The same as (A), but for period ^#2. Here, we highlight the trends corresponding to a diffusivity equal to 0.05, 0.06, or 0.07 m²/s (black, red, and blue dashed lines, respectively). Moreover, we highlight a period with events covering a narrow range of relative distances, but a high relative time (such as period ^#1; yellow rectangle it is singular), as well as a second area with a high range of distances in a narrow period of time (red rectangle it is singular).

We can summarize the main characteristics of RIS for the two periods as follows:

The swarm that occurred in period ^#1 presents:

1. Average δBe values above zero (Figures 4C,D).

2. A frequency-magnitude distribution b-value of 1.14 ± 0.02 (Figure 4E).

3. Seismicity was clustered SW of the Pertusillo reservoir (Figure 6A), mostly within 8 km of the first event (Figure 7A). Earthquakes occurred at the intersection between the southern termination of the MMFS and northwest–southeast striking faults, with a variable faulting style (Stabile et al., 2014; Improta et al., 2017; Hager et al., 2021).

The swarm that occurred in period ^#2 was characterized by:

1. Average δBe values below zero (Figures 4C,D).

2. A frequency-magnitude distribution b-value of 1.46 ± 0.02 (Figure 4F).

3. Seismicity was spread over the whole length of the MMFS (Figure 6B), up to 16 km away from the first event (Figure 7B).

4. Considering the space-time features of this swarm, we identify three main patterns (Figure 7B):

i A significant number of events occurred within 8 km of the first event (yellow rectangles in Figure 7B), similar to period ^#1.

ii A group of events followed a trend corresponding to diffusivities in the range 0.05–0.07 m²/s (black, red, and blue dashed lines in Figure 7B).

iii Finally, a number of events occurred in a narrow period of time, but covered a wide range of distances; a maximum of 16 km from the first event was observed (red rectangles in Figure 7B).

The general pattern of RIS emerging for period ^#1 (Figure 6A) is rather simple, and agrees with previous studies (e.g., Stabile et al., 2014). The system of faults close to the southern part of the Pertusillo lake exhibits different strike (both NW–SE and NE–SW) and faulting styles. Our results confirm, in agreement with Rinaldi et al. (2020), that the Pertusillo Lake played a crucial role in the generation of earthquakes during period ^#1. Likely, both the orientation of faults with respect to the regional tectonic stress (i.e., the minimum horizontal stress axis oriented N032; Bello et al., 2022), and their style are responsible for the relative high stress drops, ∆σ, (i.e., higher δBe and lower b-values) of these events with respect to the other swarm. Indeed, assuming similar frictional coefficients and initial cohesion values, strike-slip faults can show higher stress-drops with respect to normal faulting (Shapiro and Dinske, 2021).

Figure 6B shows that for period ^#2, the swarm appeared more complex. In this case, the seismicity was widespread along the MMFS; up to 16 km away from the first event. This result suggests that this seismicity was not only influenced by the Pertusillo lake water level. Indeed, if we consider that the reservoir water level does not show a particular trend for this period, we can imagine that the main triggering process is the poroelastic/elastic stress due to aquifers in the carbonate rocks. The decreasing trend in the cumulative of δBe values suggests the occurrence of microearthquakes with lower stress drops in period ^#2, compared with those in period ^#1. Assuming that the effective vertical stress is equivalent for both periods ^#1 and ^#2, such stress drop differences can be justified by the more complex fault geometry SW of the Pertusillo Lake (period ^#1, Figure 6A), with respect to the dominant faulting style of the MMFS (period ^#2, Figure 6B). This hypothesis is also supported by the higher b-value estimates for the seismic swarm that occurred in period ^#2, with respect to the swarm that occurred in period ^#1. Furthermore, this result agrees with the general framework of b-values and faulting styles proposed by Schorlemmer et al. (2005), statistically demonstrating how the b-value varies systematically for different styles of faulting, exhibiting higher values for normal faults than for strike-slip or reverse faults. However, it is worth noting that our b-value estimates for both periods are significantly above ∼1, the value estimated for this region of the Apennines chain (Gulia and Meletti, 2007; Stabile et al., 2013). This difference in b-value estimates suggests that a pore-pressure increase contributes to the effective normal stress of the seismicity considered in this study.

We have shown that the seasonal water level fluctuations of the Pertusillo lake are in good agreement with the normalized water level discharge from the Caposele spring, located in the Irpinia area approximately 80 km from our area of interest (Figure 5). This result suggests a regional-scale aquifer dynamic; the seasonal water level fluctuations of the Pertusillo lake can be used as a proxy for monitoring such dynamics. This aspect is particularly useful for interpreting the driving trigger mechanisms of the three types of seismicity behaviors observed in period ^#2 (Figures 6, 7). Events occurring within 8 km of the first event (yellow rectangle in Figure 7B) can be strictly classified as continuous local RIS (similar to the earthquakes in period ^#1). The events following a spatiotemporal trend, with corresponding diffusivities of approximately 0.05–0.07 m²/s (black, red, and blue dashed lines in Figure 7B), can be attributed to pore-pressure diffusion along the MMFS. Finally, microseismicity that occurred over a narrow period of time, yet showing relative distances from the first event up to 16 km (red rectangle in Figure 7B), suggests a rapid seismic response to groundwater recharge of the aquifer in the valley.

This kind of seismicity can have strong implications for seismic hazards in the region. This shows us that the MMFS is highly sensitive to even small external quasi-periodic perturbations over a fault segment approximately 16 km in length. Considering the empirical laws proposed by Wells and Coppersmith (1994), the scenario where this segment breaks in a unique rupture episode, would correspond to a moment magnitude 6.2 moment magnitude earthquake. The seismogenic fault system responsible for the 1857, Mw 7.0 Basilicata earthquake is still debated, with some authors suggesting that the rupture occurred on the MMFS (Maschio et al., 2005), others on the EAFS (Cello et al., 2003), whereas others call into question the role played by the Pergola-Melandro fault located to the North (Burrato and Valensise, 2008). Finally, Bello et al. (2022) recently proposed that the 1857 Basilicata earthquake could be due to CMF (Caggiano-Montemurro fault) SW-dipping.

Our work does not aim to settle the matter; however it highlights that the MMFS is an active fault system, influenced by hydrological forces and hence likely in a critical state. Therefore, we highlight the importance of monitoring spatio-temporal patterns and source characteristics associated with the evolution of the microseismicity in the MMFS. Monitoring can indeed improve our knowledge on the faults’ mechanical condition and can provide information for prioritizing hazard scenarios. Concerning the ground motion intensity parameter δBe, which is easily computable in near-real time, we believe it can become a precious tool for monitoring faults and for unveiling their strength/friction variations, which could lead to the occurrence of large earthquakes.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: Data necessary for this study are provided by ENI s. p.a. Requests to access these datasets should be directed to marco.mileti@eni.com.

Author contributions

MP designed the concept of the study. MP and VS performed the analysis. MP, TS, and VS interpreted the results and wrote the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research benefited from the financial support of the project “Detection and tracking of crustal fluid by multi-parametric methodologies and technologies” of the Italian PRIN-MIUR program (Grant no. 20174X3P29).

Acknowledgments

We would like to thank the Editor, C. Galasso, and three reviewers for their comments and suggestions that allowed us to significantly improve the content and form of the manuscript. We acknowledge ENI S.p.A. for providing the seismic data necessary for this study and the Ente per lo Sviluppo dell’Irrigazione e la Trasformazione Fondiaria (agency of Potenza, Italy) for information regarding the Pertusillo artificial lake.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.1048196/full#supplementary-material

References

Al Atik, L., Abrahamson, A., Bommer, J. J., Scherbaum, F., Cotton, F., and Kuehn, N. 2010. The variability of ground-motion prediction models and its components. Seismol. Res. Lett., 81, 5, 794–801. doi:10.1785/gssrl.81.5.794

CrossRef Full Text | Google Scholar

Allmann, B. P., and Shearer, P. M. (2007). Spatial and temporal stress drop variations in small earthquakes near Parkfield, California. J. Geophys. Res. 112, B04305. doi:10.1029/2006JB004395

CrossRef Full Text | Google Scholar

Allocca, V., Manna, F., and De Vita, P. (2014). Estimating annual groundwater recharge coefficient for karst aquifers of the southern Apennines (Italy). Hydrol. Earth Syst. Sci. 18 (2), 803–817. doi:10.5194/hess-18-803-2014

CrossRef Full Text | Google Scholar

Amitrano, D. (2003). Brittle-ductile transition and associated seismicity: Experimental and numerical studies and relationship with the b value. J. Geophys. Res. 108, B12044. doi:10.1029/2001JB000680

CrossRef Full Text | Google Scholar

Balasco, M., Cavalcante, F., Romano, G., Serlenga, V., Siniscalchi, A., Stabile, T. A., et al. (2021). New insights into the High Agri Valley deep structure revealed by magnetotelluric imaging and seismic tomography, 808. Tectonophysics: Southern Apennine, Italy, 228817. doi:10.1016/j.tecto.2021.228817

CrossRef Full Text | Google Scholar

Baltay, A. S., Hanks, T. C., and Abrahamson, N. A. (2017). Uncertainty, variability, and earthquake physics in ground-motion prediction equations. Bull. Seismol. Soc. Am. 107, 1754–1772. doi:10.1785/0120160164

CrossRef Full Text | Google Scholar

Barajas, A., Poli, P., d’Agostino, N., Margerin, L., and Campillo, M. (2021). Separation of poroelastic and elastic processes of an aquifer from tectonic phenomena using geodetic, seismic, and meteorological data in the Pollino region, Italy. Geochemistry, Geophysics, Geosystems. AGU Geochem. Soc., 65. doi:10.1029/2021GC009742.hal-03429180

CrossRef Full Text | Google Scholar

Bates, D., Maechler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67 (1), 1–48. doi:10.18637/jss.v067i01https://cran.r-project.org/web/packages/lme4/vignettes/lmer.pdf.

CrossRef Full Text | Google Scholar

Bello, S., Lavecchia, G., Andrenacci, C., Ercoli, M., Cirillo, D., Carboni, F., et al. (2022). Complex trans-ridge normal faults controlling large earthquakes. Sci. Rep. 12, Art. n. 10676. doi:10.1038/s41598-022-14406-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Bindi, D., Cotton, F., Spallarossa, D., Picozzi, M., and Rivalta, E. (2018). Temporal variability of ground shaking and stress drop in central Italy: A hint for fault healing? Bull. Seismol. Soc. Am. 108 (4), 1853–1863. doi:10.1785/0120180078

CrossRef Full Text | Google Scholar

Bindi, D., Parolai, S., Grosser, H., Milkereit, C., and Durukal, E. (2007). Empirical ground-motion prediction equations for northwestern Turkey using the aftershocks of the 1999 Kocaeli earthquake. Geophys. Res. Lett. 34 (8). doi:10.1029/2007gl029222

CrossRef Full Text | Google Scholar

Bindi, D., Spallarossa, D., and Pacor, F. (2017). Between-event and between-station variability observed in the fourier and response spectra domains: Comparison with seismological models. Geophys. J. Int. 210, 1092–1104. doi:10.1093/gji/ggx217

CrossRef Full Text | Google Scholar

Brenguier, F., Campillo, M., Hadziioannou, C., Shapiro, N. M., Nadeau, R. M., and Larose, E. (2008). Postseismic relaxation along the san andreas fault at parkfield from continuous seismological observations. Science 321 (5895), 1478–1481. doi:10.1126/science.1160943

PubMed Abstract | CrossRef Full Text | Google Scholar

Brönnimann, S. (2007). Impact of El niño–southern oscillation on European climate. Rev. Geophys. 45, RG3003. doi:10.1029/2006RG000199

CrossRef Full Text | Google Scholar

Brozzetti, F. (2011). The campania-lucania Extensional Fault system, southern Italy: A suggestion for a uniform model of active extension in the Italian Apennines. Tectonics 30 (5), TC5009. doi:10.1029/2010TC002794

CrossRef Full Text | Google Scholar

Burrato, P., and Valensise, G. (2008). Rise and fall of a hypothesized seismic gap: Source complexity in the Mw 7.0 16 december 1857 southern Italy earthquake. Bull. Seismol. Soc. Am. 98, 139–148. doi:10.1785/0120070094

CrossRef Full Text | Google Scholar

Büyükakpınar, P., Cesca, S., Hainzl, S., Jamalreyhani, M., Heimann, S., and Dahm, T. (2021). Reservoir-Triggered earthquakes around the atatürk dam (southeastern Turkey). Front. Earth Sci. 9, Art. n. 663385. doi:10.3389/feart.2021.663385

CrossRef Full Text | Google Scholar

Carder, D. S. (1945). Seismic investigations in the Boulder Dam area, 1940-1944, and the influence of reservoir loading on local earthquake activity*. Bull. Seismol. Soc. Am. 35, 175–192. doi:10.1785/bssa0350040175

CrossRef Full Text | Google Scholar

Catalano, S., Monaco, C., Tortorici, L., Paltrinieri, W., and Steel, N. (2004). Neogene-quaternary tectonic evolution of the southern Apennines. Tectonics 23, TC2003. doi:10.1029/2003tc001512

CrossRef Full Text | Google Scholar

Causse, M., and Song, S. G. (2015). Are stress drop and rupture velocity of earthquakes independent? Insight from observed ground motion variability. Geophys. Res. Lett. 42, 7383–7389. doi:10.1002/2015GL064793

CrossRef Full Text | Google Scholar

Cello, G., and Mazzoli, S. (1998). Apennine tectonics in southern Italy: A review. J. Geodyn. 27, 191–211. doi:10.1016/s0264-3707(97)00072-0

CrossRef Full Text | Google Scholar

Cello, G., Tondi, E., Micarelli, L., and Mattioni, L. (2003). Active tectonics and earthquake sources in the epicentral area of the 1857 Basilicata earthquake (Southern Italy). J. Geodyn. 36, 37–50. doi:10.1016/s0264-3707(03)00037-1

CrossRef Full Text | Google Scholar

Cinque, A., Patacca, E., Scandone, P., and Tozzi, M. (1993). Quaternary kinematic evolution of the Southern Appennines. Relationships between surface geological features and deep lithospheric structures. Ann. Geophys. 36, 249–260.

Google Scholar

Cotton, F., Archuleta, R., and Causse, M. (2013). What is sigma of the stress drop? Seismol. Res. Lett. 84, 42–48. doi:10.1785/0220120087

CrossRef Full Text | Google Scholar

Courboulex, F., Vallée, M., Causse, M., and Chounet, A. (2016). Stress-drop variability of shallow earthquakes extracted from a global database of source time functions. Seismol. Res. Lett. 87 (4), 912–918. doi:10.1785/0220150283

CrossRef Full Text | Google Scholar

D’Agostino, N. (2014). Complete seismic release of tectonic strain and earthquake recurrence in the Apennines (Italy). Geophys. Res. Lett. 41, 1155–1162. doi:10.1002/2014GL059230

CrossRef Full Text | Google Scholar

D’Agostino, N., Silverii, F., Amoroso, O., Convertito, V., Fiorillo, F., Ventafridda, G., et al. (2018). Crustal deformation and seismicity modulated by groundwater recharge of karst aquifers. Geophys. Res. Lett. 45 (12253–12), 253–262. doi:10.1029/2018GL079794

CrossRef Full Text | Google Scholar

De Landro, G., Amoroso, O., Russo, G., D’Agostino, N., Esposito, R., Emolo, A., et al. (2022). Decade-long monitoring of seismic velocity changes at the Irpinia fault system (southern Italy) reveals pore pressure pulsations. Sci. Rep. 12, 1247. doi:10.1038/s41598-022-05365-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Devoti, R., Riguzzi, F., Cinti, F. R., and Ventura, G. (2018). Long-term strain oscillations related to the hydrological interaction between aquifers in intra-mountain basins: A case study from Apennines chain (Italy). Earth Planet. Sci. Lett. 501 (1), 1–12. doi:10.1016/j.epsl.2018.08.014

CrossRef Full Text | Google Scholar

Do Nascimento, A. F., Cowie, P. A., Lunn, R. J., and Pearce, R. G. (2004). Spatio-temporal evolution of induced seismicity at Açu reservoir, NE Brazil. Geophys. J. Int. 158, 1041–1052. doi:10.1111/j.1365-246x.2004.02351.x

CrossRef Full Text | Google Scholar

Douglas, J., and Edwards, B. (2016). Recent and future developments in earthquake ground motion estimation. Earth-Science Rev. 160, 203–219. doi:10.1016/j.earscirev.2016.07.005

CrossRef Full Text | Google Scholar

Durá-Gómez, I., and Talwani, P. (2010). Hydromechanics of the koyna-warna region, India. Pure Appl. Geophys. 167, 183–213. doi:10.1007/s00024-009-0012-5

CrossRef Full Text | Google Scholar

Efron, B. (1979). Bootstrap methods: Another look at the jackknife. Ann. Stat. 7 (1), 1–26. doi:10.1214/aos/1176344552

CrossRef Full Text | Google Scholar

El Hariri, M., Abercrombie, R. E., Rowe, C. A., and do Nascimento, A. (2010). The role of fluids in triggering earthquakes: Observations from reservoir induced seismicity in Brazil. Geophys. J. Int. 181 (3), 1566–1574. doi:10.1111/j.1365-246X.2010.04554.x

CrossRef Full Text | Google Scholar

Ferranti, L., Maschio, L., and Burrato, P. (2007). Field trip guide to active tectonics studies in the high Agri Valley. http://hdl.handle.net/2122/2749 (Istituto Nazionale di Geofisica eVulcanologia).

Google Scholar

Ferranti, L., Oldow, J. S., and Sacchi, M. (1996). Pre-Quaternary orogen-parallel extension in the Southern Apennine belt, Italy. Tectonophysics 260, 325–347. doi:10.1016/0040-1951(95)00209-x

CrossRef Full Text | Google Scholar

Ferranti, L., and Oldow, J. S. (1999). History and tectonic implications of low-angle detachment faults and orogen parallel extension, Picentini Mountains, Southern Apennines fold and thrust belt, Italy. Tectonics 18 (3), 498–526. doi:10.1029/1998tc900024

CrossRef Full Text | Google Scholar

Ferranti, L., Palano, M., Cannavò, F., Mazzella, M. E., Oldow, J. S., Gueguen, E., et al. (2014). Rates of geodetic deformation across active faults in southern Italy. Tectonophysics 621, 101–122. doi:10.1016/j.tecto.2014.02.007

CrossRef Full Text | Google Scholar

Giocoli, A., Stabile, T. A., Adurno, I., Perrone, A., Gallipoli, M. R., Gueguen, E., et al. (2015). Geological and geophysical characterization of the southeastern side of the High Agri Valley (southern Apennines, Italy). Nat. Hazards Earth Syst. Sci. 15 (2), 315–323. una quindicina d'anni tra studi. doi:10.5194/nhess-15-315-2015

CrossRef Full Text | Google Scholar

Gulia, L., and Meletti, C. (2007). Testing the b-value variability in Italy and its influence on Italian PSHA. Boll. Geof. Teor. Appl. 49 (1), 59–76.

Google Scholar

Gupta, H. K., and Rastogi, B. K. (1976). Dams and earthquakes. Amsterdam, Netherlands: Elsevier, 229.

Google Scholar

Gutenberg, B., and Richter, C. F. (1942). Earthquake magnitude, intensity, energy, and acceleration. Bull. Seismol. Soc. Am. 32, 163–191. doi:10.1785/bssa0320030163

CrossRef Full Text | Google Scholar

Hager, B. H., Dieterich, J., Frohlich, C., Juanes, R., Mantica, S., Shaw, J. H., et al. (2021). A process-based approach to understanding and managing triggered seismicity. Nature 595, 684–689. doi:10.1038/s41586-021-03668-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Hainzl, S., Ben-Zion, Y., Cattania, C., and Wassermann, J. (2013). Testing atmospheric and tidal earthquake triggering at Mt. Hochstaufen, Germany. J. Geophys. Res. Solid Earth 118, 5442–5452. doi:10.1002/jgrb.50387

CrossRef Full Text | Google Scholar

Harris, R. (1998). Introduction to special section: Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res. 103 (10), 24347–24358. doi:10.1029/98JB01576

CrossRef Full Text | Google Scholar

Hsu, Y.-J., Kao, H., Bürgmann, R., Lee, Y.-T., Huang, H.-H., Hsu, Y.-F., et al. (2011). Synchronized and asynchronous modulation of seismicity by hydrological loading: A case study in taiwan. Sci. Adv. 7, eabf7282. doi:10.1126/sciadv.abf7282

PubMed Abstract | CrossRef Full Text | Google Scholar

Improta, L., Bagh, S., De Gori, P., Valoroso, L., Pastori, M., Piccinini, D., et al. (2017). Reservoir structure and wastewater-induced seismicity at the val d'Agri oilfield (Italy) shown by three-DimensionalV local earthquake tomography. J. Geophys. Res. Solid Earth 122 (11), 9050–9082. doi:10.1002/2017JB014725

CrossRef Full Text | Google Scholar

King, G., Stein, R., and Lin, J. (1994). Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 84 (3), 935–953.

Google Scholar

Kotha, S. R., Weatherill, G., Bindi, D., and Cotton, F. (2020). A regionally-adaptable ground-motion model for shallow crustal earthquakes in Europe. Bull. Earthq. Eng. 18, 4091–4125. doi:10.1007/s10518-020-00869-1

CrossRef Full Text | Google Scholar

Lomax, A., Virieux, J., Volant, P., and Berge, C. (2000). “Probabilistic earthquake location in 3D and layered models: Introduction of a Metropolis-Gibbs method and comparison with linear locations,” in Advances in seismic event location. Editors C. H. Thurber, and N. Rabinowitz (Amsterdam, Netherlands: Kluwer), 101–134.

CrossRef Full Text | Google Scholar

Maschio, L., Ferranti, L., and Burrato, P. (2005). Active extension in val d’Agri area, southern Apennines, Italy: Implications for the geometry of the seismogenic belt. Geophys. J. Int. 162, 591–609. doi:10.1111/j.1365-246x.2005.02597.x

CrossRef Full Text | Google Scholar

Mazzoli, S., Barkham, S., Cello, G., Gambini, R., Mattioni, L., Shiner, P., et al. (2001). Reconstruction of continental margin architecture deformed by the contraction of the Lagonegro Basin, southern Apennines, Italy. J. Geol. Soc. Lond. 158, 309–319. doi:10.1144/jgs.158.2.309

CrossRef Full Text | Google Scholar

Mazzoli, S., D’Errico, M., Aldega, L., Corrado, S., Invernizzi, C., Shiner, P., et al. (2008). Tectonic burial and “young” (<10 Ma) exhumation in the southern Apennines fold-and-thrust belt (Italy). Geol. 36 (3), 243–246. doi:10.1130/G24344A.1

CrossRef Full Text | Google Scholar

Montone, P., Mariucci, M. T., Pondrelli, S., and Amato, A. (2004). An improved stress map for Italy and surrounding regions (central Mediterranean). J. Geophys. Res. 109–B10410. doi:10.1029/2003JB002703

CrossRef Full Text | Google Scholar

Munafò, I., Malagnini, L., and Chiaraluce, L. (2016). On the relationship between Mw and ML for small earthquakes. Bull. Seismol. Soc. Am. 106 (5), 2402–2408. doi:10.1785/0120160130

CrossRef Full Text | Google Scholar

Oth, A., Miyake, H., and Bindi, D. (2017). On the relation of earthquake stress drop and ground motion variability. J. Geophys. Res. Solid Earth 122, 5474–5492. doi:10.1002/2017JB014026

CrossRef Full Text | Google Scholar

Papanikolaou, I. D., and Roberts, G. P. (2007). Geometry, kinematics and deformation rates along the active normal fault system in the southern Apennines: Implications for fault growth. J. Struct. Geol. 29, 166–188. doi:10.1016/j.jsg.2006.07.009

CrossRef Full Text | Google Scholar

Patacca, E., and Scandone, P. (2007) Constraints on the interpretation of the crop-04 seismic line derived from plio–pleistocene foredeep and thrust-sheet-top deposits (southern Apennines, Italy). CROP-04. (Ed. by A. Mazzotti, E. Patacca, and P. Scandone) Rome: Boll. della Soc. Geol. It. Special, 241–256.

Google Scholar

Patacca, E., and Scandone, P. (2001). “Late thrust propagation and sedimentary response in the thrust belt-foredeep system of the Southern Apennines,” in Anatomy of an orogen: The Apennines and adjacent Mediterranean basin. Editors G. B. Vai, and I. P. Martini, 401–440.

CrossRef Full Text | Google Scholar

Picozzi, M., Bindi, D., Festa, G., Cotton, F., Scala, A., and D’Agostino, N. (2021b). Spatio-temporal evolution of microseismicity seismic source properties at the Irpinia near fault observatory, southern Italy. Bull. Seismol. Soc. Am. 112 (1), 226–242. doi:10.1785/0120210064

CrossRef Full Text | Google Scholar

Picozzi, M., Bindi, D., Spallarossa, D., Oth, A., Di Giacomo, D., and Zollo, A. (2019b). Moment and energy magnitudes: Diversity of views on earthquake shaking potential and earthquake statistics. Geophys. J. Int. 216, 1245–1259. doi:10.1093/gji/ggy488

CrossRef Full Text | Google Scholar

Picozzi, M., Bindi, D., Zollo, A., Festa, G., and Spallarossa, D. (2019a). Detecting long-lasting transients of earthquake activity on a fault system by monitoring apparent stress, ground motion and clustering. Sci. Rep. 9, 16268. doi:10.1038/s41598-019-52756-8

CrossRef Full Text | Google Scholar

Picozzi, M., Cotton, F., Bindi, D., Emolo, A., Adinolfi, G. M., Spallarossa, D., et al. (2021a). Spatiotemporal evolution of ground-motion intensity at the Irpinia near-fault observatory, southern Italy. Bull. Seismol. Soc. Am. 112 (1), 243–261. doi:10.1785/0120210153

CrossRef Full Text | Google Scholar

Rinaldi, A. P., Improta, L., Catalli, F., and Urpi, L. S. (2020). Combined approach of poroelastic and earthquake nucleation applied to the reservoir-induced seismic activity in the Val d’Agri area, Italy. J. Rock Mech. Geotechnical Eng. 12 (4), 802–810. doi:10.1016/j.jrmge.2020.04.003

CrossRef Full Text | Google Scholar

Roda-Boluda, D. C., and Whittaker, A. C. (2018). Normal fault evolution and coupled landscape response: Examples from the Southern Apennines, Italy. Basin Res. 30 (Suppl. 1), 186–209. doi:10.1111/bre.12215

CrossRef Full Text | Google Scholar

Scholz, C. H. (2019). The mechanics of earthquakes and faulting. Cambridge University Press.

Google Scholar

Schorlemmer, D., Wiemer, S., and Wyss, M. (2005). Variations in earthquake-size distribution across different stress regimes. Nature 437, 539–542. doi:10.1038/nature04094

CrossRef Full Text | Google Scholar

Serlenga, V., and Stabile, T. A. (2019). How do local earthquake tomography and inverted dataset affect earthquake locations? The case study of high Agri Valley (southern Italy). Geomat. Nat. Hazards Risk 10 (1), 49–78. doi:10.1080/19475705.2018.1504124

CrossRef Full Text | Google Scholar

Shapiro, S. A., and Dinske, C. (2021). Stress drop, seismogenic index and fault cohesion of fluid-induced earthquakes. Rock Mech. Rock Eng. 54, 5483–5492. doi:10.1007/s00603-021-02420-3

CrossRef Full Text | Google Scholar

Shapiro, S. A., Krüger, O. S., and Dinske, C. (2013). Probability of inducing given-magnitude earthquakes by perturbing finite volumes of rocks. J. Geophys. Res. Solid Earth 118, 3557–3575. doi:10.1002/jgrb.50264

CrossRef Full Text | Google Scholar

Shashidhar, D., Rao, N. P., and Gupta, H. K. (2011). Waveform inversion of broad-band data of local earthquakes in the Koyna-Warna region, Western India. Geophys. J. Int. 185, 292–304. doi:10.1111/j.1365-246x.2011.04935.x

CrossRef Full Text | Google Scholar

Shiner, P., Beccaccini, A., and Mazzoli, S. (2004). Thin-skinned versus thick-skinned structural models for apulian carbonate reservoirs: Constraints from the val d’Agri fields, S Apennines, Italy. Mar. Pet. Geol. 21, 805–827. doi:10.1016/j.marpetgeo.2003.11.020

CrossRef Full Text | Google Scholar

Silverii, F., D'Agostino, N., Borsa, A. A., Calcaterra, S., Gambino, P., Giuliani, R., et al. (2019). Transient crustal deformation from karst aquifers hydrology in the Apennines (Italy). Earth Planet. Sci. Lett. 506, 23–37. doi:10.1016/j.epsl.2018.10.019

CrossRef Full Text | Google Scholar

Silverii, F., D’Agostino, N., Métois, M., Fiorillo, F., and Ventafridda, G. (2016). Transient deformation of karst aquifers due to seasonal and multi-year groundwater variations observed by GPS in Southern Apennines (Italy). J. Geophys. Res. Solid Earth 121, 8315–8337. doi:10.1002/2016jb013361

CrossRef Full Text | Google Scholar

Simpson, D. W., and Negmatullaev, S. K. (1981). Induced seismicity at nurek reservoir, tadjikistan, USSR. Bull. Seismol. Soc. Am. 71 (5), 1561–1586.

Google Scholar

Stabile, T. A., Giocoli, A., Lapenna, V., Perrone, A., Piscitelli, S., and Telesca, L. (2014). Evidence of low-magnitude continued reservoir-induced seismicity associated with the Pertusillo artificial lake (southern Italy). Bull. Seismol. Soc. Am. 104 (4), 1820–1828. doi:10.1785/0120130333

CrossRef Full Text | Google Scholar

Stabile, T. A., Giocoli, A., Perrone, A., Piscitelli, S., Telesca, L., and Lapenna, V. (2015). Relationship between seismicity and water level of the Pertusillo reservoir (southern Italy). Boll. Geof. Teor. Appl. 56, 505–517. doi:10.4430/bgta0161

CrossRef Full Text | Google Scholar

Stabile, T. A., Iannaccone, G., Zollo, A., Lomax, A., Ferulano, M. F., Vetri, M. L. V., et al. (2013). A comprehensive approach for evaluating network performance in surface and borehole seismic monitoring. Geophys. J. Int. 192 (2), 793–806. doi:10.1093/gji/ggs049

CrossRef Full Text | Google Scholar

Stabile, T. A., Serlenga, V., Satriano, C., Romanelli, M., Gueguen, E., Gallipoli, M. R., et al. (2020). The INSIEME seismic network: A research infrastructure for studying induced seismicity in the high Agri Valley (southern Italy). Earth Syst. Sci. Data 12, 519–538. doi:10.5194/essd-12-519-2020

CrossRef Full Text | Google Scholar

Telesca, L., Giocoli, A., Lapenna, V., and Stabile, T. A. (2015). Robust identification of periodic behavior in the time dynamics of short seismic series: The case of seismicity induced by Pertusillo lake, southern Italy. Stoch. Environ. Res. Risk Assess. 29, 1437–1446. doi:10.1007/s00477-014-0980-6

CrossRef Full Text | Google Scholar

Valoroso, L., Improta, L., Chiaraluce, L., Di Stefano, R., Ferranti, L., Govoni, A., et al. (2009). Active faults and induced seismicity in the Val d’Agri area (Southern Apennines, Italy). Geophys. J. Int. 178, 488–502. doi:10.1111/j.1365-246X.2009.04166.x

CrossRef Full Text | Google Scholar

Vittori, E., Maschio, L., Ferreli, L., Michetti, A. M., and Serva, L. (1997). Carta e base di dati delle faglie capaci per l’Italia centro-meridionale: Presentazione e stato di avanzamento del progetto ITHACA. Il Quat. 10 (2), 305–312.

Google Scholar

Wells, D. L., and Coppersmith, K. J. (1994). New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 84, 974–1002.

Google Scholar

Wiemer, S. (2001). A software package to analyze seismicity: Zmap. Seismol. Res. Lett. 72, 373–382. doi:10.1785/gssrl.72.3.373

CrossRef Full Text | Google Scholar