- 1School of Earth Sciences and Engineering, Suzhou University, Suzhou, China
- 2National Engineering Research Center of Coal Mine Water Hazard Controlling, Anhui, China
- 3School of Resource and Geoscience, China University of Mining and Technology, Xuzhou, China
To further understand the pore structure characteristics and their effect on CH4 adsorption capacity for high-rank coals. Based on 11 fresh coal samples from the Zhina coalfield of South China. We analyzed the pore structure characteristics of coal samples by low-temperature liquid-nitrogen adsorption (LP-N2A) measurements. On the basis of nuclear magnetic resonance (NMR), we obtained the fractal dimensions of different types of pores by the new model, studied the relationship between the fractal dimensions, and the characteristic parameters of coals (composition and pore characteristics) and discussed the influence of the fractal dimensions on CH4 adsorption. The results show that according to LP-N2A isotherms, all coals can be classified into three types. The micropores provide the largest proportion of the specific surface area (SSA) of coals. Two fractal dimensions, Da (adsorption pore) and Ds (seepage pore), ranged from 2.471 to 2.805 and from 2.812 to 2.976, which were acquired in the saturated water condition by NMR. Furthermore, Da and Ds have different correlations with ash yield, carbon contents, moisture, SSA and irreducible fluid porosity. The coal composition and pore parameters have much greater control over fractal dimensions. Moreover, the different fractal dimensions have different influences on methane adsorption. With the increase of Da, the methane adsorption capacity is enhanced, but it is weakened with the increase of Ds. The high-rank coals have more SSA with higher Da and provide more adsorption sites for CH4. Langmuir pressure PL has different correlations with fractal dimensions. Da decreases with the increase of PL. The adsorption velocity is faster with higher Da. Thus, the fractal dimensions are the comprehensive reflection of differences among the physical properties of coal and are able to show the effect of coal properties on methane adsorption fully.
1 Introduction
Coal is a complex and heterogeneous porous medium. Its internal pore surface area is much larger than its external surface area which can be neglected. The pore surface with strong adsorption ability is the primary storage and migration of coalbed methane (CBM) (Alexeev, 1977; Meyers, 1982). The structure and developmental features of pores perform a significant control function in adsorption capacity, desorption capacity and permeability of coal reservoirs, which directly affects the exploration efficiency of CBM. Meanwhile, the unstable CBM production is influenced by the complex features of pore-fracture, buried depth of coal seam and geothermal dynamics (Johnson and Flores, 1998; Saboorian-Jooybari, 2016; Zhao et al., 2019). Thus, it is a great significance to characterize coal reservoirs by researching the storage capacity and migration mechanism of pores in coal reservoirs (Dullien, 1991).
At present, defining the coal pore system, there are various classifications of qualitative descriptions of pores in coal reservoirs (Hodot, 1966; Sing, 1982; Fu et al., 2005; Cai et al., 2013a). Based on gas adsorption−desorption, Hodot’s classification (Hodot, 1966) is widely used. The pores are divided into four types: micropores (less than 10 nm), transition pores (10–100 nm), mesopores (100–1000 nm) and macropores (more than 1,000 nm). Pores (less than 100 nm) are adsorption pores which play a crucial role in CBM adsorption and diffusion pores (Cai et al., 2013b). In the present study, the pore characteristics of coal reservoir are studied by many methods and technologies, such as mercury intrusion porosimetry (MIP) (Gao et al., 2018; Ju et al., 2018), scanning electron microscopy (SEM) (Shan et al., 2015; Li et al., 2020a), N2 adsorption-desorption and CO2 gas adsorption (Acevedo and Barriocanal, 2015; Li et al., 2019; Nie et al., 2020), atomic force microscope (AFM) (Pan et al., 2015), small-angle X-ray scattering (SAXS) (Ferro et al., 2012; Coetzee et al., 2015; Liu and He, 2017) and nuclear magnetic resonance (NMR) (Lee and Lee, 2013; Li et al., 2017). The result shows that the pore structure of coal has a fractal feature within a certain scale range (Fu et al., 2005; Shi et al., 2006; Yao et al., 2009; Liu et al., 2015; Peng et al., 2017). However, these technical methods may cause the decrease of pore diameter, the damage of coal matrix system and the loss of some important details of coal reservoir (Yao and Liu, 2012). NMR is an efficient experimental method to study the pore properties of coal reservoirs. The NMR technique is widely applied in petrophysical features, shapes, sizes and porosity of pores, because of its rapid, accurate and high-resolution characteristics. NMR T2 cutoff value (T2C) is an important parameter for irreducible water saturation calculation, pore size distribution (PSD) and permeability prediction. Ge et al. (2014) studied the influential factors of T2C and proposed the predicating model for T2C value by multiple linear regressions of multifractal parameters. Yao et al. (2010) designed the NMR experiments of 100% water-saturated and irreducible water coal samples, respectively. Results show that the relaxation times corresponding to the adsorption-pore (< 100 nm), seepage-pore (> 100 nm) and fracture are 0.5–2.5 ms, 20–50 ms and >100 ms, respectively. Meanwhile, the NMR-based permeability model is built on the basis of the data of calculated irreducible and producible porosities. Zheng et al. (2020) divided T2 cutoffs into two types: the absolute irreducible fluid T2 cutoffs (T2C1) and absolute movable fluid T2 cutoff (T2C2); Based on the dual T2 cutoffs model, the pore fluid typing of coal is divided into three types: absolute irreducible fluid (T2 < T2C1), partial movable fluid (T2C1 < T2 < T2C2) and absolute movable fluid (T2 > T2C2).
Because of the complexity and anisotropy of the pore structure of the coal reservoir, it is difficult to give an accurate description by the traditional geometrical method and is unable to measure by fixed scale. The fractal theory is an effective method to quantitatively describe pore structure features (Song et al., 2013; Wang et al., 2013). Based on the isotherms of N2 gas adsorption/desorption, adopting the fractal Frenkel–Halsey–Hill (FHH) method, the fractal dimensions D1 and D2, which represent the irregularity of pore surface and heterogeneity of pore structure, are obtained (Yao et al., 2008). Coupled with CH4 isotherm adsorption experiments, D1 has more significant influence than D2 on adsorption capacity (Li et al., 2015). Song et al. (2017) analyzed the fractal characteristics of nanopores in tectonically deformed coals on the basis of mercury intrusion and N2/CO2 gas adsorption experiments. They found that the fractal dimension (<8 nm) has an important role in the adsorption capacity. Additionally, previous researchers have found that the NMR fractal theory is used to study the pore-fracture characteristics of coal (Li et al., 2013; Sun et al., 2015; Ouyang et al., 2016). Based on the NMR T2 spectrum, the fractal dimensions are divided into D1(adsorption pores) and D2(seepage pores). D2 has a significant influence on the permeability of the coal reservoir (Chen et al., 2018). Zhou et al. (2016) calculated the adsorption space fractal (DNMRA), seepage space fractal (DNMRS) and moveable fluid space fractal (DNMRM) in low-rank coals, respectively. They demonstrated the model between permeability and DNMRM. With MIP and NMR methods, MIP and NMR permeability were estimated by the modified Kozeny-Carman Equation and movable porosity-permeability model, respectively (Li et al., 2020b). Zhou et al. (2022) proposed a novel model by the low-field NMR and obtained the fractal dimensions of accessible, inaccessible and total pores, respectively. Nevertheless, the correlation between CH4 adsorption capacity and NMR fractal dimensions of coals has not been sufficiently researched.
In this paper, we collect 11 coal samples from the Zhina coalfield of South China and carry out the experiment analyses to investigate the characteristics of pores and coal adsorption by the LP-N2A, NMR and CH4 isotherm adsorption methods. According to the experimental data and results analysis, we analyze the pore characteristics of coal samples, calculate the fractal dimensions of different pore types, and study the relationships between CH4 adsorption capacity and fractal dimensions.
2 Materials and methods
2.1 Sampling
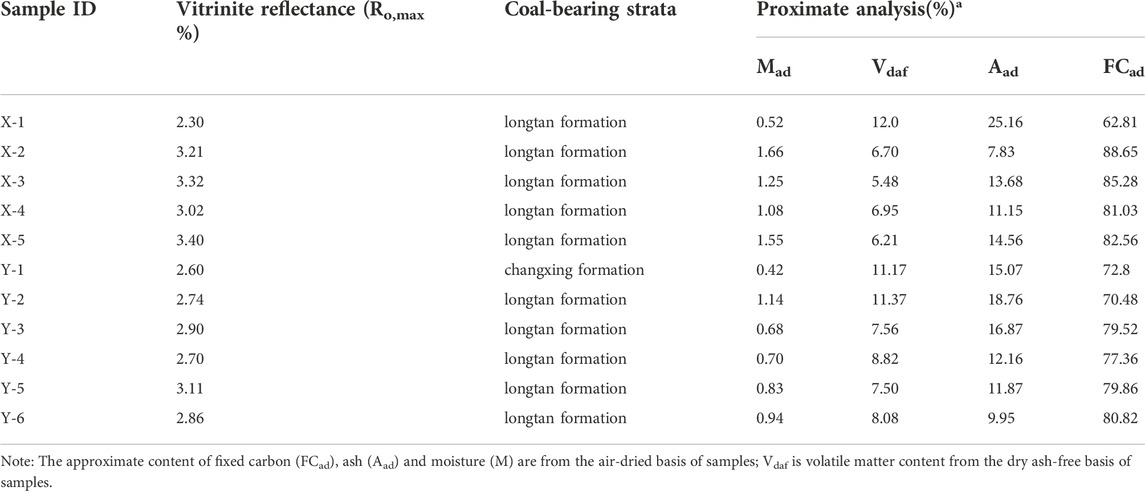
Eleven samples were collected from the Bide-Santang Basin, which is a CBM reservoir of multiple coal seams in the Zhina coalfield, Guizhou Province (Figure 1). Zhina coalfield, located in western Guizhou Province, is the largest anthracite coal occurrence area in China. The coal-bearing strata of the Bide-Santang Basin are the Longtan and Changxing formations of Upper Permian, with a formation thickness of 300–450 m. In the upper Permian, the coal-bearing formation was mainly developed at continental, continental-marine transitional and shallow marine sedimentary facies. Multiple coal-bearing strata formed during this period due to frequent sea transgression and regression. Tectonic activities during the Yanshan and Himalayan formed large synclines and synclinoria, which became important structures controlling coal in the region (Yang et al., 2019). The gas content of coal seam of in Longtan Formation is generally high. The average gas content is 10–15.78 m3/t. The reservoir pressure is 2.95–11.59 MPa. The in-situ permeability of coal reservoir is low, and its average value is 0.14 mD (Cheng et al., 2021). Table 1 shows the collected samples and their locations. All the samples whose size was 30 cm×30cm×30 cm were wrapped with plastic wrap according to the Chinese Standard (GB/T 19,222–2003) and quickly packed. The grind and screening of samples were completed in the laboratory after sampling. According to GB/T6948-2008 and GB/T212–2008, samples (less than 0.200 mm in particle diameter) were selected for proximate analysis and maximum vitrinite reflectance.
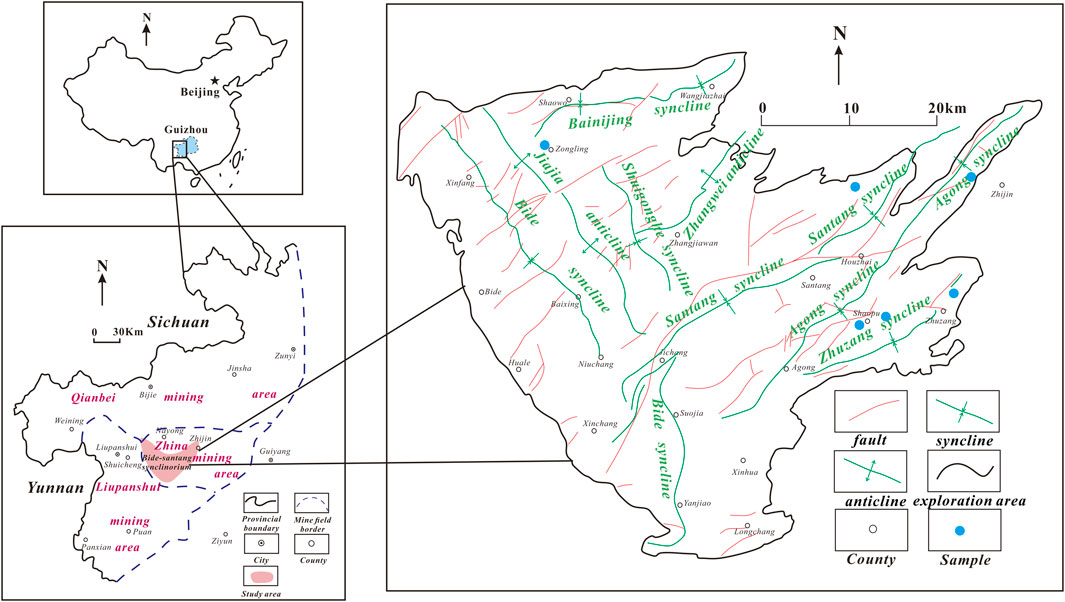
FIGURE 1. Location map showing the distribution of sampling points in the Bide-Santang Basin, China (modified from Yang et al., 2014, 2019).
2.2 CH4 isotherm adsorption experiments
Experiments were performed at the China petroleum exploration and development research institute Langfang branch using TerraTek Isothermal Adsorption and Desorption Experimental System (IS–300), according to Chinese standard (GB/T 19,560–2008). The sensitivity of the temperature sensor and pressure sensor is 0.3 C and 0.001°MPa, respectively. All the coal samples were broken, smashed and screened to a size range of 0.18–0.25 mm. Then, the moisture-equilibrium treatment of 200 g samples was carried out. The screened experimental samples were put in an incubator with oversaturated K2SO4 solution. The samples were weighed every other 24 h until the quality change was below 2 percent of their weight. The experimental temperature was 30°C, and the experimental pressure range was 0–13 MPa. The time of adsorption equilibrium kept above 12 h.
2.3 LP-N2A and NMR measurement
LPN2A was performed for the 11 coal samples using a Micromeritics ASAP 2000 surface area measurement. First, the coal samples were ground into a size range of 0.25–0.40 mm. Approximately 5 g of coal particles was placed in a vacuum oven and degassed at 105 C for 12 h to remove air, free moisture and other impurities. Then, degassed samples were exposed to N2 with purity greater than 99.99% at a temperature of 77.3°K. The range of relative pressure (P/P0) was from 0.01 to 0.995. Moreover, the Brunauer–Emmett–Teller (BET), Barrett–Joyner–Halenda (BJH) and density functional theory (DFT) models were applied to evaluate the specific surface area (SSA), pore volume (PV) and PSD, respectively (Brunauer et al., 1938; Barrett et al., 1951; Geerlings et al., 2003).
NMR measurement was performed at SGS Unconventional Petroleum Technical Testing Limited Company, following specifications of surveys SY/T 6490-2007. Firstly, several horizontal cylindrical core plugs with a diameter of 2.5 cm were drilled; Secondly, all core plugs were placed in a drying oven until drying to constant weight, then saturated with 100% saturated standard brine for 24 h; Thirdly, core plugs were placed in the probe of low magnetic field resonance core analyzer to test the transverse relaxation time T2 and worked out relaxation time spectrum of T2 by inversion. Finally, core plugs were placed in a centrifuge to dehydrate, and the centrifugal pressure was 200°psia.
2.4 Fractal theory based on NMR
Lots of papers have extensively reported the fractal dimensions of NMR (Zhang et al., 2007; Wang et al., 2011; Zhang and Weller, 2014). The fractal dimensions of NMR are obtained from the NMR data of the irreducible water and saturated water by establishing the equation of fractal dimension of coal pores (Ouyang et al., 2016; Zhou et al., 2018), But the low correlation coefficient of fractal makes these methods unsuitable for obtaining quantitative heterogeneity for porous media. We calculated the fractal dimension of pores by the new model (Zhou et al., 2022).
The critical characteristic of fractal targets in nature is self-affinity of dimension and can be quantified by a power-law function (Lai et al., 2018).
Where
The pore size distribution could be directly related to the distribution of NMR T2 relaxation time (Daigle and Johnson, 2016). The formula can be expressed as
If the coal structure is a tube, then Fs = 2; Fs = 3 for spherical; ρ is the strength of transverse relaxation;
The signal amplitude at the T2i relaxation time is a function of the number of protons, corresponding to the pore volume of pore radius
Where
The pore morphology of coal samples is assumed to be spherical, then the number of pores with a specified size
Therefore, the number of pores whose pore size is larger than
Where
By combining Equations 1, 2, and 5:
Using logarithms for Eq. 6, is revised as
Where
3 Results
3.1 Coal rank, coal component and CH4 adsorption analysis results
As seen from Table 1, the maximum vitrinite reflectance of coals ranges from 2.30 to 3.40%, which belongs to high-rank coal. Moisture contents of coals increase from 0.52 to 1.66%, ash yields of coals increase from 7.83 to 25.16%, carbon contents of coals reduce from 88.65 to 62.81% and volatile matter contents of most samples increase from 5.48 to 12.00%. The composition of coal samples is complicated, and each component concentration has the noticeable differences. Most of the coal samples are low–middle ash coal. Vitrinite is the dominant maceral composition for all coal samples.
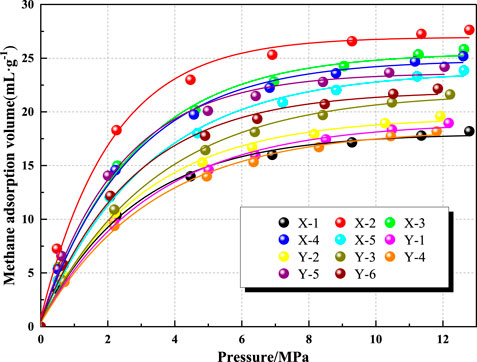
The results of the methane adsorption experiment of each coal sample are shown in Figure 2. The experimental results are fitted by the Langmuir equation:
Where P is the pressure, MPa; V is the absorption at the pressure P, m3/t; VL is the Langmuir volume, m3/t; PL is the Langmuir pressure, MPa.
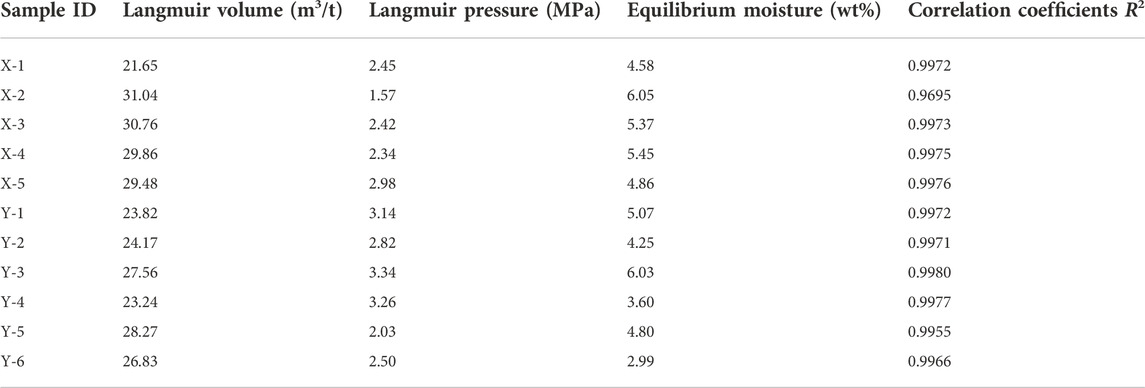
The fitted results are shown in Table 2. The degree of the fitting is high by the Langmuir equation about the methane adsorption curves of all coal samples. The Langmuir volume ranges from 21.65 ml/g to 31.04 ml/g, and the Langmuir pressure ranges from 1.57°MPa to 3.34 MPa. It shows that the adsorption capacity of different coal samples has the certain difference. But methane adsorption of coal samples has a different growth rate with increasing pressure. Methane adsorption of some coal samples increases rapidly at low pressure but flattens at high pressure. Yet methane adsorption of some other coal samples increases slowly (Li et al., 2013). For example, the methane adsorption of coal sample X-2 is about 17.4 ml/g at 2 MPa pressure, but that of coal sample X-3 is only about 13.9 ml/g at the same pressure. Although their VL has little difference, the methane adsorption at low pressure differs greatly. This illustrates that the ease of their methane adsorption is different. Coal sample X-2 is easy to adsorb methane, but coal sample X-3 is the opposite. In the process of coalbed gas production, the adsorbing methane of coal sample X-2 is difficult to desorb, but coal sample X-3 is not.
3.2 LP-N2A isotherms and pore structure characteristics
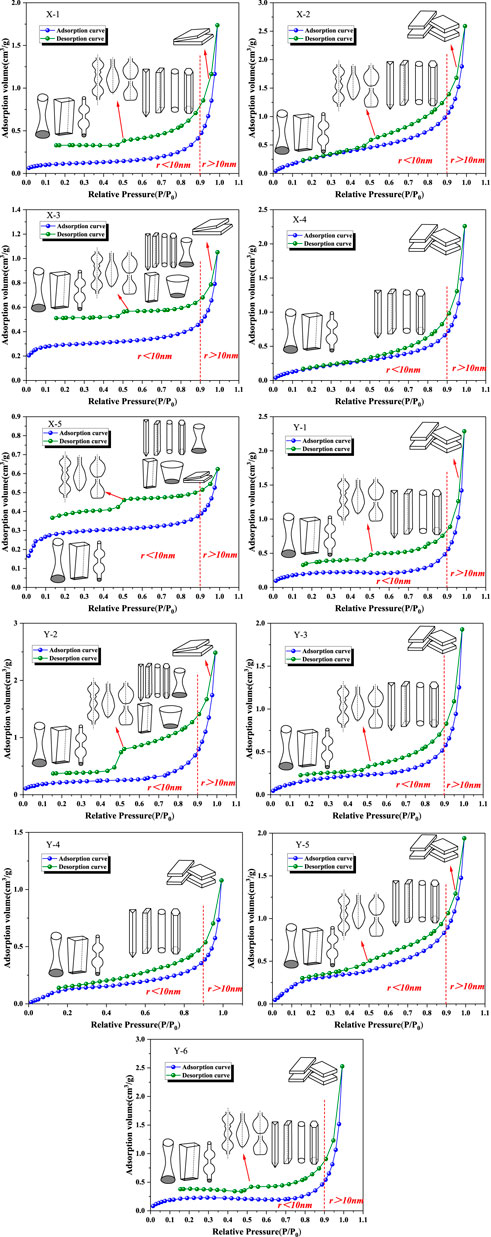
The characteristic differences of adsorption and desorption isotherms of coal samples represent the development of different types of pores (Yang et al., 2014). For porous media, the LP-N2A curves may be grouped into six types and hysteresis loops may be divided into four types (Sing, 1985). Figure 3 shows the LP-N2A isotherms for 11 coal samples. The LP-N2A isotherms of coals have remarkable differences. Based on the classification scheme proposed by De Boer (De Boer, 1958) and IUPAC (IUPAC, 1982), all coal samples can be classified as three types (A, B, and C) by the characteristics of LP-N2A isotherms.
Type A is for X-2, X-4, Y-3, Y-4 and Y-6 samples. When p/p0 < 0.8, the adsorption curves increase slowly. The adsorption curves increase rapidly at p/p0 approaching 1.0. There are inconspicuous hysteresis loops and no inflection points at 0.4 < p/p0 < 1.0. But the adsorption and desorption curves nearly overlap at p/p0 < 0.4. The adsorption volume is small at p/p0 < 0.4. At this stage, the pores consist mainly of impermeable pores closed at one end. When 0.4 < p/p0 < 0.9, the pore was dominated by cylindrical pores with openings at both ends. Due to the obvious adsorption hysteresis loops and the rapid rise of the adsorption curve, the pores are mainly open parallel plate pores at 0.9 < p/p0 < 1.0. This shows that the transition pores, mesopores and some micropores of samples have good connectivity. The samples (e.g., X-1, Y-1, Y-2 and Y-6) belong to type B. Their adsorption curves increase steadily at p/p0 < 0.8 and then increase significantly and rapidly at 0.8 < p/p0 < 1.0. It is different from type A in that it has a wide hysteresis loop at 0.5 < p/p0 < 1.0. When p/p0 < 0.4, most of the pores are impermeable pores closed at one end. But their adsorption and desorption branches have no overlap at p/p0 < 0.5, which is thought to be due to pore swelling and chemical interactions of gas and coal pore surface (Sun et al., 2015; Li et al., 2018). The hysteresis loop indicates that the pores are mainly open cylinder pores at 0.4 < p/p0 < 0.9. The desorption curve has an inflection point at a relative pressure of approximately 0.5, which reacts to the presence of thin neck and ink bottle pores. When 0.9 < p/p0 < 1.0, the pore types are also open parallel plate pores. Moreover, type C is for X-3 and X-5 samples. The pore types are similar to type B and type C at p/p0 < 0.4, but the hysteresis loop is also not completely closed. When 0.4 < p/p0 < 0.9, the appearance of wide hysteresis loops indicates that the pores are mainly composed of open pores, including cylinder pores and wedge pores. The desorption curve has a sharp inflection point at p/p0 of 0.5, which indicates the presence of a large number of fine bottleneck and ink bottle pores. When 0.9 < p/p0 < 1.0, type C differs from other types in having few plate-shaped pores.
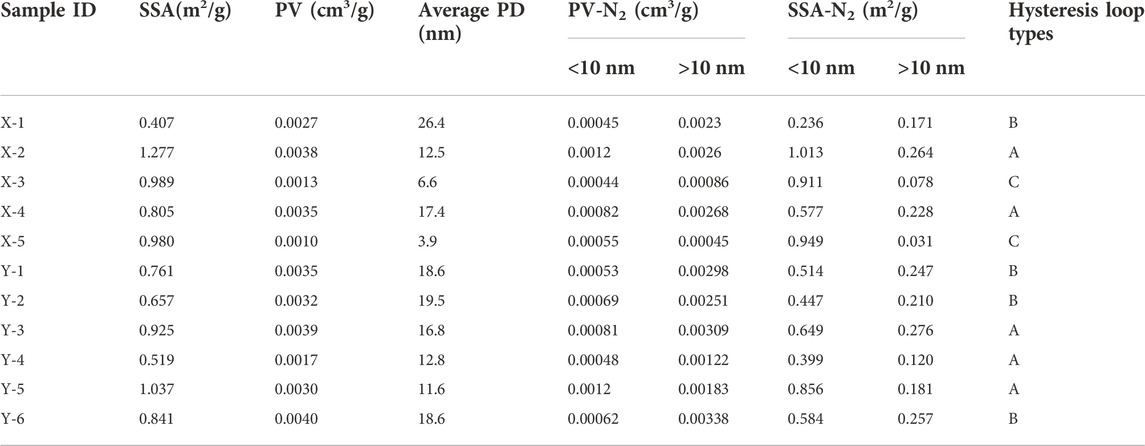
The LPN2GA test results are shown in Table 3. The SSA and PV of coal samples are obviously different. The SSA and PV range from 0.407 to 1.277 m2/g and 0.001–0.004 cm3/g, respectively. The PSD of the PV and SSA in different types of coal samples is shown in Figure 4. The SSA distribution curves suggest that all coal samples exhibit unimodality with the main peak at ∼1 nm, indicating that the SSA of coal samples is more concentrated in micropores (the SSA for < 10 nm and > 10 nm is 0.236–1.013°m2/g and 0.031–0.276°m2/g, respectively). Compared with type A, the SSA of type B/C pores is generally undeveloped at > 3 nm. Except for samples X-3 and X-5, the PV distribution shows obvious multimodality in which the peaks of the overall samples are at ∼1, ∼20 and ∼50 nm. The PV for < 10 nm and > 10 nm is 4.4×10-4-1.2×10–3°cm3/g and 4.5×10-4-3.38×10–3°cm3/g, respectively, indicating that the pores for > 10 nm provide most of the pore volume. Meanwhile, the micropores of type C provide the largest proportion of PV and SSA. Mainly because of the increasing metamorphic degree of coals, the loss of oxygen functional groups and side chains is accompanied by the significant improvement in the degree of aromatization and the increasing and orderly arrangement of aromatic ring layers in the molecular structure of coal, which results in the decrease of larger pores and the increase of smaller pores (Li et al., 2017).
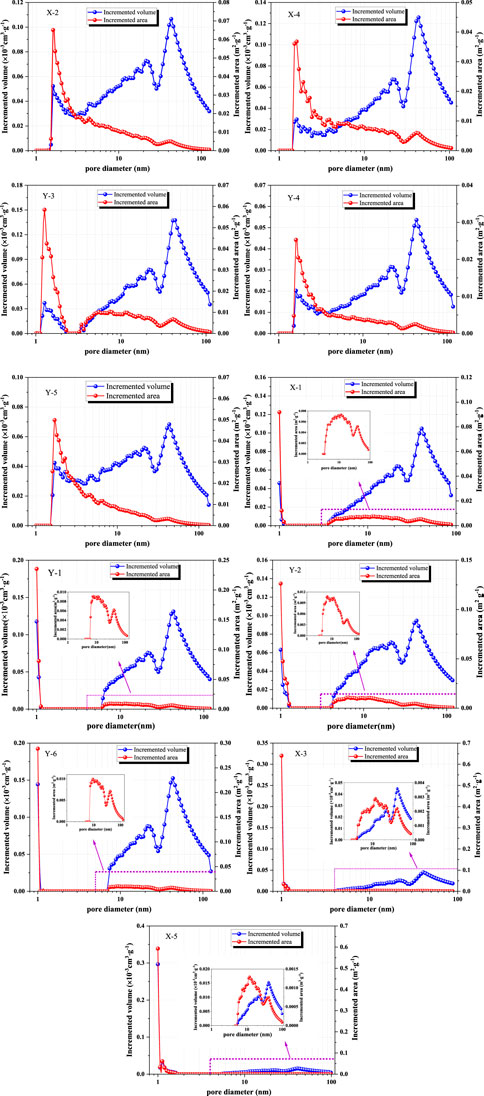
FIGURE 4. The distribution of incremental PV and SSA with LPN2GA. (X-2, X-4, Y-3, Y-4 and Y-5) Type A, (X-1, Y-1, Y-2 and Y-6) Type B, and (X-3 and X-5) Type C.
3.3 Pore size distribution of NMR
Previous researches (Cai et al., 2013a; Li et al., 2013) found that T2 can reflect the PV/size distribution in the saturated water, but cannot provide absolute full-scale PSD. There are two methods to obtain full-scale PSD by NMR measurement, namely centrifugation test and surface relaxation method.
According to the relationship between different centrifugal forces and centrifugal pore radius (Washburn equation), the pore radius r corresponding to the T2 cutoff value can be obtained at the optimal centrifugal pressure. Yao et al. (2010) propose the centrifugal experiment method of full-scale PSD of coal reservoir by NMR T2 cutoff value. The formula can be expressed as
Where rci (nm) is a pore size corresponding to a relaxation time T2i (ms), T2c is a relaxation time threshold, r (nm) is the pore size corresponding to the T2c and r is about 100 nm.
It is worth noting that there are still some movable fluids in the sample when T2 < T2C. Thus, the centrifugal experiment method is inapplicable. Then, Zheng et al., 2019 proposed a surface relaxation method to calculate the surface relaxivity of different coals, which are 2.1 μm/s, 3.0 μm/s and 1.6 μm/s for low-, medium-, and high-rank coal, respectively.
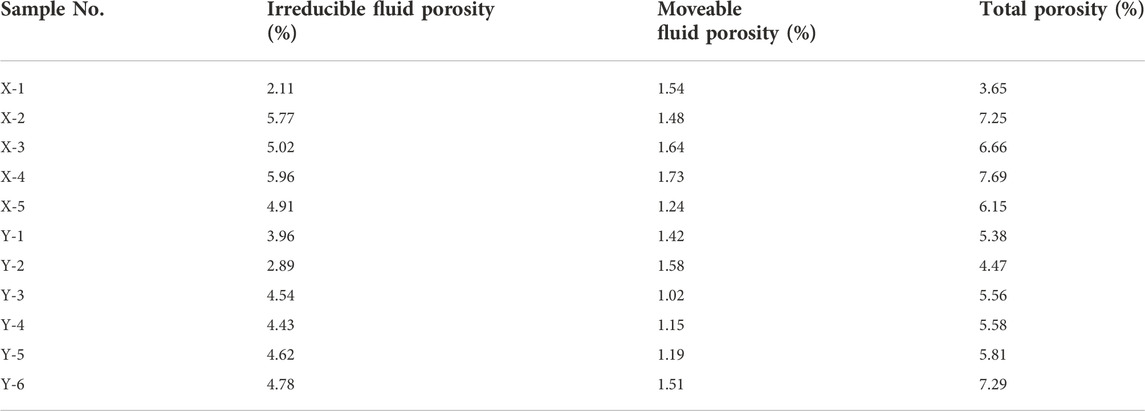
The pore of coal can be divided into micropores, transition pores, mesopores, and macropores. Micropores and transition pores belong to adsorption pores, mesopores and macropores belong to seepage pores. According to Eq. 2, the T2 spectrum of coal samples is divided into four parts, corresponding to <2.08 ms, 2.08–20.8 ms, 20.8–208 ms, > 208 ms, and representing different pores: micropore, transition pore, mesopore, macropore, respectively (Figure 5). We also calculated the cumulative porosity in two conditions. The cumulative porosity of other coal samples is given in Table 4. The irreducible and moveable fluid porosity range from 2.11% to 5.96% and 1.02%–1.73%, respectively.
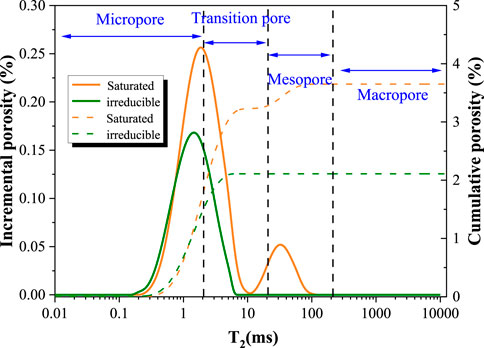
FIGURE 5. NMR T2 distribution of X-1 coal sample in the saturated water condition and the irreducible water condition.
3.4 Characteristics of fractal dimensions in NMR
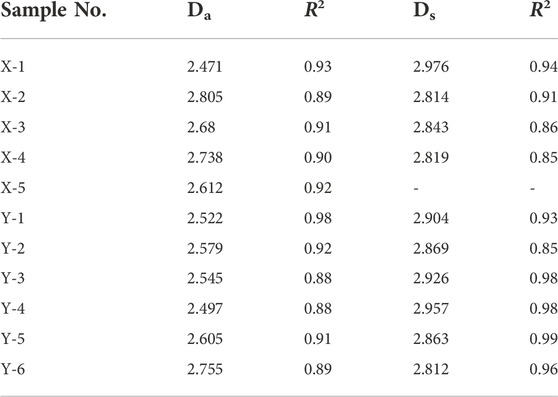
The fractal dimension of pore structure can be obtained from the slope of the equation by the linear fitting data of log(N(rj)) and log(T2). The linear correlation coefficient for sample X-1 is greater than 0.92, indicating that the adsorption and seepage pore structures of samples can be characterized by the fractal geometry theory (Figure 6). Da and Ds represent the fractal dimensions of adsorption and seepage pores under the condition of saturated water, respectively. The fractal dimension results of all samples are listed in Table 5. Generally, the fractal dimension D is between 2 and 3. When fractal dimension D is 2, the pore surface is smooth. When fractal dimension D is 3, the pore surface is rough (Zhang and Weller, 2014). The more complicated rock surface is, the larger D is (Mandelbrot and Benoit, 1998). The ranges of Da and Ds vary from 2.471 to 2.805 and from 2.812 to 2.976, with the average of 2.619 and 2.878, respectively. Because the relaxation time of the seepage pore is not detected for sample X-5, the fractal dimension of the seepage pore is missing. The fractal dimension Da is less than Ds, indicating that seepage pores are more complex than adsorption pores in all samples.
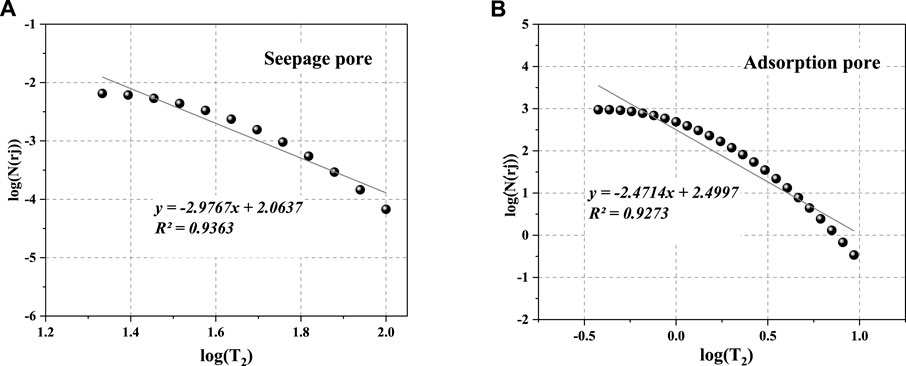
FIGURE 6. The double-logarithm relationship of different pores between log(T2) vs. log(N(rj)) for Sample X-1. (A) The double-logarithm relationship of seepage pore, (B) The double-logarithm relationship of adsorption pore.
4 Discussions
Due to the complex physical properties of coal, the methane adsorption capacity of the coal is affected by many factors, such as coal composition, pore characteristics and so on (Lin et al., 2021). Fractal represents the complexity of coal samples and can be used as a combination of comprehensive factors. However, most previous studies focused on the relationship between the coal permeability and fractal dimension by NMR, so this study mainly discussed the influence of fractal characteristics on methane adsorption capacity for high-rank coals.
4.1 Relationships between composition and fractal dimensions of coals
In order to solve the effect of coal composition on fractal characteristics of different coal pore structures by NMR, all correlations between coal compositional parameters and fractal dimensions are shown in Figures 7–9, and the data on coal composition is listed in Table 1.
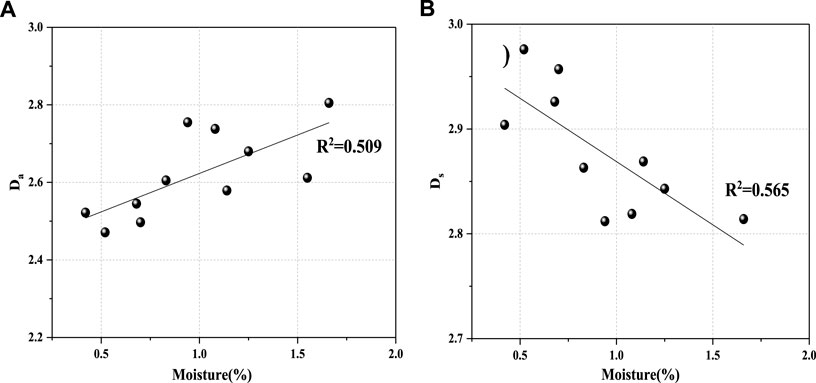
Figure 7 shows the relationships between moisture contents and fractal dimensions of coals. With the increase of moisture content, fractal dimension Ds decreases (Figure 7B). Yet fractal dimension Da increases with increasing moisture content (Figure 7A). It means that the fractal dimensions Da and Ds are greatly influenced by moisture content.
The moisture of coal reservoirs includes free water from seepage pore and irreducible water from adsorption pore. Moisture change in coal is influenced by coal rank. The volume of seepage pore is reduced by compression with the rising of coal rank, but the volume of adsorption pore increases (Yao, et al., 2008). The volume of the adsorption pore increases and that of the seepage pore decreases with the increase of moisture content of high-rank coals, and the surface of the adsorption pore may be influenced by gas-liquid interfacial tension. As a result, the adsorption pore is more complicated, and the seepage pore is more homogeneous (Li et al., 2015).
The relationships between the ash yield and the four fractal dimensions of coals are shown in Figure 8. Ash yield of coals is negatively correlated with Da (Figure 8A), and positively correlated with Ds (Figure 8B). The mineral content of coal is reflected indirectly by ash yield. If ash yield is high, mineral content is high. With increasing ash yield, adsorption pores may be more homogeneous by filling minerals, which can lead to the decreased fractal dimension Da. But Ds has a positive correlation with the ash yield of coals. The main reasons are as follows. On the one hand, with increasing ash yield, some seepage pores are partially filled with ash, leading to more heterogeneous structure of seepage pores, and greater fractal dimensions. On the other hand, the newly generated mineral pores lead to enhancing the heterogeneity of seepage pores (Yao et al., 2008; Liu and Wu, 2016).
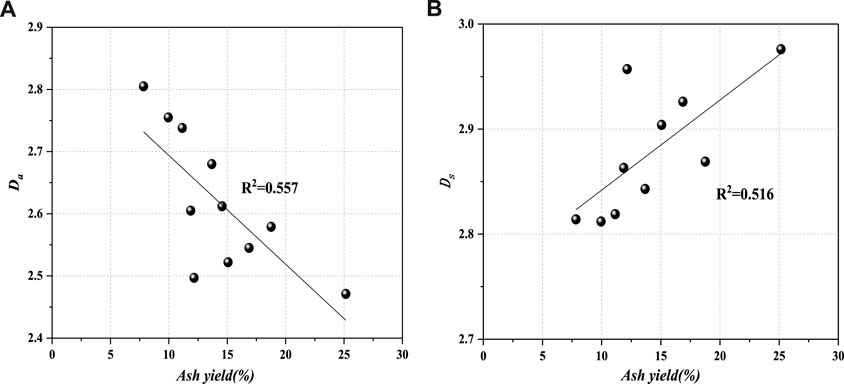
FIGURE 8. Collection between fractal dimensions (Da and Ds) and ash yield. (A) Relationship between Da and ash yield, (B) Relationship between Ds and ash yield.
Figure 9 showsthe relationships between carbon contents and fractal dimensions of coals. With the increase of carbon content, the fractal dimension Da increases and Ds decreases. We conclude that because of devolatilization and/or oxidation, the high carbon coal usually has low water content and ash yield in the coalification process. In this case, decreasing moisture content and ash yield may have caused the increase of Da and the decrease of Ds. Meanwhile, the volume and percentage of seepage pores are reducing in coals with increasing carbon contents, which leads to more homogeneous structure of seepage pores.
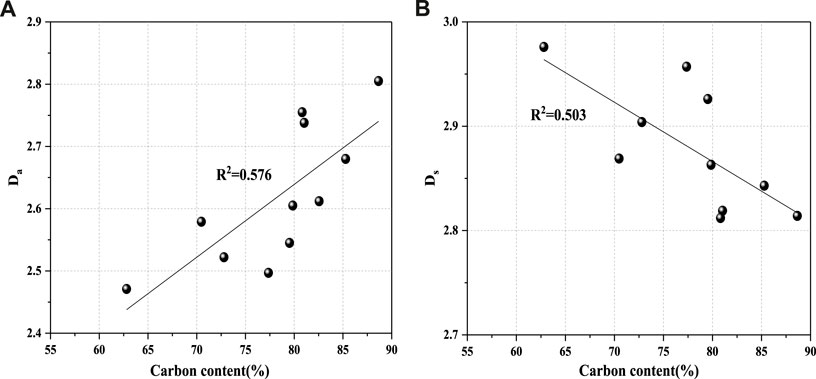
FIGURE 9. Collection between fractal dimensions (Da and Ds) and carbon content. (A) Relationship between Da and carbon content, (B) Relationship between Ds and carbon content.
4.2 Relationships between porosity and fractal dimensions of coals
Figure 10 shows the line relationship between pore structure parameters and fractal dimensions (Da and Ds). The fractal dimension Da has a positive linear correlation with the total SSA and SSA of micropore, indicating that high-rank coals with higher total SSA and micropore SSA have higher Da values (Figure 10A, Figure 10C). This means that the total surface area is mainly provided by micropores for high-rank coals. The higher the total SSA is, the higher the micropore percentage will be, resulting in more complexity of the adsorption pore structure. With the increase of total SSA and micropore SSA, Ds gradually decreases, indicating that the higher the total SSA of high-rank coals is, the smaller the content of seepage pores is, leading to more heterogeneous structure of seepage pores (Figure 10B, Figure 10D). To further reveal the correlation between fractal dimensions and pore structure characteristics, more information is needed. Table 3 shows the parameters including the total porosity, moveable fluid porosity and irreducible fluid porosity, which are obtained from NMR experimental analysis. The Da has a positive correlation with the irreducible fluid porosity (Figure 10E). In contrast, The fractal dimensions Ds has a negative correlation with the irreducible fluid porosity (Figure 10F). This means that with increasing irreducible fluid porosity, the volume and percentage of adsorption pores are increasing, which leads to the increase of SSA, more complicated structure of adsorption pores and more heterogeneous structure of seepage pores for high-rank coals. Therefore, they may result in relatively high CH4 adsorption capacity of coals with higher Da and less Ds value.
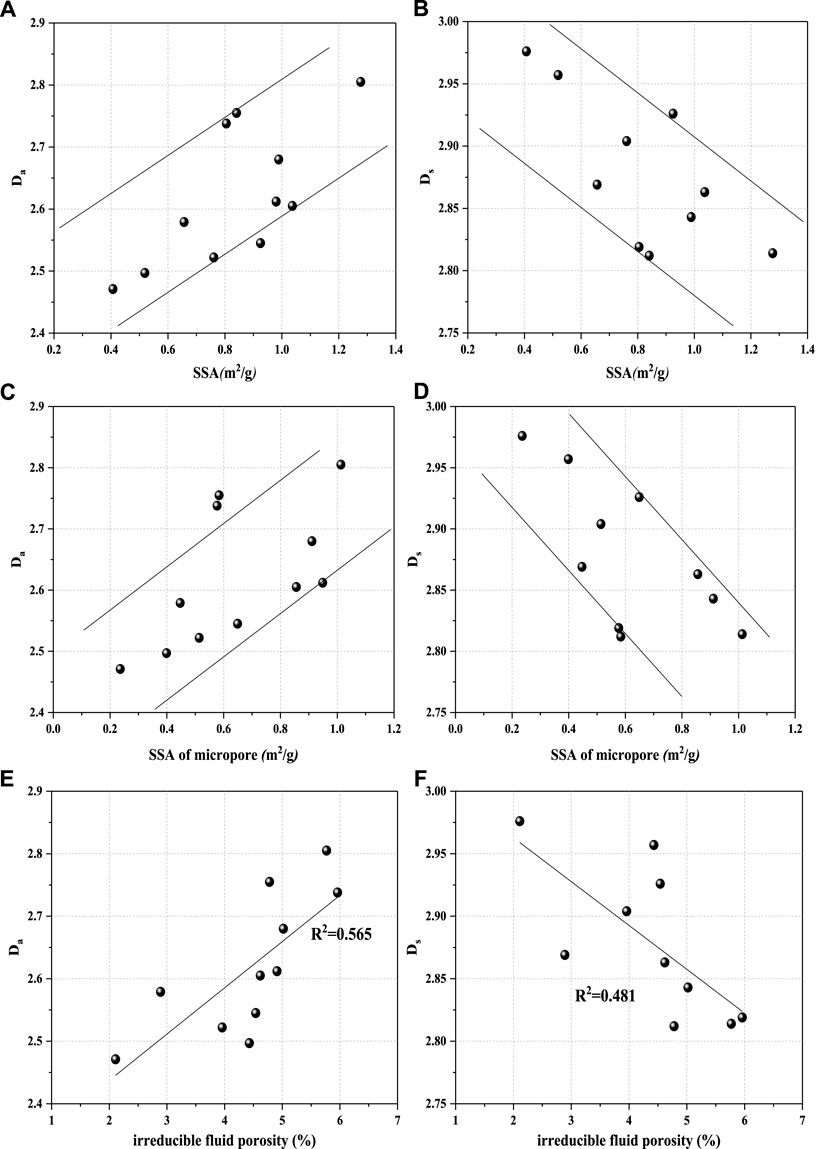
FIGURE 10. Collection between fractal dimension and pore structure. (A and B) Relationship between fractal dimensions and SSA, (C and D) Relationship between fractal dimensions and SSA of micropore, (E and F) Relationship between fractal dimensions and porosity.
4.3 Relationship between coal adsorption capacity and fractal dimension
The influence of fractal dimensions of different coal samples on VL and PL is shown in Figure 11. As shown in Figure 11A and Figure 11B, VL gradually increases with the increase of Da, which illustrates that the ultimate adsorption capacity of coal samples is gradually enhanced. VL has a positive linear correlation with Da. However, VL has a negative correlation with Ds, which means that the increase of the Ds value results in a decrease in CH4 adsorption capacity. The analysis shows that Da and Ds reflect the fractal feature of adsorption and seepage pores, respectively. As is well-known, the adsorption pore has the primary influence on the adsorption capacity of coal. On the one hand, the higher Da value represents more SSA of high-rank coals which provide more adsorption sites for CH4, so the high-rank coals have stronger adsorption capacity with higher Da. On the other hand, with the increase of Ds value, the high-rank coals have stronger heterogeneity of seepage pore structure, fewer adsorption sites for CH4 and higher capillary condensation on pore surfaces, which leads to the reduction of CH4 adsorption. Above all, the fractal dimension Da affects on CH4 adsorption capacity greater than Ds.
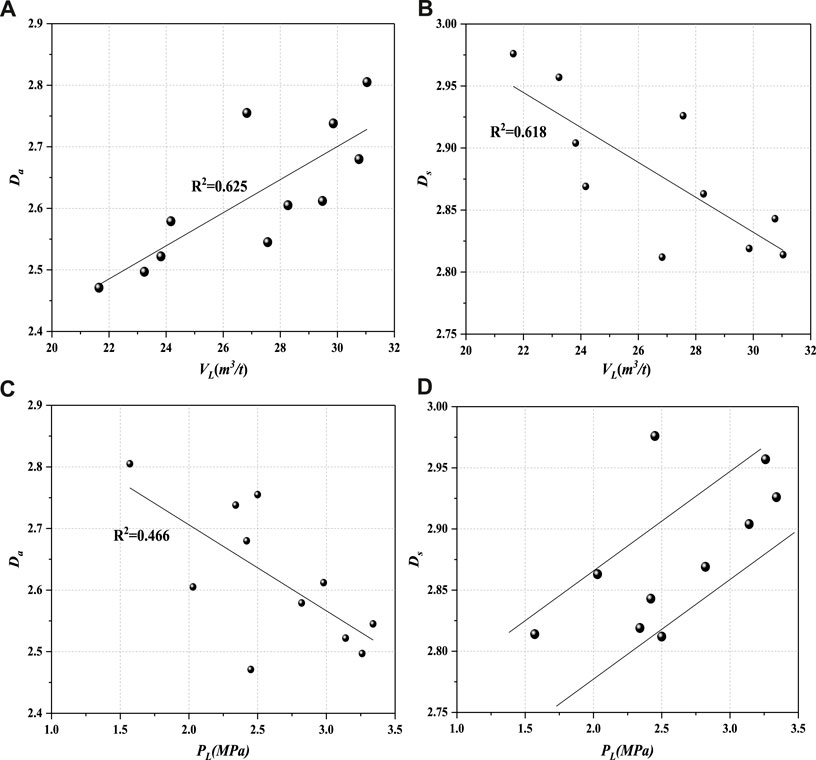
FIGURE 11. Effect of fractal dimensions on methane adsorption. (A, B) Relationship between fractal dimensions and VL, (B) Relationship between fractal dimensions and PL.
In the Langmuir equation, PL, which reflects the adsorption capacity of coal at the low-pressure stage, represents the adsorption pressure when the adsorption volume of CH4 gets to half of VL. The influence of the fractal dimensions Da and Ds on PL is shown in Figure 11C and Figure 11D. As can be seen from the figures, The Da value is negatively correlated with PL. The CH4 adsorption velocity of coal samples is increasing. According to the volume filling theory of micropores (Carrott et al., 1987), the micropores with the adsorption potential of significant superposition can reach saturation of adsorption capacity at lower pressure, and the adsorption energy has a close relationship with the surface of the micropores. With the increase of Da value, the percentage and surface of micropores will increase, which causes the increase of CH4 adsorption velocity for high-rank coals. However, there is a positive correlation between PL and Ds. With the increase of Ds, the percentage of seepage pores will increase and the surface of micropores will decrease. So the CH4 adsorption velocity decreases with higher Ds value for high-rank coals. Therefore, the fractal dimension Da has an important influence on PL.
Since the physical properties of coal are complicated, the difference in fractal dimensions of coal samples is caused by multiple factors, such as the content of each component in coal, pore size distribution, and so on. The above factors result in the heterogeneity of coal surface and structure, which will influence the methane adsorption capacity of coal. Thus, the fractal dimensions are the comprehensive reflection of differences among the physical properties of coal and are able to show the effect of coal properties on methane adsorption fully.
5 Conclusion
1. According to the characteristics of LP-N2A isotherms, all coal samples can be classified into three types. The SSA distribution curves exhibit unimodality with the main peak at ∼1 nm for all coal samples, indicating that the SSA of high-rank coals is more concentrated in micropores. The PV distribution shows obvious multimodality for most coal samples, and the peaks are at ∼1, ∼20 and ∼50 nm. The pores for > 10 nm provide most of the pore volume. Meanwhile, the micropores of type C provide the largest proportion of PV and SSA.
2. We divide the T2 spectrum of coal samples into four parts by the surface relaxivity of high-rank coal. Meanwhile, the fractal dimensions of different pore types are obtained from the slope of the equation by the linear fitting data of log(N(rj)) and log(T2). The average values of Da and Ds are 2.619 and 2.878, respectively.
3. The composition and pore parameters of coals have much greater control over fractal dimensions. The fractal dimension Da has a negative correlation with ash yield and moisture content, and a positive correlation with carbon content. The fractal dimension Ds has a positive correlation with ash yield and moisture content, and a negative correlation with carbon content. The high-rank coals with higher Da value have the more complicated structure of adsorption pores with higher SSA and irreducible fluid porosity, which results in relatively high CH4 adsorption capacity of coals.
4. The different fractal dimensions have varying effects on methane adsorption. With the increase of fractal dimension Da, VL increased and PL decreased, which illustrates that the CH4 adsorption capacity and velocity are gradually enhanced for high-rank coals. Compared with Da, Ds has the opposite effect on the CH4 adsorption capacity and velocity of high-rank coals. Thus, the fractal dimensions of different pore types, which are calculated based on NMR, are able to show the effect of coal properties on CH4 adsorption fully.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
WJ: laboratory experiments and data analysis; YZ: manuscript preparation; CW: manuscript review; and MD: sample collection.
Funding
This study was financially supported by the start-up fund for doctoral research of Suzhou University (No.2019jb16), Scientific research platform project of Suzhou University (2021XJPT54) and College Students’ innovation and entrepreneurship training program of Suzhou University (KYLXYBXM22-070).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Acevedo, B., and Barriocanal, C. (2015). Texture and surface chemistry of activated carbons obtained from tyre wastes. Fuel Process. Technol. 134, 275–283. doi:10.1016/j.fuproc.2015.02.009
Alexeev, A. D., Vasilenko, T., and Ulyanova, E. (1977). Closed porosity in fossil coals. Fuel 78, 635–638. doi:10.1016/s0016-2361(98)00198-7
Barrett, E. P., Joyner, L. G., and Halenda, P. P. (1951). The determination of pore volume and area distributions in porous substances. I. computations from nitrogen isotherms. J. Am. Chem. Soc. 73, 373–380. doi:10.1021/ja01145a126
Brunauer, S., Emmett, S., and Teller, E. J. (1938). Adsorption of gases in multi-molecular layers. J. Am. Chem. Soc. 60 (2), 309–319. doi:10.1021/ja01269a023
Cai, Y., Liu, D., Pan, Z., Yao, Y., Li, J., and Qiu, Y. (2013b). Pore structure and its impact on CH4 adsorption capacity and flow capability of bituminous and subbituminous coals from northeast China. Fuel 103, 258–268. doi:10.1016/j.fuel.2012.06.055
Cai, Y., Liu, D., Pan, Z., Yao, Y., and Qiu, Y. (2013a). Petrophysical characterization of Chinese coal cores with heat treatment by nuclear magnetic resonance. Fuel 108 (11), 292–302. doi:10.1016/j.fuel.2013.02.031
Carrott, P., Roberts, R. A., and Sing, K. (1987). Adsorption of nitrogen by porous and non-porous carbons. Carbon 25 (1), 59–68. doi:10.1016/0008-6223(87)90040-6
Chen, Y., Liu, D., and Gan, Q. (2018). Insights into fractal characteristics of pores in different rank coals by nuclear magnetic resonance (NMR). Arab. J. Geosci. 11 (19), 578. doi:10.1007/s12517-018-3943-2
Cheng, Y. Y., Cheng, Z. L., Li, S., Chen, S. D., and Guo, T. (2021). Characteristics of coalbed methane accumulation in Bide-Santang syncline, Western Guizhou and favorable sector. Geol. Bull. China 40 (7), 1140–1148.
Coetzee, G. H., Sakurovs, R., Neomagus, W., Hein, J. P., Everson, R. C., Mathews, J. P., et al. (2015). Pore development during gasification of South African inertinite-rich chars evaluated using small angle X-ray scattering. Carbon 95, 250–260. doi:10.1016/j.carbon.2015.08.030
Daigle, H., and Johnson, A. (2016). Combining mercury intrusion and nuclear magnetic resonance measurements using percolation theory. Transp. Porous Media 111, 669–679. doi:10.1007/s11242-015-0619-1
Dillinger, A., and Esteban, L. (2014). Experimental evaluation of reservoir quality in Mesozoic formations of the Perth Basin (Western Australia) by using a laboratory low field nuclear magnetic resonance. Mar. Petroleum Geol. 57, 455–469. doi:10.1016/j.marpetgeo.2014.06.010
Dullien, F. A. L. (1991). Porous media fluid transport and pore structure. Massachusetts, United States: Academic Press.
Ferro, N. D., Delmas, P., Duwig, C., Simonetti, G., and Morari, F. (2012). Coupling X-ray microtomography and mercury intrusion porosimetry to quantify aggregate structures of a cambisol under different fertilisation treatments. Soil Tillage Res. 119, 13–21. doi:10.1016/j.still.2011.12.001
Fu, X. H., Qin, Y., Zhang, W. H., Wei, C. T., and Zhou, R. F. (2005). Fractal classification and natural classification of coal pore structure based on migration of coalbed methane. Chin. Sci. Bull. 50, 66–71. doi:10.1007/bf03184085
Gao, Sh., Wang, L., Gao, J., and Zhang, R. (2018). Experimental study on pore structures of hard coal with different metamorphic grade based on fractal theory. Coal Sci. Tech. 46 (8), 93–100. doi:10.13199/j.cnki.cst.2018.08.015
Ge, X., Fan, Y., Zhu, X., Chen, Y., and Li, R. (2014). Determination of nuclear magnetic resonance T2 cutoff value based on multifractal theory-An application in sandstone with complex pore structure. Geophysics 80 (1), 11–21. doi:10.1190/geo2014-0140.1
Geerlings, P., Proft, F. D., and Langenaeker, W. (2003). Conceptual density functional theory. Chem. Rev. 103 (29), 1793–1874. doi:10.1021/cr990029p
IUPAC (1982). Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity. Pure Appl. Chem. 54 (11), 2201–2218. doi:10.1351/pac198557040603
Johnson, R. C., and Flores, R. M. (1998). Developmental geology of coalbed methane from shallow to deep in Rocky Mountain basins and in Cook inlet Matanuska basin, Alaska, USA and Canada. Int. J. Coal Geol. 35 (1), 241–282. doi:10.1016/s0166-5162(97)00016-5
Ju, Y., Sun, Y., Tan, J., Bu, H., Han, K., Li, X., et al. (2018). The composition, pore structure characterization and deformation mechanism of coal-bearing shales from tectonically altered Coalfields in Eastern China. Fuel 234, 626–642. doi:10.1016/j.fuel.2018.06.116
Lai, J., Wang, G., Fan, Z., Zhou, Z., Chen, J., and Wang, S. (2018). Fractal analysis of tight shaly sandstones using nuclear magnetic resonance measurements. Am. Assoc. Pet. Geol. Bull. 102 (2), 175–193. doi:10.1306/0425171609817007
Lee, B. H., and Lee, S. K. (2013). Effects of specific surface area and porosity on cube counting fractal dimension, lacunarity, configurational entropy, and permeability of model porous networks: Random packing simulations and NMR micro-imaging study. J. Hydrology 496, 122–141. doi:10.1016/j.jhydrol.2013.05.014
Li, P., L., Zhang, X., and Zhang, S. (2018). Structures and fractal characteristics of pores in low volatile bituminous deformed coals by low-temperature N2 adsorption after different solvents treatments. Fuel 224, 661–675. doi:10.1016/j.fuel.2018.03.067
Li, X., Kang, Y., and Haghighi, M. (2017). Investigation of pore size distributions of coals with different structures by nuclear magnetic resonance (NMR) and mercury intrusion porosimetry (MIP). Measurement 116, 122–128. doi:10.1016/j.measurement.2017.10.059
Li, Y., Yang, J., Pan, Z., and Tong, W. (2020a). Nanoscale pore structure and mechanical property analysis of coal: An insight combining AFM and SEM images. Fuel 260, 116352. doi:10.1016/j.fuel.2019.116352
Li, Z., Hao, Z., Pang, Y., and Gao, Y. (2015). Fractal dimensions of coal and their influence on methane adsorption. J. China Coal Soc. 40 (4), 863–869. doi:10.13225/j.cnki.jccs.2014.3022
Li, Z., Liu, D., Cai, Y., and Si, G. (2020b). Evaluation of coal petrophysics incorporating fractal characteristics by mercury intrusion porosimetry and low-field NMR. Fuel (Lond). 263, 116802. doi:10.1016/j.fuel.2019.116802
Li, Z., Liu, D., Cai, Y., and Teng, J. (2019). Adsorption pore structure and its fractal characteristics of coals by N2 adsorption/desorption and FESEM image analyses. Fuel 257, 116031. doi:10.1016/j.fuel.2019.116031
Li, Z. W., Lin, B. Q., Hao, Z. Y., and Gao, Y. B. (2013). Characteristics of pore size distribution of coal and its impacts on gas adsorption. J. China Univ. Min. Technol. 42 (6), 1047–1053. doi:10.13247/j.cnki.jcumt.2013.06.025
Lin, Y., Qin, Y., and Duan, Z. (2021). Pore structure, adsorptivity and influencing factors of high-volatile bituminous coal rich in inertinite. Fuel 293, 120418. doi:10.1016/j.fuel.2021.120418
Liu, H. H., Sang, S. X., Liu, S. Q., and Zhu, Q. P. (2015). Growth characteristics and genetic types of pores and fractures in a high-rank coal reservoir of the southern Qinshui basin. Ore Geol. Rev. 64, 140–151. doi:10.1016/j.oregeorev.2014.06.018
Liu, S., and Wu, C. (2016). Study on fractal characteristics of different scales pore coal reservoir in Bide-Santang Basin. Coal Sci. Technol. 44 (2), 33–38. doi:10.13199/j.cnki.cst.2016.02.006
Liu, X. F., and He, X. Q. (2017). Effect of pore characteristics on coalbed methane adsorption in middle-high rank coals. Adsorption 23 (1), 3–12. doi:10.1007/s10450-016-9811-z
Mandelbrot, B. B., and Benoit, B. (1998). The fractal geometry of nature. Am. J. Phys. 51 (3), 286–287. doi:10.1119/1.13295
Nie, B., Lun, J., Wang, K., and Shen, J. (2020). Three-dimensional characterization of open and closed coal nanopores based on a multi-scale analysis including CO2 adsorption, mercury intrusion, low-temperature nitrogen adsorption, and small-angle X-ray scattering. Energy Sci. Eng. 8, 2086–2099. doi:10.1002/ese3.649
Ouyang, Z., Liu, D., Cai, Y., and Yao, Y. (2016). Fractal analysis on heterogeneity of pore-fractures in middle-high rank coals with NMR. Energy fuels. 30, 5449–5458. doi:10.1021/acs.energyfuels.6b00563
Pan, J., Zhu, H., Hou, Q., Wang, H., and Wang, S. (2015). Macromolecular and pore structures of Chinese tectonically deformed coal studied by atomic force microscopy. Fuel 139, 94–101. doi:10.1016/j.fuel.2014.08.039
Peng, C., Zou, C., Yang, Y., Zhang, G., and Wang, W. (2017). Fractal analysis of high rank coal from southeast Qinshui basin by using gas adsorption and mercury porosimetry. J. Petroleum Sci. Eng. 156, 235–249. doi:10.1016/j.petrol.2017.06.001
Saboorian-Jooybari, H. (2016). New analytical formulas for prediction of gas-liquid relative permeabilities through fractures-Part I: Incompressible flow. J. Nat. Gas Sci. Eng. 30, 604–615. doi:10.1016/j.jngse.2016.02.002
Shan, C., Zhang, T., Guo, J., Zhang, Z., and Yang, Y. (2015). Characterization of the micropore systems in the high-rank coal reservoirs of the southern Sichuan Basin, China. Am. Assoc. Pet. Geol. Bull. 99 (11), 2099–2119. doi:10.1306/07061514240
Shi, Y. M., Zhang, Y. G., Yong, H. E., Zheng, H. F., Lu, W. Z., and Zheng, H. J. (2006). The study of flow units using fractal and fractal dimension methods of capillary pressure curve. Earth Sci. Front. 13 (3), 129–134.
Sing, K. S. W. (1982). Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (Provisional). Pure Appl. Chem. 54 (11), 2201–2218. doi:10.1351/pac198254112201
Sing, K. S. W. (1985). Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (Recommendations 1984). Pure Appl. Chem. 57, 603–619. doi:10.1351/pac198557040603
Song, X. X., Tang, Y. G., Wei, L. I., Wang, S. Q., and Yang, M. X. (2013). Fractral characteristics of adsorption pores of tectonic coal from Zhongliangshan southern coalmine. J. China Coal Soc. 38 (1), 134–139. doi:10.13225/j.cnki.jccs.2013.01.002
Song, Y., Jiang, B., and Liu, J. (2017). Nanopore structural characteristics and their impact on methane adsorption and diffusion in low to medium tectonically deformed coals: Case study in the huaibei coal field. Energy fuels. 31 (7), 6711–6723. doi:10.1021/acs.energyfuels.7b00512
Sun, W., Feng, Y., Jiang, C., and Chu, W. (2015). Fractal characterization and methane adsorption features of coal particles taken from shallow and deep coalmine layers. Fuel 155, 7–13. doi:10.1016/j.fuel.2015.03.083
Wang, C., Jiang, C. F., and Wei, C. (2013). Fractral dimension of coals and analysis of its influencing factors. J. China Univ. Min. Technol. 42 (6), 1009–1014. doi:10.13247/j.cnki.jcumt.2013.06.020
Wang, L. G., Jesus, M., and Salazar, J. (2011). Effects of surfactant-emulsified oil-based mud on borehole resistivity measurements. SPE J. 16 (3), 608–624. doi:10.2118/109946-pa
Yang, Z., Qin, Y., Wang, G. X., and An, H. (2014). Investigation on coal seam gas formation of multi-coalbed reservoir in Bide-Santang Basin Southwest China. Arab. J. Geosci. 8, 5439–5448. doi:10.1007/s12517-014-1640-3
Yang, Z., Qin, Y., Yi, T., Tang, J., Zhang, Z., and Wu, C. (2019). Analysis of multi-coalbed CBM development methods in Western Guizhou, China. Geosci. J. 23, 315–325. doi:10.1007/s12303-018-0037-9
Yao, Y., and Liu, D. (2012). Comparison of low-field NMR and mercury intrusion porosimetry in characterizing pore size distributions of coals. Fuel 95 (1), 152–158. doi:10.1016/j.fuel.2011.12.039
Yao, Y., Liu, D., Tang, D., Tang, S., and Huang, W. (2008). Fractal characterization of adsorption-pores of coals from North China: An investigation on CH4 adsorption capacity of coals. Int. J. Coal Geol. 73, 27–42. doi:10.1016/j.coal.2007.07.003
Yao, Y., Liu, D., Tang, D., Tang, S., Huang, W., Liu, Z., et al. (2009). Fractal characterization of seepage-pores of coals from China: An investigation on permeability of coals. Comput. Geosci. 35 (6), 1159–1166. doi:10.1016/j.cageo.2008.09.005
Yao, Y., Liu, D., Yao, C., Tang, D., Tang, S., and Huang, W. (2010). Petrophysical characterization of coals by low-field nuclear magnetic resonance (NMR). Fuel 89 (7), 1371–1380. doi:10.1016/j.fuel.2009.11.005
Zhang, C., Chen, Z., and Zhang, Z. (2007). Fractal characteristics of reservoir rock pore structure based on NMR T2 distribution. J. Oil Gas Technol. 29 (4), 80–86.
Zhang, Z., and Weller, A. (2014). Fractal dimension of pore-space geometry of an Eocene sandstone formation. Geophysics 79 (6), 377–387. doi:10.1190/geo2014-0143.1
Zhao, D., Guo, Y., Wang, G., and Mao, X. (2019). Characterizing nanoscale pores and its structure in coal: Experimental investigation. Energy Explor. Exploitation 37 (4), 1320–1347. doi:10.1177/0144598719831397
Zheng, S., Yao, Y., Elsworth, D., and Liu, Y. (2020). A novel pore size classification method of coals: Investigation based on NMR relaxation. J. Nat. Gas Sci. Eng. 81, 103466. doi:10.1016/j.jngse.2020.103466
Zheng, S., Yao, Y., Liu, D., Cai, Y., Liu, Y., and Li, X. (2019). Nuclear magnetic resonance T2 cutoffs of coals: A novel method by multifractal analysis theory. Fuel 241, 715–724. doi:10.1016/j.fuel.2018.12.044
Zhou, S., Liu, D., Cai, Y., and Yao, Y. (2016). Fractal characterization of pore–fracture in low-rank coals using a low-field NMR relaxation method. Fuel 181, 218–226. doi:10.1016/j.fuel.2016.04.119
Zhou, S., Liu, D., Karpyn, T., and Yao, Y. (2018). Effect of coalification jumps on petrophysical properties of various metamorphic coals from different coalfields in China. J. Nat. Gas Sci. Eng. 60, 63–76. doi:10.1016/j.jngse.2018.10.004
Keywords: nuclear magnetic resonance, fractal dimension, coalbed methane, adsorption, coal pore structure
Citation: Jiang W, Zhou Y, Wu C and Du M (2023) Fractal characteristics and theirs influence on methane adsorption in high-rank coals with NMR. Front. Earth Sci. 10:1047557. doi: 10.3389/feart.2022.1047557
Received: 18 September 2022; Accepted: 23 September 2022;
Published: 10 January 2023.
Edited by:
Mingjun Zou, North China University of Water Resources and Electric Power, ChinaReviewed by:
Taotao Cao, Hunan University of Science and Technology, ChinaTeng Li, Xi’an Shiyou University, China
Copyright © 2023 Jiang, Zhou, Wu and Du. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Jiang, amlhbmd3ZWkzcUAxNjMuY29t
 Wei Jiang
Wei Jiang Ying Zhou1,2
Ying Zhou1,2 Caifang Wu
Caifang Wu