Shear behaviors of recycled aggregate sand in constant volume simple shear tests interrelated with particle shape

Compared with quartz sand, recycled aggregate sand is characterized by the high liquefaction and shear resistance because of its irregular particle shape. However, the interrelationship between its particle shape and shear behaviors is seldom investigated. This paper investigates the role of the particle shape on the shear behaviors of recycled aggregate sand by conducting a series of monotonic and cyclic simple shear tests under undrained constant volume conditions. The particles’ morphology parameters are assessed in terms of sphericity, roundness and regularity with microscopic observation and image processing. According to the experimental results, the recycled aggregate sand with irregular shapes mobilizes greater gradients of the flow liquefaction lines under monotonic shear conditions. The irregularity of the particle shape also leads to greater peak shear stress and dynamic shear modulus, indicating stronger shear and liquefaction resistances under the cyclic shearing. Furthermore, the interrelationships between the peak shear stress, dynamic shear modulus and particle shape of the samples are revealed and established by well fitted functions, which could serve as references for the selection of recycled aggregate sand and corresponding designs of the foundation.

1 Introduction

Owing to the surge of international infrastructure construction in the last decades, the consumption of natural sand resources has been significantly increasing. It is inevitable that environmentally friendly, resource-rich, and sustainable recycled aggregate sand (RA) will replace natural sand because of its abundant mining resources, including rocks, mine tailings and industrial waste (Yang et al., 2019; Li et al., 2021; Alqarni et al., 2022).

Recently, RA has received considerable attention as an emerging construction material used in foundation backfilling. Compared with natural quartz sand (QS), RA has two noticeable characteristics. One characteristic is the chemical composition. The QS is mainly composed by silica, while the compositions of RA are various, including carbonate, ferric oxide and aluminium oxides. Another significant characteristic is the particle shape, which has been reported to have a significant impact on the mechanical behaviors of granular materials (Rui et al., 2021; Li et al., 2022; Wang et al., 2022). Compared with QS, the particle shapes of RA are more irregular and could vary in a wide range due to different production process and chemical composition. In past a few years, a number of researchers have studied the influence of particle shape on the responses of sand by experimental and numerical methods (Jensen et al., 2001; Mirghasemi et al., 2002; Chuhan et al., 2003; Tang-Tat, 2009; Ueda et al., 2013). Shinohara et al. (2000) pointed out that the irregular shapes show more intense interlocking between particles and have a noticeable impact on the internal friction angle. Yang and Wei (2012) carried out a series of undrained triaxial tests on both angular crushed silica and rounded glass beads and found that the increase of roundness could result in a decrease of the critical state angle. Maeda et al. (2010) emphasized that the shear strength, stiffness and compressibility are highly correlated to the particle shape. These studies manifest that there is an obvious interrelationship between the particle shape and mechanical behaviors of sand, especially under cyclic loading conditions (Rousé et al., 2008; Tsomokos and Georgiannou, 2010; Suh et al., 2017). Consequently, quantifying the shape of sand particles and selecting the material with suitable particles could effectively enhance its mechanical shear performance in foundation backfilling. However, although there are a number of studies about the particle shape of granular materials, the particle shape of RA and its impact on the shear behaviors have rarely been quantitatively and systematically investigated.

Meanwhile, with the rising complexity of seismic and traffic loadings, the risks of foundation deformation and sand liquefaction, which could lead to various damage, such as road collapse and pipeline leakage, kept increasing, bringing immeasurable harm to the traffic and pedestrian. A few researchers have conducted a series of experiments to evaluate the mechanical characteristics of RA under cyclic loadings and found that compared with natural sand, RA has higher liquefaction resistance and better dynamic performance. According to Wang et al. (2018), under the cyclic loading, the majority of RA materials show less permanent strain than that of natural sand. Arulrajah et al. (2013) and Li et al. (2019) conducted a series of cyclic triaxial tests to evaluate the liquefaction properties of RA and concluded that its liquefaction and shear resistance is higher than that of quartz sand. Otsubo et al. (2016) suggested that using RA for backfilling could effectively improve the shear strength and liquefaction resistance of the foundation. Huang et al. (2021) analyzed the influence of the particle grading on the cyclic shear characteristics of RA and found that the shear strength of well graded RA is higher than that of poorly graded RA. However, these experiments mainly investigated the mechanical properties of RA from macro aspects. Factors in micro scale, such as the particle shape, were paid too little attention.

Therefore, this paper aims to investigate the impact of the particle shape on shear behaviors of RA under undrained shear loading conditions by a series of monotonic and cyclic simple shear tests. The particle shapes of four kinds of RA which are crushed from different rocks were quantitatively determined and compared with natural quartz sand (QS). Based on the derived shape parameters, the connections between the particle shape and variations of the slope of liquefaction line, maximum shear stress and dynamic shear modulus were investigated and described. It should be noted that except for the particle shape, the shear behaviors could be also influenced by other factors including the grading, particle size and uniformity coefficient, which are not within the scope of this study. Therefore, these parameters are kept identical for the sample as control factors. The research findings could provide theoretical supports and reference values for the selection of RA in geotechnical engineering and facilitate the application of RA in the design and construction of foundations under cyclic loading conditions, for example, the earthquake loading condition.

2 Materials and methods

2.1 Experimental materials

Four types of RA with irregular particle shapes produced in Zhejiang Province, China, were used in this study. Each type of sand was crushed from different kinds of rocks, denoted as RASR, RAB, RAS, RAR corresponding to parent rocks of sandstone with rhyolitic crystal tuff, basalt, sandstone and river pebble respectively. The material used in the control group was quartz sand—Leighton Buzzard sand (fraction B), a type of natural sand from England, whose particles are relatively round and smooth, denoted as QS. The digital microscope photographs of the particles for each type of sand are presented in Figure 1. The compositions of RA and QS were evaluated by the XRD chemical analyze. It was found that the silicon dioxide content of QS is approximately 94.6%, while the others’ ranges from 57.4 to 74.3%.

FIGURE 1

FIGURE 1. Particle images of: (A) QS; (B) RASR; (C) RAB; (D) RAS; (E) RAR.

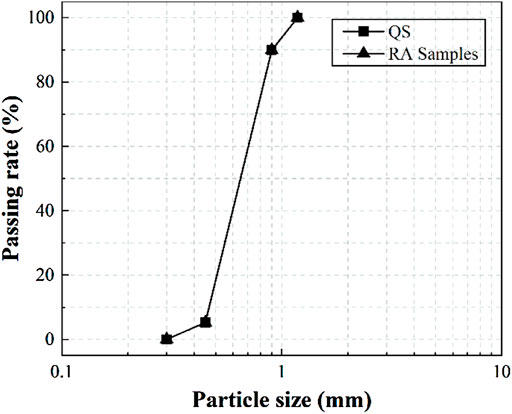
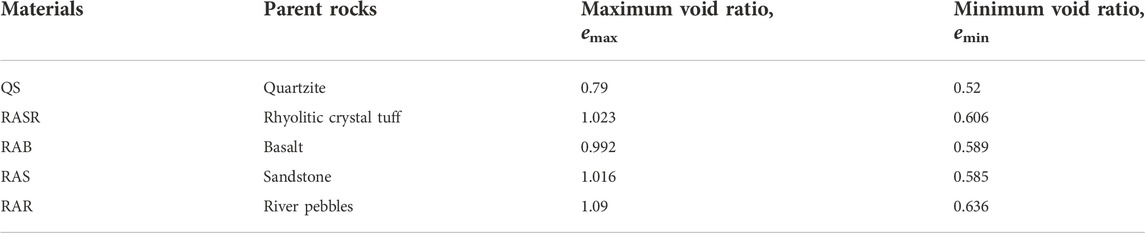
To evaluate the shear behavior of different samples and examine the impact of the particle shape on their dynamic behaviors, the particle gradations were kept consistent for the samples of both QS and RA, as shown in Figure 2, giving the identical mean particle diameter d₅₀ of 0.62 mm and the coefficient of uniformity C_u of 1.51. The maximum and minimum void ratio were assessed and utilized to control the relative density of the samples in the tests and are presented in Table 1, following the ASTM standard D4253 (2016a) and D4254 (2016b).

FIGURE 2

FIGURE 2. The grading of QS and RA samples.

TABLE 1

TABLE 1. Properties of QS and RA samples.

2.2 Particle shape evaluation

In the existing studies, a variety of parameters were proposed by researchers to quantify the particle shape (Jennings et al., 1988; Shigehisa et al., 1998; Fonseca et al., 2012; Lee et al., 2017). In this paper, the well established parameters—sphericity (S), roundness (R), and regularity (ρ) were adopted to quantitatively represent the particle shape (Wadell, 1932; Cho et al., 2007). The sphericity (S) could well describe the overall shape of the particle including the length and width while the roundness (R) could illustrate the regional shape of the principal circular surfaces. To comprehensively quantify the particle shape, the regularity (ρ) is adopted and calculated from the sphericity and roundness. The parameters can be defined as follows:

$\mathit{S}=\frac{{\mathit{r}}_{\mathit{max}-\mathit{i}\mathit{n}}}{{\mathit{r}}_{\mathit{min}-\mathit{c}\mathit{i}\mathit{r}}},(1)$

$\mathit{R}=\frac{{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\mathit{r}}_{\mathit{i}}/{\mathit{r}}_{\mathit{max}-\mathit{i}\mathit{n}}}{{\mathit{n}}_{\mathit{c}}},(2)$

$\mathit{\rho }=\frac{S+R}{2},(3)$

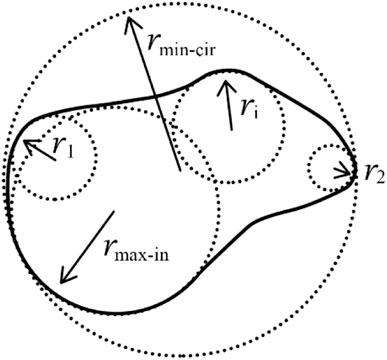
where r_i and n_c are the radius and the number of corner circles, while r_max-in is the maximum radius of the inscribe circle of the particle and r_min-cir is the minimum radius of the circumcircle. The definitions of r_i, r_max-in and r_min-cir are illustrated in Figure 3. More details can be found in Cho et al. (2006).

FIGURE 3

FIGURE 3. Illustration of particle shape parameters.

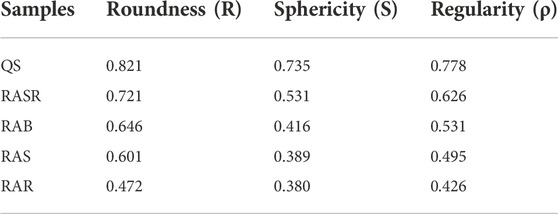
In this study, a large number of grains were picked randomly for each type of sand to quantify the shape features. The particle morphologies were obtained by the microscope. Captured pictures were firstly binarized and then the shape parameters were calculated by the MATLAB software for individual particles. The processing procedure for the pictures are shown in Figure 4. The particle regularity (ρ), which is a representative factor of sphericity and roundness, was used to quantify the overall shape for each type of samples. The computed average values o0066 for QS, RASR, RAB, RAS, RAR were 0.778, 0.626, 0.531, 0.495, 0.426 respectively (Table 2).

FIGURE 4

FIGURE 4. Binarized photos and image processing method for the particles.

TABLE 2

TABLE 2. Computed shape parameters of samples.

2.3 Experimental apparatus and methods

The simple shear tests were carried our using an electromechanical dynamic cyclic simple shear system (EMDCSS), which is capable of performing dynamic cyclic experiments with shear strain amplitudes from 0.005 to 10%, as shown in Figure 5. This device allows the stress or strain to be imposed in both the vertical direction (z-direction) and horizontal direction (x-direction). Each sample was tested in cylindrical shape with the diameter of 50 mm and the height of 30 mm. The pre-weighted and oven-dried samples were confined by an impermeable membrane and covered with low-friction stacked rings made of polytetrafluoroethylene (PTFE), which ensures a constant cross-sectional area for the sample. The rigidity of the stacked rings ensures a K0 consolidation of the sample before the shearing.

FIGURE 5

FIGURE 5. Samples prepared for monotonic and cyclic simple shear testing.

The initial relative density of samples was controlled according to the weight and void ratio and set to be 46% before the shearing. After samples were prepared in the shear box, an axial stress σ_z of 50 kPa was imposed for K₀ consolidation, lasting for 30 min.

The samples’ height remained unchanged when the shearing started, so the volume of the samples could be kept unchanged. It has been proved that the shear behavior of sand samples in constant volume is equivalent to that of those in truly undrained conditions and it is demonstrated that the loss of axial stress is equivalent to the increase of pore pressure (Dyvik et al., 1987). The method is widely adopted because the saturation of samples as well as the pore pressure sensors are not required (Mao and Fahey, 2003; Porcino et al., 2008).

Two different types of simple shear tests were carried out in this study. One is the monotonic simple shear test and the other one is the cyclic simple shear test. The test conditions are presented in Table 3. Both the monotonic and cyclic shear tests are strain-controlled. For the monotonic simple shear tests, the shear rate was set to be 0.05 mm/min. For the cyclic simple shear tests, the strain-controlled symmetric sine loading curve was applied. The loadings were imposed for 20 cycles for each sample with the frequency of 0.1 Hz to fully record the stress-strain relationship during the shearing. Four cyclic shear strain amplitudes (0.1, 0.2, 0.3, and 0.4%) were exerted to the samples in this study to investigate their cyclic shear responses.

TABLE 3

TABLE 3. Design of the monotonic and cyclic simple shear tests.

3 Results and discussion

3.1 Results of the monotonic simple shear tests

The results of the monotonic simple shear tests are shown in Figure 6. It can be seen that during the constant volume monotonic shearing, the axial stress reduces gradually, indicating the accumulation of the pore pressure. Meanwhile, the shear stress increases with the decreasing axial stress until it reaches the peak value and then reduces gradually. The peak stress ratio is determined by the ratio of the peak shear stress and the corresponding axial stress (τ_max/σ_z), which is identical to the slope of the flow liquefaction line and could reflect the stability of sandy soils (Hill, 1958). The flow liquefaction line is presented to demonstrate the initiation of failure as the instability is prone to be triggered beyond the line (Yang et al., 2022). Comparing the experimental results in Figures 6A–E, it is evident that the slope of flow liquefaction line of QS is obviously lower than RA, demonstrating its lower liquefaction resistance.

FIGURE 6

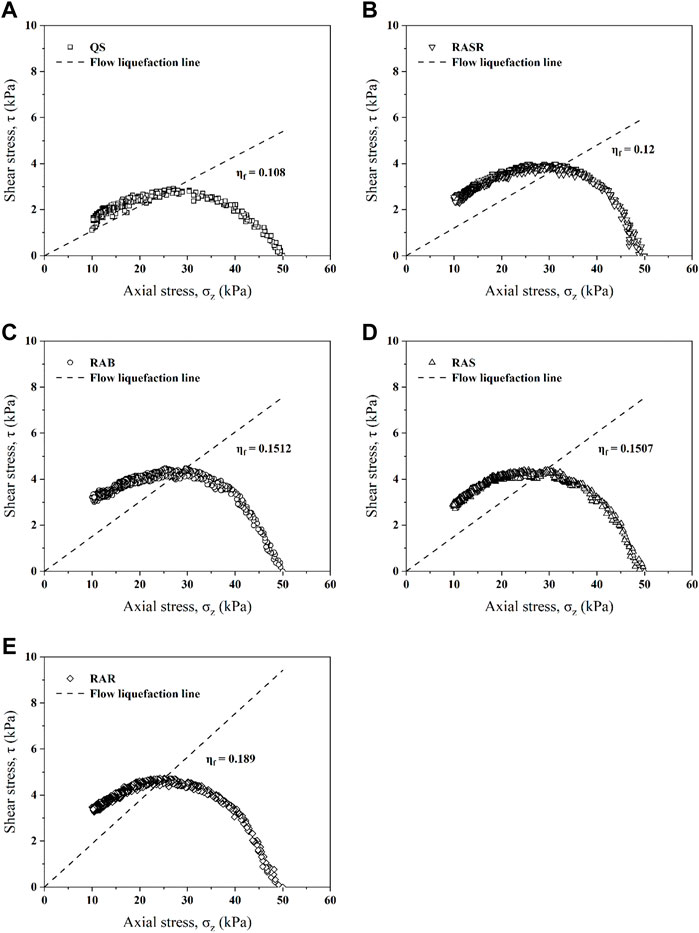
FIGURE 6. Flow liquefaction lines in the space of shear stress t versus axial stress σ_z in the monotonic simple shear tests for: (A) QS; (B) RASR; (C) RAB; (D) RAS; (E) RAR.

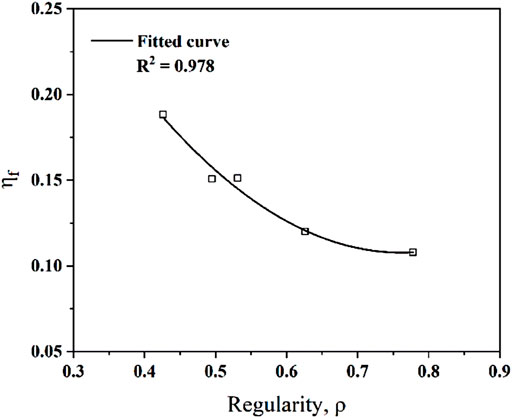
Combining the slope of liquefaction line and particle shape parameter of the samples, the influence of particle shape on the value of η_f is demonstrated in Figure 7. In general, the slope of the flow liquefaction lines tends to decrease with the increasing particle regularity in a nonlinear pattern, reflecting the instability and greater liquefaction potential of rounder particles under monotonic shear tests.

FIGURE 7

FIGURE 7. Trend of the slope of liquefaction line η_f versus particle regularity.

3.2 Results of the cyclic simple shear tests

The typical stress-strain hysteresis loops obtained from the cyclic simple shear tests with the shear strain amplitude of 0.1% are shown in Figure 8. The shear stress of RA samples comes to a peak value in the first few cycles then decreases gradually, while the shear stress of QS decreases much quicker due to its rounder particles. During the cyclic shearing, the maximum shear stress for QS, RASR, RAB, RAS, and RAR were 2.835, 3.639, 3.724, 3.893, and 4.147kPa, corresponding to the particle regularity of 0.778, 0.626, 0.531, 0.495, and 0.426. The peak shear stress is found to increase as the regularity of the particles decreases because the particle shape with greater irregularity strengthens the inter-particle locking of the samples (Yang and Elgamal, 2002; Ueng et al., 2017).

FIGURE 8

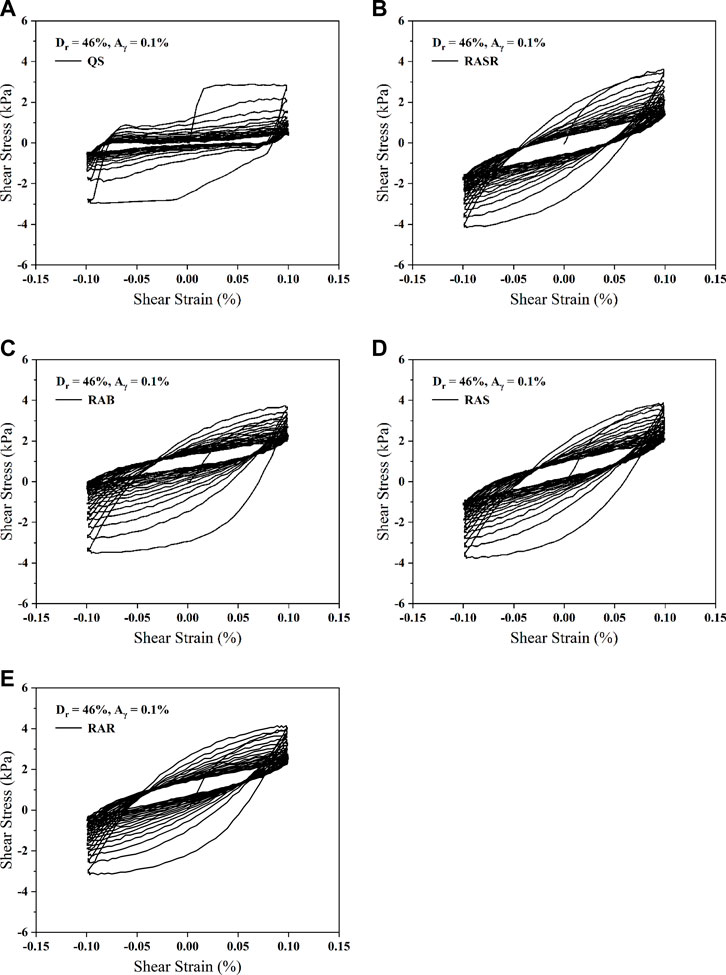
FIGURE 8. Hypothesis shear strain-stress loops of samples: (A) QS; (B) RASR; (C) RAB; (D) RAS; (E) RAR.

3.2.1 Influence of the particle shape on the maximum cyclic shear stress

From the hypothesis shear stress-strain loops, it is found that the maximum cyclic shear stress is correlated with the particle shape. Figures 9A–D show the peak value of shear stress against the particle regularity under the cyclic shearing with different shear strain amplitudes under initial normal stress of 50 kPa and relative density of 46%. A linear relationship between the peak cyclic shear stress and the particle regularity could be obtained with a given shear amplitude, which could be expressed as:

${\mathit{\tau }}_{\mathbf{max}}={\mathit{C}}_{\mathbf{1}}·\mathit{\rho }+{\mathit{C}}_{\mathbf{2}},(4)$

where C₁ and C₂ are fitting parameters for the function, depending on the initial normal stress and shear strain amplitude. In these figures, the values of C₁ and C₂ for the fitting lines both vary with the shear amplitudes. The values of C₁ are -3.537, -5.201, -6.472, and -7.995; the values of C₂ are 5.668, 7.126, 7.801, and 9.001; corresponding to the shear strain amplitude of 0.1, 0.2, 0.3, and 0.4%.

FIGURE 9

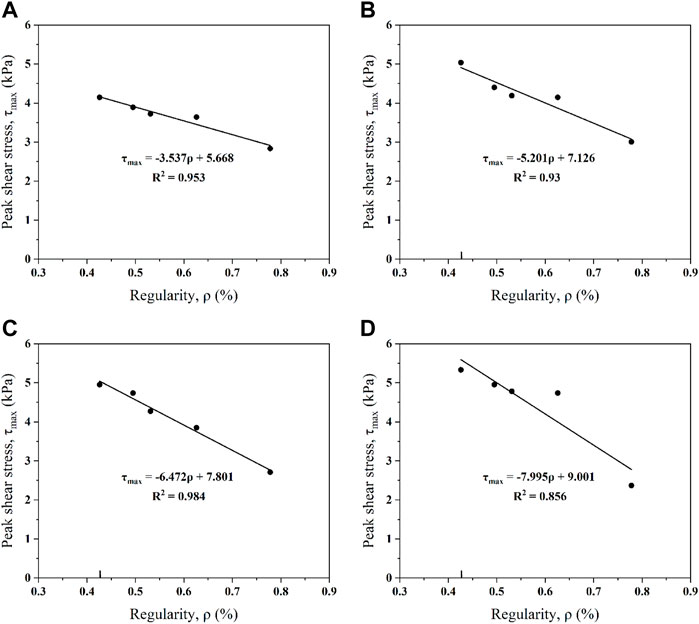
FIGURE 9. Influence of particle regularity on the maximum cyclic shear stress under different shear strain amplitudes: (A) A_γ = 0.1%; (B) A_γ = 0.2%; (C) A_γ = 0.3%; (D) A_γ = 0.4%.

To further analyze the relationship, the correlation between shear strain amplitudes and these two parameters is presented in Figures 10A,B. The results demonstrate that as the shear strain increases, the value of C₁ presents a decreasing trend, while the value of C₂ shows an increasing trend in contrast. The impact of shear strain amplitude on the values of C₁ and C₂ could be expressed as:

FIGURE 10

FIGURE 10. Influence of shear strain amplitude on the fitting parameters: (A) C₁; (B) C₂.

For value C₁

${\mathit{C}}_{\mathbf{1}}=-\mathbf{14.645}{\mathit{A}}_{\mathit{\gamma }}+\mathbf{2.14}.(5)$

For value C₂

${\mathit{C}}_{\mathbf{2}}=\mathbf{10.676}{\mathit{A}}_{\mathit{\gamma }}+\mathbf{4.73},(6)$

where A_γ is the shear strain amplitude. Combined Eqs 4–6, the maximum cyclic shear stress can be defined as:

${\mathit{\tau }}_{\mathbf{max}}={\mathit{F}}_{\mathbf{1}}\left({\mathit{A}}_{\mathit{\gamma }}\right)·\mathit{\rho }+{\mathit{F}}_{\mathbf{2}}\left({\mathit{A}}_{\mathit{\gamma }}\right),(7)$

where the F₁ (A_γ) and F₂ (A_γ) are functions of the shear strain amplitude.

3.2.2 Influence of the particle shape on the dynamic shear modulus

The dynamic shear modulus is investigated in the study as it could reflect the dynamic characteristics of granular materials under cyclic loadings, such as the earthquake loading (Nye and Fox, 2007; Vieira et al., 2013; Wang et al., 2016). Based on the hypothesis loops, the dynamic shear modulus (G_d) is defined as (Kumar et al., 2017):

${\mathit{G}}_{\mathit{d}}=\frac{{\mathit{G}}_{\mathbf{sec}\mathbf{1}}+{\mathit{G}}_{\mathbf{sec}\mathbf{2}}}{\mathbf{2}},(8)$

where the slope between the vertex of the positive half-axis and the origin of the hysteresis curve, known as G_sec1, is used to calculate the dynamic shear modulus of the loading portion while G_sec2 is used to calculate the reverse-loading part, which is determined by the slope between the vertex of the negative half-axis and the origin of the hysteresis curve. The parameter definition of dynamic shear modulus G_d in hypothesis curves is shown in Figure 11.

FIGURE 11

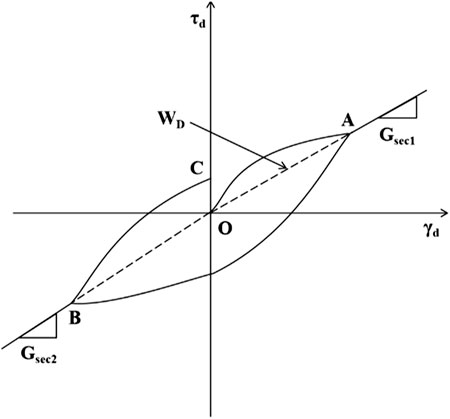
FIGURE 11. Definition of the dynamic shear modulus based on the hysteretic shear stress-strain loop.

Figure 12 shows the variation of dynamic shear modulus against the cyclic number. Different from the shear stress, the peak value of the dynamic shear modulus is reached in the first cycle. During the constant volume cyclic shearing, the dynamic shear modulus generally decreases with the imposed cyclic number as the sample contracts. The maximum dynamic shear modulus for a given tested material reduces with the increasing shear strain amplitude. Furthermore, as the shear strain amplitude increases, the reduction rate of the dynamic shear modulus increases as well. It is obvious that the value of the dynamic shear modulus of QS is less than that of RA in the same cycle and reduces faster as well. The relationship between the dynamic shear modulus and the number of cycles could be described as:

${\mathit{G}}_{\mathit{d}}=\mathit{A}·{\left({\mathit{N}}_{\mathit{c}}\right)}^{-\mathit{B}},(9)$

where A and B are parameters associated with sample properties. Generally, the given power function fits well with the reduction of dynamic shear modulus under the cyclic shearing except for the first cycle in the results of Figures 12B–D when the dramatic reduction of the dynamic shear modulus occurs, which can be difficult to predict. For a specific shear strain amplitude, it can be observed that the fitted curves of the RAR, RAS, RAB, RASR and QS are located from the top to the bottom, corresponding to the particle regularity of 0.426, 0.495, 0.531, 0.626 and 0.778. The results present a decreasing trend of the liquefaction resistance among the samples, which consists with the results obtained in Figure 7.

FIGURE 12

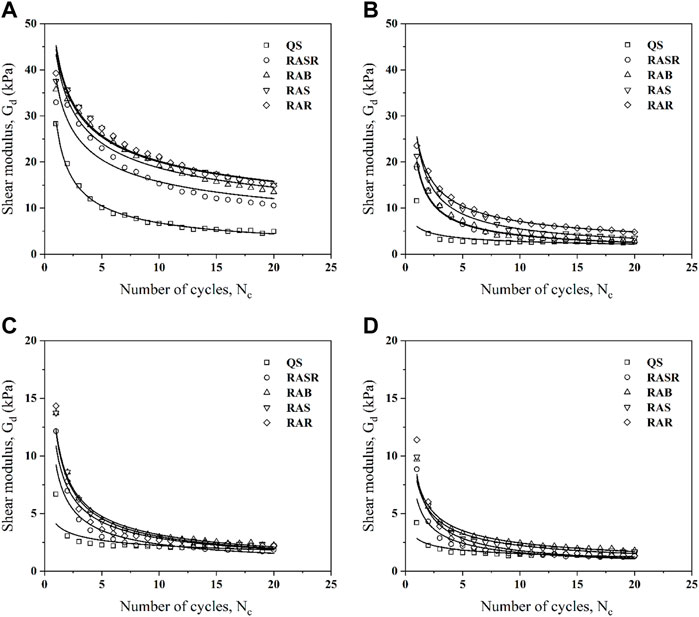
FIGURE 12. Influence of the particle regularity on the dynamic shear modulus under different shear strain amplitudes: (A) A_γ = 0.1%; (B) A_γ = 0.2%; (C) A_γ = 0.3%; (D) A_γ = 0.4%.

Figure 13 shows variations of the maximum dynamic shear modulus with the particle regularity under different shear strain amplitudes. For a given shear amplitude, the maximum dynamic shear modulus decreases with the increasing particle regularity and a linear regression is found between them. As the shear amplitude increases, the maximum dynamic shear modulus generally shows a decreasing trend. It can be observed from the fitting lines that the R² are larger than 0.9 for all the samples, which reflects the reliability of the fitting formulas. The relationship between the maximum dynamic shear modulus and the particle regularity could be established as:

${\mathit{G}}_{\mathit{d}\mathbf{max}}=-{\mathit{S}}_{\mathit{m}}·\mathit{\rho }+{\mathit{C}}_{\mathit{m}},(10)$

where S_m and C_m can be determined by the shear amplitude.

FIGURE 13

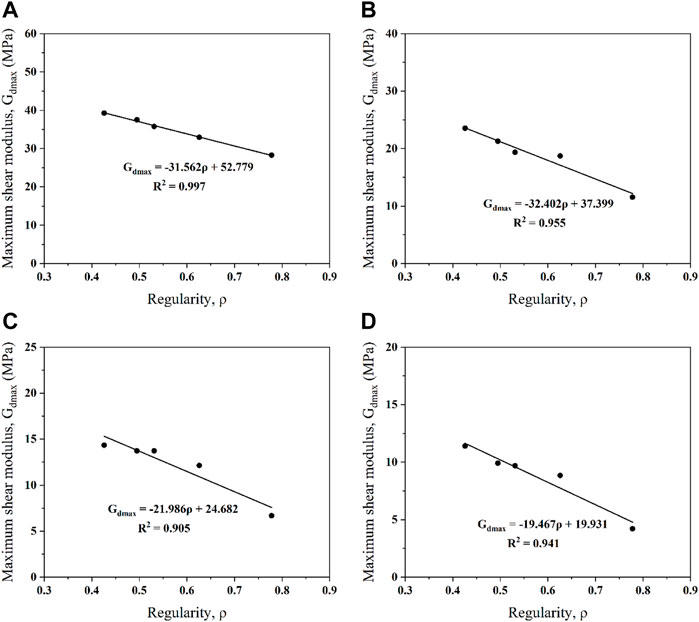
FIGURE 13. Relationship between the maximum dynamic shear modulus and particle regularity for samples under different shear strain amplitudes: (A) A_γ = 0.1%; (B) A_γ = 0.2%; (C) A_γ = 0.3%; (D) A_γ = 0.4%.

3.2.3 Energy dissipation

It is reported that the movement and relocation of sand particles would consume large energy under the cyclic loading, which is also highly related to the stability of sand (Baziar and Jafarian, 2007; Sonmezer, 2019). Therefore, the energy dissipation under the cyclic shearing is investigated as well. In this paper, the energy dissipated in one cycle is calculated by the area of the corresponding hypothesis stress-strain loop as follows (Figueroa et al., 1994):

$\mathit{\delta }\mathit{W}={\displaystyle \sum }_{\mathbf{1}}^{\mathit{i}}\frac{{\mathbf{\tau }}_{\mathit{i}+\mathbf{1}}+{\mathbf{\tau }}_{\mathit{i}}}{\mathbf{2}}·\left({\mathbf{\gamma }}_{\mathit{i}+\mathbf{1}}-{\mathbf{\gamma }}_{\mathit{i}}\right),(11)$

where τ_i and γ_i are the shear stress and shear strain recorded in one cycle. To analyze the difference of cyclic shearing resistance of sand with different particle regularity, the energy dissipation per cycle and the cumulative energy are calculated and presented in Figures 14A–D. The figures illustrate that the cumulative energy grows rapidly at the beginning of the cyclic shearing and then the increasing rate drops gradually. In the last a few cycles, the energy consumed in one cycle tend to reach a constant value, resulting in the total energy to accumulate linearly and indicating the approaching of the liquefaction. Furthermore, as the shear strain amplitude increased, the energy dissipation in one cycle drops more quickly and less cycles are required for the total energy to achieve the linear increasing rate. In general, the particles with larger regularity dissipate less energy under the same loading cycles, indicating the greater instability of the corresponding material under the cyclic shearing.

FIGURE 14

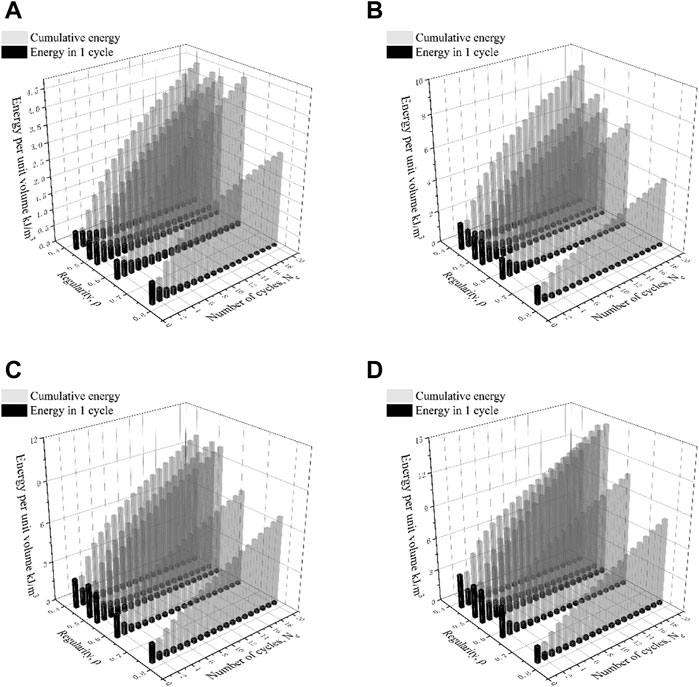
FIGURE 14. Cumulative energy consumed and energy consumed per cycle for samples under different shear strain amplitudes: (A) A_γ = 0.1%; (B) A_γ = 0.2%; (C) A_γ = 0.3%; (D) A_γ = 0.4%.

4 Conclusion

In order to explore the influence of the particle shape on the shear and liquefaction behaviors of recycled aggregate sand, a series of monotonic and cyclic simple shear tests were performed on QS and four types of RA. The shape of the particles was quantitatively evaluated in terms of sphericity, roundness and regularity. Then the regularity is selected as the representative factor to reflect the particle shape of the samples. The shear behaviors under constant volume shearing for samples with different shape characteristics were analyzed and the key findings are summarized as follows:

1) The particle regularity of QS is higher than that of RA, reflecting that the particles of RA are more irregular and angular.

2) In the monotonic simple shear tests, the shear strength and the slope of the flow liquefaction line of RA are greater than that of QS and the slope of the liquefaction line tends to decrease with the increasing particle regularity, indicating the better liquefaction resistance of RA compared with QS.

3) In the cyclic simple shear tests, the shear stress of QS decreases more quickly compared with RA because of its rounder and more regular particle shape. A linear correlation between the peak shear stress and particle shape parameters of the samples was derived under undrained cyclic shearing with different shear amplitudes.

4) During the cyclic shearing, an exponential relation was established to describe the variation of the dynamic shear modulus and imposed number of cycles of different samples. The reduction of the dynamic shear modulus is accelerated with greater shear amplitudes. A linear relationship between the particle regularity and the maximum dynamic shear modulus was proposed as well.

5) The samples with irregular particles dissipate larger energy and more cycles are required for the total energy to achieve the linear increasing rate under the same cyclic loading condition, indicating their need of greater energy to trigger instability.

The shear characteristics found in this paper and the proposed relationships between the particle shape parameters and the flow liquefaction line, peak shear stress and dynamic shear modulus could be used to predict the responses of RA under both monotonic and cyclic shear loading conditions, thus serving as the reference for its selection and application in the foundation engineering.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The research was funded by Zhejiang Provincial Natural Science Foundation of China (grant number LQ19E090003) and National Natural Science Foundation of China (grant number 51678533).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alqarni, A. S., Abbas, H., Al shwikh, K. M., and Al salloum, Y. A. (2022). Influence of treatment methods of recycled concrete aggregate on behavior of high strength concrete. Buildings 12 (4), 494. doi:10.3390/buildings12040494

CrossRef Full Text | Google Scholar

Arulrajah, A., Piratheepan, J., Disfani, M. M., and Bo, M. W. (2013). Geotechnical and geoenvironmental properties of recycled construction and demolition materials in pavement subbase applications. J. Mat. Civ. Eng. 25 (8), 1077–1088. doi:10.1061/(ASCE)MT.1943-5533.0000652

CrossRef Full Text | Google Scholar

ASTM D4253 (2016a). Standard test methods for maximum index density and unit weight of soils using vibratory table. ASTM International, West Conshohocken, PA.

Google Scholar

ASTM D4253 (2016b). Standard test method for minimum index density and unit weight of soils and calculation of relative density. ASTM International, West Conshohocken, PA.

Google Scholar

Baziar, M. H., and Jafarian, Y. (2007). Assessment of liquefaction triggering using strain energy concept and ANN model: Capacity Energy. Soil Dyn. Earthq. Eng. 27 (12), 1056–1072. doi:10.1016/j.soildyn.2007.03.007

CrossRef Full Text | Google Scholar

Cho, G. C., Dodds, J., and Santamarina, J. C. (2007). Closure to "Particle shape effects on packing density, stiffness, and strength: Natural and crushed sands by Gye-Chun Cho, Jake Dodds, and J. Carlos Santamarina. J. Geotech. Geoenviron. Eng. 133133 (11), 147411. doi:10.1061/(asce)1090-0241(2007)133:11(1474)

CrossRef Full Text | Google Scholar

Cho, G. C., Dodds, J., and Santamarina, J. C. (2006). Particle shape effects on packing density, stiffness, and strength: Natural and crushed sands. J. Geotech. Geoenviron. Eng. 133 (5), 591–602. doi:10.1061/(asce)1090-0241(2006)132:5(591)

CrossRef Full Text | Google Scholar

Chuhan, F. A., Høeg, K., Kjeldstad, A., and Bjørlykke, K. (2003). Experimental compression of loose sands: Relevance to porosity reduction during burial in sedimentary basins. Can. Geotech. J. 40, 995–1011. doi:10.1139/t03-050

CrossRef Full Text | Google Scholar

Dyvik, R., Berre, T., Lacasse, S., and Raadim, B. (1987). Comparison of truly undrained and constant volume direct simple shear tests. Geotechnique 37 (1), 3–10. doi:10.1680/geot.1987.37.1.3

CrossRef Full Text | Google Scholar

Figueroa, J. L., Saada, A. S., Liang, L., and Dahisaria, N. M. (1994). Evaluation of soil liquefaction by energy principles. J. Geotech. Engrg. 120 (9), 1554–1569. doi:10.1061/(asce)0733-9410(1994)120:9(1554)

CrossRef Full Text | Google Scholar

Fonseca, J., O'Sullivan, C., Coop, M. R., and Lee, P. D. (2012). Non-invasive characterization of particle morphology of natural sands. Soils Found. 52 (4), 712–722. doi:10.1016/j.sandf.2012.07.011

CrossRef Full Text | Google Scholar

Hill, R. (1958). A general theory of uniqueness and stability in elastic-plastic solids. J. Mech. Phys. Solids 6 (3), 236–249. doi:10.1016/0022-5096(58)90029-2

CrossRef Full Text | Google Scholar

Huang, Y., Wang, J., Ying, M., Ni, J., and Li, M. (2021). Effect of particle-size gradation on cyclic shear properties of recycled concrete aggregate. Constr. Build. Mater. 301 (3), 124143. doi:10.1016/j.conbuildmat.2021.124143

CrossRef Full Text | Google Scholar

Jennings, B., and Parslow, R. (1988). Particle size measurement: The equivalent spherical diameter. Proc. Royal Soc. A Math. 419 (1856), 137–149. doi:10.1098/rspa.1988.0100

CrossRef Full Text | Google Scholar

Jensen, R. P., Plesha, M. E., Edil, T. B., Bosscher, P. J., and Kahla, N. B. (2001). DEM simulation of particle damage in granular media — structure interfaces. Int. J. Geomech. 1 (1), 21–39. doi:10.1061/(asce)1532-3641(2001)1:1(21)

CrossRef Full Text | Google Scholar

Kumar, S. S., Krishna, A. M., and Dey, A. (2017). Evaluation of dynamic properties of sandy soil at high cyclic strains. Soil Dyn. Earthq. Eng. 99, 157–167. doi:10.1016/j.soildyn.2017.05.016

CrossRef Full Text | Google Scholar

Lee, C., Suh, H. S., Yoon, B., and Yun, T. S. (2017). Particle shape effect on thermal conductivity and shear wave velocity in sands. Acta Geotech. 12 (3), 615–625. doi:10.1007/s11440-017-0524-6

CrossRef Full Text | Google Scholar

Li, B., Wang, Y., Jin, Q., and Chen, H. (2019). Liquefaction characteristics of recycled concrete aggregates. Soil Dyn. Earthq. Eng. 120, 85–96. doi:10.1016/j.soildyn.2019.01.038

CrossRef Full Text | Google Scholar

Li, C., Liu, T., Fu, H., Zhang, X., Yang, Y., and Zhao, S. (2021). Test and evaluation of the flexural properties of reinforced concrete beams with 100% recycled coarse aggregate and manufactured sand. Buildings 11 (9), 420. doi:10.3390/buildings11090420

CrossRef Full Text | Google Scholar

Li, W., Wang, D., Chen, B., Hua, K., Su, W., Xiong, C., et al. (2022). Research on three-dimensional morphological characteristics evaluation method and processing quality of coarse aggregate. Buildings 12 (3), 293. doi:10.3390/buildings12030293

CrossRef Full Text | Google Scholar

Maeda, K., Sakai, H., Kondo, A., Yamaguchi, T., Fukuma, M., and Nukudani, E. (2010). Stress-chain based micromechanics of sand with grain shape effect. Granul. Matter 12 (5), 499–505. doi:10.1007/s10035-010-0208-5

CrossRef Full Text | Google Scholar

Mao, X., and Fahey, M. (2003). Behaviour of calcareous soils in undrained cyclic simple shear. Geotechnique 53 (8), 715–727. doi:10.1680/geot.2003.53.8.715

CrossRef Full Text | Google Scholar

Mirghasemi, A. A., Rothenburg, L., and Matyas, E. L. (2002). Influence of particle shape on engineering properties of assemblies of two-dimensional polygon-shaped particles. Geotechnique 52 (3), 209–217. doi:10.1680/geot.2002.52.3.209

CrossRef Full Text | Google Scholar

Nye, C. J., and Fox, P. J. (2007). Dynamic shear behavior of a needle-punched geosynthetic clay liner. J. Geotech. Geoenviron. Eng. 133 (8), 973–983. doi:10.1061/(asce)1090-0241(2007)133:8(973)

CrossRef Full Text | Google Scholar

Otsubo, M., Towhata, I., Hayashida, T., Liu, B., and Goto, S. (2016). Shaking table tests on liquefaction mitigation of embedded lifelines by backfilling with recycled materials. Soils Found. 56 (3), 365–378. doi:10.1016/j.sandf.2016.04.004

CrossRef Full Text | Google Scholar

Porcino, D., Caridi, G., and Ghionna, V. N. (2008). Undrained monotonic and cyclic simple shear behaviour of carbonate sand. Geotechnique 58 (8), 635–644. doi:10.1680/geot.2007.00036

CrossRef Full Text | Google Scholar

Rousé, P. C., Fannin, R. J., and Shuttle, D. A. (2008). Influence of roundness on the void ratio and strength of uniform sand. Geotechnique 58 (3), 227–231. doi:10.1680/geot.2008.58.3.227

CrossRef Full Text | Google Scholar

Rui, S., Guo, Z., Si, T., Zhou, W., and Zha, X. (2021). Particle shape influence on the deformation resistance of carbonate sands under drained condition. Soil Dyn. Earthq. Eng. 144, 106688. doi:10.1016/j.soildyn.2021.106688

CrossRef Full Text | Google Scholar

Shigehisa, E., Yoshikazu, K., Hitoshi, O., Ikeda, C., and Iwata, H. (1998). Shape estimation of anisometric particles using size measurement techniques. Part. Part. Syst. Charact. 15 (3), 145–149. doi:10.1002/(SICI)1521-4117(199817)15:3<145::AID-PPSC145>3.0.CO;2-B

CrossRef Full Text | Google Scholar

Shinohara, K., Oida, M., and Golman, B. (2000). Effect of particle shape on angle of internal friction by triaxial compression test. Powder Technol. 107 (1-2), 131–136. doi:10.1016/S0032-5910(99)00179-5

CrossRef Full Text | Google Scholar

Sonmezer, Y. B. (2019). Energy-based evaluation of liquefaction potential of uniform sands. Geomechanics Eng. 17 (2), 145–156. doi:10.12989/gae.2019.17.2.145

CrossRef Full Text | Google Scholar

Suh, H. S., Kim, K. Y., Lee, J., and Yun, T. S. (2017). Quantification of bulk form and angularity of particle with correlation of shear strength and packing density in sands. Eng. Geol. 220, 256–265. doi:10.1016/j.enggeo.2017.02.015

CrossRef Full Text | Google Scholar

Tang-Tat, N. (2009). Particle shape effect on macro- and micro-behaviors of monodisperse ellipsoids. Int. J. Numer. Anal. Methods Geomech. 33 (4), 511–527. doi:10.1002/nag.732

CrossRef Full Text | Google Scholar

Tsomokos, A., and Georgiannou, V. N. (2010). Effect of grain shape and angularity on the undrained response of fine sands. Can. Geotech. J. 47 (5), 539–551. doi:10.1139/T09-121

CrossRef Full Text | Google Scholar

Ueda, T., Matsushima, T., and Yamada, Y. (2013). DEM simulation on the one-dimensional compression behavior of various shaped crushable granular materials. Granul. Matter 15 (5), 675–684. doi:10.1007/s10035-013-0415-y

CrossRef Full Text | Google Scholar

Ueng, T. S., Wang, Z. F., Chu, M. C., and Ge, L. (2017). Laboratory tests for permeability of sand during liquefaction. Soil Dyn. Earthq. Eng. 100, 249–256. doi:10.1016/j.soildyn.2017.05.037

CrossRef Full Text | Google Scholar

Vieira, C. S., Lopes, M. L., and Caldeira, L. M. (2013). Sand-geotextile interface characterisation through monotonic and cyclic direct shear tests. Geosynth. Int. 20 (1), 26–38. doi:10.1680/gein.12.00037

CrossRef Full Text | Google Scholar

Wadell, H. (1932). Volume, shape, and roundness of rock particles. J. Geol. 40 (5), 443–451. doi:10.1086/623964

CrossRef Full Text | Google Scholar

Wang, J., Fang, Z., Cai, Y., Chai, J., Wang, P., and Geng, X. (2018). Preloading using fill surcharge and prefabricated vertical drains for an airport. Geotext. Geomembranes 46 (5), 575–585. doi:10.1016/j.geotexmem.2018.04.013

CrossRef Full Text | Google Scholar

Wang, J., Liu, F. Y., Wang, P., and Cai, Y. Q. (2016). Particle size effects on coarse soil-geogrid interface response in cyclic and post-cyclic direct shear tests. Geotext. Geomembranes 44 (6), 854–861. doi:10.1016/j.geotexmem.2016.06.011

CrossRef Full Text | Google Scholar

Wang, T., Ma, L., Wang, M., Li, Z., Zhang, X., and Geng, H. (2022). Effects of particle shape on dynamic mechanical behaviours of coral sand under one-dimensional compression. Eng. Geol. 304, 106624. doi:10.1016/j.enggeo.2022.106624

CrossRef Full Text | Google Scholar

Yang, J., Liang, L. B., and Chen, Y. (2022). Instability and liquefaction flow slide of granular soils: The role of initial shear stress. Acta Geotech. 17 (1), 65–79. doi:10.1007/s11440-021-01200-1

CrossRef Full Text | Google Scholar

Yang, J., and Wei, L. M. (2012). Collapse of loose sand with the addition of fines: The role of particle shape. Geotechnique 62 (12), 1111–1125. doi:10.1680/geot.11.P.062

CrossRef Full Text | Google Scholar

Yang, R., Yu, R., Shui, Z., Guo, C., Wu, S., Gao, X., et al. (2019). The physical and chemical impact of manufactured sand as a partial replacement material in Ultra-High Performance Concrete (UHPC). Cem. Concr. Compos. 99, 203–213. doi:10.1016/j.cemconcomp.2019.03.020

CrossRef Full Text | Google Scholar

Yang, Z., and Elgamal, A. (2002). Influence of permeability on liquefaction-induced shear deformation. J. Eng. Mech. 128 (7), 720–729. doi:10.1061/(asce)0733-9399(2002)128:7(720)

CrossRef Full Text | Google Scholar