- 1CIRES and Geological Sciences, University of Colorado, Boulder, CO, United States
- 2Central Washington University, Ellensburg, WA, United States
- 3UNAVCO, Boulder, CO, United States
- 4Department of Geosciences, University of Montana, Missoula, MT, United States
Three quarters of all Mw ≥ 6.6 earthquakes and volcanic eruptions surrounding the Caribbean plate occur preferentially during periods of decadal minima in Earth’s angular spin velocity. This correlation is revealed most clearly as a 4–6 years phase lag following the first derivative of the length of the day (LOD), Earth’s angular deceleration. We show that local strains and displacements resulting from oblateness changes, or plate boundary stresses associated with changes in tropical rotation rates are orders of magnitude lower than those typically associated with earthquake or volcano triggering. Notwithstanding the absence of a satisfactory causal physical mechanism, the relationship permits decadal trends in Caribbean tectonic hazards to be anticipated many years before their occurrence. The next period of increased tectonic activity in the Caribbean, corresponding to a probable slowing in Earth’s spin rate, will occur in the decade starting on or about 2030.
Introduction
A number of studies have established that annual fluctuations in the numbers of major earthquakes (Mw ≥ 7.0) vary over periods of decades, and that these cyclic changes in seismic productivity correlate with long period variations in Earth’s angular rotation rate (Anderson, 1974; Kanamori 1977; Shankar et al., 2001; Varga et al., 2004; Levin and Sasorova, 2015; Levin et al., 2017; Sasarova and Levin, 2018; Lutikov & Rogozhin (2014). The Mw ≥ 7 magnitude threshold in these studies arises because seismic catalogs since 1900 are decreasingly complete in lower magnitude earthquakes in the early instrumental record (see Supplementary Material S1).
Although quasi-periodic fluctuations in global seismic activity with periods from 10 to 60 years, are similar to those found in studies of fluctuations in the length of the day, an exact correspondence does not exist, and for many seismologists the relationship is not only unexpected but unconvincing. Our interests in these apparent relationships were stimulated by the identification of a dominant ≈32 years interevent interval for global Mw ≥ 7 seismicity (Bendick and Bilham, 2017), and subsequently augmented by noting the apparent 5 years lag between peak global seismicity and peak angular deceleration shown in Figure 1A (Bendick and Bilham, 2018; Bendick and Bilham, 2018).
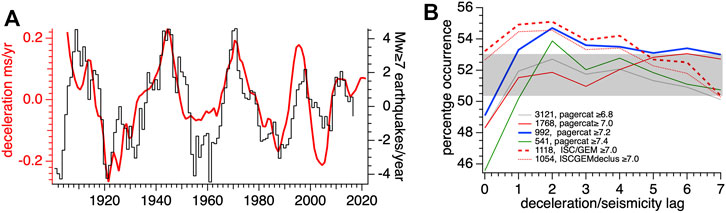
FIGURE 1. (A). Earth’s angular deceleration (red) compared to global annual deviation in numbers of Mw ≥ 7 earthquakes each year (black PagerCat, Allen et al., 2009). Both time series are band-passed with the same 5-50 year filter and the deceleration data are plotted with a five-year advance (from Bendick and Bilham, 2018). (B). Lag between global numbers of earthquakes per year and angular deceleration time series for different seismic catalogs and magnitude ranges using binary mask (see text). Were earthquakes randomly distributed in time we should anticipate each curve to lie within the shaded region of 51.7 ± 1.3% (Supplementary Material S2).
In previous and subsequent studies (e.g., Levin et al., 2017; Sasarova and Levin 2018; Jenkins et al., 2021), smoothed time series of annual counts of major earthquakes have been compared with time series of annual fluctuations in the length of the day (e.g., Figure 1A). Statistical tests to demonstrate causality are often unconvincing because of the small number of cycles involved, and results are influenced by the smoothing necessary to attenuate sub-decadal fluctuations in numerical annual earthquake counts. To overcome the brevity of the instrumental record Sasarova and Levin (2018) have with some success extended these studies to the past three centuries of historical data.
Here, to avoid artifacts from smoothing annual counts of seismicity, we adopt a different and simpler approach. As a starting point we use the first derivative of the length-of-day series, which characterizes the Earth’s secular angular deceleration, and has the attribute that zero angular acceleration corresponds to zero Euler forces (i.e., forces associated with accelerations along lines of latitude) on the Earth’s surface. We then discard numerical values in the series to form a binary mask of zeros (acceleration years) and ones (deceleration years). We use this binary series to count the numbers of earthquakes occurring during deceleration years and express this as a percentage of the total number in the catalog. We next examine the value of this percentage for various lags by advancing the earthquake catalog in increments of 1–10 years. The results are expressed as plots showing percentages of earthquakes accompanying deceleration or occurring with phase lags of up to 9 years (viz. Figure 1B).
This approach avoids arbitrary smoothing or band-passing numbers of events to form a time series and instead uses raw seismic and/or volcanic data from a region. Our null hypothesis is that in the absence of a rotational influence we should anticipate approximately equal numbers of earthquakes to occur during periods of Earth’s acceleration or deceleration. Because of an uneven slowing in the secular spin rate, the rate of occurrence for different epochs in random catalogs exceeds 50%. For example, for the 1900–2017 interval in Figure 1B random catalogs yield an average and standard deviation of 51.7 ± 1.3% (shaded).
We tested the algorithm on global seismicity as reported in previous studies using global catalogs with different magnitude cutoffs and methods of declustering. We used published declustering methods (e.g., Reasenberg, 1985; van Stiphout et al., 2012; Zaliapin and Ben-Zion, 2020), but found the results from these different approaches did not substantially alter our results. In Figure 1B we plot the global percentage of earthquakes in various catalogs occurring during periods of Earth’s deceleration at different lags following the binary time series of deceleration described above. We compare these percentages with those derived from an arbitrary number of 1250 catalogs of events with similar total numbers of global earthquakes occurring at random times. In this comparison we found that while some earthquake catalogs (irrespective of declustering) showed a distinct correlation, significantly above random, others did not.
To test whether the observed correlations were influenced by plate boundary setting, or latitude we examined the percentage ratios of Mw ≥ 7 earthquakes occurring following deceleration or acceleration at regional plate boundaries for the declustered Pagercat catalog since 1900. The percentages of events occurring during deceleration or acceleration are depicted graphically as pie diagrams (Figure 2). The percentages of roughly half of the 24 regions are close to those anticipated from random occurrence, however, for Baluchistan, the Hindu Kush, the Taiwan region and the Caribbean the percentage occurring during acceleration or deceleration approaches or exceeds 75%.
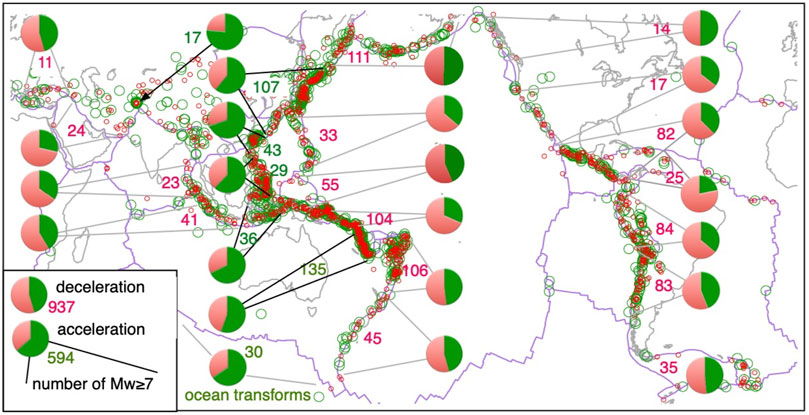
FIGURE 2. Regional distribution of Mw > 7.0 earthquakes 1900–2017 (declustered PagerCat), and global distribution lower left inset. Pie-graphs on segments of plate boundaries quantify the proportion of Mw ≥ 7 earthquakes occurring 5 years following prolonged periods of rotational deceleration (red), or acceleration (green) and the total number of earthquakes considered in each pie diagram. The number of earthquakes analyzed in regional plate boundaries varies from as few as 17 to as many as 135. Acceleration dominant pie-graphs account for only 39% of all earthquakes considered.
In the current article we focus specifically on the statistics of earthquakes and volcanic eruptions in one of these regions - the Caribbean—a plate that measures ≈2500 km east-west by ≈700 km north-south and moves eastward at ≈21 mm/yr between the Cocos subduction zone in the west and subducted Atlantic sea floor in the east (van Benthem and Govers, 2010). Its western end is bounded in the north by a sinistral transform fault system interrupted by a minor spreading center in the Cayman trough, and in the south by a dextral transform with partitioned transpressional convergence beneath eastern Venezuela and Colombia (the downgoing Maracaibo slab). In the eastern Caribbean the northern transform boundary includes minor convergence, and its southern margin is bounded by the El-Pilar/Bocono dextral transform fault system.
A record of earthquakes and eruptions in the Caribbean is available since 1660, although in some areas it is partly incomplete prior to 1900. We show that 65% of the Caribbean’s Mw ≥ 6.6 earthquakes, and more than 75% of Mw ≥ 7 earthquakes and volcanic eruptions with VEI>1 in the Antilles Arc follow periods of Earth’s deceleration with a lag of 5 ± 3 years. By comparing our results with randomly generated catalogs we show that the probability that this observed correlation occurs by chance is low.
Having demonstrated these correlations in the acceleration domain we show that they are also present in the angular velocity domain, and that the observed phase lags arise from the expected 90° phase lag in the derivative of the dominant 20 ± 10 years periods in the length of the day time series. This leads to the conclusion noted by others (referenced in our opening paragraph) on a global scale that seismic activity is enhanced during decadal periods of slow angular spin velocity. We follow this with a discussion of possible mechanisms for the observed influence of spin rate on tectonism, and a brief discussion of the utility of the observed relationship for reducing future seismic risk.
Data
We interpolated 6-month averaged length-of-day (LOD) data for the period 1656–1834 from McCarthy and Babcock (1986) to mid-year annual mean values using a smoothing spline with a smoothing coefficient of 0.2. To these data we appended additional LOD data to 1995 calculated by Gross (2001). Mid-year averages from the International Earth Rotation Service (IERS) were used complete the time series to mid-2021 (Figures 3A,B).
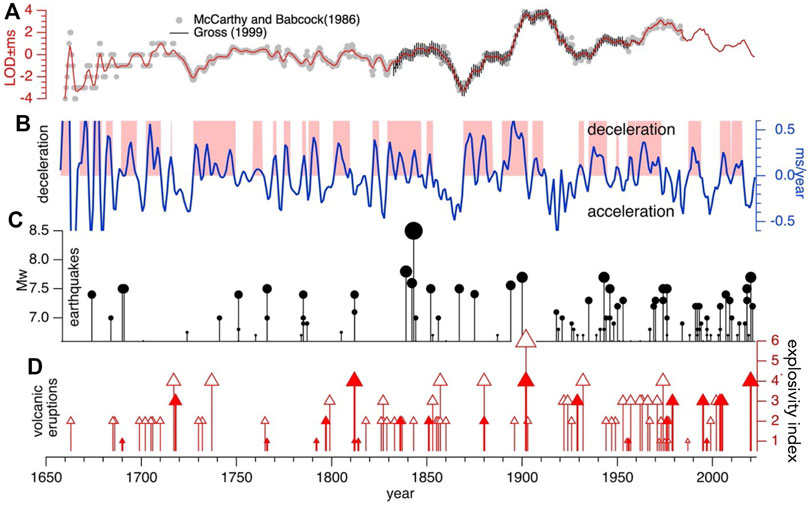
FIGURE 3. (A). Variations in the length of the day (LOD) 1656-2021 (an increase of +1 millisecond corresponds to reduction in spin velocity of 1.2 ×10−8 radians/s). Uncertainties after 1832 from Gross (2001). (B). LOD Derivative with periods of deceleration shaded red. In this plot the shaded areas include 5-year box-car smoothing. (C). Earthquakes with Mw ≥ 6.6 in the Caribbean region: 1650–1900. (D). Volcanic eruptions plotted numerically according to Volcanic Explosivity Index(VEI): eastern Caribbean (solid triangles), Guatemala (open triangles).
Two seismicity catalogs were used in the current study: the USGS Comcat/PagerCat catalog (Allen et al., 2009) for the period 1900–2022, and the ISC/GEM Version 5 catalog 1904–2017. Few differences between the on-line catalogs exist for post-1960 data, but both catalogs are incomplete for earthquakes with Mw ≤ 6.9 in the first few decades of the 20th century. For seismicity 1660–1900 we consulted an early catalog by Robson (1964) and the ISC/GEM historical catalog data and references therein (Figure 3C). The spatial distribution of seismicity is shown in Figure 4.
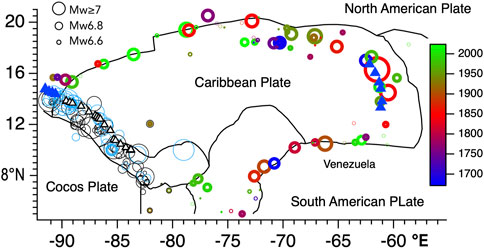
FIGURE 4. Caribbean seismicity and volcanism for the period 1665–2017. 6.6 < Mw < 8.5 colored by year and scaled by magnitude. Central American earthquakes ≥6.6 since 1904 (black circles), 1656–1900 light-blue circles. Plate boundaries from Bird (2003). Volcanoes influenced by deceleration (solid triangles): unaffected by deceleration (open triangles).
We used volcanic eruption data from the Smithsonian Global Volcanism Program (2013) which is probably complete for volcanic explosivity indices (VEI) >1 based as it is on written Caribbean archives since 1700 (Figure 3D). We examined volcanism in six separate geographical regions: Central American volcanoes in four approximately 1-degree-latitude bins between 7°N and 13°N, volcanic centers in Guatemala north of 14.5°N and finally, those in the eastern Caribbean volcanic arc, excluding Kick’em Jenny for which the early record of submarine eruptions is considered incomplete (Figure 4).
Results
In the 365-year-interval since 1656, 34 earthquakes with Mw≥6.6 are listed in the pre-instrumental catalog and 65 for the period 1900–2021. The disparity in numbers per century emphasizes incompleteness in earthquakes with Mw ≤ 7 in the early record. For each time-span of data investigated we quantified the departure from random occurrence by examining 1250 sequences of similar numbers of random earthquakes (see Supplementary Material S2) against the raw deceleration time series for each epoch. For tests that included >50 earthquakes/century, the average and standard deviation for the 365-year period was 50 ± 2.4%, and for the post-1900 interval instrumental period the average was 51.7 ± 1.3%. For subsets of data with fewer than 20 events per century the uncertainty from random catalogs increases to 18%. These 95% confidence regions are shaded or indicated by confidence intervals in Figure 5.
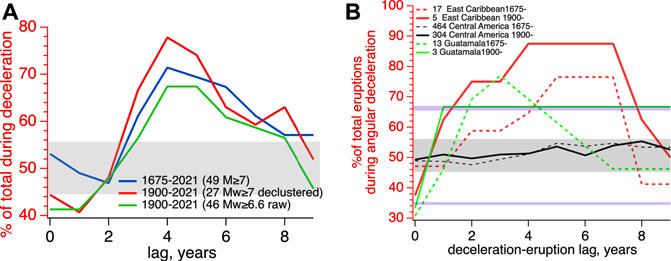
FIGURE 5. (A). Percentage earthquakes for the Caribbean plate boundary (for indicated time intervals and subsets of data) occurring following the angular deceleration time series (Figure 1B) with lags 0–9 years: 78% of Mw ≥ 7 earthquakes since 1900, and 70% since 1675 occur after a 4-year lag. (B). Percentages of volcanic eruptions in the Eastern Caribbean and Guatemala following the deceleration time series for various lags. Central American volcanoes are evidently indifferent to deceleration. The grey areas in each figure mask the percentages anticipated for random occurrence; the violet lines indicate random occurrence limits for ≈10 eruptions/century.
Smoothing of the deceleration data prior to generating the digital mask described above has no significant influence on the observed relationships (see Supplementary Material S3) and hence we used unsmoothed data in the analyses presented here. At zero lag (i.e., synchronous seismicity occurring during that year’s observed angular deceleration) a weak correlation with acceleration is observed for post-1900 data, and no correlation is observed for early data. In contrast, seismicity lagging 3–6 years after the deceleration time-series shows significant correlation for both subsets of data. Maximum percentages of 60–65% occur for lags of 4–5 years. Of 49 Mw ≥ 7 earthquakes since 1656 and 27 since 1900, 70%–77% have occurred with a lag of 4 years after deceleration (Figure 5A). More than 68% of all Mw ≥ 6.6 earthquakes since 1900 have occurred 4–5 years after deceleration.
Similar correlations are evident for the volcanic eruption data. Since 1656, 464 eruptions occur in Central America and 17 in the eastern Caribbean. We counted the number of eruptions occurring during periods of angular deceleration independent of their volcanic explosivity index (VEI). We found that each of four ≈1°-latitude subsets of central American volcanoes were indifferent to deceleration and we summarize their ensemble average in Figure 5B. In contrast, although the total number of eruuptions is small, volcanoes in Guatemala and the Eastern Caribbean show a marked preference for erupting after a two- to 7-year lag. The ≥80% correlation for the 20th century Antilles eruption record signifies that four of its five eruptive episodes appear to have been influenced by Earth’s deceleration. Similarly, 12 of its 17 pre-1900 eruptions have been likewise influenced. Eruptions typically follow nearby major earthquakes (González et al., 2021). Global correlations between volcanic eruptions and Earth’s rotation have been previously reported by Palladino and Sottili (2013) and Sottili et al. (2014).
In Supplementary Material S4 we examine the influence of Earth rotation variations on seismicity surrounding the Scotia plate and plate boundaries contiguous with the Caribbean Plate. Central American Mw > 7 seismicity for the instrumental period was found to be antiphase with the Caribbean plate correlations described above, but when earthquakes from the historical record were included, the effect was significantly suppressed. Cocos and Andean subduction seismicity is weakly influenced by deceleration at zero lag (Supplementary Figure S3B), with Cocos seismicity suppressed by 10% and Andes seismicity enhanced by 15%. In contrast, the Scotia plate responds strongly and immediately to deceleration with more than 70% of its earthquakes occurring after a lag of 2–3 years. An examination of sparse Mw ≥ 7 Mid Atlantic transform seismicity showed it to be largely indifferent to the rotational deceleration time series. Although these relationships may be important in identifying a physical mechanism for the observed effects, we do not discuss these further in this article.
Angular deceleration vs. velocity?
In the above analyses we have compared the timing of earthquakes and eruptions with angular deceleration time series. In this section we show that the 3–7 years lags evident in these correlations arise from the lag between Earth’s angular deceleration and angular spin velocity. For example, were the LOD time series a sine wave with a period of 20 years, peak LOD would lag precisely π/2, or 5 years, behind peak deceleration. Multi-taper spectral analysis of the deceleration data reveals broad spectral peaks centered near 7, 9.5, 14, 40 and 60 year periods (shaded green Figure 6B). Analyses of subsets of the deceleration data with different start and end times reveal that the peaks vary somewhat in amplitude and period indicating a non-stationary spectrum. These same peaks in a spectrum of the raw LOD time series are masked by spectral energy arising from the DC component of the LOD time series, however, they are readily apparent in a high-pass filtered version of the LOD time series. We demonstrate their presence in a residual LOD series formed by subtracting a smoothing spline filter fit to the data, from the raw data (Figure 6A). The spectral harmonics in the residual, as expected, are similar to those derived from the deceleration time series (Figure 6B).
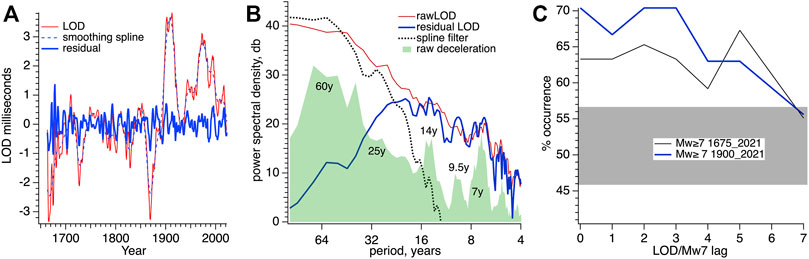
FIGURE 6. (A). LOD time series (red) and its residual (blue) after removing a smoothing spline fit to the LOD data. (B). Multi-taper spectral analyses (expressed as db with arbitrary zero) of the deceleration time series (green shading), smoothing spline (dotted black line), the raw (red) and residual (blue) length-of-day data (red). (C). percentage of earthquakes occurring during periods of positive excursions in residual shown in (A). Grey area indicates region anticipated from random occurrence.
We surmise that the deceleration correlations with 5 ± 3-year lags in Figure 5 correspond to subsequent angular spin velocity (LOD) correlations with 0–6 years lag, at periods of 20 ± 12 years. As a test of this conclusion, we convert the residual series in Figure 6A to a binary series of slow/fast angular velocities and count the percentage number of earthquakes occurring during slow velocities (Figure 6C). This shows that >65% of all earthquakes occur during times when the Earth spins at minimum velocity (maximum LOD) with zero lag, or a lag of several years.
Hence, in searching for a physical mechanism linking variations of the length-of-day with lithospheric seismicity, physical mechanisms relating angular deceleration, or velocity, are equally viable. The influence of angular velocity is instantaneous, and the influence of angular deceleration leads by an interval of T/4, where T is the forcing period in years.
This conclusion can only be defended for fluctuations in LOD with periods shorter than ≈50 years. Longer periods do not appear to contribute significantly to the observed correlations. This conclusion is consistent with the 5–50 years band-passed correlation reproduced in Figure 1A.
Mechanisms: Influence of changes in spin velocity on lithospheric stresses
We review briefly several mechanisms that have been proposed to relate changes in angular velocity to lithospheric seismicity (Figure 7). The mechanisms fall into three broad classes: velocity changes that grow or reduce the equatorial bulge (e.g., Sottili et al., 2014; Levin and Sasarova, 2017), forces that result directly from lithospheric accelerations (Euler and Coriolis forces) with or without potential phase lags resulting from near surface viscosity, Polflucht accelerations and surface-normal accelerations (changes in g) resulting from angular velocity and radius changes.
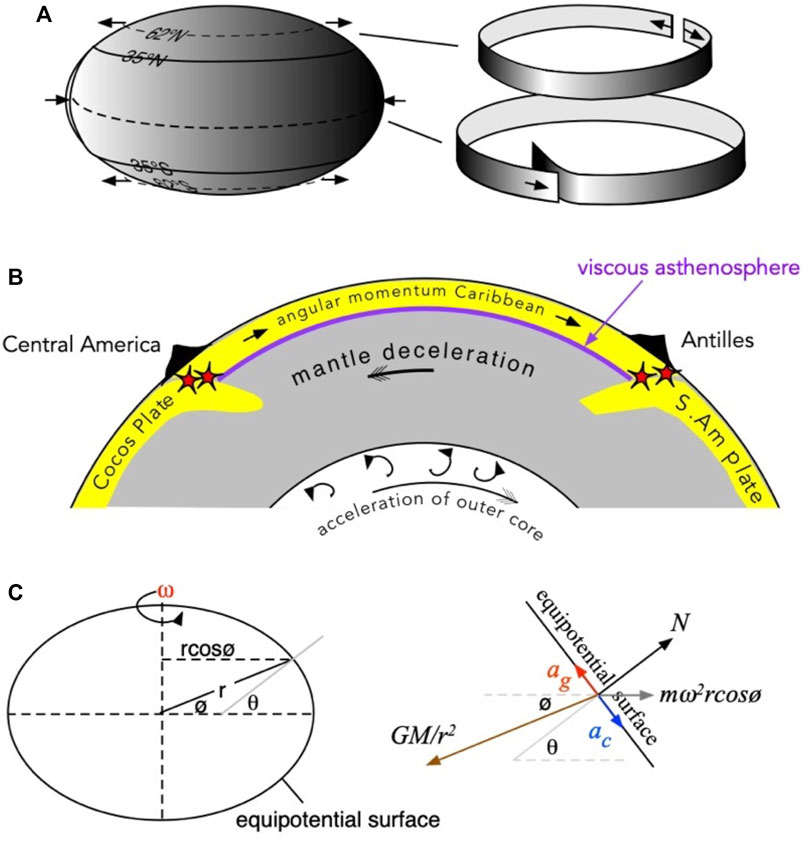
FIGURE 7. Schematic views of coupling between an incremental slowing in Earth’s spin velocity and lithospheric stresses. (A) A slowing in rotational velocity decreases Earth’s oblateness, extending small circles in polar regions and decreasing them in tropical regions. (B) Schematic section through equator viewed from south pole showing sense of Euler forces attending deceleration. (C) Resolved horizontal accelerations acting on a point mass on the equatorial bulge (ag = ac) exactly cancel, but surface-normal gravity increases with decreasing angular velocity.
Oblateness and angular velocity
Levin et al. (2017) quantify the surface strain changes that accompany a decrease in rotational velocity as follows. The change of radius of an oblate spheroid, ∆R, as a function of latitude ø is related to changes of the flattening of the earth ∆e as a function of angular velocity in the form
where R is Earth’s mean radius. This results in a change in the small-circle circumference at the Earth’s surface, ∆c as a function of latitude.
where ∆e is the product of Earth’s flattening and the angular velocity change ∆ω radians/s. Substituting A= 6378 km, ∆e = 7.78 × 10−11 for a 1 millisecond change in LOD in Eq. 2 yields extremal values for ∆c of ≈1 mm/ms at the equator, zero at the poles and at latitudes of ±35.262°, and −0.65 mm/ms at latitudes of ±62°.
Elastic oblateness adjustments are assumed to be complete within a few hours of angular velocity changes, followed by viscous adjustments of the mantle with time constants of the order of hundreds of years (Munk and McDonald, 1973). For the 2500-km-wide Caribbean plate at ≈12°N, displacements between the Cocos and Atlantic Sea floor subduction zones amount to just 0.06 mm (≈2 × 10−11 strain) per millisecond of LOD slowing. Were this convergence applied to the Antilles subduction zone alone it would be the equivalent to about 1 day of eastward plate-tectonic motion of the Caribbean plate, or 0.003% of a 100 years duration earthquake cycle. Hence, the ability for oblateness changes to influence seismicity exists, but appears to be insignificant. Moreover, these inferred displacements would not contribute directly to shear strain on Caribbean’s northern and southern transform faults.
A secondary effect of a change in velocity has been proposed by Sottili et al. (2014), and references therein. It invokes the change in the tensile hoop stress in a rotating small-circle annulus approximating the lithosphere. Supposing the lithosphere were a competent homogeneous material with density, d, rotating with uniform velocity ω, with diameter 2R, the tensile stress would be σΗ = dω2R2 ≈ 600 MPa (Hearn, 1997). Reductions in angular velocity of 10–8 rad/s associated with 1 millisecond increase in LOD, however, would change this tensile stress by only 14 Pa, and changes in differential stresses between the base and top of the crust by less than 0.04 Pa. These changes in stress are significantly smaller than those calculated by Sottili et al. (2014) and orders of magnitude smaller than those typically associated with triggering crustal volcanism or seismicity. The discrepancy between our values and theirs is that these authors introduced an “effective” change in the LOD considerably larger than the maximum mean annual LOD change (Sottili, personal communication, 2022)
Angular deceleration and angular momentum of the Caribbean plate
The second mechanism is dynamic (Figure 7B). A slowing in rotation rate results in an Euler force on a mass on the Earth’s surface directed along a line of latitude. The force is resisted by tractions between mantle and lithosphere resulting from the viscosity of the asthenosphere, and by subducting slabs anchored to the mantle. The resulting displacements are minimal at annual periods but can occur with increasing amplitude and lag at periods longer than several years. Thus, in the presence of mantle deceleration over periods of decades, eastward motion between the Caribbean and contiguous plates is decreasingly restrained by asthenospheric viscosity, and increasingly compliments plate boundary eastward motions thereby enhancing transform and subduction zone seismicity. During succeeding periods of acceleration, the process reverses and plate boundary stresses are relaxed. The Caribbean thus acts effectively as a “loose cannon” between the Central American and Atlantic subduction zones, both of which are securely anchored to the mantle. The analogy is weak because east-west motion of the Caribbean plate is also resisted by its south-dipping subducted Maracaibo slab beneath Colombia and Venezuela.
Before calculating the forces predicted by this dynamic mechanism, we first calculate whether the observed delays of several years are reasonable. We approximate the Caribbean plate as a flat rigid slab separated by a Maxwell-viscous layer (the asthenosphere) from an underlying surface undergoing simple harmonic motion (Ross and Schubert, 1986). The phase lag between induced motions of the top plate when driven by the basal plate driven at period T has the form:
where ν= viscosity and µ is the rigidity modulus of the intervening asthenospheric layer. Reasonable numbers for µ (6 × 1010 Nm−2) and ν (=3.1018 Pa s) yield a phase lag of 5 years for input periods of ≈20 years.
We next estimate the plate boundary forces arising from these long period decelerations. The linear eastward velocity (v) of Caribbean plate at 12°N is 2πr/86164.1, v= 454.9 m/s, which reduces by −5.3 μm/s for each 1 ms increase in LOD. Hence a linear deceleration of −1.7E-14 m−2 is associated with a 1 ms change in LOD at decadal periods.
Approximating the volume of the Caribbean plate as a block with area ≈2 × 1012 m2 and thickness 30 km with an average density of 2750 kg/m3 we derive a mass of ≈2 × 1020 kg. Were the asthenosphere frictionless, the plate boundary force necessary to arrest the momentum of the plate would be 2 × 1020 x 1.7 × 10−14 = 3.3 × 106 N.
If this were entirely resisted by the Antilles subduction zone with cross-sectional area ≈500 km × 20 km, the stress/unit area would amount to 3.3 × 10−4 N/m2 (330 Pa or 3.3 × 10−9 bar). These values are nine orders of magnitude lower than the incremental stresses of ≈1 bar that have been reported as sufficient to trigger earthquakes, but approach the ≈100 Pa stress changes that have been invoked as responsible for modulating seismic tremor (Thomas et al., 2009, 2012) The calculated stresses are further diminished if the contact areas of the northern and southern transforms are figured into the calculations.
Centripetal forces
The centripetal acceleration on a mass, m, on the Earth’s surface is mω2Rcosø directed normal to the spin axis, where R is the radius of the Earth, ω the angular velocity, and ø its latitude. Were the Earth spherical, its resolved component perpendicular to the Earth’s surface would be mω2Rcos2ø, with a tangential acceleration parallel to the Earth’s surface directed towards the equator of mω2Rcosø sinø. On a spherical rotating Earth this tangential acceleration would force a mass like the Caribbean plate to drift toward the equator. However, the equatorial bulge on an elastic earth adopts a figure that exactly annuls this force. i.e., the surface of the spheroid is everywhere an equipotential and the resolved horizontal components of mass attraction (ag) and centripetal acceleration (ac) are exactly equal and opposite, independent of angular velocity (Figure 7C).
While no residual north-south accelerations accompany a change in oblateness, the surface acceleration due to gravity increases during slowing of Earth’s spin, due to reduced equatorial radius and a reduction in outward directed centripetal acceleration caused by the slowing in angular velocity. The net acceleration due to gravity and centripetal forces normal to the surface can be approximated by:
The net increase in g at the mean latitude of the Caribbean (∼10°N) for a 1 ms increase in the LOD is ≈0.15 µGal (10–9 m/s−2). Thus, an increase in LOD caused by a slowing of Earth’s rotation, would tend to increase slab-pull of the subducted Caribbean plate beneath the Maracaibo Basin, and slab suction near the Antilles by ≈1 part in 1010 per millisecond LOD. Van Benthem and Govers (2010) calculate NW directed tensile stress magnitudes of 12 MPa for the region NW of the Maracaibo slab and hence these would be enhanced by a mere 10–3 Pa (10–8 bars) per millisecond LOD increase.
Chandler wobble- variations of surface strain and gravity 1848–2022
Variations in Earth’s rotation rate are superimposed on the Earth’s annual wobble and the slightly longer period Chandler wobble. In the presence of polar shifts of x and y radians along the Greenwich and 90°E meridians respectively, the variation of the Earth’s acceleration due to gravity, and easterly displacement, sλ, at colatitude θ, and east longitude λ, are
In the above first order expressions derived by Wahr (1985), the direct contribution from changes in rotational velocity on gravity and displacement are considered negligible, as are the effects of anelasticity and ocean loading. The variation of g and east-west strain at the average latitude and longitude of the Caribbean plate between 1845 and 2021 are shown in Figure 8. During this time, longitudes between 75°±12°W contract 5 ± 0.7 nanostrain and gravity increases by 3 ± 0.3 µGal, both small quantities.
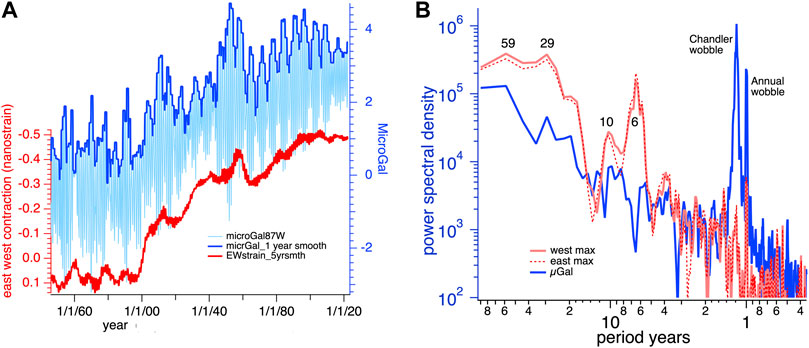
FIGURE 8. (A) E/W strain changes (red) across the Caribbean plate 1845–2022 with a 5 years moving average, compared to variations in gravity (light blue), and their peak annual value (dark blue). (B) Multi-taper spectral analyses of the raw gravity signal (blue) showing the Chandler and Annual peaks, compared to the spectral density of peak annual strain calculated for the E and W extremities of the Caribbean plate.
Though the wobble periods are too short to account for the correlations we describe above, the sum of the (≈14 months) Chandler wobble and the (12-month) annual wobble modulates the sum of the two time-series with dominant beat frequency of ≈6 years, and with secondary periods near 10, 20, 29 and 59 years (Figure 8).
The slow increase in gravity over the past 175 years is incremented at 5-year to 60-year intervals by ≈1µGal (1.5 × 10−8 Nm−2) equivalent to a 3 mm rise in sea level. We conclude that strain changes and changes in g resulting from Earth’s wobble are negligible compared to those typically associated with earthquake triggering.
Polflucht acceleration
Early in the last century Wegener (1980) invoked polflucht as a mechanism to move continents from the poles toward the equator (Epstein, 1921; Lambert 1921; Krause, 2007). Although this acceleration and its attendendent forces have been subsequently neglected, they influence Coulomb failure conditions on plate boundaries. The amplitude of polflucht acceleration on a free body depends on its latitude and the distance between the center of gravity and its center of buoyancy, being zero at the equator and the poles (Engelhardt and Englehardt, 2017) in the case of floating body, or the vertical distance between its translation surface and its center of mass, in the case of a solid body. The equator-directed acceleration arises because co-geoids (surfaces of equal gravitational potential above or below the earth’s geoid) on a rotating earth are not parallel along lines of longitude. That is, at great distances from the earth, or beneath the Earth’s surface, co-geoids tend to become more spherical, whereas at the Earth’s surface they are spheroidal. The origin of the polflucht acceleration is most easily visualized (following the discussion outlined in Lambert, 1921) by imagining a large spherical ball-bearing free to roll upon a smooth, perfectly-horizontal surface, such as a frozen body of water, or a perfectly horizontal airport runway. The base of the ball lies on a co-geoid and its point of contact is thus on an equipotential surface and is in equilibrium. However, its center of gravity lies on an higher equipotential surface, which relative to the runway, converges toward the poles. As a consequence (in the absence of friction) the ball would roll southward as its center of gravity essentially accelerates “downhill” along this higher geoid, away from the poles and toward the equator. Lambert (1921) calculates that the resulting horizontal acceleration is small (<0.001 µGal) for continents where the center-of-gravity and center-of-buoyancy may be of the order of a few hundreds of meters. The difference in radial separation between the c-of-g and the effective c-of-b of the Caribbean is considerably larger and separated also in a latitudinal sense. The net Polflucht acceleration depends on the integrated mass above and below the Caribbean’s eastward translation surface (viz. the Caribbean asthenosphere) including masses associated with the subducting Maracaibo slab and the Puerto Rico trench, and is therefore substantial. Reduced oblateness associated with slowing in Earth’s rotation would effectively reduce the Polflucht acceleration to some small fraction of this amplitude, thereby modulating fault-normal Coulomb failure conditions on the northern-Caribbean and Venezuelan transform faults, and on associated descending slabs.
These stress changes are small. At first sight it would appear that the forces of north-south compression on the northern and southern transforms and descending slabs would be antiphase, and if this prevailed we might anticipate increased seismicity in the south to be accompanied by decreased seismicity in the north and vice versa. However, the Polflucht accelerations also act on contiguous plates to the north and south of the Caribbean, resulting in monotonic stresses directed always equatorward. A complete evaluation of these cumulative effects is beyond the scope of this article. However, to test whether antiphase behavior does, or does not, exist, in Figure 9 we plot seismicity and volcanism as a function of time, distinguishing between earthquakes occurring on the northern and southern boundaries, during the largest rotational slowing in the past two centuries (1870–1910). There is a weak suggestion that seismicity was prominent on the Bocono fault system during this maximum slowing period, during which time the northern transforms between Jamaica and Puerto Rico were largely inactive. Prior to this time the northern transforms were active. No simple pattern such as that illustrated is found elsewhere in the past few centuries, possibly because the earthquakes in question have renewal intervals significantly longer than the periodic decadal fluctuations in the length of the day. Although we find this test suggestive, it is clearly inconclusive given the small number of earthquakes under consideration.
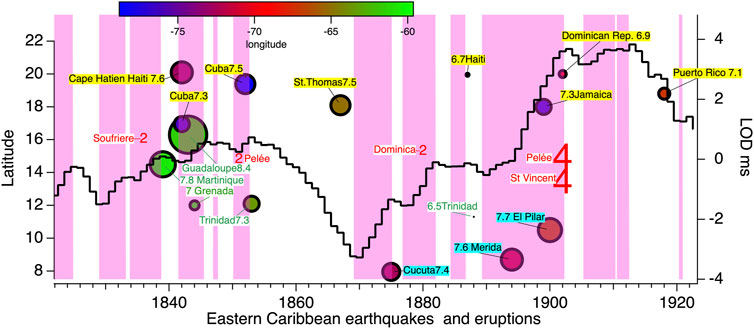
FIGURE 9. Time/space plot of Eastern Caribbean seismicity (circles 6.8 < Mw < 7.7) and volcanism (red numbers VEI 2–4), compared to length of day (LOD = black cityscape line). The color coding is according to longitude (top panel) and circle sizes are proportional to magnitude. Violet shading indicates periods of deceleration, yellow highlight = earthquakes on northern transform, blue highlight = earthquakes on southern transform, green script = eastern subduction earthquakes, red script = named eruptions. Longitudes <65°W include subduction volcanism and earthquakes in the eastern Caribbean. The plot illustrates the extreme (7 ms) increase in the LOD that occurred between 1870 and 1910, during which seismicity on the Bocono fault system was prominent, and northern seismicity largely quiescent.
Combinations of mechanisms?
The above mechanisms fall short of approaching the ±0.5 bar (±50 kPa) stress changes commonly associated with triggering of earthquakes (King et al., 1994), but some approach in magnitude the 100 Pa stress changes that have been associated with modulating seismic tremor (Thomas et al., 2009, 2012). Acting in unison a, b, and c act in the same sense to enhance Coulomb failure during a slowing Earth’s rotational velocity. Moreover, the dominant phase lag of 5 ± 2 years evident in Figure 5, which we attribute to a 20 ± 8 years forcing frequency (Figure 6B), and the apparent viscous lag of 5 years consistent with mechanism b above, provides conditions for long period synchronization between acceleration and velocity.
A further possibility is that our calculations of average plate boundary stresses for mechanisms, based as they are on average plate boundary stresses would underestimate stresses at asperities, should these dominate the failure modes of Caribbean plate boundary slip. Strain concentration in the Caribbean plate occurs in the tapered mantle wedge overlying the downgoing slab, and within volcanic magma chambers that act as weak elastic inclusions in the lithosphere (Gudmundsson, 2006).
Discussion
Global energy exchanged during periodic 10–8 variations in spin rate (LOD changes of 1 millisecond) is of the order of 1021 J, many orders of magnitude greater than that released annually by earthquakes (Kanamori, 1977) so that a potential rotational influence on seismicity is energetically feasible. The findings presented here (Figure 4), and global relationships between rotation and seismicity reported by others, confirm that such an influence apparently exists, but although several mechanisms have been proposed, the calculated stresses fall far below those usually associated with those capable of triggering plate boundary seismicity.
Bendick and Bilham (2017) suggest that synchronization of some earthquakes may be triggered by very weak forces, such as those discussed above, interacting with the earthquake renewal interval of earthquake cycles on plate boundaries. Long-period fluctuations in the LOD of ≤30 years would tend to synchronize with earthquakes with coseismic slip ≤60 cm (assuming plate boundary velocities of ≤20 mm/yr), that is, with Mw ≤ 6.6 earthquakes. Hence, if synchronization is responsible for the triggering of Mw ≥ 7 earthquakes with ≥2 m of slip (requiring ≥100 years renewal intervals), synchronization must occur at multiples of the 20–50-year LOD fluctuation periods.
Implications for future seismicity
Notwithstanding the absence of a convincing mechanism for the relationships apparent in Figure 4, the approximately 5-year lag between deceleration and Caribbean seismicity in principle permits the forecast of future earthquake activity in the region.
This serendipitous insight into future seismic and volcanic activity, however, comes with a critical caveat - the fundamental period of the deceleration must also be known and invariable. For example, a 5-year advanced warning of increased future seismicity is only possible if it can be established that the observed deceleration is associated with a persistent 20-year period periodic variation in the length of the day.
Although an adaptive approach using incoming LOD data to verify decadal periodicity permits such a forecast to be updated as necessary, in Figure 10 we demonstrate that with reasonable certainty a dominant multidecadal period is persistent in historical data. It shows the hi-passed LOD data from Figure 6A, additionally low-passed using a 25-year Gaussian filter. The spectrum of these data in Figure 10B indicate that the residual time series contains several broad overlapping spectral peaks between 12–32 years. The interaction of these contiguous peaks is the cause of the interference “beats” in Figure 6A. Of significance is that in the past 300 years, with four exceptions, peak angular deceleration advanced by 5 years coincides, within a year, with minimum angular spin velocity.
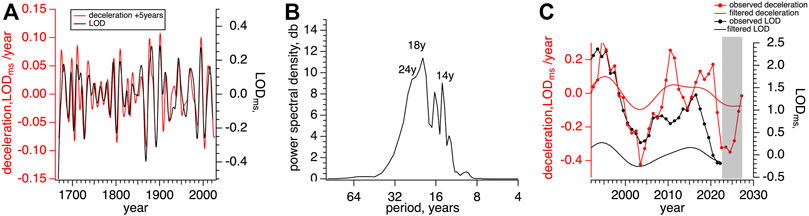
FIGURE 10. Bandpassed (20 ± 10 years) deceleration (red) and LOD data (black) The deceleration data are advanced 5 years. (B) The deceleration spectrum of these bandpassed data. Overlapping spectral peaks cause long period interference in the time series (C) shows the most recent 30 years with the last LOD derived point in mid-2021 at the start of a 5-year forecast for relative seismic quiescence (shaded grey). In the 2030 decade Earth rotation is expected to slow (maximum deceleration and maximum LOD), which we show to be associated with increased seismicity and volcanism.
The most recent 5 years (2017–2022) has seen a number of Mw ≥ 7 earthquakes in the Caribbean corresponding to the decade-long peak evident in the raw and unfiltered deceleration and velocity data (Figure 10C). The period 2022–2027, in contrast, shows a decline in angular velocity, and is hence projected to be a period of relative seismic quiescence. However, since 25% of major earthquakes in the Caribbean have occurred at times unaffected by angular deceleration, the occurrence of damaging earthquakes in the next half decade clearly cannot be excluded. Slowing of Earth’s spin velocity is anticipated to dominate the 2030 decade, signifying a resumption of increased seismic activity. To place these expectations in context, we note that the frequency of Caribbean Mw ≥ 6.6 earthquakes in the past 200 years has been 1.5 ± 1.1 per decade with extremes of 0 and 4 events per decade. These rates are low but represent more than a doubling in seismic hazard and risk during periods of minimum spin velocity compared to intervening decades of faster spin.
Conclusion
The purpose of this article is to show that Caribbean seismicity and volcanism occur preferentially during periods of minima in Earth’s angular spin velocity, and to investigate causal physical mechanisms to which we can attribute this effect.
We demonstrate the relationship between tectonic activity indirectly, by forming a binary mask from the first derivative of the length-of-the-day time series, to form a time series that permits us to count the percentages of earthquakes above a certain magnitude threshhold occurring during periods of angular deceleration. The advantage of the method is that we use raw seismicity and deceleration data without contrived filtering. The procedure reveals that 65%–75% of all Mw ≥ 6.6 to Mw ≥ 7.0 earthquakes in the Caribbean correlate with the deceleration time series with a 5 ± 2 years lag. We then show that the 5-year lag apparent between the deceleration and seismicity time series is anticipated from the lag between quasi-sinusoidal forcing at periods centered near 20 ± 8 years embedded in the LOD time series, and that these periods have remained fairly stable over the past three centuries. This leads to the conclusion that Caribbean seismicity is enhanced during periods of minimum angular rotational velocity, a conclusion that can be demonstrated directly by band-passing the LOD time series to suppress secular changes in LOD.
A quantitative causal mechanism linking variations in Earth rotation to increased or reduced seismicity or volcanism, however, has remained elusive. Several proposed physical mechanisms generate stresses at periods consistent with those proposed, yet if our calculations are correct, these accelerations or resultant stresses are many orders of magnitude smaller than those typically associated with earthquake triggering.
Notwithstanding the absence of a clear understanding of the underlying physics, the apparently strong correlation between minima in Earth’s rotation rate (maximum Length-of-Day) and increased tectonic activity provides a potential forecast tool to characterize future seismicity and/or volcanism in the Caribbean. The longevity of advanced warning depends on the stability of the underlying decadal fluctuations in rotational velocity that have been observed in past decades. Using the past century of fluctuations as a guide we believe this stability is sufficient to extrapolate present-day mean deceleration data to make a reasonable forecast of increased or subdued seismicity 5 years into the future. Annual updates of present-day annual LOD data can be used to confirm and if necessary, qualify these forecasts of future seismicity.
The current 5-year (2022–7) forecast, based on present-day rapid spin velocities (Figure 10C), is that few Mw ≥ 6.6 earthquakes should be expected in Caribbean plate boundaries, but that increased tectonism should be anticipated in the decade starting on or about 2030, when spin velocities are anticipated to slow. The total numbers of anticipated earthquakes per decade are small: in the past 200 years up to four Mw ≥ 6.6 earthquakes have occurred in decades when earth’s spin is slow, and as few as none in decades when earth’s spin is fast.
Data availability statement
Publicly available datasets were analyzed in this study. Access links to these data are indicated within the body of the text.
Author contributions
All authors contributed equally to the discussions underlying the problems addressed in this article.
Funding
We thank the University of Colorado at Boulder RFA for a grant to examine some of the issues in this article. Page charges were generously covered by the Cooperative Institute for Research in the Environmental Sciences.
Acknowledgments
We are indebted to the late Peter Molnar, Duncan Agnew, Roland Bürgmann, Jerry Mitrovica, Richard Peltier, and Gianluca Sottili with whom we have discussed some of the issues presented in this article. We thank Mason Perry for providing us with a Caribbean de-clustered seismic catalog using the Zaliapin and Ben-Zion (2020) algorithm.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.1041311/full#supplementary-material
References
Allen, T. I., Marano, K. D., and Earle, P. S., (2009). Wald, PAGER-CAT: A composite earthquake catalog for calibrating global fatality models. Seismol. Res. Lett. 80 (1), 5–7. doi:10.1785/gssrl.80.1.5
Anderson, D. L. (1974). Earthquakes and the rotation of the Earth. Science 186, 49–50. doi:10.1126/science.186.4158.49
Bendick, R., and Bilham, R. (2018). Can changes in Earth’s rotation be used to forecast earthquakes? Available at: https://temblor.net/earthquake-insights/can-changes-in-earths-rotation-be-used-to-forecast-earthquakes-5642/.
Bendick, R., and Bilham, R. (2017). Do weak global stresses synchronize earthquakes? Geophys. Res. Lett. 44, 8320–8327. doi:10.1002/2017GL074934
Bilham, R., and Bendick, R. (2017). Decelerations in Earth's rotation precede peak rates in Mw≥7 earthquakes by ≈5 years -a five year forecast for increased global seismic hazard? Geol. Soc. Amer. Annu. Meet. 15, 30. doi:10.1130/abs/2017AM-300667
Bird, P. (2003). An updated digital model of plate boundaries. Geochem. Geophys. Geosyst. 4, 1027. doi:10.1029/2001gc000252
Bucholc, M., and Steacy, S. (2016). Tidal stress triggering of earthquakes in Southern California. Geophys. J. Int. 205 (2), 681–693. doi:10.1093/gji/ggw045
Chen, Y. W., Colli, L., Bird, D. E., Wu, J., and Zhu, H. (2021). Caribbean plate tilted and actively dragged eastwards by low-viscosity asthenospheric flow. Nat. Commun. 12, 1603. doi:10.1038/s41467-021-21723-1
Di Giacomo, D., Harris, J., Villaseñor, A., Storchak, D. A., Engdahl, E. R., and Lee, W. H. K. (2015). ISC-GEM: Global Instrumental Earthquake Catalogue (1900–2009), I. Data collection from early instrumental seismological bulletins. Phys. Earth Planet. Interiors 239, 14–24. doi:10.1016/j.pepi.2014.06.003
Engelhardt, H., and Englehardt, M. (2017). An equatorward force acting on large floating ice masses: Polfluchtkraft. Ann. Glaciol. 58, 144–151. doi:10.1017/aog.2017.17
Epstein, P. S. (1921). Über die Polfluchtkraft der Kontinente. Naturwissenschaften 9 (25), 499–502. doi:10.1007/bf01494987
González, G., Fujita, E., Shibazaki, B., Hayashida, T., Chiodini, G., Lucchi, F., et al. (2021). Increment in the volcanic unrest and number of eruptions after the 2012 large earthquakes sequence in Central America. Sci. Rep. 11, 22417. doi:10.1038/s41598-021-01725-1
Gross, R. S. (2001). A combined length-of-day series spanning 1832–1997: LUNAR97. Phys. Earth Planet. Interiors 123, 65–76. doi:10.1016/s0031-9201(00)00217-x
Global Volcanism Program (2013). Volcanoes of the world. Editor E. Venzke (Smithsonian Institution), 4.10. Downloaded. doi:10.5479/si.GVP.VOTW4-2013
Jenkins, A. P., Biggs, J., Rust, A. C., and Rougier, J. C. (2021). Decadal timescale correlations between global earthquake activity and volcanic eruption rates. Geophys. Res. Lett. 48, e2021GL093550. doi:10.1029/2021GL093550
Kanamori, H. (1977). The energy release in great earthquakes. J. Geophys. Res. 82 (20), 2981–2987. doi:10.1029/jb082i020p02981
King, G. C. P., Stein, R. S., and Lin, J. (1994). Static stress changes and the triggering of earthquakes. Bull. Seism. S. Amer. 84 (3), 935–953.
Krause, R. A. (2007). Die polfluchtkraft: Der LELY-versuch – vergessene begriffe der Geologiegeschichte. Polarforschung 76 (3), 133–140. doi:10.013/epic.29962
Lambert, W. D. (1921). Some mechanical curiosities connected with the Earth's field of force. Am. J. Sci. 5th Ser. 2 (9), 129–158. Article 10. doi:10.2475/ajs.s5-2.9.129
Levin, B., Domanski, A., and Sasorova, E. (2014). Zonal concentration of some geophysical process intensity caused by tides and variations in the Earth's rotation velocity. Adv. Geosci. 35, 137–144. doi:10.5194/adgeo-35-137-2014
Levin, B., and Sasarova, E. (2017). The Earth's entry into a new phase of reduction of its angular velocity and an increase in its seismic activity. Geophys. Res. Abstr. 19, EGU2017–2933.
Levin, B. V., and Sasorova, E. V. (2015). Relationship between variations in the rotation velocity of the earth and its seismic activity. Dokl. Akad. Nauk. 464 (3), 351–355. doi:10.1134/S1028334X15090196
Levin, B. W., and Sasarova, E. V. (2015). Dynamics of seismic activity during the last 120 years. Dokl. Earth Sc. 461, 25482–25987. original Russian Text Doklady Akademii Nauk, 461(1)ISSN 1028-334X. doi:10.1134/s1028334x15030034
Levin, B. W., Sasorova, E. V., Steblov, G. M., Domanski, A. V., Prytkov, A. S., and Tsyba, E. N. (2017). Variations of the Earth's rotation rate and cyclic processes in geodynamics Geodesy and Geodynamics. Geodesy Geodyn. 8, 206. doi:10.1016/j.geog.2017.03.007
Lutikov, A. I., and Rogozhin, E. A. (2014). Variations in the intensity of the global seismic process in the 20th and the beginning of 21st centuries. Izv. Phys. Solid Earth 50 (4), 484–500. doi:10.1134/S1069351314040089
McCarthy, D. D., and Babcock, A. K. (1986). The length of day since 1656. Phys. Earth Planet. Interiors 44, 281–292. doi:10.1016/0031-9201(86)90077-4
Munk, W. H., and MacDonald, G. J. F. (1973). The rotation of the Earth. London: Cambridge University Press, 323.
Palladino, D. M., and Sottili, G. (2013). Earth's spin and volcanic eruptions: Evidence for mutual cause-and-effect interactions? Terra nova. 26, 78–84. doi:10.1111/ter.12073
Reasenberg, P. (1985). Second-order moment of central California seismicity, 1969-1982. J. Geophys. Res. 90, 5479–5495. doi:10.1029/jb090ib07p05479
Riguzzi, F., Panza, G., Varga, P., and Doglioni, C. (2010). Can Earth's rotation and tidal despinning drive plate tectonics. Tectonophysics 484, 60–73. ISSN 0040-1951. doi:10.1016/j.tecto.2009.06.012
Robson, G. R. (1964). An earthquake catalogue for the Eastern Caribbean 1530-1960. Bull. Seismol. Soc. Am. 54 (2), 785–832. doi:10.1785/bssa0540020785
Ross, M., and Schubert, G. (1986). Tidal dissipation in a viscoelastic planet. J. Geophys. Res. 91 (B4), 447–452. doi:10.1029/jb091ib04p0d447
Sasarova, E., and Levin, Boris (2018). Variations of the Earth's rotation rate and cyclic processes in geodynamics. J. Geog. ad Geolf 10 (2), 43–55. doi:10.5539/jgg.v10n2p43ISSN1916-9779
Shanker, D., Kapur, N., and Singh, V. (2001). On the spatio-temporal distribution of global seismicity and rotation of the Earth—A review. Acta Geod. Geophys. Hung. 36, 175–187. doi:10.1556/ageod.36.2001.2.5
Sottili, G., Palladino, D. M., Cuffaro, M., and Doglioni, C. (2014). Earth’s rotation variability triggers explosive eruptions in subduction zones. Earth Planet. Sp. 67, 208. doi:10.1186/s40623-015-0375-z
Thomas, A. M., Bürgmann, R., Shelly, D. R., Beeler, N. M., and Rudolph, M. L. (2012). Tidal triggering of low frequency earthquakes near Parkfield, California: Implications for fault mechanics within the brittle-ductile transition. J. Geophys. Res. 117 (05301). doi:10.1029/2011JB009036
Thomas, A. M., Nadeau, R. M., and Bürgmann, R. (2009). Tremor-tide correlations and near-lithostatic pore pressure on the deep San Andreas fault. Nature 462, 1048–1051. doi:10.1038/nature08654
van Benthem, S., and Govers, R. (2010). The Caribbean plate: Pulled, pushed, or dragged? J. Geophys. Res. 115, B10409. doi:10.1029/2009JB006950
van Stiphout, T., Zhuang, J., and Marsan, D. (2012). Seismicity declustering. Community Online Resource for Statistical Seismicity Analysis. doi:10.5078/corssa52382934
Varga, P., GambisBus, D. Z., and Bizouard, Ch. (2004). in The relationship between the global seismicity and the rotation of the earth. Journées 2004 – systèmes de référence spatio-temporels. Fundamental astronomy: New concepts and models for high accuracy observations. Editor N. Capitaine (ParisParis: Observatoire de Paris), 20115–22120. 2-901057-51-9.
Wahr, J. M. (1985). Deformation induced by polar motion. J. Geophys. Res. 90 (11), 9363–9368. doi:10.1029/jb090ib11p09363
Wegener, A. (1980). Die Entstehung der Kontinente and Ozeane. Nachdruck der 1. und 4. Berlin: Auflage. Akademie-verlag, 381.
Keywords: rotation and seismicity, LOD, earthquake forecast, polflucht, oblateness, rotational velocity, angular deceleration
Citation: Bilham R, Szeliga W, Mencin D and Bendick R (2022) Increased Caribbean seismicity and volcanism during minima in Earth’s rotation rate: Search for a physical mechanism and a 2030 forecast. Front. Earth Sci. 10:1041311. doi: 10.3389/feart.2022.1041311
Received: 10 September 2022; Accepted: 25 November 2022;
Published: 20 December 2022.
Edited by:
Peter Varga, ELKH Institute of Earth Physics and Space Research Seismological Observatory, HungaryReviewed by:
Gianluca Sottili, Faculty of Mathematics, Physics, and Natural Sciences, Sapienza University of Rome, ItalyAngelo De Santis, Istituto Nazionale di Geofisica e Vulcanologia (INGV), Italy
Copyright © 2022 Bilham, Szeliga, Mencin and Bendick. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roger Bilham, YmlsaGFtQGNvbG9yYWRvLmVkdQ==
 Roger Bilham
Roger Bilham Walter Szeliga
Walter Szeliga David Mencin
David Mencin Rebecca Bendick3,4
Rebecca Bendick3,4