Research on cemented artificial pillars to replace protective inter-block coal pillars and stope failure laws

1 Introduction

China produces huge amounts of coal (Fu et al., 2021). The associated high-intensity longwall mining has resulted in numerous irregular blocks and residual coal pillars being left behind over the years of operation (Zhang et al., 2018). Due to mining economics, surface environmental concerns, and other factors, the mining of residual coal areas (e.g., ‘under three’ pressed coal, slope pressed coal) has been limited (Zhang Y. L. et al., 2021). As a new development in mining, the short-wall block mining (SBM) method provided an effective technical solution for coal resource mining (Zhang et al., 2020; Zhang Y. et al., 2021). In the SBM process, protective inter-block coal pillars (PICPs) are part of the support system and these aid in controlling the distortion and destruction of the wall rock. However, the SBM method has a low recovery rate due to the PICPs being permanently left in the goaf after mining.

In one recent SBM study, Cao et al. (2014) determined the failure conditions of isolated coal pillars in a Datong coal mine by combining data from field-drilled peep-holes with theoretical derivations. Zhou et al. (2014) studied mine pressure behavior in an SBM working face layout based on force analysis of the PICPs and roof movement. Jiang et al. (2016) used an iterative approximation algorithm to obtain a model of the load-displacement energy of a hard roof in a short-wall block stope. Zhang et al. (2017) employed regression analysis to determine the nonlinear effect of the SBM method’s stope parameters on the development height of overburden cracks.

Studies on coal pillar recovery have also recently been carried out. For instance, Zhou et al. (2019) proposed the use of a sand-based backfilling body to recover the remaining coal pillars and analyzed the principles involved in the use of sand-based backfilling bodies to maintain the stability of the stope. Ma et al. (2017) proposed the use of solid backfill to replace the coal pillars in the lower part of an industrial square to provide effective surface-subsidence control. Sun et al. (2018) proposed the cemented paste backfilling method to recover short-strip coal pillars and studied the stability conditions of the impermeable layer. However, there have been few published results describing the recovery of PICPs generated by the SBM method, hence further analysis and exploration are needed.

To fill this gap in the literature, we here propose to maximize coal recovery through the use of cemented artificial pillars to replace PICPs. The artificial pillar replacement technology for PICPs was designed to be compatible with the features of a typical SBM working face layout. The optimal composition and characteristics of the high-strength cemented backfill material for artificial pillar construction were determined through innovative materials ratio testing. A cusp catastrophe model of an artificial pillar was developed and used to determine the necessary conditions and critical widths to prevent catastrophic instability of the artificial pillars. The theoretical analysis was verified using FLAC3D numerical simulations of the dynamic failure process of the artificial pillar and stope. Field monitoring was done to further confirm the theoretical analysis and numerical simulation results.

2 Engineering background

2.1 Test area

The test area selected was located in northern Shaanxi Province, China, and had a simple coal strata structure. The main coal mining seam at the site had five layers, and the No. 2 mining layer was used, with an average dip angle of about 2°. The test area was located 143 m underground where the height of the coal stratum was 4 m (Figure 1). The area dimensions were 152 m × 108 m. The roof was composed of mudstone and sandstone (18.0 m) and was relatively stable. The roof upward included mudstone (5.0 m), sandstone (5.2 m), mudstone (16.7 m), sandy shale (14.1 m), fine sandstone (5.0 m), mudstone (3.3 m), coarse sandstone (31.0 m), mudstone (10.7 m), and loess strata (34.0 m). The stability of the roof, floor, and roadway of the adjacent working face in the test area was good, so the SBM method was adopted in that area. Two blocks were designed for mining, and the middle of the two blocks was the retained area of a PICP.

FIGURE 1

FIGURE 1. Details of the test area used in this study.

2.2 PICP replacement

The PICP and adjacent areas within the test area were divided into two columns of several recovery areas on the left and right of the site (Figure 2A). The inner and outer coal walls were left around the recovery area as backfilling retaining walls. The thickness of the inner and outer coal walls was 1.2 m. After digging the main haulage roadway and auxiliary haulage roadway in the testing area, a branch roadway with a width of 4.3 m (set according to the width of the continuous miner) was dug close to the right side of the PICP.

FIGURE 2

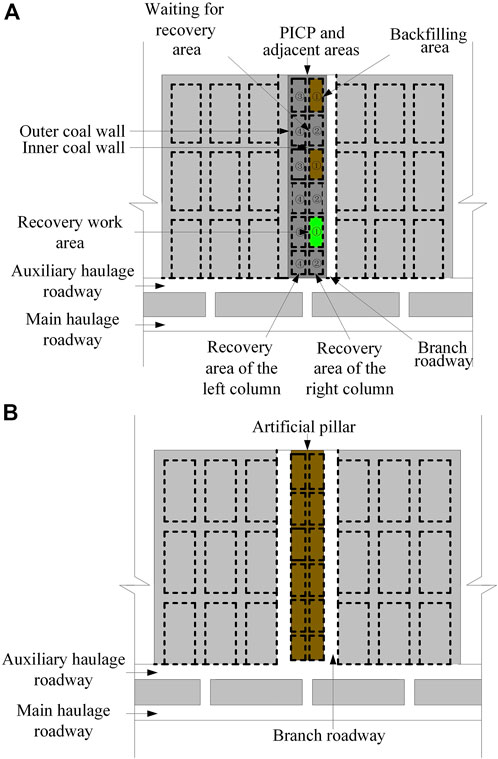
FIGURE 2. PICP replacement technique. (A) Recovery sequence of PICP; (B) completed recovery of PICP.

To reduce stress concentration, ‘leaping’ mining was then carried out in the recovery area of the right column of the PICP through a retreat mining sequence, and each recovery area was backfilled after mining. The excavation and recovery equipment used were continuous miners (Zhou et al., 2014). After all recovery areas of the right coal pillar were fully mined, another branch roadway with a width of 4.3 m was dug close to the PICP. The recovery areas in the left column were then mined one by one using the same process and sequence as the recovery areas in the right column. The recovery sequence is shown in Figure 2A. The strength of the backfill materials increased very slowly over 28 days of curing; therefore, the 28-day strength was taken as the final strength of the backfill materials and, the recovery areas in the left and right columns were backfilled and left standing for 28 days. The inner and outer coal walls were then recovered. Finally, the overall artificial pillar was obtained by backfilling the empty area formed after the inner coal wall was recovered (Figure 2B).

3 Matching experimental and mechanical property measurements of cemented backfilling materials

3.1 Experimental design and uniaxial compressive strength (UCS) tests

We employed uniaxial compressive strength (UCS) as the final target property in determining the optimum composition of the backfill materials. In the cemented backfill body, the cementitious materials were Portland cement (grade 42.5) and low-calcium secondary fly ash; fine aggregate (continuous graded fluvial sand with 0–4.75 mm particle size); and coarse aggregate (5–10 mm continuous graded coal gangue). The added concatenators were 25 mm × 0.65 mm crimped steel fiber (tensile strength >600 MPa, density of 7850 kg/m³). Tap water was used for mixing the ingredients.

To ensure sufficient liquidity of the slurry for transport and to produce reliable strength in the backfilling body, the mass fraction of the slurry concentration was set to 85% in accordance with multiple earlier tests (Li, 2021). The variable factors in the proportioning scheme of the backfill material mixtures were the proportion of fly ash in the sum of fluvial sand and fly ash, and the proportion of steel fiber. Each variable factor was divided into four levels, which means that a total of 16 mixing ratios were set (Table 1). A group of nine samples of cemented backfill materials, with each sample having dimensions of 100 mm × 100 mm × 100 mm, were produced for each of the 16 mixing ratios. The sample was taken out from the mold 12 h later and cured in a curing box at a temperature of 20 ± 2°C and a relative humidity of 95% until the specified age was reached. We used the mechanical testing and simulation electro-hydraulic servo rock loading system (loading rate of 0.6 mm/min) to test the unconfined uniaxial compression mechanical properties of the backfill material samples as they cured on day 7, day 14, and day 28.

TABLE 1

TABLE 1. Details of the 16 mixing ratios used in this study.

3.2 Tests results

3.2.1 Peak strength and residual strength

The peak strength at each measurement time and the residual strengths on day 28 are shown in Figure 3. Among the 16 mixing ratios, the 28-day peak strength values of samples of the A5, A6, A9, and A11 ratios all reached 14.7 MPa or more, showing good compressive properties (Figure 3A). The peak strength of mixing ratio A6 at 7 d was the highest, reaching 9.02 MPa (Figure 3B). Because of the addition of steel fiber to the A6 mixture, the bonding force between the steel fiber and the backfill materials improved their residual strength (Li, 2021; Ran et al., 2021), and mixture A6 had the highest residual strength at 5.4 MPa.

FIGURE 3

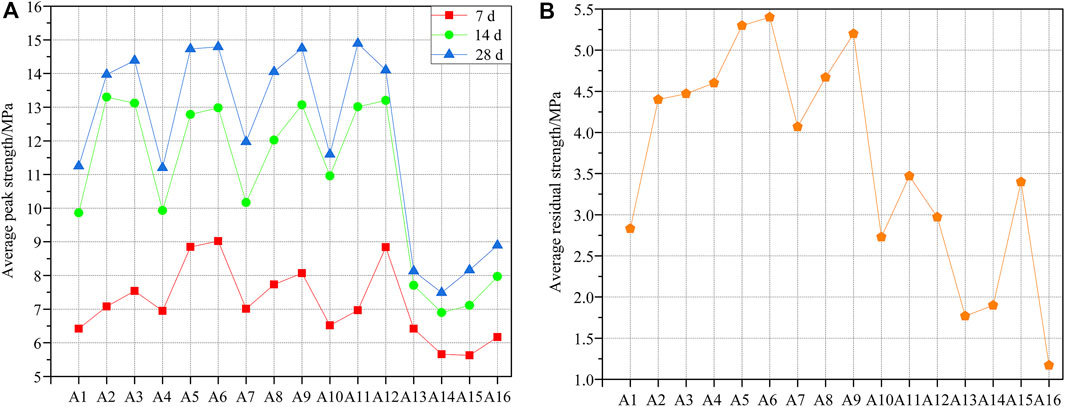
FIGURE 3. Results of the UCS tests. (A) Average peak strength at each measurement time (days 7, 14, and 28); (B) uniaxial compressive residual strength at day 28.

3.2.2 Effect of steel fiber and fly ash content on peak strength

As shown in Figures 4A,C, the steel fiber content had only a small effect on the peak strength compared to the fly ash, which had a large effect, showing that when the proportion of fly ash was larger, the peak strength was higher (Figures 4B,C). When the proportions of steel fiber and fly ash were 0.8% and 60%, respectively, the peak strength was the highest. Therefore, through comprehensive analysis of the influence of steel fiber and fly ash on peak strength, we concluded that the strength and durability of artificial pillar backfilling materials was optimal when the proportion of steel fiber and fly ash were 0.8% and 60%, respectively.

FIGURE 4

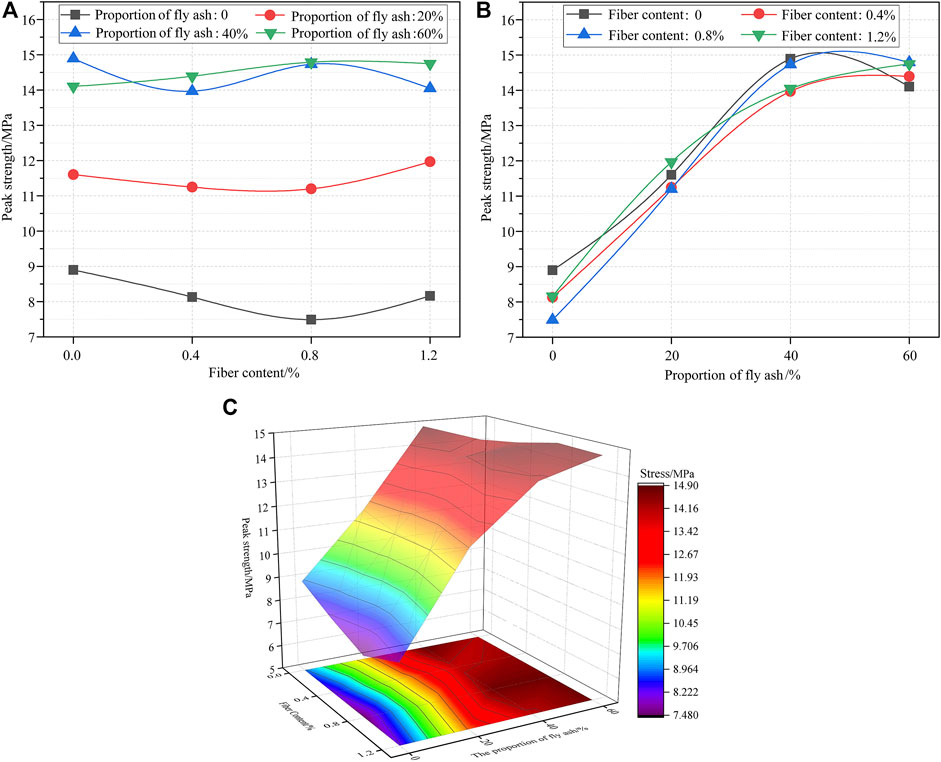
FIGURE 4. Effect of steel fiber and fly ash content on peak strength. (A) Steel fiber content; (B) proportion of fly ash; (C) interaction between steel fiber and fly ash.

Based on the above results, we determined that the mixture ratio in A6 was optimal for these tests. The mass ratios of the ingredients in this mixture were: cement (1), fluvial sand (1.6), fly ash (2.4), coal gangue (2), steel fiber (0.435), and water (1.312). The strength of the 28-day cured mixture was used as the final strength.

4 Catastrophe theory analysis of artificial pillar instability

The instability and failure of an artificial pillar are affected by geological conditions and its own anti-failure performance, which is a discontinuous mutation process with sudden, instantaneous seismic activity and significant destruction. This process corresponds to the sudden jump, divergence, and lag characteristics described by catastrophe theory (Shi et al., 2020). This theory can effectively explain artificial pillar instability, and we used it to analyze the stability characteristics of artificial pillars used to replace PICPs.

4.1 Mechanical model of a rock beam-artificial pillar system

The goaf shown in Figure 5A is formed by mining in blocks on the two sides of an artificial pillar. If the size of the coal pillars between mining tunnels is too small, they will eventually degrade and fail to support the roof (Cao et al., 2014); thus, we will not consider the influence of coal pillars between mining tunnels. According to the theory of material mechanics, it is assumed that the floor is not deformed, and the roof is deemed to be a rock beam of length 2l, which is always kept within its elastic range during the forced flexural displacement process. The flexural stiffness of the rock beam is given by EI, where $E=E_0/1-{{\mu }_0}^2$, $I=B{H}^3/12$, and B and H represent the roof width and thickness, respectively. The un-mined coal body is considered to be rigid. The artificial pillar is relatively narrow, and its supporting effect per unit length on the roof is deemed to be the support force. The gravity of the rock beam and its overlying strata is regarded as load q, and the roof subsidence is u. The rock beam is firmly embedded in the coal body on both sides so that the whole structure constitutes a clamped beam. The mechanical model is summarized in Figure 5B, which was drawn by cutting the position in Figure 5A I-I (Qin et al., 2006; Zhang et al., 2011).

FIGURE 5

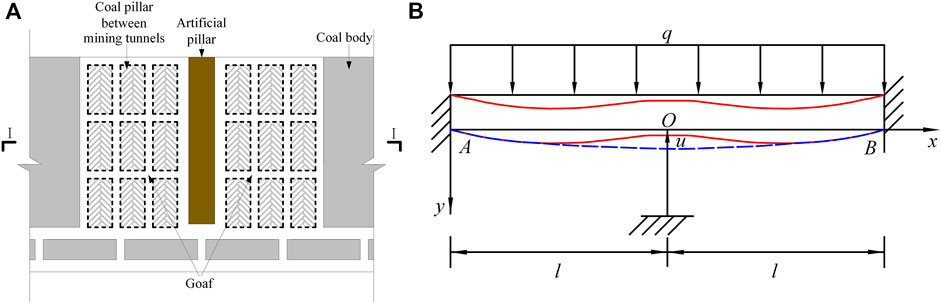
FIGURE 5. The goaf after block mining and the proposed mechanical model of the system. (A) The goaf after block mining; (B) mechanical model of the rock beam-artificial pillar system.

4.2 Cusp catastrophe model of the artificial pillar

The bending displacement energy, V_s, of the rock beam, the compressive displacement energy, V_e, of the artificial pillar, and the energy of the bending displacement process of the rock beam, V_p, constitute the total potential energy V (Xia et al., 2019; Shun et al., 2021), which is expressed as follows:

$V=V_{\mathrm{s}}+V_{\mathrm{e}}-V_{\mathrm{p}}(1)$

According to the mechanical analysis presented in the previous section, and existing research results (Zhou et al., 2018a; Shi et al., 2020), the total potential energy equation based on elastic mechanics theory is:

$\begin{array}{l}V=\frac{EI}{2}{\int }_0^{2l}{f}^{″}{\left(x\right)}^{2}dx+k_0{\int }_0^{u}u\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]du-q{\int }_0^{2l}f\left(x\right)dx\\ =\frac{{\pi }^{4}EI}{8l^3}{u}^2+k_0{u}_0\left\{u_0-\left(u_0+u\right)\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]\right\}-qlu\end{array}(2)$

where $k_0=E^{\prime }b/h$ is the stiffness of the artificial pillar ($E^{\prime }=E_0^{\prime }/1-{\mu }^{\prime }$), u₀ is the deformation at the peak strain of the artificial pillar ($u_0=h{\epsilon }_0$), and m is the index of curve homology.

According to the static equilibrium condition, the equation of the equilibrium surface, M, of V = 0 with u as the state variable can be obtained by:

$V^{\prime }=\frac{{\pi }^{4}EIu}{4l^3}+k_{0}u\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]-ql=0(3)$

At the cusp of the equilibrium surface, there is:

$V^{″}=\frac{k_0}{u_0}\left(2-\frac{u}{u_0}\right)\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]=0(4)$

According to this relation, it can be found at the cusp that $u=u_1=2u_0$.

A Taylor expansion is now performed at the cusp with respect to the state variable u₁, and the third term is intercepted to obtain:

$\begin{array}{l}{V}^{\prime }=k_0{u}_1\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]-\frac{{\pi }^{4}EI}{4l^3}\left(b-u_1\right)-ql+\left\{k_0\left(1-\frac{u_1}{u}\right)\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]+\frac{{\pi }^{4}EI}{4l^3}\right\}\left(u-u_1\right)\\ +\left\{\frac{k_0}{2u_0}\left(\frac{u_1}{u_0}-2\right)\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]\right\}{\left(u-u_1\right)}^2+\left\{\frac{k_0}{6u_0^2}\left(3-\frac{u_1}{u_0}\right)\exp \left[-{\left(\frac{u}{u_0}\right)}^m\right]\right\}{\left(u-u_1\right)}^3=0\end{array}(5)$

The state parameter x, where $x=\left(u-u_1\right)/u_1$, and the control parameters P and Q are then introduced, where equation M is given by:

$x^3+Px+Q=0(6)$

Among which:

$P=\frac{3}{2}\left(k-1\right)(7)$

$Q=\frac{3}{2}\left(1+k-\xi \right)(8)$

$k=\frac{{\pi }^{4}EI/4l^3}{k_0\exp \left(-\frac{m+1}{m}\right)}=\frac{k_2}{k_1}(9)$

$\xi =\frac{ql\exp \left(\frac{m+1}{m}\right)}{k_0{u}_1}(10)$

where k is the stiffness ratio, and ξ is a geometrical mechanical parameter.

Taking the first derivative of M, the singular value equation is expressed as:

$3x^2+P=0(11)$

By eliminating x in combination with Eqs 6, 11, the bifurcation set Δ is given by:

$∆=4P^3+27Q^2=0(12)$

As shown in Figure 6, when the three-dimensional coordinate points controlled by P, Q, and x change continuously along path I, the system is stable; at this time, Δ > 0. When the coordinate points change continuously along path II, there is a leap from the lower lobe to the upper lobe, and the system is mutational; at this time, Δ < 0. When the system is in a boundary pattern, Δ = 0 (Zhou et al., 2018b; Ma et al., 2019; Wang et al., 2021).

FIGURE 6

FIGURE 6. Equilibrium surface and control plane of the system.

Substituting Eqs 7, 8 into Eq. 12, we get:

$∆=4{\left[\frac{3}{2}\left(k-1\right)\right]}^3+27{\left[\frac{3}{2}\left(1+k-\xi \right)\right]}^2=0(13)$

According to this relation, ξ and k determine the stability of the system. When k < 1, Δ < 0, the system exhibits catastrophic instability. Therefore, the necessary condition for the catastrophic instability of an artificial pillar is expressed by:

$k=\frac{{\pi }^{4}EI/4l^3}{k_0\exp \left(-\frac{m+1}{m}\right)}=\frac{k_2}{k_1}<1(14)$

According to this equation, k₁ can be altered to improve the anti-failure capability and avoid catastrophic instability by changing the bearing capacity of the artificial pillar and determining a reasonable width. The bearing capacity of the artificial pillar was determined through the backfill materials ratio tests presented in Section 3. Here, we determine a reasonable artificial pillar width appropriate to the conditions of the test area used in this study. According to the boundary pattern of catastrophe, Δ = 0 and Eq. 14, the critical width of the artificial pillar to eliminate catastrophic instability can be obtained by:

$b=\frac{{\pi }^{4}EIh/4l^3}{E^{\prime }\exp \left(-\frac{m+1}{m}\right)}(15)$

In the test area used in this study, the roof thickness was 18 m, the elastic modulus of the roof rock was E₀ = 20.33 GPa, the Poisson’s ratio of the roof was 0.22, and the roof span was 76 m. In addition, the elastic modulus E′₀ of the A6 backfill materials group was 1.15 GPa, and the Poisson’s ratio μ′ of backfill materials was 0.35. The A6 backfill mixture ratio samples had obvious strain softening characteristics, and their homology index, m, was 1, and the height of the artificial pillar reached 4 m. Therefore, we calculated that the critical width of an artificial pillar in the test area when catastrophic instability occurred would be 13 m.

5 Stope failure: Numerical simulation and field verification

5.1 Numerical simulation analysis of stope failure laws

The FLAC3D (version 5.0) model was set up according to the field conditions of the test area. The model was then simplified to a horizontal model, with X, Y, and Z dimensions of 232 m × 40 m × 91 m, respectively (Figure 7). A 40 m coal body was set on the boundary of the model to reduce the edge effect. The mining length of the test area was 152 m, and the lengths of blocks 1 and 2 varied according to the width of the artificial pillar. To speed up numerical calculations, the weight of the rock strata applied at the height of 84 m from the top of the model to the surface had an equivalent load of 1.77 MPa. The Mohr-coulomb failure criterion was used in the constitutive model. According to the calculations above, the critical width of the catastrophic instability of the artificial pillar was 13 m, so the widths of the artificial pillars were set to 13 m, 12 m, and 14 m for comparative analysis of the stope failure laws.

FIGURE 7

FIGURE 7. Three-dimensional numerical simulation model.

5.1.1 Analysis of the failure characteristics of the artificial pillars

The plastic zone of the artificial pillars after mining the blocks is shown in Figure 8. There is still a 2 m-wide elastic zone at the top of the artificial pillar when its width is 13 m, and the width of the elastic zone accounts for about 15% of the width of the artificial pillar. Although influenced by the unit division of the FLAC3D grid, the results are close to the theoretical derivation in Cao et al. (2014) that stipulated that catastrophic instability can occur when the width of the elastic area of a PICP is less than 14% of the total width of the coal pillar.

FIGURE 8

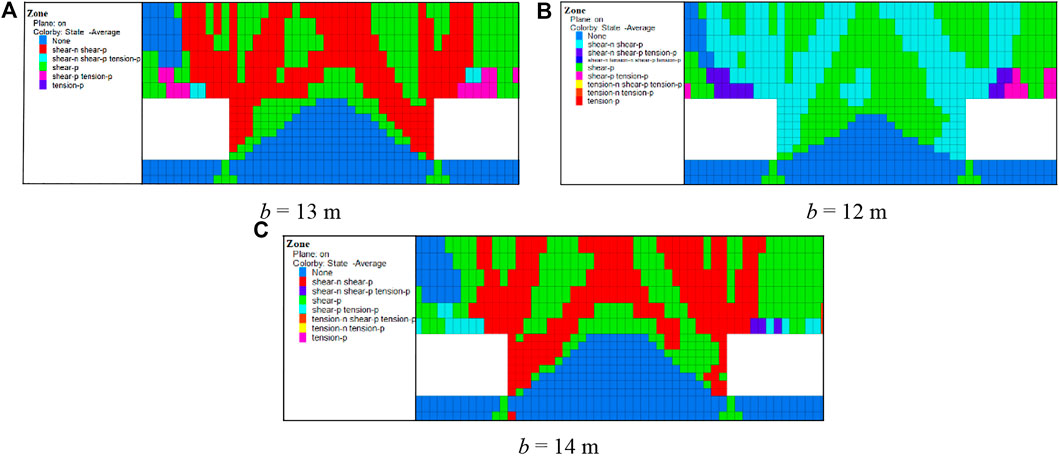
FIGURE 8. Distribution of plastic zones with different widths of artificial pillars (A) b = 13 m; (B) b = 12 m; (C) b = 14 m.

When the width of the artificial pillar is 12 m, the top is connected by the plastic zone, and it is very likely to experience catastrophic instability. However, when the width of the artificial pillar is 14 m, the large area is in the elastic zone, and only two sides of the artificial pillar experience compression-shear failure. Thus, the numerical simulation illustrates the failure characteristics of the artificial pillar, which verify the theoretical analysis presented above. The analysis confirms that an artificial pillar width of 13 m is the critical width for catastrophic instability under the conditions of the test area.

5.1.2 Analysis of stope failure laws

When the width of the artificial pillar was set to 14 m, the dynamic evolution process of stope deformation and failure was simulated for three cases: (1) after artificial pillar replacement of the PICP; (2) after the mining of block 1; and (3) after the mining of block 2.

5.1.2.1 Stope failure laws after artificial pillar replacement of the PICP

Figure 9 shows the distribution of the vertical stress and plastic zones in branch roadways and an artificial pillar after replacing the PICP. A rock mass without mining is usually in the elastic deformation state before roadway excavation (Qian et al., 2010). The excavation of the branch roadway and recovery pillar then redistributes the original rock stress. The stress is mostly concentrated in the upper and lower ends of the branch roadway, and the maximum vertical stress reaches 6.63 MPa. The roof of the branch roadway is damaged by tensile and shear stress, but the overall damage of the branch roadway is small.

FIGURE 9

FIGURE 9. Distribution of vertical stress and plastic zones in branch roadways and the artificial pillar. (A) Vertical stress distribution of the branch roadway and artificial pillar; (B) distribution of plastic zones of the branches and artificial pillar.

5.1.2.2 Stope failure laws after mining block 1

After mining block 1 (Figure 10), the immediate roof was in a state of tensile failure in a large area of the stope, and the basic roof plastic zone developed into an inverted funnel shape, while the whole overlaying rock showed failure in the shape of a saddle. Under the influence of mining in block 1, the vertical stress concentration of the left branch roadway increased and the maximum vertical stress reached 9.49 MPa. The roof tensile stress of the branch roadway increased continuously. The mining of block 1 aggravated the destruction of the coal wall and roof of the branch roadway. The artificial pillar only produced a small range of stresses concentrated on one side of the goaf and a small range of shear failure occurred on the immediate upper roof of the artificial pillar. However, the artificial pillar suffered no damage.

FIGURE 10

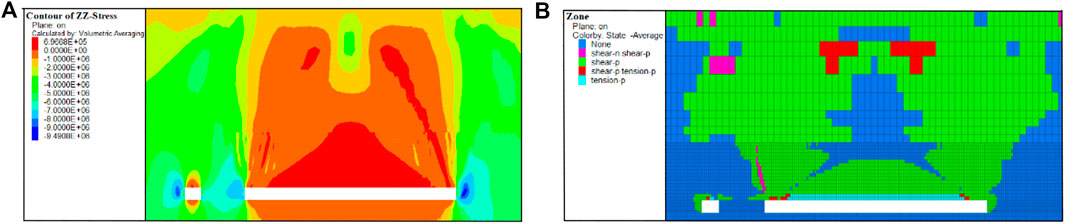
FIGURE 10. Distribution of vertical stress and plastic zones after mining block 1. (A) Vertical stress distribution after mining block 1; (B) plastic zone distribution after mining block 1.

Measuring points were arranged along the roof from the branch roadway on the left side of the artificial pillar to the mining boundary of the right goaf to monitor stope roof subsidence. As shown in Figure 11, there was only a little movement in the roof of the branch roadway after mining in block 1 as a result of the load from the overlying rock. After mining block 1, the roof on the branch roadway on the left side of the artificial pillar sank only slightly; the sinking curve of the goaf roof had a single peak of parabolic shape. The maximum sinking position was near the roof span of the goaf 118 m to the left of the mining boundary, and the peak subsidence was 2.12 m. After the mining of block 1, the roof gradually began to break, but the branch roadway and artificial pillar retained good stability.

FIGURE 11

FIGURE 11. Stope roof subsidence after mining block 1.

5.1.2.3 Stope failure laws after mining block 2

The stress on the stope was redistributed after mining block 2, and an artificial pillar-boundary coal-rock cooperative supporting system was formed (Figure 12). The stope stress was mostly concentrated in the roof’s upper artificial pillar and the top of the artificial pillar. The abutment pressure exerted by the overlying rock on the artificial pillar presented a bell-shaped distribution, and the maximum vertical stress reached 19.85 MPa. A large area inside the artificial pillar remained in the elastic state without failure. The overlying strata failure degree of block 1 was much greater than that of block 2, and the overlying strata failure of the stope as a whole presented a large saddle shape.

FIGURE 12

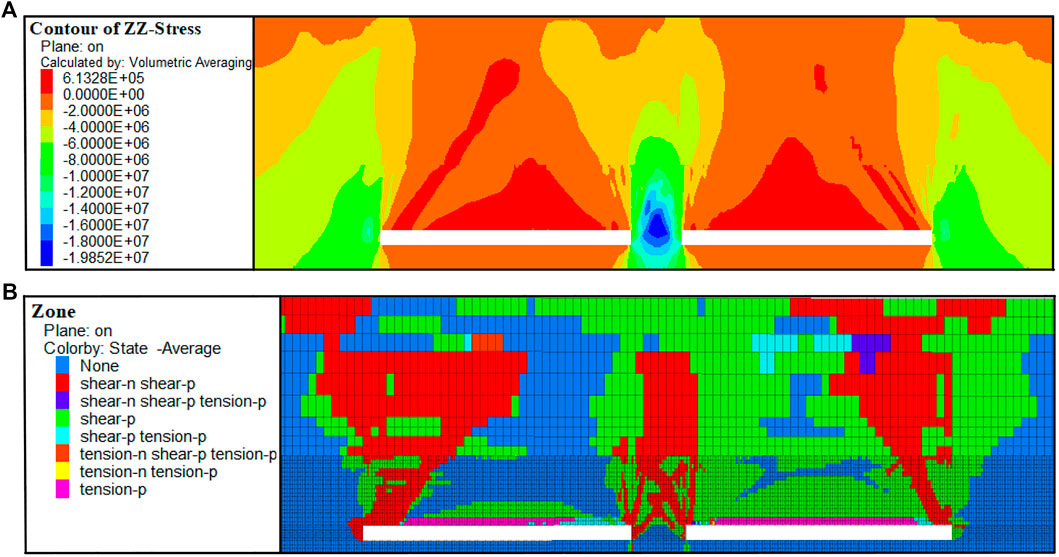
FIGURE 12. Distribution of vertical stress and plastic zones after mining block 2. (A) Vertical stress distribution after mining block 2; (B) plastic zone distribution after mining block 2.

Measuring points were arranged along the left mining boundary to the right mining boundary to monitor the vertical displacement of the stope roof after mining in block 2, as shown in Figure 13. After mining block 2, the stope roof sank significantly. The maximum sinking position of the right goaf shifted from 118 m to 102 m away from the left mining boundary (Figure 11). The maximum sinking position was close to the artificial pillar, and the maximum sinking distance was 3.41 m. The maximum sinking position of the left goaf appeared in the roof of the left side branch roadway of the original artificial pillar, 5 m away from the artificial pillar, and the maximum subsidence was 2 m. The maximum subsidence position of the left and right goaf was close to the artificial pillar. As the artificial pillar limited the roof subsidence of the whole stope, the artificial pillar bore a large load, and further compression deformation occurred. The roof subsidence of the whole goaf was large and gradually showed a trend toward collapse. The movement of the overlying strata dominated after the PICP was replaced by the artificial pillar of the new cemented backfill material, and this was consistent with SBM. Although the stability of the artificial pillar was affected by mining disturbance, roof breaking, and subsidence in the goaf, its failure only started after mining block 2 and the failure was a gradual process that significantly contributed to the overall stability of the stope.

FIGURE 13

FIGURE 13. Stope roof subsidence after mining block 2.

From the results of the simulations, we know that the damage to the artificial pillar, the roof of the goaf, and the surrounding rock of the stope followed similar laws, indicating that it was the block mined later that affected the stability of the previously formed goaf and artificial pillar, and that the stability of the stope was greatly affected by the mining. However, a reasonable width for the artificial pillar was effective in decreasing the damage caused by mining.

5.2 Field engineering verification

As shown in Figure 14, the artificial pillar backfilling system used as a test case in the coal mine consisted of systems for weighing and transporting the dry materials, mixing them, and conveying the slurry. The weighing system consisted of a transfer bin and a support. The transfer bin was installed on the support, and the weight loss of the support was determined. The main body of the conveying system for the dry materials was a plate chain conveyor. Its switch was connected to the weight sensors of the support for accurate measurement and stable feeding. The water required to be added to the slurry mixing system for slurry preparation was measured by using a tank with a controlled water height. The slurry mixing system was an intermittent operation two-axle forced mixer. A slurry transfer tank was arranged below the mixer to hold the prepared backfilling slurry. The slurry prepared by the mixing system was put into the transfer tank of the slurry conveying system and transported to the underground artificial pillar backfilling area at a constant speed through a conveying pump. The slurry conveying capacity was 30–50 m³/h.

FIGURE 14

FIGURE 14. Artificial pillar backfilling system.

Earth pressure cells were installed during the artificial pillar pouring process to monitor its internal stresses. These could be used to determine whether instability failure of the artificial pillar occurred. Three rows of earth pressure cells with a height of 2 m were arranged in the middle column of the artificial pillar. The height of each earth pressure cell was 2 m, the spacing between each earth pressure cell was 2 m, and a total of 18 cells were installed (No. 1-6 from left to right in Figure 15). A stress-mining date-change curve of the artificial pillar was then drawn using the monitoring data of the second row of earth pressure cells as it was relatively complete (Figure 16).

FIGURE 15

FIGURE 15. Earth pressure cells layout.

FIGURE 16

FIGURE 16. Artificial pillar stress–mining date-change curve.

Figure 16 shows that the stress of the artificial pillar increased during the mining of block 1, and the artificial pillar did not yield until after mining was completed. With the mining of block 2, the stress concentration degree in the artificial pillar also rose. Affected by the mining of block 2, the stress at the No. 6 monitoring point decreased sharply. Therefore, it can be inferred that the artificial pillar began to yield on the side close to block 1, but the yield range did not spread to monitoring point 5. Thus, the yield range was within 4 m. With further mining at block 2, the phenomenon of a sudden stress drop also occurred at the No. 1 monitoring point, indicating that the artificial pillar began to yield on the side close to block 2, and the yield range in the artificial pillar was further expanded. It can be inferred that the yield width was less than 8 m as no sharp decline in stress occurred at monitoring points 2-5. The artificial pillar with a width of 14 m still had an elastic area of at least 6 m without catastrophic instability occurring. Therefore, an artificial pillar with a width of 14 m was reasonable for the conditions in the test area. The field monitoring results verified the theoretical derivation and numerical simulation results presented above.

6 Conclusion

1) This work addresses the low coal-recovery rate and the waste of resources caused by PICPs in SBM by replacing them with artificial cemented pillars. A coal mine test area in northern Shaanxi Province, China, was employed to test the design and operation of an artificial pillar replacement system for PICPs.

2) Using innovative materials ratio tests, appropriate combinations of cemented backfill materials for constructing artificial pillars with reliable strengths were obtained. Their peak strength and residual strength values reached 14.7 and 5.4 MPa, respectively. The optimum mixture mass ratio was cement (1), fluvial sand (1.6), fly ash (2.4), coal gangue (2), steel fiber (0.435), and water (1.312).

3) A cusp catastrophe model of an artificial pillar was established, and the necessary conditions for catastrophic instability were deduced as the stiffness ratio, k < 1. The critical width of an artificial pillar in the test area to avoid catastrophic instability was calculated to be 13 m.

4) FLAC3D numerical simulations were used to verify the catastrophe theory analysis. The simulation results showed that when the width of the artificial pillar was 14 m, the failure of the pillar and stope progressed gradually, and no sudden instability occurred. Field monitoring results in the test area verified the theoretical derivation and numerical simulation results, confirming that it was feasible to replace PICPs with cemented artificial pillars with widths of 14 m.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and have read and approved it for publication.

Funding

This study was supported by the National Natural Science Foundation of China (51874284, 52274143).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, S. G., Cao, Y., and Jiang, H. J. (2014). Research on catastrophe instability mechanism of section coal pillars in block mining. J. Min. Saf. Eng. 31 (6), 907–913. doi:10.13545/j.issn1673-3363.2014.06.013

CrossRef Full Text | Google Scholar

Fu, Q., Yang, K., Liu, Q. J., Liu, S., He, X., and Lyu, X. (2021). Optimization of barrier pillar design in longwall mining with top coal caving in spontaneous combustion coal seam. Geofluids 2021, 1–15. doi:10.1155/2021/2749373

CrossRef Full Text | Google Scholar

Jiang, H. J., Cao, S. G., Zhang, Y., and Wang, C. (2016). Analytical solutions of hard roof’s bending moment, deflection and energy under the front abutment pressure before periodic weighting. Int. J. Min. Sci. Technol. 26 (1), 175–181. doi:10.1016/j.ijmst.2015.11.027

CrossRef Full Text | Google Scholar

Li, J. (2021). “Research and application of bearing characteristics of strong-toughness cemented backfilling materials,”. Master Thesis (Xuzhou (Jiangsu): China University of Mining and Technology). doi:10.27623/d.cnki.gzkyu.2021.000375

CrossRef Full Text | Google Scholar

Ma, C. Q., Li, H. Z., and Zhang, P. P. (2017). Subsidence prediction method of solid backfilling mining with different filling ratios under thick unconsolidated layers. Arab. J. Geosci. 10 (23), 511–512. doi:10.1007/s12517-017-3303-7

CrossRef Full Text | Google Scholar

Ma, S. W., Luo, Z. Q., Hu, J. H., Ren, Q. F., Qin, Y. G., and Wen, L. (2019). Determination of intervening pillar thickness based on the cusp catastrophe model. Adv. Civ. Eng. 2019, 1–11. doi:10.1155/2019/8253589

CrossRef Full Text | Google Scholar

Qian, M. G., Shi, P. W., and Xu, J. L. (2010). Mining pressure and strata control. Xu Zhou, China: China University of Mining and Technology Press, 197.

Google Scholar

Qin, S. Q., Jiao, J. J., Tang, C. A., and Li, Z. G. (2006). Instability leading to coal bumps and nonlinear evolutionary mechanisms for a coal-pillar-and-roof system. Int. J. solids Struct. 43 (25-26), 7407–7423. doi:10.1016/j.ijsolstr.2005.06.087

CrossRef Full Text | Google Scholar

Ran, J. L., Li, T. C., Chen, D. H., Shang, L. M., Li, W. T., and Zhu, Q. W. (2021). Mechanical properties of concrete reinforced with corrugated steel fiber under uniaxial compression and tension. Structures 34, 1890–1902. doi:10.1016/j.istruc.2021.08.135

CrossRef Full Text | Google Scholar

Shi, X. Z., Ke, W. Y., Gou, Y. G., Huo, X. F., and Kan, Z. H. (2020). Optimization of strip pillar size in upper chamber of long-span stope. J. Min. Saf. Eng. 37 (06), 1084–1093. doi:10.13545/j.cnki.jmse.2020.06.00

CrossRef Full Text | Google Scholar

Shun, P., Xu, X. D., Zhou, Y. J., Zang, G. C., and Wang, J. (2021). Investigation of instability and blasting caving technology of composite support structure in the goaf of gypsum mine. Geotech. Geol. Eng. (Dordr). 39 (6), 4377–4391. doi:10.1007/s10706-021-01769-0

CrossRef Full Text | Google Scholar

Sun, Q., Zhang, J. X., and Zhou, N. (2018). Study and discussion of short-strip coal pillar recovery with cemented paste backfill. Int. J. Rock Mech. Min. Sci. 104, 147–155. doi:10.1016/j.ijrmms.2018.01.031

CrossRef Full Text | Google Scholar

Wang, X. R., Guan, K., Yang, T. H., and Liu, X. G. (2021). Instability mechanism of pillar burst in asymmetric mining based on cusp catastrophe model. Rock Mech. Rock Eng. 54 (3), 1463–1479. doi:10.1007/s00603-020-02313-x

CrossRef Full Text | Google Scholar

Xia, K. Z., Chen, C. X., Zhou, Y. C., Liu, X. M., Zheng, Y., and Pan, Y. C. (2019). Catastrophe instability mechanism of the pillar-roof system in gypsum mines due to the influence of relative humidity. Int. J. Geomech. 19 (4), 06019004. doi:10.1061/(asce)gm.1943-5622.0001378

CrossRef Full Text | Google Scholar

Zhang, Q. L., Cao, X. G., Wang, Y. L., and Liu, H. Q. (2011). Stability analysis of stope roof-pillar based on cusp catastrophe model. China Saf. Sci. J. 21 (10), 52–57. doi:10.16265/j.cnki.issn1003-3033.2011.10.022

CrossRef Full Text | Google Scholar

Zhang, Y., Cao, S. G., Guo, S., Wan, T., and Wang, J. J. (2018). Mechanisms of the development of water-conducting fracture zone in overlying strata during shortwall block backfill mining: A case study in northwestern China. Environ. Earth Sci. 77 (14), 543–617. doi:10.1007/s12665-018-7726-6

CrossRef Full Text | Google Scholar

Zhang, Y., Cao, S. G., Lan, L. X., Gao, R., and Yan, H. (2017). Analysis of development pattern of a water-flowing fissure zone in shortwall block mining. Energies 10 (5), 734. doi:10.3390/en10050734

CrossRef Full Text | Google Scholar

Zhang, Y., Cao, S. G., Zhang, N., and Zhao, C. Z. (2020). The application of short-wall block backfill mining to preserve surface water resources in northwest China. J. Clean. Prod. 261, 121232. doi:10.1016/j.jclepro.2020.121232

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, Y. Z., Lai, X. P., and Gao, J. M. (2021a). Physical modeling of the controlled water-flowing fracture development during short-wall block backfill mining. Lithosphere 2021 (4), 2860087. doi:10.2113/2021/2860087

CrossRef Full Text | Google Scholar

Zhang, Y. L., Wang, B. K., Zhang, X. F., and Li, F. Q. (2021b). Forty years’ development and future prospect on mechanized short-wall mining technology with continuous miner in China. J. China Coal Soc. 46 (01), 86–99. doi:10.13225/j.cnki.jccs.2020.1632

CrossRef Full Text | Google Scholar

Zhou, M. P., Cao, S. G., and Jiang, X. J. (2014). The law of rock pressure in the stope with blocking mining by the continuous miner. J. Min. Saf. Eng. 31, 413–417. doi:10.13545/j.issn1673-3363.2014.03.013

CrossRef Full Text | Google Scholar

Zhou, N., Yan, H., Jiang, S. Y., Sun, Q., and Ouyang, S. Y. (2019). Stability analysis of surrounding rock in paste backfill recovery of residual room pillars. Sustainability 11 (2), 478. doi:10.3390/su11020478

CrossRef Full Text | Google Scholar

Zhou, Y. J., Li, M., Xu, X. D., Li, X. T., Ma, Y. D., and Ma, Z. G. (2018a). Research on catastrophic pillar instability in room and pillar gypsum mining. Sustainability 10 (10), 3773. doi:10.3390/su10103773

CrossRef Full Text | Google Scholar

Zhou, Y. J., Xu, X. D., Li, X. T., Li, M., and Yang, Y. G. (2018b). Study on catastrophe instability of support system in gypsum goaf based on energy dissipation theory. Adv. Civ. Eng. 2018, 1–9. doi:10.1155/2018/4293584

CrossRef Full Text | Google Scholar