Three-dimensional seismic stability of locally loaded slopes under a rotational velocity field

In practical engineering, slopes subjected to local loads, like footings of buildings, are common. This paper aims to give an insight into the effect of seismic force on the stability of locally loaded slopes. Numerical methods can be used to study this problem, but they require much computational time. Contrarily, limit analysis method is an approach to perform slope stability analysis with high computational efficiency. Thus, an accurate approach in mechanical points is proposed for this problem based on limit analysis method herein. In the framework of limit analysis, existing research about this problem used a kinematically translational velocity field. However, the velocity field of the locally loaded slope at failure is proved to be rotational possibly. Thus, to fill this gap, a 3D rotational velocity field is employed herein to obtain limit loads on the slope top, which improves the existing upper-bound solutions obtained by using the translational velocity field. The particle swarm optimization algorithm and the Nelder-Mead simplex algorithm are employed to search the global minimum of the upper-bound estimation of the limit load. Parametric analysis is performed and it shows that the limit load increases with the increase of a/H or the internal friction angle φ but decreases as the slope angle β or the length-to-width ratio (L/t) of the local load increases. Furthermore, the limit load is found to decrease with the increase of the seismic coefficient $k_h$ and it is proportional to the seismic coefficient.

Introduction

It is common to construct infrastructures, such as a building or a road, on the top of slopes in engineering practice. In this circumstance, they are prone to collapse when the stability of the slope is threatened. In some regions of the world, there are frequent seismic activities that have great adverse effects on slope stability. When an earthquake occurs, the buildings on the top surface of slopes are likely to collapse, resulting in huge losses (Song et al., 2021a; Song et al., 2021b; Song et al., 2021c; Song et al., 2021d). Thus, it is important to study the effect of seismic activities on the stability of locally loaded slopes.

Many papers have been devoted to the stability analysis of locally loaded slopes using various approaches. The slice method of limit equilibrium was used to study this problem by many scholars (Bishop, 1955; Morgenstern and Price, 1965; Spencer, 1967; Acevedo et al., 2021; Jiang et al., 2021). Using the limit equilibrium method, Azzouz and Baligh (1983) conducted circular arc limit equilibrium analysis and gave a set of charts for clay slopes bearing strip and square footings. The limit equilibrium method was also employed to provide solutions and design charts for this problem by many other scholars (Meyerhof, 1957; Saran et al., 1989). Recently, the finite element method has been widely adopted. Georgiadis (2010) employed the finite element method to investigate the undrained bearing capacity of strip footings on the top surface of slopes. The finite element method combined with a linear programming was used to compute the rigorous upper bounds of the collapse load by Sloan (1989). Leshchinsky (2015) used the discontinuity layout optimization (DLO) approach to investigate the bearing capacity of a footing on the crest of a c-φ slope. The DLO approach was also employed by Zhou et al. (2018) to study the bearing capacity and failure mechanism of locally loaded slopes.

However, the limit equilibrium method requires hypotheses about the inter-slice force, which may reduce the theoretical rigor, and the numerical method requires much computational time, which is of low efficiency. Compared with the methods introduced above, limit analysis method is equipped with a rigorous mechanics basis and high calculation efficiency. Therefore, it is studied by many scholars in recent years. The upper bound theorem of limit analysis states that an upper bound estimation of the force which drives the slope to collapse can be obtained by equating the total external work rate to the internal energy dissipation rate computed in a kinematically admissible velocity field (He et al., 2012; Khezri et al., 2016; Qin et al., 2020; Xiao et al., 2020; Zhang et al., 2022). There are many kinematically admissible 3D velocity fields that can be used in the upper bound analysis of slope stability, for instance, the cylindrical and spherical mechanism (Baligh and Azzouz, 1975), the 3D multi-blocks failure mechanism (Michalowski, 1989), and the 3D rotational failure mechanism (Michalowski and Drescher, 2009; Pan et al., 2017). Besides these mechanisms above, the mechanical mechanism at failure of granular materials, like soils, can also be derived from the view of the soil particle rearrangement (Bai et al., 2019; Bai et al., 2022). For example, based on the soil particle rearrangement, Bai et al. (2021) proposed a new coupled thermo-hydro-mechanical mechanism. Michalowski (1989) performed a 3D stability analysis of locally loaded slopes and provided a set of upper-bound solution using the 3D translational multi-blocks failure mechanism. However, this issue has never been studied using a 3D rotational failure mechanism since this scenario may concern a rotational velocity field of slope at failure. Nevertheless, the recent numerical investigation performed by Li et al. (2019) showed that, at failure, the velocity field of the locally loaded slope is rotational rather than translational, and the velocity field given by Li et al. (2019) is reprinted in Figure 1. Therefore, it is necessary to perform a 3D seismic stability analysis of locally loaded slopes based on a 3D rotational velocity field, which is the gap of the present research. In the framework of limit analysis, the widely used 3D rotational velocity field is the 3D rotational failure mechanism proposed by Michalowski and Drescher (2009). Thus, the 3D rotational failure mechanism is employed herein to perform a stability analysis of slopes subjected to local loads on the top surface.

FIGURE 1

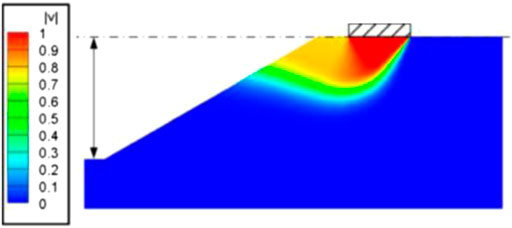
FIGURE 1. The rotational velocity field of the slope at failure [reprinted from Li et al. (2019)].

In the presented work, the 3D stability of slopes, subjected to seismic forces and local loads on the top surface, is investigated. The upper bound theorem of limit analysis is employed to calculate the critical limit load using the 3D rotational failure mechanism. To obtain the global minimum, the particle swarm optimization algorithm in combination with the Nelder-Mead simplex algorithm is adopted in searching for the least upper-bound solution. This paper extends the work of stability analysis of slopes subjected to local loads based on the 3D translational failure mechanism by Michalowski (1989) to that based on 3D rotational failure mechanism. To validate the present approach, the limit loads computed from the proposed approach are compared with the solutions of Michalowski (1989) and Zhou et al. (2018). A parametric analysis is provided at the end of this paper.

Problem description

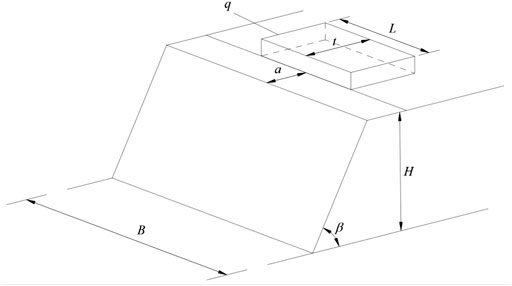
As shown in Figure 2, a slope subjected to vertical local loads on the top surface is considered. The angle of the slope is denoted by $\beta$ and the height by H. The soil in the slope body is regarded as a homogeneous and isotropic material, obeying the Mohr-Coulomb yield criterion. The cohesion and internal friction angle of the soil are denoted by c and $\phi$, respectively. The vertical local load, a cause of slope failure, is uniformly distributed on the top of the slope. The width and the length of the locally loading region are denoted by t and L, respectively, and the distance between the local load and the crest of the slope is represented by a. To study the seismic stability of the slope, earthquake forces are considered in this paper and they are described by a seismic coefficient $k_h$. The upper bound theorem of limit analysis is employed to calculate the upper bound of the limit load causing slope collapse. This issue was already studied by Michalowski (1989) using the 3D multi-block failure mechanism as a kinematically admissible velocity field in the absence of seismic forces. This paper extends the work of Michalowski (1989) by applying the 3D rotational failure mechanism as a kinematically admissible velocity field. The internal energy is only dissipated along the sliding surface, while the work rate of external forces includes those of the weight and the local load on the top surface. According to the upper bound theory of limit analysis, the upper bound of the limit local load can be found by equating the internal energy dissipation rate to the total external work rate.

FIGURE 2

FIGURE 2. The 3D slope with a local load on the top surface.

In this problem, with the increase of a/t, the failure pattern will change from toe failure and face failure to Prandtl-type failure in which the failure surface extends to the bottom surface of slopes. The Prandtl-type failure cannot be studied by the 3D rotational failure mechanism. Therefore, only the toe failure and the face failure are in the consideration of this work, which is the limitation of the proposed method.

Upper bound seismic stability analysis of locally loaded slopes

Description of 3D rotational failure mechanism

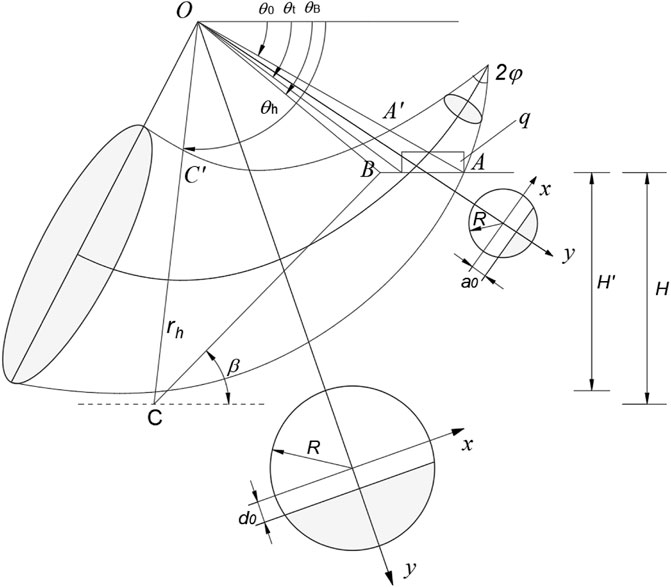
The 3D rotational failure mechanism was firstly proposed by Michalowski and Drescher (2009) to study the stability of slopes. It is a classical 3D failure mechanism for slope stability analysis and inspired many subsequent researches (Gao et al., 2013; Yang and Pan, 2015). The geometry of the 3D rotational failure mechanism is sketched in Figure 3. It can be seen from Figure 3 that the shape of the 3D rotational failure mechanism is a curvilinear cone with an apex angle, a portion of which intersects the slope body (the sliding part). The symmetry plane of the failure mechanism contains two log-spirals whose equations are as follows

$r=r_0{e}^{\left(\theta -{\theta }_0\right)\tan \phi },(1)$

$r^{\prime }=r_0^{\prime }{e}^{-\left(\theta -{\theta }_0\right)\tan \phi },(2)$

where OA= $r_0$, OA’= $r_0^{\prime }$, and ${\theta }_0$ is the angle between OA and the horizontal direction. In this work, both the toe failure and the face failure of slopes are in consideration. Thus the height of the failure mechanism, denoted by $H^{\prime }$, should not be bigger than the slope height, H. The distance between the rotation center O and the center axis of cone is denoted by $r_m$. The cross-section of the cone is a circle whose radius is denoted by R. The magnitudes of $r_m$ and R change at different values of $\theta$ and the expressions of them are

$r_m=\frac{\left(r+r^{\prime }\right)}{2}=r_0{f}_1\left(\theta \right),(3)$

$R=\frac{\left(r-r^{\prime }\right)}{2}=r_0{f}_2\left(\theta \right),(4)$

where the expressions for $f_1$ and $f_2$ are reported in the Appendix A of this paper.

FIGURE 3

FIGURE 3. 3D rotational failure mechanism of slopes.

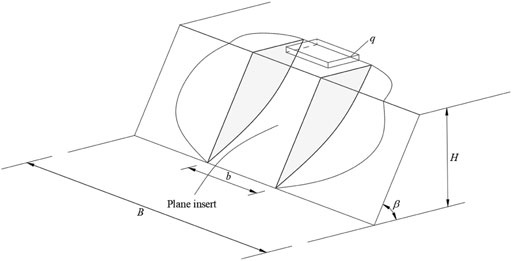
For the sake of the consistency with engineering practice, the 3D rotational failure mechanism is modified by splitting the halves of the 3D sliding body and placing a plane-strain insert between these two-halves, as shown in Figure 4. The width of the plane insert is denoted by b. It should be noted that the sum of the width of the two curved halves and the width of the plane insert, b, cannot exceed the slope width B. In addition, the width of the plane insert b is optimized together with the geometrical parameters determining the rotation center in the search for the best failure surface. In Figure 4, the local load q is symmetric about the symmetry plane of the failure mechanism. It should be noticed that the minimum width of the failure mechanism at the top surface of the slope, i.e., b, should not be smaller than the length of the local load, i.e., L, and, in other words, the constraint condition of $b/H\ge L/H$ should be enforced in the search of the optimal failure surface. The external work rate and internal energy dissipation rate of the two curved halves are calculated by complicated integrals, while those of the plane insert can be obtained by the product of b and those of the 2D situation.

FIGURE 4

FIGURE 4. The modified 3D rotational failure mechanism with a plane insert.

Calculations of external work rate

To perform work rate calculations of external forces, a local coordinate system x-o-y is set up in the circular cross-section, as shown in Figure 3 and the original point o is the center of the circular cross-section. In this paper, the considered external forces include the gravity force, the seismic force and the vertical local load q on the top surface.

The work rate of gravity force includes two parts. The first one is the gravity force work rate done by the plane insert of the 3D rotational failure mechanism and the other one is that done by the two curved halves at the two ends of the failure mechanism. By integration, the expression of the gravity force work rate for the two curved halves is (Michalowski and Drescher, 2009):

$W_{\gamma -3D}=2\omega \gamma \left[{\int }_{{\theta }_0}^{{\theta }_B}{\int }_0^{x_1^{*}}{\int }_{a_0}^{y^{*}}{\left(r_m+y\right)}^2\cos \theta dxdyd\theta +{\int }_{{\theta }_B}^{{\theta }_h}{\int }_0^{x_2^{*}}{\int }_{d_0}^{y^{*}}{\left(r_m+y\right)}^2\cos \theta dxdyd\theta \right],(5)$

where $\omega$ is the angular velocity, and $\gamma$ is the unit weight of the soil. $x_1^{*}=\sqrt{R^2-a_0^2}$, $x_2^{*}=\sqrt{R^2-d_0^2}$, $y^{*}=\sqrt{R^2-x^2}$, $a_0$ and $d_0$ are calculated from the following equations,

$a_0=\frac{\sin {\theta }_0}{\sin \theta }{r}_0-r_m=r_0{f}_3\left(\theta \right),(6)$

$d_0=\frac{\sin \left({\theta }_h+\beta \right)}{\sin \left(\theta +\beta \right)}{r}_0{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-r_m=r_0{f}_4\left(\theta \right).(7)$

Angle ${\theta }_B$ is found from the geometrical relations

${\theta }_B=\arctan \frac{\sin {\theta }_0}{\cos {\theta }_0-\kappa },(8)$

$\kappa =\frac{\sin \left({\theta }_h-{\theta }_0\right)}{\sin {\theta }_h}-\frac{e^{\left({\theta }_h-{\theta }_0\right)\tan \phi }\sin {\theta }_h-\sin {\theta }_0}{\sin {\theta }_h\sin \beta }\sin \left({\theta }_h+\beta \right).(9)$

After the integration about $y$ and $x$ which is calculated analytically, and about $\theta$ that is performed numerically, Eq. 5 is converted to

$W_{\gamma -3D}=\gamma \omega r_0^4{g}_1\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right).(10)$

$$

$W_{\gamma -insert}=\gamma \omega r_0^4{g}_2\left({\theta }_0,{\theta }_h,b/H\right).(11)$

The local load on the top of the slope is regarded as surface force whose work rate is obtained by performing integral over the intersecting region of the top of failure mechanism and the area where the load is distributed. For instance, when the failure mechanism gets through the right end point of the local load, as shown in Figure 3, the expression of the work rate of the local load is

$W_q=\omega qL{r}_0^2{g}_3\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0,H^{\prime }\right).(12)$

The angle ${\theta }_t$, the integral upper limit in the expression of $W_q$, is found from the geometrical relations

${\theta }_t=\arctan \frac{r_0\sin {\theta }_0}{r_0\cos {\theta }_0-t},(13)$

where $r_0$ is equal to $H^{\prime }/\left(H^{\prime }/r_0\right)$, thus $H^{\prime }$ is involved in the expression of $W_q$. The expression of $H^{\prime }/r_0$ is given in the Appendix A.

In this paper, the seismic force is regarded as a static inertia force and characterized by a coefficient $k_h$, which is in the range of 0 and 0.2. Similar to the calculation of gravity force work rate, the seismic force work rate is also divided into two parts. The seismic force work rate for the two curved halves is,

$W_{k_h-3D}=2k_h\omega \gamma \left[{\int }_{{\theta }_0}^{{\theta }_B}{\int }_0^{x_1^{*}}{\int }_{a_0}^{y^{*}}{\left(r_m+y\right)}^2\sin \theta dxdyd\theta +{\int }_{{\theta }_B}^{{\theta }_h}{\int }_0^{x_2^{*}}{\int }_{d_0}^{y^{*}}{\left(r_m+y\right)}^2\sin \theta dxdyd\theta \right].(14)$

After performing integration about $y$ and $x$ analytically, then Eq. 14 can be written as,

$W_{k_h-3D}=\gamma \omega k_h{r}_0^4{g}_4\left({\theta }_0,{\theta }_h,\frac{r_0^{\prime }}{r_0}\right),(15)$

where the expressions for $g_4({\theta }_0,{\theta }_h,r_0^{\prime }/r_0$) is reported in the Appendix A of this paper.

The seismic force work rate of the plane insert can be expressed as,

$W_{k_h-\mathit{insert}}=\gamma \omega k_h{r}_0^4{g}_5\left({\theta }_0,{\theta }_h,\frac{b}{H}\right),(16)$

where the expressions for $g_5\left({\theta }_0,{\theta }_h,b/H\right)$ is reported in the Appendix A of this paper.

$W=W_{\gamma -3D}+W_{\gamma -\mathit{insert}}+W_q+W_{k_h-3D}+W_{k_h-\mathit{insert}},(17)$

Thus the total external work rate can be expressed as.

Calculations of internal energy dissipation rate

The calculations of internal energy dissipation rate can be converted to integrals over the face of the slope and the top surface of the slope, which are denoted by $D_{BC}$ and $D_{AB}$ respectively. The expressions of the internal energy dissipation rate of the two curved halves is

$D_{AB-3D}=-2\omega c\cot \phi {{\displaystyle \int }}_{{\theta }_0}^{{\theta }_B}{{\displaystyle \int }}_0^{x_1^{*}}\frac{{\sin }^2{\theta }_0}{{\sin }^3\theta }\cos \theta r_0^{2}dxd\theta ,(18)$

$D_{BC-3D}=-2\omega c\cot \phi {{\displaystyle \int }}_{{\theta }_B}^{{\theta }_h}{{\displaystyle \int }}_0^{x_2^{*}}\frac{{\sin }^2\left({\theta }_h+\beta \right)}{{\sin }^3\left(\theta +\beta \right)}\cos \left(\theta +\beta \right)r_0^2{e}^{2\left({\theta }_h-{\theta }_0\right)\tan \phi }dxd\theta .(19)$

Summing $D_{AB-3D}$ and $D_{BC-3D}$ leads to the internal energy dissipation rate of the two curved halves, i.e.

$D_{3D}=D_{AB-3D}+D_{BC-3D}.(20)$

By substituting Eqs 15, 16 into Eq. 17, then Eq. 17 can be written as

$D_{3D}=\omega c\cot \phi r_0^3{g}_6\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right).(21)$

Similarly, the internal energy dissipation rate of the plane insert can be derived as follows,

$D_{AB-insert}=-2\omega c\cot \phi {\int }_{{\theta }_0}^{{\theta }_B}{\int }_0^{b/2}\frac{{\sin }^2{\theta }_0}{{\sin }^3\theta }\cos \theta r_0^{2}dxd\theta ,(22)$

$D_{BC-insert}=-2\omega c\cot \phi {{\displaystyle \int }}_{{\theta }_B}^{{\theta }_h}{{\displaystyle \int }}_0^{b/2}\frac{{\sin }^2\left({\theta }_h+\beta \right)}{{\sin }^3\left(\theta +\beta \right)}\cos \left(\theta +\beta \right)r_0^2{e}^{2\left({\theta }_h-{\theta }_0\right)\tan \phi }dxd\theta .(23)$

Similarly, summing $D_{AB-\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{t}}$ and $D_{BC-\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{t}}$ leads to the internal energy dissipation rate of the plane insert, i.e

$D_{\mathit{insert}}=D_{AB-\mathit{insert}}+D_{BC-\mathit{insert}}.(24)$

By substituting Eqs 19, 20 into Eq. 21, then Eq. 21 can be written as

$D_{insert}=\omega c\cot \phi r_0^3{g}_7\left({\theta }_0,{\theta }_h,\frac{b}{H}\right).(25)$

Therefore, the total internal energy dissipation rate of the 3D failure mechanism can be obtained by summing those of the rotational mechanism and the plane insert, i.e.,

$D=D_{3D}+D_{insert}.(26)$

For the sake of completeness, the expressions of $f_1\left(\theta \right)-f_4\left(\theta \right)$ and $g_1\left({\theta }_0,{\theta }_h,b/H\right)-g_7\left({\theta }_0,{\theta }_h,b/H\right)$ are given in the Appendix A of this paper.

Optimization of the limit load q

According to the upper bound theorem of limit analysis, equating the internal energy dissipation rate to the external work rate results in the upper bound estimation of the limit load. And its expression is as follows,

$q=\frac{\left[\omega c\cot \phi r_0^3{g}_6\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right)+\omega c\cot \phi r_0^3{g}_7\left({\theta }_0,{\theta }_h,b/H\right)-\gamma \omega r_0^4{g}_1\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right)-\gamma \omega r_0^4{g}_2\left({\theta }_0,{\theta }_h,b/H\right)-\gamma \omega k_h{r}_0^4{g}_4\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right)-\gamma \omega k_h{r}_0^4{g}_5\left({\theta }_0,{\theta }_h,b/H\right)\right]}{\omega L{r}_0^2{g}_3\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0,H^{\prime }\right)}.(27)$

It is easily found that the upper bound of the local load in this study is a function of five parameters: ${\theta }_0,{\theta }_h,r_0^{\prime }/r_0,b/H,H^{\prime }$. Each set of these parameters defines a kinematically admissible velocity field that is able to yield an upper bound estimation of the limit load. Thus the critical limit load can be obtained by cycling these parameters under the following constraint conditions until the least upper bound solution is obtained.

$\{\begin{array}{c}0<{\theta }_0<\pi ,\\ {\theta }_0<{\theta }_h<\pi ,\\ 0<r_0^{\prime }/r_0<1,\\ \frac{\left(L+B_{\mathit{max}}^{3D}\right)}{H}<\frac{\left(b+B_{\mathit{max}}^{3D}\right)}{H}<\frac{B}{H},\\ 0<H^{\prime }\le H,\end{array}(28)$

where $B_{\mathit{max}}^{3D}$ is the maximum width of rotation mechanism and B is the slope width. To find the global minimum of the limit load, the particle swarm optimization algorithm is firstly used to locate the region near the optimum point, followed by adopting Nelder-Mead simplex algorithm to search the global minimum using the solution from the particle swarm algorithm as the initial point. The obtained minimum upper bound solution $q_{cr}$ is seen as the limit load and used to perform the following analysis.

Results and discussions

Comparisons

To validate the correctness of the proposed approach, the limit loads of 10 cases computed from the proposed approach are compared with the solutions of Michalowski (1989) in which the 3D multi-blocks translational failure mechanism is used to determine the limit load. In the calculations, $L/t$ and $k_h$ are fixed to 2.0 and 0, respectively. The results are given in Table 1. It can be seen from Table 1 that the upper-bound solutions of the limit load computed from the proposed method are lower than that of Michalowski (1989), the maximum difference only reaching 6.98%. This indicates that the proposed method improves the existing upper-bound solutions of limit loads provided by the 3D translational failure mechanism. The reason why the upper bound solutions computed from the 3D rotational failure mechanism is smaller than that of the 3D translational failure mechanism may be that the 3D rotational failure mechanism is more unfavorable to the stability of slopes and is closer to the real situation in practical engineering than the 3D translational failure mechanism.

TABLE 1

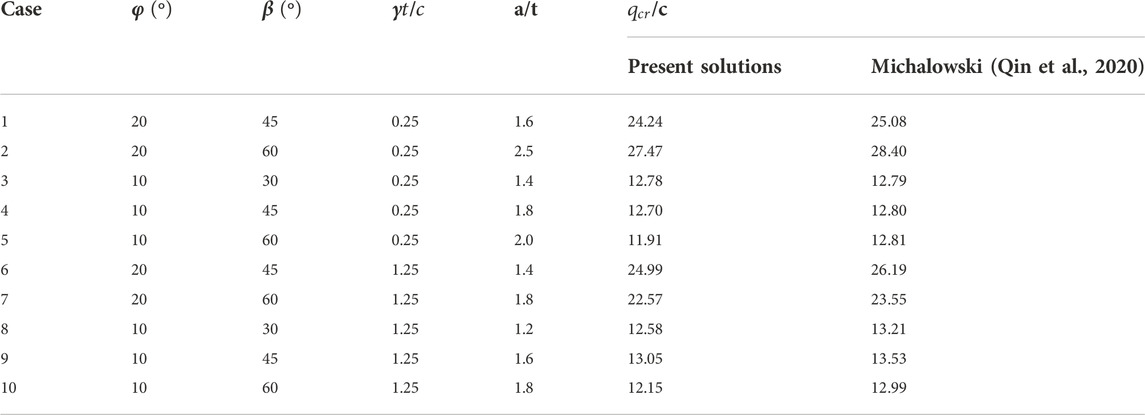
TABLE 1. Comparison between the proposed method and Michalowski (1989).

Zhou et al. (2018) evaluated the bearing capacity and failure mechanism of strip footings placed on the top of 2D slopes, using the discontinuity layout optimization (DLO) approach. The DLO approach can automatically identify the critical layout of slip-lines and the corresponding least upper bound solution of the critical load. To further validate the present approach, the limit loads computed from the proposed approach are compared with the solutions of Zhou et al. (2018) for 10 cases. In the calculations, the magnitude of H/t and $k_h$ are set to 5 and 0, respectively. For a better comparison with their 2D work, the length of the local load is fixed to the slope width, i.e., L=B. The results are given in Table 2. It is seen that the presented solutions agree well with those of Zhou et al. (2018), and the maximum difference is 8.7% for case 7 in which $\phi =10°$, $\beta =30°$, $c/t\gamma =2$ and a/t=2.5. This shows the validation of the proposed method.

TABLE 2

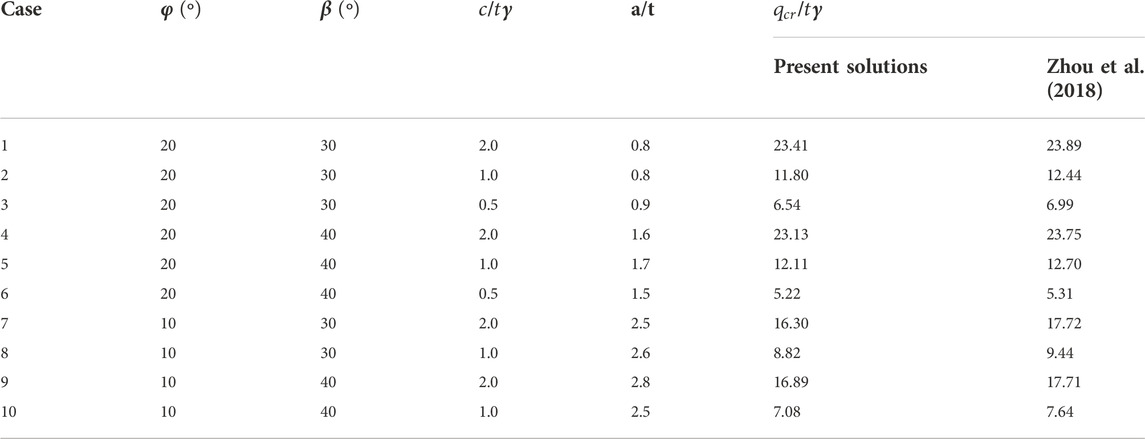
TABLE 2. Comparison between the proposed method and Zhou et al. (2018).

Parametric analysis

Several design charts are presented in Figure 5 to perform parametric analysis, each showing the limit load ratio $q_{cr}/c$ ($q_{cr}$ is the limit load leading to slope failure and c is the cohesion of soil masses) as a function of a/H. In the calculation, the B/H ratio is set as three and the vertical load is distributed in a rectangular area (L/t=2). The soil cohesion is set to 20 kPa and the internal friction angle is set as 10 $°$ or 20 $°$. The unit weight of the soil mass is equal to 20 kN/m³. Figure 5 indicates that the limit load ratio increases with the increase of a/H or the internal friction angle $\phi$ but decreases as the slope angle $\beta$ increases. It can be found by comparing Figures 5A,B that the growth rate of the limit load ratio with the increase of a/H is larger for $\phi$ =20 $°$ than $\phi$ =10 $°$. For example, limit load ratio increases by 2.64 (from 2.96 for a/H=0.2 to 5.6 for a/H=0.4) for $\phi$ =10 $°$ and $\beta$ =30 $°$, but the growth is equal to 11.26 (from 13.38 to 24.63) for $\phi$ =20 $°$.

FIGURE 5

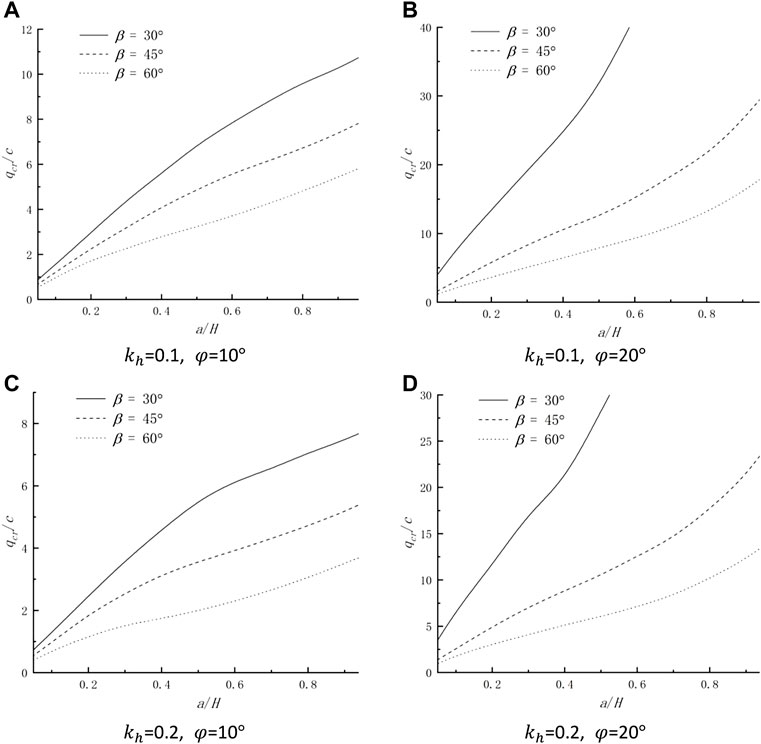
FIGURE 5. Limit load ratio $q_{cr}/c$ as a function of a/H.(A) $k_h$ =0.1, $\phi$ =10 $°$ (B) $k_h$ =0.1, $\phi$ =20 $°$ (C) $k_h$ =0.2, $\phi$ =10 $°$ (D) $k_h$ =0.2, $\phi$ =20 $°$.

Figure 6 is presented to study the effect of the seismic force on the limit load. The limit load ratio $q_{cr}/c$ is plotted as a function of the seismic coefficient $k_h$ in Figure 6. It can be found from Figure 6 that the limit load decreases with the increase of seismic coefficient $k_h$, which is because the seismic force is an adverse effect on the slope stability and can reduce the bearing capacity of slopes. Another interesting fact is that the curves in Figure 6 are almost straight lines, indicating that the limit load is proportional to the seismic coefficient $k_h$. Therefore, given some limit loads for some seismic coefficients, unknown limit loads for certain seismic coefficients can be obtained by linear interpolation.

FIGURE 6

FIGURE 6. Limit load ratio $q_{cr}/c$ as a function of seismic coefficient $k_h$.

Figure 7 is given for investigating the effect of the shape of the local load on the magnitude of the limit load. In Figure 7, the dimensionless limit load ratio ($q_{cr}/c$) is shown as a function of the length-to-width ratio (L/t) of the local load. It can be seen from Figure 7 that the limit load decreases and gradually becomes stable with the increase of the L/t ratio. In the calculation, a/H and $k_h$ are set to 0.2 and 0.1 respectively, and $\phi$ is equal to 10 $°$. The length of the local load L is less than the slope width B in the calculation.

FIGURE 7

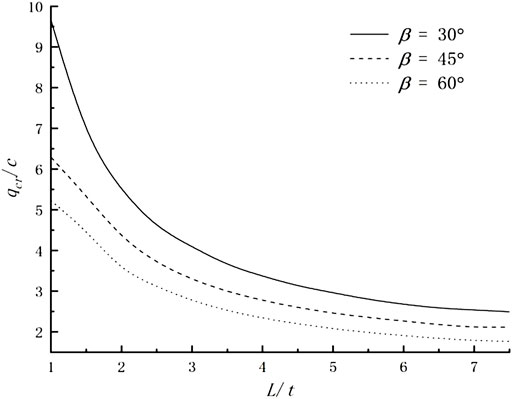
FIGURE 7. The influence of the length of the local load on the magnitude of the limit load; $\gamma b/c=1$, a/b=0.3, $\phi =15°$.

Conclusion

In light of the kinematical approach of limit analysis, this paper investigates the effect of seismic force on slope bearing capacity by calculating the limit load on the top surface of slopes. In the framework of limit analysis, the stability analysis of locally loaded slopes was performed based on the translational velocity field. However, numerical research shows that the failure velocity field seems rotational. Therefore, to fill this gap, the 3D rotational failure mechanism is employed as the kinematically admissible velocity field to investigate this problem. For validation, the limit loads computed from the proposed approach are compared with the solutions available in the literature. Parametric analyses are presented to investigate the influence of different parameters on the critical loads. Based on the work above, the conclusions are drawn:

(1) Comparisons with the results of using the 3D multi-block failure mechanism and with the DLO approach show a good agreement, indicating the correctness of the proposed approach. The upper bound of limit loads computed from the proposed method is found lower than those computed using the 3D multi-blocks failure mechanism, indicating that the 3D rotational failure mechanism can improve the upper-bound estimation of the limit load from the 3D multi-block failure mechanism.

(2) The limit load is found to decrease with the increase of the seismic coefficient $k_h$ and it is proportional to the seismic coefficient. Thus, unknown limit loads for certain seismic coefficients can be obtained by the linear interpolation method.

(3) Parametric analysis indicates that the limit load increases with the increase of a/H or the internal friction angle $\phi$ but decreases as the slope angle $\beta$ increases. And, with the increase of a/H, the growth rate of the limit load becomes larger for the larger value of $\phi$. The investigation into the effect of the shape of the local load on the limit load shows that the limit load decreases and gradually becomes stable as the length-to-width ratio (L/t) of the local load increases.

(4) The sliding surface extending to the bottom surface of the slope is not considered in this work, which is the limitation of this paper. Follow-up investigations can improve this limitation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XJ: writing original draft preparation, validation, and formal analysis. QW: conceptualization and methodology, supervision.

Funding

This research was funded by the Key Programs of Zhejiang College of Security Technology, grant number: No. AF 2021Z01.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acevedo, A. M. G., Passini, L., Talamini, A. A., Kormann, A. C. M., and Fiori, A. P. (2021). Assessing limit equilibrium method approach and mapping critical areas for slope stability analysis in serra do mar paranaense—Brazil. Environ. Earth Sci. 80, 572. doi:10.1007/s12665-021-09863-5

CrossRef Full Text | Google Scholar

Azzouz, A. S., and Baligh, M. M. (1983). Loaded areas on cohesive slopes. J. Geotech. Engrg. 109 (5), 724–729. doi:10.1061/(asce)0733-9410(1983)109:5(724)

CrossRef Full Text | Google Scholar

Bai, B., Wang, Y., Rao, D., and Bai, F. (2022). The effective thermal conductivity of unsaturated porous media deduced by pore-scale SPH simulation. Front. Earth Sci. (Lausanne). 10, 943853. doi:10.3389/feart.2022.943853

CrossRef Full Text | Google Scholar

Bai, B., Yang, G. C., Li, T., and Yang, G. S. (2019). A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials. Mech. Mater. 139, 103180. doi:10.1016/j.mechmat.2019.103180

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotechnics 137, 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Baligh, M. M., and Azzouz, A. S. (1975). End effects on stability of cohesive slopes. J. Geotech. Engrg. Div. 101 (11), 1105–1117. doi:10.1061/ajgeb6.0000210

CrossRef Full Text | Google Scholar

Bishop, A. W. (1955). The use of the slip circle in the stability analysis of slopes. Geotechnique 5 (1), 7–17. doi:10.1680/geot.1955.5.1.7

CrossRef Full Text | Google Scholar

Gao, Y. F., Zhang, F., Lei, G. H., and Li, D. Y. (2013). An extended limit analysis of three-dimensional slope stability. Géotechnique 63 (6), 518–524. doi:10.1680/geot.12.t.004

CrossRef Full Text | Google Scholar

Georgiadis, K. (2010). Undrained bearing capacity of strip footings on slopes. J. Geotech. Geoenviron. Eng. 136 (5), 677–685. doi:10.1061/(asce)gt.1943-5606.0000269

CrossRef Full Text | Google Scholar

He, S., Ouyang, C., and Luo, Y. (2012). Seismic stability analysis of soil nail reinforced slope using kinematic approach of limit analysis. Environ. Earth Sci. 66, 319–326. doi:10.1007/s12665-011-1241-3

CrossRef Full Text | Google Scholar

Jiang, Y., Cheng, H., and Liu, Z. (2021). Upper bound analysis of the stability of 3D slopes in the saturated soft clay subjected to seismic effect. Front. Earth Sci. 9, 795854. doi:10.3389/feart.2021.795854

CrossRef Full Text | Google Scholar

Khezri, N., Mohamad, H., and Fatahi, B. (2016). Stability assessment of tunnel face in a layered soil using upper bound theorem of limit analysis. Geomech. Eng. 11 (4), 471–492. doi:10.12989/gae.2016.11.4.471

CrossRef Full Text | Google Scholar

Leshchinsky, B. (2015). Bearing capacity of footings placed adjacent to c′-ϕ′ slopesslopes. J. Geotech. Geoenviron. Eng. 141 (6), 04015022. doi:10.1061/(asce)gt.1943-5606.0001306

CrossRef Full Text | Google Scholar

Li, S., Huang, M., and Yu, J. (2019). Continuous field based upper-bound analysis for the undrained bearing capacity of strip footings resting near clay slopes with linearly increased strength. Comput. Geotechnics 105, 168–182. doi:10.1016/j.compgeo.2018.10.002

CrossRef Full Text | Google Scholar

Meyerhof, G. (June 1957). The ultimate bearing capacity of foundations on slopes, Proceedings of the 4th international conference on soil mechanics and Foundation Engineering. London, England .

Google Scholar

Michalowski, R. (1989). Three-dimensional analysis of locally loaded slopes. Géotechnique 39 (1), 27–38. doi:10.1680/geot.1989.39.1.27

CrossRef Full Text | Google Scholar

Michalowski, R. L., and Drescher, A. (2009). Three-dimensional stability of slopes and excavations. Géotechnique 59 (10), 839–850. doi:10.1680/geot.8.p.136

CrossRef Full Text | Google Scholar

Morgenstern, N. R., and Price, V. E. (1965). The analysis of the stability of general slip surfaces. Géotechnique 15 (1), 79–93. doi:10.1680/geot.1965.15.1.79

CrossRef Full Text | Google Scholar

Pan, Q., Xu, J., and Dias, D. (2017). Three-dimensional stability of a slope subjected to seepage forces. Int. J. Geomech. 17 (8), 04017035. doi:10.1061/(asce)gm.1943-5622.0000913

CrossRef Full Text | Google Scholar

Qin, C., Chian, S. C., and Du, S. (2020). Revisiting seismic slope stability: Intermediate or below-the-toe failure. Géotechnique 70 (1), 71–79. doi:10.1680/jgeot.18.t.001

CrossRef Full Text | Google Scholar

Saran, S., Sud, V., and Handa, S. (1989). Bearing capacity of footings adjacent to slopes. J. Geotech. Engrg. 115 (4), 553–573. doi:10.1061/(asce)0733-9410(1989)115:4(553)

CrossRef Full Text | Google Scholar

Sloan, S. W. (1989). Upper bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 13 (3), 263–282. doi:10.1002/nag.1610130304

CrossRef Full Text | Google Scholar

Song, D., Liu, X., Huang, J., and Zhang, J. (2021). Energy-based analysis of seismic failure mechanism of a rock slope with discontinuities using Hilbert-Huang Transform and Marginal Spectrum in the time-frequency domain. Landslides 18, 105–123. doi:10.1007/s10346-020-01491-7

CrossRef Full Text | Google Scholar

Song, D., Liu, X., Huang, J., Zhang, Y., Zhang, J., and Nkwenti, B. (2021). Seismic cumulative failure effects on a reservoir bank slope with a complex geological structure considering plastic deformation characteristics using shaking table tests. Eng. Geol. 286 (3), 106085. doi:10.1016/j.enggeo.2021.106085

CrossRef Full Text | Google Scholar

Song, D., Liu, X., Li, B., Zhang, J., and Vocan, J. (2021). Assessing the influence of a rapid water drawdown on the seismic response characteristics of a reservoir rock slope using time-frequency analysis. Acta Geotech. 16, 1281–1302. doi:10.1007/s11440-020-01094-5

CrossRef Full Text | Google Scholar

Song, D., Liu, X., Huang, J., Wang, E., and Zhang, J. (2021). Characteristics of wave propagation through rock mass slopes with weak structural planes and their impacts on the seismic response characteristics of slopes: A case study in the middle reaches of jinsha river. Bull. Eng. Geol. Environ. 80, 1317–1334. doi:10.1007/s10064-020-02008-1

CrossRef Full Text | Google Scholar

Spencer, E. (1967). A method of analysis of the stability of embankments assuming parallel inter-slice forces. Géotechnique 17 (1), 11–26. doi:10.1680/geot.1967.17.1.11

CrossRef Full Text | Google Scholar

Xiao, Y., Zhao, M., Zhao, H., and Zhang, R. (2020). Numerical study on bearing capacity of ring foundations for storage tanks on a rock mass. Arab. J. Geosci. 13 (23), 1249–9. doi:10.1007/s12517-020-06255-0

CrossRef Full Text | Google Scholar

Yang, X. L., and Pan, Q. J. (2015). Three dimensional seismic and static stability of rock slopes. Geomech. Eng. 8 (1), 97–111. doi:10.12989/gae.2015.8.1.097

CrossRef Full Text | Google Scholar

Zhang, H., Wu, Y., Huang, S., Zheng, L., and Miao, Y. (2022). Analysis of flexural toppling failure of anti-dip rock slopes due to earthquakes. Front. Earth Sci. 9, 831023. doi:10.3389/feart.2021.831023

CrossRef Full Text | Google Scholar

Zhou, H., Zheng, G., Yin, X., Jia, R., and Yang, X. (2018). The bearing capacity and failure mechanism of a vertically loaded strip footing placed on the top of slopes. Comput. Geotech. 94, 12–21. doi:10.1016/j.compgeo.2017.08.009

CrossRef Full Text | Google Scholar

Appendix A

$\frac{H^{\prime }}{r_0}=\sin {\theta }_h{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-\sin {\theta }_0,(\mathrm{A1})$

$\frac{L}{r_0}=\frac{\sin \left({\theta }_h-{\theta }_0\right)}{\sin {\theta }_h}-\frac{\sin \left({\theta }_h+\beta \right)}{\sin {\theta }_h\sin \beta }\left[\sin {\theta }_h{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-\sin {\theta }_0\right],(\mathrm{A2})$

$f_1\left(\theta \right)=\frac{1}{2}\left[e^{\left(\theta -{\theta }_0\right)\tan \phi }+\frac{r_0^{\prime }}{r_0}{e}^{-\left(\theta -{\theta }_0\right)\tan \phi }\right],(\mathrm{A3})$

$f_2\left(\theta \right)=\frac{1}{2}\left[e^{\left(\theta -{\theta }_0\right)\tan \phi }-\frac{r_0^{\prime }}{r_0}{e}^{-\left(\theta -{\theta }_0\right)\tan \phi }\right],(\mathrm{A4})$

$f_3\left(\theta \right)=\frac{\sin {\theta }_0}{\sin \theta }-\frac{1}{2}\left[e^{\left(\theta -{\theta }_0\right)\tan \phi }+\frac{r_0^{\prime }}{r_0}{e}^{-\left(\theta -{\theta }_0\right)\tan \phi }\right],(\mathrm{A5})$

$f_4\left(\theta \right)=\frac{\sin \left({\theta }_h+\beta \right)}{\sin \left(\theta +\beta \right)}{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-\frac{1}{2}\left[e^{\left(\theta -{\theta }_0\right)\tan \phi }+\frac{r_0^{\prime }}{r_0}{e}^{-\left(\theta -{\theta }_0\right)\tan \phi }\right],(\mathrm{A6})$

$\begin{array}{ll}\hfill g_1\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right)& =2{\int }_{{\theta }_0}^{{\theta }_B}\left[\left(\frac{f_2^2{f}_3}{8}-\frac{f_3^3}{4}-\frac{2f_1{f}_3^2}{3}-\frac{f_3{f}_1^2}{2}+\frac{2f_1{f}_2^2}{3}\right)\sqrt{f_2^2-f_3^2}+\left(\frac{f_2^4}{8}+\frac{f_2^2{f}_1^2}{2}\right)\arcsin \left(\frac{\sqrt{f_2^2-f_3^2}}{f_2}\right)\right]\cos \theta d\theta \hfill \\ \hfill & +2{\int }_{{\theta }_B}^{{\theta }_h}\left[\left(\frac{f_2^2{f}_4}{8}-\frac{f_4^3}{4}-\frac{2f_1{f}_4^2}{3}-\frac{f_4{f}_1^2}{2}+\frac{2f_1{f}_2^2}{3}\right)\sqrt{f_2^2-f_4^2}+\left(\frac{f_2^4}{8}+\frac{f_2^2{f}_1^2}{2}\right)\arcsin \left(\frac{\sqrt{f_2^2-f_4^2}}{f_2}\right)\right]\cos \theta d\theta ,\hfill \end{array}(\mathrm{A7})$

$f_5\left({\theta }_0,{\theta }_h\right)=\frac{1}{3\left(1+9{\tan }^2\phi \right)}\left[\left(3\tan \phi \cos {\theta }_h+\sin {\theta }_h\right)e^{3\left({\theta }_h-{\theta }_0\right)\tan \phi }-\left(3\tan \phi \cos {\theta }_0+\sin {\theta }_0\right)\right],(\mathrm{A8})$

$f_6\left({\theta }_0,{\theta }_h\right)=\frac{1}{6}\frac{L}{r_0}\left(2\cos {\theta }_0-\frac{L}{r_0}\right)\sin {\theta }_0,(\mathrm{A9})$

$f_7\left({\theta }_0,{\theta }_h\right)=\frac{1}{6}{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }\left[\sin \left({\theta }_h-{\theta }_0\right)-\frac{L}{r_0}\sin {\theta }_h\right]\left[\cos {\theta }_0-\frac{L}{r_0}+\cos {\theta }_h{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }\right],(\mathrm{A10})$

$g_2\left({\theta }_0,{\theta }_h,b/H\right)=\frac{b}{H}\left(f_5-f_6-f_7\right)\left[\sin {\theta }_h{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-\sin {\theta }_0\right],(\mathrm{A11})$

$g_3\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0,H^{\prime }\right)={\int }_{{\theta }_0}^{{\theta }_t}\frac{{\left(f_1+f_3\right)}^2}{\tan \theta }d\theta ,(\mathrm{A12})$

$\begin{array}{ll}\hfill g_4\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right)& =2{\int }_{{\theta }_0}^{{\theta }_B}\left[\left(\frac{f_2^2{f}_3}{8}-\frac{f_3^3}{4}-\frac{2f_1{f}_3^2}{3}-\frac{f_3{f}_1^2}{2}+\frac{2f_1{f}_2^2}{3}\right)\sqrt{f_2^2-f_3^2}+\left(\frac{f_2^4}{8}+\frac{f_2^2{f}_1^2}{2}\right)\arcsin \left(\frac{\sqrt{f_2^2-f_3^2}}{f_2}\right)\right]\sin \theta d\theta \hfill \\ \hfill & +2{\int }_{{\theta }_B}^{{\theta }_h}\left[\left(\frac{f_2^2{f}_4}{8}-\frac{f_4^3}{4}-\frac{2f_1{f}_4^2}{3}-\frac{f_4{f}_1^2}{2}+\frac{2f_1{f}_2^2}{3}\right)\sqrt{f_2^2-f_4^2}+\left(\frac{f_2^4}{8}+\frac{f_2^2{f}_1^2}{2}\right)\arcsin \left(\frac{\sqrt{f_2^2-f_4^2}}{f_2}\right)\right]\sin \theta d\theta ,\hfill \end{array}(\mathrm{A13})$

$f_8\left({\theta }_0,{\theta }_h\right)=\frac{1}{3\left(1+9{\tan }^2\phi \right)}\left[\left(3\tan \phi \sin {\theta }_h-\cos {\theta }_h\right)e^{3\left({\theta }_h-{\theta }_0\right)\tan \phi }-\left(3\tan \phi \sin {\theta }_0-\cos {\theta }_0\right)\right],(\mathrm{A14})$

$f_9\left({\theta }_0,{\theta }_h\right)=\frac{1}{6}\frac{L}{r_0}\left(2\sin {\theta }_0+\frac{L}{r_0}\sin \alpha \right)\sin \left({\theta }_0+\alpha \right),(\mathrm{A15})$

$f_{10}\left({\theta }_0,{\theta }_h\right)=\frac{1}{6}{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }\frac{H}{r_0}\frac{\sin \left({\theta }_h+\beta \right)}{\sin \beta }\left[2\sin {\theta }_h{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-\frac{H}{r_0}\right],(\mathrm{A16})$

$g_5\left({\theta }_0,{\theta }_h,b/H\right)=\frac{b}{H}\left(f_8-f_9-f_{10}\right)\frac{\sin \beta }{\sin \left(\beta -\alpha \right)}\left[\sin \left({\theta }_h+\alpha \right)e^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-\sin \left({\theta }_0+\alpha \right)\right],(\mathrm{A17})$

$g_6\left({\theta }_0,{\theta }_h,r_0^{\prime }/r_0\right)=-2{\sin }^2{\theta }_0{{\displaystyle \int }}_{{\theta }_0}^{{\theta }_B}\frac{\cos \theta }{{\sin }^3\theta }\sqrt{f_2^2-f_3^2}d\theta -2e^{2\left({\theta }_h-{\theta }_0\right)\tan \phi }{\sin }^2\left({\theta }_h+\beta \right){{\displaystyle \int }}_{{\theta }_B}^{{\theta }_h}\frac{\cos \left(\theta +\beta \right)}{{\sin }^3\left(\theta +\beta \right)}\sqrt{f_2^2-f_4^2}d\theta ,(\mathrm{A18})$

$g_7\left({\theta }_0,{\theta }_h,b/H\right)=\frac{b}{2H}\left\{\frac{{\sin }^2{\theta }_0}{{\sin }^2{\theta }_B}-1+\left[1-\frac{{\sin }^2\left({\theta }_h+\beta \right)}{{\sin }^2\left({\theta }_B+\beta \right)}\right]e^{2\left({\theta }_h-{\theta }_0\right)\tan \phi }\right\}\bullet \left[\sin {\theta }_h{e}^{\left({\theta }_h-{\theta }_0\right)\tan \phi }-\sin {\theta }_0\right].(\mathrm{A19})$