Investigation on unfrozen water content models of freezing soils

Unfrozen water content is a significant hydro-thermal property in numerical modeling in cold regions. Although numerous models have been developed to mimic the variation of unfrozen water content with subzero temperature, comprehensive evaluation of unfrozen water content models is scarce. This study collected a total of 29 models and divided them into four categories, namely, theoretical models, soil water characteristic curve (SWCC)-based models, empirical models, and estimation models. These models were evaluated with 1278 experimental points from 16 studies covering multiple soil types, including 24 clays, 18 silty clays, 7 silts, 19 sands, and 10 sandstones. Root mean square error and average deviations were applied to judge the performance of these models. Most unfrozen water content models can well simulate the relationship between unfrozen water content and subzero temperature. Among the aforementioned four categories of unfrozen water content models, Lizhm et al. model, Fredlund and Xing (C=1)-Wen model, Kozlowski empirical model, and Kozlowski estimation model performed best in their respective categories. Compared to the rest three categories, estimation models can be applied to predict the variation of unfrozen water content with subzero temperature by some easy-to-obtain soil physical parameters and provide guidance for the development of unfrozen water content models.

1 Introduction

At subzero temperatures, not all water freezes into ice, causing unfrozen water, air, and ice to co-exist in soil pores. Unfrozen water content describes the ability of soil to retain liquid water at a subzero temperature (Wang et al., 2017; Zhang et al., 2018). The relationship between unfrozen water content and subzero temperature in frozen soils can be termed as soil freezing characteristic curve (SFCC), which is similar to the soil water characteristic curve (SWCC) in unfrozen soils (Bai et al., 2018; Wen et al., 2020). Unfrozen water content is a significant hydro-thermal property widely used in numerical modeling of heat and water transfer in engineering projects in cold regions, such as embankments (Yang et al., 2022), canals (Li et al., 2019), tunnels (Tan et al., 2013), oil pipelines (Zhao et al., 2014), and shafts (Yang et al., 2022). Therefore, understanding the unfrozen water content in freezing soils becomes a hot topic in recent years.

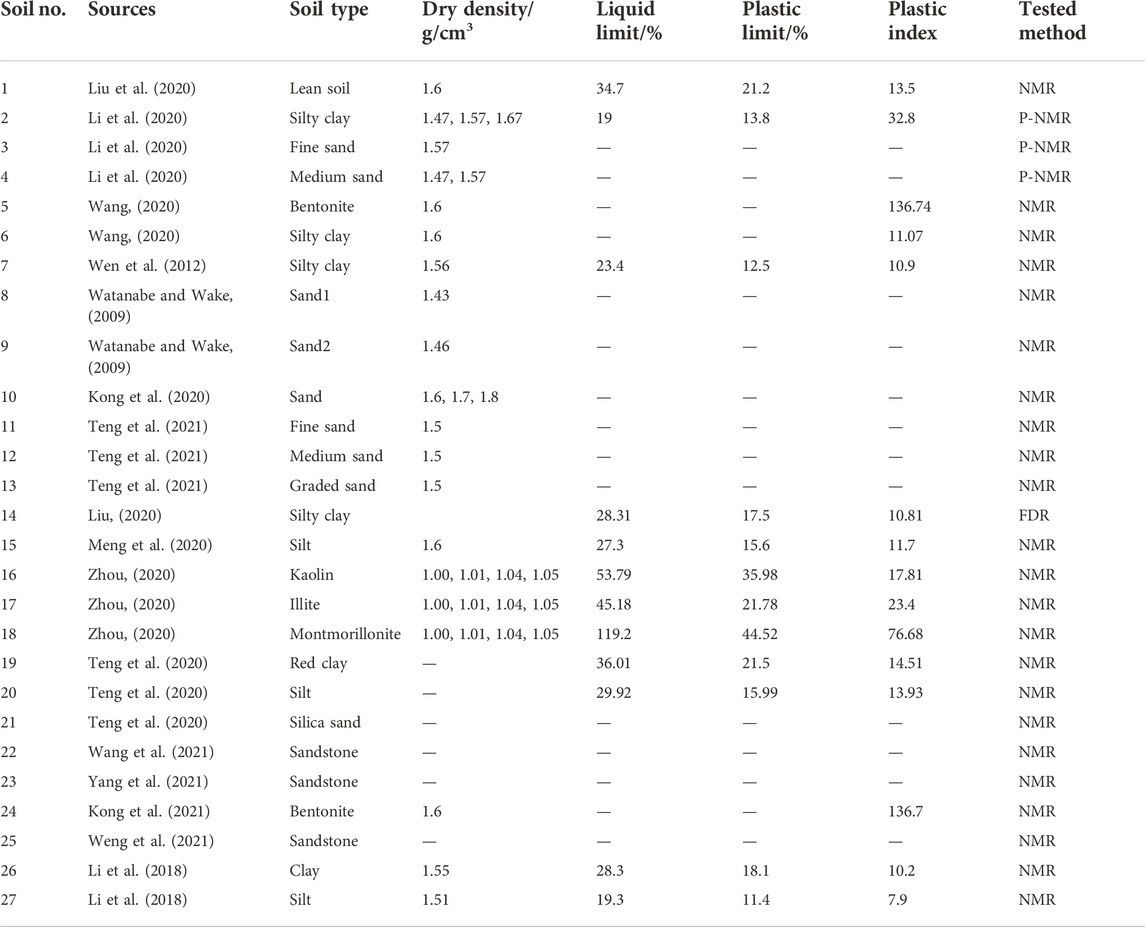
Many experimental technologies have been developed to measure unfrozen water contents at different subzero temperatures, such as low-field nuclear magnetic resonance (Chen et al., 2021), pulsed nuclear magnetic resonance (Kruse et al., 2018), differential scanning calorimetry (Kozlowski, 2004), time domain reflectometry (Liu and Yu, 2013), and frequency domain reflectometry (Lu et al., 2017). Each technology has strength and limitation. For example, frequency domain reflectometry can be applied to continuously measure the unfrozen water content during a freezing-thawing process, but it is significantly affected by salt content and soil types (Yoshikawa et al., 2004; Li et al., 2020). Over the past few decades, many attempts have shown that three distinctive stages can be applied to model the variation of unfrozen water content with subzero temperature. In Stage 1, unfrozen water content remains unchanged when the temperature decreases. In Stage 2, decreasing temperature leads to sharply decrease of temperature. The border between Stage 1 and Stage 2 refers to the freezing point (Zhang et al., 2018). When the temperature continues to decrease, the rate of change in unfrozen water content will gradual decrease in Stage 3. Extensive experimental efforts have shown that the unfrozen water content is strongly affected by initial water content (Tang et al., 2018), dry density (Li et al., 2020), plasticity (Kong et al., 2020), soil type (Zhang et al., 2018), and confining stress (Mu et al., 2019).

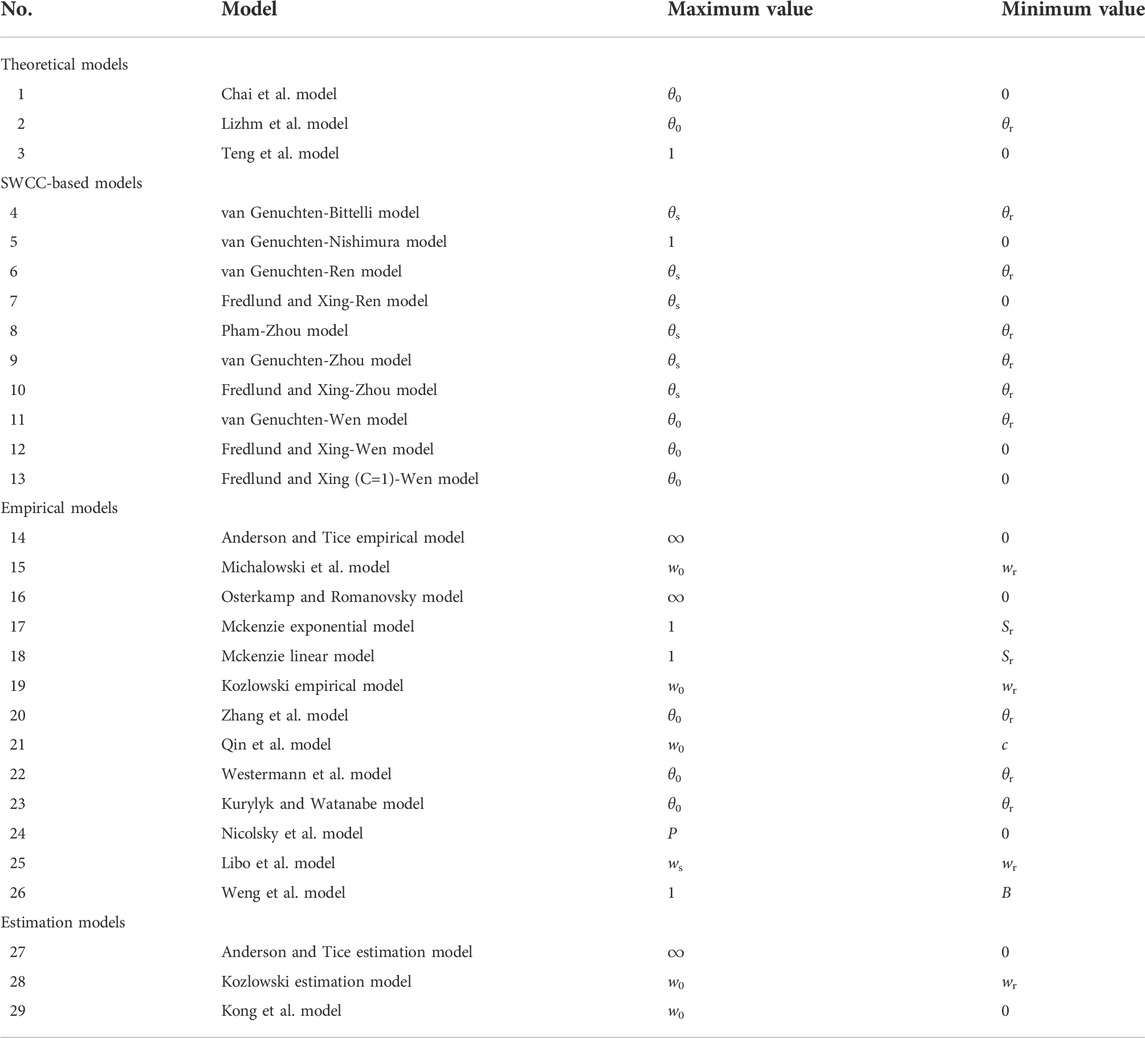
Many models have been proposed to calculate the unfrozen water content, which can be divided into four categories, namely, theoretical models, SWCC-based models, empirical models, and estimation models. The theoretical models have physical basis and most of them have complicated formulas (Chai et al., 2018; Li et al., 2020; Teng et al., 2021). These models are developed based on the pore size distribution or the microscopic geometry arrangements of solid particles. The SWCC-based models are obtained by the combination of Clapeyron equation and SWCC model or by replacing the matric suction in the SWCC model with subzero temperature (Ren et al., 2017; Wen et al., 2020; Zhou, 2020). Most SWCC-based models are developed by the Fredlund and Xing SWCC model and van Genuchten SWCC model. The empirical models are developed based on the empirical analysis of experimental data between unfrozen water content and subzero temperature (Michalowski, 1993; Osterkamp and Romanovsky, 1997; McKenzie et al., 2007; Westermann et al., 2011; Nicolsky et al., 2017). The formulas of empirical models are simple, but their parameters have no physical meanings. The estimation models are developed by relating the curve-fitting parameters of the SWCC-based models and empirical models with some easy-to-obtain physical properties, such as specific surface area (SSA), plastic index (I_p) (Anderson and Tice, 1972; Kozlowski, 2007; Kong et al., 2020). The main difference between the estimation models and other models in the first three categories is that the estimation models can be applied to estimate the unfrozen water content. Although these unfrozen water content models have good performance in modeling the relationship between unfrozen water content and subzero temperature, most models have only been tested or calibrated with a limited number of soils. Therefore, it is of critical importance to comprehensively compare and evaluate the available unfrozen water content models with a large number of experimental points from a variety of soil types.

The study aims to 1) conduct an extensive review of unfrozen water content models, 2) investigate the maximum and minimum values of the unfrozen water content models, and 3) evaluate the unfrozen water content models with a wide range of soil types.

2 A review of unfrozen water content models

29 unfrozen water content models from literature were selected and divided into four categories: 1) theoretical models (3 models), 2) SWCC-based models (10 models), 3) empirical models (13 models), and 4) estimation models (3 models). The volumetric unfrozen water content can be determined by the formula below.

${\theta }_{\mathrm{u}}=\frac{w_{\mathrm{u}}{\rho }_{\mathrm{d}}}{{\rho }_{\mathrm{w}}}=S_{\mathrm{u}}p(1)$

where θ_u is volumetric unfrozen water content, w_u is gravimetric unfrozen water content, ρ_d is dry density, ρ_w is density of water, S_u is saturation degree of unfrozen water content, and p is porosity.

2.1 Theoretical models

2.1.1 Chai et al. model

Chai et al. (2018) divided water into three parts, namely, bulk water, capillary water and bound water. They assumed that once the temperature was below 0°C, the bulk water was totally frozen and the capillary water and bound water made up the unfrozen water. The unfrozen water content was thereby taken as the sum of unfrozen capillary water and unfrozen bound water at a subzero temperature of T_i, which is given as,

${\theta }_{\mathrm{u}}\left(T_{\mathrm{i}}\right)={\theta }_{\text{cu}}\left(T_{\mathrm{i}}\right)+{\theta }_{\text{bu}}\left(T_{\mathrm{i}}\right)(2)$

where θ_cu (T_i) is the unfrozen capillary water content at a subzero temperature of T_i, and θ_bu is the unfrozen bound water content at a subzero temperature of T_i.

${\theta }_{\text{cu}}\left(T_{\mathrm{i}}\right)={\sum }_{\mathrm{d}}{v}_{\mathrm{d}}{\theta }_{\text{cu}}{\left(T_{\mathrm{i}}\right)}_{\mathrm{d}}(3)$

where v_d is proportion of soil particles with size d, and θ_cu (T_i)_d is the unfrozen capillary water content that surrounds the soil particles of size d at a subzero temperature of T_i.

${\theta }_{\text{cu}}{\left(T_{\mathrm{i}}\right)}_{\mathrm{d}}=\frac{8\left\{xy-\left[\pi {\left(R_{\mathrm{d}}+h\right)}^2\frac{{\sin }^{-1}\left(\frac{y}{R_{\mathrm{d}}+h}\right)}{2\pi }-\frac{1}{2}y\left(R_{\mathrm{d}}+h+a-x\right)\right]-\left(\pi r^2\frac{{\sin }^{-1}\left(\frac{x}{r}\right)}{2\pi }-\frac{1}{2}x\sqrt{r^2-x^2}\right)\right\}}{4{\left(R_{\mathrm{d}}+h+a\right)}^2}(4)$

where a is a variable used for describing the distance between two soil particles, R_d is radius of soil particle of size d, r is meniscus radius of capillary water, h is thickness of the bound water film, x and y are coordinate values of contact point of the meniscus.

${\theta }_{\text{bu}}\left(T_{\mathrm{i}}\right)={\rho }_{\mathrm{d}}\left(y_{\mathrm{w}}-\frac{a_{\text{wi}}{M}_{\mathrm{w}}{\sum }_{\mathrm{s}}{\eta }_{\mathrm{s}}{y}_{\mathrm{s}}}{\left(1-a_{\text{wi}}\right)M_{\mathrm{s}}}\right)(5)$

where a_wi is activity at a subzero temperature of T_i, y_w is mass fraction of water, y_s is mass fraction of solute, M_w is molar mass of water, M_s is molar mass of solute (dissociation number of salt).

2.1.2 Lizhm et al. model

Li et al. (2020) suggested that the total unfrozen water content can be calculated by the summation of unfrozen water in unfrozen water pores (θ_uu) and in frozen pores (θ_uf), which is given as,

${\theta }_{\mathrm{u}}={\theta }_{\text{uu}}+{\theta }_{\text{uf}}(6)$

where θ_uu is volumetric unfrozen water content in unfrozen water pores, and θ_uf is volumetric unfrozen water content in frozen pores.θ_uu can be developed by integrating the pore-size probability density distribution.

${\theta }_{\text{uu}}={\theta }_{\mathrm{r}}+\frac{{\theta }_0-{\theta }_{\mathrm{r}}}{1+\exp \left[b\left(T_0-T\right)-c{\left(T_0-T\right)}^d\right]}(7)$

where θ₀ is initial volumetric water content, θ_r is residual volumetric unfrozen water content, T₀ is freezing point of bulk water and equal to 273.15 K or 0°C, and b, c, and d are curve-fitting parameters related to the soil properties.

θ_uu can be calculated by integrating the product of SSA and thickness of unfrozen water film.

${\theta }_{\text{uf}}=-{\left(\frac{9H{T}_{0}SS{A}^3}{16\pi {\rho }_{\mathrm{w}}{L}_{\mathrm{f}}}\right)}^{1/3}{\left(T-T_0\right)}^{2/3}(8)$

where H is Hamaker constant, which ranges from -10^–20 to -10^–19 J, and L_f is latent heat of fusion of water.

2.1.3 Teng et al. model

Teng et al. (2021) developed a theoretical unfrozen water content model that took account of the effect of adsorption and capillarity. They considered two kinds of monodisperse particle arrangements (simple cubic (SC) arrangement and tetrahedral (TH) arrangement). The unfrozen water content can then be expressed as the linear combination of unfrozen water content from SC and TH.

$S_{\mathrm{u}}=D_{\mathrm{r}}{S}_{\mathrm{u},\text{TH}}+\left(1-D_{\mathrm{r}}\right)S_{\mathrm{u},\text{SC}}(9)$

where S_u,TH is saturation degree of unfrozen water content of TH arrangement, S_u,SC is saturation degree of unfrozen water content of SC arrangement, and D_r is relative density.

$S_{\mathrm{u},\text{TH}}=\{\begin{array}{cc}\frac{\begin{array}{l}6y_{0}R-6\arctan \left(\frac{y_0}{R}\right)R^2-\left[3\pi -6\arctan \left(\frac{y_0}{R}\right)\right]r^2\\ +\left[\pi -6\arctan \left(\frac{y_0}{R}\right)\right]\left(2R{d}_{\mathrm{f}}+d_{\mathrm{f}}^2\right)\end{array}}{\left(2\sqrt{3}-\pi \right)R^2}& y_0\le \frac{R}{\sqrt{3}}\\ \frac{6y_{0}R-6\left(y_0-\frac{R}{\sqrt{3}}\right)R-6\left[r-\left(y_0-\frac{R}{\sqrt{3}}\right)\right]\left(R-x\right)-\pi R^2}{\left(2\sqrt{3}-\pi \right)R^2}& \frac{R}{\sqrt{3}}<y_0\le \frac{\left(6-\sqrt{3}\right)}{\left(6\sqrt{3}-6\right)}R\\ 1& y_0>\frac{\left(6-\sqrt{3}\right)}{\left(6\sqrt{3}-6\right)}R\end{array}(10)$

where y₀ is the length of line segment used to distinguish different calculation intervals, R is particle radius, and d_f is water film thickness.

$S_{\mathrm{u},\text{SC}}=\{\begin{array}{cc}\frac{4y_{0}R-4\arctan \left(\frac{y_0}{R}\right)R^2-\left[2\pi -4\arctan \left(\frac{y_0}{R}\right)\right]r^2+\left[\pi -4\arctan \left(\frac{y_0}{R}\right)\right]\left(2R{d}_{\mathrm{f}}+d_{\mathrm{f}}^2\right)}{\left(4-\pi \right)R^2}& y_0\le R\\ \frac{4y_{0}R-4\left(y_0-R\right)R-4\left[r-\left(y_0-R\right)\right]\left(R-x\right)-\pi R^2}{\left(4-\pi \right)R^2}& y_0>R\end{array}(11)$

2.2 SWCC-based models

2.2.1 van Genuchten-Bittelli model

Bittelli et al. (2003) neglected the overburden pressure in the generalized Clapeyron equation, and assumed that the pore water pressure was equivalent to the negative matric head in the van Genuchten SWCC model. The van Genuchten-Bittelli model can be expressed as,

${\theta }_{\mathrm{u}}=\left({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{r}}\right){\left[1+{\left(-a_{\mathrm{v}}\frac{L_{\mathrm{f}}T}{\mathrm{g}{T}_0}\right)}^{n_{\mathrm{v}}}\right]}^{-m_{\mathrm{v}}}+{\theta }_{\mathrm{r}}(12)$

where a_v, m_v, and n_v are curve-fitting parameters of van Genuchten SWCC model, and θ_s is saturated volumetric water content.

2.2.2 van Genuchten-Nishimura model

Nishimura et al. (2009) proposed a Clausius-Clapeyron equation to model the equilibrium between liquid water and ice and then substituted this Clausius-Clapeyron equation into the van Genuchten SWCC model, yielding a new unfrozen water content model containing the temperature and ice pressure. Compared with the temperature, the effect of ice pressure on the unfrozen water content is negligible. Therefore, a simplified unfrozen water content model was adopted as (Nishimura et al., 2009; Vitel et al., 2016; Mu et al., 2018).

$S_{\mathrm{u}}={\left[1+{\left(-\frac{L_{\mathrm{f}}{\rho }_{\mathrm{w}}\ln \left(\frac{T+273.15}{273.15}\right)}{a_{\mathrm{v}}}\right)}^{\frac{1}{1-m_{\mathrm{v}}}}\right]}^{-m_{\mathrm{v}}}(13)$

2.2.3 van Genuchten-Ren model

Ren et al. (2017) assumed that the pore ice pressure in a frozen soil was equal to atmospheric pressure and the solute effect was ignored. Based on the two assumptions, the Clapeyron equation was applied to transform subzero temperature to suction, yielding the SWCC-based model. The combination of van Genuchten SWCC model and Clapeyron equation leads to the following unfrozen water content model.

${\theta }_{\mathrm{u}}={\theta }_{\mathrm{r}}+\left({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{r}}\right){\left[1+{\left(-a_{\mathrm{v}}{L}_{\mathrm{f}}{\rho }_{\mathrm{w}}\ln \frac{T+273.15}{T_0+273.15}\right)}^{n_{\mathrm{v}}}\right]}^{-m_{\mathrm{v}}}(14)$

2.2.4 Fredlund and Xing-Ren model

By substituting the Clapeyron equation into Fredlund and Xing SWCC model yielded (Ren et al., 2017).

${\theta }_{\mathrm{u}}=\frac{{\theta }_{\mathrm{s}}}{{\left\{\ln \left[2.718+{\left(-\frac{L_{\mathrm{f}}{\rho }_{\mathrm{w}}}{a_{\mathrm{f}}}\ln \left(\frac{T+273.15}{T_0+273.15}\right)\right)}^{n_{\mathrm{f}}}\right]\right\}}^{m_{\mathrm{f}}}}(15)$

where a_f, m_f, and n_f are curve-fitting parameters of Fredlund and Xing SWCC model.

2.2.5 Pham-Zhou model

Zhou (2020) suggested that SFCC was similar with SWCC, and replaced the matric suction in Pham SWCC model with temperature (-T), yielding the Pham-based SFCC model.

${\theta }_{\mathrm{u}}=\frac{{\theta }_{\mathrm{s}}\alpha +{\theta }_{\mathrm{r}}{\left(-T\right)}^m}{\alpha +{\left(-T\right)}^m}(16)$

where α is curve-fitting parameter of Pham SWCC model.

2.2.6 van Genuchten-Zhou model

Zhou (2020) reviewed the van Genuchten SWCC model and replaced the matric suction with temperature (-T), yielding van Genuchten-based SFCC model.

${\theta }_{\mathrm{u}}=\left({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{r}}\right)\frac{1}{{\left[1+{\left(a_{\mathrm{v}}\left(-T\right)\right)}^{n_{\mathrm{v}}}\right]}^{m_{\mathrm{v}}}}+{\theta }_{\mathrm{r}}(17)$

2.2.7 Fredlund and Xing-Zhou model

In the similar way, Zhou (2020) modified the Fredlund and Xing SWCC model by replacing the matric suction with temperature (-T).

${\theta }_{\mathrm{u}}=\left({\theta }_{\mathrm{s}}-{\theta }_{\mathrm{r}}\right)\frac{1}{{\left\{\ln \left[\mathrm{e}+{\left(-\frac{T}{a_{\mathrm{f}}}\right)}^{n_{\mathrm{f}}}\right]\right\}}^{m_{\mathrm{f}}}}+{\theta }_{\mathrm{r}}(18)$

2.2.8 van Genuchten-Wen model

Wen et al. (2020) indicated that the saturated water content can be replaced by the initial water content and proposed three generalized unfrozen water content models based on different SWCC models. Substituting a simplified Clapeyron equation and initial water content into van Genuchten SWCC model yielded the following unfrozen water content model,

${\theta }_{\mathrm{u}}={\theta }_{\mathrm{r}}+\left({\theta }_0-{\theta }_{\mathrm{r}}\right)\frac{1}{{\left[1+{\left(-\frac{a_{\mathrm{v}}{L}_{\mathrm{f}}{\rho }_{\mathrm{w}}T}{273.15}\right)}^{n_{\mathrm{v}}}\right]}^{m_{\mathrm{v}}}}(19)$

2.2.9 Fredlund and Xing-Wen model

The combination of a simplified Clapeyron equation, initial water content and Fredlund and Xing model yielded the Fredlund and Xing-Wen model (Wen et al., 2020).

${\theta }_{\mathrm{u}}=C\left(T\right)\frac{{\theta }_0}{{\left\{\ln \left[2.718+{\left(-\frac{L_{\mathrm{f}}{\rho }_{\mathrm{w}}T}{273.15a_{\mathrm{f}}}\right)}^{n_{\mathrm{f}}}\right]\right\}}^{m_{\mathrm{f}}}}(20)$

where C(T) is a correction factor and equal to $1-\frac{\ln \left(1-\frac{L{\rho }_{\mathrm{w}}T}{273.15C_{\mathrm{r}}}\right)}{\ln \left(1+\frac{1000000}{C_{\mathrm{r}}}\right)}$.

2.2.10 Fredlund and Xing(C=1)-Wen model

In order to simplify the Fredlund and Xing-Wen model, Wen et al. (2020) assumed that the correction factor in Eq. 20 can be equal to 1 and then produced a simplified unfrozen water content model.

${\theta }_{\mathrm{u}}=\frac{{\theta }_0}{{\left\{\ln \left[2.718+{\left(\frac{-L{\rho }_{\mathrm{w}}T}{273.15a_{\mathrm{f}}}\right)}^{n_{\mathrm{f}}}\right]\right\}}^{m_{\mathrm{f}}}}(21)$

2.3 Empirical models

2.3.1 Anderson and Tice empirical model

Anderson and Tice (1972) proposed a power formula with two parameters to calculate the gravimetric unfrozen water content.

$w_{\mathrm{u}}=\alpha {\left(-T\right)}^{\beta }(22)$

where α and β are curve-fitting parameters.

2.3.2 Michalowski et al. model

Based on the experimental unfrozen water contents of several soils in Anderson and Tice (1973), Michalowski (1993) and Michalowski and Zhu (2006) proposed an exponential formula to mimic the relationship between the gravimetric unfrozen water content and temperature. A similar formula was proposed to model the relationship between the volumetric unfrozen water content and temperature by Blanchard and Frémond (1985). Michalowski and Zhu (2006) indicated that not all water in the soil pores freeze to ice at the freezing point of water, so a discontinuity of water existed. The water content (w₀) dropped down to a smaller water content ($\overline{w}$) at T₀ and then gradually reduced to a smaller unfrozen water content (w_r) at a lower reference temperature. From calibration, the moisture content $\overline{w}$ was equal to the initial water content.

$w_{\mathrm{u}}=\{\begin{array}{cc}{w}_0& T\ge T_0\\ w_{\mathrm{r}}+\left(w_0-w_{\mathrm{r}}\right)\exp \left[\mu \left(T-T_0\right)\right]& T<T_0\end{array}(23)$

where μ is applied to describe the rate of decay.

2.3.3 Osterkamp and Romanovsky model

Osterkamp and Romanovsky (1997) modified the Anderson and Tice model by considering the freezing point, which is given as,

${\theta }_{\mathrm{u}}=a{\left|T-T_{\mathrm{f}}\right|}^c(24)$

where T_f is freezing point.

2.3.4 Mckenzie exponential model

Mckenzie et al. (2007) developed an exponential formula to model the relationship between saturation degree of unfrozen water content and temperature.

$S_{\mathrm{u}}=S_{\mathrm{r}}+\left(1-S_{\mathrm{r}}\right)\exp \left[-{\left(\frac{T-T_{\mathrm{f}}}{\gamma }\right)}^2\right](25)$

where S_r is residual saturation degree of unfrozen water content, T_f = 0 °C was recommend by Mckenzie et al. (2007), and γ is a fitting parameter.

2.3.5 Mckenzie linear model

Mckenzie et al. (2007) indicated that the unfrozen water content should be smoothly and easily differentiated, and proposed a simplest linear function (McKenzie et al., 2007).

$S_{\mathrm{u}}=\{\begin{array}{cc}mT+1& T>T_{\mathrm{r}}\\ S_{\mathrm{r}}& T\le T_{\mathrm{r}}\end{array}(26)$

where m is the slope of the unfrozen water content model, and T_r is defined as the temperature at which the linear freezing function attains residual saturation.

Due to the continuity of the unfrozen water content at T_r, the T_r can be given as,

$T_{\mathrm{r}}=\frac{S_{\mathrm{r}}-1}{m}(27)$

2.3.6 Kozlowski empirical model

Kozlowski (2007) developed a piecewise formula to model the relationship between gravimetric unfrozen water content and temperature. T_f and boundary temperature divided the model into three temperature ranges.

$w_{\mathrm{u}}=\{\begin{array}{cc}{w}_0& T>T_{\mathrm{f}}\\ w_{\text{res}}+\left(w_0-w_{\text{res}}\right)\exp \left[e{\left(\frac{T_{\mathrm{f}}-T}{T-T_{\mathrm{m}}}\right)}^f\right]& T_{\mathrm{m}}<T\le T_{\mathrm{f}}\\ w_{\text{res}}& T\le T_{\mathrm{m}}\end{array}(28)$

where T_m is the boundary temperature and equal to -12°C, e and f are non-interpretable coefficients, which are responsible for fitting the formula to the experimental gravimetric unfrozen water content in the range from T_m to T_f.

2.3.7 Zhang et al. model

A segmented linear function without a fitted parameter was proposed to model the volumetric unfrozen water content and temperature (Zhang et al., 2008), which was given as,

${\theta }_{\mathrm{u}}=\{\begin{array}{cc}{\theta }_0-\left({\theta }_0-{\theta }_{\mathrm{r}}\right)\left(T-T_{\mathrm{f}}\right)/\left(T_{\mathrm{r}}-T_{\mathrm{f}}\right)& T>T_{\mathrm{r}}\\ {\theta }_{\mathrm{r}}& T\le T_{\mathrm{r}}\end{array}(29)$

2.3.8 Qin et al. model

By analyzing the free energy in the frozen soil, a three parameter-model was developed to mimic the relationship between gravimetric unfrozen water content and temperature (Qin et al., 2009). The new model is similar to the widely-used Anderson and Tice model.

$w_{\mathrm{u}}=\{\begin{array}{cc}{w}_0& T>T_{\mathrm{f}}\\ a{\left(-T\right)}^b+c& T\le T_{\mathrm{f}}\end{array}(30)$

2.3.9 Westermann et al. model

Westermann et al. (2011) proposed a model to relate the volumetric unfrozen water content and temperature.

${\theta }_{\mathrm{u}}=\{\begin{array}{cc}{\theta }_0& T>0\\ {\theta }_{\mathrm{r}}-\left({\theta }_0-{\theta }_{\mathrm{r}}\right)\frac{\delta }{T-\delta }& T\le 0\end{array}(31)$

where δ is a fitting parameter.

2.3.10 Kurylyk and Watanabe model

In order to obtain a continuous exponential formula, the Mckenzie exponential model was modified slightly with the initial volumetric water content replacing the saturated volumetric water content to allow for unsaturated conditions (Kurylyk and Watanabe, 2013).

${\theta }_{\mathrm{u}}={\theta }_{\mathrm{r}}+\left({\theta }_0-{\theta }_{\mathrm{r}}\right)\exp \left[-{\left(\frac{T}{\gamma }\right)}^2\right](32)$

2.3.11 Nicolsky et al. model

Nicolsky et al. (2017) indicated that the unfrozen water content of fully saturated soils can be divided into two parts by T_f. The unfrozen water content in the saturated soil was equal to the soil porosity when the temperature was larger than T_f, otherwise, the unfrozen water content nonlinearly declined with the decreases of temperature.

${\theta }_{\mathrm{u}}=\{\begin{array}{cc}p& T\ge T_{\mathrm{f}}\\ p{\left|T_{\mathrm{f}}\right|}^b{\left|T\right|}^{-b}& T<T_{\mathrm{f}}\end{array}(33)$

2.3.12 Libo et al. model

Li et al. (2021) investigated the unfrozen water content of water-saturated coal and proposed a nonlinear formula with three parameters to mimic the relationship between unfrozen water content and temperature during a freezing process.

$w_{\mathrm{u}}=w_{\mathrm{r}}+\left(w_{\mathrm{s}}-w_{\mathrm{r}}\right)\frac{1}{\left[1+{\left(\frac{T}{a}\right)}^m\right]}(34)$

2.3.13 Weng et al. model

By investigating the relationship between unfrozen water content and temperature of five sandstones during a freezing process, Weng et al. (2021) developed an exponential unfrozen water content formula to fit the experimental data, which was given as,

$S_{\mathrm{u}}=\{\begin{array}{cc}1& T>0\\ A{\mathrm{e}}^{\frac{T}{t}}+B& T\le 0\end{array}(35)$

where A, B and t are curve-fitting parameters, A and t controlled the decrease speed of the unfrozen water content during a freezing process, and B is the residual unfrozen water content when the temperature closes to infinitesimally.

2.4 Estimation models

2.4.1 Anderson and Tice estimation model

Anderson and Tice (1972) related the two parameters of the power formula with SSA, yielding the Anderson and Tice estimation model.

$w_{\mathrm{u}}={\mathrm{e}}^{0.5519\ln SSA+0.2618}{\left(-T\right)}^{{-\mathrm{e}}^{0.2640\ln SSA+0.3711}}(36)$

2.4.2 Kozlowski estimation model

Six clays were applied to determine the parameters of the Kozlowski empirical model, yielding the Kozlowski estimation model (Kozlowski, 2007).

$w_{\mathrm{u}}=\{\begin{array}{cc}{w}_0& T>T_{\mathrm{f}}\\ w_{\mathrm{r}}+\left(w_0-w_{\mathrm{r}}\right)\exp \left[-3.35{\left(\frac{T_{\mathrm{f}}-T}{T-T_{\mathrm{m}}}\right)}^{0.37}\right]& T_{\mathrm{m}}<T\le T_{\mathrm{f}}\\ w_{\mathrm{r}}& T\le T_{\mathrm{m}}\end{array}(37)$

T_f was calculated by the following empirical relationship.

$T_{\mathrm{f}}=-0.0729w_{\mathrm{p}}^{2.462}{w}^{-2}(38)$

where w_p is plastic limit, %, w is total gravimetric water content, %.

$w_{\mathrm{r}}=0.042SSA+3(39)$

2.4.3 Kong et al. model

Kong et al. (2020) suggested that the classic power function proposed by Anderson and Tice (1972) contain two drawbacks. One drawback was that the parameters in Anderson and Tice empirical model had no physical meaning, and the other one was that the dimensions on left-hand and right-hand sides of the model were not uniform. To overcome the two drawbacks, Kong et al. (2020) proposed a new formula to estimate the unfrozen water content.

$w_{\mathrm{u}}=\{\begin{array}{cc}{w}_0& T>T_{\mathrm{f}}\\ w_0{\left(\frac{T}{T_{\mathrm{f}}}\right)}^g& T\le T_{\mathrm{f}}\end{array}(40)$

$T_{\mathrm{f}}=-0.015I_{\mathrm{p}}-0.063(41)$

$g=0.300I_{\mathrm{p}}-2.232(42)$

3 Data collection and analysis

3.1 Published datasets

In order to evaluate the performance of the 29 models, the unfrozen water content values were collected by the following criteria: 1) each soil sample contained unfrozen water content values under at least five subzero temperatures, 2) initial volumetric water content and saturated volumetric water content or porosity were available. 24 clays, 18 silty clays, 7 silts, 19 sands, and 10 sandstones satisfied the above criteria, as shown in Table 1. More details of their databases and experimental methodologies can be found in the following papers (Watanabe and Wake, 2009; Wen et al., 2012; Li et al., 2018; Kong et al., 2020; Li et al., 2020; Liu, 2020; Liu et al., 2020; Meng et al., 2020; Teng et al., 2020; Wang, 2020; Zhou, 2020; Kong et al., 2021; Teng et al., 2021; Wang et al., 2021; Weng et al., 2021; Yang et al., 2021).

TABLE 1

TABLE 1. Overview of the compiled unfrozen water content dataset.

3.2 Model performance metrics

The difference between calculated and measured unfrozen water contents were compared by plotting them on the same figure. To quantitatively evaluate the performance of these unfrozen water content models, two indices were adopted as criterion in this study.

1) Root mean square error (RMSE)

$RMSE=\sqrt{\frac{{\displaystyle \sum }_{i=1}^N{\left({\theta }_{\mathrm{u}-\text{ci}}-{\theta }_{\mathrm{u}-\text{mi}}\right)}^2}{N}}(43)$

2) Average deviations (AD)

$AD=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\left({\theta }_{\mathrm{u}-\text{ci}}-{\theta }_{\mathrm{u}-\text{mi}}\right)(44)$

where θ_u-ci is calculated by different unfrozen water content models, θ_u-mi is measured results, N is the number of points.

RMSE describes the absolute deviation between the calculated and measured results. AD represents the relative deviation between the calculated and measured results, which can be divided into three different conditions: 1) AD>0, θ_u-ci overestimates θ_u-mi, 2) AD=0, θ_u-ci is equal to θ_u-mi, and 3) AD<0, θ_u-ci underestimates θ_u-mi.

4 Results and discussion

4.1 Comparison of maximum and minimum values

During a freezing process, the unfrozen water content calculated by an unfrozen water content model decreased with subzero temperature, and the variation of unfrozen water content was constrained by the maximum and minimum values of the unfrozen water content model. In other words, the calculated unfrozen water content would distribute between maximum and minimum values. Table 2 summarized the results for all the unfrozen water content models.

TABLE 2

TABLE 2. The maximum and minimum values of unfrozen water content models.

For the theoretical models, the maximum values were saturated water content or initial water content, while the minimum values were residual water content or 0. For the SWCC-based models, the maximum values of most models were taken from saturated water content (θ_s or 1). The result was not surprising, since the SWCC-based models were developed from the SWCC model, and the maximum value of SWCC model was saturated water content. For the three models derived from the work of Wen et al. (2020), the maximum value was initial water content (θ₀). The minimum value of the SWCC-based models referred to θ_r or 0.

The formula of most empirical models was piecewise function, and different temperatures (0 °C, T_f and T_r) were applied to divide the unfrozen water content model into two or three segments. The maximum and minimum values for most empirical models were the same as that of the SWCC-based models. However, some empirical models had special maximum and minimum values. For example, the maximum value of Anderson and Tice model tended to infinity when the temperature approached 0 °C, while the maximum value of Osterkamp and Romanovsky model was infinity when the temperature approached T_f. The minimum values of the Qin et al. model and Weng et al. model were c and B, respectively, which can be regarded as residual unfrozen water content. For the three estimation models, the Anderson and Tice estimation model and Kozlowski estimation model were developed from the Anderson and Tice empirical model and Kozlowski empirical model, respectively. Therefore, the maximum and minimum values of the Anderson and Tice estimation model and Kozlowski estimation model were the same as that of Anderson and Tice empirical model and Kozlowski empirical model. For the Kong et al. model, the maximum and minimum values were w₀ and 0, respectively.

4.2 Model evaluation

4.2.1 Theoretical models

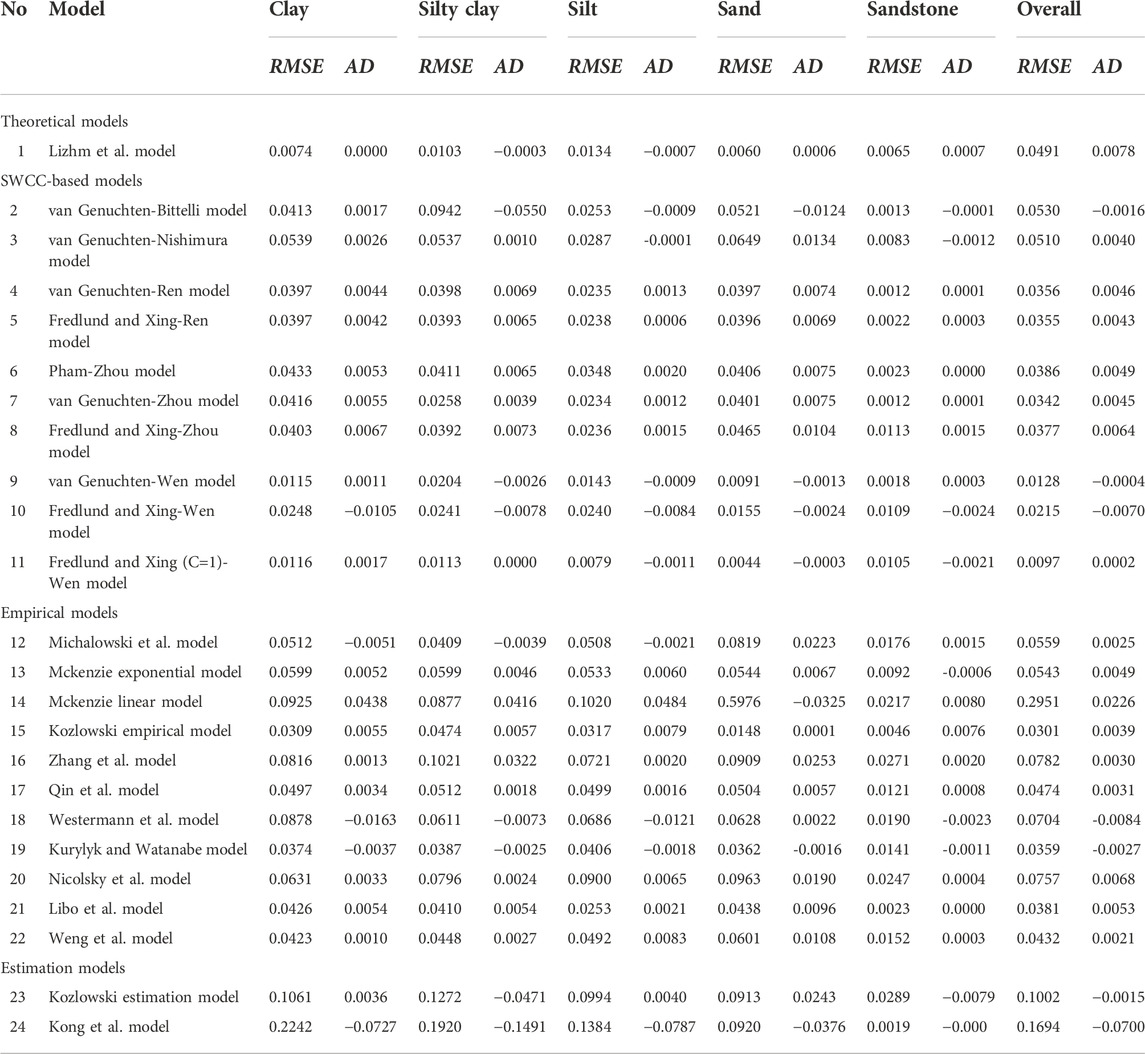
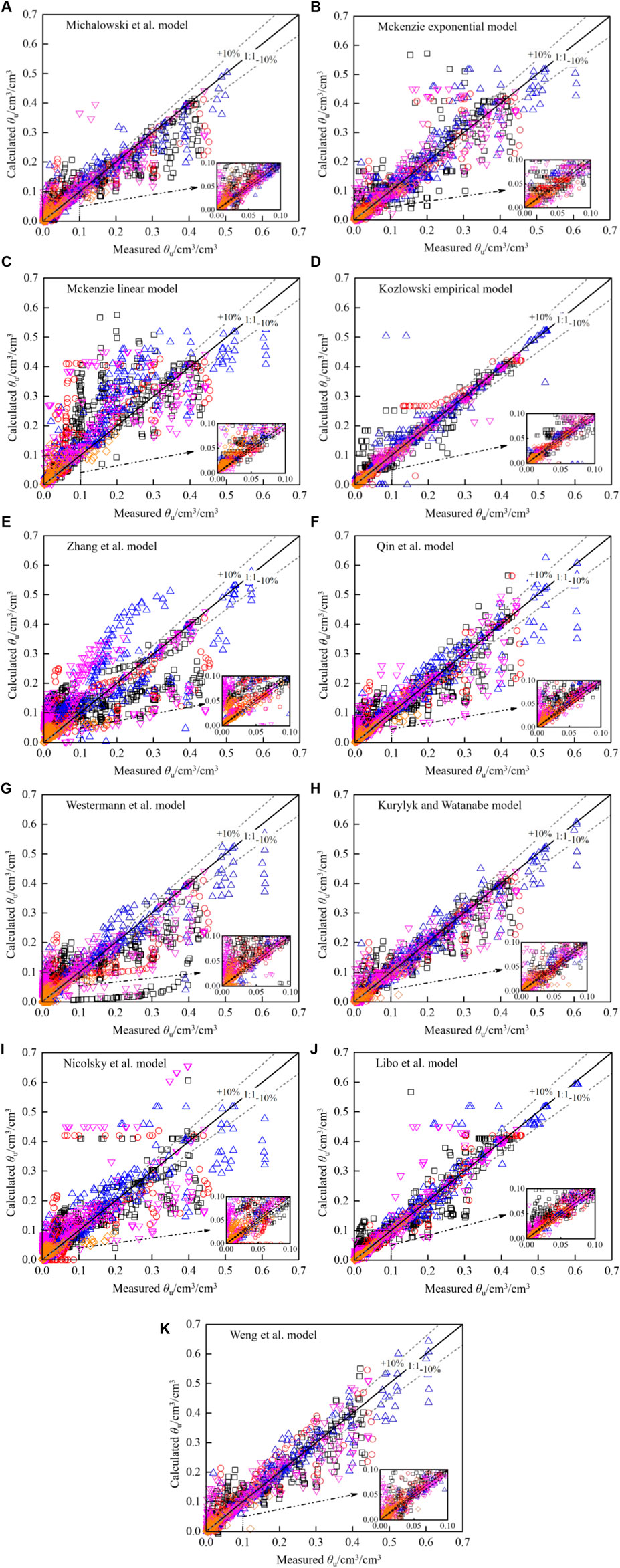
The Chai et al. model and Teng et al. model were complicated and difficult to be incorporated into the numerical modelling. Therefore, they were not included in present study. Figure 1 shows the calculated unfrozen water contents matched well with the measured results. Most of the calculated results stood between the ±10% deviation lines over the entire range of unfrozen water content. Table 3 showed that the RMSE of the Lizhim et al. model ranged from 0.0060 to 0.0134, indicating a good fitting performance of the unfrozen water content. Based on the AD values, it was found that the Lizhim et al. model underestimated the unfrozen water content for silty clay and silt, while the Lizhim et al. model overestimated the results for sand and sandstone. When unfrozen water content was larger than 0.3 cm³/cm³, the Lizhim et al. model tended to underestimate the results.

FIGURE 1

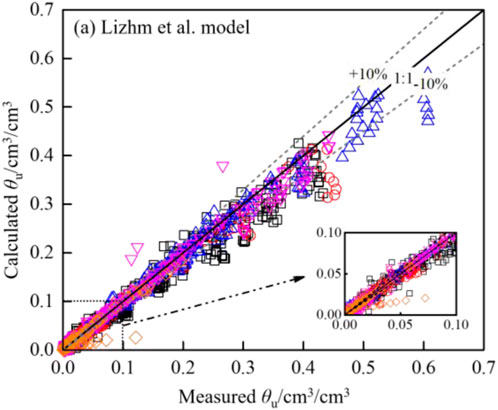
FIGURE 1. Fitting performance of 1 theoretical model. In the figure, black square stands for clay, blue up triangle stands for silty clay, red circle stands for silt, magenta down triangle stands for sand, and orange rhombus stands for sandstone.

TABLE 3

TABLE 3. Performance of the selected unfrozen water content models.

4.2.2 SWCC-based models

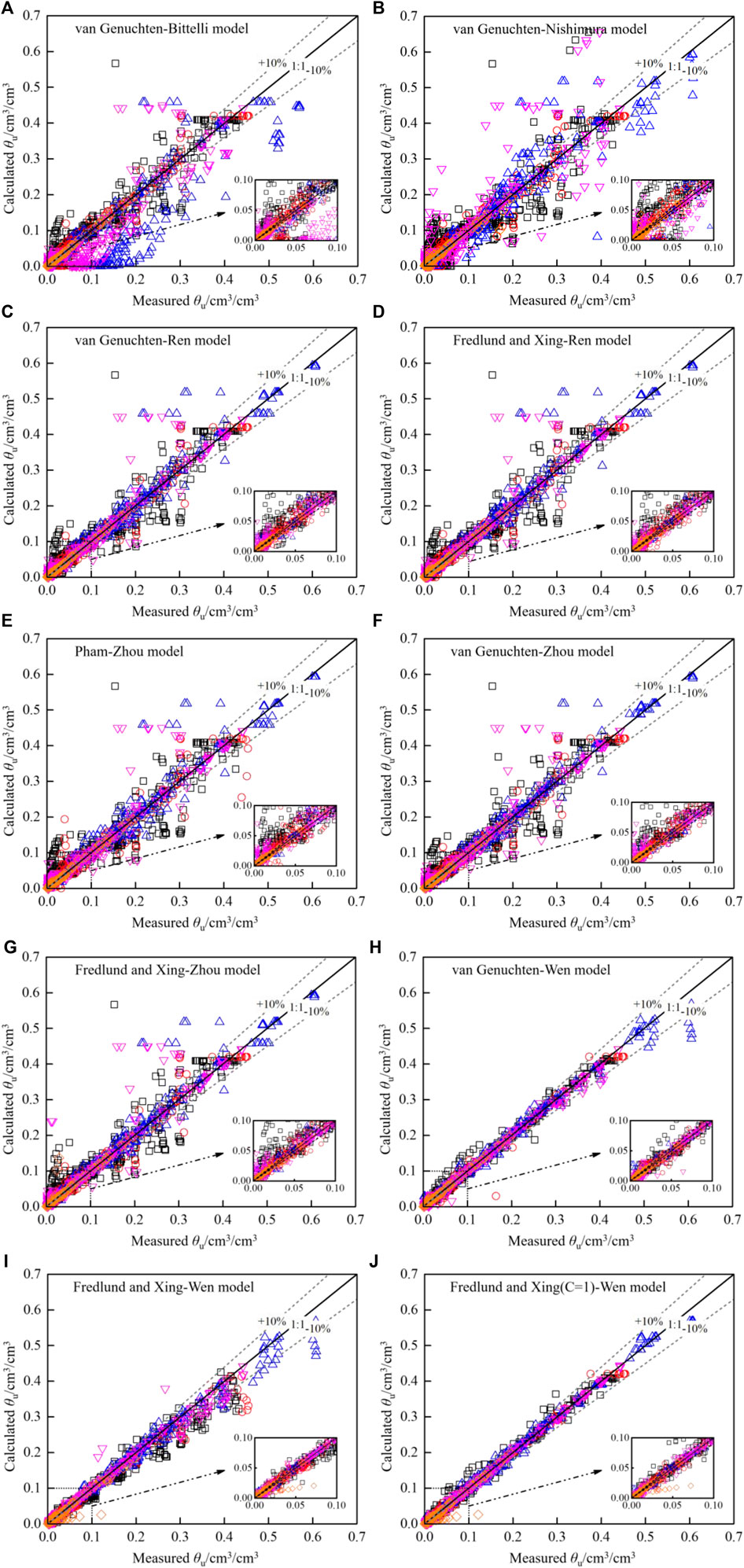
Figure 2 shows the comparison between calculated and measured unfrozen volumetric water contents for the 10 SWCC-based models. For each unfrozen water content model, most calculated results stood between the ±10% deviation lines over the entire range of unfrozen water content, implying that all models had good performance in estimating unfrozen water content for all soil samples. Besides, we can find that the Fredlund and Xing (C=1)-Wen model had the best performance with RMSE=0.0097 cm³/cm³, AD=0.0002 cm³/cm³, followed by van Genuchten-Wen model (RMSE=0.0128 cm³/cm³, AD=-0.0004 cm³/cm³) and Fredlund and Xing-Wen model (RMSE=0.0215 cm³/cm³, AD=-0.0070 cm³/cm³). This was mainly attributed to that the Fredlund and Xing (C=1)-Wen model, van Genuchten-Wen model and Fredlund and Xing-Wen model were developed by replacing the saturated volumetric water content with initial volumetric water content in the SWCC-based model, which overcome the computational oddity at 0°C.

FIGURE 2

FIGURE 2. (Continued).

Different soil types led to different model performance. In this study, Table 3 showed that Fredlund and Xing (C=1)-Wen model had best estimation for silty clay, silt and sand, the van Genuchten-Wen model showed best performance in clay, and the van Genuchten-Ren model and van Genuchten-Zhou model performed best when dealing with sandstone. The successful application of van Genuchten-Ren model and van Genuchten-Zhou model for the sandstone samples were mainly due to that the sandstones were saturated before measuring the unfrozen water content. Wen et al. (2020) evaluated the Fredlund and Xing (C=1)-Wen model, van Genuchten-Wen model and Fredlund and Xing-Wen model with uniform-sized glass powders and silty clay, and found that the Fredlund and Xing-Wen model had best performance among the three models, especially in narrower subzero temperature ranges, which is slightly different from the results in this study. The higher T_f of the soil samples of the Wen et al. (2020) research and lower T_f of the soil samples in this study may be a reason for this disagreement. Besides, the correction factor had a significant effect on the Fredlund and Xing-Wen model. Ren et al. (2017) evaluated the van Genuchten-Ren model and Fredlund and Xing-Ren model with four soils (Castor sandy loam, Lanzhou silt, Niagara silt, and Regina clay), and reported that the Fredlund and Xing-Ren model was slightly better than van Genuchten-Ren model. However, their results were different from the results in this study in terms of RMSE and AD, which may be attributed to a limited number of the soil samples used in the Ren et al. (2017) research.

4.2.3 Empirical models

The Anderson and Tice empirical model and Osterkamp and Romanovsky model were excluded in this study because the Anderson and Tice empirical model tended to infinite at 0 °C and the Osterkamp and Romanovsky model tended to infinite at T_f. T_f was determined by Eq. 41. Figure 3 showed the comparison between calculated and measured unfrozen volumetric water contents for the 11 empirical models. It indicated that the model with best performance is Kozlowski empirical model with RMSE=0.0301 cm³/cm³, AD=0.0039 cm³/cm³, followed by the Kurylyk and Watanabe model with RMSE=0.0359 cm³/cm³, AD=-0.0027 cm³/cm³ and Libo et al. model with RMSE=0.0381 cm³/cm³, AD=0.0053 cm³/cm³. It can be seen from Table 3 that the Kozlowski empirical model had best performance in clay and sand, the Libo et al. model was good at simulating the silt and sandstone, and the Kurylyk and Watanabe model showed best estimation for silty clay. Kurylyk and Watanabe (2013) used silt loam to evaluate the Kozlowski empirical model, Kurylyk and Watanabe model and Mckenzie linear model, and pointed out that the Kozlowski empirical model had best performance among the three models. Lu et al. (2019) evaluated the Michalowski et al. model, Mckenzie exponential model, and Kozlowski empirical model with two types of silty clay, and concluded that the Kozlowski empirical model was best among the three models. However, the results were slightly different from the findings in this study and the work of Wen et al. (2020) research. The present study and Wen et al. (2020) research indicated that the Michalowski et al. model had best performance among the three models for silty clay, followed by the Kozlowski empirical model, and Mckenzie exponential model. The inconsistency can be attributed to two reasons. First, the T_res=-12 °C and w_res was regarded as a fitting parameter in the present study, while the T_res and w_res were obtained from the residual unfrozen water content and its corresponding temperature in Lu et al. (2019) research. Second, the methods for determination of T_f were different.

FIGURE 3

FIGURE 3. (Continued).

4.2.4 Estimation models

The Anderson and Tice estimation model was not included in the section because it tended to be infinite at 0 °C. Results showed that the Kozlowski model had better performance for clay, silt, silty clay, and sand, while the Kong et al. model was more suitable for sandstone. The result was not surprising, since the Kozlowski estimation model was developed primarily from a data set of clays. Kozlowski (2007) used four soils (Bentonite, Kaolin clay, Silty clay and Sandy silt) to evaluate the Kozlowski estimation model and Anderson and Tice estimation model, and indicated that the Kozlowski estimation model performed better than the Anderson and Tice estimation model. The result showed that the Anderson and Tice estimation model yielded a larger unfrozen water content at a higher subzero temperature, especially near 0 °C. For the Kong et al. model, it tended to underestimate the unfrozen water content for clay, silt and silty clay.

Unlike the theoretical, SWCC-based and empirical models, the Kozlowski estimation model and Kong et al. model can be applied to calculate the unfrozen water contents under different subzero temperatures with some easy-to-obtain soil parameters. For example, the Kozlowski estimation model can be used to estimate the gravimetric unfrozen water contents at different subzero temperatures using w_p, w, and SSA. The Kong et al. model required two soil physical parameters (I_p, w), and the relationship between gravimetric unfrozen water content and subzero temperature can then be determined. The two estimation models obtained good performance for sandstone. For other soil types, the calculated results were not as good as previous models. It seems that increasing clay content of soil sample lead to unsatisfactory calculated results. However, the estimation models can still provide guidance on the development of unfrozen water content models in the future studies.

5 Conclusion

This study summarized 29 unfrozen water content models and determined the maximum and minimum values of these models. These models were compared and evaluated with 1278 measurements on clay, silty clay, silt, sand and sandstone. The results showed that the Lizhm et al. model, Fredlund and Xing (C=1)-Wen model, Kozlowski empirical model, and Kozlowski estimation model performed best in the corresponding categories. The overall performance of these models was satisfactory, especially the SWCC-based models. The estimation models can be applied to predict the relationship between unfrozen water content and subzero temperature with some easy-to-obtain soil physical parameters. These estimation models provided guidance on the development of unfrozen water content models for wider applications in the future studies (Figure 4).

FIGURE 4

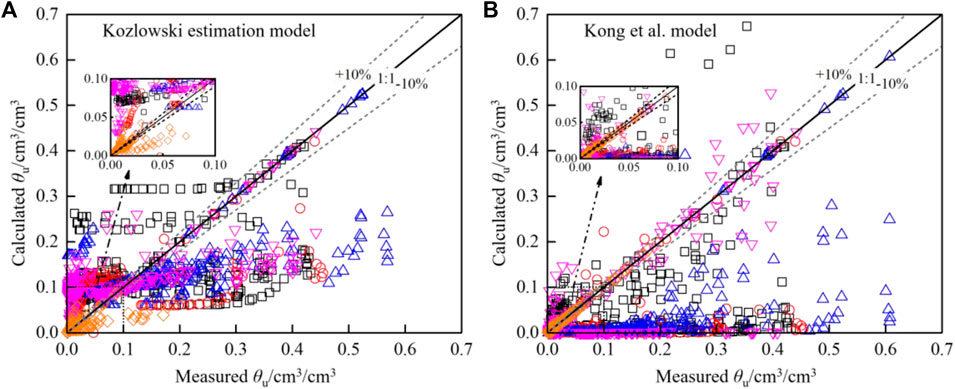
FIGURE 4. Calculating performance of 2 estimation models. In the figure, black square stands for clay, blue up triangle stands for silty clay, red circle stands for silt, magenta down triangle stands for sand, and orange rhombus stands for sandstone.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JB and ZW contributed to conception of the study, writing and discussions; GW, HW, and YZ contributed to review of the manuscript; GL and TS contributed to editing of Figures and Table.

Funding

This study was financially supported by the National Natural Science Foundation of China (Grant No. 42102306), the Second Tibetan Plateau Scientific Expedition and Research (STEP) Program (Grant No. 2019QZKK0905), the National Earthquake Science Joint Foundation of China (Grant No. U1939209), the Open Fund of State Key Laboratory of Frozen Soil Engineering (Grant No. SKLFSE202108, SKLFSE202009), and the program of the State Key Laboratory of Road Engineering Safety and Health in Cold and High-Altitude Regions (Grant No. YGY2020KYPT-07).

Conflict of interest

Authors YZ and TS were employed by CCCC First Harbor Consultants Co, Ltd and Jiangsu Sunpower Technology Co, Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, D. M., and Tice, A. R. (1972). Predicting unfrozen water contents in frozen soils from surface area measurements. Highw. Res. Rec. 393, 12–18.

Google Scholar

Anderson, D., and Tice, A. R. (1973). “The unfrozen interfacial phase in frozen soil water systems,” in Physical aspects of soil water and salts in ecosystems (Springer), 107–124.

CrossRef Full Text | Google Scholar

Bai, R., Lai, Y., Zhang, M., and Yu, F. (2018). Theory and application of a novel soil freezing characteristic curve. Appl. Therm. Eng. 129, 1106–1114. doi:10.1016/j.applthermaleng.2017.10.121

CrossRef Full Text | Google Scholar

Bittelli, M., Flury, M., and Campbell, G. S. (2003). A thermodielectric analyzer to measure the freezing and moisture characteristic of porous media. Water Resour. Res. 39 (2). doi:10.1029/2001wr000930

CrossRef Full Text | Google Scholar

Blanchard, D., and Frémond, M. (1985). Soil frost heaving and thaw settlement.

Google Scholar

Chai, M., Zhang, J., Zhang, H., Mu, Y., Sun, G., and Yin, Z. (2018). A method for calculating unfrozen water content of silty clay with consideration of freezing point. Appl. Clay Sci. 161, 474–481. doi:10.1016/j.clay.2018.05.015

CrossRef Full Text | Google Scholar

Chen, Y., Zhou, Z., Wang, J., Zhao, Y., and Dou, Z. (2021). Quantification and division of unfrozen water content during the freezing process and the influence of soil properties by low-field nuclear magnetic resonance. J. Hydrology 602, 126719. doi:10.1016/j.jhydrol.2021.126719

CrossRef Full Text | Google Scholar

Kong, L., Wang, Y., Sun, W., and Qi, J. (2020). Influence of plasticity on unfrozen water content of frozen soils as determined by nuclear magnetic resonance. Cold Regions Sci. Technol. 172, 102993. doi:10.1016/j.coldregions.2020.102993

CrossRef Full Text | Google Scholar

Kong, L., Liang, K., and Peng, l. (2021). Experimental study on the influence of specific surface area on the soil-freezing characteristic curve. Rock Soil Mech. 42 (7), 1883–1893. doi:10.16285/j.rsm.2020.1754

CrossRef Full Text | Google Scholar

Kozlowski, T. (2004). Soil freezing point as obtained on melting. Cold Regions Sci. Technol. 38 (2), 93–101. doi:10.1016/j.coldregions.2003.09.001

CrossRef Full Text | Google Scholar

Kozlowski, T. (2007). A semi-empirical model for phase composition of water in clay–water systems. Cold Regions Sci. Technol. 49 (3), 226–236. doi:10.1016/j.coldregions.2007.03.013

CrossRef Full Text | Google Scholar

Kruse, A. M., Darrow, M. M., and Akagawa, S. (2018). Improvements in measuring unfrozen water in frozen soils using the pulsed nuclear magnetic resonance method. J. Cold Reg. Eng. 32 (1), 04017016. doi:10.1061/(asce)cr.1943-5495.0000141

CrossRef Full Text | Google Scholar

Kurylyk, B. L., and Watanabe, K. (2013). The mathematical representation of freezing and thawing processes in variably-saturated, non-deformable soils. Adv. Water Resour. 60, 160–177. doi:10.1016/j.advwatres.2013.07.016

CrossRef Full Text | Google Scholar

Li, H., Yang, Z. J., and Wang, J. (2018). Unfrozen water content of permafrost during thawing by the capacitance technique. Cold Regions Sci. Technol. 152, 15–22. doi:10.1016/j.coldregions.2018.04.012

CrossRef Full Text | Google Scholar

Li, S., Lai, Y., Zhang, M., Pei, W., Zhang, C., and Yu, F. (2019). Centrifuge and numerical modeling of the frost heave mechanism of a cold-region canal. Acta Geotech. 14 (4), 1113–1128. doi:10.1007/s11440-018-0710-1

CrossRef Full Text | Google Scholar

Li, Z., Chen, J., and Sugimoto, M. (2020). Pulsed NMR measurements of unfrozen water content in partially frozen soil. J. Cold Reg. Eng. 34 (3), 04020013. doi:10.1061/(asce)cr.1943-5495.0000220

CrossRef Full Text | Google Scholar

Li, B., Huang, L., Lv, X., and Ren, Y. (2021). Variation features of unfrozen water content of water-saturated coal under low freezing temperature. Sci. Rep. 11 (1), 15398. doi:10.1038/s41598-021-94943-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C. (2020). Experimental study on freezing temperature and unfrozen water content of heavy metal contaminated loess. Lanzhou: Lanzhou University of Technology.

Google Scholar

Liu, J., Yang, P., and Yang, Z. (2020). Electrical properties of frozen saline clay and their relationship with unfrozen water content. Cold Regions Sci. Technol. 178, 103127. doi:10.1016/j.coldregions.2020.103127

CrossRef Full Text | Google Scholar

Liu, Z., and Yu, X. (2013). Physically based equation for phase composition curve of frozen soils. Transp. Res. Rec. 2349 (2349), 93–99. doi:10.3141/2349-11

CrossRef Full Text | Google Scholar

Lu, J., Zhang, M., Zhang, X., and Yan, Z. (2017). Experimental study on unfrozen water content and the freezing temperature during freezing and thawing processes. Chin. J. Rock Mech. Eng. 36 (7), 1803–1812. doi:10.13722/j.cnki.jrme.2016.1433

CrossRef Full Text | Google Scholar

Lu, J., Pei, W., Zhang, X., Bi, J., and Zhao, T. (2019). Evaluation of calculation models for the unfrozen water content of freezing soils. J. Hydrology 575, 976–985. doi:10.1016/j.jhydrol.2019.05.031

CrossRef Full Text | Google Scholar

McKenzie, J. M., Voss, C. I., and Siegel, D. I. (2007). Groundwater flow with energy transport and water–ice phase change: Numerical simulations, benchmarks, and application to freezing in peat bogs. Adv. Water Resour. 30 (4), 966–983. doi:10.1016/j.advwatres.2006.08.008

CrossRef Full Text | Google Scholar

Meng, X., Zhou, J., Wei, C., Zhang, K., Shen, Z., and Yang, Z. (2020). Effects of salinity on soil freezing temperature and unfrozen water content. Rock Soil Mech. 41 (3), 952–960. doi:10.16285/j.rsm.2019.0617

CrossRef Full Text | Google Scholar

Michalowski, R. L. (1993). A constitutive model of saturated soils for frost heave simulations. Cold Regions Sci. Technol. 22 (1), 47–63. doi:10.1016/0165-232x(93)90045-a

CrossRef Full Text | Google Scholar

Michalowski, R. L., and Zhu, M. (2006). Frost heave modelling using porosity rate function. Int. J. Numer. Anal. Methods Geomech. 30 (8), 703–722. doi:10.1002/nag.497

CrossRef Full Text | Google Scholar

Mu, Q. Y., Ng, C. W. W., Zhou, C., Zhou, G. G. D., and Liao, H. J. (2018). A new model for capturing void ratio-dependent unfrozen water characteristics curves. Comput. Geotechnics 101, 95–99. doi:10.1016/j.compgeo.2018.04.019

CrossRef Full Text | Google Scholar

Mu, Q. Y., Zhou, C., Ng, C. W. W., and Zhou, G. G. D. (2019). Stress effects on soil freezing characteristic curve: Equipment development and experimental results. Vadose zone J. 18 (1), 1–10. doi:10.2136/vzj2018.11.0199

CrossRef Full Text | Google Scholar

Nicolsky, D. J., Romanovsky, V. E., Panda, S. K., Marchenko, S. S., and Muskett, R. R. (2017). Applicability of the ecosystem type approach to model permafrost dynamics across the Alaska North Slope. J. Geophys. Res. Earth Surf. 122 (1), 50–75. doi:10.1002/2016jf003852

CrossRef Full Text | Google Scholar

Nishimura, S., Gens, A., Olivella, S., and Jardine, R. J. (2009). THM-Coupled finite element analysis of frozen soil: Formulation and application. Géotechnique 59 (3), 159–171. doi:10.1680/geot.2009.59.3.159

CrossRef Full Text | Google Scholar

Osterkamp, T., and Romanovsky, V. (1997). Freezing of the active layer on the coastal plain of the Alaskan Arctic. Permafr. Periglac. Process. 8 (1), 23–44. doi:10.1002/(sici)1099-1530(199701)8:1<23::aid-ppp239>3.0.co;2-2

CrossRef Full Text | Google Scholar

Qin, Y., Li, G., and Qu, G. (2009). “A formula for the unfrozen water content and temperature of frozen soils,” in Cold regions engineering 2009: Cold regions impacts on research, design, and construction, 155–161.

CrossRef Full Text | Google Scholar

Ren, J., Vanapalli, S. K., and Han, Z. (2017). Soil freezing process and different expressions for the soil-freezing characteristic curve. Sci. Cold Arid Regions 9 (3), 221–228. doi:10.3724/SP.J.1226.2017.00221

CrossRef Full Text | Google Scholar

Tan, X., Chen, W., Wu, G., and Yang, J. (2013). Numerical simulations of heat transfer with ice–water phase change occurring in porous media and application to a cold-region tunnel. Tunn. Undergr. Space Technol. 38, 170–179. doi:10.1016/j.tust.2013.07.008

CrossRef Full Text | Google Scholar

Tang, L., Wang, K., Jin, L., Yang, G., Jia, H., and Taoum, A. (2018). A resistivity model for testing unfrozen water content of frozen soil. Cold Regions Sci. Technol. 153, 55–63. doi:10.1016/j.coldregions.2018.05.003

CrossRef Full Text | Google Scholar

Teng, J., Kou, J., Yan, X., Zhang, S., and Sheng, D. (2020). Parameterization of soil freezing characteristic curve for unsaturated soils. Cold Regions Sci. Technol. 170, 102928. doi:10.1016/j.coldregions.2019.102928

CrossRef Full Text | Google Scholar

Teng, J., Zhong, Y., Zhang, S., and Sheng, D. (2021). A mathematic model for the soil freezing characteristic curve: The roles of adsorption and capillarity. Cold Regions Sci. Technol. 181, 103178. doi:10.1016/j.coldregions.2020.103178

CrossRef Full Text | Google Scholar

Vitel, M., Rouabhi, A., Tijani, M., and Guérin, F. (2016). Modeling heat and mass transfer during ground freezing subjected to high seepage velocities. Comput. Geotechnics 73, 1–15. doi:10.1016/j.compgeo.2015.11.014

CrossRef Full Text | Google Scholar

Wang, C., Lai, Y., and Zhang, M. (2017). Estimating soil freezing characteristic curve based on pore-size distribution. Appl. Therm. Eng. 124, 1049–1060. doi:10.1016/j.applthermaleng.2017.06.006

CrossRef Full Text | Google Scholar

Wang, T., Sun, Q., Jia, H., Ren, J., and Luo, T. (2021). Linking the mechanical properties of frozen sandstone to phase composition of pore water measured by LF-NMR at subzero temperatures. Bull. Eng. Geol. Environ. 80 (6), 4501–4513. doi:10.1007/s10064-021-02224-3

CrossRef Full Text | Google Scholar

Wang, Y. (2020). Experimental study on influence of plasticity on unfrozen water content in frozen soils based on nuclear magnetic resonance. Beijing: Beijing University of Civil Engineering and Architecture.

Google Scholar

Watanabe, K., and Wake, T. (2009). Measurement of unfrozen water content and relative permittivity of frozen unsaturated soil using NMR and TDR. Cold Regions Sci. Technol. 59 (1), 34–41. doi:10.1016/j.coldregions.2009.05.011

CrossRef Full Text | Google Scholar

Wen, Z., Ma, W., Feng, W., Deng, Y., Wang, D., Fan, Z., et al. (2012). Experimental study on unfrozen water content and soil matric potential of Qinghai-Tibetan silty clay. Environ. Earth Sci. 66 (5), 1467–1476. doi:10.1007/s12665-011-1386-0

CrossRef Full Text | Google Scholar

Wen, H., Bi, J., and Guo, D. (2020). Evaluation of the calculated unfrozen water contents determined by different measured subzero temperature ranges. Cold Regions Sci. Technol. 170, 102927. doi:10.1016/j.coldregions.2019.102927

CrossRef Full Text | Google Scholar

Weng, L., Wu, Z., Liu, Q., Chu, Z., and Zhang, S. (2021). Evolutions of the unfrozen water content of saturated sandstones during freezing process and the freeze-induced damage characteristics. Int. J. Rock Mech. Min. Sci. 142, 104757. doi:10.1016/j.ijrmms.2021.104757

CrossRef Full Text | Google Scholar

Westermann, S., Boike, J., Langer, M., Schuler, T., and Etzelmüller, B. (2011). Modeling the impact of wintertime rain events on the thermal regime of permafrost. Cryosphere 5 (4), 945–959. doi:10.5194/tc-5-945-2011

CrossRef Full Text | Google Scholar

Yang, L., Jia, H., Han, L., Zhang, H., and Tang, L. (2021). Hysteresis in the ultrasonic parameters of saturated sandstone during freezing and thawing and correlations with unfrozen water content. J. Rock Mech. Geotechnical Eng. 13 (5), 1078–1092. doi:10.1016/j.jrmge.2021.06.006

CrossRef Full Text | Google Scholar

Yang, S., Zhang, M., Pei, W., Melnikov, A., Zhang, Z., and You, Z. J. A. R. (2022a). Numerical study on snow erosion and deposition around an embankment with a snow fence under snowfall conditions. Aeolian Res. 56, 100798. doi:10.1016/j.aeolia.2022.100798

CrossRef Full Text | Google Scholar

Yang, Y., Lei, D., Chen, Y., Cai, C., and Hou, S. (2022b). Coupled thermal-hydro-mechanical model of deep artificial freezing clay. Cold Regions Sci. Technol. 198, 103534. doi:10.1016/j.coldregions.2022.103534

CrossRef Full Text | Google Scholar

Yoshikawa, K., Overduin, P. P., and Harden, J. W. (2004). Moisture content measurements of moss (Sphagnum spp.) using commercial sensors. Permafr. Periglac. Process. 15 (4), 309–318. doi:10.1002/ppp.505

CrossRef Full Text | Google Scholar

Zhang, Y., Carey, S. K., and Quinton, W. L. (2008). Evaluation of the algorithms and parameterizations for ground thawing and freezing simulation in permafrost regions. J. Geophys. Res. 113 (D17), D17116. doi:10.1029/2007jd009343

CrossRef Full Text | Google Scholar

Zhang, M., Zhang, X., Lu, J., Pei, W., and Wang, C. (2018). Analysis of volumetric unfrozen water contents in freezing soils. Exp. Heat. Transf. 32, 426–438. doi:10.1080/08916152.2018.1535528

CrossRef Full Text | Google Scholar

Zhao, Y., Yu, B., Yu, G., and Li, W. (2014). Study on the water-heat coupled phenomena in thawing frozen soil around a buried oil pipeline. Appl. Therm. Eng. 73 (2), 1477–1488. doi:10.1016/j.applthermaleng.2014.06.017

CrossRef Full Text | Google Scholar

Zhou, J. (2020). Experimental study on characteristics of unfrozen water in clay mineral and its effect on sand thawing characteristics. Xuzhou: China University of Mining and Technology.

Google Scholar