Study on rock mass failure characteristics of double-hole delayed blasting in interbedding based on particle expansion algorithm

The existence of the interface between soft and hard rock often makes it difficult to control the blasting effect. Studying the influence of structural plane and delayed initiation time on rock blasting characteristics can make the blasting effect more controllable. In this paper, by using the Particle Flow Code (PFC^2D) and particle expansion algorithm, the double-hole delayed blasting experiments of soft-hard rock are carried out, and the results are analyzed from the perspectives of fragment gradation, micro contact force and energy field. Results show that: 1) When blasting in hard rock, if the distance between structural plane and blasthole is about two times the radius of crushing area, it will easier to form large area fragments, and the fragments tend to be crushed with the increase of the distance. When the distance is 2–4 times the radius of crushing area, with the increase of delay time, the overall fragment area value increases first and then decreases, and reaches the maximum when the delay time is 4 ms. 2) When the structural plane existing in the rock mass, the delayed initiation will make the contact force become relatively uniform within a certain range. The main direction of contact force will appear in the uneven state of contact force generated by simultaneous or delayed initiation, which is close to the parallel or vertical direction of blasthole connection. 3) When blasting in hard rock, if the distance between the structural plane and the blasthole is greater than about two times the radius of the crushing area, compared with simultaneous blasting, the peak kinetic energy and peak strain energy of delayed blasting will be reduced by about 33% and 46% respectively.

1 Introduction

Layered rock in natural rock mass is quite common, accounting for about 66.7% of the land area, and reaching 77.3% in China (Bo, 2016). In addition to layered rock mass, natural rock mass with a large number of joint fissures, fault fracture zones and other structural planes is often encountered in engineering (Dong et al., 2020; Zhou and He, 2020; Dong et al., 2021). For example, in open-pit coal mines in Xinjiang, China, interbedded, alternating and soft-hard rock are often encountered (Chen et al., 2015). In tunnel excavation, the heading face often encounters soft-hard rock (Feng et al., 2012; Yang et al., 2018). Structural plane is a geological interface with a certain extension direction and relatively small thickness formed in rock mass. Due to the existence of a large number of structural planes, the rock mass has obvious anisotropy in terms of stress and deformation (Lisjak et al., 2014). Especially in blasting engineering, the structural plane will affect the propagation of stress wave, which makes the blasting characteristics of rock mass different from those of homogeneous rock mass (Duan et al., 2017; Feng et al., 2020). In addition to the structural plane, different rock lithology (Zaid et al., 2020; Zaid et al., 2021; Zaid and Rehan Sadique, 2021; Zaid and Shah, 2021; Sadique et al., 2022), different degree of weathering (Zaid et al., 2022) will show different blasting effect. What’s more, research shows that the fracture mode and crack morphology of soft rock and hard rock are quite different (Tao et al., 2020a).

Blasting technology is often used in geological engineering such as underground excavation (Tao et al., 2021), ore mining (Tao et al., 2020a; Tao et al., 2020b; Xu et al., 2020), slope engineering (Zhou et al., 2019; Yang et al., 2022). In engineering, multi-hole blasting is often used, so the interaction between blastholes needs to be considered. At present, the researches on double-hole or multi-hole initiation mainly focus on the blasthole spacing (Li C. et al., 2021), in-situ stress (Yang J. et al., 2020), initiation delayed time (Chen et al., 2017), and charging method (Guo et al., 2020). Yang L. et al. (2020) found that compared with single-hole blasting, double-hole blasting had a superposition effect, and the peak strain and stress at the midpoint of the blasthole were more than twice that of single-hole blasting. Pu et al. (2021) found that, by using numerical simulation method, increasing the spacing of blastholes was not conducive to the propagation of cracks, but also inhibited the merging of cracks at the guide holes. Wu et al. (2021) also compared the crack behavior of elliptical bipolar linear charge blasting and ordinary blasting based on numerical simulation method, and found that the charging mode had a great impact on the formation of directional cracks. Zhang et al. (2022) simulated the blasting effect under isotropic and anisotropic high stress, and found that in isotropic state, the inhibition effect of in-situ stress on blasting effect increased with the growth of in-situ stress. Under various anisotropic conditions, cracks were more likely to develop in the direction of high stress.

The research directions of double-hole blasting mainly focus on the above aspects, and most of the research objects are single lithology rock mass. According to the previous research results, rock lithology and the interface between layered rock mass (also known as structural plane) have a great influence on the blasting effect, but there are few research results on this aspect. Therefore, this paper will explore the rock failure characteristics of double-hole blasting in the geological environment which rock mass composed of hard rock and soft rock with large differences in rock mechanical properties. In addition to the complex geological condition, the delayed initiation problem also has a serious impact on the blasting characteristics under the condition of multi-hole blasting, so the delayed initiation problem has to be considered. Consequently, in this paper, the numerical simulation of double-hole blasting is carried out considering the two necessary factors of soft-hard composited rock strata and delayed detonation. The results can provide reference for practical engineering.

2 Analytical framework for cylindrical wave propagation in in-situ stress rocks

The blasting of long-length cylindrical charge in deep rock can be simplified as a plane strain problem, as shown in Figure 1. There is a circular hole with radius a in the plane of elastic medium with infinite length and width, isotropic and homogeneous, and it is subjected to the horizontal stress σ_h and vertical stress σ_v in the far field. The in-situ stress in the vertical and horizontal directions are calculated according to the empirical formula (Brown and Hoek, 1978) and the formula presented by Stephansson et al. (1986), as follows:

$\{\begin{array}{l}{\sigma }_v=\gamma H\\ {\sigma }_{h\max }=6.7+0.0444H\\ {\sigma }_{h\min }=0.8+0.0329H\end{array}(1)$

where $\gamma$ is the average bulk density of the rock mass, H is the buried depth of the blasthole.

FIGURE 1

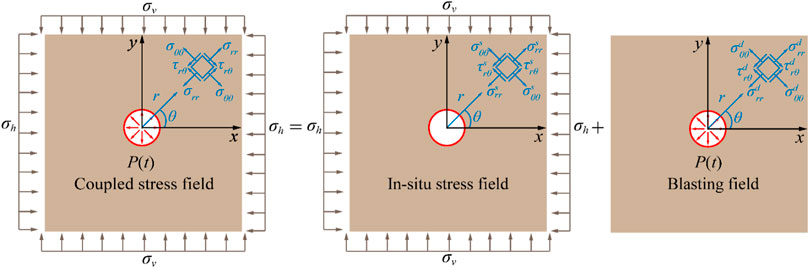
FIGURE 1. Coupling of blasting stress field in deep rock mass (Li X. et al., 2021).

Explosion dynamic load P(t) will be applied on the blasthole wall and then spread to the rock mass. The stress distribution of deep rock mass when blasting can be considered as the result of the combination of static stress distribution caused by in-situ stress and dynamic response caused by explosion load.

2.1 Static stress distribution around a blasthole

The stress distribution around a blasthole under biaxial stresses can be solved according to the formula given by Kirsch (1898):

$\{\begin{array}{l}{\sigma }_{rr}^s=\frac{1}{2}\left({\sigma }_h+{\sigma }_v\right)\left(1-\frac{a^2}{r^2}\right)+\frac{1}{2}\left({\sigma }_h-{\sigma }_v\right)\left(1-\frac{a^2}{r^2}\right)\left(1-\frac{3a^2}{r^2}\right)\cos 2\theta \\ {\sigma }_{\theta \theta }^s=\frac{1}{2}\left({\sigma }_h+{\sigma }_v\right)\left(1+\frac{a^2}{r^2}\right)-\frac{1}{2}\left({\sigma }_h-{\sigma }_v\right)\left(1+\frac{3a^2}{r^2}\right)\cos 2\theta \\ {\tau }_{r\theta }^s=\frac{1}{2}\left({\sigma }_v-{\sigma }_h\right)\left(1-\frac{a^2}{r^2}\right)\left(1+\frac{3a^2}{r^2}\right)\sin 2\theta \end{array}(2)$

where ${\sigma }_{rr}^s$, ${\sigma }_{\theta \theta }^s$ and ${\tau }_{r\theta }^s$ are the radial stress, hoop stress, and shear stress in the static state, respectively; r represents the distance from the blasthole (r≥a) and a is the radius of the blasthole.

2.2 Dynamic stress distribution when blasting

The shock wave is generated by the explosion of the cylindrical charge in the rock. In the process of continuous outward propagation, the shock wave will decay into the stress wave. The dynamic stress field generated by blasting load in elastic medium can be expressed as (Chen et al., 2009; Xue et al., 2022) :

$\{\begin{array}{l}{\sigma }_{rr}^d=P{\overline{r}}^{\left(\alpha \right)}\\ {\sigma }_{\theta \theta }^d=-\lambda {\sigma }_{rr}^d\end{array}(3)$

$\overline{r}=\frac{r}{a}(4)$

$\alpha =2\pm \frac{{\mu }_d}{1-{\mu }_d}(5)$

$\lambda =\frac{{\mu }_d}{1-{\mu }_d}(6)$

${\mu }_d=0.8\mu (7)$

where ${\sigma }_{rr}^d$ and ${\sigma }_{\theta \theta }^d$ are the radial stress and hoop stress in the rock under dynamic stress field respectively; P is the initial impact pressure transmitted into the rock; $\overline{r}$ is the distance ratio; $\alpha$ is the attenuation coefficient of stress wave, where the positive and negative signs represent the shock wave region and the stress wave region; $\lambda$ is the lateral stress coefficient; ${\mu }_d$ is the dynamic Poisson’s ratio and $\mu$ is the static Poisson’s ratio.

Combining Eqs. 2, 3, the stress state of any point in the rock under the coupled stress field can be obtained, and the expression is as follows:

$\{\begin{array}{l}\begin{array}{l}{\sigma }_{rr}={\sigma }_{rr}^s+{\sigma }_{rr}^d\\ =\frac{1}{2}\left({\sigma }_h+{\sigma }_v\right)\left(1-\frac{a^2}{r^2}\right)+\frac{1}{2}\left({\sigma }_h-{\sigma }_v\right)\left(1-\frac{a^2}{r^2}\right)\left(1-\frac{3a^2}{r^2}\right)\cos 2\theta +P{\frac{r}{a}}^{\left(2\pm \frac{0.8\mu }{1-0.8\mu }\right)}\end{array}\\ \begin{array}{l}{\sigma }_{\theta \theta }={\sigma }_{\theta \theta }^s+{\sigma }_{\theta \theta }^d\\ =\frac{1}{2}\left({\sigma }_h+{\sigma }_v\right)\left(1+\frac{a^2}{r^2}\right)-\frac{1}{2}\left({\sigma }_h-{\sigma }_v\right)\left(1+\frac{3a^2}{r^2}\right)\cos 2\theta -\frac{0.8\mu }{1-0.8\mu }P{\frac{r}{a}}^{\left(2\pm \frac{0.8\mu }{1-0.8\mu }\right)}\end{array}\end{array}(8)$

3 Basic principles of the PFC method

3.1 Simulation of rock materials in PFC^2D

In the field of geotechnical engineering, Particle Flow Code (PFC^2D) is a kind of discrete element analysis software used to simulate granular materials or can be simplified into granular materials. Among the many constitutive models provided by PFC^2D, the Parallel Bond Model (PBM) can transfer normal force, shear force and moment, so it can better simulate the mechanical behavior of rock and soil. The numerical model of rock and soil mass is mainly composed of particles and connects which between particles. The maximum tension stress and maximum shear stress of connect in the PBM can be described as follows:

$\{\begin{array}{l}{\sigma }_{t\max }=\frac{\overline{F_n}}{A}+\frac{\left|\overline{M}\right|}{I}\overline{R}\\ {\tau }_{\max }=\frac{\overline{F_S}}{A}\end{array}(9)$

Where ${\sigma }_{t\max }$ and ${\tau }_{\max }$ represent the maximum normal stress and the maximum shear stress, respectively; $\overline{F_n}$ and $\overline{F_S}$ represent the normal and tangential component of the parallel-bonded force, respectively; A and I are the area and inertial moment of the bond cross section, respectively; $\overline{R}$ is the bond radius. If the tension stress exceeds ${\sigma }_{t\max }$, tension failure occurs. If the shear stress exceeds ${\tau }_{\max }$, shear failure occurs. When the connect breaks, the Parallel Bond Model degenerates into the Linear Model.

3.2 Blasting load application based on the particle expansion algorithm

In this paper, the blasting load is applied by the particle expansion algorithm (Chong et al., 2018). The stress wave generated by the cylindrical charge propagates to surrounding rock mass, which can be generally equivalent to pulse stress wave. It is simplified as a half sine wave with the same time in the rising section and the falling section, and its expression is:

$P\left(t\right)=\frac{P_m}{2}\left[1-\cos \left(\frac{2\pi }{\Delta T}t\right)\right](10)$

where $P\left(t\right)$ is the detonation pressure; $P_m$ is the peak pressure in the hole which is 4 GPa; △T is the half sinusoidal action time, generally 10 ms, and t is the duration time which is 20 ms.

Under the condition of coupled charge, the borehole pressure P is:

$P=P_c\frac{2}{1+{\rho }_{0}D/{\rho }_r{c}_p}(11)$

Detonation wavefront pressure is $P_c$:

$P_c=\frac{{\rho }_0{D}^2}{4}(12)$

where ${\rho }_0$ is the density of the explosive; ${\rho }_r$ is the density of the rock; $c_p$ is the wave velocity of longitudinal wave propagation in the rock mass; $D=4\sqrt{Q_v}$, $Q_v$ is the explosive heat of the explosive and D is the explosive velocity.

Under the condition of uncoupled charge, the borehole pressure P will decay rapidly which is:

$P=\frac{1}{8}{\rho }_0{D}^2{\left(\frac{V_c}{V_b}\right)}^{3}n(13)$

where $V_{\mathrm{c}}$ and $V_{\mathrm{b}}$ are the volume of explosive and the volume of blasthole respectively; n is the increase factor, n = 8∼11.

As shown in Figure 2, by using particle expansion algorithm, the expanded particle will overlap with the rock particles on the hole wall. According to the particle contact principle of PFC^2D, assuming that the initial charge radius is r₀, when it expands to the blasting cavity radius, the borehole pressure is P, and the radial thrust force F is generated for the particles on the hole wall:

$F=K_{\mathrm{n}}d=2\pi r_{0}p(14)$

FIGURE 2

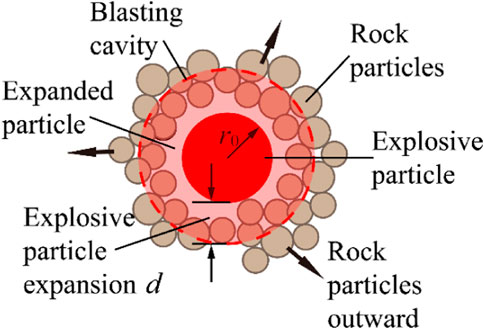
FIGURE 2. Schematic diagram of particle expansion algorithm (Zhang et al., 2020).

Then the explosion point particle expansion radius is:

$d=\frac{2\pi r_{0}p}{K_{\mathrm{n}}}(15)$

$K_{\mathrm{n}}=\frac{2\left(r_{\max }+r_{\min }\right)\pi p}{\left(r_{\max }-r_{\min }\right)}(16)$

where K_n is the contact stiffness of particles, r₀ is the initial radius of the blast point, d is the blast point radius after expansion, p is the stress acting on the rock wall, r_max and r_min are the maximum and minimum radii, respectively, of the particle expansion.

Therefore, the blasting stress wave can be applied to the rock mass as long as the expansion radius of the blasting point is changed according to Eqs. 10, 15.

3.3 Boundary conditions

This paper assumes that the rock model is an infinite medium model, so it is necessary to set a stress wave dispersion boundary to absorb the stress wave propagating to the boundary, so that the stress wave does not reflect. This paper considers the dispersion effect of viscous boundary proposed by Kouroussis et al. (2011) and the dispersion effect of stress wave propagation at the boundary of rock mass proposed by Shi (Chong et al., 2018).

The relationship between boundary force and particle moving speed is:

$F=-2\rho C\stackrel{·}{u}r(17)$

where r is the particle radius, ρ is the rock density, C is the wave velocity, $\stackrel{·}{u}$ is the particle velocity.

$F=\{\begin{array}{l}-\xi \cdot 2\rho C_{\mathrm{P}}{\stackrel{·}{u}}_{\mathrm{n}}r\\ -\eta \cdot 2\rho C_{\mathrm{s}}{\stackrel{·}{u}}_{\mathrm{s}}r\end{array}(18)$

where ζ and η are the dispersion effect correction coefficients of P-wave and S-wave respectively; C_P and C_S are P-wave velocity and S-wave velocity respectively; ${\stackrel{·}{u}}_{\mathrm{n}}$ and ${\stackrel{·}{u}}_{\mathrm{s}}$ are the normal and tangential velocities of particles respectively.

4 Construction and validation of the numerical model

4.1 Construction of the sandstone rock mass model

The single hole blasting numerical model established by PFC^2D is shown in Figure 3. The model size is 10 m × 10 m, and the red particle in the model geometric center is the explosion point, whose radius is 10 cm. The internal particles of the rock mass are generated by the particle expansion method, and the initial radius range of the particles is 5∼7.5 mm. The sandstone in the blasting numerical simulation experiment of Wei Yuan et al. is taken as the research object and the microscopic parameters are shown in Table 1 (Yuan et al., 2018). In this paper, the numerical simulation of single-hole blasting is carried out under the same in-situ stress (σ_h =σ_v = 5 MPa) as Wei Yuan et al. In addition, the servo mechanism proposed by Cundall and Strack (1979) is used to apply the in-situ stress.

FIGURE 3

FIGURE 3. Numerical model of single hole blasting.

TABLE 1

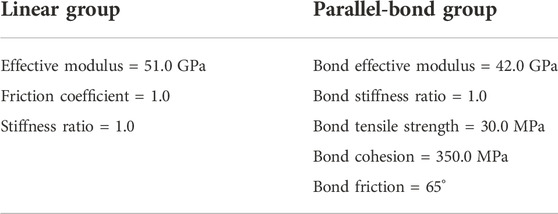
TABLE 1. Microscopic parameters of sandstone (Yuan et al., 2018).

4.2 Verification of the coupled stress field

During the verification of the coupled stress field (Eq. 8), both the horizontal stress σ_h and vertical stress σ_v are 5 MPa (without considering the influence of gravity field), the radius a of blasthole is 14.3 cm, and the Poisson’s ratio is 0.188. The values of main parameters of the explosive are shown in Table 2. In the process of blasting, the rock mass is considered to be homogeneous and isotropic. For the convenience of calculation, these measuring circles, which radii are 10 cm, shown in Figure 4 are set to monitor the peak stress at corresponding positions. The spacing between each two measuring circles is 0.5 m, and the distance between the measuring circle and blasthole is also 0.5 m.

TABLE 2

TABLE 2. Main technical indicators of explosive.

FIGURE 4

FIGURE 4. Verification of peak stress of coupled stress field. (A) Radial stress, (B) Hoop stress.

After configuring the above parameters, the peak radial stress and the peak hoop stress at measuring circle positions can be obtained. The rationality of the blasting method is verified by comparing the monitored simulated experimental values with the theoretical values.

5 Experimental cases setting

The structural plane has a serious impact on the propagation of the stress wave generated by blasting. When the stress wave propagates to the structural plane, reflection and transmission will occur. Due to the different distance between structural plane and blasthole, stress waves of different degrees are reflected and transmitted. In addition, the different initiation times of the two blasting charges will also make the stress waves propagating to the structural plane different. Therefore, in order to explore the influence of structural plane position and delayed initiation time on the blasting characteristics of rock mass, based on the verification experiment of sandstone single-hole blasting, the double-hole blasting experiments of soft-hard composite rock are carried out in this paper. The two blastholes are respectively applied with blasting load, and the load change curve of the delayed initiation blasthole is shown in Eq. 19, wherein Δt is the time difference between two blastholes. When two blastholes are detonated at different times, the left blasthole is detonated first, and the right blasthole is detonated later. The confining pressure of the sample is the same as that of the verification experiment, which is 5 MPa. In order to reduce the influence of the boundary, the numerical model size of 10 m × 10 m is changed to 15 m × 10 m. Soft rock is introduced into hard rock samples (Figure 5), to study the influence of structural plane position and delayed initiation time on blasting characteristics. Liangfu et al. (2020) used Particle Flow Code (PFC^2D) to carry out uniaxial compression test and biaxial compression test, and accurately calibrated the microscopic parameters of dolomite limestone (Table 3). Therefore, this group of parameters is taken as the parameters of soft rock in this paper. The distribution thickness of soft rock and the working cases of delayed initiation time are shown in Table 4.

$P\left(t\right)=\frac{P_m}{2}\left[1-\cos \left(\frac{2\pi }{\Delta T}\left(t-∆t\right)\right)\right](19)$

FIGURE 5

FIGURE 5. Schematic diagram of double-hole blasting model.

TABLE 3

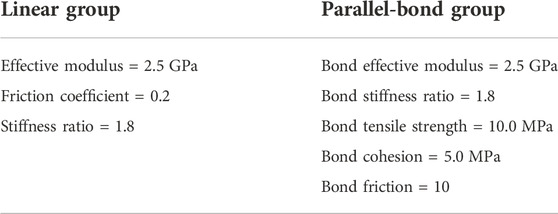
TABLE 3. Microscopic parameters of limestone (Liangfu et al., 2020).

TABLE 4

TABLE 4. Working cases of double-hole blasting.

6 Analysis of blasting results

6.1 Fragment gradation analysis

The degree of rock fragmentation during blasting has a serious impact on the productivity of civil engineering, especially mining engineering. The generation of fragments with ideal particle size distribution by blasting is crucial to improve the efficiency of all downstream processes. In order to deeply analyze the degree of rock fragmentation after blasting, this paper explores the fragment gradation produced by blasting under various working cases. The analysis results are shown in Figures 6, 7. From the analysis results, it can be seen that both soft rock thickness H_S and delayed initiation time Δt have great influence on the fragment gradation.

FIGURE 6

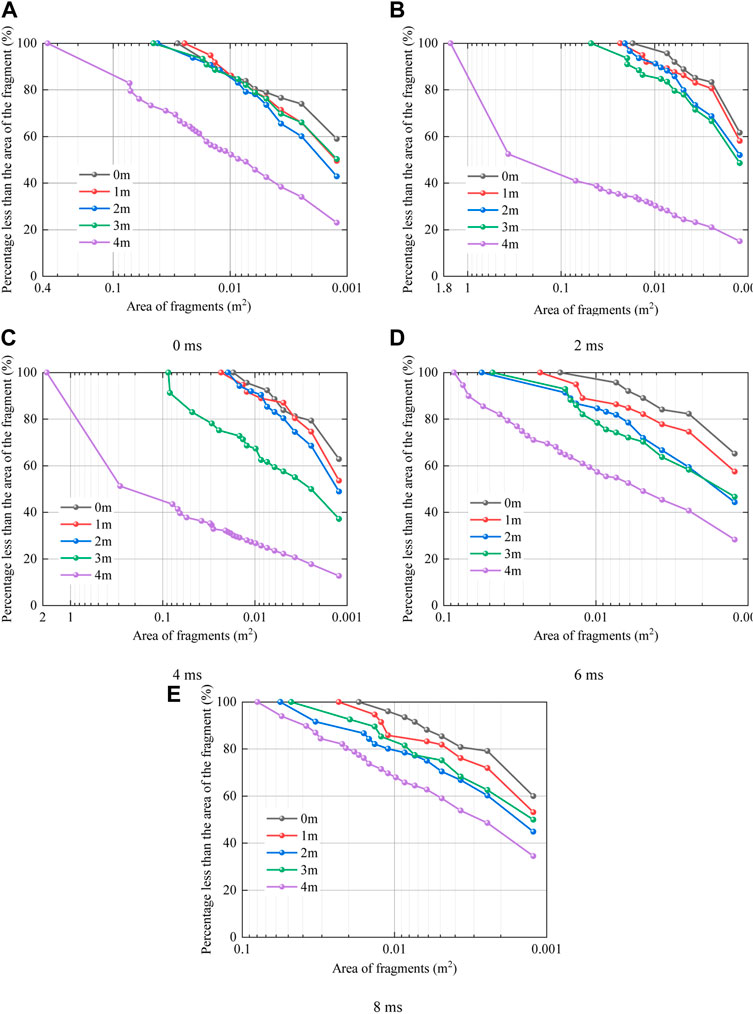
FIGURE 6. Fragment gradation curves under hard rock initiation, (A) 0 ms, (B) 2 ms, (C) 4 ms, (D) 6 ms, (E) 8 ms.

FIGURE 7

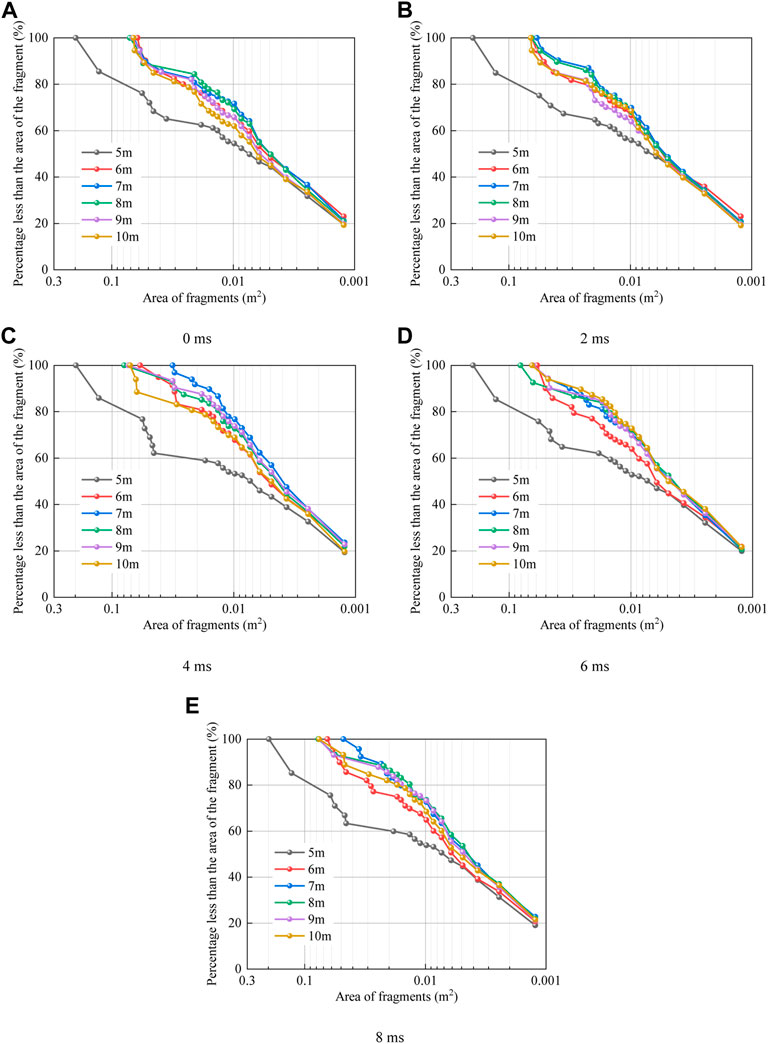
FIGURE 7. Fragment gradation curves under soft rock initiation, (A) 0 ms, (B) 2 ms, (C) 4 ms, (D) 6 ms, (E) 8 ms.

In PFC^2D, rock particles are considered to be discs per unit thickness (i.e., 1 m thick) and this paper assumes that all particles have the same density. In practice, the weight percentage is usually used to analyze the fragment gradation, so the fragment area is multiplied by the thickness and particle density to obtain the fragment weight. Since the thickness and density of all fragments are the same, in order to better reflect the expression characteristics of two-dimensional software and facilitate statistical calculation, this paper uses the area percentage, the results are the same as the weight percentage.

6.1.1 Detonation in hard rock

When simultaneous detonation of two blastholes (Δt=0 ms) and H_S <4 m, the change trend of the gradation curve is relatively consistent. When H_S = 4 m, the overall gradation curve is significantly lower than that when H_S <4 m. The comparison of two results shows that when the distance between the structural plane and blasthole is about 2 times the radius of crushing area, it is easier to form large-area fragments, and when the distance continues to increase, the fragments tend to be crushed. For example, for fragments with an area of less than 0.012 m², such fragments account for about 20% when H_S >4 m, and more than 40% when H_S <4 m. For fragments with an area less than 0.01 m², in the case of H_S >4 m and H_S <4 m, these fragments account for about 55% and 85% respectively. This rule can still be reflected in other delay time cases of initiation in hard rock.

With the increase of the delayed initiation time (Δt), the blasting results are also significantly different from those in the case of simultaneous initiation, mainly manifested in H_S = 3 m and 4 m. However, when H_S <3 m, the gradation curve is basically the same as that of simultaneous initiation under the same conditions, and there is no obvious change. Therefore, the change of the gradation curve with Δt, under the cases of H_S = 3 m and 4 m, is mainly discussed. With the increase of Δt, two gradation curves when H_S = 3 m and 4 m show a trend of decreasing first and then increasing. When H_S = 4 m, compared with simultaneous initiation, the gradation curve with a delay time of 2 ms shows an obvious downward trend, which indicates that the proportion of smaller fragments is significantly reduced, while the proportion of larger fragments is increasing. This rule is the same as that when the delay time is 4 ms, and large area fragments account for more, which indicates that when the delay time is in 0–4 ms, increasing the delay time is more likely to form larger area fragments. Such as fragments with an area of less than 0.01 m², when Δt = 0, 2 and 4 ms, the proportions are about 50%, 30%, and 25% respectively. In addition, it is also found that when the delay time was 0–4 ms, with the increase of the delay time, not only the proportion of larger fragments increased, but also the area value of the largest fragment increased. For example, when Δt = 0, 2 and 4 ms, the area values of the largest fragments are 0.36 m², 1.52 m² and 1.81 m², respectively. When Δt>4 ms and H_S = 4 m, the gradation curve shows a rising trend, indicating that compared with Δt = 4 ms and H_S = 4 m, the fragment area decreases as a whole. Such as fragments with an area of less than 0.017 m², when Δt = 4, 6, and 8 ms, the proportions are about 30%, 66%, and 77% respectively. In case of delayed initiation, the rule of H_S = 3 m is basically the same as that of H_S = 4 m, so it will not be repeated.

Combined with the results of the above discussion, it can be seen that when the distance between blasthole and structural plane is about 2 times the radius of crushing area, the area of the fragments are relatively large, and when the distance keeps increasing, the fragments tend to be crushed more. The delayed initiation time has a significant effect on the fragment gradation under conditions of H_S = 3 and 4 m. With the increase of the delay time, the fragment area generally increases first and then decreases. The fragment area reaches the maximum when the delay time is 4 ms.

6.1.2 Detonation in soft rock

As shown in Figure 7, when the blasthole is detonated in the structural plane and soft rock, the delay time has a small impact on the gradation of rock fragments, while the distance between the structural plane and the blasthole has an impact on the gradation of fragments. The fragment gradation curve when blasting in structural plane (H_S = 5 m) is obviously lower than that when blasting in soft rock. It shows that when detonating in structural plane, it is easier to form large-area fragments than in soft rock, and this rule is basically the same at various delay times.

6.2 Microscopic contact between particles

In PFC^2D, the relative size and direction of the contact force between particles can be observed. The contact force under pure hard rock (in-situ is also 5 MPa) is shown in Figure 8. Before blasting, the contact force between particles is uniform, but after blasting, due to the propagation of blasting stress wave, the contact force has a certain direction. The darker the color of the contact force, the larger the value of the contact force, and the lighter the color, the smaller the value of the contact force. The color of the contact force around the blasthole is the darkest, which indicates that the contact force around the blasthole is the largest. According to the statistics of the magnitude and direction of the contact force, it can be seen that the thickness of soft rock and the delayed initiation time affect the overall internal stress of rock mass after blasting. The angle of the contact force under each working case and the contact force value within the angle range are counted, and the results are shown in Figures 9, 10.

FIGURE 8

FIGURE 8. Schematic diagram of particle contact force before and after blasting.

FIGURE 9

FIGURE 9. Contact force information after blasting in hard rock.

FIGURE 10

FIGURE 10. Contact force information after blasting in soft rock.

6.2.1 Detonation in hard rock

When H_S = 0 m, that is, detonated in pure hard rock, it can be seen that the contact force curve after detonation is elliptical, and its long axis direction is more obvious than the short axis direction. The long axis direction (referred to as the main direction of contact force in this paper) is 120–300°, indicating that after the blasting is completed, the rock mass has a relatively large contact force in these two directions. The short axis direction is 30–210°, which indicates that the rock mass produces relatively small contact force in these two directions. The difference of contact force between the two directions can reach 1000 MN. Since the two holes are horizontally distributed, the main direction of the contact force is closer to the direction of the vertical hole connection (i.e., 90°). In addition, in the state of pure hard rock, the detonation time difference of two holes has little effect on the contact force curve.

When H_S = 1 m, due to the reflection of stress wave (the stress wave reflected by the structural plane is less in this case), the whole contact force curve begins to change from ellipse to circle, and the contact force curve follows this rule under different delay time. It shows that when the structural plane is far away from the blasthole, the reflected weak stress wave can make the overall stress more uniform. With the continuous increase of H_S, the structural plane continues to approach the blasthole, and the reflected stress wave continues to increase. Coupled with the delayed detonation time and the interaction between the blastholes, the contact force begins to change more complicated. When H_S = 2 m and 3 m, the overall trend of the two cases is consistent. At this time, the stress wave reflected by the structural plane in the rock mass is relatively more, resulting in some curves beginning to change from circular to elliptical, while the rest are still circular. For example, when H_S = 2 m and the delay time is 8 ms, the curve is obviously elliptical, and its long axis direction is 30–210° with the short axis direction is 120–300°. At other delay times, the contact force curve is close to a circle. The general rule when H_S = 3 m is almost the same as that when H_S = 2 m, the difference is that the delay time corresponding to the contact force curve close to the circle. When H_S = 4 m, the structural plane is very close to the blasthole, and the overall rule of contact force curve is quite different from H_S=1 m, 2 m, and 3 m. When the delay time is 4 ms and 6 ms, the contact force curve is oval, the long axis direction is 30–210°. In the cases of other delay time, the contact force curves are still oval, but the long axis directions are 120–300°.

Due to the existence of structural plane, the overall stress situation will change after blasting. Considering the structural plane and delayed initiation at the same time, the internal stress of rock mass will change from uneven to relatively uniform within a certain range. The main direction of the contact force will appear in the uneven state, and the main direction is close to the direction perpendicular to or parallel to the hole connection (about 120–300° or 30–210°). Because of the relative position between structural plane and blasthole, the delay time of initiation, the sequence of initiation and the interaction between two blastholes, the blasting process becomes extremely complex, so that the range of uniform contact force is difficult to determine.

6.2.2 Detonation in soft rock

When detonated in structural plane and soft rock, the contact force inside the rock mass is obviously smaller than that detonated in hard rock. When detonated in structural plane, the main direction of the contact force is about 120–300° except that the main direction of the contact force with a delay time of 4 ms is about 0–180°, and the main direction of the contact force under different delay times fluctuates slightly in 120–300°, and changes little in other directions. When detonated in soft rock and structural plane, the delay time and the position of structural plane have little effect on the direction of the contact force, and the main direction of the contact force is about 120–300°. When detonated in pure soft rock, the contact force distribution is more uniform, the main direction of contact force is not obvious.

6.3 Internal energy fields of rock mass

In order to explore the influence of delayed initiation time (Δt) and soft rock thickness (H_S) on the internal energy field of rock mass, this paper analyzes the blasting results from the perspectives of kinetic energy, friction energy and strain energy. Three energy calculation methods Eqs. 4, 5, 6 are given in the Particle Flow Code (PFC^2D). Through the energy record inside the software, the energy evolution curve (Figure 11) of rock mass under different thickness H_S and different delayed initiation time can be obtained.

FIGURE 11

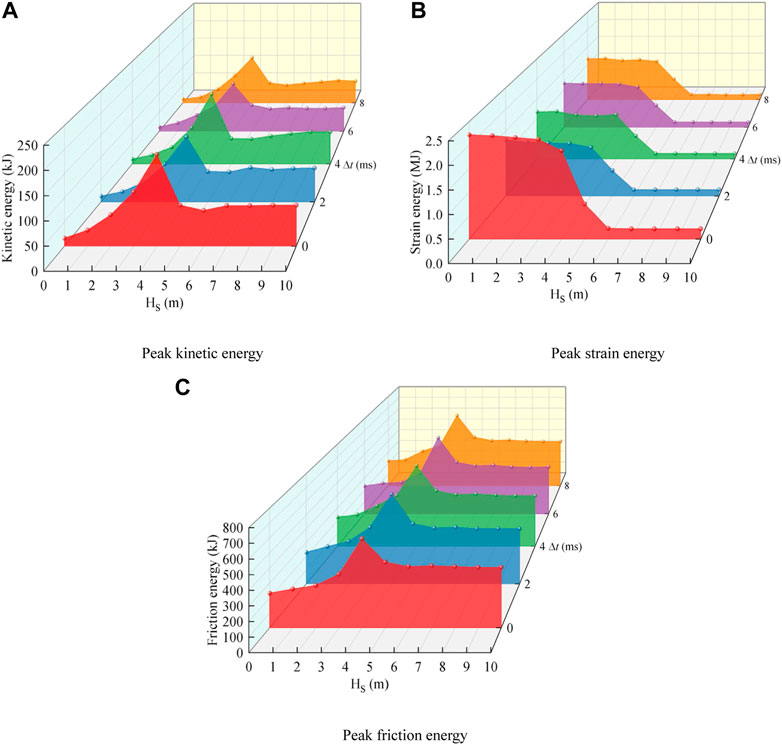
FIGURE 11. Peak energy variation curves, (A) Peak kinetic energy, (B) Peak strain energy, (C) Peak friction energy.

Kinetic energy calculation method (E_K):

$E_K={\displaystyle \sum }_{i=1}^n\frac{1}{2}{\mathrm{m}}_i{v}_i^2(20)$

where m_i is the mass of the particle, v_i is the velocity of the particle and n is the total number of particles.

Friction energy (E_F) calculation method:

$E_F=-{\mathrm{F}}^{\mathrm{d}}·\left(\begin{array}{l}·\\ \delta \end{array}t\right)(21)$

where F^d is the dashpot force, $\begin{array}{l}·\\ \delta \end{array}$ is the relative translation velocity and t is the during time.

Strain energy (E_S) calculation method:

$E_S=\frac{1}{2}\left(\frac{F_n^2}{k_{n}A}+\frac{\parallel {\mathrm{F}}_{\mathrm{s}}{\parallel }^2}{k_{s}A}+\frac{M_t^2}{k_{s}J}+\frac{\parallel {\mathrm{M}}_{\mathrm{b}}{\parallel }^2}{k_{n}I}\right)(22)$

where k_n is the normal stiffness, k_s is the shear stiffness, A is the cross-sectional area, I is the moment of inertia of the parallel bond cross-section, J is the polar moment of inertia of the parallel bond cross-section, F_n is the parallel-bonded normal force, F_s is the parallel-bonded shear force, M_t is the parallel-bonded twisting moment (2D model: M_t = 0) and M_b is the parallel-bonded bending moment.

6.3.1 Evolution process of kinetic energy

As shown in Figure 11A, the peak kinetic energy of rock mass changes with delay time (Δt) and soft rock thickness (H_S). When Δt is constant and H_S ≤4 m, the peak kinetic energy increases monotonously with the increase of H_S, and reaches the maximum at H_S = 4 m. With the increase of H_S, the stress wave reflected by the structural plane also increases, resulting in more and more energy converging in the hard rock between the structural plane and the borehole. It can be seen from Eq. 10 that the kinetic energy is mainly related to the mass and vibration velocity of the particles. In the process of rock mass failure, the mass of particles is constant. Therefore, it can be seen that when H_S is increasing, the vibration velocity of particles is increasing, and finally the peak kinetic energy of rock mass sample is increasing. When H_S = 4 m, the stress wave reflected by the structural plane is the most, and the converged energy is the highest, so the peak kinetic energy reaches the maximum. When 4 < H_S < 6 m, the peak kinetic energy decreases monotonously with the increase of H_S, indicating that when the distance between structural plane and borehole is too small, the vibration velocity of the particles decreases greatly, resulting in a sharp decline in kinetic energy. When H_S ≥6 m, with the increase of H_S, the peak kinetic energy tends to be stable and no longer changes. It shows that when detonated in soft rock, due to the low strength of soft rock, more and more cracks are generated, resulting in a large amount of energy consumption, so that the vibration speed of particles is relatively slow. This phenomenon is basically not affected by the change of structural plane position, so the kinetic energy is stable when H_S >6 m.

When H_S is constant, the peak kinetic energy of simultaneous initiation and delayed initiation are different. On the whole, when two holes are detonated simultaneously (Δt=0 ms), the peak kinetic energy curve is higher than that of delayed detonation (Δt=2, 4, 6, 8 ms). It shows that delayed initiation will reduce the kinetic energy of rock mass, and this rule is more obvious in the range of H_S <4 m. In this range, different delay time has little effect on the peak kinetic energy. When H_S is constant, the average peak kinetic energy at Δt = 2, 4, 6, 8 ms is E_ka, and it is compared with the peak kinetic energy E_k0 at Δt = 0 ms. By calculation, when the distance between structural plane and blasthole is greater than about 2 times the radius of the crushing area (H_S<4 m), E_k0 is about 33% higher than E_ka, that is, the peak kinetic energy of delayed initiation is about 33% lower than that of simultaneous initiation.

6.3.2 Evolution process of strain energy

As shown in Figure 11B, the peak strain energy of rock mass changes with time delay (Δt) and soft rock thickness (H_S). When Δt is constant and H_S < 4 m (initiation in hard rock), the peak strain energy decreases slowly with the increase of H_S. In this range, the peak strain energy curve of simultaneous initiation is obviously higher than that of delayed initiation, and the difference of delayed initiation time leads to the small change of peak strain energy. It shows that compared with simultaneous initiation, delayed initiation can significantly reduce strain energy, and the difference of delay time is little on this effect. When H_S is constant, the average peak strain energy E_sa at Δt = 2, 4, 6 and 8 ms is compared with the peak kinetic energy E_s0 at Δt=0 ms. By calculation, when the distance between structural plane and blasthole is greater than about 2 times the radius of the crushing area (H_S<4 m), E_sa is about 46% higher than E_s0, that is, the peak strain energy of delayed initiation is about 46% lower than that of simultaneous initiation. At 4 ≤H_S <6 m and different delay times, the peak strain energy decreases sharply with the increase of H_S. In this range, the curve gap between delayed detonation and simultaneous detonation is getting smaller and smaller. Until H_S = 6 m, the gap is the smallest.

6.3.3 Evolution process of friction energy

As shown in Figure 11C, the peak friction energy of rock mass changes with delay time (Δt) and thickness of soft rock (H_S). The overall change trend of peak friction energy is basically consistent with peak kinetic energy, that is, when H_S ≤4 m (initiation in hard rock), the peak friction energy increases monotonously with the increase of H_S, and reaches the maximum at H_S = 4 m. When 4 <H_S <6 m, the peak friction energy decreases monotonously with the increase of H_S. When H_S≥6 m, with the increase of H_S, the peak friction energy tends to be stable.

On the whole, the peak friction energy curves of delayed initiation and simultaneous initiation are basically coincident, indicating that delayed initiation has little effect on the peak friction energy of rock mass.

7 Discussion

According to this study, discussions are made on three aspects: explosion method, model validation and research prospect.

(1) It is well known that rock mass is destroyed under the dual action of explosion stress wave and high pressure gas. At present, there are two main methods to consider the effect of high pressure gas in the numerical simulation of discrete element method: direct application and indirect application. Direct application is to consider the effect of stress wave and high pressure gas respectively, in which the stress wave is realized by applying particle velocity (Yuan et al., 2018). In fact, it is difficult to simulate gas pressure when using discrete element method to simulate blasting. And the detonation gas can only flow through the cracks connected to the borehole, while ignoring the isolated cracks unrelated to the borehole (Yuan et al., 2019). Indirect application, namely single particle expansion loading algorithm, takes both stress wave and high pressure gas into consideration simultaneously. The load acting on the borehole wall by the indirect application method is more uniform and reliable. As long as the expansion rate of expansive particles and the peak pressure on the borehole wall are determined, the rock blasting process can be simulated ideally (Xue et al., 2022).

(2) In addition to the verification of the analytical stress field in this paper, the numerical blasting method is also compared the final state of the crack network with the results of other scholars and the specific process is explained in detail in the reference of Cui et al. (2022). Therefore, both methods prove the rationality of the blasting method used in this paper.

(3) The experiments in this paper are based on the initial stress field of 5 MPa. The change of initial stress field, the existence of joints and faults also have a serious impact on the blasting characteristics, which makes the blasting effect difficult to control accurately. Based on this research, these factors will be considered for further study.

8 Conclusion

Based on the Particle Flow Code (PFC^2D), the numerical simulation method of rock blasting is verified. Then, the double-hole soft-hard rock simultaneous initiation and delayed initiation blasting experiments are carried out. The influence of structural plane and delay time on the characteristics of double-hole blasting is analyzed from three aspects: fragment gradation, micro-contact between particles and energy field. The conclusions are as follows:

(1) When detonated in hard rock, it is easier to form large area of fragments. And when the distance between structural plane and blasthole is about 2 times the radius of the crushing area, the fragments tend to be crushed as the distance increases. When the distance is in the range of 2–4 times the radius of the crushing area, with the increase of delay time, the fragment area increases first and then decreases, and reaches the maximum at 4 ms. When detonated in the structural plane, it is easier to form large area fragments than in soft rock.

(2) When there is the structural plane inside the rock mass, delayed detonation can significantly make contact force become relatively uniform within a certain range. The main direction of contact force will appear in the uneven state of contact force, and its specific direction is close to the direction of parallel or vertical blastholes connection (about 120–300° or 30–210°).

(3) When the distance between structural plane and blasthole is greater than about 2 times the radius of the crushing area and detonated in hard rock, compared with simultaneous detonation, the peak kinetic energy and the peak strain energy of delayed detonation will be reduced by about 33% and 46% respectively. What’s more, the delay time has little effect on the peak friction energy.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JC verified the rationality of the numerical blasting method, and analyzed the blasting characteristics of soft-hard rock strata. XL guides the experimental method, LX guides the analysis of the experimental results, and writes the manuscript with JC. JQ guides the Figures and Tables in the manuscript and modifies the manuscript. All the authors completed the manuscript check work.

Funding

This research was supported by the National Natural Science Foundation of China (52068066 and 51908482) and Autonomous Region Graduate Scientific Research Innovation Project (XJ 2022G050).

Conflict of interest

Authors XL and LX were employed by the company Xinjiang Academy of Architectural Science (Limited Liability Company).

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bo, W. (2016). Study on disturbance zone evolution and anchoring mechanism of surrounding rock in layered rock tunnel. Ph.D, China University of Geosciences. Beijing, china.

Google Scholar

Brown, E. T., and Hoek, E. (1978). Trends in relationships between measured in-situ stresses and depth. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 15, 211–215. doi:10.1016/0148-9062(78)91227-5

CrossRef Full Text | Google Scholar

Chen, M., Lu, W-B., Zhou, C-B., and Luo, Y. (2009). Influence of initial in-situ stress on blasting-induced cracking zone in tunnel excavation. Yantu Lixue/Rock Soil Mech. 30, 2254–2258.

Google Scholar

Chen, S., Hu, S., and Chu, S. (2017). Study on the blasting vibration effect influenced by millisecond time and cylindrical charging characteristics. Yanshilixue Yu Gongcheng Xuebao/Chinese J. Rock Mech. Eng. 36, 3974–3983. doi:10.13722/j.cnki.jrme.2017.1163

CrossRef Full Text | Google Scholar

Chen, Y., Chang, Z., Mao, J., and Wang, W. (2015). Blasting effect analysis of hole-by-hole millisecond minute difference initiation network along V-shaped oblique line. Electron. J. Geotechnical Eng. 20, 5833–5838.

Google Scholar

Chong, S., Qiang, Z., and Sheng-nian, W. (2018). Numerical simulation technology and application with particle flow code(PFC5.0). Rock Soil Mech. 39, 36.

Google Scholar

Cui, J., Xie, L., Qiao, W., Qiu, L., Hu, Z., and Wu, L. (2022). Study on blasting characteristics of rock mass with weak interlayer based on energy field. Sci. Rep. 12, 12698. doi:10.1038/s41598-022-17028-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Cundall, P. A., and Strack, O. D. L. (1979). A discrete numerical model for granular assemblies. Géotechnique 29, 47–65. doi:10.1680/geot.1979.29.1.47

CrossRef Full Text | Google Scholar

Dong, M., Wang, L., Shahbodagh, B., Du, X., Deng, S., and Sun, Z. (2020). Effect of the soft and hard interbedded layers of bedrock on the mechanical characteristics of stabilizing piles. Appl. Sci. 10, 4760. doi:10.3390/app10144760

CrossRef Full Text | Google Scholar

Dong, Q., Li, X., Jia, Y., and Sun, J. (2021). A numerical simulation of blasting stress wave propagation in a jointed rock mass under initial stresses. Appl. Sci. 11, 7873. doi:10.3390/app11177873

CrossRef Full Text | Google Scholar

Duan, S-Q., Feng, X-T., Jiang, Q., Liu, G-F., Pei, S-F., and Fan, Y-L. (2017). In situ observation of failure mechanisms controlled by rock masses with weak interlayer zones in large underground cavern excavations under high geostress. Rock Mech. Rock Eng. 50, 2465–2493. doi:10.1007/s00603-017-1249-4

CrossRef Full Text | Google Scholar

Feng, W., Huang, R., and Li, T. (2012). Deformation analysis of a soft–hard rock contact zone surrounding a tunnel. Tunn. Undergr. Space Technol. 32, 190–197. doi:10.1016/j.tust.2012.06.011

CrossRef Full Text | Google Scholar

Feng, X., Zhang, Q., Wang, E., Ali, M., Dong, Z., and Zhang, G. (2020). 3D modeling of the influence of a splay fault on controlling the propagation of nonlinear stress waves induced by blast loading. Soil Dyn. Earthq. Eng. 138, 106335. doi:10.1016/j.soildyn.2020.106335

CrossRef Full Text | Google Scholar

Guo, D-Y., Zhao, J-C., Zhu, T-G., and Zhang, C. (2020). Crack propagation and coalescence mechanism of double-hole cumulative blasting in coal seam. Gongcheng Kexue Xuebao/Chinese J. Eng. 42, 1613–1623. doi:10.13374/j.issn2095-9389.2020.05.19.001

CrossRef Full Text | Google Scholar

Kirsch, C. (1898). Die Theorie der Elastizitat und die Bedurfnisse der Festigkeitslehre. Z. Des. Vereines Dtsch. Ingenieure 42. 240–300,

Google Scholar

Kouroussis, G., Verlinden, O., and Conti, C. (2011). Finite-dynamic model for infinite media: Corrected solution of viscous boundary efficiency. J. Eng. Mech. 137, 509–511. doi:10.1061/(asce)em.1943-7889.0000250

CrossRef Full Text | Google Scholar

Li, C., Kang, Y., Zhang, Y., and Luo, H. (2021). Effect of double holes on crack propagation in PMMA plates under blasting load by caustics method. Theor. Appl. Fract. Mech. 116, 103103. doi:10.1016/j.tafmec.2021.103103

CrossRef Full Text | Google Scholar

Li, X., Zhu, Z., Wang, M., Wan, D., Zhou, L., and Liu, R. (2021). Numerical study on the behavior of blasting in deep rock masses. Tunn. Undergr. Space Technol. 113, 103968. doi:10.1016/j.tust.2021.103968

CrossRef Full Text | Google Scholar

Liangfu, X., Qingyang, Z., Yongjun, Q., Jianhu, W., and Jiangu, Q. (2020). Study on evolutionary characteristics of toppling deformation of anti-dip bank slope based on energy field. Sustainability 12, 7544. doi:10.3390/su12187544

CrossRef Full Text | Google Scholar

Lisjak, A., Grasselli, G., and Vietor, T. (2014). Continuum–discontinuum analysis of failure mechanisms around unsupported circular excavations in anisotropic clay shales. Int. J. Rock Mech. Min. Sci. 65, 96–115. doi:10.1016/j.ijrmms.2013.10.006

CrossRef Full Text | Google Scholar

Pu, C., Yang, X., Zhao, H., Chen, Z., and Xiao, D. (2021). Numerical investigation on crack propagation and coalescence induced by dual-borehole blasting. Int. J. Impact Eng. 157, 103983. doi:10.1016/j.ijimpeng.2021.103983

CrossRef Full Text | Google Scholar

Sadique, M. R., Zaid, M., and Alam, M. M. (2022). Rock tunnel performance under blast loading through finite element analysis. Geotech. Geol. Eng. (Dordr). 40, 35–56. doi:10.1007/s10706-021-01879-9

CrossRef Full Text | Google Scholar

Stephansson, O., Särkkä, P., and Myrvang, A. (1986). State of stress in fennoscandia. Stockholm, Sweden: ISRM International Symposium. 1986-1002.

Google Scholar

Tao, J., Shi, A-C., Li, H-T., Zhou, J-W., Yang, X-G., and Lu, G-D. (2021). Thermal-mechanical modelling of rock response and damage evolution during excavation in prestressed geothermal deposits. Int. J. Rock Mech. Min. Sci. 147, 104913. doi:10.1016/j.ijrmms.2021.104913

CrossRef Full Text | Google Scholar

Tao, J., Yang, X-G., Li, H-T., Zhou, J-W., Fan, G., and Lu, G-D. (2020a). Effects of in-situ stresses on dynamic rock responses under blast loading. Mech. Mater. 145, 103374. doi:10.1016/j.mechmat.2020.103374

CrossRef Full Text | Google Scholar

Tao, J., Yang, X-G., Li, H-T., Zhou, J-W., Qi, S-C., and Lu, G-D. (2020b). Numerical investigation of blast-induced rock fragmentation. Comput. Geotechnics 128, 103846. doi:10.1016/j.compgeo.2020.103846

CrossRef Full Text | Google Scholar

Wu, B., Xu, S., Meng, G., Cui, Y., Cai, J., and Zhang, Y. (2021). Study on the dynamic evolution of through-crack in the double hole of elliptical bipolar linear-shaped charge blasting. Shock Vib. 2021, 1–7. doi:10.1155/2021/3792765

CrossRef Full Text | Google Scholar

Xu, H., Yang, X-G., Zhang, J-H., Zhou, J-W., Tao, J., and Lu, G-D. (2020). A closed-form solution to spherical wave propagation in triaxial stress fields. Int. J. Rock Mech. Min. Sci. 128, 104266. doi:10.1016/j.ijrmms.2020.104266

CrossRef Full Text | Google Scholar

Xue, Y., Jiang, X., Kong, F., Li, Z., Gong, H., Yang, F., et al. (2022). Rupture of rock with discontinuities under blasting disturbance: Insights from discrete element method modeling. Simul. Model. Pract. Theory 116, 102486. doi:10.1016/j.simpat.2022.102486

CrossRef Full Text | Google Scholar

Yang, J., Dai, J., Yao, C., Hu, Y., Zhang, X., and Zhou, C. (2022). Displacement mutation characteristics and energy mechanisms of anchored jointed rock slopes under blasting excavation disturbance. Baozha Yu Chongji/Explosion Shock Waves 42. 1021-1035. doi:10.11883/bzycj-2021-0126

CrossRef Full Text | Google Scholar

Yang, J., Sun, W., Yao, C., and Zhang, X. (2020). Mechanism of rock fragmentation by multi-hole blasting in highly-stressed rock masses. Baozha Yu Chongji/Explosion Shock Waves 40. 466–490. doi:10.11883/bzycj-2019-0427

CrossRef Full Text | Google Scholar

Yang, L., Ding, C., Yang, R., and Wang, Q. (2020). Experimental and theoretical analysis of stress superposition in double-hole blasts. J. Test. Eval. 48, 20180093. doi:10.1520/JTE20180093

CrossRef Full Text | Google Scholar

Yang, S-Q., Chen, M., Fang, G., Wang, Y-C., Meng, B., Li, Y-H., et al. (2018). Physical experiment and numerical modelling of tunnel excavation in slanted upper-soft and lower-hard strata. Tunn. Undergr. Space Technol. 82, 248–264. doi:10.1016/j.tust.2018.08.049

CrossRef Full Text | Google Scholar

Yuan, W., Su, X., Wang, W., Wen, L., and Chang, J. (2019). Numerical study of the contributions of shock wave and detonation gas to crack generation in deep rock without free surfaces. J. Petroleum Sci. Eng. 177, 699–710. doi:10.1016/j.petrol.2019.02.004

CrossRef Full Text | Google Scholar

Yuan, W., Wang, W., and Su, X., Li, J., Li, Z., Wen, L., et al. (2018). Numerical study of the impact mechanism of decoupling charge on blasting-enhanced permeability in low-permeability sandstones. Int. J. Rock Mech. Min. Sci. 106, 300–310. doi:10.1016/j.ijrmms.2018.04.029

CrossRef Full Text | Google Scholar

Zaid, M., and Rehan Sadique, M. (2021). A simple approximate simulation using coupled eulerian–Lagrangian (CEL) simulation in investigating effects of internal blast in rock tunnel. Indian Geotech. J. 51, 1038–1055. doi:10.1007/s40098-021-00511-0

CrossRef Full Text | Google Scholar

Zaid, M., Sadique, M. R., and Alam, M. M. (2021). Blast analysis of tunnels in Manhattan-Schist and Quartz-Schist using coupled-Eulerian–Lagrangian method. Innov. Infrastruct. Solut. 6, 69. doi:10.1007/s41062-020-00446-0

CrossRef Full Text | Google Scholar

Zaid, M., Sadique, M. R., and Alam, M. M. (2022). Blast resistant analysis of rock tunnel using abaqus: Effect of weathering. Geotech. Geol. Eng. (Dordr). 40, 809–832. doi:10.1007/s10706-021-01927-4

CrossRef Full Text | Google Scholar

Zaid, M., Sadique, M. R., and Samanta, M. (2020). Effect of unconfined compressive strength of rock on dynamic response of shallow unlined tunnel. SN Appl. Sci. 2, 2131. doi:10.1007/s42452-020-03876-8

CrossRef Full Text | Google Scholar

Zaid, M., and Shah, I. A. (2021). Numerical analysis of himalayan rock tunnels under static and blast loading. Geotech. Geol. Eng. (Dordr). 39, 5063–5083. doi:10.1007/s10706-021-01813-z

CrossRef Full Text | Google Scholar

Zhang, J., Liu, Z., Fu, S., and Qiao, G. (2022). Damage of Rock Mass by Double-Hole Blasting with Slit Charge and Development of Stress Wave under High in Situ Stress, Shock Vib. 2022(2):11. doi:10.1155/2022/6967057

CrossRef Full Text | Google Scholar

Zhang, Z., Gao, W., Li, K., and Li, B. (2020). Numerical simulation of rock mass blasting using particle flow code and particle expansion loading algorithm. Simul. Model. Pract. Theory 104, 102119. doi:10.1016/j.simpat.2020.102119

CrossRef Full Text | Google Scholar

Zhou, H., and He, C. (2020). Propagation law of stress wave and cracks in non-penetrating jointed rock mass: A numerical study based on particle flow code. Geotech. Geol. Eng. (Dordr). 38, 3967–3981. doi:10.1007/s10706-020-01271-z

CrossRef Full Text | Google Scholar

Zhou, W., Liang, R., Chen, J., Zhu, M., Chen, P., Lou, X., et al. (2019). Millisecond time for reducing vibration between two holes for slope blasting determined by stability coefficient of time history. Baozha Yu Chongji/Explosion Shock Waves 39. 130-137 doi:10.11883/bzycj-2018-0337

CrossRef Full Text | Google Scholar