A mechanistic model for minimizing pressure loss in the wellbore during drilling by considering the effects of cuttings

Because of the existence of cuttings in the flow, the pressure loss in the wellbore can increase significantly. Minimization of the flow pressure loss greatly benefits the drilling process. This work investigates the most important factors to the pressure loss in the wellbore during the hole cleaning process. It is found that, for the solid–liquid, two-phase flow, the fluid flow rate is not always proportional to annular pressure loss as the single-phase flow. The mechanisms behind this effect are studied, and a mechanistic model based on the solid–liquid, two-phase flow is proposed to simulate the hole cleaning process and predict the critical fluid flow rate, which gives the minimum pressure loss in the wellbore. The effect of the inclination angle, fluid rheological parameters, annulus geometry, and the rate of penetration on the critical value are investigated by using the proposed model. Results show that the critical flow rate value increases as the inclination angle increases under 60° and decreases once the inclination angle goes beyond 60°. The critical flow rate increases as the fluid viscosity and the wellbore geometry increase. This proposed model can be used to minimize the pressure loss in the wellbore in the given operational conditions and optimize the drilling parameters.

1 Introduction

For a successful extended reach well (ERW) drilling operation, accurate control of the equivalent circulation density (ECD) is essential. High ECD can lead to a series of drilling problems, such as lost circulation. ECD is the sum of equivalent static density (ESD) and additional pressure loss caused by the fluid flow. ECD controlling does not decrease the ESD but optimizes the flow rate to reduce the additional pressure loss. Considering the effect of the wellbore and drill string geometry, drilling fluid, rheology, flow rates, and drilling operations in calculating ECD are necessary. Several studies have been conducted to investigate the modeling of ECD. Luo and Peden (1987) predicted that annulus pressure loss would decrease with the increase in drill pipe rotation because of the fluid shear-thinning theory. Hemphill and Ravi (2007) focused on the effect of the drill string rotational speed on the predicted ECD. Hemphill and Ravi (2011) simplified their model in another study. The presence of the tool joint changes the annulus geometry between the drill pipe and casing/hole, resulting in strong turbulence and fluid acceleration that generate additional viscous dissipation and pressure losses. Jeong and Shah (2004) investigated the effect of the tool joint on annular pressure loss with a non-rotating drill pipe. Simoes et al. (2007) focused on the influence of tool joints on wellbore hydraulics, which was conducted considering different wellbore and tool-joint geometries, and presented results for a theoretical study conducted through computational fluid dynamics (CFD) techniques to evaluate the influence of the tool joints on the ECD for different wellbore geometries, drilling fluids, and flow rates. A high-temperature/high-pressure condition is very common in deep wells. Therefore, the effect of temperature and pressure on fluid rheology cannot be ignored. Rommetveit and Bjorkevoll (1997) presented the effects of pressure and temperature on fluid rheology for typical HPHT wells. Osisanya and Harris (2005) employed the Bingham plastic model to express the rheological behavior of the drilling fluids studied, with rheological parameters expressed as functions of temperature and pressure. Although many theoretical and experimental studies have been conducted on fluid flow through annuli to predict the ECD, most undermine or simply ignore the effect of cuttings.

Both field applications and laboratory studies show that cuttings in the wellbore can significantly affect the pressure gradient (Coley and Edwards, 2013; Zhang et al., 2014). The effects of cuttings on ECD are contributed by three aspects: the mud hydrostatics pressure, the solid phase in the mud, and the frictional pressure loss in the annulus (Yao et al., 2022). Zhang et al. (2015) were the first to investigate the relationship between the annulus pressure loss and hole cleaning in depth. Experimental results show that annulus pressure loss does not always rise with the increase in the flow rate in extended reach wells and horizontal wells. There is a critical value due to the existence of cuttings below which the annular pressure loss decreases with the increase in the flow rate. Once beyond the critical value, the annulus pressure loss begins to increase, as shown in Figure 1.

FIGURE 1

FIGURE 1. Effect of the flow rate on annulus pressure loss.

The existence of the critical value (inflection point) shown in Figure 1 is the combined effect of cuttings on the drilling fluid density, effective annulus flow area, and friction coefficient. First, the mixing of cuttings and drilling fluid changes the effective density of the flow in the wellbore. Second, in the inclined or horizontal section, cuttings settle at the lower part of the annulus, which reduces the effective annulus flow area and increases the drilling fluid velocity, thereby increasing the friction loss in the wellbore. Third, the cuttings bed increases surface roughness. At low flow rates, cuttings accumulate in the wellbore due to gravity. The formation of cutting beds reduces the annulus equivalent flow area and improves the drilling fluid density and friction coefficient, which results in high annulus pressure loss. However, with the increase in the flow rate, cuttings are suspended into the drilling fluid and circulated out of the well. Consequently, the annulus pressure loss decreases with the decrease in the height of the cuttings bed. Once the flow rate exceeds a certain value (the turning point in Figure 1), the increase in friction loss becomes more important, the influence of cuttings concentration and cuttings bed becomes minor, and annulus pressure loss increases as the flow rate increases.

This study proposes a method to determine the hole cleaning criteria and optimize drilling parameters by minimizing the ECD in deviated wells during drilling. The relationship between hole cleaning and annulus pressure loss is established based on cuttings transport mechanistic models. The effects of major factors such as the well inclination angle, annulus size, cuttings density, ROP, and rheological parameters of drilling fluid are investigated. Moreover, a workflow is presented to optimize the drilling parameters.

2 Optimization method for hole cleaning in extended reach wells

2.1 Couple hole cleaning and ECD prediction models

Depending on the inclination of the wellbore and the operational conditions, the cuttings may form different flow patterns in the wellbore (Zhang et al., 2015). Based on the flow patterns, a set of mechanistic models is developed to cover all the scenarios during the drilling process.

2.1.1 Flow pattern

The solid phase can distribute in various geometrical configurations for the flow of solid–liquid mixtures in the annulus with different inclination angles. The geometrical configurations, which are also called flow patterns, identified flow patterns to be dominated by two factors: solid settling and solid re-suspension. Four flow patterns were presented for the solid–liquid, two-phase flow in annulus geometry in drilling applications, covering the entire inclination range (from vertical to horizontal), as shown in Figure 2.

FIGURE 2

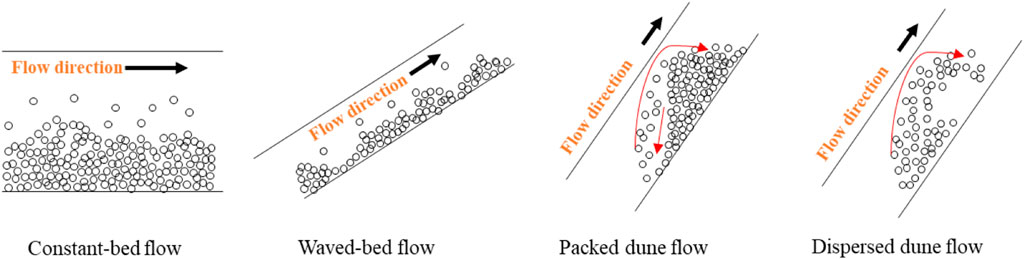
FIGURE 2. Cuttings flow patterns for the entire inclination range (Zhang et al., 2015).

A dimensionless flow pattern map is developed from the experimental results, as shown in Figure 3. The horizontal axis of the flow pattern map is the reciprocal of an extended Froude number (Fr). In this application, the Froude number is modified using Eq. 1. The vertical axis of the flow pattern map is a dimensionless number (DPG) related to the pressure loss of the mixture flow in the annulus, which is expressed by Eq. 2:

$\mathrm{F}\mathrm{r}=A\frac{v_{\mathrm{s}\mathrm{c}}}{\sqrt{\left(\frac{{\rho }_{\mathrm{s}}}{{\rho }_{\mathrm{L}}}-1\right)Dg\left|f\cdot \sin \theta -\cos \theta \right|}},(1)$

$DPG=\frac{\Delta P}{{\rho }_{\mathrm{s}}\left(1-\frac{{\rho }_{\mathrm{f}}}{{\rho }_{\mathrm{s}}}\right)g\Delta L},(2)$

where $A$ represents the status index of the Fr number, dimensionless; $v_{\mathrm{s}\mathrm{c}}$ is the superficial liquid velocity, m/s; ${\rho }_{\mathrm{s}}$ is the solid density, kg/m³; ${\rho }_{\mathrm{L}}$ is the fluid density, kg/m³; D is the equivalent diameter of the geometry, m; g is the gravity acceleration, m/s²; f is the friction factor between solid particles, dimensionless; θ is the well’s inclined angle, degree; ΔP is the pressure loss in the well, MPa; and L is the wellbore length, m.

FIGURE 3

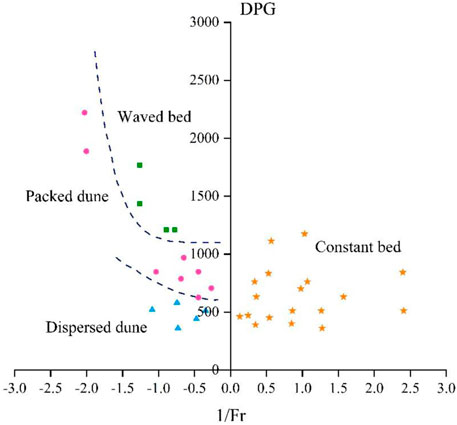
FIGURE 3. Flow pattern map (Zhang et al., 2015).

2.1.2 Mechanistic models

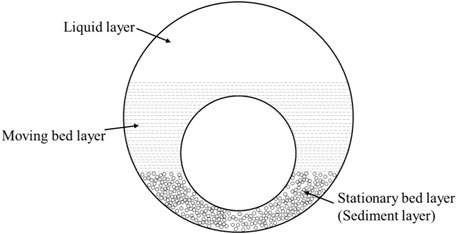
2.1.2.1 Three-layer model

The constant-bed flow commonly occurs in horizontal or highly inclined wells, and a three-layer model is applied to describe this pattern. In the model, the cross section of the annulus can be divided into three parts based on the distribution of cuttings, as shown in Figure 4.

FIGURE 4

FIGURE 4. Three-layer model geometry.

The assumptions of the model are listed as follows:

1) There are no cuttings in the upper liquid layer.

2) The moving bed layer is a mixture of cuttings and fluid, and there is no slip between the fluid and the particles.

3) The fluid velocity in the moving bed layer is constant.

4) In a control volume, the height of the stationary bed layer is constant in the direction of the borehole axis, and the porosity of the cuttings bed is constant.

5) The cuttings diameter is uniform, and all the cuttings are assumed to be spherical.

The conservation of mass of the solid phase is as follows:

${\rho }_{\mathrm{s}}{A}_{\mathrm{s}\mathrm{b}}{C}_{\mathrm{s}\mathrm{b}}{U}_{\mathrm{s}\mathrm{b}}+{\rho }_{\mathrm{s}}{A}_{\mathrm{m}\mathrm{b}}{C}_{\mathrm{m}\mathrm{b}}{U}_{\mathrm{m}\mathrm{b}}=\lambda {\rho }_{\mathrm{s}}{A}_{\mathrm{w}}{U}_{\mathrm{t}},(3)$

where $A_{\mathrm{s}\mathrm{b}}$ represents the cross-sectional area of the stationary bed layer, m²; $C_{\mathrm{s}\mathrm{b}}$ is the solids’ concentration of the stationary bed layer, dimensionless; $U_{\mathrm{s}\mathrm{b}}$ is the velocity of the stationary bed, which is 0, m/s; $A_{\mathrm{m}\mathrm{b}}$ is the cross-sectional area of the moving bed layer, m²; $C_{\mathrm{m}\mathrm{b}}$ is the solids’ concentration of the moving bed layer, dimensionless; $U_{\mathrm{m}\mathrm{b}}$ is the velocity of the moving bed, m/s; $\lambda$ is the correction factor for the feed cutting concentration, which is defined by Ozbayoglu (2002) as λ = (A_w-A^*_bed (1-φ_bed))/A_w, dimensionless; A^*_bed is the cross-sectional area of cuttings bed near bit in an open hole section, m²; φ_bed is the porosity of the cuttings bed, dimensionless; $A_{\mathrm{w}}$ is the cross-sectional area of the wellbore, m²; and $U_{\mathrm{t}}$ is the drilling speed, which is ROP, m/s.

The conservation of mass of the liquid phase is as follows:

${\rho }_{\mathrm{L}}{A}_{\mathrm{s}\mathrm{d}}{U}_{\mathrm{s}\mathrm{d}}+{\rho }_{\mathrm{L}}{A}_{\mathrm{m}\mathrm{b}}\left(1-C_{\mathrm{m}\mathrm{b}}\right)U_{\mathrm{m}\mathrm{b}}+{\rho }_{\mathrm{L}}{A}_{\mathrm{s}\mathrm{b}}\left(1-C_{\mathrm{s}\mathrm{b}}\right)U_{\mathrm{s}\mathrm{b}}={\rho }_{\mathrm{L}}Q,(4)$

where $A_{\mathrm{s}\mathrm{d}}$ represents the cross-sectional area of the dispersed liquid layer, m²; $U_{\mathrm{s}\mathrm{d}}$ is the velocity of the dispersed layer, m/s; and $Q$ is the drilling fluid flow rate, m³/s.

For the upper dispersed layer, the momentum equation is as follows:

$A_{\mathrm{s}\mathrm{d}}\left(\frac{\Delta P}{L}\right)=-{\tau }_{\mathrm{s}\mathrm{d}}{S}_{\mathrm{s}\mathrm{d}}-{\tau }_{\mathrm{s}\mathrm{d}\mathrm{m}\mathrm{b}}{S}_{\mathrm{s}\mathrm{d}\mathrm{m}\mathrm{b}}-{\rho }_{\mathrm{s}\mathrm{d}}g{A}_{\mathrm{s}\mathrm{d}}\cos \theta ,(5)$

where ${\tau }_{\mathrm{s}\mathrm{d}}$ represents the shear stress between the dispersed layer and the wellbore wall, Pa; $S_{\mathrm{s}\mathrm{d}}$ is the dispersed liquid layer wet parameter, m; ${\tau }_{\mathrm{s}\mathrm{d}\mathrm{m}\mathrm{b}}$ is the shear stress between the dispersed layer and moving bed layer, Pa; $S_{\mathrm{s}\mathrm{d}\mathrm{m}\mathrm{b}}$ is the wetted perimeter between the liquid layer and moving bed layer, m; and ${\rho }_{\mathrm{s}\mathrm{d}}$ is the dispersed liquid layer density, kg/m³.

For the moving bed layer,

$A_{\mathrm{m}\mathrm{b}}\left(\frac{\Delta P}{L}\right)=-{\tau }_{\mathrm{m}\mathrm{b}}{S}_{\mathrm{m}\mathrm{b}}+{\tau }_{\mathrm{s}\mathrm{d}\mathrm{m}\mathrm{b}}{S}_{\mathrm{s}\mathrm{d}\mathrm{m}\mathrm{b}}-\frac{F_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}}{L}-\frac{F_{\mathrm{m}\mathrm{b}}}{L}-{\tau }_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}{S}_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}-{\rho }_{\mathrm{m}\mathrm{b}}g{A}_{\mathrm{m}\mathrm{b}}\cos \theta ,(6)$

where ${\tau }_{\mathrm{m}\mathrm{b}}$ represents the shear stress between the moving bed layer and wellbore wall, Pa; $S_{\mathrm{m}\mathrm{b}}$ is the wetted perimeter between the moving bed layer and wellbore wall, m; $F_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}$ is the friction force between the moving bed layer and the stationary bed layer, N; $F_{\mathrm{m}\mathrm{b}}$ is the friction force between the moving bed layer and wellbore wall, N; ${\tau }_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}$ is the shear stress between the moving bed layer and stationary bed layer, Pa; $S_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}$ is the wetted perimeter between the moving bed layer and stationary bed layer, m; and ${\rho }_{\mathrm{m}\mathrm{b}}$ is the moving bed layer density, kg/m³.

For the stationary bed layer, the criterion keeping it from moving is that the driving force acting on the bed is less than the resistance. Eq. 7 is the case where the driving force acting on the bed is less than the resistance, and the stationary bed is at rest. Eq. 8 is the case of cuttings moving upward. At this time, the friction force between the moving bed layer and wellbore wall is the driving force, which is located on the left side of the equation. The driving force overcomes the resistance and presents an upward movement state, and some cuttings move to the moving bed layer as follows:

$A_{\mathrm{s}\mathrm{b}}\left(\frac{\Delta P}{L}\right)+\frac{F_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}}{L}+{\tau }_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}{S}_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}<\frac{F_{\mathrm{s}\mathrm{b}}}{L}+{\rho }_{\mathrm{m}\mathrm{b}}g{A}_{\mathrm{m}\mathrm{b}}\cos \theta ,(7)$

$A_{\mathrm{s}\mathrm{b}}\left(\frac{\Delta P}{L}\right)+\frac{F_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}}{L}+{\tau }_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}{S}_{\mathrm{m}\mathrm{b}\mathrm{s}\mathrm{b}}+\frac{F_{\mathrm{s}\mathrm{b}}}{L}>{\rho }_{\mathrm{m}\mathrm{b}}g{A}_{\mathrm{m}\mathrm{b}}\cos \theta ,(8)$

where $F_{\mathrm{s}\mathrm{b}}$ represents the friction force between the moving bed layer and wellbore wall, N.

When the cuttings bed is stationary, we have six unknowns: $C_{\mathrm{m}\mathrm{b}}$, $U_{\mathrm{m}\mathrm{b}}$, $U_{\mathrm{s}\mathrm{d}}$, $h_{\mathrm{s}\mathrm{b}}$, $h_{\mathrm{m}\mathrm{b}}$, and $\frac{\Delta P}{L}$. From the conservation of mass, two equations can be obtained. From the conservation of momentum, two equations can be obtained. From the critical cutting rolling velocity model (details in section Closure equations), $U_{\mathrm{m}\mathrm{b}}$ can be obtained. From the cuttings diffusion model, $C_{\mathrm{m}\mathrm{b}}$ can be obtained. In general, we have six equations and six unknowns. The model can be solved numerically.

When the cuttings bed is in motion, we have seven unknowns: $C_{\mathrm{m}\mathrm{b}}$, $U_{\mathrm{m}\mathrm{b}}$, $U_{\mathrm{s}\mathrm{d}}$, $U_{\mathrm{s}\mathrm{b}}$, $h_{\mathrm{s}\mathrm{b}}$, $h_{\mathrm{m}\mathrm{b}}$, and $\frac{\Delta P}{L}$. From the conservation of mass, two equations can be obtained. From the conservation of momentum, three equations can be obtained. From the critical cuttings rolling velocity model (details in section Closure equations), $U_{\mathrm{m}\mathrm{b}}$ can be obtained. From the cuttings diffusion model, $C_{\mathrm{m}\mathrm{b}}$ can be obtained. In general, we have seven equations and seven unknowns. The model can be solved numerically.

2.1.2.2 Segment model

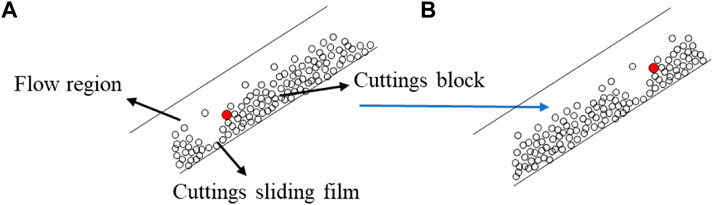
As the well inclination angle decreases, the cuttings in the stationary smooth cutting bed slide download. The sliding leads to the appearance of waves in the cuttings bed. The waved-bed flow is composed of three parts: the flow region, stationary cuttings slug region, and sliding cuttings film region (Figure 5).

FIGURE 5

FIGURE 5. Original segment model.

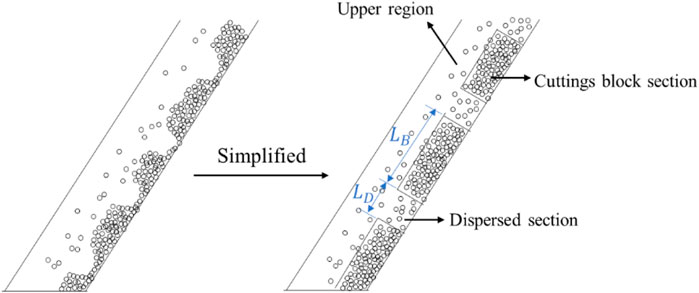
A simplified segment model is applied to simulate the cuttings transport for this flow pattern. In this model, it is assumed that the cuttings between two neighboring slugs are fully dispersed, and there is no cuttings film, as shown in Figure 6. $L_{\mathrm{B}}$ represents the cuttings block length, m; $L_{\mathrm{D}}$ is the dispersed region length, m; and ($L_B$ + $L_D$) is the unit length.

FIGURE 6

FIGURE 6. Simplified segment model.

In the segment model, the following assumptions are proposed:

1) In the upper part of the annulus, the cuttings are fully dispersed, meaning the cuttings concentration is homogeneous.

2) In the lower part of the annulus, the cuttings block region is stationary, and the dispersed regions move forward at a constant velocity. The cuttings are fully dispersed in the dispersed region. The mass exchange rate between the dispersed and block regions is constant. The sizes of the block and the dispersed regions are uniform along the test section.

3) The pressure gradient in the upper region is the same as that in the dispersed region and the cuttings block region. Because of the pressure gradient, there is fluid flow in the cuttings block. The flow is insignificant compared to the flow in the upper part of the annulus and the dispersed region. Thus, the fluid flow in the cuttings block is neglected.

4) The drill pipe rotation is not considered in this model.

5) The cuttings diameter is uniform, and all the cuttings are assumed to be spherical.

6) There is no slip between the particles and the liquid.

The conservation of mass for the solid phase is as follows:

${\rho }_{\mathrm{s}}{U}_{\mathrm{u}}{A}_{\mathrm{u}}{C}_{\mathrm{u}}+{\rho }_{\mathrm{s}}{U}_{\mathrm{d}}{A}_{\mathrm{d}}{C}_{\mathrm{d}}=\lambda {\rho }_{\mathrm{s}}{U}_{\mathrm{t}}{A}_{\mathrm{w}},(9)$

where $U_{\mathrm{u}}$ represents the velocity of the upper liquid layer in the segment model, m/s; $A_{\mathrm{u}}$ is the cross-sectional area of the upper liquid region, m²; $C_{\mathrm{u}}$ is the solids’ concentration of the upper region in the segment model, dimensionless; $U_{\mathrm{d}}$ is the velocity of the dispersed region in the segment model, m/s; $A_{\mathrm{d}}$ is the cross-sectional area of the dispersed region in the segment model, m²; and $C_{\mathrm{d}}$ is the solids’ concentration of the dispersed region in the segment model, dimensionless.

For the liquid phase,

${\rho }_{\mathrm{L}}{U}_{\mathrm{u}}{A}_{\mathrm{u}}\left(1-C_{\mathrm{u}}\right)+{\rho }_{\mathrm{L}}{U}_{\mathrm{d}}{A}_{\mathrm{d}}\left(1-C_{\mathrm{d}}\right)={\rho }_{\mathrm{L}}Q.(10)$

The momentum equation for the upper part is as follows:

$-A_{\mathrm{u}}\frac{DP}{DL}={\tau }_{\mathrm{u}\mathrm{w}}\cdot S_{\mathrm{u}\mathrm{w}}+{\tau }_{\mathrm{u}\mathrm{b}}\cdot S_{\mathrm{u}\mathrm{b}}\cdot R_{\mathrm{b}}+{\tau }_{\mathrm{u}\mathrm{d}}\cdot S_{\mathrm{u}\mathrm{d}}\cdot \left(1-R_{\mathrm{b}}\right)+{\rho }_{\mathrm{u}}\cdot g\cdot A_{\mathrm{u}}\cdot \cos \theta ,(11)$

where ${\tau }_{\mathrm{u}\mathrm{w}}$ represents the shear stress between the upper region and wellbore wall, Pa; $S_{\mathrm{u}\mathrm{w}}$ is the wetted perimeter between the upper region and wellbore wall, m; ${\tau }_{\mathrm{u}\mathrm{b}}$ is the shear stress between the upper region and solid block, Pa; $S_{\mathrm{u}\mathrm{b}}$ is the wetted perimeter between the upper region and solid block in the segment model, m; $R_{\mathrm{b}}$ is calculated by Eq. 15, dimensionless; ${\tau }_{\mathrm{u}\mathrm{d}}$ is the shear stress between the upper and dispersed regions in the segment model, Pa; $S_{\mathrm{u}\mathrm{d}}$ is the wetted perimeter between the upper and dispersed regions in the segment model, m; and ${\rho }_{\mathrm{u}}$ is the upper liquid layer density in the segment model, kg/m³.

The momentum equation for the dispersed region is as follows:

$-A_{\mathrm{d}}\frac{DP}{\mathrm{D}L}={\tau }_{\mathrm{d}\mathrm{w}}\cdot S_{\mathrm{d}\mathrm{w}}-{\tau }_{\mathrm{u}\mathrm{d}}\cdot S_{\mathrm{u}\mathrm{d}}\cdot \left(1-R_{\mathrm{b}}\right)+{\rho }_{\mathrm{d}}\cdot g\cdot A_{\mathrm{d}}\cdot \cos \theta ,(12)$

where ${\tau }_{\mathrm{d}\mathrm{w}}$ represents the shear stress between the dispersed region and wellbore wall, Pa; $S_{\mathrm{d}\mathrm{w}}$ is the wetted perimeter between the dispersed region and wellbore wall, m; and ${\rho }_{\mathrm{d}}$ is the dispersed region density in the segment model, kg/m³.

The momentum equation for the solid block region is as follows:

$-A_{\mathrm{b}}\frac{\mathrm{D}P}{DL}\le -{\tau }_{\mathrm{u}\mathrm{b}}\cdot S_{\mathrm{u}\mathrm{b}}+\frac{F_{\mathrm{u}\mathrm{b}}}{L}+{\rho }_{\mathrm{b}}\cdot g\cdot A_{\mathrm{u}}\cdot \cos \theta (13)$

and

$-A_{\mathrm{b}}\frac{\mathrm{D}P}{\mathrm{D}L}+{\tau }_{\mathrm{u}\mathrm{b}}\cdot S_{\mathrm{u}\mathrm{b}}-\frac{F_{\mathrm{u}\mathrm{b}}}{L}\ge {\rho }_{\mathrm{b}}\cdot g\cdot A_{\mathrm{u}}\cdot \cos \theta ,(14)$

where $A_{\mathrm{b}}$ represents the area of the solid block in the segment model, m²; $F_{\mathrm{u}\mathrm{b}}$ is the friction force between the upper region and solid block, N; ${\rho }_{\mathrm{b}}$ is the solid block density in the segment model, kg/m³.

$R_b$ is the packed solid block length ratio, which is the ratio of the cuttings block length and the unit length, dimensionless:

$R_{\mathrm{b}}=L_{\mathrm{B}}/\left(L_{\mathrm{B}}+L_{\mathrm{D}}\right).(15)$

In the model, we have six unknowns: $\frac{\mathrm{D}P}{\mathrm{D}L}$, $U_{\mathrm{u}}$, $U_{\mathrm{d}}$, $C_{\mathrm{u}}$, $C_{\mathrm{d}}$, and $A_{\mathrm{u}}$. From the conservation of mass, two equations can be obtained. From the conservation of momentum, two equations can be obtained. The other two equations can be obtained from the closure relationships. We have six equations and six unknowns, and the model can be solved numerically.

2.1.2.3 Dispersed model

At the low inclined position and high flow rate conditions, the cuttings in the wellbore may get totally dispersed. The local cuttings concentration in the wellbore is directly related to the cuttings slip velocity.

The superficial liquid velocity $v_{\mathrm{s}\mathrm{c}}$ is as follows:

$v_{\mathrm{s}\mathrm{c}}=\frac{U_t\cdot A_{\mathrm{w}}}{A_{\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{u}\mathrm{l}\mathrm{u}\mathrm{s}}},(16)$

and the superficial cuttings velocity $v_{\mathrm{s}\mathrm{l}}$ is as follows:

$v_{\mathrm{s}\mathrm{l}}=\frac{Q}{A_{\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{u}\mathrm{l}\mathrm{u}\mathrm{s}}},(17)$

where $A_{\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{u}\mathrm{l}\mathrm{u}\mathrm{s}}$ represents the cross-sectional area of the annulus, m².

The feeding in the cuttings concentration $C_{\mathrm{F}}$ is as follows:

$C_{\mathrm{F}}=\frac{U_t\cdot A_{\mathrm{w}}}{U_t\cdot A_{\mathrm{w}}+Q}=\frac{v_{\mathrm{s}\mathrm{c}}}{v_{\mathrm{s}\mathrm{l}}+v_{\mathrm{s}\mathrm{c}}}.(18)$

The cross-section average in situ cuttings concentration $C_{\mathrm{c}}$ is as follows:

$C_{\mathrm{c}}=\frac{1}{A}{\int }_0^A{\epsilon }_{\mathrm{c}}dA,(19)$

where ${\epsilon }_{\mathrm{c}}$ is the local in situ volume fraction of the cuttings, dimensionless.

The average slip velocity between the drilling fluid and cuttings $v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}$ is as follows:

$v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}=v_{\mathrm{l}}-v_{\mathrm{c}}=\frac{v_{\mathrm{s}\mathrm{l}}}{1-C_{\mathrm{c}}}-\frac{v_{\mathrm{s}\mathrm{c}}}{C_{\mathrm{c}}},(20)$

where $v_{\mathrm{l}}$ is the drilling fluid flow rate, m/s, and $v_{\mathrm{c}}$ is the critical velocity to roll the particle, m/s.

The mixture equation is as follows:

$v_{\mathrm{M}}=v_{\mathrm{s}\mathrm{l}}+v_{\mathrm{s}\mathrm{c}}=\frac{U_t\cdot A_{\mathrm{b}\mathrm{i}\mathrm{t}}+Q}{A_{\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{u}\mathrm{l}\mathrm{u}\mathrm{s}}},(21)$

where $v_{\mathrm{M}}$ represents the solid and liquid mixture velocity, m/s, and $A_{\mathrm{b}\mathrm{i}\mathrm{t}}$ is the cross-sectional area of the bit, m².

Substituting Eq. 20 and Eq. 21 into Eq. 19, we obtain $C_{\mathrm{c}}$ as follows:

$C_{\mathrm{c}}=-\left(\frac{v_{\mathrm{M}}-v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}}{2v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}}\right)+{\left[{\left(\frac{v_{\mathrm{M}}-v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}}{2v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}}\right)}^2+\frac{v_{\mathrm{M}}{C}_{\mathrm{F}}}{v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}}\right]}^{0.5}.(22)$

The pressure gradient for the dispersed model is obtained using standard drilling hydraulic models, by replacing the pure drilling fluid velocity with the mixture velocity and the fluid density with the new mixture density of the local cuttings and fluid:

${\rho }_{\mathrm{m}}={\rho }_{\mathrm{L}}\ast \left(1-C_{\mathrm{c}}\right)+{\rho }_{\mathrm{s}}\ast C_{\mathrm{c}},(23)$

where ${\rho }_{\mathrm{m}}$ represents the new mixture density of the local cuttings and the fluid, kg/m³.

2.2 Closure equations

According to the experimental observation, the cuttings roll forward rather than slide forward on the surface of the cuttings bed. Therefore, the fluid velocity near the cuttings bed is the critical velocity of cuttings rolling. In the mechanistic model, the average velocity above the cuttings bed can be considered as the average velocity of the mixed layer. There is a cuttings exchange between cuttings beds and mixed beds. The cuttings of the mixed layer are continuously settled to the cuttings bed because of gravity. Meanwhile, the cuttings are re-suspended to the mixed layer due to the effect of turbulent suspension and particle uplift. The mixed layer cuttings concentration profile is obtained by comparing the upward re-suspension and downward deposition. The closure equations proposed in conjunction with boundary conditions can avoid multi-solution problems and simplify the model-solving process.

2.2.1 Cuttings rolling model

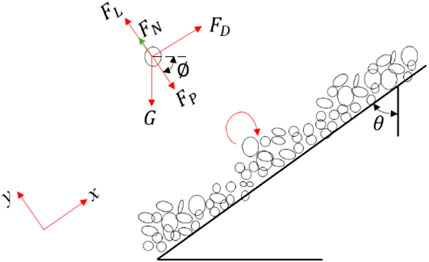
The solution mentioned previously requires the critical velocity of cuttings movement, namely, the minimum fluid velocity that enables the cuttings to move continuously forward. Particles begin to roll on the cuttings bed surface at first in highly inclined wells. Figure 7 is the free body diagram of a random rolling particle on the surface of the cuttings bed.

FIGURE 7

FIGURE 7. Particle rolling.

When the particle began to roll on the surface of the cuttings bed, the sum of the moment on the particle caused by all the forces acting on the particle $T$ is as follows:

$T=\frac{d_{\mathrm{s}}}{2}\left[F_{\mathrm{D}}\cdot \sin {\theta }_{\mathrm{p}\mathrm{c}}+F_{\mathrm{L}}\cdot \cos {\theta }_{\mathrm{p}\mathrm{c}}-F_{\mathrm{P}}\cdot \cos {\theta }_{\mathrm{p}\mathrm{c}}-G\cdot \left(\theta +\sin {\theta }_{\mathrm{p}\mathrm{c}}\right)\right],(24)$

where $T$ represents the sum of the moment on the particle, N$\cdot$m; $d_{\mathrm{s}}$ is the solid particle diameter, m; $F_{\mathrm{D}}$ is the drag force, N; ${\theta }_{\mathrm{p}\mathrm{c}}$ is the angle of repose of cutting, degree; $F_{\mathrm{L}}$ is the lift force, N; $F_{\mathrm{P}}$ is the force caused by the pressure gradient, N; and $G$ is gravity, N.

In order to make the particle roll on the cuttings bed, $T$ needs to be larger than zero. Therefore, the critical velocity of rolling the particle $v_{\mathrm{c}}$ is as follows:

$v_{\mathrm{c}}=\sqrt{\frac{6{\tau }_{\mathrm{y}}\cos {\theta }_{\mathrm{p}\mathrm{c}}+4d_{\mathrm{s}}\left({\rho }_{\mathrm{s}}-{\rho }_{\mathrm{L}}\right)g\cdot \sin \left(\theta +{\theta }_{\mathrm{p}\mathrm{c}}\right)}{3\left(C_{\mathrm{L}}{\rho }_{\mathrm{L}}\cos {\theta }_{\mathrm{p}\mathrm{c}}+C_{\mathrm{D}}{\rho }_{\mathrm{L}}\sin {\theta }_{\mathrm{p}\mathrm{c}}\right)}},(25)$

where ${\tau }_{\mathrm{y}}$ is the yield point, Pa; $C_{\mathrm{L}}$ is the lift coefficient, dimensionless; and $C_{\mathrm{D}}$ is the drag coefficient, dimensionless.

For intermediate inclined wells, the cuttings can be re-suspended to the flow more easily than rolling on the bed surface. To lift the particle away from the cuttings bed, the sum of the force in the y direction should be larger than zero, which means

$F_{\mathrm{y}}=F_{\mathrm{L}}-F_p-G\cdot \sin \theta -F_{\mathrm{N}}>0.(26)$

Therefore,

$F_{\mathrm{y}}=\frac{\pi }{2}{d}_{\mathrm{s}}^2\left[\frac{1}{4}{\rho }_{\mathrm{L}}{C}_{\mathrm{L}}{v}_{\mathrm{r}}^2-\frac{1}{2}{\tau }_{\mathrm{y}}-\frac{d_{\mathrm{s}}}{3}\left({\rho }_{\mathrm{s}}-{\rho }_{\mathrm{L}}\right)g\sin \theta \right]+F_{\mathrm{N}},(27)$

where $F_{\mathrm{y}}$ represents the sum of the forces in the y direction, N, and $F_{\mathrm{N}}$ is the support force from the cuttings bed, N.

When the particle leaves the cuttings bed, F_N goes to zero. Moreover, the critical velocity to suspend the particle is as follows:

$v_{\mathrm{c}}=\sqrt{\left[\frac{2{\tau }_{\mathrm{y}}}{C_{\mathrm{L}}{\rho }_{\mathrm{L}}}+\frac{4d_{\mathrm{s}}\left({\rho }_{\mathrm{s}}-{\rho }_{\mathrm{L}}\right)}{3C_{\mathrm{L}}{\rho }_{\mathrm{L}}}g\sin \theta \right]}.(28)$

2.2.2 Cuttings diffusion model

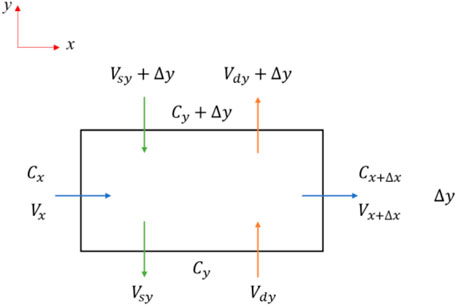
For the control volume shown in Figure 8, $C$ is the local cuttings concentration, $v$ is the local cutting velocity, the subscript $s$ represents settling, and $d$ represents diffusion. The change of cuttings quantity in unit time can be expressed as in Eq. 29:

$\frac{\Delta C\cdot \mathrm{\Delta }x\cdot \mathrm{\Delta }y}{\Delta t}=\left[C_{\mathrm{x}}{v}_{\mathrm{x}}\Delta y-C_{\mathrm{x}+\mathrm{\Delta }\mathrm{x}}{v}_{\mathrm{x}+\mathrm{\Delta }\mathrm{x}}\Delta y\right]-\left(v_{\mathrm{s}\mathrm{y}}{C}_{\mathrm{y}}-v_{\mathrm{s}\mathrm{y}+\mathrm{\Delta }\mathrm{y}}{C}_{\mathrm{y}+\mathrm{\Delta }\mathrm{y}}\right)\Delta x+\left(v_{\mathrm{d}\mathrm{y}}{C}_{\mathrm{y}}-v_{\mathrm{d}\mathrm{y}+\mathrm{\Delta }\mathrm{y}}{C}_{\mathrm{y}+\mathrm{\Delta }\mathrm{y}}\right)\Delta x,(29)$

where $v_{\mathrm{s}\mathrm{y}}$ represents the settling velocity of the solid particles in the y direction, m/s; $v_{\mathrm{d}\mathrm{y}}$ is the diffusion velocity in the y direction, m/s; $C_{\mathrm{x}}$ is the local cuttings concentration in the x direction, dimensionless; $C_{\mathrm{y}}$ is the local cuttings concentration in the y direction, dimensionless.

FIGURE 8

FIGURE 8. Cuttings diffusion in a control volume.

For the fully developed flow, $v_{\mathrm{x}}{=v}_{\mathrm{x}+\mathrm{\Delta }\mathrm{x}}$. Thus, lateral diffusion can be neglected. The equation is divided by $\Delta x\Delta y$, and the limit t is taken to be x, y → 0 to obtain the following:

$\frac{\partial C}{\partial t}=-\frac{\partial \left(v_{\mathrm{s}}C\right)}{\partial y}+\frac{\partial \left(v_{\mathrm{d}}C\right)}{\partial y},(30)$

where $v_{\mathrm{s}}$ is the solid particle settling velocity, m/s, and $v_{\mathrm{d}}$ is the diffusion velocity, m/s.

For non-horizontal wells, the settling velocity is $v_{\mathrm{s}}\sin \theta$:

$v_{\mathrm{d}}=\Gamma \ast \frac{\partial C}{\partial y},(31)$

where $\Gamma$ is the diffusion coefficient, which includes the shear-induced diffusion and turbulent diffusion, dimensionless.

In this case, because of the large cuttings, the shear-induced diffusion can be neglected, and only turbulent diffusion is considered. By rearranging Eq. 32,

$\frac{\partial C}{\partial t}=-C\frac{\partial v_s}{\partial y}-v_s\frac{\partial C}{\partial y}+\frac{\partial \Gamma }{\partial y}\frac{\partial C}{\partial y}+\Gamma \frac{{\partial }^{2}C}{\partial y^2},(32)$

$S_{C_t}=\frac{v_t}{{\Gamma }_t},(33)$

where the Schmidt number $S_{C_t}$ equals 0.9 for near-wall flows; ${\Gamma }_t$ is the turbulent diffusion coefficient, which is closely related to the turbulent viscosity, dimensionless; and $v_t$ is the turbulent viscosity.

The downward settling velocity is as follows:

$v_{\mathrm{s}}=\sqrt{\frac{4g{d}_{\mathrm{s}}\left({\rho }_{\mathrm{s}}-{\rho }_{\mathrm{l}}\right)}{3{\rho }_{\mathrm{f}}{C}_{\mathrm{D}}}}.(34)$

The boundary conditions are as follows: at the top of the moving layer, the cuttings concentration is 0. At the bottom of the moving layer, the cuttings concentration is the same as the packed cuttings bed concentration.

2.3 Methodology to use the minimum ECD model

The model is solved by using a numerical method, and detailed procedures are shown as follows:

1) Input calculation data, such as the wellbore geometry, flow rate, and fluid rheological parameters.

2) Assume the height of the cutting bed from zero, and assume the annular pressure gradient $\frac{∆P}{L}$.

3) Judge the flow pattern for the solid–liquid, two-phase flow, and calculate the Froude number using Eq. 1 and DPG using Eq. 2.

4) Calculate the wet perimeters and areas of the annular geometry (details available in previous work (Zhang et al., 2015)).

5) Calculate the velocity of every layer using Eqs. 28 and 34.

6) Update the cuttings concentration and bed height using Eqs. (3), 4.

7) Calculate the shear stress, Reynolds number, and friction coefficient using the equations in Appendix B.

8) Calculate the annular pressure gradient using Eqs. 5–8.

9) Compare the calculated results, assume that $\frac{∆P}{L}$ is equal to 1. If the margin is greater than the tolerance, go back to step 1), increase the cutting bed height by 0.001 and change the assumed value of the pressure gradient $\frac{∆P}{L}$, and then repeat steps 1)–8). Output the annulus pressure gradient $\frac{∆P}{L}$ until the margin is less than the tolerance, and convert it to the value corresponding to ECD.

10) Plot the ECD against the flow rate to establish the minimum ECD curve and then obtain the minimum flow rate.

3 Model verifications

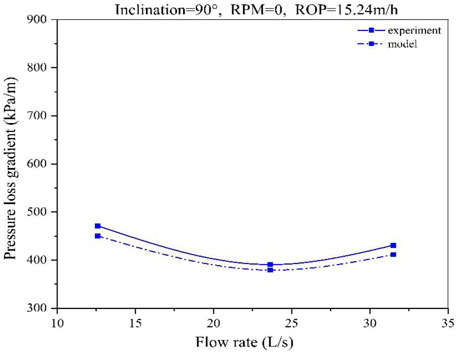
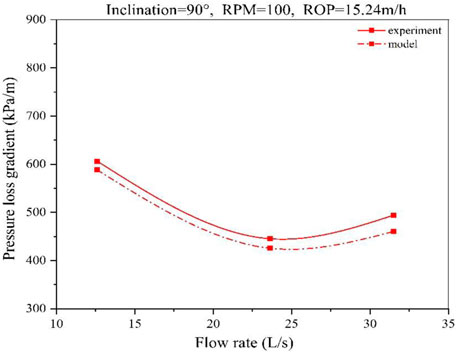
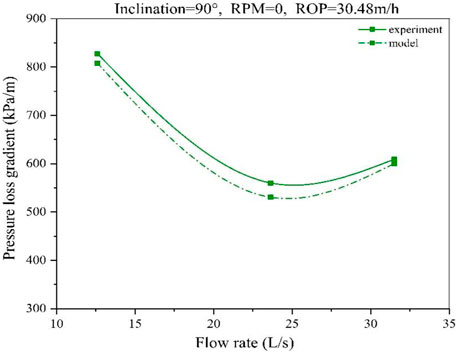
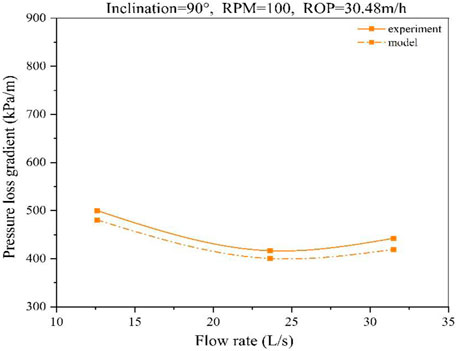
In order to verify the reliability of the model, the results are compared with the experimental data published in the literature (Zhang et al., 2015; Zhang, 2015). The accuracy and reliability of the model are verified by the comparative test data on hole inclination, rotary speed, and ROP.

The comparison results are shown in Figures 9–12. At a low flow rate (12.6 L/s), the predicted results are in good agreement with the experimental data. The average difference between predictions and experimental results is about 5%. With the increase in the flow rate, the model matches the experimental data well.

FIGURE 9

FIGURE 9. Pressure loss gradient at 90°, 15.24 m/h, and 0 RPM.

FIGURE 10

FIGURE 10. Pressure loss gradient at 90°, 15.24 m/h, and 100 RPM.

FIGURE 11

FIGURE 11. Pressure loss gradient at 90°, 30.48 m/h, and 0 RPM.

FIGURE 12

FIGURE 12. Pressure loss gradient at 90°, 30.48 m/h, and 100 RPM.

4 Results and discussion

In order to show the influence of cuttings on annulus pressure loss more clearly under the conditions of different sections, inclined angle, flow rate, ROP, and drilling fluid parameters, the annulus pressure loss in a single section under different conditions is calculated and analyzed.

4.1 Single-well section analysis

4.1.1 Effects of the inclination angle

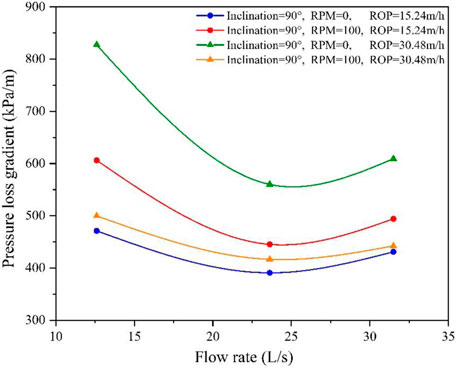
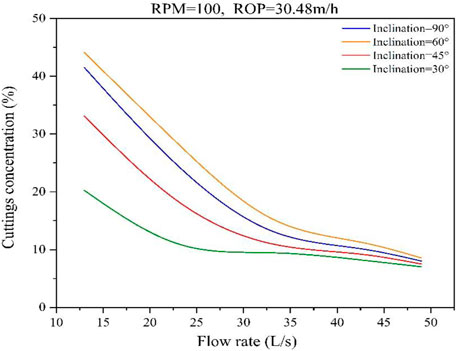
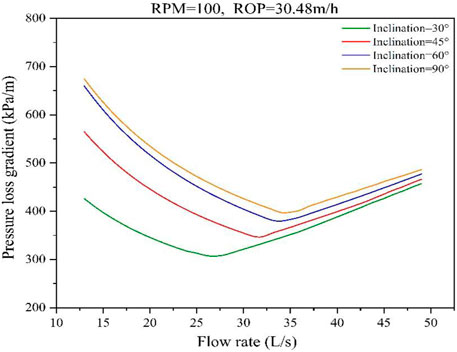
In this case, rotary speed and ROP are assumed to be constants, 100 RPM and 30.48 m/h, respectively. The relationship between the flow rate and annulus pressure loss is shown in Figure 13 as inclination changes.

FIGURE 13

FIGURE 13. Effect of the inclination angle on the cuttings concentration.

When the flow rate and inclination angle are both small, the annulus pressure loss is specifically high. However, the annulus pressure loss decreases obviously with the hole inclination increasing, as shown in Figure 14, which is caused by the concentration of cuttings at different inclination positions shown in Figure 13. For all inclination positions, there is a turning point for the pressure gradients as the flow rate increases. The flow rate value for the turning points increases as the inclination angle increases below 60° and decreases beyond 60°, which is consistent with the cuttings concentration results shown in Figure 13. It can be indicated that the flow rate of the turning point is proportional to the efforts required to clean the wellbore.

FIGURE 14

FIGURE 14. Effect of the inclination angle on pressure loss.

4.1.2 Effects of rheological parameters

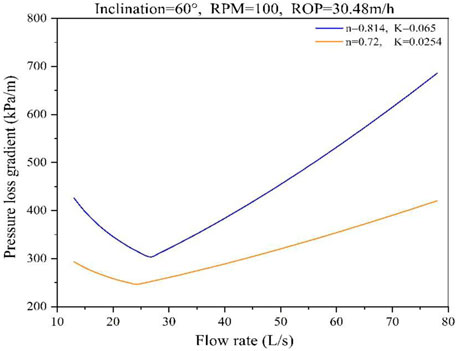
In this case, both fluids are power-low flow, and the density is 1,000 kg/m³. The first fluid behavior index (n) is 0.814, and the consistency coefficient (K) is 0.065 pasⁿ. The second fluid n is 0.72, and K is 0.0254 pasⁿ. Figure 15 shows the calculation results of the variation of the annulus pressure loss of the two different drilling fluids with the flow rate change in a deviated well with 100 RPM and an ROP of 30.48 m/h.

FIGURE 15

FIGURE 15. Effect of rheological parameters on pressure loss.

Figure 15 shows that there is little effect on the fluid flow index; the greater the fluid consistency coefficient, the greater the viscosity is. Therefore, the annulus pressure loss is larger. Moreover, the increase in the fluid viscosity reduces the value of the critical flow rate.

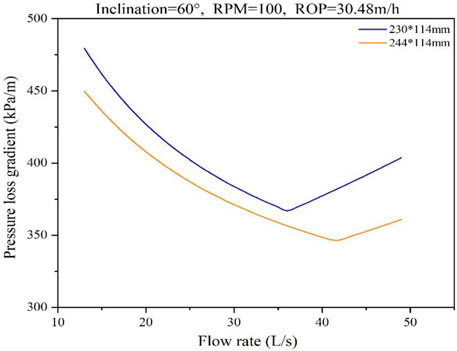
4.1.3 Effects of annulus geometry

In this case, the first geometry is 230*114 (mm), and the second is 244*114 (mm). Results are shown in Figure 16. From the diagram, we can find that the annulus pressure loss decreases with the increase in annulus geometry, but the critical flow rate is adverse. The increase in the annulus geometry reduces the annulus velocity and the consumption of drilling fluid friction resistance. However, the decrease in the flow rate reduces the carrying capacity of the drilling fluid, which increases the critical value.

FIGURE 16

FIGURE 16. Effect of annulus geometry on pressure loss.

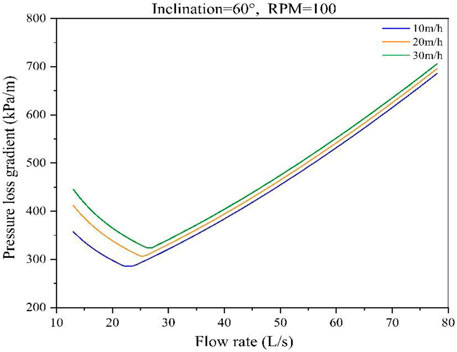
4.1.4 Effects of ROP

Figure 17 shows the variation of annulus pressure loss with flow rate change in a deviated well after ROP changed. The rotary speed is 100 RPM. The consistency coefficient (K) of the drilling fluid is 0.065 pasⁿ, and the behavior index (n) is 0.72. It can be found from the diagram that the annulus pressure loss and the critical flow rate both increase with the increase in the ROP. Because ROP increases, the number of suspended cuttings and the height of the cuttings bed in the annulus increase, resulting in an increase in the annulus velocity and the fluid average density. Therefore, the annulus pressure loss curve in Figure 17 shifts to the upper right.

FIGURE 17

FIGURE 17. Effect of ROP on pressure loss.

4.2 Real case analysis

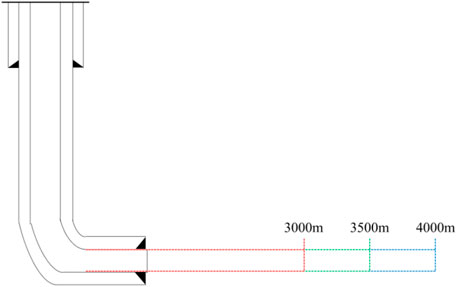
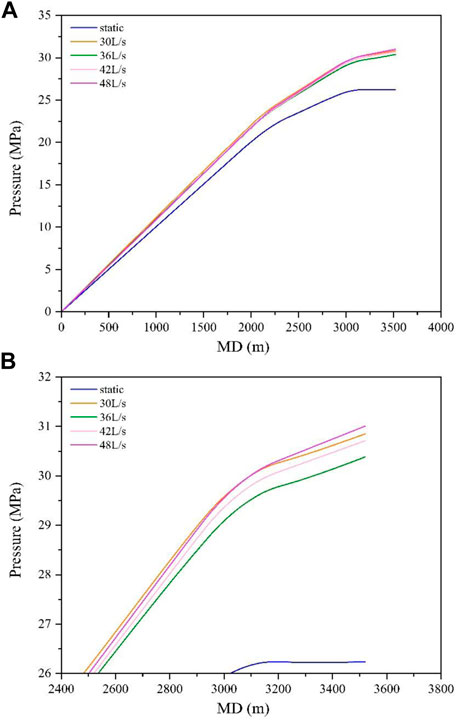
Based on this model, combined with the data on well A, the whole wellbore cleaning optimization method of extended reach wells is analyzed. The casing program is shown in Figure 18 and can be divided into vertical and horizontal sections. The basic data include the following: the length of the vertical section is 2,902 m; the outer diameter of the casing is 244.5 mm; the length of the horizontal section is assumed to be 3,000, 3,500, and 4,000 m; the diameter of the bits is 215.9 mm; the outer of the drill pipe is 127 mm; the rotary speed is 100 RPM; and the ROP is 15.24 m/h. The drilling fluid is power-low flow with a density of 1,000 kg/m³, a behavior index (n) of 0.814, and a consistency coefficient (K) of 0.065 pasⁿ. The cuttings used in the case are sandstone. The cuttings density is 2,667 kg/m³, the average diameter is 3 mm, and the packed porosity is 0.36.

FIGURE 18

FIGURE 18. Structure of the wellbore.

The bottom hole pressure under different flow rates in open hole drilling is shown in Figure 19A. Because of the presence of cuttings and friction, the annulus pressure loss in the flowing condition is larger than hydrostatic pressure. The details of the pressure near the bottom hole region are shown in Figure 19B. The optimal flow rate in this condition is about 36 L/s. A lower flow rate leads to high solid concentration in the well, which increases the bottom hole pressure; a higher flow rate leads to more friction loss, which also increases the bottom hole pressure.

FIGURE 19

FIGURE 19. (A) Wellbore pressure profile. (B) Wellbore pressure profile for the near-bottom region.

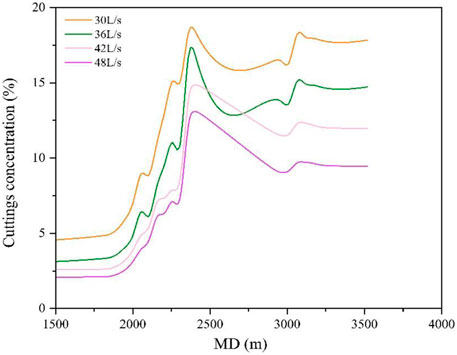
The cuttings concentration profile in the wellbore is shown in Figure 20. The cuttings concentration decreases with the increase in the flow rate. At 36 L/s, the cuttings concentration is less than 5% in the vertical part of the well, which satisfies the requirements of traditional wellbore cleaning. In the inclined and horizontal sections of the wellbore, slight cuttings deposition is acceptable during drilling.

FIGURE 20

FIGURE 20. Solids’ concentration profile in the wellbore.

In most drilling applications, it is necessary to minimize the pressure loss caused by friction and cuttings in the annulus. The pressure drop in the annulus is not always proportional to the flow rate. At a low flow rate, the concentration of cuttings in the wellbore is relatively high, which results in a high-pressure drop. In these cases, increasing the flow rate can reduce the cuttings concentration significantly, which actually reduces the total pressure drop. In the low cuttings concentration condition, the influence of cuttings on pressure loss is very small. In these cases, increasing the flow rate will lead to a significant increase in friction loss, which also increases the bottom hole pressure. Therefore, at the optimum flow rate of 36 L/s, the pressure loss in the annulus is the smallest.

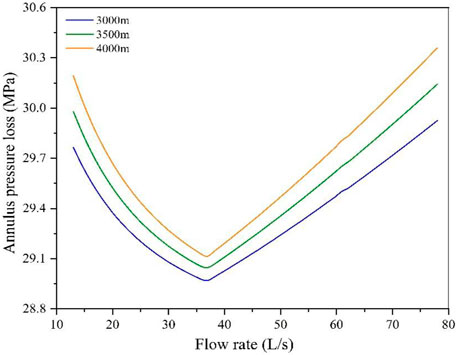
Figure 21 shows the calculation results of the annulus pressure loss changes with the variety of flow rates at different horizontal sections, which further proves the optimum flow rate.

FIGURE 21

FIGURE 21. Effect of horizontal section length on pressure loss.

5 Conclusion

Through experiments and theoretical research, the following conclusions can be drawn:

1) The annulus pressure loss is closely related to the cuttings concentration. Without effective hole cleaning, many cuttings accumulate in the annulus and significantly impact pressure loss.

2) There is a critical flow rate for the relationship value between the flow rate and annulus pressure loss. When the flow rate is less than the critical value, the annulus pressure loss decreases with the increase in the flow rate. When the flow rate exceeds the critical value, the annulus pressure loss begins to increase with the increase in the flow rate.

3) The critical value varies with the rheological parameters of the drilling fluid, ROP, hole inclination, and the annulus size.

4) According to the requirements of drilling technology, a new method for hole cleaning optimization in extended reach wells by minimizing the ECD is presented, which can be used to optimize drilling parameters and minimize the ECD during drilling ERD wells.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

BL verified the model. XW analyzed and summarized the application process of the minimum ECD model method for extended-reach wellbore cleaning. FZ analyzed the flow pattern and mechanical model. XW derived the closure equations. YW analyzed the influence of multiple factors on the cuttings concentration and pressure loss gradient in a single-well section. YW analyzed the cuttings concentration, pressure profile, and annular pressure loss distribution in the whole section of the real case well.

Funding

This work was supported by the National Natural Science Foundation of China (Grant no. 51874045) and the Hubei Provincial Science and Technology Agency (Grant no. 2019CFA093).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Coley, C. J., and Edwards, S. T. (2013). “The use of A long string annular pressure measurements to monitor solids transport and hole cleaning,” in Paper SPE 163567 presented at the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 5-7 March 2013.

CrossRef Full Text | Google Scholar

Hemphill, T., and Ravi, K. (2007). “Field validation of drill pipe rotation effects on equivalent circulating density,” in paper SPE 110470 presented at the SPE Annual Technical Conference and Exhibition in Anaheim, Anaheim, California, 11-14 November 2007.

CrossRef Full Text | Google Scholar

Hemphill, T., and Ravi, K. (2011). “Improved prediction of ECD with drill pipe rotation,” in Paper IPTC 15424 presented at International Petroleum Technology Conference, Bangkok, Thailand, 15-17 November 2011.

CrossRef Full Text | Google Scholar

Jeong, Y., and Shah, S. (2004). “Analysis of tool joint effects for accurate friction pressure loss calculation,” in Paper SPE 87182 presented at IADC/SPE Drilling Conference, Dallas, Texas, 2-4 March 2004.

Google Scholar

Luo, Y., and Peden, J. M. (1987). “Flow of drilling fluids through eccentric annuli,” in Paper SPE 16692 presented at the SPE Annual Technical Conference and Exhibition, Dallas, Texas, 27-30 September 1987.

CrossRef Full Text | Google Scholar

Osisanya, S. O., and Harris, O. O. (2005). “Evaluation of equivalent circulating density of drilling fluids under high pressure/high temperature conditions,” in Paper SPE 97018 presented at SPE Annual Technical Conference and Exhibition, Dallas, Texas, 9-12 October 2005.

CrossRef Full Text | Google Scholar

Ozbayoglu, E. M. (2002). “Cuttings transport with foam in horizontal and highly-inclined wellbore,” (Tulsa, Oklahoma, USA: The University of Tulsa). Ph.D. Dissertation.

Google Scholar

Rommetveit, R., and Bjorkevoll, K. S. (1997). “Temperature and pressure effects on drilling fluid rheology and ECD in very deep wells,” in Paper SPE 39282 presented at SPE/IADC Middle East Drilling Technology Conference, Bahrain, 23-25 November 1997.

CrossRef Full Text | Google Scholar

Simoes, S. Q., Miska, S. Z., Takach, N. E., et al. (2007). “The effect of tool joints on ECD while drilling,” in Paper SPE 106647 presented at Production and Operations Symposium, Oklahoma City, Oklahoma, U.S.A, 31 March-3 April 2007.

CrossRef Full Text | Google Scholar

Yao, Y., Qiu, Y., Cui, Y., Wei, M., and Bai, B. (2022). Insights to surfactant huff-puff design in carbonate reservoirs based on machine learning modeling. Chem. Eng. J. 451, 138022. doi:10.1016/j.cej.2022.138022

CrossRef Full Text | Google Scholar

Zhang, F., Miska, S., and Yu, M. (2014). “Application of real-time solids monitoring in well design, annulus pressure control and managed pressure drilling,” in Paper presented at the 2014 AADE Fluids Technical Conference and Exhibition, Houston, Texas, USA, 15-16 April 2014.

Google Scholar

Zhang, F., Miska, S., Yu, M., Evren, M., and Takach, N. (2015). Pressure profile in annulus: Solids play a significant role. J. Energy Resour. Technol. 137, 34–45. doi:10.1115/1.4030845

CrossRef Full Text | Google Scholar

Zhang, F. (2015). “Numerical simulation and experimental study of cuttings transport in intermediate inclined wells,” (Tulsa, Oklahoma, USA: The University of Tulsa). Ph.D. Dissertation.

Google Scholar