
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 12 January 2023
Sec. Structural Geology and Tectonics
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.1032817
This article is part of the Research Topic Unconventional Reservoir Geomechanics View all 16 articles
A large number of natural cracks exist in shale reservoirs, and the presence of natural cracks weakens the integrity of shale, which is an important factor governing the effectiveness of shale gas extraction. In this paper, shales from the Lower Cambrian Niutitang Formation in northern Guizhou were scanned by electron microscopy, their microstructures were selected for digital image processing, and uniaxial compression numerical tests were conducted on shale models containing different natural crack dips using the rock fracture process system RFPA2D-DIP to study the effects of natural cracks on the mechanical properties and fracture patterns of shales at the microscopic scale. The study shows that the peak strength and elastic modulus of shale increase with increasing natural crack inclination angle. The fracture modes of shale at the microscopic scale can be roughly divided into four categories: similar to I-type fractures (0°), oblique I-type fractures (15°, 45°, 60°, 75°), folded line fractures (30°), and V-type fractures (90°). Natural cracks within shale are found to have a significant effect on the distribution of stress. Acoustic emission can reflect the stress change and rupture process for shales containing natural cracks with different dip angles at the microscopic scale. The presence of natural cracks has a significant effect on the AE energy and fractal dimension. The magnitude of the AE energy increases with increasing stress level and reaches a maximum value at 90°, while the value of the fractal dimension is found to zigzag upwards because the value of the fractal dimension is jointly influenced by both newborn cracks and native natural cracks.
Shale gas, as an unconventional natural gas resource, has a large resource potential and wide distribution area, and is, thus, of wide interest to scholars at home and abroad (Wang et al., 2016a; Wang et al., 2016b; Shrestha et al., 2016; Nezhad et al., 2018; Liu et al., 2020a; Ban et al., 2021; Yu et al., 2021; Zhu et al., 2021). Compared with conventional natural gas, shale gas has the advantages of a long extraction life and long production cycle, and along with the consumption of conventional oil and gas, shale gas is expected to take its place in the future (Lisjak et al., 2014; Heng et al., 2015; Wu et al., 2017; Hu et al., 2020; Xu et al., 2020; Jin et al., 2021). Currently, the United States leads the world in the commercial production of shale gas (Wang et al., 2019). According to the results of exploration, China has the highest amount of shale gas in the world, and the difficulty in extracting shale gas is largely due to the low porosity and poor permeability of shale formations (Zou et al., 2016; Lan et al., 2018; Wu et al., 2018; Liu et al., 2019). For shale gas extraction, hydraulic fracturing is the preferred technology in most countries (Wang et al., 2014; Ju et al., 2018; Zhao et al., 2020; Feng et al., 2021). Therefore, studies of the mechanical properties of shale and its fracture pattern provide important theoretical support for the design of commercial shale gas extraction schemes.
Shales often contain complex natural fractures, and the presence of natural fractures affects the mechanical properties and fracture patterns of shales. Natural fractures, due to their irregularity, lead to a difficult problem in theoretically studying the damage mechanism for shales containing natural fractures. To solve this challenge, domestic and international scholars have carried out relevant mechanical tests in the laboratory. Chen et al. used the RTR-1000 triaxial rock mechanical test system to perform triaxial experiments on shales containing different fractures (controlling a single variable so that the number of fractures, dip angle, depth and filling are different) to investigate the peak stress, elastic modulus and damage forms for shales under different fracture patterns (Chen et al., 2020). Lee H et al. described the initiation, extension and coalescence of cracks at or near preexisting open cracks or defects in specimens under uniaxial compression (Lee and Jeon, 2011). Wei et al. conducted an experimental study into the deformation and fracture characteristics of brittle shales containing natural fractures under uniaxial cyclic loading in Pengshui, Chongqing, using the RMT-150C rock mechanics test system (Wei et al., 2015). Wang et al. carried out Brazilian splitting tests with disc specimens containing prefabricated fractures and monitored the damage process for the specimens using a high-speed camera and an acoustic emission monitoring device, aiming to investigate the fracture characteristics and breaking mechanism for black shale under the combined effect of laminations and prefabricated fractures. Numerous scholars have studied the damage mechanisms for shales containing defects through tests such as triaxial, uniaxial and Brazilian splitting (Wang et al., 2020). However, in the laboratory, the damage mechanism for naturally fractured shales is studied by the pre-preparation of fractures. It is difficult to prepare shale specimens with variable defects, especially for testing shales with natural fractures at the microscopic scale, which is basically impossible to do in the laboratory, and numerous factors limit researchers to study the damage mechanism of shales with natural fractures.
Numerical tests are sought after by academics as an alternative research tool because they enable more control over more variables and make it easier to perform tests that are otherwise difficult to carry out in the laboratory. Yu et al. studied the interaction mechanism between hydraulic and natural fractures and proposed a new numerical method called 2P-IKSPH (Yu et al., 2021). Zheng et al. developed a damage-stress-seepage coupled hydraulic fracture extension model based on the extended finite element method to investigate the interaction mechanism between hydraulic fracturing and natural fractures (Zheng et al., 2019). Liu et al. proposed a mixed-phase field approach and used the mixed-phase field model to numerically investigate the behavior of hydraulically fractured shale specimens containing prefractured laminae (Liu et al., 2020b). He et al. developed a model based on a validated particle flow program (PFC2D) to investigate the indirect tensile mechanical behavior of shales containing two central parallel cracks under Brazilian cleavage test conditions (He et al., 2021). Shi et al. developed numerical models for five different sets of prefabricated fractures with laminar dip angles to study the mechanism of fracture extension in black shale by hydraulic fracturing (Shi et al., 2018).
In summary, both indoor and numerical tests have focused on the effect of macroscopic cracking on the damage mechanism for shale, and few studies have been carried out that address the effect of natural cracking on the mechanical properties and fracture mode of shale at the microscopic scale due to the specificity of natural cracking.
To further study the microstructure, shale samples were observed by scanning electron microscopy. A natural crack was selected by electron microscopy, and the microstructure of shale with natural cracks was obtained by correlation processing. Seven groups of digital images of shale with natural cracks at different dip angles and a control group without cracks were imported by RFPA2D-DIP. Numerical models were established in turn, and numerical tests (uniaxial compression) were carried out for each of the eight groups. The mechanical properties and fracture patterns for shale specimens containing natural fractures at different dip angles are discussed and analyzed. The results of this study provide theoretical support and have important implications for the design of commercial shale gas extraction schemes.
Fenggang Shale Gas No.3 Block in Guizhou is an important part of the National Shale Gas Resources Strategic Investigation Pilot Project, which has a good geological research foundation and resource development prospects (Figure 1). The area is located in the northern part of Guizhou Province, and the administrative division is under the jurisdiction of Meitan County, Fenggang and Sinan County of Tongren Region in the southeastern part of Zunyi District, Guizhou Province. The geotectonic position of the study area is located in the eastern part of the Upper Yangzi platform area, and the tectonic evolution is consistent with the regional tectonic evolution of the Yangzi platform. The tectonic evolution of the Yangzi platform occurred during the Xue Feng movement period, the Early-Middle Garidon period, the Late Garidon period, the Haixi period, the Indo-Chinese period, the Yanshan period and the Xishan period. The superposition of multiple tectonic movements has resulted in a complex tectonic pattern for the Yangzi Plateau.
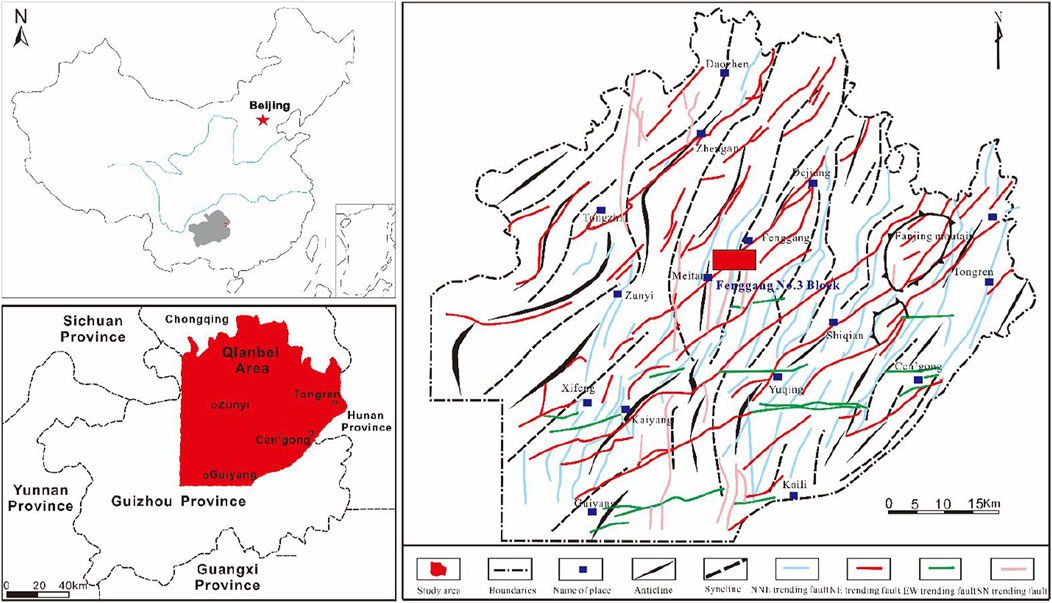
FIGURE 1. Area map of the Fenggang No.3 Block, Qianbei, Guizhou (Liu et al., 2019).
The study area is located in the southern section of the Wuling tectonic zone, and north-south, north-northeast and northeast fractures and folding structures are developed in the area and are superimposed on each other for transformation. The north-south, northeast and north-northeast folded axial surfaces and punching faults constitute the main tectonic skeleton in the area. Folds and fractures are commonly developed in the area, the folds mainly consist of north-east and north-northeast spreading “spaced trough” structures, and a series of north-east-directed compound backslopes and compound oblique structures are developed. The fractures are formed by the joint action of multiple fractures, mainly north‒northeast and northeast torsional fractures. Among these tectonic traces, the north-south oriented tectonic zone is formed at the earliest stage, the north-east oriented tectonic zone is formed at the latest stage, and the north-north-east oriented tectonic zone is formed in between the earliest and latest stages.
Observation of the fractures in the shale cores of the shale of the Niutitang Formation under the Cambrian System in Fenggang No. Three Block shows that the fracture types in the shale cores of the Niutitang Formation are mainly tectonic fractures (Figure 2A), high-angle shear fractures (Figure 2B), low-angle slip fractures (Figure 2C), construct pressure solution suture (Figure 2D), tensile fracture formed by crumping (Figure 2E) and horizontal interlayer seam (Figure 2F), among which the main fractures consist of tectonic fractures and shear fractures (Figures 2A,B).

FIGURE 2. Niutitang Formation shale fracture photos in Fenggang No.3 block. (A) Tectonic fractures. (B) High-angle shear fractures. (C) Low-angle slip fractures. (D) Construct pressure solution suture. (E) Tensile fracture formed by crumping. (F) Horizontal interlayer seam.
Scanning electron microscopy reveals that micron-to nanoscale microfractures are developed in black shale (Figure 3). The fracture lengths are approximately 1 μm–10 μm, and the widths range between 24 nm–942 nm. A few of the microfractures are filled with pyrite and clay minerals, etc., and most of them belong to the effective fractures that are not filled. For shale reservoirs with low porosity and low permeability, the development of natural fractures is of great significance for increasing shale gas production.
The shale sample used in this experiment was obtained from the Lower Cambrian Niutitang Formation stratum in the Qianbei area, and the sample color was black (Figure 4A). Scanning electron microscopy was used to further study the microstructure of the shale sample, and an electron microscope scan of the shale of the Niutitang Formation was obtained (Figure 4B). A natural fracture was selected from the electron microscope scan, and the microstructure of the shale containing natural fractures was determined by correlation processing (Figure 4C). The gray‒black color in the figure shows the shale matrix, and the dark black part shows the natural fracture inside the shale. The natural fractures in shale will affect the mechanical properties and fracture pattern of shale under uniaxial compression.

FIGURE 4. Shale macro and micro structure. (A) Macro structure of shale. (B) Scanning electron microscopy of shale. (C) Micro structure of natural fractured shale containing.
During the processing of the microstructure images of shale by RFPA2D-DIP, the selected shale microstructure images were first imported, and the differences in color and brightness were used to characterize the differences in the material and its inhomogeneity. By the threshold segmentation method, the image segmentation threshold for shale microstructure was selected based on the change in the magnitude of the I-value (which characterizes the magnitude of the brightness in the image) (Liu et al., 2020a). Figure 5A shows the selected shale microstructure image containing natural cracks under electron microscopy scanning, and in the digital image processing process, a scan line was used through the shale microstructure image containing natural cracks to obtain the curve for the change in the I value (Figure 5B). A I value threshold of 68 was obtained by multiple scanning and synthesis, which was divided into two intervals of 0–68 and 68–110, with natural cracks and the shale matrix lying in the range of 0–68 and 68–110, respectively. Figure 6 shows the digital characterization image of the processed shale from which the shape and distribution of natural cracks can be clearly observed.
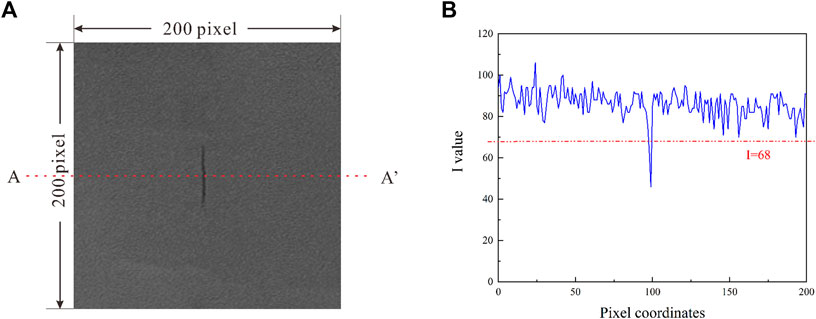
FIGURE 5. Numerical image characterization. (A) Position of scan line AA'. (B) Curve of l value on scan line AA'.
In the process of digital image processing for the shale microstructure containing natural cracks, the image consists of a large number of pixel points and each pixel point is considered as a cell; the mapping method was used to convert the cell and grid, with each small grid representing a cell, characterizing a pixel point; then, the color characteristics of each pixel point, i.e., I value, were used to classify each pixel point into different material types and assign different mechanical parameters, generating a digital image characterizing the shale. Digital images of the matrix and natural cracks were generated to establish a numerical model that corresponds to the real situation (Cui et al., 2020).
To consider the nonuniformity of shale, in RFPA2D-DIP, it was assumed that each mechanical parameter of the shale model microcell obeys a Weibull statistical distribution (Weibull, 1951):
In Eq. 1, the mechanical property parameters of the unit are characterized by α, such as the modulus of elasticity and compressive strength, where α0 characterizes the average value of the mechanical property parameters for the unit and m characterizes the homogeneity of the material; the more homogeneous the material, the larger the m. According to the literature (Zhu et al., 2011; Lou et al., 2020; Wu et al., 2020), each known mechanical parameter for the shale is shown in Table 1. In order to study the mechanical properties, rupture process and acoustic emission signal evolution characteristics of shale containing different inclination angles of natural cracks at microscopic scale, so as to establish numerical models of shale specimens with internal natural crack inclination angles of 0°, 15°, 30°, 45°, 60°, 75°, 90° and control group without natural cracks under uniaxial compression conditions, a total of 8 groups, were tested numerically by RFPA2D-DIP, and the mechanical loading model is shown in Figure 7, loaded by displacement control volume.
Figure 8 shows the stress‒strain curves for shale containing natural cracks with different inclination angles under uniaxial compression. The stress‒strain curves for the 90° and control specimens show good consistency, except that the peak compressive strength of the control specimens is higher than that of the 90° specimens, and the stress‒strain curves can be summarized in four stages: linear elastic stage, yield stage, rupture stage, and stability stage, which are typical of brittle damage.
The stress‒strain curves corresponding to 0°, 15°, 30°, 45°, 60°, and 75° specimens show inconsistency with the corresponding curves obtained for the control group, which can be mainly divided into two types: 0°, 60°, and 15°, 30°, 45°, and 75°. Both types undergo multiple stress drops during the rupture process, and the peak stresses for 0° and 60° all occur at the second stress drop, while 15°, 30°, 45°, and 75° peak stresses all occur at the first stress drop.
Taking 60° as an example, the first stage is the linear elastic stage, where with an increase in displacement loading, the stress increases linearly; the second stage is the first yielding stage, where the continued loading leads to a gradual nonlinear increase in the stress until it reaches the initial stress peak and the rock ruptures; the third stage is the initial rupture stage, where the rock ruptures for the first time, which leads to a linear decline in the stress; and the fourth stage is the second stressing. The fourth stage is the secondary stress stage, where after the initial rupture of the rock with increasing displacement loading, the stress again increases nonlinearly until the second time to reach the peak stress, with the second peak stress being higher than the peak stress of the first rupture; the fifth stage is the repetition stage, where with increasing displacement loading, the phenomenon of multiple stress drops occurs; the sixth stage is the stability stage, where the stress tends to stabilize and no longer change with increasing displacement loading stress size.
This is because the shale fractures in the 0°–75° tests were initiated by natural fractures in the shale, and after the first stress peak in the fracture process, the stress drops and then rises again, reciprocating until the fracture is complete. The shale can continue to withstand the load after the initial stress drop, and the existence of this phenomenon is related to the inclination of the natural fractures and the way the shale is fractured. The 90° test was not initiated by a natural fracture in the shale, so only one stress drop is found to occur.
The relationship between the peak stress, elastic modulus and different crack inclination angles was obtained by simulating numerical experiments with different crack inclination angles, as shown in Figure 9. The overall trend for the peak stress and elastic modulus of shale increases with increasing natural crack inclination angle, which is basically consistent with the conclusion obtained in the literature (Liu et al., 2020c). Only the 15° and 60° shale specimens show a decrease in peak stress, while the 15° and 45° shale specimens show a decrease in elastic modulus. The peak stress is found to occur at 62.8 MPa at 0°, 60.8 MPa at 15°, 67.5 MPa at 30°, 71.8 MPa at 45°, 71.1 MPa at 60°, 82.9 MPa at 75°, 86.9 MPa at 90°, and 98.7 MPa in the control group; the control group shows clearly different behavior due to the presence of natural cracks. The overall trend is that as the angle of the natural cracks contained in the shale increases, the stress loss that occurs in the uniaxial compression process for the shale is 36.4% for 0°, 38.4% for 15°, 31.6% for 30°, 27.3% for 45°, 27.9% for 60°, 16% for 75°, and 11.9% for 90°. The overall trend is that as the natural fracture angle in the shale increases, the stress loss that occurs in uniaxial compression decreases. In general, the peak stress and elastic modulus of shale increase as the natural crack angle in shale increases, and, conversely, the stress loss that occurs in shale decreases.
Figure 10 shows the fracture process and acoustic emission diagram for the microstructure of naturally fractured shale with different dip angles under uniaxial compression. It is obvious from the rupture process of natural fractured shale containing different inclination angles that the rupture process for natural fractured shale containing different inclination angles is mainly divided into three processes: crack initiation, crack expansion and crack penetration. Figure 10A shows the crack initiation stage for the shale damage process, Figure 10B shows the crack expansion stage, Figure 10C shows the crack penetration stage, and Figure 10D shows the shale crack. The acoustic emission map corresponds to the penetration stage due to the different angles of the natural fracture, which leads to different fracture initiation points, different fracture extension processes, and, finally, different fracture patterns. There are four main categories as follows:
1) Cracking perpendicular to the natural crack and finally forming a similar I-type crack (0°): In the uniaxial compression state where the natural crack is inclined at an angle of 0°, first, the natural crack in the middle of the shale is gradually compressed with increasing displacement loading, and tiny cracks sprout up and down from the middle of the natural crack. As the crack gradually expands upward and downward, new cracks begin to sprout on the right side of the lower sprouting crack and mainly along the new crack. The upper side is mainly located along the initial sprouting crack until penetration and finally connects and penetrates to form a similar I-type crack, producing more microcracks in the lower half of the main crack and fewer in the upper half.
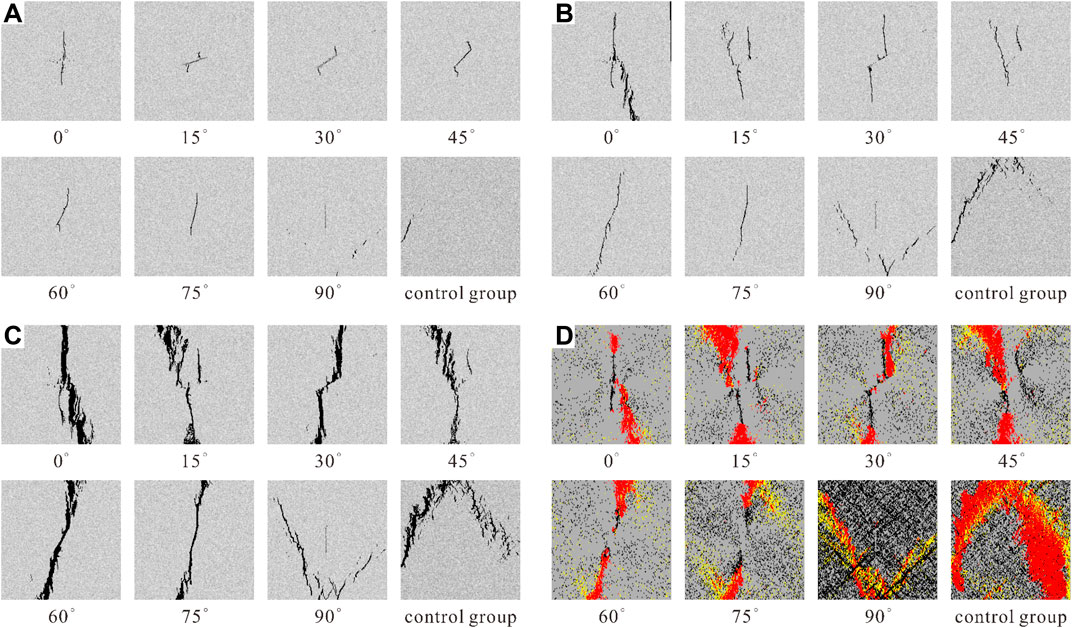
FIGURE 10. Fracturing process of microstructure of shale. (A) Crack initiation. (B) Crack propagation. (C) Fracture mode. (D) Acoustic emission.
In the process of the natural crack being compacted, due to the irregularity of the natural crack (wide in the middle and narrow at the ends), the middle of the natural crack is cracked by tension, and tensile damage occurs in the unit. As the natural crack is compacted, the crack tip is gradually extended up and down by tension, while the rest of the unit undergoes sporadic shear damage until the crack penetrates the specimen.
2) Inclined or along both sides of the natural crack, eventually forming oblique I-type cracks (15°, 45°, 60°, 75°): taking 45° as an example, in the uniaxial compression state where the natural crack is inclined at an angle of 45°, the cracks sprout at both ends of the natural crack, close to perpendicular to the natural crack, and then expand upward and downward with the starting crack, and it can be observed in the crack expansion stage that the cracks on the sitting side extend upward. The crack on the upper right side only extends upward along the emergent crack, and the natural crack with an inclination of 45° is gradually compacted in the crack extension stage, and finally extends upward and downward along the emergent crack on the lower left side to expand into a through crack. Meanwhile, the crack on the upper right side only extends partly in the extension stage and does not form a through crack, and the rupture process for the specimen at 15° is similar to that described above, which is only the initial emergent crack, which does not start at the two ends of the natural crack, but at a distance from the two ends of the natural crack. For the 60° and 75° specimens, it is obvious that the emergent crack starts from the natural crack, and the angle and direction of the crack extension is located nearly up and down along both sides of the natural crack. With continuous loading, the crack extends continuously to form an oblique I-type through crack, and more tiny cracks are produced at the upper and lower ends of the crack near the penetration cracks.
With an increase in displacement loading, tensile damage occurs at both ends of the natural crack, cracks sprout, and with the extension of the sprouted crack, in addition to tensile damage at the extended crack, the rest of the sporadic units show shear damage. When the sporadic rupture of the unit leads to the formation of a crack, crack extension occurs when tensile damage occurs, and the cracks formed penetrate each other to form the main crack and penetration.
3) Tilted cracking on both sides of the natural crack, eventually forming a folding crack (30°): in the uniaxial compression state with a natural crack tilt angle of 30°, the crack starts to form along both sides of the natural crack, the starting angle is nearly vertical, the lower left side starts cracking downward, the upper right side starts cracking upward. With continuous loading until the crack penetrates, a folding through crack is formed, with the natural crack and the sprouting crack around sprouting many tiny secondary cracks, especially with a short vertical crack sprouting in the middle of the natural crack, which does not extend and expand again.
For a natural crack inclination of 30°, with ab increase in loading, tensile damage occurs at both ends of the natural crack, sprouting cracks and expansion, sporadic shear damage units do not form through cracks, and with the extension of the crack, the formation of tensile damage mainly occurs via cracking.
4) Crack initiation not along the natural crack, eventually forming V-shaped cracks (90°) and inverted V-shaped cracks (control group): in the uniaxial compression state with a natural crack inclination angle of 90°, it is obvious that the crack initiation does not occur from the natural crack but involves the sprouting of tiny cracks on the lower right side and the lower left side of the specimen, respectively, and with continuous loading, the cracks on the left and right sides extend continuously, forming penetration cracks that are nearly V-shaped. With continuous loading, the cracks on the left and right sides are extended, forming a penetration crack that is nearly V-shaped and more micro cracks appear on the lower part, while the control specimen is cracked from the left side, and the cracks are extended diagonally upward to the top and then extended along the lower right side, finally forming an inverted V-shaped penetration crack and more secondary cracks along the main crack.
For a natural crack inclination angle of 90°, crack initiation and expansion are not affected by the natural crack. With an increase in displacement loading, unit shear damage occurs, and with an increase in the number of damaged units, cracks gradually form under tensile and shear extension and expansion.
The fracture pattern diagrams and acoustic emission diagrams for naturally fractured shale with different dip angles show good agreement between acoustic emission and the fracture pattern of the shale. In the acoustic emission diagrams of natural fractured shale with different inclination angles, the red characterized unit is damaged in tension at the current loading step, the yellow characterized unit is damaged in compression shear at the current loading step, and the black characterized unit is completely damaged at the current loading step. In the uniaxial compression state when the natural crack inclination angle is 0°, 15°, 30°, and 45°, it can be found that most of the cells in the main crack part of the rupture process suffer from tensile damage, and the rest of the cells are accompanied by a small amount of compression shear damage. In the uniaxial compression state when the natural crack inclination angle is 60° and 75°, it can be found that most of the cells in the main crack part of the rupture process suffer from tensile damage. However, for the uncracked uniaxial compression, when the natural crack inclination is 90°, it can be found that the cracking process is accompanied by tensile and compression shear damage in the main cracked units.
The stress distribution characteristics of the microstructure of naturally cracked shale containing different inclination angles under uniaxial compression are shown in Figure 11, and the color brightness in the stress distribution diagram represents the magnitude of the stress; the brighter the color, the higher the stress. In the initial stage (Figure 11A), when the natural crack inclination angle is 0°, it is obvious that there is an obvious stress concentration effect at the ends of both sides of the natural crack, while the middle of the crack has less stress; for a natural crack inclination angle of 15°, 45°, 60° and 75°, it is obvious that the stress is mainly concentrated on the left end and the right end of the natural crack; for a natural crack inclination angle of 30°, the stress is concentrated on the ends of both sides of the crack, and the stress is concentrated on the upper and lower sides of the crack, followed by the formation of irregular cracks distributed in a jagged pattern; for a natural crack inclination of 90°, the stress distribution is similar to that of the control group test, which has little relationship with the vertical natural crack, and the crack mainly affects the overall strength size of the shale. In the extension stage (Figure 11B), the 0° specimen cracks vertically upward and downward from the middle, and the stress is still concentrated at both ends of the natural crack; the 15° specimen cracks upward and downward not far from the end of the crack, and the stress is still mainly concentrated at both sides of the end of the crack; the 30°, 45°, 60°, and 75° specimens crack from both ends of the crack, and the stress follows the distribution of the new crack as the crack opens; the 90° specimen cracks from the lower part of the specimen, and the stress is mainly concentrated at both sides of the new cracks. This indicates that the presence of natural cracks within the shale has a significant effect on the stress distribution.

FIGURE 11. Stress distribution of microstructure of shale. (A) Stress distribution in the initial stage. (B) Stress distribution in the extension stage.
Figure 12 shows the relationship between the stress, loading step, acoustic emission and cumulative acoustic emission for different natural crack inclination angles. In the RFPA2D-DIP numerical test, one acoustic emission event characterizes the microrupture of a cell, and the cumulative acoustic emission is the cumulative sum of acoustic emission events, which characterizes the overall number of cell microruptures (Liu et al., 2020c). As shown in Figure 12, the stress-loading step and the acoustic emission-loading step show good agreement, and the change phase for acoustic emission basically coincides with the change phase for shale stress.
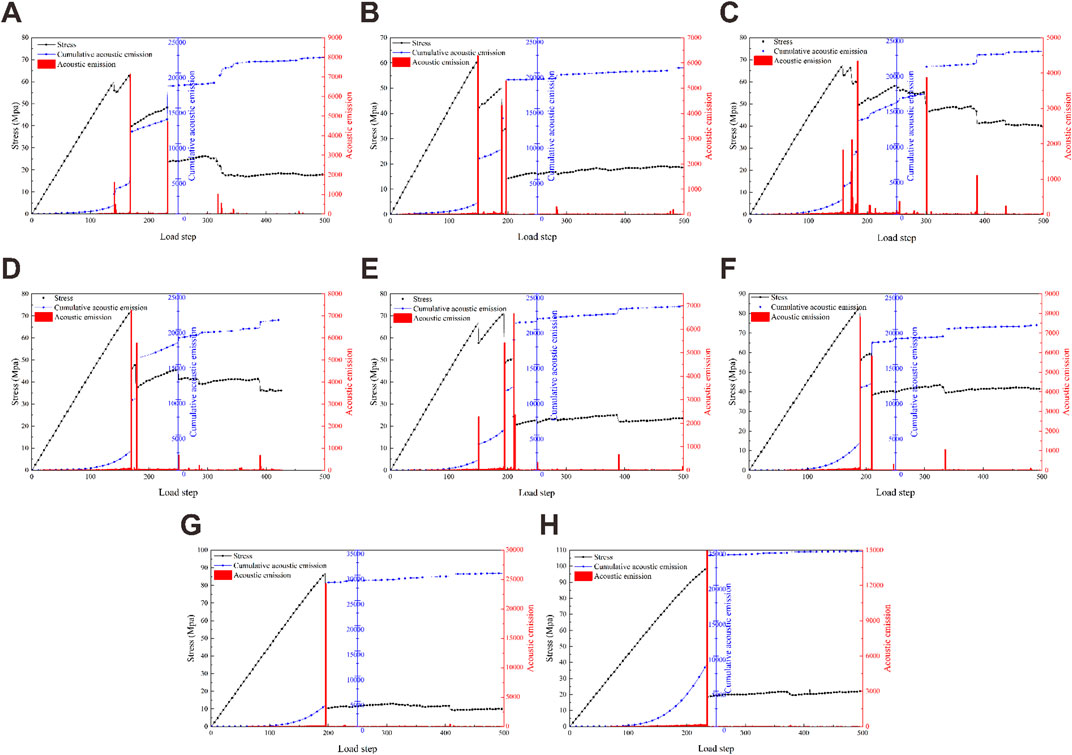
FIGURE 12. Relationship among stress, AE count, cumulative AE count and loading steps under different angle. (A) 0°, (B) 15°, (C) 30°, (D) 45°, (E) 60°, (F) 75°, (G) 90°, (H) Control group.
In the eight sets of tests described in this paper, the tests with a natural crack inclination of 90° show the same trend as that for the control group (Figures 12G,H). Taking the uniaxial compression natural crack of 90° as an example (Figure 12G), in the first stage, the specimen shows a flat - nonlinear the accumulated acoustic emission. In the initial stage of loading (loading steps of 0–63), with increasing number of loading steps, the stress gradually increases, the number of acoustic emission events is 0, the accumulated acoustic emission number is also 0, showing a flat acoustic emission. In the process of gradual loading (loading steps of 64–196), with an increase in displacement loading, the stress continues to increase, the internal units of the shale begin to gradually undergo damage, the acoustic emission events gradually increase from 0, the accumulated acoustic emission exhibits nonlinear growth, and the stress magnitude gradually approaches the peak stress; In the second stage, the cumulative acoustic emission shows a sudden change—flat, as the loading step is further increased (loading step is 196), the stress reaches a peak, and the number of acoustic emission events also reaches a peak, the shale cracks expand rapidly, and the cumulative acoustic emission grows abruptly, then the shale is completely destroyed. At this time, upon a further increase in the loading step (loading step is 197-), the stress magnitude shows a smooth change, and the number of acoustic emission events is close to 0. The cumulative acoustic emission shows a flattening. During the whole process for the natural crack dip angle of 90° and the control group, only one stress drop occurs, i.e., the stress instantaneously levels off after reaching the peak, and the acoustic emission and cumulative acoustic emission also level off after showing abrupt changes at the same loading step.
In six sets of tests with natural crack inclination angles of 0°, 15°, 30°, 45°, 60°, and 75° in uniaxial compression (Figures 12A–F), a minimum of two stress drops occur during loading, and a minimum of two sudden changes in acoustic emission and cumulative acoustic emission are observed. For the example of natural cracking in uniaxial compression at 75° (Figure 12F), the first stage of cumulative acoustic emission shows a flat—nonlinear response; in the initial stage of loading (loading steps 0–32), with an increasing number of loading steps, the stress gradually increases, the number of acoustic emission events is 0, the number of cumulative acoustic emission is also 0, showing a flat response. In the process of gradual loading (loading steps 33–189), with an increase in displacement loading, the stress continues to increase, the shale internal unit is gradually damaged, acoustic emission events gradually increase from 0, the cumulative acoustic emission shows a nonlinear growth, and the stress magnitude gradually approaches the peak stress observed for the first stress drop phenomenon; The cumulative acoustic emission in the second stage shows abrupt - nonlinear - abrupt - nonlinear - abrupt—flat behavior. With a gradual increase in the number of loading steps (190-), the specimen shows a total of three stress drop phenomena, and three abrupt changes in the corresponding acoustic emission and cumulative acoustic emission are observed to occur at loading steps of 190, 210, and 335, respectively, and the number of acoustic emission events is 7808, 5812, and 1040, corresponding to stress values of 82.97, 59.79, and 39.43 MPa, respectively, before leveling off.
Therefore, it is concluded that the acoustic emission signal shows good agreement with the variation in the mechanical properties and fracture process for naturally fractured shale containing different dip angles, as discussed above, and the acoustic emission can reflect the stress variation and fracture process for naturally fractured shale containing different dip angles at the microscopic scale.
Fractal theory can be used to quantitatively describe irregularities and complexities, which naturally includes the evolution of rock fractures. The fractal dimension DS can be used to quantitatively describe the intensity and complexity of rock fractures (Zhang et al., 2018). In this paper, images of rock fractures at different stress levels with different natural crack inclinations were imported into a MATLAB calculation program to determine their corresponding fractal dimensions. The fractal dimension DS is solved as follows (Zhang et al., 2015):
where Ds is the fractal dimension of the damaged region, r is the side length of the square box, and N(r) is the number of square boxes with side length r needed to cover the damaged region therein.
Table 2 shows the values for the AE energy and fractal dimension DS for different stress levels at different natural crack inclination angles, and Figure 13 shows the relationship between the stress level and AE energy and fractal dimension at different natural crack inclination angles. As shown in the figures, the AE energy increases with increasing stress level at any natural crack inclination angle; the overall trend is that the AE energy value corresponding to the peak stress increases with increasing natural crack inclination angle but decreases at a natural crack inclination angle of 75°, which is because at a natural crack inclination angle of 75°, the specimen extends along the direction of the crack inclination angle at both ends of the natural crack without extending the complex crack, the rupture form is simple, and the number of ruptured units is small.
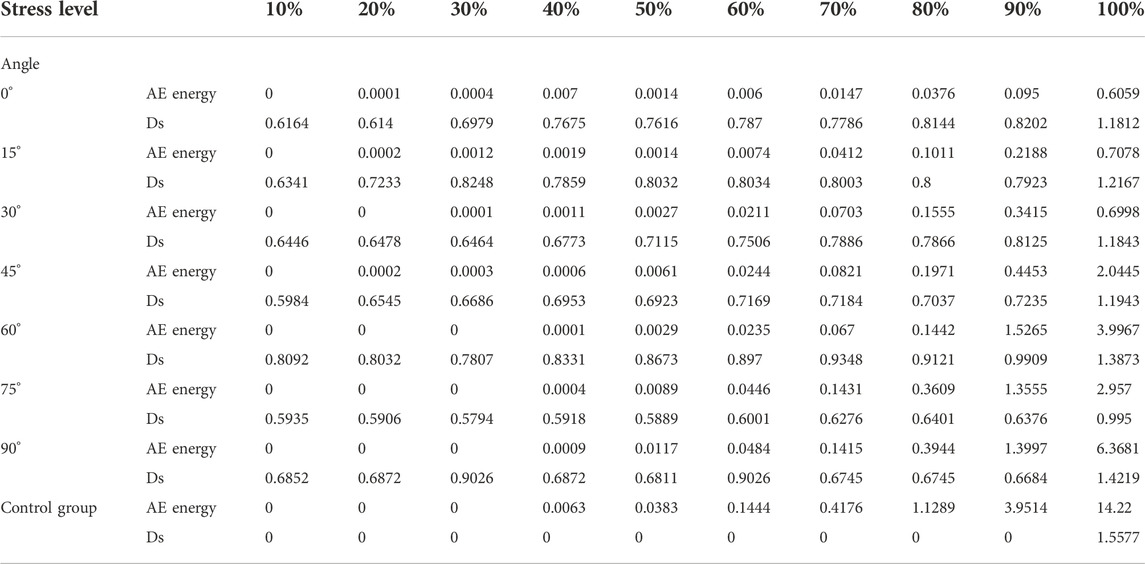
TABLE 2. AE energy and fractal dimension Ds at different stress levels for different natural crack inclination angles.
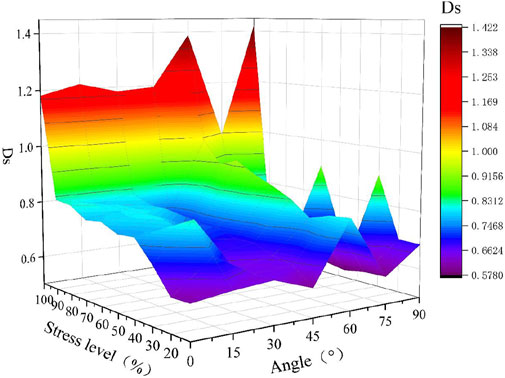
FIGURE 13. Plot of stress level versus fractal dimension Ds for different natural crack inclination angles.
As shown in the graph, the fractal dimension of the specimens from 0° to 90° is not 0 at a stress level of 10% due to the presence of natural cracks, while the fractal dimension values for the control group specimens, are 0 at the 10%–90% stress level due to the absence of natural cracks, and only when the stress level is 100% is the fractal dimension value 1.5577, which also shows the brittleness of the rock. For example, for a natural crack inclination of 0°, the fractal dimension value is 0.6164 at a stress level of 10%; due to the unevenness of the natural crack (wide at the middle and narrow at the ends), the shale is stressed to split from the middle of the natural crack up and down; when the stress level is 20%, the fractal dimension value is 0.614, which is slightly less than that at a stress level of 10%, which is because although the stress is increased (the crack splitting from the middle of the natural crack also expands) the increase in the stress also leads to compression of the natural crack to a certain extent, so the fractal dimension value is slightly reduced; in the process of increasing the stress level from 20% to 100%, the fractal dimension value zigzags upwards, which is because although the stress-induced crack expands, the natural crack is also gradually compressed, and the new cracks and the native natural cracks together affect the fractal dimension. In the test where the natural crack inclination angle ranges from 30°–90°, the value of fractal dimension is also influenced by the new cracks and the native natural cracks.
With an increase in the natural crack inclination angle, the fractal dimension value at the peak stress under the overall trend also increases, and the fractal dimension value at 90° is 1.4219, which is the maximum value of the fractal dimension in the test from 0° to 90°. However, for a natural crack inclination angle of 75°, the fractal dimension value is only 0.995, which is the same as the change law for the AE energy value because it cracks with both ends of the natural crack, and the fractal dimension value is only 0.995 for a natural crack inclination angle of 75°.
In summary, the magnitude of the AE energy is increased with increasing stress level in 0°–90° tests and reaches a maximum value at 90°, while the fractal dimension value zigzags upwards, which is due to the joint influence of the newborn cracks and the native natural cracks. In the process of increasing the stress level, the natural cracks are compacted, and the compacting phenomenon is decreased with increasing inclination angle of the natural cracks. In the control test, both AE energy and fractal dimension values are increased with increasing stress level. The overall trend for the AE energy and fractal dimension values under peak stress show a continuous increase with increasing inclination angle of the natural crack, while the maximum value is reached in the control test, and only a significant decrease is observed in the 75° test, which is because the 75° specimen extends along the direction of the crack inclination angle at both ends of the natural crack without extending the other cracks, i.e., the rupture form is simple.
Shale specimens obtained from the Lower Cambrian Niuhuitang Formation of the Qianbei region were studied in this paper. The shale samples were observed by scanning electron microscopy, a natural crack was selected, and the microstructure of the shale with natural cracks was obtained by correlation processing. Seven groups of digital images of shale with natural cracks at different dips and a control group without cracks were imported using RFPA2D-DIP. Numerical models were built in turn, numerical tests (uniaxial compression) were carried out for each of the eight groups of specimens, and the following conclusions were obtained:
1) The dip angle for the natural fracture has an important influence on the mechanical characteristics of shale. As the natural fracture inclination angle increases, the peak stress and modulus of elasticity of shale as a whole tend to increase; however, compared to the intact specimens, the strength loss due to the natural fracture tends to show an overall decrease, and during fracture, the damage is more complex compared to that for the control group, except for the specimens with a natural fracture inclination angle of 90°, where one or two stress drops occur after the peak stress.
2) The dip angle of the natural fracture has an important influence on the fracture pattern of the shale. The fracture patterns for shales containing natural fractures at the microscopic scale can be broadly divided into four categories: when the natural fracture inclination angle is 0°, the central part of the fracture is cracked in tension and is accompanied by the compression of the natural fracture to extend in the direction of loading, eventually forming a similar I-shaped fracture; when the natural fracture inclination angle is 15°, 45°, 60°, and 75°, tensile damage occurs at the ends of the natural fracture, accompanied by the extension of the budding fracture and microfracture connection. When the natural crack inclination angle is 30°, the natural crack end produces a wing-shaped crack and continues to stretch and break along the wing crack, eventually forming a folded crack; when the natural crack inclination angle is 90°, the crack initiation and expansion is not affected by the natural crack, and a V-shaped crack is eventually formed as the microcrack expands, connects and penetrates.
3) The microstructure of shale has an important influence on the main stress distribution. In the initial stage, the stresses in the 0°–75° specimens are mainly distributed at the ends of the fractures or at the top and bottom sides, while the 90° specimens show no obvious stress distribution at the natural fractures; in the rupture stage, the stresses in the 0° and 15° specimens are still mainly distributed at the ends of the fractures, while the stresses in the 30°–90° specimens are distributed in the direction of fracture expansion, and the stress concentration phenomenon is obvious. This indicates that the presence of natural cracks within the shale has a significant influence on the distribution of the principal stresses.
4) Acoustic emission can reflect the stress changes and rupture process for naturally fractured shales containing different dip angles at the microscopic scale. In the 0°–90° test, the magnitude of the AE energy is positively correlated with the stress level, and the overall trend for the AE energy increases with increasing inclination angle of natural fractures at peak stress, with a significant decrease observed only in the 75° test.
5) The presence of natural cracks has a significant effect on the fractal dimension. The fractal dimension is controlled by both natural and nascent cracks and is increased with increasing stress level, with the fractal dimension at peak stress increasing with the natural crack inclination, except for the 75° test, where it shows a significant decrease.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Writing-original draft preparation, CY; writing-review and editing, ZW; methodology, CY; software, CY; formal analysis, CY; investigation, WW; resources, HL; data curation, HQ and NR; funding acquisition, ZW All authors have read and agreed to the published version of the manuscript.
This research was funded by the National Natural Science Foundation of China, grant number 51964007, 51774101 and 52104080, Guizhou Science and Technology Fund, grant number [2020]4Y046, [2019]1075, and [2018]1107.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ban, Y., Fu, X., Xie, Q., Duan, J., and Abdullah, R. (2021). Failure characteristics of obliqued-layers shale specimens from ex-perimental observation. Arab. J. Sci. Eng. 46, 10757–10770. doi:10.1007/s13369-021-05538-2
Chen, J., Li, Y., Ma, H., Wang, X., and Li, S. (2020). Experimental study on the three-axis compression of shale considering the influence of the crack. Sci. Technol. Eng. 20 (26), 10778–10782.
Cui, H., Wu, Z., Lou, Y., Zuo, Y., Sun, W., and Liu, H. (2020). Numerical experiment on damage and fracture of shale based on micro-scale. Coal Geol. Explor. 48 (5), 137–143.
Feng, X., Ma, F., Zhao, H., and Guo, J. (2021). Numerical simulation of hydraulic fracturing in shale gas reservoirs under fault influence. J. Eng. Geol. 29 (3), 751–763.
He, B., Liu, J., Zhao, P., and Wang, J. (2021). PFC2D-based investigation on the mechanical behavior of anisotropic shale under Brazilian splitting containing two parallel cracks. Front. Earth Sci. 15 (4), 803–816. doi:10.1007/s11707-021-0895-8
Heng, S., Yang, C., Zhang, B., Guo, Y., Wang, L., and Wei, Y. (2015). Experimental research on anisotropic properties of shale. Rock Soil Mech. 36 (03), 609–616.
Hu, Y., Li, X., Zhang, Z., He, J., and Li, G. (2020). Numerical investigation on the hydraulic stimulation of naturally fractured Longmaxi shale reservoirs using an extended discontinuous deformation analysis (DDA) method. Geomech. Geophys. Geo-energ. Geo-resour. 6, 73. doi:10.1007/s40948-020-00195-5
Jin, J., Zheng, X., Fu, Y., Chen, T., Yang, D., and Zhong, H. (2021). Experimental study of acidization impact to pore topo-logical structure variation of Niutitang shale. J. Eng. Geol. 29 (3), 891–900.
Ju, W., Wu, C., and Sun, W. (2018). Effects of mechanical layering on hydraulic fracturing in shale gas reservoirs based on numerical models. Arab. J. Geosci. 11, 323. doi:10.1007/s12517-018-3693-1
Lan, H., Chen, J., and Wu, Y. (2018). Spatial characterization of micro- and nanoscale micro-cracks in gas shale before and after triaxial compression test. J. Eng. Geol. 26 (1), 24–35.
Lee, H., and Jeon, S. (2011). An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression. Int. J. Solids Struct. 48, 979–999. doi:10.1016/j.ijsolstr.2010.12.001
Lisjak, A., Grasselli, G., and Vietor, T. (2014). Continuum–discontinuum analysis of failure mechanisms around unsupported circular excavations in anisotropic clay shales. Int. J. Rock Mech. Min. Sci. (1997). 65, 96–115. doi:10.1016/j.ijrmms.2013.10.006
Liu, H., Zuo, Y., Wu, Z., Sun, W., and Xi, S. (2020). Study of concrete internal crack growth deformation law and fracture process using digital images. Concrete (01), 32–37+40.
Liu, J., Cao, X., Xu, J., Yao, Q., and Ni, H. (2020). A new method for threshold determination of gray image. Geomech. Geophys. Geo-energ. Geo-resour. 6, 72. doi:10.1007/s40948-020-00198-2
Liu, J., Liang, X., Xue, Y., Fu, Y., Yao, K., and Dou, F. (2020). Investigation on crack initiation and propagation in hydraulic fracturing of bedded shale by hybrid phase-field modeling. Theor. Appl. Fract. Mech. 108, 102651. doi:10.1016/j.tafmec.2020.102651
Liu, Y., Gao, D., Li, Q., Wan, Y., Duan, W., Zeng, X., et al. (2019). Mechanical frontiers in shale-gas development. Adv. Mech. 49 (00), 1–236.
Lou, Y., Wu, Z., Sun, W., Yin, S., Wang, A., Liu, H., et al. (2020). Study on failure models and fractal characteristics of shale under seepage-stress coupling. Energy Sci. Eng. 8, 1634–1649. doi:10.1002/ese3.621
Nezhad, M., Fisher, Q., Gironacci, E., and Rezania, M. (2018). Experimental study and numerical modeling of fracture propagation in shale rocks during Brazilian disk test. Rock Mech. Rock Eng. 51, 1755–1775. doi:10.1007/s00603-018-1429-x
Shi, X., Zhang, X., Wang, B., Tang, T., and Han, W. (2018). Hydraulic fracturing test with prefabricated crack on anisotropic shale, Laboratory testing and numerical simulation. J. Petroleum Sci. Eng. 168, 409–418. doi:10.1016/j.petrol.2018.04.059
Shrestha, N., Chilkoor, G., Wilder, J., Gadhamshetty, V., and Stone, J. J. (2016). Potential water resource impacts of hydraulic fracturing from unconventional oil production in the Bakken shale. Water Res. 108, 1–24. doi:10.1016/j.watres.2016.11.006
Wang, G., Xiao, Y., Zhao, H., Wang, Y., and Chen, Y. (2019). Application of microseismic monitoring technology to re–fracturing of shale gas horizontal wells. Geol. Explor. 55 (5), 1336–1342.
Wang, H., Li, Y., Cao, S., Pan, R., Yang, H., Zhang, K., et al. (2020). Brazilian splitting test study on crack propagation process and macroscopic failure mode of pre-cracked black shale. Chin. J. Rock Mech. Eng. 39 (05), 912–926.
Wang, R., Gu, Y., Ding, W., Gong, D., Yin, S., Wang, X., et al. (2016). Characteristics and dominant controlling factors of organic-rich marine shales with high thermal maturity, A case study of the Lower Cambrian Niutitang Formation in the Cen’gong block, southern China. J. Nat. Gas Sci. Eng. 33, 81–96. doi:10.1016/j.jngse.2016.05.009
Wang, S., Zhao, J., and Li, Y. (2014). Hydraulic fracturing simulation of complex fractures growth in naturally fractured shale gas reservoir. Arab. J. Sci. Eng. 39, 7411–7419. doi:10.1007/s13369-014-1221-5
Wang, Y., Li, X., Zhang, Y., and Zheng, B. (2016). Gas shale hydraulic fracturing, a numerical investigation of the fracturing network evolution in the Silurian Longmaxi formation in the southeast of Sichuan Basin, China, using a coupled FSD approach. Environ. Earth Sci. 75, 1093. doi:10.1007/s12665-016-5696-0
Wei, Y., Yang, C., Guo, Y., Liu, W., Wang, L., and Heng, S. (2015). Experimental investigation on deformation and fracture characteristics of brittle shale with natural cracks under uniaxial cyclic loading. Rock Soil Mech. 36 (06), 1649–1658.
Weibull, W. (1951). A statistical distribution function of wide applicability. J. Appl. Mech. 18, 293–297. doi:10.1115/1.4010337
Wu, Z., Lou, Y., Yin, S., Wang, A., Liu, H., Sun, W., et al. (2020). Acoustic and fractal analyses of the mechanical properties and fracture modes of bedding-containing shale under different seepage pressures. Energy Sci. Eng. 8, 3638–3656. doi:10.1002/ese3.772
Wu, Z., Zuo, Y., Wang, S., Chen, J., Wang, A., Liu, L., et al. (2017). Numerical study of multi-period palaeotectonic stress fields in Lower Cambrian shale reservoirs and the prediction of fractures distribution, A case study of the Niutitang Formation in Feng'gang No. 3 block, South China. Mar. Pet. Geol. 80, 369–381. doi:10.1016/j.marpetgeo.2016.12.008
Wu, Z., Zuo, Y., Wang, S., Sun, W., and Liu, L. (2018). Experimental study on the stress sensitivity and influence factors of shale under varying stress. Shock Vib. 2018, 1–9. doi:10.1155/2018/3616942
Xu, X., Shen, B., Li, Z., Zhang, W., Yu, L., and Ma, Z. (2020). Status and prospect of experimental technologies of geological evaluation for shale gas. Reserv. Eval. Dev. 10 (1), 1–8.
Yu, S., Ren, X., Wang, H., Zhang, J., and Sun, Z. (2021). Numerical simulation on the interaction modes between hydraulic and natural fractures based on a new SPH method. Arab. J. Sci. Eng. 46, 11089–11100. doi:10.1007/s13369-021-05672-x
Zhang, R., Dai, F., Gao, M., Xu, N., and Zhang, C. (2015). Fractal analysis of acoustic emission during uniaxial and triaxial loading of rock. Int. J. Rock Mech. Min. Sci. (1997). 79, 241–249. doi:10.1016/j.ijrmms.2015.08.020
Zhang, S., Shou, K., Xian, X., Zhou, J., and Liu, G. (2018). Fractal characteristics and acoustic emission of anisotropic shale in Brazilian tests. Tunn. Undergr. Space Technol. 71, 298–308. doi:10.1016/j.tust.2017.08.031
Zhao, P., Xie, L., Ge, Q., Zhang, Y., Liu, J., and He, B. (2020). Numerical study of the effect of natural fractures on shale hydraulic fracturing based on the continuum approach. J. Petroleum Sci. Eng. 189, 107038. doi:10.1016/j.petrol.2020.107038
Zheng, H., Pu, C., and Tong, I. (2019). Study on the interaction mechanism of hydraulic fracture and natural fracture in shale formation. Energies 12, 4477. doi:10.3390/en12234477
Zhu, Y., Liu, K., Zhong, X., Wang, Y., Chen, C., Zhang, H., et al. (2021). Experimental investigation on the anisotropic behaviors induced by bedding planes in mechanical properties of ma'quan oil shale. Arab. J. Sci. Eng. 47, 11385–11403. doi:10.1007/s13369-021-06027-2
Zhu, Z., Xiao, P., Sheng, Q., Liu, J., and Leng, X. (2011). Numerical simulation of fracture propagation of heterogeneous rock material based on digital image processing. Rock Soil Mech. 32 (12), 3780–3786.
Keywords: natural crack, peak stress, rupture mode, stress distribution, acoustic emission, fractal dimension
Citation: Yang C, Wu Z, Wang W, Qu H, Ren N and Li H (2023) Study on the influence of natural cracks on the mechanical properties and fracture mode for shale at the microscale: An example from the Lower Cambrian Niutitang Formation in northern Guizhou. Front. Earth Sci. 10:1032817. doi: 10.3389/feart.2022.1032817
Received: 31 August 2022; Accepted: 31 October 2022;
Published: 12 January 2023.
Edited by:
Jingshou Liu, China University of Geosciences Wuhan, ChinaReviewed by:
Jianhua He, Chengdu University of Technology, ChinaCopyright © 2023 Yang, Wu, Wang, Qu, Ren and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhonghu Wu, d3V6aG9uZ2h1Z3p1QDE2My5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.