Regulation effect of slit-check dam against woody debris flow: Laboratory test

Woody debris flows (i.e., debris flows carrying wood) are common in mountainous and forested areas. They can cause more severe hazards due to the effects of LW (woody debris larger than 1 m in length and 10 cm in width) compared to debris flows without LW. Mitigation structures for debris flows have considered little of the regulating effect on LW and the influence of LW on the regulation effect of sediment. Thus, model tests were conducted to discuss the regulation effects of slit-check dams on woody debris flow. Research results demonstrated that slit-check dams can effectively regulate woody debris flows without overflows. Once overflow occurs, sediment trapping efficiency and the wood retention rate dramatically decrease. The sediment trapping efficiency of slit-check dams on debris flows without LW shared a linear relationship with the relative opening width, the height-to-width ratio of the opening, and the opening density. However, this was also influenced by the wood retention rate for woody debris flow. A logarithmic relationship between the sediment trapping rate and wood retention rate was obtained. The wood retention rate is mainly determined by the ratio of the LW length to the opening width, the ratio of the LW length to the channel width and the opening density of the slit-check dam. Three draining patterns of woody debris flows at the slit-check dam and three clogging types of LW at the openings of the slit-check dam were observed. Some design criteria for the structure parameters of the slit-check dam were proposed. These research results promote a better understanding of the regulation effect of slit-check dams on woody debris flows and provide a basis for the optimal design of slit-check dams.

Introduction

With the recent increase of global warming and extreme weather, mountain disasters are occurring more frequently and with a high magnitude. With the phenomenon of mountain torrents and debris flows transporting woody debris, woody debris flows have been reported worldwide and the hazardous effects of LW (large wood more than 1 m in length and 10 cm in diameter) have been highlighted in many studies (Gao et al., 2005; Comiti et al., 2008; Ana et al., 2015; Henshaw et al., 2015; Steeb et al., 2016; Xie et al., 2020a). An extreme flood that occurred in August 2005 in Switzerland was considered the costliest natural disaster in the history of Switzerland (Steeb et al., 2016), and one important factor responsible for the damage was LW. More than 69000 m³ of LW were transported throughout the affected area (Steeb et al., 2016). LW accumulated at key cross sections, such as bridge piers and culverts, producing increased upstream water levels, large horizontal structural loadings, and flow field modifications that considerably exacerbated scour (Laursen 1956; Melville and Dongol, 1992; Pagliara and Carnacina, 2010; Schmocker et al., 2011; Schmocker and Hager, 2013; Jochner et al., 2015; Comiti et al., 2016; Hartlieb 2017; Panici and Almeida, 2018; Schalko et al., 2018; Schalko et al., 2019; Peng et al., 2021). LW can also block spillways of check dams, which causes sediment trapping upstream by subsequent debris flows and decreases their discharge ability and storage capacity (Doi et al., 2000; SEDALP WP6 Report 2014; Piton and Recking, 2016; Rossi and Armanini, 2019; Wang et al., 2017). LW transported by debris flow or flood waters can strike residential or other structures and exert a certain impact force that can be large enough to cause substantial damage to structures (Fu et al., 2001; Haehnel and Daly, 2002; Robert and Steven, 2004). Therefore, it is of great importance to study mitigation measures for LW and check the applicability of traditional mitigation measures based on traditional debris flows for woody debris flows.

Both engineering and non-engineering measures have been proposed to reduce the risk of flash floods and debris flows with LW. Several studies have conducted risk assessments that considered influencing factors such as LW amount and transport route. With the development of geographic information technology and advanced theories, the estimation and distribution model of LW quantity based on GIS and fuzzy decision theory has gradually developed (Rickenmann, 1999; Petraschek and Kienholz, 2003; Mazzorana et al., 2009; Mazzorana et al., 2012; Ruiz-Villanueva et al., 2014). Administrative measures include strategic and organizational procedures, such as emergency action plans, evacuation scenarios, or regional planning, that do not influence the river itself have also been developed in many countries (Lange and Bezzola, 2006; Schmocker et al., 2011). These measures lead to sustainable systems but are difficult to implement in many scenarios because the land use in densely populated regions is difficult to modify and change.

Structural engineering measures are often considered the most effective ways for debris flow mitigation (Comiti et al., 2016). Currently, woody debris mitigation structural measures can be divided into two main categories: 1) measures to guide woody debris safely downstream to protect certain objectives, such as debris deflectors and sweepers that are installed on protected objects (Bradley et al., 2004), and 2) measures to intercept woody debris at a certain location. Debris rakes and flexible barriers have been adopted to retain woody debris (Rimböck, 2004; Song et al., 2019; Wang et al., 2022; Xie et al.,2017). Slit-check dams, which are a traditional open-type check dam, have been most widely used for debris flow mitigation. Many researches have examined the sediment regulation effect of slit-check dams against debris flows through field investigations, model tests, and numerical simulations (Ishikawa and Mizuyama,1988; Han and Ou, 2006; Hassan-Esfahani and Banihabib, 2016; Chen and Tfwala, 2018; Zhao et al., 2019; Okamoto et al., 2019), while only a few researches have focused on the regulation effect of woody debris flows. D’Agostino et al. (2000) conducted investigations on open check dams for LW control. Shrestha et al. (2012) investigated the deposition process of debris flows with woody debris and woody debris jamming on slit-check dams. Kato et al. (2015) studied the characteristics of woody debris and sediment transportation around slit-check dams. Rossi and Armanini (2019) addressed the influence of intense sediment transport on the efficiency of structures aimed at the interception of wood logs. Xie et al. (2020b) conducted preliminary research on the regulation effect of slit-check dams on woody debris flows.

Although fundamental knowledge about slit-check dams and woody debris flows have been obtained from the previously mentioned studies, design criterion are still not explicit for slit-check dams regulating woody debris flows. Therefore, this study investigates the regulation effect of slit-check dams on woody debris flows through model tests. The whole process of woody debris flows including the initiation, transportation, and deposition is discussed. The regulating effect of slit-check dams on both sediment and woody components is analyzed. Certain criteria of the main parameters were obtained for the design of slit-check dams.

Methods and materials

Woody debris flow case

Many debris flows occurred in the Wenchuan earthquake area after it happened in 2008. Many of these debris flow events showed dam-breaking characteristics because of landslide dams and woody debris jams. A large number of woody debris and boulders were observed along gullies and clogged building structures, formed jams at narrow cross sections, and blocked open-type check dams (Figure 1).

FIGURE 1

FIGURE 1. Woody debris in the debris flow events in the Wenchuan earthquake area.

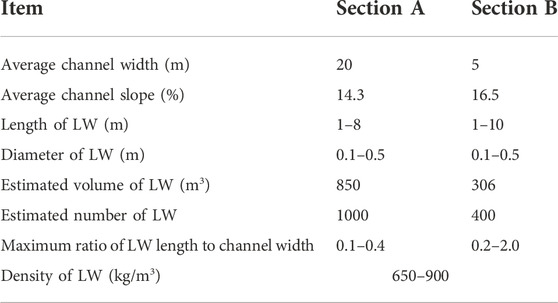
Take the large-scale debris flow in Qipangou, Wenchuan County on 11 July 2013 as an example, this debris flow event lasted for approximately one and a half hours and the solid material flushed out was up to 78.2×10⁴ m³ and caused huge casualties and economic losses (Qin et al., 2016). The main valley of Qipangou is approximately 15.1 km long, 1300–4200 m a.s.l., and 20–120 m wide with an average longitudinal slope of 19.2%; the tributary channel is approximately 5–20 m in width with an average slope of 23.0%. The largest boulders we observed in the field at approximately 2.0 m. The grain size distribution (GSD) of the sediment obtained from the deposition is shown in Figure 2A. A large number of LWs were distributed both in the main valley and the tributary channel. Some of the LWs were artificially arranged and piled together near the residential area (Figure 2B). LW in the tributary maintained a more natural status (Figure 2C). We conducted detailed measurements of LW in two sections (Figure 2D), that is, the section A (within 1 km of depositing area in the main channel) and section B (1 km upstream from the mouth of the tributary valley). The statistics obtained are listed in Table 1.

FIGURE 2

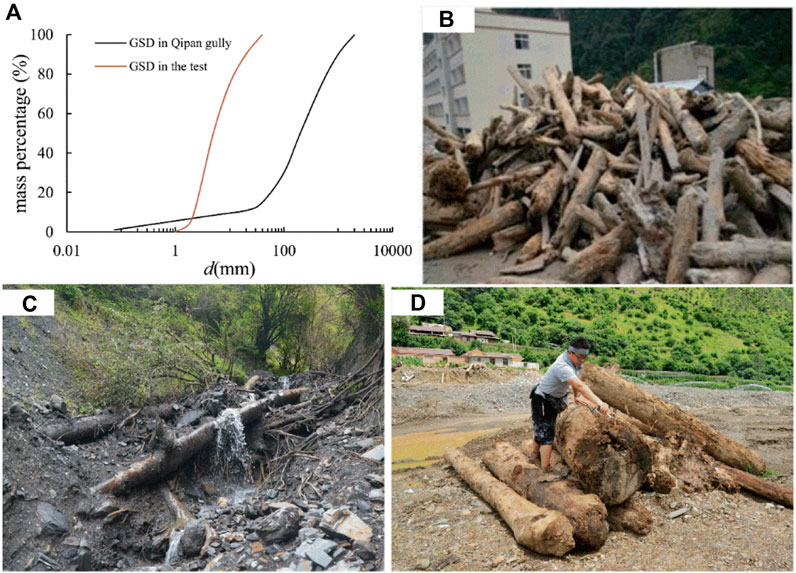
FIGURE 2. LW transported by the debris flow occurred on 11 July 2013 in Qipan Gully, (A) GSD of the sediment in the deposits, (B) LW artificially collected at the mouth of the main valley, (C) LW in the tributary channel, and (D) the measurement of LW.

TABLE 1

TABLE 1. Statistical data of LW parameters in Qipangou, Wenchuan County on 11 July 2013.

Scaling

Small-scale flume tests have been widely used to investigate the complex flow interactions between mass movement and structures. Scaling issues play a crucial role in designing experiments involving grain fluid mixtures to ensure that the test outcome is similar to that of the prototype (Rickenmann, 1999; Iverson, 2015). However, to transfer the entire dynamic process from prototype to laboratory experiment is difficult because the scaling laws are more complicated for debris flow than water (Heller, 2011; Kaitna et al., 2011). As debris flow is a type of gravity-driven motion, Froude similarity is often adopted to design the model tests for debris flow (Rickenmann, 1999; Iverson, 2015). According to the data of Qipangou debris flow, the length scale was set to be λ_L=L_p/L_m =50, where L_p and L_m are the length of the prototype and the model. The volume scale (λ_V) and velocity scale can be calculated as λ_V=λ_L³=125000 and λv=λ_L^0.5=4.47 based on Froude similarity.

Experimental device setup

The experimental device consisted of a hoper, a channel, a tailing pool and a water tank. The channel cross-section was rectangular with three dimensions of 6.0 m×0.43 m×0.5 m (length×width×depth) and a slope of 15.8% (9.0°) (Figure 3A). The right-side wall of the channel was made of transparent glass to permit easy observation. The wood sediment debris source was accumulated in the section of 0–1.5 m upstream, the slit dam was made of steel and installed in the channel 0.5 m from the downstream of the channel end, and the distance between the wood sediment source and the slit-check dam was equal to 3.5 m (Figure 3B). The wood sediment debris source was formed by the layered accumulation of sediment and wood as shown in Figure 3C. Figure 3D illustrates the slit-check dam model in which b represents the width of the openings, h is the height of the openings, and n is the number of openings. A water pump installed in the water tank was used to provide a constant water discharge of Q_w= 390 cm³/s. Three high-definition cameras were installed on the top of the source area, the transportation section and on the top of the slit dam. Another camera was installed on the side of the transportation section.

FIGURE 3

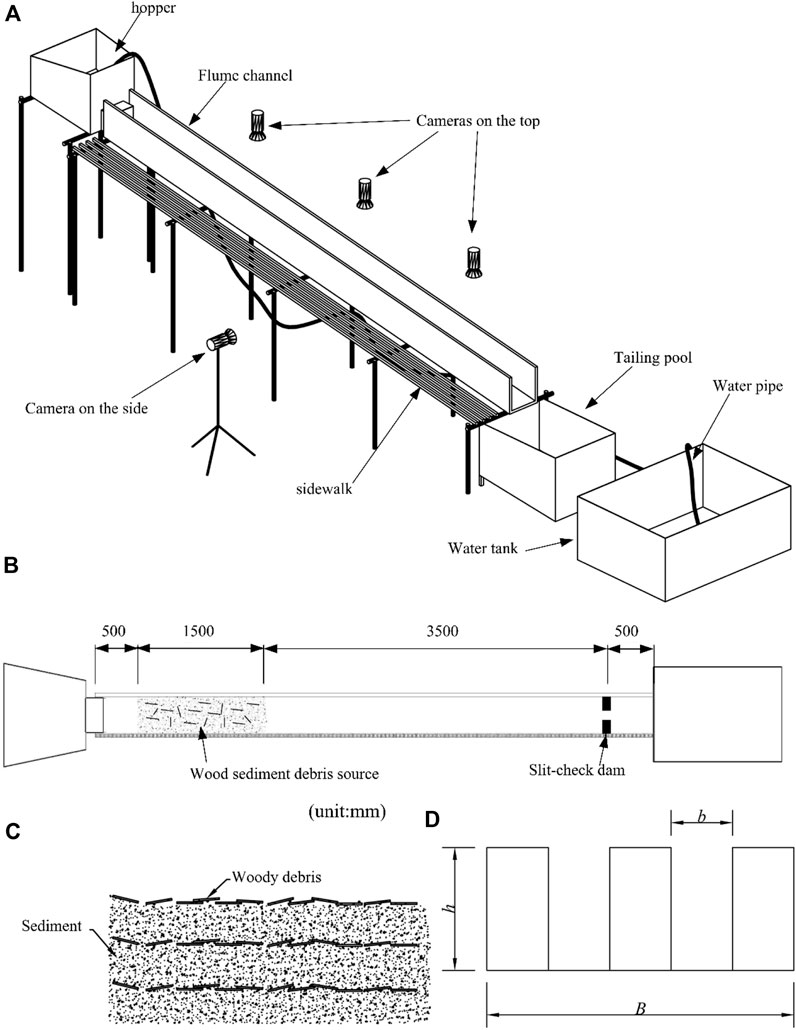
FIGURE 3. Schematic diagram of (A) a 3D view of the experimental device, (B) plain view of the experimental device, (C) accumulation of the wood sediment debris source, and (D) slit-check dam model.

Wood and sediment materials

The GSD used in the experiment was obtained from the field by removing fine particles smaller than 2 mm and coarse particles larger than 2 m, as shown in Figure 2A. There were two reasons to remove fine particles smaller than 2 mm: 1) d=2 mm was considered the lower acceptable limit particle size of the solid-liquid phase according to previous research on the two-phase flow theory regarding debris flow (Fei et al., 1991; Shu et al., 2008; Le et al., 2018) and 2) miniaturized debris flows exhibited disproportionately large effects of viscous shear resistance and cohesion exerted by the liquid phase (Iverson, 2015). The reason for removing coarse particles was related to the maximum particle size of the sediment (d_max), which should be less than 1/5 of the channel width to reduce the size effect in laboratory tests. Hence, the maximum diameter of the sediment d_max in this study was selected as equal to 40 mm with d₃₀=3.6 mm, d₅₀=5 mm, and d₉₅=30 mm. The sediment samples are shown in Figure 4A. The total mass of the sediment was 80 kg for each experiment with a bulk volume of 0.052 m³.

FIGURE 4

FIGURE 4. Sediment and LW model samples as (A) sediment samples and (B) LW model samples.

The parameters of LW were designed based on the data in Table 1. The length of the LW model was 5 cm, 10 cm, 15 cm, 20 cm, and 25 cm with a diameter of 5–10 mm. The corresponding prototype was 2.5–12.5 m in length and 25–50 cm in diameter, which are mostly within the range of the prototype in Qipan gully. All LW models were made of natural branches in a cylindrical shape with an average density of 810 kg/m³ as shown in Figure 4B. The volume and quantity of different LW are listed in Table 1. The ratio of LW volume to sediment volume (V/V_s) was set to be 0.038 and was within the range of 0.001–0.1 according to ESCD (2007). Different lengths of LW required different quantities (N) to satisfy the same V/Vs, which is also shown in Table 2.

TABLE 2

TABLE 2. Test parameters

Test conditions and measurements

Considering the different parameters of the slit-check dam and LW, two series of tests were set up. Test series A examined the regulation effect of a slit-check dam on debris flow without LW and had a total of 15 groups. Test series B was related to the regulation effect of the slit dam on woody debris flow and had a total of 45 groups. Each group of tests was coded with letters representing the different parameters of the slit-check dam and LW and the corresponding values, such as n2b5h8L5N250, which indicates quantities of the slit dam openings n = 2, the opening width b = 5 cm, the opening height h = 8 cm, the length of the LW L = 5 cm, and the quantity of LW N = 250.

A stony debris flow was formed from water eroding the accumulation of wood sediment debris. The duration of water discharge was 90 s. High-definition cameras were used to record the whole test progress. The debris flow density was measured using a cup and calculated via γ_c=m_cg/V_c, where m_c is the mass of debris flow collected by the cup and V_c is the volume of the cup. The debris flow velocity was measured using the buoy method and calculated via v=△s/△t, where △s is the length of the measured section and △t is the duration of the buoy passing the measured section. Sediment and LW in the depositing area and that remaining in the source area was collected, dried, weighed, and sieved.

Results and analysis

Five parameters were first defined to depict the characteristic of the woody debris flow dynamics and the regulating effect of slit-check dam on sediment and woody debris, which are the sediment activation rate (P_sa), sediment trapping rate (P_st), wood retention rate (P_wr), wood clogging rate (P_wc), and opening blockage rate (P_ob) as expressed by Eqs. 1–(5).

$P_{sa}=\frac{M-m_r}{M}\times 100\%,(1)$

$P_{st}=\frac{m_t}{M-m_r}\times 100\%,(2)$

$P_{wr}=\frac{N_t}{N-N_r}\times 100\%,(3)$

$P_{wc}=\frac{N_c}{N_t}\times 100\%,(4)$

$P_{ob}=\frac{A_b}{A}\times 100\%,(5)$

where M is the mass of the original source material (kg), which is 80 kg; m_r is the mass of sediment remaining in the source area (kg); m_t is the mass of sediment trapped by the slit-check dam (kg); N is the total amount of LW that is inputed; N_t is the total quantity of LW that stayed behind the slit-check dam; N_r is the quantity of LW that remained in the source area; N_c is the total amount of LW that blocked the slit-check dam openings. A_b and A are the blocked area and the total area of the slit-check dam openings, respectively.

Woody debris flow properties

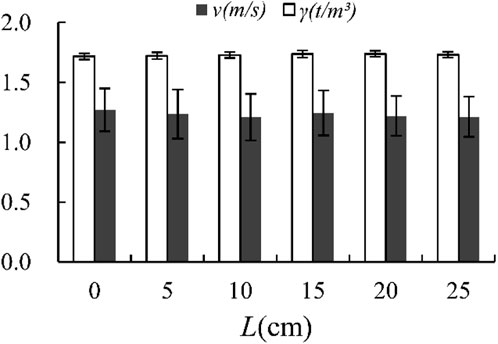
According to the test results, the density of the debris flow γ_c ranged from 1.65–1.76 t/m³ with an average of 1.73 t/m³. The sediment volume concentration C_v was calculated via $C_V=\frac{{\gamma }_c-{\gamma }_w}{{\gamma }_s-{\gamma }_w}$, where γ_w and γ_s are the density of water and sediment, respectively. The C_v ranged from 0.40 to 0.46 with a mean of 0.44. The average velocity of the debris flow under different conditions was approximately 1.2 m/s. Figure 5 shows that there was little difference in the density and velocity under debris flow conditions with or without LW, which indicates that LW exerted little influence on the properties of debris flow. The debris flow discharge Q_c was calculated according to Eq. 6 with an average of 700 cm³/s.

$Q_c=\frac{Q_w}{1-C_v}(6)$

FIGURE 5

FIGURE 5. Density and velocity of debris flows under different conditions.

Characteristics of the woody debris flow dynamic process

The initiation of the woody debris flow

The formation of woody debris flows by hydraulic scour is a gradual process of erosion that starts with surface erosion and slowly forms erosion chutes until mass erosion collapses (Zheng et al., 2021) (Figure 6). The amount of the activated wood sediment source was variable under different conditions. A certain amount of wood and sediment remained in the source section under most test conditions. When LW was oblique or perpendicular to the direction of the flow in the wood sediment debris mixture, the key log was formed as illustrated by a circle in Figure 6. The sediment around the key log was much more stable and difficult to erode, which resulted in a convex shape around the key log in the wood sediment debris residual, as shown by dashed lines in Figure 6. We defined this effect as an anchoring effect of LW on the surrounding sediment. This phenomenon was also observed in the fields (Figure 7). These key logs can even form step-pool systems that play an important role in the topographic evolution of the channel (Brenda and Davies 2002; Curran and Wohl, 2003; Faustini and Jones, 2003).

FIGURE 6

FIGURE 6. Initiation process of a woody debris flow.

FIGURE 7

FIGURE 7. LW store and anchor sediment around in the nature field.

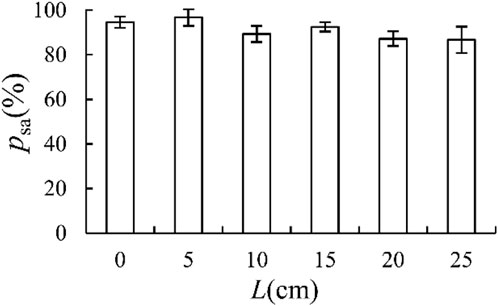
Figure 8 illustrates that the sediment activation rate (P_si) decreased with an increase of the relative length of LW (L/b). This is because the longer the LW, the greater the probability of forming key logs and the more obvious the anchoring effect. However, due to the random distribution of the LW in each layer in this study, the changing trend of the sediment activation rate was not obvious.

FIGURE 8

FIGURE 8. Sediment activation rate under different conditions of woody debris.

Transportation of woody debris flow

LW slides on the surface of the fluid with its long axis prone and parallel to the direction of the fluid. The closer the LW was to the wall of the flume, the more pronounced this phenomenon. Due to the large depth of the backwater behind the slit-check dam, LW that arrived before the sediment deposition occurrence floated and rotated in the backwater area and finally drained downstream. Sediment deposition occurred behind the slit-check dam as soon as large boulders reached the dam. Subsequent sediments accumulated and extended upstream, forming deposits within 2 m behind the slit-check dam. Many of the subsequent LW rotated along the long axis perpendicular to the direction of flow when moved to the sediment deposition section and rolled forward and then deposited on the surface of the sediment deposits due to decreased flow depth. As for those LWs that reached the slit-check dam, different draining processes at the slit dam could be observed under different conditions. We further discuss the overflow conditions and draining characteristics of LW at the slit-check dam in the following.

Overflow conditions

According to Lin et al. (2015), the designed maximum discharge of a slit-check dam with rectangular openings can be calculated by Eq. 7:

$Q_m=n5C{h}^{\frac{3}{2}}b,(7)$

$C=-0.85{\gamma }_c+0.02\theta +0.24\frac{b}{B}+1.79,(8)$

where n is the quantity of the openings; C is the flow discharge coefficient, which can be calculated by Eq. 8; b is the opening width; h is the opening height; γ_c is the flow discharge, t/m³; θ is the slope of the channel, °; and B is the width of the channel.

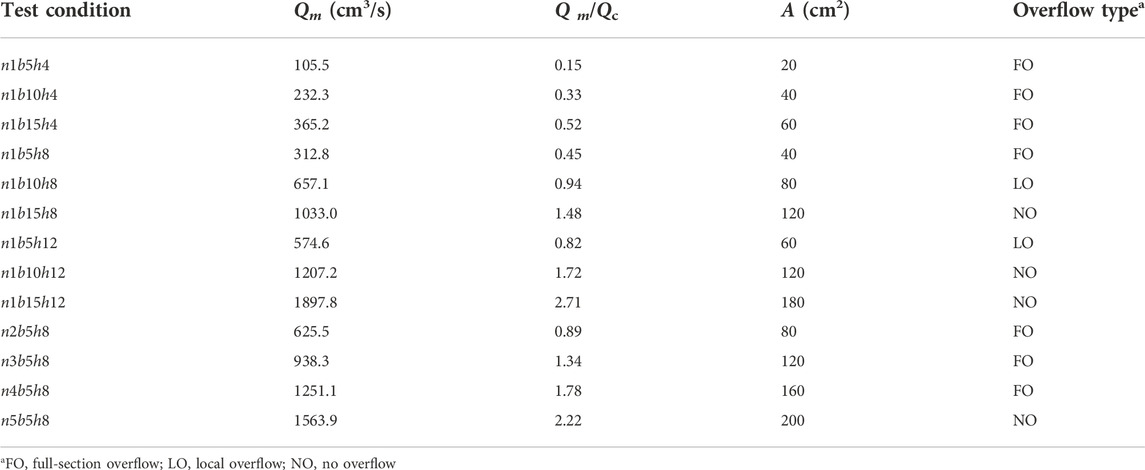
Table 3 lists the maximum discharge of the slit-check dam under different conditions and the ratio of the maximum discharge to the measured discharge (Q_m/Q_c).

TABLE 3

TABLE 3. Overflow conditions

Table 3 shows that under the single-opening slit-check dam condition, full-section overflow (FO) occurred when Q_m/Q_c<0.6, that is, h=4 cm and b=5 cm, 10 cm, and 15 cm. Local overflow (LO) occurred when Q/Q_c =0.82 (n1b5h12) and no overflow phenomenon (NO) occurred when Q_m/Q_c >0.94. Under conditions of a multiple-opening slit-check dam, FO occurred when Q_m/Q_c =0.89 and LO happened even when Q_m/Q_c=1.34 (n3b5h8) and 1.78 (n4b5h8). As Q_m/Q_c increased, the overflow degree weakened but the characteristics of the opening and the total area influenced the discharge ability. When the opening height of the slit-check dam is too small, the overflow phenomenon may still occur by increasing the opening width. Similarly, when the opening width is too small, increasing the height and quantity of openings cannot prevent the overflow phenomenon. We conclude that the reasonable values of the width and height of a single opening are a prerequisite for a better discharge capacity of the slit-check dam.

Table 3 also shows that under the same opening area conditions, the larger the opening height-to-width ratio, the larger the Q_m/Q_c and the weaker the overflows, which infers that the discharge capacity of a narrow and deep opening is greater than that of a wide and shallow type.

LW draining characteristics at the slit-check dam

Three patterns of LW draining at the slit-check dam were concluded based on the relationship of wood retention rates (P_wr) with time, as shown in Figures 9A–C.

1) Smoothly draining downstream. This pattern indicates that all LWs reaching the slit-check dam could pass through and never block the openings. No clogging occurred at the openings and two specific cases can be subdivided further. One is draining from the top of the dam. For these conditions where overflow occurred, most of the LW reaching the slit-check dam was draining from the top of the dam no matter how long the LW was. The other is passing through the openings of the slit-check dam. This type mainly happened under the L/b≤1.0 condition. The wood retention rate was always lower than 10% during the whole process as shown in Figure 9A.

2) Intermittently blocking-breaking at the slit-check dam. This pattern mainly occurred under conditions of 1.0<L/b≤2.0, where LW clogged the opening of the slit-check dam first and then partially or totally flowed away by the subsequent fluid. The wood retention rate dramatically fluctuated, as Figure 9B illustrates, and ranged from 10% to 20%.

3) Continuously clogging at the slit-check dam. This mode mostly occurred when L/b>2.0 and the logjam formed by LW was stable and hard to break once it was formed. The wood retention rate continued to increase with time and finally reached more than 30% in most cases. A slight fluctuation could also be observed from the P_wt-t curve in Figure 9C, which was caused by the phenomenon that a few members of LW were carried away by the subsequent flow without breaking the whole logjam.

FIGURE 9

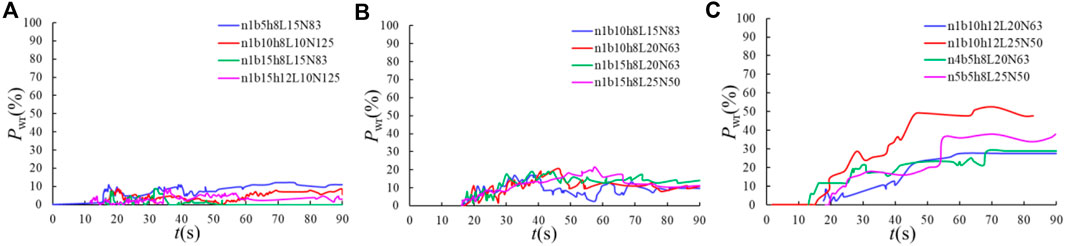
FIGURE 9. Different drainage patterns of LW at the slit-check dam. (A) Smoothly draining, (B) Intermittently blocking-breaking, and (C) Continuously clogging

The characteristics of LW accumulation at the slit-check dam

The LW directly intercepted by the slit-check dam presented three typical forms of accumulation: 1) several LW members bridge across the openings (bridging clogging for short) (Figure 10A); 2) multiple LW members intersect with each other clogging the openings (intersecting clogging for short) (Figure 10B); and 3) both bridging members and intersecting members occurred in the accumulation (hybrid clogging for short) (Figure 10C). Usually, bridging clogging and intersecting clogging were easily formed in single-opening slit-check dams and hybrid clogging was observed in multi-openings of the slit-check dam. According to statistical analysis, the opening blockage rate (P_oc) caused by bridging clogging and intersecting clogging was generally less than 20% and more than 30%, respectively, and that caused by the hybrid clogging was between 20% and 30% (Figure 11A). The opening blocking area rate shared a linear relationship with the wood retention rate (Figure 11B).

FIGURE 10

FIGURE 10. Three typical patterns of LW jams at slit-check dams. (A) bridging clogging, (B) intersecting clogging, and (C) hybrid clogging

FIGURE 11

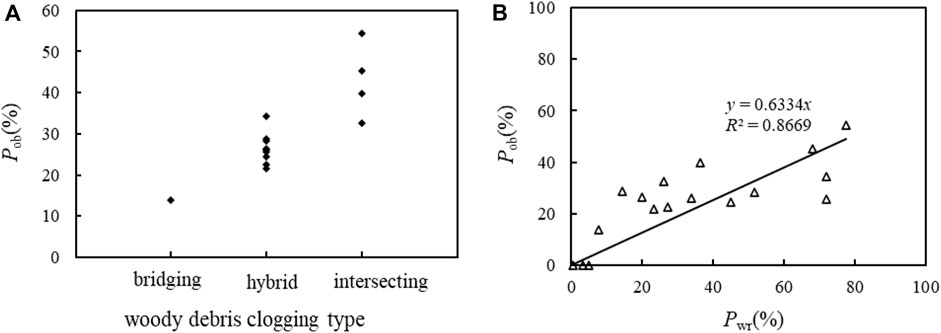
FIGURE 11. Characteristic of LW clogging at the slit-check dam. (A) Relationship of LW clogging types with the opening area blocking rate and (B) relationship between the wood retention rate and opening area blocking rate.

Regulating effect of the slit-check dam

Regulation effect of the slit-check dam on debris flow without LW

Figure 12A demonstrates that the sediment trapping rate linearly decreased with an increase of the relative opening width, especially when h=4 cm, the sediment trapping rate decreased compared to that of h=8 cm and 12 cm. The main reason was that serious overflow occurred according to Table 3, which caused a large amount of sediment discharge from the top of the dam and resulted in a lower sediment trapping rate. Mizuyama and Mizuno (1997) reported that the open check dam could capture debris flows if the relative width of an opening b/d₉₅ <2. To ensure more accurate capturing, opening of the check dams was proposed to satisfy the condition of 1.0≤b/d₉₅≤1.5 by the Technical Standards on Debris Flow Control and Woody Debris Control in Japan (Osanai et al., 2010). Based on this study, when the opening width b=5 cm (b/d₉₅=1.67), the openings were severely blocked by large boulders and severe overflows occurred. Additionally, the slit-check dam would lose its function of trapping sediment and decreasing the discharge if all openings were blocked. Thus, a preliminary condition of b/d₉₅>1.67 is suggested from the perspective of preventing serious blocking of the openings.

FIGURE 12

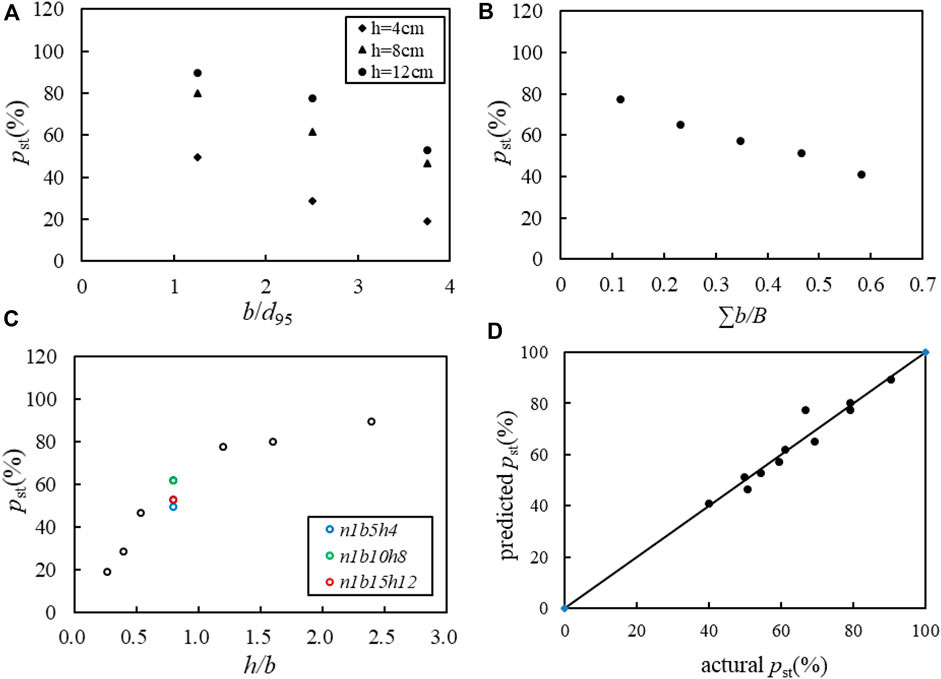
FIGURE 12. Sediment trapping rate under different conditions. (A) Different relative opening width, (B) different opening density, (C) different opening height-to-width ratio, and (D) verification of the regression result.

Figure 12B shows that sediment trapping efficiency also decreased with an increase of the opening density. With low opening density, a high sediment trapping rate would accelerate sediment accumulation behind the dam and cause the storage capacity to be quickly consumed. Thus, the opening density suggested by Li. (1997) in the range of 0.3–0.6 is reasonable.

Figure 12C indicates that the sediment trapping rate increased with an increase in the height-to-width ratio. The sediment trapping rate increased dramatically when h/b<1.2 and then the increasing rate decreased when h/b>1.2. Figure 12C also demonstrates that the sediment trapping efficiency was different under the same height-to-width ratio conditions. For example, when b₁=5 cm, h₁=4 cm, b₂=10 cm, h₂=8 cm, and b₃=15 cm, h₃=12 cm all satisfied the condition of h/b=0.8, then the sediment trapping rate appeared the largest when b=10 cm, h=8 cm. The main reason was that under the condition of n1b5 h4, a serious overflow phenomenon occurred, which caused a large amount of sediment to be discharged from the top of the dam and resulted in a lower sediment trapping rate. While b=10 cm and 15 cm, the slit-check dam was not clogged by boulders so that the sediment trapping effect decreased with an increase of the opening width.

Considering the results of previous research and this study, the opening width and height of the slit-check dam are suggested to satisfy the conditions of 1.67≤b/d₉₅≤2.0 and h/b≥1.2 to obtain a high sediment trapping efficiency without seriously clogging the openings. The opening density of the slit-check dam is suggested at a range of 0.3–0.6.

According to multiple linear regression analyses using data without overflow conditions, the sediment trapping rate had a relationship with the relative opening width (b/d₉₅), the height-to-width ratio (h/b), and the opening density of the slit-check dam (∑b/B) as follows:

$P_{st}=63.3+1.86\left(\frac{b}{d_{95}}\right)+14.1\left(\frac{h}{b}\right)-84.6\left(\frac{\sum b}{B}\right)R^2=0.902.(9)$

Figure 12D illustrates that the predicted values of the sediment trapping rate by Eq. 9 were well matched with the measured ones.

Regulation effect of the slit-check dam on woody debris flow

Figure 13A shows that the wood retention rates were mostly less than 10% under the conditions of L=5 cm, 10 cm, 15 cm, and 20 cm. For the LW with L=25 cm, the wood retention rate increased to 20%, which was mainly a contribution from the LW accumulated on the sediment deposits in the channel because of the low wood clogging rate. This is because LW is easy to deposit in the channel when the length of LW relative to the channel width L/B>0.5 (Lienkeaemper and Swanson, 1987; Abbe and Montgomery, 2003). Sediment trapping rates were relatively high and changed little under different LW conditions. We conclude that the regulation effect of a slit-check dam on LW was very poor, and the influence of LW on the sediment trapping efficiency could be neglected when overflow occurred. Thus, the follow-up analysis only focuses on cases without overflows. Figures 13B,C demonstrate that the wood retention rate linearly increased with the relative length of LW when L/b>1.0 and decreased with the increase of opening density. LW accumulation at the slit-check dam contributed to more than 60% of the wood retention rate. The intercepted LW accumulated at the opening of the slit-check dam and in turn promoted the interception of sediment.

FIGURE 13

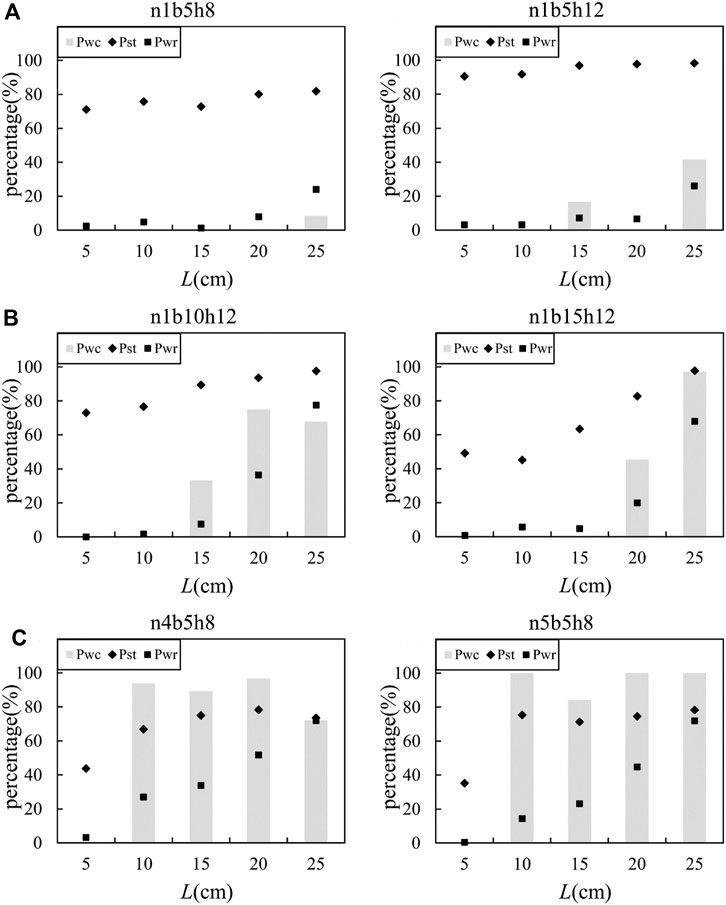
FIGURE 13. Sediment trapping rate (P_st), wood retention rate (P_wr), and wood clogging rate (P_wc) under different conditions. (A) Single-opening slit-check dams with overflows, (B) single-opening slit-check dams without overflow, and (C) multi-opening slit-check dams without overflow.

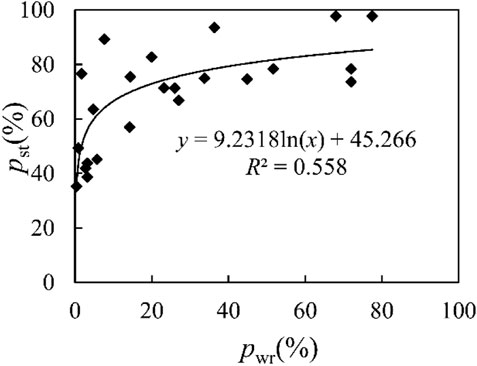
We conclude from the above analysis that the length of LW relative to the width of the channel (L/B) affects its retention during the transportation process, while the length of LW relative to the opening width of the slit-check dam (L/b) and the opening density of the slit-check dam (∑b/B) determined the interception of LW by the slit-check dam. The two aspects affected the wood retention rate together, which in turn affected the sediment trapping efficiency. Based on the regression analysis using data of all conditions without overflows, the relationship between the wood retention rate (P_wr) and L/B, L/b and ∑b/B is shown in Eq. 10 and a logarithmic relationship was satisfied between the wood retention rate (P_wr) and the sediment trapping rate (P_st) as shown in Eq. 11 and Figure 14.

$P_{wr}=-6.74+14.1\left(\frac{L}{b}\right)+24.0\left(\frac{L}{B}\right)-34.5\frac{\sum b}{B}{R}^2=0.930(10)$

$P_{st}=9.232\ln \left(P_{wr}\right)+45.266R^2=0.558(11)$

FIGURE 14

FIGURE 14. Relationship between the wood retention rate and the sediment trapping rate.

Discussion

Shrestha et al. (2012) proposed five mechanisms for LW jamming at the single-opening slit-check dam according to the geometric relationship and occurrence probability as shown in Figure 15. For this, the occurrence of (a), (b), and (c) needs to meet the basic condition of L/b>1.0. The pattern of (d) mainly occurs when the amount of LW is large, and the probability is related to the quantity and relative length of LW. The larger the amount and L/b, the greater the probability of jamming.

FIGURE 15

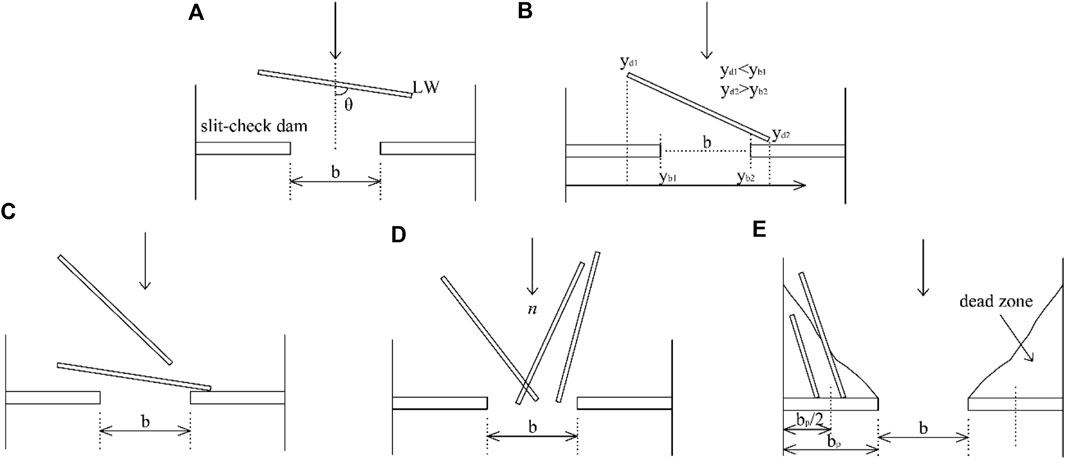
FIGURE 15. LW jamming at the slit-check dam. (A) A piece of driftwood was jammed with a large orientation ranging from 80° to 90°. (B) A piece of driftwood was jammed in a slit-check dam due to geometric conditions as yd1<yb1 and yd2<yb2. (C) A piece of driftwood coming from the rear was also jammed by the pieces of driftwood already jammed in a slit-check dam. (D) The pieces of driftwood were jammed when the number of pieces of driftwood arrived at the slit opening at the same time. (E) A piece of driftwood was jammed in an impermeable width of the slit-check dam when the centroid of the driftwood was located only inside the dead zone of flow (redrawn from Shrestha et al. (2012)).

The basic types of LW clogging at the single-opening slit-check dam proposed in our study are bridging clogging and intersecting clogging, which can be explained by the above mechanism. The bridging type can be formed by the mentioned mechanism of (a) and (b), while the intersecting type can be formed by (c) and (d). All jamming observed in this study occurred under the condition of L/b>1.0, while Chen et al. (2020) produced intersecting jamming under the condition of 0.75<L/b<1.

Our study also proposed three draining patterns of LW at the slit-check dam according to the wood retention rate, which is smoothly draining mode, intermittently blocking-breaking mode and continuously clogging mode. The main factor determining the different patterns was L/b. These basic conclusions are consistent with Chen et al. (2020), but the specific conditions for each pattern were different. In this study, the smoothly draining mode mainly occurred under the condition of L/b<1.0, the intermittently blocking-breaking mode at 1.0<L/b<2.0, and the continuous clogging at L/b≥2.0. According to Chen et al. (2020), blocking-breaking phenomenon could be observed when L/b>0.5, and an amplification effect could be observed on debris flow discharge when blocking-breaking occurred. The amplification factor could be as high as 1.6 when L/b=0.85 and V/V_max=0.75. However, no obvious amplification effect was observed in either this study or in Shrestha et al. (2012).

The reasons for these differences in the model tests may be as follows: 1) the properties of debris flows are different. Debris flows in Chen et al. (2020) were prepared from real debris flow sediment samples from Jiangjia Valley, and this slurry contained a large number of fine particles; densities of 1.5 t/m³, 1.7 t/m³, and 1.9 t/m³ were used. In this study, a stony debris flow with a density of 1.7 t/m³ was formed by water eroding coarse-grained sediment accumulation. The existence of fine particles increased the stickiness of the debris flow and also filled the pores of the logjam, which caused a large increase in the upstream sediment storage capacity, and once the logjam broke up, an amplification of peak discharge occurred. 2) The dynamic parameters of debris flow are different. Chen et al. (2020) activated the debris flow of 0.75 m³ by opening the gauge gate for a certain duration (10 s). The maximum discharge of the debris flow was approximately 3200–3600 cm³/s. However, a constant discharge of 700 cm³/s was produced by water scouring the sediment deposit in this study over a relatively long duration (90 s). Therefore, the instantaneous transport ability of debris flow to LW is different. Specifically, the larger the flow discharge, the more LWs can be transported at one time. 3) The input method of LW is different. LW was supplied in four groups upstream of the model dam with a frequency of 15 logs/s in Chen et al. (2020), which ensured the input LW to immediately participate in the movement. In this experiment, LWs were mixed with sediment in a layered occurrence as shown in Figure 3C and spread in the source area section. The quantity of LW that can participate in the movement was random in each test and the activation of LW requires more energy.

Based on the aforementioned analysis, the difference in fluid properties, dynamic parameters and input of LW all have an influence on the characteristics of LW transportation and deposition. Thus, future research should carry on stimulations based on real scenarios to make the research results more practical.

Conclusions

Through model tests, we analyzed the regulation effect of slit-check dams with different structural parameters on woody debris flows and discussed the influence of LW on the regulation effect of the slit-check dams. The main conclusions are as follows:

1) LW presented three draining modes at the slit-check dam: smoothly draining mode, intermittently blocking-breaking mode, and continuously clogging mode. Three types of logjams were observed by the intercepted LW at the slit-check dam, which are the bridging logjam, the intersecting logjam, and the hybrid logjam.

2) The opening width is a prerequisite for designing a slit-check dam concerning its regulation effects. This suggested the need to satisfy the conditions of 1.67<b/d₉₅<2.0 and 1.0<L/b<2.0 to obtain high sediment and woody trapping efficiency without serious clogging. A narrow and deep opening shape is preferred compared to a wide and shallow type. The height-to-width ratio is suggested to satisfy the condition of h/b≥1.2. Multiple opening slit-check dams present a better regulation effect than single- opening slit-check dams when the opening area is the same. The opening density ∑b/B is recommended and ranges from 0.3 to 0.6.

3) Overflow conditions should be taken into consideration when discussing the regulation effect of slit-check dams on woody debris flows. The ratio of the maximum discharge of the slit-check dam to the discharge of debris flow Q_m/Q_c is suggested to evaluate whether overflow would occur. Overflow will happen for a single-opening slit-check dam when Q_m/Q_c <1 and the value is even higher for multi-opening slit-check dams. Slit-check dams have a weak regulation effect on LW when overflow occurs, but exert strong effects on LW without overflows. The sediment trapping rate could be predicted according to Eq. 9 for the debris flow without LW. The wood retention rate and sediment trapping rate could be predicted by Eqs. 10, 11, respectively, for woody debris flow.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author contributions

XX and XW contributed to the conception and design of the study. XX, XW, Zhe L, Zhi L, SZ carried out all experiments and XW, Zhe L, and Zhi L organized the database. XW performed the statistical analysis and wrote the first draft of the manuscript. XX was responsible for the improvement of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No 41907258) and Doctoral Research Start-up Fund of Anyang Institute of Technology (BSJ2019011).

Conflict of interest

The authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbe, T. B., and Montgomery, D. R. (2003). Patterns and processes of wood debris accumulation in the Queets River basin, Washington. Geomorphology 51 (1-3), 81–107. doi:10.1016/S0169-555X(02)00326-4

CrossRef Full Text | Google Scholar

Ana, L., Comiti, F., Borga, M., Cavalli, M., and Marchi, L. (2015). Dynamics of large wood during a flash flood in two mountain catchments. Nat. Hazards Earth Syst. Sci. 12 (8), 1741–1755. doi:10.5194/nhess-15-1741-2015

CrossRef Full Text | Google Scholar

Bocchiola, D., Rulli, M. C., and Rosso, R. (2006). Transport of large woody debris in the presence of obstacles. Geomorphology 76 (1–2), 166–178. doi:10.1016/j.geomorph.2005.08.016

CrossRef Full Text | Google Scholar

Bradley, J. B., Richards, D. L., and Bahner, C. D. (2005). Debris control structures–Evaluation and countermeasures[R], Hydraulic Engineering Circular 9, 179.

Google Scholar

Braudrick, C. A., and Grant, G. E. (2001). Transport and deposition of large woody debris in streams: A flume experiment. Geomorphology 41 (4), 263–283. doi:10.1016/S0169-555X(01)00058-7

CrossRef Full Text | Google Scholar

Braudrick, C., Grant, G., and Ishikawa, Y. (1997). Dynamics of wood transport in streams: A flume experiment. Earth Surf. Process. Landforms 22 (7), 669–683. doi:10.1002/(SICI)1096-9837(199707)22:7<669::AID-ESP740>3.0.CO;2-L

CrossRef Full Text | Google Scholar

Brenda, R. B., and Davies, R. T. (2002). Influence of large woody debris on channel morphology in native forest and pine plantation streams in the Nelson region, New Zealand. N. Z. J. Mar. Freshw. Res. 36 (4), 763–774. doi:10.1080/00288330.2002.9517129

CrossRef Full Text | Google Scholar

Chen, J., Wang, D., Zhao, W., Chen, H., Wang, T., Nepal, N., et al. (2020). Laboratory study on the characteristics of large wood and debris flow processes at slit-check dams. Landslides 17 (2), 1703–1711. doi:10.1007/s10346-020-01409-3

CrossRef Full Text | Google Scholar

Chen, S. C., and Tfwala, S. (2018). Evaluating an optimum slit check dam design by using a 2D unsteady numerical model. E3S Web Conf. 40, 03027. doi:10.1051/e3sconf/20184003027

CrossRef Full Text | Google Scholar

Collins, B. D., Montgomery, D. R., Fetherston, K. L., and Abbe, T. B. (2012). The floodplain large-wood cycle hypothesis: A mechanism for the physical and biotic structuring of temperate forested alluvial valleys in the north pacific coastal ecoregion. Geomorphology 139-140, 460–470. doi:10.1016/j.geomorph.2011.11.011

CrossRef Full Text | Google Scholar

Comiti, F., Lucía, A., and Rickenmann, D. (2016). Large wood recruitment and transport during large floods: A review. Geomorphology 269, 23–39. doi:10.1016/j.geomorph.2016.06.016

CrossRef Full Text | Google Scholar

Comiti, F., Mao, L., Perciso, E., Picco, L., Marchi, L., and Borga, M. (2008). Large wood and flash floods: Evidence from the 2007 event in the davča basin (Slovenia). WIT Trans. Eng. Sci. 60. doi:10.2495/DEB080181

CrossRef Full Text | Google Scholar

Curran, J. H., and Wohl, E. E. (2003). Large woody debris and flow resistance in step-pool channels, Cascade Range, Washington. Geomorphology 51, 141–157. doi:10.1016/S0169-555X(02)00333-1

CrossRef Full Text | Google Scholar

D’Agostino, V., Degetto, M., and Righetti, M. (2000). “Experimental investigation on open check dam for coarse woody debris control,” in Dynamics of water and sediments in mountain basins Quaderni diIdronomia Montana (Cosenza: Editoriale Bios), 201–212.

Google Scholar

Davidson, S. L., and Eaton, B. C. (2013). Modeling channel morphodynamic response to variations in large wood: Implications for stream rehabilitation in degraded watersheds. Geomorphology 202, 59–73. doi:10.1016/j.geomorph.2012.10.005

CrossRef Full Text | Google Scholar

Doi, Y., Minami, N., and Yamada, T. (2000). Experimental analysis of woody debris trapping by impermeable type Sabo dam, filled with sediment woody debris carried by debris flow. J. Jpn. Soc. Eros. Control Eng. 52 (6), 49–55. doi:10.11475/sabo1973.52.6_49

CrossRef Full Text | Google Scholar

Erosion and Sediment Control Division (2007). Manual of Technical Standard for establishing Sabo plan for debris flow and driftwood. Technical Note of National Institute for Land and Infrastructure Management. AvaliableAt: http://www.sabo-int.org/guideline/index.html.

Google Scholar

Faustini, J. M., and Jones, J. A. (2003). Influence of large woody debris on channel morphology and dynamics in steep, boulder-rich mountain streams, Western Cascades, Oregon. Geomorphology 51 (1), 187–205. doi:10.1016/S0169-555X(02)00336-7

CrossRef Full Text | Google Scholar

Fei, X. J., Kang, Z. C., and Wang, Y. Y. (1991). Effect of fine grain and debris flow slurry bodies on debris flow motion. Mountain Research. Mountain Research(3), 143–152.

Google Scholar

Fu, Z. P., Liu, M. M., and Liu, J. C. (2001). Study on measurement and characteristics of percussive force of float timber. Adv. Sci. Technol. Water Resour. 3, 33–34+6370.

Google Scholar

Gao, K. C., Meng, C. G., and Wei, F. Q. (2005). Analysis and countermeasure for the large-scale landslide debris flow hazard in DeShong, Yunnan, China. J. Disaster Prev. Mitig. Eng. 25 (3), 251–257. doi:10.1360/gs050303

CrossRef Full Text | Google Scholar

Gurnell, A. M., Bertoldi, W., and Corenblit, D. (2012). Changing river channels: The roles of hydrological processes, plants and pioneer fluvial landforms in humid temperate, mixed load, gravel bed rivers. Earth-Science Rev. 111, 129–141. doi:10.1016/j.earscirev.2011.11.005

CrossRef Full Text | Google Scholar

Haehnel, R. B., and Daly, S. F. (2002). Maximum impact force of woody debris on floodplain structures. J. Hydraul. Eng. 130 (2), 112–120. doi:10.1061/(asce)0733-9429(2004)130:2(112)(2004)130:2(112)

CrossRef Full Text | Google Scholar

Han, W. B., and Ou, G. Q. (2006). Efficiency of slit dam prevention against non-viscous debris flow. Wuhan. Univ. J. Nat. Sci. 11 (4), 865–869. doi:10.1007/bf02830178

CrossRef Full Text | Google Scholar

Hartlieb, A. (2017). Decisive parameters for backwater effects caused by floating debris jams. Open J. Fluid Dyn. 07 (7), 475–484. doi:10.4236/ojfd.2017.74032

CrossRef Full Text | Google Scholar

Hassan-Esfahani, L., and Banihabib, M. E. (2016). The impact of slit and detention dams on debris flow control using GSTARS 3.0. Environ. Earth Sci. 75, 328. doi:10.1007/s12665-015-5183-z

CrossRef Full Text | Google Scholar

Heller, V. (2011). Scale effects in physical hydraulic engineering models. J. Hydraulic Res. 49 (3), 293–306. doi:10.1080/00221686.2011.578914

CrossRef Full Text | Google Scholar

Henshaw, A. J., Bertoldi, W., and Harvey, G. L. (2015). Large wood dynamics along the taliento river, Italy: Insights from field and remote sensing investigations. Springer International Publishing. doi:10.1007/978-3-319-09054-2_30

CrossRef Full Text | Google Scholar

Ishikawa, Y., and Mizuyama, T. (1988). “An experimental study of per-meable sediment control dams as a countermeasure against floating logs,” in 6th congress asian and pacific regional division int. Association for hydraulic research kyoto (Kyoto, Japan: Dept. of Civil Engineering, Kyoto Univ.).

Google Scholar

Iverson, R. M. (2015). Scaling and design of landslide and debris-flow experiments. Geomorphology 2 (44), 9–20. doi:10.1016/j.geomorph.2015.02.033

CrossRef Full Text | Google Scholar

Jochner, M., Turowski, J. M., Badoux, A., Stoffel, M., and Rickli, C. (2015). The role of log jams and exceptional flood events in mobilizing coarse particulate organic matter in a steep headwater stream. Earth Surf. Dynam. 3, 311–320. doi:10.5194/esurf-3-311-2015

CrossRef Full Text | Google Scholar

Kaitna, R., Chiari, M., Kerschbaumer, M., Kapeller, H., Zlatic-Jugovic, J., Hengl, M., et al. (2011). Physical and numerical modelling of a bedload deposition area for an Alpine torrent. Nat. Hazards Earth Syst. Sci. 11, 1589–1597. doi:10.5194/nhess-11-1589-2011

CrossRef Full Text | Google Scholar

Kato, Y., Hinokidani, O., Kajikawa, Y., and Nagatani, N. (2015). Characteristics of driftwoods and sediment transportation around a slit sabo dam. Hydroengineering 71 (4), 985–990. doi:10.2208/jscejhe.71.i_985

CrossRef Full Text | Google Scholar

Lancaster, S. T., Hayes, S. K., and Grant, G. E. (2001). Effects of wood on debris flow run-out in small mountain watersheds. Water Resour. Res. 39 (6), 1168. doi:10.1029/2001WR001227

CrossRef Full Text | Google Scholar

Lange, D., and Bezzola, G. R. (2006). in Driftwood: Problems and solutions. Rep. VAW-mitteilung 188. Editor H.-E. Minor (Zurich, Switzerland: Swiss Federal Institute of Technology).

Google Scholar

Laursen, E. M. (1956). Scour around bridge piers and abutments. Bulletin 4 (60), 28–31.

Google Scholar

Le, M. H., Han, Q. W., and Fang, C. M. (2018). The critical grain size of debris flow. J. Sediment Res. 43 (03), 1–6. doi:10.16239/j.cnki.0468-155x.2018.03.001

CrossRef Full Text | Google Scholar

Li, D. J. (1997). Debris flow mitigation theory and practices. Beijing: Science Press.

Google Scholar

Lienkaemper, G. W., and Swanson, F. J. (1987). Dynamics of large woody debris in streams in old-growth Douglas-fir forests. Can. J. For. Res. 17, 150–156. doi:10.1139/x87-027

CrossRef Full Text | Google Scholar

Lin, X. P., You, Y., and Liu, J. F. (2015). Experimental study on discharge capacity of spillway of check dam for debris flow. J. Nat. Disasters 24 (1), 9–14.

Google Scholar

Massong, T. M., and Montgomery, D. R. (2000). Influence of sediment supply, lithology, and wood debris on the distribution of bedrock and alluvial channels. Geol. Soc. Am. Bull. 112, 591–599. doi:10.1130/0016-7606(2000)112<591:iossla>2.0.co;2

CrossRef Full Text | Google Scholar

Mazzorana, B., Comiti, F., Scherer, C., and Fuchs, S. (2012). Developing consistent scenarios to assess flood hazards in mountain streams. J. Environ. Manag. 94 (1), 112–124. doi:10.1016/j.jenvman.2011.06.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Mazzorana, B., Zischg, A., Largiader, A., and Hubl, J. (2009). Hazard index maps for woody material recruitment and transport in alpine catchments. Nat. Hazards Earth Syst. Sci. 9 (1), 197–209. doi:10.5194/nhess-9-197-2009

CrossRef Full Text | Google Scholar

Melville, B. W., and Dongol, D. M. (1992). Bridge pier scour with debris accumulation. J. Hydraul. Eng. 118118 (9), 1306–1310. doi:10.1061/(asce)0733-9429(1992)118:9(1306)

CrossRef Full Text | Google Scholar

Mizuyama, T., and Mizuno, H. (1997). “Prediction of debris flow hydrograph passing through grid type control structure,” in Proceedings of first international conference on debris-flow hazard mitigation (ASCE), 74–82.

Google Scholar

Okamoto, T., Takebayashi, H., Sanjou, M., Suzuki, R., and Toda, K. (2019). Log jam formation at bridges and the effect on floodplain flow: A flume experiment. J. Flood Risk Manag. 13 (S1), 12562. doi:10.1111/jfr3.12562

CrossRef Full Text | Google Scholar

Osanai, N., Mizuno, H., and Mizuyama, T. (2010). Design standard of control structures against debris flow in Japan. J. Disaster Res. 5, 307–314. doi:10.20965/jdr.2010.p0307

CrossRef Full Text | Google Scholar

Pagliara, S., and Carnacina, I. (2010). Temporal scour evolution at bridge piers: Effect of wood debris roughness and porosity. J. Hydraulic Res. 48 (1), 3–13. doi:10.1080/00221680903568592

CrossRef Full Text | Google Scholar

Panici, D., and de Almeida, G. A. M. (2018). Formation, growth, and failure of debris jams at bridge piers. Water Resour. Res. 54 (9), 6226–6241. doi:10.1029/2017WR022177

CrossRef Full Text | Google Scholar

Peng, M., Guan, S., and Feng, S. (2021). Deposition characteristics of debris flows in a lateral flume considering upstream entrainment. Geomorphology 394, 1–16. doi:10.1016/j.geomorph.2021.107960

CrossRef Full Text | Google Scholar

Petraschek, A., and Kienholz, H. (2003). Hazard assessment and mapping of mountain risks in Switzerland. Bull. Eng. Geol. Environ. 61 (3), 263–268. doi:10.1007/s10064-002-0163-4

CrossRef Full Text | Google Scholar

Piton, G., and Recking, A. (2016) Design of sediment traps with open check dams II: Woody debris. J. Hydraul. Eng. 142, 04015046. doi:10.1061/(asce)hy.1943-7900.0001049

CrossRef Full Text | Google Scholar

Qin, H. K., Zhang, H. Q., and Zhang, B. (2016). Formation conditions of the Qipangou multi stage dam-breaking debris flows in Wenchuan area after the earthquake. J. Eng. Geol. suppl, 100–107. doi:10.13544/j.cnki.jeg.2016.s015

CrossRef Full Text | Google Scholar

Rickenmann, D. (1999). Empirical relationships for debris flows. Nat. Hazards (Dordr). 19 (1), 47–77. doi:10.1023/A:1008064220727

CrossRef Full Text | Google Scholar

Rimböck, A. (2004). Design of rope net barriers for woody debris entrapment: Introduction of a design concept. Klagenfurt, Austria: International Research Society INTERPRAEVENT, 265–276.

Google Scholar

Robert, B., and Steven, F. D. (2004). Maximum impact force of woody debris on floodplain structures. J. Hydraul. Eng. 130 (2), 112–120. doi:10.1061/(asce)0733-9429(2004)130:2(112)

CrossRef Full Text | Google Scholar

Rossi, G., and Armanini, A. (2019). Experimental analysis of open check dams and protection bars against debris flows and driftwood. Environ. Fluid Mech. (Dordr). 1, 559–578. doi:10.1007/s10652-019-09714-9

CrossRef Full Text | Google Scholar

Ruiz-Villanueva, V., Bodoque, J. M., Díez-Herrero, A., and Blade, E. (2014). Large wood transport as significant influence on flood risk in a mountain village. Nat. Hazards (Dordr). 74, 967–987. doi:10.1007/s11069-014-1222-4

CrossRef Full Text | Google Scholar

Schalko, I., Lageder, C., Schmocker, L., Weitbrecht, V., and Boes, R. (2019). Laboratory flume experiments on the formation of spanwise large wood accumulations: I. Effect on backwater rise. Water Resour. Res. 55, 4854–4870. doi:10.1029/2018WR024649

CrossRef Full Text | Google Scholar

Schalko, I., Schmocker, L., Weitbrecht, V., and Boes, R. M. (2018). Backwater rise due to large wood accumulations. J. Hydraul. Eng. 144 (9), 04018056. doi:10.1061/(ASCE)HY.1943-7900.0001501

CrossRef Full Text | Google Scholar

Schmocker, L., Hager, W. H., and Asce, F. (2011). Probability of drift blockage at bridge decks. J. Hydraul. Eng. 137 (4), 470–479. doi:10.1061/(ASCE)HY.1943-7900.0000319

CrossRef Full Text | Google Scholar

Schmocker, L., and Hager, W. H. (2013). Scale modeling of wooden debris accumulation at a debris rack. J. Hydraul. Eng. 139 (8), 827–836. doi:10.1061/(asce)hy.1943-7900.0000714

CrossRef Full Text | Google Scholar

SEDALP WP6 Report (2014). Interactions with structures. Available at: http://www.sedalp.eu/download/dwd/reports/WP6_Report.pdf.191

Google Scholar

Sediment Control (Sabo) Division (2000). Driftwood countermeasure guideline (proposal). Japan: Sediment Control (Sabo) Department.

Google Scholar

Shrestha, B. B., Nakagawa, H., Kawaike, K., Baba, Y., and Zhang, H. (2012). Driftwood deposition from debris flows at slit-check dams and fans. Nat. Hazards (Dordr). 61 (2), 577–602. doi:10.1007/s11069-011-9939-9

CrossRef Full Text | Google Scholar

Shu, A. P., Zhang, Z. D., and Wang, L. (2008). Method for determining the critical grain size of viscous debris flow based on energy dissipation principle. J. Hydraulic Eng. 38 (3), 257–263. doi:10.3321/j.issn:0559-9350.2008.03.001

CrossRef Full Text | Google Scholar

Song, D., Zhou, G. G., Xu, M., Choi, C., Li, S., and Zheng, Y. (2019). Quantitative analysis of debris-flow flexible barrier capacity from momentum and energy perspectives. Eng. Geol. 251, 81–92. doi:10.1016/j.enggeo.2019.02.010

CrossRef Full Text | Google Scholar

Steeb, N., Rickenmann, D., Badoux, A., Rickli, C., and Waldner, P. (2016). Large wood recruitment processes and transported volumes in Swiss mountain streams during the extreme flood of August 2005. Geomorphology 279, 112–127. doi:10.1016/j.geomorph.2016.10.011

CrossRef Full Text | Google Scholar

Uchiogi, T., Shima, J., and Tajima, H. (1996). Design methods for wood-debris entrapment. Interpraevent Int. Symp. Klagenf. Austria 5 (1), 279–288.

Google Scholar

Wang, D. Z., Chen, X. Q., Zhao, W. Y., Xu, M., and Choi, C. E. (2017). Movement and intercept characteristics of driftwood in debris flow. Sci. Soil Water Conservation 15 (06), 9–18. doi:10.16843/j.sswc.2017.06.002

CrossRef Full Text | Google Scholar

Wang, L., Song, D., and Zhou, G. (2022). Debris flow overflowing flexible barrier: Physical process and drag load characteristics. Landslides 19, 1881–1896. doi:10.1007/s10346-022-01880-0

CrossRef Full Text | Google Scholar

Wohl, E. (2011). Threshold-induced complex behavior of wood in mountain streams. Geology 39, 587–590. doi:10.1130/G32105.1

CrossRef Full Text | Google Scholar

Xie, X. P. (2017). The control effect of multi-herringbone water-separation system to debris flow and its design method based on experimental research. Beijing: Chinese Academy of Sciences University.

Google Scholar

Xie, X. P., Wang, X. J., and Qu, X. (2020b). Experimental study on mitigation effect of slit dam to debris flow with driftwood. J. Eng. Geol. 28 (6), 1300–1310. doi:10.13544/j.cnki.jeg.2020-130

CrossRef Full Text | Google Scholar

Xie, X. P., Wang, X. J., and Yan, C. L. (2020a). A review of the research on woody debris related disaster and its prospect. Mt. Res. 38 (04), 552–560. doi:10.16089/j.cnki.1008-2786.000533

CrossRef Full Text | Google Scholar

Xie, X. P., Wei, F. Q., Yang, H. J., and Xie, T. (2017). Experimental study on large wood filtration performance by herringbone water-sediment separation structure. J. Mt. Sci. 14 (2), 269–281. doi:10.1007/s11629-016-3922-6

CrossRef Full Text | Google Scholar

Zhao, G. D., Hu, H., Song, D., Zhao, T., and Chen, X. Q. (2019). Experimental study on the regulation function of slit dam against debris flows. Landslides 16 (1), 75–90. doi:10.1007/s10346-018-1065-2

CrossRef Full Text | Google Scholar

Zheng, H., Shi, Z., Yu, S., Zhao, T., and Chen, X. Q. (2021) Erosion mechanisms of debris flow on the sediment bed', Water Resources Research. Water Resour. Res. 57 (12), e2021WR030707. doi:10.1029/2021WR030707

CrossRef Full Text | Google Scholar

Nomenclature

L the length of LW

N the quantity of LW

B the width of the channel, which equals the total width of the slit-check dam

b the width of a single opening of the slit-check dam

h the height of the opening of the slit-check dam

n the quantity of the openings of the slit-check dam

A the area of the openings of the slit-check dam

P_sa sediment activation rate

P_st sediment trapping rate

P_wr wood retention rate

P_wc wood clogging rate

P_ob opening blockage rate

γ_c debris flow density

C_v sediment volume concentration

Q_c debris flow discharge

v_c debris flow velocity Q_m: maximum discharge of the slit-check dam

V the volume of LW

V_s the volume of sediment