
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 27 September 2022
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.1018432
This article is part of the Research Topic Advanced Application of Deep Learning, Statistical Modelling, and Numerical Simulation on Geo-Environmental Hazards View all 59 articles
The forecast of failure time of unstable slope and the definition of early warning threshold are very important for preventing landslide disaster and reducing its losses. Based on the monitoring curve of unstable slope deformation varying with time, the mathematical models are used to accurately describe the nonlinear creep behavior in the initial creep stage and the unstable creep stage of unstable slope and a forecasting method for creep landslide is proposed. In addition, this study examines an improved tangential angle criterion obtained by a new forecasting method. The results show that the initial creep stage of unstable slope can not be neglected for forecasting the failure time. The initial creep velocity v0 and the viscoelastic hysteresis coefficient
Landslide hazards not only threatened the human life but also cause serious and destructive effects on the environment, resources, and construction practices. An analysis of historical records showed that from 1410 to 1999, at least 996 landslides occurred in Italy, resulting in 12,421 casualties (Guzzetti, 2000). As recently as October 1963, the catastrophic Vaiont landslide occurred in Italy, approximately 2.5×108 m3 in volume, the Vaiont landslide caused more than 2000 deaths (Tika and Hutchinson. 1999). An analysis of Canada’s fatal landslide data-base from 1840 to 1996 shows that approximately 600 people died in 84 landslide events (Evans, 1997). In Newfoundland alone, as many as 68 fatalities due to landslides have occurred (Liverman et al., 2001; Evans et al., 2005). In the data-base of landslide records from 1978 to 2005, Nepal has suffered a total of 397 fatal landslides, causing 22,179 deaths -an average of 78 deaths per year (Petley et al., 2007). Recently in Nepal, from June 10 to 15 August 2007, 70 people died in landslides (Dahal and Hasegawa, 2008). In China, 10,000 people were killed as a result of a series of catastrophic landslides triggered by the 1920 Haiyuan earthquake (Ms=8.5) (Wang et al., 2014; Pei et al., 2017; Zhou et al., 2021; Cui et al., 2022). At present, landslides occur in almost all areas of China, the most serious of which have been recorded from provinces in Western China. In the past 20 years, landslides have caused about 1,000 deaths per year in Western China (Huang, 2009; Zhang et al., 2019a; Ye et al., 2020a; Li et al., 2021a; Cui et al., 2021). Therefore, landslides and their related ensuing hazards have caused significant casualties and economic losses worldwide (Borgatti et al., 2006; Collins, 2008; Zhang et al., 2017; Ye et al., 2020b; Li et al., 2021b; Li et al., 2022).
In order to reduce the serious damage caused by landslide disasters, accurate warning and forecasting is critical. The evolution and development of landslides are affected by many factors, such as topography, geological structure and extreme environment, which cause the deformation behavior of landslides to be nonlinear, making the early warning and forecasting of landslides very difficult. Nevertheless, great achievements have been obtained by the study of landslide warning and forecasting methods. For example, regression predicting methods to perform the forecasting relied on Lyapunov functions (Huang et al., 2009), extreme learning machines (Huang et al., 2017), artificial neural networks (Mayoraz and Vulliet 2002), and bionics algorithm (Gao 2014). Complex correlations between triggering factors and landslide failure were used for landslide prediction (Li et al., 2018). However, the intrinsic failure behavior and critical failure criteria of landslide are typically not taken into account in these approaches to landslide forecasting and warning. In these past approaches, the methods of regression and bionics algorithm for prediction failure time of the landslide are considered only a coincidence, and further verification and improvement in engineering practice was proposed (Qin et al., 2002; Chen et al., 2018). Further research shows slow creep of landslide to be the strain of rock and soil material itself, which is time-dependent under constant load dominated by the gravity field. For the soil and rock unstable slopes with time -dependent failure, this kind of slope is a dynamic development process, which undergoes long-term deformation from beginning to failure, and sliding deformation had the characteristics of slow creep. The failure of this unstable slope is termed “creep landslide” (Terzaghi, 1950; Haefeli, 1953; Xu et al., 2011; Marin and Velásquez, 2020; Zhang et al., 2021; Bao et al., 2022). Compared with the above-mentioned regression and bionics algorithm predicting methods, the intrinsic creep behavior of the failure in the geological body is seen to be more important for the early warning of the landslide with creep characteristics. Saito and Uezawa (1961) obtained the relationship between creep rupture time of soil and strain rate in creep experiments of soil, and an empirical prediction equation for landslide failure time was proposed. Fukuzono (1985) proposed a phenomenological method based on Saito theory in small-scale model tests. The results showed that the inverse velocity of deformation velocity in the tertiary creep decreased with the increased of time, and then the inverse-velocity method was used to predict the time of landslide failure. Voight (1988) conducted a detailed study and verification of the Fukuzono model describing the behavior of materials in the final stage of failure. This was interpreted as the basic law for various forms of material failure and it successfully predicted volcanic eruptions. Due to the simplicity of the application of the inverse-velocity method, it was widely used in the prediction of the failure time of soil and rock unstable slopes (Rose and Hungr, 2007; Mufundirwa et al., 2010; He and Kusiak, 2017). However, a prediction error may be caused by neglecting the influence of initial creep process on the slope. For example, the predicted error of the empirical prediction equation of landslide failure time proposed by Saito was10±0.59.
For the application of various prediction methods such as empirical equations, phenomenological methods, regression methods, and bionics algorithm, a generalised early warning thresholds criterion was critical to the accuracy of landslide early warning and forecast (Pei et al., 2016; Zhang et al., 2019b; Zhang et al., 2020). Intrieri et al. (2012) defined three different velocity threshold levels, ordinary level, attention level and alarm level, by studying the most critical period of the completely monitoring data for the Torgiovannetto landslide. Xu et al. (2011) developed a quantitative method–based on statistical analysis of a large number of landslide events–which was used to describe the tangential angle of the deformation vs. time curve of the landslide, and following that, the criterion of the landslide tangential angle was proposed. Chen et al. (2018) conducted research on the critical deformation criterion for first locked segment and multi-locking segment were respectively, based on the rupture behavior at the volume dilation point during the shearing process of locked segments in landslide (Qin et al., 2010a, 2010b; Xue et al., 2014). However, there is currently no reasonable forecasting method combined with appropriate generalised early warning thresholds criterion to improve the accuracy of early warning and forecasting in order to reduce the serious damage caused by landslides.
Therefore, in order to reduce the serious damage caused by landslides, this paper mainly explores the forecasting methods of landslide, and then the generalised early warning thresholds criterion is studied, in order to improve the accuracy of early warning and forecasting for landslides. To achieve these objectives, firstly, this study is based on the monitoring curve of unstable slope deformation varying with time. The creep mathematical models describing the initial creep stage and the unstable creep stage of unstable slope is selected. Meanwhile, according to the analysis of the forecast parameters of the unstable slope, combined with the critical tangential angle warning criterion and an improved tangential angle criterion comparison study, the warning prediction of landslide is proposed. Finally, the forecasting method applied to the early warning and forecasting analysis of reported soil and rock landslides cases with creep characteristics is presented. In the process of landslide forecasting, the principle of the combination of generalised early warning thresholds criterion and predicted failure time, the combination of monitoring and field observation, and the combination of empirical prediction and theoretical analysis to carry out comprehensive landslide prediction is adhered to.
The deformation and failure characteristics of rock and soil mass are notably reflected by landslide deformation, which is the external manifestation of landslide deformation. Landslide deformation monitoring plays an important role in evaluating stability, deformation evolution, early warning, and forecasting of landslides. The failure of unstable slopes with characteristics of long-term creep deformation are usually caused by unstable slopes under various factors (such as topography, geological structure, and physical and mechanical properties of anisotropic rocks and soils), which form a constant load dominated by the gravity field. The deformation of the slope starts from the region where the internal local shear stress concentrated, which reaches the final destruction process (Tavenas and Leroueil. 1981). The whole creep deformation process includes an initial creep stage and an unstable creep stage, wherein the unstable creep stage includes secondary creep stage and tertiary creep stage (Saito. 1969), as shown in Figure 1.
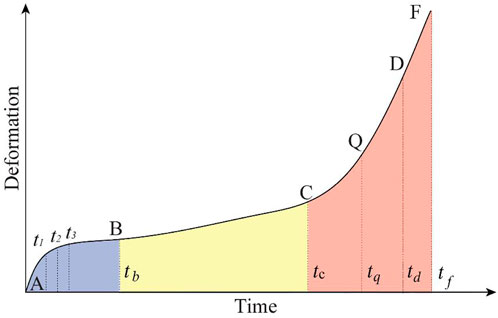
FIGURE 1. Deformation stage of landslide with creep characteristics. Note: AB, primary creep; BF, unstable creep; BC, secondary creep; CF, tertiary creep; CQ, initial accelerated sub-phase; QD, medium accelerated sub-phase; DF, critical failure sub-phase.
Yang (2010) proposed that the deformation of the initial creep stage of the landslide was far beyond the strain of the geomaterial in the viscoelastic range, rather it showed the deformation characteristics of viscoelastic hysteresis. Numerous studies have proposed many viscoelastic hysteretic models with hysteretic deformation by combining laboratory tests with long-term monitoring of landslide deformation (Miao et al., 1999; Christensen, 2012). The most typical models are the Maxwell model and the Kelvin model.
The mathematical expression of Maxwell model is as follows:
Where the
When the sliding surface of the landslide is formed, it would be controlled by the constant force of gravity field. From the initial creep state to the whole creep state, the stress state of the soil is constant. For Eq. 1 with respect to time derivation, the deformation velocity is obtained as follows:
Among them, the dimension of viscous coefficient is kPa•s, the dimension of load stress is kPa, and the dimension of velocity is ms−1. Therefore, in terms of nonlinear creep, the Maxwell creep mathematical model is as follows:
The expression of the Kelvin model is
Where the
Eq. 6 available from Eq. 5, with respect the derivative of time
Since when
Saito and Uezawa (1961) established logarithmic empirical formulas of time and deformation velocity based on a series of creep tests.
Where
Fukuzono (1985) and Vioght 1988) established the relationship between acceleration and velocity of deformation based on Saito theory as follows:
where A and α are constants under time invariant external conditions (i.e., load and temperature) (Crosta and Agliardi 2003).
Eq. 8 not only shows the macroscopical integrity and non-linear deformation characteristics in creep failure of slope at the unstable creep stage, but it also is coupled with Eq. 6.
Qin et al. (2010a, 2010b) and Xue et al. (2014) established a physical prediction model based on the Weibull distribution that couples the renormalization group model with the constitutive relation. The research shows that, the rupture behavior at the volume dilation point during the shearing process of locked segments in landslide, proposed the critical deformation criterion for first locked segment and multi-locking segment, as shown in the following:
Where
1) the initial creep stage
When t≤tb, the boundary condition: t=0, y=0 dy/dt=0
2) the unstable creep stage
When t≥tb,
The function-fitting method is used to calculate the unknown parameters in Eq. 12, and the fitted assignment points (t1, y1) (t2, y2) and (t3, y3) are selected on the initial creep curve. Note that the t1, t2 and t3 should be under condition of t3-t2=2 (t2-t1). The mathematical expression of v0 and
At the initial creep stage and the unstable creep stage of the landslide, the deformation and deformation velocity are equal at t=tb, indicating that the two curves are continuous and tangent at tb, and there exists a unique solution.
Eq. 19 available from Eq. 17 and 18
(tc, yc) and (tq, yq) are selected on the curve of unstable creep stage, where c is the starting deformation value of tertiary creep of landslide. Note that the tq and tc should be under condition of tq>tc.
Eq. 23 available from Eq. 20 and 21 and Eq. 22
Eq. 24 available from Eq. 19 and 23
The unknown parameters tb and tf are solved by the transcendental equations of Eq. 24 and 25. The d point is the deformation of the locked section at the peak strength, which is the critical deformation criterion when the landslide locked section is broken Eq. 9 and 10. The corresponding time td is used as the forecasting time of the landslide failure.
Eq. 27 available from Eq. 20 and 21 and Eq. 25
Eq. 28 available from Eq. 9 and 21 and Eq. 24
During the formation and evolution of slope failure, the cumulative deformation is characterised by increasing with time, but the increasing speed was different in different stages. It can be seen from the cumulative deformation curve that the tangential angle had different characteristics at different stages. However, the dimension of the vertical and horizontal coordinates is different, and the magnitude change of the vertical and horizontal coordinates caused the tangential angle to change accordingly. Therefore, the tangential angle defined by S (deformation) - t (time) curve was not unique.
After that, Xu, et al. (2011) proposed that the velocity of the landslide was considered to be a constant value in an infinitesimal period of time, as shown in the following:
Where Si is the cumulative deformation of the unstable slope in time ti, v is the average velocity of the secondary creep stage, Ti was the ordinate value of the same dimension and unit as the horizontal axis after transformation. According to the Ti combined monitoring time t, which corresponds to the curve of deformation vs. time, the T - t curve can be obtained,
In order to obtain the unique tangential angle in T-t curve, it could be seen from Eq. 29 and 30 that the tangential angle is inseparable from the determination of the secondary creep stage velocity v of landslide, the v is shown in the following:
where vi is the deformation velocity of the ith time intervals in the secondary creep stage, and n is the number of time intervals.
Assume that the average velocity was
According to new forecasting method, the tangential angle criterion was studied. For the landslide with creep characteristics, under the influence of various factors (such as topography, geomorphology, geological structure and physical and mechanical properties of anisotropic rocks and soils), a constant driving force based on gravity field was formed. According to Eq. 2 and 5, the initial creep velocity v0 and the viscoelastic hysteresis coefficient
When the external conditions of the landslide with creep characteristics are unchanged, the average velocity in the secondary creep stage corresponds to the only critical tangential angle. According to the 15 typical landslide data with creep characteristics collected from the scientific literature, the deformation stage and T-t transformation were carried out. The average velocity in secondary creep stage and the critical tangential angle of each landslide was obtained respectively, as shown in Table 1. The results of Table 1 demonstrate the difference of landslide characteristics and external factors. There was a significant difference between the duration of each deformation stage of the landslide, the average velocity in the secondary creep stage, and the improved tangential angle of the critical failure stage. The average velocity in the secondary creep stage ranged from 0.055 mm/d to 4.45 mm/d, and the improved tangential angle of the critical failure stage ranged from 82.05° to 89.66°. The larger the average velocity v in secondary, the smaller the critical tangential angle was, and the linear decreasing trend was obtained, as shown in Figure 2.
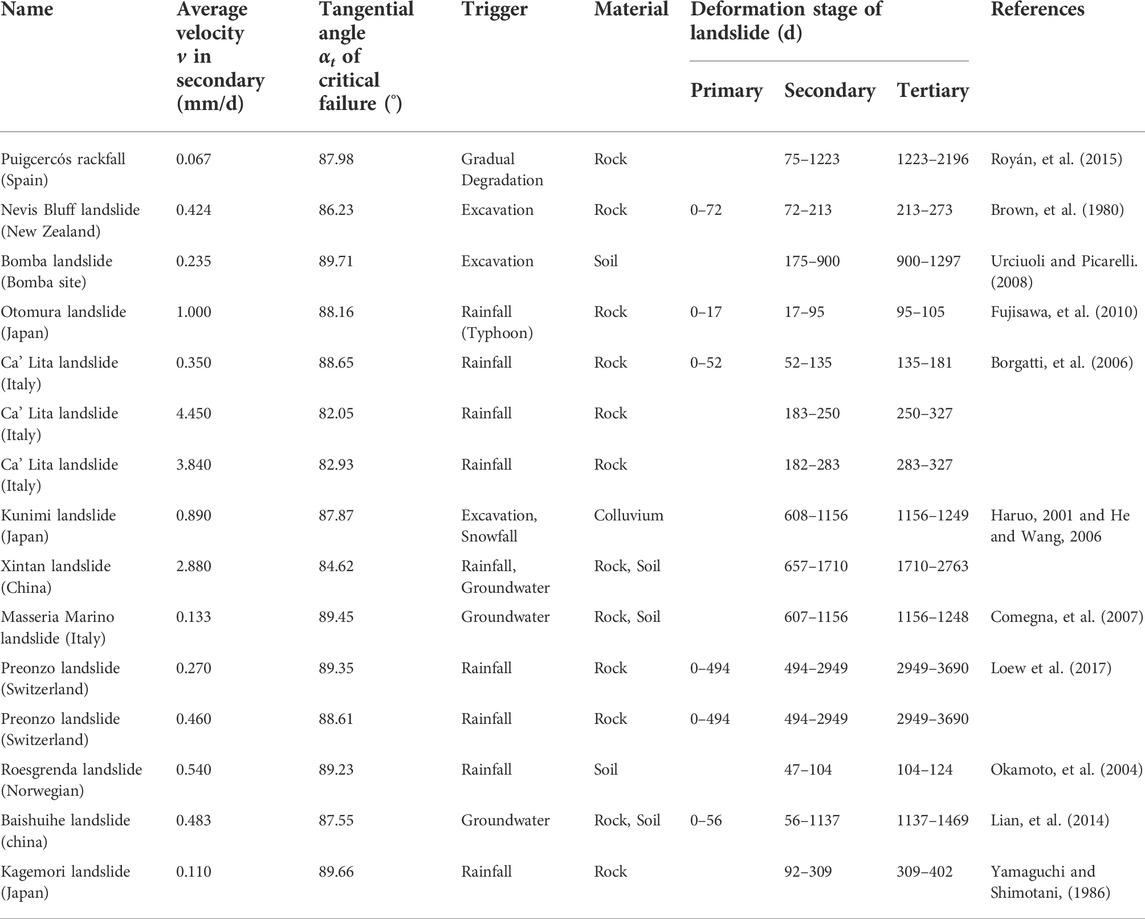
TABLE 1. Landslides database collected from scientific literature including details about average velocity in secondary, tangential, material, triggering factors, duration of the deformation stage of landslide, and reference.
According to the above analysis, the relationship between the critical tangential angle and the average velocity v in secondary is calculated by fitting as follows:
Where αt and v are the critical tangential angle and the average velocity in the secondary creep stage of the landslide with creep characteristics, respectively.
From Eq. 35, it can be seen that the improved tangential angle of the critical failure stage is mainly determined by the average velocity in the secondary creep stage, it is a comprehensive response of the creep parameters. The tangential angle of the critical failure is calculated according to the average velocity in the secondary creep stage of the landslide. Therefore, combined with the monitoring of the average velocity in secondary and the new forecasting method, the landslide prediction with creep characteristics is carried out. The early warning and forecasting system of the landslide is established, as shown in Figure 3.
Cut-and-fill methods to form steep slopes were used in the investigation areas. Focusing on the filling slope with a maximum height of 40.0 m, the original landform was more complicated, which represented by a naturally created V-shaped valley together with a U-shaped valley with original slope angle of 50°∼70°. The total filling volume was 6.12×104 m3 in fill slope with the elevation starting at 409 m and ending at 446 m (Figure 4). The soil structure in the high fill slope was horizontal Holocene Series (Q4), which was recently deposited loess consisting of silt and silty clay. The bedding and vertical joints structure of the original slope was well-developed, and the stratum lithology was the alluvial silty clay and clay of the Holocene Series (Q4al+pl).
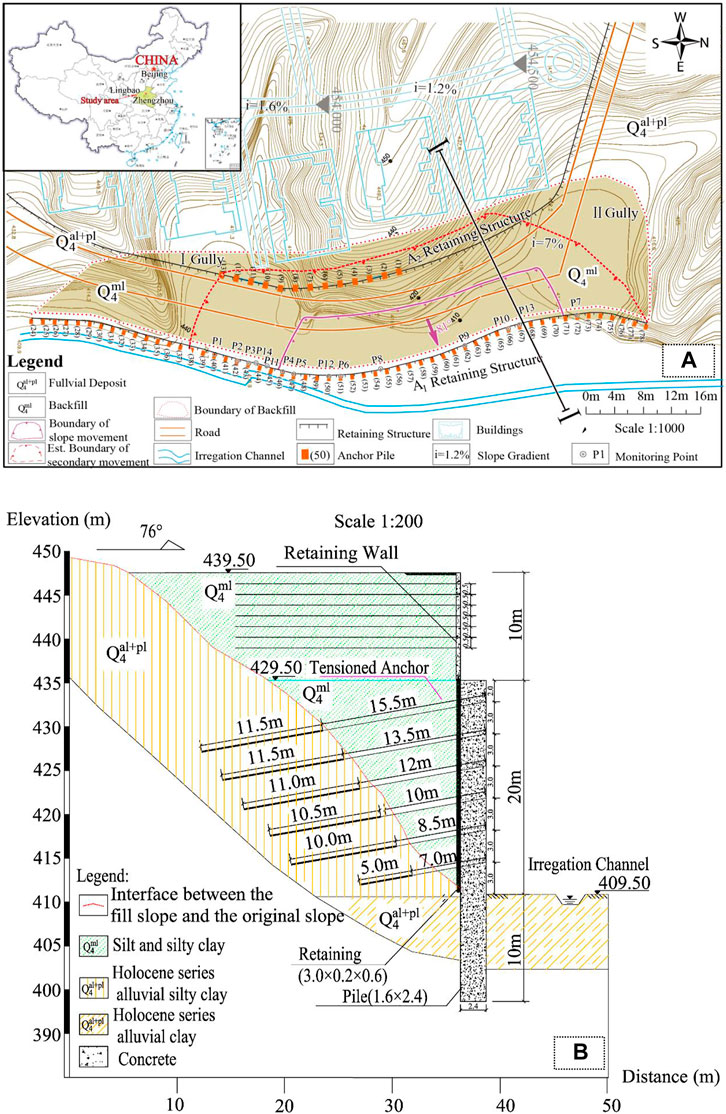
FIGURE 4. (A) Planar view of the high fill loess slope; (B)Engineering geological section of the high loess fill slope.
Two structure forms were constructed for the fill slope in the region of A1 retaining structure: retaining walls and pile boards connected to pile foundations were used in the upper and the lower of the fill slope, respectively. A total of 55 piles were distributed in the A1 area. At 4:51 a.m., fourth May 2015, the A1 retaining structures between 46# pile and 70# pile failed and collapsed after the rainfall on 1 May 2015, see Figure 5. The collapse region with dimensions of 78 m × 13 m × 22.6 m (length × width × height) was formed, approximately 2.31×104 m3 in volume (Figure 5B). The landslides buried 20 houses and damaged another 23. Fortunately, due to successful early warning, numerous people in the landslide danger zone were transferred to a safe place as a matter of urgency. When the landslide occurred, there were no casualties. Generally speaking, the stage of deformation and failure of the high fill slope was summarised as the following three stages: 1) Creep of slope under progressive gravity, bending-shear deformation of the piles. 2) Acceleration of slope sliding, development stage of pile dumping. (iii)The sliding surface of fill slope rapidly transfixion and the local failure occurring in the slope and piles. In summary, the deformation and failure of loess high fill slope presented a retrogressive failure mode of landslide.

FIGURE 5. The panorama and after failure of the high loess fill slope (A) Panorama of the high loess fill slope; (B) The high loess fill slope after failure.
In the conventional appearance monitoring methods, the main methods include electronic total station and GPS monitoring. These methods are monitored by setting monitoring points, resulting in a small monitoring range, low monitoring frequency, and low monitoring accuracy. For this study, the real-time monitoring on the fill slope was achieved by the IBIS-L terrain deformation monitoring system. This monitoring system combines synthetic aperture radar tech and stepped frequency—continuous wave tech to achieve resolution up to 0.1 mm (Pei et al., 2016). As for the full extent of the monitoring region, the changes in the temperature and humidity could affect the monitoring results. Because of the propagation velocity of electromagnetic wave varies in different environments, two ground control points (GCP) were selected as check points in the study region through which the final monitoring results were corrected to avoid the influence of different environments factors (Rödelsperger et al., 2010).
In the real-time monitoring of the study area, the IBIS-L monitoring device was used to monitor the fill slope in the A1 area, in which the deformation change at any position in the monitoring area at any stage of the line of sight was obtained (Figure 6). In addition, the centre of the linear orbital was taken as the origin, the linear orbital direction was the X-axis, and the vertical linear orbital direction was the Y-axis. The deformation symbol of the monitoring area was defined as the direction away from the instrument was positive.
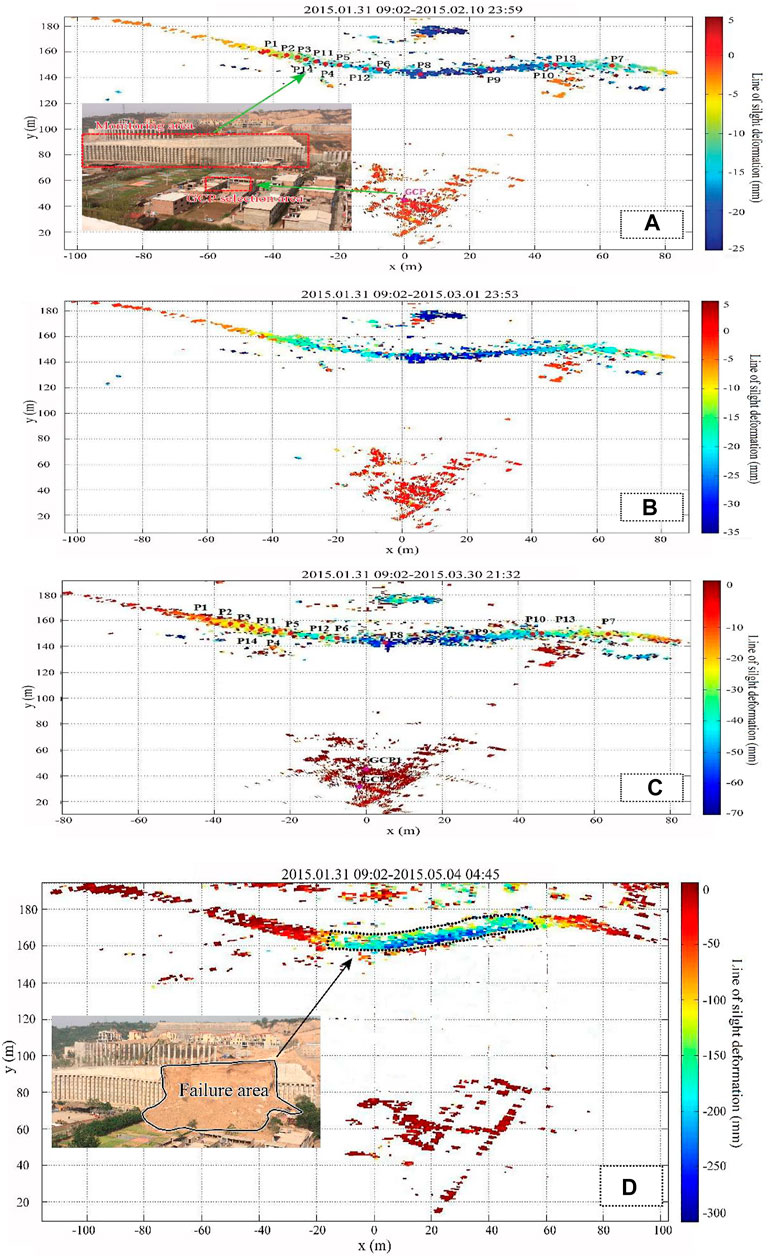
FIGURE 6. Deformation cloud diagrams during different monitoring periods were obtained by IBIS-L monitoring device (A) between 31 January 2015 and 10 February 2015; (B) between 31 January 2015 and 1 March 2015; (C) between 31 January 2015 and 30 March 2015; (D) between 31 January 2015 and 4 May 2015.
It is seen from Figure 6 that within the monitoring interval from January 31 to 4 May 2015, the deformation of the high fill slope in the A1 area gradually produces the deformation in the line of sight. As the monitoring time increases, the cumulative deformation in the deformation cloud diagram gradually increases, indicating that the deformation of the high fill slope gradually increases. From January 31st to 10 February 2015, the deformation generated in the fill slope ranged from 6.4 to 19.5 mm approximately. From January 31 to 1 March 2015, the deformation generated in the fill slope ranged from 11.72 to 31.34 mm approximately. From January 31 to 30 March 2015, the deformation generated in the fill slope ranged from 18.60 to 69.77 mm approximately. From January 31st to 4 May 2015, the deformation generated in the fill slope was ranged from 35.91 to 320.11 mm approximately. The fill slope entered the tertiary creep stage on 30 April 2015. The maximum increase of the deformation of the fill slope from April 30 and 4 May 2015 was 189.71 mm. In the monitoring process of the study area, the deformation of the monitoring cloud diagram had been increasing and the monitoring deformation had not been in convergence. It was shown that the stability of the high fill slope in the A1 area was still relatively weak. From the difference of the colour of the monitoring deformation cloud, the deformation of the filling slope in the study area showed obvious regional characteristics. The area with larger deformation increment was located in the middle of the monitoring area, followed by the right side of the monitoring area and the deformation with relatively small increment was located in the left monitoring area.
Numerous typical monitoring points were selected at different areas in the monitoring cloud diagram for this study, as shown in Figure 6A. The deformation evolution of high fill slope was mainly controlled by gravity field. In the initial and secondary creep stages, the slope of the cumulative deformation curve is smaller, the cumulative deformation increases slowly and the duration is longer. However, in the tertiary creep stage, the curve of deformation vs. time showed a sudden increase. The slope of the curve was relatively larger and the duration was relatively short (Figure 7A).
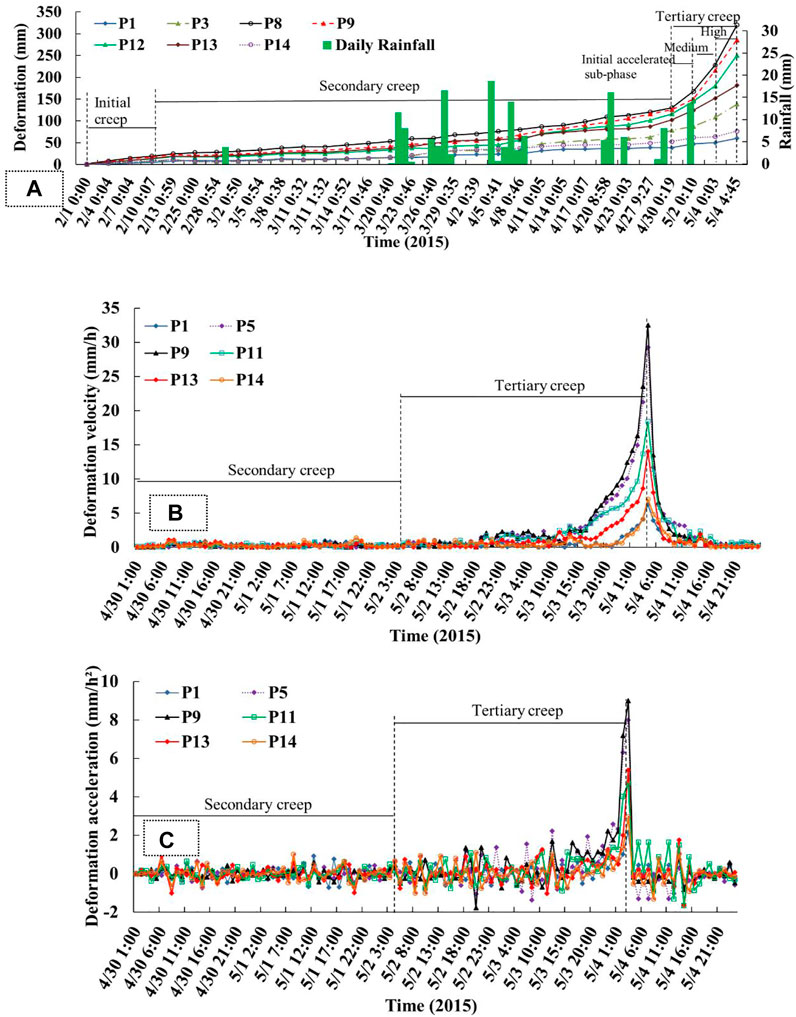
FIGURE 7. (A)Curves of deformation and rainfall events with time; (B) Velocity variation during formation and evolution of slope failure; (C) Acceleration variation during formation and evolution of slope failure.
The deformation velocity remains almost unchanged in the secondary creep stage and enters the initial accelerated sub-phase in the tertiary creep stage. The deformation velocity increases significantly compared with the previous stage, while in the high acceleration sub-phase, the deformation velocity increases sharply to its maximum value (Figure 7B). The acceleration of the deformation fluctuates with a small amplitude mainly around 0 mm/h2 in the secondary creep stages and enters the initial accelerated sub-phase in the tertiary creep stage, which fluctuates around 0 mm/h2, but with an obviously larger fluctuation amplitude. Regarding the acceleration in the high acceleration sub-phase, the deformation process accelerates intensively, which shows the characteristics of a sharp rise in acceleration rate (Figure 7C), where the acceleration increases from 0 mm/h2 to the maximum. Compared with the initial and secondary creep stage, the acceleration of the high acceleration sub-phase in tertiary creep stage plays a guiding role in the early warning of high fill slopes.
Referring to the curve of deformation vs. time at the P8 and P9 monitoring points in Figure 7A, the fitted assignment points t1, t2, t3 and tc, tq were selected on the initial creep stage and the unstable creep stage of the curve of deformation vs. time. It was noted that the t1, t2 and t3 should be under condition of t3-t2=2 (t2-t1) and c was the starting deformation value of tertiary creep, moreover, the tc and tq should be under condition of tc>tq. Then, the deformation fitting assignment points at the P8 and P9 monitoring points were brought into the new forecasting method for failure time of creep landslide. Based on the fitting assignment points of the deformation curve at the P8 monitoring point, combined with the critical deformation criterion for the failure of landslide (as shown in Eq. 9). The corresponding failure time td of the landslide locked segment was predicted to be 94.233 days, i.e., the time of landslide failure was predicted to be 3 May 2015, and the time tf of landslide occurrence was predicted to be 99.8 days, i.e., 8 May 2015. The corresponding results of the new forecasting method at the P8 monitoring point showed that the high fill slope would be failure between 3 May 2015 and 8 May 2015. The high fill slope failure occurred at 4:51 on 4 May 2015, i.e., the forecasting failure time, based on the new forecasting method, was used to warn the failure of high fill slope 1 day earlier. Based on the fitting assignment points of the deformation curves at the P9 monitoring point, the corresponding failure time td of landslide locked segment was predicted to be 95.94days, that is, the time of landslide failure was predicted to be 4 May 2015, and the time tf of the landslide occurrence was predicted to be 105.65 days, i.e., 14 May 2015. Therefore, based on the deformation curve at the positions of P8 and P9 monitoring points, the failure time of the high fill slope was between 3 May 2015 and 4 May 2015, while the high fill slope was in a state of critical failure after the fracture of the locked section. The failure time of the landslide was advanced due to the rainfall on 1 May 2015. The P8 and P9 monitoring curve fitting assignment points and the creep parameters of the landslide and the warning forecast time are shown in Table 2, respectively.
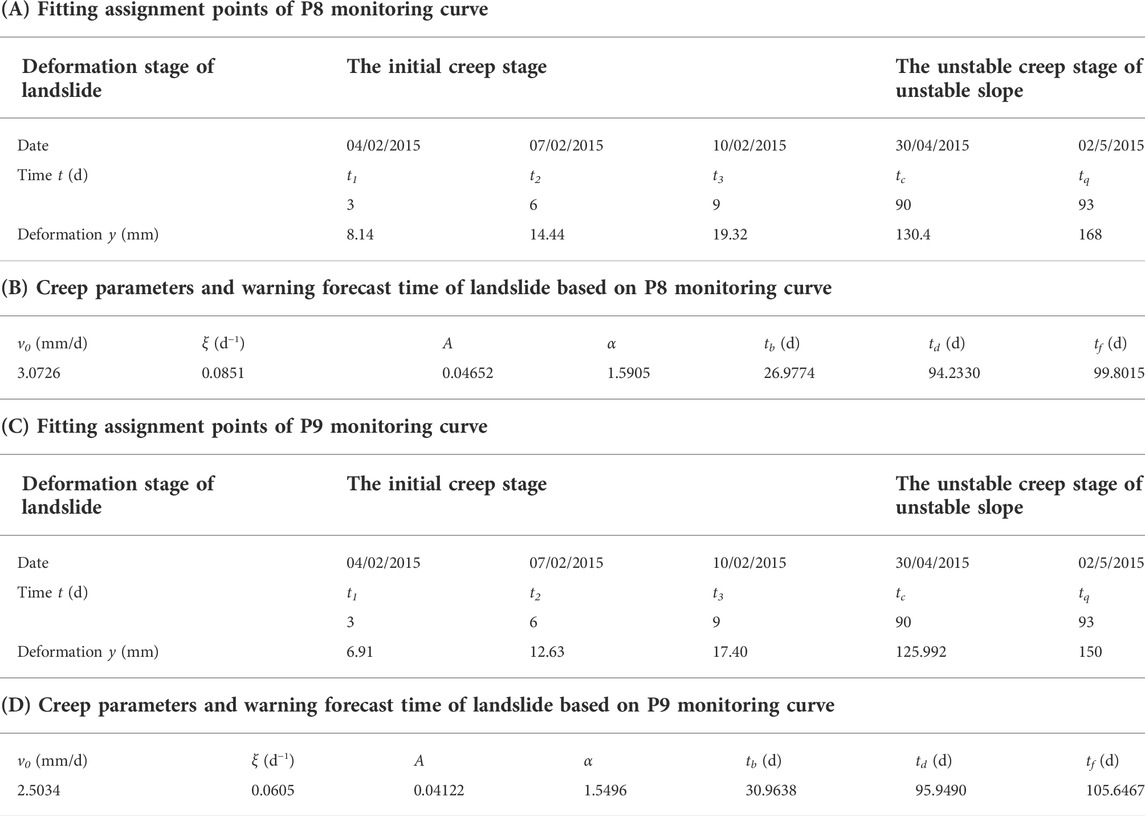
TABLE 2. Fitting assignment points of P8 or P9 monitoring curve and creep parameters and warning forecast time of landslide based on P8 or P9 monitoring curve.
Based on the new forecasting method of creep landslide, failure time td and occurrence time tf of the landslide were proposed, but in order to provide more accurate warning, the improved tangential angle criterion based on the new early warning method was studied. By comparing the deformation curve in the new forecasting method of creep landslide at the monitoring points of P8 and P9 with the field monitoring deformation curve (Figures 8A,B). Location of the P8 monitoring point, the average velocity in the secondary creep stage of the deformation curve based on the new forecasting method and field monitoring were 1.48 mm/d and 1.66 mm/d, respectively. The relationship between the critical tangential angle αt and the average velocity v in secondary was considered, as shown in Eq. 35. The corresponding critical tangential angles of landslide were 86.82° and 86.53° at P8 monitoring point, respectively. At the location of the P9 monitoring point, the average velocity in the secondary creep stage of deformation curve based on new forecasting method and field monitoring were 1.51 mm/d and 1.52 mm/d, respectively. The corresponding the critical tangential angles of landslide were 86.77° and 86.73° at the P9 monitoring point, respectively. The critical tangential angle of real time curves in field monitoring at the P8 and P9 monitoring points transformed from eq. 29 and 30 to T-t curves were 87.46° and 87.60°, respectively (Figures 8C,D). The results showed that the deformation curve obtained by the new forecasting method of creep landslide could reflect the characteristics of each deformation stage of the landslide. The critical tangential angle of the curves in the new forecasting method was compared with the critical tangential angle of real time curves in field monitoring and the error was within 1°. The improved tangential angle based on new forecasting method had a good indication for the warning of landslides. Combined with the new forecasting method of creep landslide, failure time td and occurrence time tf of landslide were proposed, and the failure of creep landslide could be accurately predicted.
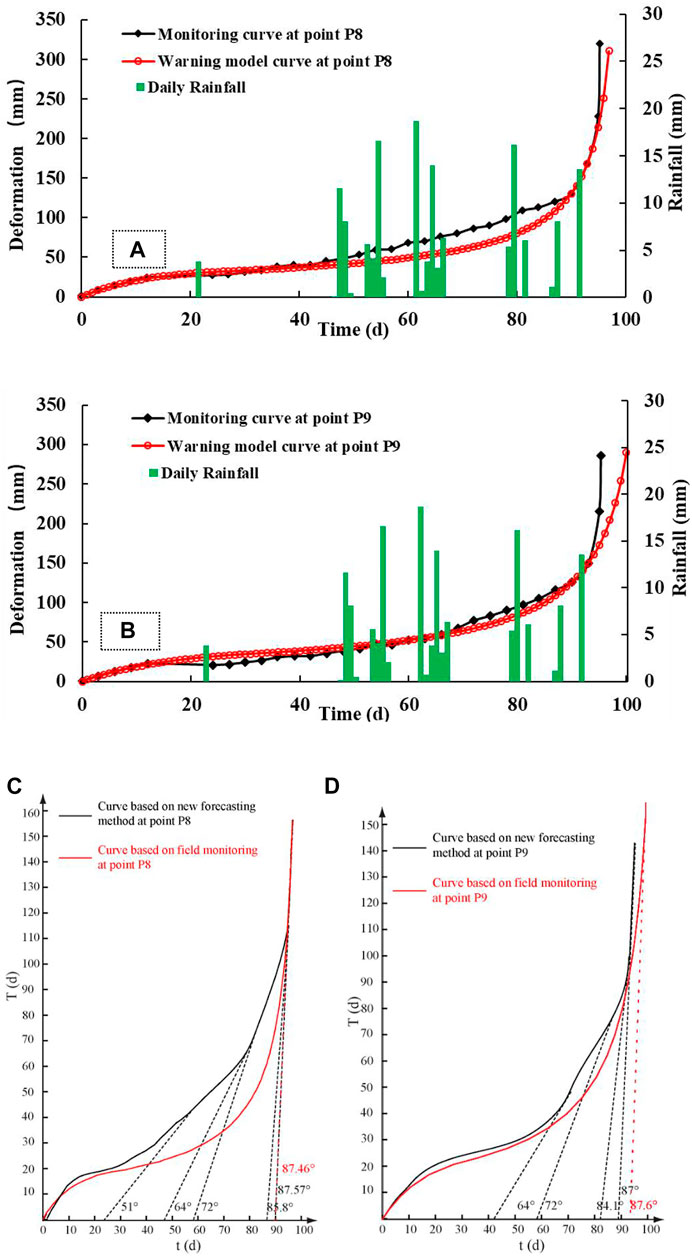
FIGURE 8. Comparison among rainfall events and deformation (the real time monitoring in field and in the new forecasting method of creep landslide) as a function of time, (A) P8 monitoring point (B) P9 monitoring point; (C) T-t curve of point P8; (D) T-t curve of point P9.
At 5:39 on 24 June 2017, a large landslide–consisting of hard rock predominantly composed of metamorphic sandstone–occurred in village of Xinmo, in Maoxian County, Sichuan Province, China and 64 houses were buried, 83 people were lost or died. The Songping River, a tributary of the Min River, was blocked for nearly 2 km, causing heavy casualties and property losses (Fan et al., 2017). It was mainly due to the cumulative damage of rock mass caused by historical seismic activity and long-term gravitational deformation, and then the catastrophic landslide event triggered by rainfall (Pei et al., 2018). The Maoxian landslide can be divided into two regions, namely the landslide region and the landslide-affected region. The landslide region from top to bottom was the A scarping region, the B transportation region and the C deposit region. The landslide-affected region was the region affected by the potential catastrophic danger of the landslide. It was mainly the potential unstable rock mass in region D and the sliding body in region E, as shown in Figure 9A. InSAR (Interferometric Synthetic Aperture Radar) is developing rapidly in detecting and monitoring surface deformation associated with landslides (Bovenga et al., 2017). Intrieri et al. (2018) used InSAR technology on the obvious pre-event ground deformation of this landslide, which was obtained by ESA Sentinel-1 satellite from 9 October 2014 to 19 June 2017 (Figure 9B). It shows that there was obvious precursory deformation before the occurrence of the Maoxian landslide. The acceleration zone was located at the trailing edge of the northwestern part in the landslide. In this region, the monitoring point MP was selected and the precursory deformation vs. time curve was analyzed. The positive values of the curve correspond to the movement towards the satellite, while the negative values correspond to the movement away from the satellite. After 20 April 2017, the Maoxian landslide was in the initial acceleration sub-phase of the tertiary creep stage, and led to the period from 7 June 2017 to the 19th, the landslide was in the medium accelerated sub-phase, during which the average velocity of the landslide was about 2 mm/day.
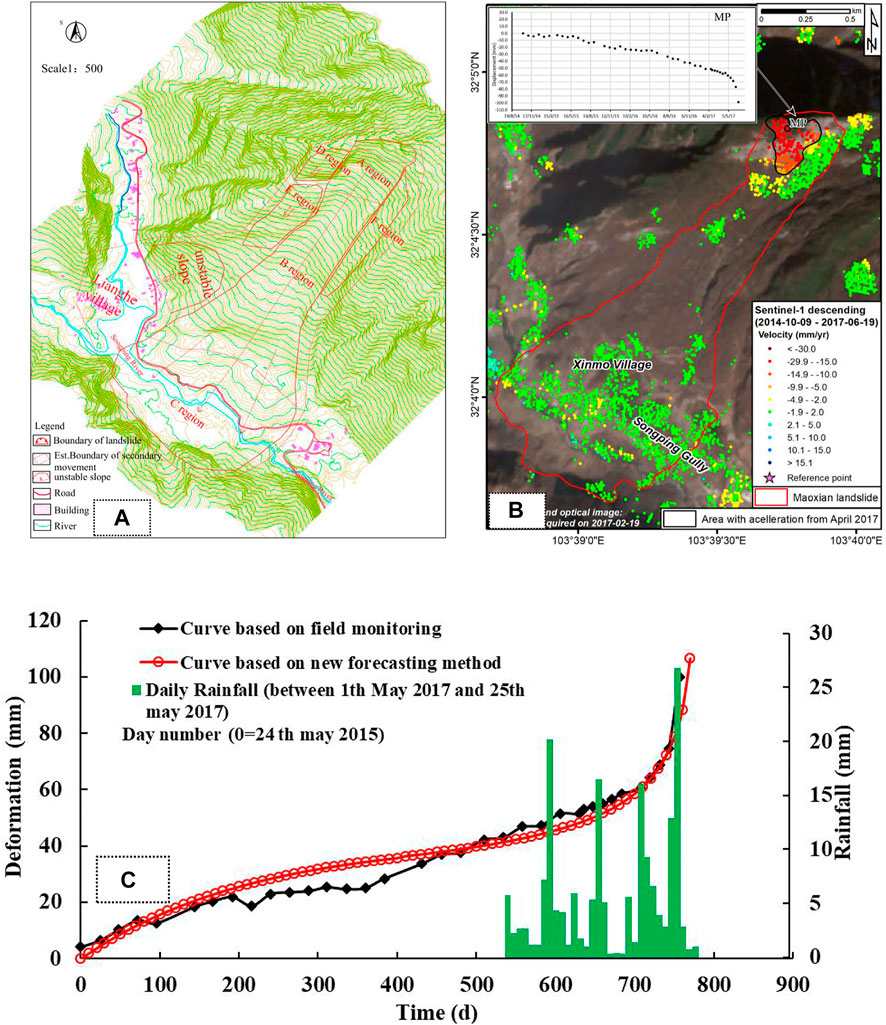
FIGURE 9. (A)Planar view of Maoxian landslide; (B) Pre-event ground deformation of the Maoxian landslide (modified after Intrieri et al., 2018); (C) Comparison among rainfall events and deformation (the real time monitoring in field and in the new forecasting method of creep landslide) as a function of time in Maoxian landslide.
From Figure 9C, the fitting assignment points in new forecasting method were selected for each stage of the deformation curve from 24 May 2015 to 19 June 2017, as shown in Table 3A. The corresponding failure time td of the landslide locked segment was predicted to be 760.841days, i.e., the time of landslide failure was predicted to be 22 June 2017, 2 days before the Maoxian landslide occurred. The time tf of landslide occurrence was predicted to be 782.292 days, i.e., 14 July 2017 (Table 3B). The results of the new forecasting method indicated that failure time of the Maoxian landslide locked section was 22 June 2017, after that, this landslide was in a state of critical failure. Research by Fan et al. (2017) showed that the cumulative rainfall exceeded 200 mm from 1 May 2017 to the time of landslide failure. It was possible that the landslide failure time was advanced due to rainfall. In order to obtain an accurate warning, the deformation curves between the real time monitoring in field and in the new forecasting method of creep landslide were compared (Figure 9C). The average velocity at the secondary creep stage in deformation vs. time curve of the new method and the real time monitoring were 0.055 mm/d and 0.07612 mm/d, respectively. Combined with the relationship between the critical tangential angle αt and the average velocity v in secondary, the corresponding the critical tangential angle of landslide were 89.11° and 89.07°, respectively. Meanwhile, the critical tangential angle in T-t curve of the Maoxian landslide was 89.41°. The critical tangential angle of the curves in the new forecasting method was compared with the critical tangential angle in T-t curve, the error was within 1°. The improved tangential angle based on new forecasting method had a good indication for the warning of Moxian landslides. Moreover, combined with failure time td and occurrence time tf, the early warning and forecasting system of landslide was applied, the failure of creep landslide could be accurately predicted.
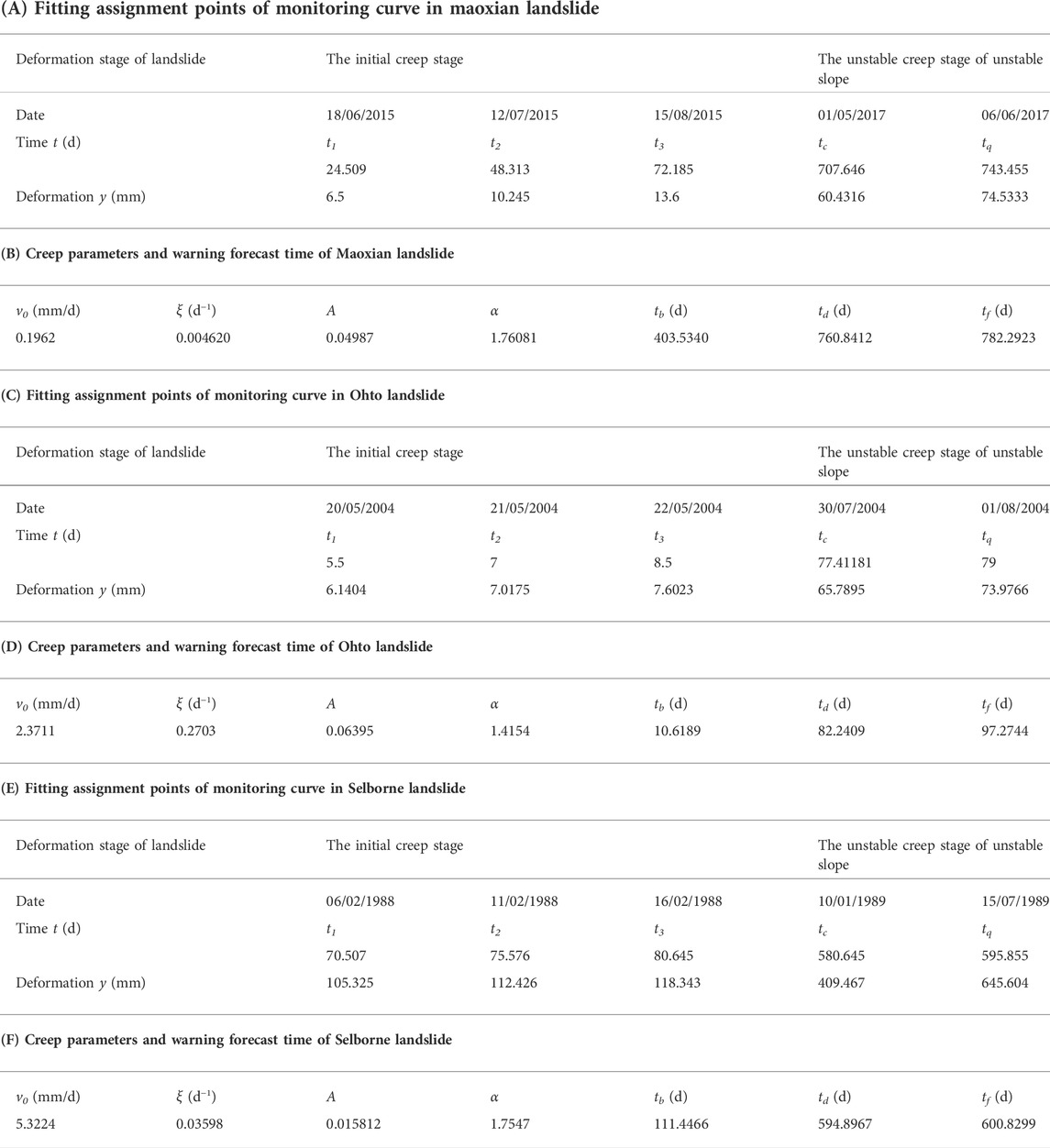
TABLE 3. Fitting assignment points of monitoring curve in landslide of case verification and creep parameters and warning forecast time of landslide in case verification.
At 0:15 a.m. on 10 August 2004, a rock slope of 120 m wide and 100 m high failed in Ohto, Nara, Japan. The total amount of landslide was approximately 2.0×105 m3, consisting of soft rock with an alternation of sandstone and mudstone/shale. Fortunately, the landslide did not cause casualties (Suwa et al., 2010). Ohto landslide occurred on a steep slope opposite the Kumano River (Figures 10A–E). As shown in Figure 10F, the slope was steep, with an average slope angle of 40 °and the steeper in the lower part, i.e., the slope was convex. The convex-slope condition also caused slope instability. In January 2004, several extensometers were installed to monitor the deformation of the unstable slope as shown in Figure 10D. It shows that the creep velocity was constant before 31 July 2004, and then began to accelerate. At 5:10 a.m. on August 8, when the creep velocity reached 4 mm/2h, the Route 168 was closed and the landslide occurred 43 h later.
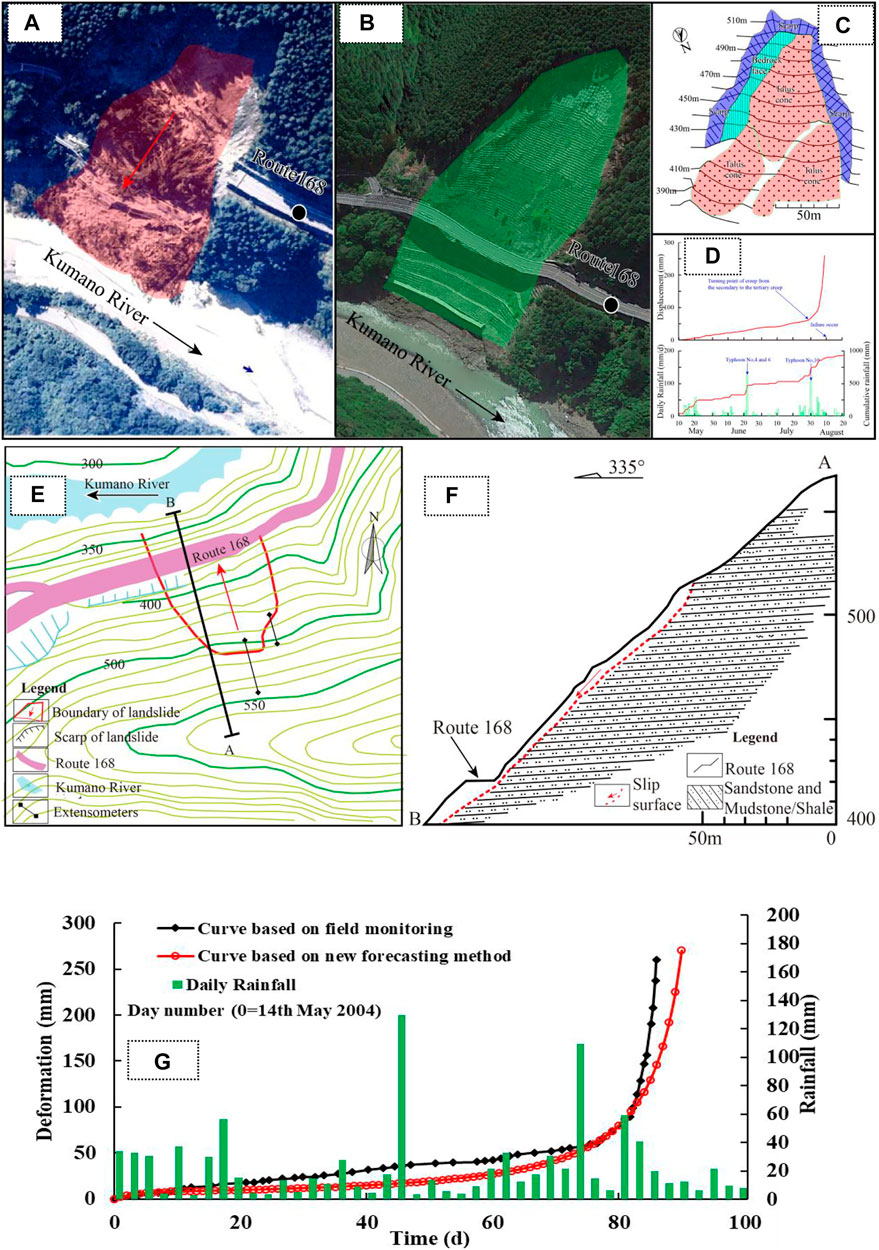
FIGURE 10. (A) Aerial view of landslide; (B) Aerial view after landslide treatment; (C) Detail of landslide; (D) The trailing edge deformation of the landslide and the daily rainfall (modified after Suwa et al., 2010); (E) Planar view of landslide;(F) Engineering geological section of landslide (modified after Suwa et al., 2010); (G) Comparison among rainfall events and deformation (the real time monitoring in field and in the new forecasting method of creep landslide) as a function of time in Ohto landslide.
The fitting assignment points in new forecasting method were selected in each stage of the deformation curve, as shown in Table 3C. The corresponding failure time td of landslide locked segment was predicted to be 82.2409 days, i.e., the time of landslide failure was predicted to be 4 August 2004, 6 days before the Ohto landslide occurred. The time tf of landslide occurrence was predicted to be 97.2744days, i.e., 19 August 2004 (Table 3D). The results of the new forecasting method indicated that the failure time of the Ohto landslide locked section was 4 August 2004, after that, this landslide would be in a state of critical failure. Suwa et al. (2010) research showed that the creep stage of landslides changes from a secondary creep to tertiary creep, which coincided with a heavy rainstorm caused by typhoon Namtheun. It was possible that the landslide failure time was advanced due to a heavy rainstorm. In order to obtain an accurate warning, the deformation curves between the real time monitoring in field and in the new forecasting method of creep landslide were compared (Figure 10G). The average velocity at the secondary creep stage in deformation vs. time curve of the new method and the real time monitoring were 0.83 mm/d and 0.89 mm/d, respectively. Combined with the relationship between the critical tangential angle αt and the average velocity v in secondary, the corresponding critical tangential angles of the landslide were 87.86° and 87.77°, respectively. Meanwhile, the critical tangential angle in T-t curve of Ohto landslide was 88.94°. The critical tangential angle of the curves in the new forecasting method was compared with critical tangential angle in the T-t curve, the error was within 1°. Combined with the new forecasting method of creep landslide, a failure time td and an occurrence time tf of the landslide were proposed, and the accurate warning of the failure of landslide with creep characteristics was achieved.
Petley (2004) studied the failure of a soil slope caused by the rise of groundwater level on 20 July 1989. This experiment in Selborne, Hampshire, United Kingdom, controlled the replenishment of pore water pressure, which resulted in the failure of a 9 m deep excavation terraced slope composed of gault clay. After the slope excavation and instrument installation were carried out from August 1987 to August 1988, the pore water pressure in the slope was gradually increased in January 1989, and the slope failure occurred on 20 July 1989. A near-circular slip surface appeared at the trailing edge and the middle of the slope. The before and after test views of Selborne landslide are shown in Figures 11A,B. In the process of landslide failure evolution, the deformation process was monitored in real time through inclinometers at different positions, the deformation of an unstable slope was monitored as shown in Figures 11C,D.
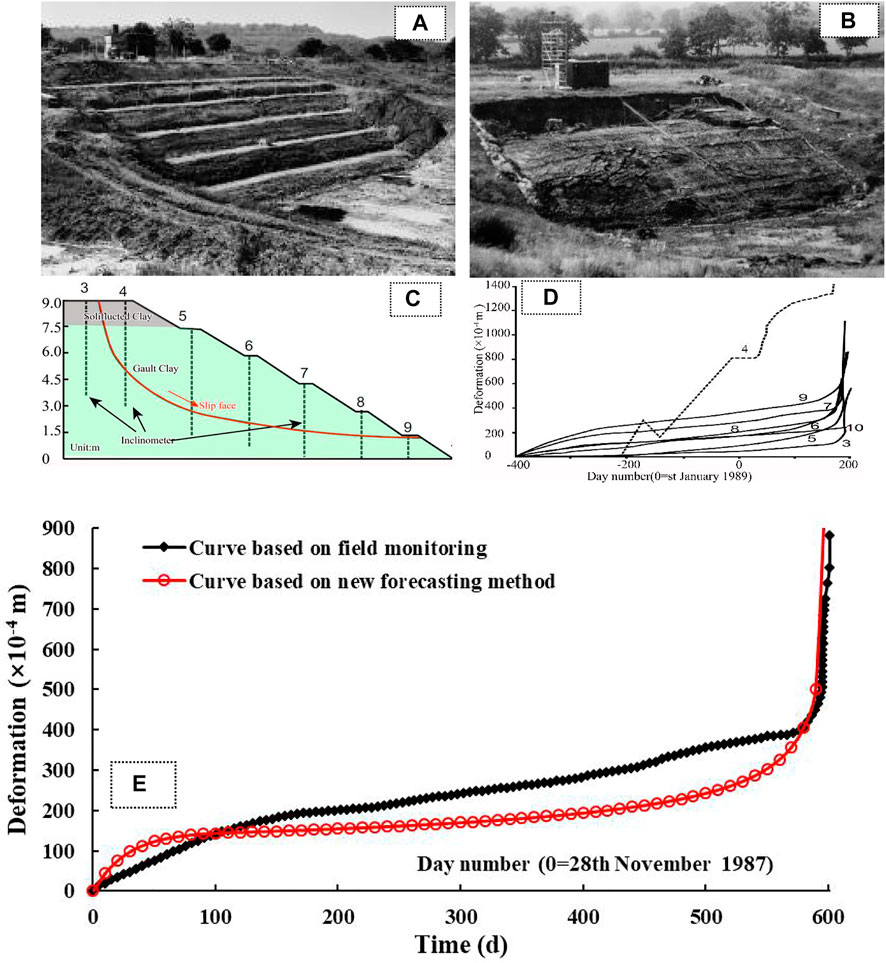
FIGURE 11. (A) View of Selborne landslide before test;(B) View of Selborne landslide after test (after Cooper et al., 1998); (C) Engineering geological section of Selborne landslide; (D) Variations of deformation time at different positions of the Selborne landslide (modified after Petley 2004); (E) Comparison of deformation curves of Selborne landslide between the real time monitoring in field and in the new forecasting method.
The fitting assignment points in new forecasting method were selected in each stage of the deformation curve, as shown in Table 3E. The corresponding failure time td of the landslide locked segment was predicted to be 594.897days, i.e., the time of landslide failure was predicted to be 14 July 1989, 6 days before the Selborne landslide occurred. The time tf of the landslide occurrence was predicted to be 600.830days, i.e., 20 July 1989 (Table 3F), which was consistent with the time that the Selborne landslide failure occurred. Moreover, in order to obtain an accurate warning, the deformation curves between the real time monitoring in field and the new forecasting method of creep landslide were compared (Figure 11F). The average velocity at the secondary creep stage in deformation vs. time curve of the new method and the real time monitoring were 0.46 mm/d and 0.55 mm/d, respectively. Combined with the relationship between the critical tangential angle αt and the average velocity v in the secondary. The corresponding the critical tangential angles of the landslide were 88.46° and 88.31°, respectively. Meanwhile, the critical tangential angle in T-t curve of the Selborne landslide was 89.94°. When the critical tangential angle of the curves in the new forecasting method was compared with the critical tangential angle in T-t curve, the error was within 1°. The result showed that the early warning and forecasting system (Figure 3) based on landslide deformation could curve obtain an accurate warning of creep landslide.
The empirical prediction equation for landslide failure time proposed by Saito (1969), based on laboratory soil creep experiments, is shown in Eq. 7 while the mathematical model of unstable creep stage, established by Fukuzono (1985) is shown in Eq. 8. The proposals of Saito and Fukuzono are both used in the forecasting and warning process of landslides, however, in these approaches the prediction error may be caused by neglecting the influence of initial creep process on the slope. Nevertheless, their exploration of the use of creep theory to forecast the failure of landslides has been indispensable and creative. The creep theory of rock and soil is the basis for the prediction of landslide failure time. Following to the creep mathematical model of viscoelastic hysteretic, such as the Maxwell model and the Kelvin model, the initial creep stage was analysed. The results of this study confirm that determining the initial creep velocity v0 and the viscoelastic hysteresis coefficient
In the Fukuzono model, the α parameter represented the linear or nonlinear trend of the inverse velocity vs. time curve. When α=2, the trend of the curve was linear. When α>2 and 1>α<2, the curve shape was convex and concave, respectively, showing a nonlinear trend, which was crucial for the prediction of landslide failure time (Bozzano et al., 2014). According to studies by Fukuzono (1985) and Varnes (1983), the α value of natural landslides was between 1.5 and 2.2. Specifically, for approximately 80% of the available landslide data sets, α was larger than 1. Bozzano et al. (2014) suggested that when unstable slope influenced by man-made retaining structures were considered, lower values of α were obtained. The analysis of the creep parameter α for the verified cases of landslide events are shown in Tables 2B, 2D, 3B, 3D, 3F. The α at different monitoring positions in the fill slope composed of the same soil were 1.5905 and 1.5496 at the P8 and P9 monitoring points respectively, and there was also a difference of 0.0409 (Table 2B and Table 2D). The maximum difference of α in different rock and soil mass composition of unstable slope was 0.3454. If only α is used to forecast the failure time of unstable slope, a large error occurred. For a landslide with creep characteristics, the creep parameters controlling the deformation process of unstable slope are not unique. For the different rock and soil composition slopes, the study of the unique corresponding creep parameters is very important for landslide warning and prediction.
Since the evolution process of landslide geological bodies is extremely complicated and variable, it is not enough to predict landslides successfully only by theoretical methods, and more consideration should be given to a generalised criterion for the prediction of landslide failure time. Therefore, the critical deformation criterion and the critical tangential angle warning criterion were used in this paper, the combination of these not only improved the accuracy of landslide warning and forecast, but also supplemented the early warning parameters of unstable slope when combined with the new forecasting method of landslide.
When applying the new forecasting method of creep landslide for the hard rock slope, because the elastic deformation was not significant, the real creep curve had the characteristic of viscoelastic hysteresis, which reflected the actual deformation curve varying with time. Consequently, the selection of the fitting assignment points in the initial creep stage not only satisfied the condition of t3-t2=2 (t2-t1) but also closer to the region with viscosity hysteresis characteristic of this stage. However, the selections of the fitting assignment points for soft rock or soil slope in the initial creep stage are opposite to that for hard rock slope. For example, in the early warning process of the Maoxian landslide of hard rock composition, the selections of t1, t2 and t3 were closer to the region with viscosity hysteresis characteristic in the initial creep stage, while the Ohto landslide of soft rock composition, t1, t2 and t3 were mainly selected in the elastic characteristic area in this stage, which was opposite to Maoxian landslide. In addition, the starting point for the tertiary creep of the slope from the secondary creep stage to the tertiary creep stage is a precursor to the instability of the slope. Therefore, in order to better identify the deformation stage of the unstable slope and more accurately selected the fitting assignment points for each stage, the author strongly recommend monitoring the whole process of the unstable slope to obtain an accurate and complete slope evolution process. At present, the new forecasting method has a good early warning and forecasting effect for the creep landslide.
Based on the monitoring curve of unstable slope deformation with time, a new forecasting method for failure time of creep landslide is proposed. Meanwhile, combined with the critical tangential angle warning criterion and an improved tangential angle criterion comparison study, an early warning and forecasting of landslide with creep characteristic is carried out. The following conclusions can be drawn:
1) The initial creep stage of unstable slope cannot be neglected for forecasting the failure time. The initial creep velocity v0 and the viscoelastic hysteresis coefficient
2) According to the creep mathematical model of viscoelastic hysteretic, the nonlinear creep law of unstable slope in the initial creep stage is described. Moreover, the Fukuzono model describing the behavior of materials in the final stage of failure is used to study the nonlinear characteristics of the slope deformation in the unstable creep stage, and then a new forecasting method for failure time of creep landslide is proposed.
3) Based on the new forecasting method, the tangential angle criterion is studied. The average velocity in the secondary creep stage is regarded as the comprehensive external manifestation of various parameters in the process of creep deformation in landslide, and there is an inverse relationship with the critical tangential angle. From this, the critical tangential angle criterion of landslide failure is proposed.
4) For a landslide with creep characteristics, the creep parameters controlling the deformation process of unstable slope are not unique. For the different rock and soil composition slopes, the study of the unique corresponding creep parameters is very important for landslide warning and prediction.
5) The failure time and occurrence time of landslides are obtained by using the new forecasting method of creep landslide, and then the forecast parameters are analysed. Meanwhile, based on the analysis of the forecast parameters of the unstable slope, combined with the critical tangential angle warning criterion and an improved tangential angle criterion comparison study, the warning prediction of landslide is proposed. An early warning and forecasting system of landslide with creep characteristic is established.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
SZ and TJ: study methodology and wrote the original draft. XP and RH: data curation. QX: conceptualizing the study. YX: data analysis and investigation. XP: review and editing. LZ: data curation, program development.
This project was partially supported by the National Natural Science Foundation of China (Grant Nos. 42107169; 42090052), the Major Program of the National Natural Science Foundation of China (Grant Nos. 41790445; 41572302), the open Fund of State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology (Grant Nos. SKLGP2021K016), and the Key Research & Development and Promotion Project of Henan Province (Grant Nos. 222102320463).
We would like to acknowledge the editors and reviewers for their invaluable comments, leading to a substantial improvement of this manuscript. Saito M., Fukuzono T., and Yang R. G. are sincerely acknowledged for their contribution to exploration forecasting the failure of landslides base on creep theory.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bao, C., Zhan, L., Xia, Y., Huang, Y., and Zhao, Z. (2022). Development trend and stability analysis of creep landslide with obvious slip zone under rainfall taking xinchang xiashan basalt slope as an example. Front. Earth Sci. 9, 808086. doi:10.3389/feart.2021.808086
Borgatti, L., Corsini, A., Barbieri, M., Sartini, G., Truffelli, G., Caputo, G., et al. (2006). Large reactivated landslides in weak rock masses: A case study from the northern apennines (Italy). Landslides 3, 115–124. doi:10.1007/s10346-005-0033-9
Bovenga, F., Pasquariello, G., Pellicani, R., Refice, A., and Spilotro, G. (2017). Landslide monitoring for risk mitigation by using corner reflector and satellite SAR interferometry: The large landslide of carlantino (Italy). Catena 151, 49–62. doi:10.1016/j.catena.2016.12.006
Bozzano, F., Cipriani, I., Mazzanti, P., and Prestininzi, A. (2014). A field experiment for calibrating landslide time-of-failure prediction functions. Int. J. Rock Mech. Min. Sci. (1997). 67, 69–77. doi:10.1016/j.ijrmms.2013.12.006
Brown, I., Hittinger, M., and Goodman, R. (1980). Finite element study of the Nevis Bluff (New Zealand) rock slope failure. Rock Mech. 12, 231–245. doi:10.1007/BF01251027
Chen, H. R., Qin, S. Q., Xue, L., and Xu, C. (2021). Why the Xintan landslide was not triggered by the heaviest historical rainfall: Mechanism and review. Eng. Geol. 294, 106379. doi:10.1016/j.enggeo.2021.106379
Chen, H. R., Qin, S. Q., Xue, L., Yang, B. C., and Zhang, K. (2018). A physical model predicting instability of rock slopes with locked segments along a potential slip surface. Eng. Geol. 242, 34–43. doi:10.1016/j.enggeo.2018.05.012
Collins, T. K. (2008). Debris flows caused by failure of fill slopes: Early detection, warning, and loss prevention. Landslides 5 (1), 107–120. doi:10.1007/s10346-007-0107-y
Comegna, L., Picarelli, L., and Urciuoli, G. (2007). The mechanics of mudslides as a cyclic undrained–drained process. Landslides (4), 217–232. doi:10.1007/s10346-007-0083-2
Cooper, M. R., Bromhead, E. N., Petley, D. J., and Grant, D. I. (1998). The Selborne cutting stability experiment. Geotechnique 48, 83–101. doi:10.1680/geot.1998.48.1.83
Crosta, G. B., and Agliardi, F. (2003). Failure forecast for large rock slides by surface displacement measurements. Can. Geotech. J. J40, 176–191. doi:10.1139/t02-085
Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a bedding fault: Understanding the initiation and movement of the Daguangbao landslide triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geol. 295, 106455. doi:10.1016/j.enggeo.2021.106455
Cui, S., Wu, H., Pei, X., Yang, Q., Huang, R., and Guo, B. (2022). Characterizing the spatial distribution, frequency, geomorphological and geological controls on landslides triggered by the 1933 Mw 7.3 Diexi Earthquake, Sichuan, China. Geomorphology 403, 108177. doi:10.1016/j.geomorph.2022.108177
Dahal, R. K., and Hasegawa, S. (2008). Representative rainfall thresholds for landslides in the Nepal Himalaya. Geomorphology 100 (3), 429–443. doi:10.1016/j.geomorph.2008.01.014
Evans, S. G., Cruden, D. M., Bobrowsky, P. T., Guthrie, R. H., Keegan, T. R., Liverman, D. G. E., et al. (2005). “Landslide risk assessment in Canada: A review of recent developments,” in Landslide risk management. Editors O. Hungr, R. Fell, R. Couture, and R. Eberhardt (London: Taylor and Francis Group), 351–363.
Evans, S. G. (1997). “Fatal landslides and landslide risk in Canada,” in Landslide risk assessment (London, UK: ICE Virtual Library), 1–7.
Fan, X., Xu, Q., Scaringi, G., Dai, L., Li, W., Dong, X., et al. (2017). Failure mechanism and kine-matics of the deadly June 24th 2017 Xinmo landslide, maoxian, sichuan, China. Landslides 14 (6), 2129–2146. doi:10.1007/s10346-017-0907-7
Fujisawa, K., Marcato, G., Nomura, Y., and Pasuto, A. (2010). Management of a typhoon-induced landslide in Otomura (Japan). Geomorphology 124, 150–156. doi:10.1016/j.geomorph.2010.09.027
Fukuzono, T. (1985). “A new method for predicting the failure time of a slope,” in Proceedings of the 4th international conference and field workshop in landslides (Tokyo: Tokyo University Press), 145–150.
Gao, W. (2014). Forecasting of landslide disasters based on bionics algorithm (Part 1: Critical slip surface searching). Comput. Geotechnics 61, 370–377. doi:10.1016/j.compgeo.2014.06.007
Guzzetti, F. (2000). Landslide fatalities and the evaluation of landslide risk in Italy. Eng. Geol. 58, 89–107. doi:10.1016/s0013-7952(00)00047-8
Haefeli, R. (1953). Creep problems in soils, snow and ice. Soil Mech. Found. Eng. 3, 238–251. Proc. 3rd Int. Conf.
Haruo, S. Z. (2001). Process of slip-surface development and formation of slip-surface clay in landslides in Tertiary volcanic rocks, Japan. Eng. Geol. 68, 289–317.
He, K. Q., and Wang, S. J. (2006). Double-parameter threshold and its formation mechanism of the colluvial landslide: Xintan landslide, China. Environ. Geol. 49 (5), 696–707. doi:10.1007/s00254-005-0108-x
He, Y., and Kusiak, A. (2017). Performance assessment of wind turbines: Data-derived quantitative metrics. IEEE Trans. Sustain. Energy 9 (1), 65–73. doi:10.1109/tste.2017.2715061
Huang, F., Huang, J., Jiang, S., and Zhou, C. (2017). Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 218, 173–186. doi:10.1016/j.enggeo.2017.01.016
Huang, R. Q. (2009). Some catastrophic landslides since the twentieth century in the southwest of China. Landslides 6, 69–81. doi:10.1007/s10346-009-0142-y
Huang, Z. Q., Law, K. T., Liu, H. D., and Tong, J. (2009). The chaotic characteristics of landslide evolution: A case study of xintan landslide. Environ. Geol. 56 (8), 1585–1591. Available at: http://dx.doi.org/10.1007/s00254-008-1256-6.
Intrieri, E., Gigli, G., Mugnai, F., Fanti, R., and Casagli, N. (2012). Design and implementation of a landslide early warning system. Eng. Geol. 147–148, 124–136. doi:10.1016/j.enggeo.2012.07.017
Intrieri, E., Raspini, F., Fumagalli, A., Lu, P., Del Conte, S., Farina, P., et al. (2018). The maoxian landslide as seen from space: Detecting precursors of failure with sentinel-1 data. Landslides 15 (Issue 1), 123–133. doi:10.1007/s10346-017-0915-7
Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D., and Cheng, Q. (2021a). Short-term nacelle orientation forecasting using bilinear transformation and ICEEMDAN framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928
Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. (2021b). Monitoring and identifying wind turbine generator bearing faults using deep belief network and EWMA control charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039
Li, H., He, Y., Xu, Q., Deng, j., Li, W., and Wei, Y. (2022). Detection and segmentation of loess landslides via satellite images: A two-phase framework. Landslides 19, 673–686. doi:10.1007/s10346-021-01789-0
Li, H., Xu, Q., He, Y., and Deng, J. (2018). Prediction of landslide displacement with an ensemble-based extreme learning machine andcopula models. Landslides 15 (10), 2047–2059. doi:10.1007/s10346-018-1020-2
Lian, C., Zeng, Z. G., Yao, W., and Tang, H. M. (2014). Extreme learning machine for the displacement prediction of landslide under rainfall and reservoir level. Stoch. Environ. Res. Risk Assess. 28, 1957–1972. doi:10.1007/s00477-014-0875-6
Liverman, D. G. E., Batterson, M. J., Taylo, r. D., and Ryan, J. (2001). Geological hazards and disasters in Newfoundland. Can. Geatecltnical J. 38, 936–956.
Loew, S., Gschwind, S., Gischig, V., Keller-Signer, A., and Valenti, G. (2017). Monitoring and early warning of the 2012 Preonzo catastrophic rock slope failure. Landslides 14 (2), 141–154. doi:10.1007/s10346-016-0701-y
Marin, R. J., and Velásquez, M. F. (2020). Influence of hydraulic properties on physically modelling slope stability and the definition of rainfall thresholds for shallow landslides. Geomorphology 351, 106976. doi:10.1016/j.geomorph.2019.106976
Mayoraz, F., and Vulliet, L. (2002). Neural networks for slope movement prediction. Int. J. Geomech. 2 (2), 153–173. doi:10.1061/(asce)1532-3641(2002)2:2(153)
Miao, T. D., Ma, C. W., and Wu, S. Z. (1999). Evolution model of progressive failure of landslides. J. Geotech. Geoenviron. Eng. 125 (10), 827–831. doi:10.1061/(asce)1090-0241(1999)125:10(827)
Mufundirwa, A., Fujii, Y., and Kodama, J. (2010). A new practical method for prediction of geomechanical failure-time. Int. J. Rock Mech. Min. Sci. (1997). 47 (7), 1079–1090. doi:10.1016/j.ijrmms.2010.07.001
Okamoto, T., Larsen, J. O., Matsuura, S., Asano, S., Takeuchi, Y., and Grande, L. (2004). Displacement properties of landslide masses at the initiation of failure in quick clay deposits and the effects of meteorological and hydrological factors. Eng. Geol. 72, 233–251. doi:10.1016/j.enggeo.2003.09.004
Pei, X. J., Guo, B., Cui, S. H., Wang, D. P., Xu, Q., and Li, T. T. (2018). On the initiation, movement and deposition of a large landslide in Maoxian County, China. J. Mt. Sci. 15 (6), 1319–1330. doi:10.1007/s11629-017-4627-1
Pei, X. J., Zhang, S., Huang, R. Q., Wei, K. H., Liu, F. Z., and Duan, Y. X. (2016). Deformation propagation and identification of an impending disaster of a retained high embankment based on monitoring of minor deformation, China. Landslides Eng. Slopes Exp. 3, 1583–1590.
Pei, X. J., Zhang, X. C., Guo, B., Wang, G. H., and Zhang, F. Y. (2017). Experimental case study of seismically induced loess liquefaction and landslide. Eng. Geol. 223, 23–30. doi:10.1016/j.enggeo.2017.03.016
Petley, D. N., Hearn, G. J., Hart, A., Rosser, N. J., Dunning, S. A., Oven, K., et al. (2007). Trends in landslide occurrence in Nepal. Nat. Hazards 43 (1), 23–44. doi:10.1007/s11069-006-9100-3
Petley, D. N. (2004). The evolution of slope failures: Mechanisms of rupture propagation. Nat. Hazards Earth Syst. Sci. 4 (1), 147–152. Copernicus Publications on behalf of the European Geosciences Union. doi:10.5194/nhess-4-147-2004
Qin, S., Jiao, J. J., and Wang, S. (2002). A nonlinear dynamical model of landslide evolution. Geomorphology 43, 77–85. doi:10.1016/s0169-555x(01)00122-2
Qin, S. Q., Wang, Y. Y., and Ma, P. (2010a). Exponential laws of critical displacement evolution for landslides and avalanches. Chin. J. Rock Mech. Eng. 29 (05), 873–880.
Qin, S. Q., Xu, X. W., Hu, P., Wang, Y. Y., Huang, X., and Pan, X. H., (2010b). Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction. Chin. J. Geophysics-English Ed. 53 (04), 1001–1014. http://dx.doi. org/10.3969/j.issn.0001-5733.2010.04.025.
Rödelsperger, S., Becker, M., Gerstenecker, C., Läufer, G., Schilling, K., and Steineck, D. (2010). Digital elevation model with the ground-based SAR IBIS-L as basis for volcanic deformation monitoring. J. Geodyn. 49, 241–246. doi:10.1016/j.jog.2009.10.009
Rose, N. D., and Hungr, O. (2007). Forecasting potential rock slope failure in open pit mines using the inverse-velocity method. Int. J. Rock Mech. Min. Sci. (1997). 44 (2), 308–320. doi:10.1016/j.ijrmms.2006.07.014
Royán, M. J., Abellán, A., and Vilaplana, J. M. (2015). Progressive failure leading to the 3 December 2013 rockfall at Puigcercós scarp (Catalonia, Spain). Landslides 12, 585–595. doi:10.1007/s10346-015-0573-6
Saito, M. (1969). “Forecasting time of slope failure by tertiary creep,” in Proceedings of the 7th international conference on soil mechanics and foundation engineering (Mexico: Sociedad Mexicana de Mecanica de Suelos A.C), 677–683.
Suwa, H., Mizuno, T., and Ishii, T. (20102010). Prediction of a landslide and analysis of slide motion with reference to the 2004 Ohto slide in Nara, Japan. Geomorphology 124, 157–163. doi:10.1016/j.geomorph.2010.05.003
Tavenas, F., and Leroueil, S. (1981). Creep and failure of slopes in clays. Can. Geotech. J. 18 (1), 106–120. doi:10.1139/t81-010
Terzaghi, K. (1950). “Mechanism of landslides,” in Application of geology to engineering practice (berkey volume). Editor S. Paige (Washington, DC: Geological Society of America), 83–123.
Tika, T. E., and Hutchinson, J. N. (1999). Ring shear tests on soil from the Vaiont landslide slip surface. Geotechnique 49 (1), 59–74. doi:10.1680/geot.1999.49.1.59
Urciuoli, G., and Picarelli, L. (2008). Interaction between landslides and man-made work. London: Landslides and Engineered Slopes Taylor & Francis Group, 1301–1307.
Varnes, D. J. (1983). Time-deformation relations in creep to failure of Earth materials. Proc. seventh Southeast Asian Geotechnical Conf. 2, 107–130.
Voight, B. (1988). A method for prediction of volcanic eruptions. Nature 332, 125–130. doi:10.1038/332125a0
Wang, G. H., Zhang, D. X., Furuya, G., and Yang, J. (2014). Pore-pressure generation and fluidization in a loess landslide triggered by the 1920 haiyuan earthquake, China: A case study. Eng. Geol. 174, 36–45. doi:10.1016/j.enggeo.2014.03.006
Xu, Q., Yuan, Y., Zeng, Y. P., and Hack, R. (2011). Some new pre-warning criteria for creep slope failure. Sci. China Technol. Sci. 54, 210–220. doi:10.1007/s11431-011-4640-5
Xue, L., Qin, S. Q., Li, P., Li, G., Adewuyi Oyediran, I., and Pan, X. (2014). New quantitative displacement criteria for slope deformation process: From the onset of the accelerating creep to brittle rupture and final failure. Eng. Geol. 182 (Part A), 79–87. doi:10.1016/j.enggeo.2014.08.007
Yamaguchi, U., and Shimotani, T. (1986). 10. A case study of slope failure in a limestone quarry. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 23 (1), 95–104. Available at: https://doi.org/10.1016/0148-9062(86)91670-0.
Yang, R. G. (2010). Theory of rock and soil structural stability and prediction of landslide. Beijing: Sichuan Science and Geological Publishing House, 2–13. (in Chinese).
Ye, X. Y., Wang, S. Y., Li, Q., Zhang, S., and Sheng, D. C. (2020a). Negative effect of installation on performance of a compaction-grouted soil nail in poorly graded stockton beach sand. J. Geotech. Geoenviron. Eng. 146 (8), 04020061. doi:10.1061/(asce)gt.1943-5606.0002301
Ye, X. Y., Wang, S. Y., Zhang, S., Xiao, X., and Xu, F. (2020b). The compaction effect on the performance of a compaction-grouted soil nail in sand. Acta Geotech. 15 (10), 2983–2995. doi:10.1007/s11440-020-01017-4
Zhang, F. Y., Kang, C., Chan, D., Zhang, X. C., Pei, X. J., and Peng, J. B. (2017). A study of a flow slide with significant entrainment in loess areas in China. Earth Surf. Process. Landf. 42 (14), 2295–2305. doi:10.1002/esp.4184
Zhang, S., Li, Y., Peng, R., Ye, X. Y., and Wang, S. Y. (2021). A semi-analytical model for a compaction-grouted soil nail with double grout bulbs considering compaction effect in sand. Transp. Geotech. 31, 100670. doi:10.1016/j.trgeo.2021.100670
Zhang, S., Pei, X. J., Wang, S. Y., Huang, R. Q., and Zhang, X. C. (2020). Centrifuge model testing of loess landslides induced by excavation in Northwest China. Int. J. Geomech. 20. doi:10.1061/(ASCE)GM.1943-5622.0001619
Zhang, S., Pei, X. J., Wang, S. Y., Huang, R. Q., Zhang, X. C., and Chang, Z. L. (2019a). Centrifuge model testing of a loess landslide induced by rising groundwater in Northwest China. Eng. Geol. 259, 105170. doi:10.1016/j.enggeo.2019.105170
Zhang, S., Zhang, X. C., Pei, X. J., Wang, S. Y., Huang, R. Q., Xu, Q., et al. (2019b). Model test study on the hydrological mechanisms and early warning thresholds for loess fill slope failure induced by rainfall. Eng. Geol. 258, 105135. doi:10.1016/j.enggeo.2019.05.012
Keywords: creep landslide, failure-time prediction, nonlinear creep behavior, tangential angle, early warning
Citation: Zhang S, Jiang T, Pei X, Huang R, Xu Q, Xie Y, Pan X and Zhi L (2022) A new forecasting method for failure time of creep landslide based on nonlinear creep behavior and new pre-warning criterion. Front. Earth Sci. 10:1018432. doi: 10.3389/feart.2022.1018432
Received: 13 August 2022; Accepted: 06 September 2022;
Published: 27 September 2022.
Edited by:
Jingren Zhou, Sichuan University, ChinaCopyright © 2022 Zhang, Jiang, Pei, Huang, Xu, Xie, Pan and Zhi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qiang Xu, eHFAY2R1dC5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.