Expanding the theory for reducing the CO2 disaster—Hypotheses from partial least-squares regression and machine learning

The rapid increase in atmospheric CO₂ concentration has caused a climate disaster (CO₂ disaster). This study expands the theory for reducing this disaster by analyzing the possibility of reinforcing soil CO₂ uptake (F_x) in arid regions using partial least-squares regression (PLSR) and machine learning models such as artificial neural networks. The results of this study demonstrated that groundwater level is a leading contributor to the regulation of the dynamics of the main drivers of F_x–air temperature at 10 cm above the soil surface, the soil volumetric water content at 0–5 cm (R²=0.76, RMSE=0.435), and soil pH (R²=0.978, RMSE=0.028) in arid regions. F_x can be reinforced through groundwater source management which influences the groundwater level (R²=0.692, RMSE=0.03). This study also presents and discusses some basic hypotheses and evidence for quantitively reinforcing F_x.

1 Introduction

The Earth is a complicated system with considerable uncertainties regarding the biotic/abiotic processes in many ecosystems (Caers, 2011). The Earth’s surface temperature is widely recognized to be heavily influenced by greenhouse gases, among which CO₂ is the major contributor (Joos et al., 1999). The rapid increase of atmospheric CO₂ concentration and the resulting climate disaster (the CO₂ disaster) have attracted attention (Mercer, 1978). With the intensification of the CO₂ disaster, arid regions are getting more arid and, hence, are facing more serious threats (Huang et al., 2017). The warming trends in arid and semi-arid regions are significantly higher than those in non-arid regions (Schlaepfer et al., 2017). Moreover, the CO₂ disaster may reduce the extent of temperate drylands and intensify drought in deep soils, such that approximately 15%–30% of the temperate dry area might be transformed into arid areas by the late 21st century (Schlaepfer et al., 2017). Global warming accelerates not only dryland expansion but also soil CO₂ release in some regions (Jenkinson et al., 1991; Huang et al., 2016). Therefore, any possible technologies for reducing the CO₂ disaster are worthy of investigation (Murata and Cheolsong, 2008; Edmonds and Smith, 2011).

Since 2006, a series of studies have demonstrated soil CO₂ uptake in arid regions (Wang et al., 2015a; Wang et al., 2016a). In the traditional ecological paradigm, soils can only release CO₂ (Baldocchi et al., 2001; Wang et al., 2015a). Soil CO₂ release was defined as the sum of two organic components: plant root respiration (autotrophic respiration) and soil organic carbon decomposition by soil fauna and soil microbes (Falge et al., 2001; Farifteh et al., 2007; Baldocchi et al., 2015). Many observations of soil CO₂ fluxes with both chambers and open- or closed-path eddy systems have highlighted anonymous CO₂ uptake (Hastings et al., 2005; Jasoni et al., 2005; Mielnick et al., 2005; Reichstein et al., 2005; Chapin et al., 2006). The components of soil CO₂ fluxes are the sum of its inorganic (soil inorganic respiration) and organic (soil organic respiration) components, respectively (Wohlfahrt et al., 2008). Moreover, soil inorganic respiration temporally dominates the net ecosystem exchange of CO₂ (Schlesinger, 2001; Kowalski et al., 2008; Inglima et al., 2009; Sanchez-Cañete et al., 2011; Chen et al., 2013). Hence, we are motivated to investigate the possibility of reinforcing soil CO₂ uptake to reduce the CO₂ disaster. The environmental contributions to the main drivers of soil CO₂ uptake and whether such contributions can be reinforced through human activities remain unknown (Chen et al., 2013). However, if possible, soil CO₂ uptake not only indicates a hidden carbon cycle loop potentially contributing to the long-sought “missing sink” (Stone, 2008; Xie et al., 2008; Serrano-Ortiz et al., 2010; Ma et al., 2013; Chen et al., 2014; Wang et al., 2015b; Wang et al., 2016b) but also promises an emerging technology to reduce the CO₂ disaster (Wang et al., 2016a; Wang et al., 2016b).

The risk of soil salinization in arid regions is increasing due to the combined effects of global warming, drought intensification, and population growth (Utset and Borroto, 2001). Many studies have demonstrated the high sensitivity of arid regions to the CO₂ disaster (Gök et al., 2000; Rey et al., 2012; Rey, 2014; Li et al., 2015). However, few studies have addressed the feasibility of reinforcing soil CO₂ uptake in these regions (Wang et al., 2015a; Wang et al., 2016a). The utilization of CO₂ uptake as a practical technology for reducing the CO₂ disaster requires the reliable quantification of environmental influences on the main drivers of soil CO₂ uptake and the assessment of the possibility of reinforcing these influences (Wang et al., 2016b). Until now, considerable uncertainties remain regarding the underlining mechanisms of soil CO₂ uptake (Wang et al., 2015b; Wang et al., 2016b). Nevertheless, a global model of soil CO₂ uptake has been established (Chen et al., 2014), which can be used to expand the theory for reducing the CO₂ disaster by analyzing the main drivers involved in the model. The main challenges are as follows. First, since the mechanisms of such CO₂ uptake remain undetermined, any possible environmental contributors to these main drivers must be comprehensively considered. Second, since the influencing modes of most environmental controls are not fully understood, their possible interactions cannot be ignored. These two challenges have not been explicitly tackled in previous studies. Addressing these challenges and clarifying the environmental contributors of the main drivers could allow an assessment of the feasibility of artificially enhancing CO₂ uptake and the limits of such enhancement. Scientists could then determine whether such enhancements could provide a new method to replace reduced industrial emissions and, ultimately, reduce the CO₂ disaster.

Therefore, the objectives of the present study were to 1) examine the leading environmental contributors to the main drivers for soil CO₂ uptake in arid regions, 2) evaluate the most interpretable proportion of all considered contributors and determine the need to introduce other environmental contributors, and 3) discuss the feasibility of reinforcing soil CO₂ uptake in arid regions by human activities. The organization of this article is as follows. Section 2 illustrates the methods for computing soil CO₂ uptake, along with the subsequent regression and machine learning theory. Partial least-squares regression (PLSR) is used to exclude interactions among the considered environmental contributors. A machine learning model (ANN) is used for cross-validation by excluding the secondary contributors. Hypotheses are developed from the PLSR-ANN and discussed in Section 3. We also assess the largest proportions of these contributors in explaining soil CO₂ uptake and further clarify their leading roles. In addition, we evaluate the most interpretable proportion of all the contributors considered in the present study and determine whether other contributors need to be involved in subsequent studies. Based on the results from the PLSR-ANN calibrations, Section 4 establishes and discusses the theory of a conceptual framework to reinforce soil CO₂ uptake through effective activities in the background of global warming. The conclusions and some outstanding remarks are presented in Section 5.

2 Theory and methodology

2.1 Computation of soil CO₂ uptake

Soil CO₂ uptake involves not only fluxes of CO₂ over the soil surface but also beneath the soil. To compute CO₂ fluxes over the soil surface, a PVC column is set to measure CO₂ concentration above the soil in a closed chamber. As shown in Eqs 1, 2 in Wang et al. (2016c), the net soil CO₂ release (F_c) can be computed by

$F_c=\frac{dC\left(t\right)}{dt}=\frac{k\left(t\right){\rho V}_{pvc}}{S_{pvc}}\ast \frac{∆{CO}_{\mathrm{2}}}{∆t}=\frac{k\left(t\right)\rho rh}{r+\mathrm{2}h}\ast \frac{∆{CO}_{\mathrm{2}}}{∆t}(1)$

where r, h, V_pvc, and S_pvc are the height, radius volume, and surface area of the PVC column, respectively; ρ is the CO₂ density under the standard state; and k is a dynamic transform coefficient.

A temperature-dependent Q₁₀ model has been widely utilized, in which Q₁₀ is the derivative of the exponential chemical reaction-temperature equation originally developed by Van’t Hoff (1898). With T_as defined as the air temperature at 10 cm above the soil surface, θ_s the soil volumetric water content at 0–5 cm, and R₁₀ the referred F_c at 10°C, then Q₁₀ is the factor by which F_c is multiplied when T increases by 10°C. According to Eqs 1–3 described by Wang et al. (2015b), the part of F_c unexplained by the Q₁₀ model is attributed to the inorganic component of F_c. Alternatively, the soil CO₂ uptake (F_x) can be computed by

$F_o=R_{\mathrm{10}}{Q}_{\mathrm{10}}^{\left(T_{as}-\mathrm{10}\right)/\mathrm{10}}(2)$

$F_i=F_c-F_o(3)$

$F_i^{+}=\left(F_i+\left|F_i\right|\right)/\mathrm{2},F_i^{-}=\left(F_i-\left|F_i\right|\right)/\mathrm{2}(4)$

$F_x=F_i^{-}(5)$

$F_x=f\left(pH\right)+g\left(T_{as},{\theta }_s\right)(6)$

where F_o and F_i are the organic and inorganic components of F_c, respectively.

Equation 6 can be further reconciled as

$F_x=F_{xnp}\left({EV}_{np}\right)+F_{xlp}\left({EV}_{lp}\right)(7)$

where F_xnp and F_xlp are the linear and nonlinear components of F_x, respectively. EV_np and EV_lp are the sets of environmental variables for the linear and nonlinear components, respectively.

As seen in Chen et al. (2014), the main drivers for F_x are pH, T_as, θ_s; thus,

$F_{xnp}\left({EV}_{np}\right)=f\left(pH\right)=r_{\mathrm{7}}{q}_{\mathrm{7}}^{pH-\mathrm{7}},F_{xlp}\left({EV}_{lp}\right)=g\left(T,{\theta }_s\right)=\lambda T+\mu {\theta }_s+e(8)$

where the pH belongs to EV_np and T_as and θ_s belong to EV_lp.

For computation, the empirical coefficients from Chen et al. (2014) and Wang et al. (2015b) can be directly used. That is,

$F_{xnp}\left({EV}_{np}\right)=\mathrm{3.0191}\times {\mathrm{0.7625}}^{pH-\mathrm{7}}(9)$

$F_{xlp}\left({EV}_{lp}\right)F_{xlp}\left({EV}_{lp}\right)=\mathrm{0.0059}{T}_{as}+\mathrm{0.0003}{\theta }_s-\mathrm{2.5081}(10)$

where F_x is hypothetically attributed as pH-driven, T_as-driven, and θ_s-driven CO₂ uptake by soils.

2.2 PLSR and machine learning theory

Two adaptive methods—partial least-squares regression (PLSR) and a machine learning model (ANN)—were used to examine the environmental contributors of pH, T_as, and θ_s. Backpropagation was utilized in the machine learning processes with ANN. The performance statistics of the ANN calibration were explicitly displayed and the environmental contributors with relatively small contributions (<5%) were excluded from the ANN model performance. The PLSR model was performed on a random partition of the dataset (70% for training, 30% for testing) and ANN models were assessed against the whole data set. The major steps of the PLSR calibration are shown in Figure 1 (Zhou et al., 2021).

FIGURE 1

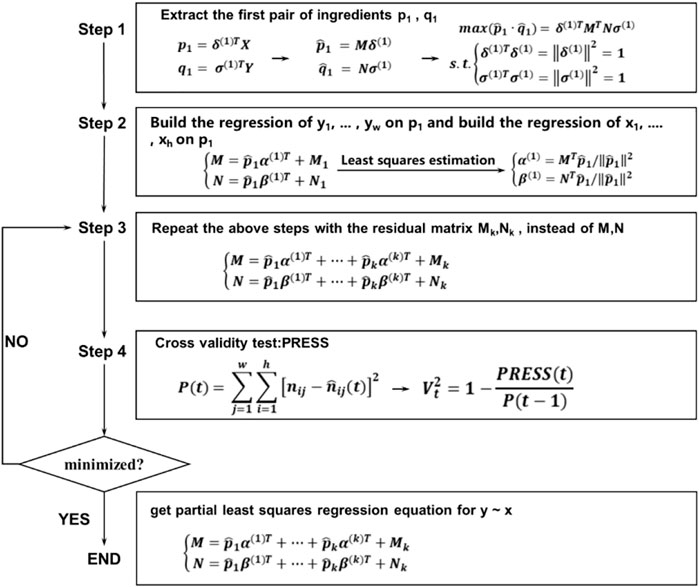
FIGURE 1. Major steps of PLSR calibration. Note: X and Y are the data on environmental variables and soil CO₂ uptake respectively. The corresponding matrices of X and Y are M and N, respectively. The corresponding eigenvectors of M and N are δ and σ, respectively. To calculate the coefficients α and β in the principal components from PLSR, we extract as much variation information as possible from each variable group. This is a conditional extremum problem, which is solved using the Lagrange multiplier method.

Six calibration processes were performed during PLSR. The first was the standardization, which was done before Step 1. The second process was to find the correlation coefficient matrix, where X and Y were put into an augmented matrix that was included in Steps 2 and 3. The third process was to find the pair of principal components. This process was included in Step 4, where the Lagrange multiplier method was utilized. The fourth subsequent process involved the calculation of the contribution rate table, in which the contributions of each environmental contributor were determined individually. The fifth process was to select k principal component pairs according to the contribution rate table, which was used in the sixth and seventh processes to carry out the final regressions between environmental contributors and the main drivers for soil CO₂ uptake. The eighth process performed cross-validation with the above PLSR components.

However, PLSR also has some limits. PLSR is a linear model, which is advantageous for determining the contributions of individual environmental variables. However, the best model might be nonlinear. Meanwhile, ANN cross-validation is also required to ensure that the selected determining factors from PLSR remain dominant in nonlinear models. The ANN aims to imitate the working mechanisms of the human brain. Neurons are connected to form each layer of the neural network. Each layer transmits information through a function operation running on the connection between each layer. By adjusting the connected weights between each layer, the neural network can output the desired target. This goal needs to be achieved through the training of the neural network, which is within the allowable range of error. The basic information transfer function for the connection between each connection layer is xw + b, where x is the information passed from the previous layer, w is the weight reflecting the relevance, and b is the deviation. As the brain sometimes needs to choose to transmit or ignore received information, neural networks filter information through an activation function. The major steps in ANN for updating parameters are shown in Figure 2 (Zhou et al., 2021; Zhuang et al., 2021).

FIGURE 2

FIGURE 2. Major steps in machine learning processes with ANN. Note: After obtaining a training set, the ANN can extract the features of each part of the observed object by learning. If the training effect is not satisfied, error data will be generated and back-propagated and relevant parameters will be adjusted according to the error value to minimize the target. The parameter adjustment is mainly based on the prediction results of the errors in each layer.

Environmental data-driven PLSR-ANNs were collected from a series of previous studies (Chen et al., 2014; Zhou et al., 2021; Zhuang et al., 2021). The present study further hypothesized that the precipitation amounts (P_a) and groundwater level (GL) were another two elements in EV_np. Based on the results of PLSR and machine learning, the other environmental variables; namely, air humidity (AH), air pressure (AP), soil temperature (T_s), soil salinity (SS), and wind speed (WS) and direction (WD) were included in EV_lp. Evidence for the above two hypotheses is presented in Sections 3 and 4. The calibration errors were quantified using R² and RMSE, as described by Farifteh et al. (2007) and Zhou et al. (2021).

3 Hypotheses and evidence

3.1 Reinforcement of T_as-driven CO₂ uptake

According to Eq. 10, soil CO₂ uptake can be reinforced by reducing T_as. The reinforcement degree is −0.0059 μmol m⁻² s⁻¹ when T_as decreases by 1°C. We hypothesized that T_as was a function of other environmental variables; that is,

$T_{as}=T_{asf}\left(AH,AP,T_s,SS,WS,WD,pH,GL,{\theta }_s,P_a\right)(11)$

The hypothetical mechanisms in the function T_f are as follows. T_s can affect T_as because T_s is a direct reflection of the surface heat condition. Since the volume heat capacity of water is much larger than that of air, AH, GL, WD, WS, P_a, and θ_s can affect T_as. Decreases in AP indicate that the air above the soil is expanding and T_as is increasing. Since soil water and salt transport can be aggravated by higher T_as, SS and pH are also potential indicators for local T_as. Under these hypotheses, the reinforcement of T_as-driven CO₂ uptake is possible if one of the environmental variables AH, AP, T_s, SS, WS, WD, pH, GL, θ_s, and P_a can be changed through human activities.

The results of the PLSR-ANN analyses present some basic evidence for Eq. 11. As shown in Figure 3, the PLSR results demonstrated the very accurate prediction of T_as by a linear combination of other environmental variables (R²=0.894 and RMSE=2.975 on the training data set, R²=0.939 and RMSE=2.507 on the testing data set). These results were further demonstrated by the ANN (R²=0.924 and RMSE=2.495 before excluding the secondary contributors, R²=0.887 and RMSE=2.966 after excluding the secondary contributors).

FIGURE 3

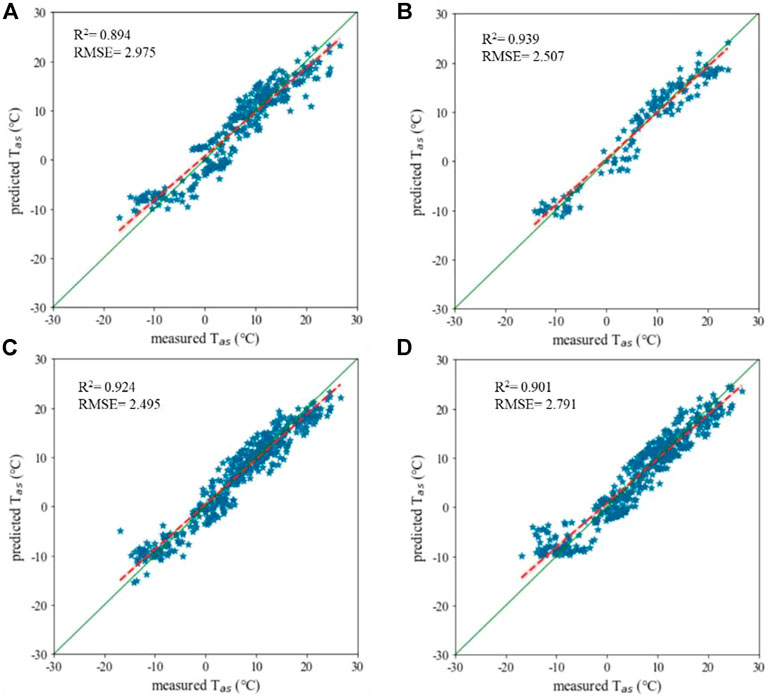
FIGURE 3. Evidence for Eq. 11 from the PLSR training stage (A), testing stage (B), and ANN analyses before excluding the secondary contributors (C) and after excluding the secondary contributors (D). Note: T_as is the air temperature at 10 cm above the soil surface. All other environmental variables are considered potential contributors to T_as.

From the PLSR results, the function T_asf can be approximated by

$T_{as}=c_{\mathrm{0}}+c_{\mathrm{1}}AH+c_{\mathrm{2}}AP+c_{\mathrm{3}}{T}_s+c_{\mathrm{4}}SS+c_{\mathrm{5}}WS+c_{\mathrm{6}}WD+c_{\mathrm{7}}pH+c_{\mathrm{8}}GL+c_{\mathrm{9}}{\theta }_s+c_{\mathrm{10}}{P}_a(12)$

where the contributions of AH, AP, T_s, SS, WS, WD, pH, GL, θ_s, and P_a to T_as can be calculated from the coefficients c₁, c₂, …, c₁₀, in which c₀ is the residual.

The computed coefficients for Eq. 12 were c₁=−2.0413, c₂=−1.4424, c₃=2.3231, c₄=−1.3964, c₅=0.3635, c₆=−0.1313, c₇=1.6382, c₈=−1.9786, c₉=0.6742, c₁₀=0. Hence, the leading environmental contributors to T_as were T_s, AH, GL, pH, AP, SS and θ_s, with contributions to T_as of 19.4%, 17%, 16.5%, 13.7%, 12%, 11.6%, and 5.6%, respectively. Among these leading environmental contributors, GL was significantly affected by human activities and can also influence pH, SS, and θ_s. Therefore, we can try to reinforce T_as-driven soil CO₂ uptake in arid regions through groundwater management, which is associated not only with irrigation decisions but also with living plans and industrial water use. A decrease in GL by 1 m means a T_as reduction of 1.9786°C and a reinforcement of F_x by −0.0117 μmol m⁻² s⁻¹ according to Eqs 10, 12.

3.2 Reinforcement of θ_s-driven CO₂ uptake

According to Eq.10, soil CO₂ uptake can be reinforced by reducing θ_s. The reinforcement degree is −0.0003 μmol m⁻² s⁻¹ when θ_s decreases by 1%. We hypothesized that θ_s was a function of other environmental variables; that is,

${\theta }_s={\theta }_{sf}\left(AH,AP,T_s,SS,WS,WD,pH,GL,T_{as},P_a\right)(13)$

The hypothetical mechanisms in the function θ_sf are as follows. Precipitation and evaporation are the two most important factors influencing θ_s. Therefore, P_a affects θ_s. Since T_s and T_as can directly reflect the surface heat conditions, the θ_s values under different temperatures can vary. Except for precipitation and evaporation, atmospheric environments, soil properties, and surface vegetation also affect θ_s. Hence, AP, AH, WD, WS, SS, and pH can potentially affect θ_s. The influence of GL on θ_s is easily understood. In arid regions, soil water is mainly supplied by groundwater. A decrease in GL can directly induce the decrease of θ_s. Under these hypotheses, θ_s-driven CO₂ uptake can be reinforced if one of these environmental variables can be changed through human activities.

The results of the PLSR-ANN analyses present some basic evidence for Eq. 13. As shown in Figure 4, the PLSR results suggest that the best linear combination of other environmental variables can only explain about half of the variations in θ_s (R²=0.552 and RMSE=0.577 on the training data set, R²=0.51 and RMSE=0.663 on the testing data set). However, we cannot conclude that the function θ_sf in Eq. 13 does not exist. The ANN results suggest that θ_s can be correctly predicted by a nonlinear combination of the considered environmental variables (R²=0.9 and RMSE=0.274 before excluding the secondary contributors, R²=0.904 and RMSE=0.283 after excluding the secondary contributors).

FIGURE 4

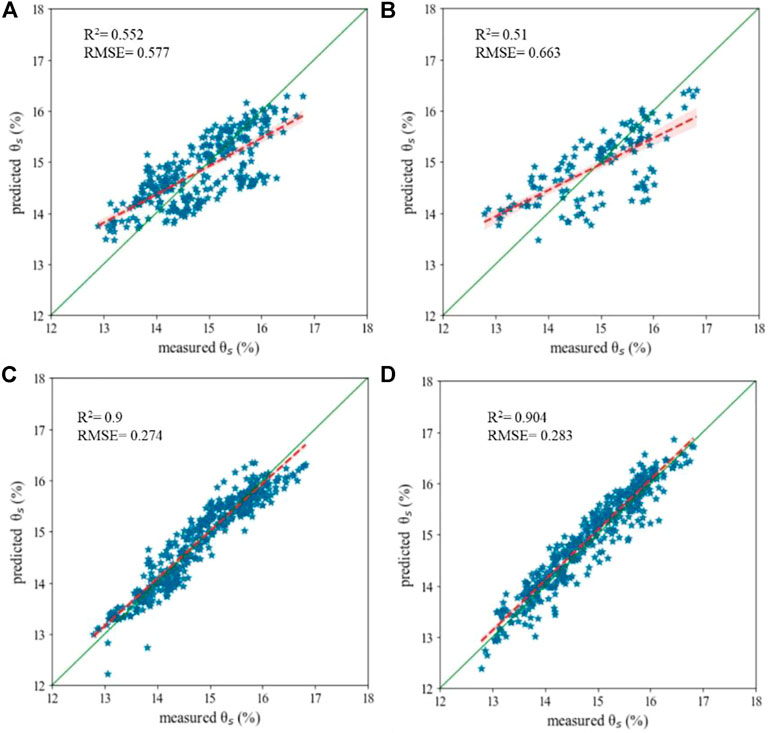
FIGURE 4. Evidence for Eq. 13 from the PLSR training stage (A), testing stage (B), and ANN analyses before excluding the secondary contributors (C) and after excluding the secondary contributors (D). Note: θ_s is the soil volumetric water content at 0–5 cm. All other environmental variables are considered potential contributors to θ_s.

From the PLSR results, the function θ_sf cannot be approximated by

${\theta }_s=c_{\mathrm{0}}+c_{\mathrm{1}}AH+c_{\mathrm{2}}AP+c_{\mathrm{3}}{T}_s+c_{\mathrm{4}}SS+c_{\mathrm{5}}WS+c_{\mathrm{6}}WD+c_{\mathrm{7}}pH+c_{\mathrm{8}}GL+c_{\mathrm{9}}{T}_{as}+c_{\mathrm{10}}{P}_a(14)$

where the computed coefficients from PLSR are c₁=−0.1691, c₂=−0.0238, c₃=0.2133, c₄=0.3858, c₅=0.0326, c₆=−0.102, c₇=−0.0202, c₈=−0.219, c₉=0.1813, c₁₀=0.

These computed coefficients further reveal that the PLSR results are not convincing. Thus, the leading contributors are SS, GL, T_s, T_as, AH, and WD, with contributions to θ_s of 28.6%, 16.3%, 15.8%, 13.5%, 12.6%, and 7.6%, respectively. While the results are wrong to exclude P_a, we can obtain significant information from the two subfigures in Figures 4C,D. No significant differences in ANN performance were observed before and after excluding the secondary contributors. They were both very robust. Since Eq. 14 excluded WS, AP, pH, and P_a as the second contributors to θ_s, there must be another important contributor among T_s, T_as, GL, WD, SS, and AH.

Although the ANN results present a very accurate prediction of θ_s by a nonlinear combination of the considered environmental variables, we cannot determine the best θ_sf from ANN. Consequently, we are motivated to choose the most important contributor to θ_s among T_s, T_as, GL, WD, SS, and AH. Since GL can be influenced by human activities and the management of groundwater sources has attracted attention (Daliakopoulos et al., 2005; Wang et al., 2016d; Cruz-Paredes et al., 2021), we prefer to choose GL. As shown in Figure 5, θ_s fluctuates when GL varies from 65 to 90 m in irrigation seasons.

FIGURE 5

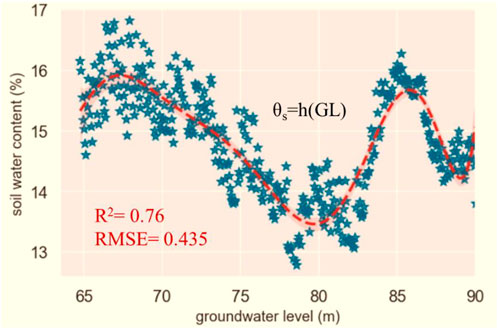
FIGURE 5. Evidence for groundwater level (GL) as a leading variable in Eq. 13 showing evident fluctuations in θ_s when GL varies from 65 to 90 m in irrigation seasons. Note: function h is an eight-degree polynomial. The coefficients of the 8th, 7th, 6th, 5th, 4th, 3rd, 2nd, and 1st order terms are 3.488e−08, −2.114e−05, 0.005591, −0.8432, 79.32, −4765, 1.786e+05, and −3.815e+06, respectively. The constant is 3.559e+07.

GL is also a well-known factor associated with θ_s (Buttle, 1989). Irrigation decisions can significantly affect θ_s and other soil properties (Rawls et al., 1982). In Section 3.1, GL is a suitable controller to reinforce T_as-driven soil CO₂ uptake. Benefitting from a suitable plan on water use for living and industry, we can effectively control GL that can, in turn, affect θ_s. In particular, we can try to reinforce θ_s-driven soil CO₂ uptake in arid regions through proper irrigation decisions and groundwater use plans. Considering Figure 5 as an example, it is easy to see that the relationships between GL and θ_s are complicated. When GL increased from 68 to 78 m, θ_s decreased from 15.88% to 13.70%. Thus, an increase in GL at this stage led to a 2.18% decrease in θ_s, which reinforced F_x by −0.001 μmol m⁻² s⁻¹ according to Eqs 10, 13.

3.3 Reinforcement of pH-driven CO₂ uptake

According to Eq. 9, soil CO₂ uptake can be reinforced by increasing soil pH. Both T_as and θ_s belong to EV_lp, while pH belongs to EV_np. Since F_x(EV_np) is an exponential function, the reinforcement degree of F_x can differ when the pH is increased from different starting points. For example, F_x can be reinforced by −0.7170 μmol m⁻² s⁻¹ with a pH increase from 7 to 8. However, when the pH is increased from 8 to 9, the F_x is reinforced by only −0.5467 μmol m⁻² s⁻¹.

We can hypothesize that pH is a function of other environmental variables; that is

$pH={pH}_f\left(AH,AP,T_s,SS,WS,WD,{\theta }_s,GL,T_{as},P_a\right)(15)$

However, as we learned in Section 3.2, the PLSR-ANN results cannot help us directly identify the leading contributor unless the hypothesized function can be approximated by a linear function. Thus, pH_f may be approximated by a linear function. As proper irrigation decisions and groundwater source management have been recommended to reinforce both T_as-driven and θ_s-driven CO₂ uptake, we directly hypothesize that pH is a nonlinear function of GL; that is

$pH={pH}_f\left(GL\right)(16)$

The hypothetical mechanisms in the function pH_f are as follows. Fluctuation of GL significantly affects soil salt transport, which in turn changes the salt composition of the soil. Since soil pH is majorly influenced by salt composition, pH can be approximated by a nonlinear function of GL. Eq. 16 is proved to be robust (R²=0.978, RMSE=0.028), as shown in Figure 6. Hence, the hypotheses with Eq. 16 are not only reasonable but are also robust in predicting soil pH.

FIGURE 6

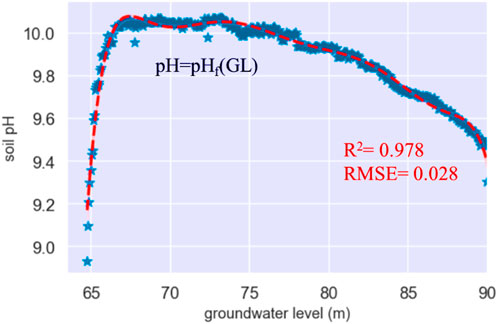
FIGURE 6. Evidence for Eq. 16 showing the close relationship between pH and groundwater level (GL) when GL varies from 65 to 90 m in irrigation seasons. Note: function h is an eighth-degree polynomial. The coefficients of the 8th, 7th, 6th, 5th, 4th, 3rd, 2nd, and 1st order terms are −8.034e−09, −5.022e−06, 0.001371, 0.2137, −20.77, 1291, −5.005e+04, and 1.107e+06, respectively. The constant is −1.07e+07.

Under these hypotheses, pH-driven CO₂ uptake can be reinforced through human activities. Similar to the strategies in Sections 3.1 and 3.2, only a suitable plan on water use for living and industry is required to ensure that the GL fluctuations are advantageous for reinforcing soil CO₂ uptake. Considering Figure 6 as an example, it is easy to see that the relationships between GL and pH are also complicated. When GL increased from 65 to 70 m, the pH increased from 9.40 to 10.03. Therefore, a GL increase at this stage caused a pH increase of 0.63, leading to a −0.2473 μmol m⁻² s⁻¹ reinforcement of F_x according to Eqs 10, 16. However, when GL increased from 70 to 90 m, the pH increased from 10.03 to 9.40. Therefore, a GL increase at this stage caused a decrease in pH of 0.63, which cannot reinforce F_x.

4 Perspectives and discussions

The CO₂ disaster has led to global warming and environmental deterioration (Zekai, 2009; Wani et al., 2012). This crisis can further exacerbate violent conflicts in countries and regions over territory or water supply, which lead to energy, ecological, food, and even economic crises (Pimentel et al., 1973; Coyle and Simmons, 2014; Weston, 2014). Protecting the Earth (and ourselves) requires expanding the theory for reducing the CO₂ disaster. The mechanisms of CO₂ uptake by soils in arid regions are not fully understood. This uptake might be one way for the Earth to repair itself. The present study analyzed whether there is a way for humans to enhance CO₂ uptake. As previous studies identified the main drivers of soil CO₂ uptake, our analyses focused on the influences of other environmental variables on these drivers. However, precipitation in arid regions is limited and we have not collected sufficient and continuous data to accurately quantify the contributions of P_a to T_as, θ_s, and soil pH. Both the PLSR and machine learning results in this study suggested GL as a common controller for the main drivers of soil CO₂ uptake. T_as, θ_s, and soil pH may each show changes in groundwater discharge or recharge, which will in turn influence CO₂ uptake. Therefore, groundwater source management may be a way to reinforce CO₂ uptake by soils in arid regions. There are still considerable uncertainties regarding the influences of P_a and GL on F_x. Their influences on soil CO₂ uptake are complicated, as shown in Figure 7.

FIGURE 7

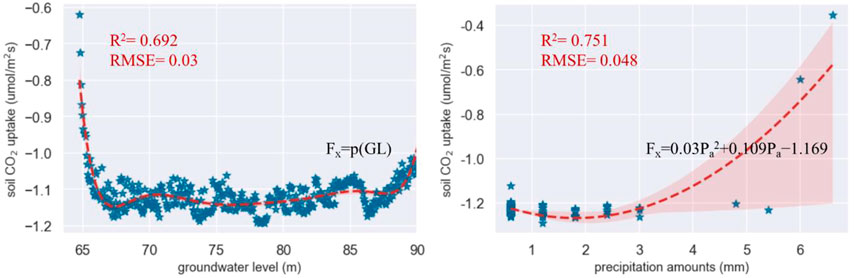
FIGURE 7. Complicated influences of groundwater level (GL) and precipitation amounts (P_a) on soil CO₂ uptake (F_x). Note: p is an eighth-order polynomial. The coefficients of the 8th, 7th, 6th, 5th, 4th, 3rd, 2nd, and 1st order terms are 2.658e−09, −1.66e−06, 0.0045, 0.0705, 6.853, −425.8, 1.652e+04, and 3.655e+05, respectively. The constant is 3.535e+06.

Besides the methodology discussed in this study, many other methods have been proposed to regulate T_as, θ_s, and soil pH. For example, increasing vegetation can shield the direct radiation of the Sun to soil. Because the T_as-driven reinforcement coefficient is almost 20 times that of the θ_s-driven reinforcement coefficient, there is no need to consider the increase in θ_s caused by the reduction of T_as. In addition, increased θ_s is also conducive to the growth of vegetation and photosynthetic CO₂ absorption. Meanwhile, the adjustment of soil pH requires a comprehensive consideration of soil conditions. If the soil conditions are good, then increasing vegetation can provide photosynthetic CO₂ absorption. In most situations, it is not wise to directly increase soil pH to reinforce soil CO₂ uptake. The total reinforcement of photosynthetic CO₂ absorption and soil CO₂ uptake must be comprehensively considered when making decisions, as shown in Figure 8.

FIGURE 8

FIGURE 8. Perspective scheme to comprehensively consider the total reinforcement of photosynthetic CO₂ absorption and soil CO₂ uptake.

The methods in this study allow us to assess soil CO₂ uptake on different scales and also minimize the influences on soil structure. If P_t is the period for measurements, the contribution of soil CO₂ uptake to reducing CO₂concentration can be inferred through Eqs 11–17, as follows:

$\frac{∆C\left(t\right)}{∆t}=F_x\frac{\left(r+\mathrm{2}h\right)}{rh\rho k\left(t\right)}(17)$

$∆C\left(t\right)=F_x\frac{\left(r+\mathrm{2}h\right)∆t}{rh\rho k\left(t\right)}(18)$

$C\left(n{P}_t+P_t\right)-C\left(n{P}_t\right)=F_x\left(n{P}_t\right)\frac{\left(r+\mathrm{2}h\right)P_t}{rh\rho k\left(n{P}_t\right)}(19)$

${\sum }_{n=\mathit{1}}^{N}C\left(n{P}_t+P_t\right)-C\left(n{P}_t\right)={\sum }_{n=\mathit{1}}^N{F}_x\left(n{P}_t\right)\frac{\left(r+\mathrm{2}h\right)P_t}{rh\rho k\left(n{P}_t\right)}(20)$

${\sum }_{n=\mathit{1}}^{N}C\left(n{P}_t+P_t\right)-C\left(n{P}_t\right)={\sum }_{n=\mathit{1}}^N{F}_{xnp}\left(n{P}_t\right)\frac{\left(r+\mathrm{2}h\right)P_t}{rh\rho k\left(n{P}_t\right)}+{\sum }_{n=\mathit{1}}^N{F}_{xlp}\left(n{P}_t\right)\frac{\left(r+\mathrm{2}h\right)P_t}{rh\rho k\left(n{P}_t\right)}(21)$

$\int dC\left(t\right)=\int F_{xnp}\left(t\right)\frac{\left(r+\mathrm{2}h\right)}{rhk\left(t\right)\rho }dt+\int F_{xlp}\left(t\right)\frac{\left(r+\mathrm{2}h\right)}{rhk\left(t\right)\rho }dt(22)$

$\iint dC\left(t\right)dx=\iint F_{xnp}\left(t\right)\frac{\left(r+\mathrm{2}h\right)}{rhk\left(t\right)\rho }dtdx+F_{xlp}\left(t\right)\frac{\left(r+\mathrm{2}h\right)}{rhk\left(t\right)\rho }dtdx(23)$

where dx represents the changes in soil depth and the soil CO₂ uptake corresponding to the environmental changes, which can be computed from Eqs 1–10.

The presentation of reliable decisions in Figure 8 requires determining whether the interactions between photosynthetic CO₂ absorption and soil CO₂ uptake should be involved. The reliable partition of soil CO₂ uptake requires improving the current NEE model.

5 Conclusion

Groundwater level is a leading environmental contributor to the main drivers for soil CO₂ uptake in arid regions. The reinforcement of soil CO₂ uptake through groundwater source management is possible. The results of the PLSR-ANN presented evidence of the theoretical feasibility of reinforcing soil CO₂ uptake in arid regions by human activities. Groundwater discharge and recharge can regulate changes in T_as, θ_s, and soil pH. However, the influences of groundwater are complicated. Meanwhile, we must comprehensively consider the total reinforcement of photosynthetic CO₂ absorption and soil CO₂ uptake when making decisions. Further expansion of the theory for reducing the CO₂ disaster requires further investigation of the need to consider the interactions between photosynthetic CO₂ absorption and soil CO₂ uptake. Thus, these are the next research priorities.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author contributions

B-ZX was mainly responsible for data collection, code convenience, and paper writing as the core contributor of this paper. X-LL assisted in the completion of experiments and compilation of the data tables. W-FW led the project and conceived the main idea of this research. XC was responsible for guiding the experimental code and language polishing of the paper.

Funding

This research was funded by the National Natural Science Foundation of China (41571299) and the High-level Base-building Project for Industrial Technology Innovation (1021GN204005-A06).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baldocchi, D., Falge, E., Gu, L., Olson, R., Hollinger, D., Running, S., et al. (2001). Fluxnet: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 82 (11), 2415–2434. doi:10.1175/1520-0477(2001)082<2415:fantts>2.3.co;2

CrossRef Full Text | Google Scholar

Baldocchi, D., Sturtevant, C., and Contributors, F. (2015). Does day and night sampling reduce spurious correlation between canopy photosynthesis and ecosystem respiration? Agric. For. Meteorol. 207, 117–126. doi:10.1016/j.agrformet.2015.03.010

CrossRef Full Text | Google Scholar

Buttle, J. M. (1989). Soil moisture and groundwater responses to snowmelt on a drumlin sideslope. J. Hydrology 105 (3), 335–355. doi:10.1016/0022-1694(89)90112-1

CrossRef Full Text | Google Scholar

Caers, J. (2011). Modeling uncertainty in the earth sciences[M]. Wiley.

Google Scholar

Chapin, F. S., Woodwell, G. M., Randerson, J. T., Rastetter, E. B., Lovett, G. M., Baldocchi, D. D., et al. (2006). Reconciling carbon-cycle concepts, terminology, and methods. Ecosystems 9 (710), 1041–1050. doi:10.1007/s10021-005-0105-7

CrossRef Full Text | Google Scholar

Chen, X., Wang, W. F., Luo, G. P., Li, L. H., and Li, Y. (2013). Time lag between carbon dioxide influx to and efflux from bare saline-alkali soil detected by the explicit partitioning and reconciling of soil CO₂ flux. Stoch. Environ. Res. Risk Assess. 27 (3), 737–745. doi:10.1007/s00477-012-0636-3

CrossRef Full Text | Google Scholar

Chen, X., Wang, W. F., Luo, G. P., and Ye, H. (2014). Can soil respiration estimate neglect the contribution of abiotic exchange? J. Arid. Land 6 (2), 129–135. doi:10.1007/s40333-013-0244-1

CrossRef Full Text | Google Scholar

Coyle, E. D., and Simmons, R. A. (2014). Understanding the global energy crisis[M]. Purdue University Press.

Google Scholar

Cruz-Paredes, C., Tájmel, D., and Rousk, J. (2021). Can moisture affect temperature dependences of microbial growth and respiration?[J]. Soil Biology and Biochemistry, 108223.

CrossRef Full Text | Google Scholar

Daliakopoulos, I. N., Coulibaly, P., and Tsanis, I. K. (2005). Groundwater level forecasting using artificial neural networks. J. Hydrology 309 (1), 229–240. doi:10.1016/j.jhydrol.2004.12.001

CrossRef Full Text | Google Scholar

Edmonds, I., and Smith, G. (2011). Surface reflectance and conversion efficiency dependence of technologies for mitigating global warming. Renew. Energy 36 (5), 1343–1351. doi:10.1016/j.renene.2010.11.001

CrossRef Full Text | Google Scholar

Falge, E., Baldocchi, D., Tenhunen, J., Aubinet, M., Bakwin, P., Berbigier, P., et al. (2001). Seasonality of ecosystem respiration and gross primary production as derived from FLUXNET measurements. Agric. For. Meteorol. 113, 53–74. doi:10.1016/s0168-1923(02)00102-8

CrossRef Full Text | Google Scholar

Farifteh, J., Meer, F. V. D., Atzberger, C., and Carranza, E. (2007). Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN). Remote Sens. Environ. 110 (1), 59–78. doi:10.1016/j.rse.2007.02.005

CrossRef Full Text | Google Scholar

Gök, M., Coupé, V. M. H., Berkhof, J., Schulze, E. D., Rebmann, C., Moors, E. J., et al. (2000). Respiration as the main determinant of carbon balance in European forests. Nature 404 (6780), 861–865. doi:10.1038/35009084

PubMed Abstract | CrossRef Full Text | Google Scholar

Hastings, S. J., Oechel, W. C., and Muhlia-Melo, A. (2005). Diurnal, seasonal and annual variation in the net ecosystem CO2 exchange of a desert shrub community (Sarcocaulescent) in Baja California, Mexico. Glob. Chang. Biol. 11 (6), 927–939. doi:10.1111/j.1365-2486.2005.00951.x

CrossRef Full Text | Google Scholar

Huang, J. P., Yu, H. P., Dai, A. G., Wei, Y., and Kang, L. (2017). Drylands face potential threat under 2 °C global warming target. Nat. Clim. Chang. 7, 417–422. doi:10.1038/nclimate3275

CrossRef Full Text | Google Scholar

Huang, J. P., Yu, H. P., Guan, X. D., Wang, G., and Guo, R. (2016). Accelerated dryland expansion under climate change. Nat. Clim. Chang. 6, 166–171. doi:10.1038/nclimate2837

CrossRef Full Text | Google Scholar

Inglima, I., Alberti, G., Bertolini, T., Vaccari, F. P., Gioli, B., Miglietta, F., et al. (2009). Precipitation pulses enhance respiration of mediterranean ecosystems: the balance between organic and inorganic components of increased soil CO₂ efflux[J]. Glob. Change Biol. 15 (5), 1289–1301. doi:10.1111/j.1365-2486.2008.01793.x

CrossRef Full Text | Google Scholar

Jasoni, R., Smith, S., and Arnone, J. (2005). Net ecosystem CO₂ exchange in Mojave Desert shrublands during the eighth year of exposure to elevated CO2. Glob. Chang. Biol. 11 (5), 749–756. doi:10.1111/j.1365-2486.2005.00948.x

CrossRef Full Text | Google Scholar

Jenkinson, D. S., Adams, D. E., and Wild, A. (1991). Model estimates of CO₂ emissions from soil in response to global warming[J]. Nature 351 (6324), 304–306. doi:10.1038/351304a0

CrossRef Full Text | Google Scholar

Joos, F., Plattner, G. K., Stocker, T. F., Marchal, O., and Schmittner, A. (1999). Global warming and marine carbon cycle feedbacks on future atmospheric CO₂[J]. Science 284 (5413), 464–467. doi:10.1126/science.284.5413.464

PubMed Abstract | CrossRef Full Text | Google Scholar

Kowalski, A. S., Serrano-Ortiz, P., Janssens, I. A., Sanchez-Moral, S., Cuezva, S., Domingo, F., et al. (2008). Can flux tower research neglect geochemical CO₂ exchange? Agric. For. Meteorol. 148 (148), 1045–1054. doi:10.1016/j.agrformet.2008.02.004

CrossRef Full Text | Google Scholar

Li, Y., Wang, Y., Houghton, R. A., and Tang, L. S. (2015). Hidden carbon sink beneath desert. Geophys. Res. Lett. 42 (14), 5880–5887. doi:10.1002/2015gl064222

CrossRef Full Text | Google Scholar

Ma, J., Wang, Z. Y., Stevenson, B. A., Zheng, X. J., and Li, Y. (2013). An inorganic CO₂ diffusion and dissolution process explains negative CO₂ fluxes in saline/alkaline soils. Sci. Rep. 3, 2025. doi:10.1038/srep02025

PubMed Abstract | CrossRef Full Text | Google Scholar

Mercer, J. H. (1978). West antarctic ice sheet and CO₂ greenhouse effect: A threat of disaster[J]. Nature 271 (5643), 321–325. doi:10.1038/271321a0

CrossRef Full Text | Google Scholar

Mielnick, P., Dugas, W. A., Mitchell, K., and Havstad, K. (2005). Long-term measurements of CO₂, flux and evapotranspiration in a Chihuahuan desert grassland. J. Arid Environ. 60 (3), 423–436. doi:10.1016/j.jaridenv.2004.06.001

CrossRef Full Text | Google Scholar

Murata, A., and Cheolsong, L. I. (2008). A modeling analysis of the deployment of energy efficient industrial technologies in China under CO₂ emission constraints[J]. J. Jpn. Inst. Energy 87 (87), 938–945. doi:10.3775/jie.87.938

CrossRef Full Text | Google Scholar

Pimentel, D., Hurd, L. E., Bellotti, A. C., Forster, M. J., Oka, I. N., Sholes, O. D., et al. (1973). Food production and the energy crisis. Science 182 (4111), 443–449. doi:10.1126/science.182.4111.443

PubMed Abstract | CrossRef Full Text | Google Scholar

Rawls, W. J., Brakensiek, D. L., and Saxtonn, K. E. (1982). Estimation of soil water properties[J]. Trans. Am. Soc. Agric. Eng. 25 (5), 1316–1320.

Google Scholar

Reichstein, M., Falge, E., Baldocchi, D., Papale, D., Aubinet, M., Berbigier, P., et al. (2005). On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm. Glob. Chang. Biol. 11 (9), 1424–1439. doi:10.1111/j.1365-2486.2005.001002.x

CrossRef Full Text | Google Scholar

Rey, A., Belelli-Marchesini, L., Were, A., Serrano-ortiz, P., Etiope, G., Papale, D., et al. (2012). Wind as a main driver of the net ecosystem carbon balance of a semiarid Mediterranean steppe in the South East of Spain. Glob. Chang. Biol. 18 (2), 539–554. doi:10.1111/j.1365-2486.2011.02534.x

CrossRef Full Text | Google Scholar

Rey, A. (2014). Mind the gap: non-biological processes contributing to soil CO₂ efflux. Glob. Chang. Biol. 21 (5), 1752–1761. doi:10.1111/gcb.12821

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez-Cañete, E. P., Serrano-Ortiz, P., Kowalski, A. S., et al. (2011). Subterranean CO₂ ventilation and its role in the net ecosystem carbon balance of a karstic shrubland. Geophys. Res. Lett. 38 (9), 159–164.

Google Scholar

Schlaepfer, D. R., Bradford, J. B., Lauenroth, W. K., Munson, S. M., Tietjen, B., Hall, S. A., et al. (2017). Climate change reduces extent of temperate drylands and intensifies drought in deep soils. Nat. Commun. 8, 14196. doi:10.1038/ncomms14196

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlesinger, W. H. (2001). Carbon sequestration in soils: some cautions amidst optimism. Agric. Ecosyst. Environ. 82 (1-3), 121–127. doi:10.1016/s0167-8809(00)00221-8

CrossRef Full Text | Google Scholar

Serrano-Ortiz, P., Roland, M., Sanchez-Moral, S., Janssens, I. A., Domingo, F., Godderis, Y., et al. (2010). Hidden, abiotic CO₂ flows and gaseous reservoirs in the terrestrial carbon cycle: Review and perspectives. Agric. For. Meteorol. 151 (4), 321–329. doi:10.1016/j.agrformet.2010.01.002

CrossRef Full Text | Google Scholar

Stone, R. (2008). Have desert researchers discovered a hidden loop in the carbon cycle? Science 320 (5882), 1409–1410. doi:10.1126/science.320.5882.1409

PubMed Abstract | CrossRef Full Text | Google Scholar

Utset, A., and Borroto, M. (2001). A modeling-GIS approach for assessing irrigation effects on soil salinisation under global warming conditions. Agric. Water Manag. 50 (1), 53–63. doi:10.1016/s0378-3774(01)00090-7

CrossRef Full Text | Google Scholar

Van't Hoff, J. H. (1898). Lectures on theoretical and physical chemistry[M]. Edward Arnold.

Google Scholar

Wang, W. F., Chen, X., and Pu, Z. (2015). Negative soil respiration fluxes in unneglectable arid regions. Pol. J. Environ. Stud. 24 (2), 905–908. doi:10.15244/pjoes/23878

CrossRef Full Text | Google Scholar

Wang, W. F., Chen, X., Wang, L., Zhang, H., Yin, G., and Zhang, Y. (2016). Approaching the truth of the missing carbon sink. Pol. J. Environ. Stud. 25 (4), 1799–1802. doi:10.15244/pjoes/62357

CrossRef Full Text | Google Scholar

Wang, W. F., Chen, X., Zhang, H., Jing, C., Zhang, Y., and Yan, B. (2015). Highlighting photocatalytic H₂-production from natural seawater and the utilization of quasi-photosynthetic absorption as two ultimate solutions for CO₂ mitigation. Int. J. Photoenergy, 1–11. Article ID: 481624. doi:10.1155/2015/481624

CrossRef Full Text | Google Scholar

Wang, W. F., Chen, X., and Zhang, H. W. (2016). Intelligence in ecology: How internet of things expands insights into the missing CO₂ sink. Scientific Programming, 589723.

Google Scholar

Wang, W. F., Chen, X., and Zhang, H. W. (2016). Soil CO₂ uptake in deserts and its implications to the groundwater environment. doi:10.3390/w8090379Water

CrossRef Full Text

Wang, W. F., Chen, X., Zhang, Y. F., Yu, J., Ma, T., Lv, Z., et al. (2016). Nanodeserts: A conjecture in nanotechnology to enhance quasi-photosynthetic CO₂ absorption. Int. J. Polym. Sci. 2016, 1–10. Article ID 5027879. doi:10.1155/2016/5027879

CrossRef Full Text | Google Scholar

Wani, S A, Asif, M, and Lone, S (2012). Global warming and its impact on environment.[J]. J. Indian Med. Assoc. 111 (6), 376–376.

Google Scholar

Weston, D. (2014). The political economy of global warming: The terminal crisis[M]. Routledge.

Google Scholar

Wohlfahrt, G., Fenstermaker, L. F., and Arnone, J. A. (2008). Large annual net ecosystem CO₂ uptake of a Mojave Desert ecosystem. Glob. Change Biol. 14 (7), 1475–1487. doi:10.1111/j.1365-2486.2008.01593.x

CrossRef Full Text | Google Scholar

Xie, J. X., Li, Y., Zhai, C. X., Li, C., and Lan, Z. (2008). CO₂ absorption by alkaline soils and its implication to the global carbon cycle. Environ. Geol. 56 (5), 953–961. doi:10.1007/s00254-008-1197-0

CrossRef Full Text | Google Scholar

Zekai, Şen. (2009). Global warming threat on water resources and environment: A review. Environ. Geol. 57, 321–329. doi:10.1007/s00254-008-1569-5

CrossRef Full Text | Google Scholar

Zhou, J. L., Li, X. Q., and Wang, W. F. (2021). Analysis of environmental controls on the quasi-ocean and ocean CO₂ concentration by two intelligent algorithms. Mathematical Problems in Engineering, 6666139.

Google Scholar

Zhuang, Z. K., Li, X. Q., and Wang, W. F. (2021). Analysis of environmental controls on the quasi-ocean and ocean CO₂ concentration by two intelligent algorithms. Mathematical Problems in Engineering, 9840335.

Google Scholar