Two-phase Flow Model and Productivity Evaluation of Gas and Water for Dual-Medium Carbonate Gas Reservoirs

Fluid flow in the dual-medium carbonate gas reservoir is characterized by stress sensitivity and non-Darcy flow effect. In order to accurately describe the unsteady flow of gas and water in the dual-medium gas reservoir, a two-phase flow model of gas and water is built. First, reservoir space and fluid flow characteristics of carbonate gas reservoirs are investigated, and the flow model that considers both the stress sensitivity and non-Darcy flow is built based on the fundamental flow theory, after fully investigating the reservoir space and fluid flow characteristics of carbonate gas reservoirs. Then, the perturbation theory is introduced, and the model is solved in the Laplace space, after which the obtained Laplace space analytical solution is converted into the real-space solution. Finally, the productivity evaluation model for the dual-medium gas reservoir with the gas-water two-phase flow is built, based on the flowing material balance method and Newton iteration. The presented productivity evaluation model is applied to analyze the effects of stress sensitivity and non-Darcy flow on the two-phase flow model of gas and water for the dual-medium gas reservoir and the reservoir productivity. The results indicate that a higher stress sensitivity coefficient is demonstrated to indicate higher stress sensitivity and accelerated production decline of the reservoir, while a lower non-Darcy flow effect coefficient represents a stronger non-Darcy effect and boosted drop of initial production of the reservoir. Hence, it is not reasonable to neglect the effects of stress sensitivity and non-Darcy flow during the evaluation of the productivity of a dual-medium carbonate gas reservoir. The model presented in this research provides important references for improving the recovery performance of dual-medium gas reservoirs.

Introduction

Carbonate reservoirs are important targets for hydrocarbon exploration and exploitation, because they contain abundant oil and gas resources (Xu et al., 2007). Compared with conventional gas reservoirs, the dual-medium carbonate gas reservoir is associated with greatly different reservoir characteristics that may result from the relatively developed pores and fractures. Its flow is typically characterized by stress sensitivity, non-Darcy effect, and unique relative gas-water permeability relationship.

In terms of stress sensitivity, Fan et al. (2011) develop a flow model incorporating the stress-sensitive permeability of fracture systems via analyzing the medium deformation of the dual-medium gas reservoir. Zhao et al. (2013) carry out stress sensitivity experiments using four types of cores, namely the matrix type, the fully-filled-fracture type, the semi-filled-fracture type, and the non-filled-fracture type. They rank the stress sensitivity of these four types of cores in the increasing order of matrix, fully-filled-fracture, semi-filled-fracture, and non-filled-fracture types. Moreover, they identify a power-law relationship between permeability and stress. Peng et al. (2015) experimentally analyzed the stress sensitivity of cores under the constant confining pressure and varied pressure and its effects on the reservoir productivity. Zhang R et al. (2016) compare five frequently-used formulas for stress sensitivity via an experimental-theoretical-integrated approach and conclude that the stress sensitivity of fractured reservoirs can be characterized using the power-law formula. Luo et al. (2021) considered the stress-sensitive effects of natural fractures based on the dual-medium flow theory model.

Also, studies on the characteristics of non-Darcy flow have been reported. Cheng and Chen (1998) probe the characteristics of low-speed non-Darcy flow in the case of two-phase flow of oil and gas and point out that non-Darcy flow to some extent impacts (reduces) oil production. Moreover, with the same water content, the productivity index of non-Darcy flow is smaller than that of Darcy flow. Lu (2010) experimentally investigates the fluid flow characteristics under the varied fracture and fracture-vug conditions and identifies the critical parameter values for non-Dary flow, and builds the flow model by introducing Forchheimer number to characterize non-Darcy flow. Zhang F et al. (2016) study the effects of high-speed non-Darcy flow on the productivity of gas wells with certain water cut, via theoretical derivation. Furthermore, the analysis based on the derived productivity equation and actual data of production wells demonstrates that the productivity of gas wells with a certain water cut is considerably lower than that of gas wells with no water production; the non-Darcy effect of productivity of gas wells declines after water production starts. Javadpour et al. (2021) considered the non- Darcy flow of shale gas, and reviewed the dominant gas-flow processes in a single nanopore based on theoretical models and molecular dynamics simulations, and Lattice Boltzmann modeling.

As for the relative permeability of gas and water, Esmaeili et al. (2020) use a newmethodology and conduct limited steady-state relative permeability measurements at different temperatures to confirm the validity of displacement-based relative permeability. Fang et al. (2015) study the pattern of the relative permeability curves of gas and water in high-temperature, high-pressure tight gas reservoirs. Their research identifies that gas permeability under high temperature and high pressure is found to be higher than that under conventional conditions, which means high temperature and high pressure are in favor of gas flow. Liao (2016) investigates the characteristics of the two-phase flow of gas and water in the fractured gas reservoir using numerical models. In his research, he discussed the effects of numerous factors on the production characteristics of the gas reservoir based on the mechanism model, including geological parameters, aquifer parameters, production schemes, water intrusion patterns, and heterogeneity.

At last, for the flow model and productivity evaluation model of gas reservoirs, Zhang et al. (2017a) combine the material balance equation and stress-dependent production equation in the case of over-pressurization to analyze the stress sensitivity of formations and derive the productivity prediction model. The result indicate the critical role of stress sensitivity in reducing the production of gas wells and shortening the duration of stable production. Brown et al. (2009) analyze the pressure and productivity characteristics of stage-fractured horizontal wells of shale gas reservoirs using an analytical tri-linear flow model. Deng et al. (2011), based on their analysis of the gas-water relative permeability regularity, modify the productivity prediction model of water-producing gas wells and the production decline analysis method for water-involved gas reservoirs with the non-Darcy flow. Chen (2016) probes the fluid flow patterns of low-permeability gas reservoirs and develops the productivity calculation formulas for fractured horizontal wells and those with inclined fractures and gas-water two-phase flow, respectively. The presented models are validated by the good application performance of the models to the production data of actual production wells. In 2017, a productivity evaluation method for abnormally over-pressurized gas reservoirs, incorporating both the reservoir rock deformation and gas-water relative permeability, is developed by Zhang et al. (2017b), which is then applied to investigating the factors affecting the production performance of gas wells via actual production data. Based on the material balance theory, Zhang W et al. (2017) derive the pressure calculation formula and production prediction equation for gas wells featuring two-phase flow, which provide theoretical support to production forecasting of gas wells with coexisting gas and water.

The above review demonstrates substantial progress in studying the flow regularity and productivity prediction of carbonate gas reservoirs. Nonetheless, most research only considers the effects of a single factor, and rare studies have been reported to investigate the joint impacts of stress sensitivity, non-Darcy flow, and two-phase relative permeability of gas and water on carbonate gas reservoirs. Moreover, complete, systematic productivity evaluation methods for carbonate gas reservoirs haven’t been presented yet. Given these, this study aims and manages to build a gas-water two-phase flow model of carbonate gas reservoirs, incorporating both stress sensitivity and non-Darcy flow. Results of this study are expected to provide references for improving the recovery performance of dual-medium carbonate gas reservoirs.

Fluid Flow Patterns for Carbonate Gas Reservoirs

Dual-medium carbonate gas reservoirs are different from conventional reservoirs, and they are composed of matrix and fracture systems (Li et al., 2017)—the low-porosity, high-permeability fracture system is the main flow channel for fluids, while the high-porosity, low-permeability matrix system is the main storage space for gas. Such dual-medium carbonate reservoirs have greatly different pore-throat structures and more complicated fluid flow than conventional pore-dominated gas reservoirs (Jia et al., 2013).

Stress Sensitivity of Reservoirs

During the recovery process of carbonate gas reservoirs, the reservoir rock framework deforms, as the effective stress grows (e.g., the overburden stress) owing to the sustained production of natural gas and consequent pore pressure decline (Li et al., 2011). The ultimate resultant variation of the reservoir physical parameters such as permeability and porosity is referred to as stress sensitivity (Peng et al., 2015). It is known that with the progress in hydrocarbon recovery, the reservoir permeability and productivity are both degraded.

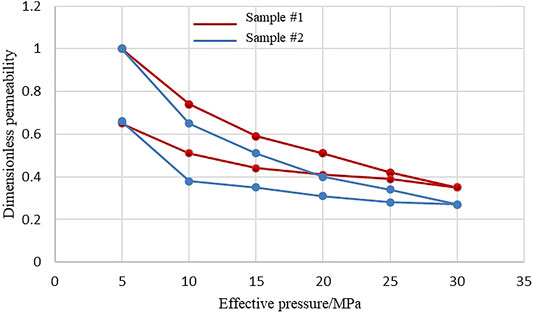
The core porosity and permeability measurements under the overburden pressure of the L carbonate gas reservoir of the A gas field (Figure 1) shows that the tendencies of permeability to decline with increasing overburden pressure are generally consistent; as the overburden pressure reaches 30 MPa, the core permeability declines by 60%; as the overburden pressure restores to the initial value, the permeability recovers to about 60% of the initial permeability (in other words, a permanent permeability loss of 40% is caused). The dimensionless permeability in Figure 1 is the ratio of permeability under certain pressure conditions to initial permeability (k_i/k₀).

FIGURE 1

FIGURE 1. Relationship between core permeability and overburden pressure.

The stress sensitivity can be characterized using the power-law function (Petrosa, 1986):

$k_f=k_{fi}{e}^{-{\gamma }_f\left({\psi }_i-{\psi }_f\right)}(1)$

where $k_f$ is the permeability of the fracture system, mD; $k_{fi}$ is the fracture system permeability corresponding to the original formation conditions, mD; ${\gamma }_f$ is the permeability modulus, MPa⁻¹; ${\psi }_i$ is the initial pseudo-pressure of formations, MPa²/(mPa·s); ${\psi }_f$ is the pseudo-pressure of the fracture system, MPa²/(mPa·s).

The pseudo-permeability modulus is defined as:

${\gamma }_f=\frac{1}{k_f}\frac{\partial k_f}{\partial {\psi }_f}(2)$

Effects of High-Speed Non-Darcy Flow

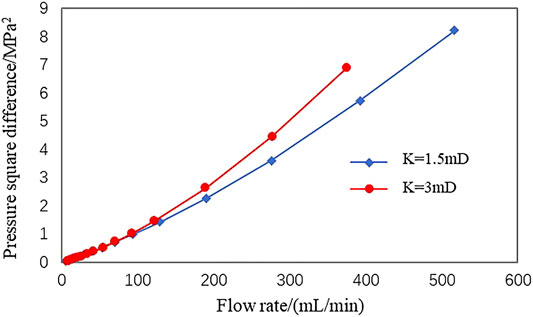
Due to the reservoir rock property, the dual-medium carbonate reservoir is subjected to considerable gas turbulence and thus the intensive non-Darcy effect (Chen et al., 2015). The non-Darcy flow regularity of the fracture-pore type reservoir rock of the L gas reservoir in the A gas field is illustrated in Figure 2. When the flow rate grows, the non-linearity between the pressure square difference and the gas flow rate gradually climbs up. Gas wells, subjected to the non-Darcy effect, are expected to present a certain degree of production decline.

FIGURE 2

FIGURE 2. Non-Darcy feature of the fracture-pore type reservoir rock.

The non-Darcy effect can be characterized by introducing a correction factor dependent on fluid flow rates (Huang et al., 2004).

$-\frac{dP}{dr}=\frac{{\mu }_g{u}_g}{K}+\delta \rho u_g^2(3)$

where ${\mathit{\mu }}_{\mathit{g}}$ is the fluid viscosity, mPa·s; ${\mathit{u}}_{\mathit{g}}$ is the flow rate, cm/s; $\mathbf{\delta }$ is the non-Darcy coefficient, cm⁻¹; $\mathbf{\rho }$ is the fluid density, kg/m³.

Two-phase Relative Permeability Pattern of Gas and Water

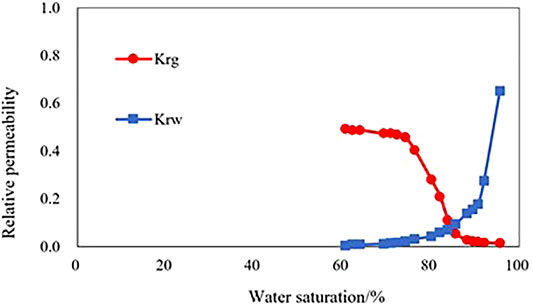
Because of the presence of dual media composed of pores and fractures and the substantial difference of fluid flow space between them, the fracture-pore type carbonate reservoir presents highly complex flow characteristics. Accordingly, the two-phase relative permeability pattern of gas and water is also greatly different from that in the conventional gas reservoir (Figure 3). Cores in the study area are proven to be highly hydrophilic, with the relative permeability intersection point occurring at the water saturation of above 70%. This is caused by the micropore structure of the gas reservoir—some tiny throats in the pore structure are too small to allow water to form a continuous flowing phase after penetrating such space.

FIGURE 3

FIGURE 3. Two-phase relative permeability of gas and water for the dual-medium.

Two-Phase Productivity Evaluation Model for Gas and Water in Dual-Medium Gas Reservoirs

Flow Model

The fracture-pore type dual-medium has been demonstrated to primarily consist of two types of pore structures, namely primary inter-granular pores and secondary pores. Primary pores are largely affected by deposition and diagenesis processes, dimensions, distributions, and shapes of reservoir rock grains, thereby presenting heterogeneous features of permeability and porosity. As for secondary pores, they are composed of fractures, joints, and dissolved pores. In other words, the dual-medium consists of two systems, namely pore and fracture systems. In most cases, the fracture system serves as the main fluid flow channel, while the rock matrix provides the main storage space.

The fractured reservoir has the following characteristics:

1) Dual structural characteristics. The reservoir rock is associated with the extensive development of both primary and secondary pores (in other words, it consists of dual media of pores and fractures, respectively). Both the pore and fracture media have their own porosity and permeability features and the two media are connected.

2) The compressibility of the fracture system is considerably higher than that of the pore system. Therefore, as the fluid (pore) pressure decreases, the fracture may close under the overburden pressure; moreover, such fracture closure is irreversible. Ultimately, the fracture permeability is reduced.

3) Anisotropy. The reservoir permeability is highly anisotropic. For productivity evaluation, if the goal is only to investigate the formation characteristics in a vertical well, the medium can be considered isotropic.

The fracture-pore medium model assumes that the reservoir is a dual-medium for fluid storage and flow composed of the matrix and fracture systems. The assumptions of the physical model for production decline of wells in the fracture-pore type reservoir are summarized below:

1) The vertical well is producing at a constant production rate from a reservoir with the closed outer boundary.

2) The payzone is producing across its whole thickness and the fluid flows into the wellbore via the radial flow regime.

3) The rock compressibility is neglected, while the gas compressibility and stress-dependency of the fracture system permeability are considered.

4) Fluids have two components, namely gas and water.

5) The effects of capillary pressure and gravity are ignored.

6) Fractures are the only channel for fluids to flow into the wellbore. Fluids in the matrix system flow into fractures via the pseudo-steady cross flow and then enter the wellbore through fractures.

The mathematic model of the fracture system is described below:

The continuity equation:

$\frac{1}{r}\frac{\partial }{\partial r}\left[r\left({\rho }_{\text{g}}{v}_{\text{g}}+{\rho }_{\text{w}}{v}_{\text{w}}\right)\right]=\frac{\partial \left({\rho }_{\text{g}}{S}_{\text{g}}+{\rho }_{\text{w}}{S}_{\text{w}}\right)}{\partial t}-q_{\text{mf}}(4)$

where ${\rho }_{\text{g}}$ is the gas density, kg/m³; $v_{\text{g}}$ is the gas flow rate, cm/s; ${\rho }_{\text{w}}$ is the water density, kg/m³; $v_{\text{w}}$ is the water flow rate cm/s; $S_{\text{g}}$ is the gas saturation, decimals; $S_{\text{w}}$ is the water saturation, decimals.

Equations of motion:

$v_{\text{g}}=-\delta \frac{k{k}_{\text{rg}}}{{\mu }_{\text{g}}{B}_{\text{g}}}\frac{\partial p}{\partial r}(5)$

where $k_{\text{rg}}$ is the relative permeability of gas, decimals; ${\mu }_{\text{g}}$ is the gas viscosity, mPas; $B_{\text{g}}$ is the formation volume coefficient of gas, decimals.

$v_{\text{w}}=-\delta \frac{k{k}_{\text{rw}}}{{\mu }_{\text{w}}{B}_{\text{w}}}\frac{\partial p}{\partial r}(6)$

where $k_{\text{rw}}$ is the relative permeability of water, decimals; ${\mu }_{\text{w}}$ is the water viscosity, mPa·s; $B_{\text{w}}$ is the formation volume coefficient of water, decimals.

The cross-flow rate between the matrix and fracture systems can be determined by:

$q_{\text{jmf}}=\frac{{\alpha }_m{k}_m{k}_{\text{rjm}}{S}_j}{B_j}\left(p_m-p_f\right),j=\text{w},\text{g}(7)$

By combing the above equations, basic control equations of flow for the fracture system can be obtained:

$\frac{{\lambda }_{\text{g}}{k}_{\text{f}}}{r}\frac{\partial p_{\text{f}}}{\partial r}+{\lambda }_{\text{g}}\frac{\partial k_f}{\partial p_{\text{f}}}{\left(\frac{\partial p_{\text{f}}}{\partial r}\right)}^2+{\lambda }_{\text{g}}{k}_{\text{f}}\frac{{\partial }^2{p}_{\text{f}}}{\partial r^2}+\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{\delta k_{\text{rgf}}{B}_{\text{g}}}\left(p_m-p_f\right)=\frac{{\varphi }_{\text{f}}}{0.0864\delta k_{\text{rgf}}}\frac{\partial }{\partial t}\left(\frac{S_{\text{g}}}{B_{\text{g}}}\right)(8)$

where $k_{\text{rgm}}$ is the relative permeability of gas for the matrix system, decimals; $k_{\text{rgf}}$ is that for the fracture system, decimals.

$\frac{{\lambda }_w{k}_{\text{f}}}{r}\frac{\partial p_{\text{f}}}{\partial r}+{\lambda }_w\frac{\partial k_f}{\partial p_{\text{f}}}{\left(\frac{\partial p_{\text{f}}}{\partial r}\right)}^2+{\lambda }_w{k}_{\text{f}}\frac{{\partial }^2{p}_{\text{f}}}{\partial r^2}+\frac{{\alpha }_m{k}_m{k}_{\text{rwm}}{S}_w}{\delta k_{\text{rwf}}{B}_w}\left(p_m-p_f\right)=\frac{{\varphi }_{\text{f}}}{0.0864\delta k_{\text{rwf}}}\frac{\partial }{\partial t}\left(\frac{S_w}{B_w}\right)(9)$

where $k_{\text{rwm}}$ is the relative permeability of water for the matrix system, decimals; $k_{\text{rwf}}$ is that for the fracture system, decimals.

Similarly, the basic control equations of flow for the matrix system can be obtained:

$\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{B_{\text{g}}}\left(p_m-p_f\right)=\frac{{\varphi }_{\text{m}}}{0.0864k_{\text{m}}}\frac{\partial }{\partial t}\left(\frac{S_{\text{g}}}{B_{\text{g}}}\right)(10)$

$\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{B_{\text{g}}}\left(p_m-p_f\right)=\frac{{\varphi }_{\text{m}}}{0.0864k_{\text{m}}}\frac{\partial }{\partial t}\left(\frac{S_{\text{w}}}{B_{\text{w}}}\right)(11)$

The pseudo-pressure is defined as:

${\psi }_{\text{g}}={\displaystyle \underset{0}{\overset{p}{\int }}{\lambda }_{\text{g}}\text{d}p},j=f,m(12)$

where ${\lambda }_{\text{g}}=\frac{1}{{\mu }_{\text{g}}{B}_{\text{g}}}$.

Thus, the basic control equation for gas flow in the fracture system is

$\frac{1}{r}\frac{\partial {\psi }_{\text{f}}}{\partial r}+{\gamma }_{\text{f}}{\left(\frac{\partial {\psi }_{\text{f}}}{\partial r}\right)}^2+\frac{{\partial }^2{\psi }_{\text{f}}}{\partial r^2}+\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{k_{\text{f}}{\lambda }_g^2\delta k_{\text{rgf}}{B}_{\text{g}}}\left({\psi }_m-{\psi }_f\right)=\frac{1}{k_{\text{f}}{\theta }_{\text{f}}}\frac{\partial {\psi }_{\text{f}}}{\partial t}(13)$

where

$\frac{1}{{\theta }_{\text{f}}}=\frac{{\varphi }_{\text{f}}}{0.0864\delta k_{\text{rgf}}}\frac{1}{{\lambda }_{\text{g}}^2}\left(-\frac{S_{\text{g}}}{B_g^2}\frac{\text{d}{B}_{\text{g}}}{\text{d}{p}_{\text{f}}}\right)(14)$

The basic control equation for gas flow in the matrix system is

$\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{{\lambda }_g{B}_{\text{g}}}\left({\psi }_m-{\psi }_f\right)=\frac{1}{{\theta }_m}\frac{\partial {\psi }_m}{\partial t}(15)$

where

$\frac{1}{{\theta }_{\text{m}}}=\frac{{\varphi }_{\text{m}}}{0.0864k_{\text{m}}{k}_{\text{rgm}}}\frac{1}{{\lambda }_{\text{g}}}\left(-\frac{S_{\text{g}}}{B_{\text{g}}^2}\frac{\text{d}{B}_{\text{g}}}{\text{d}{p}_{\text{m}}}\right)(16)$

The initial condition is:

${{\psi }_{\text{f}}\left(r,t\right)|}_{t=0}={{\psi }_{\text{m}}\left(r,t\right)|}_{t=0}={\psi }_{\text{i}}(17)$

The inner boundary condition is:

${\delta \frac{\partial {\psi }_{\text{f}}}{\partial r}|}_{r=r_w}=\frac{T{q}_{\text{sc}}}{78.489K_{\text{fi}}h}(18)$

The outer boundary condition is:

${\frac{\partial {\psi }_{\text{f}}}{\partial r}|}_{r=r_e}=0(19)$

Solving the Model

The duration for productivity prediction is divided into numerous time intervals. The parameters dependent on saturations are calculated explicitly, which means that within a time step, the saturation remains the same. In contrast, parameters dependent on pressure are determined implicitly. The gas production is determined by solving our model, and meanwhile, the water production is predicted using the gas/water ratio. In other words, the model solving involves only the gas equation. After the gas production is determined, the average pressure and saturation across the production-affected (pressure drawdown) zone of the gas reservoir are computed via the flowing material balance method, according to which the model parameters are updated. Finally, the semi-analytical solutions of the model are obtained after numerous iterations. The solving workflow is summarized below:

1) Parameter normalization and equation linearization

The parameter normalization is shown below:

The dimensionless stress sensitivity coefficient is defined as:

${\gamma }_{\text{fD}}=\frac{T{q}_{\text{sc}}}{78.489K_{\text{fi}}h}{\gamma }_f(20)$

The dimensionless time:

$t_{\text{D}}=\frac{3.6k_{\text{fi}}}{{\mu }_i{r}_{\text{w}}^2{({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}})}_i}t(21)$

The dimensionless radius:

$r_{\text{D}}=\frac{r}{r_{\text{wa}}}=\frac{r}{r_{\text{w}}{\text{e}}^{-S}}(22)$

The dimensionless pseudo-pressure:

${\psi }_{\text{fD}}=\frac{78.489K_{\text{fi}}h}{T{q}_{\text{sc}}}\left({\psi }_{\text{i}}-{\psi }_{\text{f}}\right)(23)$

${\psi }_{\text{mD}}=\frac{78.489K_{\text{fi}}h}{T{q}_{\text{sc}}}\left({\psi }_{\text{i}}-{\psi }_{\text{m}}\right)(24)$

Accordingly, the fracture control equation can be rewritten as:

$\frac{1}{r_D}\frac{\partial {\psi }_{fD}}{\partial r_D}-{\gamma }_{fD}{\left(\frac{\partial {\psi }_{fD}}{\partial r_D}\right)}^2+\frac{{\partial }^2{\psi }_{fD}}{\partial r_D^2}=e^{{\gamma }_{fD}{\psi }_{fD}}\left[\frac{3.6k_{fi}{e}^{-2S}}{{\theta }_f{\mu }_i{\left({\varphi }_m{C}_m+{\varphi }_f{C}_f\right)}_i}\frac{\partial {\psi }_{fD}}{\partial t_D}-\frac{r_w^2{e}^{-2S}{\alpha }_m{k}_m{k}_{rgm}{S}_g}{{\lambda }_g^2\delta k_{rgf}{B}_g}\left({\psi }_{fD}-{\psi }_{mD}\right)\right](25)$

The matrix control equation can be rewritten as:

$\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{{\lambda }_g{B}_{\text{g}}}\left({\psi }_{fD}-{\psi }_{mD}\right)=\frac{1}{{\theta }_m}\frac{3.6k_{\text{fi}}}{{\mu }_i{r}_w^2{\left({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}}\right)}_i}\frac{\partial {\psi }_{mD}}{\partial t_D}(26)$

The rewritten expression of the initial condition:

${{\psi }_{\text{fD}}\left(r_{\text{D}},t_{\text{D}}\right)|}_{t_{\text{D}}=0}={{\psi }_{\text{mD}}\left(r_{\text{D}},t_{\text{D}}\right)|}_{t_{\text{D}}=0}=0(27)$

The inner boundary condition:

${\left(e^{-{\gamma }_{\text{mD}}{\psi }_{\text{fD}}}\delta \frac{\partial {\psi }_{\text{fD}}}{\partial r_{\text{D}}}\right)|}_{rD=1}=-1(28)$

The outer boundary condition:

${\frac{\partial {\psi }_{\text{fD}}}{\partial r_{\text{D}}}|}_{r_{\text{D}}=r_{\text{eD}}}=0(29)$

The perturbation theory is introduced:

${\psi }_{\text{fD}}\left(r_{\text{D}},t_{\text{D}}\right)=-\frac{1}{{\gamma }_{\text{fD}}}\ln \left[1-{\gamma }_{\text{fD}}{\eta }_{\text{fD}}\left(r_{\text{D}},t_{\text{D}}\right)\right](30)$

${\psi }_{\text{mD}}\left(r_{\text{D}},t_{\text{D}}\right)=-\frac{1}{{\gamma }_{\text{fD}}}\ln \left[1-{\gamma }_{\text{fD}}{\eta }_{\text{mD}}\left(r_{\text{D}},t_{\text{D}}\right)\right](31)$

The zeroth-order solution for perturbation is adopted and simplified as:

$\frac{1}{r_D}\frac{\partial {\eta }_{\text{0fD}}}{\partial r_D}+\frac{{\partial }^2{\eta }_{\text{0fD}}}{\partial r_D^2}=\frac{3.6k_{\text{fi}}{\text{e}}^{-2S}}{{\theta }_{\text{f}}{\mu }_i{({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}})}_i}\frac{\partial {\eta }_{\text{0fD}}}{\partial t_D}-\frac{r_w^2{\text{e}}^{-2S}{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{{\lambda }_{\text{g}}^2\delta k_{\text{rgf}}{B}_{\text{g}}}\left({\eta }_{0fD}-{\eta }_{0mD}\right)(32)$

$\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{{\lambda }_g{B}_{\text{g}}}\left({\eta }_{0fD}-{\eta }_{0mD}\right)=\frac{3.6k_{\text{fi}}}{{\theta }_m{\mu }_i{r}_{\text{w}}^2{({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}})}_i}\frac{\partial {\eta }_{0mD}}{\partial t_D}(33)$

Correspondingly, the initial condition:

${{\eta }_{\text{fD}}\left(r_{\text{D}},t_{\text{D}}\right)|}_{t_{\text{D}}=0}={{\eta }_{\text{mD}}\left(r_{\text{D}},t_{\text{D}}\right)|}_{t_{\text{D}}=0}=0(34)$

The inner boundary condition:

${\left(\delta \frac{\partial {\eta }_{\text{0fD}}}{\partial r_{\text{D}}}\right)|}_{r_{\text{D}}=1}=-1(35)$

The outer boundary condition:

${\frac{\partial {\eta }_{\text{0fD}}}{\partial r_{\text{D}}}|}_{r_{\text{D}}=r_{\text{eD}}}=0(36)$

2) Laplace transform and solutions of the mathematic model

For the convenience of derivation, we perform the Laplace transform to solve the model in the Laplace space. Subsequently, the Stehfest numerical inversion method is applied to obtain the solutions of the real space of the model.

The equation group is re-arranged using the Laplace transform of t_D:

$\frac{1}{r_D}\frac{\partial {\overline{\eta }}_{\text{0fD}}}{\partial r_D}+\frac{{\partial }^2{\overline{\eta }}_{\text{0fD}}}{\partial r_D^2}=\frac{3.6k_{\text{fi}}{\text{e}}^{-2S}}{{\theta }_{\text{f}}{\mu }_i{\left({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}}\right)}_i}{\overline{\eta }}_{\text{0fD}}-\frac{r_{\text{w}}^2{\text{e}}^{-2S}{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{{\lambda }_{\text{g}}^2\delta k_{\text{rgf}}{B}_{\text{g}}}\left({\overline{\eta }}_{0fD}-{\overline{\eta }}_{0mD}\right)(37)$

$\frac{{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}}{{\lambda }_g{B}_{\text{g}}}\left({\overline{\eta }}_{0fD}-{\overline{\eta }}_{0mD}\right)=\frac{3.6k_{\text{fi}}}{{\theta }_m{\mu }_i{r}_{\text{w}}^2{({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}})}_i}{\overline{\eta }}_{\text{0mD}}(38)$

The initial condition:

${{\overline{\eta }}_{\text{fD}}\left(r_{\text{D}},t_{\text{D}}\right)|}_{t_{\text{D}}=0}={\overline{\eta }}_{\text{mD}}{\left(r_{\text{D}},t_{\text{D}}\right)|}_{t_{\text{D}}=0}=0(39)$

The inner boundary condition:

${\left(\delta \frac{\partial {\overline{\eta }}_{\text{0fD}}}{\partial r_{\text{D}}}\right)|}_{r_{\text{D}}=1}=-1(40)$

The outer boundary condition:

${\frac{\partial {\overline{\eta }}_{\text{0fD}}}{\partial r_{\text{D}}}|}_{r_{\text{D}}=r_{\text{eD}}}=0(41)$

Combining Eqs 37, 38 yields:

$\frac{1}{r_D}\frac{\partial {\overline{\eta }}_{\text{0fD}}}{\partial r_D}+\frac{{\partial }^2{\overline{\eta }}_{\text{0fD}}}{\partial r_D^2}-f\left(\xi \right){\overline{\eta }}_{\text{0fD}}=0(42)$

where

$f\left(\xi \right)=\frac{{\text{e}}^{-2S}3.6k_{\text{fi}}}{{\theta }_{\text{f}}{\mu }_i{\left({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}}\right)}_i}-\frac{{\text{e}}^{-2S}{\lambda }_g{B}_{\text{g}}3.6k_{\text{fi}}}{{\theta }_m{\mu }_i{r}_{\text{w}}^2{\alpha }_m{k}_m{k}_{\text{rgm}}{S}_{\text{g}}{\left({\varphi }_{\text{m}}{C}_{\text{m}}+{\varphi }_{\text{f}}{C}_{\text{f}}\right)}_i+{\lambda }_g{B}_{\text{g}}3.6k_{\text{fi}}}(43)$

Substituting the inner and outer boundary conditions into Eq. 42, the solution is obtained:

${\overline{\eta }}_{\text{0fD}}=\frac{1}{\delta D}{I}_0\left(r_D\sqrt{f\left(\xi \right)}\right)K_1\left(r_{eD}\sqrt{f\left(\xi \right)}\right)+\frac{1}{\delta D}{I}_1\left(r_{eD}\sqrt{f\left(\xi \right)}\right)K_0\left(r_D\sqrt{f\left(\xi \right)}\right)(44)$

where

$D=\sqrt{f\left(\xi \right)}\left[I_1\left(r_{eD}\sqrt{f\left(\xi \right)}\right)K_1\left(\sqrt{f\left(\xi \right)}\right)-I_1\left(\sqrt{f\left(\xi \right)}\right)K_1\left(r_{eD}\sqrt{f\left(\xi \right)}\right)\right](45)$

The production is expressed as below:

${\overline{q}}_{\text{gf}}=-2\pi k_{\text{f}}{k}_{\text{rgf}}h{r}_{\text{w}}{\frac{\partial \Delta {\overline{\eta }}_{\text{f}}}{\partial r}|}_{r\to r_{\text{w}}}(46)$

3) Calculating the average formation pressure using the material balance method

We manage to linearize the two-phase equation by introducing the pseudo- time and pressure. However, the obtained general solution is a function of the pseudo-time, while the pseudo-time is a function of pressure. Hence, the iterative calculation is required to compute the productivity corresponding to the real time and its composition (gas and water production). In iteration, the average gas reservoir pressure needs to be computed at each time step.

The overall material balance equation of the gas system is presented below:

$IGIP-RGIP=G_{\text{p}}(47)$

where $IGIP$ is the initial gas in place, m³; $RGIP$ is the remaining gas in place, m³; $G_{\text{p}}$ is the cumulative gas production, m³.

Moreover, the IGIP can be calculated using the following equation:

$IGIP=\pi r_{{\text{ginv}}^2}h\varphi \left(\frac{S_{\text{gi}}}{B_{\text{gi}}}\right)(48)$

where $r_{\text{ginv}}$ is the drainage radius of gas, m; $S_{\text{gi}}$ is the initial gas saturation, decimals; $B_{\text{gi}}$ is the initial formation volume coefficient of gas, decimals.

The RGIP is determined as below:

$RGIP=\pi r_{{\text{ginv}}^2}h\varphi \left(\frac{{\overline{S}}_{\text{g}}}{{\overline{B}}_{\text{g}}}\right)(49)$

where ${\overline{S}}_{\text{g}}$ is the average gas saturation, decimals; ${\overline{B}}_{\text{g}}$ 为is the average formation volume coefficient of gas, decimals.

The cumulative gas production:

$G_{\text{p}}={\displaystyle \underset{0}{\overset{t}{\int }}{q}_{\text{g}}\text{d}t}(50)$

where $q_g$ is the daily gas production, m³/d.

By substituting Eqs 48–50 into Eq. 47, we have:

$\frac{{\overline{S}}_g}{{\overline{B}}_g}=\frac{S_{\text{gi}}}{B_{\text{gi}}}-\frac{G_{\text{p}}}{\pi r_{{\text{ginv}}^2}h\varphi }(51)$

The overall material balance equation of water is:

$IWIP-RWIP=N_{\text{w}}(52)$

where $IWIP$ is the initial water in place, m³; $RWIP$ is the remaining water in place, m³; $N_{\text{w}}$ is the cumulative water production, m³.

The IWIP can be calculated using the following equation:

$IWIP=\pi r_{{\text{winv}}^2}h\varphi \left(\frac{S_{\text{wi}}}{B_{\text{wi}}}\right)(53)$

where $r_{\text{winv}}$ is the drainage radius of water, m; $S_{\text{wi}}$ is the initial water saturation, decimals; $B_{\text{wi}}$ is the initial formation volume coefficient of water, decimals.

The RWIP can be calculated as below:

$RWIP=\pi r_{{\text{winv}}^2}h\varphi \left(\frac{{\overline{S}}_{\text{w}}}{{\overline{B}}_{\text{w}}}\right)(54)$

where ${\overline{S}}_w$ is the average water saturation, decimals; ${\overline{B}}_w$ is the average formation volume coefficient of water, decimals.

The cumulative water production:

$N_{\text{w}}={\displaystyle \underset{0}{\overset{t}{\int }}{q}_{\text{w}}\text{d}t}(55)$

where $q_{\text{w}}$ is the daily water production, m³/d.

Substituting Eqs 53–55 into Eq. 50 yields:

$\frac{{\overline{S}}_{\text{w}}}{{\overline{B}}_{\text{w}}}=\frac{S_{\text{wi}}}{B_{\text{wi}}}-\frac{N_{\text{w}}}{\pi r_{{\text{winv}}^2}h\varphi }(56)$

The correlation between the water and gas saturation is shown below:

${\overline{S}}_{\text{g}}+{\overline{S}}_{\text{w}}=1(57)$

By combining Eqs 51, 56, 57, we have:

$f\left(\overline{p}\right)=\frac{1}{{\overline{B}}_{\text{g}}}+\left(\frac{{\overline{B}}_{\text{w}}}{{\overline{B}}_{\text{g}}}\right)m_1-m_2(58)$

where

$m_1=\left(\frac{S_{\text{wi}}}{B_{\text{wi}}}\right)-\frac{N_{\text{w}}}{\pi r_{{\text{inv}}^2}h\varphi }(59)$

$m_2=\left(\frac{S_{\text{gi}}}{B_{\text{gi}}}\right)-\frac{G_{\text{p}}}{\pi r_{{\text{inv}}^2}h\varphi }(60)$

The derivative of Eq. 58 is:

$f^{\prime }\left(\overline{p}\right)=-\frac{1}{{\overline{B}}_{\text{g}}^2}\frac{\text{d}{B}_{\text{g}}}{\text{d}p}+m_1\left(-\frac{1}{{\overline{B}}_{\text{w}}}\frac{\text{d}{B}_{\text{w}}}{\text{d}p}+\frac{B_{\text{w}}}{{\overline{B}}_{\text{g}}^2}\frac{\text{d}{B}_{\text{g}}}{\text{d}p}\right)(61)$

Then the Newton iteration equation can be written as Eq. 62:

${\overline{p}}_{\text{k}+1}={\overline{p}}_{\text{k}}-\omega \frac{f\left(\overline{p_{\text{k}}}\right)}{f^{\prime }\left(\overline{p_{\text{k}}}\right)}(62)$

The two-phase flow model of gas and water is solved in a semi-analytical approach. The productivity prediction workflow for the two-phase flow of gas and water is illustrated in Figure 4. The duration for productivity prediction is divided into numerous time steps. The saturation-dependent parameters are calculated explicitly, while the pressure-dependent ones are computed implicitly. Specifically, within one time step, the saturation is defined as a constant, and the pressure-dependent parameter is calculated using the pseudo-pressure. After obtaining the gas production, the average reservoir pressure and saturation across the pressure drawdown-affected zone are determined using the flowing material balance method. Subsequently, the model parameters are updated according to the new average reservoir pressure and saturation and the production is calculated again. The semi-analytical solutions of the model are finally obtained after multiple iterations.

FIGURE 4

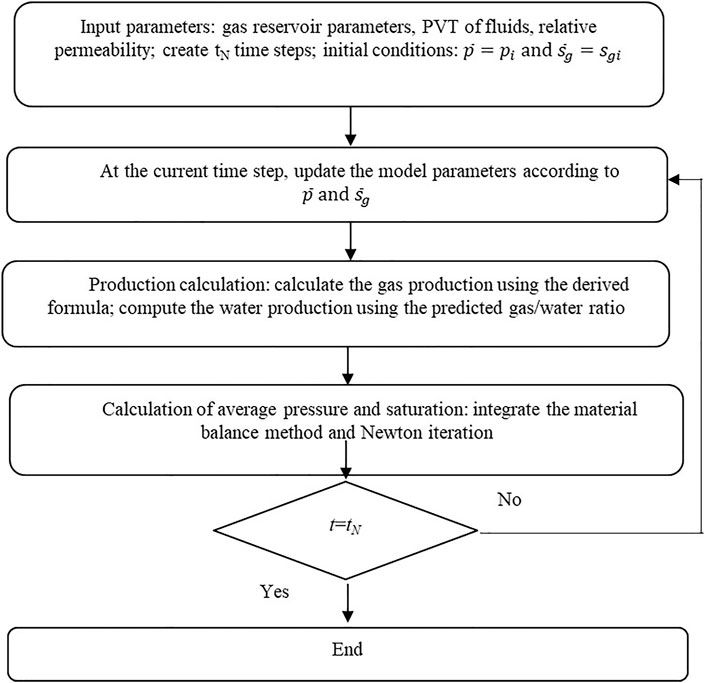
FIGURE 4. Productivity prediction workflow based on the semi-analytic model for two-phase flow of gas and water.

Analysis of Factors Affecting Productivity of Carbonate Gas Reservoirs

The value of the permeability modulus γ represents how much the production performance of gas wells is affected by stress sensitivity (Figure 5). A higher permeability modulus indicates higher stress sensitivity of the reservoir, which is associated with lowering down of the type curve and faster production decline. The dual-medium carbonate reservoir is found with extensive development of fractures. During the recovery process, the increase of the effective overburden pressure results in deformation of the rock framework and decline of permeability, accelerating production decline. Moreover, with the elapsed time of recovery, the effect of stress sensitivity grows. Hence, the recovery of carbonate gas reservoirs shall adopt a proper recovery rate and drawdown pressure to minimize the impact of stress sensitivity and improve recovery performance.

FIGURE 5

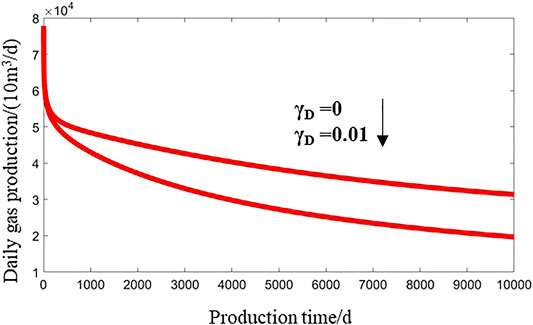
FIGURE 5. The effect of stress sensitivity on the productivity of gas wells with the two-phase flow of gas and water.

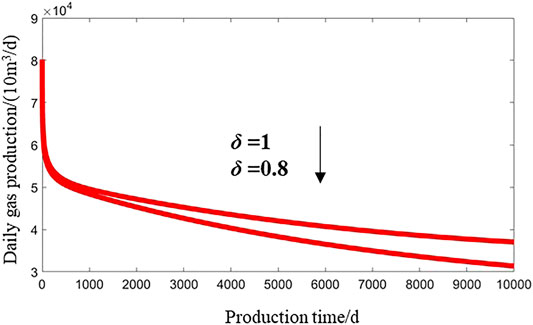
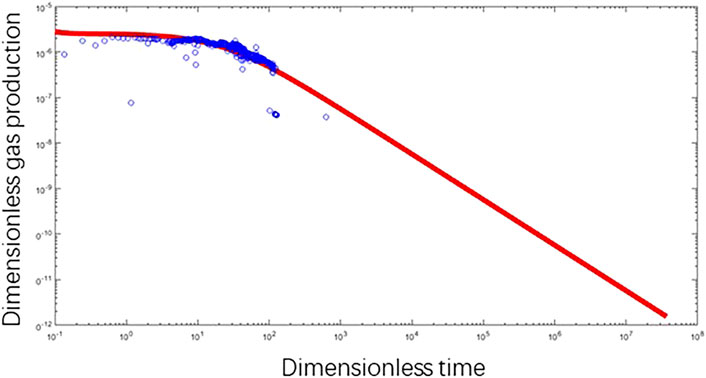
The high-speed non-Darcy coefficient δ represents the effect of the high-speed non-Darcy flow on the type curve (Figure 6). With a smaller value of the high-speed non-Darcy coefficient, the non-Darcy effect grows, the type curve is lowered, and the initial production is reduced. Therefore, the productivity evaluation of the dual-medium carbonate gas reservoir cannot neglect the non-Darcy effect.

FIGURE 6

FIGURE 6. The effect of non-Darcy flow on gas wells with two-phase flow of gas and water.

Case Study

Here the L carbonate gas reservoir of the A gas field is taken as an example and the developed two-phase flow model of gas and water based on the dual-medium is applied to productivity prediction of the production well, Well M2. This well presents an initial gas production of 17 × 104 m³/d during the production testing, and after 1 month of production, the production is raised to 28 × 104 m³/d. After 3 years of production, the daily gas production of this well is 9.6 × 104 m³/d, the daily water is 9.8 m³/d, and the water/gas ratio is 0.98 m³/10⁴m³. The basic parameters of this well are summarized in Table 1.

TABLE 1

TABLE 1. Basic parameters of Well M2.

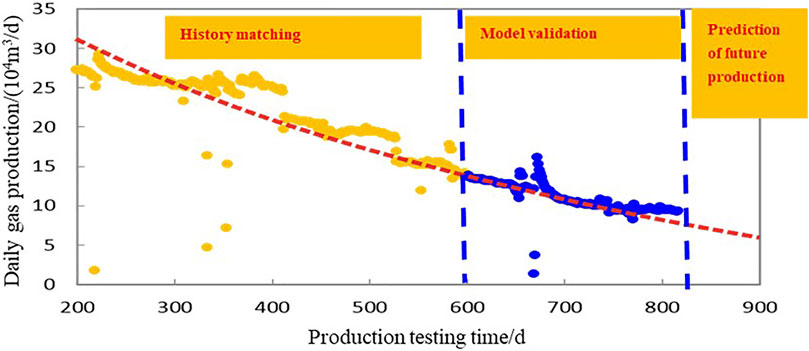
The developed productivity evaluation model is used for fitting the interpretation of the reservoir drilled by this well, based on its production performance. The fitting interpretation results are concluded in Figure 7; Table 2.

FIGURE 7

FIGURE 7. The fitting interpretation curve of production decline of Well M2.

TABLE 2

TABLE 2. Fitting interpretation results for production decline of Well M2.

The future production of Well M2 at a constant flowing bottomhole pressure is forecasted, based on the model parameters interpreted from its actual production performance. The results are summarized in Figure 8; Table 3.

FIGURE 8

FIGURE 8. Production prediction of Well M2.

TABLE 3

TABLE 3. Production prediction of Well M2.

The error analysis of the predicted production shows that on Day 800, the predicted daily production of Well M2 is 9.47 × 104 m³/d, while the actual production rate is 9.61 × 104 m³/d. The error of the calculation is 1.5%, which is within the allowed error range and thus means that the productivity prediction results meet the engineering criterion.

Conclusion

1) The dual-medium carbonate gas reservoir is grealtly different from the conventional gas reservoir, in terms of the storage space and fluid flow characteristics. Therefore, the flow model shall consider both the stress sensitivity and high-speed non-Darcy flow effect.

2) The stress sensitivity and non-Darcy effect coefficients are introduced into the flow model of the dual-medium gas reservoir, which results in the nonlinearity of the flow equations. Then, the perturbation theory is applied to eliminate the nonlinearity and the flow equations are transformed into the Laplace space for solutions. The solution of fluid production is obtained via the Stehfest numerical inversion, and the semi-analytical solutions of the model are calculated via the flowing material balance method and Newton iteration.

3) The analysis of the production decline type curve of the dual-medium carbonate gas reservoir shows that the dual-medium gas reservoir with higher stress sensitivity is associated with accelerated production decline; that with a more intensive non-Darcy flow effect is found with lower initial production.

4) The developed model is used for the case study of an actual production well. The analysis results show that the error of the predicted production of the analyzed well is within the engineering-permissible range, which validates the high applicability and practicability of our model.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

LK, WG, XZ, and YL contributed to design of the study and method establishment, wrote the first draft of the manuscript. JG, ZS, ML, and YS wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The work was funded by R&D Department of Petrochina (No. 2021DJ2 005). The APC was funded by R&D Department of Petrochina (No. 2021DJ2 005). The funders had no role in the design, execution, interpretation, or writing of the study.

Conflict of Interest

Author ML was employed by Beijing Gas Group Co., Ltd. Author YS was employed by PetroChina Southwest Oil and Gasfield Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Brown, M. L., Ozkan, E., Raghavan, R. S., and Kazemi, H. (2009). Practical Solutions for Pressure-Transient Responses of Fractured Horizontal wells in Unconventional Shale Reservoirs. SPE Reservoir Eval. Eng. 14 (6), 663–676. doi:10.1016/s1876-3804(17)30031-9

CrossRef Full Text | Google Scholar

Chen, C. (2016). Research on Productivity of Fractured Horizontal wells with Steady-State Two-phase Flow of Gas and Water in the YD Gas Reservoir. Chengdu: Southwest Petroleum University.

Google Scholar

Chen, Y.-F., Zhou, J.-Q., Hu, S.-H., Hu, R., and Zhou, C.-B. (2015). Evaluation of Forchheimer Equation Coefficients for Non-darcy Flow in Deformable Rough-Walled Fractures. J. Hydrol. 529, 993–1006. doi:10.1016/j.jhydrol.2015.09.021

CrossRef Full Text | Google Scholar

Cheng, S., and Chen, M. (1998). Numerical Simulation of Two-Dimensional Two-phase Non-Darcy Slow Flow. Pet. Exploration Develop. 25 (1), 41–43.

Google Scholar

Deng, Q., Tang, H., Lv, Z., Wang, Q., Lv, D., and Liu, Q. (2011). The Study of Productivity Forecast in Water-Producing Gas Well. Pet. Geology. Eng. 25 (3), 68–69. doi:10.3969/j.issn.1673-8217.2011.03.020

CrossRef Full Text | Google Scholar

Esmaeili, S., Sarma, H., Harding, T., and Maini, B. (2020). Effect of Temperature on Bitumen/water Relative Permeability in Oil Sands. Energy Fuels 34 (10), 12314–12329. doi:10.1021/acs.energyfuels.0c02180

CrossRef Full Text | Google Scholar

Fan, H., Li, X., Dou, T., Chen, J., and Yuan, F. (2011). Study on the Flowing Performance of Gas Wells in Dual-Porosity Deformable Fractal Reservoirs. J. Southwest Pet. Univ. (Science Technol. Edition) 33 (2), 115–120. doi:10.3863/j.issn.1674-5086.2011.02.019

CrossRef Full Text | Google Scholar

Fang, J., Guo, P., Xiao, X., Du, J., Dong, C., Xiong, Y., et al. (2015). Gas-Water Relative Permeability Measurement of High Temperature and High Pressure Tight Gas Reservoirs. Pet. Exploration Develop. 42 (1), 84–87. doi:10.1016/s1876-3804(15)60010-6

CrossRef Full Text | Google Scholar

Huang, B., Ran, X., and Li, X. (2004). Analysis Method of Gas Reservoir Engineering. Beijing: Petroleum industry Press, 87–90.

Google Scholar

Javadpour, F., Singh, H., Rabbani, A., Babaei, M., and Enayati, S. (2021). Gas Flow Models of Shale: A Review. Energy & Fuels 35 (4), 2999–3010. doi:10.1021/acs.energyfuels.0c04381

CrossRef Full Text | Google Scholar

Jia, A. L., Yan, H. J., Guo, J. L., He, D. B., Cheng, L. H., and Jia, C. Y. (2013). Development Characteristics for Different Types of Carbonate Gas Reservoirs. Acta Petrolei Sinica 34 (5), 914–923. doi:10.7623/syxb201305012

CrossRef Full Text | Google Scholar

Li, D., Kang, Y., and You, L. (2011). “Experimental Study on Permeability Stress Sensitivity of Carbonate Rocks,” in The Chinese Conference on Theoretical and Applied Mechanics 2011 in Memorial of Tsien Hsue-Shen’s 100th Anniversary, Harbin, China, August 22–24, 2011.

Google Scholar

Li, X., Guo, Z., Wan, Y., Liu, X., Zhang, M., Xie, W., et al. (2017). Geological Characteristics and Development Strategies for Cambrian Longwangmiao Formation Gas Reservoir in Anyue Gas Field, Sichuan Basin, SW China. Pet. Exploration Develop. 44 (3), 398–406. doi:10.1016/s1876-3804(17)30049-6

CrossRef Full Text | Google Scholar

Liao, Z. (2016). Research on the Water Production Pattern and Production Performance of Water Flooding in Fractured Gas Reservoirs. Chengdu: Southwest Petroleum University.

Google Scholar

Lu, Z. (2010). Fluid Flow Law in Fractured Vuggy media. Qingdao: China University of Petroleum.

Google Scholar

Luo, A., Li, Y., Wu, L., Peng, Y., and Tang, W. (2021). Fractured Horizontal Well Productivity Model for Shale Gas Considering Stress Sensitivity, Hydraulic Fracture Azimuth, and Interference between Fractures. Nat. Gas Industry B 8 (3), 278–286. doi:10.1016/j.ngib.2021.04.008

CrossRef Full Text | Google Scholar

Peng, X., Lu, Y., Liu, X., Duan, C., Li, Z., Liu, S., et al. (2015). Rock Stress Sensitivity and its Influence on Productivity of Overpressured Gas Reservoir: A Case Study in Yinggehai Basin, China. Int. J. Oil Gas Coal Eng. 3 (3), 33. doi:10.11648/j.ogce.20150303.11

CrossRef Full Text | Google Scholar

Petrosa, O. A. (1986). “Pressure Transient Response in Stress-Sensitive Formation,” in SPE California Regional Meeting, SPE15115, Oakland, CA, April 2–4, 1986. doi:10.2118/15115-ms

CrossRef Full Text | Google Scholar

Xu, J. L., Cheng, X. B., Pan, X. H., and Fei, H. Y. (2007). Fracture and Cavity Prediction Method in Carbonate Reservoirs and its Application. Nat. Gas Industry 11 (11), 56–63. doi:10.3321/j.issn:1000-0976.2007.11.011

CrossRef Full Text | Google Scholar

Zhang, F., Wu, Y., and Wang, X. (2016). Effect of High-Speed Non-Darcy Flow on Productivity for Gas-Well with Producing Water. Petrochemical Industry Appl. 35 (1), 34–36. doi:10.3969/j.issn.1673-5285.2016.01.010

CrossRef Full Text | Google Scholar

Zhang, H., Wang, J., Jin, S., Chen, H., and Wang, L. (2017a). Rational Production of Water Producing Gas wells in the South Area of Sulige Gasfield, Ordos Basin. Nat. Gas Exploration Develop. 40 (3), 72–77. doi:10.12055/gaskk.issn.1673-3177.2017.03.011

CrossRef Full Text | Google Scholar

Zhang, H., Wang, L., Wang, X., Zhou, W., Zeng, X., Liu, C., et al. (2017b). Productivity Analysis Method for Gas-Water wells in Abnormal Overpressure Gas Reservoirs. Pet. Exploration Develop. 44 (2), 258–262. doi:10.1016/s1876-3804(17)30031-9

CrossRef Full Text | Google Scholar

Zhang, R., Ning, Z., Zhang, H., and Xie, Q. (2016). New Insights and Discussions on Stress Sensitivity of Fractured Tight Reservoir. Nat. Gas Geosci. 27 (5), 918–923. doi:10.11764/j.issn.1672-1926.2016.05.0918

CrossRef Full Text | Google Scholar

Zhang, W., Meng, Z., and Li, H. (2017). Study on Development Performance Pattern Prediction of Gas Reservoirs with Abnormal Overpressure. China Pet. Chem. Stand. Qual. 37 (17), 94–95. doi:10.3969/j.issn.1673-4076.2017.17.045

CrossRef Full Text | Google Scholar

Zhao, L., Chen, Y., Ning, Z., Wu, X., Liu, L., and Chen, X. (2013). Stress Sensitive Experiments for Abnormal Overpressure Carbonate Reservoirs: A Case from the Kenkiyak Fractured-Porous Oil Field in the Littoral Caspian Basin. Pet. Exploration Develop. 40 (2), 208–215. doi:10.1016/s1876-3804(13)60024-5

CrossRef Full Text | Google Scholar