- PetroChina Research Institute of Petroleum Exploration and Development, Beijing, China
The flow of shale gas in nano scale pores is affected by multiple physical phenomena. At present, the influence of multiple physical phenomena on the transport mechanism of gas in nano-pores is not clear, and a unified mathematical model to describe these multiple physical phenomena is still not available. In this paper, an apparent permeability model was established, after comprehensively considering three gas flow mechanisms in shale matrix organic pores, including viscous slippage Flow, Knudsen diffusion and surface diffusion of adsorbed gas, and real gas effect and confinement effect, and at the same time considering the effects of matrix shrinkage, stress sensitivity, adsorption layer thinning, confinement effect and real gas effect on pore radius. The contribution of three flow mechanisms to apparent permeability under different pore pressure and pore size is analyzed. The effects of adsorption layer thinning, stress sensitivity, matrix shrinkage effect, real gas effect and confinement effect on apparent permeability were also systematically analyzed. The results show that the apparent permeability first decreases and then increases with the decrease of pore pressure. With the decrease of pore pressure, matrix shrinkage, Knudsen diffusion, slippage effect and surface diffusion effect increase gradually. These four effects will not only make up for the permeability loss caused by stress sensitivity and adsorption layer, but also significantly increase the permeability. With the decrease of pore radius, the contribution of slippage flow decreases, and the contributions of Knudsen diffusion and surface diffusion increase gradually. With the decrease of pore radius and the increase of pore pressure, the influence of real gas effect and confinement effect on permeability increases significantly. Considering real gas and confinement effect, the apparent permeability of pores with radius of 5 nm is increased by 13.2%, and the apparent permeability of pores with radius of 1 nm is increased by 61.3%. The apparent permeability model obtained in this paper can provide a theoretical basis for more accurate measurement of permeability of shale matrix and accurate evaluation of productivity of shale gas horizontal wells.
1 Introduction
Shale gas is an unconventional natural gas that is mainly stored in shale as adsorption gas and free gas. Scanning electron microscopy (SEM) shows the development of numerous connected nanoscale pores in shale matrix. The mechanism of gas flow in nanoscale pores differs significantly from that in conventional reservoirs, and the classical Darcy’s law cannot be used to describe the flow pattern of shale gas. Therefore, elucidating the flow mechanism of shale gas in nanoscale pores and establishing a mathematical model to characterize the flow behavior of shale gas for numerical simulation and production prediction of shale gas reservoirs has considerable theoretical significance.
The special occurrence mechanism of shale gas and nano scale gas transmission space lead to the complexity of flow behavior. Currently, many scholars have used the apparent permeability as an important parameter to comprehensively characterize this complex gas flow behavior. Sakhaee-Pour and Bryant (2012) analyzed the effect of the methane adsorption layer and gas slip at the pore wall on the flow behavior of shale gas to determine the permeability of shale reservoirs. Swami et al. (2012) used an apparent permeability model for various nanopores of shale matrix to analyze the effect of the pore radius and formation pressure on the apparent permeability and Darcy permeability ratio. Song et al. (2016) developed a model of the apparent permeability of inorganic and organic matter considering stress-sensitivity effects. Cao et al. (2017) proposed a three-dimensional coupled model for inorganic and organic matter to calculate the permeability of shale. Singh et al. (2014) derived an analytical model for the apparent permeability that does not require empirical parameters to characterize the effects of the pore size, pore geometry, temperature, gas properties and average reservoir pressure on the apparent permeability. Akkutlu and Fathi, (2012) developed an apparent permeability model considering the stress sensitivity, mainly considering surface diffusion and Knudsen diffusion in the flow mechanism. Wang et al. (2015) developed an apparent permeability model considering stress-sensitivity effects and the pore gas adsorption layer. The evolution of the apparent permeability during production and the effects of the stress sensitivity and adsorption layer on the permeability were determined. Wu et al. (2016a) developed a model for the apparent permeability considering slip flow, Knudsen diffusion, surface diffusion, stress sensitivity and the adsorption layer. A bulk phase gas transport model was formulated by superposing the two transport mechanisms of slip flow and Knudsen diffusion with a weighting factor. Zhao et al. (2016) established mass flux equations for four shale gas flow regimes based on the Knudsen number and derived a unified apparent permeability calculation model for the different flow regimes. Jia et al. (2018) considered the comprehensive effects of effective stress increase and gas desorption on pore size, established an apparent permeability model considering slippage, Knudsen diffusion and surface diffusion and analyzed the permeability changes during shale gas production. Huang et al. (2018) considered the dense gas effect and introduced a surface diffusion correction factor to study the effect of the adsorption layer on the apparent permeability under different mass transfer mechanisms (slip flow, surface diffusion and Knudsen diffusion). Sheng et al. (2018) analyzed the effect of the microscale compressibility on the apparent permeability and porosity. Geng et al. (2016) proposed a viscous-diffusive model to simulate the transport of shale gas in nanopores. The extended Navier-Stokes equation was used to describe multiple flow mechanisms, including viscous flow, slip and transition flow. Sun et al. (2019) proposed a model for gas transport in elliptical nanotubes based on a weighted superposition of continuous flow and Knudsen diffusion. The contribution of Knudsen diffusion contribution to the apparent permeability was found to increase with the aspect ratio. Tian et al. (2018) proposed a model for shale gas transport in circular nanotubes with weighted contributions from slip flow, bulk phase diffusion and Knudsen diffusion. Yin et al. (2017) proposed an analytical model for gas transport in nanopores considering real gas effects and surface diffusion. Wang et al. (2019) derived a model for the apparent shale gas permeability based on fractal theory, considering gas slip flow, Knudsen diffusion and surface diffusion transport mechanisms. Chai et al. (2019) divided the gas flow in a circular tube into viscous, Knudsen diffusion and surface diffusion zones. Coefficients were introduced for the viscous slip flow and Knudsen diffusion contributions to establish a unified apparent gas permeability model. Shi et al. (2013) studied pore size and water phase distribution in shale matrix. Combined with the mechanism of gas transportation, a new diffusion and slip flow model is proposed. Zhang et al. (2017) established a gas-water two-phase permeability model. The model considers not only the gas slippage and water film thickness in the whole Knudsen diffusion range, but also the real gas effect and stress sensitivity. Zhang T. et al. (2018) proposed an apparent permeability model for shale considering the initial water content saturation distribution. Surface diffusion and Knudsen diffusion were found to be the key factors affecting the permeability. Nanopores smaller than 2 nm in organic matter were found to exhibit a higher permeability than macro-pores at pressures below 6 MPa. Wang et al. (2018) used a logarithmic normal distribution function to characterize the pore size distribution and derived a gas transport model for organic and inorganic matter. The effects of a real gas, the water film thickness and the stress sensitivity on the gas transport were considered in the model. The permeability was found to increase with the organic carbon content at pressures above 5 MPa. Sun et al. (2018a) modeled the apparent permeability of circular organic nanopores and inorganic matrix slit pores, considering the water distribution characteristics. The effects of the bulk phase gas slip flow, stress sensitivity and real gas effects on the apparent permeability were considered. In addition, the effect of the water film thickness on the apparent permeability was considered for the inorganic pore. Although water saturation was considered in the model, matrix shrinkage was neglected. Sheng et al. (2019) considered the effect of the adsorption layer, stress sensitivity and desorption-induced shrinkage on the pore radius and proposed an apparent permeability model for organic pore. The matrix porosity and apparent permeability were found to decrease under the stress-sensitivity effect for pore pressures above 20 MPa, where matrix shrinkage and adsorption layer thinning compensated for the reduction in the permeability after the pore pressure decreased to 20 MPa. Zhang L. et al. (2020) developed a unified apparent permeability model for a shale matrix considering gas transport behavior in organic and inorganic pores. Zhang Q. et al. (2020) established a unified apparent permeability model for inorganic and organic matter by considering the effects of the adsorption layer, matrix shrinkage and stress sensitivity on the pore radius. The main innovation of this model was to consider the effect of surface diffusion on slip flow, whereas the effect of the gas flow patterns over the full range of Knudsen numbers was neglected.
A literature search shows that three flow mechanisms have mainly been considered in apparent permeability models of shale matrix: surface diffusion (Wasaki and Akkutlu, 2015; Wang and Marongiu-Porcu, 2015; Wang et al., 2015; Wu et al., 2016b; Wu et al. 2016c; Wu et al.2016d; Wu et al. 2017; Sun et al., 2017; Zhang L. et al., 2018; Jia et al., 2019), Knudsen diffusion and slip flow (Sakhaee-Pour and Bryant, 2012; Akkutlu and Fathi, 2012; Xiong et al., 2012; Sheng et al., 2015; Zhang et al., 2015; Song et al., 2016; Li et al., 2019). Stress sensitivity (Dong et al., 2010; Pang et al., 2017; Cui et al., 2018a; Cui et al., 2018b), the water film thickness (Li et al., 2016; Sun et al., 2017; Li et al., 2018; Peng et al., 2018) and adsorption layer thinning (Li et al., 2020) are the three main factors affecting the pore radius. A few scholars believe that the matrix shrinkage effect (An et al., 2017; Sheng et al., 2019) has a certain impact on the porosity and apparent permeability of shale matrix, but the influence degree of matrix shrinkage is not clear enough. The factors considered in these models are not comprehensive enough. In this paper, a apparent permeability model is established, after comprehensively considering three gas flow mechanisms in shale matrix organic pores, including viscous slippage flow, Knudsen diffusion and surface diffusion of adsorbed gas, and real gas effect and confinement effect, and at the same time considering the effects of matrix shrinkage, stress sensitivity, adsorption layer thinning, confinement effect and real gas effect on pore radius. The contribution of three flow mechanisms to apparent permeability under different pore pressure and pore size is analyzed. The effects of adsorption layer thinning, stress sensitivity, matrix shrinkage effect, real gas effect and confinement effect on apparent permeability are also systematically analyzed.
2 Model Description and Formulation
2.1 Model Description
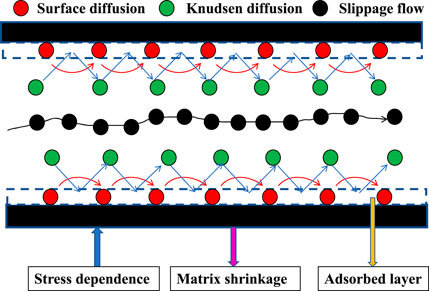
Gas transport in organic pores includes slip flow, Knudsen diffusion, and surface diffusion of the adsorption gas. The adsorption gas occupies a portion of the transport space of pores, which reduces the effective pore radius for gas transport. During production, adsorption layer thinning and matrix shrinkage expand the organic matrix pore radius because the adsorption gas desorbs from the matrix pore walls, whereas stress sensitivity decreases the pore radius. The pore radius and porosity of the shale organic matrix are in a dynamic change state under this triple effect (the stress sensitivity, adsorption layer thinning and matrix shrinkage), as shown in Figure 1. Considering the effects of dynamic pore radius, real gas effect and confinement effect on gas transport, in the next part, we will establish the mathematical models of slippage flow, Knudsen diffusion and surface diffusion respectively.
2.2 Mathematical Model
2.2.1 Real Gas Effect and Confinement Effect
Shale gas is dense under high reservoir pressures. Intermolecular forces and the gas molecular size affect the gas transport capacity. This effect of real gas on the gas transport can be described by using a dimensionless gas deviation factor Z, the gas viscosity and the mean free path of the gas molecules (Sun et al., 2018a):
where
and P denotes the reservoir pore pressure, MPa; T denotes the reservoir temperature, K; Pr is the dimensionless contrast pressure; Tr is the dimensionless gas contrast temperature; and Pcb and Tcb denote the critical pressure (MPa) and temperature (K) of the bulk phase gas, respectively.
The force between gas molecules and pore wall will have a certain impact on the gas transport mechanism and ability. This effect is called confinement effect. Due to the confinement effect, the critical pressure and temperature of gas will change. The critical parameters of the gas in the nanopores are related to the pore size as follows (Sun et al., 2018b):
where D denotes the pore diameter, nm; σ denotes the Lennard-Jones parameter, which is taken as 0.28 nm in this study; da denotes the thickness of the adsorption layer, nm; and Tcc and Pcc denote the critical gas temperature (K) and pressure (MPa) considering the confinement effect, respectively.
The real gas viscosity μg, mPas, varies with the pressure and temperature as follows (Zhang L. et al., 2020):
The coefficients in Equation 6 are shown in Table 1:
where ρg denotes the gas density, kg/m3; Mg denotes the gas molecular mass, kg/mol; and R denotes the universal gas constant, Pa/mol/K.
The mean free path λr, m of real gas molecules is defined as
The true Knudsen number Knr (dimensionless) of the real gas in the nanopores is defined as
where r denotes the pore radius, nm.
2.2.2 Variation in the Pore Radius of an Organic Matrix
1) Effect of the Stress Sensitivity on the Pore Radius
During shale gas production, the intrinsic permeability, porosity and nanopore radius of shale decrease as the effective stress increases, and the gas flow capacity decreases accordingly. Dong et al. (2010) used the results of shale core experiments to propose a power law for the variation in the shale porosity and permeability with the pressure:
where Po denotes the atmospheric pressure, MPa; and Pe denotes the overlying effective stress, MPa, which is defined as
where σc denotes the overlying stress, MPa; K denotes the intrinsic permeability under the effective stress, μm2; Ko denotes the intrinsic permeability under atmospheric pressure, μm2;
The organic pore radius under effective stress, rs, nm is related to K and
where τ denotes the dimensionless pore tortuosity.
Equations 11, 12, 14 can be used to express rs as follows:
where ro denotes the pore radius at atmospheric pressure, nm.
2) Effect of Gas Desorption on the Pore Radius
The large quantity of adsorption gas on the organic pore wall reduces the pore radius. However, gas desorption thins the adsorption layer and thus increases the pore radius. Therefore, during the production of shale gas wells, the effects of both the adsorption layer thinning and the stress sensitivity on the pore radius need to be considered.
In the equation above, resd denotes the pore radius, nm considering both stress sensitivity and the adsorption layer thinning; dm denotes the methane molecular diameter, 0.4 nm; and θ denotes the dimensionless gas coverage, which is defined considering the real gas effect as:
where PL denotes the Langmuir pressure, MPa.
3) Effect of matrix Shrinkage on the Pore Radius
Most gas has been shown to be stored as adsorbed state in the organic kerogen. During depressurization production, the pore pressure decreases, and the desorption of adsorption gas leads to the shrinkage of shale organic matrix. The dimensionless matrix volume strain εm caused by gas desorption can be expressed as
where εL denotes the dimensionless Langmuir strain; and pin denotes the initial pore pressure, MPa. The change in the matrix volume from the shrinkage of the organic matrix ∆Vm, m3, can be expressed as
The initial dimensionless matrix porosity φint and pore volume Vp_in are defined as
where np denotes the dimensionless number of pores; lp denotes the pore length, m; and rin denotes the initial pore radius, m.
The initial volume of the organic substrate is obtained by substituting Equation 21 into Equation 20:
Shrinkage of the organic matrix shrinkage increases the nanopore radius. The matrix pore volume Vp considering the matrix shrinkage can be expressed as
Substituting Equations 21, 19 into Equation 23 yields
where rds denotes the pore radius considering the shrinkage of the organic matrix, nm:
4) Pore Radius under the Triple Effect
During the production of shale gas wells, an increase in the effective stress produces a decrease in pore radius, whereas matrix shrinkage increases the pore radius. In addition, adsorption layer thinning at the pore wall expands the pore radius. Thus, the dynamically changing nanopore radius of the shale organic matrix ref, nm, under these three effects is expressed as:
2.2.3 Viscous Slip Flow
Knr is an important indicator of the gas flow state. For 10–3 < Knr < 10–1, the gas in the nanopores is in slip flow. Using a slip flow correction factor for the viscous flow yields the real gas slip flow mass flux Jvs, kg/(m2·s) (Wu et al., 2017):
where
and αo is the dimensionless coefficient for the rarefaction effect at infinite Knr; α1 and β are dimensionless fitting constants; αr is the dimensionless ideal gas rarefaction effect coefficient; and b is the dimensionless gas slip constant.
2.2.4 Knudsen Diffusion
For Knr > 10, Knudsen diffusion is the main contribution to the gas flow in the nanopores. The real gas mass flux under Knudsen diffusion Jkn, kg/(m2·s) is obtained by considering the influence of the pore wall roughness on the gas flow:
where δ denotes the dimensionless ratio of the molecular diameter to the local pore diameter; Df denotes the dimensionless fractal dimension of the pore wall; and Cg is the gas compression factor, 1/MPa.
2.2.5 Surface Diffusion of Adsorption Gas
There is a large concentration gradient of adsorption gas in organic matter over a large specific surface area. In addition to desorption, surface diffusion will occur in shale organic matrix under concentration gradient. The surface diffusion mass flux Jsa, kg/(m2·s), is expressed as
where ρs denotes the shale matrix density, kg/m3; VL denotes the Langmuir volume, m3/kg; Vstd denotes the gas molar volume in the standard state, m3/mol; and Ds denotes the surface diffusion coefficient (m2/s) considering the effect of coverage on surface diffusion and is expressed as (Huang et al., 2018):
where
and
2.2.6 Mass Flow Equation for Gas in Organic Matrix
The gas transport mechanism in the pores of the shale organic matrix consists of the slip flow of free gas and Knudsen and surface diffusion of adsorption gas. The total mass flow is obtained by linear superposition, in which the slippage flow and Knudsen diffusion of bulk free gas are weighted by contribution coefficient. The total mass flow in the organic matrix pores is expressed as:
Substituting Equations 25, 27, 29 into Equation 31 yields:
where φmt denotes the dimensionless total matrix porosity under the effective stress. The dimensionless coefficient for the slip flow contribution fs is given as the ratio of the collision frequency between molecules to the total collision frequency, and the dimensionless coefficient for the Knudsen diffusion contribution fk is given as the ratio of the collision frequency of molecules with the pore wall to the total collision frequency:
2.2.7 Apparent Permeability of the Shale Organic Matrix
The definition of the apparent permeability can be used to relate the total mass flow to the apparent permeability of the organic matric to gas Kmap, expressed in the form of Darcy’s equation as:
Combining Equations 39, 44 yields Kmap:
3 Results and Discussion
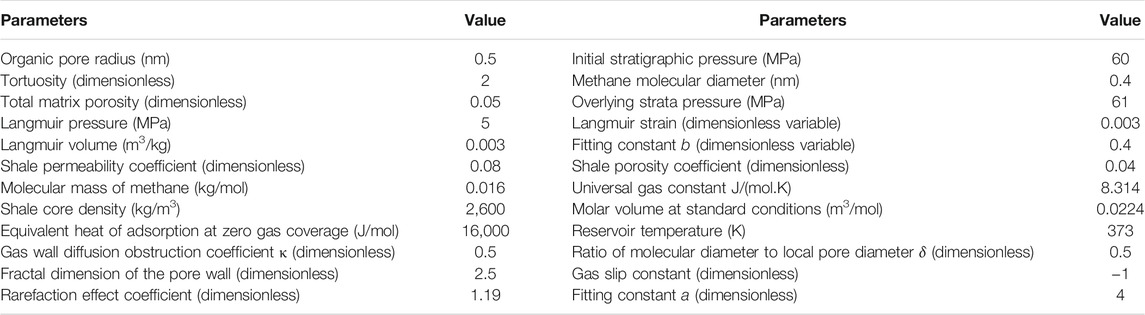
Basic parameters presented in Table 2 were used to analyze how the pore pressure, pore radius, stress sensitivity, adsorption layer and matrix shrinkage affect the apparent permeability of the shale organic matrix.
Figure 2 shows the ratio of the apparent permeability to the intrinsic permeability for different pore radii. This ratio increases as the pore pressure decreases, especially for pressures below 10 MPa. The ratio decreases as the pore radius increases. The apparent permeability differs from the intrinsic permeability in this study in accounting for three flow mechanisms: gas slip flow, Knudsen diffusion and surface diffusion. The variation in the permeability ratio with the pore pressure in Figure 2 indicates that the pore pressure and especially the pore radius are the key factors affecting the gas flow mechanism.
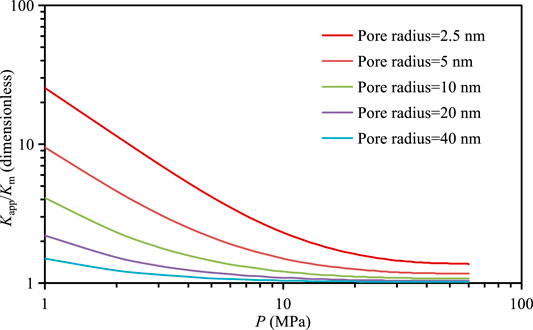
FIGURE 2. Ratio of the apparent permeability to the intrinsic permeability for different pore radii.
Figure 3A and Figure 3B show the contribution of viscous slippage flow, Knudsen diffusion and surface diffusion to apparent permeability with the change of pore radius under low pressure (P = 3 Mpa) and high pressure (p = 30 MPa), respectively. With the decrease of pore radius, the contribution of viscous slippage flow gradually decreases, while the contributions of surface diffusion and Knudsen diffusion gradually increase. When the pore radius is less than 10 nm, this phenomenon becomes more significant. Under high pressure, when the pore radius is greater than 2 nm, the contribution of Knudsen diffusion and surface diffusion to the apparent permeability is almost negligible ( <5%). Under low pressure, when the pore radius is greater than 20 nm, the contribution of Knudsen diffusion and surface diffusion to the apparent permeability can be ignored ( <5%). Under both low pressure and high pressure, the slippage coefficient decreases to nearly 1 with the increase of pore radius, which indicates that the bulk fluid gradually changes from slippage to viscous flow with the increase of pore radius. Pore pressure and pore size are the key factors affecting surface diffusion, slippage effect and Knudsen diffusion. The smaller the pore pressure and pore radius, the greater the contribution of surface diffusion and Knudsen diffusion to the apparent permeability.
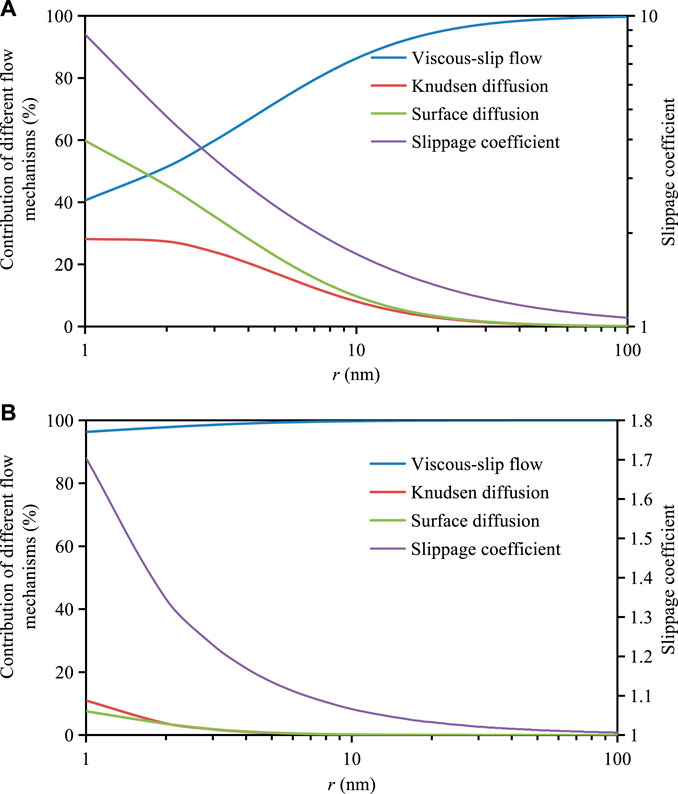
FIGURE 3. (A) Percentage contribution of different flow mechanisms to the apparent permeability (p = 3 MPa). (B) Percentage contribution of different flow mechanisms to the apparent permeability (p = 30 MPa).
The deviation of apparent permeability Ψ, % is defined as:
where Kmat and Kma denote the apparent permeability of shale matrix with and without the triple flow mechanisms, nD, respectively.
Figure 4 shows the variation of apparent permeability deviation with pore pressure under different pore radius with or without considering the influence of triple flow mechanism. The average deviation of apparent permeability in two cases is given in Table 3. When the pore radius is 2.5, 5, 10, and 20 nm, the corresponding apparent permeability decreases by 59.4, 57.6, 56.4 and 55.7% respectively. Generally speaking, with the decrease of pore pressure, the permeability deviation first decreases and then increases. When the pore pressure is greater than 8Mpa, the permeability deviation decreases with the increase of pore radius; When the pore pressure is less than 8Mpa, the permeability deviation increases with the increase of pore radius. This is because the smaller the pore radius, the more significant the influence of the adsorption layer on the apparent permeability. With the decrease of pore pressure, the nano scale effect will increase significantly, so as to improve the apparent permeability and weaken the negative impact of the triple flow mechanisms on the permeability.
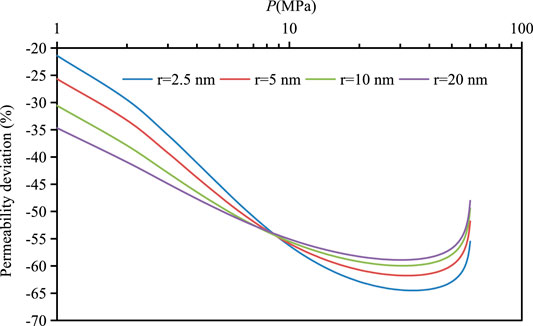
FIGURE 4. Difference in apparent permeability deviation with and without the triple flow mechanisms for different pore radii.

TABLE 3. Average apparent permeability deviation considering the triple flow mechanisms for different pore radius.
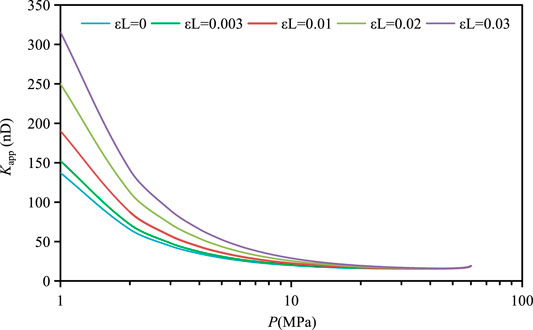
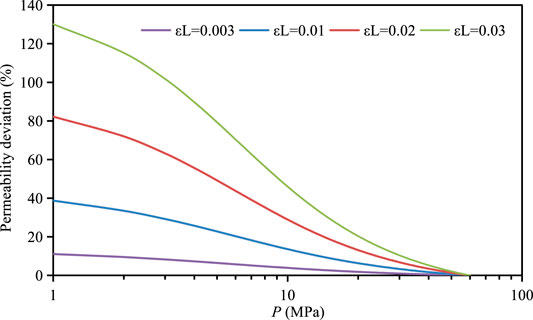
Figure 5 and Figure 6 show the effects of Langmuir strain (matrix shrinkage effect)on apparent permeability and permeability deviation respectively. The apparent permeability increases with the increase of Langmuir strain. As shown in Table 4, when the Langmuir strain is 0.003, 0.01, 0.02 and 0.03, the permeability considering matrix shrinkage effect increases by 1.95, 6.76, 14.3, and 22.6% respectively. When the pore pressure drops to 10MPa, the effect of matrix shrinkage on permeability becomes more obvious with the decrease of pore pressure and the increase of Langmuir strain.
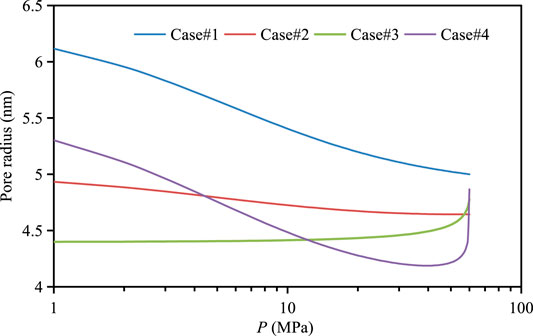
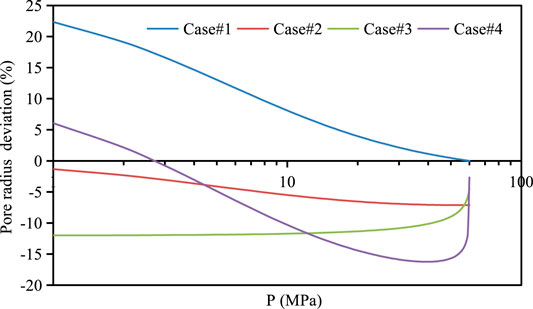
Figure 7 and Figure 8 show the effect of different mechanisms on pore radius in organic pores (shown in Table 5). Table 6 shows the percentage of influence of different mechanisms on pore radius. According to the results in the table, it can be seen that the matrix shrinkage effect increases the pore radius by 4% on average, and the existence of stress sensitive and adsorption layer reduces the pore radius by 10.3 and 6.4% on average. If the effects of stress sensitivity, adsorption layer thinning and matrix shrinkage are considered at the same time, the average pore radius decreases by 13%, and the maximum pore radius decreases by 17% to about 6%. This shows that with the decrease of pore pressure, the matrix shrinkage effect and the thinning of adsorption layer will make up for the loss of pore radius caused by stress sensitivity and increase the pore radius.
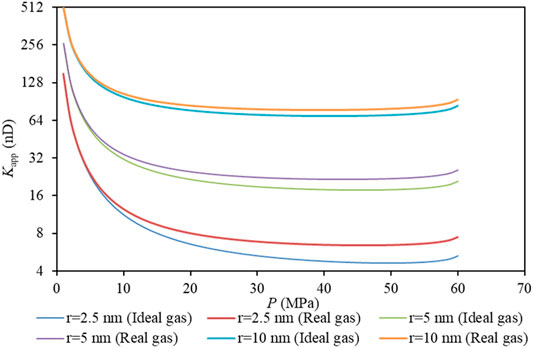
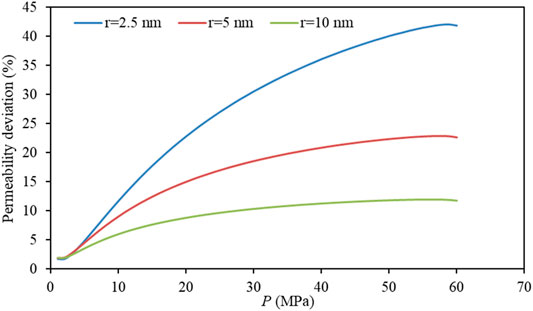
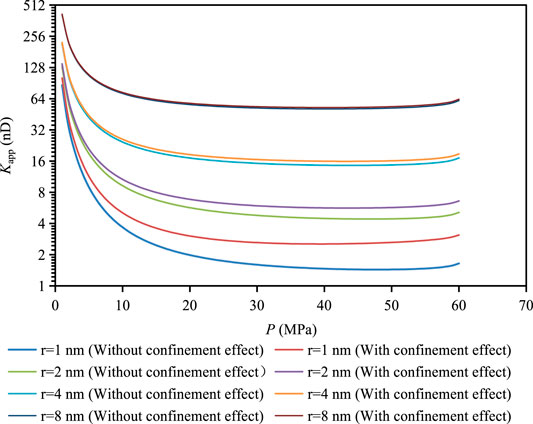
Figure 9 shows the variation of apparent permeability of ideal gas and real gas with pore pressure under different pore radius. Table 7 shows the permeability deviation of ideal gas and real gas under different pore radius and pore pressure. It can be found from the figure that the apparent permeability of the real gas is higher than that of the ideal gas. With the decrease of pore pressure, the permeability deviation between ideal gas and real gas gradually decreases, which is due to the repulsion of gas molecules under high pressure and attraction under low pressure. As shown in the data in Table 7 and Figure 10, when the pore radius is 2.5, 5 and 10 nm respectively, the apparent permeability of the real gas is increased by 27.5, 16.5 and 9.3% on average compared with the ideal gas. Therefore, it can be found that with the decrease of pore radius, the influence of real gas effect on permeability increases, and the influence of real gas effect on permeability is more obvious under high pressure. At a pore pressure of 60MPa, the apparent permeability calculated based on real gas in pores with a pore radius of 2.5 nm is about 42% higher than that of ideal gas. Therefore, the influence of real gas effect on shale permeability can not be ignored.
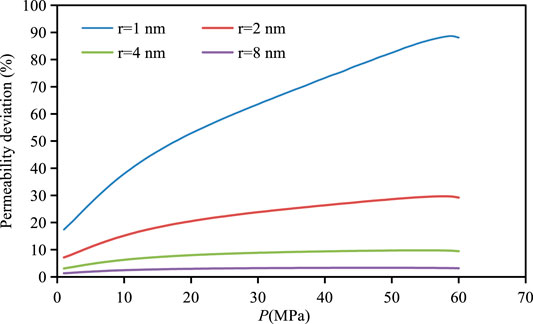
Figure 11 shows the influence of confinement effect on permeability under different pore radius. Figure 11 and Table 8 show the variation of permeability deviation and average permeability deviation with pore pressure under different pore radius with and without confinement effect. Figure 11 shows that the apparent permeability is improved after considering the influence of confinement effect compared with not considering confinement effect. According to the data in Figure 12 and Table 8, when the pore radius is 1 nm, 2 nm, 4 nm and 8 nm, the apparent permeability considering the confinement effect is increased by 61.3, 22.4, 8.2, and 2.9% respectively. The permeability deviation decreases with the decrease of pore pressure and increases with the decrease of pore radius. Under the pore pressure of 60MPa, the influence of confinement effect on permeability in organic pores with pore radius of 1 nm can be increased by 88%. Therefore, the influence of confinement effect can not be ignored for small pore radius and high pressure.
4 Conclusion
A apparent permeability model is established, after comprehensively considering three gas flow mechanisms in shale matrix organic pores, including viscous slippage flow, Knudsen diffusion and surface diffusion of adsorbed gas, and real gas effect and confinement effect, and at the same time considering the effects of matrix shrinkage, stress sensitivity, adsorption layer thinning, confinement effect and real gas effect on pore radius. The contribution of three flow mechanisms to apparent permeability under different pore pressure and pore size is analyzed. At the same time, the effects of adsorption layer thinning, stress sensitivity, matrix shrinkage effect, real gas effect and confinement effect on apparent permeability are systematically analyzed. The results show that:
1) Pore pressure and pore radius are the key factors affecting the gas flow mechanism. With the decrease of pore radius, the contribution of viscous slippage flow decreases gradually, and the contributions of surface diffusion and Knudsen diffusion increase gradually. When the pore radius is less than 10 nm, this phenomenon becomes more significant; The apparent permeability decreases first and then increases with the decrease of pore pressure.
2) Adsorption layer and stress sensitivity will reduce the effective radius of pores. With the increase of Langmuir strain and the decrease of pore pressure, the matrix shrinkage effect increases, and the matrix shrinkage will increase the effective pore radius. When the pore pressure drops to 10 MPa, with the decrease of pore pressure and the increase of Langmuir strain, the influence of matrix shrinkage effect on permeability will become more obvious. The matrix shrinkage effect may make up for the loss of effective radius of organic pores caused by stress sensitivity and the existence of adsorption layer.
3) The real gas effect can improve the apparent permeability. With the increase of pore pressure and the decrease of pore radius, the effect of real gas effect on the apparent permeability increases. The influence of real gas effect on shale permeability can not be ignored.
4) The confinement effect can improve the apparent permeability. With the increase of pore pressure and the decrease of pore radius, the influence of confinement effect on apparent permeability increases rapidly. Under the conditions of nano pores and high pressure, the influence of confinement effect can not be ignored.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
WG, XZ, and RY contributed to conception and design of the study. wrote the first draft of the manuscript. LK, JG, and YL wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Conflict of Interest
Authors WG, XZ, RY, LK, JG and YL were employed by PetroChina.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, orclaim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
An, C., Fang, Y., Liu, S., Alfi, M., Yan, B., Wang, Y., et al. (2017). “Impacts of Matrix Shrinkage and Stress Changes on Permeability and Gas Production of Organic-Rich Shale Reservoirs,” in [C] //Society of Petroleum Engineers-SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 1–16. doi:10.2118/186029-ms
Cao, G., Lin, M., Jiang, W., Li, H., Yi, Z., and Wu, C. (2017). A 3D Coupled Model of Organic Matter and Inorganic Matrix for Calculating the Permeability of Shale. Fuel 204, 129–143. doi:10.1016/j.fuel.2017.05.052
Chai, D., Fan, Z., and Li, X. (2019). A New Unified Gas-Transport Model for Gas Flow in Nanoscale Porous Media. SPE J. 24 (02), 698–719. doi:10.2118/194208-pa
Cui, G., Liu, J., Wei, M., Feng, X., and Elsworth, D. (2018a). Evolution of Permeability during the Process of Shale Gas Extraction. J. Nat. Gas Sci. Eng. 49, 94–109. doi:10.1016/j.jngse.2017.10.018
Cui, G., Liu, J., Wei, M., Shi, R., and Elsworth, D. (2018b). Why Shale Permeability Changes under Variable Effective Stresses: New Insights. Fuel 213, 55–71. doi:10.1016/j.fuel.2017.10.068
Dong, J.-J., Hsu, J.-Y., Wu, W.-J., Shimamoto, T., Hung, J.-H., Yeh, E.-C., et al. (2010). Stress-dependence of the Permeability and Porosity of sandstone and Shale from TCDP Hole-A. Int. J. Rock Mech. Mining Sci. 47, 1141–1157. doi:10.1016/j.ijrmms.2010.06.019
Geng, L., Li, G., Zitha, P., Tian, S., Sheng, M., and Fan, X. (2016). A Diffusion-Viscous Flow Model for Simulating Shale Gas Transport in Nano-Pores. Fuel 181, 887–894. doi:10.1016/j.fuel.2016.05.036
Huang, S., Wu, Y., Cheng, L., Liu, H., Xue, Y., and Ding, G. (2018). Apparent Permeability Model for Shale Gas Reservoirs Considering Multiple Transport Mechanisms. Geofluids. doi:10.1155/2018/2186194
Jia, B., Tsau, J.-S., and Barati, R. (2018). A Workflow to Estimate Shale Gas Permeability Variations during the Production Process. Fuel 220, 879–889. doi:10.1016/j.fuel.2017.11.087
Jia, B., Tsau, J.-S., and Barati, R. (2019). Investigation of Shale-Gas-Production Behavior: Evaluation of the Effects of Multiple Physics on the Matrix. SPE Reservoir Eval. Eng. 23 (01), 068–080. doi:10.2118/197069-pa
Li, J., Chen, Z., Wu, K., Zhang, T., Zhang, R., Xu, J., et al. (2018). Effect of Water Saturation on Gas Slippage in Circular and Angular Pores. Aiche J. 64 (9), 3529–3541. doi:10.1002/aic.16196
Li, J., Li, X., Wang, X., Li, Y., Wu, K., Shi, J., et al. (2016). Water Distribution Characteristic and Effect on Methane Adsorption Capacity in Shale clay. Int. J. Coal Geology. 159, 135–154. doi:10.1016/j.coal.2016.03.012
Li, Z., Qi, Z., Yan, W., Xiang, Z. P., Ao, X., Huang, X. L., et al. (2020). Prediction of Production Performance of Refractured Shale Gas Well Considering Coupled Multiscale Gas Flow and Geomechanics. Geofluids 2020, 1–21. doi:10.1155/2020/9160346
Li, Z., Yan, W., Qi, Z., Dong, D., Huang, X., and Yu, R. (2019). Production Performance Model Based on Quadruple-Porosity Medium in Shale Gas Reservoirs Considering Multi-Transport Mechanisms. Energy Sourc. A: Recovery, Utilization, Environ. Effects, 1–19. doi:10.1080/15567036.2019.1662520
Pang, Y., Soliman, M. Y., Deng, H., and Emadi, H. (2017). Analysis of Effective Porosity and Effective Permeability in Shale-Gas Reservoirs with Consideration of Gas Adsorption and Stress Effects. SPE J. 22 (06), 1–739. doi:10.2118/180260-pa
Peng, Y., Liu, J., Pan, Z., Qu, H., and Connell, L. (2018). Evolution of Shale Apparent Permeability under Variable Boundary Conditions. Fuel 215, 46–56. doi:10.1016/j.fuel.2017.11.024
Sakhaee-Pour, A., and Bryant, S. L. (2012). Gas Permeability of Shale. SPE Reservoir Eval. Eng. 15 (04), 401–409. doi:10.2118/146944-pa
Sheng, G., Javadpour, F., and Su, Y. (2019). Dynamic Porosity and Apparent Permeability in Porous Organic Matter of Shale Gas Reservoirs. Fuel 251, 341–351. doi:10.1016/j.fuel.2019.04.044
Sheng, G., Javadpour, F., and Su, Y. (2018). Effect of Microscale Compressibility on Apparent Porosity and Permeability in Shale Gas Reservoirs. Int. J. Heat Mass Transfer 120, 56–65. doi:10.1016/j.ijheatmasstransfer.2017.12.014
Sheng, G., Su, Y., Wang, W., Liu, J., Lu, M., Zhang, Q., et al. (2015). A Multiple Porosity media Model for Multi-Fractured Horizontal wells in Shale Gas Reservoirs. J. Nat. Gas Sci. Eng. 27, 1562–1573. doi:10.1016/j.jngse.2015.10.026
Shi, J. T., Zhang, L., Li, Y. S., Yu, W., He, X., Liu, N., et al. (2013). “Diffusion and Flow Mechanisms of Shale Gas through Matrix Pores and Gas Production Forecasting,” in Paper SPE 167226 Presented at the SPE Unconventional Resources Conference Canada, Calgary, Alberta, Canada, 1–14. doi:10.2118/167226-ms
Singh, H., Javadpour, F., Ettehadtavakkol, A., and Darabi, H. (2014). Nonempirical Apparent Permeability of Shale. SPE Reservoir Eval. Eng. 17 (03), 414–424. doi:10.2118/170243-pa
Song, W., Yao, J., Li, Y., Sun, H., Zhang, L., Yang, Y., et al. (2016). Apparent Gas Permeability in an Organic-Rich Shale Reservoir. Fuel 181, 973–984. doi:10.1016/j.fuel.2016.05.011
Sun, Z., Li, X., Shi, J., Zhang, T., and Sun, F. (2017). Apparent Permeability Model for Real Gas Transport through Shale Gas Reservoirs Considering Water Distribution Characteristic. Int. J. Heat Mass Transfer 115, 1008–1019. doi:10.1016/j.ijheatmasstransfer.2017.07.123
Sun, Z., Shi, J., Wu, K., and Li, X. (2018a). Gas Flow Behavior through Inorganic Nanopores in Shale Considering Confinement Effect and Moisture Content. Ind. Eng. Chem. Res. 57 (9), 3430–3440. doi:10.1021/acs.iecr.8b00271
Sun, Z., Shi, J., Wu, K., Xu, B., Zhang, T., Chang, Y., et al. (2018b). Transport Capacity of Gas Confined in Nanoporous Ultra-tight Gas Reservoirs with Real Gas Effect and Water Storage Mechanisms Coupling. Int. J. Heat Mass Transfer 126, 1007–1018. doi:10.1016/j.ijheatmasstransfer.2018.05.078
Sun, Z., Shi, J., Wu, K., Zhang, T., Feng, D., Huang, L., et al. (2019). An Analytical Model for Gas Transport through Elliptical Nanopores. Chem. Eng. Sci. 199, 199–209. doi:10.1016/j.ces.2019.01.013
Swami, V., Clarkson, C. R., and Settari, A. (2012). “Non Darcy Flow in Shale Nanopores:Do We Have a Final Answer?,” in Paper SPE 162665 Presented at the SPE Canadian Unconventional Resources Conference, Calgary, Alberta, Canada, 1–15.
Tian, S., Wang, T., Li, G., Sheng, M., Liu, Q., and Zhang, S. (2018). An Analytical Model for Shale Gas Transport in Circular Tube Pores. Int. J. Heat Mass Transfer 127, 321–328. doi:10.1016/j.ijheatmasstransfer.2018.07.046
Wang, H. Y., and Marongiu-Porcu, M. (2015). “A Unified Model of Matrix Permeability in Shale Gas Formations,” in Paper SPE 173196 Presented at the SPE Reservoir Simulation Symposium, Houston, Texas, USA, 1–10. doi:10.2118/173196-ms
Wang, J., Liu, H., Wang, L., Zhang, H., Luo, H., and Gao, Y. (2015). Apparent Permeability for Gas Transport in Nanopores of Organic Shale Reservoirs Including Multiple Effects. Int. J. Coal Geology. 152, 50–62. doi:10.1016/j.coal.2015.10.004
Wang, Q., Hu, Y., Zhao, J., Ren, L., Zhao, C., and Zhao, J. (2019). Multiscale Apparent Permeability Model of Shale Nanopores Based on Fractal Theory. Energies 12 (17), 3381. doi:10.3390/en12173381
Wang, S., Shi, J., Wang, K., Sun, Z., Miao, Y., and Hou, C. (2018). Apparent Permeability Model for Gas Transport in Shale Reservoirs with Nano-Scale Porous media. J. Nat. Gas Sci. Eng. 55, 508–519. doi:10.1016/j.jngse.2018.05.026
Wasaki, A., and Akkutlu, I. Y. (2015). Permeability of Organic-Rich Shale. SPE J. 20 (06), 1–384. doi:10.2118/170830-pa
Wu, K., Chen, Z., Li, X., and Dong, X. (2016c). Methane Storage in Nanoporous Material at Supercritical Temperature over a Wide Range of Pressures. Sci. Rep. 6, 33461. doi:10.1038/srep33461
Wu, K., Chen, Z., Li, X., Guo, C., and Wei, M. (2016d). A Model for Multiple Transport Mechanisms through Nanopores of Shale Gas Reservoirs with Real Gas Effect-Adsorption-Mechanic Coupling. Int. J. Heat Mass Transfer 93, 408–426. doi:10.1016/j.ijheatmasstransfer.2015.10.003
Wu, K., Chen, Z., Li, X., Xu, J., Li, J., Wang, K., et al. (2017). Flow Behavior of Gas Confined in Nanoporous Shale at High Pressure: Real Gas Effect. Fuel 205, 173–183. doi:10.1016/j.fuel.2017.05.055
Wu, K., Li, X., Guo, C., Wang, C., and Chen, Z. (2016a). A Unified Model for Gas Transfer in Nanopores of Shale-Gas Reservoirs: Coupling Pore Diffusion and Surface Diffusion. SPE J. 21 (05), 1–583. doi:10.2118/2014-1921039-pa
Wu, K., Li, X., Guo, C., Wang, C., and Chen, Z. (2016b). A Unified Model for Gas Transfer in Nanopores of Shale-Gas Reservoirs: Coupling Pore Diffusion and Surface Diffusion. SPE J. 21 (05), 1583–1611. doi:10.2118/2014-1921039-pa
Xiong, X. Y., Devegowda, D., Villazon, M., Sigal, R., and Civan, F. (2012). “A Fully-Coupled Free and Adsorptive Phase Transport Model for Shale Gas Reservoirs Including Non-darcy Flow Effects,” in SPE annual technical conference and exhibition (SPE-159758-MS), San Antonio, Texas, USA, 1–16. doi:10.2118/159758-ms
Yin, Y., Qu, Z. G., and Zhang, J. F. (2017). An Analytical Model for Shale Gas Transport in Kerogen Nanopores Coupled with Real Gas Effect and Surface Diffusion. Fuel 210, 569–577. doi:10.1016/j.fuel.2017.09.018
Yucel Akkutlu, I., and Fathi, E. (2012). Multiscale Gas Transport in Shales with Local Kerogen Heterogeneities. SPE J. 17, 1002–1011. doi:10.2118/146422-pa
Zhang, L., Liang, H., Zhao, Y., Xie, J., Peng, X., and Li, Q. (2020). Gas Transport Characteristics in Shale Matrix Based on Multiple Mechanisms. Chem. Eng. J. 386, 124002. doi:10.1016/j.cej.2019.124002
Zhang, L., Shan, B., Zhao, Y., Du, J., Chen, J., and Tao, X. (2018). Gas Transport Model in Organic Shale Nanopores Considering Langmuir Slip Conditions and Diffusion: Pore Confinement, Real Gas, and Geomechanical Effects. Energies 11 (1), 223. doi:10.3390/en11010223
Zhang, M., Yao, J., Sun, H., Zhao, J.-l., Fan, D.-y., Huang, Z.-q., et al. (2015). Triple-continuum Modeling of Shale Gas Reservoirs Considering the Effect of Kerogen. J. Nat. Gas Sci. Eng. 24, 252–263. doi:10.1016/j.jngse.2015.03.032
Zhang, Q., Wang, W.-D., Kade, Y., Wang, B.-T., and Xiong, L. (2020). Analysis of Gas Transport Behavior in Organic and Inorganic Nanopores Based on a Unified Apparent Gas Permeability Model. Pet. Sci. 17 (1), 168–181. doi:10.1007/s12182-019-00358-4
Zhang, T., Li, X., Sun, Z., Feng, D., Miao, Y., Li, P., et al. (2017). An Analytical Model for Relative Permeability in Water-Wet Nanoporous media. Chem. Eng. Sci. 174, 1–12. doi:10.1016/j.ces.2017.08.023
Zhang, T., Li, X., Wang, X., Li, J., Sun, Z., Feng, D., et al. (2018). A Discrete Model for Apparent Gas Permeability in Nanoporous Shale Coupling Initial Water Distribution. J. Nat. Gas Sci. Eng. 59, 80–96. doi:10.1016/j.jngse.2018.08.024
Keywords: apparent permeability, shale gas, adsorption layer, stress sensitivity, matrix shrinkage, multiple transport mechanisms
Citation: Guo W, Zhang X, Yu R, Kang L, Gao J and Liu Y (2022) A Model for the Apparent Gas Permeability of Shale Matrix Organic Nanopore Considering Multiple Physical Phenomena. Front. Earth Sci. 9:813585. doi: 10.3389/feart.2021.813585
Received: 12 November 2021; Accepted: 14 December 2021;
Published: 10 January 2022.
Edited by:
Xiaohu Dong, China University of Petroleum, ChinaReviewed by:
Bailu Teng, China University of Geosciences, ChinaLuo Zuo, Sinopec, China
Dong Feng, China University of Petroleum, China
Copyright © 2022 Guo, Zhang, Yu, Kang, Gao and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaowei Zhang, emhhbmd4dzY5QHBldHJvY2hpbmEuY29tLmNu; Rongze Yu, eXVyejIwMTE2OUBwZXRyb2NoaW5hLmNvbS5jbg==
 Wei Guo
Wei Guo Xiaowei Zhang*
Xiaowei Zhang* Lixia Kang
Lixia Kang