Construction and Programming of Bivariate Model for Unsaturated Soil Seepage Calculation

The seepage calculation of unsaturated soil has always been an important subject in the field of geotechnical engineering, and it greatly influences the stability of geotechnical engineering. Currently, most of the unsaturated soil seepage calculation formulas consider only the saturation. In fact, the seepage of the soil is also affected by other factors, such as pore size. Therefore, considering the influence of void ratio in the seepage calculation of unsaturated soil is worthy of further investigation. In this study, a seepage function of unsaturated soil, which considers the influence of dry density and saturation, was constructed and introduced into ABAQUS program. An engineering case was calculated, and the difference between the results considering two variables and that only considering saturation was compared and analyzed. The analysis of the results indicates that this function can better characterize unsaturated seepage, and its subprogram is applicable.

1 Introduction

The study on seepage calculation of unsaturation soil is important in geotechnical engineering. Many projects need to conduct unsaturated soil seepage calculation, such as foundation excavation, hydropower dam engineering, and slope stability engineering. (Jennings and Burland, 1961;Fredrond and Laharzo, 1997; Xie and Zhiyan, 2006; Han et al., 2016; Fan et al., 2019; Jiang et al., 2021). Many researchers (Wang et al., 2013; Chen, 2014; Zhou et al., 2018; Shao et al., 2019; Xie et al., 2019; Liu et al., 2020; Liu et al., 2020; Han et al., 2021; Huang et al., 2021; Kang et al., 2021; Lu et al., 2021; Sun et al., 2021; Wang et al., 2021) have studied unsaturated seepage from different aspects. (Yu et al., 2008; Han et al., 2018: Zhang et al., 2021) studied the stability of unsaturated soil slope under unsteady seepage condition. Tang et al. (2002) and Xiong et al. (2005) explored the influence of seepage on slope stability. Liu and others (Mao, 2003; Liu et al., 2005; Han et al., 2019; Liu et al., 2020; Yao et al., 2021) examined the mechanism of slope instability when water level rises. Neuman (1973) proposed a unified consideration of saturated and unsaturated seepage state, which has been recognized by academia in seepage calculation. Fu and Jin (2008) and Fan et al. (2020) proposed a saturated–unsaturated seepage model with the total head of porous media and seepage field. Tao et al. (Han et al., 2018; Tao et al., 2019; Liu et al., 2020; Wang et al., 2021) analyzed the influence of initial void ratio on permeability coefficient of unsaturated soil through experiments and model calculation. Wu and Zhang, (2009) proposed a numerical analysis method for one-dimensional coupling of seepage and deformation of elastic soil. Jia et al. (2007) and Liu et al. (2021) derived the basic equation of unsteady seepage in unsaturated soil. Zhang et al. (2006, 2020) calculated the influence of water level decline on slope safety factor under different slopes of soil–water characteristic curves. Wu et al. (2009) proposed a general finite element method for solving Richards equation of unsaturated seepage. Ma et al. (2018) and Sheng et al. (2008) analyzed the influence of dry density on permeability coefficient.

The aforementioned analysis shows that the existing seepage calculation methods of unsaturated soil only consider the variable of saturation. However, in the process of permeability deformation of actual soil, unsaturated permeability coefficient will be influenced by many factors, such as the size of soil particles, the density, the pressure, and the void ratio. Therefore, the factors should be considered comprehensively to better calculate and simulate the actual state of unsaturated seepage Liu et al. (2010). In this study, a permeability function for unsaturated soil considering bivariate of dry density and saturation was proposed. It was introduced into the ABAQUS finite element program by subprogram development. One engineering case was calculated, and the difference between the results considering two variables and that only considering saturation was compared and analyzed. The analysis of the results indicates that this function can better characterize unsaturated seepage, and its subprogram is applicable.

2 Bivariate Permeability Model of Unsaturation Soil

2.1 Permeability Function of Unsaturated Soil With Bivariate of Dry Density and Saturation

The relationship between seepage coefficient and saturation of samples under different wetting cycles is measured using an improved water-gas motion measuring instrument developed by institute of Geotechnical Engineering, Xi’an University of Technology. The dry density of the samples ρ_d = 1.40–1.67 g/cm³. The variation in relative permeability coefficient ratio (k_r = k_w/k_s) with saturation under different dry densities is comprehensively analyzed by selecting a set of test data with most humidifying cycles. The permeability function of unsaturated soil considering bivariate of dry density and saturation is derived, as shown in Equations 1–3:

$k_r=a\cdot \exp \left[b\cdot S^{b_1\exp (b_2\cdot {\rho }_d)}\right](1)$

$k_s=\alpha \cdot \exp \left[\beta \cdot {\rho }_d\right](2)$

$k_w/k_s=k_r=a\cdot \alpha \cdot \exp \left[b\cdot S^{b_1\exp (b_2\cdot {\rho }_d)}+\beta \cdot {\rho }_d\right](3)$

where a and b and b₁ and b₂ and α and β are all parameters of loess used in the test, and a = 4 × 10⁻⁵, b = 9.8385, b₁ = 1182.2, b₂ = −4.8569, α = 10⁹, β = −12.757; ${\rho }_d$ is dry density (g/cm³); $S$ is saturation of soil samples; k_r is the ratio of permeability coefficient; k_s is the permeability coefficient of saturated soil (×10⁻⁷ cm/s); k_w is the seepage coefficient of unsaturated soil (×10⁻⁷ cm/s, independent variables are density and saturation).

The model considers the influence of the change in both saturation and dry density on the permeability coefficient in seepage process. This calculation process is considered to be more consistent with the stress state in seepage engineering.

2.2 Soil–Water Characteristic Curve

Zhang (2009) tested the soil–water characteristic curves of unsaturated loess under different axial stress and lateral confinement. The soil–water characteristic curves of measured under no pressure are compared with that under a certain consolidation pressure. The influence of initial density and stress on the soil–water characteristic curve is qualitatively analyzed. Through the verification of the test data in Huang et al. (1994) and Huang et al. (1998) paper, a new model considering the density change caused by stress is proposed, namely the modified van-Genuchten model, as shown in Equation 4:

$S_w={\left\{1+{[{\left(\frac{e}{a}\right)}^{\frac{1}{b}}\cdot S]}^n\right\}}^{\frac{b}{n}}(4)$

where a is a parameter related to intake value; n is a soil parameter related to the soil dehydration rate after the matric suction is greater than the intake value; m is a parameter related to the residual water content.

3 Program Development of Bivariate Model

USDFLD is a subroutine module in ABAQUS. Its main function is to change the field variable (FV) value at the material point through the subroutine for altering the parameter value of the material. The subroutine is based on the calculation principle of Newton iterative method. Stress increment and state variables are updated by the strain increment introduced by ABAQUS main program, and the Jacobian matrix əΔσ/əΔε of the material is given for calculation.

The USDFLD subroutine can define the custom field variable as a function of time or of other available material point. The material property is defined as a function of the field variable related to the calculation solution (SDV). When USDFLD is called, it must be defined by initial conditions, predefined field variables, or initial field variables. In the process of calculation, although the field variable has been defined by the initial conditions, the one at the integral point is obtained by field variable interpolation at the corresponding node, that is, the field variable value of the node is interpolated to calculate the value at the integral point. USDFLD only redefines the field variables at the integration point. Therefore, we first deform the unsaturated permeability function of two variables, namely, Equations 1, 3, and obtain Equations 5, 6.

$k_w=a\cdot \exp \left(b\cdot S\right)\cdot \alpha \exp \left[b\cdot S^{b_1\exp \left(b_2{\rho }_d\right)}-b\cdot S+\beta \cdot {\rho }_d\right](5)$

We define $k_s^{\prime }=\alpha \cdot \exp \left[b\cdot S^{b_1\exp \left(b_2{\rho }_d\right)}-b\cdot S+\beta \cdot {\rho }_d\right]$, and then Equation 6 can be derived:

$k_r^{\prime }=a\cdot \exp \left[b\cdot S\right](6)$

where k_s’ is equivalent saturated permeability coefficient, k_r′ is equivalent unsaturated soil relative permeability coefficient, and S is saturation.

The equivalent saturated permeability coefficient k_s′ is expressed as a function of dry density and suction by converting the aforementioned formulas. The equivalent relative permeability coefficient k_r’ is expressed as a function of saturation. Given that the dry density ρ_d can be expressed by the void ratio, the saturated permeability coefficient is also the function of void ratio and saturation. In ABAQUS, only a custom field variable is needed to realize the aforementioned function because the saturated permeability coefficient can be directly defined as a function of void ratio.

In Equation 5, the value of k_w is not equal to the saturated permeability coefficient when the saturation is 1. Therefore, the function cannot be directly used to calculate the permeability coefficient in the saturated region. The saturated permeability coefficient should be calculated according to Equation 2 ($k_s=\alpha \cdot \exp [\beta \cdot {\rho }_d]$) in the DATE LINE step of ABAQUS when the saturation S = 1.

The field variable FV1 to S should be updated through the USDFLD subroutine in the calculation process to realize the variation in permeability coefficient with dry density and saturation in the program. The redefinition of permeability coefficient is realized.

The development of the bivariate model is realized by programming in FORTRAN language. The bivariate permeability function model of unsaturated soil is successfully introduced into ABAQUS. The USDFLD subroutine is as follows:

4 Verification by an Engineering Example

4.1 Introduction of the Example

A homogeneous earth dam project in Xi’an is selected for modeling calculation, and a two-dimensional model is established. The Cambridge model is used for calculation. This earth dam is shown in Figure 1.

FIGURE 1

FIGURE 1. The schematic diagram of the homogeneous earth dam model.

The bottom of the dam is taken as the elevation of 0. The height of the dam crest is 12.0 m, the width of the dam crest is 4.0 m, and the width of the dam bottom is 52.0 m. The upstream slope and downstream slope are both 1:2.0.

The water level on upstream slope is 10 m, and the downstream slope is considered without water. The seepage boundaries are the bottom of the dam and the downstream. The saturated permeability coefficient of the dam soil is 1.3E−5 m/s. The applicable range of dry density in Equation 5 is ρ_d = 1.40–1.67 g/cm³, which is converted to void ratio as e = 0.56–0.89. The initial void ratio value of this example is in this range.

The FV can be updated at Gaussian integral points in USDFLD. Thus, the unsaturated permeability function with bivariate of saturation and dry density can be realized in ABAQUS by assigning corresponding permeability coefficients to different void ratios in this example.

The permeability coefficient of the dam is shown in Table 1. The effect of temperature field is not considered in this paper, so the values of temperature field all are 0 (can also be omitted).

TABLE 1

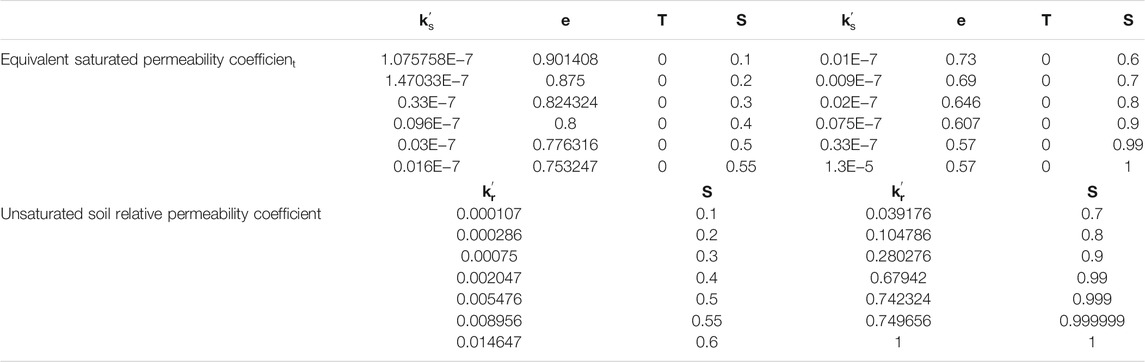
TABLE 1. The definition data of equivalent saturated permeability coefficient k_s′ and unsaturated soil relative permeability coefficient k_r′

The data in the original example (2009) is shown in Table 2, and the soil–water characteristic curve is shown in Figure 2.

TABLE 2

TABLE 2. Pore pressure and saturation of the soil–water characteristic curve

FIGURE 2

FIGURE 2. Soil–water characteristic curve.

4.2 Calculation Schemes

The earth dam model is calculated under two schemes, under constant permeability coefficient and permeability coefficient varying with void ratio (dry density) and saturation.

Considering the change in the void ratio and saturation, the influence of non-constant permeability coefficient on seepage calculation is compared and analyzed. The results of FV are further extracted for analysis to verify the introduced of the bivariate function model subroutine for seepage calculation.

4.3 Results and Analysis

The seepage paths are the same under the two calculation schemes. The pore water pressure, saturation, and flow velocity in the unsaturated region will be different in the seepage process. Due to the different seepage calculation model, the differences in pore water pressure and saturation under two calculation schemes are emphatically compared.

4.3.1 Results and Analysis of Pore Water Pressure

Figure 3 shows the cloud pictures of pore water pressure extracted after simulation calculation under the two schemes. The maximum value of pore water pressure is located in the upstream slope angle, and the minimum is located in the downstream slope top. These findings reflect that the downstream slope is unsaturated zone.

FIGURE 3

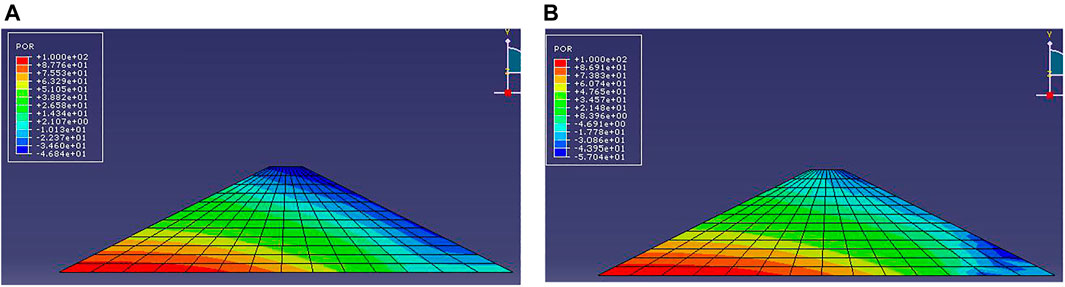
FIGURE 3. The pore water pressure cloud picture calculated under two schemes. (A) The pore water pressure cloud picture calculated under Scheme 1. (B) The pore water pressure cloud picture calculated under Scheme 2.

Figure 3 shows the approximate distribution trend of pore water pressure, but the specific variation cannot be known. Therefore, the pore water pressure data of each section node are extracted for analysis, as shown in Figures 4, 5.

FIGURE 4

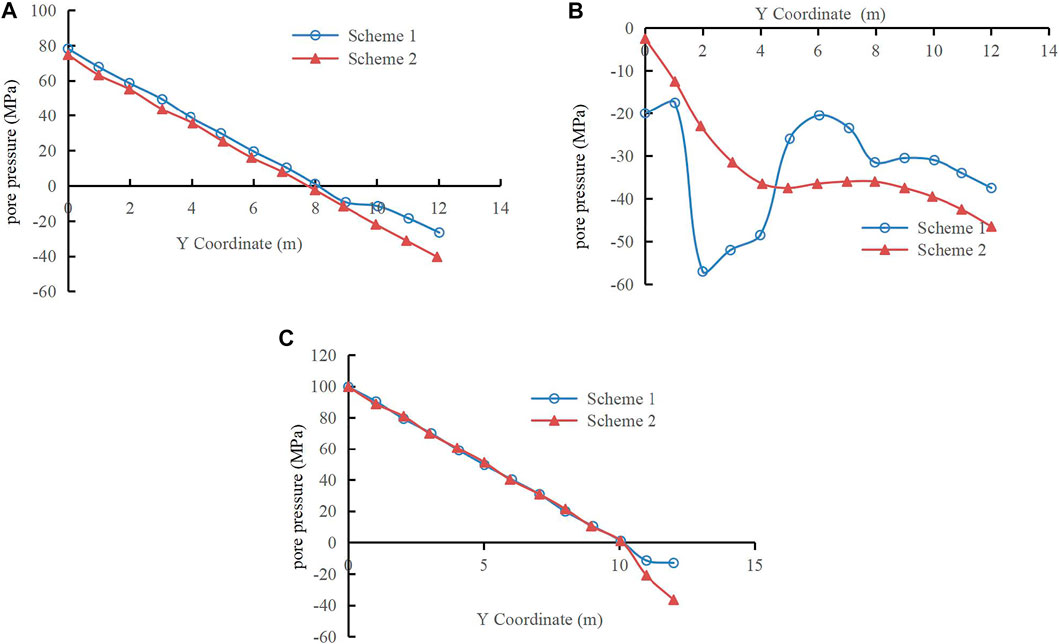
FIGURE 4. The curve of pore pressure with Y coordinate. (A) The curve of pore water pressure with Y coordinate in the middle of earth dam. (B) The curve of pore water pressure with Y coordinate on downstream slope of earth dam. (C) The curve of pore pressure with Y coordinate on upstream slope of earth dam.

FIGURE 5

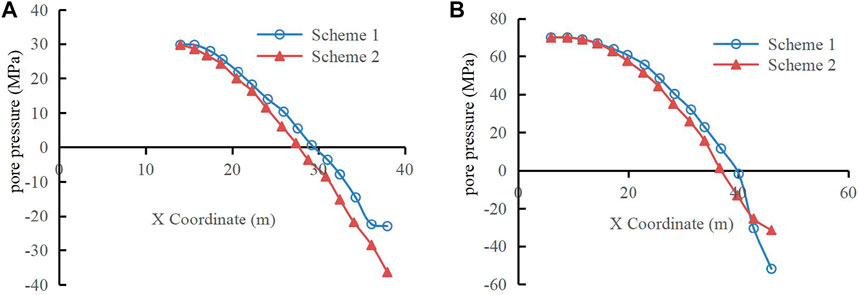
FIGURE 5. The curve of pore pressure with X coordinate. (A) The curve of pore water pressure with X coordinate at Y = 8 m. (B) The curve of pore water pressure with X coordinate at Y = 4 m.

The Y coordinate in the figure represents the height direction of the dam, and the X coordinate represents the width direction of the dam.

Figure 4A presents the variation in pore water pressure with Y coordinate in the middle of the earth dam. Figure 4B shows the variation in pore water pressure with Y coordinate in the downstream slope. Figure 4C displays the variation in pore water pressure with Y coordinate in the upstream slope.

Figure 4A shows that the pore water pressure in the middle position of the dam varies linearly with the coordinate under the two schemes. These pressures transit from saturation to unsaturated zone at Y = 8 m. The pore water pressure calculated by considering the change in void ratio is larger than that calculated by constant void ratio. This feature is more pronounced in unsaturated zone. In the unsaturated region, the matrix suction calculated by Scheme 1 is smaller than that calculated by Scheme 2. In addition, the zero pore pressure position calculated by Scheme 2 is higher than that of Scheme 1.

Figure 4B shows that the downstream of the dam is completely unsaturated zone, and the pore water pressure calculated considering the change in void ratio is greater than that when the void ratio is constant in the region of 4–12 m. However, the opposite situation is observed in the region of 0–4 m. This result is due to that the permeability coefficient will reduce when considering the void ratio change.

As shown in Figure 4C, the pore water pressure variation of the two schemes is the same in the saturated region on the upstream slope of the dam. However, the pore pressure calculated considering the change in void ratio in the unsaturated region is significantly greater than that considering it is constant. Analysis shows that this finding is mainly due to that the permeability coefficient in the unsaturated zone is smaller. This condition results in that the infiltration line of the former is higher than that of the latter. Thus, the pore water pressure increases significantly in the unsaturated zone.

Figure 5 presents the curves of pore water pressure of dam cross section with X and Y coordinates of 4 m and 8 m, respectively. The curves show that the calculated pore water pressure considering the change in void ratio is larger than that of constant void ratio. At the downstream slope (i.e., X > 24 m), the calculated pore pressure considering the change in void ratio is smaller than that when the void ratio is constant when Y = 4 m.

The comprehensive analysis of the aforementioned figures shows that the saturation line for seepage will change when the influence of the change in void ratio on unsaturated permeability coefficient is considered. Specifically, the calculation result of saturation line shifts to the left as a whole compared with that of Scheme 1 in the region of Y = 0–4 m. The saturation line will be lower than that of Scheme 1 in the region of Y = 4–12 m. These feature are more in line with the actual seepage process.

4.3.2 Results and Analysis of Saturation

Saturation is also an important index in the calculation and analysis of unsaturated seepage. The saturation under different schemes of the same section is extracted for comparative analysis by referring to the section selected in pore water pressure. Figure 6 shows the saturation cloud pictures under the two schemes.

FIGURE 6

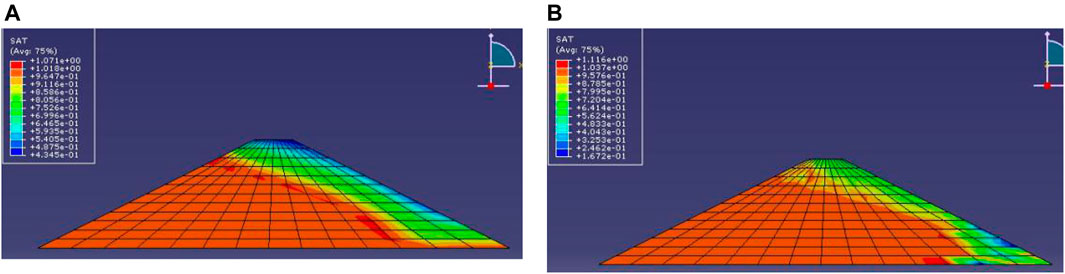
FIGURE 6. The saturation calculated under two schemes. (A) The saturation calculated without considering the change of void ratio. (B) The saturation calculated considering void ratio change.

As shown in Figure 6, the wetting surface of the downstream slope in Scheme 1 is obviously shifted to the left compared with that in Scheme 2. The minimum saturation of Scheme 2 is on the upper right side of the unsaturated zone, while it is at the foot of the downstream slope of Scheme 1. The reason is that the void ratio is linearly distributed along the dam height. Therefore, the unsaturated permeability coefficient of Scheme 1 will be greatly reduced at the bottom of the slope. The saturation line shifts to the left accordingly. As a result, the saturation at the foot of the downstream slope is smaller than that at the left and upper parts of the downstream slope.

Figure 7 shows the curves of the saturation at the middle of the dam and the downstream slope and the upstream slope under the two schemes. Figure 8 presents the curves of the saturation of the sections with Y = 4 m and Y = 8 m under the two schemes.

FIGURE 7

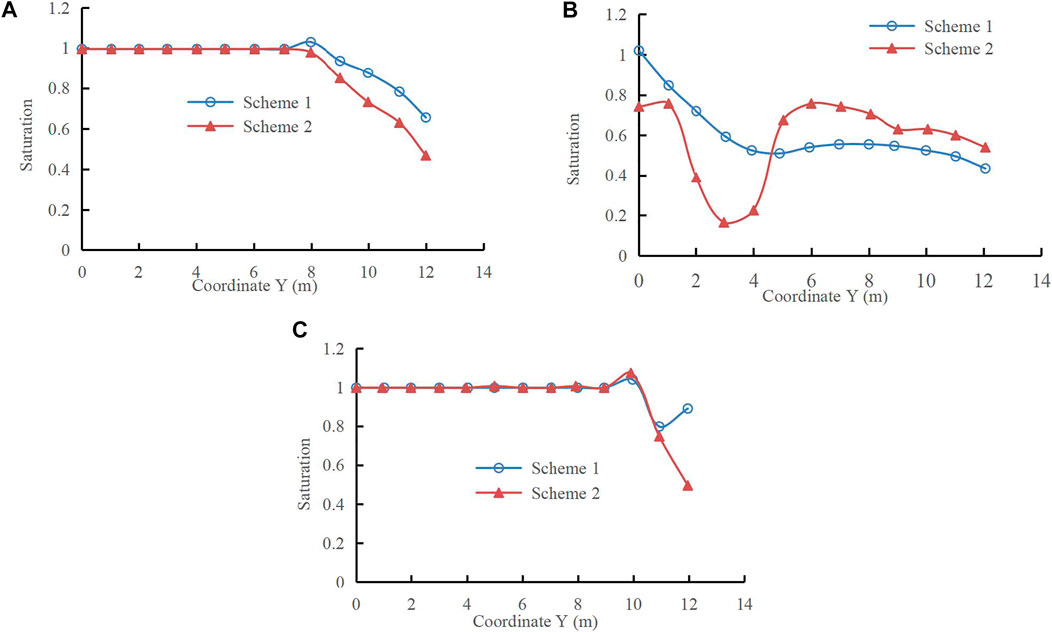
FIGURE 7. The curve of saturation with Y coordinate. (A) The curve of saturation with Y coordinate in the middle of earth dam. (B) The curve of saturation with Y coordinate on the slope downstream of earth dam. (C) The curve of saturation with Y coordinate on upstream slope of earth dam.

FIGURE 8

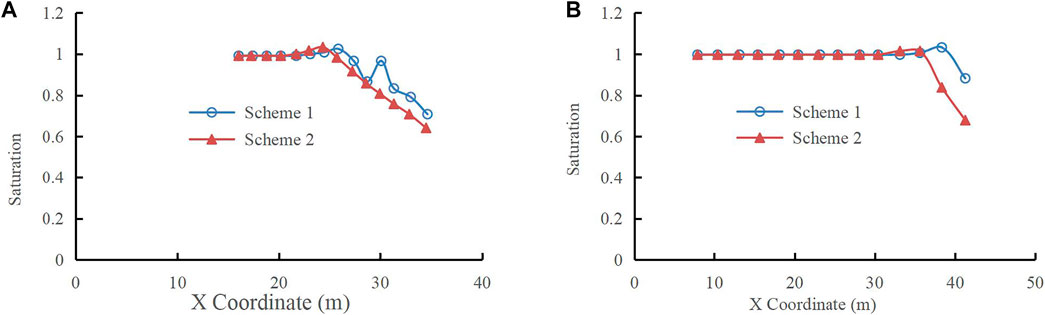
FIGURE 8. The curve of calculated saturation with X coordinate. (A) The curve of calculated saturation with X coordinate at Y=8 m. (B) The curve of calculated saturation with X coordinate at Y=4 m.

Figures 7, 8 show the comparison of saturation at each section. The figures indicate that the saturation values under the two schemes are equal in the saturated region, but a lag in the transition is observed between the saturated and unsaturated regions. The feature is most obvious in the downstream slope of the unsaturated region. The change in saturation is similar to the change trend of pore water pressure in Section 4.2.1. The saturation calculated by Scheme 1 is larger than that of Scheme 2 in the unsaturated zone in the upper part of the dam. The saturation of Scheme 2 is larger than that of Scheme 1 in the unsaturated zone in the lower part of the dam downstream. Analysis shows that this finding is due to that the permeability coefficient will decrease considering the influence of dry density (void ratio) on unsaturated permeability coefficient.

4.3.3 Results and Analysis of Seepage Velocity

The cloud pictures of seepage velocity under the two schemes are shown in Figure 9.

FIGURE 9

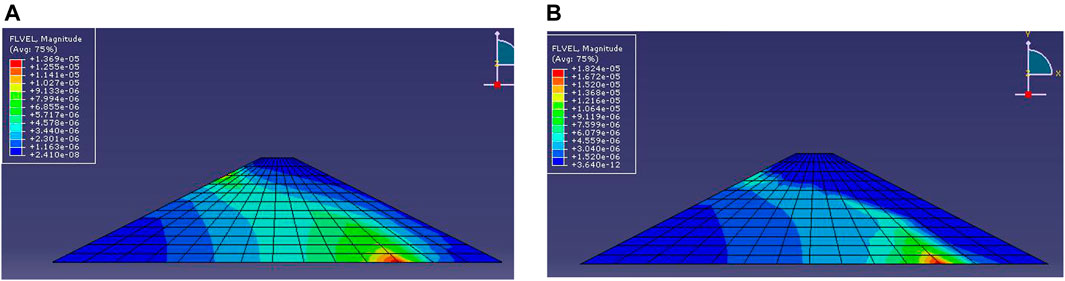
FIGURE 9. The flow velocity cloud picture calculated under two schemes. (A) The flow velocity cloud picture calculated under Scheme 1. (B) The flow velocity cloud picture calculated under Scheme 2.

The data are extracted to draw the curves of the seepage velocity and Y at the middle position of the dam X = 0, the downstream slope and the upstream slope, and the relationship between the seepage velocity and X at Y = 4 m and 8 m sections. They are shown in Figures 10, 11.

FIGURE 10

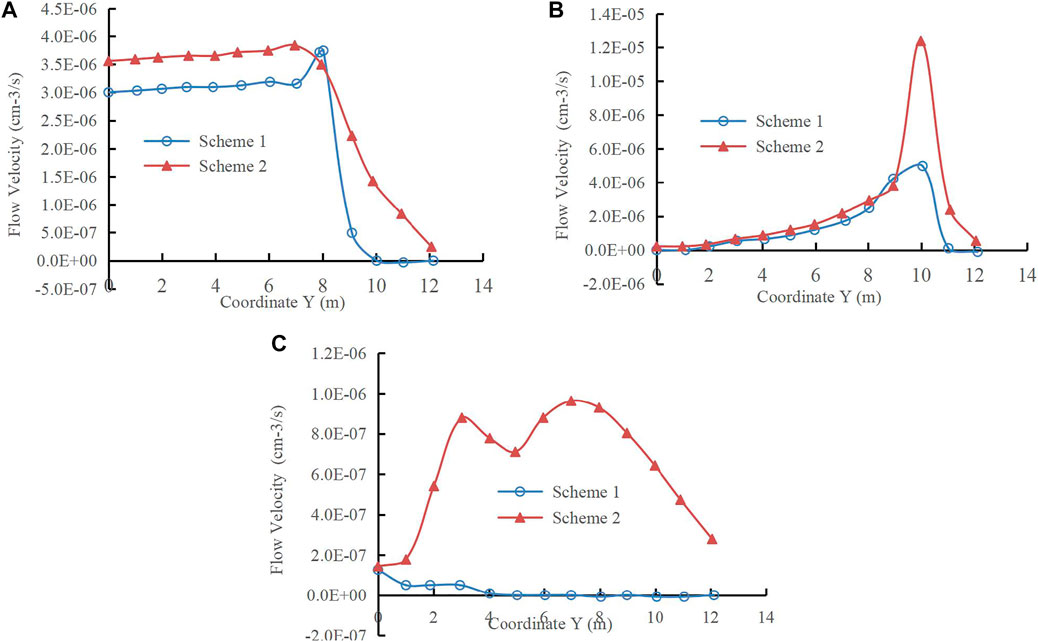
FIGURE 10. The curve of seepage velocity with Y coordinate. (A) The curve of seepage velocity with Y coordinate in the middle of dam body. (B) The curve of seepage velocity with Y coordinate on the slope downstream of earth dam. (C) The curve of seepage velocity with Y coordinate on upstream slope of earth dam.

FIGURE 11

FIGURE 11. The curve of seepage velocity with X coordinate. (A) The curve of seepage velocity with X coordinate at Y=4 m. (B) The curve of seepage velocity with X coordinate at Y=8 m.

Figure 10 shows that the seepage velocity considering the void ratio’s change is significantly smaller than that under constant void ratio. Figure 10A shows that the middle and lower parts of the earth dam are saturated regions, and the upper part is unsaturated regions. Therefore, a slight difference in unsaturated seepage velocity is observed between the two schemes when Y < 8 m.

Figure 11 reveals a large difference in the seepage velocity under the two schemes, and the maximum value reaches more than one order of magnitude.

As shown in Figure 10B, the velocity is the same when Y < 10.0 m. However, the difference in permeability coefficient between the two schemes increases sharply when Y > 10.0 m. Figure 11A shows similar laws. Specifically, the difference in seepage velocity is not large when Y < 35 m, but the permeability coefficients of the two are also quite different when Y is greater than 35. As shown in Figure 11B, the difference is also small when Y < 24 m, while the difference is large when Y > 24 m.

These results show that the seepage velocity of the two schemes is quite different. This finding also verifies the change rule of pore water pressure caused by the aforementioned change in void ratio. In particular, the permeability coefficient of Scheme 1 is reduced compared with that of Scheme 2 due to the decrease in seepage velocity, and the infiltration line will shift to the left lower part in the process of seepage.

4.4 Verification of the Introduction of Subroutines

The value of custom field variables can be extracted in the post-processing module of ABAQUS. The FV and saturation values at the integral point are extracted to verify whether the USDFLD subroutine is used in seepage calculation. Figure 12 shows the FV cloud picture and saturation cloud picture of this example model.

FIGURE 12

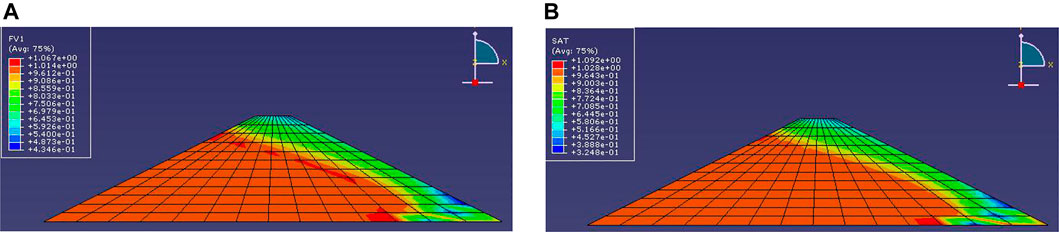
FIGURE 12. The cloud picture of FV and saturation. (A) The FV cloud picture. (B) The saturation cloud picture.

As shown in Figure 12, the cloud pictures of the field variable FV1 and saturation are nearly the same in term of the distribution law and order of magnitude. This finding means that the USDFLD subroutine updates the saturation in the calculation process, which also verifies that the subroutine is successfully called in ABAQUS calculation. Therefore, the seepage calculation can be conducted in finite element by using the seepage model considering bivariate of void ratio (dry density) and saturation.

The void ratio is assumed to be linearly distributed along the dam height, but the coupling between stress and seepage is not fundamentally considered. In practical engineering, the void ratio changes with stress, and the permeability coefficient of soil decreases with the decrement in void ratio. Therefore, the calculation results considering the change in void ratio in Scheme 2 are more consistent with the actual situation.

5 Conclusion

In this study, the bivariate permeability function of unsaturated soil is derived and introduced into ABAQUS program by subroutine development. A homogeneous earth dam is calculated for the verification of the model. The calculation results are compared and analyzed. The unsaturated seepage model considering bivariate of dry density and saturation can be introduced into the finite element method.

1) After considering bivariate of dry density and saturation, the calculated saturation is different from those without this consideration with the decrease in permeability coefficient of unsaturated soil.

2) The calculated saturation line considering bivariate of dry density and saturation has a tendency to move left lower than that without considering the influence of density on permeability coefficient.

3) When considering bivariate of dry density and saturation, the calculated pore water pressure in unsaturated region is smaller than that of the unsaturated seepage calculated by the traditional method.

4) The FV cloud picture is compared with the saturation cloud picture by using the custom field variable function in ABAQUS to verify that the subroutine is successfully called during the ABAQUS calculation.

5) The unsaturated seepage model considering bivariate of dry density and saturation can be introduced into the material model of ABAQUS Finite Element.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

FYL contributed to the conception of the study; LJZ executed numerical calculation; LJZ and BW contributed significantly to analysis and article preparation; FYL and DZ performed the data analyses and wrote the article.

Funding

This study was funded by the National Natural Science Foundation of China (No. 12072260) and the State Key Laboratory of Eco-hydraulics in Northwest Arid Region of China (No. QNZX-2019-07).

Conflict of Interest

BW was employed by the Company Ji Kan Research Institute of Engineering Investigation and Design, Co., Ltd. DZ was employed by the Company Yellow River Engineering Consulting Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, Z. (2014). On Basic Theories of Unsaturated Soils and Special Soils. Chin. J. Geotechnical Eng. 36 (2), 201–271. doi:10.11779/CJGE201402001

CrossRef Full Text | Google Scholar

Fan, J., Jiang, D., Liu, W., Wu, F., Chen, J., and Daemen, J. (2019). Discontinuous Fatigue of Salt Rock with Low-Stress Intervals. Int. J. Rock Mech. Mining Sci. 115 (3), 77–86. doi:10.1016/j.ijrmms.2019.01.013

CrossRef Full Text | Google Scholar

Fan, J., Liu, W., Jiang, D., Chen, J., Tiedeu, W. N., and Daemen, J. J. K. (2020). Time Interval Effect in Triaxial Discontinuous Cyclic Compression Tests and Simulations for the Residual Stress in Rock Salt. Rock Mech. Rock Eng. 53, 4061–4076. doi:10.1007/s00603-020-02150-y

CrossRef Full Text | Google Scholar

Fredrond, D. G., and Laharzo, H. (1997). Mechanics of Unsaturated Soils. Beijing: China Construction Press.

Google Scholar

Fu, J., and Jin, S. (2008). The Seepage Computation Based on Saturation Description. Chin. J. Hydrodynamics 23 (6), 668–674.

Google Scholar

Han, T., Li, Z., and Chen, Y. (2021). Sulfate Attack Induced Dry-Wet Failure Modes and a Constitutive Model for Mortar Specimens with a Single Intermittent Fracture. Int. J. Geomech. 21 (2), 04020249. doi:10.1061/(ASCE)GM.1943-5622.0001909

CrossRef Full Text | Google Scholar

Han, T., and Li, Z. (2021). Mechanical Characteristics and Freezing-Thawing Degradation Mechanism for Mortar Samples under Sodium Sulfate Solutions Attack. Arab J. Geosci. 14, 2069. doi:10.1007/s12517-021-08403-6

CrossRef Full Text | Google Scholar

Han, T., Shi, J., and Cao, X. (2016). Fracturing and Damage to Sandstone under Coupling Effects of Chemical Corrosion and Freeze-Thaw Cycles. Rock Mech. Rock Eng. 49 (11), 4245–4255. doi:10.1007/s00603-016-1028-7

CrossRef Full Text | Google Scholar

Han, T., Shi, J., Chen, Y., and Cao, X. (2018). Quantifying Microstructural Damage of sandstone after Hydrochemical Corrosion. Int. J. Geomech. 18 (10), 04018121. doi:10.1061/(ASCE)GM.1943-5622.0001237

CrossRef Full Text | Google Scholar

Han, T., Wang, X., Li, D., Li, D., Han, N., and Xing, F. (2019). Damage and Degradation Mechanism for Single Intermittent Cracked Mortar Specimens under a Combination of Chemical Solutions and Dry-Wet Cycles. Construction Building Mater. 213, 567–581. doi:10.1016/j.conbuildmat.2019.04.085

CrossRef Full Text | Google Scholar

Huang, S., Barbour, S. L., and Fredlund, D. G. (1998). Development and Verification of a Coefficient of Permeability Function for a Deformable Unsaturated Soil. Can. Geotech. J. 35, 411–425. doi:10.1139/t98-010

CrossRef Full Text | Google Scholar

Huang, S. Y., Barbour, S. L., and Fredlund, D. G. (1994). “A History of the Coefficient of Permeability Function,” in Proceedings of Sino-Canadian Symposium on Unsaturated/ Expansive Soils. China.

Google Scholar

Huang, T., Liao, X., Huang, Z., and Wang, R. (2021). Numerical Simulation of Ferrofluid Flow in Heterogeneous and Fractured Porous Media Based on Finite Element Method. Front. Earth Sci. 9. doi:10.3389/feart.2021.693531

CrossRef Full Text | Google Scholar

Jennings, J. E. B., and Burland, J. B. (1961). Limitation to the Use of Effective Stress in Partly Saturated Soils. Geotechnique 12 (2), 125–144. 10.1680/geot.1962.12.2.125.

Google Scholar

Jia, C., Huang, M., and Wang, G. (2007). Strength Reduction Fem in Stability Analysis of Soil Slopes Subjected to Transient Unsaturated Seepage. Chin. J. Rock Mech. Eng. 26 (6), 1290–1296.

Google Scholar

Jiang, D., Meng, W., Huang, Y., Yu, Y., Zhou, Y., Jiang, Z., et al. (2021). Characterization of Physical Field and Flow Assurance Risk Analysis of Subsea Cage-Sleeve Throttling Valve. Front. Earth Sci. 9. doi:10.3389/feart.2021.786996

CrossRef Full Text | Google Scholar

Kang, Y., Fan, J., Jiang, D., and Li, Z. (2021). Influence of Geological and Environmental Factors on the Reconsolidation Behavior of fine Granular Salt. Nat. Resour. Res. 30 (1), 805–826. doi:10.1007/s11053-020-09732-1

CrossRef Full Text | Google Scholar

Liu, B., Chen, J., and Ding, X. (2021). Research on Permeability Coefficient of Heterogeneous Geomaterials Based on Digital Images. Adv. Civil Eng. Technology) 2021 (1), 1–11. doi:10.13764/j.cnki.ncdg.2021.01.00110.1155/2021/6616546

CrossRef Full Text | Google Scholar

Liu, C., Chen, C., and Feng, X. (2005). Study on Mechanism of Slope Instability Due to Reservoir Water Level Rise. Rock Soil Mech. 26 (5), 769–773. doi:10.16285/j.rsm.2005.05.019

CrossRef Full Text | Google Scholar

Liu, F. Y., Zhang, Z., and Zhou, D. (2010). Saturation-density Dependent Permeability Function for Unsaturated Loess. SHUILI XUEBAO 41 (9), 1054–1060. doi:10.13243/j.cnki.slxb.2010.09.014

CrossRef Full Text | Google Scholar

Liu, N., Cui, L., and Wang, Y. (2020). Analytical Assessment of Internal Stress in Cemented Paste Backfill. Adv. Mater. Sci. Eng. 2020, 1–13. doi:10.1155/2020/6666548

CrossRef Full Text | Google Scholar

Liu, N., Li, N., Xu, C., Li, G., Song, Z., and Yang, M. (2020). Mechanism of Secondary Lining Cracking and its Simulation for the Dugongling Tunnel. Rock Mech. Rock Eng. 53 (9), 4539–4558. doi:10.1007/s00603-020-02183-3

CrossRef Full Text | Google Scholar

Liu, W., Zhang, X., Fan, J., Zuo, J., Zhang, Z., and Chen, J. (2020). Study on the Mechanical Properties of Man-Made Salt Rock Samples with Impurities. J. Nat. Gas Sci. Eng. 84, 103683. doi:10.1016/j.jngse.2020.103683

CrossRef Full Text | Google Scholar

Liu, W., Zhang, Z., Fan, J., Jiang, D., Li, Z., and Chen, J. (2020). Research on Gas Leakage and Collapse in the Cavern Roof of Underground Natural Gas Storage in Thinly Bedded Salt Rocks. J. Energ. Storage 31, 101669. doi:10.1016/j.est.2020.101669

CrossRef Full Text | Google Scholar

Lu, J., Fu, X., Kang, J., Cheng, M., and Wang, Z. (2021). Characterization of Full Pore and Stress Compression Response of Reservoirs with Different Coal Ranks. Front. Earth Sci. 9. doi:10.3389/feart.2021.764853

CrossRef Full Text | Google Scholar

Ma, Y., Chen, W., Bi, J., and Guo, G.-H. (2018). Influence of Dry Density on Coefficient of Permeability of Unsaturated Loess. Chin. J. Geotechnical Eng. 40 (S1), 165–170. doi:10.11779/CJGE2018S1027

CrossRef Full Text | Google Scholar

Mao, C. (2003). Analysis and Control of Seepage Calculation. Beijing: China Water Resources and Hydropower Press.

Google Scholar

Neuman, S. P. (1973). Saturated-unsaturated Seepage by Finite Elements. J. Hydr. Div. 99 (12), 2233–2250. doi:10.1061/jyceaj.0003829

CrossRef Full Text | Google Scholar

Shao, L., Wen, T., and Guo, X. (2019). Direct Measurement Method and Prediction Formula for Permeability Coefficient of Unsaturated Soils. Chin. J. Geotechnical Eng. 41 (5), 806–812. doi:10.11779/CJGE201905002

CrossRef Full Text | Google Scholar

Sheng, D., Gens, A., Fredlund, D. G., and Sloan, S. W. (2008). Unsaturated Soils: From Constitutive Modelling to Numerical Algorithms. Comput. Geotechnics 35, 810–824. doi:10.1016/j.compgeo.2008.08.011

CrossRef Full Text | Google Scholar

Sun, J., Xiao, X., Wei, Q., Cheng, P., and Tian, H. (2021). Occurrence of Irreducible Water and its Influences on Gas-Bearing Property of Gas Shales from Shallow Longmaxi Formation in the Xishui Area, Guizhou, Southern China. Front. Earth Sci. 9. doi:10.3389/feart.2021.654136

CrossRef Full Text | Google Scholar

Tang, H., Ma, S., Liu, Y., and Jia, H. (2002). Stability and Control Measures of Zhaoshuling Landslide Badong County Three Gorges Reservoir. Earth Science-Journal China Univ. Geosciences 27 (5), 621–625.

Google Scholar

Tao, G., Wu, X., and Gan, S. (2019). Experimental Study and Model Prediction of Permeability Coefficient of Unsaturated clay with Different Initial Void Ratios. Rock Soil Mech. 40 (5), 1761–1770. doi:10.16285/j.rsm.2018.0857

CrossRef Full Text | Google Scholar

Wang, D., Tong, L., and Qiu, Y. (2013). Rankine's Earth Pressure Analysis of Unsaturated Soil under Condition of Rainfall Infiltration. Rock Soil Mech. 34 (11), 3192–3196. doi:10.16285/j.rsm.2013.11.017

CrossRef Full Text | Google Scholar

Wang, S., Tan, X., Xia, Y., Tian, B., and Liang, B. (2021). Progress on Modeling of Dynamic Productivity of Fractured Gas Condensate Reservoir Based on a Fluid-Solid Coupling Method. Front. Earth Sci. 9. doi:10.3389/feart.2021.722787

CrossRef Full Text | Google Scholar

Wang, X., Zhang, Z., Gong, R., and Wang, S. (2021). Pore Network Modeling of Oil-Water Flow in Jimsar Shale Oil Reservoir. Front. Earth Sci. 9. doi:10.3389/feart.2021.738545

CrossRef Full Text | Google Scholar

Wu, L. Z., and Zhang, L. M. (2009). Analytical Solution to 1D Coupled Water Infiltration and Deformation in Unsaturated Soils. Int. J. Numer. Anal. Meth. Geomech. 33, 773–790. doi:10.1002/nag.742

CrossRef Full Text | Google Scholar

Wu, M. (2009). Finite-element Algorithm for Richards' Equation for Saturated-Unsaturated Seepage Flow. SHUILI XUEBAO 40 (10), 1274–1279. doi:10.13243/j.cnki.slxb.2009.10.010

CrossRef Full Text | Google Scholar

Xie, Di., and Zhiyan, F. (2006). Consideration of Some Fundamental Viewpoints in Studying Effective Stress of Unsaturated Soils. Chin. J. Geotechnical Eng. 28 (2), 170–173. doi:10.1007/s00603-016-1028-7

CrossRef Full Text | Google Scholar

Xie, Q., Tian, D., and Jin-hui, L. (2019). Simulation of Seepage Flow on Soil Slope and Special Stress-Correction Technique. Rock Soil Mech. 40 (3), 879–892. doi:10.16285/j.rsm.2017.1827

CrossRef Full Text | Google Scholar

Xiong, G., Ruan, Y., and Yang, J. (2005). Analysis on Relation between Rainfall and Slope Stability. Chin. J. Underground Space Eng. 1 (6), 1017–1020.

Google Scholar

Yao, Y., Li, J., Xiao, Z., and Xiao, H. (2021). Soil-Water Characteristics and Creep Deformation of Unsaturated Expansive Subgrade Soil: Experimental Test and Simulation. Front. Earth Sci. 9. doi:10.3389/feart.2021.783273

CrossRef Full Text | Google Scholar

Yu, Y., Lin, H., Li, R., and Li, G. (2008). Stability Analysis of Unsaturated Soil Slope under Transient Seepage Flow State. Rock Soil Mech. 29 (11), 2892–2898. doi:10.16285/j.rsm.2008.11.016

CrossRef Full Text | Google Scholar

Zhang, T., Zhang, H., and Huang, W. (2020). Finite Element Analysis of the Stability of Unsaturated Soil Slope under Surface Water Drawdown Conditions. J. Chongqing Univ. 43 (6), 12–20. doi:10.11835/j.issn.1000-582X.2020.06.002

CrossRef Full Text | Google Scholar

Zhang, W., Yan, L., and Ling, D. (2006). Influence of Reservoir Water Level Fluctuations on Stability of Unsaturated Soil banks. J. Zhejiang Univ. (Engineering Science) 40 (8), 1365–1428.

Google Scholar

Zhang, X., Liu, W., Jiang, D., Qiao, W., Liu, E., Zhang, N., et al. (2021). Investigation on the Influences of Interlayer Contents on Stability and Usability of Energy Storage Caverns in Bedded Rock Salt. Energy 231, 120968. doi:10.1016/j.energy.2021.120968

CrossRef Full Text | Google Scholar

Zhang, Z. (2009). Experimental Study on Permeability Function of Unsaturated Soil and its Application. Xian: Xi'an University of Technology.

Google Scholar

Zhou, Y., Deng, A., and Lu, Q. (2018). A One-Dimensional Consolidation Model Considering Large Strain for Unsaturated Soil. Rock Soil Mech. 39 (5), 1675–1682. doi:10.16285/j.rsm.2017.1804

CrossRef Full Text | Google Scholar