Structural Vibration Analysis of Historical Drum Tower Structure Caused by Underground Train Running

The vibration induced by underground metro operation could have significant impacts on the safety of building structures. In this study, the dynamic response of the Nanjing Drum Tower affected by the metro line four operation was investigated by a three-dimensional FEM coupling train-track-tunnel-foundation-soil-basement–Drum Tower model performed on a 64 CPU parallel computing cluster platform. The results show that the vertical vibration caused by the subway operation has a more serious impact on the historical structure of the Drum Tower than the horizontal vibration. The vertical vibration attenuates rapidly from the basement bottom to the top of the tower. The horizontal vibration amplifies along the height of the historical building. The truss roof significantly weakens the vibration. As the speed of the train increases, the amplitude of horizontal and vertical vibration increases gradually from the bottom to the roof of the Drum Tower despite a relatively smaller increase for the horizontal vibration. As for the double-track operation case, the vertical vibration amplitude is much greater than that for the single-track operation, and no significant difference is observed in the horizontal direction. The amplitudes of horizontal vibration velocity for the basement and Drum Tower are 0.131 and 0.060 mm/s, respectively.

Introduction

Historical buildings, which may have a history of thousands of years, have undergone countless natural disasters and man-made damages. Hence, different degrees of damages are induced. Subway, one of the most important railway transportation tools in modern cities, may inevitably be designed to go through the adjacency of historical buildings due to traffic demands and space constraints. More severe vibration damages on these historical buildings have thus been caused by the metro train operation. For example, some historical masonry churches near rail transit lines in the Republic of Czech cracked due to the vibration caused by the running vehicles. Bata (1971) first studied the influence of traffic vibration on historical buildings, and some European scholars have done studies on the protection of historical buildings against traffic vibration in their own countries (Ellis, 1987; Clemente and Rinaldis, 1998). In China, many historical buildings were affected by the vibration of the subway, and the walls were cracked and damaged. Beijing Railway Line six was once planned to pass underneath the Forbidden City moat, but the tunnel was only 20 m away from the northwest turret of the Forbidden City. To avoid damage to the Forbidden City, the route had to be changed. Lines 8 and 16 have also been adjusted to avoid the Drum Tower and Changchun Tower. The running trains of Beijing–Shanghai caused unignorable vibrations to the Huqiu Pagoda in Suzhou. The Xi’an subway line 4 re-planned its route to avoid the Wild Goose Pagoda. Besides, the wood structure is the main form of the Chinese historical bell towers, drum towers, and other buildings, most of which take on frame structures. However, the structural and mechanical characteristics are very different from reinforced concrete buildings. Nevertheless, few studies on the influence of railway traffic load on historical wooden structures have been conducted. Taking Xi’an bell tower as the research background, some scholars established the 3-D finite element model of the bell tower, soil layer, and tunnel structure, and obtained the dynamic response of historical buildings under the vibration load of rail transit (Lei, 2010; Ma et al., 2010; Qian et al., 2010; Wang and An, 2010; Qian et al., 2012). However, oversimplification was made in the model, which led to a significant difference from the actual project.

The Nanjing Drum Tower is composed of the upper and lower parts (Figure 1A). The upper part is the wooden structure city building rebuilt in the early Qing Dynasty, the lower is the masonry arch basement preserved in the early Ming Dynasty. It is regarded as a typical historical high wooden-frame building and is protected by the government. Having experienced numerous natural disasters and man-made disturbances, the Drum Tower is damaged: cracks are found around the surfaces of the basement, a part of the cracks is chiseled, chiseled cracks have entered the masonry, and the bricks are cracking. A large area of cracking is found in the parapet painting layer around the top of the castle, and horizontal cracks are shown under the slab coping. The paints on the eave columns, columns, and wood beams of the tower have fallen off, the woods are cracked, and the surfaces are rotten. Leaks and dry shrinkage cracks are observed in the roof frame. Figures 1B,C show the damages of the Drum Tower. Figure 1D shows the relative position between the interval structure of the metro station and the Drum Tower. The Drum Tower is surrounded by ground and underground traffic. The operation of the subway is bound to bring significant vibration impact on the historical structure of the Drum Tower. Hence, it is very necessary to conduct an evaluation before the subway is opened to traffic.

FIGURE 1

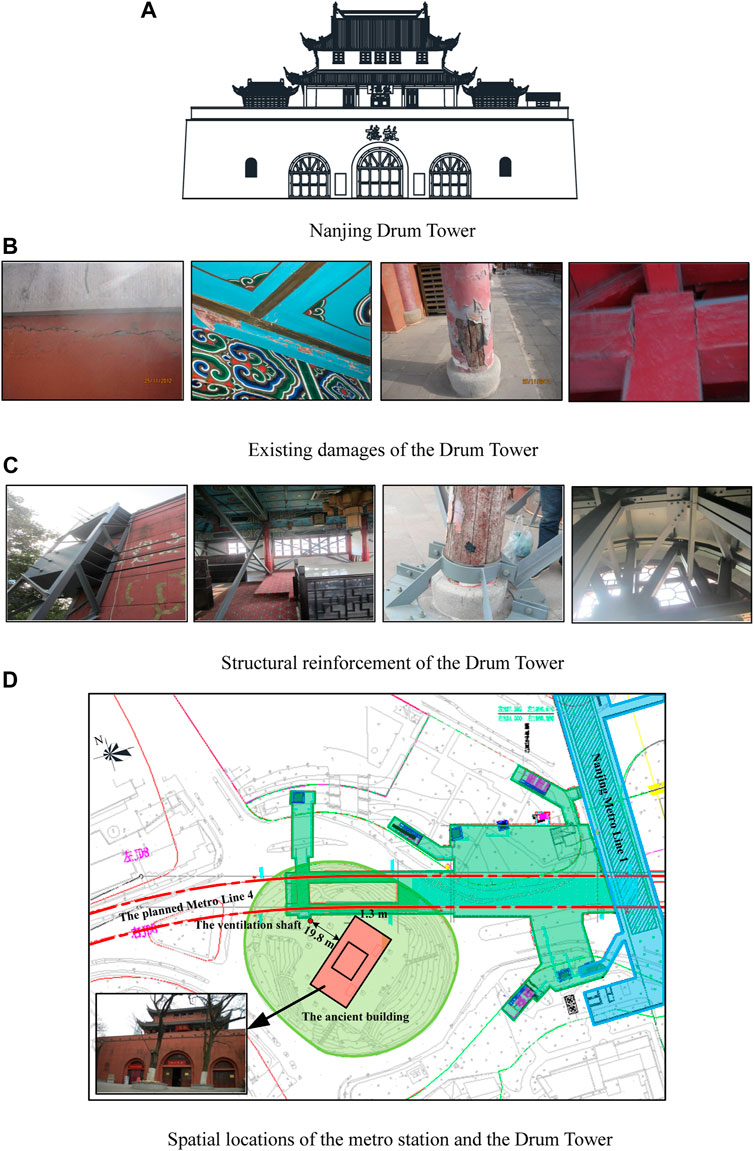
FIGURE 1. Overview of Nanjing Drum Tower. (A) Nanjing Drum Tower, (B) existing damages of the Drum Tower, (C) structural reinforcement of the Drum Tower, (D) spatial locations of the metro station and the Drum Tower.

Numerical Coupling Modeling

Numerical Model Parameters of Building and Foundation

The commercial finite element software Abaqus is used for 3D dynamic coupling simulation (Chen et al., 2011; Kan et al., 2011; Mao and Chen, 2011; Zhao et al., 2019). The model is composed of five parts: wooden-frame tower, basement, soil, tunnel, and vehicle–track system. The whole model is formed by defining the contact forms of each other. The Drum Tower and basement models are shown in Figure 2A. The mesh size should be large enough so that the external boundary can represent an infinitely extended medium, that is, at the two lateral boundaries, the horizontal and vertical displacements vanish. To eliminate the influence of soil far-field boundary on the calculation results, the left boundary was 35 m away from the castle, the right boundary was 55 m away from the right tunnel (about 8 times the tunnel diameter), and the lower boundary was 30 m away from the tunnel bottom plate (about 5 times the tunnel diameter). To obtain more accurate simulation results, a refined model was adopted, which was composed of 875,523 elements, among which there were 532,987 soil elements, 9,599 elements for the station structures and tunnel lining, 294,388 elements for the basement, and 33915 elements for the Drum Tower. The total degrees of freedom (DOF) were 2,817,333. Solid elements were used for the soil and basement, the beam and shell elements were used for the wooden-frame tower, and the shell elements were used for the tunnel lining. The Goodman interface element is used to model the interaction behavior between the soil and the tunnel segmental linings in the numerical model. In this study, we adopt $\Delta t$ = 10⁻⁵ s by the trial-and-error analysis to achieve the balance of computational efficiency and accuracy. Note that this dynamic explicit analysis takes around 3 days using the 64 CPU parallel computing cluster platform.

FIGURE 2

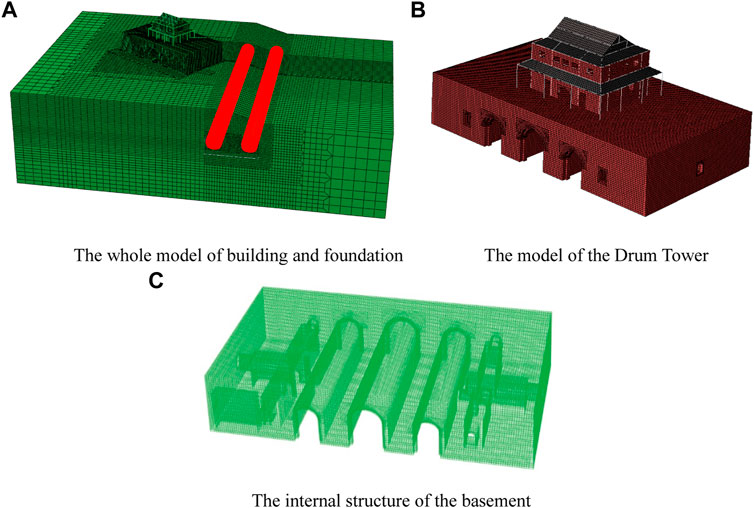
FIGURE 2. Finite element model of the Nanjing Drum Tower. (A) The whole model of building and foundation. (B) The model of the Drum Tower. (C) The internal structure of the basement.

The Drum Tower is a wooden structure like other historical buildings in China. The upper part of the tower can be divided into four layers: truss roof, paving layer, beam–column frame, and column base. This structure is similar to the frame structure. The load transmitted from the roof is mainly borne by the beam–column system and eventually transmitted to the column base, while the wall does not participate in the load-bearing system. The truss roof and beam–column system are simplified as space frame structures in the model. The beams, the columns, and the roof are interconnected to form a frame structural system, as shown in Figure 2B. The lower part of the tower is made of bricks. The interior is hollow and has a rich spatial structure. There are three coupons in the red wall, extending through the whole width of the tower, and the city structure and internal structure are shown in Figure 2C. In the upper part model, the deformation behavior was simulated by refining mesh, with an element size of 0.3 × 0.3 × 0.3 m. For the key parts such as the entrance of doors and windows in the basement, a more refined mesh was used to truly reflect the deformation characteristics of the vulnerable area of the structure.

According to the on-site detection and evaluation, lots of vertical cracks were found in the wall, and some had extended through the masonry and might lead to a more complicated mechanical behavior. For the sake of convenience, the initial mechanical parameters of Nanjing Drum Tower were selected by referring to the investigation result of the Xi’an historical Bell Tower structure that was built at the close time. Then, an inversion analysis based on the natural vibration characteristics test of the Drum Tower structure in the early stage was carried out. The model parameters of the historical structure (i.e., the wooden-frame tower and the basement) are calibrated by back analysis of the field testing on the natural frequency of the historical structure incorporating the damage-induced material deterioration as shown in Figure 1, as well as by the testing results of historical buildings conducted by Professor Yu Maohong’s research group in Xi’an Jiaotong University for many years, as shown in Table 1. The normal DOF was fixed by the model side, and the underside displacement freedom of the model was constrained in three directions. The grids near the tunnel and the city threshold were densely divided, while the grids in the far area were gradually sparser. This strategy can not only ensure sufficient calculation accuracy but also reduce the number of DOF as much as possible. The Davidenkov viscoelastic constitutive model was used to describe the dynamic nonlinear characteristics of the soil. We implemented the Davidenkov model in Abaqus as a user-defined-model routine by using Fortran (Zhao et al., 2021). The constants A, B, and r₀ of the Davidenkov model can be calibrated by the modulus reduction and damping curves obtained by conventional cyclic laboratory tests. Its specific parameters are shown in Table 2.

TABLE 1

TABLE 1. Computational parameters of the model.

TABLE 2

TABLE 2. Soil profile and parameters of the Davidenkov model.

Vehicle–Track Coupling System

The running vehicle–track system can be regarded as a multi rigid body system imposed with a certain speed, which is determined according to the real metro operation (Zhai, 2020). The vertical model was simulated by a secondary suspension (Figure 3A). Its specific parameters are shown in Table 3. The wheelsets, bogies, and carriages were simplified as rigid bodies with a symmetric center of mass, which are all connected by spring damping. The finite element model of the train is shown in Figure 3B. Its specific parameters of slab ballastless track are shown in Table 4. The track was simulated by beam elements, and the spring and damping were simulated by the fastening and gel pad (Figure 3C), respectively. The rest are simulated by solid elements. The coupling mode between the wheel and rail was simulated by the rolling contact. The penalty contact algorithm and the finite slip displacement formulation were applied to describe the contact behaviors between the wheel and rail. The normal action between the wheel and rail adopted forced contact, and the tangential action adopted friction of penalty.

FIGURE 3

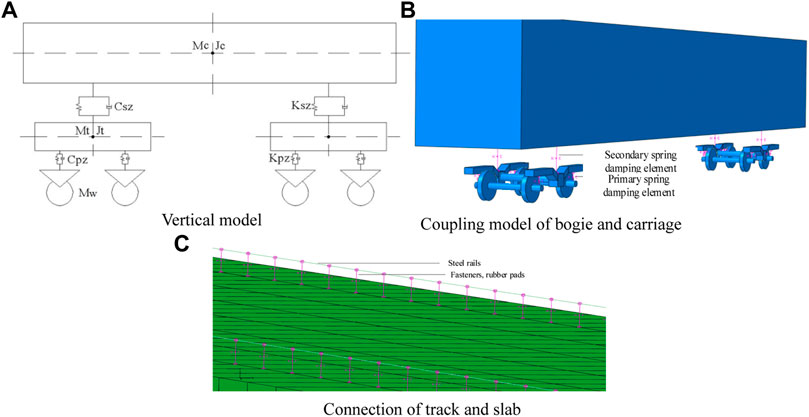
FIGURE 3. Finite element coupling model of the train. (A) Vertical model. (B) Coupling model of bogie and carriage. (C) Connection of track and slab.

TABLE 3

TABLE 3. Parameters of the vehicle model.

TABLE 4

TABLE 4. Parameters of the slab track.

Results and Discussion

Natural Frequency Analysis

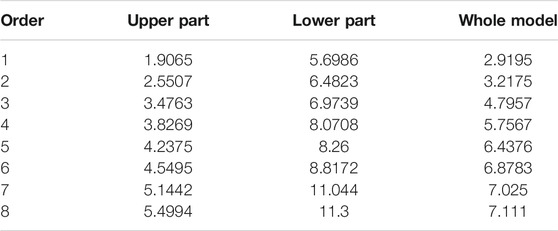
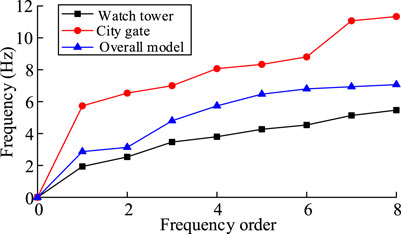
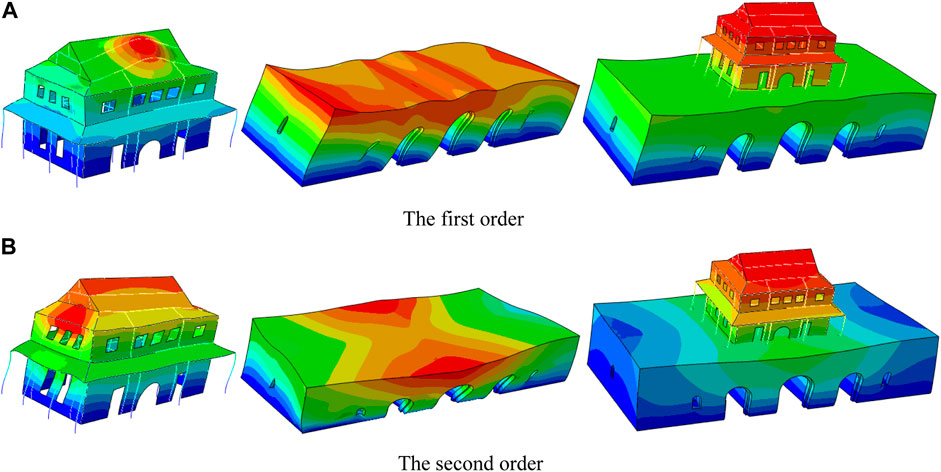
Table 5 shows the calculated natural frequency of each order of the Drum Tower model of a high watchtower on either side of a basement wooden structure, and Figure 4 shows the variation curve of natural frequency. It can be seen that the natural frequencies of the watchtower on either side of a basement model and the overall model are relatively dense, the adjacent frequencies have little difference, and the performance is relatively stable. The second, third, fifth, and sixth frequency of the monument building model differ greatly, and the difference between the other frequencies is small, indicating that the natural frequency of the wooden-frame structure model changes greatly and is easy to disperse, and thus the performance is not very stable. Figure 5 shows the first two vibration modes of the three finite element models.

TABLE 5

TABLE 5. Natural frequency of the Drum Tower model.

FIGURE 4

FIGURE 4. Variation trend of the natural frequency of the Drum Tower model.

FIGURE 5

FIGURE 5. Vibration modes of the Drum Tower model. (A) The first order. (B) The second order.

Time–History Analysis

Vibration velocity is a common physical quantity to measure the impact of environment vibration on the historical buildings. The vibration speed and frequency are directly related to the damage of frame structure, and can directly reflect the damage intensity and the energy of structure response to vibration. Therefore, these two indices play an important role in the evaluation of the impact of environment vibration on the historical buildings. Figure 6 shows the time–history curves of horizontal and vertical vibration velocities at the Drum Tower and the basement caused by subway operation, respectively. It can be seen that the vertical vibration velocity is greater than the horizontal vibration velocity at the Drum Tower and the basement under subway operation loading.

FIGURE 6

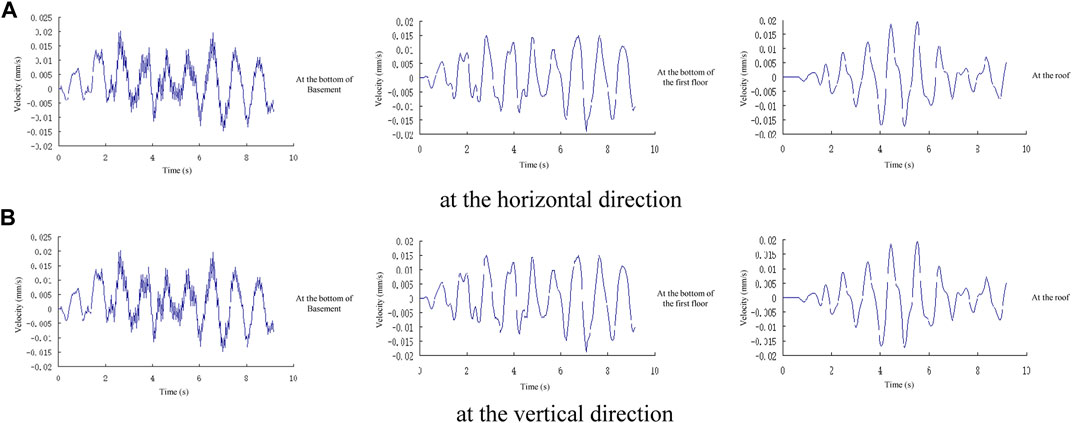
FIGURE 6. The time–history curve of vibration velocity (A) at the horizontal direction, (B) at the vertical direction.

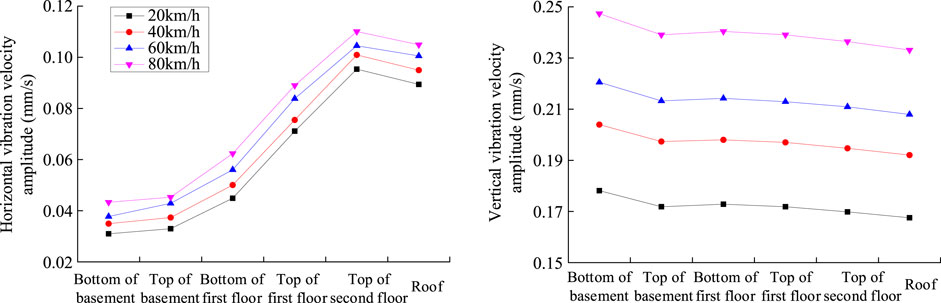
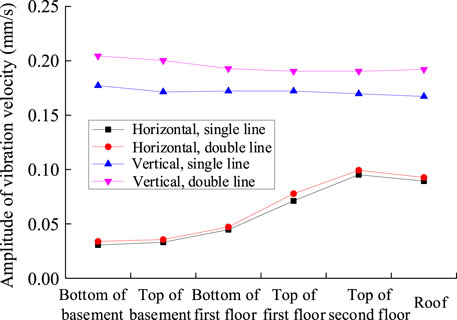
The amplitude of vibration velocity at different positions of the Drum Tower in Figure 7 illustrates that:

1) When the subway runs through the Drum Tower at a speed of 20 km/h, the maximum horizontal and vertical vibration speeds at the basement are 0.033 and 0.178 mm/s, respectively. The maximum horizontal and vertical vibration speeds at the Drum Tower are 0.095 and 0.173 mm/s, respectively. When the subway runs through the Drum Tower at a speed of 40 km/h, the horizontal and vertical vibration amplitudes are 0.038 and 0.203 mm/s at the basement, and 0.101 and 0.198 mm/s at the Drum Tower, respectively. When the subway runs at a speed of 60 km/h through the Drum Tower, the horizontal and vertical vibration velocities are 0.044 and 0.204 mm/s at the basement, and 0.106 and 0.236 mm/s at the Drum Tower, respectively. When the subway runs through the Drum Tower at a speed of 80 km/h, the horizontal and vertical vibration speeds reach 0.105 and 0.22 mm/s at the basement, and 0.11 and 0.236 mm/s the Drum Tower, respectively.

2) From the bottom of the basement to the roof of the Drum Tower, the horizontal vibration increases gradually, but decreases at the roof; the vertical vibration attenuates gradually along the height of the historical structure. The reasons are as follows: the horizontal vibration of the frame structure is generally amplified along the structure height. However, the lateral stiffness and weight of the truss roof of the Drum Tower is greater, which can prevent the horizontal vibration propagation. The transmission of vertical vibration is a simple energy attenuation process. The masonry structure of the basement is able to absorb energy, which therefore leads to a faster attenuation.

3) With the increase of vehicle speed, the horizontal and vertical vibration amplitudes gradually increase from the bottom of the basement to the roof of the Drum Tower, and the vibration intensifies with the increase of vehicle speed. The attenuation trend increases with the increase of vehicle speed. The vertical vibration increases significantly, while the amplification of horizontal vibration is relatively small.

4) When the vehicle speed is low (20 km/s and 40 km/s), the horizontal vibration increases from the bottom of the basement to the roof of the Drum Tower. But when the vehicle speed is high (60 km/s and 80 km/s), the horizontal vibration maintains an increasing trend in the basement but decreases in the Drum Tower, and the attenuation degree increases with the increase of vehicle speed.

FIGURE 7

FIGURE 7. The amplitude of vibration velocity at different parts of the Drum Tower.

Figure 8 shows the comparison of vibration caused by double-track operation and single-track operation when the vehicle speed is 40 km/h. It can be seen that when the train runs on double-track, the vertical vibration amplitude is significantly higher than that on single-track, but the horizontal direction slightly changes. According to Technical Specifications for protection of historic buildings against man-made vibration (GB/T50452-2008) issued by the Ministry of Housing and Urban–Rural Development, PRC, the allowable vibration speeds of Drum Tower (wooden structure) and the basement (masonary structure) in provincial cultural relics protection units are 0.27 mm/s (horizontal direction) and 0.25 mm/s (horizontal direction), respectively. The numerical results show that the maximum horizontal vibration velocity amplitudes of the Drum Tower and the basement are 0.105 mm/s and 0.045 mm/s, respectively, which meet the limit requirements of the specification.

FIGURE 8

FIGURE 8. Comparison of vibration caused by single and double line operation.

Conclusion

A three-dimensional finite element model of vehicle-railway-viaduct-foundation coupling model was established for evaluating the dynamic response of the Nanjing Drum Tower affected by the metro line four operation. The characteristics of ground vibration caused by the train operation under different working conditions were investigated, and the attenuation curve of ground vibration level with the increase of distance from bridge pier was analyzed by parameterization. Some main conclusions were obtained as follows:

1) When the subway runs at a speed of 80 km/h through the drum tower, the maximum horizontal and vertical vibration speeds at the basement are 0.045 and 0.47 mm/s, respectively. The maximum horizontal and vertical vibration speeds of the Drum Tower are 0.011 and 0.236 mm/s, respectively.

2) From the bottom of the basement to the roof of the Drum Tower, the horizontal vibration increases gradually but decreases at the truss roof. The vertical vibration decreases, and the decrease from the bottom to the top of the basement is relatively greater.

3) With the increase of vehicle speed, the amplitude of horizontal and vertical vibration increases gradually from the bottom of the basement to the roof of the Drum Tower, but the amplitude of horizontal vibration is relatively small. When the train is running on double track, the vertical vibration amplitude is significantly higher than that on single track, but the horizontal vibration amplitude changes little.

4) According to the numerical calculation results, the vertical vibration of the historical structure caused by train operation is much greater than the horizontal vibration. However, the current code demands the limiting requirements at the horizonal vibration, neglecting the vertical vibration.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

Investigation and data analysis of the work, YZ and XB; Funding acquisition and formal writing of the work, SW and HS; review of the work, KZ and HW. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. 41902282).

Conflict of Interest

Author YZ was employed by The 4th Construction Co., Ltd. of China 15th Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bata, M. (1971). Effects on Buildings of Vibrations Caused by Traffic. Building Sci. 6 (4), 221–246. doi:10.1016/0007-3628(71)90014-4

CrossRef Full Text | Google Scholar

Chen, G. X., Chen, L., Jing, L. P., and Long, H. (2011). Comparison of Implicit and Explicit Finite Element Methods with Parallel Computing for Seismic Response Analysis of Metro Underground Structures. J. China Railway Soc. 33 (11), 111–118. doi:10.3969/j.issn.1001-8360.2011.11.019

CrossRef Full Text | Google Scholar

Clemente, P., and Rinaldis, D. (1998). Protection of a Monumental Building against Traffic-Induced Vibrations. Soil Dyn. Earthquake Eng. 17 (5), 289–296. doi:10.1016/S0267-7261(98)00012-8

CrossRef Full Text | Google Scholar

Ellis, P. (1987). Effects of Traffic Vibration on Historic Buildings. Sci. Total Environ. 59, 37–45. doi:10.1016/0048-9697(87)90429-3

CrossRef Full Text | Google Scholar

Kan, S. Z., Chen, G. X., and Chen, L. (2011). Construction and Optimization of Parallel Computing Cluster Platform Based on Abaqus Software. J. Disaster Prev. Mitigation Eng. 33 (11), 111–117. doi:10.1016/S1874-8651(10)60080-4

CrossRef Full Text | Google Scholar

Lei, Y. S. (2010). Research on Protective Measures of City Wall and BellTower Due to underneath Crossing Xi'an Metro Line No.2. Rock Soil Mech. 31 (1), 223–236. doi:10.16285/j.rsm.2010.01.006

CrossRef Full Text | Google Scholar

Ma, M., Liu, W., and Ding, D. (2010). Influence of Metro Train-Induced Vibration on Xi'an Bell Tower. Beijing Jiaotong Daxue Xuebao/Journal Beijing Jiaotong Univ. 34 (4), 88–92. doi:10.3969/j.issn.1673-0291.2010.04.0088.05

CrossRef Full Text | Google Scholar

Mao, K., and Chen, G. (2011). Construction of Parallel Computing Heterogeneous Cluster Platform Based on Abaqus Software. J. Earthquake Eng. Eng. Vibration 31 (5), 184–189. doi:10.13197/j.eeev.2011.05.009

CrossRef Full Text | Google Scholar

Qian, C. Y., Zheng, J. G., and Dong, X. (2012). Dynamic Response of Xi'an Bell Tower under the Situation of Metro Train Running. J. Guilin Univ. Technology 32 (3), 375–380. doi:10.3969/j.issn.1674-9057.2012.03.017

CrossRef Full Text | Google Scholar

Qian, C., Zheng, J., and Song, C. (2010). Dynamic Response Analysis of Bell Tower Foundation Induced by Train Running on Metro in Xi'an. World Earthquake Eng. 16, 177–181. doi:10.3969/j.issn.1007-6069.2010.04.0177.05

CrossRef Full Text | Google Scholar

Wang, X., and An, X. (2010). Dynamic Response of a Timber Structure with High-Platform Foundation under Traffic Loads. Mech. Eng. 32 (4), 40–46. doi:10.6052/1000-0992-lxysj2009-463

CrossRef Full Text | Google Scholar

Zhai, W. (2020). Vehicle–Track Coupled Dynamics: Theory and Applications. Singapore: Springer.

Google Scholar

Zhao, K., Wang, Q., Chen, Q., Zhuang, H., and Chen, G. (2021). Simplified Effective Stress Simulation of Shear Wave Propagation in Saturated Granular Soils. Géotechnique Lett. 11 (1), 1–22. doi:10.1680/jgele.19.00023

CrossRef Full Text | Google Scholar

Zhao, K., Wang, Q. Z., and Mao, K. M. (2019). 3D FE Analysis on Building Vibration Induced by Train Running. J. Disaster Prev. Mitigation Eng. 39 (2), 209–216. doi:10.13409/j.cnki.jdpme.2019.02.003

CrossRef Full Text | Google Scholar