A Granular Thermodynamic Model to Describe the Temperature/Mechanical Characteristics of Sandy Soil

Based on the granular-solid-hydrodynamic theory, the constitutive model considering the thermo-hydro-mechanical (THM) coupled action is established, and the dilatancy property of sandy soil under coupled high mechanical pressure and temperature is simulated. The relationship between the energy dissipation and the macroscopic stress-strain changes at the grain level of saturated sandy soil is connected by defining the transfer coefficient and the energy function, without considering the concepts of yield surface and hardening parameters in classical plastic mechanics. Additionally, the changes in temperature, relative density and confining pressure during the shearing process cause particle rolling, slipping and friction. The energy dissipation in this process is described by defining the concept of particle entropy and particle temperature. In the calculation, the isotropic compression test, drained and undrained shear test of sandy soil under high stress are simulated respectively. The validity of the model is proved by comparing with the test results. Meanwhile, the stress-strain relationship and pore pressure variation law of sandy soil under different temperatures are predicted. The results show that the effect of temperature on shear strength is limited, and the pore pressure will gradually increase and become stable with the increase of temperature. Thus, this work establishes the soil THM coupled model from the perspective of micro energy dissipation, which can provide new theoretical support for the prediction of natural disasters such as landslides and debris flow.

Introduction

In mountainous areas, under the action of high ground stress, water flow and temperature, sandy soil will be disturbed by the construction of gravity dams, deep-buried tunnels and other large-scale projects, which will generate pore water pressure in the sandy soil, and cause particles to roll or even break (Bai et al., 2014; Wang et al., 2021). This process intensifies the occurrence of natural disasters such as debris flow and landslide, and seriously affects the environmental change and sustainable development in mountainous areas (Bai et al., 2018; Zhou et al., 2021). Through the triaxial drained and undrained shear tests of sandy soil under high confining pressure and temperature, researchers found that the higher the confining pressure, the more obvious the strain softening trend of sandy soil samples. Meanwhile, with the increase of the confining pressure, the axial strain at failure reaches the peak value, then decreases, and the volumetric strain gradually changes from dilatancy to shear shrinkage (Billam, 1971; Bai et al., 2021a). Attempts have been made to consider the factors that influence the mechanical properties of sandy soil including initial density, temperature and stress level. Researchers (Bai and Li, 2013; Bai et al., 2020a; Taherdangkoo et al., 2020a) introduced that the sand particles were broken obviously under high stress, and the isotropic compression curves of different initial density samples finally coincided with each other. At the same time, when the confining pressure is large enough, the initial relative density has little effect on the stress-strain relationship and pore pressure, and the sandy soil sample shows the nature of normally consolidated clay. Hagerty et al. (1993) divided the compression characteristics of sandy soil into three stages through one-dimensional compression test: under low pressure, the volume of sample decreases due to the rearrangement of particles; under high pressure, the crushing and rearrangement of sand particles produce stronger compression performance; under higher pressure, the contact between particles increases greatly, and the material properties are controlled by particle crushing. The results of the above experiments provide guidance for the establishment of constitutive relationship of sandy soil under high stress.

In the earlier studies considering the impact of particle breakage on the mechanical properties of sandy soil, a variety of mathematical models were established by the modification and expansion of the existing soil model. Scholars (Taherdangkoo et al., 2020b; Meng et al., 2020; Bai et al., 2021b) have improved the yield surface or hardening law in the Cambridge model and established the constitutive model of sandy soil by using the unrelated flow law, which can well predict the characteristics of sandy soil. Meanwhile, the theory of sub plasticity based on thermodynamics has been increasingly applied in the establishment of sand’s constitutive model. The theory uses tensor function as a tool, abandons the concepts of strain decomposition into elastic strain and plastic strain, yield surface and loading and unloading in traditional elastic-plastic theory, and directly establishes the relationship between stress rate and strain rate (Wu and Kolymbas, 1990; Bai, 2006a; Cui et al., 2021). In order to describe the material state change of sandy soil during loading, some scholars introduced state parameters into the constitutive relation of sandy soil. Been and Jefferies (1985) successfully carried out a series of triaxial test against Kogyuk sand and proposed the concept of state parameters, which have been used by many researchers to study the dilatancy of sandy soil. For better reflection of the deformation behavior of saturated sandy soil in general stress space, Manzati and Dafalias (1997) established a constitutive model, which was based on the basic framework of critical state soil mechanics, and combined the theory of bilateral plastic model with state parameters. Rowe (1962) verified that the dilatancy of granular soil was controlled by the distribution of contact stress between particles through experiments on different materials, and deduced the stress dilatancy relationship under plane strain condition on the assumption that the minimum energy ratio is reached when the soil is damaged. Bolton (1986) proposed to use dilatancy index to reflect the current state of sandy soil, which can estimate the dilatancy of sandy soil samples. However, the constitutive equations used in these models cannot effectively describe the coupled characteristic of soil under multi field action, and are only suitable for soil samples under a certain condition.

Different from the above methods, some scholars used the granular-solid-hydrodynamic (GSH) theory, which has been applied in solid materials such as polymers and crystals, to establish the constitutive model of soil. The GSH theory is based on the method of fluid dynamics, and constructs the constitutive relationship of materials on the basis of non-equilibrium theory and physical conservation law. Using the definitions of particle entropy and particle temperature, Jiang and Liu (2009) established the theoretical constitutive model of single granular material, which can comprehensively consider the macro and micro behaviour of granular material. On this basis, some researchers (Zhang and Cheng, 2017; Bai et al., 2019a) extended the GSH theory to saturated soil and unsaturated soil, respectively, to simulate the mechanical characteristics of related soil, which confirmed the effectiveness of the model. Bai et al. (2019b) further extended the theory and focused on the factors that influence the characteristics of unsaturated soil including over consolidation ratio, temperature and stress path. The traditional plastic theory is to choose the yield function, plastic potential surface and hardening function independently, which is not rigorous enough in theory, and GSH theory can effectively avoid this point (Bai et al., 2019b). In addition, the constitutive equation of soil based on the GSH theory can automatically meet the first and second laws of thermodynamics. However, taking into account the complexity of the interaction between the various phases in the soil, the application of the theory in various types of soil needs to be further promoted.

In the present study, based on the GSH theory and the dilatancy equation considering the state variables, a THM coupled model is established, and the shear test of saturated sandy soil under the coupled action of temperature and stress is simulated. The new THM coupled model considers the energy dissipation of sandy soil material from the micro mechanism by using the linear non-equilibrium theory and the critical state theory, and further defines the entropy and temperature of the particle to link the energy dissipation at particle level with the change of system energy. The effectiveness of the proposed model is verified by the simulation of sandy soil samples under different initial void ratios and confining pressures. The simulation tests include isotropic compression test, drained and undrained shear test. At the same time, based on undrained test, the stress-strain relationship and pore pressure change of sandy soil under different temperatures are predicted, which provides a reference for the development of follow-up experiments.

Methods

Granular-Solid-Hydrodynamic Theory in Sandy Soil

It is assumed that both the solid and liquid phases of geomaterials are incompressible and have the same temperature at the same location. In the closed system, the change of internal energy of granular materials caused by unit time and unit volume can be divided into two categories: recoverable energy and irrecoverable energy. For granular materials, the irrecoverable energy dissipation is mainly due to the sliding, collision, rolling and friction between granular materials, while the recoverable energy is mainly due to the mutual extrusion between particles, which transforms the external input energy into elastic potential energy for storage. Thus, the composition of energy density of granular materials in the closed system can be obtained, as shown in Eq. 1:

$w=w_e+w_g+w_k+w_0(1)$

where $w_e$ is the elastic potential energy stored by the granular material under the action of external force; $w_g$is the irrecoverable energy produced in the mesoscopic scale; $w_k$is the kinetic energy of the granular material itselfp; w is the energy density in isolated system; $w_0$is the heat energy of the material itself in the closed system.

In addition, when characterizing the independent state variables of granular materials, there are inelastic collisions between particles in the mesoscopic scale of granular materials. This further results in the dissipation of system energy, which shows as the change of system entropy. Jiang and Liu (2009) linked the entropy generation caused by the dissipation of granular materials at mesoscopic level with the change of macroscopic entropy, and determined the thermodynamic independent state variable $\left\{i.e\text{.,}.,\rho ,m_i,S,S_g,{\epsilon }_{ij}^e\right\}$ and their conjugate quantities of granular materials$\left\{i.e.,u_c,v_i,T,T_g,{\pi }_{ij}\right\}$. By constructing thermodynamic identities, the energy density expression is obtained:

$\text{d}w={\pi }_{ij}{\text{d}}_{\text{t}}{\epsilon }_{ij}^e+T_g\text{d}{S}_g+T\text{d}S+u_c\text{d}\rho +v_i\text{d}{m}_i(2)$

In combination with Eq. 1, it is concluded that:

$w_e={\pi }_{ij}{\text{d}}_{\text{t}}{\epsilon }_{ij}^e(3)$

$w_g=T_g\text{d}{S}_g(4)$

where $T_g$ is the particle temperature; ${\pi }_{ij}$is the elastic stress; ${\epsilon }_{ij}^e$ is the elastic strain; $T$ is the material temperature; $S$ is material entropy; $u_c$ is the chemical potential; $\rho$ is the material density; $S_g$ is particle entropy; $v_i$ is the velocity; $m_i$ is momentum.

According to the second law of thermodynamics, the entropy transformation rate R caused by the irreversible process in the closed system is always greater than zero. The higher the entropy of the system, the closer the isolated system will be to the equilibrium state, and the entropy will reach the maximum. The linear non-equilibrium theory defines the factor that drives the closed system to deviate from the equilibrium state as dissipative force, and the energy dissipation caused by the unit dissipative force in unit time is called dissipative flow. At the same time, when the system is close to the equilibrium state, it can be considered that there is a linear relationship between the dissipative force and the dissipative flow. The dissipative force $\left\{i.e.,{\pi }_{ij},T_g,{\nabla }_{i}T,{\text{d}}_t{\epsilon }_{ij},{\psi }_{ij}^l,{\psi }_{ij}^g\right\}$ and the corresponding dissipative flow $\left\{i.e{\text{., d}}_t{\epsilon }_{ij}^p,I_g,\frac{q_k}{T},{\sigma }_{ij}^{vs},{\sigma }_{ij}^{vL},{\sigma }_{ij}^{vG}\right\}$ of granular materials in the closed system can be determined by using the conservation equations of mass, momentum and energy combined with the entropy increasing equation of the closed system. It shows that the elastic stress ${\pi }_{ij}$ and the plastic strain rate ${\text{d}}_t{\epsilon }_{ij}^p$ are the corresponding dissipative force and flow. The dissipative force and dissipative flow at the particle level are ${\sigma }_{ij}^{vg}$ and ${\text{d}}_t{\epsilon }_{kl}$, respectively, which can be used to represent the entropy generation rate of particles R_g at the mesoscopic level (Yang and Bai, 2019). The following results can be obtained:

${\text{d}}_t{\epsilon }_{ij}^p={\mathit{\eta }}_{\mathit{i}jkl}{\pi }_{ij}(5)$

${\sigma }_{ij}^{vg}={\lambda }_{ijkl}^g{\text{d}}_t{\epsilon }_{kl}(6)$

where ${\eta }_{ijkl}$ is the transfer coefficient corresponding to the elastic stress ${\pi }_{ij}$, ${\lambda }_{ijkl}^g$ is the transfer coefficient at the particle level.

According to the basic function form of the elastic potential energy density function of cohesive soil materials given by Bai et al. (2019b) and the basic concept of the specific elastic energy proposed by Jiang and Liu (2007), for the saturated sandy soil without considering the influence of the cohesive force, the expression of the elastic potential energy stored in the sandy soil under the action of temperature is obtained as follows:

${\omega }_e=B{\left(\Delta +{\beta }_T\Delta T\right)}^{\beta }\left[{({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T})}^2+\xi {\left(u_s\right)}^2\right](7)$

where B is the parameter describing the degree of hardness or softness of the material. ${\beta }_T$ is the thermal expansion coefficient of soil, ${\epsilon }_v^e$is the elastic volume strain ${\epsilon }_v^e={\epsilon }_{kk}^e$, $u_s$is the elastic shear strain ${\epsilon }_{\text{s}}^e$, $\xi$is the friction angle coefficient, e is the void ratio, $\beta$reflects the material property of sandy soil, and$\lambda$is the slope of e-logp curve in consolidation test of sandy soil sample. Combined with the isotropic compression consolidation curve, B is assumed to be the form$B=B_{0}exp(-\frac{e}{\lambda })$.

By using the Expressions (3), (4) and (5) and referring to the expressions ${\eta }_{ijkl}$ in reference (Yang and Bai, 2019; Bai et al., 2021c), the elastic stress and plastic strain rate are obtained:

${\pi }_{ij}=\frac{\partial {\omega }_e}{\partial {\epsilon }_{ij}^e}=B\left[\left(2+\beta \right){\left({\epsilon }_v^e+{\beta }_T\Delta T\right)}^{\beta +1}{\delta }_{ij}+\beta \xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{\beta -1}{\left({\epsilon }_{\text{s}}^e\right)}^2{\delta }_{ij}+2\xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{\beta }{e}_{ij}^e\right](8)$

${\text{d}}_t{\epsilon }_{ij}^p={\eta }_v{\left(T_g\right)}^{0.5}{\epsilon }_v^e{\delta }_{ij}+{\eta }_s{\left(T_g\right)}^{0.5}{e}_{ij}^e(9)$

where elastic stress ${\pi }_{ij}$is equal to the effective stress between particles (Jiang et al., 2017), $e_{ij}^e$is the elastic deviator strain $e_{ij}^e={\epsilon }_{ij}^e-\frac{1}{3}{\epsilon }_{kk}^e{\delta }_{ij}$, ${\eta }_v$ and ${\eta }_s$ are the corresponding transfer coefficients.

When the sandy soil is in the critical state, there exists liquefaction phenomenon. At this time, the elastic volume strain ${\epsilon }_v^e$ is 0, the average effective stress $p\prime$ is 0, and $\beta$will be taken as 1.5. Combined with Eq. 8, the specific expressions of average effective stress and shear stress q are obtained as follows:

$p\prime =\frac{1}{3}{\pi }_{kk}=B\left[3.5{\left({\epsilon }_v^e+{\beta }_{\mathrm{T}}\Delta \mathrm{T}\right)}^{2.5}+1.5\xi {\left({\epsilon }_v^e+{\beta }_{\mathrm{T}}\Delta \mathrm{T}\right)}^{0.5}{\left({\epsilon }_s^e\right)}^2\right](10)$

$q=\sqrt{\left({\pi }_{ij}-p\text{'}{\delta }_{ij}\right)\left({\pi }_{ij}-p\text{'}{\delta }_{ij}\right)}=\sqrt{6}B\xi {\left({\epsilon }_v^e+{\beta }_{\mathrm{T}}\Delta \mathrm{T}\right)}^{1.5}{\epsilon }_s^e(11)$

In reference Jiang and Liu (2009), the energy carried by particle motion is expressed as $w_g$ = $\frac{1}{2}b{\rho }_s{\left(T_g\right)}^2$. According to the linear non-equilibrium theory, the entropy generation rate at the particle level is $R_g={\sigma }_{ij}^{vg}{\text{d}}_t{\epsilon }_{kl}$. The motion equation of particle entropy at the mesoscopic level is obtained by combining Eqs 4–6

${\text{d}}_t\left(T_g\right)=\frac{{\mathit{\lambda }}_{sg}}{b}\frac{{\left({\text{d}}_t{e}_{ij}\right)}^2}{{\rho }^s}+\frac{{\mathit{\lambda }}_{vg}}{b}\frac{{\left({\text{d}}_t{\epsilon }_v\right)}^2}{{\rho }^s}+\frac{\varsigma }{b}\frac{{\text{d}}_{t}T}{{\rho }^s}-\frac{\gamma }{b}\frac{T_g}{{\rho }^s}(12)$

For the convenience of parameter calculation, Eq. 12 is simplified as follows:

${\text{d}}_t\left(T_{gg}\right)=c_2{c}_5\frac{{\left({\text{d}}_t{e}_{ij}\right)}^2}{{\rho }^s}+c_3{c}_5\frac{{\left({\text{d}}_t{\epsilon }_v\right)}^2}{{\rho }^s}+c_4\frac{{\text{d}}_{t}T}{{\rho }^s}-c_5\frac{T_{gg}}{{\rho }^s}(13)$

where $e_{ij}={\epsilon }_{ij}-\frac{1}{3}{\epsilon }_{kk}{\delta }_{ij}$ is the deviator strain; ${\epsilon }_v={\epsilon }_{kk}$ is the volume strain; ${\lambda }_{vg}$ and ${\lambda }_{sg}$ are the transport coefficients at the particle level, respectively; $\varsigma$is the dissipation at particle level caused by temperature. b is a material properties parameter, $c_2=\frac{{\eta }_s^{1/\alpha }{\lambda }_{sg}}{\gamma }$,$c_3=\frac{{\eta }_s^{1/\alpha }{\lambda }_{vg}}{\gamma }$,$c_4=\frac{{\eta }_s^{1/\alpha }}{b}$,$c_5=\frac{\gamma }{b}$,$T_{\text{gg}}={\eta }_s^{1/\alpha }{T}_{\text{g}}$. According to the hypothesis in references (Bai and Su, 2012; Zhang and Cheng, 2016), a is a material constant and is taken as 0.5 (Zhang and Cheng, 2016).

Dilatancy in Sandy Soil

When the sandy soil sample reaches the critical state, the volume strain increment is zero and the deviator strain increment increases continuously in the last stage of shear deformation. The critical state of sandy soil is not a straight line in the e-logp plane (Verdugo and Ishihara, 1996; Taherdangkoo et al., 2021). Li and Dafalias (Li and Dafalias, 2000) expressed the critical state of sandy soil as follows:

$e_c=e_{\kappa }-{\mathit{\lambda }}_c{\left(p\prime /p_a\right)}^{\theta }(14)$

where $e_{\kappa }$ is the void ratio corresponding to the critical state line when p = 0; e_c is the critical void ratio; ${\lambda }_c$ is the slope in$e$-${(p^{\prime }/p_a)}^{\theta }$plane; P_a is the standard atmospheric pressure, usually 100kPa; θ is the critical state line parameter.

By comparing the test data of Toyoura sandy soil by Verdugo and Ishihara (1996) with the critical state curve proposed by Li and Dafalias (2000), it is found that Eq. 14 can better reflect the critical state condition of sandy soil.

The state parameter is usually expressed by relative density and confining pressure. Been and Jefferies (1985) regard the dilatancy of sandy soil as an independent state variable, and proposed the difference between critical void ratio $e_c$ and current void ratio e to represent the state of sandy soil samples:

$\psi =e-e_c(15)$

In this way, the current state (e, p) of sandy soil can be determined. When $\psi$>0, the sandy soil is in a loose state, and shear shrinkage occurs during shearing. On the other side ($\psi$<0), the sandy soil is in a relatively dense state, and shear dilatation occurs during shearing.

Referring to Li and Dafalias (2000), the dilatancy ratio is the ratio of plastic volumetric strain $(i.e.{\text{,d}}_t{\epsilon }_v^p)$ to plastic shear strain $(i.e.{\text{,d}}_t{\epsilon }_s^p)$, and the state parameter is introduced into the dilatancy equation to establish the dilatancy expression of sandy soil.

$d=d_0\left(e^{m\psi }-\frac{\eta }{M}\right)(16)$

where$M$is the critical state stress ratio; $\eta$ = $q/p\prime$ is the stress ratio in the current state; $\psi$is the state parameter, which is determined by combining Eq. 15; $d_0$ and $m$ are the fitting parameters.

The above is the constitutive model of sandy soil under high stress and temperature coupled based on GSH theory. The main governing equations are Eqs 9–11, Eqs 13–16. The model establishes the constitutive relationship from the point of microscopic energy dissipation and can well reflect the mechanical properties of sandy soil. The state variables required for the constitutive equation of GSH theoretical model are shown in Table 1.

TABLE 1

TABLE 1. State variables in GSH theoretical model.

Determination of Model Parameters

There are 15 parameters in the model, including thermodynamic parameter$\left\{B_0,\xi ,\lambda ,{\beta }_T{\text{,c}}_1{\text{,c}}_2{\text{,c}}_3{\text{,c}}_4{\text{,c}}_5\right\}$ and parameter $\left\{M,e_k,{\lambda }_c,\theta \text{,}{d}_0\text{,}m\right\}$ in the dilatancy equation with state variable. Most of the parameters can be obtained through the conventional soil mechanics test, and the available specific parameter calibration method is provided here.

1) B₀ and$\lambda$are calibrated by the curve of isotropic compression and rebound. B₀ is the elastic stiffness parameter, and a set of elastic strain ${\epsilon }_{v1}^e$ under confining pressure$p_1\text{'}$ are obtained by using the rebound curve of soil. Because the shear strain is ignored in the rebound process, the value of B₀ can be obtained by combining Eq. 10. $\lambda$is the slope of e-logp curve in one-dimensional consolidation test of sandy soil sample.

2) ξ is the parameter related to the friction angle of sandy soil (Jiang and Liu, 2009). In the critical state, the volume and stress of sandy soil remain unchanged, while the shear strain develops continuously. In the simulation, it is shown as${\text{d}}_t{\epsilon }_v=0$${\text{d}}_t{T}_g=0$, ${\text{d}}_t{\epsilon }_v^e=0$. Eq. 9 is simplified as:

${\text{d}}_t{\epsilon }_{ij}^p=\frac{{\eta }_v}{{\eta }_s}{\left({\eta }_s^{1/0.5}{T}_g\right)}^{0.5}{\epsilon }_v^e{\delta }_{ij}+{\left({\eta }_s^{1/0.5}{T}_g\right)}^{0.5}{e}_{ij}^e(17)$

where the parameter $c_1=\frac{{\eta }_v}{{\eta }_s}$ is defined.

3) The dilatancy ratio d is the ratio of plastic volumetric strain rate $d_t{\epsilon }_v^p$ to plastic shear strain rate$d_t{\epsilon }_s^p$. Eq. 18 is obtained by combining Eq. 17. Simultaneous Eqs 16–18 determine the value of c₁.

$d=\frac{{\text{d}}_t{\epsilon }_v^p}{{\text{d}}_t{\epsilon }_s^p}=\frac{3c_1{\left(T_{gg}\right)}^{0.5}{\epsilon }_v^e}{{\left(T_{gg}\right)}^{0.5}{\epsilon }_s^e}(18)$

4) The value of c₂ can be obtained through Eq. 17 and Eq. 13, Eqs 10–11 as well as the critical state ratio.

5) The parameter c₃ is determined by isotropic compression curve; c₄ is determined by the thermal response caused by heating, and c₄ = 0.003 kg m⁻³ kPa⁻¹ by referring to Bai et al. (2017); Bai and Shi, 2017); c₅ is determined by stress relaxation test, and the value in reference Bai et al. (2021c) is 800 kg m⁻³ s⁻¹.

6) The method of parameter selection in the dilatancy equation is explained in detail in reference Li and Dafalias (2000).

Model Verification

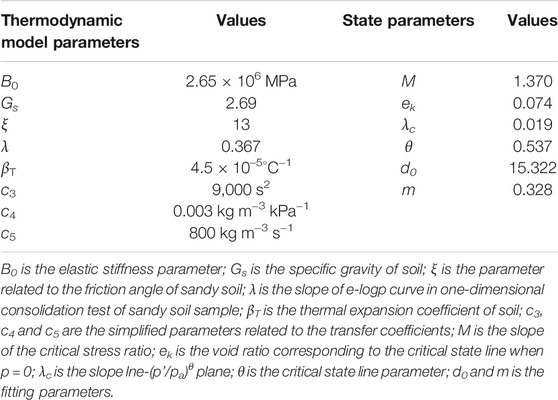
Lade and Yamamuro (Yamamuro, 1996; Lade and Yamamuro, 1997; Lade et al., 2005; Poul et al., 2020) carried out a series of experimental studies on the mechanical properties of three different initial densities of Cambria sandy soil under different pressures using a standard triaxial apparatus. The particle size distribution of Cambria sandy soil ranges from 0.83 to 2 mm, the particle specific gravity G_s is 2.69, and the maximum and minimum void ratio are 0.792 and 0.503, respectively. The temperature of sample test is set at 25°C, and the experimental results are estimated by the sandy soil model. Through the parameter analysis of part 2.3, the values of relevant control symbols including thermodynamic model parameters and state parameters are listed in Table 2.

TABLE 2

TABLE 2. Thermodynamic parameters and state parameters in the model.

Isotropic Compression Test

According to Eqs 10, 11, the corresponding differential expression is obtained as follows:

${\text{d}}_{t}p\prime =\frac{{\rho }_L{G}_{s}p\prime }{\mathit{\lambda }{\rho }_d}{\text{d}}_t{\epsilon }_{\text{v}}+B\left[8.75{\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{1.5}+0.75\xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{-0.5}{\left({\epsilon }_{\text{s}}^e\right)}^2\right]\left({\text{d}}_t{\epsilon }_v^e+{\beta }_{\mathrm{T}}{\text{d}}_t\mathrm{T}\right)+3B\xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{0.5}\left({\epsilon }_{\text{s}}^e\right){\text{d}}_t{\epsilon }_s^e(19)$

${\text{d}}_{t}q=\frac{{\rho }_L{G}_{s}q}{\mathit{\lambda }{\rho }_d}{\text{d}}_t{\epsilon }_{\text{v}}+1.5\sqrt{6}B\xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{0.5}{\epsilon }_{\text{s}}^e\left({\text{d}}_t{\epsilon }_v^e+{\beta }_{\mathrm{T}}{\text{d}}_t\mathrm{T}\right)+\sqrt{6}B\xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{1.5}{\text{d}}_t{\epsilon }_s^e(20)$

In the isotropic compression experiment, the elastic shear strain ${\epsilon }_{\text{s}}^e$ is 0, and the effect of temperature is not considered. According to Eq. 19, the stress expression is described as:

${\text{d}}_{t}p\prime =\frac{{\rho }_L{G}_{s}p\prime }{\mathit{\lambda }{\rho }_d}{\text{d}}_t{\epsilon }_{\text{v}}+8.75B{\left({\epsilon }_v^e\right)}^{1.5}{\text{d}}_t{\epsilon }_v^e(21)$

where ${\rho }_d$is the density of soil particles, obtained by ${\rho }_d=\frac{{\rho }_L{G}_s}{1+e}$; ${\rho }_L$ is the water density, ${\rho }_L$ = 1,000 kg/m³.

Figure 1 illustrates the simulation of sandy soil isotropic compression test using the newly proposed model, where the initial relative densities are 30, 60, and 90%, respectively. The results show that when the confining pressure exceeded 12 MPa, the sandy soil samples with different initial void ratios have similar void ratios under the same confining pressure, indicating that the initial relative density has no significant effect on the deformation and strength of sandy soil when the stress level exceeds a certain value. This is due to the fact that under the action of larger confining pressure, the rolling and extrusion deformation of soil particles in the sandy soil sample gradually turns into the crushing of soil particles. Meanwhile, with the increase of stress level, the amount of broken sandy soil particles increases gradually, and the broken particles fill the gap, resulting in the compression phenomenon of clay like materials. Through comparison, the proposed model can well reflect the compression characteristics of sandy soil under high stress.

FIGURE 1

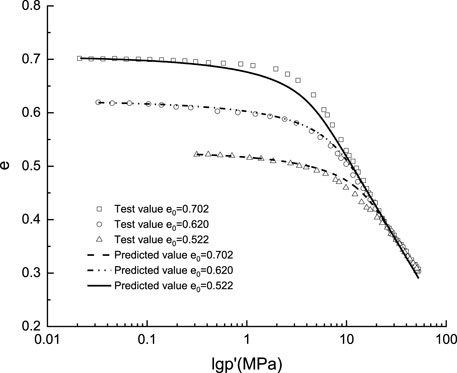
FIGURE 1. Isotropic compression test and simulation results of loose, medium dense and dense Cambria sandy soil.

Uudrained Shear Test

In the undrained shear test of sandy soil, ${\text{d}}_t{\sigma }_3=0$,${\text{d}}_t{\epsilon }_{\text{v}}=0$, it can be deduced that:

${\text{d}}_{t}p\text{'}=\frac{1}{3}{\text{d}}_t{\sigma }_1-{\text{d}}_t{u}_w(22)$

${\text{d}}_{t}q={\text{d}}_t{\sigma }_1(23)$

By introducing Eqs 19–20 into Eqs 22, 23, the pore pressure growth rate can be written as:

${\text{d}}_t{u}_w=B\left\{0.5\sqrt{6}\xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{0.5}{\epsilon }_{\text{s}}^e-\left[8.75{\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{1.5}+0.75\xi {\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{-0.5}{\left({\epsilon }_{\text{s}}^e\right)}^2\right]\right\}\left({\text{d}}_t{\epsilon }_v^e+{\beta }_{\mathrm{T}}{\text{d}}_t\mathrm{T}\right)+B\xi \left[\frac{\sqrt{6}}{3}{\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{1.5}-3{\left({\epsilon }_v^e+{\beta }_T\Delta \mathrm{T}\right)}^{0.5}{\epsilon }_{\text{s}}^e\right]{\text{d}}_t{\epsilon }_s^e(24)$

It can be found from Figure 2 that, at lower confining pressure (6.4 MPa), the deviator stress increases and tends to be stable with the increase of axial strain, and there exists no peak point, showing strain hardening characteristics. However, when the confining pressure is more than 34 MPa, under the condition of small strain, the deviator stress increases rapidly, then the growth rate slows down and the peak value appears. In the final stage, as the increase of axial strain, the deviator stress decreases and tends to be stable. It is worth noting that the higher the confining pressure, the higher the peak strength, and the greater the difference between the peak strength and the bias stress under the stable state. The confining pressure increased from 34 to 52 MPa, the difference between them was 3.67 and 6.65 MPa, and the relative increase rate was 37.7 and 48.6% respectively. This phenomenon can be explained as the breakage of particles in the sample. When the confining pressure is low, at the initial stage of shear deformation, the shear strength of sandy soil samples is mainly affected by sliding friction, dilatancy effect and particle rearrangement, and the particle breakage rate is low. The higher the confining pressure is, the higher the particle breakage rate is under the same axial strain condition. When the shear strength reaches the maximum value, the particle breakage inside the sample becomes the main factor affecting the shear strength, and its shear strength gradually decreases and tends to be stable, which is similar to the softening characteristics of clay soil.

FIGURE 2

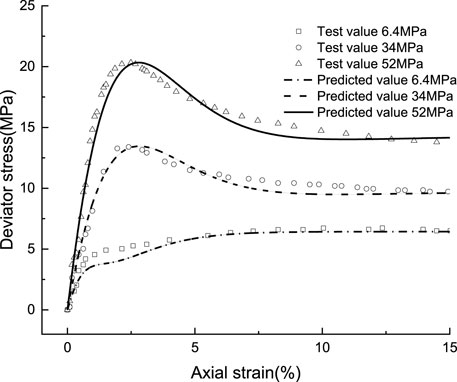
FIGURE 2. Stress-strain relationship and model prediction results of triaxial undrained shear test on dense sandy soil.

Moreover, in conjunction with Figure 3, it can be seen that under the confining pressure of 6.4 MPa, the average effective stress decreases rapidly and then increases. This is mainly due to the fact that in the initial stage of shear deformation, the volume of the sandy soil sample has a faster trend of shrinking, resulting in a rapid increase in pore pressure. With the further development of shear deformation, pore pressure gradually decreases, and the sample shows the tendency of volume expansion and finally the sample is damaged. The simulation results are in good agreement with the experimental results, which verifies the validity of the proposed model.

FIGURE 3

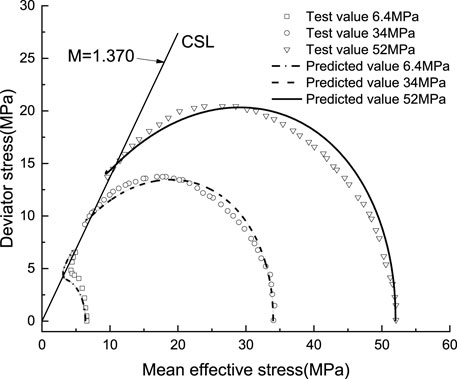
FIGURE 3. Effective stress paths and model prediction results of undrained compression tests on dense Cambria sandy soil.

Figure 4 indicated that the stress-strain curves of sandy soil with different initial densities have similar changing trends. Under the condition of small axial strain (<3%), loose sandy soil and medium dense sandy soil reach the same peak strength. However, after the peak value, the shear strength of medium dense sandy soil is always higher than that of loose sandy soil under the same axial strain. This is mainly due to the influence of two aspects on the mechanical properties of sandy soil under larger confining pressure, namely, the rearrangement of particles and particle breakage. The former is affected by initial relative density, while the latter is affected by confining pressure.

FIGURE 4

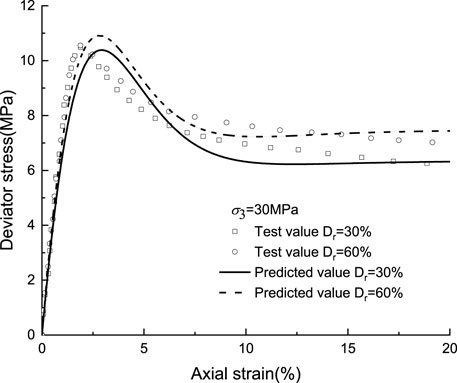
FIGURE 4. Stress-strain relationship and model prediction results of sandy soil under different initial relative density.

Three temperature gradients (25°C, 40°C and 80°C) are set according to the method in the reference (Bai et al. (2020b); Bai, 2006b; Zarifi et al., 2021). The undrained shear tests of sandy soil samples at different temperatures were simulated. The stress-strain relationship and pore pressure relation with strain under different temperature conditions are presented in Figure 5 and Figure 6. Figure 5 illustrates that the stress variation law of sandy soil samples under different temperatures is consistent, showing that the higher temperature lead to an increase of the peak strength. It is indicating that within a certain strain range, the increase in temperature can affect the undrained shear strength of sandy soil samples, which is consistent with the conclusion in literature (Abuel-Naga et al., 2007; Wang et al., 2020). It is worth noting that when the strain exceeds a certain value (15%), with the further development of shear deformation, the deviatoric stress values under different temperatures are finally close to each other. At this time, the ambient temperature during shear test has no significant effect on the strength of sandy soil. The variation of pore pressure under different temperatures is presented in Figure 6. The pore pressure increased gradually with increasing shear deformation and finally reached a constant value until axial strain reached 10%, which is caused by the decrease trend of volume in the initial stage of shear. At the same time, the comparison of pore pressure changes at different temperatures indicate that the higher the temperature is, the higher the pore pressure is, which is mainly caused by the difference of thermal expansion coefficient between water and sandy soil particles.

FIGURE 5

FIGURE 5. Stress-strain relationship and model prediction results of dense sandy soil under different temperatures.

FIGURE 6

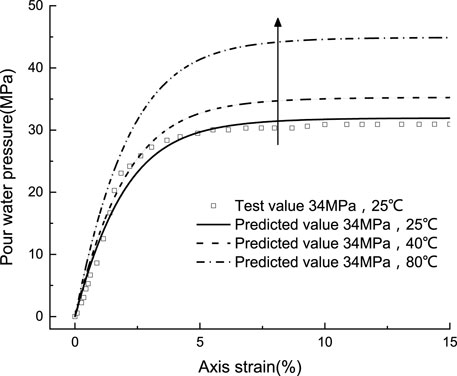
FIGURE 6. The change of pore pressure in undrained shear test of dense sandy soil under different temperatures.

Drained Shear Test

In the sandy soil drainage shear test, the relationship between shear stress and average effective stress are as follows:

${\text{d}}_{t}p\text{'}=\frac{1}{3}{\text{d}}_{t}q(25)$

By substituting Eqs 19, 20 into Eq. 25, the specific expression of volume strain rate without considering temperature effect is obtained as follows:

${\text{d}}_t{\epsilon }_v=\frac{B\left\{\left[26.25{\left({\epsilon }_v^e\right)}^{1.5}+2.25\xi {\left({\epsilon }_v^e\right)}^{-0.5}{\left({\epsilon }_{\text{s}}^e\right)}^2\right]-1.5\sqrt{6}\xi {\left({\epsilon }_v^e\right)}^{0.5}{\epsilon }_{\text{s}}^e\right\}{\text{d}}_t{\epsilon }_v^p-B\xi [3{\left({\epsilon }_v^e\right)}^{0.5}{\epsilon }_{\text{s}}^e-\sqrt{6}{\left({\epsilon }_v^e\right)}^{1.5}]{\text{d}}_t{\epsilon }_s^e}{\frac{{\rho }_L{G}_s\left(3p\text{'}-q\right)}{\lambda {\rho }_d}+B\left\{\left[26.25{\left({\epsilon }_v^e\right)}^{1.5}+2.25\xi {\left({\epsilon }_v^e\right)}^{-0.5}{\left({\epsilon }_{\text{s}}^e\right)}^2\right]-1.5\sqrt{6}\xi {\left({\epsilon }_v^e\right)}^{0.5}{\epsilon }_{\text{s}}^e\right\}}(26)$

Specifying that the volume strain of the specimen is negative with volume shrinkage and positive with volume expansion. It can be seen in Figure 7 that when the confining pressure is 2.1 MPa, with the axial strain increases, the sandy soil sample experiences two trends: shear shrinkage first and then shear expansion, until the sample is destroyed. This is in line with the volume change trend of medium density sandy soil under the action of low confining pressure. Figure 8 demonstrates that, at the lower confining pressure (2.1 MPa), the relationship between axial strain and shear stress ratio can be divided into two stages: surge section and platform section. In the initial stage, when the axial strain is in 0–5%, the stress ratio increases obviously. With the increase of axial strain, an obvious platform section appears, and the stress increase trend is gradually gentle until the sandy soil sample is destroyed. In contrast, when the confining pressure gradually increases (5.8 and 11.5 MPa), the volumetric strain presents the deformation dominated by shear shrinkage. Meanwhile, with the increase of confining pressure, the initial slope of stress-strain curve decreases, the platform section gradually decreases, and the maximum principal stress ratio of the specimen decreases. The main reason for the formation of the platform section is that under the action of small confining pressure (2.1 MPa), the load-bearing particles in the sandy soil sample change from the initial mutual extrusion and rolling to the particle breakage and particle reorientation, which is also the main reason for the specimen deformation from shear shrinkage to shear dilatation. This conclusion is consistent with the point of reference (Zhou et al., 2021). When the confining pressure is large (5.8 and 11.5 MPa), the plateau section in the stress-strain curve is no longer obvious, indicating that a large number of particles are broken in the initial stage and distributed throughout the test process, which can be verified by the fact that the slope of volume strain in Figure 7 remains basically constant.

FIGURE 7

FIGURE 7. Volume strain variation of undrained shear under different initial confining pressures.

FIGURE 8

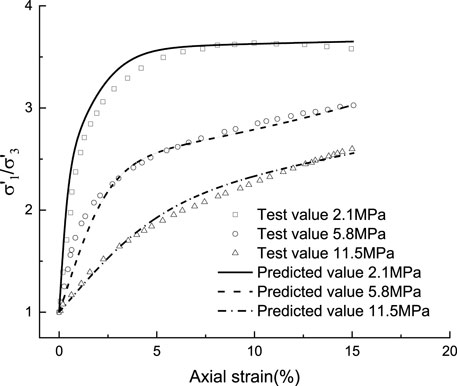
FIGURE 8. The change of undrained shear stress ratio of dense sandy soil under different initial confining pressures.

Conclusion

By introducing the state variable into the dilatancy equation and using the theory of GSH and critical state, an inelastic coupled model of thermo-hydro-mechanical is established without considering the concepts of yield surface and flow rule, and the characteristics of sandy soil under the action of high stress and temperature are simulated. The effectiveness of the model is proved by the isotropic compression tests and the shear tests of drained and undrained. Moreover, based on the undrained shear test of sandy soil, the stress-strain relationship and pore pressure of sandy soil under different temperature conditions are predicted. The following conclusions are drawn:

Under the action of high stress, the microscopic mechanism of sandy soil sample deformation is gradually transformed from the rolling and extrusion of the particles to the particles broken and filled with pores. The particle breakage rate and the degree of shear shrinkage deformation of sandy soil samples are positively correlated with the pressure on the samples.

The stress-strain relationship of sandy soil under atmospheric pressure is strain hardening type, which gradually changes to strain softening type with the increase of confining pressure, and the peak strength value increases with the increase of confining pressure.

The higher the temperature is, the greater the pore pressure of sandy soil under undrained shear condition are. However, with the increase of shear strain, the effect of temperature on shear strength is gradually weakened, while the pore pressure is gradually increased and tends to be flat.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The contribution of RZ is methodology, and the others are investigation and analysis.

Funding

Hebei Province Postdoctoral Research Projects Merit-based Funding Program (B2020005008).

Conflict of Interest

WW was employed by Hebei Research Institute of Construction and Geotechnical Investigation Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

Abuel-Naga, H. M., Bergado, D. T., and Lim, B. F. (2007). Effect of Temperature on Shear Strength and Yielding Behavior of Soft Bangkok clay. Soils Found. 47 (3), 423–436. doi:10.3208/sandf.47.423

CrossRef Full Text | Google Scholar

Bai, B., and Li, T. (2013). Irreversible Consolidation Problem of a Saturated Porothermoelastic Spherical Body with a Spherical Cavity. Appl. Math. Model. 37 (4), 1973–1982. doi:10.1016/j.apm.2012.05.003

CrossRef Full Text | Google Scholar

Bai, B., and Shi, X. (2017). Experimental Study on the Consolidation of Saturated Silty clay Subjected to Cyclic thermal Loading. Geomech. Eng. 12 (4), 707–721. doi:10.12989/gae.2017.12.4.707

CrossRef Full Text | Google Scholar

Bai, B., and Su, Z. (2012). Thermal Responses of Saturated Silty Clay during Repeated Heating-Cooling Processes. Transp. Porous Med. 93 (1), 1–11. doi:10.1007/s11242-012-9939-6

CrossRef Full Text | Google Scholar

Bai, B., Guo, L., and Han, S. (2014). Pore Pressure and Consolidation of Saturated Silty clay Induced by Progressively Heating/cooling. Mech. Mater. 75, 84–94. doi:10.1016/j.mechmat.2014.04.005

CrossRef Full Text | Google Scholar

Bai, B., Long, F., Rao, D., and Xu, T. (2017). The Effect of Temperature on the Seepage Transport of Suspended Particles in a Porous Medium. Hydrol. Process. 31 (2), 382–393. doi:10.1002/hyp.11034

CrossRef Full Text | Google Scholar

Bai, B., Rao, D., Xu, T., and Chen, P. (2018). SPH-FDM Boundary for the Analysis of thermal Process in Homogeneous media with a Discontinuous Interface. Int. J. Heat Mass Transfer 117, 517–526. doi:10.1016/j.ijheatmasstransfer.2017.10.004

CrossRef Full Text | Google Scholar

Bai, B., Rao, D., Chang, T., and Guo, Z. (2019). A Nonlinear Attachment-Detachment Model with Adsorption Hysteresis for Suspension-Colloidal Transport in Porous media. J. Hydrol. 578, 124080. doi:10.1016/j.jhydrol.2019.124080

CrossRef Full Text | Google Scholar

Bai, B., Yang, G.-c., Li, T., and Yang, G.-s. (2019). A Thermodynamic Constitutive Model with Temperature Effect Based on Particle Rearrangement for Geomaterials. Mech. Mater. 139, 103180. doi:10.1016/j.mechmat.2019.103180

CrossRef Full Text | Google Scholar

Bai, B., Zhang, J., Liu, L., and Ji, Y. (2020). The Deposition Characteristics of Coupled lead Ions and Suspended Silicon Powders along the Migration Distance in Water Seepage. Transp. Porous Med. 134 (3), 707–724. doi:10.1007/s11242-020-01464-3

CrossRef Full Text | Google Scholar

Bai, B., Xu, T., Nie, Q., and Li, P. (2020). Temperature-driven Migration of Heavy Metal Pb2+ along with Moisture Movement in Unsaturated Soils. Int. J. Heat Mass Transfer 153, 119573. doi:10.1016/j.ijheatmasstransfer.2020.119573

CrossRef Full Text | Google Scholar

Bai, B., Nie, Q., Zhang, Y., Wang, X., and Hu, W. (2021). Cotransport of Heavy Metals and SiO2 Particles at Different Temperatures by Seepage. J. Hydrol. 597, 125771. doi:10.1016/j.jhydrol.2020.125771

CrossRef Full Text | Google Scholar

Bai, B., Jiang, S., Liu, L., Li, X., and Wu, H. (2021). The Transport of Silica Powders and lead Ions under Unsteady Flow and Variable Injection Concentrations. Powder Techn. 387, 22–30. doi:10.1016/j.powtec.2021.04.014

CrossRef Full Text | Google Scholar

Bai, B., Nie, Q., Wu, H., and Hou, J. (2021). The Attachment-Detachment Mechanism of Ionic/nanoscale/microscale Substances on Quartz Sand in Water. Powder Techn. 394, 1158–1168. doi:10.1016/j.powtec.2021.09.051

CrossRef Full Text | Google Scholar

Bai, B. (2006). Fluctuation Responses of Saturated Porous media Subjected to Cyclic thermal Loading. Comput. Geotechn. 33 (8), 396–403. doi:10.1016/j.compgeo.2006.08.005

CrossRef Full Text | Google Scholar

Bai, B. (2006). Thermal Consolidation of Layered Porous Half-Space to Variable thermal Loading. Appl. Math. Mech. 27, 1531–1539. doi:10.1007/s10483-006-1111-1

CrossRef Full Text | Google Scholar

Been, K., and Jefferies, M. G. (1985). A State Parameter for Sands. Géotechnique 35 (2), 99–112. doi:10.1680/geot.1985.35.2.99

CrossRef Full Text | Google Scholar

Billam, J. (1971). “Some Aspects of the Behaviour of Granular Materials at High Pressures,” in Proceedings of the Roscoe Memorial Symposium, Cambridge, March (Cambridge University), 69–80.

Google Scholar

Bolton, M. D. (1986). The Strength and Dilatancy of Sands. Géotechnique 36 (1), 65–78. doi:10.1680/geot.1986.36.1.65

CrossRef Full Text | Google Scholar

Cui, C., Meng, K., Xu, C., Liang, Z., Li, H., and Pei, H. (2021). Analytical Solution for Longitudinal Vibration of a Floating Pile in Saturated Porous media Based on a Fictitious Saturated Soil Pile Model. Comput. Geotechn. 131, 103942. doi:10.1016/j.compgeo.2020.103942

CrossRef Full Text | Google Scholar

Hagerty, M. M., Hite, D. R., Ullrich, C. R., and Hagerty, D. J. (1993). One‐Dimensional High‐Pressure Compression of Granular Media. J. Geotechn. Eng. 119 (1), 1–18. doi:10.1061/(asce)0733-9410(1993)119:1(1)

CrossRef Full Text | Google Scholar

Jiang, Y., and Liu, M. (2007). A Brief Review of “Granular Elasticity”. Eur. Phys. J. E 22, 255–260. doi:10.1140/epje/e2007-00009-x

CrossRef Full Text | Google Scholar

Jiang, Y., and Liu, M. (2009). Granular Solid Hydrodynamics. Granular Matter 11 (3), 139–156. doi:10.1007/s10035-009-0137-3

CrossRef Full Text | Google Scholar

Jiang, Y., Einav, I., and Liu, M. (2017). A Thermodynamic Treatment of Partially Saturated Soils Revealing the Structure of Effective Stress. J. Mech. Phys. Sol. 100, 131–146. doi:10.1016/j.jmps.2016.11.018

CrossRef Full Text | Google Scholar

Lade, P., and Yamamuro, J. (1997). Undrained Sand Behavior in Axisymmetric Tests at High Pressures. J. Geotechn. Eng. 122 (2), 120–129.

Google Scholar

Lade, P., Yamamuro, J., and Bopp, P. (2005). “Relative Density Effects on Drained and Undrained Strengths of Sand at High Pressures,” in Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering: Geotechnology in Harmony with the Global Environment, Osaka, Japan, 537–541. doi:10.3233/978-1-61499-656-9-537

CrossRef Full Text | Google Scholar

Li, X. S., and Dafalias, Y. F. (2000). Dilatancy for Cohesionless Soils. Géotechnique 50 (4), 449–460. doi:10.1680/geot.2000.50.4.449

CrossRef Full Text | Google Scholar

Manzati, M., and Dafalias, Y. (1997). A Critical State Two-Surface Plasticity Model for Sands. Geotechnique 47 (2), 255–272.

Google Scholar

Meng, K., Cui, C., Liang, Z., Li, H., and Pei, H. (2020). A New Approach for Longitudinal Vibration of a Large-Diameter Floating Pipe Pile in Visco-Elastic Soil Considering the Three-Dimensional Wave Effects. Comput. Geotechn. 128, 103840. doi:10.1016/j.compgeo.2020.103840

CrossRef Full Text | Google Scholar

Poul, V., Lade, P., and Bopp, P. (2020). Relative Density Effects on Drained Sand Behavior at High Pressures. Soils and Foundations 45 (1), 1–13. doi:10.3208/sandf.45.1_1

CrossRef Full Text | Google Scholar

Rowe, P. (1962). The Stress–Dilatancy Relation for Static Equilibrium of an Assembly of Particles in Contact. Proc. R. Soc. Lond. 269 (1339), 500–527.

Google Scholar

Taherdangkoo, R., Tatomir, A., and Sauter, M. (2020a). Modeling of Methane Migration from Gas Wellbores into Shallow Groundwater at basin Scale. Environ. Earth Sci. 79 (432), 3–16. doi:10.1007/s12665-020-09170-5

CrossRef Full Text | Google Scholar

Taherdangkoo, R., Tatomir, A., Taherdangkoo, M., Qiu, P., and Sauter, M. (2020b). Nonlinear Autoregressive Neural Networks to Predict Hydraulic Fracturing Fluid Leakage into Shallow Groundwater. Water 12 (3), 841. doi:10.3390/w12030841

CrossRef Full Text | Google Scholar

Taherdangkoo, R., Liu, Q., Xing, Y., Yang, H., Cao, V., Sauter, M., et al. (2021). Predicting Methane Solubility in Water and Seawater by Machine Learning Algorithms: Application to Methane Transport Modeling. J. Contam. Hydrol. 242, 103844. doi:10.1016/j.jconhyd.2021.103844

CrossRef Full Text | Google Scholar

Verdugo, R., and Ishihara, K. (1996). The Steady State of sandy Soils. Soils Found. 36 (2), 81–91. doi:10.3208/sandf.36.2_81

CrossRef Full Text | Google Scholar

Wang, Y., Chen, F., Li, X., Yin, X., and Lei, Y. (2020). The Variable-Mass Seepage Law of Broken Porous Rock: an Experimental Study. Geomatics Nat. Hazards Risk 11 (1), 1991–2005. doi:10.1080/19475705.2020.1821791

CrossRef Full Text | Google Scholar

Wang, Y., Li, Z., Jing, H., Li, Y., and Wang, M. (2021). Study on the Seepage Characteristics of Deep Buried Tunnels under Variable High-Pressure Water Heads. Bull. Eng. Geol. Environ. 80 (2), 1477–1487. doi:10.1007/s10064-020-01986-6

CrossRef Full Text | Google Scholar

Wu, W., and Kolymbas, D. (1990). Numerical Testing of the Stability Criterion for Hypoplastic Constitutive Equations. Mech. Mater. 9, 245–253. doi:10.1016/0167-6636(90)90006-2

CrossRef Full Text | Google Scholar

Yamamuro, J. (1996). Drained Sand Behavior in Axisymmetric Tests at High Pressures. J. Geotechn. Eng. 122, 109. doi:10.1061/(asce)0733-9410(1996)122:2(109)

CrossRef Full Text | Google Scholar

Yang, G., and Bai, B. (2019). Thermo-hydro-mechanical Model for Unsaturated clay Soils Based on Granular Solid Hydrodynamics Theory. Int. J. Geomech. 19 (10), 04019115. doi:10.1061/(asce)gm.1943-5622.0001498

CrossRef Full Text | Google Scholar

Zarifi, M., Kvamme, B., and Kuznetsova, T. (2021). Modeling Heat Transport in Systems of Hydrate-Filled Sediments Using Residual Thermodynamics and Classical Nucleation Theory. Appl. Sci. 11 (9), 4124. doi:10.3390/app11094124

CrossRef Full Text | Google Scholar

Zhang, Z.-C., and Cheng, X.-H. (2016). A Thermo-Mechanical Coupled Constitutive Model for clay Based on Extended Granular Solid Hydrodynamics. Comput. Geotechn. 80, 373–382. doi:10.1016/j.compgeo.2016.05.010

CrossRef Full Text | Google Scholar

Zhang, Z., and Cheng, X. (2017). A Fully Coupled THM Model Based on a Non-equilibrium Thermodynamic Approach and its Application. Int. J. Numer. Anal. Meth. Geomech. 41, 527–554. doi:10.1002/nag.2569

CrossRef Full Text | Google Scholar

Zhou, H.-f., Liu, B., Ye, F., Fu, W.-x., Tang, W.-q., Qin, Y.-d., et al. (2021). Landslide Distribution and Sliding Mode Control along the Anninghe Fault Zone at the Eastern Edge of the Tibetan Plateau. J. Mt. Sci. 18, 2094–2107. doi:10.1007/s11629-020-6573-6

CrossRef Full Text | Google Scholar