Equilibration Times of Dissolved Inorganic Carbon During pH Transitions

Equilibration times of dissolved inorganic carbon (DIC) depend on conversion reactions between CO₂(aq) and the dissociation products of carbonic acid [S = (H₂CO₃) + (HCO₃⁻) + (CO₃²⁻)]. Here, we develop analytical equations and a numerical model to calculate chemical equilibration times of DIC during pH transitions in buffered and unbuffered solutions. We approximate the equilibration degree of the DIC reservoir by the smaller of the CO₂(aq) and S pools at the new pH, since the smaller pool is always farther from equilibrium during the chemical evolution. Both the amount of DIC converted and the rate of conversion differ between a pH increase and decrease, leading to distinct equilibration times for these general cases. Alkalinity perturbations in unbuffered solutions initially drive pH overshoots (increase or decrease) relative to the new equilibrium pH. The increased rates of DIC conversion associated with the pH overshoot yield shorter equilibration times compared to buffered solutions. Salinity has opposing effects on buffered and unbuffered solutions, decreasing and increasing equilibration times, respectively.

1 Introduction

Knowledge of the dissolved inorganic carbon (DIC) system is central to a range of research fields and applications, among which are chemical oceanography, environmental geochemistry, carbon sequestration, and experimental geochemistry (e.g., Stumm and Morgan, 1996; Zeebe et al., 1999; Rollion-Bard et al., 2003; Lal, 2008; Hansen et al., 2013; Daëron et al., 2019; Christensen et al., 2021). An understanding of the DIC kinetics factors into such fields, for example, when planning experiments, when deciding on dynamic versus equilibrium representation of reactions in models of aqueous environments, when evaluating the likelihood of isotopic equilibrium for applications in paleoclimate and paleohydrology, and when engineering applications of descaling or carbon sequestration.

The chemical reactions in the DIC system progress at different rates (e.g., Zeebe and Wolf-Gladrow, 2001; Sade and Halevy, 2017; Sade and Halevy, 2018). Dissociation of carbonic acid and water are rapid reactions, whose reactants may be considered to be in equilibrium on a time scale of seconds:

${\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3\rightleftharpoons \mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}+{\mathrm{H}}^{+},(1)$

$\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}\rightleftharpoons \mathrm{C}{\mathrm{O}}_3^{2–}+{\mathrm{H}}^{+},(2)$

${\mathrm{H}}_2\mathrm{O}\rightleftharpoons {\mathrm{H}}^{+}+\mathrm{O}{\mathrm{H}}^{–}.(3)$

In contrast, CO₂ hydration and hydroxylation are slower reactions, which determine the equilibration times of the sum of H₂CO₃, HCO₃⁻, and CO₃²⁻ with aqueous CO₂ (henceforth CO₂(aq)), and therefore, the equilibration time of the entire DIC reservoir:

$\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)+{\mathrm{H}}_2\mathrm{O}\begin{array}{c}{k}_{+4}\\ \rightleftarrows \\ k_{–4}\end{array}{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3,(4)$

$\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)+\mathrm{O}{\mathrm{H}}^{–}\begin{array}{c}{k}_{+5}\\ \rightleftarrows \\ k_{–5}\end{array}\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–},(5)$

where k_+i and k_−i are the forward and reverse rate constants of reaction i. In freshwater at 25°C, k₊₄ and k₋₄ are 0.026 s⁻¹ and 27 s⁻¹, whereas k₊₅ and k⁻₅ are 8,416 L mol⁻¹ s⁻¹, and 0.00019 s⁻¹, respectively (Roughton, 1941; Pinsent et al., 1956).

Usdowski (1982) derived equations to describe the time required to achieve chemical equilibrium in a DIC system that is closed to gas exchange with the atmosphere during pH transitions in buffered solutions. The equations of Usdowski (1982) specifically regard an initial low-pH solution composed exclusively of CO₂(aq), which re-equilibrates at an arbitrary, new, fixed pH. The mathematical derivation is based on a schematic reaction between two distinct DIC pools, CO₂(aq) and S,

$\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]\begin{array}{c}k\\ \rightleftarrows \\ k^{\prime }\end{array}S,(6)$

where S is the sum of [H₂CO₃], [HCO₃⁻] and [CO₃²⁻], which are internally equilibrated with each other {DIC = [CO₂(aq)] + S}. In reaction 6, k, and k’ are rate constants of composite, rather than elementary reactions. Specifically, k and k’ are related to the CO₂ hydration and hydroxylation reactions, and their values depend on the solution pH,

$k=k_{+4}+k_{+5}\left[\mathrm{O}{\mathrm{H}}^{–}\right],(7)$

$k^{\prime }=k_{–4}\frac{\left[{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3\right]}{S }+k_{–5}\frac{\left[\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–} \right]}{S }=\frac{k_{–4}}{1+\frac{K_{{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3}}{\left[{\mathrm{H}}^{+}\right]}+\frac{K_{{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3}\cdot K_{\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}}}{{\left[{\mathrm{H}}^{+}\right]}^2}}+\frac{k_{–5}}{1+\frac{\left[{\mathrm{H}}^{+}\right]}{K_{{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3}}+\frac{K_{\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}}}{\left[{\mathrm{H}}^{+}\right]}}.(8)$

In Eq. 8, $K_{{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3}$ and $K_{\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}}$ are the first and second carbonic acid dissociation constants. Note that $K_{{\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3}$ is distinct from Ka1, the first acid dissociation constant for the sum of CO₂(aq) and H₂CO₃ (Supplementary Information). Then, the equilibration time following a pH transition from an initially CO₂(aq)-dominated DIC solution to a new buffered solution is given by (cf. Eq. I-2–22 in Usdowski, 1982):

$t=\frac{\mathrm{l}\mathrm{n}\left(1-\frac{S}{S_{\mathrm{e}\mathrm{q}}}\right)}{–\left(\mathit{k}+k^{\prime }\right)},(9)$

where the subscript “eq” denotes the equilibrium concentration at the new pH, and the ratio S/S_eq, the equilibration degree of the S reservoir, approximates the equilibration degree of the entire DIC reservoir at a given time t.

The derivation of Usdowski (1982) closely approximates the chemical equilibration time only under certain conditions. A general derivation should accurately represent a DIC solution at any initial pH and associated DIC speciation. Furthermore, a conservative estimate of the equilibration degree of the DIC reservoir should consider the smaller of the CO₂(aq) and S pools at the new pH, which is always farther from equilibrium. For example, consider an initial solution with 100 units of DIC, all as CO₂(aq), which re-equilibrates to a new buffered pH, at which CO₂(aq):S is 60:40. As equilibrium is approached, for example, when CO₂(aq):S is 65:35, the CO₂(aq) pool is 8.3% away from equilibrium ([CO₂(aq)]/[CO₂(aq)]_eq = 65/60 = 1.083), whereas the S reservoir is 12.5% away from equilibrium (S/S_eq = 35/40 = 0.875). Conversely, during equilibration to a pH at which CO₂(aq):S is 40:60, at 5 units away from equilibrium, the CO₂(aq) pool is 12.5% away from equilibrium and the S pool is 8.3% away from equilibrium. In both cases, the smaller pool at the new pH is farther from equilibrium during the chemical evolution.

In this study, we expanded the equations of Usdowski (1982) to derive general analytical expressions for the chemical equilibration time of DIC solutions of any initial speciation, at any new, buffered pH. We additionally used a numerical model to explore the equilibration times of the DIC in unbuffered solutions. Lastly, we compared the equilibration times of the DIC during pH transitions in buffered and unbuffered solutions with equilibration times calculated by perturbation theory at a given pH (Zeebe and Wolf-Gladrow, 2001), and discussed the sensitivity of these equilibration times to the ionic strength (salinity) of the solution.

2 Methods

2.1 Analytical Expressions for DIC Equilibration Times in Buffered Solutions

The derivation of the general case, describing equilibration times of DIC during transition from any initial pH to any buffered pH, follows the approach of Usdowski (1982), but additionally considers the DIC speciation at the new pH. Specifically, the smaller of the CO₂(aq) and S pools at the new pH is used to represent the equilibration degree of the DIC reservoir. This is done by comparing the new pH to pKa1, the pH at which CO₂(aq) composes 50% of the DIC (e.g., in freshwater at 25°C, pKa1 = 6.35; Harned and Davis, 1943). If the new pH is higher than pKa1, the degree of equilibration is calculated using the CO₂(aq) pool ([CO₂(aq)]/[CO₂(aq)]_eq), and if the new pH is lower than pKa1, the degree of equilibration is calculated using the S pool (S/S_eq). The equilibration time depends on the initial distance from equilibrium, requiring the additional terms [CO₂(aq)]₀/[CO₂(aq)]_eq and S₀/S_eq, which represent the initial equilibration degree of the DIC reservoir (the subscript “0” denotes the initial concentrations). The concentrations of CO₂(aq) and S in any equilibrated solution are:

$\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]=\frac{\mathrm{DI}\mathrm{C}}{1+K^{\prime }+\frac{Ka1\left(1 +K^{\prime }\right)}{\left[{\mathrm{H}}^{+}\right]}+\frac{Ka1\left(1+K^{\prime }\right)K_{\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}}}{{\left[{\mathrm{H}}^{+}\right]}^2}},(10)$

$S=\mathrm{DI}\mathrm{C}-\left[\mathrm{C}\mathrm{O}2\left(\mathrm{a}\mathrm{q}\right)\right],(11)$

where ${\mathit{K}}^{\prime }=k_{+4}/k_{-4}$.

The equilibration time during transition from an arbitrary solution pH to another buffered pH is given by (see Supplementary Information for a detailed derivation and the values of the thermodynamic and rate constants required for these equations):

$t=\frac{\mathrm{l}\mathrm{n}\left(\left(\frac{S}{S_{eq}}–1\right)/\left(\frac{S_0}{S_{eq}}–1\right)\right)}{–\left(k+k^{\prime }\right)}\mathrm{for}\mathrm{new}\mathrm{pH<pKal,}(\mathrm{12a})$

$t=\frac{\ln \left(\left(\frac{\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]}{{\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]}_{eq}}–1\right)/\left(\frac{{\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]}_0}{{\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]}_{eq}}–1\right)\right)}{–\left(k+k^{\prime }\right)}\mathrm{for}\mathrm{new}\mathrm{pH>pKal.}(\mathrm{12b})$

The time required to achieve 99% equilibrium is:

$t_{99}=\frac{\ln \left(\left|0.01/\left(\frac{S_0}{S_{eq}}–1\right)\right|\right)}{–\left(k+k^{\prime }\right)}\mathrm{for}\mathrm{new}\mathrm{pH<pKal,}(\mathrm{13a})$

$t_{99}=\frac{ln\left(\left|0.01/\left(\frac{{\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]}_0}{{\left[\mathrm{C}{\mathrm{O}}_2\left(\mathrm{a}\mathrm{q}\right)\right]}_{eq}}–1\right)\right|\right)}{–\left(k+k^{\prime }\right)}\mathrm{for}\mathrm{new}\mathrm{pH>pKal.}(\mathrm{13b})$

2.2 Numerical Model for DIC Equilibration Times in Unbuffered Solutions

We used a numerical model to calculate the equilibration times of the DIC reservoir during pH transitions in unbuffered solutions, and to validate the analytical equilibration times in buffered solutions (Eqs. 12, 13). The model is based on a previously developed model (Sade et al., 2021), which was here simplified to focus solely on the aqueous phase and to neglect diffusion and advection. The simplified model consists of a set of differential equations, which describe the chemical evolution of the DIC species with time, based on reactions 1–5. The differential equations are forward integrated using the ode15s solver in the Matlab^® software, under an assumption of instantaneous equilibrium among H⁺, OH⁻, CO₃²⁻, HCO₃⁻, and H₂CO₃. In simulations of the buffered solutions, the new pH was fixed. In simulations of the unbuffered solutions, we set the new pH by introducing Ca²⁺ or Cl⁻ ions (i.e., changing the alkalinity). Water dissociation and DIC speciation reactions then release H⁺ and OH⁻ to conserve electrical neutrality, determining the new pH.

2.3 Salinity Effects

In both the numerical model and the analytical expressions, we explicitly account for neither activity coefficients nor ion pairs. Instead, we account for the effects of salinity by using thermodynamic and rate constants for either freshwater or seawater (Supplementary Tables S1, S2). In simulated Ca-Cl-DIC solutions with a low ionic strength (here freshwater solutions), activity coefficients are near unity and the concentration of ion pairs is low. In simulated seawater, we used stoichiometric equilibrium constants and kinetic rate constants measured in seawater, which account for the effect of salinity. Hence, both in freshwater and in seawater, we expect that our results provide a reasonable approximation of DIC equilibration times. An investigation of the effect of a larger range of ionic strength (and chemical composition) requires better constraints on the salinity dependence of the equilibrium and kinetic constants and is beyond the scope of this study.

3 Results

3.1 Equilibration Times During a pH Transition in Buffered Solutions

Equilibration times are different during pH transitions towards lower and higher values, and are bounded by two end members (Figure 1A). An initially CO₂(aq)-dominated solution (99.9% of the DIC as CO₂(aq) at pH₀ = 0; blue curve in Figure 1) bounds the maximal equilibration times during a pH increase, and an initially S-dominated solution (100.0% of the DIC as S at pH₀ = 14; red curve in Figure 1) bounds the maximal equilibration times during a pH decrease. The longest calculated equilibration times during transitions to lower and higher pH values, 150 and 245 s, are at pH 7.4 and 7.8, respectively. At the edges of the examined pH range, equilibration times reduce to a few seconds. The equilibration times of solutions with any other initial DIC speciation (i.e., 0 < pH₀ < 14) are generally shorter than those of the end members described above (e.g., pH₀ = 7; black curve in Figure 1A). However, at final pH values that are lower than 6 or higher than 10, where equilibration times markedly decrease, the curves closely converge (Figure 1A). Our numerical model yielded equilibration times within a tenth of a second of the analytical model, validating the analytical equations (Eqs. 12, 13).

FIGURE 1

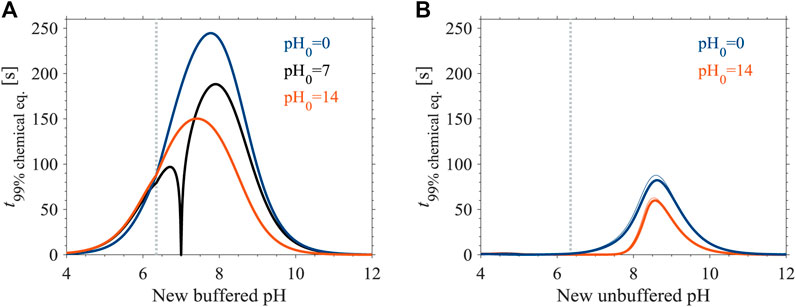
FIGURE 1. Equilibration times of DIC in freshwater at 25°C during a pH transition (A) in buffered solutions (Eq. 13) and in (B) unbuffered solutions (as calculated by our numerical model). The pH of the initial solution (“pH₀”) is given in the figure legends, and a vertical line marks the pKa1 value. In panel B, we illustrated equilibration times for 10 mM DIC (thick lines), enveloped by equilibration times for 1 and 100 mM DIC (thin lines). See Supplementary Figure S1 for an enlarged version of panel B.

3.2 Equilibration Times During a pH Transition in Unbuffered Solutions

We evaluated the DIC equilibration times in unbuffered solutions using a numerical model (Figure 1B). Equilibration times during a pH increase (blue curve) are longer than during a pH decrease (red curve), both reaching a maximum at pH 8.6 of 82 and 60 s, respectively. At pH < 6 and pH > 11, equilibration times are shorter than a few seconds. Overall, the maximal equilibration times in unbuffered solutions are shorter by a factor of 2.5–3, relative to buffered solutions, with peaks that are located at a higher pH value (pH 8.6 and 7.4–7.8 in unbuffered and buffered solutions, respectively). In addition, unlike in buffered solutions, in unbuffered solutions the DIC concentration affects the equilibration time, with lower equilibration times corresponding to higher DIC concentrations. However, over the examined range of DIC concentration, 1–100 mM, differences in equilibration times approach 8 s, at most (Figure 1B).

4 Discussion

Equilibration times of DIC during pH transitions are determined by 1) the initial distance from the equilibrium speciation at the new pH and 2) the rates of DIC conversion during the chemical evolution (Figure 2). Given a fixed DIC concentration, the DIC speciation depends upon the solution pH. Therefore, the difference between the initial and new (buffered or unbuffered) pH values of the solution determines how much of the DIC needs to be converted during the chemical evolution at the new pH. Specifically, if the new pH is higher than the initial pH, CO₂(aq) is converted to S by CO₂(aq) hydration and hydroxylation reactions (forward reaction 6). In contrast, if the new pH is lower than the initial pH, CO₂(aq) is produced by H₂CO₃ dehydration and HCO₃⁻ dehydroxylation reactions (reverse reaction 6). However, the solution pH affects not only the amount of DIC that must be converted, but also the conversion rate. The rate constants of CO₂(aq) hydration and hydroxylation, H₂CO₃ dehydration, and HCO₃⁻ dehydroxylation, alongside pH-dependent fractions of H₂CO₃ and HCO₃⁻ out of S, result in a pH-dependence of the rate of DIC conversion. Specifically, with increasing pH, rates of CO₂(aq) consumption increase whereas rates of CO₂(aq) production decrease (Figure 2B).

FIGURE 2

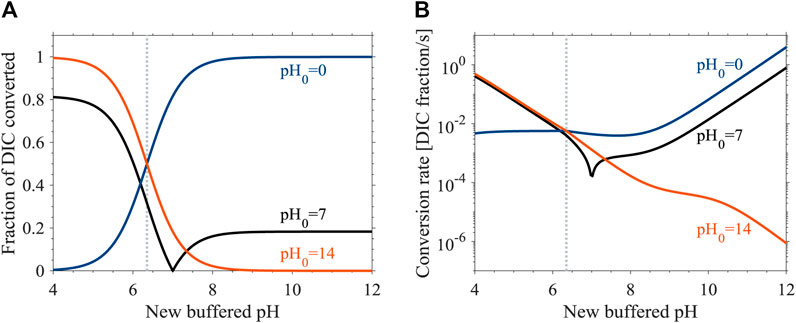
FIGURE 2. Chemical equilibration of DIC in pH-buffered freshwater solutions at 25°C (Eq. 13). (A) Fractions of DIC converted between the CO₂(aq)-S pools during transitions from an initial pH₀ to a new equilibrium pH. (B) The average DIC conversion rates during these pH transitions.

Overall, equilibration times are shorter when the converted DIC fractions are smaller, and when the CO₂(aq)-S conversion rates are higher. For instance, the maximal equilibration time in buffered solutions is achieved during a transition of a CO₂(aq)-dominated solution to a new pH of 7.8 (245 s; Figure 1A). During this transition, 97% of the DIC is converted from CO₂(aq) to S (Figure 2A, blue) at rates that are close to the minimum rates of CO₂(aq) consumption under these conditions (Figure 2B, blue). In comparison, the equilibration of an S-dominated solution at the same buffered pH of 7.8 is faster (142 s; Figure 1A), despite CO₂(aq) production rates in this case that are lower by an order of magnitude than the CO₂(aq) consumption rates in the CO₂(aq)-dominated solution described above (Figure 2B, red). The equilibration time of the S-dominated solution is shorter because only 3% of the DIC needs to be converted from S to CO₂(aq) (Figure 2A, red).

Notably, equilibration times of DIC in unbuffered solutions are shorter relative to buffered solutions (Figure 1). In unbuffered solutions, introduction of Ca²⁺ or Cl⁻ ions (as simulated in our numerical model) immediately alters the solution alkalinity, resulting in a transient pH excursion to higher and lower values, respectively, than the final equilibrium pH value. The reason for this transient excursion is that it takes time for DIC speciation [through CO₂(aq) production/consumption] to compensate for the instantaneous change in the solution’s alkalinity. For example, introduction of 5.1 mM Ca²⁺ into a CO₂(aq)-dominated 10 mM DIC solution (pH₀ = 0) instantaneously increases the simulated pH to 12, before decreasing back to the new equilibrium pH of 8.6 (Supplementary Figure S3). Since CO₂(aq) production/consumption rates are higher at lower/higher pH values, these overshoots to higher-than-equilibrium and lower-than-equilibrium pH values decrease the overall equilibration times relative to conditions of a fixed, buffered pH (Figure 2).

Our numerical equilibration times for a pH decrease in unbuffered solutions are comparable to equilibration times calculated by perturbation theory, which are commonly cited in the literature (Zeebe and Wolf-Gladrow, 2001). This similarity arises from the decay of a perturbation to DIC speciation being the driver of the chemical evolution in both cases. In the perturbation theory, DIC is perturbed directly, whereas in our numerical simulations of unbuffered solutions the alkalinity is changed, and the DIC speciation is “perturbed” relative to what it would be at the final new pH. Differences between our numerical equilibration times for both pH decrease and increase and the perturbation theory stem from different amounts and rates of CO₂(aq) consumption/production during the relaxation from the perturbed to the equilibrium pH (Supplementary Information).

Salinity affects the DIC equilibration times in buffered and unbuffered solutions differently (Figure 3). Applying equilibrium and rate constants for seawater (Supplementary Information) in Eq. 13 and in our numerical model results in shorter and longer equilibration times in buffered and unbuffered solutions, respectively, relative to freshwater. For example, the maximal equilibration time of initially CO₂(aq)-dominated seawater buffered solution (Figure 3A), is 25% shorter than in freshwater. In both cases (buffered and unbuffered solutions), the seawater curves shift towards lower pH values relative to freshwater, in accordance with the shift of pKa1 (in seawater, pKa1 = 5.86; Zeebe and Wolf-Gladrow, 2001).

FIGURE 3

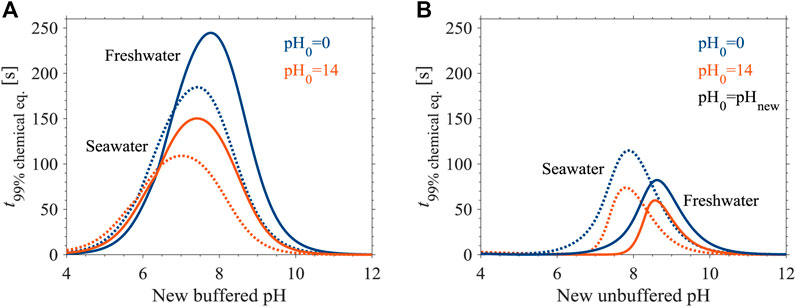
FIGURE 3. Equilibration times during pH transitions at 25°C in 10 mM DIC seawater (dotted lines) and freshwater (solid lines) in (A) buffered and (B) unbuffered solutions. Perturbation theory equilibration times are shown in panel B for comparison (pH₀ = pH_new; Eq. C.7.25 in Zeebe and Wolf-Gladrow, 2001).

Our analytical expressions for the chemical equilibration times of DIC in (strongly) buffered solutions are applicable to a range of artificial settings, such as laboratory experiments of mineral precipitation. The numerical model for equilibration times in unbuffered solutions expands the applicability to a wide range of natural and artificial settings. Examples include rapid productivity-driven changes in DIC concentration and speciation in the photic zone of lakes and oceans, exhalation of hydrothermal fluids into seawater, injection of CO₂-bearing fluids into marine sediments, or pH variations driven by oxidation of sulfide and/or ferrous iron in initially anoxic spring water or acid mine drainage. As the relaxation to equilibrium is governed by the rates of reaction among the DIC species and with water (H₂O in the case of hydration, OH⁻ in the case of hydroxylation), the chemical equilibration times presented here bear also on the time to carbon isotopic equilibrium within the DIC system and on the time to DIC-water oxygen isotopic equilibrium.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

IH and ZS conceived, and IH oversaw the study. ZS, SH, and IH developed the numerical model and analytical equations. ZS and SH performed the simulations. All authors participated in writing the article.

Funding

IH acknowledges funding from a European Research Council Starting Grant 755053.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank two reviewers for helpful comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.792858/full#supplementary-material

References

Christensen, J. N., Watkins, J. M., Devriendt, L. S., DePaolo, D. J., Conrad, M. E., Voltolini, M., et al. (2021). Isotopic Fractionation Accompanying CO2 Hydroxylation and Carbonate Precipitation from High pH Waters at the Cedars, California, USA. Geochimica et Cosmochimica Acta 301, 91–115. doi:10.1016/j.gca.2021.01.003

CrossRef Full Text | Google Scholar

Daëron, M., Drysdale, R. N., Peral, M., Huyghe, D., Blamart, D., Coplen, T. B., et al. (2019). Most Earth-Surface Calcites Precipitate Out of Isotopic Equilibrium. Nat. Commun. 10 (1), 429. doi:10.1038/s41467-019-08336-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, M., Dreybrodt, W., and Scholz, D. (2013). Chemical Evolution of Dissolved Inorganic Carbon Species Flowing in Thin Water Films and its Implications for (Rapid) Degassing of CO2 during Speleothem Growth. Geochimica et Cosmochimica Acta 107, 242–251. doi:10.1016/j.gca.2013.01.006

CrossRef Full Text | Google Scholar

Harned, H. S., and Davis, R. (1943). The Ionization Constant of Carbonic Acid in Water and the Solubility of Carbon Dioxide in Water and Aqueous Salt Solutions from 0 to 50°. J. Am. Chem. Soc. 65, 2030–2037. doi:10.1021/ja01250a059

CrossRef Full Text | Google Scholar

Lal, R. (2008). Carbon Sequestration. Phil. Trans. R. Soc. B 363, 815–830. doi:10.1098/rstb.2007.2185

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinsent, B. R. W., Pearson, L., and Roughton, F. J. W. (1956). The Kinetics of Combination of Carbon Dioxide with Hydroxide Ions. Trans. Faraday Soc. 52, 1512–1520. doi:10.1039/tf9565201512

CrossRef Full Text | Google Scholar

Rollion-Bard, C., Chaussidon, M., and France-Lanord, C. (2003). pH Control on Oxygen Isotopic Composition of Symbiotic Corals. Earth Planet. Sci. Lett. 215, 275–288. doi:10.1016/s0012-821x(03)00391-1

CrossRef Full Text | Google Scholar

Roughton, F. J. W. (1941). The Kinetics and Rapid Thermochemistry of Carbonic Acid. J. Am. Chem. Soc. 63, 2930–2934. doi:10.1021/ja01856a018

CrossRef Full Text | Google Scholar

Sade, Z., and Halevy, I. (2018). Corrigendum to “New Constraints on Kinetic Isotope Effects during CO₂(aq) Hydration and Hydroxylation: Revisiting Theoretical and Experimental Data” (Geochim. Cosmochim. Acta 214(2017) 246–265). Geochim. Cosmochim. Acta 225, 237–240. doi:10.1016/j.gca.2018.01.030

CrossRef Full Text | Google Scholar

Sade, Z., and Halevy, I. (2017). New Constraints on Kinetic Isotope Effects during CO2(aq) Hydration and Hydroxylation: Revisiting Theoretical and Experimental Data. Geochimica et Cosmochimica Acta 214, 246–265. doi:10.1016/j.gca.2017.07.035

CrossRef Full Text | Google Scholar

Sade, Z., Hegyi, S., Hansen, M., Scholz, D., and Halevy, I. (2021). The Effects of Drip Rate and Geometry on the Isotopic Composition of Speleothems: Evaluation with an Advection-Diffusion-Reaction Model. Geochim. Cosmochim. Acta 317, 409–432. doi:10.1016/j.gca.2021.10.008

CrossRef Full Text | Google Scholar

Stumm, W., and Morgan, J. J. (1996). Aquatic Chemistry. 3rd edn. New York: Wiley.)

Google Scholar

Usdowski, E. (1982). Reactions and Equilibria in the Systems CO2-H2O and CaCO3-CO2-H2O (0°-50 °C) - A Review. njma 144, 148–171. doi:10.1127/njma/144/1982/148

CrossRef Full Text | Google Scholar

Zeebe, R. E., and Wolf-Gladrow, D. A. (2001). CO2 in Seawater: Equilibrium, Kinetics, Isotopes. Amsterdam: Elsevier Oceanography Series.

Google Scholar

Zeebe, R. E., Wolf-Gladrow, D. A., and Jansen, H. (1999). On the Time Required to Establish Chemical and Isotopic Equilibrium in the Carbon Dioxide System in Seawater. Mar. Chem. 65, 135–153. doi:10.1016/s0304-4203(98)00092-9

CrossRef Full Text | Google Scholar