- 1China Three Gorges Corporation, Beijing, China
- 2CAUPD Beijing Planning & Design Consultants Co., Ltd., Beijing, China
- 3Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing, China
- 4College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing, China
- 5Innovation Academy for Earth Science, Chinese Academy of Sciences, Beijing, China
- 6Sinopec Green Energy Geothermal Development Co.,Ltd., Xiong'an, China
Recoverable geothermal resources are very important for geothermal development and utilization. Generally, the recovery factor is a measure of available geothermal resources in a geothermal field. However, it has been a pre-determined ratio in practice and sustainable utilization of geothermal resources was not considered in the previous calculation of recoverable resources. In this work, we have attempted to develop a method to calculate recoverable geothermal resources based on a numerical thermo-hydraulic coupled modeling of a geothermal reservoir under exploitation, with an assumption of sustainability. Taking a geothermal reservoir as an example, we demonstrate the effectiveness of the method. The recoverable geothermal resources are 6.85 × 1018 J assuming a lifetime of 100 years in a well doublet pattern for geothermal heating. We further discuss the influence of well spacing on the recoverable resources. It is found that 600 m is the optimal well spacing with maximum extracted energy that conforms to the limit of the pressure drop and no temperature drop in the production well. Under the uniform well distribution pattern for sustainable exploitation, the recovery factor is 26.2%, which is higher than the previous value of 15% when depending only on lithology. The proposed method for calculating the recoverable geothermal resources is instructive for making decisions for sustainable exploitation.
Introduction
Geothermal energy is a clean energy that barely pollutes the atmosphere or emits greenhouse gases (Lund et al., 2011; Pang et al., 2012). Compared with solar and wind energy, geothermal energy is continuous and stable. Geothermal energy usage has increased substantially in recent decades, and geothermal direct use is the most versatile and common form in many countries (Dickson and Fanelli, 2013; Shortall et al., 2015). In China, direct use of geothermal energy is widely distributed, and the total amount of heat has been the largest in the world (Zhu et al., 2015). Xiongxian geothermal field is currently supplying heat for 4.5 million square meters of houses, the largest district heating capacity in the world from a single geothermal field (Pang, 2018). Therefore, we have taken Xiongxian geothermal field as the example in our study of recoverable geothermal resources.
Over-exploitation of geothermal water may lead to a continuous decline in the groundwater level as well as reservoir temperature (Sanyal et al., 2000; Allis et al., 2009; Duan et al., 2011). Sustainable utilization of geothermal resources is a challenge facing the scientific community (Mongillo and Axelsson, 2010). The amount of recoverable resources is very important for sustainable geothermal resource management. There was a 30-m drop in the groundwater level from 2001 to 2009 in the majority of wells in the Xiongxian geothermal field (Kong et al., 2014). The recoverable geothermal resources in Xiongxian geothermal field are calculated by using a recovery factor of 15%, as set in the national standard (DZ40-85, 1985; Yang et al., 2015; Wang, 2009; Pang et al., 2017), which does not consider sustainability issues such as thermal breakthrough and pressure drop.
The renewability and sustainability of geothermal energy have attracted the attention of many scholars (White and Williams, 1975; Rybach et al., 1999; Stefansson, 2000; Axelsson et al., 2001; Rybach, 2003; Sanyal, 2005). Sustainability is reasonably defined as the ability to economically maintain the installed capacity over the amortized life of a power plant by taking practical steps (such as make-up well drilling) to compensate for resource degradation (pressure drawdown and/or cooling) (Sanyal, 2005). The project or amortized life is usually 20–50 years (O’Sullivan and O’Sullivan, 2016). Franco and Donatini (2017), who agree with Sanyal’s (2005) opinion on sustainability, believe that the geothermal potential of a particular area is to assess the maximum water yield to keep the heat extraction energy unchanged for an amortized time considering the temperature and pressure variation in the geothermal field. Williams et al. (2008) think any estimate of reservoir production potential should evaluate longevity from the perspective of injection and eventual thermal breakthrough. However, regrettably, few people consider sustainable use of geothermal resources when calculating the recoverable geothermal resources. It is therefore crucial and urgent to determine recoverable geothermal resources under conditions where temperature drop does not occur and pressure drop is within the threshold value in the production well, keeping the energy output of the well unchanged during the project lifetime; assumed to be 100 years. The lifetime of a geothermal field is defined as the thermal breakthrough time in the well doublet, that also meets the pressure drop limit (Gringarten, 1978).
Comerford et al. (2018) estimated geothermal heat recovery from a hot sedimentary aquifer in Guardbridge, Scotland using coupled groundwater flow and heat transport numerical model combining the heterogeneity of the medium. Simulation indicated production is sustainable for over 50 years in assumed extraction scenarios. However, the maximum thermal exploitation amount that keeps sustainable and the pressure change is not taken into account. Bodvarsson and Tsang (Bödvarsson and Tsang, 1982) and Williams (2007) estimated the recoverable geothermal resources for fracture reservoirs based on analytical equation and for fracture spacing of less than 30 m, the cold sweep will not achieve the production well in 30 years. The maximum extraction rate is not given. Kong et al. (2017) has put forward an optimistic well spacing using economic analysis which does not consider the sustainable exploration of a geothermal reservoir. Williams (2007), Williams (2010) established an idealized fractural reservoir model exploited by a single production and injection well doublet to describe the cold water injection front. The temperature of the production well began to decrease at about 5 years. The annual recoverable geothermal resources and recovery factor were evaluated with the change of production years. However, due to the decrease in temperature, recoverable geothermal resources cannot be maintained in a sustainable way. Sanyal et al. (2004) summarized the results of a national assessment of hydrothermal resources undertaken by USGS and GeothermEX according to industry experience over 26 years and estimated minimum sustainable capacity of 17 fields. GeothermEX assessment considered recovery factor 0.131 according to statistical fit. He also gave a semi-empirical equation that sustainable heat production capacity is the sum of natural heat discharge rate and the maximum heat production rate and indicated the value range from 3 to 17%, with a mean of 11%. However, in the calculation, the empirical coefficient of sustainability factor ranges so widely that the error is ±70% about the median of 10% (Grant, 2015). In the national standard of China, the recovery factor (Rg for simplicity) is set as 15% to calculate recoverable resources for thermal reservoirs with fractured carbonate rock (DZ40-85, 1985). The mean recovery factor recommended by the Australian code for sedimentary reservoirs is 17.5% with a range of 10–25% with a uniform probability (Williams et al., 2008; AGRCC, 2010a; AGRCC, 2010b; O’Sullivan and O’Sullivan, 2016). However, it is very unreliable to assess recoverable resources by depending on a pre-determined Rg decided by the reservoir lithology. Simple analytical models for a homogeneous and isotropic aquifer have been adopted to assess the recoverable geothermal resources that the extraction can be economically maintained in a geothermal field for urban heating (Gringarten, 1978; AGRCC, 2010a; Ferguson and Grasby, 2014; Ufondu, 2017).
In this study, a numerical thermo-hydraulic coupled modeling based on a trial method is proposed to calculate the recoverable geothermal resources in Xiongxian geothermal field. The recoverable geothermal resources and lifetime are related to the exploitation amount that can maintain the heat extraction unchanged throughout the authorized life of the field. The numerical model is established using many parameters, such as thermal conductivity, permeability, viscosity, and others, which are more accurate than using the predetermined Rg set in the standard. Additionally, lateral water flow and seasonal district heating are also considered in the numerical model, which was not taken into account in the analytical model. Therefore, the optimal well spacing that maintains the temperature of the fluid unchanged and the drawdown in the production well within the allowed value is discussed in this study.
Modeling Method
The procedures include two steps. One step is the numerical simulation, which is related to the geological and physical processes. The other step analyses the recoverable geothermal resources and recovery factors according to water pressure drop and thermal breakthrough.
Numerical Model
The present work focuses on numerical modeling for maximum heat extraction. The model in this study contains the 1D injection/production wells and 2D porous matrix of the Xiongxian Jixian system reservoir. Lateral runoff, seasonal heating, and different well spacing in well doublet patterns are considered in the model. The numerical model is based on a two-dimensional transient heat transfer model, and the following two Equations 1, 2 are used to realize the common simulation of the thermal front and pressure drawdown.
Mass conservation equation for control of flow in porous media is as follows:
where
The processes of heat conduction and convection are governed by the following constitutive Equation 2:
where
Recoverable Geothermal Resources Analysis
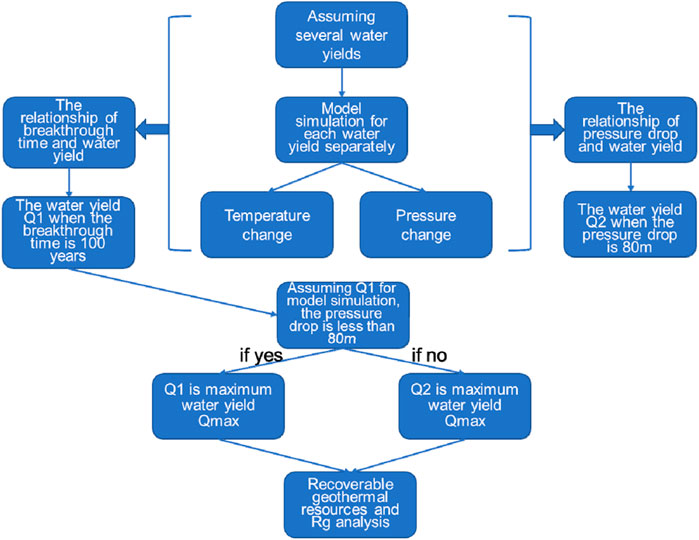
The changes in temperature and pressure at the production well can be known from the model. The following is a description of the steps taken to acquire the recoverable resources and Rg (Figure 1).
1) Assuming multiple mining scenarios with a series of water yields, the other conditions of the model in these scenarios, including initial conditions, boundary conditions, and grid settings are all the same;
2) Carry out numerical simulations for multiple scenarios with different water yields separately. In every scenario, temperature change and hydraulic pressure change with the mining time of the reservoir are obtained through model simulation;
3) Based on the simulation results, the temperature change curve of the production well can be obtained in every mining scenario. Reinjection of geothermal water into reservoirs could help maintain the reservoir pressure but may lead to thermal breakthrough. Therefore, each water yield corresponds to the thermal breakthrough time when the temperature of the production well drops. Therefore, the corresponding relationship between water yield and thermal breakthrough time is obtained.
By analogy, the pressure change curve of the production well can be obtained in every mining scenario. The corresponding relationship between water yield and the maximum value of the pressure drop is obtained.
4) According to the relationship between water yield and thermal breakthrough time, assuming that the thermal breakthrough time is 100 years, the corresponding water yield Q1 in this scenario can be obtained.
Similarly, according to the relationship between water yield and the maximum value of the pressure drop, assuming that the maximum pressure drop is the pressure threshold, the corresponding water yield Q2 in this scenario can be obtained.
5) Assuming that the water yield is Q1, a numerical model simulation is performed to obtain the pressure change of the production well over time. If the maximum value of the pressure drop is less than the threshold, Q1 is the maximum water yield Qmax all over the multiple scenarios.
If the maximum value of the pressure drop with the water yield Q1 is more than the threshold, Q2 is the maximum water yield Qmax all over the multiple scenarios.
The pressure drop threshold is assumed to be 80 m. This pressure threshold can be changed according to the actual situation of the geothermal field. In order to prevent atmospheric corrosion, the pump should be about 70 m below the surface of the water. If the water pump of the production well is located at about 150 m under the water level, the maximum water level can only drop another 80 m.
6) Based on the maximum water yield Qmax, the geothermal recoverable resource for a single well doublet at the wellhead
Where,
where
7) The layout of the well doublet pattern in the geothermal field area is arranged as follows. In Figure 2,
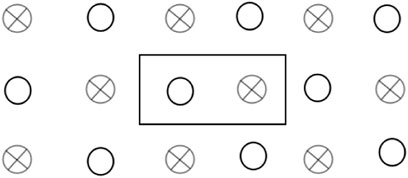
FIGURE 2. Selected reference volume (doublet in a closed rectangle) in a multiple well doublet production pattern.
The well spacing is D (m). The number of well doublets n in the exploitation area S (m2) is
Then, the total maximum water yield is as follow
Where
8) Recoverable geothermal resources can be obtained as follows:
9) To calculate the recovery factor, the total geothermal resource is needed to be obtained. The volumetric method is applied to calculate the total geothermal resource. The volumetric method was originally proposed in the USGS Assessment of Geothermal Resources (Nathenson, 1975; White and Williams, 1975; Muffler and Cataldi, 1978), and the total geothermal resource in a reservoir is calculated as
Here,
The recovery factor is defined as the ratio of the extracted thermal energy (measured at the wellhead) to the total geothermal energy contained originally in a given subsurface volume of rock and water (Axelsson et al., 2001), and this factor can be deduced by Equations 1, 6 as follows:
Where,
Model Configuration
In order to illustrate the sustainable recoverable resources of a geothermal reservoir, a two-dimensional hydro-thermal coupling model was established to simulate the hydro-thermal distribution in the field and the temperature and pressure change of the production well. The numerical model can be used to calculate the maximum water yield of sustainable exploitation for which the outlet temperature does not drop and the pressure does not exceed the critical value in the production well within 100 years of geothermal field life. Then, the recoverable resources can be calculated. This numerical model simulates the seasonal heating under the conditions of well doublet production patterns. The amount of recoverable resources is not fixed but varies with the production flow rate and production pattern, such as well spacing. The influence of well spacing is analyzed using the numerical model, and the optimal well spacing was found in this section.
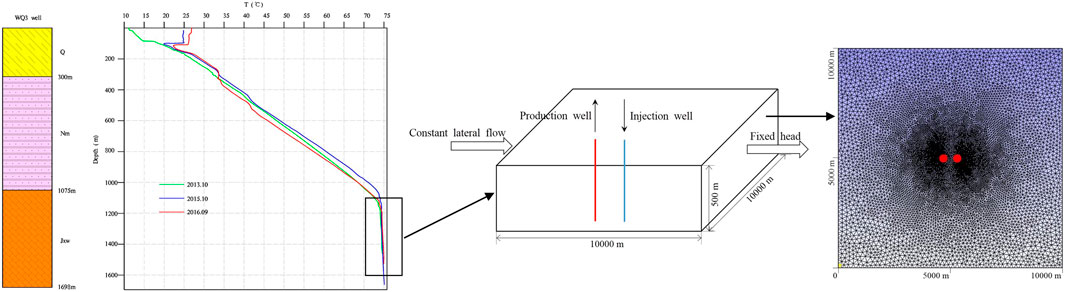
A few assumptions are made in the model for simplicity. These are listed as follows: the reservoir is supposed to be horizontal and of uniform thickness; the model of the reservoir is a rectangle of 10 km in length and 10 km in width to ignore the boundary effects; the permeability and thermal conductivity of the reservoir rock is assumed to be isotropic; the reservoir is regarded as a homogeneous aquifer; the thermal reservoir is mined at a constant water yield; the production and reinjection rate is balanced. The model is a cross-section horizontal two-dimensional (2-D) model. Since the reservoir in Jixian system formation encountered by drilling is about 500 m, the reservoir thickness in the model is set to 500 m. The reservoir is approximately located at a depth of 1 km underground (Figure 3). The main parameter values are listed in Table 1.
Grid System
The numerical model is spatially discretized and is refined near the production well and reinjection well (Figure 3). The specific heat capacity and density of reservoir rocks are 920 J/kg°C and 2,700 kg/m3 respectively. The permeability of the whole reservoir is set to be 1 × 10–13 m2, the porosity is 0.03 (Kong et al., 2017; Pang, 2018).
Initial Condition
The temperature of the layer is set at 75°C, and its hydraulic pressure is 0 Pa in the whole model range in the beginning. A steady-state simulation was performed first with the lateral recharge, the result of which was adopted as the initial condition for the transient flow model. The details are as follows. First, run the numerical model with the consistent temperature and pressure throughout the model area with the lateral recharge. Then the initial hydraulic pressure distribution is achieved. Lastly, this new hydraulic pressure distribution is used as the initial condition for simulation.
Boundary Condition
A hydraulic fixed head is set as a constant value of 0 m on the right side, and the lateral recharge of 1.6 × 10–6 m2/s from the left side is considered in the numerical model (Kong et al., 2017).
Source Term
Assuming that all of the water from the production well is reinjected into the recharge well, the pumping rate is equal to the quantity of water recharge. The temperature of the injection water is 30°C. Seasonal heating in 3 months of the year (from November 15th to March 15th) is considered in the numerical model.
In this work, the numerical model was developed with OpenGeoSys (OGS), which is a finite element and open-source software for solving multiple problems (Kolditz et al., 2012). A 2-D numerical model was established using OGS to simulate fluid and thermal transfer in the reservoir.
Case Study
The numerical modeling is applied to Xiongxian in northern China as our study area, in which space heating is already on the way. The geothermal field in Xiongxian is located southwest of the Niutuozhen uplift, in the northern part of the Jizhong Depression, which is situated in the Bohai Bay Basin. The Bohai Bay Basin is a large Mesozoic-Cenozoic Cratonian sedimentary basin filled with continental Paleocene, Neogene, and Quaternary sediments. This basin was developed in the Tertiary on the basement of the North China Platform and includes many independent Paleogene fault depressions. The entire area settled into a large depression during the Neogene period (Kong et al., 2014; Kong et al., 2020).
There are four main faults forming the boundaries of the Niutuozhen uplift, including the Niudong fault, the Rongcheng fault, the Daxing fault, and the Niunan fault (Figure 4). These faults were formed from the Late Jurassic to the Cretaceous by folding movement. The Xiongxian geothermal field is in the southern part of the Niutuozhen uplift, the bedrock of which is consisted of middle-upper Proterozoic Jixian system dolomite and Sinian dolomite. The Niutuozhen geothermal field has excellent geological structural conditions for the formation of geothermal resources. The Middle and Upper Proterozoic basement uplift causes the distribution of terrestrial heat flow and the geothermal gradient to have the characteristics of being high at the bulge axis and gradually decreasing toward the edge of the bulge. The high value of the geothermal gradient of the Cenozoic caprock in the geothermal field spreads in the NEE direction, and the overall trend is higher in the southwest and lower in the northeast. The geothermal gradient of the Quaternary and Neogene caprocks in the Xiongxian district in the southern area of Niutuozhen geothermal field is between 4.86–7.64 °C/100 m, showing the characteristics of a conductive geothermal field. The geothermal gradient of the geothermal reservoir of the Wumishan group is much smaller than that of the upper caprock, with an average of 0.62°C/100 m, showing obvious convective heat transfer characteristics. The terrestrial heat flow in the southern area of the Niutuozhen geothermal field is between 83.13 and 119.65 mW/m2. The terrestrial heat flow mainly comes from the heat generated by the radioactive decay of shallow rocks in the crust and the heat conducted by the upper mantle. According to the lithology and drilling information in the Xiongxian district, the lithology of geothermal reservoirs includes Neogene sandstone and lower Proterozoic Jixian system dolomite bedrock. Jixian system dolomite bedrock, especially the Wumishan group, is the main aquifer for space heating due to higher reservoir temperature, water yield, and wide distribution (Pang et al., 2018). The geothermal fluid in the bedrock thermal reservoir is mainly recharged by the lateral runoff from the Taihang Mountain in the west and the Yanshan Mountain in the north. After deep circulation heating, the geothermal water is stored in the bedrock thermal reservoir. In geologic history, the degree of rock karst weathering is approximately uniform. A homogeneous isotropic aquifer in the Jixian system dolomite was assumed in this study to establish a method to calculate the recoverable resources for district heating (Kong et al., 2014). According to the work of our research group, there are six wells in Xiongxian for continuous temperature measurement in the borehole, including one mining well, one monitoring well, and four recharge wells. In this paper, since the monitoring well does not produce geothermal water, the temperature profile is less affected and more presentative (Pang, 2018). The location of the monitoring well and the measured temperature are in Figure 4. The temperature logging is respectively from September 2013, September 2015, and October 2016. The average temperature gradient is about 5.13°C/100 m for the Cenozoic cap and 0.16°C/100 m for bedrock, which is small. The temperature is about 75°C at the bottom of the hole.
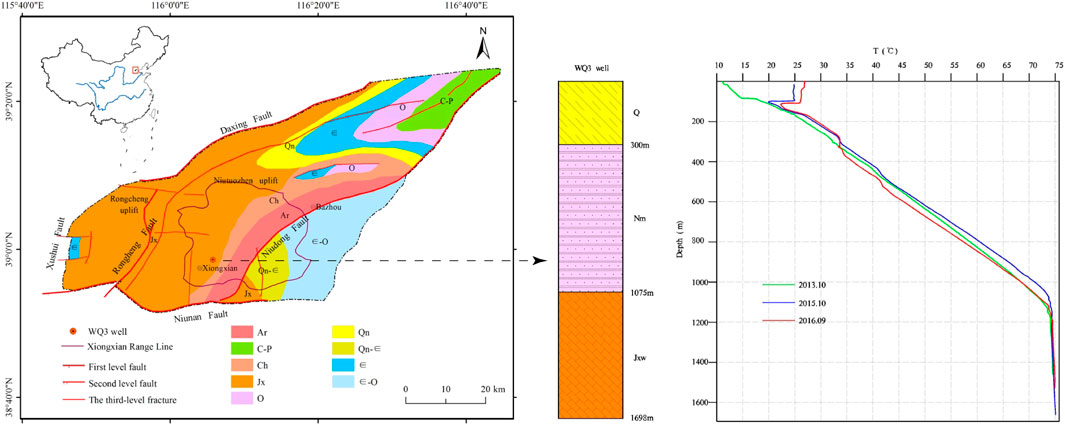
FIGURE 4. Pre-Cenozoic geological map in the Niutuozhen uplift; the location and temperature profile of monitoring well in the Xiongxian geothermal field (C-P: Carboniferous–Permian; O: Ordovician; Ch: Changcheng system; Qn: Qingbaikou system; Jx: Jixian; ∈: Cambrian; Q-Quaternary; Nm-Neogene minghuazhen group; Jxw-Jixian wumishan group) [adapted by Pang et al. (2018)].
Results and Discussion
Assuming different water yields, the pressure and temperature changes should be different. A total of 12 scenarios have been simulated to have a grasp of the effect of pressure and temperature to obtain the recoverable geothermal resources. The water yields of 12 scenarios are 100, 120, 150, 180, 200, 208, 220, 250, 292, 300, 333, and 417 m3/h respectively. In order to optimize the well spacing, the scenarios with several well spacing 300, 400, 500, 600, and 700 m are simulated respectively.
Maximum Water Yield
Assuming an arbitrary production water yield, the model simulates the temperature change of a production well with the production time. When the temperature of the production well begins to drop, this is referred to as thermal breakthrough time. Similarly, the thermal breakthrough time for each water yield can be acquired. By using the trial method and setting several water yields for the production well, the corresponding lifetime of the geothermal field can be obtained. Then, the correlation diagram between the water yield and the lifetime of the geothermal field can be established (Figure 5). The corresponding water yield can be acquired when the lifetime is 100 years. When the well spacing is 600 m, the fitting curvilinear equation of the correlation between the water yield and the lifetime of the geothermal field is
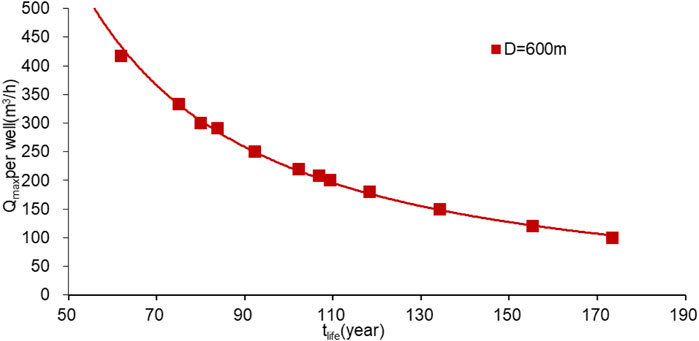
FIGURE 5. Relationship between the time when thermal breakthrough occurred and the water yield per production well.
When the lifetime of the geothermal field is 100 years, the maximum water yield per well
When the water yield per well is 223.64 m3/h, the model simulates the variation diagram of the temperature distribution from the recharge well to the production well with time, as shown in Figure 6. Figure 7 shows that when the well spacing is 600 m and the water yield per well is 223.64 m3/h, the temperature of the production well changes with the mining time. The temperature of the production well starts to decline when 100 years (Figure 7).
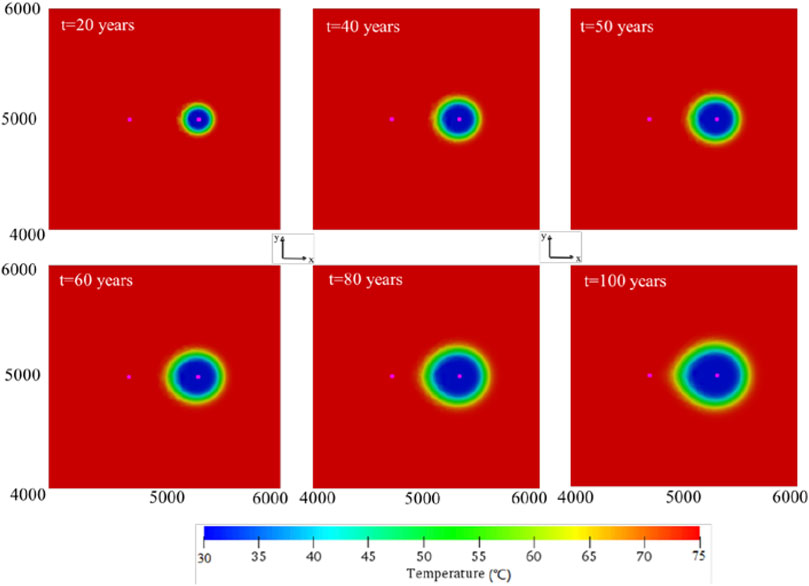
FIGURE 6. When the well spacing is 600 m and the water yield per production well is 223.64 m3/h, the temperature distribution displays in the geothermal field in the year 100.
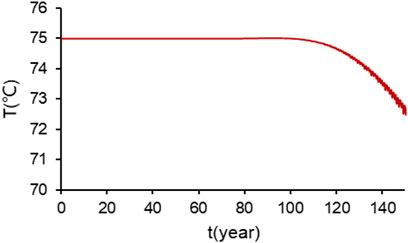
FIGURE 7. When the well spacing is 600 m and the water yield per production well is 223.64 m3/h, the temperature of the production well changes with the production time.
When
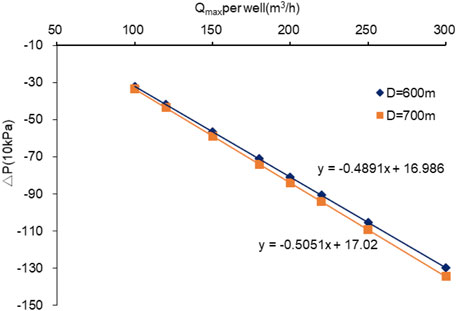
FIGURE 8. The relationship of maximum drawdowns and different water yields when the well spacing is 600 m and 700 m.
Well Spacing Optimization
Well spacing has an impact on the recoverable resources. If the well spacing increases, the time for thermal breakthrough becomes longer, but the pressure drop of the production well increases, which may lead to exceeding the limit value. Also, the larger the well spacing is, the lower the number of wells in a geothermal field and the lower the drilling costs. The optimal well spacing with the maximum water yield to meet the pressure drop limit can then be obtained.
In the numerical model, under different well spacing, multiple sets of thermal breakthrough times can be obtained by assuming multiple groups of water yields, as shown in Figure 9. The curvilinear fitting is based on the relationship between the water yield and the lifetime of the geothermal field for different well spacing. When the well spacing is 300 m, the fitting curvilinear equation is
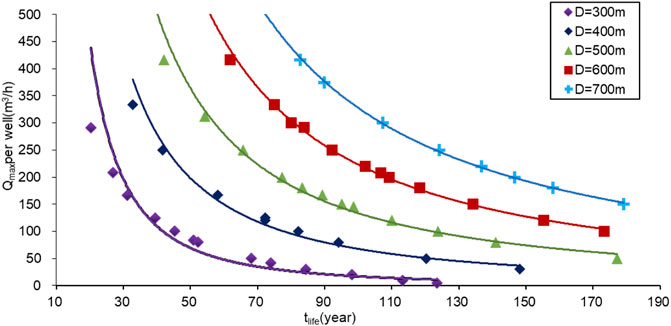
FIGURE 9. Relationship between the time when thermal breakthrough occurred and the maximum water yield per well under different well spacing.
Similarly,
When the well spacing is 300, 400, 500, and 700 m and the geothermal field lifetime is 100 years, the maximum water yield per well
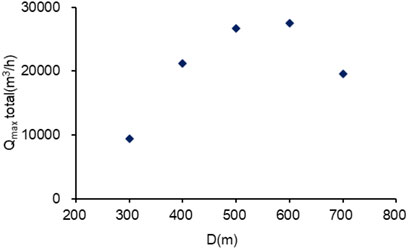
FIGURE 10. When the lifetime of the geothermal field is 100 years, the relationship between the total maximum water yield and the well spacing.
The pressure simulation results for each well spacing were obtained under the premise that the maximum water yield is consistent with the assumption that the temperature does not decrease during the production period of 100 years. The change in the pressure of the production well could be acquired by simulation. The maximum pressure drawdown occurred at the end of the 120-days heating season. With increasing well spacing, the pressure of the production well decreased greatly.
Owing to the drawdown value limit of 80 m, the pressure drawdown was within the acceptable limits of 80 m in the well doublet pattern. Also, at this point, the total water yield reaches the maximum. Thus, 600 m is the optimal spacing and conforms to the requirements of sustainable production with maximum water yield and therefore, maximum recoverable resource.
Geothermal Recoverable Resources
According to the drilling temperature data and the kriging interpolation algorithm in Xiongxian, the reservoir temperature distribution in the Jixian system of Xiongxian is obtained (Pang, 2018). Based on the aforementioned uniform well distribution with the optimal spacing of 600 m under the condition of sustainable assumption, Xiongxian can be divided into the well layout diagram as shown in Figure 11.
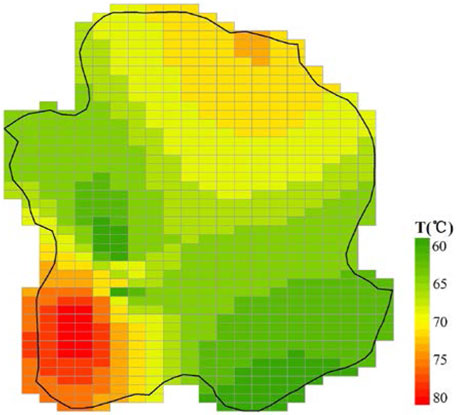
FIGURE 11. The study area is divided into several rectangles and the reservoir temperature distribution in the Jixian reservoir is superimposed.
Maximum water yield can be extracted when the length of the rectangular boundary is twice that of the well spacing and the width is equal to the well spacing, as arranged in Figure 11. In each rectangular square, there is a pair of wells. According to this pattern, the number of well doublets n in the exploitation area can be obtained as 803. Assuming that mining is carried out at the maximum water yield, the total maximum water yield is from Equation 9
The recoverable geothermal resources can be calculated according to the following Equation 10
Based on the above-calculated results, the recovery factor can be computed according to Equation 12
When the well spacing
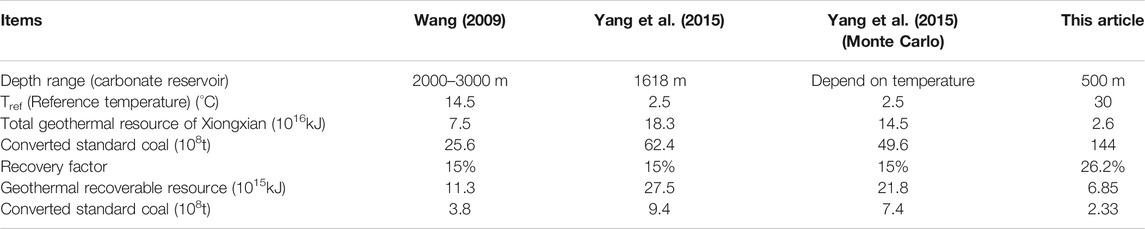
In the Xiongxian geothermal field, the total geothermal resources have been estimated by the Volume method (Wang, 2009; Yang et al., 2015). In their work, the recoverable geothermal resource is calculated by multiplying the total amount of resources by 15% (DZ40-85, 1985). Their results are listed in Table 2 to compare with our results.
It could be found that different total geothermal resources were obtained. This is attributed to the difference in the parameters including reservoir thickness and the reference temperature. Since the reference temperature used in this article is the temperature of the recharge water, and the reference temperature chosen by the others is the underground constant temperature zone or the average temperature of the atmosphere, the total amount of resources we calculated is low. However, here we insist on using the temperature of the recharge water as the reference temperature, because the heat we use for district heating is actually the heat released by the geothermal water circulation once, that is, the heat contained in the difference between the production temperature and the recharge temperature. Anyway, it can be known from the calculation formula
Conclusion
A numerical thermo-hydraulic coupled modeling in a geothermal reservoir is set up to investigate the geothermal recoverable resources during an operation time of 100 years with sustainability assumption. This work provides another way for sustainable exploitation and the calculation of recoverable resources.
The maximum water yield for per production well in well doublet pattern that keeps the heat extraction energy unchanged for an amortized time is 16.86, 67.69, 133.44, 198.29, and 192.08 m3/h, respectively, when the well spacing is 300, 400, 500, 600, and 700 m. According to the relationships among the well spacing, the drawdown of production wells, and maximum water yield of total wells, it is found that 600 m is the optimal well spacing with maximum exploitation amount and conforming to sustainability. The optimal well spacing can guide the management of geothermal fields.
The amount of recoverable geothermal resources in the Jixian system reservoir was calculated under the optimal spacing layout. The recoverable resources in 100 years are 6.85 × 1018 J. The calculation result of the recovery factor is 26.2%, which is higher than the previous value of 15% when only depending on lithology.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
YF and YH conceived and designed the numerical investigation; YF created the numerical model; YH examined the accuracy of the proposed model; YF and SZ designed the graphics and analyzed the result; YF wrote the manuscript; SZ, YF, and HL revised the manuscript; ZP proposed instructive suggestions to the manuscript.
Conflicts of Interest
Author YF is employed by China Three Gorges Corporation. Author SZ is employed by CAUPD Beijing Planning & Design Consultants Co., Ltd. Author HL is employed by Sinopec Green Energy Geothermal Development Co.,Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Dr. Yanlong Kong for his valuable advice on the manuscript. Many thanks to Dr. Jumei Pang, Dr. Ji Luo, Dr. Chaofan Chen, Dr. Yingchun Wang, Dr. Yiman Li, and Dr. Tianming Huang for discussions and constructive comments on an earlier version of the manuscript. Appreciation goes to for their guidance.
References
Allis, R., Bromley, C., and Currie, S. (2009). Update on Subsidence at the Wairakei-Tauhara Geothermal System, New Zealand. Geothermics 38, 169–180. doi:10.1016/j.geothermics.2008.12.006
Australian Geothermal Reporting Code Committee (AGRCC) (2010a). Australian Code for Reporting of Exploration Results, Geothermal Resources and Geothermal Reserves: The Geothermal Reporting Code. second edition. Adelaide: Australian Geothermal Energy Group AGEG and the Australian Geothermal Energy Association.
Australian Geothermal Reporting Code Committee (AGRCC) (2010b). Geothermal Lexicon for Resources and Reserves Definition and Reporting. second edition. Adelaide: Australian Geothermal Energy Group AGEG and the Australian Geothermal Energy Association.
Axelsson, G., Gudmundsson, A., Steingrimsson, B., Palmason, G., Armannsson, H., Tulinius, H., et al. (2001). Sustainable Production of Geothermal Energy: Suggested Definition. IGA-News. 43, 1–2.
Bödvarsson, G. S., and Tsang, C. F. (1982). Injection and thermal Breakthrough in Fractured Geothermal Reservoirs. J. Geophys. Res. 87, 1031–1048. doi:10.1029/jb087ib02p01031
Böttcher, N., Blöcher, G., Cacace, M., and Kolditz, O. (2012). “Heat Transport,” in Thermo-hydro-mechanical-chemical Processes in Porous media. Editors O. Kolditz,, and U. J. Görke (Berlin,Germany: Springer), 89–105. doi:10.1007/978-3-642-27177-9_4
Chen, C., Lin, M., and Cheng, J. (2011). Groundwater Dynamics. 5th ed. Beijing: Geological Publishing House.
Comerford, A., Fraser-Harris, A., Johnson, G., and McDermott, C. I. (2018). Controls on Geothermal Heat Recovery from a Hot Sedimentary Aquifer in Guardbridge, Scotland: Field Measurements, Modelling and Long Term Sustainability. Geothermics 76, 125–140. doi:10.1016/j.geothermics.2018.07.004
Dickson, M. H., and Fanelli, M. (2013). Geothermal Energy: Utilization and Technology. NewYork: Routledge Press.
Duan, Z., Pang, Z., and Wang, X. (2011). Sustainability Evaluation of limestone Geothermal Reservoirs with Extended Production Histories in Beijing and Tianjin, China. Geothermics 40, 125–135. doi:10.1016/j.geothermics.2011.02.001
DZ40-85 (1985). Method for Geothermal Resource Assessment Ministry of Geology and mineral Resources of the People's Republic of China. Beijing, China: GEOLOGICAL PUBLISHING HOUSE.
Ferguson, G., and Grasby, S. E. (2014). The Geothermal Potential of the Basal Clastics of Saskatchewan, Canada. Hydrogeol. J. 22, 143–150. doi:10.1007/s10040-013-1061-5
Franco, A., and Donatini, F. (2017). Methods for the Estimation of the Energy Stored in Geothermal Reservoirs. Proc. J. Phys. Conf. Ser. 796, 12025. doi:10.1088/1742-6596/796/1/012025
Garg, S. K., and Combs, J. (2015). A Reformulation of USGS Volumetric “Heat in Place” Resource Estimation Method. Geothermics 55, 150–158. doi:10.1016/j.geothermics.2015.02.004
Grant, M. A. (2015). Resource Assessment, a Review, with Reference to the Australian Code. Resource 19, 25.
Gringarten, A. C. (1978). Reservoir Lifetime and Heat Recovery Factor in Geothermal Aquifers Used for Urban Heating. Pageoph 117, 297–308. doi:10.1007/bf00879755
Gringarten, A. C., and Sauty, J. P. (1975). A Theoretical Study of Heat Extraction from Aquifers with Uniform Regional Flow. J. Geophys. Res. 80, 4956–4962. doi:10.1029/jb080i035p04956
Kolditz, O., Bauer, S., Bilke, L., Böttcher, N., Delfs, J. O., Fischer, T., et al. (2012). OpenGeoSys: an Open-Source Initiative for Numerical Simulation of Thermo-Hydro-Mechanical/chemical (THM/C) Processes in Porous media. Environ. Earth Sciearth Sci. 67, 589–599. doi:10.1007/s12665-012-1546-x
Kong, Y., Pang, Z., Shao, H., Hu, S., and Kolditz, O. (2014). Recent Studies on Hydrothermal Systems in China: a Review. Geotherm. Energ. 2, 19. doi:10.1186/s40517-014-0019-8
Kong, Y., Pang, Z., Shao, H., and Kolditz, O. (2017). Optimization of Well-Doublet Placement in Geothermal Reservoirs Using Numerical Simulation and Economic Analysis. Environ. Earth Sci. 76, 118. doi:10.1007/s12665-017-6404-4
Kong, Y., Pang, J., Pang, Z., Li, J., and Pan, S. (2020). Fault-Affected Fluid Circulation Revealed by Hydrochemistry and Isotopes in a Large-Scale Utilized Geothermal Reservoir. Geofluids 24, 1–13. doi:10.1155/2020/2604025
Lund, J. W., Freeston, D. H., and Boyd, T. L. (2011). Direct Utilization of Geothermal Energy 2010 Worldwide Review. Geothermics 40 (3), 159–180. doi:10.1016/j.geothermics.2011.07.004
Mongillo, M. A., and Axelsson, G. (2010). Preface to Geothermics Special Issue on Sustainable Geothermal Utilization. Geothermics 39, 279–282. doi:10.1016/j.geothermics.2010.09.011
Muffler, P., and Cataldi, R. (1978). Methods for Regional Assessment of Geothermal Resources. Geothermics 7, 53–89. doi:10.1016/0375-6505(78)90002-0
Nathenson, M. (1975). Physical Factors Determining the Fraction of Stored Energy Recoverable from Hydrothermal Convection Systems and Conduction-Dominated areas[R]. Menlo Park, Calif.(USA): Geological Survey.
O'Sullivan, M. J., and O'Sullivan, J. P. (2016). “Reservoir Modeling and Simulation for Geothermal Resource Characterization and Evaluation,” in Geothermal Power Generation. Editor R. DiPippo (Amsterdam, Netherlands: Elsevier), 165–199. doi:10.1016/B978-0-08-100337-4.00007-3
Pang, J. (2018). “A Study on the Responsing Mechanism of Karstic Geothermal Reservoir to Large Scale Production and Reinjection in Niutuozhen Geothermal Field,”. [PhD thesis] (Beijing, China: University of Chinese Academy of Sciences).
Pang, J., Pang, Z., Lv, M., Tian, J., and Kong, Y. (2018). Geochemical and Isotopic Characteristics of Fluids in the Niutuozhen Geothermal Field, North China. Environ. Earth Sci. 77, 1–21. doi:10.1007/s12665-017-7171-y
Pang, Z. H., Kong, Y. L., Pang, J. M., Hu, S., and Wang, J. (2017). Geothermal Resources and Development in Xiongxian New Area. Bull. Chin. Acad. Sci. 32, 1224–1230. doi:10.16418/j.issn.1000-3045.2017.11.007
Pang, Z., Hu, S., and Wang, J. (2012). A Roadmap to Geothermal Energy Development in China. Keji Daobao/Sci. Technol. Rev. 30, 18–24.
Rybach, L. (2003). Geothermal Energy: Sustainability and the Environment. Geothermics 32, 463–470. doi:10.1016/s0375-6505(03)00057-9
Rybach, L., Mégel, T., and Eugster, W. J. (1999). How Renewable Are Geothermal Resources? Geotherm. Resour. Counc. Trans. 23, 563–566.
Sanyal, S. K., Butler, S. J., Brown, P. J., Goyal, K., and Box, T. (2000). An Investigation of Productivity and Pressure Decline Trends in Geothermal Steam Reservoirs. Trans. Resour. Counc. 24, 325–330.
Sanyal, S. K., Klein, C. W., Lovekin, J. W., and Henneberger, R. C. (2004). National Assessment of U.S. Geothermal Resources—A Perspective. United States: Geothermal Resources Council Transactions.
Sanyal, S. “Sustainability and Renewability of Geothermal Power Capacity,” in Proceedings of the World Geothermal Congress, Antalya, Turkey, April 2005.
Shortall, R., Davidsdottir, B., and Axelsson, G. (2015). Geothermal Energy for Sustainable Development: A Review of Sustainability Impacts and Assessment Frameworks. Renew. Sustain. Energ. Rev. 44 (C), 391–406. doi:10.1016/j.rser.2014.12.020
Stefansson, V. “The Renewability of Geothermal Energy,” in Proceedings of the Proceedings of the World Geothermal Congress, Kyushu-Tohoku, Japan, May-June 2000, 883–888.
Ufondu, L. S. (2017). “Assessment of the Potential Heat Stored in the Deep Aquifers of the Willison basin for Geothermal Energy Production,”. Doctoral dissertation (Canada: University of Saskatchewan).
Wang, S. “Geothermal Resource Assessment in Xiongxian,” in Proceedings of Chinese Geophysical Society, China, July 2009, 1. Chinese geophysics.
White, D. E., and Williams, D. L. (1975). Assessment of Geothermal Resources of the United States. Geological Survey (Menlo Park, California (USA): US Department of the Interior).
Williams, C. F. “Development of Revised Techniques for Assessing Geothermal Resources,” in Proceedings of the Proceedings, 29th Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, California, January 2004, 7.
Williams, C. F., Reed, M., and Mariner, R. H. (2008). A Review of Methods Applied by the US Geological Survey in the Assessment if Identified Geothermal Resources. University Park, Pennsylvania, United States: Citeseer.
Williams, C. F. “Thermal Energy Recovery from Enhanced Geothermal Systems-Evaluating the Potential from Deep, High-Temperature Resources,” in Proceedings of 35th Workshop on geothermal reservoir engineering, Stanford University, U.S, February 2010.
Williams, C. F. “Updated Methods for Estimating Recovery Factors for Geothermal Resources,” in Proceedings of Thirty-Second Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, California, January 2007.
Yang, F. T., Liu, S. L., Liu, J. X., Pang, Z., and Zhou, D. “Combined Monte Carlo Simulation and Geological Modeling for Geothermal Resource Assessment: a Case Study of the Xiongxian Geothermal Field, China,” in Proceedings of the Proceedings of the World Geothermal Congress, Australia-Newzealand, April 2015.
Keywords: recoverable geothermal resources, numerical model, sustainable exploitation, reinjection, well spacing
Citation: Fan Y, Zhang S, Huang Y, Pang Z and Li H (2022) Determining the Recoverable Geothermal Resources Using a Numerical Thermo-Hydraulic Coupled Modeling in Geothermal Reservoirs. Front. Earth Sci. 9:787133. doi: 10.3389/feart.2021.787133
Received: 30 September 2021; Accepted: 19 November 2021;
Published: 14 January 2022.
Edited by:
Haibing Shao, Helmholtz Association of German Research Centres (HZ), GermanyReviewed by:
Fengtian Yang, Jilin University, ChinaChaofan Chen, Helmholtz Association of German Research Centres (HZ), Germany
Copyright © 2022 Fan, Zhang, Huang, Pang and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yifan Fan, ZmFuX3lpZmFuQGN0Zy5jb20uY24=
 Yifan Fan
Yifan Fan Shikuan Zhang2
Shikuan Zhang2 Yonghui Huang
Yonghui Huang Zhonghe Pang
Zhonghe Pang