Fracture Network Localization Preceding Catastrophic Failure in Triaxial Compression Experiments on Rocks

McBeck, Jessica; Ben-Zion, Yehuda; Renard, François

doi:10.3389/feart.2021.778811

ORIGINAL RESEARCH article

Front. Earth Sci., 29 November 2021

Sec. Geohazards and Georisks

Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.778811

This article is part of the Research Topic Recent Advances in Mechanics and Physics of Rock Fractures across Scales View all 7 articles

Fracture Network Localization Preceding Catastrophic Failure in Triaxial Compression Experiments on Rocks

Jessica McBeck¹*

Yehuda Ben-Zion²

François Renard^1,3

¹The Njord Centre, Departments of Geosciences and Physics, University of Oslo, Oslo, Norway
²Department of Earth Sciences and Southern California Earthquake Center, University of Southern California, Los Angeles, CA, United States
³University Grenoble Alpes, University Savoie Mont Blanc, CNRS, IRD, ISTerre, Grenoble, France

We quantify the spatial distribution of fracture networks throughout six in situ X-ray tomography triaxial compression experiments on crystalline rocks at confining stresses of 5–35 MPa in order to quantify how fracture development controls the final macroscopic failure of the rock, a process analogous to those that control geohazards such as earthquakes and landslides. Tracking the proportion of the cumulative volume of fractures with volumes >90th percentile to the total fracture volume, $\sum v_{90} / v_{t o t}$ indicates that the fracture networks tend to increase in localization toward these largest fractures for up to 80% of the applied differential stress. The evolution of this metric also matches the evolution of the Gini coefficient, which measures the deviation of a population from uniformity. These results are consistent with observations of localizing low magnitude seismicity before large earthquakes in southern California. In both this analysis and the present work, phases of delocalization interrupt the general increase in localization preceding catastrophic failure, indicating that delocalization does not necessarily indicate a reduction of seismic hazard. However, the proportion of the maximum fracture volume to the total fracture volume does not increase monotonically. Experiments with higher confining stress tend to experience greater localization. To further quantify localization, we compare the geometry of the largest fractures, with volumes >90th percentile, to the best fit plane through these fractures immediately preceding failure. The r² scores and the mean distance of the fractures to the plane indicate greater localization in monzonite than in granite. The smaller mean mineral diameter and lower confining stress in the granite experiments may contribute to this result. Tracking these various metrics of localization reveals a close association between macroscopic yielding and the acceleration of fracture network localization. Near yielding, $\sum v_{90} / v_{t o t}$ and the Gini coefficient increase while the mean distance to the final failure plane decreases. Macroscopic yielding thus occurs when the rate of fracture network localization increases.

Introduction

Preexisting weaknesses control how and when rocks fail because they concentrate shear and tensile stresses that promote fracture propagation under relatively low differential stress (e.g., Griffith, 1921). These early fractures tend to propagate parallel to the maximum compression direction, $σ_{1}$ , and open perpendicular to it in rocks (e.g., Peng and Johnson, 1972; Moore and Lockner, 1995; Wu et al., 2000; Miao et al., 2021). Following the wing crack model of fracture network development (e.g., Brace et al., 1966; Horii and Nemat-Nasser, 1986; Sammis and Ashby, 1986; Kemeny and Cook, 1991), the initial propagation of a fracture from an inclined preexisting fracture is stable, so increasing stress must drive further propagation. Laboratory observations suggest that when the length of a fracture is comparable to the interfracture spacing, fractures begin to interact with each other, prompting linkage and coalescence (e.g., Wong, 1982; Kranz, 1983; Rawling et al., 2002). This transition from distributed, isolated fractures to coalescing, interacting, and localizing arrays of fractures is associated with a transition from stable to unstable propagation (e.g., Figure 1). The spatial distribution of the evolving fracture network thus may provide key information about the proximity of the system to failure. Indeed, fracture network clustering is a key predictor of the timing of catastrophic failure in triaxial compression experiments (McBeck J. A. et al., 2020). Similarly, increasing localization and clustering of low magnitude seismicity preceded several M > 7 earthquakes in southern and Baja California (Ben-Zion and Zaliapin, 2020).

FIGURE 1

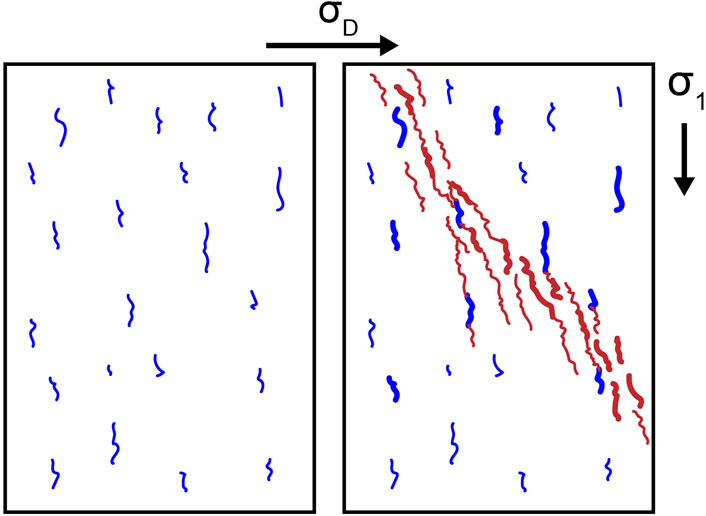
FIGURE 1. Transition from stable (left) to unstable (right) fracture network development via coalescence of fractures with increasing differential stress, $σ_{D}$ . Left: Under lower $σ_{D}$ , microfractures nucleate and grow parallel to the main compressive stress, $σ_{1}$ . Right: With increasing $σ_{D}$ , approaching system-size failure, the microfractures grow, interact, and link to form a connected fault.

Field observations and laboratory experiments show how deformation can become more localized toward macroscopic failure in the laboratory, and with increasing total slip and slip-rate along faults in the field (e.g., Segall and Pollard, 1983; Chen and Spetzler, 1993; Bergbauer and Martel, 1999; Ben-Zion and Sammis, 2003; Schubnel et al., 2003; Kattenhorn and Marshall, 2006; De Joussineau et al., 2007; Moir et al., 2010; Zhao et al., 2018; Kandula et al., 2019; Renard et al., 2019a; Renard et al., 2019b; McBeck et al., 2020a; McBeck et al., 2020b). Locations of acoustic emissions (AEs) captured during rock deformation experiments under triaxial compression loading suggest that the AEs localize from a diffuse cloud to a narrower zone with increasing deformation (Lockner et al., 1991; Aben et al., 2019). Some experiments show that AEs can propagate across the rock sample, from a smaller cluster of AEs at one edge of the rock sample to a system-spanning, elongate cluster (Benson et al., 2007). Some clusters of AEs may include a process zone and subsequent damage zone (Lei et al., 2000). Tensile fracturing and relatively low b values with a few large events characterize deformation in the process zone, while shear fracturing and lower b values with a greater number of larger events characterize deformation in the damage zone. These laboratory observations suggest that fracture linkage is the dominant form of fracture network development following macroscopic fault formation. Additional analyses identify a link between b values and the spatial distribution of AEs in experiments on precut granite cores that contain faults with varying degrees of roughness (Goebel et al., 2017). Rougher faults have more distributed AEs and higher b values than smoother faults, which produce more localized deformation with larger rupture areas and thus lower b values.

In situ X-ray tomography experiments that capture images of three-dimensional fracture networks at different times provide additional evidence of deformation localization preceding catastrophic failure. Observations from X-ray tomography experiments indicate that fracture networks can evolve from isolated fractures that trend parallel to $σ_{1}$ , to a linked array of fractures that trends oblique to $σ_{1}$ (Zabler et al., 2008; Kandula et al., 2019; Renard et al., 2018; Renard et al., 2019a). Similar experiments on granite and other low porosity crystalline rocks show a similar tendency of increasing localization toward failure: from initially distributed fractures to a system-spanning fault network (Renard et al., 2017; Renard et al., 2019b). However, some experiments on these rock types do not reveal such system-spanning faults preceding macroscopic failure (Renard et al., 2019a; Renard et al., 2019b; McBeck et al., 2021). In these experiments, the fracture networks remain relatively distributed with several large fractures, rather than one dominant system-spanning fault.

These previous analyses did not systematically compare the varying expressions of fracture network localization, and did not examine why different experiments, under varying confining stresses and on different rock types, experienced varying expressions of localization. Here, we quantify and compare the evolving spatial distribution of fracture networks throughout six in situ X-ray tomography triaxial compression experiments on low porosity crystalline rocks: granite and monzonite. We assess the idea that one dominant fracture continually grows at the expense of others by tracking the proportion of the volume of the maximum fracture, v_max, to the total fracture volume, v_tot, throughout each experiment. We also examine if the set of the largest fractures continually dominates deformation by tracking the sum of the volume of the fractures with volumes >90th percentile, relative to the total fracture volume, $\sum v_{90} / v_{t o t}$ , and the Gini coefficient, which measures the deviation of a population from a uniform distribution (Gini, 1921). To further quantify the localization of the fracture networks, we compare the geometry of the set of the largest fractures to a plane. We find the best fit plane through the fractures with volumes >90th percentile in the tomogram immediately preceding failure, and then calculate the distance between these fractures and the plane, and the r² score of the fractures and the plane. Tracking these various metrics of localization reveals fundamental insights into the temporal evolution of localization toward failure, including intermittent phases of delocalization, the influence of confining stress and rock type on localization, and the temporal correlation between macroscopic yielding and fracture network localization.

Methods

In situ X-Ray Tomography

We use the X-ray transparent triaxial deformation apparatus Hades (Renard et al., 2016) installed at beamline ID19 at the European Synchrotron and Radiation facility to deform the rock cores. This apparatus enables acquiring X-ray tomograms of the rock core while it is inside the apparatus at the applied differential stress conditions. In these experiments, we apply a constant confining stress between 5 and 35 MPa (Table 1) using oil surrounding the jacket that contains the rock core, and then increase the axial stress in steps of 0.5–5 MPa, with smaller increases of axial stress closer to macroscopic failure (Figure 2), at ambient temperature conditions. After each stress step, we acquire 1,600 radiographs at 32 bytes gray scale resolution of X-ray absorption while the sample is rotated over 180° within 1.5 min. The final reconstructed tomogram contains 1,600 × 1600 × 1,600 voxels with 6.5 µm/voxel spatial sampling. Due to the stress-controlled loading conditions, the rocks fail in a sudden stress drop. The final scan is acquired typically within 0.5 MPa of the final failure stress. We measure the axial contraction of the rock sample using the tomograms because the shortening of the rock core is visible in the three-dimensional images.

TABLE 1

TABLE 1. Conditions of each experiment.

FIGURE 2

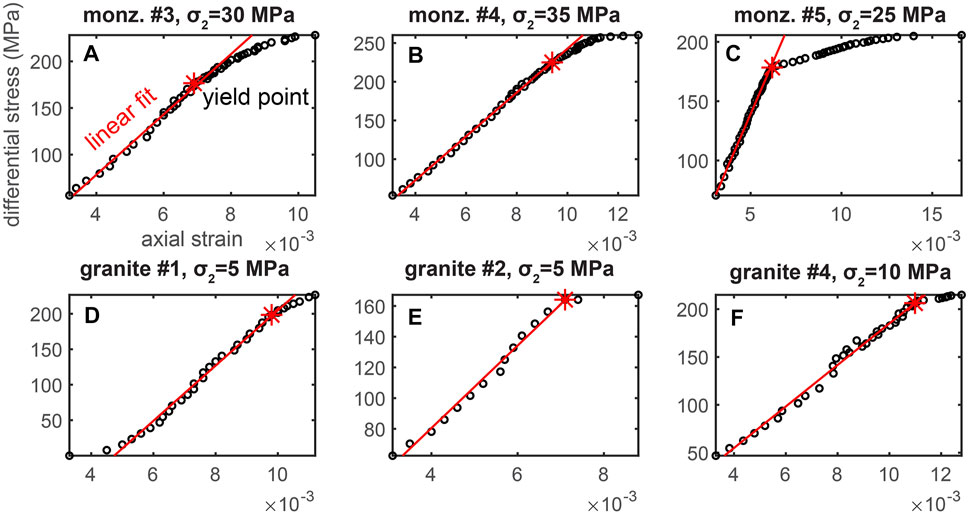
FIGURE 2. Differential stress versus axial strain relationships for the six examined experiments: (A) monzonite #3, (B) monzonite #4, (C) monzonite #5, (D) granite #1, (E) granite #2, and (F) granite #4. Black circles show the conditions when an X-ray tomogram was acquired. Red lines show the linear fit of the early portion of the data. Red stars show the identified yield point, when the data diverges from the linear fit. The title of each plot shows the experiment abbreviation (Table 1), and applied confining stress, $σ_{2}$ . In experiment monz. #4, we applied a pore fluid pressure, p = 5 MPa.

The rock samples are cylinders 1 cm tall and 4 mm wide. We perform three experiments on Westerly granite and three experiments on monzonite. Granite and monzonite are both low porosity crystalline rocks dominated by quartz and feldspar. The main difference between these rocks is that the mean grain size of the granite is 100–200 μm, while monzonite has a mean grain size of 300–400 μm (e.g., Aben et al., 2016). Each rock sample was deformed without fluid, except for monzonite #4, which included 5 MPa of deionized water as pore fluid pressure.

Each experiment includes the typical three stages of rock deformation in the brittle regime: (1) an early linear phase, (2) yielding, and (3) macroscopic failure (Figure 2). Due to the approximately linear relationship between the axial contraction and differential stress early in each experiment, we may fit a line through the data to identify the yield point. We identify the yield point when the data begins to diverge from the linear fit by more than 5%. Later, we compare the microscopic observations of fracture network development to the timing of the macroscopic yielding. The images of the X-ray tomograms of each experiment are publicly available (Renard, 2017, 2018, 2021).

Segmentation of Fracture Networks

During the reconstruction of the radiographs to three-dimensional volumes, we applied corrections to remove acquisition noise, including ring artefacts, and to smooth variations in the intensity of the X-ray source during the experiment. To remove noise from the reconstructed images, we preprocessed these data using the commercial image analysis software AvizoFire™, including denoising the volumes using a non-local-means filter (Buades et al., 2005).

The reconstructed tomograms are three-dimensional representations of the local density of the material. Pores and fractures may be distinguished from the solid rock because they have distinct ranges of densities. We segment the rock into solid and fractures using a standard global thresholding technique. We identify the local minimum in the histogram of the gray scale values of the tomogram, indicative of density, that separates the solid material from the fractures and pores (Supplementary Figure S1). We identify this minimum threshold by fitting two Gaussian distributions to the two portions of the histogram that correspond to the solid material and fractures. We identify the threshold between the phases at the gray scale value when the second derivative of this cumulative Gaussian distribution is closest to zero. A second derivative equal to zero indicates an inflection point between the two Gaussian distributions, which we use as the threshold to separate the solid from the voids.

Gini Coefficient

We use several metrics to quantify localization, including the Gini coefficient. The Gini coefficient uses the Lorenz curve of a distribution to measure the deviation from a uniform distribution (e.g., Gini, 1921; Ben-Zion and Zaliapin, 2020). The Lorenz curve shows the proportion of the total amount of a population, such as fracture volume, that is included in the bottom percentile of a population. The Gini coefficient is one minus twice the integral of the Lorenz curve (Supplementary Figure S2). Thus, larger Gini coefficients indicate that the total volume of the fractures in a network is dominated by a few fractures, whereas lower Gini coefficients indicate that the total volume is more equally distributed among all the fractures.

Results

Localization Toward the Largest Fractures

To gain a general understanding of fracture network localization in these experiments, we first examine the fracture networks in the final five scans before system-size failure in two experiments (Figure 3). These two experiments share some fundamental similarities in fracture network development preceding macroscopic failure. In the final stages of the monzonite #5 experiment (Figure 3A), the largest fractures appear first relatively randomly spread throughout the rock core. With increasing differential stress, the fractures grow in volume and link with each other. In the scan immediately preceding failure, the fracture network extends from the top to the bottom of the core. Similar to the monzonite #5 experiment, initially the fracture and pore network in the granite #2 experiment is relatively diffusely distributed (Figure 3B). Then, with increasing differential stress, several fractures propagate and coalesce to form elongated system-spanning fault networks.

FIGURE 3

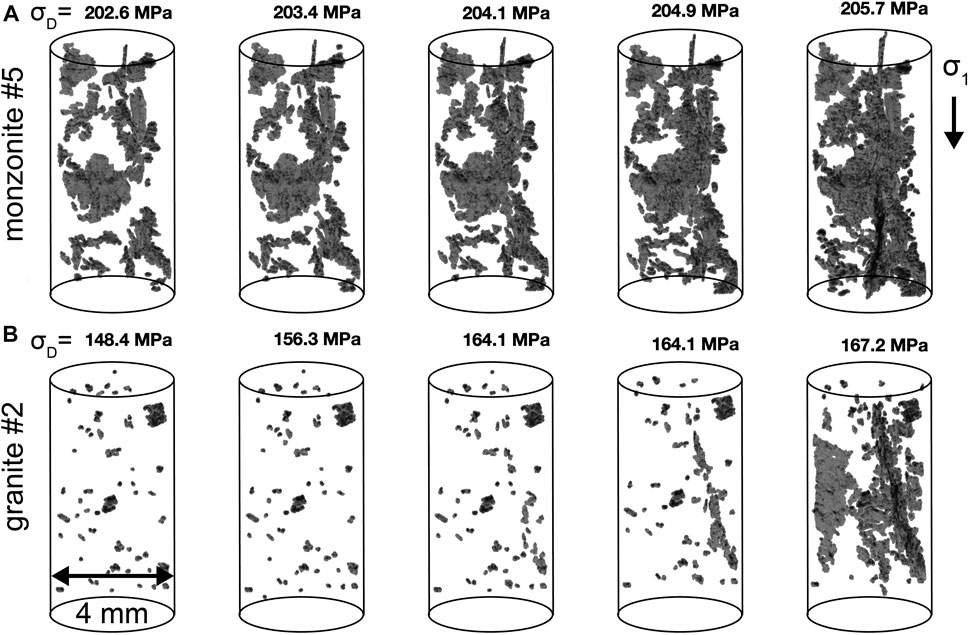
FIGURE 3. Fracture network development in the final five tomograms preceding macroscopic failure in experiment monzonite #5 (A) and granite #2 (B). Black regions show the fractures with volumes greater than the 90th percentile of the population. Numbers at the top of the cores show the differential stress applied on the sample when the scan was acquired.

The fracture networks in these experiments also suggest differences in the localization process between rock types. In the monzonite #5 experiment, the identified fracture network extends from the top to the bottom of the core, and also has a wide lateral extent, perpendicular to $σ_{1}$ . In the granite #2 experiment, the largest fractures extend from the top to the bottom of the core, but are more narrowly constrained in the lateral direction. Thus, the fracture network appears more localized in the granite #2 experiment immediately preceding failure than the monzonite #5 experiment. Next, we assess the validity of these observations by quantifying the localization of the fracture networks.

To quantify the coalescence of the fracture networks throughout triaxial compression, we first track the proportion of the maximum fracture volume to the total volume of all the fractures, v_max/v_tot, in each scan acquired throughout the experiments (Figure 4). High v_max/v_tot indicates that the largest, most volumetric, fracture in the network dominates the network. Increasing v_max/v_tot indicates that the largest fracture continually dominates an increasing proportion of the fracture network. Following the idea that the fracture networks coalesce into one dominant fracture, v_max/v_tot should continually increase with differential stress. However, only two of the experiments (monzonite #3 and granite #4) show generally increasing v_max/v_tot, with a few episodic decreases. Instead, the majority of the experiments experience delocalization away from the largest fracture, with prolonged phases of decreasing v_max/v_tot. The granite #1 and #2 experiments host relatively constant v_max/v_tot until near macroscopic failure, and then sharp drops in v_max/v_tot. The monzonite #4 experiment also hosts a sharp drop in v_max/v_tot near failure. These sharp drops indicate that many smaller fractures are propagating and lengthening in the final stages preceding failure, while the largest fracture is growing at a slower rate relative to the cumulative influence of all of the smaller fractures.

FIGURE 4

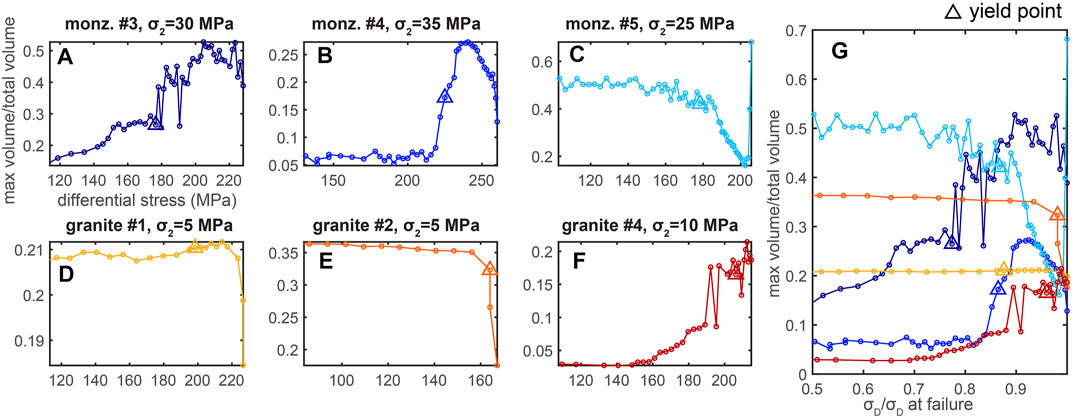
FIGURE 4. Evolution of the maximum fracture volume divided by the total volume of fractures, v_max/v_tot, throughout each individual experiment (A–F), and for all the experiments (G). Color of the lines in (G) matches the colors of each experiment shown in (A–F). Triangles show the conditions of the yield point. Increasing v_max/v_tot indicates that the fracture network is localizing toward the one largest fracture.

The experiments that do not host a sharp drop in v_max/v_tot near failure show either sharp (monzonite #5) or more gradual (monzonite #3, granite #4) increases in v_max/v_tot following yielding and preceding macroscopic failure. Thus, following yielding, the final fracture network that develops in half of the experiments is dominated by the largest fracture that grows at the expense of the other fractures, and likely coalesces with several of the preexisting large fractures. In the other set of the experiments, the final fracture network is dominated by several large fractures, and not only one.

The metric of localization, v_max/v_tot, reveals that fracture network development does not always follow the idealized evolution of one fracture continually growing at the expense of others. Rather, the rocks experience phases of delocalization away from the largest fracture, as well as the localization of deformation toward it. Due to this contrasting behavior, we next examine the localization of the few largest fractures, rather than only the absolute maximum. We track the set of fractures with volumes >90th percentile of the fracture volumes in each tomogram (i.e., the cumulative volume of the top 10th percentile fractures at each stress step). We then examine the evolution of the proportion of the sum of their fracture volumes, $\sum v_{90}$ , to the total fracture volume, v_tot, with increasing differential stress. Increasing $\sum v_{90} / v_{t o t}$ indicates increasing localization toward the largest set of fractures in the network, with volumes >90th percentile. We also test the influence of changing this threshold, and do not observe significant differences in the results.

In all but one of the experiments (granite #1), the largest fractures host generally increasing proportions of the total fracture network throughout loading (Figure 5). The granite #1 experiment experiences only small changes in $\sum v_{90} / v_{t o t}$ (Figure 5D, g). Several of the experiments host accelerations in $\sum v_{90} / v_{t o t}$ near macroscopic failure (e.g., monzonite #5, granite #4, granite #2). Other experiments show more continuous increases toward failure, without significant changes in the rate of $\sum v_{90} / v_{t o t}$ accumulation relative to differential stress (monzonite #3 and #4). The timing of macroscopic yielding and the observed acceleration in $\sum v_{90} / v_{t o t}$ are similar in the majority of the experiments (granite #2 and #4, monzonite #4 and #5), but appear to lack a strong correlation in other experiments (e.g., monzonite #3). To test the influence of using different thresholds, we performed this analysis using the 25th, 50th, and 75th percentile thresholds (Supplementary Figure S3). This analysis shows that the overall trends of $\sum v_{90} / v_{t o t}$ when x is 25, 50 and 75 is similar to when x is 90. Although the precise magnitude of $\sum v_{90} / v_{t o t}$ decreases with increasing x, the overall trends remain unchanged. In addition, the evolution of the Gini coefficient matches the evolution of $\sum v_{90} / v_{t o t}$ for each experiment (Supplementary Figure S4).

FIGURE 5

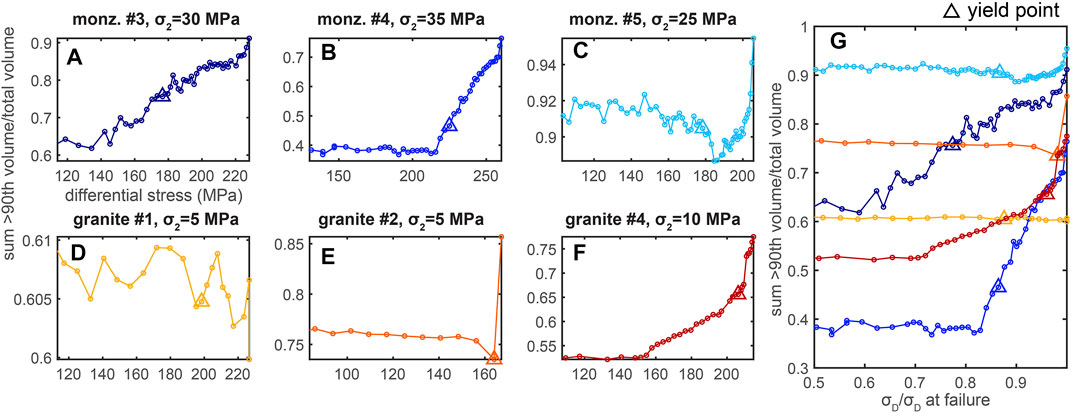
FIGURE 5. Evolution of the sum of the fracture volumes with values >90th percentile divided by the total volume of fractures, $\sum v_{90} / v_{t o t}$ , throughout each individual experiment (A–F), and for all the experiments (G). Color of the lines in (G) matches the colors of each experiment shown in (A–F). Triangles show the conditions of the yield point. Increasing $\sum v_{90} / v_{t o t}$ indicates increasing localization toward the largest fractures in the network, with volumes >90th percentile.

In summary, the majority of the experiments experience increasing localization of fracture development toward the largest fractures (Figure 5, Supplementary Figure S3 and S4), and the majority of the experiments experience some phases of delocalization away from the one largest fracture (Figure 4). Thus, the fracture network that grows at the expense of the other fractures is generally comprised of several fractures, rather than only the largest fracture. Counting the number of the largest fractures throughout each experiment indicates that these fracture networks, composed of fractures with volumes >90th percentile, host hundreds of fractures between the yielding point and macroscopic failure (Supplementary Figure S5).

To more directly compare the signals of localization with the three metrics of the Gini coefficient, $\sum v_{90} / v_{t o t}$ , and v_max/v_tot, we now examine the differences of these metrics calculated in the final and initial tomogram of each experiment (Figure 6). Comparing the difference in v_max/v_tot indicates that four of the six experiments experience increasing localization toward the largest fracture from the final to initial scan. Thus, the proportion of the total fracture network contained by the largest fracture increases from the initial to the final scan in four of the six experiments. All but one of the experiments (granite #1) experience localization toward the largest set of fractures, as measured with $\sum v_{90} / v_{t o t}$ , and the Gini coefficient. The outlier experiment granite #1 produces only a small decrease in $\sum v_{90} / v_{t o t}$ from the final to initial scan. Thus, the largest set of fractures, with volumes >90th percentile, comprises a larger proportion of the total fracture network immediately preceding failure than earlier in loading.

FIGURE 6

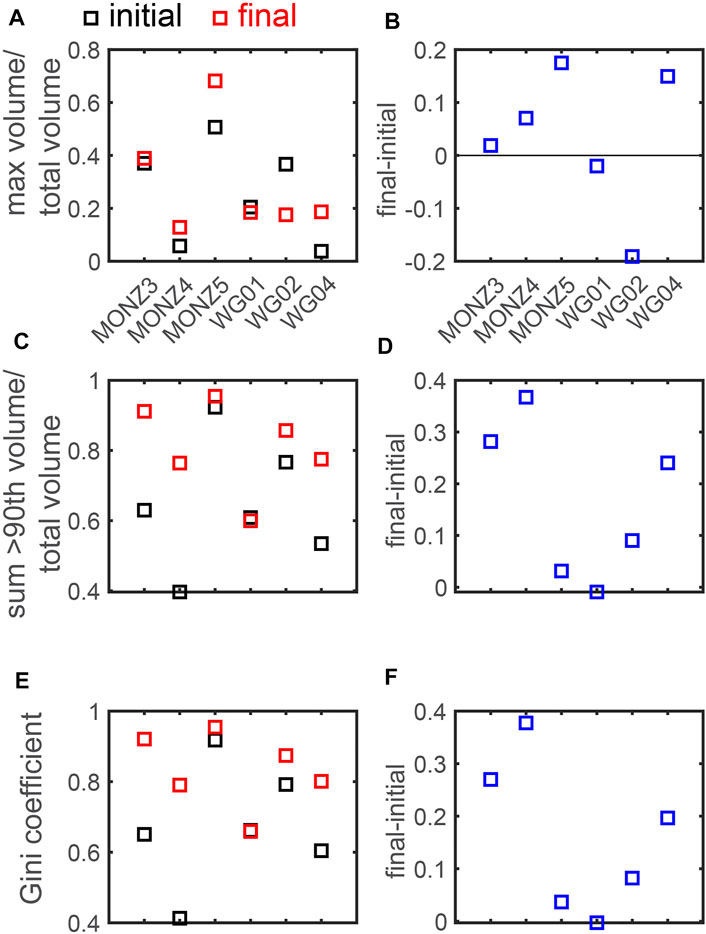
FIGURE 6. Difference in the v_max/v_tot (A, B), $\sum v_{90} / v_{t o t}$ (C, D), and the Gini coefficient (E, F) from the initial and final tomogram acquired in each experiment. Positive changes from the initial to final scan indicate increasing localization. The results of the Gini coefficient and $\sum v_{90} / v_{t o t}$ are nearly identical.

The monzonite #5 and granite #4 experiments produce the largest increases in v_max/v_tot, whereas monzonite #3 and #4 produce the largest increases in $\sum v_{90} / v_{t o t}$ and the Gini coefficient. These experiments have higher applied confining stress than the other experiments (granite #1, #2). Thus, higher confining stresses appear to promote larger increases in localization. However, we note that the differences between these confining stresses are not exceptionally large, and that variability between individual rock cores may also contribute to the varying localization behavior.

The granite #1 experiment experiences the smallest absolute changes in the localization metrics. The lower applied confining stress and associated shorter yielding phase of the granite #1 experiment (Figure 2) may produce the relatively constant localization. Although granite #1 and granite #2 both experience 5 MPa confining stress, granite #1 accumulates less axial strain between yielding and macroscopic failure than granite #2 (Figure 2). This shorter yielding phase suggests that the fracture networks grew relatively slowly during yielding in granite #1, producing smaller changes in the axial strain, and smaller changes in the fracture network localization compared to granite #2.

To gain further insight into the different expressions of localization in each experiment, we calculate the proportion of the accumulated differential stress (i.e., time) of the experiment in which the three metrics of localization show increasing localization (Figure 7). The differential stress that the system experiences is a proxy for time because we increase the differential stress in steps toward failure, and acquire an X-ray tomogram of the system after each increase in differential stress. Increases in the Gini coefficient, $\sum v_{90} / v_{t o t}$ , and v_max/v_tot indicate that the fracture network increases in localization. Thus, we calculate the proportion of the applied differential stress in which each of these three metrics increase from the previous scan (and thus differential stress state). For each metric, we apply a median filter with a bin size of five in order to limit the influence of small perturbations, calculate the slope of the median filtered data, count the number of instances of positive slope, and then sum the differential stress experienced by each scan for all of the scans with a positive slope.

FIGURE 7

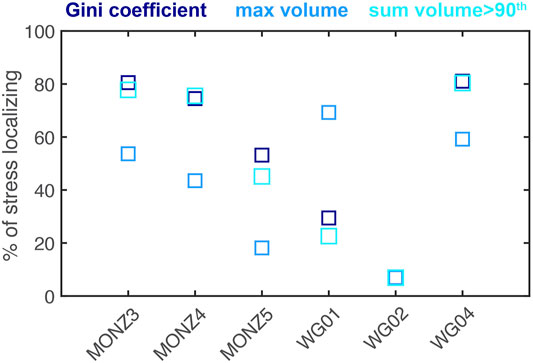
FIGURE 7. Percentage of the applied differential stress in which the Gini coefficient, v_max/v_tot, and $\sum v_{90} / v_{t o t}$ show localization, i.e., increase from one scan to the next.

Comparing the percentage of the differential stress in which each of these metrics are localizing indicates that the Gini coefficient or $\sum v_{90} / v_{t o t}$ produce higher percentages than v_max/v_tot in all but one of the experiments (granite #1) (Figure 7). Thus, the largest fractures in the network are localizing for longer periods of time than the absolute largest fracture in all but one experiment. Granite #1 is the only experiment in which the largest fracture dominates fracture network localization, rather than the set of the top 10th percentile of the fractures. This experiment increases in localization for about 80% of the time, whereas the Gini coefficient and $\sum v_{90} / v_{t o t}$ increase in localization for <40% of the time.

Using the metric that produces the largest percentages of the experimental time (typically the Gini coefficient or $\sum v_{90} / v_{t o t}$ , none of the experiments experience localization for more than 80% of the time (Figure 7). Two of the experiments (monzonite #5, granite #2) experience localization for shorter time intervals, for only about 50 and 5%. Both of these experiments host extended periods of generally decreasing localization early in the experiments, and then brief periods of localization immediately preceding failure (e.g., Figure 5). In contrast, the other experiments that host significant degrees of increasing localization, in terms of magnitude and time (monzonite #3, monzonite #4, granite #4), show more prolonged phases of increasing localization that begin before the macroscopic yield point (Figure 5).

Localization Toward the Final Failure Plane

The analyses in the previous section indicate that the largest fractures in the network, with volumes >90th percentile, tend to localize for up to 80% of the experimental time (Figure 7). To examine the evolving spatial distribution of these largest fractures toward failure, we compare them to the plane that represents the final fracture network immediately preceding failure (e.g., Figure 8). We fit this plane to the fractures with volumes >90th percentile in the final scan acquired preceding macroscopic failure using least squares regression in two-dimensions. We fit the plane to the largest set of fractures, rather than only the largest fracture, because the fracture networks generally localize toward the largest set of fractures (Figure 5), rather than the largest fracture (Figure 4). To assess how the fracture networks coalesce toward their final geometry, we examine the r² score of this final failure plane and the largest set of fractures throughout each experiment (Figure 9), and the mean distance between these fractures and the failure plane (Figure 10, Figure 11, Supplementary Figure S6). We calculate the mean distance by finding the closest distance between each large fracture and the failure plane, and then finding the mean of the distances in a given scan.

FIGURE 8

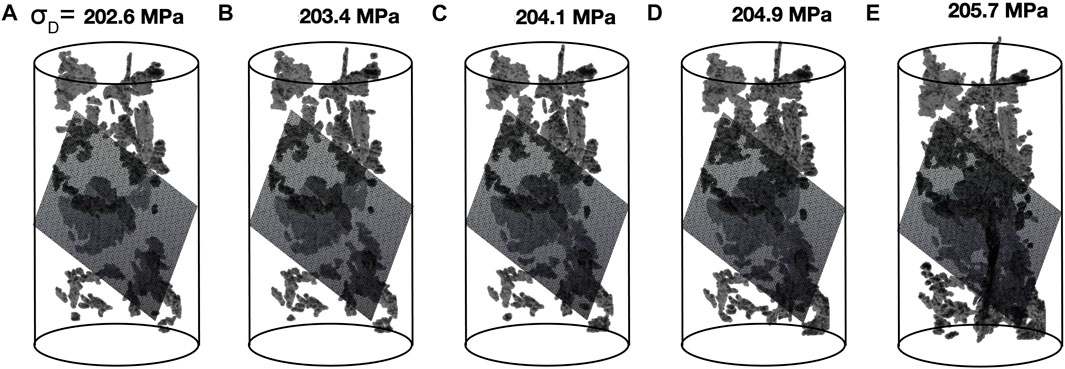
FIGURE 8. Largest fractures, with volumes >90th percentile, in the five scans acquired before failure in the monzonite #5 experiment, and best fit plane of the final fault geometry. The final failure plane is built from the scan acquired immediately preceding failure. Numbers at the top of the cores show the differential stress when the scan was acquired.

FIGURE 9

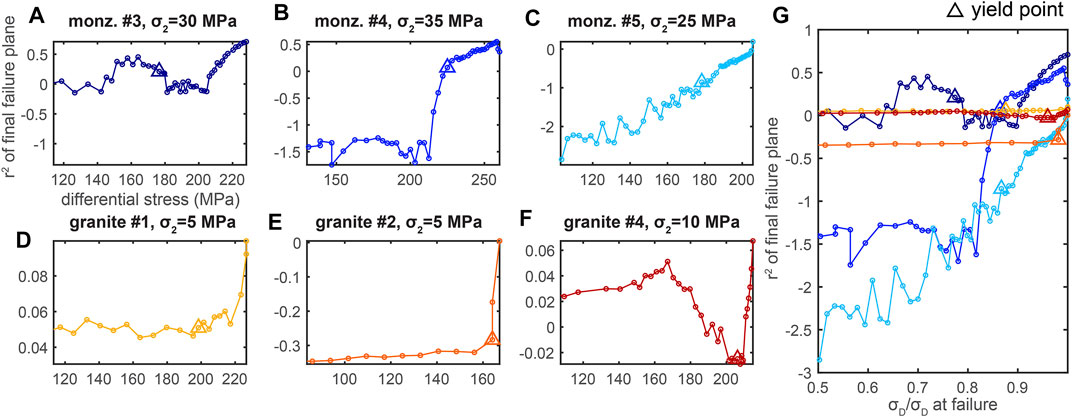
FIGURE 9. Evolution of the r² of the largest fractures and the final failure plane throughout each individual experiment (A–F), and for all the experiments (G). Color of the lines in (G) matches the colors of each experiment shown in (A–F). Triangles show the conditions of the yield point.

FIGURE 10

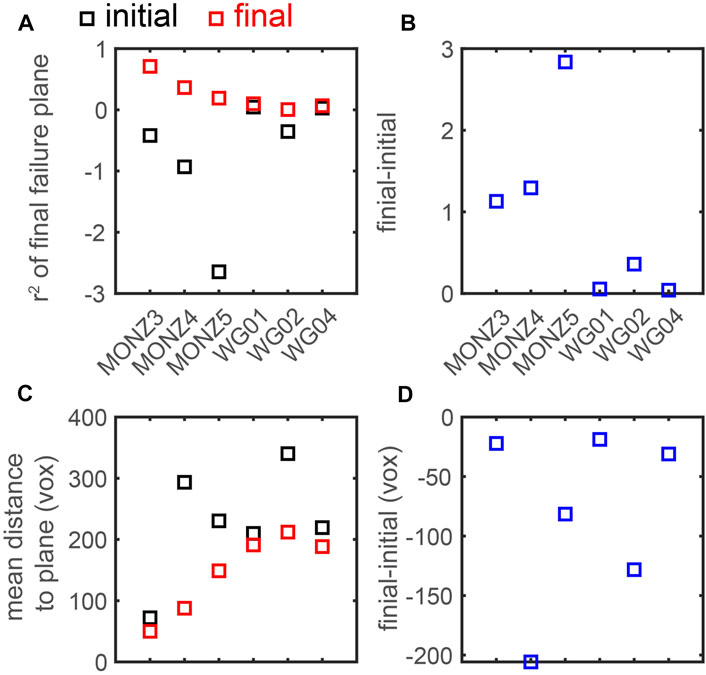
FIGURE 10. Difference in the r² score (A, B), and mean distance between the 10% largest fractures and the failure plane (C, D) from the initial and final tomogram acquired in each experiment. Positive and negative changes from the initial to final scan indicate increasing localization for the r² score and mean distance, respectively.

FIGURE 11

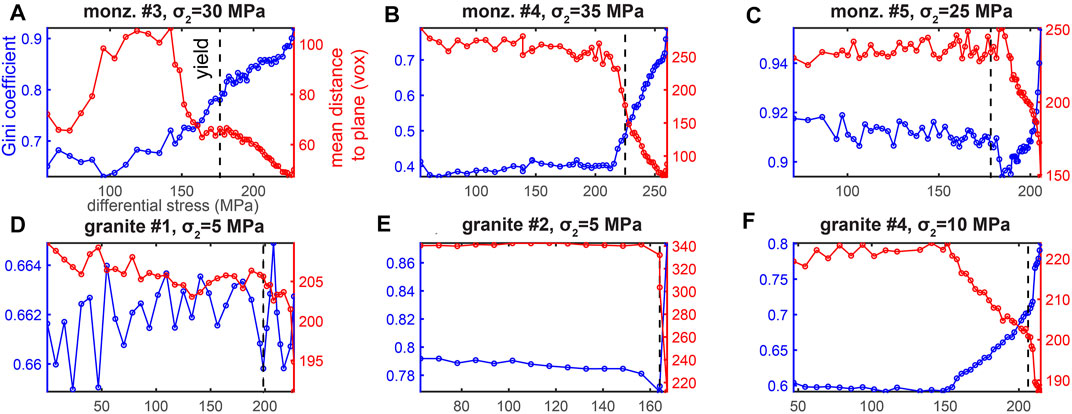
FIGURE 11. Evolution of the Gini coefficient and mean distance to the final failure plane in each experiment. Increasing Gini coefficient indicates increasing localization, while decreasing distance indicates increasing localization. Vertical black dashed lines indicate the macroscopic yield point.

The fit between the final failure plane and the largest fractures (r² score) generally increases toward failure (Figure 9). This trend is expected because we calculate the final failure plane using the largest fractures identified in the final scan. However, the fit does not increase monotonically, and instead shows some phases of delocalization away from the plane. The granite #4 experiment hosts the most significant of these drops, in terms of the difference relative to the maximum achieved r² score (Figure 9F). The monzonite #3 experiment also shows a phase of delocalization, and then stagnating r² scores following the macroscopic yield point. Monzonite #3 is also the experiment with the fracture network that most closely fits a plane in the final scan, producing the highest r² score (Figure 9G).

The granite experiments all show sharp increases in the r² score in the final few scans preceding failure. These increases coincide in time with the macroscopic yield point. In contrast, the monzonite experiments show more continuous increases over longer intervals of differential stress. Two of the monzonite experiments reveal changes in the r² score near the yield point: decreasing in monzonite #3 and slowing in monzonite #4. The general trends observed in the r² score match the trends in the mean distance between each fracture and the plane (Supplementary Figure S6, Figure 11).

To further examine the evolving spatial distribution of the largest fractures relative to the final failure plane, we compare the r² score and mean distance between the fractures and the plane in the initial and final scans acquired in each experiment (Figure 10). The monzonite experiments experience larger r² scores in the final scan, and larger increases in the r² score than the granite experiments. Thus, the top 10th percentile largest fractures in the final scan more closely match the geometry of a plane in the monzonite experiments than those in the granite experiments. In addition, at the onset of loading, the largest fractures in the monzonite experiments deviate more significantly from a plane than those in the granite experiments. The higher confining stress applied to the monzonite experiments may contribute to the greater localization of the largest fractures toward a plane in this suite of experiments.

Consistent with the trend in the r² scores, the monzonite experiments also host lower mean distances between the largest fractures and the failure plane in the final scan compared to the granite experiments (Figure 10C). The final mean distance is relatively consistent, near 200 voxels, for the granite experiments. Thus, the largest fractures are more tightly clustered around the final failure plane in the monzonite experiments than the granite experiments. The monzonite experiments also tend to host the largest changes in the mean distance. However, granite #2 also produces a significant change, while monzonite #3 produces a smaller change. These changes occur at least in part because the mean distance in the initial scan is larger (monzonite #3) and smaller (granite #2) than the other experiments.

The mean distance to the final failure plane and the Gini coefficient may correlate with each other. If the largest fractures coalesce from a diffuse to localized distribution, the mean distance should decrease while the Gini coefficient increases. This inverse relationship generally applies to these experiments (Figure 11). Following yielding, the Gini coefficient increases while the mean distance decreases toward failure, in all but the granite #1 experiment (Figure 11D). Thus, the fracture networks coalesce from many small distributed fractures to larger well-connected fractures that increasingly localize toward the largest set of fractures, and their approximate failure plane.

Discussion

Fracture Network Domination

Fracture networks develop through the linkage and coalescence of fractures. In an idealized system without significant mechanical heterogeneities or interaction between neighboring fractures, the localization process should be monotonic (e.g., Lyakhovsky et al., 2011). The relationship between the fracture length and stress intensity factor (e.g., Isida, 1971) suggests that the largest fracture in a network should grow at the expense of the others (e.g., Figure 12A). If fracture networks under triaxial compression follow this evolution, then the proportion of the maximum fracture volume of the total fracture volume, v_max/v_tot, should increase continuously toward macroscopic failure. However, the experiments show that v_max/v_tot does not increase monotonically, but instead experiences phases of delocalization of the fracture network away from the largest fracture (Figure 4). In some experiments, v_max/v_tot is smaller at the end of the experiment, immediately preceding failure, than at the beginning of the experiment (Figure 6). Only one experiment (granite #4) experiences a systematic increase in v_max/v_tot with only small perturbations. Thus, the fracture network in this experiment is dominated by one large fracture that grows and perhaps coalesces relatively faster than the other largest fractures. In general, however, the fracture networks are not dominated by the one largest fracture. The proportion of the experimental time (differential stress) in which the fracture networks experience localization toward the one largest fracture generally ranges from 40–70%, with two experiments hosting <20% (Figure 8).

FIGURE 12

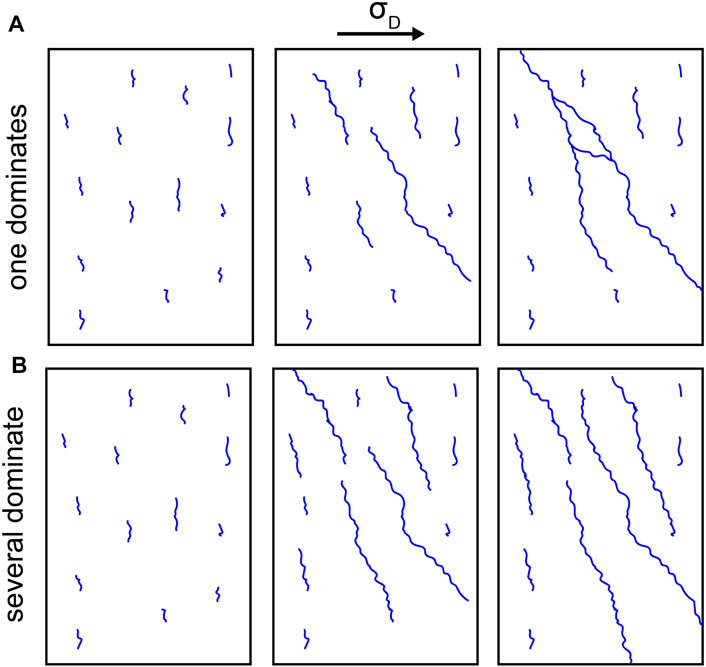
FIGURE 12. Fracture network development in a rock in which the one largest fracture dominates development (A) and in which several of the largest fractures dominate (B). The localization observed in experiments monzonite #3 and granite #4 most closely match (A), while the other experiments most closely match (B) (e.g., Figure 4).

In contrast, the experiments experience localization toward the largest set of fractures (with volumes >90th percentile) for a longer period of time than toward the one largest fracture, up to 80% of the applied differential stress (Figure 8). Tracking the proportion of the sum of the volumes >90th percentile to the total fracture volume, $\sum v_{90} / v_{t o t}$ , shows that all of the experiments host larger $\sum v_{90} / v_{t o t}$ in the scan acquired immediately preceding failure than in the initial scan. Moreover, $\sum v_{90} / v_{t o t}$ generally increases throughout each experiment, with only small episodes of delocalization (Figure 5). Thus, a more general description of fracture network development includes the growth and coalescence of several tens or hundreds of large fractures, rather than only one (e.g., Figure 12).

Using the localization metric that produces longest periods of increasing localization, the experiments tend to host localization for only up to 80% of the time (Figure 8). Thus, the fracture network does not continually localize toward the largest set of fractures, but also experiences phases with only minor changes in localization and short periods of delocalization. This evolution matches observations of low magnitude seismicity in southern and Baja California preceding several M > 7 earthquakes (Ben-Zion and Zaliapin, 2020). These results indicate that episodes of delocalization do not necessarily imply a reduced seismic hazard.

The evolving fracture geometry and how it interacts with fractures and other heterogeneities likely triggers these episodes of delocalization. For example, a fracture may begin to grow and coalesce in one portion of the rock core, but then become impeded when it propagates into the stress shadow of another fracture or a mechanical heterogeneity. When this first fracture arrests its growth, other large fractures may propagate and coalesce faster. Whether one fault propagates or not, and thus how fault networks develop, depend on the local tensile and shear stresses that develop at the fault tips (e.g., Paterson and Wong, 2005). These local stress concentrations influence the global mechanical efficiency of the system, suggesting that the efficiency of a system can predict whether a fault will propagate, and fault network development in general (e.g., Cooke and Madden, 2014). Numerical models suggest that fracture propagation will only occur when the energetic cost of propagation is lower than the gain in efficiency produced by that propagation (Del Castello and Cooke, 2007). Following this energy budget formulation, fracture propagation and subsequent slip can reduce the total internal work expended in diffuse host rock deformation while increasing the frictional work done against slip (e.g., Madden et al., 2017; McBeck et al., 2018; McBeck et al., 2019). Thus, faults may propagate and slip only when the efficiency gained by reducing off-fault deformation (the decrease in internal work) is greater than the energy consumed in fracture growth and slip (the increase in frictional work and work of fault propagation).

The precise geometry of a fracture network, and whether it is dominated by one large fracture or several large fractures, has significant implications for fluid flow in the network, and the relationship between porosity and permeability. If the porosity of a rock volume arises from one dominant fracture, then the resulting permeability may be at the higher end of estimates. Instead, if the porosity arises from several large unconnected fractures, then the permeability may be lower than expected. The evolving and varying dominance of the largest fracture in these experiments underscore the importance of fluid flow simulations and experimental measurements when constraining permeability (e.g., Dardis and McCloskey, 1998; Bernabé et al., 2003; Costa, 2006; Watanabe et al., 2009).

Fracture Network Planarity

Tracking the similarity of the largest set of fractures to a plane with the r² score indicates that this set of fractures does not systematically localize toward the final failure plane throughout the experiment. Instead, each experiment hosts short phases of delocalization in which the r² score temporarily decreases or remains at similar values (Figure 9). If fracture networks develop from one dominant fracture that continually grows at the expense of others (Figure 12), then the r² score may tend to increase monotonically. However, because one fracture does not tend to dominate the full fracture network throughout all of the experiments, the evolving geometry of the largest set of fractures does not systematically increase toward planarity.

The planarity immediately preceding failure of the largest set of fractures, with volumes >90th percentile, differs in the experiments on granite and monzonite (Figure 10). The r² score is generally higher for the monzonite experiments than for the granite experiments. Similarly, the mean distance of the largest fractures to the failure plane is generally smaller for the monzonite experiments than for the granite experiments. Thus, the fracture network that develops immediately preceding failure in the monzonite experiments more closely matches a plane than the network that develops in the granite experiments. This difference may arise from the higher confining stress applied to the monzonite experiments (25–35 MPa) compared to the granite experiments (5–10 MPa). The higher confining stress could promote greater localization of the fracture network to a plane in the monzonite experiments. However, due to the potential influence of variability between rock cores, additional experiments are required to confirm this idea. Previous laboratory experiments demonstrate that higher confining stress can produce localized shear failure planes, while rocks under lower confinement fail via more distributed axial splitting (e.g., Amann et al., 2012). These laboratory results are also consistent with observations that indicate that earthquake-induced rock damage in southern California is more localized and continuous at greater depth than near the surface (Ben-Zion and Zaliapin, 2019).

The larger mean grain size of the monzonite compared to the granite could also contribute to this difference in localization. Grain boundaries in crystalline rocks can influence where fractures nucleate because the constitutive minerals have varying stiffness (e.g., Tapponnier and Brace, 1976; Moore and Lockner, 1995). The material contrast produces differential compaction that leads to stress concentrations. The smaller grain size in the granite could lead to more sites of fracture nucleation and termination at the edges of minerals of different stiffnesses than the monzonite. The resulting greater number of sites of nucleation and termination could then produce more delocalized fracture networks in the granite than the monzonite.

In most experiments, the Gini coefficient and the mean distance to the failure plane are relatively constant, and then accelerate and decelerate close to macroscopic failure, respectively (Figure 11). The timing of this change in rate occurs near or slightly before the macroscopic yield point (within 10 MPa of differential stress) in some of the experiments (e.g., granite #2, monzonite #4 and #5), while in others this change occurs at least 20 MPa of differential stress before the yield point (e.g., granite #4). Thus, the reorganization of the fracture network that includes accelerating localization toward the largest set of fractures often precedes the macroscopic yield point. The acceleration of fracture network localization produces increasingly larger changes in the axial contraction for equal increments of differential stress. Fracture network localization may coincide in time with a transition from slower to faster fracture growth (e.g., Thompson et al., 2006). Because we load the rock core with differential stress steps, and stop increasing the differential stress to acquire a tomogram, the fracture growth that we capture in the tomograms is stable, and does not occur with an accelerating, unstable rate. Thus, in our experiments, the acceleration of fracture network localization may coincide in time with the transition from slower to faster fracture growth. Under more continuous differential stress or axial strain loading conditions, the localization of the fracture network may coincide with the transition from stable to unstable fracture growth. Previous work has also inferred a link between unstable fracture growth and fracture coalescence (e.g., Nicksiar and Martin, 2012). Other work has linked the transition from quasi-static to unstable fracture growth to a critical crack length (e.g., Ohnaka and Kuwahara, 1990).

Conclusion

We quantify the spatial distribution of fracture networks throughout six in situ X-ray tomography triaxial compression experiments as they are loaded toward system-size failure under confining stress conditions of the upper crust. We assess the idea that one dominant fracture monotonically grows at the expense of others by tracking the ratio v_max/v_tot of the largest fracture volume relative to the total fracture volume throughout each experiment. The ratio v_max/v_tot does not systematically increase in the experiments. Following this result, we test if a set of the largest fractures continually dominates deformation by tracking the sum of the volume of the fractures with volumes >90th percentile relative to the total fracture volume, $\sum v_{90} / v_{t o t}$ . This metric indicates that the fracture networks tend to increase in localization toward the largest set of fractures for up to 80% of the experimental time. The evolution of this metric matches the evolution of the Gini coefficient. Experiments with higher applied confining stress tend to experience greater increases in localization. However, we applied higher confining stress to the monzonite cores, and lower confining stress to the granite cores. Thus, the observed variation in localization behavior may be due to both confining stress and rock type. Further experiments are required to differentiate between the two effects.

Comparing the geometry of the set of the largest fractures to a plane with the r² score indicates that it is more similar to a plane in the monzonite experiments than the granite experiments immediately preceding failure. In addition, the mean distance between the plane and the set of fractures is smaller in the monzonite experiments than the granite experiments immediately preceding failure. The smaller mean grain size in the granite may produce more sites of fracture nucleation and termination, leading to more delocalized fracture networks that deviate further from a plane. The higher applied confining stress of the monzonite experiments (25–35 MPa) relative to the granite experiments (5–10 MPa) may also contribute to the more localized fracture networks in the monzonite experiments. Tracking these metrics of localization reveals a close association between the macroscopic yielding of the rock and the acceleration of the localization of the fracture network. Near yielding, $\sum v_{90} / v_{t o t}$ and the Gini coefficient increase while the mean distance between the largest set of fractures and the final failure plane decreases. Macroscopic yielding occurs when the rate of fracture network localization increases. The macroscopic yielding may occur when the fractures begin to grow and coalesce faster, producing increasingly localized fracture networks.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Renard, F. (2017). Critical evolution of damage towards system size failure in a crystalline rock [Data set]. Norstore. doi: 10.11582/2017.00025. Renard, F. (2018). Volumetric and shear processes in crystalline rock during the approach to faulting [Data set]. Norstore. doi: 10.11582/2018.00023. Renard, F. (2021). X-ray tomography data of Westerley granite [Data set]. Norstore. doi: 10.11582/2021.00002.

Author Contributions

JM designed the analysis and wrote the paper. YB-Z refined the analysis and helped write the paper. FR performed the experiments and helped write the paper.

Funding

The Research Council of Norway (Grant 300435 to JAM) and U.S. Department of Energy (Award DE-SC0016520 to YBZ) funded this work. Sigma2-NIRD provided data storage (Grant NS9073K). Beamtime was allocated at the European Synchrotron Radiation Facility (Long Term Proposal ES-295).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Elodie Boller, Paul Tafforeau, and Alexander Rack for advice about the design of the tomography setup, Benoît Cordonnier for the help with experiments, and Sanchez Technology for building the deformation apparatus. The Research Council of Norway (Grant 300435 to JAM) and U.S. Department of Energy (award DE-SC0016520 to YBZ) funded this work. Sigma2-NIRD provided data storage (Grant NS9073K). Beamtime was allocated at the European Synchrotron Radiation Facility (Long Term Proposal ES-295). The experimental data of time series of X-ray tomograms are available on Norstore: including the three monzonite samples (Renard, 2017, 2018), and the three Westerly granite samples (Renard, 2021). We thank Guest Editor Ernie Rutter, and Reviewers Alexis Cartwright-Taylor and Joern Lauterjung for suggestions that improved this manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.778811/full#supplementary-material

References

Aben, F. M., Brantut, N., Mitchell, T. M., and David, E. C. (2019). Rupture Energetics in Crustal Rock from Laboratory‐Scale Seismic Tomography. Geophys. Res. Lett. 46 (13), 7337–7344. doi:10.1029/2019gl083040