- 1Key Laboratory of Coalbed Methane Resources and Reservoir Formation Process, Ministry of Education, China University of Mining and Technology, Xuzhou, China
- 2School of Resources and Geosciences, China University of Mining and Technology, Xuzhou, China
Over the last three decades, molecular dynamics (MD) has been extensively utilized in the field of coalbed methane geology. These uses include but are not limited to 1) adsorption of gaseous molecules onto coal, 2) diffusion of gaseous molecules into coal, 3) gas adsorption-induced coal matrix swelling and shrinkage, and 4) coal pyrolysis and combustion. With the development of computation power, we are entering a period where MD can be widely used for the above higher level applications. Here, the application of MD for coalbed methane study was reviewed. Combining GCMC (grand canonical Monte Carlo) and MD simulation can provide microscopic understanding of the adsorption of gaseous molecules onto coal. The experimental observations face significant challenges when encountering the nanoscale diffusion process due to coal structure heterogeneity. Today, all types of diffusion coefficients, such as self-, corrected-, and transport-diffusion coefficients can be calculated based on MD and the Peng-Robinson equation. To date, the MD simulation for both pure and multi-components has reached a situation of unprecedented success. Meanwhile, the swelling deformation of coal has been attracting an increasing amount of attention both via experimental and mimetic angles, which can be successfully clarified using MD and a poromechanical model incorporating the geothermal gradient law. With the development of computational power and physical examination level, simulation sophistication and improvements in MD, GCMC, and other numerical models will provide more opportunities to go beyond the current informed approach, gaining researcher confidence in the engagement in the estimation of coal-swelling deformation behaviors. These reactive MD works have clarified the feasibility and capability of the reactive force field ReaxFF to describe initial reactive events for coal pyrolysis and combustion. In future, advancing MD simulation (primarily characterized by the ReaxFF force field) will allow the exploration of the more complex reaction process. The reaction mechanism of pyrolysis and spontaneous combustion should also be a positive trend, as well as the potential of MD for both visualization and microscopic mechanisms for more clean utilization processes of coal. Thus, it is expected that the availability of MD will continue to increase and be added to the extensive list of advanced analytical approaches to explore the multi-scaled behaviors in coalbed methane geology.
Introduction
Here, the applicability of molecular dynamics (MD) to the study of coalbed methane geology is examined, specifically the role in visualizing the multimember behaviors accompanying adsorption/diffusion of gaseous molecules, gas-induced coal swelling, pyrolysis, and combustion. A review of MD applications to the study of geoscience is available (Cygan and Kubicki, 2018). Its applications to estimate the microscopic behaviors in coalbed methane geology have yet to be reviewed however. The earliest work for the application of MD aimed to reveal the dynamics damage of the materials exposed to radiation (Gibson et al., 1960), highlighting the non-equilibrium boundary conditions for particles with continuous forces. This preliminary work led to qualitative estimation of thermodynamic properties and to quantitative study of microscopic processes. In 1964, Rahman simulated liquid hydrogen with an MD method in periodic boundary conditions (PBCs) and surprisingly discovered that even a few particles represented the thermodynamic properties of the whole system (Rahman, 1964). Since then, MD simulation of condensed matter has become available, attracting worldwide physicochemical scholars to invest in this research work, taking advantage of the zero approximation nature, tracking particle trajectory, and accurate simulation results. The application of MD to visualize coal physico-chemical processes can date from 1992 as “The minimum-energy conformations obtained after MD calculations have provided insights into the types of bonding that provide the rigid structure observed for coals.” using Given, Wiser, Solomon, and Shinn’s molecular representations of coal in Carlson’s work (Carlson, 1992). Since then, the coal literature, over the last 29 years, has generated a surprisingly large number of MD applications in coal studies. The MD work using those predominantly classical molecular representations of coal slices remains state-of-the-art until advances in the analytical techniques as well as modeling software can be obtained (Mathews and Chaffee, 2012).
The jumps in computation power have also helped us to overcome some of the simulation challenges in model construction and calculation scale, and also aided scholar confidence in the microscopic representations, bridging the macroscopic characteristics and microscopic behaviors of coal. Figure 1A depicts the gradual emergence of journal publications utilizing MD for coal or coal-related research over the last ∼20 years, covering disciplines such as engineering, chemistry, energy fuels, environmental science ecology, and physics (Figure 1B). Although, this is likely an underestimation of the work since it was assessed from only the Web of Science Core Collection. It is expected that this simulation method will become more common for exploring coal behaviors. This paper provides a dedicated review of the history advances, and state-of-the-art availability for MD utility, along with applications in adsorption/diffusion of gaseous molecules, gas-induced coal swelling, pyrolysis, and combustion.
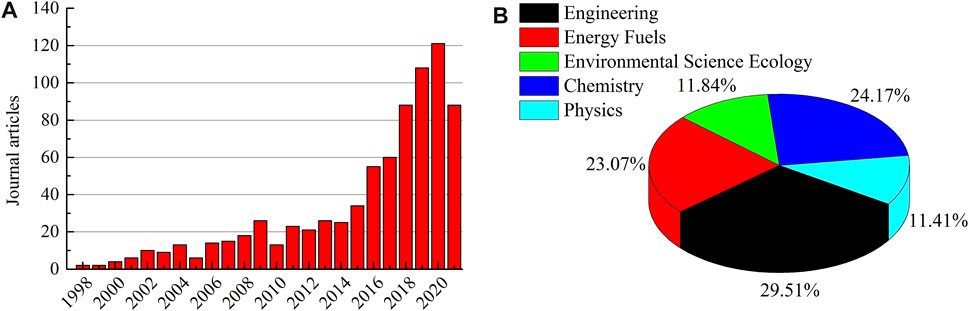
FIGURE 1. (A) Journal articles from the Web of Science Core Collection for the application of MD to coal research and (B) the corresponding field distribution.
Molecular Dynamics
Advantages of MD
The inadequate mathematical apparatus which has already been able to solve the many-body problem still finds it challenging to depict the physical and chemical systems. The behaviors for the systems composed of a fairly large number of interacting particles cannot be described in a theoretically exact way despite the fact that the characteristics of an isolated particle or even the initial processes of two particles can be clarified via the Newtonian equation of motion (Alder and Wainwright, 1959). As a deterministic method of MD, the system composed of N particles will be abstracted into N interacting particles prior to MD simulation. The MD theory was to solve the motion trajectory of each particle using the typical second law of Newton, where the force exerted on these particles is determined by the potential energy of the system (Hu et al., 2010). The critical issue lies in the determination of the potential energy functions (molecular force field) of different systems (Zhao et al., 2016a; Hu et al., 2017), which describes the motion of particles via the Schrödinger equation of the steady (time-independent) state neglecting the spin orbit and other related effects (Naber, 2004). Thus, the determination is to choose the analytic function form and the corresponding parameters (Halgren, 1996; Canongia and Pádua, 2004; Canongia Lopes and Pádua, 2006).
The primary principle of designing a basic force field is to minimize the computational energy cost per unit time step. This can also maximize the simulation geometric scale, which is important for the all-atom force field and even for the coarse-grained model as well. For the microsecond and even millisecond level simulation, the geometric scale should be carefully considered, and Cai and Christophe (2013) have established the typical relationship between time scale and spatial scale in the classical molecular dynamics framework (Figure 2). The large-scale parallelization or dedicated architecture technology can be embedded into the extensible molecular dynamics program with the increasing computation power and the development of large-scale parallel computing architecture (Gonalves et al., 2017). Today, computer simulation has included the whole grain size ranging from dislocation to grain boundary-based deformation mechanism, setting a promising Frontier to explore the material system using MD. For coal macromolecular systems, the common molecular force fields such as OPLS (optimized potentials for liquid simulations) (Jorgensen et al., 1996), polymer-consistent force field (PCFF) (Sun et al., 1994), Dreiding (Carlson, 1992; Takanohashi et al., 1999; Fan et al., 2019), condensed phase optimized molecular potential for atomistic simulation studies (COMPASS) (Hu et al., 2010), and universal force field (Zhao et al., 2016a) can all be used to calculate the macroscopic physical properties, for example, the cohesive energy density and porosity, where the Dreiding and COMPASS force fields have displayed good applicability for coal representations (Figures 3A,B) (Xiang et al., 2014; Song et al., 2017a, Song et al., 2017b).
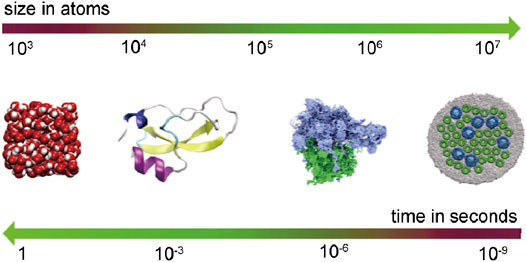
FIGURE 2. Typical relationship between time scale and spatial scale in the classical molecular dynamics framework (Cai and Christophe, 2013) (from left to right: water molecules; an enzyme; the ribosome; a 25-million-atom patch of the photosynthetic membrane of purple bacteria).
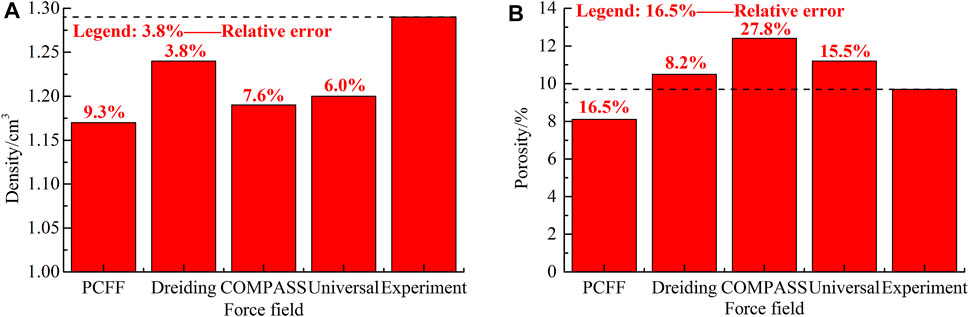
FIGURE 3. Comparisons in the density (A) and porosity (B) of coal calculated from different force fields.
Realization of MD
The classical MD theory can be classified into two schemes: 1) equilibrium MD and 2) non-equilibrium MD, and there also exists quantized MD for the case of Gaussian approximations, including frozen and thawed Gaussians (Brüschweiler and Ernst, 1992; Prezhdo, 2002; Manzhos, 2013). Equilibrium MD is further comprised of four types: micro canonical ensemble (NVE), canonical ensemble (NVT), isothermal isobaric ensemble (NPT), and grand canonical ensemble (VTμ) (Rokach, 2010; Zhao et al, 2016a). The common ensemble classification and their properties under macro constraints are depicted in Table 1. There are frequently four types of temperature control mode for the NVT and NPT ensembles, consisting of velocity scale, Berendsen hot bath, Gaussian hot bath, and Nose-Hoover hot bath (Kraska, 2006). In isobaric simulation (NPT), volume changes can be achieved by adjusting the size of the simulated cell in three or one direction(s). In general, the Berendsen-, Anderson-, and Parrinello-Rahman method were utilized frequently for MD simulation (Ulander and Haymet, 2003).
The iso-energetic process was the initial motivation to conduct MD where the starting point is to describe the interaction of the N particles by Hamiltonian equation (Magri., 1978). The success of the calculation depends on the setting of the initial position and initial velocity, where the system studied is usually placed on an ideal lattice. The initial velocity is set according to the Boltzmann distribution (sometimes the initial velocity is set to 0 directly) (Bonomi et al., 2009; Bodendorfer et al., 2019). However, the initial conditions related to the given energy cannot be accurately known frequently. Thus, the system should be adjusted according to the given initial position and initial speed until reaching the required energy (Bonomi et al., 2009). In many practical situations, what we focus on is the isothermal system rather than an iso-energetic system, equivalent to an isolated system immersed in a large heat source of constant temperature (canonical ensemble). The way to keep the temperature constant is to rescale the speed of each step by multiplying a factor (β) before the speed to ensure the constant kinetic energy (Luo et al., 1996). Other scholars such as Haile and Gupta (1983) improved the calibration method via introducing the constant kinetic energy, proposing a method of rescaling momentum.
The iso-pressure molecular dynamics method was first proposed by Anderson (1980) and then extended to the calculation of the cell shape changes (Parrinello and Rahman, 1980; Nosé, 1984). In the isobaric process, the NPT ensemble can be achieved if the system is not adiabatic. The molecular dynamics algorithm of this ensemble was essentially identical to the NPH ensemble, achieving the isothermal isobaric process by adjusting the velocity of each step. Another approach to this process, also proposed by Anderson, is the MD and MC (Monte Carlo) bridging approach to simulate isothermal pressure systems (Luo et al., 1996). This method alters the particle velocity by random collision, and the distribution of particle velocity after collision is used to generate a canonical ensemble (Luo et al., 1996). In addition, Car and Parrinello (1985) developed CP (Car-Parrinello) dynamics by combining density functional theory and the molecular dynamics method. In addition to the above advantages of molecular dynamics, this method can also calculate the ground state electronic structure of solid materials. Due to the large amount of calculation, its application is still limited by the development of computation power (Luo et al., 1996).
Frequently, the MD method can be implemented via three common pathways: quenched dynamics, simulated annealing, and impulse dynamics (Adcock and McCammon, 2006; Lobato et al., 2012; Bando et al., 2020). Quenched dynamics refers to the calculation of atomic displacement versus time at a constant temperature. A sample configuration was extracted in a given internal time (Barbiero et al., 2018). On the contrary, simulated annealing is temperature cycling in a given time to achieve the purpose of sampling in the whole configuration space, making use of the possibility to cross a large energy barrier at a certain high temperature (Righettoni and Pratsinis, 2014; Krumeich et al., 2016). Song et al. and Fu and Song have also devoted some effort to annealing kinetics in the material studio platform (Song et al., 2017a, Song et al., 2017b; Fu and Song, 2018). Annealing dynamics is an advanced process to approach geometrically optimal configuration superior to the pure geometry and energy optimization of this platform (Song et al., 2017a; Song et al., 2017b). The impulse dynamics method firstly assigns an initial velocity vector to the selected atom prior to dynamics simulation, which was frequently used to push the interaction molecules across the energy barrier before the molecular structure relaxed.
Adsorption of Gaseous Molecules Onto Coal
The molecular mechanism of microscopic interactions between CH4/CO2/H2O and coal is the base to understanding the occurrence state of these gaseous molecules and the induced swelling (Xiang et al., 2014). No experimental technology has been found to operate perfectly, especially for the microscopic interactions of the molecular scale. The traditional experimentations have patent limitations to detect the molecular mechanism of microscopic interactions between the gaseous molecules and coal. MD simulation has been a powerful tool to reveal the relationship between the structure and properties of coal and the interaction mechanism of physical chemistry system compared with the various instrumental analysis technologies. The flow chart for the adsorption process was designed based on the minimum energy principle (Figure 4). Combining GCMC and MD simulation could provide the quantitative understanding of gaseous molecules adsorbing onto coal. The different contributions from van der Waals force, electrostatic force, and hydrogen bond force to the reduction in non-bonding energy suggest that the interaction of coal-CH4 typically exhibits as physical adsorption (Song et al., 2017a). However, the interaction between coal and CO2 is dominated by physical adsorption and incorporates weak chemical adsorption; for coal-H2O, the case encounters the simultaneous existence of physical and chemical adsorption (Xiang et al., 2014).
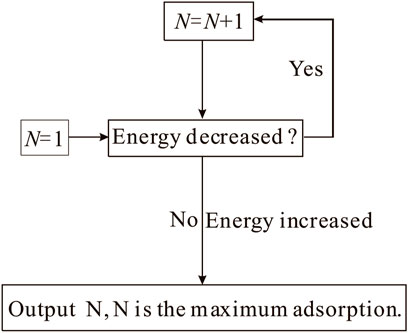
FIGURE 4. Adsorption process flow chart for MD and GCMC (Song et al., 2017b).
The initial efforts of simulating the adsorption of gaseous molecules onto coal were based on perfect graphite or defective graphite (Thierfelder et al., 2011). Also, the methane adsorption of MD calculation has been reported to amplify the gas storage in open-ended single-walled carbon nanotubes, where the hybrid isotherm model of Langmuir and Sips was nicely in line with the calculated results (Shokri et al., 2010). The present implementation of MD over-binds about as much as bare DFT (density function theory) calculations under bind, but yields a meaningful adsorption height. Thierfelder et al. (2011) conducted methane adsorption on graphene from the first principles including dispersion interaction, and presented a microscopic picture of the reliability of approximate schemes in which van der Waals forces were limited. For quite a long time, the MD simulation of methane adsorption on graphite (0 0 0 1) was used as the platform to evaluate the gas behaviors onto coal in the molecular scale via state-of-the-art surface science analysis and computation approaches (Dash., 1975; Vidali et al., 1991; Bruch et al., 2007). Mosher et al. (2013) investigated methane adsorption in carbon-based 3D pore networks and found that the simulation estimates overpredict excess adsorption. This discrepancy is potentially induced from the limitation of the experimental model. Liu et al. (2013) simulated the CH4 adsorption on N- and B-containing carbon models of coal and proposed that the physical adsorption of CH4 on coal depends slightly upon the adsorption sites, orientation of CH4, and the electronegativity of the dopant in coal. Hu et al. (2010) calculated the adsorption properties of CH4 and CO2 onto coal in an attempt to shed light on the adsorption at the atomistic level, demonstrating the successful utilization of MD in the study of the adsorption field. The MD simulation indicates the stronger adsorption affinity of CO2 over CH4 almost in all the published literature to date. Compared with the experimental-based characterization, MD can be understood as a “virtual experiment” at the molecular level, serving as an interface between laboratory experimentation and physicochemical theories (Liu et al., 2013). From the last decade on, MD work has been extended to more complex cases, for example, the contributions from water and oxidation on the adsorption process.
The coal macromolecular representation used in Hu et al. (2010) was the Wiser model and the MD results proved that the coal could absorb more CO2 than CH4 at the given temperature, providing an alternative technique to clarify the interactions between coal and adsorbates even for practically unreachable conditions. The general outcomes of MD are frequently consistent for different coal macromolecular representations, proving MD to be a promising tool incorporating the coincidences between the experimental and simulation results. Since the last decade, the coal geology community has witnessed a blowout increase in the generation of coal macromolecular representations with the gradually popularizing analysis and modeling technologies. The combined Monte Carlo and molecular dynamics is the most favored method to reveal the single and competitive adsorption of gaseous adsorbates onto coal. Zhang et al. (2014) conducted MC and MD simulations at a temperature ranging from 308 to 370 K to investigate the methane adsorption on dry and moist coal, providing a quantitative insight into the impacts of moisture and temperature on methane adsorption. The experimentations of Goodman et al. (2007) suggested good agreement of adsorption amount for pressure up to 8 MPa, however, for higher pressures, the results of different laboratories diverged distinctly in ranks, maceral, ash content, porosity, surface functional groups, temperature, and moisture.
Aiming at this issue, Liu and Wilcox (2011), Liu and Wilcox (2012a), Liu and Wilcox (2012b) conducted detailed simulation to articulate the CO2 adsorption onto microporous carbons of heterogeneous surface functional groups, and the results suggested that the oxygen functional groups were favored for CO2 adsorption, where the opposite effects can be indicated for the hydrated graphite. Based on the CS1000 coal model, the competitive adsorption behavior of CO2 and CH4 in coal micropores was also clarified based on the poromechanical model and MD and proposed a safe and long-term carbon sequestration resulting from the preferential adsorption of CO2 to CH4 (Brochard et al., 2012). Figure 5a∼fdepict the coal macromolecular representations which were frequently used in the publications. The consistent results among different macromolecular representations suggest the rationality of the MD method to depict the adsorption behaviors of gaseous adsorbates onto coal. Recently, MD has been prevalently used to optimize macromolecular representations prior to the adsorption process. Compared with the GCMC method, the adsorption process calculated from the MD simulation could provide more force and energy state parameters both for the initial and final status of the coal-gas compounds. However, MD requires much more computing memory and time than the MC calculation to acquire the normal termination status (Zhao et al., 2016a).
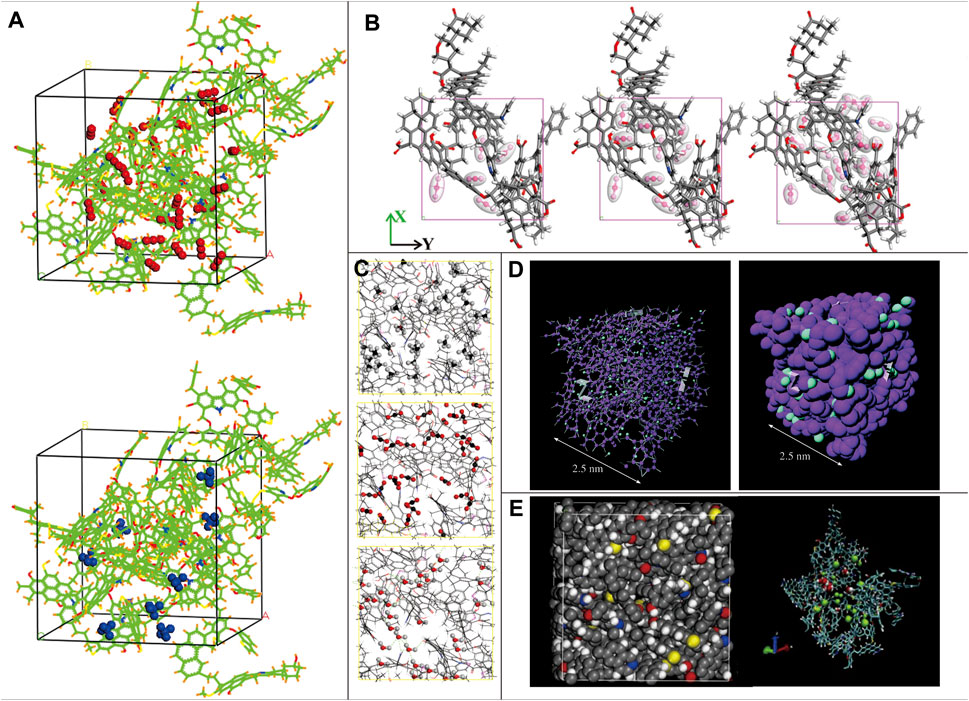
FIGURE 5. Typical coal macromolecular representations used to simulate the adsorption process (A): Wiser model absorbing the CO2 and CH4 (Zhao et al., 2016b); (B): the typical vitrinite model absorbing different amounts of CO2 (Song et al., 2018); (C): the Yanzhou coal model absorbing CH4, CO2, and H2O (Xiang et al., 2014); (D): CS1000 coal model absorbing CO2 (Brochard et al., 2012); (E): intermediate-rank bituminous coal building block absorbing H2O and CH4 (Zhang et al., 2014).
As increasingly dependable MD models are being developed for coal macromolecular representations, the adsorption processes of CH4/CO2/N2/H2O have been prevailing using the MD theory and method, providing a microscopic insight of high fidelity to present the structural heterogeneity of coal. In addition, the single maceral has been separated from the whole coal to represent the compositional complexity, as well as the macromolecular representations (Song et al., 2017a; Song et al., 2017b). For common gases such as CH4, CO2, H2O, and N2, the adsorption priority follows the order of CO2> H2O > CH4> N2, independent of the coal macromolecular representations used. For the outcomes of MD, Song et al. (2017a) exhibited the typical results and a comparison with the experimental results. As seen in Figures 6A–C, the maximum adsorption amounts of MD were close to the experimental result using the IS-100 isothermal adsorption desorption instrument (at 298 K), indicating the rationality of MD. However, their variation laws differ significantly, especially for the low pressure region. The adsorption amount of MD first increases sharply at low pressures and then remains stable with the increasing pressure. However, the experimental results gradually increase with the increasing pressure until 5 MPa. This was induced from the existence of ash in coal and may be the limitation of the coal macromolecular representations for the ash-related analysis. The D-A model fit better than the Langmuir model, which perhaps indicates the microporous filling properties for adsorption processes. For CO2, the experimental adsorption amount was slightly lower than the MD results and their difference tended to decrease with the increasing pressure. When approaching the saturation state, the relative error of MD was reduced to 1.2%, maintaining an acceptable error (Song et al., 2018).
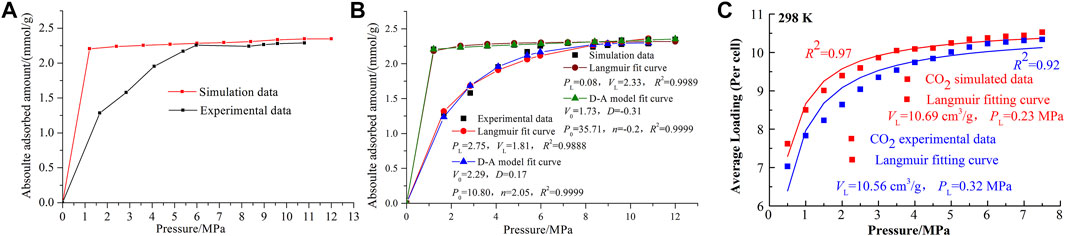
FIGURE 6. (A) Comparison between MD and experiment results for CH4, (B) their Langmuir and D-A model fitting results (Song et al., 2017a), and (C) comparison between MD and experiment results for CO2 (Song et al., 2018).
Diffusion of Gaseous Molecules Through Coal Matrix
Single Component Diffusion
As early as 1905, Einstein established the movement of small particles suspended in a stationary liquid based on the molecular-kinetic theory of heat, indicating the direction of calculating the diffusion of gaseous molecules into porous medium (Einstein, 1905). The hypothesis of the diffusion investigation of MD was the identification of the adsorption process, which assumes that the atom motions follow Newton’s first law and can be described via the empirical potential functions (Song et al., 2018). Thus, MD has long been an appropriate approach to explore the underlying interaction mechanism of gas-coal and gas-gas during the diffusion process. Generally, the diffusion mechanisms can be classified into four mechanisms with the increasing observation scale, i.e., self-diffusion, Fickian diffusion, Knudsen diffusion, and surface diffusion. Self-diffusion occurs in the pure crystals and is independent of concentration gradient (Hu et al., 2017). Frequently, self-diffusion, following the Einstein equation, can be directly calculated via the Dynamics module of Materials Studio and utilized as the starting point to initiate the more advanced diffusion processes (Xiang et al., 2014). Fickian diffusion was derived by molecule-molecule collisions, where the diffusion mass flow per unit time through the unit cross-section perpendicular to the diffusion direction is proportional to the concentration gradient at the cross-section under the conditions of steady diffusion (Charrière et al., 2010; Liu et al., 2015). Fickian diffusion is the apparent diffusion process and can be examined experimentally, characterized via Fickian/transport diffusion coefficients (Zhao et al., 2016b). Knudsen diffusion occurs in pores whose diameter is smaller than the mean-free path length of gas molecules and can be quantified by Knudsen diffusion coefficients (Yang and Liu, 2019). The flux equation of Knudsen diffusion can be induced from the theory of molecular motion. Surface diffusion refers to the movement of atoms, ions, molecules, and clusters along the surface direction on the solid surface and occurs when there exists a chemical potential gradient field on the solid surface (Karacan and Mitchell, 2003). As the surface area is about unit surface spacing, the surface diffusion mainly occurs at the distance of 2-3 layers of atomic surface to the solid surface (Song et al., 2018). This diffusion mechanism is not only dependent on external environment (temperature, pressure, humidity, atmosphere, etc.), but is also affected by crystal orientation, electronic structure of surface chemical composition, and surface potential (Liu and Lin, 2019).
Scholars from around the world have invested great efforts to investigate the diffusion behaviors of gaseous adsorbates in coal from both experimentation and molecular/numerical simulations over the last two decades. The apparent diffusion coefficient was physically observable via experiments (Saghafi et al., 2007; Jian et al., 2012), however, the experimental observations face significant challenges when encountering the nanoscale diffusion process due to the heterogeneity of coal structure. MD could offer one approach to simulate the nanoscale diffusion process even for binary and ternary mixtures. An excellent review on the diffusion coefficients calculated from MD for binary and ternary mixtures is currently available (Liu et al., 2013). These MD works not only focus on self-diffusion coefficients, but also on the corrected (or Maxwell-Stefan) and transport diffusion coefficients (Zhao et al., 2016b; Song et al., 2018). Hu et al. (2010) simulated the diffusion of the small-molecule gas in coal via the Einstein diffusion law and Wiser model, proposing an alternative method for directly studying the interactions between coal macromolecules and small molecule gases. This work firstly introduces the calculation of self-diffusion coefficients from the mean square displacement (MSD) curves. The linear region suggests the occurrence of the Einstein diffusion, however, an anomalous (non-Einstein) diffusion also exists before the Einstein diffusion resulting from the extra tortuosity of the coal macromolecular structure (Hu et al., 2010). It is notable that the slopes of the MSD-t curve in the anomalous and Einstein diffusion stage were 1.0 and 0.5, respectively, (Hu et al., 2010; Song et al., 2017b) (Figures 7A–D), indicating the consistent motion laws of the microscopic particles. The consistent slope of the MSD-t curve in the literature suggests the reliability of the MD work for calculating the diffusion coefficients. Then, Xiang et al. (2014) calculated the self-diffusion coefficients of CO2, CH4, and H2O in Yanzhou coal based on Einstein’s diffusion law and found that the self-diffusion coefficients of these three gases follow the order of CO2>H2O > CH4.
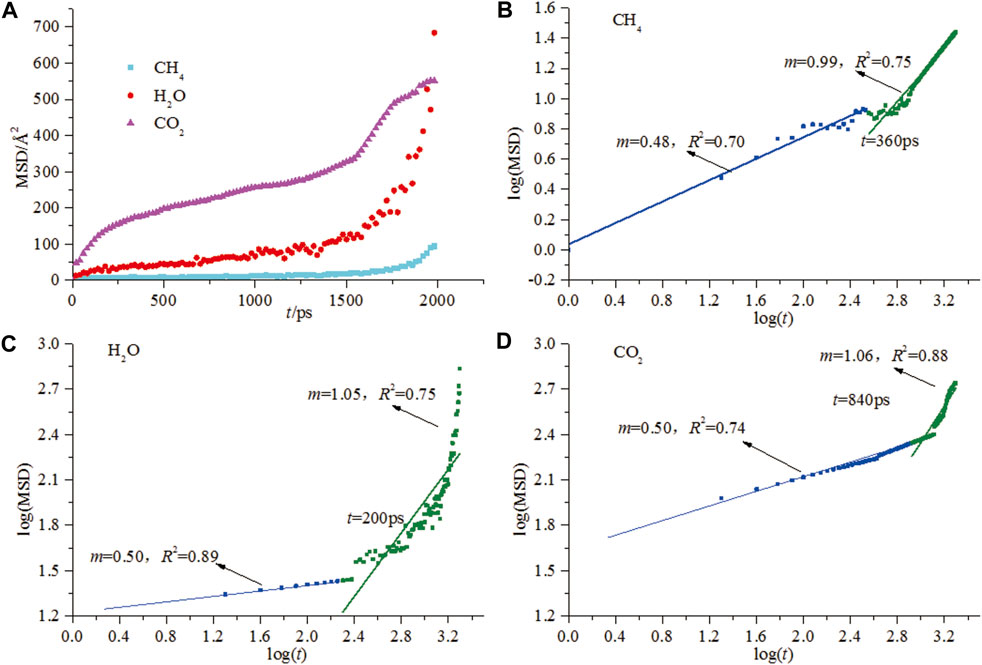
FIGURE 7. MSD vs. time plot of CH4, CO2, and H2O diffusion (A) and logarithmic plot of CH4 (B), CO2 (C), and H2O, (D) MSD vs. t (from Song et al., 2017b).
Other than these self-diffusion coefficient works, Zhao et al., 2016b conducted an MD work for the self- and transport diffusion of CO2 and CH4 in coal, where the corrected (or Maxwell-Stefan) and transport diffusion coefficients were induced based on Fick’s first law and the Peng-Robinson state equation. Based on the GCMC and MD on the coal building block (C100H82O5N2S2) of 191 atoms, Zhang et al. (2016) applied the Maxwell- Stefan diffusion model to correlate the self and transport diffusivities and discovered that the transport coefficients increased with the increasing reservoir pressure due to the enhancement of the thermodynamic factor incorporating with the Peng-Robinson equation of state. Song et al. (2018) combined the GCMC and MD simulation method to orderly relate the adsorption state and the self and transport diffusion for CO2/CH4/N2 in low-rank coal vitrinite and clarified that the diffusion process for N2 is the easiest to induce compared to CO2 and CH4. From the research paths of Hu et al. (2010), Zhang et al. (2014), Zhao et al., 2016b, and Song et al. (2018), MD has become a gradually perfect method to depict the diffusion behaviors of gaseous molecules into coal, reflecting the advanced process of MD for the single component. Both the activation energy calculated from the Arrhenius law and the output configuration of the diffusion behaviors were also collected during the MD simulation, yielding the optimal configurations of coal-CH4, coal-CO2, and coal-N2 at varying adsorption states (Song et al., 2018). The activation energy (ΔEs) of the diffusion process was independent of the temperature, however, it increased with the increasing adsorbate number. All types of the diffusion coefficients, such as the self, corrected, and transport diffusion coefficients, increased with the increasing temperature, indicating the higher probabilities of a big jump for the gaseous adsorbates from one site to another neighboring site. To date, the MD simulation of a single component has reached a situation of unprecedented success after Song et al. (2018). To the best of our knowledge, this series is the most microscopically appropriate method to determine the diffusion properties in coal using the realistic coal model accounting for the heterogeneities of the physical and chemical structures in natural coal. Future efforts will clarify the impacts from the guest-host and guest-guest interactions on the transport properties in coal macromolecular representations.
To verify the MD results, the comparison between simulation and experimental results is depicted in Table 2. The Ds, Dc, and Dt refer to the self-diffusion coefficients, corrected-diffusion coefficients, and transport-diffusion coefficients, respectively, where Dt corresponds to the experimental results. The self-diffusion coefficients of vitrinite+5 CO2 (representing 5 CO2 molecules diffusing in a vitrinite macromolecule) and vitrinite+5 CH4 are 8.53 and 3.47 × 10−11 m2/s, respectively, at 298 K and 0.1 MPa, which are higher than the values calculated by Zhao et al. (2016a) in the Wiser coal model (5.4 × 10−11 m2/s for CO2 and 1.6 × 10−11 m2/s for CH4, MD in the Compass force field for 2000 ps) and by Xiang et al. (2014) in the Yanzhou coal model (1.42 × 10−11 m2/s for CO2 and 0.335 × 10−11 m2/s for CH4, MD in the Dreding force field for 1,500 ps) however significantly lower than the values calculated by Hu et al. (2010) in the Wiser model (1 × 10−9 m2/s for CO2 and 1.2 × 10−9 m2/s for CH4). As the total simulation time for MD is the signature for the diffusion behaviors, the running time for MD time is 500 ps, which is significantly shorter than the transformation time of 1,000 ps established by Müller-Plathe et al. (1992). The short MD runs used and the resulting poor definition of the anomalies in MSD involved in the diffusions of small gas molecules in the polymer materials may have not shown up in earlier MD simulations, which on the other hand will result in improper diffusion coefficient results (Müller-Plathe et al., 1992; Zhao et al., 2016a). The transport diffusion coefficients of CO2 and CH4 are close to the experimental results by Saghafi et al. (2007) with a relative error of 2.9–64.0% and 5.9–27.7%, respectively, verifying the rationality of the calculated method.
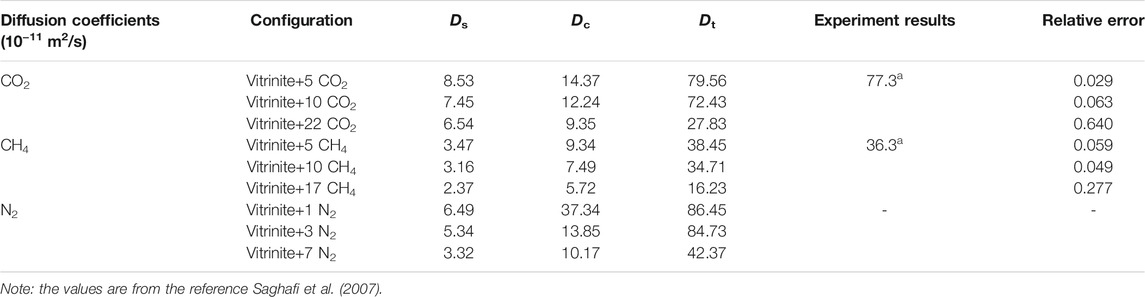
TABLE 2. Three diffusion coefficients for different amounts of CO2, CH4, and N2 in vitrinite (Song et al., 2018).
Diffusion of Binary and Ternary Mixtures
Except for the diffusion behaviors of the single component, MD can also calculate the diffusion properties of gaseous adsorbates of the binary and ternary mixtures in coal, which has gained considerable and increasing interest as it reflects the multi-component characteristics of the coalbed methane and shale gas. The methods for calculating diffusion coefficients of the binary and ternary mixtures can propose predictive engineering models for the field data. For the Fick diffusion coefficients, the method is always consistent using the MD simulation. The multicomponent Darken equation was also developed to depict the concentration dependence of Maxwell-Stefan diffusion coefficients (Liu et al., 2012), providing an expression of Di, jxk to parametrize the generalized Vignes equation. The Maxwell-Stefan (M-S) theory established to depict the multicomponent diffusion and the diffusion mechanism was dominated by the surface diffusion process (Maxwell, 1867). The diffusion particles were always derived by the force field of the pore walls (Hu et al., 2017). When n types of gaseous adsorbates diffused in coal which was presented as the (n+1)th component, M-S diffusion equations of mutual diffusion can well characterize the motion properties for the coal-gas system (Krishna and Wesselingh, 1997; Skoulidas et al., 2003). Compared with the diffusion of the pure component, the M-S diffusion equations of mutual diffusion can provide the binary exchange coefficient (Dij) to reflect the cross influence of different components in the mixture diffusion system (Hu et al., 2017). The thermodynamic factor and modified Onsager coefficient matrix can also be calculated to obtain the phenomenological coefficients incorporating with the MD simulation. For the Accelrys Materials Studio software, MD can be conducted in the Dynamics Task of the Forcite module, whose details can be referred to in Adsorption of Gaseous Molecules Onto Coal. Prior to the Dynamics Task, the configuration should be subjected to geometry optimization, energy optimization, and annealing simulation. The gaseous adsorbates were inserted into the coal macromolecular representations via the GCMC or MC. In this work process, MD was also used to minimize the configuration for relaxation (Hu et al., 2017).
Frequently, the trajectories of the last several seconds were saved and used for the diffusion calculation. For the results of the mutual diffusion coefficient matrix [D], the diagonal elements such as D11 and D22 quantify the interaction extent of gas-coal, however, the cross exchange (correlation) coefficients such as D21 and D12 reflect the interactions of gas-gas for the binary and ternary mixtures (Liu et al., 2013; Hu et al., 2017). The increasing diffusion coefficients with the increasing temperature indicated in almost all the literature suggest the enhancement of the activity at high temperatures (Hu et al., 2010, 2017; Zhao et al., 2016b; Song et al., 2018). The coupling intensity (RD = Di/Dij) which was defined to quantify the contributions of gas-gas and gas-coal to the diffusion of gaseous adsorbates in coal increases with the increasing temperature (Hu et al., 2017), suggesting that the interactions between gas and gas weakens at higher temperature. The first term for the right hand of M-S diffusion equations for the mutual diffusion is negligible, indicating that the case is infinitely close to single-component diffusion at a high enough temperature. For the pressure dependence, there exists divergence on whether high pressure could promote or impede the diffusion speed of the guest molecules (Table 3). Staib et al. (2013) summarized the pressure dependence of diffusion coefficients for various gaseous adsorbates in coal and also proposed a numerical model to characterize the pressure and concentration dependence of CO2 diffusion in coal, clarifying the importance of the pressure step used for calculating the diffusion coefficients at the given conditions. However, the MD results exhibit high consistency for the pressure dependence. Generally, the transport diffusion coefficients first increase until peak pressure and then decrease with the increasing pressure.

TABLE 3. Effects of the pressure on the diffusion coefficients for various gaseous adsorbates in coal (modified from Staib et al. (2013)).
Gas-Induced Coal Swelling and Shrinkage
For the U.S., CO2 emissions from fossil fuel combustion accounts for about 94% (Liu and Wilcox, 2011), and worldwide economic stability and development require energy, which today is also largely dominated by the direct combustion of fossil fuels (Markewitz et al., 2012; Middleton et al., 2012; Moore., 2012). As indicated in almost all the literature, coal has the advantage of adsorption of CO2 over CH4, thus, the injection of CO2 into coal seams could not only improve the recovery of the coalbed methane (Xiang et al., 2014) but also minimize global emissions (Chen et al., 2021). This provides a promising continuable technique for carbon capture and storage. Although the recovery rate of CBM can be enhanced to 95% after injecting CO2 compared with the original 77% (Reeves et al., 2004; Wang K. et al., 2020, Wang et al., 2021a), the adsorption of CO2 onto coal could induce the differential swelling of the coal matrix, which will narrow (or even lead to the closure of the fracture network) the seepage channel and result in the reduction of permeability by ∼1 order of magnitude next to the injection well (Brochard et al., 2011; Wang R. et al., 2020).
The differential swelling of coal is caused by the reduction of mechanical strength after absorbing the gaseous adsorbates (Fan et al., 2020). For the last four decades, the swelling deformation of coal has been attracting increasing attention both via the experimental and mimetic angle. Green et al. (1984) firstly applied the volumetric swelling procedure to examine the coal swelling of the coal matrix and compared the results with the gravimetric swelling experiments, verifying the consistent results between the volumetric and gravimetric procedure. Reucroft and Sethuraman (1987) conducted dilatometric studies on swelling deformation induced from CO2 adsorption and quantified that the swelling deformation induced from CO2 adsorption can account for 20–50% of the specific surface area estimated from the low pressure CO2 adsorption experiments. Aida et al. (1991) examined the steric effects on the solvent swelling of Illinois No. 6 coal and discovered good correlations between cross-link densities and swelling deformation behaviors. Then, Pan and Connell, 2007 established a theoretical model to depict adsorption-induced coal swelling and strain equilibrium, successfully describing the differences in swelling behaviors among different gas species. There also exist anisotropic properties for coal swelling, where more swelling occurs in the bedding direction than that parallel to the bedding (Pan and Connell, 2011). Larsen, 2014 proposed that the dissolved CO2 serves as a plasticizer which can enable the physical structure rearrangements and make the coal into a more associated form in which fluids will be less soluble. Romanov et al. (2006) calculated the errors induced from coal swelling for CO2 adsorption measurements and found that the true adsorption amount is at least 10% more than the observed values for the gravimetric experiment. For the swelling of pressure dependence, the swelling rate firstly increases with the increasing pressure until 8–10 MPa and remains stable (Day et al., 2008), indicating the existence of the swelling limit. The rank and sorbate used also impact the swelling rate in coals and these have been experimentally clarified by Astashov et al. (2008) and Majewska et al., 2010. Niu et al. (2017) estimated the adsorption swelling of natural and reconstituted anthracite coals using an experimental platform and discovered the swelling hysteresis phenomenon.
As mentioned above, the experimental methodology has achieved the quantification of the swelling rate and the influencing factors with the development of the physical analog. However, the experimentation could not reveal the microscopic mechanism of the swelling deformation in essence. MD was another efficient method to reproduce the swelling behaviors of gaseous adsorbates into coal. Narkiewicz and Mathews (2009) calculated the CO2-induced swelling of coal via MD and proposed that the anisotropic swelling was greater perpendicular to the bedding plane. The deformation of coal induced by CH4 adsorption was also quantified via the quenched solid density functional theory (QSDFT) and clarified the adsorption-induced deformation effect (Yang et al., 2010). Compared with MD, two qualitatively different types of swelling mechanisms can be identified depending upon the pore size. However, the QSDFT requires the minimization of the grand thermodynamic potential, which needs a lot of computation power. Based on the poromechanical model, Brochard et al. (2011) conducted effective MD work for swelling deformation behaviors of the CS1000 model induced from the adsorption of CO2 and CH4 in micropores, clarifying that the differential swelling was independent of the geological temperatures and pressures. This work highlights the foundation of the research for swelling deformation, and works as a guide for future coal scholars. Then, the solvent-coal interactions during solvent swelling were examined using the self-built macromolecular representations of Permian-aged South African coals and the results indicated that the nonbonding interactions play an important role during coal-solvent swelling. Xiang et al. (2014) conducted MD simulation for the competitive adsorption of CH4/CO2/H2O and swelling of Yanzhou coal macromolecular representation. This GCMC and MD work clarifies that the reduction in valence electronic energy suggests the molecular mechanism of the swelling deformation for the “stressed coal” formed from the stress (Xiang et al., 2014). Using the extended poromechanical model developed by Brochard et al. (2011), the MC work for the Wiser model suggested that the swelling deformation enhances with the increasing mole fraction of CO2 (Zhang et al., 2015). The calculation flow of the swelling deformation using GCMC and MD is depicted in Figures 8A–D using the coal vitrinite macromolecular representations built in our previous work (Song et al., 2017a). The adsorption process for the CO2 molecules can be simulated via GCMC. Also, the pore volume, specific surface area, and pore size distribution can be calculated using the Atom Volumes & Surface Tool in the Materials Studio software. Then, the swelling ratio of coal vitrinite at this given condition was 5.4%, indicating the loss of porosity correspondingly. This provides a promising method to estimate the swelling deformation of coal and has achieved consistent outcomes (Song et al., 2019).

FIGURE 8. The calculation flow of the swelling deformation for low-rank coal vitrinite macromolecular representation (at 273 K and 0.1 MPa; the occupied and free volume are depicted as the gray zone and blue zone, respectively.).
Zhao et al., 2016b proposed that the swelling deformation of coal was negligible at relatively low pressures and becomes significant with increasing pressure. We also calculated the volumetric change using the GCMC and MD based on the coal vitrinite macromolecular representation and proposed that higher temperature is conducive for the swelling equilibrium (Song et al., 2018), which is considered to be related to chemical thermodynamics. Frequently, the swelling rate, always following the order of [CO2] > [CH4] > [N2], first increases sharply and then slowly when reaching a temperature >348 K independent of the adsorbate type and adsorption state. This reduction in the increase rate of swelling deformation was orientated from the structural variation under high temperatures. For the Materials Studio software environment, the swelling rate can be calculated via the difference in the configuration volume before and after MD. The research synchronously using the GCMC and MD suggests that the swelling rate is almost proportional to the adsorption quantity of CH4/CO2/H2O before the adsorption limit (Song et al., 2018). The occurrence of the swelling deformation should overcome the non-bond potential energy, and thus the proneness of the swelling deformation can be estimated from the composition of molecular potential energy, which can be referred to in detail in Eq. 3. For the pressure dependence, the swelling rate increases slowly at low pressures and sharply at high pressures, in line with the results that higher pressures lead to the closure of the fractures and thus delay the gas diffusion speed (Zhao et al., 2016a; Song et al., 2018).
As the temperature and pressure dependence have been clarified, the differentiated swelling deformation of coal could be revealed in response to the geological conditions using the GCMC and MD (Chen et al., 2021; Wang H. et al., 2021, Wang et al., 2021c, Wang et al., 2021 J.). The work of Chen et al. (2021) has reached the quantification of differentiated swelling deformation for the binary mixture. For the binary mixture of n CO2+ m CH4 (binary mixture of N2+ CH4 with the molar ratio of n: m) and n N2+m CH4, the differentiated swelling deformation was dominated by the mole fraction of CO2 and CH4, respectively (Figure 9). It is noteworthy that, as the geological conditions were actually determined by the pressure and temperature, the variations of the swelling deformation for the coal matrix in response to the geological conditions is of great significance for the extraction of CBM and CO2 capture and storage, especially for the deep un-minable coalbeds (Van Niekerk and Mathews, 2011). Based on the consistent results for the temperature and pressure dependence of swelling deformation, the variation of swelling deformation can be clarified using MD and a poromechanical model incorporating the geothermal gradient law. Chen et al. (2021) investigated the differential swelling of coal vitrinite at geological conditions and proposed that the differential swelling ratio increases regularly with the increase of the burial depth. Although both the swelling ratios for the binary mixtures of n CO2+m CH4 and the n N2+m CH4 increase with the increasing burial depth, there exist distinctly different variations between them (Figure 10). For the former, the differential swelling ratio first increases and then remains stable with the increasing bulk mole fraction of CO2. However, for the latter, it gradually increases with the increasing bulk mole fraction of N2 despite of the low increase rate at a higher bulk mole fraction of N2. With the development of computational power and physical examination level, the simulation sophistication and improvement in MD, GCMC, and other numerical models will provide more opportunities to go beyond our current informed approach, gaining our confidence in the engagement in the estimation of coal swelling deformation behaviors.
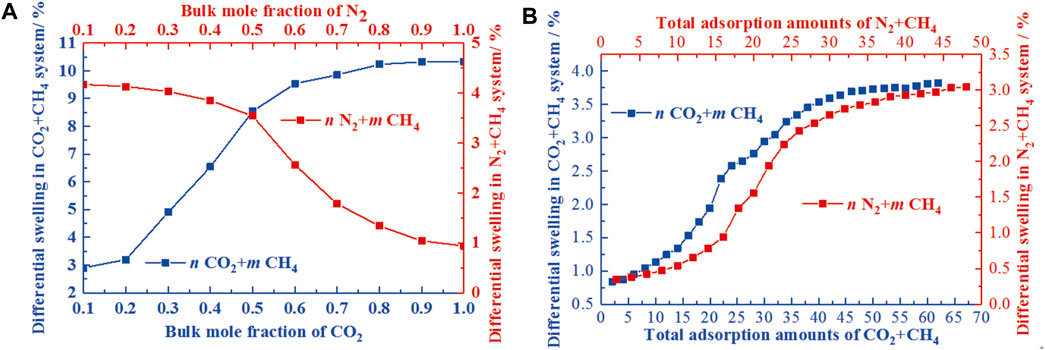
FIGURE 9. The variations of the differential swelling of the n CO2+ m CH4 and the n N2+m CH4 systems under the influence of mole fraction and adsorption amount (Chen et al., 2021).
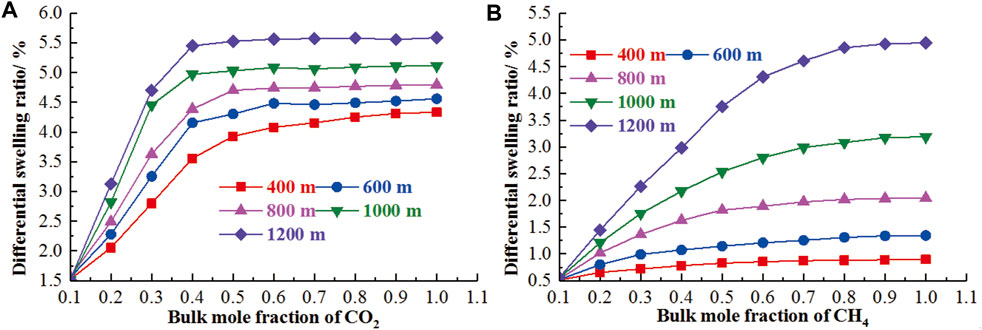
FIGURE 10. The variations of the differential swelling of the n CO2+ m CH4 and the n N2+m CH4 systems in geological conditions (Chen et al., 2021).
There also exist properties for matrix shrinkage for coal. Durucan et al. (2009) conducted matrix deformation experiments on a range of different rank coals subjected to carbon dioxide and methane sorption at representative in situ reservoir pressures under unconfined conditions. These experiments were complemented by a set of simultaneous gas permeability and strain measurements, relating to coal rank and the mechanical and elastic properties. The matrix volume of coal shrinks when occluded gases desorb from its structure. In coalbed gas reservoirs, matrix shrinkage could cause the fracture aperture width to increase, causing an increase in permeability. Levine (1996) developed a computer model to evaluate the potential effect of matrix shrinkage on the absolute permeability and the results indicated that permeability changes as large as +250 mD are predicted for the upper case value of matrix shrinkage. Harpalani and Schraufnagel (1990) established gas pressure-volumetric strain relationships and proposed that the volume of the coal matrix shrinks by ≈0.4% when the gas pressure falls from 6.9 MPa to atmospheric pressure. The permeability increase as a result of matrix shrinkage was also observed in Bowen Basin coal where the matrix shrinkage becomes a dominant factor on cleat permeability over the effective horizontal stress. Liu and Harpalani (2013) reviewed the experimental and theoretical studies on coal matrix shrinkage and also developed a new theoretical approach to model sorption-induced coal shrinkage or swelling. Connell (2016) established a new interpretation of the response of coal permeability to changes in matrix shrinkage and found that considerable fines production at lower pore pressures with this reservoir could contribute to permeability damage, a mechanism not considered in the current model or the Shi-Durucan model.
Coal Pyrolysis and Gas Generation
As the first and necessary reaction step, coal pyrolysis, also termed as coal dry distillation, occurs at almost all the thermal upgrading processes of coal, producing CH4, CO2, H2O, etc. (Hou et al., 2017; Wang et al., 2021a). Although the methodology for pyrolysis includes the physical method, chemical method, physical chemistry method, and computer-aided molecular design (CAMD), the traditional physical methodology faces great challenges when monitoring complex reaction processes and variations for free radicals (Khare et al., 2011; Ashraf et al., 2019). Mathews et al. (2011) proposed the combined experimental examinations and MD of ReaxFF to reveal the pyrolysis mechanisms of coal. ReaxFF MD can estimate the variations of free radicals in the pyrolysis process and adequately consider the weak interaction of chemical bond formation, Coulomb force, and van der Waals force. Therefore, the method of ReaxFF MD is more and more widely used in the coal pyrolysis process (Chenoweth et al., 2008; Zheng et al., 2013; Gao et al., 2018). The ReaxFF force field was proposed by Van Duin et al. (2001) to simulate the break and generation of the chemical bonds between atoms, thus systematically analyzing the continuous chemical reaction process involved in the pyrolysis process.
The simulation process for the ReaxFF MD includes 1) selection or construction of the coal macromolecular representations, 2) geometrical and energetic optimization for the coal macromolecular representations, and 3) simulation of the ReaxFF force field (Yang et al., 2020, Yang et al., 2021). The appropriate selection of the ReaxFF force field should enable the estimation and capture of the products and free radicals resulting from the pyrolysis reaction to obtain the product distribution and elementary reaction of the reaction (Kitsuka et al., 2007; Ashraf et al., 2019). The coal pyrolysis process can be simulated by ReaxFF MD, as well as the effects of pyrolysis temperature, which is of great significance for further study of the coal pyrolysis mechanism. ReaxFF MD can also be used to reproduce the large scale (above 1,000 of atoms) reactive system. For the pyrolysis/combustion process, ReaxFF MD can produce the results 100 times faster than the methods of quantum mechanics (QM) (Bhoi et al., 2014). Although kinetic chemical models have been established to depict the pyrolysis/combustion process of coal, they face utility challenges due to very expensive validation with experimental results and their time-consuming process. In light of this, MD simulation could provide a fundamental reaction mechanism based on the coal macromolecular representation. As mentioned above, the force field characterizing coal pyrolysis/combustion could depict the generation, transformation, and dissociation of the chemical bonds (Weismiller et al., 2010), whose results were in line with those from QM. Bhoi et al. (2014) conducted the MD simulation of spontaneous combustion using brown coal representation and proposed that the combustion of brown coal was initialized by thermal degradation at simulated temperatures high enough to enable chemical reaction within a computationally affordable time. Zheng et al. (2013) investigated the pyrolysis reaction of bituminous coal at 1,000–2000 K (250 ps in duration) based on the Wister and Shinn coal macromolecular representations and highlighted the consistency of the three types of pyrolysis products between MD and experimental results. The comparison of ReaxFF MD and thermogravimetric experimental results could verify the coal macromolecular representation constructed via the elemental analysis, nuclear magnetic resonance (NMR), and infrared spectroscopy (Wang et al., 2017).
The appropriate utilization of the force field enables us to clarify the complex reactions of hydrocarbons. As an extremely complex mechanism, the temperature of ReaxFF MD for the coal pyrolysis reaction mechanism was significantly higher than the actual reaction temperature, where the quantitative relation between the simulated and actual temperature was via the simple harmonic transition state theory. The background processing time of ReaxFF MD can be shortened by programming. Combined with the advantages of the ReaxFF reaction MD in exploring the mechanisms and behaviors of coal pyrolysis, the numbers of calculation cores and force field parameters should be furtherly optimized to improve the calculation efficiency, chemical analysis ability, authenticity, and conclusion accuracy of ReaxFF MD in simulating the pyrolysis mechanisms. Since the parameters of the reactive force fields (RFFs) were frequently derived from QM results, the reactive MD was a powerful tool for exploring complex reactive systems (Castro-Marcano et al., 2012). With the computational resources of the state of the art, the time scale required for ReaxFF MD simulation is of several orders of magnitude shorter than that required for the experiments (Castro-Marcano et al., 2012). Despite the traditional ReaxFF MD, the newly trained ReaxFF which incorporates sulfur-containing hydrocarbons has been found to correctly simulate pyrolysis and combustion dynamics of coal (Castro-Marcano et al., 2012), which provides an improved char construction methodology and demonstrates that the chemical events occurred during the combustion as well (Figure 11). ReaxFF MD simulation has been successfully utilized to reveal the atomic-scaled mechanism of the combustion of an Illinois No. 6 coal char combining the appropriate char representation and ReaxFF reactive force field. These reactive MD works have clarified the feasibility and capability of ReaxFF to describe the initial reactive events for coal pyrolysis and combustion.
FIGURE 11. Conversion of six-membered ring into five- and seven-membered rings demonstrated via ReaxFF MD combustion at 3000 K (for interpretation of the references to color in this figure legend, the reader is referred to the web version of this article) (from Castro-Marcano et al., 2012).
Factors affecting the pyrolysis process such as rank, pulverized coal particle size, temperature, heating rate, pyrolysis atmosphere, residence duration, and catalyst could interact and mutually restrain, dividing the pyrolysis process into three stages, i.e., primary pyrolysis reaction, secondary pyrolysis reaction, and later condensation reaction (Kitsuka et al., 2007; Casal et al., 2018). The outcomes of the hydrocarbon yield with the temperature is depicted in Figure 12. There are three peaks during the pyrolysis process, which exhibit at 350–380°C, 380–470°C, and 480–520°C. There, the yields are low (C1: 1.98–4.39 mg/g*TOC, C2–C5: 2.35–2.93 mg/g*TOC) (TOC, the content of the total organic carbon) for the first stage. The majority of C2–C5 in this stage comes from the initial cracking of aliphatic chains and oxygen functional groups. The instantaneous rate was also low at this stage, which was perhaps induced from limited heat accumulation to trigger the thermal cracking of coal macromolecules (Bhoi et al., 2014). For the second stage, production of C1 and C2–C5 stably increased with temperature, where C1 likely comes from the initial cracking of coal macromolecules but also from the secondary cracking of C2–C5 molecules. The instantaneous rates of C2–C5 decrease with the increasing temperature. The increasing yield of C2–C5 indicates that the generation rate of C2–C5 was higher than their cracking rates, which is consistent with the results of ReaxFF MD (Castro-Marcano et al., 2012). The third peak is from 480 to 520°C with a high hydrocarbon yield (C1: 30.23–40.38 mg/g*TOC, C2–C5: 7.65–7.71 mg/g*TOC), as well as generation rates. In this stage, the faster rate of reactive dynamics time of MD enables us to initiate chemical reactions within a computational affordable time. The ReaxFF could detect the types of free radical intermediates to obtain the distribution and elementary reaction of general products during coal pyrolysis, which is of wider significance for explaining the mechanism of pyrolysis behaviors. The corresponding temperatures are representative of the loss of short chain aliphatic structures such as -CH3 and -CH2, and the condensation of aromatic structures.
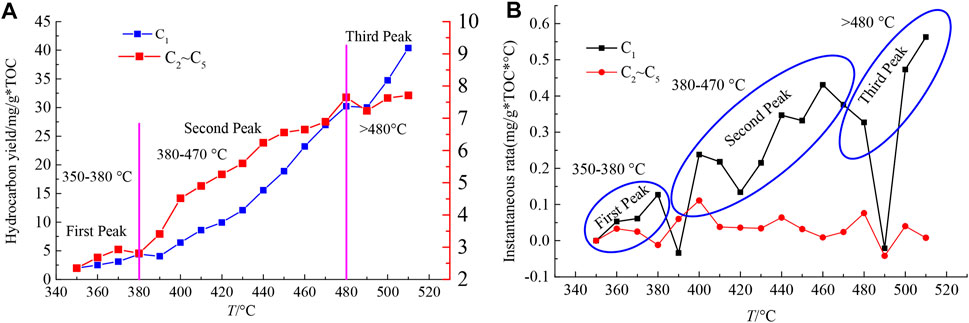
FIGURE 12. (A) Hydrocarbon yield and (B) instantaneous rate under different pyrolysis temperatures (Song et al., 2017c).
The temperature programmed pyrolysis work is of great interest in coal utilization processes where there is a slow-heating rate. The pyrolysis products of vitrinite are mainly gaseous hydrocarbon C1–5. Gaseous hydrocarbon yield and change law of functional groups were obtained. Light hydrocarbon (C6–C14) content of M1 (Ro, max = 0.58%), M2 (Ro, max = 0.80%), M3 (Ro, max = 1.59%), M4 (Ro, max = 1.61%), and M5 (Ro, max = 2.46%) calculated by experiment results of the closed system and open system are respectively 4 mg/g·TOC, 110 mg/g·TOC, 111 mg/g·TOC, 104 mg/g·TOC, and 38 mg/g·TOC. Thus, the yields of C6–C14 first increase and then decrease with the increasing rank. During pyrolysis, the higher carboxyl content and H-bonding were an essential contributor to the stability of coal macromolecules with the different lost rate of oxygen-containing functional groups and alkyl side chains with the increasing coal rank (Li et al., 2013).
As mentioned above, the main components of CBM were generated from the thermal evolution of the organic matters. Thus, the ReaxFF MD is an appropriate method to clarify the gas generation mechanism. The enrichment in coal is closely related to the occurrence of CH4, which primarily can be divided into three states, i.e., adsorption, free, and dissolved states. These were related to the microscopic interactions between coal macromolecules and CH4. Using MD we clarified the dominance of physical adsorption for CH4 from different contributions of van der Waals force, electrostatic force, and hydrogen bond force. For CBM industry, CH4 first desorbed from the micropores surface, then diffused into fractures of the coalbed, and finally was extracted through permeation flow. The hypothesis of the diffusion investigation of MD was the identification of the adsorption process, which assumes that the atom motions follow Newton’s first law and can be described via the empirical potential functions. Thus, MD has long been an appropriate approach to explore the underlying interaction mechanism of gas-coal and gas-gas during the diffusion process. MD could offer one approach to simulate the nanoscale diffusion process even for binary and ternary mixtures. An excellent review on the diffusion coefficients calculated from MD for binary and ternary mixtures is currently available (Liu et al., 2013). There also exist properties for matrix swelling and shrinkage for coal during the adsorption and desorption of CH4. MD was another efficient method to reproduce the swelling behaviors of gaseous adsorbates into coal. Narkiewicz and Mathews (2009) calculated the CO2-induced swelling of coal via MD and proposed that anisotropic swelling was greater perpendicular to the bedding plane. Based on the poromechanical model, Brochard et al. (2011) conducted effective MD work for swelling deformation behaviors of the CS1000 model induced from the adsorption of CO2 and CH4 in micropores, clarifying that the differential swelling was independent of the geological temperatures and pressures. These basic enrichment and transportation processes for coalbed methane geology are closely related to the interactions among coal and gaseous adsorbates, where MD can be appropriately used to reproduce these processes.
Concluding Comments and Prospects
MD has applicability over a wide range of applications in coalbed methane geology. While much of the early work was categorized into “biological systems” that were of high performance and large-scaled, later work has been extended to quantify and rationalize coal’s complex behaviors. Compared with the experimental work, MD simulation can provide insights into the molecular mechanism of microscopic interactions between CH4/CO2/H2O/N2 and coal. With the development of the computation power, we are entering a period where MD will be used for higher level applications such as 1) adsorption of gaseous molecules onto coal, 2) diffusion of gaseous molecules into coal, 3) gas induced coal swelling, and 4) coal pyrolysis and combustion.
Combining GCMC and MD simulation can provide a quantitative understanding of gaseous molecules onto coal. MD simulation indicates the stronger adsorption affinity of CO2 over CH4 almost for all the published literature to date. Compared with the experimental-based characterization, MD can be understood as a “virtual experiment” at the molecular level, serving as an interface between laboratory experimentation and physicochemical theories. Since the last decade, the MD work has been extended to more complex cases, for example, the contributions from water and oxidation on the adsorption process. The hypothesis of the diffusion investigation of MD was identified to the adsorption process, assuming that the atom motions follow Newton’s first law and can be described via the empirical potential functions. Thus, MD has long been an appropriate approach to explore the underlying interaction mechanism of gas-coal and gas-gas during the diffusion process. The experimental observations face significant challenges when encountering the nanoscale diffusion process due to the heterogeneity of coal structure. Today, all types of the diffusion coefficients, such as the self, corrected, and transport diffusion coefficients can be calculated based on MD and the Peng-Robinson equation. To date, MD simulation of a single component has reached a situation of unprecedented success after Song et al. (2018). To the best of our knowledge, the current research origin is the most microscopically appropriate method to determine the diffusion properties in coal using the realistic coal model accounting for the heterogeneities of the physical and chemical structures in natural coal. Future efforts will clarify the impacts from the guest-host and guest-guest interactions on the transport properties in coal macromolecular representations.
Although the recovery rate of CBM can be enhanced after injecting CO2 compared with the original 77%, the adsorption of CO2 onto coal could induce the differential swelling of the coal matrix, which is caused by the reduction of mechanical strength after absorbing the gaseous adsorbates. For the last four decades, the swelling deformation of coal has been attracting increasing attention both via the experimental and mimetic angle. Based on the consistent results for the temperature and pressure dependence of swelling deformation, the variation of swelling deformation can be clarified using MD and a poromechanical model incorporating the geothermal gradient law. With the development of computational power and physical examination level, simulation sophistication and improvement in MD, GCMC, and other numerical models will provide more opportunities to go beyond our current informed approach, gaining our confidence in the engagement in the estimation of coal swelling deformation behaviors. Coal pyrolysis, also termed as coal dry distillation, occurs at almost all the thermal upgrading processes of coal. The faster rate of reactive dynamics time of MD enables us to initiate chemical reactions within an affordable computational time. The background processing time of ReaxFF MD can be shortened by programming. These reactive MD works have clarified the feasibility and capability of ReaxFF to descript the initial reactive events for coal pyrolysis and combustion. Combined with the advantages of the ReaxFF reaction MD in exploring the mechanisms and behaviors of coal pyrolysis, the representation construction method, auxiliary construction program, pyrolysis simulation temperature range, and pyrolysis time should be furtherly optimized to improve the calculation efficiency, chemical analysis ability, authenticity, and conclusion accuracy of ReaxFF MD in simulating the pyrolysis mechanisms. Advancing MD simulation (primarily characterized by a force field) will also allow the exploration of the more complex reaction process. The reaction mechanism of pyrolysis and spontaneous combustion should be a positive trend. The potential of MD for both visualization and microscopic mechanisms is also an interesting possible direction. Thus, it is expected that the availability of MD will continue to increase and will be added to the extensive list of advanced analytical approaches to explore the behaviors of multi-scale mechanisms in coalbed methane geology.
Author Contributions
SY: Formal analysis, Writing–original draft. JB: Conceptualization, Funding acquisition, Supervision. WC: Supervision. DX: Software, Supervision, Visualization, Data curation, Formal analysis. QF, HC, and CG: Supervision: Supervision.
Funding
This research was sponsored by the National Natural Science Foundation of China (Nos. 42102210, 41430317) and Natural Science Foundation of Jiangsu Province (Grant No. BK20200663).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adcock, S. A., and McCammon, J. A. (2006). Molecular Dynamics: Survey of Methods for Simulating the Activity of Proteins. Chem. Rev. 106 (5), 1589–1615. doi:10.1021/cr040426m
Aida, T., Fuku, K., Fujii, M., Yoshihara, M., Maeshima, T., and Squires, T. G. (1991). Steric Requirements for the Solvent Swelling of Illinois No. 6 Coal. Energy fuels 5 (1), 79–83. doi:10.1021/ef00025a013
Alder, B. J., and Wainwright, T. E. (1959). Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 31 (2), 459–466. doi:10.1063/1.1730376
Anderson, J. B. (1980). Quantum Chemistry by Random Walk: Higher Accuracy. J. Chem. Phys. 73 (8), 3897–3899. doi:10.1063/1.440575
Ashraf, A., Sattar, H., and Munir, S. (2019). Thermal Decomposition Study and Pyrolysis Kinetics of Coal and Agricultural Residues Under Non-Isothermal Conditions. Fuel 235, 504–514. doi:10.1016/j.fuel.2018.07.120
Astashov, A. V., Belyi, A. A., and Bunin, A. V. (2008). Quasi-Equilibrium Swelling and Structural Parameters of Coals. Fuel 87, 3455–3461. doi:10.1016/j.fuel.2008.04.027
Bando, Y., Susa, Y., Oshiyama, H., Shibata, N., and Nishimori, H. (2020). Probing the Universality of Topological Defect Formation in a Quantum Annealer: Kibble-Zurek Mechanism and beyond. Phys. Rev. Res. 2 (3), 033369. doi:10.1103/physrevresearch.2.033369
Barbiero, L., Santos, L., and Goldman, N. (2018). Quenched Dynamics and Spin-Charge Separation in an Interacting Topological Lattice. Phys. Rev. B 97 (20), 201115. doi:10.1103/physrevb.97.201115
Bhoi, S., Banerjee, T., and Mohanty, K. (2014). Molecular Dynamic Simulation of Spontaneous Combustion and Pyrolysis of Brown Coal Using ReaxFF. Fuel 136 (6), 326–333. doi:10.1016/j.fuel.2014.07.058
Bodendorfer, N., Mele, F. M., and Münch, J. (2019). A Note on the Hamiltonian as a Polymerisation Parameter. Class. Quan. Grav. 36 (18), 187001. doi:10.1088/1361-6382/ab32ba
Bonomi, M., Barducci, A., and Parrinello, M. (2009). Reconstructing the Equilibrium Boltzmann Distribution from Well-Tempered Metadynamics. J. Comput. Chem. 30 (11), 1615–1621. doi:10.1002/jcc.21305
Brochard, L., Vandamme, M., Pellenq, R. J.-M., and Fen-Chong, T. (2012). Adsorption-Induced Deformation of Microporous Materials: Coal Swelling Induced by CO2-CH4 Competitive Adsorption. Langmuir 28, 2659–2670. doi:10.1021/la204072d
Brüschweiler, R., and Ernst, R. R. (1992). Molecular Dynamics Monitored by Cross-Correlated Cross Relaxation of Spins Quantized along Orthogonal Axes. J. Chem. Phys. 96 (3), 1758–1766. doi:10.1063/1.462131
Bruch, L. W., Cole, M. W., and Zaremba, E. (2007). Physical Adsorption: Forces and Phenomena. Mineola, NY: Dover Publications.
Busch, A., Gensterblum, Y., Krooss, B. M., and Littke, R. (2004). Methane and Carbon Dioxide Adsorption-Diffusion Experiments on Coal: Upscaling and Modeling. Int. J. Coal Geol. 60 (2), 151–168. doi:10.1016/j.coal.2004.05.002
Cai, W., and Christophe, C. (2013). Frontiers in High-Performance, Large-Scale Molecular Dynamics. 35 Years of Molecular-Dynamics Simulations of Biological Systems. Acta Chim. Sinica 71 (2), 159–168. doi:10.6023/a12110930
Canongia Lopes, J. N., and Pádua, A. A. H. (2004). Molecular Force Field for Ionic Liquids Composed of Triflate or Bistriflylimide Anions. J. Phys. Chem. B 108 (43), 16893–16898. doi:10.1021/jp0476545
Canongia Lopes, J. N., and Pádua, A. A. H. (2006). Molecular Force Field for Ionic Liquids III: Imidazolium, Pyridinium, and Phosphonium Cations; Chloride, Bromide, and Dicyanamide Anions. J. Phys. Chem. B 110 (39), 19586–19592. doi:10.1021/jp063901o
Car, R., and Parrinello, M. (1985). Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 55 (22), 2471–2474. doi:10.1103/physrevlett.55.2471
Carlson, G. A. (1992). Computer Simulation of the Molecular Structure of Bituminous Coal. Energy fuels 6 (6), 771–778. doi:10.1021/ef00036a012
Casal, M. D., Vega, M. F., Diaz-Faes, E., and Barriocanal, C. (2018). The Influence of Chemical Structure on the Kinetics of Coal Pyrolysis. Int. J. Coal Geology. 195, 415–422. doi:10.1016/j.coal.2018.06.014
Castro-Marcano, F., Kamat, A. M., Russo, M. F., van Duin, A. C. T., and Mathews, J. P. (2012). Combustion of an Illinois No. 6 Coal Char Simulated Using an Atomistic Char Representation and the ReaxFF Reactive Force Field. Combustion and Flame 159, 1272–1285. doi:10.1016/j.combustflame.2011.10.022
Charrière, D., Pokryszka, Z., and Behra, P. (2010). Effect of Pressure and Temperature on Diffusion of CO2 and CH4 into Coal from the Lorraine basin (France). Int. J. Coal Geol. 81 (4), 373–380. doi:10.1016/j.coal.2009.03.007
Chen, L., Wang, L., Yang, T., and Yang, H. M. (2021). Deformation and Swelling of Coal Induced from Competitive Adsorption of CH4/CO2/N2. Fuel 286, 119356. doi:10.1016/j.fuel.2020.119356
Chenoweth, K., Van Duin, A. C. T., and Goddard, W. A. (2008). ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Hydrocarbon Oxidation. J. Phys. Chem. A. 112 (5), 1040–1053. doi:10.1021/jp709896w
Ciembroniewicz, A., and Marecka, A. (1993). Kinetics of CO2 Sorption for Two Polish Hard Coals. Fuel 72 (3), 405–408. doi:10.1016/0016-2361(93)90062-7
Clarkson, C. R., and Bustin, R. M. (1999). The Effect of Pore Structure and Gas Pressure upon the Transport Properties of Coal: a Laboratory and Modeling Study. 1. Isotherms and Pore Volume Distributions. Fuel 78 (11), 1333–1344. doi:10.1016/s0016-2361(99)00055-1
Connell, L. D. (2016). A New Interpretation of the Response of Coal Permeability to Changes in Pore Pressure, Stress and Matrix Shrinkage. Int. J. Coal Geology. 162, 169–182. doi:10.1016/j.coal.2016.06.012
Cui, X., Bustin, R. M., and Dipple, G. (2004). Selective Transport of CO2, CH4, and N2 in Coals: Insights from Modeling of Experimental Gas Adsorption Data. Fuel 83 (3), 293–303. doi:10.1016/j.fuel.2003.09.001
Cygan, R. T., and Kubicki, J. D. (2018). Molecular Modeling Theory: Applications in the Geosciences. Washington, DC: Walter de Gruyter GmbH & Co KG.
Dash, J. G. (1975). Films on Solid Surfaces: Physics and Chemistry of Physical Adsorption. New York, NY: Academic Press.
Day, S., Fry, R., and Sakurovs, R. (2008). Swelling of Australian Coals in Supercritical CO2. Int. J. Coal Geology. 74 (1), 41–52. doi:10.1016/j.coal.2007.09.006
Durucan, S., Ahsanb, M., and Shia, J.-Q. (2009). Matrix Shrinkage and Swelling Characteristics of European Coals. Energ. Proced. 1 (1), 3055–3062. doi:10.1016/j.egypro.2009.02.084
Einstein, A. (1905). Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 322 (8), 549–560. doi:10.1002/andp.19053220806
Fan, C., Li, S., Luo, M., Zhou, L., Zhang, H., and Yang, Z. (2019). Effects of N and S Functionalities on Binary Gas Co-Adsorption on a Coal Macromolecule. Energy Fuels 33 (5), 3934–3946. doi:10.1021/acs.energyfuels.8b04410
Fan, C., Li, S., Elsworth, D., Han, J., and Yang, Z. (2020). Experimental Investigation on Dynamic Strength and Energy Dissipation Characteristics of Gas Outburst‐Prone Coal. Energy Sci. Eng. 8 (4), 1015–1028. doi:10.1002/ese3.565
Fu, Y., and Song, Y. (2018). CO2-Adsorption Promoted CH4-Desorption onto Low-Rank Coal Vitrinite by Density Functional Theory Including Dispersion Correction (DFT-D3). Fuel 219 (1), 259–269. doi:10.1016/j.fuel.2018.01.127
Gao, M., Li, X., and Guo, L. (2018). Pyrolysis Simulations of Fugu Coal by Large-Scale ReaxFF Molecular Dynamics. Fuel Process. Techn. 178, 197–205. doi:10.1016/j.fuproc.2018.05.011
Gibson, J. B., Goland, A. N., Milgram, M., and Vineyard, G. H. (1960). Dynamics of Radiation Damage. Phys. Rev. 120 (4), 1229–1253. doi:10.1103/physrev.120.1229
Gonalves, W., Morthomas, J., Chantrenne, P., Perez, M., and Martin, C. L. (2017). Elasticity and Strength of Silica Aerogels: A Molecular Dynamics Study on Large Volumes. Acta Mater. 145, 165–174. doi:10.1016/j.actamat.2017.12.005
Goodman, A. L., Busch, A., Bustin, R. M., Chikatamarla, L., Day, S., Duffy, G. J., et al. (2007). Inter-Laboratory Comparison II: CO2 Isotherms Measured on Moisture-Equilibrated Argonne Premium Coals at 55 °C and up to 15 MPa. Int. J. Coal Geology. 72, 153–164. doi:10.1016/j.coal.2007.01.005
Green, T. K., Kovac, J., and Larsen, J. W. (1984). A Rapid and Convenient Method for Measuring the Swelling of Coals by Solvents. Fuel 63 (7), 935–938. doi:10.1016/0016-2361(84)90313-2
Haile, J. M., and Gupta, S. (1983). Extensions of the Molecular Dynamics Simulation Method. II. Isothermal Systems. J. Chem. Phys. 79 (6), 3067–3076. doi:10.1063/1.446137
Halgren, T. A. (1996). Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94. J. Comput. Chem. 17 (5-6), 490–519. doi:10.1002/(sici)1096-987x(199604)17:5/6<490:aid-jcc1>3.0.co;2-p
Harpalani, S., and Schraufnagel, R. (1990). Shrinkage of Coal Matrix with Release of Gas and its Impact on Permeability of Coal. Fuel 69 (5), 551–556. doi:10.1016/0016-2361(90)90137-f
Hou, Q., Han, Y., Wang, J., Dong, Y., and Pan, J. (2017). The Impacts of Stress on the Chemical Structure of Coals: A Mini-Review Based on the Recent Development of Mechanochemistry. Sci. Bull. 62 (13), 965–970. doi:10.1016/j.scib.2017.06.004
Hu, H., Li, X., Fang, Z., Wei, N., and Li, Q. (2010). Small-Molecule Gas Sorption and Diffusion in Coal: Molecular Simulation. Energy 35 (7), 2939–2944. doi:10.1016/j.energy.2010.03.028
Hu, H., Du, L., Xing, Y., and Li, X. (2017). Detailed Study on Self- and Multicomponent Diffusion of CO2-CH4 Gas Mixture in Coal by Molecular Simulation. Fuel 187, 220–228. doi:10.1016/j.fuel.2016.09.056
Jian, X., Guan, P., and Zhang, W. (2012). Carbon Dioxide Sorption and Diffusion in Coals: Experimental Investigation and Modeling. Sci. China Earth Sci. 55 (4), 633–643. doi:10.1007/s11430-011-4272-4
Jorgensen, W. L., Maxwell, D. S., and Tirado-Rives, J. (1996). Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 118 (45), 11225–11236. doi:10.1021/ja9621760
Karacan, C. Ö., and Mitchell, G. D. (2003). Behavior and Effect of Different Coal Microlithotypes during Gas Transport for Carbon Dioxide Sequestration into Coal Seams. Int. J. Coal Geology. 53 (4), 201–217. doi:10.1016/s0166-5162(03)00030-2
Khare, P., Baruah, B. P., and Rao, P. G. (2011). Application of Chemometrics to Study the Kinetics of Coal Pyrolysis: A Novel Approach. Fuel 90 (11), 3299–3305. doi:10.1016/j.fuel.2011.05.017
Kitsuka, T., Bayarsaikhan, B., Sonoyama, N., Hosokai, S., Li, C.-Z., Norinaga, K., et al. (2007). Behavior of Inherent Metallic Species as a Crucial Factor for Kinetics of Steam Gasification of Char from Coal Pyrolysis. Energy fuels 21 (2), 387–394. doi:10.1021/ef0603986
Kraska, T. (2006). Molecular-Dynamics Simulation of Argon Nucleation from Supersaturated Vapor in the NVE Ensemble. J. Chem. Phys. 124 (5), 054507. doi:10.1063/1.2162882
Krishna, R., and Wesselingh, J. A. (1997). The Maxwell-Stefan Approach to Mass Transfer. Chem. Eng. Sci. 52, 861–911. doi:10.1016/s0009-2509(96)00458-7
Krumeich, F., Waser, O., and Pratsinis, S. E. (2016). Thermal Annealing Dynamics of Carbon-Coated LiFePO4 Nanoparticles Studied by In-Situ Analysis. J. Solid State. Chem. 242, 96–102. doi:10.1016/j.jssc.2016.07.002
Larsen, J. W. (2014). The Effects of Dissolved CO2 on Coal Structure and Properties. Int. J. Coal Geol. 57, 63–70. doi:10.1016/j.egypro.2012.06.070
Levine, J. R. (1996). Model Study of the Influence of Matrix Shrinkage on Absolute Permeability of Coal Bed Reservoirs. Geol. Soc. Lond. Spec. Publications 109 (1), 197–212. doi:10.1144/gsl.sp.1996.109.01.14
Li, W., Zhu, Y., Chen, S., and Zhou, Y. (2013). Research on the Structural Characteristics of Vitrinite in Different Coal Ranks. Fuel 107, 647–652. doi:10.1016/j.fuel.2012.10.050
Liu, S., and Harpalani, S. (2013). A New Theoretical Approach to Model Sorption-Induced Coal Shrinkage or Swelling. Bulletin 97 (7), 1033–1049. doi:10.1306/12181212061
Liu, T., and Lin, B. (2019). Time-Dependent Dynamic Diffusion Processes in Coal: Model Development and Analysis. Int. J. Heat Mass Transfer 134, 1–9. doi:10.1016/j.ijheatmasstransfer.2019.01.005
Liu, Y., and Wilcox, J. (2011). CO2 Adsorption on Carbon Models of Organic Constituents of Gas Shale and Coal. Environ. Sci. Technol. 45, 809–814. doi:10.1021/es102700c
Liu, Y., and Wilcox, J. (2012a). Molecular Simulation of CO2 Adsorption in Micro- and Mesoporous Carbons with Surface Heterogeneity. Int. J. Coal Geology. 104, 83–95. doi:10.1016/j.coal.2012.04.007
Liu, Y., and Wilcox, J. (2012b). Effects of Surface Heterogeneity on the Adsorption of CO2 in Microporous Carbons. Environ. Sci. Technol. 46, 1940–1947. doi:10.1021/es204071g
Liu, X., Schnell, S. K., Simon, J.-M., Krüger, P., Bedeaux, D., Kjelstrup, S., et al. (2013). Diffusion Coefficients from Molecular Dynamics Simulations in Binary and Ternary Mixtures. Int. J. Thermophys. 34 (7), 1169–1196. doi:10.1007/s10765-013-1482-3
Liu, X.-Q., Xue, Y., Tian, Z.-Y., Mo, J.-J., Qiu, N.-X., Chu, W., et al. (2013). Adsorption of CH4 on Nitrogen- and Boron-Containing Carbon Models of Coal Predicted by Density-Functional Theory. Appl. Surf. Sci. 285, 190–197. doi:10.1016/j.apsusc.2013.08.035
Liu, Q., Cheng, Y., Zhou, H., Guo, P., An, F., and Chen, H. (2015). A Mathematical Model of Coupled Gas Flow and Coal Deformation with Gas Diffusion and Klinkenberg Effects. Rock Mech. Rock Eng. 48 (3), 1163–1180. doi:10.1007/s00603-014-0594-9
Liu, J., Li, S., and Wang, Y. (2019). Molecular Dynamics Simulation of Diffusion Behavior of CH4, CO2, and N2 in Mid-Rank Coal Vitrinite. Energies 12 (19), 3744. doi:10.3390/en12193744
Lobato, F. S., Assis, E. G., Steffen, V., and Neto, A. J. D. S. (2012). Design and Identification Problems of Rotor Bearing Systems Using the Simulated Annealing Algorithm. Simulated Annealing-Single and Multiple Objective Problems. Marcos de Sales Guerra Tsuzuki: IntechOpen, 197–216.
Luo, L., Fei, W., Li, C., and Yao, Z. (1996). Advance of Molecular Dynamics Simulation in Materials Science. Mat. Sci. Technol. 1, 125–128.
Magri, F. (1978). A Simple Model of the Integrable Hamiltonian Equation. J. Math. Phys. 19 (5), 1156–1162. doi:10.1063/1.523777
Majewska, Z., Majewski, S., and Ziętek, J. (2010). Swelling of Coal Induced by Cyclic Sorption/desorption of Gas: Experimental Observations Indicating Changes in Coal Structure Due to Sorption of CO2 and CH4. Int. J. Coal Geology. 83 (4), 475–483. doi:10.1016/j.coal.2010.07.001
Manzhos, S. (2013). Effects of Nuclear Vibrations on the Energetics of Polythiophene: Quantized Energy Molecular Dynamics. Aust. J. Chem. 66 (9), 1021–1028. doi:10.1071/ch13112
Markewitz, P., Kuckshinrichs, W., Leitner, W., Linssen, J., Zapp, P., Bongartz, R., et al. (2012). Worldwide Innovations in the Development of Carbon Capture Technologies and the Utilization of CO2. Energy Environ. Sci. 5 (6), 7281–7305. doi:10.1039/c2ee03403d
Mathews, J. P., and Chaffee, A. L. (2012). The Molecular Representations of Coal - A Review. Fuel 96, 1–14. doi:10.1016/j.fuel.2011.11.025
Mathews, J. P., Van Duin, A. C. T., and Chaffee, A. L. (2011). The Utility of Coal Molecular Models. Fuel Process. Techn. 92 (4), 718–728. doi:10.1016/j.fuproc.2010.05.037
Maxwell, J. C. (1867). On the Dynamical Theory of Gases. Philos. Trans. R. Soc. Lond. 35, 185–217. doi:10.1142/9781848161337_0014
Middleton, R. S., Keating, G. N., Stauffer, P. H., Jordan, A. B., Viswanathan, H. S., Kang, Q. J., et al. (2012). The Cross-Scale Science of CO2 Capture and Storage: From Pore Scale to Regional Scale. Energ. Environ. Sci. 5 (6), 7328–7345. doi:10.1039/c2ee03227a
Moore, T. A. (2012). Coalbed Methane: A Review. Int. J. Coal Geology. 101, 36–81. doi:10.1016/j.coal.2012.05.011
Mosher, K., He, J., Liu, Y., Rupp, E., and Wilcox, J. (2013). Molecular Simulation of Methane Adsorption in Micro- and Mesoporous Carbons with Applications to Coal and Gas Shale Systems. Int. J. Coal Geology. 109-110, 36–44. doi:10.1016/j.coal.2013.01.001
Müller-Plathe, F., Rogers, S. C., and Gunsteren, W. F. V. (1992). Computational Evidence for Anomalous Diffusion of Small Molecules in Amorphous Polymers. Chem. Phys. Lett. 199 (3-4), 237–243. doi:10.1016/0009-2614(92)80112-O
Naber, M. (2004). Time Fractional Schrödinger Equation. J. Math. Phys. 45 (8), 3339–3352. doi:10.1063/1.1769611
Narkiewicz, M. R., and Mathews, J. P. (2009). Visual Representation of Carbon Dioxide Adsorption in a Low-Volatile Bituminous Coal Molecular Model. Energy fuels 23, 5236–5246. doi:10.1021/ef900314j
Niu, Q., Cao, L., Sang, S., Zhou, X., Wang, Z., and Wu, Z. (2017). The Adsorption-Swelling and Permeability Characteristics of Natural and Reconstituted Anthracite Coals. Energy 141, 2206–2217. doi:10.1016/j.energy.2017.11.095
Nosé, S. (1984). A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mole Phys. 52 (2), 255–268. doi:10.1080/00268978400101201
Pan, Z., and Connell, L. D. (2007). A Theoretical Model for Gas Adsorption-Induced Coal Swelling. Int. J. Coal Geology. 69 (4), 243–252. doi:10.1016/j.coal.2006.04.006
Pan, Z., and Connell, L. D. (2011). Modelling of Anisotropic Coal Swelling and its Impact on Permeability Behaviour for Primary and Enhanced Coalbed Methane Recovery. Int. J. Coal Geol. 85 (3-4), 257–267. doi:10.1016/j.coal.2010.12.003
Pan, Z., Connell, L. D., Camilleri, M., and Connelly, L. (2010). Effects of Matrix Moisture on Gas Diffusion and Flow in Coal. Fuel 89 (11), 3207–3217. doi:10.1016/j.fuel.2010.05.038
Parrinello, M., and Rahman, A. (1980). Crystal Structure and Pair Potentials: A Molecular-Dynamics Study. Phys. Rev. Lett. 45 (14), 1196–1199. doi:10.1103/physrevlett.45.1196
Pone, J. D. N., Halleck, P. M., and Mathews, J. P. (2009). Sorption Capacity and Sorption Kinetic Measurements of CO2 and CH4 in Confined and Unconfined Bituminous Coal. Energy Fuels 23, 4688–4695. doi:10.1021/ef9003158
Prezhdo, O. V. (2002). Classical Mapping for Second-Order Quantized Hamiltonian Dynamics. J. Chem. Phys. 117 (7), 2995–3002. doi:10.1063/1.1493776
Rahman, A. (1964). Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev. 136 (2A), A405–A411. doi:10.1103/physrev.136.a405
Reeves, S., Davis, D., and Oudinot, A. (2004). A Technical and Economic Sensitivity Study of Enhanced Coalbed Methane Recovery and Carbon Sequestration in Coal. Washington, DC: DOE topical report.
Reucroft, P. J., and Sethuraman, A. R. (1987). Effect of Pressure on Carbon Dioxide Induced Coal Swelling. Energy fuels 1 (1), 72–75. doi:10.1021/ef00001a013
Righettoni, M., and Pratsinis, S. E. (2014). Annealing Dynamics of WO 3 by In Situ XRD. Mater. Res. Bull. 59, 199–204. doi:10.1016/j.materresbull.2014.07.018
Rokach, L. (2010). Ensemble-Based Classifiers. Art. Intell. Rev. 33 (1), 1–39. doi:10.1007/s10462-009-9124-7
Romanov, V. N., Goodman, A. L., and Larsen, J. W. (2006). Errors in CO2 Adsorption Measurements Caused by Coal Swelling. Energy fuels 20 (1), 415–416. doi:10.1021/ef050318i
Saghafi, A., Faiz, M., and Roberts, D. (2007). CO2 Storage and Gas Diffusivity Properties of Coals from Sydney Basin, Australia. Int. J. Coal Geol. 70 (1-3), 240–254. doi:10.1016/j.coal.2006.03.006
Shi, J. Q., and Durucan, S. (2003). A Bidisperse Pore Diffusion Model for Methane Displacement Desorption in Coal by CO2 Injection☆. Fuel 82, 1219–1229. doi:10.1016/s0016-2361(03)00010-3
Shokri, S., Mohammadikhah, R., Abolghasemi, H., Mohebbi, A., Hashemipour, H., Ahmadi-Marvast, M., et al. (2010). Molecular Dynamic Simulation of Multilayer Methane Adsorption On/in Open Ended Single-Walled Carbon Nanotubes. Ijcea 1, 63–70. doi:10.7763/ijcea.2010.v1.11
Siemons, N., Wolf, K. H. A. A., and Bruining, J. (2017). Interpretation of Carbon Dioxide Diffusion Behavior in Coals. Int. J. Coal Geol. 72, 315–324. doi:10.1016/j.coal.2007.04.004
Skoulidas, A. I., Sholl, D. S., and Krishna, R. (2003). Correlation Effects in Diffusion of CH4/CF4 Mixtures in MFI Zeolite. A Study Linking MD Simulations with the Maxwell−Stefan Formulation. Langmuir 19, 7977–7988. doi:10.1021/la034759a
Song, Y., Zhu, Y., and Li, W. (2017a). Macromolecule Simulation and CH4 Adsorption Mechanism of Coal Vitrinite. Appl. Surf. Sci. 396, 291–302. doi:10.1016/j.apsusc.2016.10.127
Song, Y., Jiang, B., and Li, W. (2017b). Molecular Simulation of CH4/CO2/H2O Competitive Adsorption on Low Rank Coal Vitrinite. Phys. Chem. Chem. Phys. 19 (27), 17773–17788. doi:10.1039/C7CP02993D
Song, Y., Jiang, B., Mathews, J. P., Yan, G., and Li, F. (2017c). Structural Transformations and Hydrocarbon Generation of Low-Rank Coal (Vitrinite) during Slow Heating Pyrolysis. Fuel Process. Techn. 167, 535–544. doi:10.1016/j.fuproc.2017.08.003
Song, Y., Jiang, B., and Qu, M. (2018). Molecular Dynamic Simulation of Self-and Transport Diffusion for CO2/CH4/N2 in Low-Rank Coal Vitrinite. Energy Fuels 32 (3), 3085–3096
Song, Y., Jiang, B., and Lan, F. (2019). Competitive Adsorption of CO2/N2/CH4 onto Coal Vitrinite Macromolecular: Effects of Electrostatic Interactions and Oxygen Functionalities. Fuel 235 (1), 23–38. doi:10.1016/j.fuel.2018.07.087
Staib, G., Sakurovs, R., and Gray, E. M. A. (2013). A Pressure and Concentration Dependence of CO2 Diffusion in Two Australian Bituminous Coals. Int. J. Coal Geology. 116-117, 106–116. doi:10.1016/j.coal.2013.07.005
Sun, H., Mumby, S. J., Maple, J. R., and Hagler, A. T. (1994). An Ab Initio CFF93 All-Atom Force Field for Polycarbonates. J. Am. Chem. Soc. 116 (7), 2978–2987. doi:10.1021/ja00086a030
Švábová, M., Weishauptová, Z., and Přibyl, O. (2012). The Effect of Moisture on the Sorption Process of CO2 on Coal. Fuel 92, 187–196. doi:10.1016/j.fuel.2011.08.030
Takanohashi, T., Nakamura, K., and Iino, M. (1999). Computer Simulation of Methanol Swelling of Coal Molecules. Energy fuels 13 (4), 922–926. doi:10.1021/ef980276g
Thierfelder, C., Witte, M., Blankenburg, S., Rauls, E., and Schmidt, W. G. (2011). Methane Adsorption on Graphene from First Principles Including Dispersion Interaction. Surf. Sci. 605 (7-8), 746–749. doi:10.1016/j.susc.2011.01.012
Ulander, J., and Haymet, A. D. J. (2003). Permeation across Hydrated DPPC Lipid Bilayers: Simulation of the Titrable Amphiphilic Drug Valproic Acid. Biophysical J. 85 (6), 3475–3484. doi:10.1016/s0006-3495(03)74768-7
Van Duin, A. C. T., Dasgupta, S., Lorant, F., and Goddard, W. A. (2001). ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A. 105 (41), 9396–9409. doi:10.1021/jp004368u
Van Niekerk, D., and Mathews, J. P. (2011). Molecular Dynamic Simulation of Coal-Solvent Interactions in Permian-Aged South African Coals. Fuel Process. Techn. 92 (4), 729–734. doi:10.1016/j.fuproc.2010.08.011
Vidali, G., Ihm, G., Kim, H.-Y., and Cole, M. W. (1991). Potentials of Physical Adsorption. Surf. Sci. Rep. 12 (4), 135–181. doi:10.1016/0167-5729(91)90012-m
Wang, J.-P., Li, G.-Y., Guo, R., Li, A.-Q., and Liang, Y.-H. (2017). Theoretical and Experimental Insight into Coal Structure: Establishing a Chemical Model for Yuzhou lignite. Energy fuels 31 (1), 124–132. doi:10.1021/acs.energyfuels.6b01854
Wang, K., Pan, J., Wang, E., Hou, Q., Yang, Y., and Wang, X. (2020a). Potential Impact of CO2 Injection into Coal Matrix in Molecular Terms. Chem. Eng. J. 401, 126071. doi:10.1016/j.cej.2020.126071
Wang, R., Wang, Q., Niu, Q., Pan, J., Wang, H., and Wang, Z. (2020b). CO2 Adsorption and Swelling of Coal under Constrained Conditions and Their Stage-Change Relationship. J. Nat. Gas Sci. Eng. 76, 103205. doi:10.1016/j.jngse.2020.103205
Wang, Z., Deng, Z., Fu, X., Chen, H., Pan, J., and Zhou, H. (2021a). Dynamic Monitoring of Induced Strain during N2-ECBM of Coal with Different Gas Contents. Energy fuels 35 (4), 3140–3149. doi:10.1021/acs.energyfuels.0c04405
Wang, H., Shi, X., Tian, J., Pan, J., Yao, L., and Feng, X. (2021b). Macromolecular Structure Changes of Tectonically Deformed Coal: Evidence from Coal Pyrolysis, 13C NMR, and XRD Experiments. Energy fuels 35 (10), 8711–8722. doi:10.1021/acs.energyfuels.1c00435
Wang, Z., Fu, X., Deng, Z., Pan, J., Wang, H., and Wang, Z. (2021c). Investigation of Adsorption–Desorption, Induced Strains and Permeability Evolution during N2–ECBM Recovery. Nat. Resour. Res. 30, 1–18. doi:10.1007/s11053-021-09884-8
Wang, J., Hou, Q., Zeng, F., and Guo, G.-J. (2021d). Gas Generation Mechanisms of Bituminous Coal under Shear Stress Based on ReaxFF Molecular Dynamics Simulation. Fuel 298, 120240. doi:10.1016/j.fuel.2021.120240
Weismiller, M. R., van Duin, A. C. T., Lee, J., and Yetter, R. A. (2010). ReaxFF Reactive Force Field Development and Applications for Molecular Dynamics Simulations of Ammonia Borane Dehydrogenation and Combustion. J. Phys. Chem. A. 114, 5485–5492. doi:10.1021/jp100136c
Xiang, J., Zeng, F., Liang, H., Li, B., and Song, X. (2014). Molecular Simulation of the CH4/CO2/H2O Adsorption onto the Molecular Structure of Coal. Sci. China Earth Sci. 57 (8), 1749–1759. doi:10.1007/s11430-014-4849-9
Yang, Y., and Liu, S. (2019). Estimation and Modeling of Pressure-dependent Gas Diffusion Coefficient for Coal: A Fractal Theory-Based Approach. Fuel 253, 588–606. doi:10.1016/j.fuel.2019.05.009
Yang, K., Lu, X., Lin, Y., and Neimark, A. V. (2010). Deformation of Coal Induced by Methane Adsorption at Geological Conditions. Energy fuels 24, 5955–5964. doi:10.1021/ef100769x
Yang, Y., Pan, J., Wang, K., and Hou, Q. (2020). Macromolecular Structural Response of Wender Coal under Tensile Stress via Molecular Dynamics. Fuel 265, 116938. doi:10.1016/j.fuel.2019.116938
Yang, Y., Pan, J., Hou, Q., Wang, K., and Wang, X. (2021). Stress Degradation Mechanism of Coal Macromolecular Structure: Insights from Molecular Dynamics Simulation and Quantum Chemistry Calculations. Fuel 303, 121258. doi:10.1016/j.fuel.2021.121258
Zhang, J., Clennell, M. B., Dewhurst, D. N., and Liu, K. (2014). Combined Monte Carlo and Molecular Dynamics Simulation of Methane Adsorption on Dry and Moist Coal. Fuel 122, 186–197. doi:10.1016/j.fuel.2014.01.006
Zhang, J., Liu, K., Clennell, M. B., Dewhurst, D. N., and Pervukhina, M. (2015). Molecular Simulation of CO2-CH4 Competitive Adsorption and Induced Coal Swelling. Fuel 160, 309–317. doi:10.1016/j.fuel.2015.07.092
Zhang, J., Clennell, M. B., Liu, K., Dewhurst, D. N., Pervukhina, M., and Sherwood, N. (2016). Molecular Dynamics Study of CO2 Sorption and Transport Properties in Coal. Fuel 177, 53–62. doi:10.1016/j.fuel.2016.02.075
Zhao, Y., Feng, Y., and Zhang, X. (2016a). Molecular Simulation of CO 2/CH 4 Self- and Transport Diffusion Coefficients in Coal. Fuel 165, 19–27. doi:10.1016/j.fuel.2015.10.035
Zhao, Y., Feng, Y., and Zhang, X. (2016b). Selective Adsorption and Selective Transport Diffusion of CO2-CH4 Binary Mixture in Coal Ultramicropores. Environ. Sci. Technol. 50 (17), 9380–9389. doi:10.1021/acs.est.6b01294
Keywords: molecular dynamics, adsorption, diffusion, swelling, pyrolysis and combustion, coalbed methane geology
Citation: Yu S, Bo J, Chongtao W, Xuguang D, Fangkai Q, Chenliang H and Guoxi C (2021) A Review on the Application of Molecular Dynamics to the Study of Coalbed Methane Geology. Front. Earth Sci. 9:775497. doi: 10.3389/feart.2021.775497
Received: 14 September 2021; Accepted: 08 November 2021;
Published: 09 December 2021.
Edited by:
Jienan Pan, Henan Polytechnic University, ChinaReviewed by:
Chaojun Fan, Liaoning Technical University, ChinaJiahao Wu, Tsinghua University, China
Qiming Huang, Shandong University of Science and Technology, China
Copyright © 2021 Yu, Bo, Chongtao, Xuguang, Fangkai, Chenliang and Guoxi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiang Bo, amlhbmdib0BjdW10LmVkdS5jbg==; Wei Chongtao, d2VpZ2hjdEAxNjMuY29t
 Song Yu
Song Yu Jiang Bo1,2*
Jiang Bo1,2* Wei Chongtao
Wei Chongtao Quan Fangkai
Quan Fangkai Hou Chenliang
Hou Chenliang