A Cloudier Picture of Ice-Albedo Feedback in CMIP6 Models

1 Introduction

Recent analyses of the nearly 20-year Clouds Earth Radiation and Energy System Energy Balance and Filled (CERES-EBAF) record of top of atmosphere (TOA) outgoing shortwave radiation (OSR) reveal that the Arctic is absorbing more sunlight now than at the start of this century, even when inter-annual variability is explicitly considered (Sledd and L’Ecuyer, 2021a). This result, coupled with the finding that clouds have delayed the emergence of this trend by about 5 years, indicates that the satellite record is now sufficiently long to provide a useful benchmark for assessing predicted increases in Arctic absorbed shortwave radiation due to sea ice loss, a major contributor to accelerated rates of Arctic warming relative to globe.

As the Arctic warms, reduced areas of bright snow and ice covers expose darker land and ocean surfaces that absorb more solar radiation in the sunlit summer months. This extra energy input induces additional Arctic warming that melts more ice creating an ice-albedo feedback (Budyko, 1969; Sellers, 1969; Serreze et al., 2009; Screen and Simmonds, 2010b). The impact of surface albedo changes on the net Arctic energy balance is strongly modulated by the atmosphere, though. Cloud cover, in particular, plays a large role modulating the surface energy budget, warming the surface by trapping longwave radiation and cooling the surface by reflecting SW radiation. The latter effect of clouds also obscures changes in the surface albedo that would otherwise be viewed from space (Sedlar et al., 2011; Wu et al., 2020). Sledd and L’Ecuyer (2019) showed that this “cloud masking” effect reduces the sensitivity of the Arctic-mean all-sky albedo to changes in sea ice area (SIA) by a factor of two relative to clear-skies.

Thus, while declines in sea ice and their associated impacts on surface albedo could be detected in observations some time ago (Stroeve et al., 2012; Letterly et al., 2018; Stroeve and Notz, 2018), secular trends in net solar absorption at the TOA have only recently emerged in the satellite record (Sledd and L’Ecuyer, 2021a). This stems in part from the need for direct measurements of TOA fluxes across polar regions that only became available with the launch of the CERES instruments aboard the Terra and Aqua satellites in early 2000 (Loeb et al., 2018). Using these new observations, Kato et al. (2006) quickly identified trends in Arctic shortwave (SW) irradiances, but their statistical significance was low owing to the short 4 year data record available at the time. Subsequent analyses by Hartmann and Ceppi (2014) using 13 years of CERES data indicated robustly negative trends in SW reflection over the high northern latitudes but increased interannual variability in subsequent years obscured this signal until very recently.

Increasing Arctic solar absorption is also evident in reanalyses (Perovich et al., 2007) and climate models (Choi et al., 2020; Hahn et al., 2021). Figure 1 shows recent trends in Arctic absorbed solar radiation in the ensemble of 6^th Climate Model Intercomparison Project (CMIP6) models listed in Table 1. Despite the short period covered (2000–2014 is chosen to overlap the observational record), the model ensemble shows that many ocean regions are absorbing more SW radiation than at the start of the century. Also evident in Figure 1 is the fact that clear-sky trends are frequently larger than those in all-sky conditions, consistent with the notion that clouds mask the impact of surface albedo changes on TOA or planetary albedo.

FIGURE 1

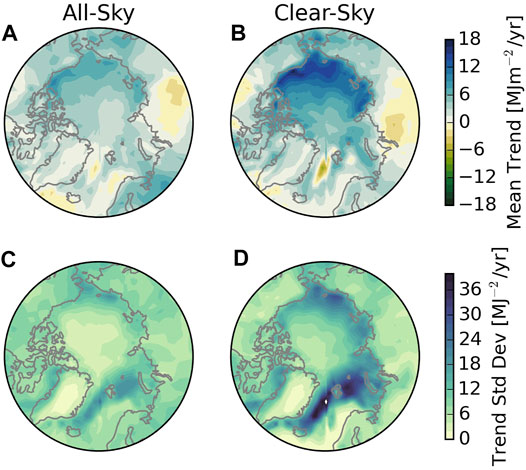
FIGURE 1. CMIP6 mean ensemble accumulated SW (SW_acc) trends (A,B) and ensemble standard deviations (C,D) for all-sky (A,C) and clear-sky (B,D) conditions. SW_acc is the total net SW energy absorbed over the melt season (Eq. 6). SW fluxes are interpolated onto the same 2.5^ox2.5^o grid as CERES in ArORIS. The models included are listed in Table 2. Results from individual models are shown in the Supplementary Material.

TABLE 1

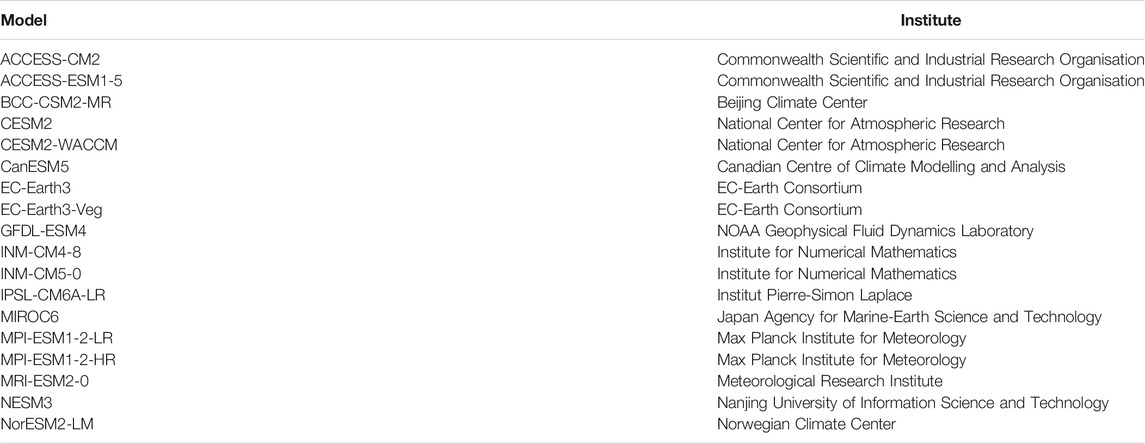
TABLE 1. Output is used from the following models from phase six of the Coupled Model Intercomparison Project.

While these trends qualitatively reflect basic physical principles, Figures 1C,D reveal that the standard deviation across models is often larger than the ensemble mean trend. Thus, while the ensemble agrees with recent observational evidence that most regions of the Arctic are absorbing more solar radiation than they were at the start of the century, individual models exhibit a wide range of behaviors over this relatively short analysis period (Supplementary Figures S1, S2). This is consistent with many recent studies that caution against using individual model realizations to assess trends on such short timescales due to internal variability. It has been well-documented that any single model realization represents just one of many possible climate trajectories that would all be consistent with model physics (Deser et al., 2012; Kay et al., 2015; Deser et al., 2020).

While this internal variability precludes direct comparison against observations which, themselves, correspond to one particular Arctic climate trajectory from the physically plausible states (evidenced by inter-annual variability), it is encouraging to note that the observations (denoted by CERES) fall within the range of states captured by the CMIP6 ensemble (Notz and Community, 2020). However, while there is value in confirming that the Arctic is absorbing more solar radiation than it was just two decades ago, these comparisons don’t address the causes of these increases or establish the combination of factors responsible for the rate of change. Establishing and modeling the coupled influences of sea ice and clouds on absorbed SW radiation and how they evolve as the Arctic warms, is essential for predicting future Arctic climate.

Many previous studies have evaluated the representation of sea ice and snow cover in CMIP6 models using satellite observations (Davy and Outten, 2020; Notz and Community, 2020; Shu et al., 2020). Yet, to quantify and ultimately predict ice-albedo feedbacks and their influence on the Arctic climate, it is equally important to establish how well models simulate the impact of changes in these bright surfaces on Arctic energy flows. Fewer studies make this important connection directly using both models and observations. This paper applies new metrics that explicitly connect sea ice changes to their influence on Arctic albedo to assess the evolution of Arctic solar absorption in the latest generation of climate models in the context of observed changes. We seek to establish how tightly CMIP6 models constrain the Arctic albedo response to changing sea ice concentration, quantify differences in their representation of the role of clouds in modulating this relationship and the emergence of trends in Arctic solar absorption, and determine how these have changed since CMIP5. For a thorough assessment of other drivers of Arctic Amplification, the reader is directed to Cai et al. (2021) or Hahn et al. (2021).

2 Materials and Methods

To answer these questions, observations are extracted from the Arctic Observations and Reanalysis Integrated System (ArORIS). ArORIS is a collection of satellite observations, ground measurements, and atmospheric reanalyses that supports Arctic climate research (Christensen et al., 2016) by collocating and interpolating all included datasets to a uniform monthly, 2.5^ox2.5^o grid. We use TOA all-sky and total-region clear-sky shortwave (SW) fluxes from CERES-EBAF that leverage in situ ocean heat content observations to adjust TOA fluxes within their ranges of uncertainty for consistency (Loeb et al., 2018). Total-region clear-sky fluxes are calculated with an adjustment factor based on the difference between clear-sky fluxes for cloud-free regions compared to fluxes from a radiative transfer calculation with a cloud-free atmospheric column (Loeb et al., 2020). This method of calculating total-region clear-sky fluxes is intended to allow direct comparison between observational and model generated clear-sky fluxes. TOA net SW flux uncertainty is 3 (6) Wm⁻² for March 2000-June 2002 and 2.5 Wm⁻² after for all-sky (clear-sky) conditions (Loeb et al., 2018). At the surface, uncertainty for all-sky upwelling (downwelling) SW flux is 6 (5) Wm⁻² (Kato et al., 2018).

Sea ice concentration (SIC) is obtained from the NSIDC Equal-Area Scalable Earth grid (EASE) weekly product, estimated with brightness temperatures from the Nimbus-7 Scanning Multichannel Microwave Radiometer (SMMR), the Defense Meteorological Satellite Program (DMSP) F8, F11, and F13 Special Sensor Microwave/Imagers (SSM/Is), and the DMSP F17 Special Sensor Microwave Imager/Sounder (SSMIS) (Brodzik and Armstrong, 2013). SIC is used to calculate sea ice area (SIA) by multiplying SIC in a grid box by its area and summing over all area north of the Arctic circle (66.56 N). SIC has an uncertainty of 15% during the melt season.

Observed relationships between surface and TOA albedo and SIA as well as trends in Arctic solar absorption are compared to similar metrics derived from the models participating in CMIP5 and 6 (Taylor et al. (2012); Eyring et al. (2016)). The specific models included in this study are listed in Tables 1 and 2. We use the historical forcing up to 2005 (2014) in CMIP5 (CMIP6), and the “business as usual” future scenario (SSP585 for CMIP6, RCP8.5 for CMIP5) through 2100. In all cases, monthly output from the first ensemble member (r1i1p1f1 in CMIP6, r1i1p1 in CMIP5) of each model is adopted, and we maintain the native model resolution prior to averaging or summing variables.

TABLE 2

TABLE 2. Output is used from the following models from phase five of the Coupled Model Intercomparison Project.

2.1 Albedo Partitioning

To correctly simulate the disposition of sunlight incident at the Arctic TOA and predict its evolution in a warming Arctic, models must correctly represent albedo changes due to both changing sea ice cover as well as the modulating effects of the intervening cloud cover. To isolate these effects, we adopt the framework of Donohoe and Battisti (2011) to separate the atmospheric and surface contributions to the planetary, or TOA, albedo. This simplified framework considers each grid cell to have a single layer atmosphere over a reflective surface. The atmosphere is assumed to be isotropic and can absorb and reflect SW radiation. The surface and TOA albedos (α_SFC, α_TOA) can be calculated from upwelling (SW^↑) and downwelling (SW^↓) fluxes at each interface:

$\alpha =\frac{S{W}^{\uparrow }}{S{W}^{\downarrow }}.(1)$

The TOA albedo can be further decomposed into a sum of two parts, one from the atmosphere:

${\alpha }_{TOA,ATM}=\frac{S{W}_{SFC}^{\downarrow }\times S{W}_{SFC}^{\uparrow }-S{W}_{TOA}^{\downarrow }\times S{W}_{TOA}^{\uparrow }}{{(S{W}_{SFC}^{\uparrow })}^2-{(S{W}_{TOA}^{\downarrow })}^2}=R(2)$

and one from the surface:

${\alpha }_{TOA,SFC}={\alpha }_{SFC}\frac{{(1-R-A)}^2}{1-R\times {\alpha }_{SFC}},(3)$

where A is the atmospheric absorption

$A=\frac{S{W}_{TOA}^{\downarrow }-S{W}_{TOA}^{\uparrow }-S{W}_{SFC}^{\downarrow }+S{W}_{SFC}^{\uparrow }}{S{W}_{SFC}^{\uparrow }+S{W}_{TOA}^{\downarrow }}.(4)$

The atmospheric contribution (α_TOA,ATM) to the TOA albedo is equal to the direct reflectance by the atmosphere (R), and the surface contribution (α_TOA,SFC) is the SW radiation reflected by the surface that passes through the atmosphere and exits at the TOA. Interested readers are directed to Donohoe and Battisti (2011) for a more detailed derivation. Together, α_TOA,ATM and α_TOA,SFC provide additional insights into model performance than α_TOA alone since the former is more directly related to clouds while the latter depends on both surface conditions and the intervening atmospheric conditions.

For albedo partitioning in observations, the uncertainty is propagated for each term assuming the errors are independent. For the TOA and surface albedos, fractional errors are calculated for up- and downwelling SW fluxes using annual uncertainties and averages (Kato et al., 2018; Loeb et al., 2018). These fractional uncertainties are added in quadrature to give 0.01 (0.12) for the TOA (surface) albedo. They are multiplied by the monthly values for each albedo. For each of the TOA albedo contributions, the absolute uncertainty, Δα, is calculated using

$\mathrm{\Delta }\alpha =\sqrt{\sum _i{\left(\frac{\partial \alpha }{\partial S{W}_i}*\mathrm{\Delta }S{W}_i\right)}^2},(5)$

where SW_i refers to the four all-sky SW fluxes used in Eqs 2, 3. The partial derivatives are evaluated using annual average values, and the absolute uncertainty is divided by the annual average albedo contribution. The resulting fractional uncertainties are 0.05 for the atmospheric contribution and 0.07 for the surface contribution.

2.2 Accumulated Shortwave

Ultimately, our ability to simulate the ice-albedo feedback and predict changes in Arctic climate depends on how well we can model the amount of solar radiation absorbed in the Arctic and the associated feedbacks. To provide a stationary time-series suitable for assessing the emergence of solar absorption trends, we adopt the accumulated net SW radiation absorbed in the Arctic climate system over the melt season, defined as:

$S{W}_{acc}=\sum _{m=3}^9\sum _{i,j}{(S{W}_{TOA}^{\downarrow }-S{W}_{TOA}^{\uparrow })}_{i,j}\times A_{i,j}\times t_m,(6)$

where A_i,j is the area of grid box i, j and t_m is the seconds in each month m. SW_acc is computed separately using all-sky and clear-sky SW fluxes integrated over the area north of the Arctic circle to assess both the total SW energy absorbed into the Arctic over the year and quantify the influence of clouds.

Quantifying changes in SW_acc provides an important measure of the Arctic climate response to increased greenhouse gas concentrations. Systematic increases in annual SW_acc (relative to an initial equilibrium where incoming solar radiation balances thermal emission and heat transport from lower latitudes) supplies energy for melting additional sea ice and snow or warming the Arctic ocean. As a result, the strength of SW_acc trends are closely linked to both Arctic and global temperature changes. Climate models that produce detectable trends in SW accumulation sooner have been shown to exhibit the largest global temperature responses under multiple shared societal pathways (Sledd and L’Ecuyer, 2021b).

In this study, to bridge the timescales between monthly albedo partitioning and seasonal SW_acc, we further calculate the total SW energy reflected over the melt season by the atmosphere:

$S{W}_{re{f}_{atm}}=\sum _{m=3}^9\sum _{i,j}{\alpha }_{TOA,AT{M}_{i,j}}S{W}_{TOA}^{\downarrow }\times A_{i,j}\times t_m(7)$

and the surface:

$S{W}_{re{f}_{sfc}}=\sum _{m=3}^9\sum _{i,j}{\alpha }_{TOA,SF{C}_{i,j}}S{W}_{TOA}^{\downarrow }\times A_{i,j}\times t_m.(8)$

2.3 Time to Emergence

Beyond the response of SW_acc to warming from increasing greenhouse gas concentrations, there is also considerable natural variability owing to year-to-year variations in cloud cover and sea ice extent. To compare the statistical significance of forced responses between models and evaluate them against the recent observational record, we adopt criteria from Weatherhead et al. (1998) that assesses the time required for trends in SW_acc to exceed its natural variability. A measured trend ($\widehat{\omega }$) must be twice as great as its standard deviation to be considered statistically significant with 95% confidence, or $|\widehat{\omega }/{\sigma }_{\widehat{\omega }}|>2$, where the standard deviation of the trend, ${\sigma }_{\widehat{\omega }}$, is given by:

${\sigma }_{\widehat{\omega }}\approx {\sigma }_N{\left[\frac{12dt}{T^3}\frac{(1+\varphi )}{(1-\varphi )}\right]}^{1/2}.(9)$

In Eq. 9, T is the length of the time series, dt is the time interval (dt = 1 for annual observations), σ_N is the standard deviation, and ϕ is the 1-lag autocorrelation. The number of years needed to measure a statistically significant trend is termed the time to emergence (TTE). This method assumes the detrended anomalies can be modeled as a first order autoregressive (AR(1)) process, although Phojanamongkolkij et al. (2014) showed it can also be used for AR(0) processes. Over the CERES record, autocorrelations in SW_acc are not significant for any number of lags due to the high uncertainty in correlations from so few years of observations. Furthermore, SW_acc appears as white or red noise in CMIP6 models tested over the historical period (Sledd and L’Ecuyer, 2021b).

While the TTE can be calculated for a single time series, internal variability can result in a range of TTE even for the same magnitudes of trend, variance, and autocorrelation (Sledd and L’Ecuyer, 2021b). We therefore follow Chepfer et al. (2018) and use synthetic time series of SW_acc to calculate a mean TTE from observations and models. A synthetic time series is created by adding a linear trend to random noise based on the statistical properties (variance and 1-lag autocorrelation) of the original time series. The synthetic time series is extended out for 150 years, which is long enough for trends to emerge in observations and all models. The mean TTE is found from a synthetic ensemble of 300 synthetic time series from each data source. Creating synthetic ensembles, as opposed to using large ensembles from GCMs, allows us to evaluate more models, as well as to compare observations with the same method. Further details concerning the application of these methods can be found in Sledd and L’Ecuyer (2021b).

3 Results and Discussion

3.1 Mean State Arctic Albedo

The planetary or TOA albedo governs how much solar energy is absorbed in a region after reflection by the surface and atmosphere. The CMIP6 models examined here broadly agree on the seasonal cycles of Arctic mean TOA albedo and the relative magnitudes of its surface and atmospheric contributions (Figure 2). In fact, the ensemble mean TOA albedo (black) tracks CERES-EBAF (red) very closely over the entire melt season with the exception of March when models predict a slightly less reflective Arctic than observed. Despite this agreement in the ensemble mean, there is significant spread between models, upwards of 0.1 difference in July and August. Thus models with the highest albedos reflect 10% more incoming solar radiation than the models with the lowest albedos, which translates to differences of more than 40 Wm⁻² in solar energy input to the region in these summer months. This far exceeds year-to-year variations in TOA albedo that are generally less than 0.01 in both the observations and individual models in all months except June (Figure 2B).

FIGURE 2

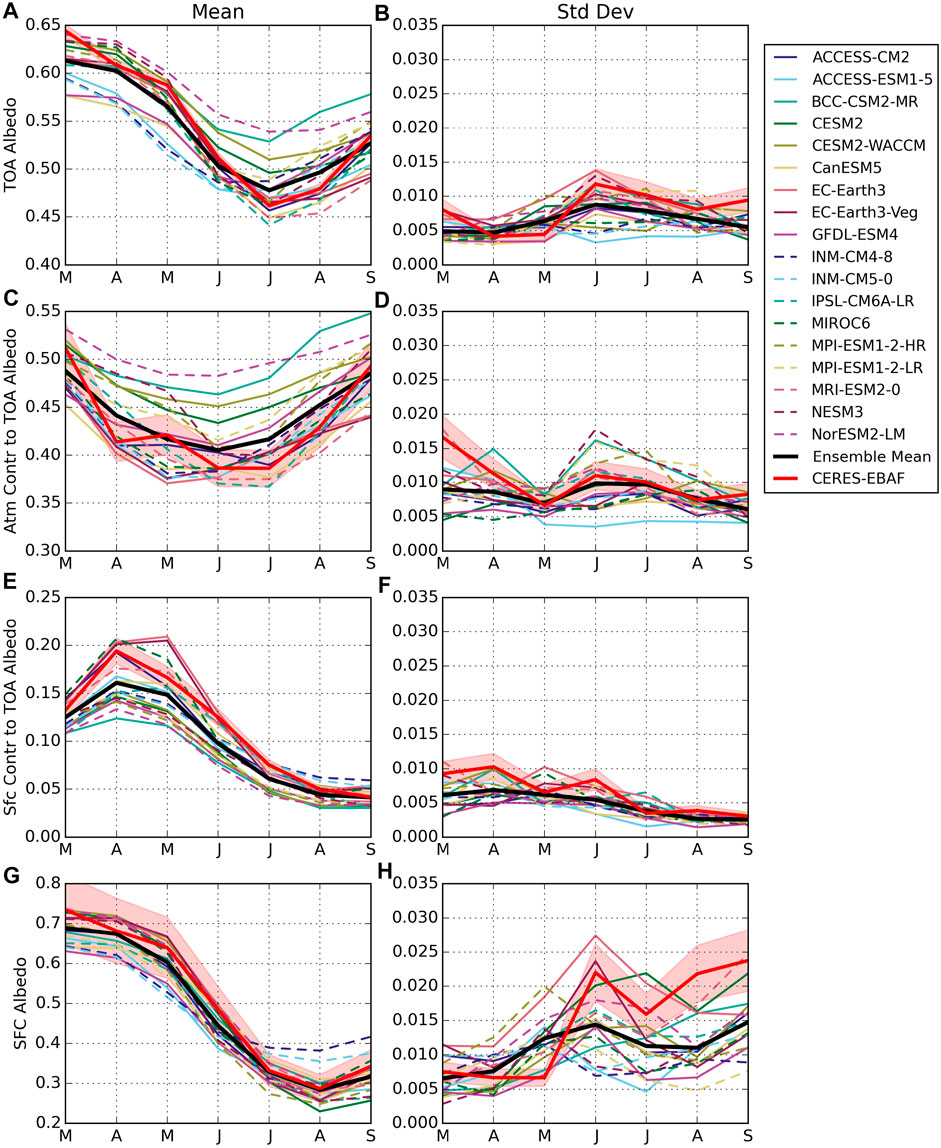
FIGURE 2. Monthly means (left column) and standard deviations (right column) of TOA and surface albedos and TOA albedo partitions in CMIP6 during the melt season, March through September. Values are calculated from historical forcing years 1900–2014 and averaged over the area north of the Arctic Circle. Ensemble means are shown in black, and observations from CERES-EBAF are shown in red. Light red shading represents uncertainty in CERES-EBAF, found by calculating annual fractional errors for each component and multiplying by the monthly values.

Similar conclusions can be drawn for surface albedo. The ensemble mean quite closely follows the CERES observations throughout the melt season, but models exhibit a spread of 0.1 in spring that increases to more than 0.16 in September. However, despite similar model spreads in SFC and TOA albedos, SFC albedo differences are not responsible for the observed range in modeled Arctic TOA albedo. Both the models and CERES observations agree that the surface contributes less than a third of the TOA albedo in the Arctic, and this contribution falls to a narrow range around 10% in late summer. Consistent with previous studies, e.g. (Qu and Hall, 2005; Sledd and L’Ecuyer, 2019), the atmosphere contributes at least twice as much as the surface to the TOA albedo at all times of year. As a result, model spread in the atmospheric contribution dominates the range of TOA albedos as evidenced by the ordering of individual models within the ensemble in Figures 2A,C.

This spread in model representations of present day Arctic albedo has implications for achieving consensus in predicting future changes in Arctic absorption. Figure 3B shows that all CMIP6 models predict that the Arctic will be darker (in other words the Arctic will absorb more solar radiation) by the end of the 21st century, consistent with the ice-albedo feedback. The largest decreases occur in early summer due to lower surface contributions (not shown). These changes occur when incident solar radiation is strong and present-day sea ice extents are relatively large, but the magnitude of these changes, and, by extension, the strength of the ice-albedo feedback, vary by a nearly a factor of 6 between models.

FIGURE 3

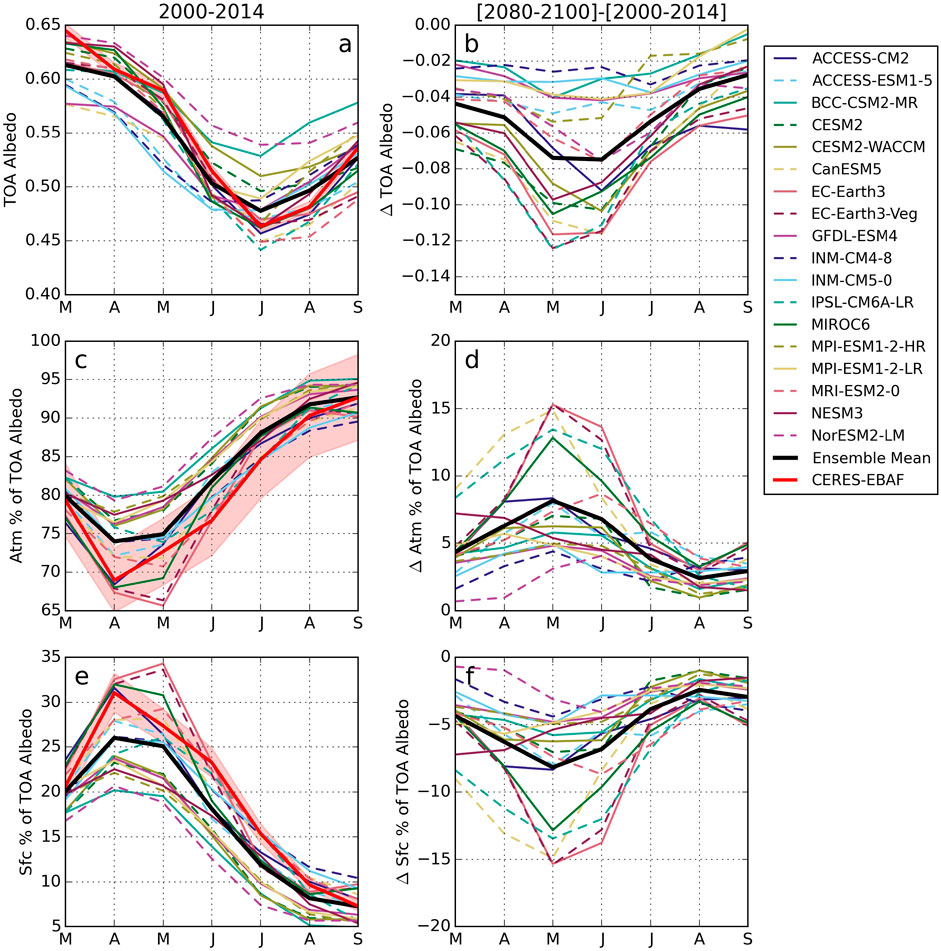
FIGURE 3. Mean TOA albedo (A) and fraction of the TOA albedo contributed by the atmosphere (C) and surface (E) over 2000–2014 in CMIP6 and observations (CERES-EBAF), March through September. Differences between historical and end of century (2080–2100) fractional TOA contributions are shown in (B,D,F), calculated with SSP585. Ensemble means are shown in black. Light red shading represents uncertainty in CERES-EBAF, found by calculating annual fractional errors for each component and multiplying by the monthly values.

To understand the source of this wide range of predictions, Figure 3 also shows the changes in atmospheric and surface contributions to TOA albedo by the end of the century. Note that here the surface and atmosphere contributions are expressed as percents of the TOA albedo as opposed to absolute values in Figure 2 to focus on relative changes. Figure 3C shows that, on average, the atmosphere accounts for 67% of the TOA albedo in late spring and as much as 93% of the TOA albedo by the end of summer based on CERES observations. Many CMIP6 models actually predict even stronger atmospheric contributions than observations. In some models, such as NESM3 and BCC-CSM3-MR, the surface never accounts for more than 20% of the TOA albedo. This may indicate that their atmospheres are too cloudy, their sea ice is too dark or too little, or some combination of these factors. In addition, it is possible model atmospheres absorb too much SW radiation, i.e. their atmospheres are too moist.

CMIP6 models also exhibit a wide range of behaviors that far exceed interannual variations in the CERES observations (less than 3% based on Figure 2D). This is especially true in spring when the models span a range of approximately 15%. Models converge in late summer when the atmosphere contributes most of the TOA albedo. To put the magnitude of this model spread into perspective, Figures 3D,F show how the contributions from the atmosphere and surface change over the 21st century. The surface contribution declines as the Arctic loses sea ice and snow cover and the atmospheric absorption slightly increases (not shown) with a moister Arctic (Nygård et al., 2020). In other words, all models predict that the atmosphere contributes a larger percentage of the TOA albedo at the end of the century. Yet some models predict increases of less than 5% throughout the year while others suggest that increases peak at 15% in May and June. These differences may be connected to the present day mean state in the models since models with larger surface contributions today (e.g. EC-Earth3, solid rose line) tend to predict the largest changes with increased greenhouse gas concentrations. However, given the important role that the atmosphere plays in defining the net radiation absorbed at TOA, differences in the distribution of water vapor and clouds and, especially, how they may change in the future, likely contribute to the spread in model predictions as well, e.g. Alkama et al. (2020). Once again, models converge in late summer since the surface contributes so little in the present day that there is little room for further decline.

3.2 The Radiative Impact of Sea Ice Changes

While the atmosphere always contributes more than the surface to TOA albedo, Figure 2 shows that surface albedo plays a significant role in determining the shape of the annual cycle of Arctic albedo. Higher albedos associated with widespread sea ice in spring lead to the highest TOA albedos across the Arctic, and melting sea ice in mid-summer coincides with the lowest TOA albedos. Only in late summer, when sea ice reaches a minimum, do we observe an apparent decoupling of TOA and SFC albedo where the Arctic becomes more reflective as a whole in August and September despite having its darkest surface. This demonstrates very clearly that the Arctic albedo is sensitive to sea ice cover but that this sensitivity is modulated by the cloudy atmosphere. As a result, the amplitude of the annual cycle of observed SFC albedo in Figure 2, defined as the difference between the maximum and minimum value over the months examined, is about 2.5 times larger than that at the TOA.

However, this ratio of surface to TOA annual cycle amplitudes is far from constant across CMIP6 models. The amplitude of the annual cycle of SFC albedo in EC-EARTH3 (solid rose line in Figure 2), for example, is 2.7 times larger than at the TOA, similar to observations. On the other hand, the amplitude of the SFC albedo annual cycle in BCC-CSM2-MR (solid light green line in Figure 2) is 4.2 times larger than that at the TOA. This is consistent with the fact that the Beijing Climate Center model exhibits larger than average atmospheric contributions to TOA albedo, suggesting that its clouds are more effective at masking surface albedo changes.

These inter-model differences in the extent to which surface albedo changes are realized at the TOA indicate that Arctic solar absorption responds differently to the annual cycle of sea ice extent across the CMIP6 models. To test whether these distinct responses extend to inter-annual variations in sea ice extent, Figure 4A summarizes how TOA and SFC albedos correlate to SIA. There is broad consensus across CMIP6 that the surface albedo is highly correlated with SIA over the historical period from 1900–2014. In June (yellow markers) correlations are all greater than 0.7, and in August and September (blue and black) correlations are above 0.9 for all models. This agreement makes physical sense as reduced areas of brighter sea ice reveal more dark open ocean.

FIGURE 4

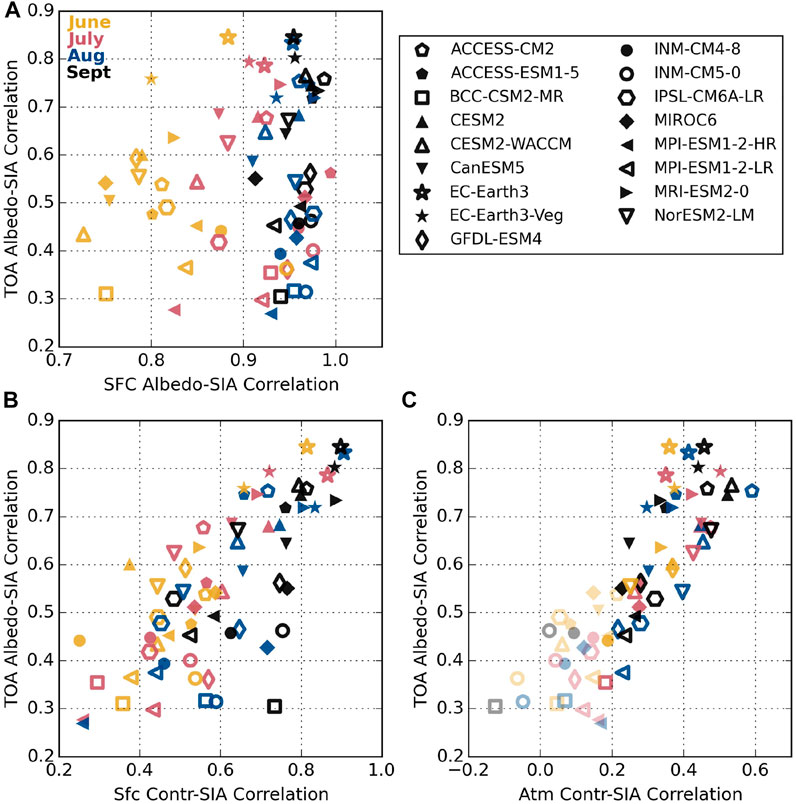
FIGURE 4. Correlations between albedos and SIA as they relate to each other during summer months. Correlation coefficients are calculated over the historical period, 1900–2014, using detrended anomalies. Correlation coefficients that are considered statistically significant using a t-test with 95% significance level and effective sample sizes that take into autocorrelation have opaque markers; statistically insignificant correlations are semi-transparent.

This close agreement between models breaks down when considering TOA albedo, though. Correlations between the TOA albedo and SIA plotted on the y-axis in Figure 4A range from less than 0.3 to more than 0.8 in all 4 months. This spread means that, in some models the TOA albedo is strongly linked to the surface and sea ice (e.g. EC-Earth3, EC-Earth3-Veg, MRI-ESM2-0), while in other models the response is relatively weak (e.g. BCC-CSM2-MR, MPI-ESM1-2-HR, MPI-ESM1-2-LR), i.e. what happens at the surface stays at the surface.

Figures 4B,C show that, like the annual cycle, the extent to which changes in TOA albedo are correlated with longer-term sea ice declines is related to the atmospheric influence. Like TOA albedo, correlations between both surface and atmospheric contributions to TOA albedo and SIA vary widely across the CMIP6 models. Correlations between surface contribution and SIA range from about 0.2 to 0.9 while atmospheric contribution correlations range from −0.1 to 0.6, although correlations with magnitudes below approximately 0.2 are not statistically significant at the 95% confidence level (represented as semi-transparent markers in Figure 4C, determined using an effective sample size that takes into account autocorrelation present in each time series). While models with the largest correlations between TOA albedo and SIA tend to also exhibit strong correlations between surface contributions and SIA, the SFC contribution is not the main driver, as indicated by the substantial spread below 0.7 in Figure 4B. Notice, for example, that in September BCC-CSM2-MR (black hexagon) shows a strong correlation between the surface contribution and SIA (0.7) but that it has one of the lowest TOA albedo-SIA correlations in the ensemble (0.3). A strong correlation between the atmospheric contribution and SIA is required for TOA albedo to be highly correlated with SIA. This reflects the fact that the atmosphere contributes a large percentage of the TOA albedo, so the disparate model behaviors may have significant implications for their responses to systematic declines in sea ice cover associated with Arctic warming.

This is confirmed in Figure 5 that shows the sensitivity of TOA and surface albedo to a 1 million square kilometer change in sea ice area, found by regressing albedos against SIA for the months of June and September. Results are presented for both the historic period 1900–2014 (left column) and the shorter modern period from 2000–2014 (right column) to allow comparison with CERES-EBAF. The corresponding ensemble means are given in Table 3. Using the longer historical time period allows for more robust statistics compared to only the years that overlap with CERES-EBAF, although it does assume that the response of albedos to SIA changes do not deviate too much in the latter time period. As expected, the surface albedo (indicated by the more transparent shading) is more sensitive to changes in SIA than the TOA albedo in all months, consistent with observations (Sledd and L’Ecuyer, 2019). Surface albedo sensitivities also tend to be better constrained between models, particularly in September when a 10⁶ km⁻² reduction in sea ice area decreases surface albedo by 0.03–0.04 in a majority of models in both epochs. This is consistent with the 0.04 sensitivity derived from CERES-EBAF observations from 2000–2014. Larger inter-model differences in June surface albedo responses, especially in the recent 2000–2014 period, are likely caused by differences in sea ice albedo (Davy and Outten, 2020).

TABLE 3

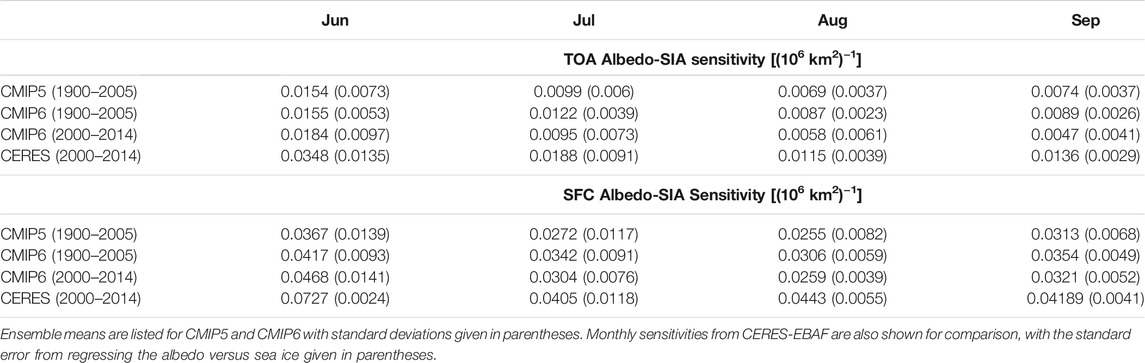
TABLE 3. Monthly TOA and surface (SFC) albedo sensitivities to sea ice area in June through September.

FIGURE 5

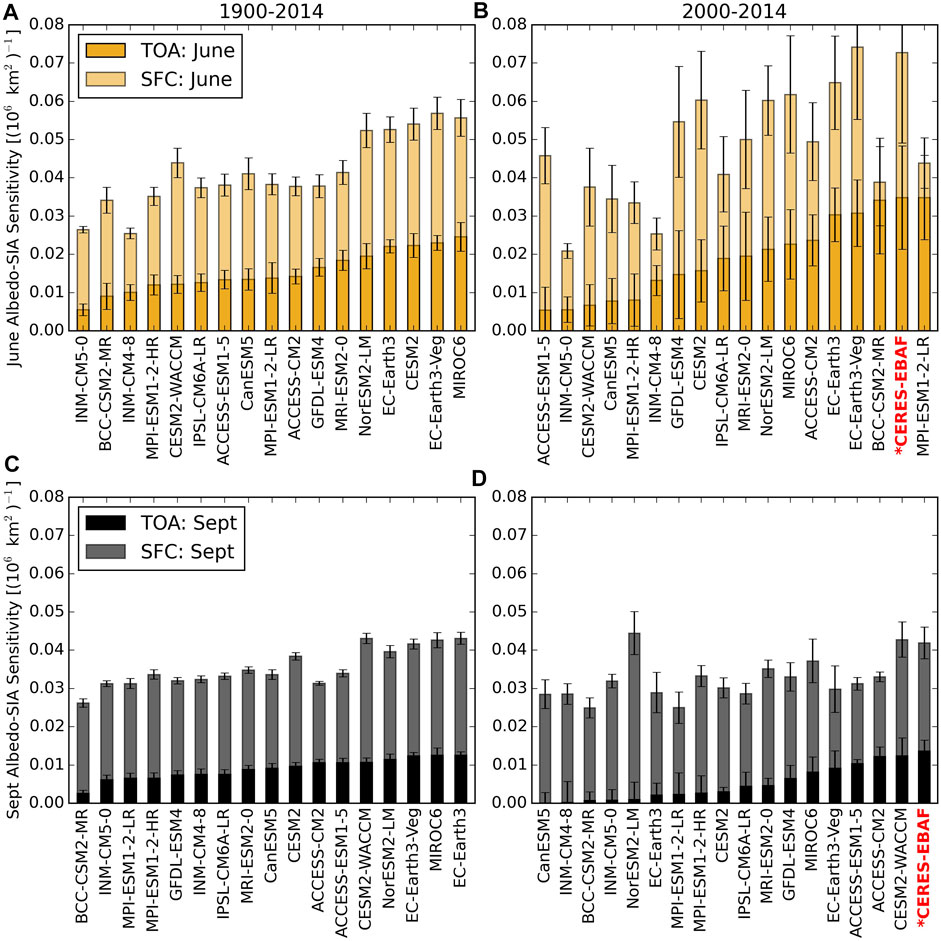
FIGURE 5. Sensitivity of TOA and surface albedos to sea ice area (SIA) in June (A,B) and September (C,D). Sensitivity is found from the regression of each albedo against SIA for a given month across the historical time period, 1900–2014 (A,C) and the overlap with the CERES observational record, 2000–2014 (B,D). Models are sorted from lowest (left) to highest (right) TOA sensitivity to SIA. Error bars represent the standard error of the estimated gradient for each sensitivity.

Recall, though, that Arctic energy balance and warming are primarily governed by the TOA albedo that determines how much solar radiation is absorbed in the region. The magnitude of the TOA response to SIA changes is much more variable across CMIP6 models in both June and September in both epochs. For example, MIROC6 is about five times more sensitive to sea ice changes than INM-CM5-0 in June over the historical 1900–2014 period with sensitivities of 2.5 and 0.5 %/10⁶ km², respectively. Assuming an average incident SW radiation at the TOA of 500 Wm⁻² (typical of the Arctic in June), a 1 million km² loss of sea ice, would result in an average of (Δ SW_absorbed=−Δα_TOA×SW ↓) 12.5 Wm⁻² more solar absorption in MIROC6 but only 2.5 Wm⁻² in INM-CM5-0. For context, this difference of 10 Wm⁻² is more than double the anticipated global mean radiative forcing from doubling current carbon dioxide concentrations (Etminan et al., 2016).

In most models, the TOA albedo is about half as sensitive to SIA in September as in June over the historical period, a direct consequence of the increased atmospheric contributions in fall compared to summer. Furthermore, changes in albedo exert a smaller influence on Arctic absorbed SW radiation in September due to the lower mean incident solar radiation. Never-the-less, September TOA albedo sensitivity to SIA over the last century varies by about a factor of 5 across CMIP6 models bracketed by BCC-CSM2-MR (0.25) and EC-Earth3 (1.25). While the precise ordering of models from lowest to highest TOA albedo sensitivity in Figure 5 varies somewhat from June to September, models with higher sensitivities in June tend to also have higher sensitivities to SIA in September.

Sensitivities calculated over the modern Arctic (2000–2014), characterized by more seasonal ice coverage, exhibit signatures consistent with this change in base state relative to the last century (Figures 5B,D). In most models, the TOA albedo in June is at least as sensitive to sea ice changes in the modern epoch compared to during the longer historical period. This is clearly evident in Figure 6 where TOA albedo sensitivity to SIA in the modern Arctic is plotted against that in the historical period for all CMIP6 models. While a few models show decreased sensitivity in June (e.g. ACCESS-ESM1-5, CESM2, and CanESM5), other models exhibit much larger increases (e.g. BCC-CSM2-MR and MIP-ESM1-2-LR). The latter models have TOA albedos that are at least three times as sensitive to SIA changes over 2000–2014 as compared to 1900–2000, which may suggest their climates are already changing significantly. A more robust but opposite trend is evident in September where the TOA albedo is less sensitive to SIA across all CMIP6 models in the modern epoch compared to the last century. In extreme cases (e.g. CanESM3, NorESM-2-LM, and EC-Earth3), the TOA albedo in September has almost no sensitivity to changing SIA in today’s climate while it varied by more than 1% per 10⁶ km⁻¹ over the past century. This is a consequence of the diminished September SIA in recent years that has increased the atmospheric contribution to TOA albedo even relative to last century (not shown but analogous to Figure 3D).

FIGURE 6

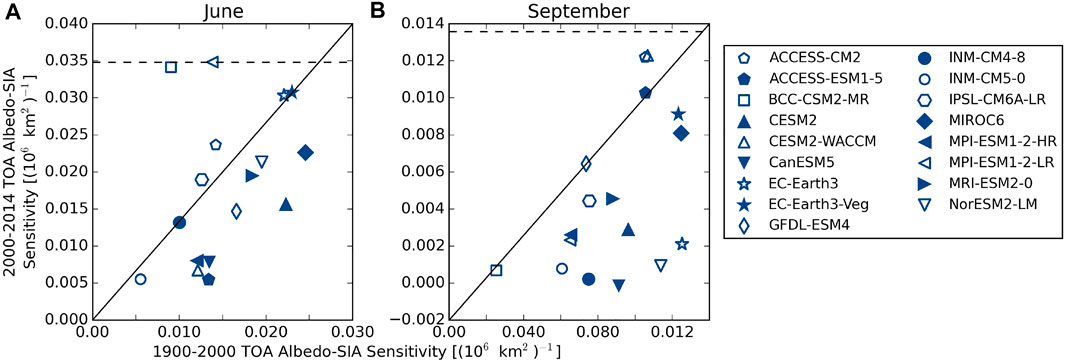
FIGURE 6. Sensitivity of TOA albedo to SIA in CMIP6 calculated over 1900–2005 compared to 2000–2014 for June (A) and September (B). Sensitivity from CERES over 2000–2014 is plotted as the horizontal line for reference.

While the modern period from 2000–2014 has fewer years and, therefore, less robust statistics than the full historical 1900–2014 record, it provides a snapshot of the modern Arctic that overlaps the observational record provided by CERES-EBAF. Furthermore, unlike the trends shown in Supplementary Figures S1, S2, the regressions shown in Figure 5 are less sensitive to internal model variability since they do not depend on the time-evolution of the modeled climate but rather the statistical relationship between two quantities: TOA albedo and SIA. The computed regressions do not depend on the specific model years that exhibit higher or lower SIA nor the actual magnitude of the SIA changes and are, therefore, less dependent on the specific trajectory of the model. Never-the-less, these relationships do depend on the mean state of the system as noted above, so some additional scatter among models should be expected relative to the longer historical period.

CERES-EBAF observations confirm that the TOA albedo sensitivity to SIA is more than two and a half times larger in June than in September. However, the observed sensitivities are larger than those in almost all of the CMIP6 in both months suggesting that Arctic solar absorption is more sensitive to changes in SIA than models predict. While internal variability likely plays a role in model behavior over this shorter period, it is not clear how it could result in all models underestimating Arctic albedo sensitivity to changes in sea ice cover. It may, instead, point to a more systematic bias in the way clouds covary with sea ice in models compared to observations, but identifying such biases would require more detailed analysis beyond that presented here.

3.3 Comparison with CMIP5

These comparisons against CERES-EBAF reveal some basic characteristics about the representation of absorbed solar radiation in the Arctic. The CMIP6 ensemble captures the observed mean annual cycle of TOA and surface albedo very well and generally simulates the observed partitioning of TOA albedo into its surface and atmospheric contributions. And yet, inter-model spread in TOA albedo, which governs the net energy input into the Arctic, is large owing primarily to substantial disagreement in the contributions from the atmosphere (i.e. clouds). This has significant implications for reconciling predicted increases in Arctic absorbed solar radiation owing to ice-albedo feedbacks over the next century, and CMIP6 models tend to systematically underestimate the sensitivity of TOA albedo to changing sea ice cover.

To put this snapshot of climate model behavior into the broader context of model development, the mean state and sensitivity of Arctic albedo to SIA in CMIP6 are compared against the preceding generation of models, CMIP5, in Figures 7, 8. Since there are only 5 years over overlap between CERES observations and historical forcing from CMIP5, observations are omitted from these comparisons.

FIGURE 7

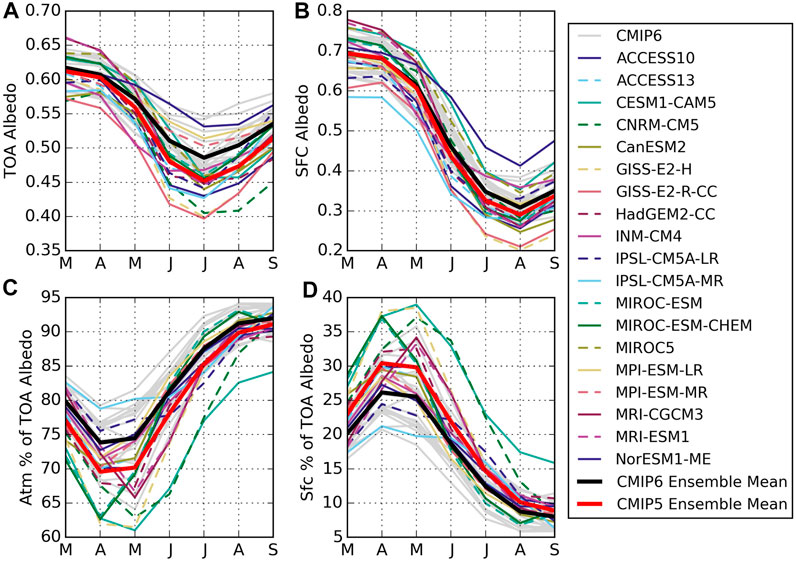
FIGURE 7. Annual cycles of TOA and surface (SFC) albedos (A,B) and percent contributions of the atmosphere (C) and surface (D) to the TOA albedo from CMIP5 (color lines) and CMIP6 (grey). Averages are calculated over 1986–2005. Ensemble means are shown in black for CMIP6 and red for CMIP5.

FIGURE 8

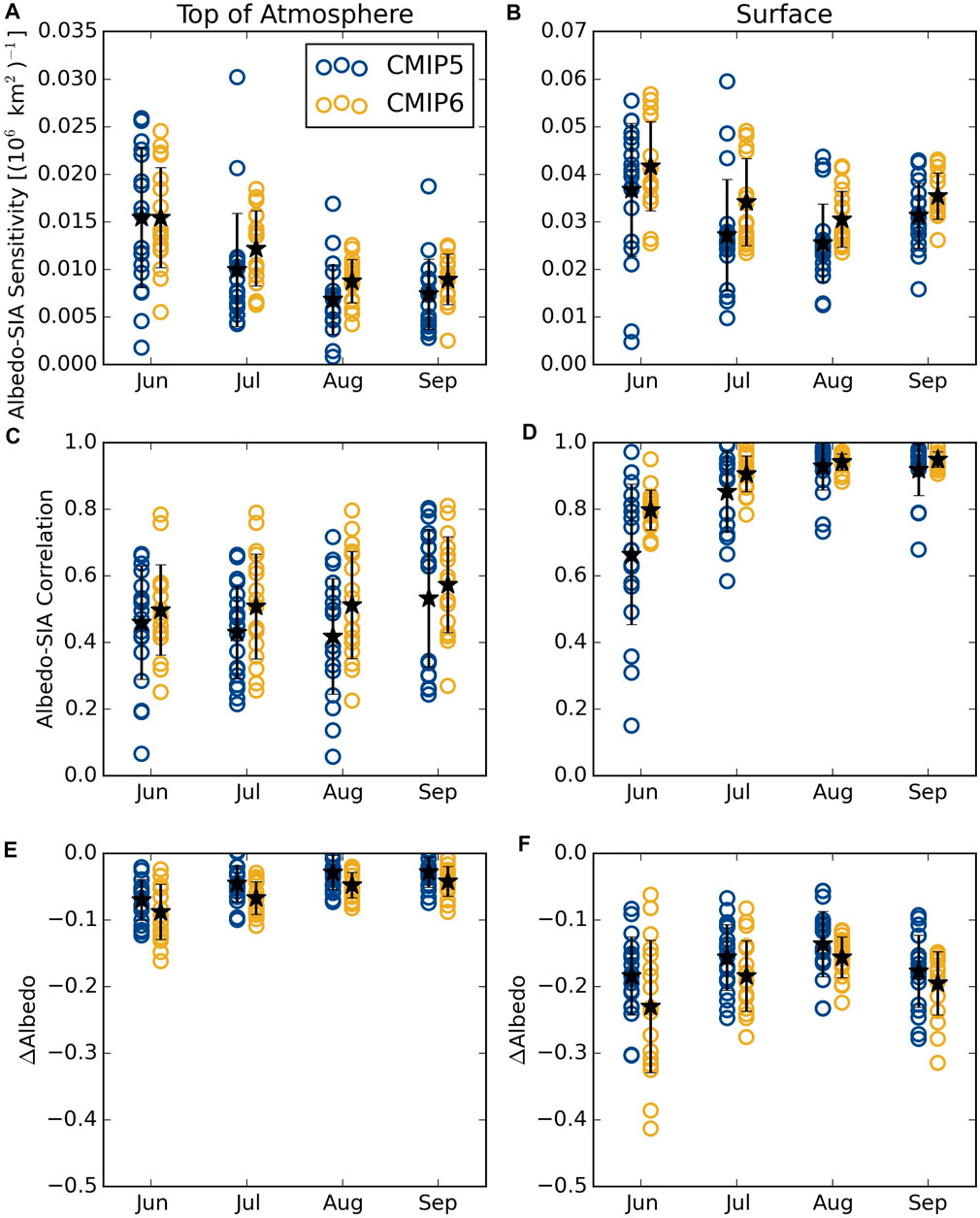
FIGURE 8. Comparison of albedo-SIA sensitivities (A,B) and correlations (C,D) at the top of the atmosphere (A,C) and surface (B,D). Values are calculated over 1900–2005 from CMIP5 and CMIP6. Changes over the 21st century ([2080–2100] minus [1900–2005]) are also shown for the TOA albedo (E) and surface albedo (F). Ensemble means are shown as stars for each month.

Annual cycles of albedos from 1986–2005 are presented in Figure 7. Note that this period has slightly larger TOA and surface albedos and marginally higher (lower) surface (atmospheric) contributions in CMIP6 relative to 2000–2014 (Figure 2) because sea ice concentrations were somewhat larger at the end of the 20^th century. The spread of albedos has narrowed between CMIP5 and CMIP6 and the Arctic is somewhat brighter in the summer months (June-August) in the latest generation of models. Although the ensemble means are very similar, CMIP5 had a notably larger spread in surface albedos over the melt season (e.g. Koenigk et al., 2014), fully encompassing the current CMIP6 ensemble (Figure 7B). The reduced spread in CMIP6 surface albedo is consistent with efforts to more closely align Arctic sea ice extents to observations (Shu et al., 2020). The actual spread in sea ice albedo is larger than that shown since averaging over the Arctic includes dark open ocean areas. The lowest average surface albedos are from the GISS models that have documented low sea ice albedos due to excessive melt pond formation (Schmidt et al., 2014). NorESM1-ME has the highest average surface albedos in summer, likely because of its high sea ice albedo (Koenigk et al., 2014).

CMIP5 models also show a larger spread in monthly TOA albedos (15% versus 10%), particularly after May. As in CMIP6, this spread is more closely linked to differences in atmospheric contributions than surface behavior, which follows the diverging representations of Arctic clouds in CMIP5 (Cesana and Chepfer, 2012). For example, although NorESM1-ME shows average summer surface albedos larger than the CMIP6 ensemble, its average TOA albedos during summer are within the CMIP6 spread since its surface contributes relatively little to the TOA albedo and its atmospheric albedo aligns well with the ensemble average, likely due to higher cloud fractions and LWP as compared to observations (Seland et al., 2020).

Overall, CMIP5 models exhibit lower atmospheric contributions to TOA albedo compared to CMIP6, both in terms of raw values (not shown) and percent contributions (Figure 7C). This larger atmospheric contribution to TOA albedo in CMIP6 is responsible for the brighter Arctic in the latest generation of models. This is consistent with increased total cloud fractions in CMIP6 compared to CMIP5 and improvements in the representation of super-cooled liquid containing clouds (Wu et al., 2019; McIlhattan et al., 2020). Such changes may stem from an increased focus on improving polar cloud parameterizations by the modeling community in recent years (Seland et al., 2020; Vignesh et al., 2020; Wei et al., 2021). This effort may also have helped to narrow the model spread in atmospheric contributions to TOA albedo between CMIP5 and CMIP6. There is about a 15% range in the percentage of TOA albedo contributed by the atmosphere across CMIP5 models in all months. Conversely, while CMIP6 exhibits similar spreads in spring, their atmospheric contributions agree to within about 5% in September, a sign that simulated late-season sea ice and cloud cover has converged in the latest generation of climate models.

There may be evidence of another significant impact of changes to Arctic cloud parameterizations in the latest generation of climate models evident in Figure 8 that compares TOA and surface albedo sensitivities to SIA changes in CMIP5 and CMIP6. Here the period 1900–2005 is adopted to ensure overlap between model generations, but omitting the last decade has a minimal impact on the magnitudes of these values in CMIP6. The corresponding mean all-sky and clear-sky TTE are given in Tables 4 and 5 for CMIP5 and CMIP6, respectively. Although the relative contributions of the atmosphere and surface to the TOA albedo shift between CMIP5 to CMIP6, there is less change in the response of surface and TOA albedos to SIA between CMIP generations. More surprising, however, is that there has been a modest shift toward stronger TOA albedo sensitivity to (and higher correlations with) SIA in CMIP6 even though the surface contributes less to TOA albedo in CMIP6 than in CMIP5. This suggests that the atmospheric albedo itself (i.e. cloud cover) may respond more strongly to sea ice changes in CMIP6 hinting that Arctic cloud feedbacks may be stronger in the current generation of climate models (Zelinka et al., 2020; Sledd and L’Ecuyer, 2021b).

TABLE 4

TABLE 4. Mean TTE in years for all-sky and clear-sky SW_acc trends from CMIP6 models.

TABLE 5

TABLE 5. Mean TTE in years for all-sky and clear-sky SW_acc trends from CMIP5 models.

Figure 8 also shows that the spread in SIA sensitivity has improved relative to CMIP5. In fact, the inter-model range of both sensitivities to SIA and correlations with SIA are smaller in the latest generation of climate models. This is consistent with reduced uncertainty in sea ice albedo feedback from CMIP5 to CMIP6 (Zelinka et al., 2020). Never-the-less, CMIP6 albedos continue to exhibit a wide range of sensitivities to SIA that have significant implications for predicted changes in absorbed SW radiation and, ultimately, the evolution of Arctic climate. This is evident in the wide range of predicted decreases in Arctic TOA and surface albedos shown in Figures 8E,F that highlight the compounding effects of model differences in both the mean state solar absorption and its sensitivity to sea ice changes. The surprisingly large spread in predicted changes in surface albedo by the end of the century, especially in June, reflects the impacts of large discrepancies in absorbed solar radiation amplified by the myriad of associated feedbacks on SIA at the end of the century (Hahn et al., 2021). CMIP6 models also predict larger increases in overall Arctic solar absorption (lower albedos) by the end of the century than their CMIP5 counterparts, but the spread between individual models has also increased.

3.4 Implications for Solar Absorption Trends

Given the reduced spread in TOA and surface albedo sensitivities to SIA in CMIP6 relative to CMIP5, the increased uncertainty in 21^st century predictions is somewhat surprising. This, together with the shift toward greater atmospheric contributions to TOA albedo in CMIP6, suggests that the diverging predictions of future Arctic albedo may stem from differing cloud responses to changing SIA in the latest generation of some models (Hahn et al., 2021).

The increased role of the atmosphere in defining future Arctic albedo has significant implications for the time to emergence of trends in models. Sledd and L’Ecuyer (2021a) recently showed that clouds have delayed the emergence of trends in observed Arctic SW absorption by about 5 years relative to clear-sky conditions by reducing the magnitude of accumulated shortwave radiation (SW_acc) trends. A similar analysis applied to CMIP6 models, however, shows a more varied picture possibly related to cloud cover feedbacks that amplify the impacts of surface albedo changes.

Figure 9 examines the connection between the TTE of SW_acc trends and SIA responses explicitly and documents an apparent divergence of model behavior from CMIP5 to CMIP6. The y-axis on all plots shows the ratio of the TTE of clear-sky SW_acc trends to those in all-sky conditions. For reference, CERES observations since 2000 predict a ratio of 0.8. The choice of September SIA regressions on the x-axis is motivated by the fact that it represents the integrated effects of the melt season. Recall that SW_acc represents the net input of SW energy at the TOA into the Arctic system over the melt season, March through September. SIA reaches its minimum in September, the result of energy exchanged throughout the preceding melt season, including SW, so it is not unreasonable for there to be a connection across these different time scales.

FIGURE 9

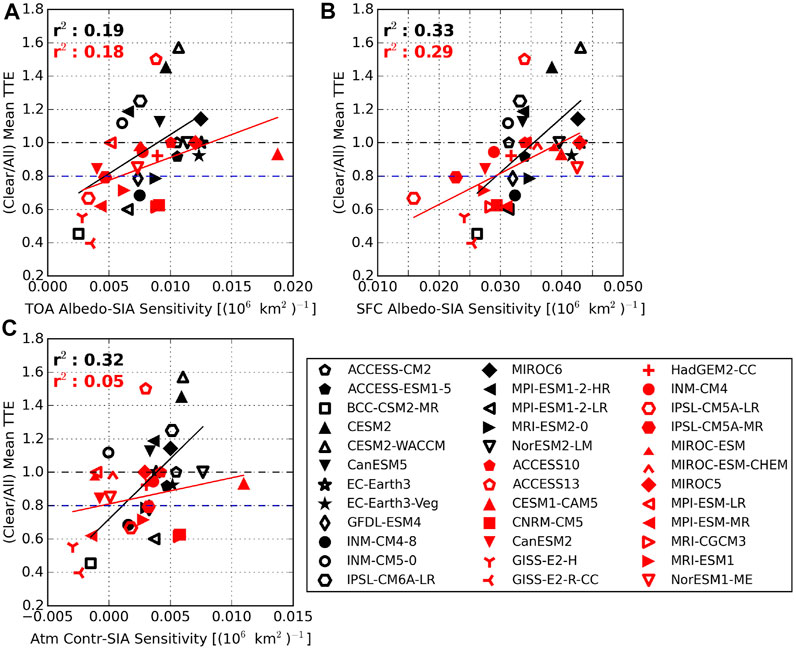
FIGURE 9. Relationships between the ratio of all-sky to clear-sky SW_acc TTE and the sensitivity of (A) TOA albedo, (B) surface albedo, and (C) the atmospheric contribution to September SIA. Results calculated from CMIP6 SSP585 are shown in black or while those from CMIP5 RCP8.5 are in red. Wherever possible, similar symbols have been adopted for models from the same center. TTE ratio from CERES (0.8) is shown as the blue dashed horizontal line for reference.

While it is challenging to compare observed TTE to those from the different CMIP5 and CMIP6 emissions pathways directly, the clear to all-sky ratio isolates the role of clouds in modifying TTE, a physical characteristic we may expect to be less sensitive to subtle differences in climate trajectories. This is confirmed by the fact that the TTE ratio is very consistent between SSP245 and SSP585 (Sledd and L’Ecuyer, 2021b). Two striking results are immediately evident in Figure 9: 1) while all but one of the CMIP5 models agree with observations that clear-sky trends emerge more quickly than all-sky trends (ratios $<$ 1), CMIP6 models are equally divided in whether clouds accelerate or delay the emergence of trends; and 2) the TTE ratio is correlated with the sensitivity of the atmospheric contribution to SIA in CMIP6 while no such correlation existed in CMIP5 (Figure 9C).

These findings are likely related. In CMIP6 models where the atmospheric contribution shows little response to September SIA, the all-sky SW_acc trend takes relatively longer to emerge than the clear-sky SW_acc trend. These are the models where clouds presumably exhibit little change with SIA and the primary role of constant cloud cover is to mask surface changes, slowing the emergence of trends in solar absorption. CMIP5 models, on the other hand, exhibit no statistically significant relationship between TTE ratio and atmospheric contribution response to SIA, and all but one outlier reproduce the observed cloud delaying of TTE (although some models show ratios very near 1).

While Figure 9 does not examine cloud feedbacks directly, it suggests that, in some CMIP6 models, increases in atmospheric contributions to TOA albedo in response to sea ice loss may enhance trends in SW_acc more than in CMIP5. For example, the Community Earth System Model (CESM) has undergone a significant shift from CESM1 (▲) where clouds slowed the emergence of SW_acc trends to CESM2 (▲) where clouds accelerate these trends by nearly 50%. Such a strong shift could be due to changes in cloud parameterizations that can have a dramatic influence on surface radiative balance, e.g. Huang et al. (2021). In Figure 10, the integrated solar radiation reflected by the atmosphere over the melt season, ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ (Eq. 7), has increased by nearly 30% between CESM1 and CESM2, consistent with McIlhattan et al. (2020) who showed that increased cloud cover and cloud liquid water path in summer led to decreased downwelling SW at the surface in CESM2 as compared to CESM1. The more SW energy the atmosphere reflects compared to the surface, the greater the impact clouds have on the Arctic mean SW_acc. This is true across all models in both CMIP generations (Figure 10B). In the case of CESM, brighter clouds in CESM2 reduce absorbed SW radiation across the Arctic by 33%, more than double their effect in CESM1 (16%). More generally, the population of CMIP6 models has shifted toward brighter atmospheres that suppress more SW_acc relative to clear skies than the population of CMIP5 models.

FIGURE 10

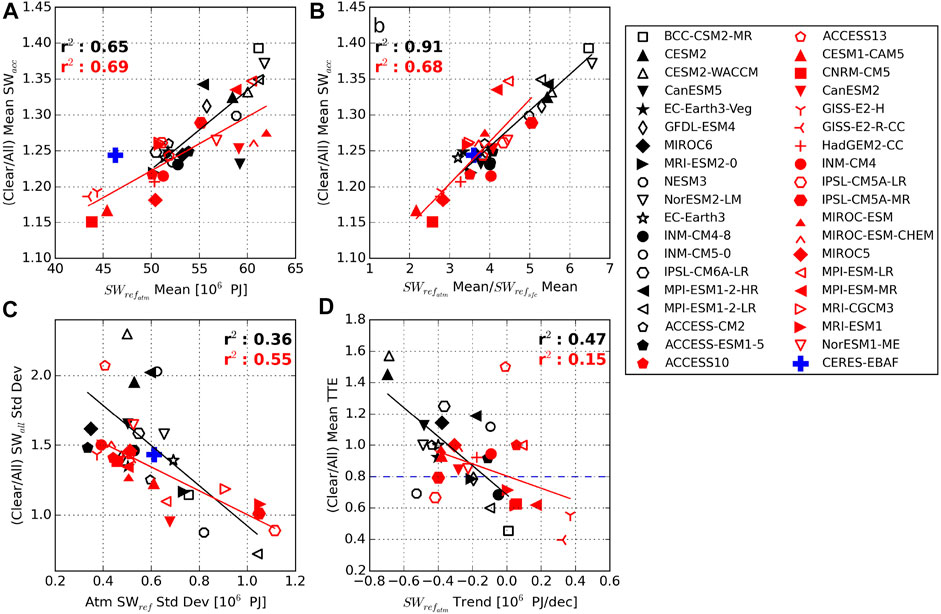
FIGURE 10. Total SW reflected due to the atmosphere ($S{W}_{re{f}_{atm}}$) as it relates to accumulated SW (SW_acc) ratios of all-sky to clear-sky for (A) means, (B) standard deviations, and (C) trends and time to emergence (TTE). Means and standard deviations are calculated over 2000–2014, and trends and SW_acc TTE are calculated using SSP585 over 2000–2100 for CMIP6 (black) and RCP8.5 for CMIP5 (red). CERES observations are shown for values calculated over 2000–2014. Wherever possible, similar symbols have been adopted for models from the same center.

The standard deviation of ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ influences whether internal variability in cloud reflection increases or decreases SW_acc variability across models. This is notable because the relative “noisiness” of all-sky versus clear-sky SW_acc is a determining factor in whether clouds increase or decrease SW_acc TTE. If clouds increase SW_acc variability, they can increase TTE because it takes longer for a trend to emerge from a noisier timeseries, and vice versa. ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ standard deviations vary by almost a factor of three across CMIP6 models in Figure 10C. Models with the greatest ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ standard deviations (MPI-ESM1-2-LR and NESM3) are the only models where clouds increase the variability of SW_acc. In models where the atmospheric reflectivity is less variable, clouds decrease SW_acc variability (ratio $>$ 1) potentially reducing time to emergence relative to clear skies. In CESM2, for example, clouds decrease the standard deviation of SW_acc by nearly a factor of two while they had a minimal impact in CESM1. This may explain the shift in CESM from clouds delaying the emergence of SW_acc trends in CESM1 (consistent with observations) to accelerating it in CESM2. In observations, clouds only slightly decrease SW_acc variability when averaged over the full Arctic, although the regional impact of clouds on SW_acc depends on the underlying surface (Sledd and L’Ecuyer, 2021a). Model biases could, therefore, stem directly from their representations of clouds or from covariability with the underlying distribution of sea ice and snow cover.

Since variability in ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ influences the noise in the ratio of clear-sky to all-sky SW_acc time-series, one might anticipate that trends in ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ may also influence the ratio of clear-sky to all-sky TTE. If cloud feedbacks are involved in accelerating the TTE of SIA trends, i.e. if cloud cover becomes less reflective as SIA decreases, we would anticipate a negative relationship between TTE ratio and trends in ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$. Figure 10D suggests that the clear-sky to all-sky TTE ratio is more strongly inversely related to the ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ trend over the 21^st century in CMIP6 than CMIP5. Some inverse relationship is expected since Eq. 2 shows that the atmospheric contribution depends on multiple reflections from the surface. A lower surface albedo will generate less upwelling SW from the surface and consequently reduce SW reflection by the atmosphere to space over the melt season in spite of the fact that the atmospheric contribution to TOA albedo increases. However, the inverse relationship between between TTE ratio and ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ trend is much weaker in CMIP5 models, lending further evidence that cloud feedbacks may be responsible for the increased ambiguity in SW_acc trends in CMIP6.

All CMIP6 models agree that the melt-season integrated SW reflected by the atmosphere decreases in the future, but the magnitude of that decline ranges from near zero (BCC-CSM2-MR, □) to about −0.7×10⁶ PJ/decade (CESM2-CAM5 and CESM2-WACCM, ▲ and △). Like the shift toward brighter present-day atmospheres, there is a systematic shift toward larger dimming trends in CMIP6 compared to CMIP5. Sledd and L’Ecuyer (2021b) attributed ambiguity in TTE ratios to cloud fraction (CF) trends. These results support that hypothesis by showing that models where clouds enhance TTE of SW_acc trends exhibit larger declines in ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$. For example, the two versions of CESM2 predict the largest 21^st century declines in ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ and have the highest TTE ratios of all CMIP6 models while CESM1 predicted less than half the decline in ${\mathrm{S}\mathrm{W}}_{re{f}_{atm}}$ and a TTE ratio of 0.9. This analysis, however, only provides a broad comparison of the characteristics of absorbed SW radiation in the CMIP6 models and documents changes relative to CMIP5. Tracing the specific causes of the wide range of atmospheric influences on Arctic absorbed shortwave radiation in CMIP6 models will require comprehensive analysis of cloud fraction, opacity, phase, and other characteristics that is beyond the current scope of this work.

4 Conclusion

An accelerated rate of Arctic warming relative to the globe has been a robust feature of observed and modeled anthropogenic climate change for many years (Serreze et al., 2009; Screen and Simmonds, 2010a). While numerous processes and feedbacks are ultimately responsible for the overall Arctic temperature response to anthropogenic forcings (Pithan and Mauritsen, 2014; Goosse et al., 2018; Hahn et al., 2021), this study examines the factors that modulate solar absorption, a direct consequence of ice-albedo feedback that can be probed using modern satellite data records. We use a simple framework to quantify the sensitivity of planetary or TOA albedo to changing sea ice cover and establish the relative roles of the atmosphere (clouds) and surface in defining this response in the last two generations of climate models in the context of satellite-derived solar reflection and sea ice cover estimates. While the framework used is not intended as a predictive model, it provides a means for collapsing the atmospheric influence on planetary albedo into a single number that is entirely defined using fluxes at the TOA and surface boundaries, allowing models and observations to be compared. The growing satellite record is further used to statistically assess the emergence of trends in Arctic absorbed radiation over the summer season, providing a measure of when the radiative impacts of ice-albedo feedbacks have exceeded internal variability.

Multiple parameters characterizing the influence of sea ice changes on Arctic solar absorption suggest that CMIP6 models have converged to a more accurate representation of present day Arctic albedo and its sensitivity to sea ice cover than their predecessors in CMIP5, which had known biases in terms of clouds and SW fluxes (e.g. Karlsson and Svensson (2013); Taylor et al. (2019)). Ensemble mean TOA and surface albedos agree more closely with CERES-EBAF, and inter-model spreads have reduced in the latest generation of climate models. As a whole, CMIP6 models simulate a brighter present-day Arctic than CMIP5 and predict stronger responses to declining sea ice cover in better agreement with observations. However, observed Arctic solar absorption remains more sensitive to changes in SIA in the modern era of seasonal sea ice cover than climate models predict.

The improved representation of present-day Arctic albedo in CMIP6 has not, however, translated into reduced spread in predicted changes. In fact, CMIP6 models exhibit wider variation in predicted declines in both surface and TOA albedos by the end of the century than CMIP5. These differences, that exceed 10% in mid-summer when incoming solar radiation is strongest, can be traced to the wide range of atmospheric contributions to TOA albedo across models. The atmosphere generally contributes more to the TOA albedo in CMIP6 and is predicted to change more dramatically by the end of the 21^st century than in CMIP5.

This lack of consensus in atmospheric reflectance among models is also evident in the estimated time to emergence of predicted trends in solar absorption in the modern Arctic. While models generally agree with observations that the cloud-free Arctic is absorbing more solar radiation than at the start of the century, CMIP6 model paint contradictory pictures regarding whether clouds suppress or enhance this trend. All but one of the CMIP5 models analyzed (Table 2) agree with observations that clouds have delayed the emergence of trends since the start of the century (Sledd and L’Ecuyer, 2021b). However, the influence of clouds on absorbed SW trends is ambiguous in CMIP6 with nearly half of the models examined (Table 1) diverging from observations and suggesting that clouds decrease TTE.

Though specific cloud parameterizations are not explicitly examined here, the increased ambiguity in the role of clouds in modulating ice-albedo feedback appears to be linked to different cloud responses to sea ice changes across models. CMIP6 models exhibit a distinct relationship between how strongly the atmospheric contribution to TOA albedo responds to SIA and how clouds influence the TTE of SW absorption trends that wasn’t present in CMIP5. Models with strong atmospheric responses to SIA tend to predict that clouds accelerate the emergence of solar absorption trends while models with weaker atmospheric responses to SIA tend to reproduce the observed cloud delays. The CMIP6 ensemble also predicts stronger seasonally-integrated atmospheric reflectance trends than the CMIP5 ensemble. The models that predict clouds reduce TTE are those that exhibit the largest declines in atmospheric reflectance with time, suggesting that ice-albedo and cloud feedbacks may work in concert to produce the most rapid changes in Arctic albedo.

Thus, while CMIP6 is converging to a better representation of current Arctic TOA and surface albedo, increased sensitivity to sea ice changes in some models amplifies initial state differences and leads to divergent cloud responses between models that were not present in CMIP5. When acting in concert with the numerous other feedbacks that amplify Arctic warming, the resulting range of Arctic absorption may have significant implications for the trajectories of Arctic temperature and sea ice across models. Continued investigation into the interplay of sea ice and clouds and their mutual impact on absorbed solar radiation in both observations and models is warranted.

Data Availability Statement

Publicly available datasets were analyzed in this study. Observational fluxes and sea ice concentration from ArORIS can be found at http://www.cloudsat.cira.colostate.edu/community-products/arctic-observation-and-reanalysisintegrated-system. Model output can be downloaded from https://esgf-node.llnl.gov/projects/esgfllnl.

Author Contributions

The authors have contributed equally to this work.

Funding

This work was supported by NASA CloudSat/CALIPSO Science Team grant 80NSSC20K0135.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank the CloudSat Data Processing Center where ArORIS data is available. We acknowledge the World Climate Research Programme, which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP. We thank the climate modeling groups for producing and making available their model output, the Earth System Grid Federation (ESGF) for archiving the data and providing access, and the multiple funding agencies who support CMIP and ESGF. We are also grateful to the anonymous reviewers whose comments helped improve this paper.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.769844/full#supplementary-material

References

Alkama, R., Taylor, P. C., Garcia-San Martin, L., Douville, H., Duveiller, G., Forzieri, G., et al. (2020). Clouds Damp the Radiative Impacts of Polar Sea Ice Loss. The Cryosphere 14, 2673–2686. doi:10.5194/tc-14-2673-2020

CrossRef Full Text | Google Scholar

Brodzik, M. J., and Armstrong, R. (2013). Northern Hemisphere EASE-Grid 2.0 Weekly Snow Cover and Sea Ice Extent. Available at: https://doi.org/10.5067/P7O0HGJLYUQU.

Google Scholar

Budyko, M. I. (1969). The Effect of Solar Radiation Variations on the Climate of the Earth. Tellus 21, 611–619. doi:10.3402/tellusa.v21i5.10109

CrossRef Full Text | Google Scholar

Cai, S., Hsu, P.-C., and Liu, F. (2021). Changes in Polar Amplification in Response to Increasing Warming in CMIP6. Atmos. Oceanic Sci. Lett. 14, 100043. doi:10.1016/j.aosl.2021.100043

CrossRef Full Text | Google Scholar

Cesana, G., and Chepfer, H. (2012). How Well Do Climate Models Simulate Cloud Vertical Structure? A Comparison between CALIPSO-GOCCP Satellite Observations and CMIP5 Models. Geophys. Res. Lett. 39. doi:10.1029/2012gl053153

CrossRef Full Text | Google Scholar

Chepfer, H., Noël, V., Chiriaco, M., Wielicki, B., Winker, D., Loeb, N., et al. (2018). The Potential of a Multidecade Spaceborne Lidar Record to Constrain Cloud Feedback. J. Geophys. Res. Atmos. 123, 5433–5454. doi:10.1002/2017jd027742

CrossRef Full Text | Google Scholar

Choi, Y. S., Hwang, J., Ok, J., Park, D. S. R., Su, H., Jiang, J. H., et al. (2020). Effect of Arctic Clouds on the Ice‐albedo Feedback in Midsummer. Int. J. Climatol. 40, 4707–4714. doi:10.1002/joc.6469

CrossRef Full Text | Google Scholar

Christensen, M. W., Behrangi, A., L’ecuyer, T. S., Wood, N. B., Lebsock, M. D., and Stephens, G. L. (2016). Arctic Observation and Reanalysis Integrated System: A New Data Product for Validation and Climate Study. Bull. Am. Meteorol. Soc. 97, 907–916. doi:10.1175/bams-d-14-00273.1

CrossRef Full Text | Google Scholar

Davy, R., and Outten, S. (2020). The Arctic Surface Climate in CMIP6: Status and Developments Since CMIP5. J. Clim. 33, 8047–8068. doi:10.1175/jcli-d-19-0990.1

CrossRef Full Text | Google Scholar

Deser, C., Lehner, F., Rodgers, K. B., Ault, T., Delworth, T. L., DiNezio, P. N., et al. (2020). Insights from Earth System Model Initial-Condition Large Ensembles and Future Prospects. Nat. Clim. Chang. 10, 277–286. doi:10.1038/s41558-020-0731-2

CrossRef Full Text | Google Scholar

Deser, C., Phillips, A., Bourdette, V., and Teng, H. (2012). Uncertainty in Climate Change Projections: The Role of Internal Variability. Clim. Dyn. 38, 527–546. doi:10.1007/s00382-010-0977-x

CrossRef Full Text | Google Scholar

Donohoe, A., and Battisti, D. S. (2011). Atmospheric and Surface Contributions to Planetary Albedo. J. Clim. 24, 4402–4418. doi:10.1175/2011jcli3946.1

CrossRef Full Text | Google Scholar

Etminan, M., Myhre, G., Highwood, E., and Shine, K. (2016). Radiative Forcing of Carbon Dioxide, Methane, and Nitrous Oxide: A Significant Revision of the Methane Radiative Forcing. Geophys. Res. Lett. 43, 12–614. doi:10.1002/2016gl071930

CrossRef Full Text | Google Scholar

Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) Experimental Design and Organization. Geoscientific Model. Dev. (Online) 9, 1937–1958. doi:10.5194/gmd-9-1937-2016

CrossRef Full Text | Google Scholar

Goosse, H., Kay, J. E., Armour, K. C., Bodas-Salcedo, A., Chepfer, H., Docquier, D., et al. (2018). Quantifying Climate Feedbacks in Polar Regions. Nat. Commun. 9, 1919. doi:10.1038/s41467-018-04173-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Hahn, L. C., Armour, K. C., Zelinka, M. D., Bitz, C. M., and Donohoe, A. (2021). Contributions to Polar Amplification in CMIP5 and CMIP6 Models. Front. Earth Sci. 9, 710036. doi:10.3389/feart.2021.710036

CrossRef Full Text | Google Scholar

Hartmann, D. L., and Ceppi, P. (2014). Trends in the CERES Dataset, 2000-13: The Effects of Sea Ice and Jet Shifts and Comparison to Climate Models. J. Clim. 27, 2444–2456. doi:10.1175/jcli-d-13-00411.1

CrossRef Full Text | Google Scholar

Huang, Y., Dong, X., Kay, J. E., Xi, B., and McIlhattan, E. A. (2021). The Climate Response to Increased Cloud Liquid Water Over the Arctic in CESM1: A Sensitivity Study of Wegener-Bergeron-Findeisen Process. Clim. Dyn. 56, 3373–3394. doi:10.1007/s00382-021-05648-5

CrossRef Full Text | Google Scholar

Karlsson, J., and Svensson, G. (2013). Consequences of Poor Representation of Arctic Sea-Ice Albedo and Cloud-Radiation Interactions in the CMIP5 Model Ensemble. Geophys. Res. Lett. 40, 4374–4379. doi:10.1002/grl.50768

CrossRef Full Text | Google Scholar

Kato, S., Loeb, N. G., Minnis, P., Francis, J. A., Charlock, T. P., Rutan, D. A., et al. (2006). Seasonal and Interannual Variations of Top-Of-Atmosphere Irradiance and Cloud Cover Over Polar Regions Derived from the CERES Data Set. Geophys. Res. Lett. 33. doi:10.1029/2006gl026685

CrossRef Full Text | Google Scholar

Kato, S., Rose, F. G., Rutan, D. A., Thorsen, T. J., Loeb, N. G., Doelling, D. R., et al. (2018). Surface Irradiances of Edition 4.0 Clouds and the Earth's Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Data Product. J. Clim. 31, 4501–4527. doi:10.1175/jcli-d-17-0523.1

CrossRef Full Text | Google Scholar

Kay, J. E., Deser, C., Phillips, A., Mai, A., Hannay, C., Strand, G., et al. (2015). The Community Earth System Model (CESM) Large Ensemble Project: A Community Resource for Studying Climate Change in the Presence of Internal Climate Variability. Bull. Am. Meteorol. Soc. 96, 1333–1349. doi:10.1175/bams-d-13-00255.1

CrossRef Full Text | Google Scholar

Koenigk, T., Devasthale, A., and Karlsson, K.-G. (2014). Summer Arctic Sea Ice Albedo in CMIP5 Models. Atmos. Chem. Phys. 14, 1987–1998. doi:10.5194/acp-14-1987-2014

CrossRef Full Text | Google Scholar

Letterly, A., Key, J., and Liu, Y. (2018). Arctic Climate: Changes in Sea Ice Extent Outweigh Changes in Snow Cover. The Cryosphere 12, 3373–3382. doi:10.5194/tc-12-3373-2018

CrossRef Full Text | Google Scholar

Loeb, N. G., Doelling, D. R., Wang, H., Su, W., Nguyen, C., Corbett, J. G., et al. (2018). Clouds and the Earth's Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-Of-Atmosphere (TOA) Edition-4.0 Data Product. J. Clim. 31, 895–918. doi:10.1175/jcli-d-17-0208.1

CrossRef Full Text | Google Scholar

Loeb, N. G., Rose, F. G., Kato, S., Rutan, D. A., Su, W., Wang, H., et al. (2020). Toward a Consistent Definition Between Satellite and Model Clear-sky Radiative Fluxes. J. Clim. 33, 61–75. doi:10.1175/jcli-d-19-0381.1

CrossRef Full Text | Google Scholar

McIlhattan, E. A., Kay, J. E., and L'Ecuyer, T. S. (2020). Arctic Clouds and Precipitation in the Community Earth System Model Version 2. J. Geophys. Res. Atmos. 125, e2020JD032521. doi:10.1029/2020JD032521

CrossRef Full Text | Google Scholar

Notz, D., and Community, S. (2020). Arctic Sea Ice in CMIP6. Geophys. Res. Lett. 47, e2019GL086749. doi:10.1029/2019gl086749

CrossRef Full Text | Google Scholar

Nygård, T., Naakka, T., and Vihma, T. (2020). Horizontal Moisture Transport Dominates the Regional Moistening Patterns in the Arctic. J. Clim. 33, 6793–6807. doi:10.1175/jcli-d-19-0891.1

CrossRef Full Text | Google Scholar

Perovich, D. K., Light, B., Eicken, H., Jones, K. F., Runciman, K., and Nghiem, S. V. (2007). Increasing Solar Heating of the Arctic Ocean and Adjacent Seas, 1979–2005: Attribution and Role in the Ice-Albedo Feedback. Geophys. Res. Lett. 34. doi:10.1029/2007gl031480

CrossRef Full Text | Google Scholar

Phojanamongkolkij, N., Kato, S., Wielicki, B. A., Taylor, P. C., and Mlynczak, M. G. (2014). A Comparison of Climate Signal Trend Detection Uncertainty Analysis Methods. J. Clim. 27, 3363–3376. doi:10.1175/jcli-d-13-00400.1

CrossRef Full Text | Google Scholar

Pithan, F., and Mauritsen, T. (2014). Arctic Amplification Dominated by Temperature Feedbacks in Contemporary Climate Models. Nat. Geosci. 7, 181–184. doi:10.1038/ngeo2071

CrossRef Full Text | Google Scholar

Qu, X., and Hall, A. (2005). Surface Contribution to Planetary Albedo Variability in Cryosphere Regions. J. Clim. 18, 5239–5252. doi:10.1175/jcli3555.1

CrossRef Full Text | Google Scholar

Schmidt, G. A., Kelley, M., Nazarenko, L., Ruedy, R., Russell, G. L., Aleinov, I., et al. (2014). Configuration and Assessment of the GISS ModelE2 Contributions to the CMIP5 Archive. J. Adv. Model. Earth Syst. 6, 141–184.

CrossRef Full Text | Google Scholar

Screen, J. A., and Simmonds, I. (2010b). Increasing Fall-winter Energy Loss from the Arctic Ocean and its Role in Arctic Temperature Amplification. Geophys. Res. Lett. 37. doi:10.1029/2010gl044136

CrossRef Full Text | Google Scholar

Screen, J. A., and Simmonds, I. (2010a). The central Role of Diminishing Sea Ice in Recent Arctic Temperature Amplification. Nature 464, 1334–1337. doi:10.1038/nature09051

PubMed Abstract | CrossRef Full Text | Google Scholar

Sedlar, J., Tjernström, M., Mauritsen, T., Shupe, M. D., Brooks, I. M., Persson, P. O. G., et al. (2011). A Transitioning Arctic Surface Energy Budget: The Impacts of Solar Zenith Angle, Surface Albedo and Cloud Radiative Forcing. Clim. Dyn. 37, 1643–1660. doi:10.1007/s00382-010-0937-5

CrossRef Full Text | Google Scholar

Seland, Ø., Bentsen, M., Olivié, D., Toniazzo, T., Gjermundsen, A., Graff, L. S., et al. (2020). Overview of the Norwegian Earth System Model (NorESM2) and Key Climate Response of CMIP6 DECK, Historical, and Scenario Simulations. Geosci. Model. Dev. 13, 6165–6200. doi:10.5194/gmd-13-6165-2020

CrossRef Full Text | Google Scholar

Sellers, W. D. (1969). A Global Climatic Model Based on the Energy Balance of the Earth-Atmosphere System. J. Appl. Meteorol. 8, 392–400. doi:10.1175/1520-0450(1969)008<0392:agcmbo>2.0.co;2

CrossRef Full Text | Google Scholar

Serreze, M. C., Barrett, A. P., Stroeve, J. C., Kindig, D. N., and Holland, M. M. (2009). The Emergence of Surface-Based Arctic Amplification. The Cryosphere 3, 11–19. doi:10.5194/tc-3-11-2009

CrossRef Full Text | Google Scholar

Shu, Q., Wang, Q., Song, Z., Qiao, F., Zhao, J., Chu, M., et al. (2020). Assessment of Sea Ice Extent in CMIP6 with Comparison to Observations and CMIP5. Geophys. Res. Lett. 47, e2020GL087965. doi:10.1029/2020gl087965

CrossRef Full Text | Google Scholar

Sledd, A., and L’Ecuyer, T. (2019). How Much Do Clouds Mask the Impacts of Arctic Sea Ice and Snow Cover Variations? Different Perspectives from Observations and Reanalyses. Atmosphere 10, 12. doi:10.3390/atmos10010012

CrossRef Full Text | Google Scholar

Sledd, A., and L’Ecuyer, T. (2021a). Emerging Trends in Arctic Solar Absorption. In review.

Google Scholar

Sledd, A., and L’Ecuyer, T. (2021b). Uncertainty in Forced and Natural Arctic Solar Absorption Variations in CMIP6 Models. J. Clim. 34, 931–948. doi:10.1175/jcli-d-20-0244.1

CrossRef Full Text | Google Scholar

Stroeve, J. C., Serreze, M. C., Holland, M. M., Kay, J. E., Malanik, J., and Barrett, A. P. (2012). The Arctic's Rapidly Shrinking Sea Ice Cover: A Research Synthesis. Climatic Change 110, 1005–1027. doi:10.1007/s10584-011-0101-1

CrossRef Full Text | Google Scholar

Stroeve, J., and Notz, D. (2018). Changing State of Arctic Sea Ice Across All Seasons. Environ. Res. Lett. 13, 103001. doi:10.1088/1748-9326/aade56

CrossRef Full Text | Google Scholar

Taylor, K. E., Stouffer, R. J., and Meehl, G. A. (2012). An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 93, 485–498. doi:10.1175/bams-d-11-00094.1

CrossRef Full Text | Google Scholar

Taylor, P. C., Boeke, R. C., Li, Y., and Thompson, D. W. J. (2019). Arctic Cloud Annual Cycle Biases in Climate Models. Atmos. Chem. Phys. 19, 8759–8782. doi:10.5194/acp-19-8759-2019

CrossRef Full Text | Google Scholar

Vignesh, P. P., Jiang, J. H., Kishore, P., Su, H., Smay, T., Brighton, N., et al. (2020). Assessment of CMIP6 Cloud Fraction and Comparison with Satellite Observations. Earth Space Sci. 7, e2019EA000975. doi:10.1029/2019ea000975

CrossRef Full Text | Google Scholar

Weatherhead, E. C., Reinsel, G. C., Tiao, G. C., Meng, X.-L., Choi, D., Cheang, W.-K., et al. (1998). Factors Affecting the Detection of Trends: Statistical Considerations and Applications to Environmental Data. J. Geophys. Res. 103, 17149–17161. doi:10.1029/98jd00995

CrossRef Full Text | Google Scholar

Wei, J., Wang, Z., Gu, M., Luo, J.-J., and Wang, Y. (2021). An Evaluation of the Arctic Clouds and Surface Radiative Fluxes in CMIP6 Models. Acta Oceanol. Sin. 40, 85–102. doi:10.1007/s13131-021-1705-6

CrossRef Full Text | Google Scholar

Wu, D. L., Lee, J. N., Kim, K.-M., and Lim, Y.-K. (2020). Interannual Variations of TOA Albedo over the Arctic, Antarctic and Tibetan Plateau in 2000-2019. Remote Sensing 12, 1460. doi:10.3390/rs12091460

CrossRef Full Text | Google Scholar

Wu, T., Lu, Y., Fang, Y., Xin, X., Li, L., Li, W., et al. (2019). The Beijing Climate Center Climate System Model (BCC-CSM): The Main Progress from CMIP5 to CMIP6. Geosci. Model. Dev. 12, 1573–1600. doi:10.5194/gmd-12-1573-2019

CrossRef Full Text | Google Scholar

Zelinka, M. D., Myers, T. A., McCoy, D. T., Po-Chedley, S., Caldwell, P. M., Ceppi, P., et al. (2020). Causes of Higher Climate Sensitivity in CMIP6 Models. Geophys. Res. Lett. 47, e2019GL085782. doi:10.1029/2019gl085782

CrossRef Full Text | Google Scholar