
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 05 October 2021
Sec. Geohazards and Georisks
Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.769257
This article is part of the Research TopicAdvances in Modeling, Assessment, and Prevention of Geotechnical and Geological DisastersView all 44 articles
Loess landslides induced by rainfall and traffic load are significant hazards during the construction and operation of highways in many loess-covered areas. Studies of the deformation and stability of loess slopes with seepage fissures are limited. In the study, a case study of the Yangpoyao loess slope with seepage fissures in China’s Loess Plateau was conducted to reveal the deformation development mechanism and assess the landslide hazards of such fissured loess slopes. First, the hydraulic-mechanical properties of the Q2 loess were investigated through experiments, and the mathematical expressions of the relationships between various mechanical parameters and water content were fitted, indicating that the mechanical parameters, such as cohesion, angle of internal friction, and deformation modulus, vary in a quasi-linear manner with the water content. Then, a new numerical method was proposed to simulate the mechanical behaviours of the loess considering its water sensitivity and transverse isotropy, where the water sensitivity was considered through the implementation of the mathematical expressions of the hydraulic-mechanical relationships, and the transverse isotropy was considered by the modified constitutive model that combined the logics of transversely elastic model and a ubiquitous-joint model. Finally, the deformation development mechanism of the fissured loess slope under rainfall and traffic load was revealed by using the proposed method. The roles of the rainfall and traffic load in the fissure propagation and deformation development process of the slope were explored, and some stabilisation measures are recommended for the prevention of its failure. The proposed method and findings arising therefrom may provide references for future studies of the stability and landslide hazard assessment of fissured loess slopes.
Loess covers
These fissures destroy the integrity of a slope, resulting in increased rainfall infiltration and a gradual reduction in the strength of the soil (Jin et al., 2012; Wang J. et al., 2018). Also, the fissures lead to stress concentration and large deformation in the slope body, resulting in slope instability (Wang et al., 2017; Wang J. et al., 2019). Previous studies on rainfall-induced landslides of fissured loess slopes have generally discovered that the failure process of the slopes can be divided into three stages: water infiltration, fissure-deformation development, and sliding (Wang et al., 2017; Zhuang et al., 2018), where the fissure-deformation development stage is of most importance in the formation of loess landslides (Jin et al., 2012; Wang J. et al., 2018; Chen et al., 2018).
Various physical model experiments have been conducted to reveal the fissure-deformation development process of loess slopes with fissures subjected to rainfall or human activities. For example, Wu et al. (2017) and Zhang et al. (2019) conducted flume experiments to study dynamic behaviours of a loess slope subject to rainfall and found a relationship between the slope stability and the rainfall infiltration. Sun et al. (2019) undertook different model experiments to assess the effects of rainfall patterns on the process of the deformation and failure of fissured loess slopes. Zhang S. et al. (2020) conducted a centrifuge model test of a loess slope and revealed the landslide process induced by excavation. Chen et al. (2018) observed three stages of a rainfall-induced loess landslide from an in-situ experiment involving artificial rainfall. Wang J. et al. (2018) analysed the failure modes of loess-filled fissured slopes based on the combination of field survey, in-situ monitoring, and laboratory testing. These physical model experiments have restored the destruction of fissured loess slope to a certain extent; however, they suffer numerous drawbacks due to the small simulation scale and high cost of materials.
To overcome the shortcomings of physical model experiments, numerical analysis was conducted to examine the deformation processes in fissured loess slopes. Through the employment of seepage-stress coupling via finite element analysis, researchers investigated the deformation and sliding mechanism of a fissured loess slope subjected to rainfall and excavation (Wang et al., 2014; Li et al., 2020), rainfall and earthquakes (Carey et al., 2017; Wang et al., 2020; Pu et al., 2021), and upon variation of prevailing hydraulic conditions (Hou et al., 2018). Moreover, other numerical methods were used to explore this problem. For example, Zhou et al. (2014a) proposed a moving boundary algorithm for mechanical-hydraulic coupled analysis and used it to investigate the failure mechanism of a loess slope along cracks caused by infiltration of water. Chang et al. (2021) simulated the failure process of fissured loess slope under rainfall and earthquake load via the PFC3D discrete element software.
As can be seen from the physical model experiments and numerical analysis above, triggering factors including rainfall, earthquakes, and human activities, intensify the fissure-deformation development process in loess slopes (Zhang and Li, 2011). Among the triggers of loess landslides, rainfall and traffic load emerge as the most important on China’s Loess Plateau (Derbyshire, 2001; Tu et al., 2009; Zhang and Li, 2011; Juang et al., 2019) where many important highways have been built upon implementation of the Western Development Drive in China in recent years. Therefore, a good understanding of the deformation development mechanism of fissured loess slope under rainfall and traffic load is of engineering concern in the loess-rich area. Moreover, previous studies are insufficient in terms of the analytical methods: most of the studies (Tu et al., 2009; Jin et al., 2012; Wang et al., 2014; Carey et al., 2017; Li et al., 2020; Wang et al., 2020; Pu et al., 2021) were based on the theory of unsaturated soil mechanics (Bishop et al., 1961) to ascertain the effects of water infiltration on loess slopes, while ignoring the two most important properties of the loess, the collapsibility (water sensitivity) (Zhou et al., 2014b; Garakani et al., 2015) and transverse isotropy (Jiang et al., 2014; Wen and Yan, 2014; Xu and Coop, 2016).
In the study, a typical loess slope of the highway engineering on China’s Loess Plateau, the Yangpoyao loess slope with a seepage fissure, was taken as a case study. The hydraulic-mechanical properties of the loess were obtained by experiment. A new numerical method was used to simulate the fissure-deformation development process of the slope under rainfall and traffic load by considering the collapsibility and transverse isotropy of the loess; the simulated results were verified by in-situ monitoring data. Based on the analysis of the simulation and field monitoring results, some stabilisation treatments are recommended for the prevention of fissured loess slope failure.
The Yangpoyao slope is located in Ganquan County, Yan’an City, Shaanxi Province, China. The slope is a typical loess slope along Huang-Yan Highway (from Huangling to Yan’an) through the centre of China’s Loess Plateau (Figures 1A,B). The total length of the slope is about 100 m, and its cross-section is shown in Figure 1C. The slope is filled with a typical loess
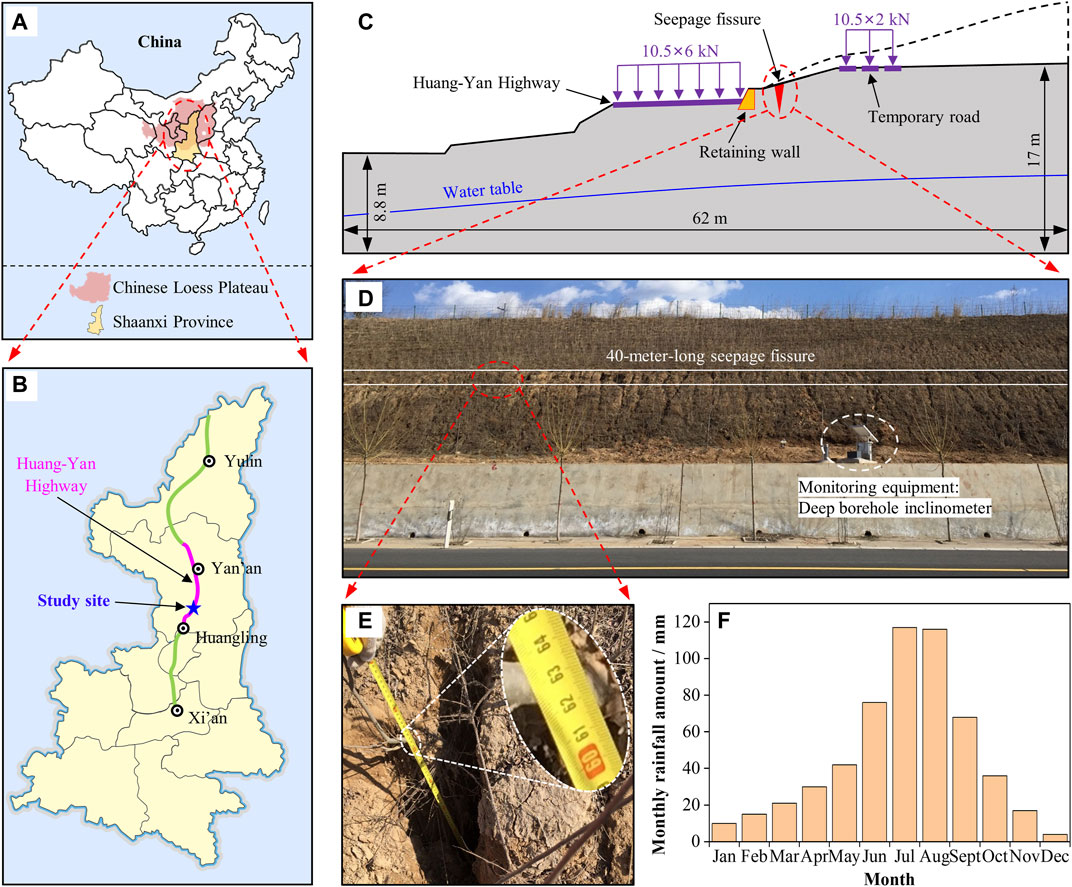
FIGURE 1. Overview of the Yangpoyao slope: (A,B) location of the site, (C) cross-section of the slope, (D,E) a fissure on the slope and (F) statistical distribution of monthly average rainfall.
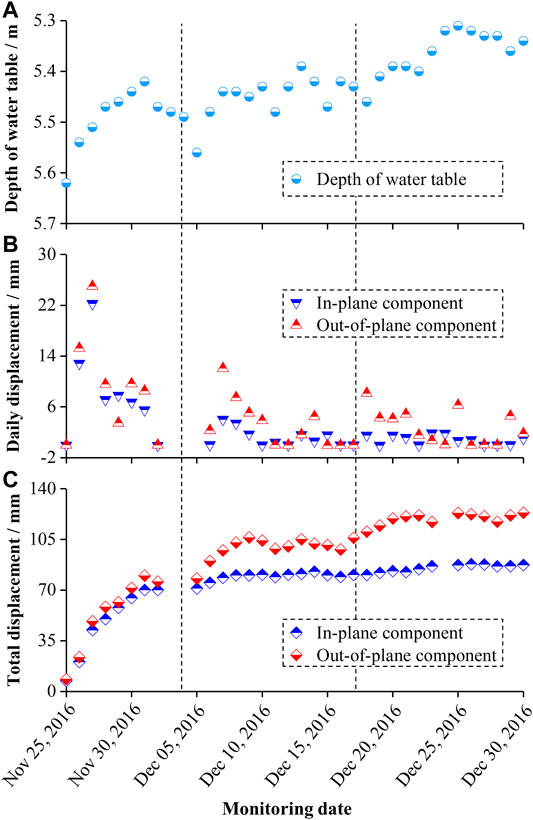
FIGURE 2. Monitoring data of the slope: (A) depth of water table, (B) daily displacement, and (C) total displacement.
The climate of the slope site is arid or semi-arid with an annual rainfall amount of about 550 mm. The distribution of annual rainfall is concentrated seasonally, about 70% of which occurs in the rainy season between June and September (Figure 1F). The maximum monthly rainfall amount appears in July or August, accounting for about 40% of the annual rainfall amount. Furthermore, the maximum daily rainfall with an average amount of 50 mm/day usually occurs in July or August. The concentrated rainfall creates the conditions for the formation of seepage fissures on the loess slope.
Monitoring work (Figure 1D) was immediately carried out on the slope when the seepage fissure appeared. The data (Figure 2) were monitored from 25 November to December 30, 2016, including the rise of the underground water table (associated with rainfall infiltration), the total horizontal deformation and the daily horizontal deformation of the slope. As illustrated in Figure 2, the monitored process of the changes in the depth of water table and the deformation of the slope can be divided into three periods according to their growth trends, which indicates that the rise of the water table is related to the increase in deformation (Xu et al., 2014); however, it also shows that the deformation increment does not explicitly vary with the water table in each period, suggesting that the deformation increment is not completely controlled by the rising water table (Mirus et al., 2018). The change in the water table is just one of the key factors influencing the deformation and other factors, such as the traffic load on the highway and temporary haul road, also contribute to the deformation. Therefore, it is necessary to study the hydraulic-mechanical response of the slope under the action of rainfall infiltration and traffic load to reveal the fissure-deformation development mechanism of this loess slope with its seepage fissure.
Loess is extremely sensitive to water and its strength reduces rapidly upon wetting (Xing et al., 2016; Yan et al., 2018). Research has revealed that water sensitivity of loess is manifest by the collapse of the original soil structures and the decrease in the shear strength and stiffness after encountering water (Feda, 1988; Zhou et al., 2014b; Garakani et al., 2015); however, in terms of loess landslides, previous studies (Tu et al., 2009; Jin et al., 2012; Wang et al., 2014; Carey et al., 2017; Li et al., 2020; Wang et al., 2020; Pu et al., 2021) usually evaluated stability of a loess slope by using the general theory of unsaturated soil mechanics, such as the Bishop’s shear strength formula (Bishop et al., 1961) which considers pore-water and pore-air pressure in soils but does not consider the water sensitivity of mechanical parameters of the loess (Xu L. et al., 2018; Xu Y. et al., 2018). This analysis method usually overestimates the slope stability due to neglecting the water sensitivity of loess, therefore, loess slopes should consider not only the effects of rainfall infiltration on the increase of the pore water pressure but also the variations in the mechanical parameters with increasing water content.
To demonstrate such specific hydraulic-mechanical characteristics of loess in slope stability analysis, especially for loess slopes with seepage fissures under the action of rainfall infiltration and traffic load, a new simulation method is proposed, as shown in Figure 3.
First, the hydraulic conductivity curve and soil-water characteristic curve of the loess are experimentally derived, and the unsaturated steady seepage theory is used to inversely calculate the initial water content and initial pore water pressure of the slope based on the pore water pressure and the water table as measured on-site.
Second, the water content increment field of the slope under rainfall is calculated based on the fields of water content before and after infiltration, and then the mechanical parameter fields, such as the distributions of cohesion, angle of internal friction, deformation modulus, and unit weight, are fitted based on the measured hydraulic-mechanical properties of the loess and the distribution of the increment in water content.
Finally, a constitutive model suitable for the loess (presented in Consideration of Transverse Isotropy of Loess ) is adopted to conduct mechanical analysis of the slope based on the pore water pressure and fitted mechanical parameters of the slope. The fissure-deformation development mechanism of the slope is revealed by analysing the calculated results, and the slope stability is evaluated.
It is noted that this method is an equivalent method of mechanical parameters to consider the water sensitivity of loess. The changes in mechanical parameters of the loess after encountering water, such as the decrease in strength and stiffness and the increase in unit weight, are fully considered in the method, but the collapse of the soil structure and the change in volume are not involved.
Soil structures are the inherent determinants of the strength and stiffness of the soils, especially for loess (Jiang et al., 2014; Wen and Yan, 2014; Xu and Coop, 2016). Figure 4A depicts the
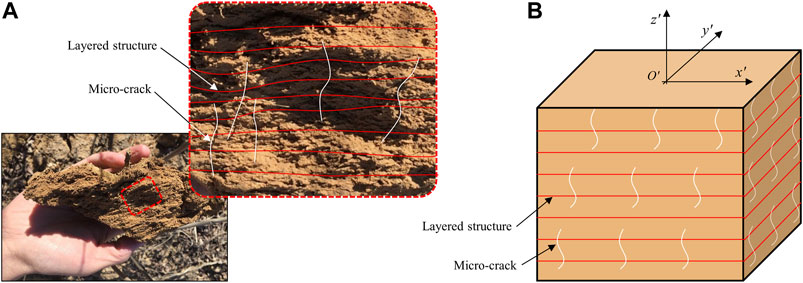
FIGURE 4. Structural characteristics of the loess: (A) loess sampled at the study site and (B) generalised model of the structure of the loess.
The Anisotropic-Elasticity Ubiquitous-Joint Model in Flac3D (Itasca Consulting Group, 2018) was modified to simulate the transversely isotropic strength and stiffness of the loess. The modified model integrates the logic of the transversely elastic model (which is used to simulate the transverse isotropy of the deformation of the loess) with that of the ubiquitous-joint model (which is employed to simulate the yield of the loess in a specific direction, i.e., the anisotropic strength of the loess). In calculation using the model, the elastic stress and strain of the elements are first calculated by the transversely elastic model (i.e., elastically trial calculation). Then, the plastic elements are determined based on the elastic stress and the yield function, and accordingly, the stress is corrected based on the distribution of the plastic elements. Followed by the stress correction, the strain of the plastic elements is corrected using the plastic flow rules to determine the incremental plastic strains. The main modification of this model is the stress and strain correction in the
The Mohr-Coulomb strength criterion is employed to judge the yield elements and correct the stress, and then the associated or non-associated plastic flow rule is accordingly used for the strain correction. Let
where
where
where
where
where
It is noteworthy that the main modification of the Anisotropic-Elasticity Ubiquitous-Joint Model involves the yield judgment and stress correction in the
The undisturbed Q2 loess collected from the Yangpoyao loess slope is brown yellow, hard, and dense, with layered structures and micro-cracks in the soil (Figure 4A). The physical properties were listed in Table 1. The main particle components of the loess are silt particles: the proportion of the loess particles with a diameter larger than 0.05 mm is 12.9%, the proportion of those from 0.005 to 0.05 mm is 71.5%, and the proportion of those smaller than 0.005 mm is 15.6%. The liquid limit and plastic limit of the soil are 31.4 and 16.7%, respectively. The unit weight of the loess varies with the water content. In the natural state, the lowest water content of the loess is about 14%, and the corresponding unit weight is 1.52 g/cm3; the saturated water content is about 30%, and the corresponding unit weight is 1.73 g/cm3. The relationship between the water content and the bulk unit weight is roughly linear:
where
To measure the hydraulic characteristics of the loess, the tests of soil-water characteristic curve were conducted using a volumetric pressure plate apparatus under pressures of 10, 50, 100, 200, 300, 500, 750, 850, and 1,000 kPa. The test data are shown in Figure 5A. Generally, the soil-water characteristic curve can be described by some models, such as van Genuchten function (van Genuchten, 1980), Fredlund-Xing function (Fredlund and Xing, 1994), and modified Kovacs function (Aubertin et al., 2003). In the present study, as the main particle components of the loess are silt particles, the Fredlund-Xing function (Eq. 8) is used to fit the soil-water characteristic curve, and the fitted function is displayed in Eq. 9.
where
The hydraulic conductivity curves can be fitted based on the existing models, such as the van Genuchten model (van Genuchten, 1980) and Fredlund-Xing-Huang model (Fredlund et al., 1994). In the study, Fredlund-Xing-Huang model (Eq. 10) is used to fit the hydraulic conductivity function based on the water-soil characteristic curve function and the soil properties, such as the saturated hydraulic conductivity, and saturated and residual water contents. The fitted hydraulic conductivity curve obtained by using the estimation techniques of Seep/W (part of the Geostudio suite) is demonstrated in Figure 5B.
where
Hydraulic-mechanical characteristics and their mathematical expressions in the loess are necessary for the seepage-stress coupling simulation of the slope under rainfall and traffic load. Previous studies revealed some hydraulic-mechanical characteristics of loess, including the variation in the matric suction, shear strength and stiffness with the water content (van Genuchten, 1980; Fredlund et al., 1994; Aubertin et al., 2003; Haeri et al., 2014; Wang W. et al., 2018; Xu Y. et al., 2018; Liang et al., 2018). However, these studies rarely propose mathematical expressions of the variation in the mechanical parameters with the water content, so, it is difficult to apply the results to numerical simulation in any direct sense.
These mathematical expressions were further studied by using direct shear tests. The tests were conducted using the direct shear apparatus at a horizontal (shear) speed of 0.8 mm/min under the condition of the vertical stresses of 100, 200, 300, and 400 kPa, respectively. Six groups of the remoulded samples with the water contents of 14 (initial water content), 16, 18, 20, 22, and 24%, respectively, were prepared for the direct shear tests. The relationships between the shear stress and shear deformation of the samples with varying water contents tested under the vertical stress of 100 kPa (those at 200, 300, and 400 kPa had similar patterns and are not given) were revealed, as illustrated in Figure 6A.
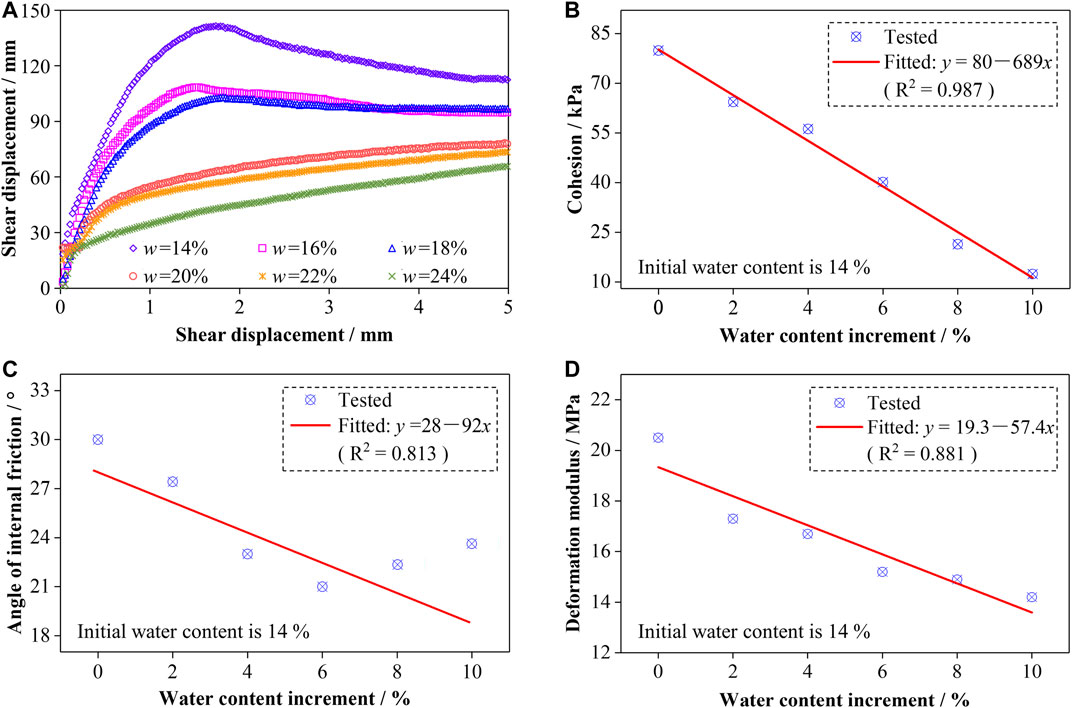
FIGURE 6. Variations of shear stress-shear stress curves (A), cohesion (B), angle of internal friction (C) and deformation modulus (D) of the loess with the water content.
The mechanical parameters, including the cohesion (Figure 6B), angle of internal friction (Figure 6C), and deformation modulus (Figure 6D), were obtained based on the results of the direct shear tests. The fitted functions of the variation in the mechanical parameters with the water content increment are shown in Eqs. 10–13, where
It is noted that due to the limitations imposed by the prevailing conditions at the study site, it is difficult to obtain undisturbed Q2 loess samples with different water contents, such that remoulded samples with a 14–24% water content were formed in the laboratory. According to related studies (Wang Y. et al., 2019; Chang et al., 2021), the difference in mechanical parameters between the undisturbed loess and remoulded samples gradually decreases with an increasing water content and is acceptable when the water content is 14–24%. As the remoulded samples lose their structural characteristics compared with the undisturbed loess, it is necessary to convert the mechanical parameters of remoulded loess into those of undisturbed loess. Based on the transformation method proposed in previous studies (Jiang et al., 2014; Zhang L. et al., 2020; Liu et al., 2020), the strength and stiffness parameters of undisturbed loess is about 1.05 times that of remoulded loess in the isotropic plane and 0.9 times that of remoulded loess out of the isotropic plane. In general, this relatively small difference between the remoulded loess and undisturbed loess does not affect our investigation of the deformation development and destabilisation mechanism of fissured loess slopes.
The seepage boundary conditions are set as shown in Figure 7A based on the water table revealed in the site investigation and the rainfall conditions over the study area. In the seepage model, the boundary conditions at the bottom and on the highway are impervious boundaries with zero water flux (WF), those on the left and right sides below the water table are constant pore-water head (PWH) boundaries, those on the left and right sides above the water table are water unit gradient (WUG) boundaries and that on the upper surface is a water-infiltration boundary with a water flux (WF) of 50 mm/d (the seepage lasts for 1 day). To simulate the fissure development process, the depth of the fissure is set to 0, 0.5, 1.0, and 1.5 m, respectively. The boundary condition at the fissure is pore-water pressure head varying with the depth of the fissure. The saturated/unsaturated seepage theory is used in seepage calculations, and the material parameters, including the soil-water characteristic curve and hydraulic conductivity curve, are assigned to the model according to the fitted results (Unsaturated Hydraulic Characteristics of the Loess).
The mechanical boundary conditions are set as shown in Figure 7B. In the mechanical model, the horizontal displacements of the left and right boundaries and the vertical displacement of the bottom boundary are fixed. The boundary conditions of the highway (with six lanes) and temporary road (with two lanes) are stress boundaries with a normal stress thereon of 10.5 kN/m (per unit width out of the plane of analysis) per lane. Other boundary conditions of the model, including the slope surface and the fissure with varying depth, are free (stress boundary with zero stress). Moreover, the pore water pressure distribution is applied to the model based on the calculation results of the seepage. The modified constitutive model in Consideration of Transverse Isotropy of Loess is used for the mechanical calculation, and the material parameters, including the cohesion, friction, deformation modulus, and bulk unit weight of the loess, are fitted based on the seepage results and assigned to the model, as shown in Settings for the Seepage-Coupled Stability Simulation.
Figures 8A–D show the results of the seepage calculation on the slope with a 1.5-meter-deep fissure. It can be seen from the figures that the water content and pore-water pressure on the slope surface, especially at the fissure, have increased significantly after infiltration (Jin et al., 2012; Zhou et al., 2014a; Chang et al., 2021). The seepage results are used for the mechanical analysis of the slope by the method proposed in Consideration of Water Sensitivity of Loess and the steps are as described below.
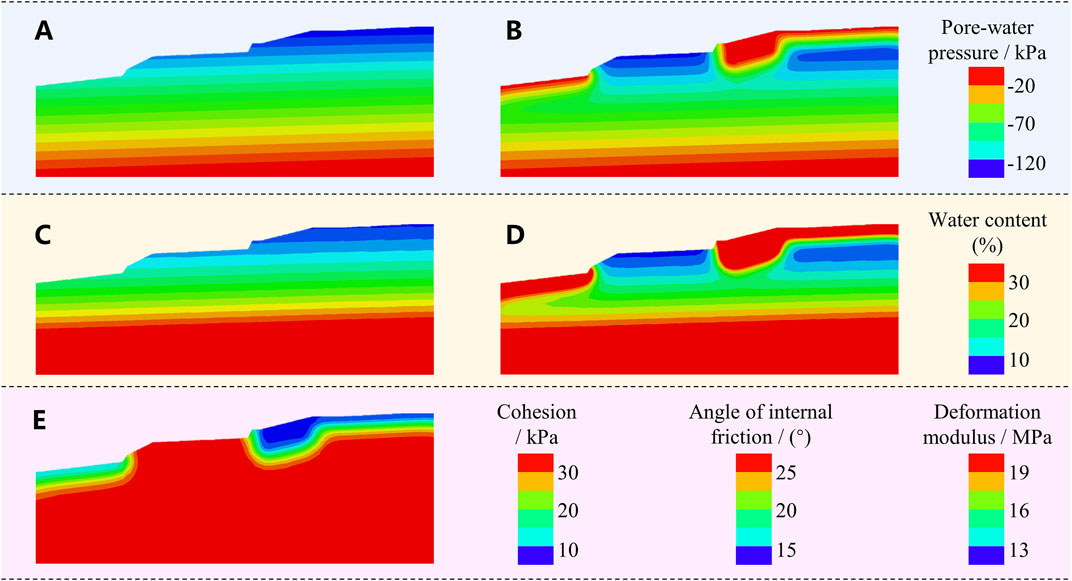
FIGURE 8. Fields of the pore-water pressure before (A) and after (B) rainfall infiltration; fields of the water content before (C) and after (D) rainfall infiltration; and the fitted fields of the cohesion, angle of internal friction and deformation modulus (E).
Firstly, the pore-water pressure field after rainfall infiltration (Figure 8B) is directly applied to the mechanical calculation model of the slope.
Secondly, the water content increment can be obtained by subtracting the water content field before (Figure 8C) from that after (Figure 8D) water infiltration. The mechanical parameter fields (Figure 8E), including those pertaining to the cohesion, angle of internal friction, and deformation modulus, can be calculated via Eqs. 11–13 based on the water content increment. A similar method is used to fit the bulk unit weight field via Eq. 7 based on the water content distribution after water infiltration (Figure 8D).
Finally, the fields pertaining to the cohesion, angle of internal friction, deformation modulus, unit weight and pore-water pressure are assigned to the mechanical model for slope stability analysis.
Previous studies (Ma et al., 2016; Tan et al., 2017) divided the fissure-deformation development process of soil slopes under internal and external actions into the trailing-edge tensile fissure stage (initial deformation stage), side-edge shear fissure stage (uniform deformation stage), leading-edge tensile fissure stage (accelerated deformation stage), and fissure penetration stage (sharp deformation stage); however, in terms of loess slopes with seepage fissures, the fissure-deformation development process is different.
Figure 9 illustrates the schematic diagrams of the shear strength field, the distribution of the plastic zones and the displacement counter at different fissure development stages of the slope under rainfall and traffic load. The fissure-deformation development process can be back-analysed based on the data shown in Figure 9.
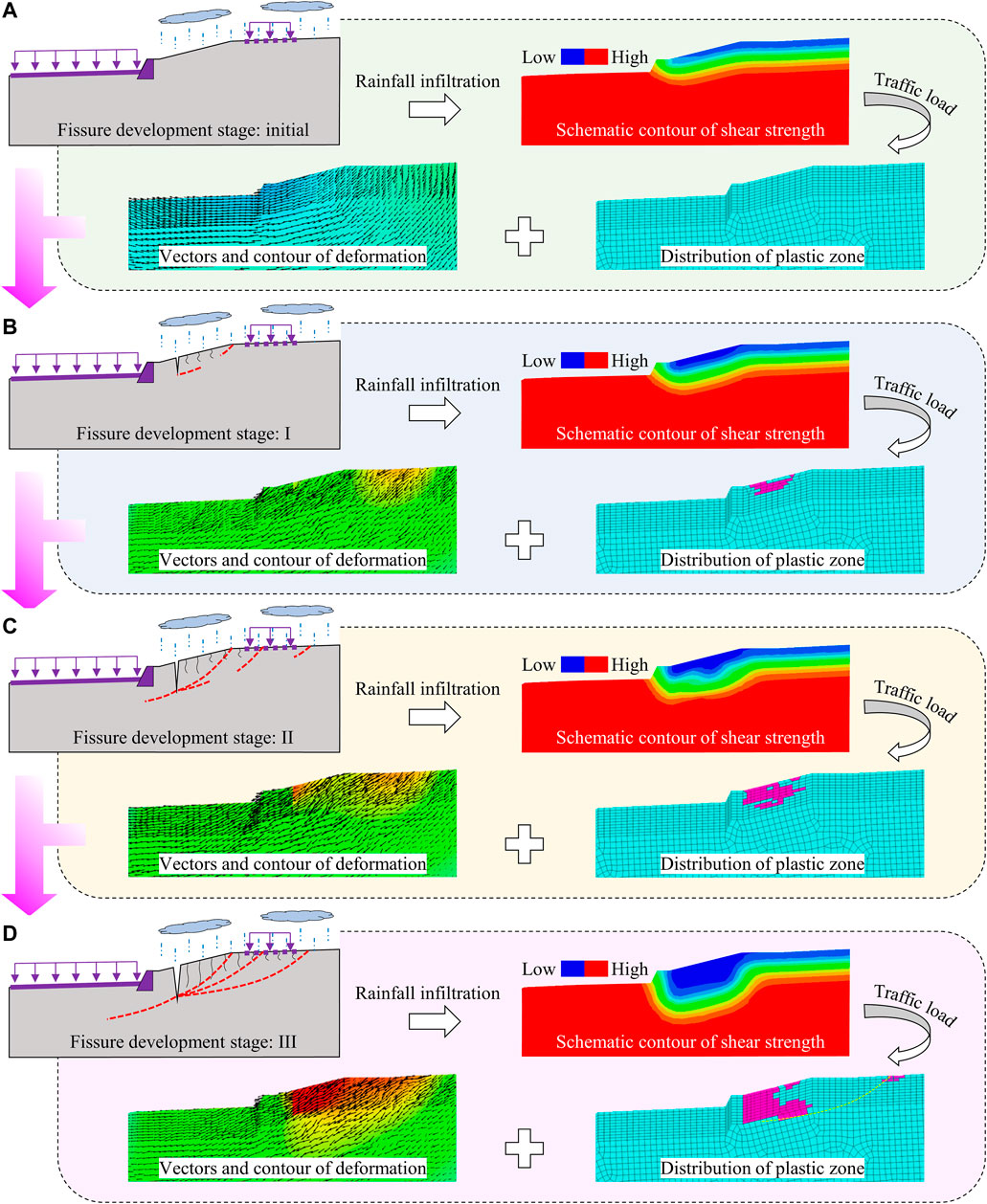
FIGURE 9. Fissure-deformation development process of the slope under rainfall and traffic load: initial stage (A), micro-crack penetration stage (B), fissure propagation stage (C) and sliding surface formation stage (D).
Initial stage (Figure 9A): there are no fissures on the slope at this stage. The slope, with a depth of soil of only about 300 mm, reaches a saturated state after rainfall infiltration (Wu et al., 2017; Hou et al., 2018), which causes a minor reduction in the strength and stiffness of the slope. The deformation of the slope under the traffic load is small, and the slope remains stable.
Micro-crack penetration stage (Figure 9B): loess contains many micro-cracks inherently, but these micro-cracks do not penetrate in a natural state (Jiang et al., 2014; Wen and Yan, 2014; Xu and Coop, 2016); however, under traffic load on the trailing-edge of the slope, the middle part of the slope surface is subjected to tensile stress, which contributes to the expansion and penetration of the micro-cracks in the soil. Rainfall infiltration reduces the strength of the soil within a certain depth of the slope surface, promoting micro-crack penetration.
Fissure propagation stage (Figure 9C): after rainfall infiltrates the soil along the penetrating micro-cracks, the strength and stiffness of the slope are significantly reduced. The reduction of the stiffness causes an increase in the deformation of the slope, and that of the strength leads to an increase in the shear and tensile failure on the slope surface. With the development of the deformation and failure zone of the slope, the fissure developed from the penetrating micro-cracks gradually propagates downwards, with further increases in the depth, width, and length of the fissure.
Sliding surface formation stage (Figure 9D): a sliding surface is initially formed along the fissure under the continuous action of rainfall and traffic load. The fissure becomes an express channel for water infiltration under precipitation (Jin et al., 2012; Zhou et al., 2014a; Chang et al., 2021). The seepage field near the fissure is greatly affected so that the strength and stiffness of the soil are correspondingly reduced, resulting in a failure zone expanding around the fissure. Meanwhile, with propagation of the fissure, the constraint of the slope near the fissure is gradually reduced, and as a result, the slope becomes more prone to deforming under traffic load. When the area of the failure zone and the magnitude of the deformation reach a certain level, the slope sliding surface gradually forms.
The study of deformation development process of the slope after stabilisation treatment is key to early warning and hazard assessment of landslides (Tu et al., 2009; Springman et al., 2013; Zhang et al., 2019). Previous studies found that the slope deformation-sliding development process is mainly divided into four stages: initial deformation, uniform deformation, accelerated deformation, and sharp deformation (sliding) (Tu et al., 2009; Xu L. et al., 2018; Chen et al., 2018; Sun et al., 2019; Li et al., 2020). However, the deformation-stabilisation development process for slopes with fissures after stabilisation treatment under rainfall and traffic load is much less frequently explored.
Figure 10 illustrates the monitored horizontal displacement of the Yangpoyao slope and the rainfall over the study site. The displacement was monitored using the deep borehole inclinometer labelled in Figure 10A, and the rainfall was monitored by rain gauges at the study site. The displacement was recorded from January 1, 2017 to June 1, 2019 (the data recorded thereafter are not presented since they are generally unchanged compared with those recorded within the first few months of 2019). During the monitoring period, two stabilisation measures were taken to prevent the fissure from further propagating. One of the treatments was that the traffic load on the slope trailing-edge was removed from February 2017, and the other was that a lawn was planted on the slope surface in the spring (especially April) of 2017, which restrained infiltration into the slope.
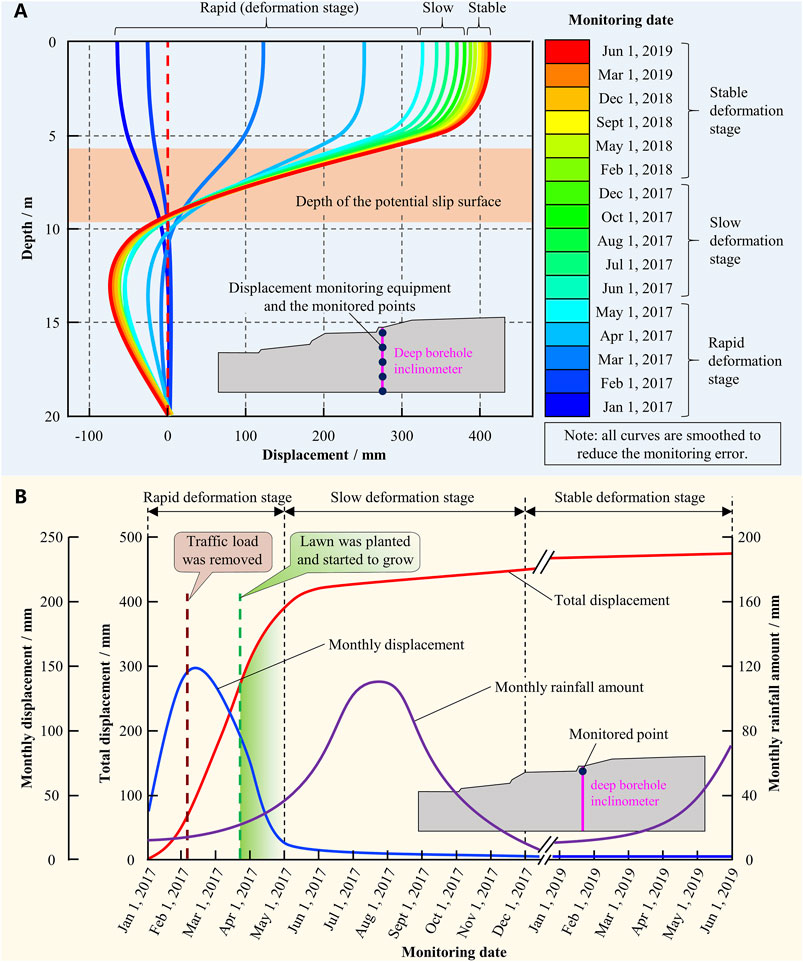
FIGURE 10. Distribution of horizontal deformation along the depth (A) and development of horizontal deformation on the surface (B) of the slope monitored by the deep borehole inclinometer.
From the deep horizontal displacements in the middle of the slope (Figure 10A), the displacements are large within the depth range from 0 to 6 m and are small at the depth below 9 m. The displacements change greatly within the depth range from 6 to 9 m, indicating that the depth of the potential sliding surface is mainly within that range. On the other hand, the depth of the potential sliding surface shown in the figure generally matches that predicted in Figures 9C,D, which indicates that the simulation in is reasonable.
From the monitored horizontal displacements of the slope surface (Figure 10B), the slope deformation development process can be divided into three stages: rapid deformation (from January 2017 to April 2017), slow deformation (from May 2017 to November 2017), and stable deformation (from December 2017). There is a significant boundary between the rapid deformation stage and the slow deformation stage, but the boundary between the slow deformation stage and the stable deformation stage is not obvious. The characteristics of each stage are described below.
In the rapid deformation stage, the total horizontal deformation of the slope increased from 0 to 400 mm in the 4 months from January 2017 to April 2017. The monthly deformation increment was 80 mm in January 2017 and increased to 150 mm in February 2017. To suppress the growing deformation and improve the stability of the slope, the traffic load on the trailing edge of the slope was removed in February 2017, as a result of which the monthly deformation increment was reduced to about 90 mm in March 2017. A lawn was planted on the slope in March 2017, preventing infiltration, reducing the monthly deformation increment in April 2017 to 10 mm.
In the slow deformation stage, the total horizontal deformation of the slope increased from 400 to 440 mm with a monthly deformation increment of 6 mm in the 7 months from May 2017 to November 2017. The average rainfall amount in July and August in 2017 reached 110 mm, but because the lawn (planted in March 2017) had grown on the slope by this stage and prevented rainfall from infiltrating into the slope along the fissure, the rainfall scarcely affected the deformation.
In the stable deformation stage, the increment of the total horizontal deformation of the slope within the 2 years (2018 and 2019) was about 30 mm. Since the deformation of the slope is very slow, it can now be recognised as a stable slope without risk of landslide.
Slope stabilisation treatments generally include reducing driving forces, increasing resisting forces, or both (Chen and Liu, 2007; Wang et al., 2014). Many effective techniques have been developed to prevent landslides, such as the pile-anchor combined structure, anchor-lattice beam combined structure and micro-pile structure (Iverson et al., 2000; Chen and Liu, 2007; Tu et al., 2009; Wang et al., 2014; Tang et al., 2015); however, these methods are not completely suitable for the stabilisation treatments of loess slopes with seepage fissures considering the efficiency and cost. Based on the analysis in Fissure-deformation Development Process Under Rainfall and Traffic Load and Deformation Development Process After Stabilisation Treatment, some insights are obtained from the stabilisation measures applied to the Yangpoyao slope.
1) The presence of fissures is one of the important internal factors that affect the trend in deformation development and the stability of loess slopes (Zhou et al., 2014a; Chang et al., 2021). To avoid the development of further fissure-deformation on fissured loess slopes, it is necessary to avoid loading on the trailing edge which results in tensile stress on the slope surfaces. The tensile stress on the slopes will cause the existing micro-cracks in the loess to expand and penetrate, resulting in the formation of fissures on the slopes. The fissures act as channels for rainwater infiltration, greatly weakening the loess and posing serious threats to the stability of such slopes (Jin et al., 2012; Tang et al., 2015). For the fissured slope in the present study, one of the treatments used to avoid tensile stress zones occurring on the slope surface is to avoid traffic load too close to the trailing edge of the slope.
2) When a fissure already occurs on a loess slope (such as the Yangpoyao slope in the present study), intervention should be timeous to prevent rainwater from infiltrating through the fissure. Rainwater infiltration into the interior of the slope will greatly reduce the strength and stiffness of the loess, causing larger deformation and plastic zones under the roadway. Furthermore, the existing fissure propagates with greater rainwater infiltration to the further detriment of the stability, eventually resulting in a landslide. For the fissured slope in the present study, one of the efficient and economical treatments to prevent rainwater from infiltrating through the fissure is to plant lawns on the slope.
3) The increasing deformation and decreasing stability of fissured loess slopes are related to the rise of water table and the increase in pore-water pressure (as shown in Figure 2). For the fissured slopes after stabilisation measures were implemented, monitoring of the displacement and seepage field (including the depth of groundwater table and pore-water pressure) should be strengthened to ensure the long-term stability of the slope.
The fissure-deformation development process is an important stage of the failure evolution process of loess slopes under rainfall and traffic load, and understanding the mechanism of fissure-deformation development is key to the hazard assessment and prevention of slope failures. In the present study, a typical highway slope on the Chinese Loess Plateau was taken as a case study to investigate such mechanism. The hydraulic-mechanical properties of the Q2 loess were studied through experiments, and a new simulation method that considers the water sensitivity and transverse isotropy of the loess was proposed. The following conclusions can be drawn:
1) The Q2 loess exhibits strong water sensitivity, which is reflected in the mechanical parameters exhibiting a high correlation with the water content: the cohesion, angle of internal friction, and deformation modulus vary in a quasi-linear manner with the water content.
2) The water sensitivity and transverse isotropy of the loess can be considered in numerical simulation using the proposed method: the water sensitivity is considered by correlating the mechanical parameter fields with the seepage field, and the transverse isotropy is considered by using the enhanced model which combines the logic of the transversely elastic model with that of the ubiquitous-joint model.
3) The fissure-deformation development process of the loess slope under rainfall and traffic load can be summarised into three stages: micro-crack penetration, fissure propagation, and sliding surface formation. Each stage is affected by the combined effects of the rainfall and load, where the role of the load is to create the stress conditions necessary for fissure-deformation development, and that of the rainfall infiltration is to reduce the strength and stiffness of the slope soil.
4) Loess slopes should not be loaded close to their trailing edge to prevent fissures from occurring on the slope surface, however, when a fissure already has developed on the slope, planting lawn on the slopes is an effective and economical means of preventing rainwater infiltration into the body of the slope. The stabilisation process of fissured loess slopes after treatment can be summarised as one involving three stages: rapid deformation, slow deformation, and stable deformation; the transition from the rapid deformation stage to the slow deformation stage is a sign that the slope tends to be stable.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
XL designed the research. CW processed the corresponding data. XL and CW wrote the first draft of the manuscript. JZ and QS helped to organize the manuscript. SC and JC revised and edited the final version.
This work was supported by the National Natural Science Foundation of China (No. 52079135), the International Partnership Program of the International Cooperation Bureau of Chinese Academy of Sciences (No. 131551KYSB20180042), and the National Key Research and Development Program of China (No. 2017YFF0108705).
JZ and SC were employed by the company CCCC First Highway Consultants Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Aubertin, M., Mbonimpa, M., Bussière, B., and Chapuis, R. P. (2003). A Model to Predict the Water Retention Curve from Basic Geotechnical Properties. Can. Geotech. J. 40, 1104–1122. doi:10.1139/t03-054
Bishop, A. W., Alpan, I., Blight, G. E., and Donald, I. B. (1961). “Factors Controlling the Strength of Partly Saturated Cohesive Soils,” in Research Conference on Shear Strength of Cohesive Soils, 503–532.
Carey, J. M., Mcsaveney, M. J., and Petley, D. N. (2017). Dynamic Liquefaction of Shear Zones in Intact Loess during Simulated Earthquake Loading. Landslides 14, 789–804. doi:10.1007/s10346-016-0746-y
Chang, W., Wang, P., Wang, H., Chai, S., Yu, Y., and Xu, S. (2021). Simulation of the Q2 Loess Slope with Seepage Fissure Failure and Seismic Response via Discrete Element Method. Bull. Eng. Geol. Environ. 80, 3495–3511. doi:10.1007/s10064-021-02139-z
Chen, G., Meng, X., Qiao, L., Zhang, Y., and Wang, S. (2018). Response of a Loess Landslide to Rainfall: Observations from a Field Artificial Rainfall experiment in Bailong River Basin, China. Landslides 15, 895–911. doi:10.1007/s10346-017-0924-6
Chen, H., and Liu, S. H. (2007). Slope Failure Characteristics and Stabilization Methods. Can. Geotech. J. 44, 377–391. doi:10.1139/t06-131
Derbyshire, E. (2001). Geological Hazards in Loess Terrain, with Particular Reference to the Loess Regions of China. Earth-Science Rev. 54, 231–260. doi:10.1016/s0012-8252(01)00050-2
Derbyshire, E., Meng, X., and Kemp, R. A. (1998). Provenance, Transport and Characteristics of Modern Aeolian Dust in Western Gansu Province, China, and Interpretation of the Quaternary Loess Record. J. Arid Environments 39, 497–516. doi:10.1006/jare.1997.0369
Feda, J. (1988). Collapse of Loess upon Wetting. Eng. Geology 25, 263–269. doi:10.1016/0013-7952(88)90031-2
Fredlund, D. G., and Xing, A. (1994). Equations for the Soil-Water Characteristic Curve. Can. Geotech. J. 31, 521–532. doi:10.1139/t94-061
Fredlund, D. G., Xing, A., and Huang, S. (1994). Predicting the Permeability Function for Unsaturated Soils Using the Soil-Water Characteristic Curve. Can. Geotech. J. 31, 533–546. doi:10.1139/t94-062
Garakani, A. A., Haeri, S. M., Khosravi, A., and Habibagahi, G. (2015). Hydro-mechanical Behavior of Undisturbed Collapsible Loessial Soils under Different Stress State Conditions. Eng. Geology 195, 28–41. doi:10.1016/j.enggeo.2015.05.026
Haeri, S. M., Akbari Garakani, A., Khosravi, A., and Meehan, C. L. (2014). Assessing the Hydro-Mechanical Behavior of Collapsible Soils Using a Modified Triaxial Test Device. Geotech. Test. J. 37, 20130034. doi:10.1520/gtj20130034
Hou, X., Vanapalli, S. K., and Li, T. (2018). Water Infiltration Characteristics in Loess Associated with Irrigation Activities and its Influence on the Slope Stability in Heifangtai Loess highland, China. Eng. Geology 234, 27–37. doi:10.1016/j.enggeo.2017.12.020
Itasca Consulting Group (2018). Itasca Flac3D V6.0, Fast Lagrangian Analysis of Continua in 3 Dimensions, User’s Guide. Minneapolis, Minnesota: Itasca Consulting Group, Inc.
Iverson, R. M., Reid, M. E., Iverson, N. R., Lahusen, R. G., Logan, M., Mann, J. E., et al. (2000). Acute Sensitivity of Landslide Rates to Initial Soil Porosity. Science 290, 513–516. doi:10.1126/science.290.5491.513
Jiang, M., Zhang, F., Hu, H., Cui, Y., and Peng, J. (2014). Structural Characterization of Natural Loess and Remolded Loess under Triaxial Tests. Eng. Geology 181, 249–260. doi:10.1016/j.enggeo.2014.07.021
Jin, A. B., Deng, F. G., Li, L. F., and Zhang, M. Z. (2012). Research on Stability Mechanism of Fissured Loess Slope Influenced by Rainfall and Evaporation. Amm 170-173, 380–385. doi:10.4028/www.scientific.net/AMM.170-173.380
Juang, C. H., Dijkstra, T., Wasowski, J., and Meng, X. (2019). Loess Geohazards Research in China: Advances and Challenges for Mega Engineering Projects. Eng. Geology 251, 1–10. doi:10.1016/j.enggeo.2019.01.019
Krzeminska, D. M., Bogaard, T. A., Malet, J.-P., and Van Beek, L. P. H. (2013). A Model of Hydrological and Mechanical Feedbacks of Preferential Fissure Flow in a Slow-Moving Landslide. Hydrol. Earth Syst. Sci. 17, 947–959. doi:10.5194/hess-17-947-2013
Leng, X., Wang, C., Sheng, Q., Chen, J., and Li, H. (2021). An Enhanced Ubiquitous-Joint Model for a Rock Mass with Conjugate Joints and its Application on Excavation Simulation of Large Underground Caverns. Front. Earth Sci. 9, 744900. doi:10.3389/feart.2021.744900
Li, Q., Wang, Y. M., Zhang, K. B., Yu, H., and Tao, Z. Y. (2020). Field Investigation and Numerical Study of a Siltstone Slope Instability Induced by Excavation and Rainfall. Landslides 17, 1485–1499. doi:10.1007/s10346-020-01396-5
Liang, C., Cao, C., and Wu, S. (2018). Hydraulic-mechanical Properties of Loess and its Behavior when Subjected to Infiltration-Induced Wetting. Bull. Eng. Geol. Environ. 77, 385–397. doi:10.1007/s10064-016-0943-x
Liu, D. (2002). Loess and Environment. J. Xi'an Jiaotong Univ. (Social Sci. Edition) 62, 7–12. doi:10.15896/j.xjtuskxb.2002.04.002
Liu, J., Li, X. A., Xue, Q., and Guo, Z. (2020). Experimental Study on Air Permeability and Microscopic Mechanism of Intact and Remolded Malan Loess, Loess Plateau, China. Bull. Eng. Geol. Environ. 79, 3909–3919. doi:10.1007/s10064-020-01810-1
Luo, H., Wu, F., Chang, J., and Xu, J. (2018). Microstructural Constraints on Geotechnical Properties of Malan Loess: A Case Study from Zhaojiaan Landslide in Shaanxi Province, China. Eng. Geology 236, 60–69. doi:10.1016/j.enggeo.2017.11.002
Ma, J., Tang, H., Hu, X., Bobet, A., Zhang, M., Zhu, T., et al. (2016). Identification of Causal Factors for the Majiagou Landslide Using Modern Data Mining Methods. Landslides 14, 311–322. doi:10.1007/s10346-016-0693-7
Mirus, B. B., Becker, R. E., Baum, R. L., and Smith, J. B. (2018). Integrating Real-Time Subsurface Hydrologic Monitoring with Empirical Rainfall Thresholds to Improve Landslide Early Warning. Landslides 15, 1909–1919. doi:10.1007/s10346-018-0995-z
Pu, X., Wan, L., and Wang, P. (2021). Initiation Mechanism of Mudflow-like Loess Landslide Induced by the Combined Effect of Earthquakes and Rainfall. Nat. Hazards. 105, 3079–3097. doi:10.1007/s11069-020-04442-6
Pu, X., Wang, L., Wang, P., and Chai, S. (2020). Study of Shaking Table Test of Seismic Subsidence Loess Landslides Induced by the Coupling Effect of Earthquakes and Rainfall. Nat. Hazards. 103, 923–945. doi:10.1007/s11069-020-04019-3
Springman, S. M., Thielen, A., Kienzler, P., and Friedel, S. (2013). A Long-Term Field Study for the Investigation of Rainfall-Induced Landslides. Géotechnique 63, 1177–1193. doi:10.1680/geot.11.P.142
Sun, P., Wang, G., Wu, L. Z., Igwe, O., and Zhu, E. (2019). Physical Model Experiments for Shallow Failure in Rainfall-Triggered Loess Slope, Northwest China. Bull. Eng. Geol. Environ. 78, 4363–4382. doi:10.1007/s10064-018-1420-5
Tan, F., Hu, X., He, C., Zhang, Y., Zhang, H., Zhou, C., et al. (2017). Identifying the Main Control Factors for Different Deformation Stages of Landslide. Geotech. Geol. Eng. 36, 469–482. doi:10.1007/s10706-017-0340-7
Tang, Y. M., Xue, Q., Li, Z. G., and Feng, W. (2015). Three Modes of Rainfall Infiltration Inducing Loess Landslide. Nat. Hazards. 79, 137–150. doi:10.1007/s11069-015-1833-4
Tu, X. B., Kwong, A. K. L., Dai, F. C., Tham, L. G., and Min, H. (2009). Field Monitoring of Rainfall Infiltration in a Loess Slope and Analysis of Failure Mechanism of Rainfall-Induced Landslides. Eng. Geology 105, 134–150. doi:10.1016/j.enggeo.2008.11.011
van Genuchten, M. T. (1980). A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. America J. 44, 892–898. doi:10.2136/sssaj1980.03615995004400050002x
Wang, G., Sun, P., Wu, L., Shi, L., and Zhu, E. (2017). Experimental Study on Mechanism of Shallow Loess Landslides Induced by Rainfall. J. Eng. Geology 25, 1252–1263. doi:10.13544/j.cnki.jeg.2017.05.010
Wang, H., Sun, P., Zhang, S., Han, S., Li, X., Wang, T., et al. (2020). Rainfall-induced Landslide in Loess Area, Northwest China: a Case Study of the Changhe Landslide on September 14, 2019, in Gansu Province. Landslides 17, 2145–2160. doi:10.1007/s10346-020-01460-0
Wang, J.-J., Liang, Y., Zhang, H.-P., Wu, Y., and Lin, X. (2014). A Loess Landslide Induced by Excavation and Rainfall. Landslides 11, 141–152. doi:10.1007/s10346-013-0418-0
Wang, J., Xu, Y., Ma, Y., Qiao, S., and Feng, K. (2018). Study on the Deformation and Failure Modes of Filling Slope in Loess Filling Engineering: a Case Study at a Loess Mountain Airport. Landslides 15, 2423–2435. doi:10.1007/s10346-018-1046-5
Wang, J., Zhang, D., Wang, N., and Gu, T. (2019). Mechanisms of Wetting-Induced Loess Slope Failures. Landslides 16, 937–953. doi:10.1007/s10346-019-01144-4
Wang, T.-T., and Huang, T.-H. (2014). Anisotropic Deformation of a Circular Tunnel Excavated in a Rock Mass Containing Sets of Ubiquitous Joints: Theory Analysis and Numerical Modeling. Rock Mech. Rock Eng. 47, 643–657. doi:10.1007/s00603-013-0405-8
Wang, W., Wang, Y., Sun, Q., Zhang, M., Qiang, Y., and Liu, M. (2018). Spatial Variation of Saturated Hydraulic Conductivity of a Loess Slope in the South Jingyang Plateau, China. Eng. Geology 236, 70–78. doi:10.1016/j.enggeo.2017.08.002
Wang, Y., Liu, H., Huang, M., Xu, M., and Liu, K. (2019). Experimental Study on Collapsibility of Luochuan Loess under Low Load. Sci. Tech. Engrg. 19, 310–316.
Wen, B.-P., and Yan, Y.-J. (2014). Influence of Structure on Shear Characteristics of the Unsaturated Loess in Lanzhou, China. Eng. Geology. 168, 46–58. doi:10.1016/j.enggeo.2013.10.023
Wu, L. Z., Zhou, Y., Sun, P., Shi, J. S., Liu, G. G., and Bai, L. Y. (2017). Laboratory Characterization of Rainfall-Induced Loess Slope Failure. Catena 150, 1–8. doi:10.1016/j.catena.2016.11.002
Xing, X., Li, T., and Fu, Y. (2016). Determination of the Related Strength Parameters of Unsaturated Loess with Conventional Triaxial Test. Environ. Earth Sci. 75, 11. doi:10.1007/s12665-015-4797-5
Xu, L., and Coop, M. R. (2016). Influence of Structure on the Behavior of a Saturated Clayey Loess. Can. Geotech. J. 53, 1026–1037. doi:10.1139/cgj-2015-0200
Xu, L., Coop, M. R., Zhang, M., and Wang, G. (2018). The Mechanics of a Saturated Silty Loss and Implications for Landslides. Eng. Geology 236, 29–42. doi:10.1016/j.enggeo.2017.02.021
Xu, L., Dai, F., Tu, X., Tham, L. G., Zhou, Y., and Iqbal, J. (2014). Landslides in a Loess Platform, North-West China. Landslides 11, 993–1005. doi:10.1007/s10346-013-0445-x
Xu, Y., Leung, C. F., Yu, J., and Chen, W. (2018). Numerical Modelling of Hydro-Mechanical Behaviour of Ground Settlement Due to Rising Water Table in Loess. Nat. Hazards 94, 241–260. doi:10.1007/s11069-018-3385-x
Yan, C.-g., Wan, Q., Xu, Y., Xie, Y., and Yin, P. (2018). Experimental Study of Barrier Effect on Moisture Movement and Mechanical Behaviors of Loess Soil. Eng. Geology 240, 1–9. doi:10.1016/j.enggeo.2018.04.007
Zhang, L., Qi, S., Ma, L., Guo, S., Li, Z., Li, G., et al. (2020). Three-dimensional Pore Characterization of Intact Loss and Compacted Loess with Micron Scale Computed Tomography and Mercury Intrusion Porosimetry. Sci. Rep. 10, 1–15. doi:10.1038/s41598-020-65302-8
Zhang, M., and Li, T. (2011). Triggering Factors and Forming Mechanism of Loess Landslides. J. Eng. Geology 19, 530–540. doi:10.1007/s12182-011-0118-0
Zhang, S., Pei, X. J., Wang, S. Y., Huang, R. Q., and Zhang, X. C. (2020). Centrifuge Model Testing of Loess Landslides Induced by Excavation in Northwest China. Int. J. Geomech. 20, 1–18. doi:10.1061/(asce)gm.1943-5622.0001619
Zhang, S., Zhang, X., Pei, X., Wang, S., Huang, R., Xu, Q., et al. (2019). Model Test Study on the Hydrological Mechanisms and Early Warning Thresholds for Loess Fill Slope Failure Induced by Rainfall. Eng. Geology 258, 1–14. doi:10.1016/j.enggeo.2019.05.012
Zhou, Y. F., Tham, L. G., Yan, R. W. M., and Xu, L. (2014a). The Mechanism of Soil Failures along Cracks Subjected to Water Infiltration. Comput. Geotechnics 55, 330–341. doi:10.1016/j.compgeo.2013.09.009
Zhou, Y. F., Tham, L. G., Yan, W. M., Dai, F. C., and Xu, L. (2014b). Laboratory Study on Soil Behavior in Loess Slope Subjected to Infiltration. Eng. Geology 183, 31–38. doi:10.1016/j.enggeo.2014.09.010
Zhuang, J., Peng, J., Wang, G., Javed, I., Wang, Y., and Li, W. (2018). Distribution and Characteristics of Landslide in Loess Plateau: A Case Study in Shaanxi Province. Eng. Geology 236, 89–96. doi:10.1016/j.enggeo.2017.03.001
Keywords: fissured loess slope, hydraulic-mechanical property, seepage fissure, deformation development mechanism, stabilisation treatment, landslide hazard
Citation: Leng X, Wang C, Zhang J, Sheng Q, Cao S and Chen J (2021) Deformation Development Mechanism in a Loess Slope With Seepage Fissures Subjected to Rainfall and Traffic Load. Front. Earth Sci. 9:769257. doi: 10.3389/feart.2021.769257
Received: 01 September 2021; Accepted: 20 September 2021;
Published: 05 October 2021.
Edited by:
Min Wang, Los Alamos National Laboratory (DOE), United StatesCopyright © 2021 Leng, Wang, Zhang, Sheng, Cao and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xianlun Leng, eGxsZW5nQHdocnNtLmFjLmNu
†These authors have contributed equally to this work and share first authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.