Microbial Alkalinity Production and Silicate Alteration in Methane Charged Marine Sediments: Implications for Porewater Chemistry and Diagenetic Carbonate Formation

A numerical reaction-transport model was developed to simulate the effects of microbial activity and mineral reactions on the composition of porewater in a 230-m-thick Pleistocene interval drilled in the Peru-Chile Trench (Ocean Drilling Program, Site 1230). This site has porewater profiles similar to those along many continental margins, where intense methanogenesis occurs and alkalinity surpasses 100 mmol/L. Simulations show that microbial sulphate reduction, anaerobic oxidation of methane, and ammonium release from organic matter degradation only account for parts of total alkalinity, and excess CO₂ produced during methanogenesis leads to acidification of porewater. Additional alkalinity is produced by slow alteration of primary aluminosilicate minerals to kaolinite and SiO₂. Overall, alkalinity production in the methanogenic zone is sufficient to prevent dissolution of carbonate minerals; indeed, it contributes to the formation of cemented carbonate layers at a supersaturation front near the sulphate-methane transition zone. Within the methanogenic zone, carbonate formation is largely inhibited by cation diffusion but occurs rapidly if cations are transported into the zone via fluid conduits, such as faults. The simulation presented here provides fundamental insight into the diagenetic effects of the deep biosphere and may also be applicable for the long-term prediction of the stability and safety of deep CO₂ storage reservoirs.

Introduction

Microbial activity below the seafloor (in the deep biosphere) affects global cycling of carbon. In sediments on many continental margins, microbes convert buried organic matter through a series of reactions to methane (CH₄) and dissolved inorganic carbon (DIC), both of which can return back to the water column through advection or diffusion (e.g., Dickens, 2003; Krumins et al., 2013). In some areas, high rates of organic carbon decomposition lead to oversaturation of porewater with respect to different carbonate minerals (e.g., Baker and Burns, 1985; Moore et al., 2004; Meister et al., 2006; Meister et al., 2007; Meister, 2015; Wehrmann et al., 2016). Precipitation of diagenetic carbonates can even occur within carbonate-free ocean margin sediment sequences (e.g., Pisciotto and Mahoney, 1981; Kelts and McKenzie, 1984; Baker and Burns, 1985). Importantly, these carbonates add to the total worldwide carbon burial flux, and variations in their accumulation over time may have contributed to past changes in global carbon cycling, such as during times of widespread anoxia (Schrag et al., 2013; Sun and Turchyn, 2014). Nevertheless, gaps remain in the understanding of organic carbon decomposition and diagenetic carbonate formation, particularly in sediment sequences characterized by strong methanogenesis.

While production of DIC drives diagenetic carbonate precipitation, a simultaneous increase in the pH buffering capacity and total alkalinity must happen to increase the activity of dissolved CO₃²⁻ and, hence, the saturation state with respect to various carbonate phases. The total alkalinity (titration alkalinity) has been defined as “excess of proton acceptors over donors with respect to carbonic acid”: TA = [HCO₃⁻] + 2 [CO₃²⁻] + [OH⁻] + [B(OH)₄⁻] + [HPO₄²⁻] + 2 [PO₄³⁻] + [H₃SiO₄⁻] + [NH₃] + [HS⁻] + 2 [S²⁻] − [H⁺] − [HF] − [HSO₄⁻] − [H₃PO₄] (Dickson, 1981; Middelburg et al., 2020). Several microbially mediated reactions increase alkalinity, including iron-reduction (Raiswell and Fisher, 2000; Wehrmann et al., 2009), organoclastic sulphate reduction (OSR), and anaerobic oxidation of methane (AOM; Moore et al., 2004; Ussler and Paull, 2008; Meister, 2013). In general, these processes progress with depth below the seafloor, according to their redox potential and free energy yield (e.g., Froelich et al., 1979). They also affect alkalinity differently. Notably, OSR produces two moles of DIC and two moles of alkalinity per mole of sulphate consumed, with a 1:1 ratio of TA:DIC (Eq. 1):

$\mathrm{S}{\mathrm{O}}_4^{2-}+2\left[\mathrm{C}{\mathrm{H}}_2\mathrm{O}\right]\to \mathrm{H}{\mathrm{S}}^{-}+2\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{-}+{\mathrm{H}}^{+}(1)$

By contrast, AOM generates more alkalinity relative to DIC (TA:DIC = 2:1; Eq. 2):

$\mathrm{S}{\mathrm{O}}_4^{2-}+\mathrm{C}{\mathrm{H}}_4\to \mathrm{H}{\mathrm{S}}^{-}+\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{-}+{\mathrm{H}}_2\mathrm{O}(2)$

In the absence of any terminal electron acceptor, subseafloor fermentation of organic matter can still occur, releasing CH₄, organic acids, and CO₂ to porewater. A dominant overall process is “methanogenesis”, which proceeds mainly through autotrophic reduction of CO₂ with H₂ as an electron donor (Conrad, 1999; Meister and Reyes, 2019):

$2 \left[{\text{CH}}_2\text{O}\right]\stackrel{+2{\text{H}}_2\text{O}}{\to }2{\text{ CO}}_2+4{\text{ H}}_2\stackrel{-2{\text{H}}_2\text{O}}{\to }{\text{CO}}_2+{\text{CH}}_4(3)$

Crucially, the overall pathway results in excess CO₂, but without producing further alkalinity.

A current problem in our collective knowledge of the deep biosphere and the role of methanogenesis for subseafloor biogeochemical processes revolves around the fate of CO₂ and extreme porewater alkalinity. Production of CO₂ (Eq. 3) should lead to acidification and undersaturation of porewater with respect to carbonate minerals. This is because CO₂ dissolves in water and generates protons, but does not change alkalinity (Eq. 4):

$\mathrm{C}{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\to \mathrm{H}\mathrm{C}{\mathrm{O}}_3^{-}+{\mathrm{H}}^{+}(4)$

However, porewaters along continental margins and within zones of significant methanogenesis consistently exhibit very high alkalinity, often exceeding 50 mmol/L (Figure 1) and sometimes surpassing 160 mmol/L (Wefer et al., 1998). Furthermore, the high alkalinity mostly reflects dissolved HCO₃⁻ concentrations (except near depths of HS⁻ production), the pH usually exceeds 7, and early diagenetic carbonate (dolomite) often has positive δ¹³C values, indicative of precipitation under methanogenenic conditions (Claypool and Kaplan, 1974; Kelts and McKenzie, 1984). As side-stepped in various works (e.g., Chatterjee et al., 2011; Meister et al., 2011), there is a “lost proton problem”. How can sufficient alkalinity, as HCO₃⁻, occur in such sub-seafloor environments to the point of driving significant amounts of carbonate precipitation?

FIGURE 1

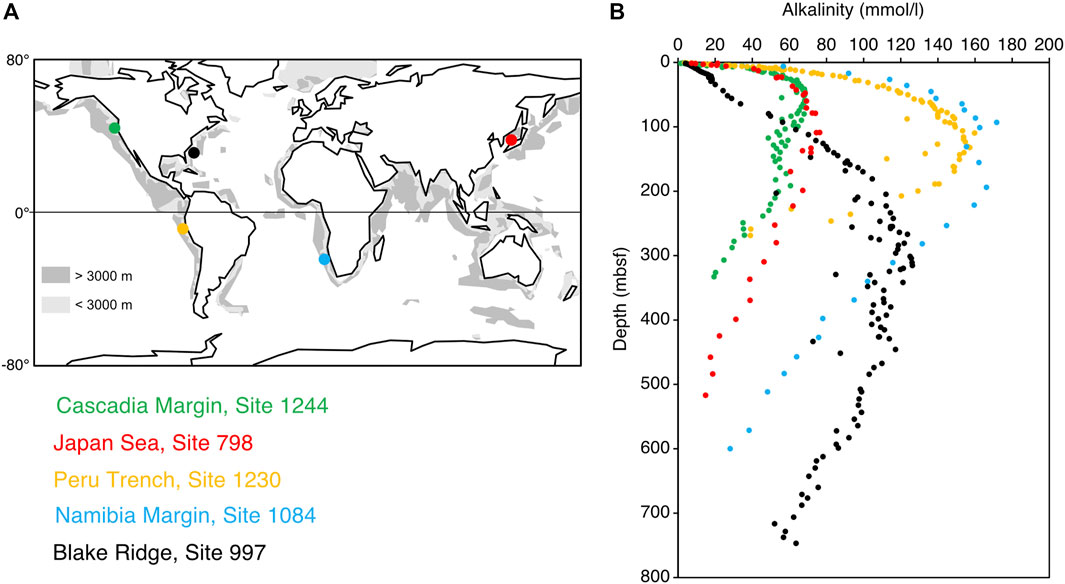
FIGURE 1. Global map showing representative ODP sites along continental margins with thick methanogenic zones (A) and compilation of their porewater alkalinity profiles with respect to metres below seafloor (mbsf), highlighting greatly elevated alkalinity in the upper few hundreds of metres of sediment (B). Data are from Ingle et al. (1990; Japan Sea, Site 798), Paull et al. (1996; Blake Ridge, Site 997), Wefer et al. (1998; Namibia Margin, Site 1084), D’Hondt et al. (2003; Peru Margin, Site 1230), and Tréhu et al. (2003; Hydrate Ridge, Site 1244).

Several additional sources of alkalinity in marine sediments have been discussed in previous studies (e.g., Chatterjee et al., 2011; Meister et al., 2011). Given a nominal C/N ratio >7:1, organic matter degradation generally produces ammonia in most continental margin sediments (e.g., Arndt et al., 2013). Due to uptake of a proton, each mole of NH₄⁺ (from NH₃) also produces one mole of alkalinity:

$\mathrm{N}{\mathrm{H}}_3+{\mathrm{H}}^{+}\to \mathrm{N}{\mathrm{H}}_4^{+}(5)$

While NH₄⁺ accumulates in the porewater, it may adsorb to clay mineral surfaces, in exchange for Ca²⁺ and Mg²⁺, which are readily released into the porewater (Von Breymann et al., 1990; Ockert et al., 2014; Mavromatis et al., 2015). Dissolved organic species, which almost certainly form in methanogenic systems, also need consideration (Smith, 2005).

Several authors (e.g., Aloisi et al., 2004; Wallmann et al., 2008; Meister et al., 2011; Archer et al., 2012; Solomon et al., 2014) have suggested that alteration of silicate minerals, particularly clay minerals, occurs within methanogenic zones and may produce sufficient alkalinity to drive diagenetic carbonate precipitation. At low pH and low temperatures, silicates may alter to secondary minerals by loss of oxides of alkali and earth alkali metals, which react to hydroxides upon protonation, thereby buffering acidification of dissolved CO₂ (Amiotte Suchet et al., 2003; Colbourn et al., 2015; Eq. 6):

$\mathrm{M}\mathrm{g}\mathrm{O}+2{\mathrm{H}}^{+}\to \mathrm{M}{\mathrm{g}}^{2+}+{\mathrm{H}}_2\mathrm{O}(6)$

Often silicate alteration reactions also show a loss of SiO₂, which upon water uptake reacts to H₄SiO₄ and which, hence, does not contribute to total alkalinity production. As a consequence of Eq. 6, alkalinity also can be expressed by the balance of conservative ions. This has been shown by Wolf-Gladrow et al. (2007), who derived an explicit conservative expression of total alkalinity: TA_ec = [Na⁺] + 2 [Mg²⁺] + 2 [Ca²⁺] + [K⁺] − [Cl⁻] − [TNH₃] − 2 [TSO₄] (here only including the components relevant for the considered system). The advantage of this expression is that all parameters are conservative and can be directly measured. TA_ec also provides a clearer understanding of how mineral reactions affect the porewater alkalinity.

Both ion exchange with NH₄⁺ and silicate mineral alteration may enrich porewaters in dissolved Mg²⁺, Na⁺, and K⁺ (Von Breymann et al., 1990; Wallmann et al., 2008), while Ca²⁺ typically becomes depleted due to carbonate precipitation. But which scenario is correct, and why and how extremely high alkalinity arises in zones of high microbial activity, remains unclear. Understanding the production of alkalinity and its effect on carbonate equilibrium is not only essential for understanding diagenetic carbonate formation and the natural carbon cycle, but also links to long-term storage of CO₂ in geological rock reservoirs (Bickle et al., 2007; Kasina et al., 2014).

In this study, we examine data from Ocean Drilling Program (ODP) Site 1230 on the Peru Margin (D’Hondt et al., 2003; Donohue et al., 2006). This site was drilled to examine microbiological and porewater expressions in an exemplary modern-day methanogenic system. Although Site 1230 has one of the most complete porewater datasets in ocean drilling history, the available information has yet to be placed into context. We developed a numerical reaction-transport model to simulate alkalinity production and its effect on the carbonate equilibrium as a result of microbial activity and mineral reactions in natural methanogenic zones over millions of years. Rates of microbial metabolic reactions (OSR and methanogenesis) are linked to an overall organic matter degradation rate. The rate of organic matter degradation (R_TOC; TOC = total organic carbon) was determined using a presumed decay function and determining the decay parameters by fitting the simulated porewater profiles to the measured porewater data. Also rates of ion exchange on clay mineral surfaces and rates of dissolution/precipitation of the minerals detected by X-ray diffraction analysis were determined in this way. We then assessed how the different processes affect total alkalinity and carbonate saturation. This simulation aims at clarifying the longstanding enigma of how diagenetic carbonates form in deep methanogenic zones below the seafloor.

Study Site and Measured Porewater Profiles

Intense coastal upwelling and high primary productivity characterize surface waters along the Peruvian continental margin. In 2002, ODP Leg 201 drilled and cored Site 1230 on the lower slope of the Peru margin (9° 6.7525′ S / 80° 35.0100′ W; Supplementary Figure S1A) at 5,086 m water depth, and within 100 m from ODP Site 685. The site comprises five holes (A-E), from which cores collected sediment to 278 m below seafloor (mbsf). Except for a few short pressure cores to collect gas, sediment recovery over the upper 216 m was accomplished using an advanced hydraulic piston core (APC) tool while recovery below this depth was accomplished mostly using an extended core barrel (XCB) tool.

The overall sequence has two main lithological units, which match those recovered at Site 685 (Supplementary Figure S1B; D’Hondt et al., 2003). The upper 230 m (Unit I) consist of Pleistocene-Holocene diatom ooze with variable mud content, traces of biogenic carbonate (nannofossils and foraminifera) and commonly pyrite. Total organic carbon content ranges between 2 and 3.5 wt%, with a nearly constant C/N ratio of about 9 (Prokopenko et al., 2006). By contrast, total inorganic carbon (TIC) content of bulk sediment mostly lies below 0.2 wt%, but reaches up to 1 wt% in the middle part of the unit (Meister et al., 2005). A 10-m-scale cyclicity in chromaticity (D’Hondt et al., 2003) spans the upper 118 m and reflects alternating domains enriched in diatom-ooze or dark-green clay, presumably linked to glacial and interglacial intervals. A change in chromaticity coincides with an interval of lower diatom content between 118 and 148 mbsf. The clay-rich diatom ooze shows signs of increasing consolidation and fissility towards the base of Unit I (D’Hondt et al., 2003).

A sharp boundary at 216 mbsf delineates Unit I and Unit II, and marks a downward shift to strongly consolidated Miocene sediments. The boundary likely represents a décollement surface within the accretionary prism (D’Hondt et al., 2003; Matmon and Bekins, 2006), as it is characterized by a 20-cm-thick fault breccia cemented by syntectonic dolomite (Meister et al., 2011) and a ∼4 Ma gap in age (Suess 1988).

Porewater profiles show major changes in fluid composition with depth, including a steep and near linear negative sulphate gradient with a thin sulphate-methane transition zone (SMT) at approximately 9 mbsf. Sulphide reaches ca. 10 mmol/L at the SMT and decreases to zero at 20 mbsf. Below the SMT, a methanogenic zone prevails throughout the sequence. Extremely high concentrations of up to 300 mmol/L methane were reconstructed by Spivack et al. (2006), and gas hydrates were detected at 82 and 148 mbsf (D’Hondt et al., 2003). Measured DIC and alkalinity both reach concentrations of more than 150 mmol/L near 150 mbsf (D’Hondt et al., 2003). Below 150 mbsf, alkalinity, ammonia, and Mg²⁺ concentrations decrease downwards towards the Unit I-II boundary (D’Hondt et al., 2003; Donohue et al., 2006). A sudden change in porewater chemistry occurs at this depth (D’Hondt et al., 2003), as indicated by more radiogenic Sr isotope values; likely this is due to fluid transported along the fault (Kastner et al., 1990; Meister et al., 2011).

Material and Methods

Mineral Analysis

Sediment samples from ODP Site 1230 were selected from undisturbed core sections recovered from 6 to 254 mbsf. For bulk mineralogical analysis, powdered sediment samples were analysed by X-ray diffraction (XRD) using a Panalytical X’Pert PRO diffractometer (Cu-Kα radiation, 40 kV, 40 mA, step size 0.0167, 5 s per step).

For clay mineral separations, six sediment samples were slightly crushed by hand to pieces of approximately 3 mm. Organic matter was removed by oxidation with diluted H₂O₂, and the samples were further disaggregated with a 400 W ultrasonic probe for 3 min. The <2 μm grain-size fraction was separated from bulk sediment by sedimentation in an Atterberg-cylinder for 24 h and 33 min (Engelhardt et al., 1974; Gaucher et al., 2004) and dried at 50°C. The homogenized samples were then saturated with K⁺ and Mg²⁺ ions and oriented samples were prepared by dispersing 10 mg of clay in 1 ml of water, pipetting the suspensions onto glass slides, and drying at room temperature. The oriented, K- and Mg-saturated samples were analysed in air-dried state and after vapour solvation with either ethylene glycol (K-samples) or glycerol (Mg-samples) at 60°C for 24 h to identify expandable clay minerals like smectite and vermiculite. Additional K-saturated samples were heated to 550°C to destroy kaolinite and expandable clay minerals (Eslinger and Pevear, 1988; Jasmund and Lagaly, 1993; Moore and Reynolds, 1997).

Reaction Transport Model

Concentrations of dissolved species were simulated with a one-dimensional reaction-transport model (Figure 2) according to Fick’s second law of diffusion in the form given by Boudreau (1997):

$\frac{\partial \mathrm{\varphi }\mathrm{C}}{\partial \mathrm{t}}=-\frac{\partial \mathrm{\varphi }\mathrm{\omega C}}{\partial \mathrm{z}}+\frac{\partial }{\partial \mathrm{z}}\left(\frac{\mathrm{\varphi }\mathrm{D}}{{\mathrm{\tau }}^2}\cdot \frac{\partial \mathrm{C}}{\partial \mathrm{z}}\right)\pm {{\displaystyle \sum }}^{\text{}}\mathrm{\varphi }\mathrm{R}(7)$

where C is the concentration of a solute (mmol/L), z is the depth in metres below seafloor (mbsf), dt is the time interval (years), and ϕ is porosity. The first term on the righthand side is a downward advection term, simulating burial with the sedimentation rate ω, whereby a steady-state compaction (dϕ/dt = 0; ϕ⋅ω is constant) was assumed. The downward decreasing porosity was calculated as:

$\mathrm{\varphi }\left(\mathrm{z}\right)={\mathrm{\varphi }}_{\mathrm{\infty }}+\left({\mathrm{\varphi }}_0-{\mathrm{\varphi }}_{\mathrm{\infty }}\right){\mathrm{e}}^{-\mathrm{z}/\mathrm{b}}(8)$

where ϕ₀ and ϕ_∞ are constant porosities at sediment depth z = 0 and ∞, respectively, and b is the porosity e-folding distance (the distance over which (ϕ₀–ϕ_∞) decreases by a factor of e).

FIGURE 2

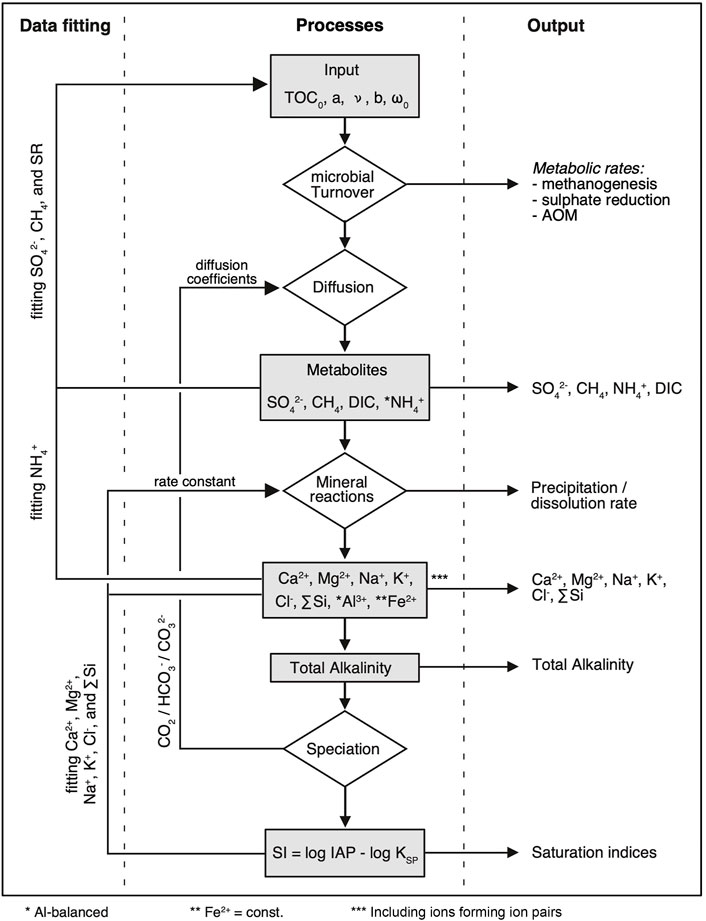
FIGURE 2. Flow chart representation of the basic reaction-transport and precipitation model, including feedbacks, data fitting, and output. TOC₀ is the initial total organic carbon content (wt%) at the time of sediment deposition. The parameters a and ν describe the function of organic matter degradation according to Boudreau and Ruddick (1991), ω is the sedimentation rate after compaction, and b defines the compaction with depth. AOM = anaerobic oxidation of methane.

The second term on the righthand side of Eq. 7 accounts for diffusion, where D is the diffusion constant (m²/s; see below). The tortuosity τ was calculated from porosity according to Boudreau (1997):

${\text{τ}}^2=1-\text{ln}{\mathrm{\varphi }}^2(9)$

The third term on the righthand side of Eq. 7 represents any source or sink (or combination thereof), where R is the rate of production or consumption of the solute (mmol L⁻¹ a⁻¹). For dissimilatory metabolic reactions (sulphate reduction and methanogenesis, according to Eqs 1, 3), the source and sink terms are stoichiometrically related to the degradation rate of TOC. The degradation of TOC was calculated using the reactive continuum (RC) model of Boudreau and Ruddick (1991):

$\text{TOC}\left(\text{t}\right)={\text{TOC}}_0{\left[\frac{{\text{a}}_{\text{RC}}}{\left({\text{a}}_{\text{RC}}+\text{t}\right)}\right]}^{\text{ν}}(10)$

where TOC(t) is the TOC at sediment age t, TOC₀ is the initial TOC upon sedimentation, and a_RC and ν are fitting parameters in the reactive continuum model. The source/sink s_TOC was calculated from the derivative of organic matter decay after time:

${\text{s}}_{\text{TOC}}=\partial \left(\frac{{\text{TOC ρ}}_{\text{s}}(1-\varphi )}{100{\text{ M}}_{\text{C}}\mathrm{\varphi }}\right)/\partial \text{t}(11)$

where ρ_s is the density of the dry sediment and M_C is the molecular weight of carbon. Also, TOC degradation is linked stoichiometrically to the release of ammonium via a prescribed C/N ratio.

For sulphate reduction and AOM, a Monod kinetic term was applied (Treude et al., 2003; Arndt et al., 2006; Arndt et al., 2009; Knab et al., 2008):

${\text{s}}_{\text{AOM}}={\text{k}}_{\text{AOM}}\left[{\text{CH}}_4\right]\frac{\left[{\text{SO}}_4^{2-}\right]}{{\text{K}}_{\text{S},\text{AOM}}+\left[{\text{SO}}_4^{2-}\right]}(12)$

where K_s and K_AOM are the half saturation constants for sulphate reduction and AOM, respectively, and k_AOM is the first-order rate constant for methane. Most sulphide produced by sulphate reduction is consumed by Fe-sulphide formation at the sulphide-iron front below the SMT. To calculate the sink of sulphide, FeS-precipitation was stoichiometrically coupled with reductive dissolution of Fe, with a Monod-term to limit reaction at very small sulphide concentrations. The rate constant was varied to fit the measured sulphide profile.

Due to the high pressure and low temperature at >5,000 m water depth, free gas phase should not reside within the porewater over the upper few hundred metres below the seafloor. However, dissolved CH₄ concentrations can surpass those for gas hydrate saturation. The saturation conditions were calculated according to an approach given by Tishchenko et al. (2005), based on Duan et al. (1992). Gas hydrate formation and dissociation was included in the transport model as a source/sink-term, with a rate depending on the oversaturation of dissolved CH₄. Burial of the solid phase (given in mmol equivalents per litre of porewater) was calculated using the sedimentation rate.

Cation Exchange on Mineral Surfaces

For the calculation of cation exchange on clay minerals, we assumed that adsorbed ions are in equilibrium with surrounding pore fluids. This is justified, because radiotracer experiments (Ockert et al., 2014) show that Ca²⁺-NH₄⁺ exchange occurs very rapidly, over a few hours. The conditional exchange coefficients (K_Ex) were found by solving a partition function with respect to ammonium for each cation (here exemplary for Ca²⁺):

${\text{K}}_{\text{NH}4-\text{Ca}}=\frac{{\text{X}}_{\text{NH}4}^2}{{\text{X}}_{\text{Ca}}}\cdot \frac{\left[\text{Ca}\right]}{{\left[{\text{NH}}_4\right]}^2}(13)$

and by assuming the sum of all mole fractions (X) equals to one (Boatman and Murray, 1982). The cation concentrations were fitted to the porewater concentrations by varying the exchange coefficients. Rates of adsorption and desorption were calculated from the depth gradients of each adsorbed ion times the burial velocity and were included as source/sink terms in the reaction-transport function.

Speciation and Mineral Reactions

Measured concentrations of dissolved ions in porewater of marine sediment generally do not account for speciation. For example, Mg concentrations determined via inductively coupled plasma atomic emission spectrometry, such as done on ODP Leg 201, inextricably include those from Mg²⁺, MgCl⁺, and MgSO₄⁽⁰⁾ (e.g., Katz and Ben-Yaakov, 1980). For the aqueous speciation and calculation of mineral saturation states the program Phreeqc (Version 3.5.0; Parkhurst and Appelo, 2013) was used. The reaction-transport model was linked to the PhreeqRM module (Parkhurst and Wissmeier, 2015). From the initial ion concentrations (here assumed as seawater concentrations), an initial (hypothetical) solution containing up to 90 species was calculated (Figure 2). The speciation was then renewed at each time step. Charge balance during transport was maintained, using the correction factor for Coulombic effects (Boudreau et al., 2004) and leaving chloride concentration variable. Charge balance also was maintained for reactions. The program determines ion activity product (IAP) and the solubility product (K_SP).

The saturation indices (SI = log IAP – log K_SP) of calcite, dolomite, and all silicate phases detected by XRD were calculated for in-situ temperature and pressure conditions. Rates of mineral precipitation or dissolution were calculated as k·SI (cf. Lasaga, 1998; Morse et al., 2007), whereby the rate constants k were assumed to exponentially decrease with depth, and the decay parameters were found by fitting the porewater profiles to measured data (Supplementary Material). Sources and sinks of ions were calculated in stoichiometric proportion to the amounts of mineral dissolved or precipitated. Since Al in porewater is extremely depleted, it was not possible with the present model to simulate reaction rates with respect to Al species using a reasonable time step. For this reason, Al was kept constant at a meaningful concentration, i.e., at an intermediate concentration at which kaolinite remains always supersaturated while other silicate minerals remain undersaturated. Mineral dissolution and precipitation were then stoichiometrically coupled so that no Al was added to or removed from the solution.

Activity correction was calculated according to the Brønsted-Guggenheim-Satchard model (also known as specific ion interaction theory, SIT; Brønsted, 1921; Guggenheim and Turgeon, 1955), using the formalism presented by Grenthe and Plyasunov (1997; Eq. 14).

$\log {\text{γ}}_{\text{i}}=-\frac{0.51\cdot {\text{ z}}_{\text{i}}^2\sqrt{\text{I}}}{1+1.5{\text{ r}}_{\text{i}}\sqrt{\text{I}}}+{\displaystyle \sum }\text{k}{\mathrm{ϵ}}_{\text{i},\text{k}}{\text{ c}}_{\text{k}}(14)$

In Eq. 14 the activity coefficient γ_i is calculated for ion “i” as a function of ionic charge z, the ion radius r, the ionic strength I of the solution, and the sum of interactions with each ion k in the solution, with the interaction coefficient ϵ between ions “i” and “k” and the molar concentration c_k.

Parameterization and Boundary Conditions

The reaction-transport equation was solved using the finite differences method with an explicit-implicit scheme. The non-linear terms, including different source and sink terms, were solved explicitly. The simulations were run until a steady state was reached. All parameters, their symbols, values (or ranges), units, and references are listed in Table 1. The porewater concentration data used for fitting the model are mostly ODP Leg 201 shipboard data (D’Hondt et al., 2003; 2004) supplemented with shore-based measurements of Ca, K, Mg, and Na by Donohue et al. (2006). For the initial solution, major ion concentrations of seawater (Table 1) were used, and the calculated solution was also set at the seafloor as an upper domain boundary condition. Elevated DIC concentrations may occur in deep-sea bottom water due to accumulation of CO₂ from aerobic respiratory production (Zeebe, 2007), which accordingly affects the pH of the boundary condition. The lower domain boundary was defined at 230 mbsf, where the concentrations are assumed as constant. This stipulation is necessary because diverse species show a gradient across the lower boundary due to the influence of fluid advection along the fault at 230 mbsf.

TABLE 1

TABLE 1. List of parameters and values used for the reaction transport model.

A minimal long-term sedimentation rate of 0.1 m/ka was assumed based on the thickness of the Pleistocene-Holocene interval of 230 m according to the Leg 112 age model (Suess, 1988). The porosity function was fitted to the measured porosity data. Diffusion coefficients were calculated for P, T, and salinity at each depth, using the functions and constants given in Boudreau (1997). No temperature and pressure derivatives of the diffusion coefficients were considered, since these effects were determined to be negligible.

We used the rate constants of AOM given in Arndt et al. (2006) and references therein and the half-saturation constant for organoclastic sulphate reduction as reported by Tarpgaard et al. (2017). Initial TOC content and parameters a and ν were found by fitting the concentration profiles of metabolites, such as sulphate and ammonium to the measured data and by fitting the SMT to 9 mbsf (Supplementary Material). In particular, varying a and ν also affects the curvature of the sulphate profile (Meister et al., 2013). Production of NH₄⁺ was stoichiometrically linked to the rate of TOC-degradation, assuming a C/N ratio of 9 (Prokopenko et al., 2006; also consistent with ratios given in; Burdige and Komada, 2013).

Cation concentrations were fitted to the measured porewater data by varying the adsorption constants, using a CEC of 100 meq/100 g based on Ockert et al. (2014). The conditional exchange coefficients only control the relative proportions in which the ions are adsorbed or desorbed, and they were adjusted to fit the data. Downward decreasing dissolution rate constants for individual clay minerals were found by fitting the data (Supplementary Material), while the precipitation of kaolinite was linked via the transfer of aluminium (see discussion for details).

For speciation and calculation of saturation states we used the parameters in the database for the specific ion interaction theory, given in the Phreeqc package (sit.dat database). The minerals were selected from the database according to the mineral assemblage detected by XRD and according to their stoichiometric composition commonly observed in marine sediments (e.g., Marinoni et al., 2008; Park et al., 2019; Table 2). For thermodynamic calculations in-situ pressure and temperature at each depth were used, with a linear temperature gradient between the mudline-temperature of 1.7 and 11.2°C at 278 mbsf at Site 1230 (D’Hondt et al., 2003).

TABLE 2

TABLE 2. List of minerals and their stoichiometric compositions selected from the sit.dat database.

Analytical Results

Bulk Mineralogy

Bulk XRD-analyses (Figure 3A) show quartz (peak at 3.34 Å; 26.67° 2θ) as the most abundant phase. The second most abundant phase is feldspar, whereby albite/anorthite (3.19 Å; 27.92° 2θ) is more abundant than K-feldspar (3.24 Å, 27.53° 2θ) in all samples. Small amounts of mica or illite (peak-positions at 10 Å, 8.83° 2θ) are present in all samples. Calcite is detected in the samples from 6 mbsf and 57 to 144 mbsf. Two separate carbonate phases, a low-Mg calcite at 3.03 Å (29.4° 2θ) and a Mg calcite at 3.02 Å (29.5° 2θ), occur. A halite (NaCl) peak at 2.82 Å (31.7° 2θ) is usually present as the samples were not washed before analysis.

FIGURE 3

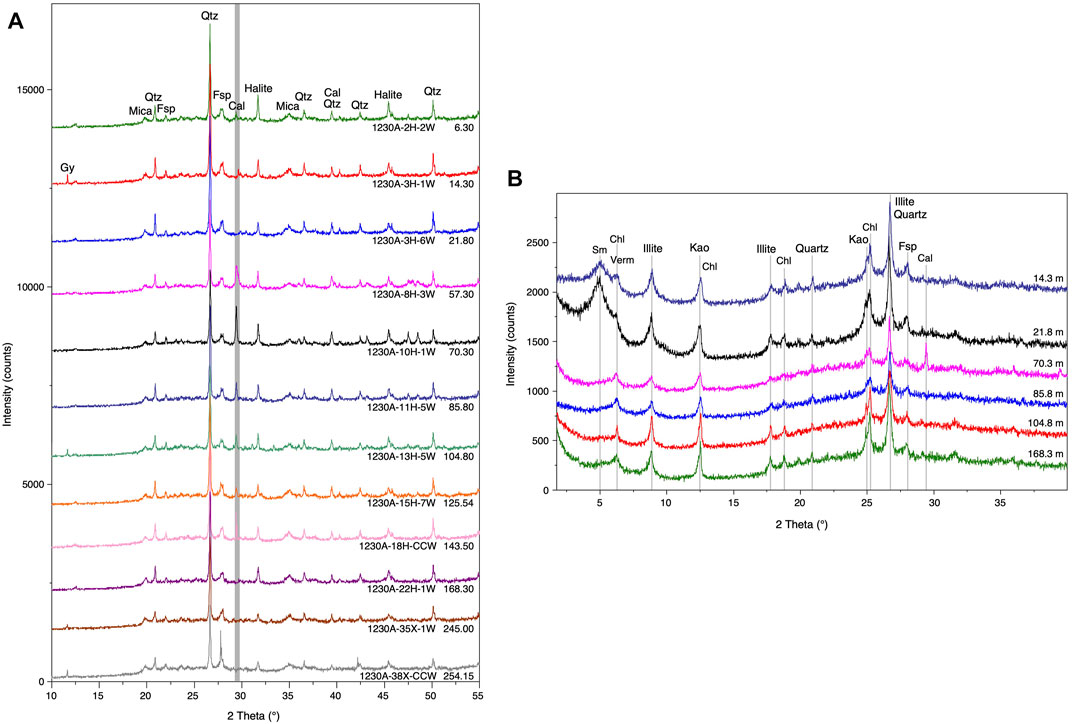
FIGURE 3. X-ray pattern of analysed sediment samples from ODP Site 1230. (A) Bulk sediment showing quartz (Qtz), feldspar (Fsp), mica, and calcite (Cal). The spectra are arranged in the sequence as they occur through the drilled core. Halite and gypsum (Gy) usually form due to evaporation during sample storage. (B) X-ray patterns of Mg-glycerol saturated clay fractions, arranged in the same sequence as they occur through the drilled core. The spectra were interpreted to indicate smectite (Sm), vermiculite (Verm), chlorite (Chl), kaolinite (Kao), and illite, based on comparison of spectra from the fractions treated with Mg-ions, K-saturated fractions treated with ethylene glycol, and fractions heated to 550°C (shown for sample 21.8 mbsf; Supplementary Material).

Clay Mineral Analysis

All analysed samples contain different amounts of smectite, vermiculite, chlorite, kaolinite, and illite (Figure 3B). Additionally, the clay fractions contain small amounts of quartz, feldspar, and calcite (only in one sample at 70.3 mbsf). Here, the identification of the clay minerals is explained for the sample from 21.8 mbsf (Supplementary Figure S2). Smectite was identified by a broad peak at 14.1 Å (6.3° 2θ) with Mg saturation which shifted to 11.8 Å (7.5° 2θ) with K saturation and collapsed to 9.9 Å (8.9° 2θ) after heating to 550°C. Saturation of the K-sample with ethylene glycol expanded smectite again to 16.8 Å (5.3° 2θ), the Mg-sample with glycerol to 18 Å (4.9° 2θ). Chlorite was identified by the peaks at 14.1, 7.07, 4.7 and 3.53 Å (6.3°, 12.5°, 18.8°, and 25.1° 2θ), which did not change position during treatments. Illite peaks at 9.9, 4.97 Å, and 3.33 Å (8.9°, 17.8°, and 26.7° 2θ) also kept their positions. Kaolinite peaks at 7.13 Å and 3.57 Å (12.4° and 24.9° 2θ) disappeared after heating to 550°C. Mg-saturated vermiculite was recognized based on a strong peak at 14 Å (6.3° 2θ), which shifted to 10 Å (8.83° 2θ) with K saturation, while saturation with Mg and glycerol (MgGly) did not change the 14 Å peak position (only present in traces in the sample from 21.8 mbsf, but more abundant in the other samples).

Looking at a depth plot of the Mg + glycerol saturated clay fractions (Figure 3B), it is obvious that only the uppermost two samples contain large amounts of smectite (18 Å, 4.9° 2θ). The deeper samples show only small smectite peaks, but additionally contain another expandable clay mineral, vermiculite (14 Å, 6.3° 2θ). Illite, chlorite, and kaolinite are present in samples of all depths.

Model Results and Discussion

Biogeochemical Reactions and Effects on Alkalinity

The basic parameters used for the geochemical simulation, temperature, pressure, sedimentation rate, porosity, TOC content, and C/N ratio were fitted as good as possible to the measured data (Figures 4A–D; Supplementary Figure S3). Modelled porewater profiles, shown in Figure 5, reach a steady state after <1 Ma, even though 2.3 Ma are needed for burial of the gas hydrates below 230 m at a sedimentation rate of 0.1 m/ka. Therefore, the time needed to reach a steady state is well within the time frame of deposition of the Pleistocene interval, throughout which the sediment composition does not fundamentally change. The geochemistry within the underlying Miocene interval is decoupled by fluid flow along the décollement, essentially setting the boundary conditions for the Pleistocene evolution of the porewater profiles.

FIGURE 4

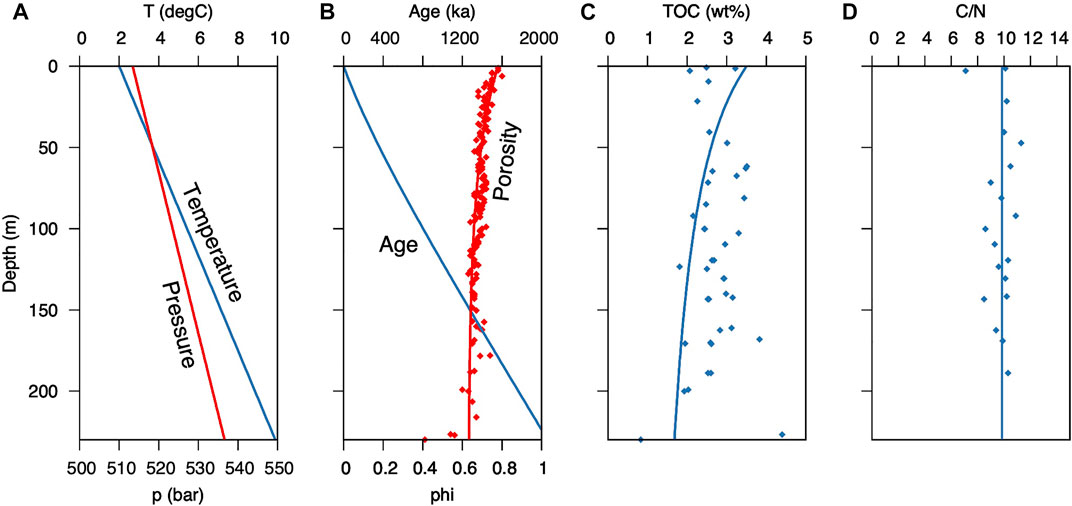
FIGURE 4. Sediment properties and organic matter content vs. depth at ODP Site 1230: (A) porewater temperature and hydrostatic pressure; (B) sediment age and porosity (data from D’Hondt et al., 2003); (C) total organic carbon content (data from Meister et al., 2005); (D) measured C/N ratios from Site 1230 (Prokopenko et al., 2006). The solid lines indicate the values assumed for the model.

FIGURE 5

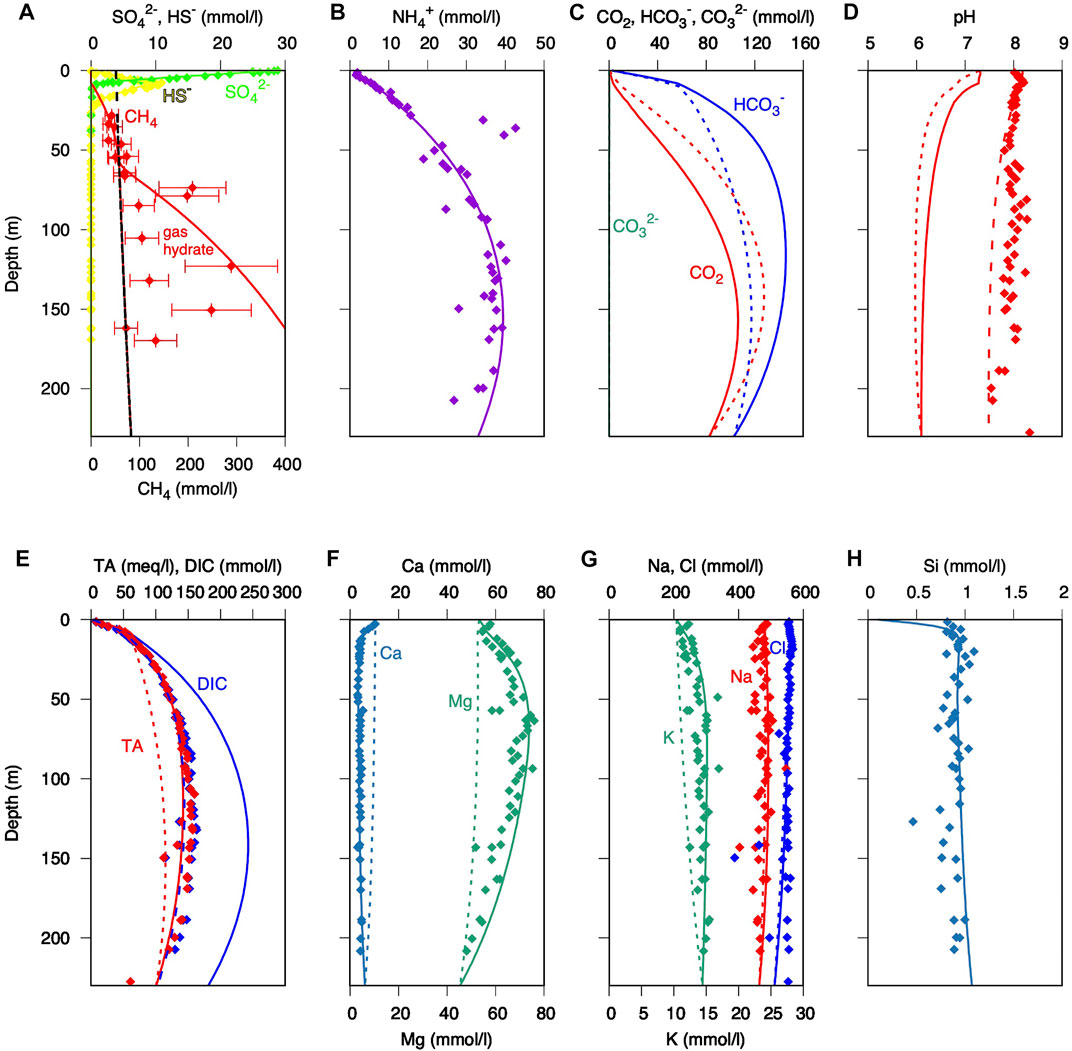
FIGURE 5. Measured (solid symbols) and simulated porewater concentration profiles (lines) vs. depth: (A) sulphate and methane; (B) ammonium; (C) inorganic carbon species; (D) pH (dashed line: after equilibration with headspace); (E) dissolved inorganic carbon and total alkalinity; (F) Ca and Mg; (G) K, Na, and Cl; and (H) total Si. All concentrations are reported in mmol/L. Dotted lines: simulation including microbial reactions; solid lines: simulation including microbial and mineral reactions. Measured data are from D’Hondt et al. (2003) and Donohue et al. (2006).

The measured sulphate profile is well reproduced by the model (Figure 5A), with an SMT at 9 mbsf. However, the rather linear gradient of the measured sulphate profile is difficult to reconcile with sulphate reduction rates of more than 1,000 pmol/cm³d typically measured near the surface using radiotracer experiments (e.g., Parkes et al., 2005), which are about three orders of magnitude higher than the ones used in the present simulation (cf. also several magnitudes lower values modelled by Wang et al., 2008). Such high rates of organoclastic sulphate reduction should result in a more curved sulphate profile (Meister et al., 2013) and a lower contribution of methanogenic activity. Our simulation clearly shows that, assuming a C/N ratio of 9.85 and a TOC₀ of 3.5 wt% and the organic carbon degradation parameters a = 25,000 a and ν = 0.33, not only the solid phase parameters, but also the distribution of sulphate and methane could be well reproduced (Supplementary Figure S3). Methane falls within the range of concentrations determined with the argon method (Spivack et al., 2006) down to a depth of 60 mbsf (Figure 5A), where gas hydrate saturation is reached. Below this depth, a large scatter in the methane data probably reflects a heterogeneous distribution of gas hydrates, which contrasts with the simulation showing gas hydrate contents increasing continuously with burial and microbial production of methane. Besides sulphate and methane, ammonium concentration provides a reliable indicator for dissimilatory microbial activity (Heini et al., 2015), and the ammonium profile is well reproduced by the model in consistency with the measured C/N ratios (Figure 5B). It is important to notice that the ammonium curve strongly depends on the parameters used for the organic carbon degradation function. Generally, a more reactive organic matter pool, with a smaller value for “a”, leads to a steeper increase of ammonium in the upper part and a lower increase in the lower part of the profile. Hence, ammonium distribution can be used as a further constraint to fine-tune the organic matter degradation function.

As a result of the constrained metabolic activity, bicarbonate shows a steep increase above the SMT, while dissolved CO₂ reaches its highest concentrations only below 100 mbsf (Figure 5C). The high CO₂ concentrations relate to the pH drop to about 6 in the methanogenic zone (short-dashed line in Figure 5D). The simulated DIC increases with depth to more than 250 mmol/L around 150 mbsf (Figure 5E), which is considerably larger than measured data, which reach only ca. 150 mmol/L. This is expected, since a significant portion of DIC was probably lost during core recovery. In-situ loss of CO₂ (e.g., Paull et al., 1996) due to partitioning of CO₂ into escaping methane gas bubbles can be excluded, as no gas phase is present at the high pressure at 5,000 m water depth. Sampling loss of CO₂ would also explain the offset of the simulated pH from the measured pH. Indeed, the measured pH could be largely restored by re-equilibrating the simulated porewater solutions with 2 L of headspace per litre of porewater at atmospheric pressure (dashed lines in Figures 5D,E). This means that CO₂ escape would have mainly occurred by equilibration with a closed headspace during core recovery or sample storage (in the core liner or in a sample container), whereas an equilibration with the open atmosphere did not occur.

The top 10 mbsf are characterized by a strong increase in porewater alkalinity, which is largely the result of sulphate reduction and AOM. However, below the SMT (∼9 mbsf) methanogenesis would only cause a small increase in alkalinity, due to the release of ammonium. Phosphate concentrations only reach up to 0.5 mmol/L (D’Hondt et al., 2003), so that the effect on alkalinity would be small. Assuming microbial activity alone, alkalinity only reaches ∼100 mmol/L between 100 and 150 mbsf (Figure 5E, dotted line), which is lower than in the measured profile. Thus, the model scenario that includes microbial activity without ion exchange or mineral reactions reproduces the concentration profiles of the main metabolites relatively well, but it cannot explain the concentrations of some of the cations (mainly Mg²⁺ and K⁺) and the full extent of alkalinity in the porewater.

Mineral Reactions and Their Effect on Porewater Chemistry

In the microbial activity scenario discussed above several conservative ions that count towards total alkalinity are not reproduced correctly (Figures 5F,G; dotted lines). Most prominently, the increase in Mg²⁺ significantly contributes to total alkalinity (TA_ec). The increase in Mg²⁺ may be a result of release in exchange for NH₄⁺ (Von Breymann et al., 1990). It is well known that especially smectites have a high ion exchange capacity due to their large surface area and also due to their ability to expand (e.g., Boatman and Murray, 1982). Therefore, we tested the effect of ion exchange, assuming a relatively high CEC of 100 meq/100 mg, which is typical for smectites (Ockert et al., 2014), and an extremely high content of exchanger of 50% in the sediment (approx. 10% smectite occurs in the uppermost two samples), however this did not show any significant effect on major cations Ca²⁺, Mg²⁺, Na⁺, K⁺, and NH₄⁺ in the porewater. This may seem surprising, because such a high content of an exchanger provides an ion exchange capacity on the order of hundreds of meq per liter of porewater solution. However, the minimal effect can be explained by the low sedimentation rate of 0.1 m/ka resulting in a very slow exchange of ions. Therefore, another explanation must be found for the discrepancy in simulated and measured alkalinity and conservative ion concentrations.

The alternative effect that could modify the ion content of the porewater would be recrystallization (Wallmann et al., 2008, and further references above). Unlike during ion exchange, the minerals are structurally decomposed and/or modified during this process, as commonly observed during the degradation of sheet silicates by weathering. Under diffusion-limited conditions in sediments and with a high rock/water ratio, concentrations would increase upon dissolution of some minerals until equilibrium is reached. If several different mineral phases are present, as in the modelled case, some minerals dissolve, others precipitate, allowing for larger mass transfer to occur (e.g., Michalopoulos and Aller, 1995). Effectively, the water acts as a medium, and mineral reactions are driven by the thermodynamic stabilities of the minerals under prevailing P/T conditions.

Analysed samples contain various amounts of vermiculite, chlorite, illite, smectite, and kaolinite, but there is no significant change in the peak pattern with depth indicative of ongoing phyllosilicate alteration. Also, the depletion of smectite below 70 mbsf must result from changing sedimentation, because smectite remains supersaturated and would rather form than dissolve throughout the profile. The coexistence of more phases than allowed by the Gibbs phase rule is indicated by the results from XRD (Figures 3A,B), so that equilibrium of the solution with all mineral phases cannot be reached. Instead, they are probably limited by reaction kinetics.

The model results show that increasing acidification leads to a minor decrease in the saturation indices of the silicate phases k-feldspar, albite, smectite, and illite, (Figures 6A,B), while they remain supersaturated at the SMT. In contrast, vermiculite and chlorite are strongly undersaturated below the SMT (Figure 6C). Porewater (Figure 6D) is most supersaturated with respect to kaolinite throughout the section and only slightly undersaturated at the sediment-water interface. Even if the simulated saturation indices are somewhat arbitrary, because the Al concentrations in porewater are assumed, the response to pH and ionic compositions seems reasonable. In particular, the suggested dissolution and precipitation reactions based on the saturation states correspond to known mineral alteration reactions: vermiculite and chlorite commonly weather to illite, and illite weathers to smectite (Chamley, 1989). According to the classical Goldich series, silicate-rich minerals are more resistant to chemical weathering at low temperature (Goldich, 1938; Kowalewski and Rimstidt, 2003). Most insoluble are Al₂O₃ octahedra, and accordingly the solubility decreases with increasing Al-content (Chamley, 1989). Saturation states in Figure 6 are consistent with this rule, showing Al-poor minerals chlorite and vermiculite to be more undersaturated and more susceptible to acidification of porewater. In contrast, Al-rich minerals, feldspar and kaolinite are supersaturated. Kaolinite precipitation is then limited by Al available from the dissolving clay minerals. As a result of alteration of Al-poor to Al-rich minerals, alkali and Earth alkali metal ions are preferentially released to the solution, along with some silica. During dissolution and precipitation, charge balance is maintained as the cations dissolve from the silicates in oxide form and the oxide is readily protonated upon dissolution, yielding free ions and H₂O (Eq. 6), hence, contributing to the excess of conservative cations and increasing TA_ec.

FIGURE 6

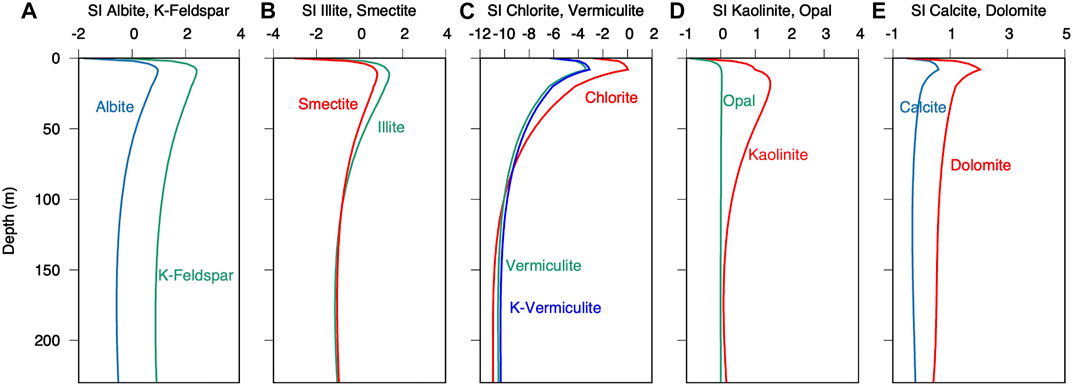
FIGURE 6. Saturation indices (SI) of silicate minerals (A) albite and K-feldspar, (B) illite and smectite, (C) vermiculite and chlorite, (D) kaolinite and cristobalite, and (E) calcite and dolomite.

By allowing the undersaturated silicates to dissolve and supersaturated silicates to precipitate, while adjusting the kinetic constants of different mineral phases, it was possible to improve the fit of porewater profiles to the measured data, in particular the increase of Mg²⁺ and K⁺ (Figures 5F,G; solid lines). It was found that the simulated porewater profiles best fit to the measured data if the reaction rate decreases exponentially with depth (Supplementary Figure S4). The dissolution of minerals other than chlorite and vermiculite had no significant effect on porewater chemistry, as their departure from equilibrium was minimal (Supplementary Figure S5). While the dissolution of chlorite only delivers Mg²⁺, K-vermiculite also provides sufficient K⁺ to reproduce the K⁺ profile. Also, a minor amount of Na⁺ may originate from mineral reactions, although albite, the Na-endmember of plagioclase, is not undersaturated and is, thus, unlikely a significant source of Na. After inclusion of additional conservative cations released from silicate alteration, the simulated alkalinity almost entirely matches the measured alkalinity (Figure 5E, solid line).

Alternatively, also volcanic glass may react with porewater and provide in particular K⁺ and Na⁺. Volcanic glass in ash layers is fairly reactive and may undergo the generalized reaction (Scholz et al., 2013):

$\begin{array}{l}\left[{\left(\mathrm{K},\mathrm{N}\mathrm{a}\right)}_2\mathrm{O};\mathrm{M}\mathrm{g}\mathrm{O};\mathrm{C}\mathrm{a}\mathrm{O};\cdot \mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3;\cdot \mathrm{S}\mathrm{i}{\mathrm{O}}_2\right]+{\mathrm{H}}_4\mathrm{S}\mathrm{i}{\mathrm{O}}_4+6\mathrm{C}{\mathrm{O}}_2+3{\mathrm{H}}_2\mathrm{O}\to \\ \mathrm{A}{\mathrm{l}}_2\mathrm{S}{\mathrm{i}}_2{\mathrm{O}}_5{\left(\mathrm{O}\mathrm{H}\right)}_4+{\mathrm{K}}^{+}+\mathrm{N}{\mathrm{a}}^{+}+\mathrm{M}{\mathrm{g}}^{2+}+\mathrm{C}{\mathrm{a}}^{2+}+6\mathrm{H}\mathrm{C}{\mathrm{O}}_{3^{-}}\end{array}(15)$

Although this has been suggested as a source of alkalinity for diagenetic carbonate formation elsewhere (e.g., Wehrmann et al., 2016), no major ash layers were reported from the sedimentary record at Site 1230. Interlayers of expandable smectites could furnish a further source of Na⁺. For example, a strong increase in Na⁺ with depth, which is decoupled from the chlorinity, occurs at Namibia margin Site 1084 and was interpreted as being derived from clay-rich sediment with up to 30% smectite in the clay fraction (Kastanja et al., 2006). However, as discussed above, ion exchange alone did not significantly affect the porewater chemistry.

Below 150 mbsf, full speciation using the measured concentrations and alkalinity would result in a charge imbalance. Since the model conserves charges, it cannot be forced to adopt this unbalance. Chloride was arbitrarily chosen to compensate the excess of negative charges, so that charge balance is maintained, which results in a decrease in Cl⁻ concentration. Despite this uncertainty near the bottom of the domain, the high alkalinity between 50 and 200 mbsf is real and can only be reached by including silicate alteration.

In addition to these mineral reactions, opal needs discussion as the sediment contains abundant diatoms (D’Hondt et al., 2003), as also indicated by an elevated baseline in the XRD-patterns. The measured concentrations of dissolved silica are clearly below the saturation of opal-A, but the simulations follow the data fairly well with opal-C/T as an equilibrium phase (Figures 5H, 6D). Indeed, it is surprising that the dissolution of opal-A, which is available in large amounts, does not dominate silica concentrations in the porewater. But it is known that opal-A dissolution can be inhibited, as diatoms are covered by organic matter (Van Cappellen, 1996). Opal-C/T as the thermodynamically more stable phase then should form, according to Ostwald’s step rule (e.g., Meister et al., 2014). The curve in the silica concentration profile near the seafloor is due to the fact that silica is strongly undersaturated in seawater. The slight increase with depth is explained by the increasing solubility with temperature.

Overall, alteration of silicate minerals contributes to the very high total alkalinity (∼150 mmol/L) measured at ODP Site 1230. This additional alkalinity effect significantly buffers acidification of the porewater by the production of CO₂ during microbial methanogenesis. In contrast, the production of alkalinity by anaerobic metabolisms (organoclastic sulphate reduction and AOM) and the dissimilatory release of ammonium alone would not be sufficient to explain the measured alkalinity. High (>80 mmol/L) alkalinity concentrations characterize porewaters recovered from within the uppermost few hundred metres below the seafloor at many drill sites along continental margins of the world. Away from the Peru Margin, examples include DSDP Site 262 (Timor Sea, Indian Ocean; Cook, 1974), ODP Sites 994, 995, and 997 (Blake Ridge, Atlantic Ocean; Paull et al., 1996), Site 1019 (California Margin, Pacific; Lyle et al., 1997), Site 1082 (Namibian Margin, Atlantic; Murray and Wigley, 1998) and IODP Sites U1426 and U1427 (Sea of Japan, west Pacific; Tada et al., 2015; see also the examples in Figure 1). All these sites have several commonalities: high accumulation rates of clay and organic carbon, a shallow SMT, and within underlying porewaters, high methane, elevated NH₄⁺ and K⁺, and low Ca²⁺ concentrations. However, unlike Site 1230, some of them have low Mg²⁺ concentrations in porewater and lack gas hydrate. We suspect that microbial methane production and consequent mineral reactions are ubiquitous processes on continental margins around the world, but the rates and details vary depending on parameters embedded in our modelling. These would include pressure and temperature, but also the rate and composition of sedimentary inputs, from organic carbon to aluminosilicates. Not all minerals react equally. In particular, the Mg-rich clay minerals, vermiculite and chlorite dominating in areas of physical weathering under cold and temperate conditions (Chamley, 1989), and to some extent probably also volcanic ash, provide a strong capacity to buffer the pH by increasing alkalinity in the porewater. Future modelling efforts at other sites should lead to further testing and refinement of ideas presented here.

Factors Controlling Carbonate Precipitation

Having established the effects of biogeochemical activity and silicate alteration on the alkalinity and DIC content, we can now assess the factors controlling the saturation state of carbonates (Figure 6E). Calcite and dolomite are only slightly supersaturated or undersaturated in the bottom water, which is partially due to high amounts of CO₂ produced by aerobic respiration in the water column, below the oxygen minimum zone at a water depth of 5,000 m (e.g., Zeebe, 2007). In the top few metres of the sediment, pH generally converges to values near 7 as a result of sulphate reduction (Soetaert et al., 2007; Meister, 2013; Meister, 2014), whereby additional alkalinity from AOM results in a sharp terrace at the SMT at 9 mbsf (solid line in Figure 5D), and saturation indices of calcite and dolomite reach maxima (Figure 6E). Ca²⁺ concentration decreases from the surface to the SMT and also Mg²⁺ shows a kink at this depth, suggesting recent or ongoing precipitation of calcite and dolomite. The kinks can be largely reproduced by the model if dolomite precipitation is included. Indeed, a hard-lithified dolomite from 6.5 mbsf shows δ¹³C values more negative than −30‰, which is a clear indication of an AOM-induced dolomite (Meister et al., 2007; Meister et al., 2011; Meister et al., 2019a).

In the methanogenic zone below 9 mbsf, DIC increase to 250 mmol/L would cause a pH decrease to <6, but taking into account alkalinity production from mineral reactions more moderate pH values above 6 are reached (Figure 5D). The saturation indices of carbonates remain near saturation, which is due to the buffering effect of the alkalinity reaching 150 mmol/L near 100 mbsf. Hence, alkalinity production due to NH₄⁺ release and silicate alteration largely prevents the dissolution of carbonates in the methanogenic zone, as it would be expected based on CO₂ production alone. Carbonates may even become slightly supersaturated due to this effect, but their precipitation would be hampered by the slow supply of Ca²⁺ due to the long diffusion distances from the seafloor.

Calcite was detected by XRD in the bulk sediments in the top 150 mbsf, with higher amounts between 50 and 150 mbsf (Figure 3A). This carbonate is clearly part of the sediment, whereas an ex-situ precipitation due to degassing during core recovery can be excluded, as from porewater with 4 mmol/L Ca²⁺ only ca. 1 g CaCO₃ per kg sediment could precipitate, which would be far below the detection limit of the XRD analysis. Besides low-Mg calcite also traces of Mg-calcite were detected. While the calcite may be diagenetic, precipitation of significant amounts of carbonate is probably not possible at present core depth, due to lack of Ca supply. Thus, the disseminated calcite detected between 50 and 150 mbsf formed most likely in the past, when the according sediment was located sufficiently near to the sediment surface to allow for a sufficient supply of Ca²⁺ from seawater, but not as shallow as during the formation of the lithified layer of dolomite at 6.5 mbsf.

The formation of hard lithified diagenetic carbonates vs. fine disseminated carbonate is a longstanding problem (cf. Garrison et al., 1984). At Site 1230 no dolomite layers occur between 6.5 and 220 mbsf throughout the zone of abundant methane production. Having demonstrated that porewaters are not carbonate-undersaturated in the methanogenic zone, it cannot be argued that past dolomite layers have been dissolved in the methanogenic zone. Apparently, they have never formed, despite the intense methane production that should have maintained a pronounced SMT. However, a possible explanation for the lack of dolomite layers could be that initially methane was not available for intense AOM at the SMT (scenario in Figure 7A). Due to the great water depth, a gas hydrate zone established and expanded as the Pleistocene interval increased in thickness. At this stage, disseminated calcite or dolomite could have formed (Figure 7B). Only when the thickness of the methanogenic zone became sufficiently large to induce an SMT at shallow depth, a dolomite layer could have formed at 6.5 mbsf (Figure 7C). The SMT may have migrated a few metres upward and downward, possibly due to variation of bottom water temperature or variation of TOC and sedimentation rate, which are not resolved by the simulation.

FIGURE 7

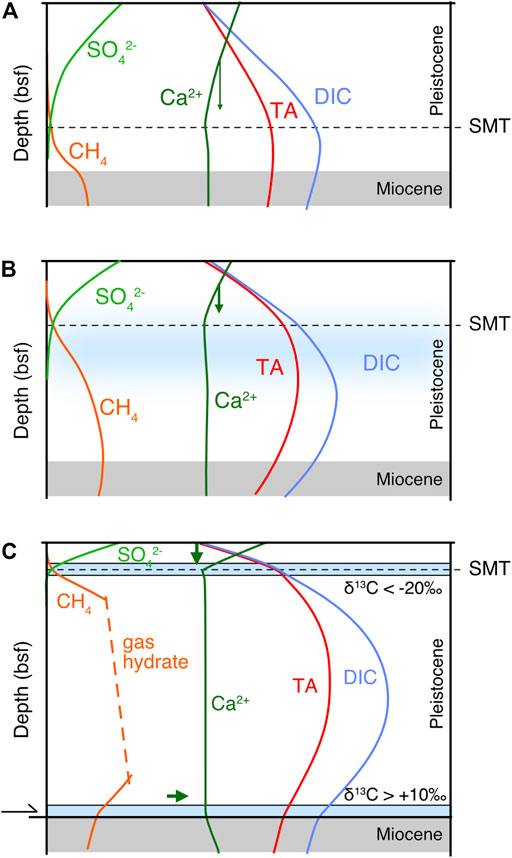
FIGURE 7. Conceptual model to explain the formation of diagenetic carbonates in relation to the evolution of the methanogenic zone: (A) During Pleistocene sedimentation over the Miocene, dissimilatory reactions lead to the onset of a methanogenic zone. (B) Within the expanding methanogenic zone alkalinity builds up, but insignificant carbonates (disseminated calcite or dolomite; blue shaded area) are precipitated as the diffusion distance for Ca²⁺ and Mg²⁺ are too long. (C) The methanogenic zone has now further expanded and a gas hydrate zone has established. The gradients near the surface are steep, with a shallow SMT driving carbonate precipitation (lithified dolomites; blue bars). Also at depth, fluid flow along the décollement provides Ca²⁺, inducing carbonate precipitation. The two types of dolomite show contrasting δ¹³C values, derived from dissimilatory sulphate reduction and methanogenesis, respectively.

While carbonate formation in relation with AOM has been discussed, it is still not clear how carbonates (in particular dolomite) with a strongly positive carbon isotope signature may form. A 20-cm-thick, hard-lithified dolomite breccia was recovered from 230 mbsf at Site 1230, exhibiting a δ¹³C of up to 15‰ (Meister et al., 2011). Inorganic carbon in methanogenic zones typically shows positive δ¹³C values, as DIC becomes enriched and CH₄ depleted in ¹³C as a result of fractionation within the methanogenic pathways (see Meister and Reyes, 2019 for details). At Site 1230, Meister et al. (2011) showed the influence of fluid with more radiogenic ⁸⁷Sr/⁸⁶Sr ratios transported along an active fault zone at 230 mbsf, providing Ca²⁺ and inducing precipitation of a dolomitic fault breccia. As Ca²⁺ was delivered into the midst of a zone with high alkalinity, large amounts of dolomite could have precipitated (Figure 7C). The formation of a dolomite breccia showing a syntectonic cement structure with compromise boundaries (Meister et al., 2011) also suggests a rapid precipitation. However, these conditions are specific to the tectonic situation in an accretionary prism, where fluid is driven upwards, but they still do not explain how hard lithified dolomite layers form in methanogenic zones elsewhere.

More extensive dolomite layers showing a methanogenic δ¹³C signature are found, for example, in the Miocene Monterey Fm. of California (e.g., Murata et al., 1969; Burns and Baker, 1987; Mozley and Burns, 1993; Loyd et al., 2012) and in many organic carbon rich marine sediments drilled by ODP (e.g., Kelts and McKenzie, 1984; Thornburg and Suess, 1992; Rodriguez et al., 2000). As these sites are partially located on the shelf, they may often be affected by CH₄ loss under dynamic conditions (Arning et al., 2012; Contreras et al., 2013), and gas escape must be taken into account, whereby partitioning of CO₂ in methane bubbles could lead to escape of CO₂ and thereby inducing carbonate formation via pH increase (Meister and Reyes, 2019; Meister et al., 2019b). However, none of these effects would be expected in the deep sea, where free gas is not present at low temperatures. In order to simulate carbonate diagenesis on the shelf, gas transport will have to be included in future modelling studies.

Conclusion

The Neogene sediment sequence at ODP Site 1230 in the Peru-Chile Trench contains porewaters with extreme alkalinity, reaching ∼150 mmol/L at ca. 100 mbsf. Full-speciation reaction-transport modelling shows that these concentrations result from several reactions. Much of the alkalinity is produced by organoclastic sulphate reduction and AOM in the upper part of the profile but also through release of ammonium from organic matter degradation throughout the sequence. The alteration of silicate minerals, in particular vermiculite and chlorite to kaolinite and opal-C/T, contributes substantial amounts of Mg²⁺ and K⁺ and further increases alkalinity in the methanogenic zone. In combination, microbial processes and clay mineral alteration produce sufficient alkalinity within the methanogenic zone to buffer acidification caused by increased DIC (up to 250 mmol/L) from dissimilation of organic matter and, thus, to prevent undersaturation and dissolution of carbonates. Within the methanogenic zone, diagenetic carbonate formation is largely calcium-limited, due to the long diffusion distances, but dolomite beds readily form if Ca²⁺ is supplied, such as at the SMT or along a fault zone. The SMT dolomites generally show a negative δ¹³C signature, whereas dolomites forming within the methanogenic zone show a positive δ¹³C signature, but in the absence of a gas phase, a shift of the dolomitization front due to CO₂ degassing does not occur within the gas hydrate stability zone.

While our simulation provides insight into carbonate diagenesis in deep methanogenic zones, it also would be applicable to human-made CO₂ storage reservoirs. Our study shows that reservoirs rich in specific clay minerals, vermiculite and chlorite, would have an extremely high capacity to trap CO₂ as bicarbonate, although the kinetics of these reactions are rather slow. In any case, having a quantitative model at hand that can realistically simulate carbonate diagenesis in marine sediments will be essential to understand the role of sub-surface fluid-microbe-mineral interactions in the global carbon cycle.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

PM: Design of the study, supervision, developing the model, interpretion, writing the manuscript; GH: Modelling with Phreeqc, wrote early version; EP: Advising numerical modelling, provided comments to the manuscript; SG: X-ray diffraction, clay mineral analysis, comments to the manuscript; GD: Shipboard and shore-based porewater analysis, comments to the manuscript; CB: Code writing in C++; BL: Code writing, code testing, advice for mathematical solutions, comments to the manuscript.

Funding

This research used samples and data provided by the Ocean Drilling Program (now International Ocean Discovery Program, IODP), sponsored by the participating countries. PM was further supported by the European Union through Marie-Curie Actions MRTN-CT-2006-035868 (project GRASP), and PIEF-GA-2013-626025 (project TRIADOL) and be the Swiss National Science Foundation SNF through project PA00P2-126221. BL acknowledges additional funding from the Helmholtz Association (Alfred Wegener Institute Helmholtz Centre for Polar and Marine Research).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank David Parkhurst for providing helpful explanations to the programme Phreeqc by responding to our question on the Phreeqc forum (https://www.phreeqcusers.org). We thank Benjamin Huet, Martin Schöpfer, and Bernhard Grasemann for providing help to solve problems with programming. Rainer Abart and Stephan Krämer provided further advice to the geochemistry. We also thank Steve Schäfer and Mischa Kim of the MathWorks Support Team for help with connecting the Matlab code to Phreeqc in an earlier version of our model. We thank two reviewers for their constructive comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.756591/full#supplementary-material

References

Aloisi, G., Wallmann, K., Drews, M., and Bohrmann, G. (2004). Evidence for the Submarine Weathering of Silicate Minerals in Black Sea Sediments: Possible Implications for the marine Li and B Cycles. Geochem. Geophys. Geosyst. 5, Q04007. doi:10.1029/2003gc000639

CrossRef Full Text | Google Scholar

Amiotte Suchet, P., Probst, J. L., and Ludwig, W. (2003). Worldwide Distribution of continental Rock Lithology: Implications for the Atmospheric/soil CO₂ Uptake by continental Weathering and Alkalinity River Transport to the Oceans. Glob. Biogeochem. Cycles 17, 1038–1051. doi:10.1029/2002gb001891

CrossRef Full Text | Google Scholar

Archer, D. E., Buffett, B. A., and McGuire, P. C. (2012). A Two-Dimensional Model of the Passive Coastal Margin Deep Sedimentary Carbon and Methane Cycles. Biogeosciences 9, 2859–2878. doi:10.5194/bg-9-2859-2012

CrossRef Full Text | Google Scholar

Arndt, S., Brumsack, H.-J., and Wirtz, K. W. (2006). Cretaceous Black Shales as Active Bioreactors: A Biogeochemical Model for the Deep Biosphere Encountered during ODP Leg 207 (Demerara Rise). Geochimica et Cosmochimica Acta 70, 408–425. doi:10.1016/j.gca.2005.09.010

CrossRef Full Text | Google Scholar

Arndt, S., Hetzel, A., and Brumsack, H.-J. (2009). Evolution of Organic Matter Degradation in Cretaceous Black Shales Inferred from Authigenic Barite: a Reaction-Transport Model. Geochimica et Cosmochimica Acta 73, 2000–2022. doi:10.1016/j.gca.2009.01.018

CrossRef Full Text | Google Scholar

Arndt, S., Jørgensen, B. B., LaRowe, D. E., Middelburg, J. J., Pancost, R. D., and Regnier, P. (2013). Quantifying the Degradation of Organic Matter in marine Sediments: A Review and Synthesis. Earth-Science Rev. 123, 53–86. doi:10.1016/j.earscirev.2013.02.008

CrossRef Full Text | Google Scholar

Arning, E. T., Berk, W., and Schulz, H. M. (2012). Quantitative Geochemical Modeling along a Transect off Peru: Carbon Cycling in Time and Space, and the Triggering Factors for Carbon Loss and Storage. Glob. Biogeochem. Cycles 26, GB4012. doi:10.1029/2011GB004156

CrossRef Full Text | Google Scholar

Baker, P. A., and Burns, S. J. (1985). Occurrence and Formation of Dolomite in Organic-Rich continental Margin Sediments. AAPG Bull. 69, 1917–1930. doi:10.1306/94885570-1704-11d7-8645000102c1865d

CrossRef Full Text | Google Scholar

Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M., and Lyle, S. (2007). Modelling Carbon Dioxide Accumulation at Sleipner: Implications for Underground Carbon Storage. Earth Planet. Sci. Lett. 255, 164–176. doi:10.1016/j.epsl.2006.12.013

CrossRef Full Text | Google Scholar

Boatman, C. D., and Murray, J. W. (1982). Modeling Exchangeable NH4 + Adsorption in marine Sediments: Process and Controls of Adsorption1,2. Limnol. Oceanogr. 27, 99–110. doi:10.4319/lo.1982.27.1.0099

CrossRef Full Text | Google Scholar

Boudreau, B. P. (1997). Diagenetic Models and Their Implementation: Modelling Transport and Reactions in Aquatic Sediments. Berlin, Heidelberg, New York: Springer.

Google Scholar

Boudreau, B. P., Meysman, F. J. R., and Middelburg, J. J. (2004). Multicomponent Ionic Diffusion in Porewaters: Coulombic Effects Revisited. Earth Planet. Sci. Lett. 222, 653–666. doi:10.1016/j.epsl.2004.02.034

CrossRef Full Text | Google Scholar

Boudreau, B. P., and Ruddick, B. R. (1991). On a Reactive Continuum Representation of Organic Matter Diagenesis. Am. J. Sci. 291, 507–538. doi:10.2475/ajs.291.5.507

CrossRef Full Text | Google Scholar

Brønsted, J. N. (1921). Studies on Solubility. IV. The Principle of the Specific Interaction of Ions. J. Am. Chem. Soc. 44, 877–898.

Google Scholar

Burdige, D. J., and Komada, T. (2013). Using Ammonium Pore Water Profiles to Assess Stoichiometry of Deep Remineralization Processes in Methanogenic continental Margin Sediments. Geochem. Geophys. Geosyst. 14, 1626–1643. doi:10.1002/ggge.20117

CrossRef Full Text | Google Scholar

Burns, S. J., and Baker, P. A. (1987). A Geochemical Study of Dolomite in the Monterey Formation, California. J. Sediment. Petrol. 57, 128–139. doi:10.1306/212f8ac6-2b24-11d7-8648000102c1865d

CrossRef Full Text | Google Scholar

Chamley, H. (1989) Clay Sedimentology. Springer, Berlin, Heidelberg, 623 pp. ISBN 978-3-540-50889-2.

Google Scholar

Chatterjee, S., Dickens, G. R., Bhatnagar, G., Chapman, W. G., Dugan, B., Snyder, G. T., et al. (2011). Pore Water Sulfate, Alkalinity, and Carbon Isotope Profiles in Shallow Sediment Above Marine Gas Hydrate Systems: A Numerical Modeling Perspective. J. Geophys. Res. 116, 1–25. doi:10.1029/2011JB008290

CrossRef Full Text | Google Scholar

Claypool, G. E., and Kaplan, I. R. (1974). “The Origin and Distribution of Methane in marine Sediments,” in ” in Natural Gases In Marine Sediments. Editor I. R. Kaplan (New York: Plenum Press), 99–139. doi:10.1007/978-1-4684-2757-8_8

CrossRef Full Text | Google Scholar

Colbourn, G., Ridgwell, A., and Lenton, T. M. (2015). The Time Scale of the Silicate Weathering Negative Feedback on Atmospheric CO2. Glob. Biogeochem. Cycles 29 (5), 583–596. doi:10.1002/2014GB005054

CrossRef Full Text | Google Scholar

Conrad, R. (1999). Contribution of Hydrogen to Methane Production and Control of Hydrogen Concentrations in Methanogenic Soils and Sediments. FEMS Microbiol. Ecol. 28, 193–202. doi:10.1111/j.1574-6941.1999.tb00575.x

CrossRef Full Text | Google Scholar

Contreras, S., Meister, P., Liu, B., Prieto-Mollar, X., Hinrichs, K.-U., Khalili, A., et al. (2013). Cyclic 100-ka (Glacial-interglacial) Migration of Subseafloor Redox Zonation on the Peruvian Shelf. Proc. Natl. Acad. Sci. 110, 18098–18103. doi:10.1073/pnas.1305981110

PubMed Abstract | CrossRef Full Text | Google Scholar

Cook, P. J. (1974). Geochemistry and Diagenesis of Interstitial Fluids and Associated Calcareous Oozes, Deep Sea Drilling Project, Leg 27, Timor Trough. Init. Rep. Deap Sea Drill. Project 27, 463–480. doi:10.2973/dsdp.proc.27.119.1974

CrossRef Full Text | Google Scholar

D’Hondt, S., Jørgensen, B. B., Miller, J., Batzke, A., Blake, R., Cragg, B. A., et al. (2004). Distributions of Microbial Activities in Deep Subseafloor Sediments. Science 306, 2216–2221.

PubMed Abstract | Google Scholar

D’Hondt, S. L., Jørgensen, B. B., and Miller, D. J. (2003). Proc. ODP, Init. Repts. 201. College Station TXUSA: Ocean Drilling Program, Texas A&M University. 77845-9547. The shipboard scientific party

Google Scholar

Dickens, G. R. (2003). Rethinking the Global Carbon Cycle with a Large, Dynamic and Microbially Mediated Gas Hydrate Capacitor. Earth Planet. Sci. Lett. 213, 169–183. doi:10.1016/s0012-821x(03)00325-x

CrossRef Full Text | Google Scholar

Dickson, A. G. (1981). An Exact Definition of Total Alkalinity and a Procedure for the Estimation of Alkalinity and Total Inorganic Carbon from Titration Data. Deep Sea Res. A: Oceanographic Res. Pap. 28, 609–623. doi:10.1016/0198-0149(81)90121-7

CrossRef Full Text | Google Scholar

Donohue, C. M., Snyder, G. T., and Dickens, G. R. (2006). “Data Report: Major Cation Concentrations of Interstitial Waters Collected from Deep Sediments of Eastern Equatorial Pacific and Peru Margin (ODP Leg 201),” in Proc. ODP, Sci. Results 201. Editors B. B. Jørgensen, 1–19, Ocean Drilling Program, College Station, Texas. doi:10.2973/odp.proc.sr.201.104.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, Z., Møller, N., and Weare, J. H. (1992). An Equation of State for the CH4-CO2-H2O System: I. Pure Systems from 0 to 1000°C and 0 to 8000 Bar. Geochimica et Cosmochimica Acta 56, 2605–2617. doi:10.1016/0016-7037(92)90347-l

CrossRef Full Text | Google Scholar

Engelhardt, W., Füchtbauer, H., and Müller, G. (1974). Sedimentary Petrology, Part 1: Methods in Sedimentary Petrology, Vol. 1. Stuttgart, Germany: Schweizerbart’sche Verlagsbuchhandlung.

Google Scholar

Eslinger, E., and Pevear, D. R. (1988). “Clay Minerals and Sandstone Diagenesis,” in Clay Minerals For Petroleum Geologists And Engineers. Editors E. Eslinger, and D. Pevear, 22, 6. 1–6.29.SEPM Short Course

Google Scholar

Froelich, P. N., Klinkhammer, G. P., Bender, M. L., Luedtke, N. A., Heath, G. R., Cullen, D., et al. (1979). Early Oxidation of Organic Matter in Pelagic Sediments of the Eastern Equatorial Atlantic: Suboxic Diagenesis. Geochimica et Cosmochimica Acta 43 (7), 1075–1090. doi:10.1016/0016-7037(79)90095-4

CrossRef Full Text | Google Scholar

Garrison, R. E., Kastner, M., and Zenger, D. H. (1984). Dolomites of the Monterey Formation and Other Organic-Rich Units. Los Angeles, California: SEPM, Pacific Section, 215.

Google Scholar

Gaucher, E., Robelin, C., Matray, J. M., Négrel, G., Gros, Y., Heitz, J. F., et al. (2004). ANDRA Underground Research Laboratory: Interpretation of the Mineralogical and Geochemical Data Acquired in the Callovian-Oxfordian Formation by Investigative Drilling. Phys. Chem. Earth, Parts A/B/C 29, 55–77. doi:10.1016/j.pce.2003.11.006

CrossRef Full Text | Google Scholar

Goldich, S. S. (1938). A Study in Rock-Weathering. J. Geology. 46, 17–58. doi:10.1086/624619

CrossRef Full Text | Google Scholar

Grenthe, I., and Plyasunov, A. (1997). On the Use of Semiempirical Electrolyte Theories for Modeling of Solution Chemical Data. Pure Appl. Chem. 69, 951–958. doi:10.1351/pac199769050951

CrossRef Full Text | Google Scholar

Guggenheim, E. A., and Turgeon, J. C. (1955). Specific Interaction of Ions. Trans. Faraday Soc. 51, 747–761. doi:10.1039/tf9555100747

CrossRef Full Text | Google Scholar

Ingle, J. C., Suyehiro, K., and von Breymann, M. T. (1990). “Japan Sea,” in Proc. ODP, Init. Repts. (College Station, TX, 128. (Ocean Drilling Program).

Google Scholar

Jasmund, K., and Lagaly, G. (1993). Tonminerale und Tone: Struktur, Eigenschaften, Anwendungen und Einsatz in Industrie und Umwelt. Darmstadt: Steinkopff. 3-7985-0923-9.

Google Scholar

Kasina, M., Morozova, D., Michalik, M., Pudlo, D., and Wuerdemann, H. (2014). Impact of Gas Storage on Reservoir Rocks - Long-Term Study to Investigate the Effects on Mineral Content and Fluid Chemistry. Energ. Proced. 59, 418–424. doi:10.1016/j.egypro.2014.10.397

CrossRef Full Text | Google Scholar

Kastanja, M. M., Diekmann, B., and Henrich, R. (2006). Controls on Carbonate and Terrigenous Deposition in the Incipient Benguela Upwelling System during the Middle to the Late Miocene (ODP Sites 1085 and 1087). Palaeogeogr. Palaeoclimatol. Palaeoecol. 241, 515–530. doi:10.1016/j.palaeo.2006.05.004

CrossRef Full Text | Google Scholar

Kastner, M., Elderfield, H., Martin, J. B., Suess, E., Kvenvolden, K. A., and Garrison, R. E. (1990). “Diagenesis and Interstitial-Water Chemistry at the Peruvian Continental Margin, Major Constituents and Strontium Isotopes,” in, Proc. ODP, Sci. Results. Editors E. Suess, and R. von Huene, 112, 413–440, Ocean Drilling Program, College Station, TX.doi:10.2973/odp.proc.sr.112.144.1990

CrossRef Full Text | Google Scholar

Katz, A., and Ben-Yaakov, S. (1980). Diffusion of Seawater Ions. Part II. The Role of Activity Coefficients and Ion Pairing. Mar. Chem. 8, 263–280. doi:10.1016/0304-4203(80)90016-x

CrossRef Full Text | Google Scholar

Kelts, K., and McKenzie, J. A. (1984). “A Comparison of Anoxic Dolomite from Deep-Sea Sediments: Quaternary Gulf of California and Messinian Tripoli Formation of Sicily,” in Dolomites Of the Monterey Formation And Other Organic-Rich Units. Editors R. E. Garrison, M. Kastner, and D. H. Zenger (Los Angeles, CA: Pacific Section SEPM), 41, 19–28.

Google Scholar

Knab, N. J., Dale, A. W., Lettmann, K., Fossing, H., and Jørgensen, B. B. (2008). Thermodynamic and Kinetic Control on Anaerobic Oxidation of Methane in marine Sediments. Geochimica et Cosmochimica Acta 72, 3746–3757. doi:10.1016/j.gca.2008.05.039

CrossRef Full Text | Google Scholar

Kowalewski, M., and Rimstidt, J. D. (2003). Average Lifetime and Age Spectra of Detrital Grains: toward a Unifying Theory of Sedimentary Particles. J. Geology. 111, 427–439. doi:10.1086/375284

CrossRef Full Text | Google Scholar

Krumins, V., Gehlen, M., Arndt, S., Van Cappellen, P., and Regnier, P. (2013). Dissolved Inorganic Carbon and Alkalinity Fluxes from Coastal marine Sediments: Model Estimates for Different Shelf Environments and Sensitivity to Global Change. Biogeosciences 10, 371–398. doi:10.5194/bg-10-371-2013

CrossRef Full Text | Google Scholar

Kutvonen, H., Rajala, P., Carpén, L., and Bomberg, M. (2015). Nitrate and Ammonia as Nitrogen Sources for Deep Subsurface Microorganisms. Front. Microbiol. 6, 1079. doi:10.3389/fmicb.2015.01079

PubMed Abstract | CrossRef Full Text | Google Scholar

Lasaga, A. C. (1998). Kinetic Theory in the Earth Sciences. Princeton Series in Geochemistry. Princeton, Chichester: Princeton University Press, 811.

Google Scholar

Loyd, S. J., Corsetti, F. A., Eiler, J. M., and Tripati, A. K. (2012). Determining the Diagenetic Conditions of Concretion Formation: Assessing Temperatures and Pore Waters Using Clumped Isotopes. J. Sediment. Res. 82, 1006–1016. doi:10.2110/jsr.2012.85

CrossRef Full Text | Google Scholar

Lyle, M., Koizumi, I., and Richter, C. Shipboard Scientific Party (1997). Proceedings of the Ocean Drilling Program. Initial Rep. 167, 353–387. doi:10.2973/odp.proc.ir.167.113.1997

CrossRef Full Text | Google Scholar

Marinoni, L., Setti, M., Salvi, C., and López-Galindo, A. (2008). Clay Minerals in Late Quaternary Sediments from the South Chilean Margin as Indicators of Provenance and Palaeoclimate. Clay miner. 43, 235–253. doi:10.1180/claymin.2008.043.2.07

CrossRef Full Text | Google Scholar

Matmon, D., and Bekins, B. A. (2006). Hydromechanics of a High Taper Angle, Low-Permeability Prism: A Case Study from Peru. J. Geophys. Res. 111, B07101. doi:10.1029/2005JB003697

CrossRef Full Text | Google Scholar

Mavromatis, V., Meister, P., and Oelkers, E. H. (2015). Using Stable Mg Isotopes to Distinguish Dolomite Formation Mechanisms: A Case Study from the Peru Margin. Chem. Geology. 385, 84–91.

Google Scholar

Meister, P., Brunner, B., Picard, A., Böttcher, M. E., and Jørgensen, B. B. (2019a). Sulphur and Carbon Isotopes as Tracers of Past Sub-seafloor Microbial Activity. Sci. Rep. 9 (604), 604–609. doi:10.1038/s41598-018-36943-7

CrossRef Full Text | Google Scholar

Meister, P., Chapligin, B., Picard, A., Meyer, H., Fischer, C., Rettenwander, D., et al. (2014). Early Diagenetic Quartz Formation at a Deep Iron Oxidation Front in the Eastern Equatorial Pacific - A Modern Analogue for Banded Iron/chert Formations? Geochimica et Cosmochimica Acta 137, 188–207. doi:10.1016/j.gca.2014.03.035

CrossRef Full Text | Google Scholar

Meister, P. (2015). For the Deep Biosphere, the Present Is Not Always the Key to the Past: what We Can Learn from the Geological Record. Terra Nova 27, 400–408. doi:10.1111/ter.12174

CrossRef Full Text | Google Scholar

Meister, P., Gutjahr, M., Frank, M., Bernasconi, S. M., Vasconcelos, C., and McKenzie, J. A. (2011). Dolomite Formation within the Methanogenic Zone Induced by Tectonically Driven Fluids in the Peru Accretionary Prism. Geology 39, 563–566. doi:10.1130/g31810.1

CrossRef Full Text | Google Scholar

Meister, P., Liu, B., Ferdelman, T. G., Jørgensen, B. B., and Khalili, A. (2013). Control of Sulphate and Methane Distributions in marine Sediments by Organic Matter Reactivity. Geochimica et Cosmochimica Acta 104, 183–193. doi:10.1016/j.gca.2012.11.011

CrossRef Full Text | Google Scholar

Meister, P., Liu, B., Khalili, A., Böttcher, M. E., and Jørgensen, B. B. (2019b). Factors Controlling the Carbon Isotope Composition of Dissolved Inorganic Carbon and Methane in marine Porewater: An Evaluation by Reaction-Transport Modelling. J. Mar. Syst. 200, 1032271–1032318. doi:10.1016/j.jmarsys.2019.103227

CrossRef Full Text | Google Scholar

Meister, P., McKenzie, J. A., Vasconcelos, C., Bernasconi, S., Frank, M., Gutjahr, M., et al. (2007). Dolomite Formation in the Dynamic Deep Biosphere: Results from the Peru Margin. Sedimentology 54, 1007–1032. doi:10.1111/j.1365-3091.2007.00870.x

CrossRef Full Text | Google Scholar

Meister, P., McKenzie, J. A., Warthmann, R., and Vasconcelos, C. (2006). “Mineralogy and Petrography of Diagenetic Dolomite, Peru Margin, ODP Leg 201,” in Proc. ODP, Sci. Results. Editors B. B. Jørgensen, S. L. D’Hondt, and D. J. Miller, 1–34. doi:10.2973/odp.proc.sr.201.102.2006

CrossRef Full Text | Google Scholar

Meister, P., Prokopenko, M., Skilbeck, C. G., Watson, M., and McKenzie, J. A. (2005). “Data Report: Compilation of Total Organic and Inorganic Carbon Data from Peru Margin and Eastern Equatorial Pacific Drill Sites (ODP Legs 112, 138, and 201),” in Proc. ODP, Sci. Results. Editors B. B. Jørgensen, S. L. D’Hondt, and D. J. Miller, 201. doi:10.2973/odp.proc.sr.201.105.2005

CrossRef Full Text | Google Scholar

Meister, P., and Reyes, C. (2019). “The Carbon-Isotope Record of the Sub-seafloor Biosphere,” in Tracking the Deep Biosphere through Time. Editors H. Drake, M. Ivarsson, and C. Heim, 9, 1–25. doi:10.3390/geosciences9120507

CrossRef Full Text | Google Scholar

Meister, P. (2013). Two Opposing Effects of Sulfate Reduction on Carbonate Precipitation in normal marine, Hypersaline, and Alkaline Environments. Geology 41, 499–502. doi:10.1130/g34185.1

CrossRef Full Text | Google Scholar

Meister, P. (2014). Two Opposing Effects of Sulfate Reduction on Carbonate Precipitation in normal marine, Hypersaline, and Alkaline Environments: Reply. Geology 42, e315. doi:10.1130/g35240y.1

CrossRef Full Text | Google Scholar

Michalopoulos, P., and Aller, R. C. (1995). Rapid Clay Mineral Formation in Amazon Delta Sediments: Reverse Weathering and Oceanic Elemental Cycles. Science 270, 614–617. doi:10.1126/science.270.5236.614

CrossRef Full Text | Google Scholar

Middelburg, J. J., Soetaert, K., and Hagens, M. (2020). Ocean Alkalinity, Buffering and Biogeochemical Processes. Rev. Geophys. 58, e2019RG000681. doi:10.1029/2019RG000681

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, D. M., and Reynolds, R. C. (1997). X-ray Diffraction and the Identification and Analysis of clay Minerals. 2nd ed. Oxford, New York: Oxford University Press.

Google Scholar

Moore, T. S., Murray, R. W., Kurtz, A. C., and Schrag, D. P. (2004)., 229. Amsterdam: Elsevier B.V., 141–154. doi:10.1016/j.epsl.2004.10.015Anaerobic Methane Oxidation and the Formation of DolomiteEarth Planet. Sci. Lett.

CrossRef Full Text | Google Scholar

Morse, J. W., Arvidson, R. S., and Lüttge, A. (2007). Calcium Carbonate Formation and Dissolution. Chem. Rev. 107, 342–381. doi:10.1021/cr050358j

PubMed Abstract | CrossRef Full Text | Google Scholar

Mozley, P. S., and Burns, S. J. (1993). Oxygen and Carbon Isotopic Composition of marine Carbonate Concretions – an Overview. J. Sediment. Petrol. 63, 73–83.

Google Scholar

Murata, K. J., Friedman, I., and Madsen, B. H. (1969). Isotopic Composition of Diagenetic Carbonates in Marine Miocene Formations of California and Oregon. U.S. Geological Survey Professional Paper. Washington, DC: U.S. Government Printing Office 614-B, 1–24. doi:10.3133/pp614B

CrossRef Full Text | Google Scholar

Murray, R. W., and Wigley, R. Shipboard Scientific Party (1998). Interstitial Water Chemistry of Deeply Buried Sediments from the Southwest African Margin: A Preliminary Synthesis of Results from Leg 175. Proc. Ocean Drill. Prog. Initial Rep. 175, 547–553. doi:10.2973/odp.proc.ir.175.120.1998

CrossRef Full Text | Google Scholar

Nauhaus, K., Boetius, A., Krüger, M., and Widdel, F. (1995). In Vitro demonstration of Anaerobic Oxidation of Methane Coupled to Sulphate Reduction in Sediment from a marine Gas Hydrate Area. Environ. Microbiol. 4, 296–305. doi:10.1046/j.1462-2920.2002.00299.x

CrossRef Full Text | Google Scholar

Ockert, C., Wehrmann, L. M., Kaufhold, S., Ferdelman, T. G., Teichert, B. M. A., and Gussone, N. (2014). Calcium-ammonium Exchange Experiments on clay Minerals Using a45Ca Tracer Technique in marine Pore Water. Isotopes Environ. Health Stud. 50, 1–17. doi:10.1080/10256016.2013.806505

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, Y. K., Lee, J. I., Jung, J., Hillenbrand, C.-D., Yoo, K.-C., and Kim, J. (2019). Elemental Compositions of Smectites Reveal Detailed Sediment Provenance Changes during Glacial and Interglacial Periods: the Southern Drake Passage and Bellingshausen Sea, Antarctica. Minerals 9 (322), 1–14. doi:10.3390/min9050322

CrossRef Full Text | Google Scholar

Parkes, R. J., Webster, G., Cragg, B. A., Weightman, A. J., Newberry, C. J., Ferdelman, T. G., et al. (2005). Deep Sub-seafloor Prokaryotes Stimulated at Interfaces over Geological Time. Nature 436, 390–394. doi:10.1038/nature03796

PubMed Abstract | CrossRef Full Text | Google Scholar

Parkhurst, D., and Appelo, C. (2013). Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. U.S. Geol. Surv. Tech. Methods 6-A43, 497.

Google Scholar

Parkhurst, D. L., and Wissmeier, L. (2015). PhreeqcRM: A Reaction Module for Transport Simulators Based on the Geochemical Model PHREEQC. Adv. Water Resour. 83, 176–189. doi:10.1016/j.advwatres.2015.06.001

CrossRef Full Text | Google Scholar

Paull, C. K., Matsumoto, R., and Wallace, P. J. Shipboard Scientific Party (1996). Gas Hydrate Sampling on the Blake Ridge and Carolina Rise Proc. ODP, Init. Repts. 164. College Station, TX: Ocean Drilling Program. doi:10.2973/odp.proc.ir.164.1996

CrossRef Full Text | Google Scholar

Pisciotto, K. H., and Mahoney, J. J. (1981). Isotopic Survey of Diagenetic Carbonates, Deep Sea Drilling Project Leg 63. Drilling Project 63, 595–609. doi:10.2973/dsdp.proc.63.118.1981

CrossRef Full Text | Google Scholar

Prokopenko, M. G., Hammond, D. E., Spivack, A. J., and Stott, L. D. (2006). Sediment and Pore Water C and N Composition of ODP Holes 201-1227A, 201–1230A. doi:10.1594/PANGAEA.773410

CrossRef Full Text | Google Scholar

Raiswell, R., and Fisher, Q. J. (2000). Mudrock‐hosted Carbonate Concretions: a Review of Growth Mechanisms and Their Influence on Chemical and Isotopic Composition. J. Geol. Soc. 157, 239–251. doi:10.1144/jgs.157.1.239

CrossRef Full Text | Google Scholar

Rodriguez, N. M., Paull, C. K., and Borowski, W. S. (2000). “Zonation of Authigenic Carbonates within Gas Hydrate-Bearing Sedimentary Sections on the Blake ridge: Offshore southeastern North America,” in Proc. ODP, Sci. Results. Editors C. K. Paull, R. Matsumoto, P. J. Wallace, and W. P. Dillon College Station, TX: Ocean Drilling Program, 164, 301–312. doi:10.2973/odp.proc.sr.164.227.2000

CrossRef Full Text | Google Scholar

Scholz, F., Hensen, C., Schmidt, M., and Geersen, J. (2013). Submarine Weathering of Silicate Minerals and the Extent of Pore Water Freshening at Active continental Margins. Geochimica et Cosmochimica Acta 100, 200–216. doi:10.1016/j.gca.2012.09.043

CrossRef Full Text | Google Scholar

Schrag, D. P., Higgins, J. A., Macdonald, F. A., and Johnston, D. T. (2013). Authigenic Carbonate and the History of the Global Carbon Cycle. Science 339, 540–543. doi:10.1126/science.1229578

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, D. C. (2005). “Data Report: Dissolved Organic Carbon in Interstitial Waters, Equatorial Pacific and Peru Margin, ODP Leg 201,” in Proc. ODP, Sci. Results 201. Editors B. B. Jørgensen, S. L. D’Hondt, and D. J. Miller. doi:10.2973/odp.proc.sr.201.111.2005

CrossRef Full Text | Google Scholar

Soetaert, K., Hofmann, A. F., Middleburg, J. J., Meysman, F. J. R., and Greenwood, J. (2007). The Effect of Biogeochemical Processes on pH. Marine Chem. 105, 30–51. doi:10.1016/j.marchem.2006.12.012

CrossRef Full Text | Google Scholar

Solomon, E. A., Spivack, A. J., Kastner, M., Torres, M. E., and Robertson, G. (2014). Gas Hydrate Distribution and Carbon Sequestration Through Coupled Microbial Methanogenesis and Silicate Weathering in the Krishna–Godavari Basin, Offshore India. Marine Petrol. Geol. 58, 233–253. doi:10.1016/j.marpetgeo.2014.08.020

CrossRef Full Text | Google Scholar

Spivack, A. J., McNeil, C., Holm, N. G., and Hinrichs, K.-U. (2006). “Determination of In Situ Methane Based on Analysis of Void Gas,” in Proc. ODP, Sci. Results. Editors B. B. Jørgensen, S. L. D’Hondt, and D. J. Miller, 1–11. doi:10.2973/odp.proc.sr.201.119.2006

CrossRef Full Text | Google Scholar

Suess, E. (1988). Peru continental Margin. Proc. ODP, Init. Repts. College Station, TX: Ocean Drilling Program.

Google Scholar

Sun, X., and Turchyn, A. V. (2014). Significant Contribution of Authigenic Carbonate to marine Carbon Burial. Nat. Geosci 7, 201–204. doi:10.1038/ngeo2070

CrossRef Full Text | Google Scholar

Tada, R., Murray, R. W., and Alvarez Zarikian, C. A. Expedition 346 Scientists (2015). Site U1426. Proc. Integr. Ocean Drill. Prog. 346, 1–113. doi:10.2204/iodp.proc.346.107.2015

CrossRef Full Text | Google Scholar

Tarpgaard, I. H., Jørgensen, B. B., Kjeldsen, K. U., Kjeldsen, K. U., and Røy, H. (2017). The marine Sulfate Reducer Desulfobacterium Autotrophicum HRM2 Can Switch between Low and High Apparent Half-Saturation Constants for Dissimilatory Sulfate Reduction. FEMS Microbiol. Ecol. 93, 12. doi:10.1093/femsec/fix012

CrossRef Full Text | Google Scholar

Thornburg, T. M., and Suess, E. (1992). “Carbonate Cementation of Granular and Fracture Porosity: Implications for the Cenozoic Hydrologic Development of the Peru Continental Margin,” in Proc. ODP, Sci. Results. Editor M. Suess, 112, 95–109.

Google Scholar

Tishchenko, P., Hensen, C., Wallmann, K., and Wong, C. S. (2005). Calculation of the Stability and Solubility of Methane Hydrate in Seawater. Chem. Geology. 219, 37–52. doi:10.1016/j.chemgeo.2005.02.008

CrossRef Full Text | Google Scholar

Tréhu, A. M., Bohrmann, G., Rack, F. R., and Torres, M. E.Shipboard Scientific Party (2003). “Drilling Gas Hydrates on Hydrate Ridge, Cascadia Continental Margin,” in Proc. ODP, Init. Repts. (College Station, TX: Ocean Drilling Program), 1–75.

Google Scholar

Treude, T., Boetius, A., Knittel, K., Wallmann, K., and Barker Jørgensen, B. (2003). Anaerobic Oxidation of Methane above Gas Hydrates at Hydrate Ridge, NE Pacific Ocean. Mar. Ecol. Prog. Ser. 264, 1–14. doi:10.3354/meps264001

CrossRef Full Text | Google Scholar

Ussler, W., and Paull, C. K. (2008). Rates of Anaerobic Oxidation of Methane and Authigenic Carbonate Mineralization in Methane-Rich Deep-Sea Sediments Inferred from Models and Geochemical Profiles. Earth Planet. Sci. Lett. 266, 271–287. doi:10.1016/j.epsl.2007.10.056

CrossRef Full Text | Google Scholar

Van Cappellen, P. (1996). Reactive Surface Area Control of the Dissolution Kinetics of Biogenic Silica in Deep-Sea Sediments. Chem. Geology. 132, 125–130. doi:10.1016/s0009-2541(96)00047-2

CrossRef Full Text | Google Scholar

Von Breymann, M. T., Collier, R., and Suess, E. (1990). Magnesium Adsorption and Ion Exchange in marine Sediments: a Multi-Component Model. Geochimica et Cosmochimica Acta 54, 3295–3313. doi:10.1016/0016-7037(90)90286-t

CrossRef Full Text | Google Scholar

Wallmann, K., Aloisi, G., Haeckel, M., Tishchenko, P., Pavlova, G., Greinert, J., et al. (2008). Silicate Weathering in Anoxic marine Sediments. Geochim. Cosmochim. Acta, 72, 3067–3090. doi:10.1016/j.gca.2008.03.026

CrossRef Full Text | Google Scholar

Wang, G., Spivack, A. J., Rutherford, S., Manor, U., and D’Hondt, S. (2008). Quantification of Co-occurring Reaction Rates in Deep Subseafloor Sediments. Geochimica et Cosmochimica Acta 72, 3479–3488. doi:10.1016/j.gca.2008.04.024

CrossRef Full Text | Google Scholar

Wefer, G., Berger, W. H., and Richter, C. Shipboard Scientific Party (1998). “Benguela Current,” in Proc. ODP, Init. Repts. 175 (College Station, TX: Ocean Drilling Program). doi:10.2973/odp.proc.ir.175.1998

CrossRef Full Text | Google Scholar

Wehrmann, L. M., Ockert, C., Mix, A. C., Gussone, N., Teichert, B. M. A., and Meister, P. (2016). Repeated Occurrences of Methanogenic Zones, Diagenetic Dolomite Formation and Linked Silicate Alteration in Southern Bering Sea Sediments (Bowers Ridge, IODP Exp. 323 Site U1341). Deep Sea Res. Part II 125–126, 117–132. doi:10.1016/j.dsr2.2013.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Wehrmann, L. M., Knab, N. J., Pirlet, H., Unnithan, V., Wild, C., and Ferdelman, T. G. (2009). Carbon Mineralization and Carbonate Preservation in Modern Cold-Water Coral Reef Sediments on the Norwegian Shelf. Biogeosciences 6, 663–680. doi:10.5194/bg-6-663-2009

CrossRef Full Text | Google Scholar

Wolf-Gladrow, D. A., Zeebe, R. E., Klaas, C., Körtzinger, A., and Dickson, A. G. (2007). Total Alkalinity: the Explicit Conservative Expression and its Application to Biogeochemical Processes. Mar. Chem. 106, 287–300. doi:10.1016/j.marchem.2007.01.006

CrossRef Full Text | Google Scholar

Zeebe, R. E. (2007). Modeling CO2 Chemistry, δ13C, and Oxidation of Organic Carbon and Methane in Sediment Porewater: Implications for Paleo-Proxies in Benthic Foraminifera. Geochimica et Cosmochimica Acta 71, 3238–3256. doi:10.1016/j.gca.2007.05.004

CrossRef Full Text | Google Scholar