Interface Properties in Binary Fluid Using Lattice Boltzmann Method

Emulsified behaviors are of importance for chemical flooding. Properties of emulsifiers relate droplets coalescence and transport. Since experiments do not provide access to observables of interest. Numerical simulations with mesoscale scheme pose attractive method to gain insight into emulsifying stability, which is defined as a period of oil droplets movements at fixed ranges. A phase field based lattice Boltzmann model is used which simulate interface behavior. Various parameters including emulsified droplet size, interface thickness, viscosity ratio and density ratio have been discussed. The aim of this study is to provide a critical suggestion that predictive emulsifying behaviors of small oil droplets immersed in water environment.

Introduction

Chemical flooding is an effective technique that plays an important role in oil production at the middle and late stages, in which basic theory is to improve mobility of the hydrocarbon by altering the interfacial conditions. Interfacial tension between oil and water can be realized by adding surfactant. Generally, some additives including high-viscosity polymer are injected with water to improve oil displacement efficiency, and therefore, oil recovery is enhanced. We found that the interfacial phenomenon produced by an emulsifier greatly impacts its emulsifying performance (Sun, Z., et al.). However, the knowledge of the interfacial properties is still lacking (Mohammed and Babadagli) (Sun, Z., et al.) (Cui, Ren, et al.) (Dicharry et al.) (Moran et al.) (Wang et al.) (Temple-Heald et al.) (Cui, Pei, et al.).

Many surfactant studies in oil production have been focused on designs of molecular structures and corresponding evaluations (Dong et al.) (Zhang and Feng) (Ding et al.) (Zhang et al.). In fact, the response time provided by an emulsifier in a target environment is directly and firstly related to its emulsifying performance. However, there are few studies regarding emulsion response time to investigate interfacial behavior. The interfacial interaction can be treated as the attractive/repulsive forces, or as both representing emulsion in numerical models (H.Nour et al.).

Unfortunately, capturing interfacial properties accurately is a challenge, numerically. The interface in numerical treatment has different strategies due to the steep gradients of properties in the normal direction. Here, the lattice Boltzmann equation (LBE) is proposed to study interfacial behavior, which should integrate both microscopic models for the interface and meso-scopic kinetic equations (Lamura et al.) (Song et al.). In the present study, the LBE with interface capturing is used to solve the velocity field, and the basic idea is developed by (Zheng et al.). Instead of recovering the fluid momentum macrodynamic equation (Swift et al.), it has better performance by recovering the fluid velocity based one (Zheng et al.).

Governing Equations of Motion Fluids

Phase Field Theory

A brief outline of this method will be in this section and for more detailed discussion refer to Jacqmin (1999). An order parameter $\varphi$ is used to define two fluids in this diffuse interface method, and a Landau free energy function is defined as

$\psi ={\displaystyle \underset{V}{\int }dV\left[\psi \left(\varphi \right)+\frac{k}{2}\left|\nabla {\varphi }^2\right|\right]}(1)$

$V$ is the control volume, k is the coefficient of surface tension,$\psi \left(\varphi \right)$ is the bulk free energy density (Tóth and Kvamme), which is related to physical intermolecular interactions in gas or fluids. The free energy density in an isothermal system can be used:

$\psi \left(\varphi \right)=\beta {\left(\varphi -{\varphi }_w\right)}^2{\left(\varphi -{\varphi }_o\right)}^2(2)$

Where $\beta$ is the constant dependence on the interfacial properties including thickness and surface tension. ${\varphi }_w$ and ${\varphi }_o$ are the constants based on the equilibrium state corresponding marked bulk fluids A and B, respectively (Van Der Sman and Meinders). Generally, ${\varphi }_o=-{\varphi }_w$. The free energy $\psi$ yields the chemical potential

${\mu }_{\varphi }=\frac{\partial \psi }{\partial \varphi }-k{\nabla }^2\varphi (3)$

$=4\beta \left(\varphi -{\varphi }_w\right)\left(\varphi -{\varphi }_o\right)\left(\varphi -\overline{\varphi }\right)-k{\nabla }^2\varphi (4)$

Where $\overline{\varphi }=\left({\varphi }_o+{\varphi }_w\right)/2$. The interface plane profile can be obtained by solving ${\mu }_{\varphi }=0,$then the interface is

$\varphi \left(\xi \right)=\frac{\left({\varphi }_w+{\varphi }_o\right)}{2}-\frac{\left({\varphi }_w-{\varphi }_o\right)}{2}\tanh \left(\frac{2\xi }{d}\right)(5)$

Where$\text{ ξ}$ is the coordinate normal to the interface and $d$ is the interfacial thickness that is given by

$d=\frac{4}{\left|{\varphi }_w-{\varphi }_o\right|}\sqrt{\frac{k}{2\beta }}(6)$

The surface tension between fluid and fluid is represented as

${\sigma }_{wo}=\frac{{\left|{\varphi }_w-{\varphi }_o\right|}^3}{6}\sqrt{2k\beta }(7)$

Cahn and Hillard approximated interfacial diffusion fluxes which is proportional to chemical potential gradients (Zu and He). The interface profile can be described with respect to $\varphi$:

$\frac{\partial \varphi }{\partial t}+\nabla \cdot \left(\varphi \mathbf{u}\right)=\mathbf{M}{\nabla }^2{\mu }_{\varphi }(8)$

Where $\mathit{u}$ and t are the velocity and time, and $\mathbf{M}$ is a mobility coefficient.

Hydrodynamic equations in the phase-field model for incompressible multiphase flows are given by

$\nabla \cdot \mathbf{u}=0(9)$

$\rho \frac{\partial \mathbf{u}}{\partial t}+\rho \nabla \cdot \left(\mathbf{uu}\right)=-\nabla \cdot p+\nabla \cdot \text{Π}+{\mathit{F}}_{\mathit{s}}(10)$

$\rho$ is the density of fluid; $\text{p}$ is the hydrodynamic pressure which emphasizes incompressibility; $\text{Π}=\mu \left(\nabla \mathbf{u}+\mathbf{u}\nabla \right)$ is the viscous stress tensor, and$\mu$is the dynamic viscosity; $F_s=-\varphi \nabla {\mu }_{\varphi }$ is the force associated with surface tension.

LBE for a Velocity Based Method

A standard LBE form for hydrodynamic properties is represented as

$f_i\left(\mathbf{r}+{\mathbf{c}}_{\mathbf{i}}\Delta t, t+\Delta t\right)-f_i\left(\mathbf{r},t\right)=-\frac{f_i\left(\mathbf{r},t\right)-f_i^{eq}\left(\mathbf{r},t\right)}{{\tau }_f}+\frac{2{\tau }_f-1}{2{\tau }_f}{F}_i\Delta t(11)$

For particle distribution function in the phase space, it has the microscopic velocity ${\mathit{c}}_{\mathit{i}}$ and an external body force may be added $F_i$ at the $\text{r}$ space coordinate and time $t$; $f_i^{eq}\left(\mathbf{r},t\right)$ is the its corresponding equilibrium state; ${\tau }_f$ is dimensionless relaxation time for velocity field; $\Delta t$ is a time step.

In the present study, a 2-dimensional 9-velocity (D2Q9) LBM structure is used to solve the field in 2D.

The particle velocity in the D2Q9 structure can be given using Gauss-Hermite quadrature in

$\left[e_{\alpha }\right]=\{\begin{array}{cc}\left(\mathrm{0,0}\right)& \alpha =0\\ c\left([\frac{\cos \left[\alpha -1\right)\pi }{2}\right],\sin \left[\frac{\left(\alpha -1\right)\pi }{2}\right])& \alpha =\mathrm{1,2,3,4}\\ \sqrt{2}c\left(\cos \left[\frac{\left(2\alpha -1\right)\pi }{4}\right],\sin \left[\frac{\left(2\alpha -1\right)\pi }{4}\right]\right)& \alpha =\mathrm{5,6,7,8}\end{array}(12)$

Where $c=\Delta x/\Delta t$ and $\Delta x$ is the streaming length. In performing LBM in recovering the incompressible flow condition, we introduced a set of relations to be compiled by the zeroth, first and second moments of the equilibrium distribution function $f_i^{eq}\left(\mathbf{r},t\right)$:

${\displaystyle {\sum }_i{f}_i^{eq}=0}(13)$

${\displaystyle {\sum }_i{\mathbf{c}}_{\mathbf{i}}{f}_i^{eq}=0}(14)$

To satisfy the function above, the following equilibrium distribution function is.

Introduced as:

$f_i^{eq}={\omega }_i \rho \left[1+\frac{3\left({\mathbf{c}}_{\mathbf{i}}\cdot \mathbf{u}\right)}{c_s^2}+\frac{9{\left({\mathbf{c}}_{\mathbf{i}}\cdot \mathbf{u}\right)}^2}{2c_s^4}-\frac{3{\mathbf{u}}^2}{2c_s^2}\right],i\ne 0(15)$

For D2Q9 model, weighting factor ${\omega }_i$ is given by

${\omega }_i=\{\begin{array}{cc}1/4,& i=0\\ 1/18,& i=1\sim 6\\ 1/36,& i=7\sim 18\end{array}(16)$

The reference speed of sound $c_s=\frac{1}{\sqrt{3}}$.

Interface Capturing

Interface capturing is proposed to be given as:

$g_i\left(\mathbf{r}+{\mathit{c}}_{\mathit{i}}\Delta t,\mathit{ }t+\Delta t\right)=-\frac{g_i\left(\mathbf{r},t\right)-g_i^{eq}\left(\mathbf{r},t\right)}{{\tau }_g}+\eta \left[g_i^{eq}\left(\mathbf{r}+{\mathbf{c}}_{\mathbf{i}}\Delta t,\mathit{ }t\right)-g_i^{eq}\left(\mathbf{r},t\right)\right](17)$

Where ${\text{g}}_{\text{i}}\left(\mathbf{r},t\right)$ is the distribution for the order parameter; ${\text{g}}_{\text{i}}^{\text{eq}}\left(\mathbf{r},\text{t}\right)$ is its corresponding equilibrium state; ${\tau }_g$ is a relaxation time for the order parameter; and $\eta$ is a constant as $\eta =2{\tau }_g-1$.

The moments of the equilibrium distribution satisfy

${\displaystyle {\sum }_i{g}_i^{eq}=\varphi }(18)$

${\displaystyle {\sum }_i{\mathit{c}}_{\mathit{i}}{g}_i^{eq}}=\frac{\varphi u}{1-\eta }(19)$

Then, density can be calculated according to mass conservation as in Owengrub and Truskinovsky (1998)

$\rho =\frac{\varphi -{\varphi }_B}{{\varphi }_A-{\varphi }_B}\left({\rho }_A-{\rho }_B\right)+{\rho }_B(20)$

The viscosity distribution within interface in the LB is given by

$\mu =\frac{\varphi -{\varphi }_B}{{\varphi }_A-{\varphi }_B}\left({\mu }_A-{\mu }_B\right)+{\mu }_B(21)$

Discretization

The Laplacian of the force terms can be discretized and interfacial force is adopted

$\nabla \phi =\frac{{{\displaystyle \sum }}_{i\ne 0}{\omega }_i{\mathbf{c}}_{\mathbf{i}}\left({\mathbf{c}}_{\mathbf{i}}\cdot \nabla \phi \right)}{c_s^2}(21)$

${\nabla }^2\phi =\frac{{{\displaystyle \sum }}_{i\ne 0}{\omega }_i{\left({\mathit{c}}_{\mathit{i}}\cdot \nabla \right)}^2\phi }{c_s^2}(22)$

Where $\phi$ is any macroscopic quantity. We use second-order central difference to the directional derivatives in ${\mathit{c}}_{\mathit{i}}$direction as

${{\mathit{c}}_{\mathit{i}}\cdot \nabla \phi |}_r=\frac{\phi \left(\mathbf{r}+{\text{c}}_{\text{i}}\Delta \text{t}\right)-\phi (\mathbf{r}-{\text{c}}_{\text{i}}\Delta \text{t})}{2\Delta t}(23)$

${{\left({\mathit{c}}_{\mathit{i}}\cdot \nabla \right)}^2\phi |}_r=\frac{\phi \left(\mathbf{r}+{\text{c}}_{\text{i}}\Delta \text{t}\right)-2\phi \left(\mathbf{r}\right)+\phi (\mathbf{r}-{\mathbf{c}}_{\mathbf{i}}\Delta \text{t})}{\Delta t^2}(24)$

Validation

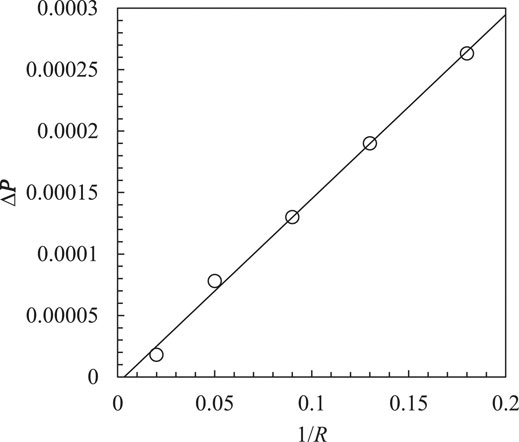
A test with one static droplet is to verify the phase field multiphase lattice Boltzmann model. Initially, a static water droplet is placed in the middle region of a computational domain. Periodic boundary conditions are applied to all boundaries. Physical properties of two phases are given by ${\rho }_w={\rho }_o=1000\text{ kg}/{\text{m}}^3$, ${\mu }_w=0.125{\mu }_o=0.001\text{Pa}\cdot \text{s}$, and surface tension is 0.0005 N/m the lattice spacing $\Delta x$ is 1 $\text{ μm}$ in physical units. $\xi =1.5\Delta x$. Order parameter relaxation time ${\tau }_g$ is $1/(3-\sqrt{3})$. At last, the bubble reaches the equilibrium. The pressure difference $\Delta p=p_{in}-p_{out}$ across a static bubble is related to the surface tension $\sigma$ according to Laplace’s law:

$\Delta p=\frac{\sigma }{R}(25)$

The radius of the droplet $R$ occupies several lattice units, which are surrounded by a quiescent phase. The boundaries of the computational domain are set to be periodic.

There is a good agreement between simulation results and the theoretical predictions, see Figure 1. The maximum error is less than 2.5%. This indicates that the surface tension simulations in the LB multiphase model have great accuracy.

FIGURE 1

FIGURE 1. Theoretical prediction (solid line) and numerical measurements of Laplace law (circles).

Results and Discussions

The parameters in the model are specified as dimensionless ratios between oil and water including viscosity and density ratios that represent external conditions. Interface thickness reflects the chemical properties of various surfactants. Radius depicts the size of the potential emulsified droplet.

Simulations of the binary droplet collision were carried out. Slip and no penetration boundary conditions are imposed at all boundaries of the computational domain. Two droplets are initially located at a far-center distance of 4$R$, and are moved towards each other by an attractive force until contact.

Head-On Collisions and Pre-coalescence of Binary Droplets

In order to evaluate the effects of various dominant parameters on emulsifier performance, a measurement is proposed. Two moving oil droplets immersed in water (light fluid) have interfacial behavior with the following procedures, see Figure 2. Initially, two bodies move from far afield. When the two reach the region where the distance between the two body centers is smaller than 2R, the first time is reckoned in as $t_1$. The two droplets continue to move until they make contact; the second time point is then recorded at the contact, $t_2$. Later, they start to merge into one, since the interface with double thickness would become small, if enough time would be given.

FIGURE 2

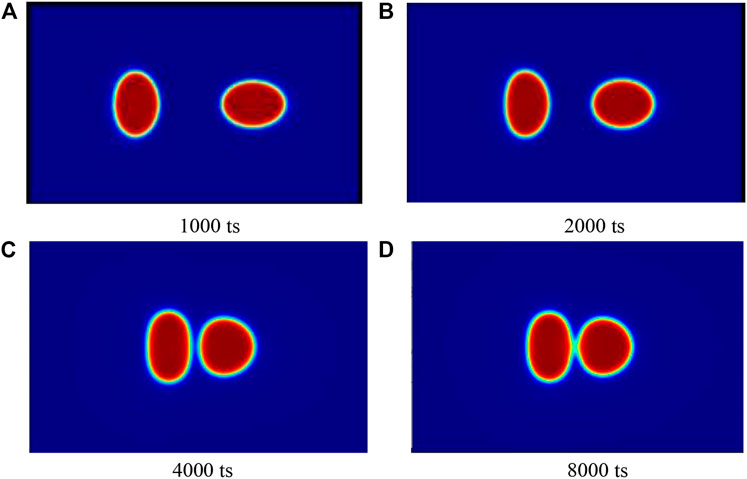
FIGURE 2. Temporal snapshots of two moving droplets within the time window from start time point to contact time point: $\sigma =1.0\times {10}^{-4}$, surface thickness d = 25 lattice units, viscosity ratio, and density ratio are set to be 10.

To quantify the balance between surface tension and interactive strength numerically, the selection of time window is defined as effective moving time. Here, effective moving time starts from the distance between droplets smaller than two radiuses to the nearest boundary distance equal to twice interface thickness, $t_2-t_1$. This time window represents degree of emulsified stability, i.e. the larger the time window is offered by specified emulsion, the better performance is showed, and vice versa.

Quantitative Measurements of Time Windows

To advise engineers to select one surfactant with good expectation, the effects of various parameters on the time window have been studied quantitatively.

Sizes of Existing Droplets, $\mathit{R}$ and Interface Thickness $\mathit{d}$

Surface tension is used to reflect the interactive strength of the two emulsified droplets and has significant effect on two phase interfacial behavior, and thereby the time window within effective contact distance between two droplets is measured as defined in Head on Collisions and Pre Coalescence of Binary Droplets. In order to keep surface tension acting on two phase systems at a reasonable level, various parameters are evaluated. In Figures 3, 4, effective time windows are decreased with the increase of magnitudes of surface tensions in systems with different radiuses and surface thicknesses. Weak interfacial strengths from two phases induce large time windows in which emulsifiers perform small surface tensions that are convenient for managing and controlling the cost of emulsifying stability.

FIGURE 3

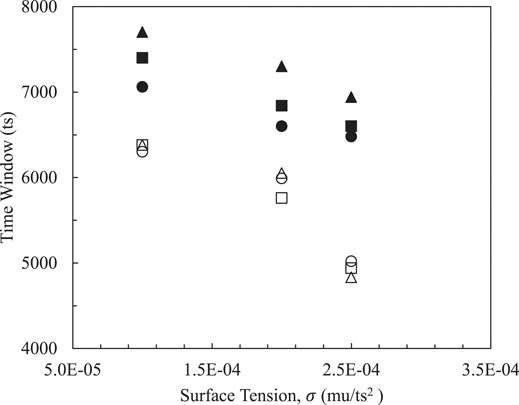
FIGURE 3. Effects of droplets sizes on time windows: circles ($R$= 35 lu), squares ($R$= 25 lu) and triangles ($R$= 15 lu) represent three specified droplet sizes, respectively; empty symbols stand for thick surfaces (d = 10 lu) and solid symbols mean thin surfaces (d = 5 lu), respectively.

FIGURE 4

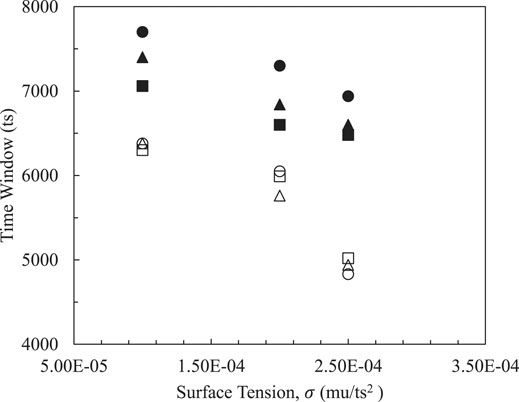
FIGURE 4. Effects of surface thicknesses on time windows with ${\rho }^{\ast }=10$ and ${\mu }^{\ast }=10$: empty symbols stand for thicker surfaces (d = 10 lu) and solid symbols mean thin surfaces (d = 5 lu), respectively; squares ($R$= 35 lu), triangles ($R$= 25 lu), and circles ($R$= 15 lu) represent three specified droplet sizes, respectively.

Figures 3, 4 both show the same trends on sizes of dispersed phases in terms of the effective time window. Smaller droplets have a wider time window due to increased total surface energy. Therefore, smaller ones are able to perform better stability and improve flow capability. On the other hand, larger droplets remain with a short duration that is used to govern contact behavior.

Shells of oil droplets and dimensions of emulsified droplets relate to emulsifying performance from chemical components of a specified emulsifier. To assess the effects of surface thicknesses and droplet radius on the time window, two thicknesses were specified on droplets surfaces as 5 and 10 lattice units and three droplets R = 15, 25 and 35 lattice unit (lu) are simulated, respectively. As the interface thickness is increased (empty symbols), the overlapped symbols indicate that sizes of internal phases have little effect on effective contact time. Meanwhile, if the thin shells with small surface thicknesses are attached onto oil droplets, the impact of the existing droplet dimension becomes significant, especially when surface tension is small. This means that the emulsifier with a capability of forming small oil droplets and a thick interface would be recommended. Furthermore, slopes of systems with thicker interfaces in both figures point out that it is sensitive to interface thickness as it changes faster at relatively high surface tension coefficients from 2.0$\times {10}^{-4}$ to 2.5$\times {10}^{-4}$ mu/ts². Surface energy of the dispersed phase under high surface tensions is declined, so droplets carrying thicker interfaces are easier to shrink. Therefore, time windows are decreased dramatically.

Effect of Density Ratio, μ^∗

In Figure 5, differences in viscosities between oil and water are dimensionlized as ${\mu }^{\ast }$ = ${\mu }_o⁄{\mu }_w$. Simulation results imply that emulsified heavy oil droplets have less time than emulsified lighter oil droplets due to narrow time windows in high viscosity ratio systems, while this does not mean, conflictingly, that heavy oil is easier to emulsify. Once the oil phase has been emulsified, such a dispersed state would have stayed longer in the water phase. Decreased viscosity differences between oil and water can increase the retention time of the dispersed phase, so some emulsifiers like polymer with high viscosities have been widely applied to enhanced oil recovery. The emulsifiers with different properties are represented by three different surface tensions, but the same interfacial thickness is kept. It suggests that to decreased surface tension is still an efficient way to manage emulsifying behavior easily. Besides, decreasing the dimension of droplets can enhance the impact on time windows shown from more dispersed symbols (empty). It is thereby confirmed that some emulsifiers can make small droplets stay dispersed longer when the viscosity of the external phase is high, and it does agree with our common sense.

FIGURE5

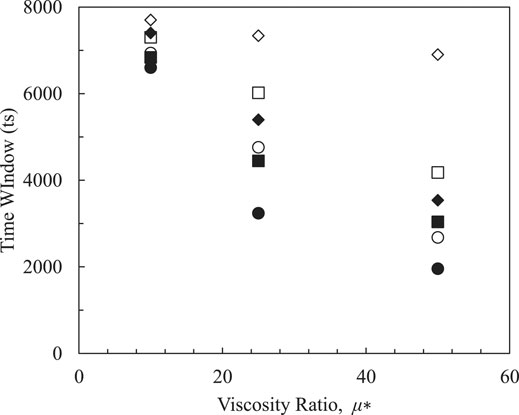
FIGURE5. Effects of viscosity ratio ${\text{μ}}^{\text{*}}$ on time windows: solid symbols represent large droplets (R = 25 lu) and empty symbols stand for small droplets (R = 15 lu), respectively; diamond ($\sigma$= 1$\times {10}^{-4}$ mu/ts²), squares ($\sigma$= 2$\times {10}^{-4}$ mu/ts²) and circles ($\sigma$= 2.5e-4 mu/ts2) represent three specified surface tensions, respectively.

Effect of Density Ratio ${\mathit{\rho }}^{\mathit{*}}$

Density is one of the most remarkable parameters in oil production. Density ratios in our LB simulations are varied from 0.8 to 1.4 recovering ranges of light to heavy oil extraction in reality. Simulation results from Figure 6 demonstrate that emulsifiers having increasing probability of emulsifying smaller droplets are recommended which not only show good emulsifying performance, but also are beneficial to manage the emulsifying process due to the large time windows left for engineers. Generally, physical properties of oil and water are fixed, small slopes (empty symbols) of systems with small droplets impact on time windows denote that increased density ratios between oil and water that can ensure relatively long durations of being dispersed. Therefore, the emulsifier carried by water should be designed to increase the density of the external phase comparing the density of the internal phase. This is to say that the less difference in density between the internal and external phases, the better emulsifying performance should be expected.

FIGURE 6

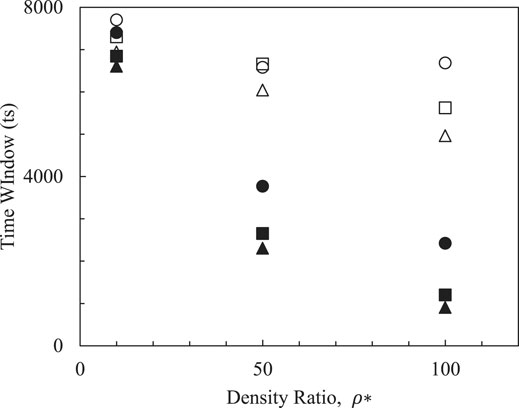
FIGURE 6. Effects of density ratio ${\text{ρ}}^{\text{*}}$ on time windows: solid symbols represent large droplets (R = 25 lu) and empty symbols stand for small droplets (R = 15 lu), respectively; circles ($\sigma$= 1$\times {10}^{-4}$ mu/ts²), squares ($\sigma$= 2$\times {10}^{-4}$ mu/ts²) and triangles ($\sigma$= 2.5$\times {10}^{-4}$ mu/ts²) represent three specified surface tensions coefficients, respectively.

Remark Conclusions

In this study, an effective time window is defined to measure emulsifying properties via staying times of dispersed phases. Interfacial tension, interfacial thickness, and differences of density and viscosity between dispersed and continuous phases have been simulated for the management and design of the emulsifiers.

1)Emulsifiers with a capability of forming small droplets and a thin interface outside are suggested, since small time windows indicate the good emulsifying performance can keep the droplets dispersed longer.

2)Small interfacial tensions provided by emulsifiers are still desired.

3)Decreasing differences of viscosities and densities between oil and water are also advised to design a binary emulsifying system.

4)A suitable emulsifier is not controlled by only one parameter. The difficulty in designing better performing emulsifiers relies on balancing these various parameters.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XL has contributed to simulation and datat analysis, JF has worked on double check manuscript, and BJ has worked for supervisor.

Funding

This work is financially supported by Chinese National Key Research and Development Program (No.SQ2018YFA070028) and SINOPEC Technical Project (No. P21085-18).

Conflicts of Interest

Authors XL, JF, BJ are employed by SINOPEC.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cui, Guodong., Pei, Shufeng., Rui, Zhenhua., Dou, Bin., Ning, Fulong., and Wang, Jiaqiang. (2020). Whole Process Analysis of Geothermal Exploitation and Power Generation from a Depleted High-Temperature Gas Reservoir by Recycling CO2. Energy 217, 119340 doi:10.1016/j.energy.2020.119340

CrossRef Full Text | Google Scholar

Cui, Guodong., Ren, Shaoran., Bin, Dou., and Fulong, Ning. (2020). Geothermal Energy Exploitation from Depleted High-Temperature Gas Reservoirs by Recycling CO2: The Superiority and Existing Problems. Geosci. Front. in press, doi:10.1016/j.gsf.2020.08.014

CrossRef Full Text | Google Scholar

Dicharry, C., Arla, D., Sinquin, A., Graciaa, A., and Bouriat, P. (2006). Stability of Water/Crude Oil Emulsions Based on Interfacial Dilatational Rheology. J. Colloid Interf. Sci. 297 (2), 785–791. doi:10.1016/j.jcis.2005.10.069

CrossRef Full Text | Google Scholar

Ding, D., Sun, Z., and Xu, M. (1998). Properties of Surface Film of Oil Components. J. Univ. Petroleum 22 (3), 82–83

Google Scholar

Dong, Z., Lin, M., Wang, H., and Li, M. (2010). Influence of Surfactants Used in Surfactant-Polymer Flooding on the Stability of Gudong Crude Oil Emulsion. Pet. Sci. 7 (2), 263–267. doi:10.1007/s12182-010-0031-y

CrossRef Full Text | Google Scholar

Jacqmin, D. (1999). Calculation of Two-phase Navier-Stokes Flows Using Phase-Field Modeling. J. Comput. Phys. 155 (1), 96–127. doi:10.1006/jcph.1999.6332

CrossRef Full Text | Google Scholar

Lamura, A., Gonnella, G., and Yeomans, J. M. (1999). A Lattice Boltzmann Model of Ternary Fluid Mixtures. Europhys. Lett. 45 (3), 314–320. doi:10.1209/epl/i1999-00165-4

CrossRef Full Text | Google Scholar

Mohammed, M., and Babadagli, T. (2021). New Insights into the Interfacial Phenomena Occurring between Hydrocarbon Solvent and Heavy Oil. J. Pet. Sci. Eng. 196, 108022. doi:10.1016/j.petrol.2020.108022

CrossRef Full Text | Google Scholar

Moran, K., Yeung, A., and Masliyah, J. (2006). The Viscoplastic Properties of Crude Oil-Water Interfaces. Chem. Eng. Sci. 61 (18), 6016–6028. doi:10.1016/j.ces.2006.05.026

CrossRef Full Text | Google Scholar

Nour, H. A., Yunus, R. M., and Anwaruddin, H. (2007). Water-in-Crude Oil Emulsions: Its Stabilitzation and Demulsification. J. Appl. Sci. 15, 12–130

Google Scholar

Owengrub, J., and Truskinovsky, L. (1998). Quasi-Incompressible Cahn-Hilliard Fluids and Topological Transitions. Proc. R. Soc. A: Math. Phys. Eng. Sci. 454, 2617–2654. doi:10.1098/rspa.1998.0273

CrossRef Full Text | Google Scholar

Song, W., Yin, Y., Landry, C. J., Prodanovic, M., Qu, Z., and Yao, J. (2021). A Local-Effective-Viscosity Multirelaxation-Time Lattice Boltzmann Pore-Network Coupling Model for Gas Transport in Complex Nanoporous Media. SPE J. 26 (01), 461–481. doi:10.2118/203841-pa

CrossRef Full Text | Google Scholar

Sun, Z., Li, X., Liu, W., Zhang, T., He, M., and Nasrabadi, H. (2020). Molecular Dynamics of Methane Flow Behavior through Realistic Organic Nanopores under Geologic Shale Condition: Pore Size and Kerogen Types. Chem. Eng. J. 398 (124341), 1–10. doi:10.1016/j.cej.2020.124341

CrossRef Full Text | Google Scholar

Sun, Z., Shi, J., Wu, K., Zhang, T., Feng, D., and Li, X. (2019). Effect of Pressure-Propagation Behavior on Production Performance: Implication for Advancing Low-Permeability Coalbed-Methane Recovery. SPE J. 24 (02), 681–697. doi:10.2118/194021-pa

CrossRef Full Text | Google Scholar

Swift, M. R., Orlandini, E., Osborn, W. R., and Yeomans, J. M. (1996). Lattice Boltzmann Simulations of Liquid-Gas and Binary Fluid Systems, Phys. Rev. E, 54, 5, 5041–5052. doi:10.1103/physreve.54.5041

CrossRef Full Text | Google Scholar

Temple-Heald, C., Davies, C., Wilson, N., and Readman, N. (2014). Developing New Surfactant Chemistry for Breaking Emulsions in Heavy Oil. J. Pet. Technology 66 (01), 30, doi:10.2118/0114-0030-jpt

CrossRef Full Text | Google Scholar

Tóth, G. I., and Kvamme., B. (2015). Phase Field Modelling of Spinodal Decomposition in the Oil/Water/Asphaltene System, Phys. Chem. Chem. Phys. 17. (31), 20259–20273. doi:10.1039/c5cp02357b

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Der Sman, R. G. M., and Meinders, M. B. J. (2016). Analysis of Improved Lattice Boltzmann Phase Field Method for Soluble Surfactants, Computer Phys. Commun. 199, 12–21. doi:10.1016/j.cpc.2015.10.002

CrossRef Full Text | Google Scholar

Wang, H. Y., Liu, Ai-qin., and Wen, Xin-min. (2008). Factors Influencing Interfacial Electric Properties of Produced Water from Oilfield Jining: Journal of the University of Petroleum, 143–146+151

Google Scholar

Zhang, Bingzhu., and Feng, Shubo. (2010). Advances in the Modelling and Simulation of Emulsion Polymerisation. Int. J. Model. 11 (Nov), 262–273. doi:10.1504/ijmic.2010.037038

CrossRef Full Text | Google Scholar

Zhang, J. Y., Wang, X. P., Liu, H. Y., Tang, J. A., and Jiang, L. (1998). Interfacial Rheology Investigation of Polyacrylamide-Surfactant Interactions. Colloids Surf. A: Physicochemical Eng. Aspects 132 (1), 9–16. doi:10.1016/s0927-7757(97)00151-9

CrossRef Full Text | Google Scholar

Zheng, H. W., Shu, C., Chew, Y. T., and Sun, J. H. (2008). Three-dimensional Lattice Boltzmann Interface Capturing Method for Incompressible Flows. Int. J. Numer. Meth. Fluids 56, 1653–1671. doi:10.1002/fld.1563

CrossRef Full Text | Google Scholar

Zu, Y. Q., and He, S. (2013). Phase-Field-Based Lattice Boltzmann Model for Incompressible Binary Fluid Systems with Density and Viscosity Contrasts. Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys. 87 (4), 1–23. doi:10.1103/physreve.87.043301

CrossRef Full Text | Google Scholar