- Department of Earth Sciences, Uppsala University, Uppsala, Sweden
Although many convincing, diverse, and sometimes competing models of glacier surging have been proposed, the observed behavior of surging glaciers does not fit into distinct categories, and suggests the presence of a universal mechanism driving all surges. On the one hand, recent simulations of oscillatory flow behavior through the description of transient basal drag hint at a fundamental underlying process. On the other hand, the proposition of a unified model of oscillatory flow through the concept of enthalpy adopts a systems based view, in an attempt to rather unify different mechanisms through a single universal measure. While these two general approaches differ in perspective, they are not mutually exclusive, and seem likely to complement each other. A framework incorporating both approaches would see the mechanics of basal drag describing ice flow velocity and surge propagation as a function of forcing by conditions at the glacier bed, in turn modulated through the unified measure of enthalpy.
1 Introduction
Surges are broadly defined as semi-periodic increases in ice flow velocity through basal sliding that are unrelated to direct climatic influences. Surging glaciers alternate between relatively short mass redistributing active phases and longer quiescent phases, during which flow speeds are low and mass accumulates in a reservoir area (Meier and Post, 1969). This behavior has been identified in about 1% of the world’s glaciers, and seems to occur more frequently in certain geographic clusters (Sevestre and Benn, 2015). Relatively few uniform characteristics are identifiable between glaciers exhibiting oscillatory flow velocities, leading to difficulties in determining a universal underlying mechanism driving surges (Clarke, 1991; Frappé and Clarke, 2007).
Founding models of glacier surging include the proposition that 1) flow acceleration is driven by a switch from cold to temperate conditions at the bed (Svalbard-type surges, Clarke, 1976; Murray et al., 2003), and 2) basal water pressure build up drives surge propagation and water release causes surge termination (Alaskan-type surges, Kamb et al., 1985). The two models have been co-existing in the literature as they are generally invoked to explain different types of surge behavior, the latter mechanism causing much more rapid flow acceleration during shorter active phases.
Since the 1980s, a growing body of research describes a wide range of observed surge behavior that does not fit neatly within one of the two originally suggested categories of surges (e.g. Fowler et al., 2001; Murray et al., 2003; Dunse et al., 2015; Lovell et al., 2018; Haga et al., 2020). Perhaps as a result, the various additions and revisions to initial surging theories suggested by these newer studies often transcend the boundaries between the initially proposed mechanisms; and the once clear distinction between two separate surging regimes somewhat wanes. Finally, investigations of conditions at the ice-bed interface show that stated prerequisites in previous models are not unequivocally valid, implying surge types are not solely linked to the glacier’s physical and thermal attributes (Harrison and Post, 2003; Sevestre et al., 2015). In an extensive study of properties of surging glaciers worldwide, Sevestre and Benn (2015) identify strong influences of climate and glacier geometry on surging, but this materialises as a range in oscillatory flow behavior, rather than as distinct categories. A similar observation is made through regional monitoring of flow acceleration in Herreid and Truffer (2016). Finally, (Frappé and Clarke, 2007), build on the example of Trapridge glacier exhibiting different types of surge behavior in subsequent active phases to argue against the distinction between surge types, and in favour of the presence of a single underlying mechanism.
As advanced by Frappé and Clarke (2007), placing surges on a spectrum of the same phenomenon rather than considering them in different categories implies that there is potentially a single universal mechanism. This creates a tension with the various previously proposed models, many of which have been illustrated rather convincingly in case studies. There seem to be two ways to reconcile this tension: either all processes must be secondary to a single fundamental mechanism that describes all surges, or surging can be explained as the result of the interaction between various mechanisms, providing a unified theory through a systems based approach. This review briefly discusses recent work towards a universal model of glacier surges, how these advances fit in either of the two approaches, and offers suggestions for further progress towards an all encompassing model of unstable flow.
2 A Process Based View on Surging
Basal processes are difficult to observe during an active phase (Harrison and Post, 2003), and the physics of basal drag are generally simplified or circumvented altogether in numerical models of surging (e.g. Van Pelt and Oerlemans, 2012; Benn et al., 2019a; Ou, 2021). This gap in understanding makes basal mechanics an obvious avenue for identifying a fundamental mechanism regulating all surge motion.
Thøgersen et al. (2019) recently proposed a rate and state friction model describing surge initiation and propagation entirely through the evolution of friction at hard glacier beds, validating model results through comparisons with the Variegated glacier surge documented in Kamb et al. (1985). The paper builds on concepts from Gagliardini et al. (2007), who model the influence of subglacial bed roughness on the friction term. Thøgersen et al. (2019) identify threshold shear stresses at which friction flips from velocity strengthening to velocity weakening (Figure 1). The authors note that if the initial velocity weakening friction instability occurs in an area larger than a certain threshold, it can propagate over the glacier, producing characteristics such as a bulge at the surge front. The study identifies mass build up, common to all surging glaciers, as the only required process leading to a transgression of the shear stress threshold that triggers an active phase. Nevertheless, the authors add that increased meltwater supply can facilitate and/or lead to a switch towards velocity weakening friction by reducing the glacier sole’s ability to adhere to the bed surface. Meanwhile, the study’s focus lies on motion of the ice over a hard bed surface, and motion incurred from the deformation of soft substrates is not directly accounted for in the model. Harrison and Post (2003) suggest such deformation to play an important role in active phase flow in most observed surges, including that of Variegated glacier, thus somewhat limiting the present iteration of rate and state friction as the fundamental process governing surging.
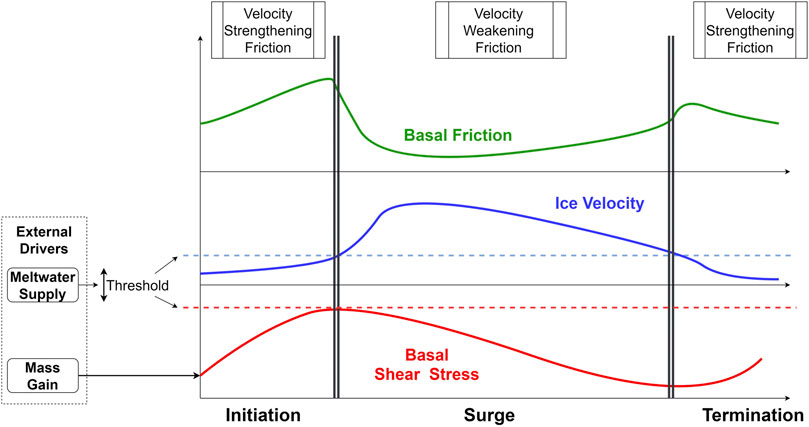
FIGURE 1. Conceptual and simplified temporal evolution of mechanism parameters described in Thøgersen et al. (2019). During initiation basal shear stress increases with mass gain, flow velocity is restrained by velocity strengthening friction. Water presence influences level of threshold in shear stress and velocity that results in velocity weakening friction. During surge, friction is low, velocity is high, driving stress gradually decreases. At low driving stress velocity decreases and friction returns to velocity strengthening thus following basal slip rates, surge is terminated. View is strongly simplified: detail of cavity formation, spatial propagation and influence of valley side friction not included here.
Recent work has shown that strain driven till dilation can lead to increased weakening and strain if the material has high hydraulic diffusivity (e.g. Hart et al., 2019). Minchew and Meyer (2020) propose a model for surge initiation through till dilation weakening, sustained throughout surge initiation and propagation by the reduced effective normal stress resulting from dynamic thinning of the overlying ice. The model relies on effective pressure changes to drive till deformation, but crucially these changes are produced from the behavior of the till itself and can occur with unvaried water volume at the bed. The mechanism is independent of changes at its boundaries, but the authors explicitly mention that considering variations in water pressure is an avenue for further research. Nevertheless, if most glaciers exhibiting surges are indeed underlain by soft sediments (Harrison et al., 2015) and no examples are brought forward of surge initiation in cold based areas, the Minchew and Meyer model might go a long way towards acting as a fundamental mechanism.
Thøgersen et al. (2019) and Minchew and Meyer (2020) describe different components of basal motion, and they are not necessarily mutually exclusive. Zoet and Iverson (2020) propose a slip law that is non-specific to surging, but incorporates both rate strengthening basal sliding over hard beds at low slip rates to plastic behavior through a deforming bed at higher flow speeds. The transition between the two mechanisms occurs at a threshold in till shear strength, which is dependent on effective pressure. Although Zoet and Iverson’s model reflects an idealized experimental scenario and requires further testing, it hints at a universal slip law (Minchew and Joughin, 2020). The behavior it describes echoes surge type flow acceleration, while once again presenting a link to influences of water pressure at the base.
3 A Systems Based View on Surging
Rather than narrowing the boundaries around a single key process from which other mechanisms follow, one can also widen the boundaries and consider the interaction of all mechanisms as the underlying process driving surging. Several recent studies can be viewed as efforts towards widening the boundaries of the considered system. This happens through the incorporation of mechanisms of surge initiation driven by water supply from englacial sources (Lingle and Fatland, 2003), the transfer of surface melt to the bed through enhanced crevassing during surge onset (e.g. Dunse et al., 2015) and water removal from the bed through perennial conduits at surge termination (Benn et al., 2009). Considerations of the effects of glacier geometry on thermodynamics (Sevestre et al., 2015) and of bed topography on mass build-up (Lovell et al., 2018) further widen understanding of processes affecting surges. The growing complexity resulting from the widening boundaries naturally leads to a larger number of possible system outcomes, with a specific surge resulting from a specific set of interacting processes and their respective specific amplitudes. This vast amount of possibilities then produces the diverse range of observed surging behavior. Sevestre and Benn (2015) catalogue this range as a surge envelope, with the boundaries of the said envelope representing the edges of the possible combinations of conditions that lead to oscillatory flow. Such a consideration requires a universal medium through which these diverse characteristics could interact, and ideally a universal unit through which they can be studied, and modelled numerically, within a single framework.
Sevestre and Benn (2015), and in further detail Benn et al. (2019a), propose enthalpy as precisely such a unit. Enthalpy quantifies glacier-internal energy regardless of the thermal regime of the ice, as it is measured by ice-water content at the pressure melting point and by ice-temperature below it. At the bed of an incompressible glacier, enthalpy gains occur through geothermal heating, frictional heating and melt water supply. Enthalpy losses occur through heat conduction from the bed to the surface, and drainage of melt water. Glaciers would then show periodic oscillations in flow velocity if there is an imbalance in either enthalpy or mass balance versus mass transfer, with a reinforcing feedback driving increased basal sliding at surge onset, and termination occurring when enthalpy loss through meltwater discharge exceeds enthalpy gains from sliding (Benn et al., 2019a). The first numerical models of enthalpy budgets and the associated ice flow velocity response simulate a wide range in oscillation frequencies and amplitude; and prove successful at mirroring the observed behavior of a surge of Morsnevbreen, on Svalbard (Benn et al., 2019a,b).
While considering glacier flow velocity oscillations and instability propagation through systemically driven enthalpy imbalances is certainly a new approach, it can hardly be described as a new mechanism. All the physical processes involved in the enthalpy model had been introduced in previous research. The diversity and complexity of these many processes is still present, and enthalpy is not driving one single mechanism that explains all surges. Rather, the enthalpy approach has the merit to provide a framework within which to consider the intricate dynamics of surging through a single universal measure. In this view, the enthalpy model does not invalidate or compete with specific models of glacier surging but rather incorporates them as components of a larger unified framework.
4 Fundamental Processes Within the Enthalpy Framework
Where do models that produce surge type flow acceleration independently of changes in enthalpy such as Thøgersen et al. and Minchew and Meyer’s models, fit within the enthalpy framework? As argued before, the enthalpy model is a means to quantify conditions at the bed rather than a physical formulation of basal slip.
Enthalpy theory ascribes surge initiation to a runaway feedback loop between sliding rates and basal melt that ultimately leads to surge-type ice velocities (Benn et al., 2019a), relying on (Lliboutry’s, 1968) widely used relation linking high ice flow velocities to low effective pressure. The resulting gradual surge build-up does reflect the multi-year activation of certain Svalbard surges but is less representative of sudden onsets of the active phase that characterise Alaskan-type surges (e.g. Nolan et al., 2021). Here, the non monotonic response of basal drag to increasing sliding rates caused by a regime change towards low basal friction in Thøgersen et al. (2019) and by till failure at yield strength in Minchew and Meyer (2020) could provide specific thresholds above which initial acceleration starts to occur.
The validity of the simplified effective pressure—sliding velocity relation in Benn et al. (2019a) also seems to be put into question when considering up or down-glacier surge propagation. If local low effective pressure is necessary for fast flow, surge propagation must be explained by pressurized water penetrating below slow flowing regions of the glacier to allow for subsequent local acceleration of basal slip. Enthalpy transfer is then the driving agent for surge propagation. Such a mechanism echoes the model of thermally controlled surging where water penetrates into frozen tills (Clarke, 1976) and where frozen bed surface conditions constrain the rather gradual spatial transfer of basal enthalpy necessary to explain observed slow surge front propagation. Similar solutions are also hinted at in Murray et al. (2000) and Benn et al. (2019b), with control on basal enthalpy transfer being shouldered by the hydraulic diffusivity properties of till in the absence of frozen substrate during observed surges on Svalbard. The mechanism further resonates as valid in instances where (enthalpy driven) propagation speeds exceed ice flow velocities (e.g. Murray et al., 2003) and in situations where the lower reaches of the glacier are subject to sudden destabilisation after basal water intrusions (Haga et al., 2020). Nevertheless, examples of up-glacier propagation (e.g. Sevestre et al., 2018) and of terminus advance (e.g. Kamb et al., 1985) logically imply that the stress balance plays a consequent role in the spatial propagation of zones with high basal sliding rates. This is further supported by areas of the glacier being isolated from draw down by the kinematic barrier provided by an ice fall (Echelmeyer et al., 1987; Nolan et al., 2021). Down-glacier surge propagation is then simply driven by the increase in compressive longitudinal stress induced by fast upstream motion, and up-glacier propagation is caused by longitudinal stretching (e.g. Halfar, 2020; Ou, 2021). Incorporating the new theories describing transient basal drag solves the problematic dependence of ice motion, and more importantly surge propagation, on water pressure at the base. Unchanged or even decreasing basal drag with increasing slip rates would allow the driving force behind propagation to be changes in the glacier’s stress balance rather than subglacial water transfer.
It needs to be underlined however that the influence of internal heat and water on surge occurrence remains undisputed. Geographic clustering of surge type glaciers implies that there is some form of external influence on the surging process (Sevestre and Benn, 2015). The critical role of water supply to the bed at various stages of the active phase has been demonstrated repeatedly (e.g. Lingle and Fatland, 2003; Gladstone et al., 2014), and Benn et al. (2019b) convincingly illustrate the impact of different enthalpy states of the bed surface. Both Thøgersen et al. and Minchew and Meyer insist their respective models are only partial representations, and the described processes would be clearly affected by variations especially in water pressure, offering an obvious coupling point to a wider enthalpy framework. Through the consideration of transient basal drag, thresholds for surge onset and termination, and propagation direction and velocity, can be described by a combination of the stress balance and the resistance to basal slip provided by the bed.
Maybe this framework can then be divided into two components: a fundamental component describing the transient behavior of friction and deformation at and in the bed, and a forcing component describing the supply of enthalpy to the first component (Figure 2). From observational evidence, it seems obvious that this forcing plays a crucial role: geothermal heat retention, basal water accumulation, and surface meltwater pulses to the base have all been shown to lead to surge initiation (Frappé and Clarke, 2007; Dunse et al., 2015; Kamb, 1987). Surge propagation speed has been linked to basal enthalpy and to dissipation of basal water (Murray et al., 2000; Benn et al., 2019b). Finally, termination can clearly be caused by sudden enthalpy diffusion rather than mass diffusion (Benn et al., 2009). The above listed processes play important roles in specific cases but are non universal. The shared component in all descriptions of surging is the complex translation of water pressure at the base to ice motion, which seems likely to be improved by new advances in understanding transient basal drag.
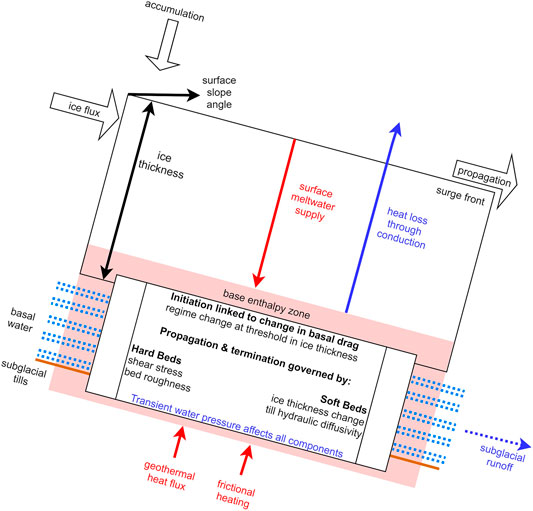
FIGURE 2. Enthalpy components based on Benn et al. (2019a). Enthalpy gains are in blue, enthalpy losses in red. Initiation of flow velocity through changes in basal drag are independent but linked to the enthalpy framework trough the impact of effective pressure.
5 Solidifying the Framework
Enthalpy could be a powerful tool in describing interactions between water, sediment and overburden pressure at the bed, providing a standardised unit to describe energy budgets and gradients over time, as well as lateral and vertical transfers of heat and water. Where enthalpy budgets can explain the likelihood of a glacier to surge, widening the system boundaries further and considering spatial variation in enthalpy over the glacier bed during the different phases of the surge cycle could provide insight towards the interactions with subglacial topography and the thermal properties of the bed surface that drive enthalpy accumulation. Such glacier specific features that promote enthalpy pooling in reservoir areas have been identified as overdeepenings (Lovell et al., 2018; Benn et al., 2019b), barriers of cold based ice (Haga et al., 2020), transverse basal crevasses (Zhan, 2019), and clast-rich substrates (Crompton et al., 2018). Their presence could provide a possible hint as to the propensity of specific glaciers within the surge envelope to surge or not. Furthermore, enthalpy gradients could perhaps be used to describe the surge front, with the steepness of such a gradient acting as an indicator of the glacier’s temporal position in the surge cycle. The propagation of a surge could then be viewed as enthalpy dissipation, and its termination might be predicted as a function of enthalpy depletion. Two dimensional models of enthalpy evolution over time within a glacier have been developed to monitor non-surge type polythermal glaciers (e.g. Hewitt and Schoof, 2017), and their coupling to the foundations of a lumped parameter type model such as presented in Benn et al. (2019b) could be a promising pursuit. Such a distributed model would likely resemble previous idealized ice sheet simulations that have been shown to produce oscillatory behavior (Van Pelt and Oerlemans, 2012; Feldmann and Levermann, 2017), but with a more detailed representation of the enthalpy variable, allowing for transfers through water drainage and englacial penetration rather than heat conduction only.
Thøgersen et al. and Minchew and Meyer (2020) describe separate components of basal motion, and a complete model of transient basal drag during the surge cycle would be critical in constraining thresholds in fast flow initiation. Coupling the models of basal drag with subglacial hydrology and temperature could advance understanding in the interaction between the fundamental and forcing components of the proposed expanded enthalpy framework. A coupled numerical model could prove a helpful tool in determining the combinations of subglacial conditions that lead to surging, for example through parameter sensitivity analysis.
A remaining weakness in the enthalpy model noted in Benn et al. (2019a) is estimating contributions of surface melt to basal enthalpy and basal discharge away from the reservoir or surging area. Observing water pathways and basal effective pressures during surges will be an essential avenue towards accurately determining enthalpy stock at the bed and thus critical to understanding transient basal drag and surge dynamics more widely. Novel measurement strategies towards this aim are being developed: Gimbert et al. (2016) demonstrate that basal pressure gradients and subglacial channel sizes can be observed through the analysis of glacio-hydraulic tremor, while Zhan (2019) identifies shifts in drainage systems through the analysis of seismic background noise. In turn, Lipovsky et al. (2019) suggest that rate weakening friction could be identified through increased seismicity caused by sediment entrainment along the glacier bed. Finally (Borstad et al., 2018), suggest implementing pressure and motion sensors during an active surge on Svalbard, recovering data through telemetry.
6 Conclusion
The wide variety of suggested processes affecting glacier surging is in tension with the supposition that all surges share a similar underlying mechanism, based on the absence of clearly distinguishable categories of unstable flow. This tension can be resolved either through identifying a single fundamental process that trumps all others, or through a system-based explanation that attributes case-specific influence to all its components. This paper argues that recently proposed models of surging roughly fit within these two approaches, although none claims the identification of a single conclusive explanation of oscillatory flow. Rather, these models seem to complement each other. Fundamental descriptions of transient basal drag could explain the translation of high enthalpy conditions to basal slip, and provide the physical basis explaining the mechanics of surge behavior, including initiation thresholds and propagation. These mechanics are nevertheless governed by the conditions they occur in. The concept of enthalpy offers a wider systemic framework to describe and monitor the forcing of flow acceleration by conditions at the glacier bed through a single measure, thus potentially facilitating further research towards surges. This could include spatially distributed considerations and modelling of surging, supported by advances in observational techniques. While the recent advances seem a step in the direction of a comprehensive description of all oscillatory flow, known processes remain to be described with more certainty and new mechanisms could still be uncovered, at which point they could be added to the extended framework or transcend it altogether.
Author Contributions
YT wrote the initial draft; WVP provided suggestions, guidance and comments; VP, and RP provided suggestions and feedback.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors WVP.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful to Doug I. Benn for his suggestions and feedback on an earlier version of the manuscript; and to Martin Truffer and two reviewers for their sharp and constructive comments.
References
Benn, D. I., Fowler, A. C., Hewitt, I., and Sevestre, H. (2019a). A General Theory of Glacier Surges. J. Glaciol. 65, 701–716. doi:10.1017/jog.2019.62
Benn, D. I., Jones, R. L., Luckman, A., Fürst, J. J., Hewitt, I., and Sommer, C. (2019b). Mass and Enthalpy Budget Evolution during the Surge of a Polythermal Glacier: a Test of Theory. J. Glaciol. 65, 717–731. doi:10.1017/jog.2019.63
Benn, D. I., Kristensen, L., and Gulley, J. D. (2009). Surge Propagation Constrained by a Persistent Subglacial Conduit, Bakaninbreen-Paulabreen, Svalbard. Ann. Glaciol. 50, 81–86. doi:10.3189/172756409789624337
Borstad, C. P., Porter, P. R., Luckman, A. J., Main, B., and Jenssen, E. (2018). Open-source Telemetry Instrumentation for Networked and Real-Time Glacier Monitoring. AGUFM 2018, C33D–C1601.
Clarke, G. K. C. (1991). Length, Width and Slope Influences on Glacier Surging. J. Glaciol. 37, 236–246. doi:10.3189/S0022143000007255
Clarke, G. K. C. (1976). Thermal Regulation of Glacier Surging. J. Glaciol. 16, 231–250. doi:10.3189/S0022143000031567
Crompton, J. W., Flowers, G. E., and Stead, D. (2018). Bedrock Fracture Characteristics as a Possible Control on the Distribution of Surge-type Glaciers. J. Geophys. Res. Earth Surf. 123, 853–873. doi:10.1002/2017JF004505
Dunse, T., Schellenberger, T., Hagen, J. O., Kääb, A., Schuler, T. V., and Reijmer, C. H. (2015). Glacier-surge Mechanisms Promoted by a Hydro-Thermodynamic Feedback to Summer Melt. The Cryosphere 9, 197–215. doi:10.5194/tc-9-197-2015
Echelmeyer, K., Butterfield, R., and Cuillard, D. (1987). Some Observations on a Recent Surge of Peters Glacier, Alaska, U.S.A. J. Glaciol. 33, 341–345. doi:10.1017/s0022143000008935
Feldmann, J., and Levermann, A. (2017). From Cyclic Ice Streaming to Heinrich-like Events: the Grow-And-Surge Instability in the Parallel Ice Sheet Model. The Cryosphere 11, 1913–1932. doi:10.5194/tc-11-1913-2017
Fowler, A. C., Murray, T., and Ng, F. S. L. (2001). Thermally Controlled Glacier Surging. J. Glaciol. 47, 527–538. doi:10.3189/172756501781831792
Frappé, T.-P., and Clarke, G. K. (2007). Slow Surge of Trapridge Glacier, yukon Territory, canada. J. Geophys. Res. Earth Surf. 112. doi:10.1029/2006jf000607
Gagliardini, O., Cohen, D., Råback, P., and Zwinger, T. (2007). Finite-element Modeling of Subglacial Cavities and Related Friction Law. J. Geophys. Res. 112. doi:10.1029/2006JF000576
Gimbert, F., Tsai, V. C., Amundson, J. M., Bartholomaus, T. C., and Walter, J. I. (2016). Subseasonal Changes Observed in Subglacial Channel Pressure, Size, and Sediment Transport. Geophys. Res. Lett. 43, 3786–3794. doi:10.1002/2016gl068337
Gladstone, R., Schäfer, M., Zwinger, T., Gong, Y., Strozzi, T., Mottram, R., et al. (2014). Importance of Basal Processes in Simulations of a Surging Svalbard Outlet Glacier. The Cryosphere 8, 1393–1405. doi:10.5194/tc-8-1393-2014
Haga, O. N., McNabb, R., Nuth, C., Altena, B., Schellenberger, T., and Kääb, A. (2020). From High Friction Zone to Frontal Collapse: Dynamics of an Ongoing Tidewater Glacier Surge, Negribreen, Svalbard. J. Glaciology, 1–13. doi:10.1017/jog.2020.43
Halfar, P. (2020). Surging Glaciers I: Dynamics and Geometry. Acta Mech. 231, 827–842. doi:10.1007/s00707-020-02614-w
Harrison, W. D., Osipova, G. B., Nosenko, G. A., Espizua, L., Kääb, A., Fischer, L., et al. (2015). “Glacier Surges,” in Snow and Ice-Related Hazards, Risks and Disasters (Elsevier), 437–485. doi:10.1016/B978-0-12-394849-6.00013-5
Harrison, W. D., and Post, A. S. (2003). How Much Do We Really Know about Glacier Surging? Ann. Glaciol. 36, 1–6. doi:10.3189/172756403781816185
Hart, J. K., Martinez, K., Basford, P. J., Clayton, A. I., Robson, B. A., and Young, D. S. (2019). Surface Melt Driven Summer Diurnal and winter Multi-Day Stick-Slip Motion and till Sedimentology. Nat. Commun. 10, 1599–1611. doi:10.1038/s41467-019-09547-6
Herreid, S., and Truffer, M. (2016). Automated Detection of Unstable Glacier Flow and a Spectrum of Speedup Behavior in the alaska Range. J. Geophys. Res. Earth Surf. 121, 64–81. doi:10.1002/2015JF003502
Hewitt, I. J., and Schoof, C. (2017). Models for Polythermal Ice Sheets and Glaciers. The Cryosphere 11, 541–551. doi:10.5194/tc-11-541-2017
Kamb, B. (1987). Glacier Surge Mechanism Based on Linked Cavity Configuration of the Basal Water Conduit System. J. Geophys. Res. 92, 9083–9100. doi:10.1029/JB092iB09p09083
Kamb, B., Raymond, C. F., Harrison, W. D., Engelhardt, H., Echelmeyer, K. A., Humphrey, N., et al. (1985). Glacier Surge Mechanism: 1982-1983 Surge of Variegated Glacier, alaska. Science 227, 469–479. doi:10.1126/science.227.4686.469
Lingle, C. S., and Fatland, D. R. (2003). Does Englacial Water Storage Drive Temperate Glacier Surges? Ann. Glaciol. 36, 14–20. doi:10.3189/172756403781816464
Lipovsky, B. P., Meyer, C. R., Zoet, L. K., McCarthy, C., Hansen, D. D., Rempel, A. W., et al. (2019). Glacier Sliding, Seismicity and Sediment Entrainment. Ann. Glaciol. 60, 182–192. doi:10.1017/aog.2019.24
Lliboutry, L. (1968). General Theory of Subglacial Cavitation and Sliding of Temperate Glaciers. J. Glaciol. 7, 21–58. doi:10.1017/s0022143000020396
Lovell, A. M., Carr, J. R., and Stokes, C. R. (2018). Topographic Controls on the Surging Behaviour of Sabche Glacier, nepal (1967 to 2017). Remote Sensing Environ. 210, 434–443. doi:10.1016/j.rse.2018.03.036
Meier, M. F., and Post, A. (1969). What Are Glacier Surges? Can. J. Earth Sci. 6, 807–817. doi:10.1139/e69-081
Minchew, B., and Joughin, I. (2020). Toward a Universal Glacier Slip Law. Science 368, 29–30. doi:10.1126/science.abb3566
Minchew, B. M., and Meyer, C. R. (2020). Dilation of Subglacial Sediment Governs Incipient Surge Motion in Glaciers with Deformable Beds. Proc. R. Soc. A. 476, 20200033–0033. doi:10.1098/rspa.2020.0033
Murray, T., Strozzi, T., Luckman, A., Jiskoot, H., and Christakos, P. (2003). Is There a Single Surge Mechanism? Contrasts in Dynamics between Glacier Surges in Svalbard and Other Regions. J. Geophys. Res. 108. doi:10.1029/2002JB001906
Murray, T., Stuart, G. W., Miller, P. J., Woodward, J., Smith, A. M., Porter, P. R., et al. (2000). Glacier Surge Propagation by thermal Evolution at the Bed. J. Geophys. Res. 105, 13491–13507. doi:10.1029/2000JB900066
Nolan, A., Kochtitzky, W., Enderlin, E. M., McNabb, R., and Kreutz, K. J. (2021). Kinematics of the Exceptionally-Short Surge Cycles of Sít' Kusá (Turner Glacier), Alaska, from 1983 to 2013. J. Glaciol. , 1, 1–15. doi:10.1017/jog.2021.29
Ou, H.-W. (2021). A Theory of Glacier Dynamics and Instabilities Part 1: Topographically Confined Glaciers. J. Glaciology, 1–12. doi:10.1017/jog.2021.20
Sevestre, H., and Benn, D. I. (2015). Climatic and Geometric Controls on the Global Distribution of Surge-type Glaciers: Implications for a Unifying Model of Surging. J. Glaciol. 61, 646–662. doi:10.3189/2015JoG14J136
Sevestre, H., Benn, D. I., Hulton, N. R. J., and Bælum, K. (2015). Thermal Structure of Svalbard Glaciers and Implications for thermal Switch Models of Glacier Surging. J. Geophys. Res. Earth Surf. 120, 2220–2236. doi:10.1002/2015jf003517
Sevestre, H., Benn, D. I., Luckman, A., Nuth, C., Kohler, J., Lindbäck, K., et al. (2018). Tidewater Glacier Surges Initiated at the Terminus. J. Geophys. Res. Earth Surf. 123, 1035–1051. doi:10.1029/2017JF004358
Thøgersen, K., Gilbert, A., Schuler, T. V., and Malthe-Sørenssen, A. (2019). Rate-and-state Friction Explains Glacier Surge Propagation. Nat. Commun. 10, 1–8. doi:10.1038/s41467-019-10506-4
Van Pelt, W. J. J., and Oerlemans, J. (2012). Numerical Simulations of Cyclic Behaviour in the Parallel Ice Sheet Model (Pism). J. Glaciol. 58, 347–360. doi:10.3189/2012jog11j217
Zhan, Z. (2019). Seismic Noise Interferometry Reveals Transverse Drainage Configuration beneath the Surging Bering Glacier. Geophys. Res. Lett. 46, 4747–4756. doi:10.1029/2019GL082411
Keywords: glacier surges, glacier dynamics, oscillatory flow, enthalpy, basal drag, ice and climate
Citation: Terleth Y, Van Pelt WJJ, Pohjola VA and Pettersson R (2021) Complementary Approaches Towards a Universal Model of Glacier Surges. Front. Earth Sci. 9:732962. doi: 10.3389/feart.2021.732962
Received: 29 June 2021; Accepted: 09 September 2021;
Published: 22 September 2021.
Edited by:
Matthias Huss, ETH Zürich, SwitzerlandReviewed by:
Duncan Joseph Quincey, University of Leeds, United KingdomMartin Truffer, University of Alaska Fairbanks, United States
Rachel Joanne Carr, Newcastle University, United Kingdom
Copyright © 2021 Terleth, Van Pelt, Pohjola and Pettersson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yoram Terleth, eW9yYW0udGVybGV0aEBnbWFpbC5jb20=
†Present address: Yoram Terleth, Department of Geological Sciences, University of Idaho, Moscow, ID, USA
 Yoram Terleth
Yoram Terleth Ward J. J. Van Pelt
Ward J. J. Van Pelt Veijo A. Pohjola
Veijo A. Pohjola Rickard Pettersson
Rickard Pettersson