Sparse Constrained Least-Squares Reverse Time Migration Based on Kirchhoff Approximation

Least-squares reverse time migration (LSRTM) is powerful for imaging complex geological structures. Most researches are based on Born modeling operator with the assumption of small perturbation. However, studies have shown that LSRTM based on Kirchhoff approximation performs better; in particular, it generates a more explicit reflected subsurface and fits large offset data well. Moreover, minimizing the difference between predicted and observed data in a least-squares sense leads to an average solution with relatively low quality. This study applies L1-norm regularization to LSRTM (L1-LSRTM) based on Kirchhoff approximation to compensate for the shortcomings of conventional LSRTM, which obtains a better reflectivity image and gets the residual and resolution in balance. Several numerical examples demonstrate that our method can effectively mitigate the deficiencies of conventional LSRTM and provide a higher resolution image profile.

Introduction

Seismic migration is an inverse procedure of forward modeling, which can restore the interior of the earth medium with record data. Specifically, migration attempts to eliminate the effects caused by the process of physical propagation and obtain an image that clearly depicts the structural information of interest. Reverse time migration (RTM), a state-of-the-art seismic imaging method (Baysal et al., 1983; McMechan, 1983), identifies the aforementioned acausal procedure appropriately. Based on two-way wave equation, RTM is powerful for handling complex geological settings and velocity with dramatic variation in the lateral direction. Therefore, it can deal with steep dips and salt dome better than conventional migration (Zhu and Lines, 1998; Yoon et al., 2003; Liu et al., 2010). However, most migration methods, including RTM, use the adjoint operator to compute the image instead of the inverse operator (Tarantola, 1984). Practical data suffers from many factors, such as irregular acquisition geometry and limited aperture of the acquisition system. These deficiencies generate artifacts and degrade the resolution. To overcome these limitations, least-squares migration (LSM) was proposed to combine with RTM (Liu et al., 2011; Dai et al., 2012). Therefore, seismic imaging can be regarded as a linearized inverse problem. With a proper initial velocity model, seismic records can be inverted to a more accurate profile. LSRTM iteratively reduces the residual between predicted data and observed data in a least-squares framework; therefore, the adjoint operator can keep approaching the inverse operator. Many results have indicated that LSRTM has a better performance than conventional RTM and migration (Zhang et al., 2015; Dutta and Schuster, 2014; Liu et al., 2016).

The precondition of seismic inversion is forward modeling, which maps the parameter model to seismic data. There are two main approaches to build linear approximation between physical model and wavefield (Yang and Zhang, 2019). One is the most commonly used Born approximation based on small perturbation (Beylkin, 1985; Bleistein, 1987). This requires that high-order scattered wavefields are much weaker than primary field. The Born operator describes a linear relationship between model perturbation and primary reflected wave. It divides the wavefield into two parts: background wavefield and perturbation wavefield. LSRTM based on Born approximation can achieve model perturbation with these two fields. In addition, an alternative scheme for modeling is Kirchhoff approximation (Bleistein, 1987). Compared with Born modeling, the Kirchhoff operator delineates the connection between primary reflected wave and reflectivity. Different operators lead to distinctive results under these two physical contexts. However, neither Born nor Kirchhoff approximation can avoid the impact on seismic image in a least-squares sense. Because minimizing the L2 norm only provides an average solution (Wang, 2016; Wu et al., 2016). It is essential to seek a balance between the residual and resolution. According to geological recognition, the earth medium usually presents a layered spatial distribution. The reflection coefficient that mirrors strata attributes should be sparsity, that is, the part of model that does not generate reflected wave ought to be zero. Therefore, the inverted model needs a sparse limitation.

This study implements a Kirchhoff modeling formula for LSRTM promoted by sparsity. The reflectivity model should be regularized with L1 norm while minimizing the residual of wavefield in the form of the L2 norm. Referring to ‘least absolute shrinkage and selection operator’ (Lasso) problem (Tibshirani, 1996), this reformed LSRTM can be solved by the algorithm of spectral projected gradient for L1 minimization (SPGL1), which is designed to solve sparse least squares (van den Berg and Friedlander, 2011). Examples show that our method can effectively overcome the problems mentioned above.

Method

RTM has great advantages in imaging steep strctures such as salt dome. However, it suffers from low-frequency noise compared to conventional migration. Least-squares migration can get closer iteratively to the optimal solution and eventually obtain a relatively high signal-to-noise ratio, high resolution and amplitude equalized profile that eliminates the influence of the acquisition system. It contains three steps: constructing a linear modeling problem first, using the forward and backward propagation wavefields to image, and finally updating the physics model according to the residual.

Linear Modeling Operators

The linearization of nonlinear forward problem is essential to seismic inversion, making the physical progress more explicit; moreover, converting the medium parameter becomes easier. The choice of a linear operator will lead to different physical significance and images. It is a common way to use Born approximation to realize linearization. The real velocity model is divided into two parts: background velocity $v_0$ and velocity perturbation $\delta v$. Given a perturbation $\delta v$, it generates a corresponding wavefield perturbation $\delta u.$ The Born operator describes the relationship between reflected wave and model perturbation. Specifically, the incident wave interacting with model perturbation becomes a new source, namely the Huygens principle, and then the new source generates wavefield perturbations. This can be expressed as follows in time domain:

$\begin{array}{c}\left(\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2}{\partial t^2}-{\nabla }^2\right)u_0\left(\mathit{x},t;{\mathit{x}}_s\right)=f\left(t;{\mathit{x}}_s\right)\end{array}(1)$

$\begin{array}{c}\begin{array}{c}\begin{array}{c}\left(\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2}{\partial t^2}-{\nabla }^2\right)\delta u_b\left(\mathit{x},t;{\mathit{x}}_s\right)=m\left(x\right)\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2{u}_0\left(\mathit{x},t;{\mathit{x}}_s\right)}{\partial t^2}\end{array}\end{array}\end{array}(2)$

where $u_0$ represents the background field propagating in $v_0$, $f\left(t;{\mathit{x}}_s\right)$ is the source signature located at ${\mathit{x}}_s$ and excited at $t$, the model perturbation is denoted by $m\left(\mathit{x}\right)=2\delta v\left(\mathit{x}\right)/v_0\left(\mathit{x}\right)$, which describes velocity changes compared to background velocity. $\mathit{x}$ is a point in model. This study assumes that the density $\rho$ is a constant (Eq. 1) and (Eq. 2) can be rewritten in form of an integral using Green’s theorem:

$\begin{array}{c}{u}_0\left(\mathit{x},t;{\mathit{x}}_s\right)=f\left(t;{\mathit{x}}_s\right)G_0\left(\mathit{x},t;{\mathit{x}}_s\right)\end{array}(3)$

$\begin{array}{c}\delta u_b\left({\mathit{x}}_g,t;{\mathit{x}}_s\right)={\displaystyle \int m\left(\mathit{x}\right)\frac{1}{v_0^2\left(\mathit{x}\right)}\frac{{\partial }^2{u}_0\left(\mathit{x},t;{\mathit{x}}_s\right)}{{\partial }^{2}t}{G}_0\left({\mathit{x}}_g,t;\mathit{x}\right)d\mathit{x}}\end{array}(4)$

where $G_0\left(\mathit{x},t;{\mathit{x}}_s\right)$ is the Green’s function from ${\mathit{x}}_s$ to $\mathit{x}$, $G_0\left({\mathit{x}}_g,t;\mathit{x}\right)$ propagates from $\mathit{x}$ to ${\mathit{x}}_g$. Green’s function is governed by:

$\begin{array}{c}\left(\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2}{\partial t^2}-{\nabla }^2\right)G_0\left(\mathit{x},t;{\mathit{x}}_s\right)=\delta \left(t;{\mathit{x}}_s\right)\end{array}(5)$

where the $\delta \left(t;{\mathit{x}}_s\right)$ is Dirac function.

Born approximation represents scattered phenomenon caused by model perturbation, which could be a means of linearizing seismic inversion. However, this approximation is accurate when scattered field $\delta u$ is much weaker than background field $u_0$ (Schuster, 2017), which is a disadvantage of Born approximation. It cannot describe kinematic and dynamic information of seismic waves well with strong reflector. And studies have shown that Born approximation has limited angle validity and it cannot appropriately predict the reflections generated with large incident angle (Yang and Zhang, 2019).

Compared to the Born operator, the Kirchhoff operator relates the reflectivity to wavefield perturbation. Therefore, it depicts the interaction between the incident field and reflectivity rather than velocity perturbation. There is a relationship between reflectivity and model perturbation when the perturbation and incident angle are small (Stolt and Weglein, 2012):

$r\left(\mathit{x},\alpha \right)=\frac{i\omega }{2v_0\left(\mathit{x}\right)\cos \left(\mathit{x},\alpha \right)}m\left(\mathit{x}\right)(6)$

where the $r\left(\mathit{x},\alpha \right)$ is the reflection coefficient at point $\mathit{x}$ with incident angle $\alpha$ between the incidence and the normal line (Figure 1). This means that we can obtain the wavefield perturbation under the Kirchhoff approximation by substituting (Eq. 6) into (Eq. 4), and we have

$\begin{array}{c}\delta u_b\left({\mathit{x}}_g,t;{\mathit{x}}_s\right)={\displaystyle \int \frac{2v_0\left(\mathit{x}\right)}{i\omega }r\left(\mathit{x},\alpha \right)\cos \left(\mathit{x},\alpha \right)\frac{1}{v_0^2\left(\mathit{x}\right)}\frac{{\partial }^2{u}_0\left(\mathit{x},t;{\mathit{x}}_s\right)}{{\partial }^{2}t}{G}_0\left({\mathit{x}}_g,t;\mathit{x}\right)d\mathit{x}}\end{array}(7)$

Here we turn Kirchhoff modeling equation into the same form as Born approximation. Then Eq. 7 can be rewritten as.

$\begin{array}{c}\left(\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2}{\partial t^2}-{\nabla }^2\right)u_0\left(\mathit{x},t;{\mathit{x}}_s\right)=-{\displaystyle \int f\left(t;{\mathit{x}}_s\right)dt}\end{array}(8)$

$\begin{array}{c}\begin{array}{c}\begin{array}{c}\left(\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2}{\partial t^2}-{\nabla }^2\right)\delta u_k\left(\mathit{x},t;{\mathit{x}}_s\right)=2v_0\left(\mathit{x}\right)r\left(\mathit{x},\alpha \right)\cos \left(\mathit{x},\alpha \right)\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2{u}_0\left(\mathit{x},t;{\mathit{x}}_s\right)}{\partial t^2}\end{array}\end{array}\end{array}(9)$

FIGURE 1

FIGURE 1. Schematic illustration of incident wave and reflected wave. And $\alpha$ is the incident angle.

It should be noted that the term $r\left(\mathit{x},\alpha \right)$ can be replaced by the generalized angle-dependent reflectivity model to get rid of the limitations of small perturbation and incident angle. Although there are some methods to solve the propagation direction of wave, such as Poynting vector and Plane Wave Decomposition (PWD), it is still tedious and time-consuming to obtain the angle term. Here we give an approximate scheme (Yang and Zhang, 2019).

Each shot can invert a reflectivity image, here we sum the images obtained by all shots. Then, we regard the summation as the final reflectivity model and use it to iterate. Approximately, we can get an averaged reflectivity model by multiple shots stacking. Therefore, we can get the predicted data by using this stacked reflectivity $R\left(\mathit{x}\right)$ rather than the angle-dependent term $r\left(\mathit{x},\alpha \right)\cos \left(\mathit{x},\alpha \right)$. Note that $R\left(\mathit{x}\right)$ is an averaged reflectivity over all illuminated angles.

$R\left(\mathit{x}\right)\approx {\displaystyle \sum _{shot}r\left(\mathit{x},\alpha \right)\cos \left(\mathit{x},\alpha \right)}(10)$

With this approximate reflectivity $R\left(\mathit{x}\right)$, we can express Eq. 9 as

$\begin{array}{c}\left(\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2}{\partial t^2}-{\nabla }^2\right)\delta u_k\left(\mathit{x},t;{\mathit{x}}_s\right)=2v_0\left(\mathit{x}\right)R\left(\mathit{x}\right)\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2{u}_0\left(\mathit{x},t;{\mathit{x}}_s\right)}{\partial t^2}\end{array}(11)$

In sum, with the relationship of reflectivity and model perturbation, two linear approximations have a similar form, which expresses their common ground. The difference between two approximations is also evident. From Eq. 6, $\cos \alpha$ approximately equals to one and can be ignored for a small incident angle. Therefore, reflectivity can be regarded as the spatial derivative of model perturbation. The inverted model after spatial derivation has a higher resolution, that is, the spectrum has been improved. More details are provided in the numerical tests.

Least-Squares With Sparse Optimization

In contrast to full waveform inversion (FWI) (Liu, et al., 2020), LSRTM first establishes a linear relationship between physical model and corresponding response (Tarantola, 1984), then it implements the inverse problem. The least-squares method (LSM) only requires the construction of a migration operator and inverse migration operator, which is conjugated to each other. It can reduce the residual between the observed and predicted data iteratively to approach the optimal solution of the inverse problem gradually. According to the linear approximation above, we can express them in the form of a matrix:

$\begin{array}{c}\mathbf{d}=\mathbf{L}\mathbf{m}\end{array}(12)$

where the $\mathit{d}$ is predicted data, such as background or perturbation fields. $\mathit{L}$ represents modeling operator and $\mathit{m}$ is the physics model. Usually, it is assumed that the background velocity has been obtained in advance, and then the data can be predicted. Hence, the misfit function can be expressed as:

$\begin{array}{c}E\left(\mathit{m}\right)={\Vert \mathit{Lm}-{\mathit{d}}_{obs}\Vert }_2\end{array}(13)$

The model $\mathit{m}$, which makes $\frac{\partial E\left(\mathit{m}\right)}{\partial \mathit{m}}$ (the Jacobian matrix) equal to 0, is the optimal solution of Eq. 13. However, the computation of the Jacobian matrix is quite time consuming, particularly for seismic exploration. We adopt the adjoint-state method to calculate the adjoint operator ${\mathit{L}}^{\mathit{T}}$ of modeling operator $\mathit{L}$, Specifically, the gradient of $E\left(\mathit{m}\right)$ can be obtained by back propagation of the wavefield residual and background field, here we give the gradient based on Kirchhoff approximation (Plessix, 2006; Wang et al., 2021):

${\mathit{m}}_{mig}={\mathit{L}}^{\text{T}}\mathit{d}=2v_0\left(\mathit{x}\right){\displaystyle \sum _{shot}{\displaystyle \int \frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^2{u}_0\left(\mathit{x},t;{\mathit{x}}_s\right)}{\partial t^2}q\left(\mathit{x},t;{\mathit{x}}_s\right)\text{d}t}}(14)$

Where $q\left(\mathit{x},t;{\mathit{x}}_s\right)$ is the adjoint wavefield governed by:

$\begin{array}{c}\frac{1}{v_0{\left(\mathit{x}\right)}^2}\frac{{\partial }^{2}q\left(\mathit{x},t;{\mathit{x}}_{\text{s}}\right)}{\partial t^2}-{\nabla }^{2}q\left(\mathit{x},t;{\mathit{x}}_{\text{s}}\right)=\delta u\left({\mathit{x}}_{\text{r}},t;{\mathit{x}}_{\text{s}}\right)\end{array}(15)$

According to Eq. 13, we can obtain a least-squares solution $\mathit{m}={\left({\mathit{L}}^{\mathit{T}}\mathit{L}\right)}^{-1}{\mathit{L}}^{\mathit{T}}\mathit{d}$. Note that LSM provides a smooth solution of the model, which is determined by the properties of the L2 norm. As a result, LSM has a limited ability to improve the quality of the image. Here we give a simple model to display the impact of LSM. In this example, we use the Ricker wavelet with a center frequency of 30 Hz and a time sampling interval of 1 ms. With convolution model theory, we can get seismic records via the convolution of Ricker wavelet and reflection coefficients, which can be obtained by $\mathit{d}=\mathit{Lm}$. Conversely, reflection coefficients can be obtained by the deconvolution of seismic records and wavelet, that is, ${\mathit{m}}_{mig}={\mathit{L}}^{\text{T}}\mathit{d}$. Figure 2C is the result of deconvolution, and it is hard to identify the reflectors. Compared to deconvolution, Figure 2D shows that LSM improves the resolution obviously. However, many oscillations caused by ${\left({\mathit{L}}^{\mathit{T}}\mathit{L}\right)}^{-1}$ near the real reflection coefficients should not exist. That’s why we regard the least-squares solution as a smooth or average solution. The actual model indicates that the medium presents a layered spatial distribution, as shown in Figure 2A or Figure 2B, that is, the sub-surfaces are sparse. In Figure 2E, the inversion result with sparse constrained LSM performs quite well, and these oscillations generated by LSM are suppressed; thus, the resolution and sparsity of the reflection coefficient series are improved effectively.

FIGURE 2

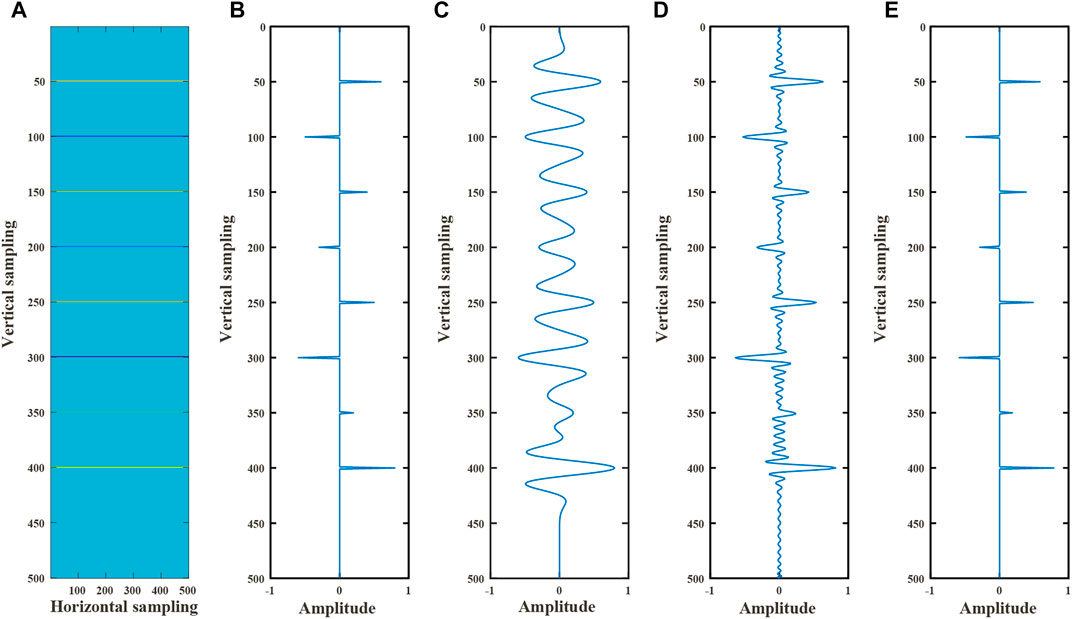
FIGURE 2. (A) reflectivity model; (B) reflection coefficient series extracted in Figure 2A; (C) deconvolution of single record; (D) the result inverted by LSM; (E) the result inverted by sparse constrained LSM.

Due to the feasibility and sparse property of L1-norm, we modify the objective function with L1 norm to realize sparse reconstruction of the model in this study. Generally, Eq. 13 can be reformed with two new problems.

1 Basis Pursuit (BP) problem

$\left(BP\right)min {\Vert \mathit{m}\Vert }_1,subjectto\mathit{Lm}=\mathit{d}(16)$

Eq. 16 depicts a BP problem that comes from compressed sense theory, and it aims to seek a sparse solution that satisfies $\mathit{Lm}=\mathit{d}$. However, practical seismic data inevitably contain noise, and Eq. 16 can be modified as a basis pursuit denoising (BPDN) problem:

$\left(B{P}_{\sigma }\right)min {\Vert \mathit{m}\Vert }_1, subject to {\Vert \mathit{Lm}-{\mathit{d}}_{obs}\Vert }_2\le \sigma (17)$

where the $\sigma$ describes the noise level in the data, and Eq. 16 and Eq. 17 are equivalent to each other when $\sigma =0$.

2 Least Absolute Shrinkage and Selection Operator (LASSO) problem

$\left(L{S}_{\tau }\right)min {\Vert \mathit{Lm}-{\mathit{d}}_{obs}\Vert }_2 ,subject to {\Vert \mathit{m}\Vert }_1\le \tau (18)$

where the $\tau \ge 0$ is an explicit limitation of sparsity on $\mathit{m}$. Problems $\left(B{P}_{\sigma }\right)$ and $\left(L{S}_{\tau }\right)$ are different descriptions of the same question. They are equivalent in the sense that there exists a solution ${\mathit{m}}^{\mathit{*}}$ of $\left(B{P}_{\sigma }\right)$ for a given $\sigma$, and there exists a corresponding $\tau$ that makes ${\mathit{m}}^{\mathit{*}}$ also be a solution of $\left(L{S}_{\tau }\right)$.

Both problems mentioned above can be solved by the algorithm of spectral projected gradient for L1 minimization (SPGL1). Given a constraint $\tau$, we can obtain the residual norm from Eq. 18:

$\begin{array}{c}\phi \left(\tau \right)= {\Vert {\mathit{r}}_{\tau }\Vert }_{2}with{\mathit{r}}_{\tau }=L{\mathit{m}}_{\tau }-{\mathit{d}}_{obs}\end{array}(19)$

Let

$\begin{array}{c}\phi \left(\tau \right)= \sigma \end{array}(20)$

Eq. 20 recasts $\left(L{S}_{\tau }\right)$ as a problem of finding the root of a nonlinear equation and defines a continuous curve, the Pareto curve (Figure 3).

FIGURE 3

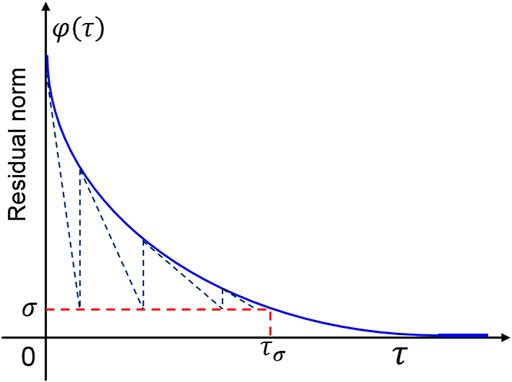
FIGURE 3. Schematic diagram of the Pareto curve. A Newton-based root-finding method is used to update the solution of Eq. 20.

For a given $\sigma$, SPGL1 uses the Newton method to approach the root, and as the $\tau$ updates iteratively, the optimal solution ${\mathit{m}}_{{\mathit{\tau }}_{\mathit{\sigma }}}$ of problems $\left(B{P}_{\sigma }\right)$ and $\left(L{S}_{\tau }\right)$ can be obtained. Therefore, we balance the 2-norm of the residual against the 1-norm of the solution eventually (van den Berg and Friedlander, 2009). From Figure 3, the question is degraded to a simple Lasso problem $\left(L{S}_{\tau }\right)$ when the noise level factor $\sigma$ is equal to 0. In this study, we set $\sigma =0$. Note that synthetic seismic records do not contain noise in general, so we set the noise level factor to be zero. Actually, the algorithm of SPGL1 can deal with noisy data, and we can add some random noise or set some traces to be zero in synthetic data. Besides, the determination of parameter $\tau$ is quite important. According to the theoretical model, we can calculate the perturbation model or reflectivity model and make a rough estimate of $\tau$. In general, it is appropriate to set the value of tau to tens of times that of the calculated perturbation model or reflectivity model. Then, the parameter $\tau$ can be adjusted according to the inversion results.

Here we summarize the workflow of L1-regularized LSRTM as follows:

1) Obtain the predicted data ${\mathit{d}}_0$ with migration velocity $v_0$, and get the ${\mathit{d}}_{res}$ with ${\mathit{d}}_{res}={\mathit{d}}_{obs}-{\mathit{d}}_0$;

2) Set the initial model ${\mathit{m}}_0$ and predict the data $\mathit{L}{\mathit{m}}_0$ based on Born or Kirchhoff approximation, therefore we can get the residual ${\mathit{r}}_0=\mathit{L}{\mathit{m}}_0-{\mathit{d}}_{res}$ and gradient operator ${\mathit{g}}_0={\mathit{L}}^{\mathit{T}}{\mathit{r}}_0$;

3) Input the parameters of $\tau$, $\sigma$ and set $k=0$;

4) Solve the Lasso problem $\left(L{S}_{\tau }\right)$ with the algorithm of SPGL1, and update the ${\mathit{m}}_k$, ${\mathit{r}}_k$ and ${\mathit{g}}_k$ until $k=k_{max}$;

5) Output the result ${\mathit{m}}_{k_{max}}$.

Numerical Example

In this study, two theoretical models are used to test the validity of the proposed method, including a single diffraction point and complex fault model. Both are based on the two-way acoustic wave equation. Here we use the finite difference method on regular grid.

Single-Diffraction Point

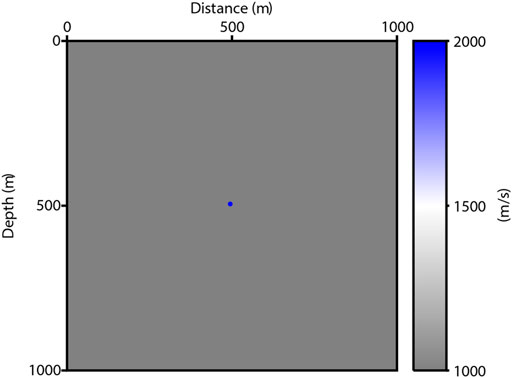
To verify the effectiveness of this method, we first set a simple model with a diffraction point of 2000 m/s embedded in the background velocity of 1,000 m/s (Figure 4), and the entire model has been discretized into 201 × 201 grids in the horizontal and vertical directions, respectively, with the same interval of 5m. The geometry system is arranged as follows: a total of 21 shots are uniformly distributed on the surface of this model with an interval of 50m. Geophones are also placed on each grid point on the surface. We use the Ricker wavelet with a center frequency of 25 Hz for modeling, and the sampling interval is 0.5 ms. In this example, we set 1,000 m/s as the migration velocity.

FIGURE 4

FIGURE 4. A simple diffraction point velocity model.

As shown in Figure 5A, the image is obtained by LSRTM based on Born approximation. This is consistent with the actual situation to a certain degree. The single scatter point is blurred with a disturbing cross pattern (marked by a yellow arrow). However, it should be a dot on the image (Lecomte and Kjeller, 2008). This is because we use the adjoint operator to migrate rather than the inverse operator in Eq. 14. Specifically, Eq. 13 defines a normal equation with ${\mathit{L}}^{\mathit{T}}\mathit{Lm}={\mathit{L}}^{\mathit{T}}\mathit{d}$. The term ${\mathit{L}}^{\mathit{T}}\mathit{L}$, Hessian matrix, is equivalent to a blur operator acting on the true image $\mathit{m}$. Furthermore, ${\mathit{L}}^{\mathit{T}}\mathit{L}$ includes the influence of irregular acquisition, limited acquisition aperture, band limited source, etc., which generate artifacts and degrade the resolution of the image (Jiang and Zhang, 2019). Compared to LSRTM, the same method in Figure 5C with the L1 constraint performs better; it mitigates the distortion caused by the blur operator. Therefore, with the promotion of sparsity, the resolution in the least-squares method has been improved significantly, and the image looks more like a scatter point.

FIGURE 5

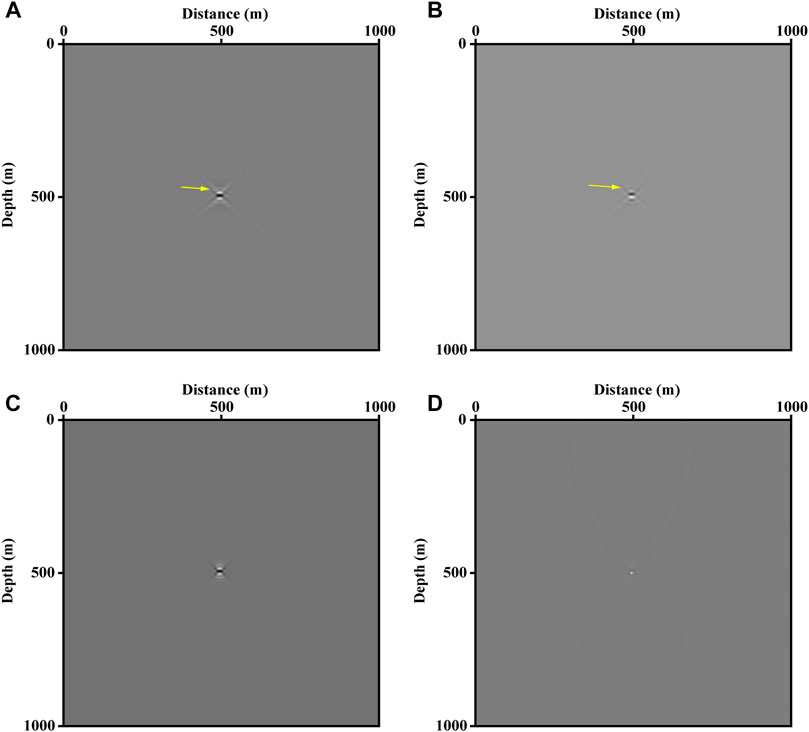
FIGURE 5. The images invert by LSRTM and LSRTM with L1 norm constraint based on Born and Kirchhoff approximation. (A) Unconstrained LSRTM based on Born approximation. (B) Unconstrained LSRTM using Kirchhoff approximation. (C) The image of the LSRTM with L1 norm regularization based on Born approximation. (D) The migrated image with sparse constrained LSRTM based on Kirchhoff approximation.

The LSRTM based on the Kirchhoff operator inverts the reflectivity directly from the seismic records. Figure 5B displays the image produced by Kirchhoff approximation. Compared to Figure 5A, least-squares RTM based on Kirchhoff operator suffers from the same problems. Similarly, we implement the L1 norm on LSRTM, which is shown in Figure 5D. The cross pattern is eliminated clearly, and we obtain an explicit dot rather than a blurred spot. Therefore, for a simple model, the sparsity-promoting LSRTM based on Kirchhoff approximation can effectively improve the resolution of the image. The results calculated by LSRTM in Figures 5A,B iterate 5 times. Figures 5C,D use the SPGL1 algorithm for iterating 10 times with $\tau =2$.

Fault Model

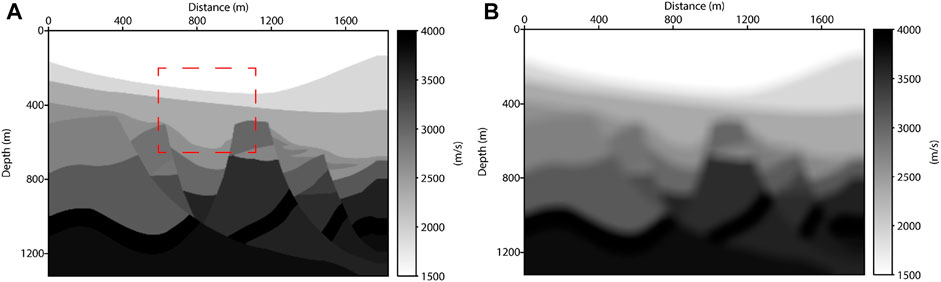
We also test the other relative complex model. In this fault model (Figure 6A), there are some classical geological structures, including folds, fault blocks, and depressions. Therefore, it appropriately shows the complex structure of near-surface media. The maximum and minimum velocities are 4,000 m/s and 1,500 m/s, respectively. Similarly, we discretize it into 265 × 367 grids with an interval of 5 m. Thus, a total of 25 shots are uniformly located at the surface of this model. The modeling seismic wavelet is same to last experiment.

FIGURE 6

FIGURE 6. (A) The real velocity of fault model. (B) the background velocity model after smooth.

As shown in Figures 7A,B, images inverted by LSRTM based on two approximations fit the fault model well, and the contact relationship between structures can be clearly depicted. To further improve the resolution of these images, we combined L1 norm regularization with LSRTM to reconstruct the model. From Figures 7C,D, the method based on Kirchhoff approximation recovers the stratum’s sparsity more effectively. The results in Figures 7A,B are calculated by LSRTM with 10 iterations. Figures 7C,D use the SPGL1 algorithm for iterating 10 times with $\tau =2000$ and $\tau =500$, respectively. Note that the amplitude of inverted results is different because of the value of parameter $\tau$.

FIGURE 7

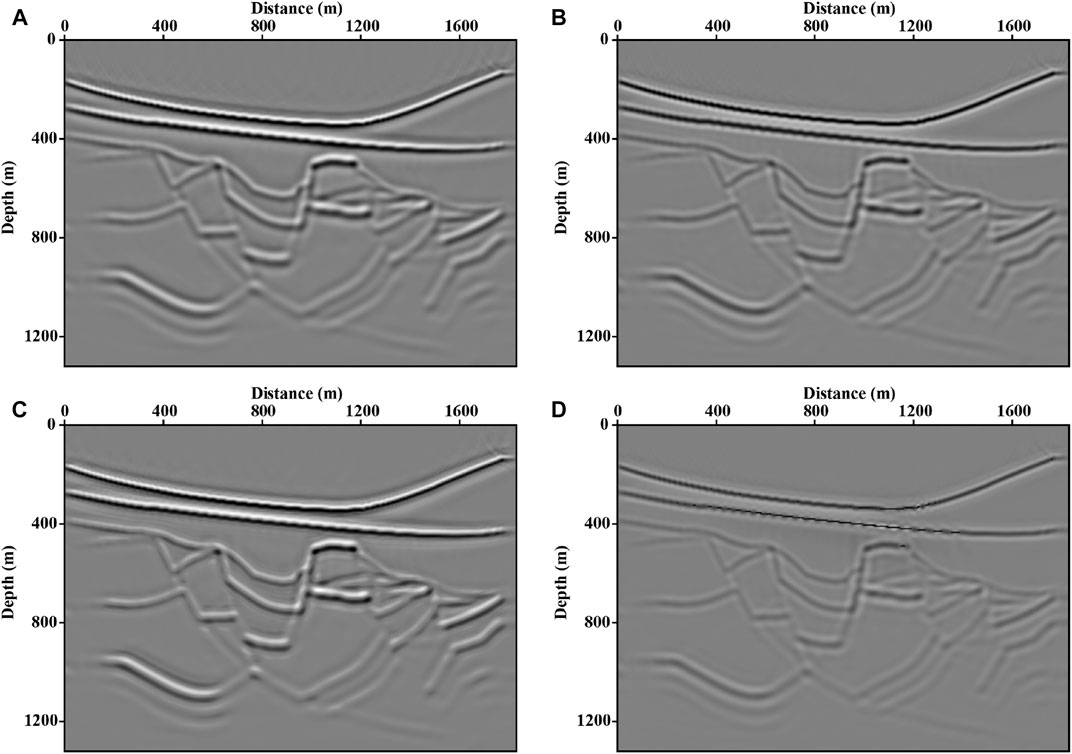
FIGURE 7. Fault images inverted by (A) Unconstrained LSRTM based on Born approximation. (B) Unconstrained LSRTM with Kirchhoff approximation. (C) LSRTM with L1 norm regularization based on Born approximation. (D) sparse constrained LSRTM based on Kirchhoff approximation.

Furthermore, we enlarge the model framed by red rectangle in Figure 6A, which has step-like strata (marked by yellow arrows in Figure 8A). After inverting, the reflectivity image in Figure 8D produced by constrained LSRTM based on Kirchhoff operator agrees with the actual situation.

FIGURE 8

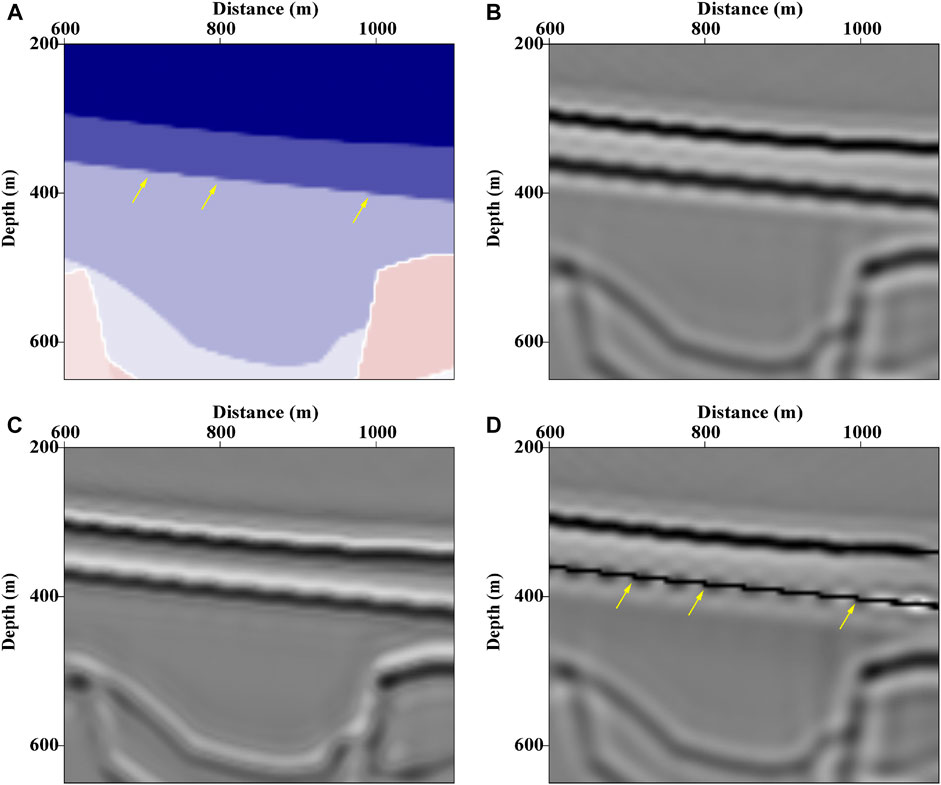
FIGURE 8. (A) true velocity model in the red rectangle in Figure 6A, (B) corresponding image inverted by LSRTM based on Kirchhoff approximation, (C) LSRTM with sparse constraint based on Born approximation, (D) LSRTM with sparse constraint based on Kirchhoff approximation.

Furthermore, images inverted by two different approximations have different phases. According to Eq. 6, reflectivity can be derived from model perturbation. With the assumption of a small incident angle, $\cos \left(\mathit{x},\alpha \right)$ is roughly equivalent to 1 and can be ignored. Then, Eq. 6 can be rewritten as $r\left(\mathit{x}\right) = ikm\left(\mathit{x}\right)/2$, where the wavenumber $k=\frac{\omega }{c}$. Therefore, reflectivity $r\left(\mathit{x}\right)$ is the spatial derivative of model perturbation $m\left(\mathit{x}\right)$. As a result, the image inverted by Kirchhoff performs sparser and sharper, and there is a phase shift of 90° between perturbation model and reflectivity model.

Figure 9 shows the amplitude spectra of the images in Figures 7B–D, respectively. The spectra curves are the sum of each trace by the spatial Fourier transform along the depth. The red one is generated from the image inverted by L1-regularized LSRTM based on Born approximation. The blue and green spectrum curves are produced by unconstrained and constrained LSRTM with Kirchhoff approximation, respectively. Because of the spatial derivative and sparse constraint, the spectrum of the image inverted by L1-LSRTM with Kirchhoff approximation has more high-wavenumber components than that of Born approximation, which explains that Kirchhoff approximation improves the resolution of the image.

FIGURE 9

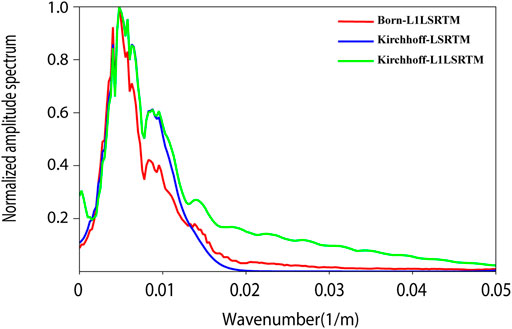
FIGURE 9. The spectrum of inverted images form Figure 6.

Conclusion

The LSRTM recasts classical seismic inversion as a linear inverse problem. By means of linear approximation, physical model is related to the corresponding wavefield. Thereafter, we can reduce the residual between predicted and observed data iteratively to directly invert the interest parameters. This study introduces two linearization methods. Born approximation obtains the relationship between the model and physical response based on perturbation theory. With the help of the Born operator, we derive another type of linear method, namely the Kirchhoff operator, which relates the reflectivity to wavefield explicitly. Moreover, these two methods have a relationship of a spatial derivative, and there is a phase shift between perturbation model and reflectivity model. Although two operators are different physical quantities, the resolution can be improved by Kirchhoff approximation.

LSRTM can mitigate the shortcomings of other migration methods, while the solution is smooth and deviates from the true model. Specifically, there are redundant oscillatory axes in the strata that should be sparsely distributed. Therefore, we reform the question as a sparsity-promoting LSRTM. The SPGL1 algorithm can effectively solve this problem and invert a sparse image that matches the model well. Examples prove the validity of our study.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

XH-Q: Methodology, Investigation, Formal analysis, Visualization, Writing—Original Draft WX-Y: Conceptualization, Writing—Review and Editing, Project administration WC-Y: Validation, Data Curation, Writing—Review and Editing ZJ-J: Supervision, Writing—Review and Editing, Funding acquisition.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the National Natural Science Fund of China (under grant 42074158) for supporting this work. And we are grateful for the comments provided by reviewers, which improve the quality of this paper a lot.

References

Baysal, E., Kosloff, D. D., and Sherwood, J. W. C. (1983). Reverse Time Migration. Geophysics 48, 1514–1524. doi:10.1190/1.1441434

CrossRef Full Text | Google Scholar

Beylkin, G. (1985). Imaging of Discontinuities in the Inverse Scattering Problem by Inversion of a Causal Generalized Radon Transform. J. Math. Phys. 26, 99–108. doi:10.1063/1.526755

CrossRef Full Text | Google Scholar

Bleistein, N., Cohen, J. K., and Hagin, F. G. (1987). Two and One‐half Dimensional Born Inversion with an Arbitrary Reference. Geophysics 52, 26–36. doi:10.1190/1.1442238

CrossRef Full Text | Google Scholar

Bleistein, N. (1987). On the Imaging of Reflectors in the Earth. Geophysics 52, 931–942. doi:10.1190/1.1442363

CrossRef Full Text | Google Scholar

Dai, W., Fowler, P., and Schuster, G. T. (2012). Multi-source Least-Squares Reverse Time Migration. Geophys. Prospecting 60, 681–695. doi:10.1111/j.1365-2478.2012.01092.x

CrossRef Full Text | Google Scholar

Dutta, G., and Schuster, G. T. (2014). Attenuation Compensation for Least-Squares Reverse Time Migration Using the Viscoacoustic-Wave Equation. Geophysics 79, S251–S262. doi:10.1190/geo2013-0414.1

CrossRef Full Text | Google Scholar

Jiang, B., and Zhang, J. (2019). Least-squares Migration with a Blockwise Hessian Matrix: A Prestack Time-Migration Approach. Geophysics 84, R625–R640. doi:10.1190/geo2018-0533.1

CrossRef Full Text | Google Scholar

Lecomte, I. (2008). Resolution and Illumination Analyses in PSDM: A ray-based Approach. The Leading Edge 27, 650–663. doi:10.1190/1.2919584

CrossRef Full Text | Google Scholar

Liu, H. W., Li, B., Liu, H., Tong, X. ‐L., and Liu, Q. (2010). The Algorithm of High Order Finite Difference Pre-stack Reverse Time Migration and GPU Implementation. Chin. J. Geophys. 53, 1725–1733. doi:10.1002/cjg2.1530(in Chinese)

CrossRef Full Text | Google Scholar

Liu, Y., Chang, X., Jin, D., He, R., Sun, H., and Zheng, Y. (2011). Reverse Time Migration of Multiples for Subsalt Imaging. Geophysics 76, WB209–WB216. doi:10.1190/geo2010-0312.1

CrossRef Full Text | Google Scholar

Liu, Y., He, B., and Zheng, Y. (2020). Controlled-order Multiple Waveform Inversion. Geophysics 85, R243–R250. doi:10.1190/geo2019-0658.1

CrossRef Full Text | Google Scholar

Liu, Y., Liu, X., Osen, A., Shao, Y., Hu, H., and Zheng, Y. (2016). Least-squares Reverse Time Migration Using Controlled-Order Multiple Reflections. Geophysics 81, S347–S357. doi:10.1190/geo2015-0479.1

CrossRef Full Text | Google Scholar

McMechan, G. A. (1983). Migration by Extrapolation of Time-dependent Boundary Values*. Geophys. Prospect 31, 413–420. doi:10.1111/j.1365-2478.1983.tb01060.x

CrossRef Full Text | Google Scholar

Plessix, R.-E. (2006). A Review of the Adjoint-State Method for Computing the Gradient of a Functional with Geophysical Applications. Geophys. J. Int. 167, 495–503. doi:10.1111/j.1365-246X.2006.02978.x

CrossRef Full Text | Google Scholar

Schuster, G. T. (2017). Seismic Inversion. Tulsa: Society of Exploration Geophysicists. doi:10.1190/1.9781560803423

CrossRef Full Text

Stolt, R. H., and Weglein, A. B. (2012). Seismic Imaging and Inversion: Application of Linear Inverse Theory. New York: Cambridge University Press, 1–404. doi:10.1017/CBO9781139056250

CrossRef Full Text

Tarantola, A. (1984). Inversion of Seismic Reflection Data in the Acoustic Approximation. Geophysics 49, 1259–1266. doi:10.1190/1.1441754

CrossRef Full Text | Google Scholar

Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodological) 58, 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x

CrossRef Full Text | Google Scholar

van den Berg, E., and Friedlander, M. P. (2009). Probing the Pareto Frontier for Basis Pursuit Solutions. SIAM J. Sci. Comput. 31, 890–912. doi:10.1137/080714488

CrossRef Full Text | Google Scholar

van den Berg, E., and Friedlander, M. P. (2011). Sparse Optimization with Least-Squares Constraints. SIAM J. Optim. 21, 1201–1229. doi:10.1137/100785028

CrossRef Full Text | Google Scholar

Wang, X. Y., Zhang, J. J., Xu, H. Q., and Tian, B. Q. (2021). Least-squares Reverse Time Migration with Wavefield Decomposition Based on the Poynting Vector. Chin. J. Geophys. (in Chinese) 64, 645–655. doi:10.6038/cjg2021O0120

CrossRef Full Text | Google Scholar

Wang, Y. H. (2016). Seismic Inversion: Theory and Applications. Oxford: Wiley, 85–86. doi:10.1002/9781119258032.ch7

CrossRef Full Text

Wu, D., Yao, G., Cao, J., and Wang, Y. (2016). Least-squares RTM with L1 Norm Regularisation. J. Geophys. Eng. 13, 666–673. doi:10.1088/1742-2132/13/5/666

CrossRef Full Text | Google Scholar

Yang, K., and Zhang, J. (2019). Comparison between Born and Kirchhoff Operators for Least-Squares Reverse Time Migration and the Constraint of the Propagation of the Background Wavefield. Geophysics 84, R725–R739. doi:10.1190/geo2018-0438.1

CrossRef Full Text | Google Scholar

Yoon, K., Shin, C., Suh, S., Lines, L. R., and Hong, S. (2003). 3D Reverse-Time Migration Using the Acoustic Wave Equation: An Experience with the SEG/EAGE Data Set. The Leading Edge 22, 38–41. doi:10.1190/1.1542754

CrossRef Full Text | Google Scholar

Zhang, Y., Duan, L., and Xie, Y. (2015). A Stable and Practical Implementation of Least-Squares Reverse Time Migration. Geophysics 80, V23–V31. doi:10.1190/geo2013-0461.1

CrossRef Full Text | Google Scholar

Zhu, J., and Lines, L. R. (1998). Comparison of Kirchhoff and Reverse‐time Migration Methods with Applications to Prestack Depth Imaging of Complex Structures. Geophysics 63, 1166–1176. doi:10.1190/1.1444416

CrossRef Full Text | Google Scholar