VSP Imaging Using Free-Surface Multiples With Wavefield Decomposition: Synthetic and Field Data Examples

Vertical seismic profiling (VSP) is an effective technique to provide high-resolution seismic images of the reservoir area. However, the quality of the images is limited by the poor illumination of primary reflection wave. In conventional VSP imaging, only the upgoing primaries are used. Adding free-surface–related multiples into the imaging process can significantly improve the coverage of the illuminated area. Conventional migration methods using multiples need the complex process of multiple prediction. Data-to-data migration (DDM) is an effective imaging technique for multiples in which the recorded data is migrated directly. To improve the imaging quality of DDM in VSP imaging, we propose separating the wavefield into downgoing and upgoing components using Hilbert transform when reverse-time migration (RTM) is implemented in DDM, and the inverse-scattering imaging condition is further applied to the decomposed wavefields. The proposed method eliminates low-frequency noises and false images generated from the conventional cross-correlation imaging condition, and further enhance the illumination in the VSP imaging. Synthetic examples and application to a walkaway field data demonstrate that it can attenuate the noise and improve the imaging resolution effectively. By using DDM with inverse scattering imaging condition and wavefield decomposition based on Hilbert transform, VSP imaging using free-surface–related multiples becomes a practical complement for conventional VSP imaging.

Introduction

Vertical seismic profiling (VSP) surveys differ from surface seismic surveys or crosswell surveys in that the surface sources and the borehole receivers are used to record both upgoing and downgoing wavefields (Stewart et al., 1984; Hardage, 1985; Chang and McMechan, 1986; Hinds et al., 1996). The receiver well is placed near the target area to obtain sufficient reflection waves generated from the reservoir (Burch et al., 2010). The configuration of VSP gives the benefits to understand corresponding geologic logs and provide additional seismic interpretation insights. However, the results of VSP imaging are restricted by the illuminated area of the primary reflections (O’Brien, et al., 2013). To greatly extend the subsurface illumination, free-surface related multiples recorded in the VSP surveys are also used in the migration of VSP data (Yu and Schuster, 2001). Jiang et al. (2005) use the mirror imaging condition to migration the first-order multiples in the VSP data. But the method needs to calculate the traveltimes of the raypath. To avoid the picking of traveltimes, seismic interferometry theory (Wapenaar and Fokkema, 2006; Schuster, 2009) is employed to transform different orders of free-surface related multiples into virtual primaries and then applied in the migration process (Yu and Schuster, 2002; Jiang et al., 2007). He et al. (2007) demonstrated the wave-equation interferometric migration generates an image volume with wide coverage for 3D VSP data. Soni and Verschuur (2015) used full-wavefield migration to enhance the illumination for VSP measurements. Recently Marchenko imaging also emerges as an alternative tool to analyze the response of multiple reflections (Singh et al., 2015; Wapenaar et al., 2017; Lomas et al., 2018; Zhang and Slob, 2019) and include the contribution for VSP imaging.

Several methods have been developed to image free-surface related multiples directly in surface seismic surveys. Instead of taking as coherent noise, the multiples are used as areal sources in the migration process (Guitton, 2002; Shan 2003; Verschuur and Berkhout, 2005; Artman, 2006; Muijs et al., 2007). Recently, migration of multiples has shown the significant advantages for enhancing areal illumination to image subsurface structures (Lu et al., 2015; Li et al., 2017; Liu et al., 2018; Zhang et al., 2020). However, most methods involve the process to separate the surface-related multiples from the original data, which is complex and prone to error for real data applications. To avoid the separation of the primaries and free-surface related multiples, Wang et al. (2014a) propose an approach that can simultaneously migrate the primaries and free-surface related multiples. The recorded data containing primaries and free-surface related multiples are backward-propagated as the receiver wavefield, and the recorded data, together with a synthetic wavelet, are forward-propagated as the source wavefield. Wang et al. (2014b) isolate the contribution of multiples and name it as data-to-data migration (DDM), in which the recorded data containing primaries and free-surface related multiples are forward and backward propagated simultaneously. The algorithm is designed for surface seismic profile and can also be applied in the VSP data processing. Using the source-receiver reciprocity, the common receiver gathers is similar to the common shot gathers in the surface seismic surveys except that the virtual source is located in the borehole.

Kirchhoff migration (Keho and Beydoun, 1988; Gray and May 1994; Bevc, 1997; Hua and McMechan, 2003) and wave-equation migration (Gazdag, 1978; Stoffa et al., 1990; Ristow and Rühl, 1994; Sava and Vasconcelos, 2011) are the most common migration algorithms in the migration of free-surface related multiples for VSP (Jiang et al., 2005; He et al., 2007). For the surface seismic surveys, reverse-time migration (RTM, Baysal et al., 1983; McMechan, 1983) has shown its superiority in handling complex geologic structures and potential for true-amplitude, high-resolution migration. The main problem for RTM is that low-frequency noise and false images are generated when the source and receiver wavefields are cross-correlated near the strong velocity gradients (Liu et al., 2011; Fei et al., 2015). This is due to the two-way wave-equation is used in the wavefield simulation. To eliminate the high-amplitude, low-frequency noise along the wave paths, Fletcher et al. (2005) propose to apply the directional damping factor. Yoon and Marfurt (2006) use the Poynting vector to calculate the direction of the wavefields and cross-corelate the desired component. The most practical method is the Laplace filter proposed by Zhang and Sun (2009), which has been widely applied in the applications of RTM. Liu et al. (2011) use Hilbert transform to separate the upgoing and downgoing components and avoid the storage of the entire wavefields. Fei et al. (2015) point out that only the cross-correlation of the downgoing source wavefield and upgoing receiver wavefield are the correct imaging condition when strong velocity contrasts exist in the velocity model. Wang et al. (2017) show the wavefield decomposition method based on Hilbert transform can eliminate the noises and false images in the DDM for surface seismic survey. Zheng et al. (2018) use the similar approach to separate the upgoing and downgoing components in the 3D forward modeling and 3D RTM. The method can be also applied in the migration of VSP data. With the decomposed wavefields, it is possible to apply some advanced imaging condition to obtain better estimation of subsurface reflectivity, such as the deconvolution imaging condition (Valenciano and Biondi, 2003; Guitton et al., 2007; Lu et al., 2015) and inverse-scattering imaging condition (Whitmore and Crawley, 2012; Suh and Wang, 2013). The inverse-scattering imaging condition is derived from the inverse theory and high-frequency approximation, which can generate subsurface images with preserved amplitudes and high resolution (Pestana et al., 2014; Duprat et al., 2015). The wavefield separation used in the imaging can be achieved with high accuracy with Hilbert transform instead of Poynting vectors (Yoon and Marfurt, 2006).

In the following sections, we first introduce the theory of DDM for VSP data, and then we illustrate how to use inverse-scattering imaging condition and wavefield decomposition with Hilbert transform to improve the results. Synthetic examples are used to validate the effectiveness of our approach. Then the method is applied to walkaway field data which is collected to monitor the injection process of CO₂. The final part is the conclusion of our work.

Methodology

DDM for VSP Data

The DDM method for surface seismic data has been demonstrated by Wang et al. (2014b). Using the source-receiver reciprocity theory, if the VSP data are resorted into common receiver gathers and the receiver in the borehole is taken as a source. They are similar to the common shot gathers of surface seismic survey except that the source in reciprocal domain is located in the well. Figure 1 illustrates the wavepath in the VSP surveys with free surface. In the gathers recorded at R, the data contains the direct wave excited at S₁, the primary excited at S₂, first-order free-surface related multiple excited at S₂ and second-order free-surface related multiple excited at S₃. Only the primary is the upgoing components and can be separated from the original data by f-k filtering. In the conventional migration of VSP data, the primary is backward propagated and cross-correlated with the forward-propagated source wavelet excited at R to image X₁. Here the source-receiver reciprocity is used. In migration of free-surface related multiples, the first-order free-surface related multiple excited at S₂ is backward propagated and cross-correalted with the direct wave excited at S₁ to image the reflector X₂. And the second-order free-surface related multiple excited at S₃ is backward propagated and cross-correalted with the first-order free-surface related multiple excited at S₂ to image the reflector X₃. From the comparison of the wavepaths in the diagram illustration, the imaging results of free-surface related multiples has wider coverage than the conventional migration. Moreover, it can clarify the shallow reflectors, which are usually not imaged when using primaries only.

FIGURE 1

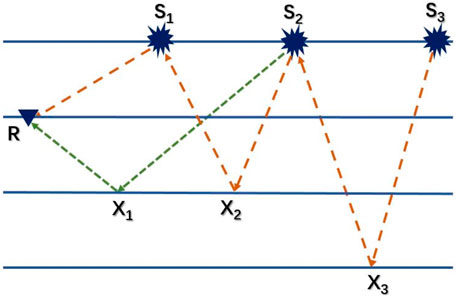
FIGURE 1. Schematic diagram of DDM method for VSP data. In conventional migration of walkaway VSP data, the upgoing component recorded at R is backward propagated and cross-correlated with the forward-propagated source wavelet excited at S₂ to image X₁; In migration of multiples. In migration of multiples, the receivers are considered to be virtual sources in the borehole and the sources located at the surface are taken as receivers for imaging multiples. The fist-order multiples are backward extrapolated from S₂ and cross-correlated with the forward-propagated direct wave from S₁ to image X₂; Similarly, the second-order multiples are backward extrapolated and cross-correlated with the forward-propagated first-order multiple to image X₃.

The imaging condition of DDM is (Wang et al., 2014b)

$I=D_F\ast D_B(1)$

For VSP data, D represents the downgoing components in the common receiver gathers. The subscript F denotes forward propagated, and B denotes backward propagated. The same data are forward and backward propagated and cross-correlated to form the subsurface image. The results of DDM contain some artifacts related with the undesired cross-correlations, such as the cross-correlation of direct waves from different shots or the cross-correlation of the direct wave and second-order free-surface related multiple. The first type mainly exists at the surface and can be muted easily. The second has longer wavepath and much weaker energy.

DDM With Inverse-Scattering Imaging Condition

There are different algorithms to implement DDM, such as one-way wave-equation (Zheng et al., 2016) or two-way wave-equation (Wang et al., 2014b). Now RTM based on two-way wave-equation has shown its benefits in offering high-resolution images and handling complex subsurface structures. The original imaging condition in RTM is

$I\left(\mathit{x}\right)={\displaystyle \int S\left(\mathit{x},t\right)R\left(\mathit{x},t\right)dt}(2)$

where $\mathit{x}$ represents the space location and $t$ represents the time. In the DDM for VSP data, $S\left(\mathit{x},t\right)$ and $R\left(\mathit{x},t\right)$ are the forward and backward propagated wavefields of the common receiver gathers from the shot locations.

As the two-way wave-equation is used in the wavefield simulation of $S\left(\mathit{x},t\right)$ and $R\left(\mathit{x},t\right)$, the upgoing and downgoing components both exist in the wavefields. The subscripts $d$ and $u$ are used to represent the downgoing and upgoing components respectively. Then the image in RTM can be divided into four parts

$I\left(\mathit{x}\right)={\displaystyle \int S_d\left(\mathit{x},t\right)R_u\left(\mathit{x},t\right)dt}+{\displaystyle \int S_u\left(\mathit{x},t\right)R_d\left(\mathit{x},t\right)dt}$

$+{\displaystyle \int S_d\left(\mathit{x},t\right)R_d\left(\mathit{x},t\right)dt}+{\displaystyle \int S_u\left(\mathit{x},t\right)R_u\left(\mathit{x},t\right)dt}(3)$

The last two terms, $S_d\left(\mathit{x},t\right)R_d\left(\mathit{x},t\right)$ and $S_u\left(\mathit{x},t\right)R_u\left(\mathit{x},t\right)$, generate the high-amplitude, low-frequency noise in the RTM results. Liu et al. (2011) use Hilbert transform to eliminate such kind of noise. Fei et al. (2015) show that the second term, $S_u\left(\mathit{x},t\right)R_d\left(\mathit{x},t\right)$, generates false images near the velocity interface or strong velocity contrasts. Thus the de-primary imaging condition is proposed (Fei et al., 2015; Wang et al., 2016; Wang et al., 2017):

$I\left(\mathit{x}\right)={\displaystyle \int S_d\left(\mathit{x},t\right)R_u\left(\mathit{x},t\right)dt}(4)$

It is the cross-correlation imaging with wavefield decomposition. True-amplitude imaging is an attractive topic for RTM. Based on the high-frequency asymptotic and the imaging/inversion theory, it is possible to obtain the estimation of slowness perturbations in wave-equation migration (Kiyashchenko et al., 2007). In RTM, the inverse-scattering imaging condition is proposed and shown the benefit of better amplitude recovery and higher resolution (Whitmore and Crawley, 2012; Pestana et al., 2014; Duprat et al., 2015). The imaging formula can be expressed as:

$I\left(\mathit{x}\right)=\frac{{\displaystyle \int \left[\frac{1}{v^2\left(\mathit{x}\right)}{I}_1-I_2\right]dt}}{{\displaystyle \int {\left|S_d\left(\mathit{x},t\right)\right|}^{2}dt}},$

$I_1={\partial }_t{S}_d\left(\mathit{x},t\right){\partial }_t{R}_u\left(\mathit{x},t\right)\hspace{0.17em},\hspace{0.17em}{I}_2=\nabla S_d\left(\mathit{x},t\right)\cdot \nabla R_u\left(\mathit{x},t\right)(5)$

where $v\left(\mathit{x}\right)$ represents the velocity. ${\partial }_t$ and $\nabla$ are the time derivative and spatial gradient operator, respectively. Compared to the conventional cross-correlation imaging condition, Eq. 5 can preserve the amplitudes and improve the resolution. In the imaging process, it is necessary to separate the wavefields to attenuate the backscattered noise introduced by two-way wave-equation. Pestana et al. (2014) uses the Poynting vector to obtain the separated components. However, their results show that the method may damage some reflections and has poor performance on receiver field. In this work, we followed the approach based on Hilbert transform to decompose the wavefield effectively.

Wavefield Decomposition Based on Hilbert Transform

According to the definition of Hilbert transform, the Hilbert transform of a signal $f\left(t\right)$ has the following quality:

${\mathrm{ℱ}}_t\left\{{\mathrm{\mathscr{H}}}_t\left[f\left(t\right)\right]\right\}=-isgn\left(\omega \right){\mathrm{ℱ}}_t\left[f\left(t\right)\right](6)$

where ${\mathrm{\mathscr{H}}}_t$ and ${\mathrm{ℱ}}_t$ represent the Hilbert transform and Fourier transform along the time axis, respectively. $i$ is the imaginary unit, $\omega$ is the frequency, and $sgn\left(\omega \right)$ is the sign function. With Hilbert transform, the downgoing and upgoing wavefields can be computed by (Zheng et al., 2018):

$S_d\left(\mathit{x},t\right)=\frac{1}{2}\left\{S\left(\mathit{x},t\right)+{\mathrm{\mathscr{H}}}_z{\mathrm{\mathscr{H}}}_t\left[S\left(\mathit{x},t\right)\right]\right\},$

$R_u\left(\mathit{x},t\right)= \frac{1}{2}\{R\left(\mathit{x},t\right)-{\mathrm{\mathscr{H}}}_z{\mathrm{\mathscr{H}}}_t\left[R\left(\mathit{x},t\right)\right]\}(7)$

where ${\mathrm{\mathscr{H}}}_z$ and ${\mathrm{\mathscr{H}}}_t$ represent the Hilbert transform in depth and time, respectively. As the wavefield modeling and Hilbert transform are both linear operators, the ${\mathrm{\mathscr{H}}}_t\left(S\left(\mathit{x},t\right)\right)$ and ${\mathrm{\mathscr{H}}}_t\left(R\left(\mathit{x},t\right)\right)$ in Eq. 7 is calculated by the forward modeling of the Hilbert transformed wavelet and data to avoid the wavefield storage. At each time step, Hilbert transform in depth is applied to the two wavefields, ${\mathrm{\mathscr{H}}}_t\left(S\left(\mathit{x},t\right)\right)$and ${\mathrm{\mathscr{H}}}_t\left(R\left(\mathit{x},t\right)\right)$ to get the final image.

The workflow for VSP imaging using free-surface related multiples with inverse scattering imaging condition and wavefield decomposition consists of the following steps: 1) separate the upgoing and downgoing components by f-k filter and resort the shotgathers to common receiver gathers; 2) forward propagate the downgoing data from the source locations and store the boundary values; 3) apply Hilbert transform to the downgoing data and forward propagate it to construct ${\mathrm{\mathscr{H}}}_t\left(S\left(\mathit{x},t\right)\right)$; 4) use the boundary value to reconstruct the wavefield $S\left(\mathit{x},t\right)$ and ${\mathrm{\mathscr{H}}}_t\left(S\left(\mathit{x},t\right)\right)$; 5) back propagate the downgoing data from the source locations to construct $R\left(\mathit{x},t\right)$; 6) apply Hilbert transform to the downgoing data and back propagate it to construct ${\mathrm{\mathscr{H}}}_t\left(R\left(\mathit{x},t\right)\right)$; 7) apply imaging condition in Eq. 5 and stack all the images at all time steps.

Synthetic Examples

To better illustrate the advantages of VSP imaging using the proposed method, we applied it on a part of the Sigsbee 2A model. Figure 2 shows the velocity model. 500 shots are deployed on the surface and 80 geophones are placed evenly in the observation well located at the center of the model. The time sampling interval is 1 ms and the grid spacing of the model is 10 m. A Ricker wavelet with peak frequency of 15 Hz is used as the source wavelet. Figure 3 shows the synthetic data generated without and with free-surface related multiples. Figure 4 shows the data for VSP imaging after f-k filtering. The upgoing components are used for conventional imaging with primaries only while the downgoing components are used for VSP imaging using free-surface related multiples. Figure 5 shows the input common receiver gathers for VSP imaging. Figures 6A,B shows the conventional cross-correlation imaging (Eq. 2) results using primaries and free-surface related multiples, respectively. The comparison clearly demonstrates the benefits of VSP imaging using multiples. Figure 6B has much wider imaging area and the reflectors above the geophones are also imaged. The results using cross-correlation imaging condition with wavefield decomposition (Eq. 4) are shown in Figure 7. Figure 7A is the result using primaries only and Figure 7B is the result using multiples. The noised are suppressed but the amplitudes decrease with the depth. We apply the inverse scattering imaging condition with wavefield decomposition (Eq. 5) to the data and the results are shown in Figure 8. Figures 8A,B are the results using primaries only and multiples, respectively. Compared to Figure 7, the proposed approach yields a better estimation of the true subsurface reflectivity with improved resolution and amplitude recovery. And there are no obvious artifacts shown in Figure 8B, as the true images has stronger contribution to the final image.

FIGURE 2

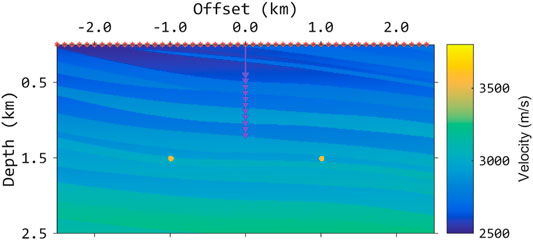
FIGURE 2. A part of Sigsbee 2A model. The VSP survey consists of 80 geophones evenly placed in the borehole between a depth of 400–1,200 m. 500 shots are evenly located at the surface.

FIGURE 3

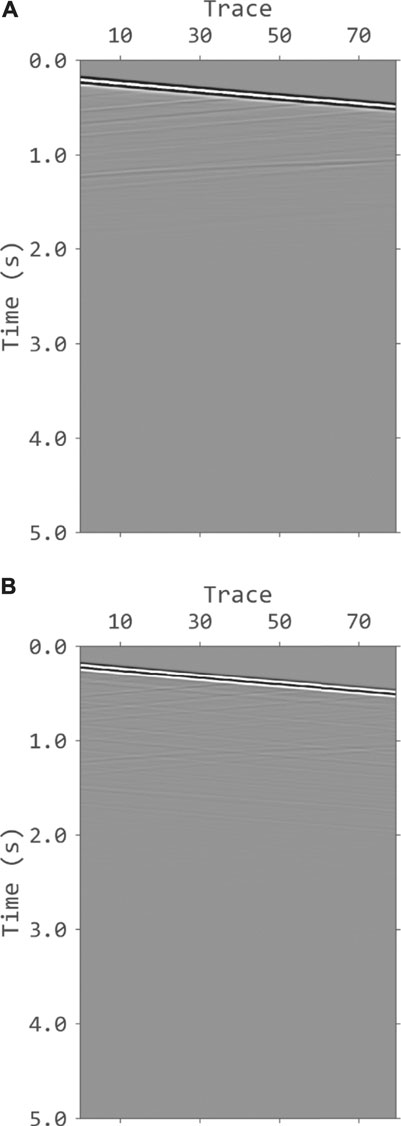
FIGURE 3. The common shot gathers generated from the Sigsbee 2A model. (A) The generated data without free-surface–related multiples, which contains downgoing direct waves and upgoing primaries. (B) The gathers generated with free surface, which contains direct waves, primaries and free-surface related multiples.

FIGURE 4

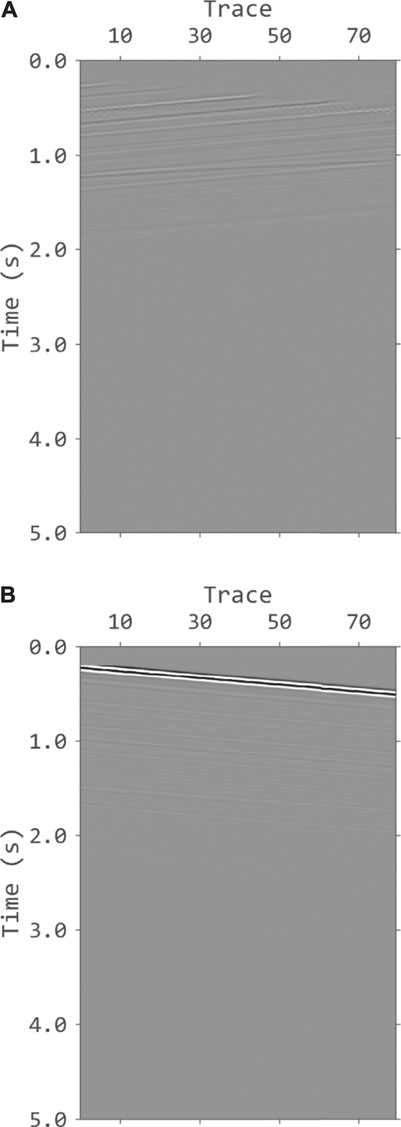
FIGURE 4. The separated components of the data shown in Panel 3 after f-k filtering. (A) The upgoing components of the data generated without free surface, it is the primaries in the original data. (B) The downgoing components of the data modeled with free surface, containing direct waves and free-surface–related multiples.

FIGURE 5

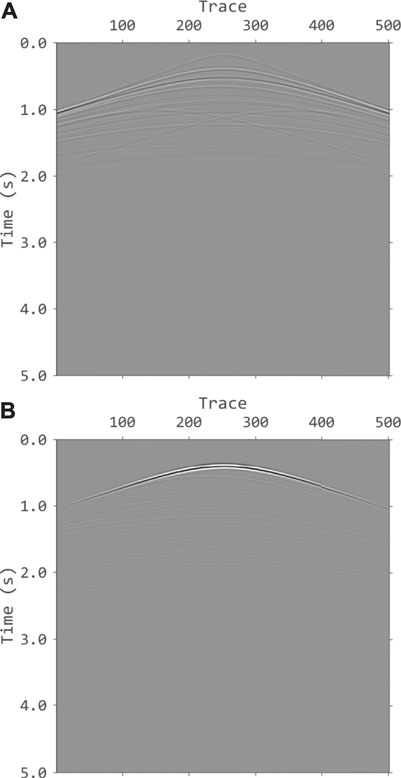
FIGURE 5. The generated input data using Sigsbee 2A model for VSP imaging. (A) a common receiver gathers of VSP data containing primaries only. (B) Common receiver gathers of VSP data containing direct waves and free-surface–related multiples.

FIGURE 6

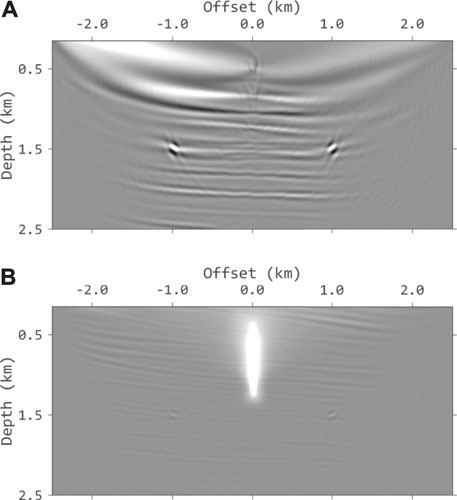
FIGURE 6. The images generated by conventional cross-correlation imaging condition. (A) The image using primaries only. (B) The image using DDM. (B) has wider coverage by involving multiples in the migration. They both have noises introduced by the two-way wave-equation used in RTM.

FIGURE 7

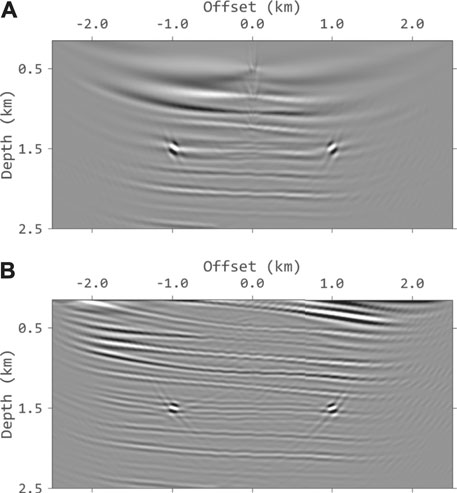
FIGURE 7. The results using cross-correlation imaging condition with wavefield decomposition. (A) The image using primaries only. (B) The image using DDM. The noises in Panel 6 are suppressed. There is no obvious artifacts in (B).

FIGURE 8

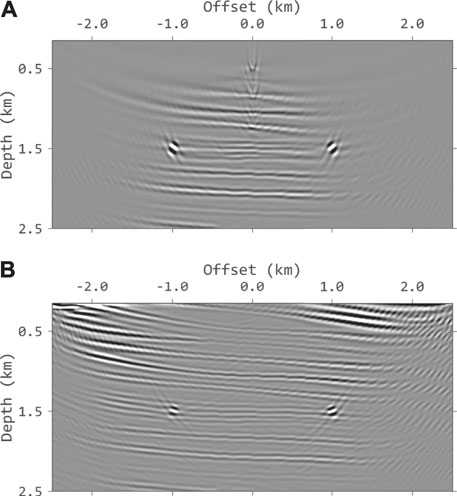
FIGURE 8. The results using inverse‐scattering imaging condition with wavefield decomposition. (A) The image using primaries only. (B) The image using DDM. Compared to Panel 7, the resolution is well improved.

Field Data Application

To verify the adaptability of the proposed method to field data, we use a walkaway field data for further test. The walkaway VSP data is collected to monitoring the reservoir changes during the CO2 injection in northwestern China. Figure 9A shows the migration velocity and seismic geometry in the walkaway VSP survey. The data are recorded by 40 receivers equally spaced from the depth of 390–1,170 m.

FIGURE 9

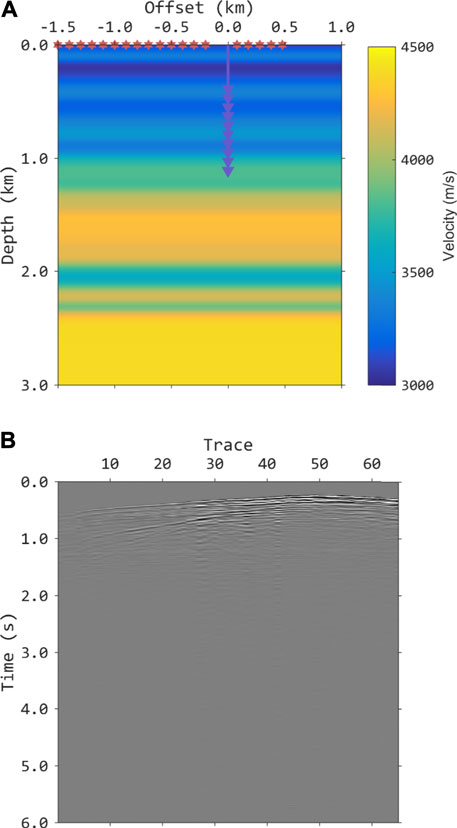
FIGURE 9. (A) The migration velocity and walkaway VSP acquisition used in field application. (B) The common receiver gathers obtained from the data containing multiples. Note that several near-offset traces are missing.

The time sampling interval is 1 ms and the grid spacing of the model is 10 m. Figure 9B shows a common receiver gather for imaging using multiples. Several shots near the wellbore are missing, which can lead to the lack of multiples with small reflection angles in the generated data.

Figures 10A,B shows the images obtained from conventional cross-correlation imaging condition with wavefield decomposition using primaries only and free surface related multiples, respectively. Figures 11A,B shows the results of the proposed method. The inverse-scattering imaging condition with wavefield decomposition improves the resolution and balances the amplitudes.

FIGURE 10

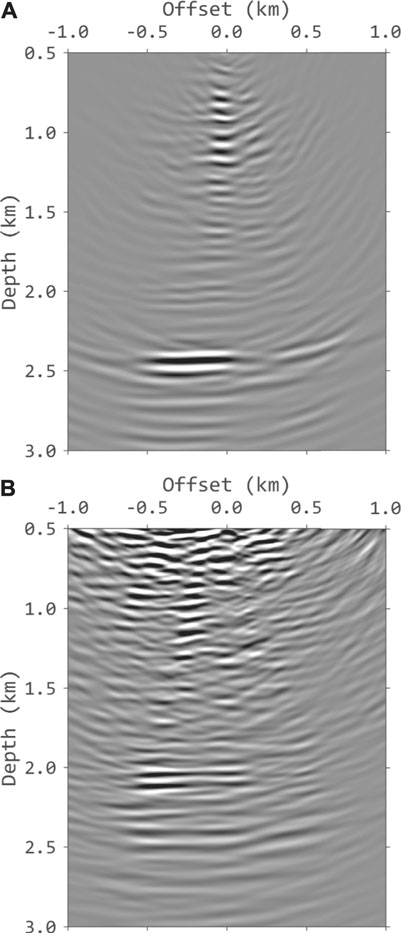
FIGURE 10. Imaging results of the walkaway VSP field data using cross-correlation imaging condition with wavefield decomposition: (A) The image using primaries only. (B) The image using DDM. Compared to (A, B) has enhanced illumination away from the well and images the shallow reflectors. Due to the lack of near-offset traces, the zone near the well is not accurately imaged in (B).

FIGURE 11

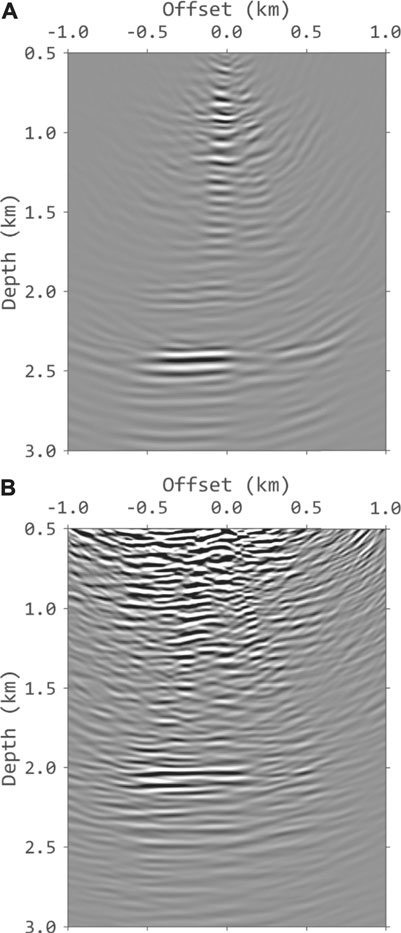
FIGURE 11. Imaging results of the walkaway VSP field data using inverse‐scattering imaging condition with wavefield decomposition: (A) The image using primaries only. (B) The image using DDM. Compared to Panel 10, the reflection amplitudes are well preserved, and the resolution is improved.

As we can see from the results, migration with multiples can effectively image the reflector in the shallow zone and enlarge the image range. But the illumination near the borehole is influenced by the reflection angle and missing near-offset traces in the data. Note that it also contains the crosstalk generated from undesired cross-correlation of different seismic events. Figure 12 illustrates the migration result that combines the contribution of primaries and multiples. Compared to the conventional images, the joint migration enhances the illumination and achieves the high-quality seismic images for monitoring the CO₂ injection. Overall, we see that VSP imaging using inverse-scattering imaging condition with wavefield decomposition is capable of handling real datasets.

FIGURE 12

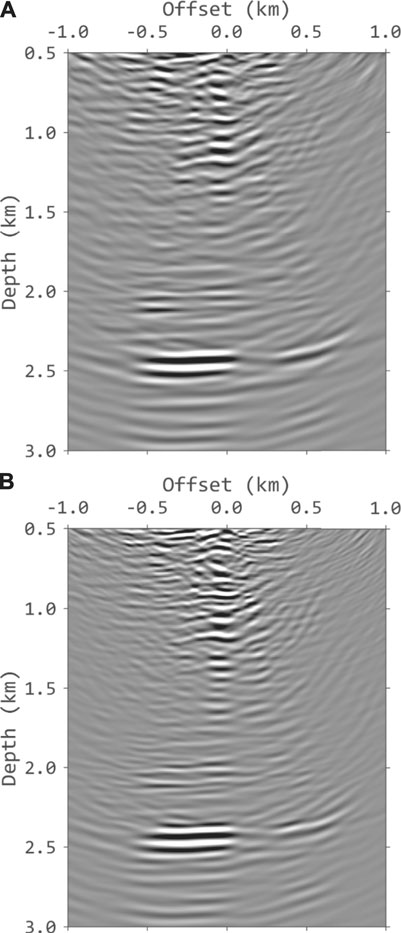
FIGURE 12. The joint migration images using primaries and multiples. (A) The result using cross-correlation imaging condition with wavefield decomposition, (B) the result using inverse-scattering imaging condition with wavefield decomposition. (B) provides the best result in resolution and frequency content.

Discussion

In the proposed workflow, the downgoing components of VSP data are included in the imaging process. Combined with the conventional VSP imaging using upgoing waves, we can have improved imaging results. An important advantage of DDM is that it can image the subsurface without any knowledge of the source information. Thus, the reflector in DDM images can be used to calibrate the conventional images when the source wavelet is inaccurate. The matching filter used in the multiple subtraction (Verschuur et al., 1992; Wang, 2003; Fomel, 2009) can be modified to find the correct combination of the two kinds of imaging results. In the application of DDM to VSP walkway data, the imaging quality is contaminated by the large-amplitude, low frequency noises around the well. By using wavefield decomposition based on Hilbert transform, this kind of noises can be suppressed effectively.

In the wavefield separation using Poynting vectors, the reflection angle between the source wavefield and receiver wavefield is calculated, and the components with the opening angle more than certain values are excluded to obtain the final imaging results. Compared to the approach using Hilbert transform, the method using Poynting vectors can not remove the false images, which are generated by the second term on the right side of Eq. 3. But it is able to generate angle domain common image gathers. The proposed approach is only designed to separate upgoing and downgoing components in the propagated wavefields, and to provide imaging results without low-frequency noise and false images. If the finite-difference time-domain method and staggered grid are used in RTM, the extra computation cost is negligible for the wavefield separation using Poynting vectors. The computation cost in the proposed approach is doubled compared to traditional RTM, thus some high-performance computation techniques, such as MPI or GPU, are necessary to increase the efficiency of the method.

The images generated from conventional cross-correlation imaging condition may suffer from poor resolution and incorrect amplitude responses while inverse-scattering imaging condition partly overcomes the drawbacks. To make the results obtained from inverse-scattering imaging condition become suitable estimation of the slowness perturbation, wavefield decomposition is necessary to avoid the noises introduced by the two-way wave equation when strong velocity gradients exist. It is an approximated solution for true amplitude RTM. The final workflow can generate subsurface images with balanced amplitude and high resolution, which is important for amplitude variation with offset analysis.

As we have demonstrated with numerical examples, the final images obtained from DDM can be superior to conventional imaging results. However, it relies on the designed geometry. The sparse shot array and shallow receiver locations may lead to limited free-surface related multiples in the recorded data. In practice, the results of DDM can be used as import complement of conventional imaging, as shown in the field example.

In the theory of DDM, because we have to cross-correlate all orders of multiples to avoid multiple prediction, the results of DDM contains undesirable artifacts. Assume that the amplitude of the true image is one, then the strongest artifact has the strength of the reflectivity. The final imaging result of DDM is still acceptable in most cases. The noise that leaks into the images can be further suppressed in image domain to improve the imaging quality. Least-squares migration (Nemeth et al., 1999; Dai et al., 2011) can be applied to remove the artifacts (Zhang and Schuster, 2014; Liu et al., 2018; Zheng et al., 2019; Li et al., 2020). Another option is high-resolution parabolic Radon filtering in angle domain common image gathers (Wang et al., 2014b; Zheng et al., 2016) or using 3D wide-azimuth acquisition (VerWest and Lin, 2007).

Conclusion

We present an effective method to imaging free-surface related multiples in VSP data. The downgoing components, which are muted in conventional VSP imaging, are used to image the subsurface. The separated downgoing components are resorted into common receiver gathers and then DDM method is used to image the subsurface. The inverse-scattering imaging condition with wavefield decomposition is applied to generate a better approximation of the subsurface reflectivity. We have illustrated the explicit workflow to apply the proposed approach with Hilbert transform in RTM. Results with synthetic VSP data and field data validate the effectiveness of the proposed approach. Compared to VSP imaging using primaries only, the results have significantly enhanced coverage and shallow reflectors with improved resolution. The algorithm handles free-surface related multiples without the need of multiple prediction in preprocessing. The method has the potential to improve the results using primaries only and offer better estimation of the geological structures.

Data Availability Statement

The field data analyzed in this study was obtained from National Institute of Clean-and-Low-Carbon Energy and used for research purposes only. Requests to access these datasets should be directed to NICE (nice_contact@chnenergy.com.cn).

Author Contributions

YZ and YW developed the theory and performed the applications. XC supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.

Funding

This study was funded by the CAS Project for Young Scientists in Basic Research (Grant No. YSBR-020), the National Natural Science Foundation of China (Grant No. 42025403) and the Youth Innovation Promotion Association CAS (Grant No. Y201917).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank National Institute of Clean-and-Low-Carbon Energy for providing research data. We thank the reviewers for their valuable comments that greatly improved the quality of this paper.

References

Artman, B. (2006). Imaging Passive Seismic Data. Geophysics 71 (4), SI177–SI187. doi:10.1190/1.2209748

CrossRef Full Text | Google Scholar

Baysal, E., Kosloff, D. D., and Sherwood, J. W. C. (1983). Reverse Time Migration. Geophysics 48, 1514–1524. doi:10.1190/1.1441434

CrossRef Full Text | Google Scholar

Bevc, D. (1997). Imaging Complex Structures with Semirecursive Kirchhoff Migration. Geophysics 62, 577–588. doi:10.1190/1.1444167

CrossRef Full Text | Google Scholar

Burch, T., Hornby, B., Sugianto, H., and Nolte, B. (2010). Subsalt 3D VSP Imaging at Deimos Field in the deepwater Gulf of Mexico. The Leading Edge 29, 680–685. doi:10.1190/1.3447781

CrossRef Full Text | Google Scholar

Chang, W. F., and McMechan, G. A. (1986). Reverse‐time Migration of Offset Vertical Seismic Profiling Data Using the Excitation‐time Imaging Condition. Geophysics 51, 67–84. doi:10.1190/1.1442041

CrossRef Full Text | Google Scholar

Dai, W., Wang, X., and Schuster, G. T. (2011). Least-squares Migration of Multisource Data with a Deblurring Filter. Geophysics 76 (5), R135–R146. doi:10.1190/geo2010-0159.1

CrossRef Full Text | Google Scholar

Fei, T. W., Yang, J., Liu, H., Qin, F., and Luo, Y. (2015). Removing False Images in Reverse Time Migration: The Concept of De-primary. Geophysics 80 (6), S237–S244. doi:10.1190/geo2015-0289.1

CrossRef Full Text | Google Scholar

Fletcher, R. F., Fowler, P., Kitchenside, P., and Albertin, U. (2005). Suppressing Artifacts in Prestack Reverse Time Migration: 75th Annual International Meeting. Houston: SEG, 2049–2051.

Google Scholar

Fomel, S. (2009). Adaptive Multiple Subtraction Using Regularized Nonstationary Regression. Geophysics 74 (1), V25–V33. doi:10.1190/1.3043447

CrossRef Full Text | Google Scholar

Gazdag, J. (1978). Wave Equation Migration with the Phase‐shift Method. Geophysics 43, 1342–1351. doi:10.1190/1.1440899

CrossRef Full Text | Google Scholar

Gray, S. H., and May, W. P. (1994). Kirchhoff Migration Using Eikonal Equation Traveltimes. Geophysics 59, 810–817. doi:10.1190/1.1443639

CrossRef Full Text | Google Scholar

Guitton, A. (2002). Shot-profile Migration of Multiple Reflections: 72nd Annual International Meeting. Salt Lake City: SEG, 1296–1299.

Google Scholar

Guitton, A., Valenciano, A., Bevc, D., and Claerbout, J. (2007). Smoothing Imaging Condition for Shot-Profile Migration. Geophysics 72 (3), S149–S154. doi:10.1190/1.2712113

CrossRef Full Text | Google Scholar

Hardage, B. A. (1985). Vertical Seismic Profiling. The Leading Edge 4, 59. doi:10.1190/1.1487141

CrossRef Full Text | Google Scholar

He, R., Hornby, B., and Schuster, G. (2007). 3D Wave-Equation Interferometric Migration of VSP Free-Surface Multiples. Geophysics 72 (5), S195–S203. doi:10.1190/1.2743375

CrossRef Full Text | Google Scholar

Hinds, R. C., Anderson, N. L., and Kuzmiski, R. D. (1996). VSP Interpretive Processing: Theory and Practice. Tulsa: Society of Exploration Geophysicists.

Google Scholar

Hua, B., and McMechan, G. A. (2003). Parsimonious 2D Prestack Kirchhoff Depth Migration. Geophysics 68, 1043–1051. doi:10.1190/1.1581075

CrossRef Full Text | Google Scholar

Jiang, Z., Sheng, J., Yu, J., Schuster, G. T., and Hornby, B. E. (2007). Migration Methods for Imaging Different-Order Multiples. Geophys. Prospect 55, 1–19. doi:10.1111/j.1365-2478.2006.00598.x

CrossRef Full Text | Google Scholar

Jiang, Z., Yu, J., Schuster, G. T., and Hornby, B. E. (2005). Migration of Multiples. The Leading Edge 24, 315–318. doi:10.1190/1.1895318

CrossRef Full Text | Google Scholar

Keho, T. H., and Beydoun, W. B. (1988). Paraxial ray Kirchhoff Migration. Geophysics 53, 1540–1546. doi:10.1190/1.1442435

CrossRef Full Text | Google Scholar

Kiyashchenko, D., Plessix, R.-E., Kashtan, B., and Troyan, V. (2007). A Modified Imaging Principle for True-Amplitude Wave-Equation Migration. Geophys. J. Int. 168, 1093–1104. doi:10.1111/j.1365-246x.2006.03187.x

CrossRef Full Text | Google Scholar

Li, Z., Li, Z., Li, Q., Li, Q., Sun, M., Hu, P., et al. (2020). Least-squares Reverse Time Migration of Multiples in Viscoacoustic media. Geophysics 85 (5), S285–S297. doi:10.1190/geo2019-0464.1

CrossRef Full Text | Google Scholar

Li, Z., Li, Z., Wang, P., and Zhang, M. (2017). Reverse Time Migration of Multiples Based on Different-Order Multiple Separation. Geophysics 82 (1), S19–S29. doi:10.1190/geo2015-0710.1

CrossRef Full Text | Google Scholar

Liu, F., Zhang, G., Morton, S. A., and Leveille, J. P. (2011). An Effective Imaging Condition for Reverse-Time Migration Using Wavefield Decomposition. Geophysics 76 (1), S29–S39. doi:10.1190/1.3533914

CrossRef Full Text | Google Scholar

Liu, X., Liu, Y., and Khan, M. (2018). Fast Least-Squares Reverse Time Migration of VSP Free-Surface Multiples with Dynamic Phase-Encoding Schemes. Geophysics 83 (4), S321–S332. doi:10.1190/geo2017-0419.1

CrossRef Full Text | Google Scholar

Lomas, A., Singh, S., and Curtis, A. (2018). Marchenko Imaging of Both Vertical and Horizontal Interfaces Using VSP Data: 88th Annual International Meeting. Anaheim: SEG, 5027.

Google Scholar

Lu, S., Whitmore, D. N., Valenciano, A. A., and Chemingui, N. (2015). Separated-wavefield Imaging Using Primary and Multiple Energy. The Leading Edge 34, 770–778. doi:10.1190/tle34070770.1

CrossRef Full Text | Google Scholar

McMechan, G. A. (1983). Migration by Extrapolation of Time-dependent Boundary Values*. Geophys. Prospect 31, 413–420. doi:10.1111/j.1365-2478.1983.tb01060.x

CrossRef Full Text | Google Scholar

Muijs, R., Robertsson, J. O., and Holliger, K. (2007). Prestack Depth Migration of Primary and Surface-Related Multiple Reflections: Part I - Imaging. Geophysics 72 (2), S59–S69. doi:10.1190/1.2422796

CrossRef Full Text | Google Scholar

Nemeth, T., Wu, C., and Schuster, G. T. (1999). Least‐squares Migration of Incomplete Reflection Data. Geophysics 64, 208–221. doi:10.1190/1.1444517

CrossRef Full Text | Google Scholar

O'Brien, J., Farmani, B., and Atkinson, B. (2013). VSP Imaging Using Free-Surface Multiples: A Case Study from the Gulf of Mexico. The Leading Edge 32, 1258–1266. doi:10.1190/tle32101258.1

CrossRef Full Text | Google Scholar

Pestana, R. C., dos Santos, A. W., and Araujo, E. S. (2014). RTM Imaging Condition Using Impedance Sensitivity Kernel Combined with Poynting Vector: 84th Annual International Meeting. Denver: SEG, 3763–3768.

Google Scholar

Ristow, D., and Rühl, T. (1994). Fourier Finite‐difference Migration. Geophysics 59, 1882–1893. doi:10.1190/1.1443575

CrossRef Full Text | Google Scholar

Sava, P., and Vasconcelos, I. (2011). Extended Imaging Conditions for Wave-Equation Migration. Geophys. Prospecting 59, 35–55. doi:10.1111/j.1365-2478.2010.00888.x

CrossRef Full Text | Google Scholar

Schuster, G. T. (2009). Seismic Interferometry. Cambridge: Cambridge University Press.

Google Scholar

Shan, G. (2003). Source-receiver Migration of Multiple Reflections: 73rd Annual International Meeting. Dallas: SEG, 1008–1011.

Google Scholar

Singh, S., Snieder, R., Behura, J., van der Neut, J., Wapenaar, K., and Slob, E. (2015). Marchenko Imaging: Imaging with Primaries, Internal Multiples, and Free-Surface Multiples. Geophysics 80 (5), S165–S174. doi:10.1190/geo2014-0494.1

CrossRef Full Text | Google Scholar

Soni, A. K., and Verschuur, D. J. (2015). Imaging Blended Vertical Seismic Profiling Data Using Full-Wavefield Migration in the Common-Receiver Domain. Geophysics 80 (3), R123–R138. doi:10.1190/geo2014-0193.1

CrossRef Full Text | Google Scholar

Stewart, R. R., Huddleston, P. D., and Kan, T. K. (1984). Seismic versus Sonic Velocities: A Vertical Seismic Profiling Study. Geophysics 49, 1153–1168. doi:10.1190/1.1441745

CrossRef Full Text | Google Scholar

Stoffa, P. L., Fokkema, J. T., de Luna Freire, R. M., and Kessinger, W. P. (1990). Split‐step Fourier Migration. Geophysics 55, 410–421. doi:10.1190/1.1442850

CrossRef Full Text | Google Scholar

Suh, S., and Wang, B. (2013). Improving Salt Boundary Imaging Using an RTM Inverse Scattering Imaging Condition: 83rd Annual International Meeting. Houston: SEG, 3953–3957.

Google Scholar

Valenciano, A. A., and Biondi, B. (2003). 2-D Deconvolution Imaging Condition for Shot-Profile Migration: 72nd Annual International Meeting. Dallas: SEG, 1059–1062.

Google Scholar

Verschuur, D., and Berkhout, A. (2005). Transforming Multiples into Primaries: Experience with Field Data: 75th Annual International Meeting. Houston: SEG, 2103–2106.

Google Scholar

Verschuur, D. J., Berkhout, A. J., and Wapenaar, C. P. A. (1992). Adaptive Surface‐related Multiple Elimination. Geophysics 57, 1166–1177. doi:10.1190/1.1443330

CrossRef Full Text | Google Scholar

VerWest, B. J., and Lin, D. (2007). Modeling the Impact of Wide-Azimuth Acquisition on Subsalt Imaging. Geophysics 72 (5), SM241–SM250. doi:10.1190/1.2736516

CrossRef Full Text | Google Scholar

Wang, Y., Chang, X., and Hu, H. (2014a). Simultaneous Reverse Time Migration of Primaries and Free-Surface Related Multiples without Multiple Prediction. Geophysics 79 (1), S1–S9. doi:10.1190/geo2012-0450.1

CrossRef Full Text | Google Scholar

Wang, Y. (2003). Multiple Subtraction Using an Expanded Multichannel Matching Filter. Geophysics 68, 346–354. doi:10.1190/1.1543220

CrossRef Full Text | Google Scholar

Wang, Y., Zheng, Y., Xue, Q., Chang, X., Fei, T. W., and Luo, Y. (2017). Reverse Time Migration of Multiples: Reducing Migration Artifacts Using the Wavefield Decomposition Imaging Condition. Geophysics 82 (4), S307–S314. doi:10.1190/geo2016-0354.1

CrossRef Full Text | Google Scholar

Wang, Y., Zheng, Y., Xue, Q., Chang, X., Fei, T. W., and Luo, Y. (2016). Reverse Time Migration with Hilbert Transform Based Full Wavefield Decomposition. Chin. J. Geophys. 59, 4200–4211.

Google Scholar

Wang, Y., Zheng, Y., Zhang, L., Chang, X., and Yao, Z. (2014b). Reverse Time Migration of Multiples: Eliminating Migration Artifacts in Angle Domain Common Image Gathers. Geophysics 79 (6), S263–S270. doi:10.1190/geo2013-0441.1

CrossRef Full Text | Google Scholar

Wapenaar, K., and Fokkema, J. (2006). Green's Function Representations for Seismic Interferometry. Geophysics 71 (4), SI33–SI46. doi:10.1190/1.2213955

CrossRef Full Text | Google Scholar

Wapenaar, K., van der Neut, J., and Slob, E. (2017). On the Role of Multiples in Marchenko Imaging. Geophysics 82, A1–A5. doi:10.1190/geo2016-0323.1

CrossRef Full Text | Google Scholar

Whitmore, N. D., and Crawley, S. (2012). Applications of RTM Inverse Scattering Imaging Conditions: 82nd Annual International Meeting. Las Vegas: SEG, 1–6. doi:10.1190/segam2012-0779.1

CrossRef Full Text | Google Scholar

Yoon, K., and Marfurt, K. J. (2006). Reverse-time Migration Using the Poynting Vector. Exploration Geophys. 37, 102–107. doi:10.1071/eg06102

CrossRef Full Text | Google Scholar

Yu, J., and Schuster, G. T. (2001). Crosscorrelogram Migration of IVSPWD Data: 71st Annual International Meeting. San Antonio: SEG, 456–459.

Google Scholar

Yu, J., and Schuster, G. T. (2002). Joint Migration of Primary and Multiple Reflections in RVSP Data: 72nd Annual International Meeting. Salt Lake City: SEG, 2373–2376.

Google Scholar

Zhang, D., and Schuster, G. T. (2014). Least-squares Reverse Time Migration of Multiples. Geophysics 79 (1), S11–S21. doi:10.1190/geo2013-0156.1

CrossRef Full Text | Google Scholar

Zhang, L., and Slob, E. (2019). Free-surface and Internal Multiple Elimination in One Step without Adaptive Subtraction. Geophysics 84 (1), A7–A11. doi:10.1190/geo2018-0548.1

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, Y., Liu, X., and Zhou, X. (2020). Reverse Time Migration Using Water‐bottom‐related Multiples. Geophys. Prospecting 68, 446–465. doi:10.1111/1365-2478.12851

CrossRef Full Text | Google Scholar

Zhang, Y., and Sun, J. (2009). Practical Issues in Reverse Time Migration: True Amplitude Gathers, Noise Removal and Harmonic Source Encoding. First break 27, 53–59. doi:10.3997/1365-2397.2009002

CrossRef Full Text | Google Scholar

Zheng, Y., Wang, Y., and Chang, X. (2018). 3D Forward Modeling of Upgoing and Downgoing Wavefields Using Hilbert Transform. Geophysics 83 (1), F1–F8. doi:10.1190/geo2016-0637.1

CrossRef Full Text | Google Scholar

Zheng, Y., Wang, Y., and Chang, X. (2016). Eliminating Artifacts in Migration of Surface-Related Multiples: An Application to marine Data. Interpretation 4 (4), SQ51–SQ57. doi:10.1190/int-2016-0020.1

CrossRef Full Text | Google Scholar

Zheng, Y., Wang, Y., and Chang, X. (2019). Least-squares Data-To-Data Migration: An Approach for Migrating Free-Surface-Related Multiples. Geophysics 84 (2), S83–S94. doi:10.1190/geo2018-0080.1

CrossRef Full Text | Google Scholar