Real-Time Prediction of Impending Ground Shaking: Review of Wavefield-Based (Ground-Motion-Based) Method for Earthquake Early Warning

Earthquake early warning (EEW) systems aim to provide advance warning of impending ground shaking, and the technique used for real-time prediction of shaking is a crucial element of EEW systems. Many EEW systems are designed to predict the strength of seismic ground motions (peak ground acceleration, peak ground velocity, or seismic intensity) based on rapidly estimated source parameters (the source-based method), such as hypocentral location, origin time, magnitude, and extent of fault rupture. Recently, however, the wavefield-based (or ground-motion-based) method has been developed to predict future ground motions based directly on the current wavefield, i.e., ground motions monitored in real-time at neighboring sites, skipping the process of estimation of the source parameters. The wavefield-based method works well even for large earthquakes with long duration and huge rupture extents, highly energetic earthquakes that deviate from standard empirical relations, and multiple simultaneous earthquakes, for which the conventional source-based method sometimes performs inadequately. The wavefield-based method also enables prediction of the ongoing seismic waveform itself using the physics of wave propagation, thus providing information on the duration, in addition to the strength of strong ground motion for various frequency bands. In this paper, I review recent developments of the wavefield-based method, from simple applications using relatively sparse observation networks to sophisticated data assimilation techniques exploiting dense networks.

Introduction

Earthquake early warning (EEW) aims to prevent/mitigate earthquake disasters by providing people with enough time to take appropriate safety measures in advance of impending strong ground motion. EEW systems have been researched and developed in Japan, Mexico, Taiwan, the United States, European countries, China, Turkey, south Korea, and many other regions (e.g., Hoshiba et al., 2008; Cuellar et al., 2014; Chen et al., 2015; Cochran et al., 2018). The prediction of strong ground motions is an important element of EEW, and many methods have been proposed; the basic algorithms are classified into three prediction concepts:

1): Predicting seismic wave propagation;

2): Predicting the amplitude of S-waves from those of preceding P-wave; and

3): Predicting an entire rupture based on the initial rupture.

EEW algorithms are constructed based on one or combination of these concepts. For example, the operational EEW system of the Japan Methodological Agency (JMA) combines Concepts 1) and 2) but does not adopt Concept 3) (Hoshiba, 2014).

Concept 1) is based on the fact that modern communication speeds (∼10⁵ km/s) are much faster than seismic wave velocity (∼10⁰–10¹ km/s); information about seismic waves detected near a hypocenter can be relayed to distant locations much faster than the seismic waves propagate. This concept assumes that observation sites are closer to the hypocenter than the prediction (target) site; the seismic observation network thus plays an important role.

Concept 2) is based on the fact that amplitudes of early P-wave arrivals are usually smaller than those of late arriving S-waves. The S-wave/P-wave amplitude ratio has been estimated theoretically or empirically, and many authors take a value of ∼5. Because communication is not necessarily required, this concept can be used for even a single isolated site. However, this concept cannot be used in cases when the earthquake rupture duration is longer than S-P time (the time between P and S wave arrives), because P waves from later large ruptures may be contaminated by S waves from earlier small ruptures. This situation usually occurs at sites near the hypocenter (that is, short S-P time) of large (that is, long rupture duration) earthquakes. Discrimination of P waves in S wave train is required.

Concept 3) is based on the hypothesis that initial parts of small and large earthquake ruptures differ. Some authors have claimed that the final moment magnitude (Mw) can be estimated from the first several seconds of P-wave portion even for large events of long rupture duration (typical durations are ∼10 and 30 s for Mw7 and 8 earthquakes, respectively), and that it may be possible to rapidly estimate the final Mw while the rupture is still ongoing (e.g., Olson and Allen, 2005; Zollo et al., 2006; Noda and Ellsworth, 2016; Melgar and Hayes, 2019). However, many authors have challenged this deterministic view of ruptures claiming that they are nondeterministic and statistically common rupture growth (e.g., Rydelek and Horiuchi, 2006; Meier et al., 2016; Okuda and Ide, 2018; Trugman et al., 2019). The debate over the deterministic nature of earthquake rupture has continued for more than 2 decades in research on EEW and the physics of earthquake rupture dynamics. Although some EEW algorithms are based on this concept, but many others are not.

In this review paper, I focus on Concept (1). When the characteristics of wave propagation are expressed simply and the source location and strength are estimated quickly, it is possible to easily predict waves strength at a given location. Many authors have thus proposed methods to rapidly estimate origin time, hypocentral location, and earthquake magnitude for EEW purposes (the point-source algorithm). Moreover, the rapid estimation of source extent has also been investigated (the finite fault algorithm) (Yamada, 2014; Böse et al., 2018). In these “source-based methods,” the strength of ground motion (e.g., peak ground acceleration, PGA; peak ground velocity, PGV; and/or seismic intensity) is usually evaluated based on Mw and distance (e.g., hypocentral distance, epicentral distance, or fault distance) using a ground motion prediction equation (GMPE). Nonetheless, the source-based methods have vulnerabilities, including underpredicting ground motion for extended ruptures in point-source algorithms, and incorrectly identifying multiple simultaneous earthquakes. Even when the hypocenter and magnitude are estimated precisely, the precision of predicted ground-motion strengths are controlled by the uncertainty in the GMPE. Recent theoretical works have suggested that the source-based methods are inherently limited in terms of the timeliness and accuracy of its prediction (Minson et al., 2018, 2019; Hoshiba, 2020).

As an alternative to source-based methods, another algorithm that has been intensively investigated over recent decade does not necessarily require source parameters to predict the strength of ground motion. Instead, future ground motions are predicted directly from observed ground motion, skipping the process of source estimation. The “wavefield-based method” or “ground-motion-based method” (hereinafter “wavefield-based method” for simplicity) first estimates the current wavefield, then predicts future wavefield based on the physics of wave propagation. Because source parameters are not estimated, this method avoids the vulnerabilities of the source-based method (rupture extent, and simultaneous multiple earthquakes).

This paper reviews recent developments, the current situation, and future prospects of the wavefield-based method by comparison with the source-based method.

Theoretical Background

Prediction of seismic wave propagation is a key element of Concept (1). Because seismic wave is controlled by the physics of wave propagation, future wavefield can be predicted by wave propagation theory. In this section, I explain the theoretical background based on three independent approaches (summarized in Table 1): the finite difference method, the boundary integral equation method, and radiative transfer theory (RTT). In the following subsections, scalar wave expression is used for simplicity although seismic waves are vector waves.

TABLE 1

TABLE 1. Summary of wavefield-based (ground-motion-based) methods for real-time prediction of ground motion.

Finite Difference Method

Wave propagation is expressed by the wave equation:

$\frac{1}{c{\left(\mathit{x}\right)}^2}\ddot{\mathit{u}}\left(\mathbf{x},t\right)={\nabla }^2\mathit{u}\left(\mathbf{x},t\right),(1)$

where u (x, t) is the wave amplitude at location x and at time t, c is phase velocity, ∇² is the Laplacian, and ü is the second order differential of u with respect to t (i.e., ∂²u/∂t²). This equation implies that the time-evolution of a wave’s amplitude, ü, is determined by its spatial distribution (∇²u). Therefore, future wavefields can be predicted from the spatial distribution of a known wavefield when the velocity structure, c(x), is known (Figure 1). Eq. 1 is approximated as

$\mathit{u}\left(\mathit{x},t+\Delta t\right)\approx 2\mathit{u}\left(\mathit{x},t\right)-\mathit{u}\left(\mathit{x},t-\Delta t\right)+ \Delta t^2\cdot c{\left(\mathit{x}\right)}^2\cdot {\nabla }^2\mathit{u}\left(\mathit{x},t \right).(2)$

FIGURE 1

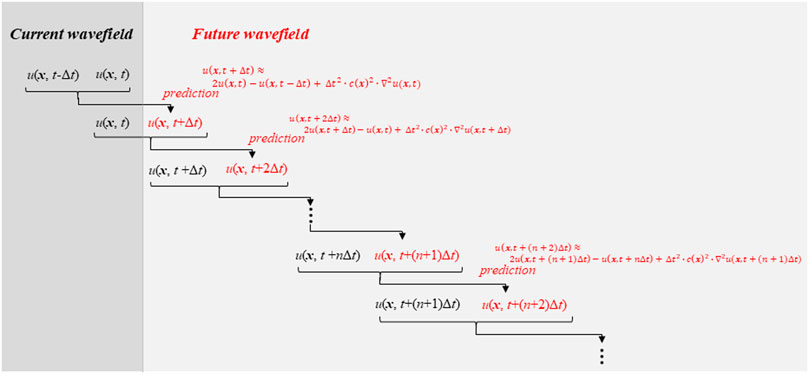
FIGURE 1. The process for predicting future wavefield using the finite difference method. From the current wavefield, u (x, t-Δt) and u (x, t), the future wavefield, u (x, t+Δt), is predicted, and then, from u (x, t) and u (x, t+Δt), u (x, t+2Δt) is forecast. Repeating this process makes it possible to obtain the wavefields at any time in the future.

The wavefield one time step Δt in the future, u (x, t+Δt), can be estimated from the current wavefield, u (x, t), and that one time step prior, u (x, t-Δt). Then, u (x, t+2Δt) is computed from u (x, t+Δt) and u (x, t) as,

$\mathit{u}\left(\mathit{x},t+2\Delta t\right)\approx 2\mathit{u}\left(\mathit{x},t+\Delta t\right)-\mathit{u}\left(\mathit{x},t\right)+ \Delta t^2\cdot c{\left(\mathit{x}\right)}^2\cdot {\nabla }^2\mathit{u}\left(\mathit{x},t+\Delta t\right) .(3)$

Thus, the wavefield at any future time can be obtained by repeating this procedure as needed. Note that this assumes that no new waves are radiated in the future, i.e., that no new earthquakes occur over the prediction period.

In this approach, precise monitoring of the spatial distribution of u (x, t) and u (x, t-Δt) is important for precise predictions. Once the detailed distribution of u (x, t) and u (x, t-Δt) are obtained, source parameters (radiation location and the strength of radiated waves, i.e., hypocenter location and magnitude) are not needed to predict the future wavefield. For precise estimation of the current wavefield, data assimilation is a powerful tool, which will be explained in a later section.

Furumura et al. (2019) and Oba et al. (2020) applied the finite difference approach to predict long-period ground motions (>3–10 s). Because they used a three-dimensional (3-D) velocity structure, they were able to predict not only the waveforms of direct P- and S-waves, but also those of reflected, refracted and surface (Rayleigh and Love) waves. At present, however, the finite difference method is not useful for computing short-period ground motions (<1 s) because the very fine mesh size required exceeds modern computing capabilities and the very precise velocity structure required to simulate wave propagation is not easily obtained by current survey techniques.

Boundary Integral Equation Method

Whereas the finite differential method represents wave propagation using differential form of the wave equation (Eq. (1)), boundary integral equation takes its integral form;

$\mathit{u}\left({\mathit{x}}_p,t\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}d\tau {\displaystyle \int \left(\mathit{u}\left({\mathit{x}}_1,\tau \right)\frac{\partial G\left({\mathit{x}}_p,t-\tau ; {\mathit{x}}_1, 0\right)}{\partial n}-G\left({\mathit{x}}_p,t-\tau ;{\mathit{x}}_1, 0\right)\frac{\partial \mathit{u}\left({\mathit{x}}_1,\tau \right)}{\partial n}\right) dS},(4)$

in 3-D space, where S is the surface enclosing the target site, x_p, x₁ is a location on S, $\partial /\partial n$ is the derivative with respect to the normal vector to S at x₁, and G is the Green’s function. S can be taken arbitrarily (Figure 2A). Here, the integrations are performed with respect to x₁ on S (i.e., the 2D integral), and with respect to the convolution integral $\tau$. Eq. 4 is valid when there are no radiations (i.e., no sources) inside S. Eq. 4 is known as the Kirchhoff-Fresnel integral in wave propagation theory. Huygens’ principle is its preliminary qualitative description, in which points on wavefront are virtual sources of secondary waves aligned along the wavefront.

FIGURE 2

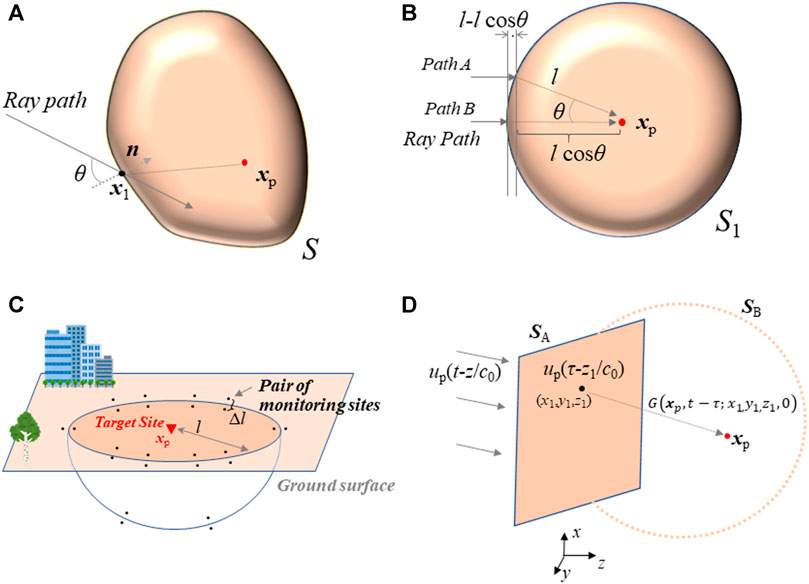
FIGURE 2. Schematic illustration of the boundary integral equation method (After Hoshiba, 2013a). The surface S can be taken arbitrarily around the target site x_p, and x₁ is a location on S, and n is the normal vector to S at x₁. Here θ is the angle of incoming ray paths from the surface normal. (B) Surface S₁ is taken around x_p as a sphere of radius l. When an incident plane wave is assumed, travel distance of path A is larger than B by l-l cos θ. (C) An example of deploying pairs of monitoring sites to predict ground motion at target site x_p. The seismometer pairs are located at radius l on the ground surface and underground. Each seismometer in each pair is spaced by Δl. (D) An example of plane wave propagation. The surface S is divided into S_A and S_B. S_A is an infinite plane normal to the z axis, and S_B is a half space of infinite radius. Incident plane wave normal to S_A is assumed.

As an example, let us take S₁ as a sphere of radius of l and centered on x_p in a homogenous velocity structure, c₀, such that |x_p-x₁| = l (Figure 2B). Because G (x_p, t; x₁, 0) = 0 when t < l/c₀, and taking travel-time into consideration, G (x_p, t + l/c₀-$\tau$ ; x₁, 0) = 0 when t + l/c₀-$\tau$ < l/c₀, i.e., when $\tau$> t, so that

$\mathit{u}\left({\mathit{x}}_p,t+l/c_0\right)=\underset{-\infty }{\overset{t}{{\displaystyle \int }}}d\tau {\displaystyle \int \left(\mathit{u}\left({\mathit{x}}_1,\tau \right)\frac{\partial G\left({\mathit{x}}_p,t+l/c_0-\tau ; {\mathit{x}}_1, 0\right)}{\partial n}- G\left({\mathit{x}}_p,t+l/c_0-\tau ;{\mathit{x}}_1, 0\right)\frac{\partial \mathit{u}\left({\mathit{x}}_1,\tau \right)}{\partial n} \right)d{S}_1}.(5)$

This means that the waveform at the target site at time l/c₀ in the future is predicted based on u (x₁, $\tau$) between the past (time -∞) and present (time t).

Green’s function in a homogeneous 3-D structure is expressed as,

$G\left({\mathit{x}}_p,t-\tau ,{\mathit{x}}_1, 0\right)=\frac{1}{4\pi |{\mathit{x}}_p-{\mathit{x}}_1|}\delta \left(t-\tau -|{\mathit{x}}_p-{\mathit{x}}_1|/c_0\right)=\frac{1}{4\pi l}\delta \left(t-\tau -l/c_0\right).(6)$

When the wavelength is much smaller than the spatial fluctuation of the absolute amplitudes of u (x_p, t) and G (x_p, t-$\tau$ ; x₁, 0), the high frequency approximation is valid, and Eq. 5 is approximated as

$\mathit{u}\left({\mathit{x}}_p,t+l/c_0\right)\approx {\displaystyle \int \frac{1}{4\pi c_{0}l}\left(\cos \theta +1\right) \dot{\mathit{u}}\left({\mathit{x}}_1, t\right) d{S}_1},(7)$

where $\theta$ (=$\theta$(x₁, t)) is the angle of incoming ray paths from the surface normal (Shearer 1999; Hoshiba 2013a). The waveform at time t + l/c₀ is the weighted sum of the time differential of waveforms at x₁ and t. This means that when $\dot{\mathit{u}}\left({\mathit{x}}_1, t\right)$ and $\theta$(x₁, t) are obtained on surface S₁, we can predict the wave motion at x_p with a lead time of l/c₀. Here, source information (hypocentral location and magnitude) is not required. For near future predictions small values of l (i.e., small S₁) are used, and for predictions of more distant future larger values of l (larger S₁) are accordingly required. When the angle of waves approaching x_p is 0°, cos $\theta$ = 1 and cos $\theta$ +1 = 2, indicating their large contribution to constitute waveforms at x_p. When the angle of waves travelling away from x_p is 180°, cos $\theta$ = -1 and cos $\theta$ +1 = 0, indicating no contribution. Thus, waves approaching x_p are important for predicting waveforms at x_p, and those traveling away from x_p are negligible. At $\theta$ = 90° (as for large-angle refractions), cos $\theta$ +1 = 1; such waves are weighted half as strongly as those of $\theta$ = 0°. However, taking wavelength into consideration, the contribution is more concentrated around $\theta$ = 0. Based on Fresnel theory, the area that mainly affects the wave motion at x_p is approximately given by the relation of “(half wavelength) ≥(Path A)-(Path B)” in Figure 2B,

$\lambda \text{/}\mathrm{2}\ge l-l\cos \theta \approx l\cdot {\theta }^2/2.(8)$

where an incident plane wave is assumed. This area is large for low-frequency waves, and small for high-frequency waves. For example, in a homogeneous velocity structure (c₀ = 3 km/s) and with l = 30 km, $\theta$ ≤0.32 rad (18°) for a 1 Hz wave, and $\theta$ ≤0.14 rad (8°) for a 5 Hz wave. Because contributions from outside this area are small, large angle refractions do not affect high-frequency waves, and the ray theory approach is valid.

Nagashima et al. (2008) and Kuyuk and Motosaka (2009) proposed a front-detection method. They tried to predict ground motion using waveforms of halfway applying empirical transfer function, which corresponds to empirically estimated Green’s function. Iervolino et al. (2007) and Iervolino (2014) proposed to deploy some observation sites on a circle whose center location is the target site, which is similar to Eqs 5, 7; this idea is essentially the basis of the boundary integral equation method. Hoshiba (2013a) explicitly introduced the boundary integral equation method for predicting future ground motion. Although it is relatively easier to take high-frequency waves in the boundary integral equation method than in the finite difference method, information on the time-dependent propagation direction ($\theta$) is required. An array technique is useful to estimate $\theta$. When pairs of seismometers are deployed as shown in Figure 2C and Eq. 5 is approximated as

$\left({\mathit{x}}_p,t+l/c_0\right)\approx \underset{-\infty }{\overset{t}{{\displaystyle \int }}}d\tau {\displaystyle \int \left(\mathit{u}\left({\mathit{x}}_1,\tau \right)\frac{G\left({\mathit{x}}_p,t+\frac{l}{c_0}-\tau ; {\mathit{x}}_1+{\mathit{n}}_1\Delta l, 0\right)-G\left({\mathit{x}}_p,t+\frac{l}{c_0}-\tau ; {\mathit{x}}_1, 0\right)}{\Delta l} - G\left({\mathit{x}}_p,t+\frac{l}{c_0}-\tau ;{\mathit{x}}_1, 0\right)\frac{\mathit{u}\left({\mathit{x}}_1+{\mathit{n}}_1\Delta l,\tau \right)-\mathit{u}\left({\mathit{x}}_1,\tau \right)}{\Delta l}\right) d{S}_1}(9)$

where n₁ is the inward-facing normal vector to S₁ at x₁, and Δl is the distance between the seismometers in each pair. Each pair simply takes the place of an array.

At this point I wish to return to Eq. 4 to review a relation between the boundary integral equation method and the source-based method. A point source at x₀ instantaneously radiating at t = t₀ of amplitude A₀ is expressed by the source A₀δ(x - x₀) δ(t - t₀). Waveforms at x₁ on the surface S are given as A₀G (x₁, t; x₀, t₀). When the source has volume V₀ and an arbitrary duration, and the source function is expressed as A (x₀, t₀), the waveforms at x₁ are described as:

$\mathit{u}\left({\mathit{x}}_1,t\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d{t}_0{\displaystyle \int G\left({\mathit{x}}_1,t;{\mathit{x}}_0, t_0\right)A\left({\mathit{x}}_0,t_0\right) d{V}_0}}.(10)$

In the source-based method, A (x₀, t₀) is first estimated from waveforms u (x₁, t) observed at multiple x₁ locations, and then the waveform at x_p is predicted as:

$\mathit{u}\left({\mathit{x}}_p,t\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d{t}_0{\displaystyle \int G\left({\mathit{x}}_p,t;{\mathit{x}}_0, t_0\right)A\left({\mathit{x}}_0,t_0\right) d{V}_0}} .(11)$

In the boundary integral equation method, the surface S is taken such that all x₁ are located on S, but the source volume V₀ is outside S. Note that surface S can be of arbitrary shape. Using Eqs. 4, 10,

$\begin{array}{l}\mathit{u}\left({\mathit{x}}_p,t\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d\tau {\displaystyle \int \left[\left({\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d{t}_0{\displaystyle \int G\left({\mathit{x}}_1,\tau ;{\mathit{x}}_0, t_0\right)A\left({\mathit{x}}_0,t_0\right) d{V}_0}}\right) \frac{\partial G\left({\mathit{x}}_p,t-\tau ; {\mathit{x}}_1, 0\right)}{\partial n}-G\left({\mathit{x}}_p,t-\tau ;{\mathit{x}}_1, 0\right)\frac{\partial }{\partial n}\left({\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d{t}_0{\displaystyle \int G\left({\mathit{x}}_1,\tau ;{\mathit{x}}_0, t_0\right)A\left({\mathit{x}}_0,t_0\right) d{V}_0}}\right)\right]}dS,}\\ ={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d{t}_0{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d\tau }{\displaystyle \int \left[{\displaystyle \int \left(G\left({\mathit{x}}_1,\tau ;{\mathit{x}}_0, t_0\right) \frac{\partial G\left({\mathit{x}}_p,t-\tau ; {\mathit{x}}_1, 0\right)}{\partial n}- G\left({\mathit{x}}_p,t- \tau ;{\mathit{x}}_1, 0\right)\frac{\partial G\left({\mathit{x}}_1,\tau ;{\mathit{x}}_0, t_0\right)}{\partial n}\right)dS}\right]}A\left({\mathit{x}}_0,t_0\right) d{V}_0,}\\ ={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}d{t}_0{\displaystyle \int G\left({\mathit{x}}_p,t;{\mathit{x}}_0, t_0\right) A\left({\mathit{x}}_0,t_0\right) d{V}_0}}\end{array}.(12)$

where

$\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}d\tau {\displaystyle \int \left(G\left({\mathit{x}}_1,\tau ; {\mathit{x}}_0, t_0\right) \frac{\partial G\left({\mathit{x}}_p,t-\tau ; {\mathit{x}}_1, 0\right)}{\partial n}- G\left({\mathit{x}}_p,t- \tau ;{\mathit{x}}_1, 0\right)\frac{\partial G\left({\mathit{x}}_1,\tau ;{\mathit{x}}_0, t_0\right)}{\partial n}\right)dS = G\left({\mathit{x}}_p,t;{\mathit{x}}_0, t_0\right)}(13)$

is used, because G (x₁, t; x₀, t₀) satisfies Eq. 4, Eq. 12 means that the boundary integral equation method bypasses the process of estimating source function, A (x₀, t₀), to predict the waveform at x_p by using observations at many x₁ locations. In the source-based method, the hypocentral distance is required to evaluate geometrical spreading attenuation (for example, the inverse of hypocentral distance for body waves). However, wave propagation physics suggests that geometrical spreading attenuation is determined by the local curvature of the wavefront: large curvatures give strong attenuation, small curvatures weak attenuation, and no curvature (e.g., plane wave) no attenuation. When the wavefield is estimated precisely and the curvature of wavefront is obtained, it is not necessary to estimate hypocentral distance to evaluate geometrical spreading attenuation.

Radiative Transfer Theory (RTT)

When the ray theory approach is valid, radiative transfer theory (RTT) is a powerful tool for representing high frequency wave propagation; scattering, attenuation and reflection are easily treated, although it is not easy to include refraction. In RTT, the propagation of energy is calculated instead of propagation of the wave itself. Many authors obtain the time history of energy, F (x, t), from the running average of the squared amplitude of the band-pass filtered waveform, u (x, t), at location x and time t (e.g., Hoshiba, 1995; Sato et al., 2012; Ogiso et al., 2018). RTT has been widely used to represent the envelope shape of high-frequency (≳1 Hz) seismic waveforms (Sato et al., 2012).

Hoshiba and Aoki (2015) applied RTT to EEW, but they considered in 2-D space. Here, I explain RTT in 3-D space. Following Hoshiba and Aoki (2015), when isotropic scattering is assumed, RTT is expressed as:

$\dot{f}\left(\mathit{x}, t:\mathit{q}\right)+c\left(\mathit{x}\right) \mathit{q}\mathit{ }\nabla f\left(\mathit{x}, t:\mathit{q}\right)=-\left(g_s\left(\mathit{x}\right)+h_s\left(\mathit{x}\right)\right)\cdot c\left(\mathit{x}\right)\cdot f\left(\mathit{x}, t:\mathit{q}\right)+\frac{c\left(\mathit{x}\right)}{4\pi }{\displaystyle \int g_s\left(\mathit{x}\right)f\left(\mathit{x}, t:\mathit{q}\mathrm{\prime }\right)d\mathit{q}\mathrm{\prime }},(14)$

where f is the energy density at location x and time t traveling in direction q (here q is the unit vector), c(x) is the velocity of seismic wave at x, and g_s(x) and h_s(x) are the strength of scattering and intrinsic absorption at x, respectively (Sato et al., 2012). Here it is assumed that scattering does not cause wave conversion (i.e., P→S or S→P). The time history of energy, F (x, t), is the sum of f (x, t: q) in all directions:

$F\left(\mathit{x},t\right)= {\displaystyle \int f\left(\mathit{x},t:\mathit{q}\right)\mathrm{d}\mathit{q}}.(15)$

Here, for simplicity, I assume that both the velocity and attenuation structures are homogeneous; thus, velocity, scattering strength, and intrinsic absorption are independent of x: c(x) = c₀, g_s(x) = g₀ and h_s(x) = h₀. Then Eq. 14 is expressed as,

$\dot{f}\left(\mathit{x}, t:\mathit{q}\right)+c_0\mathit{q}\nabla f\left(\mathit{x}, t:\mathit{q}\right)=-\left(g_0+h_0\right)c_{0}f\left(\mathit{x}, t:\mathit{q}\right)+\frac{c_0}{4\pi }{\displaystyle \int g_{0}f\left(\mathit{x}, t:\mathit{q}\mathrm{\prime }\right)d\mathit{q}\mathrm{\prime }}.(16)$

The left-hand side of Eq. 16 represents advection, the first term on the right-hand side means attenuation, and the second term represents scattering from direction q′ to q. Because the first term on the left-hand side is the differential of f with respect to time, Eq. 16 means that it is possible to predict future f provided that the current spatial and directional distributions of f are known. Eq. 16 is approximated as:

$f\left(\mathit{x}, t+\Delta t:\mathit{q}\right)\approx f\left(\mathit{x}, t:\mathit{q}\right)+\Delta t \left\{-c_0\mathit{q}\nabla f\left(\mathit{x}, t:\mathit{q}\right)-(g_0+h_0)v_{0}f\left(\mathit{x}, t:\mathit{q}\right)+\frac{c_0}{4\pi }{\displaystyle \int g_{0}f\left(\mathit{x}, t:\mathit{q}\mathrm{\prime }\right)d\mathit{q}\mathrm{\prime }} \right\}.(17)$

Repeating this process makes it possible to predict f at any future time. Note that information about the earthquake hypocenter and magnitude is not required for this prediction.

To efficiently calculate RTT simulation, a particle method based on the Monte-Carlo technique has been widely used in recent decades (e.g., Gusev and Abubakirov, 1987; Hoshiba, 1991, 1995, 1997; Yoshimoto, 2000). In this method, the propagation of wave energy is simulated by the movement of a very large number of particles. Instead of the Eulerian representation expressed in Eq. 16, I use the Lagrangian representation,

$\frac{Df\left(\mathit{x}, t:\mathit{q}\right)}{Dt}=-\left(g_0+h_0\right)c_{0}f\left(\mathit{x}, t:\mathit{q}\right)+\frac{c_0}{4\pi }{\displaystyle \int g_{0}f\left(\mathit{x}, t:\mathit{q}\mathrm{\prime }\right)d\mathit{q}\mathrm{\prime } =-g_0{c}_{0}f\left(\mathit{x}, t:\mathit{q}\right)+\frac{c_0}{4\pi }{\displaystyle \int g_{0}f\left(\mathit{x}, t:\mathit{q}\mathrm{\prime }\right)d\mathit{q}\mathrm{\prime }-h_0{c}_{0}f\left(\mathit{x}, t:\mathit{q}\right)}}.(18)$

First, let us consider the case of h₀ = 0, which means no attenuation due to absorption. The first term on the right-hand side means that the energy propagating in direction q is attenuated by scattering in proportion to f. The energy density, f, decreases exponentially as travel distance increases. The second term is the contribution of energy changing direction from q′ to q. As shown in Figure 3, this physical process is simulated by many particles through a probabilistic process (Hoshiba and Aoki, 2015). The probability that energy travels without scattering during the time interval ∆t is exp (-g₀c₀∆t), which is approximated as 1-g₀c₀∆t when g₀c₀∆t <<1. The probability that scattering occurs during this time interval is given by 1- exp (-g₀c₀∆t) ≈ g₀c₀∆t. When scattering occurs, the probability density of scattering from q′ toward q is 1/(4π) because scattering is assumed to be isotropic. These processes are simulated by using a very large number of particles.

FIGURE 3

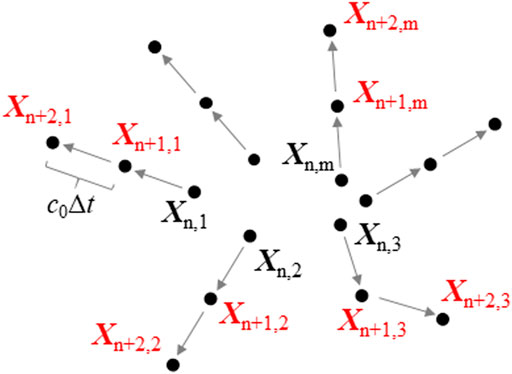
FIGURE 3. Schematic illustration of radiative transfer theory, simulated using a very large number of particles. When the propagation direction, q_m, is known, the future locations of the mth particle (X_n+1,m, X_n+2,m, … ) are easily predicted from its current location X_n,m, that is X_n+1,m = X_n,m + c₀Δtq_m and X_n+2,m = X_n,m + 2c₀Δtq_m, if scattering does not occur. If scattering occurs, the propagation direction is newly given by the probability density as shown for X_n+1,3.

Let the number of particles be M, and let X_n,m be the location of the mth particle at time, n. When traveling in direction q_m, the particle is expected to move by v₀∆tq_m over the time interval ∆t, if scattering does not occur. In contrast, if scattering occurs, the particle changes direction. Let R₁, R₂ and R₃ be independent uniform random variables between 0 and 1. When R₁ ≥ g₀v₀∆t (i.e., no scattering), the particle moves to X_n,m = X_n-1,m + c₀∆tq_m in the next time step. When R₁ < g₀c₀∆t (i.e., with scattering), the particle’s new direction is determined as q_N =(2π R₂, cos⁻¹ (1–2R₃)) and the particle is located at X_n,m = X_n-1,m + c₀∆tq_N after ∆t. At the next time step, q_m= q_N is used as the propagation direction.

The third term on the right-hand side of Eq. 18 represents attenuation due to absorption. When the mth particle has energy q_n-1,m at time n-1, the energy is attenuated as:

$q_{n,m}=q_{n-1,m}\cdot \exp \left(-h_0{c}_0\Delta t\right)\approx q_{n-1,m}\left(1-h_0{c}_0\Delta t\right)(19)$

with increasing n, where h₀v₀∆t <<1 is assumed. The energy of the particle is attenuated as the elapsed time increases regardless of scattering. In this paper, because h₀ is assumed to be homogeneous (i.e., independent of x), amount of attenuation of each particle is assumed to be the same for all m.

Hoshiba and Aoki (2015) and Ogiso et al. (2018) applied RTT to real-time predictions of the strength of seismic ground motion for EEW. They called the method “Numerical Shake Prediction,” because of its analogy to numerical weather prediction in meteorology, in which physical processes are simulated from a precise estimate of the present conditions. Because they focused on predicting seismic intensity, which is mainly determined by relatively high frequency component of waveforms, ray theory is a good approximation and RTT is applicable. They succeeded in predicting the time trace of future seismic intensities. Whereas the finite difference method is a good approach for predicting low-frequency waveforms but not high frequency waveforms, RTT is valid for high-frequency but does not necessarily hold for low-frequency because RTT is based on ray theory.

Propagation of Local Undamped Motion (PLUM) Method

For real-world application of the boundary integral equation method, a precise estimation of the wavefield distribution is required. Because quite dense observation networks are not yet available at present except few cases, it is not easy to directly apply the boundary integral equation method. Some approximations have been introduced, and the propagation of local undamped motion (PLUM) method is one of them (Kodera et al., 2018).

For plane wave propagation, let us assume the surface enclosing x_p to be an infinite plane, S_A, and half sphere of infinite radius, S_B, as shown in Figure 2D. Because S_B is located infinitely far from x_p, contribution from S_B is negligible. Plane waves propagating in the +z direction are expressed as u (x, t) = u (x, y, z, t) = u_p (t-z/c₀). Then$,$as ∂/∂n = ∂/∂z, ∂u/∂n = ∂u/∂z. The contribution from S_A is

$\mathit{u}\left({\mathit{x}}_p,t\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}d\tau \underset{-\infty }{\overset{\infty }{{\displaystyle \mathrm{\iint }}}}\left({\mathit{u}}_p\left(\tau -\frac{z_1}{c_0}\right)\frac{\partial G\left({\mathit{x}}_p,t-\tau ; x_{1, }{y}_{1, }z=z_1, 0\right)}{\partial z}-G\left({\mathit{x}}_p,t-\tau ;x_{1, }{y}_{1, }{z}_1, 0\right)\frac{\partial \mathit{u}\left(\tau -z_1/c_0\right)}{\partial z}\right) d{x}_{1}d{y}_1= {\mathit{u}}_p\left(t-\frac{\left|z_{p-}{z}_1\right|}{c_0}-\frac{z_1}{c_0}\right)=\mathit{u}\left({\mathit{x}}_1,t-\frac{\left|z_{p-}{z}_1\right|}{c_0}\right).(20)$

Here

$\underset{-\infty }{\overset{\infty }{{\displaystyle \mathrm{\iint }}}}G\left(0, 0, z_p,t-\tau ; x_{1, }{y}_{1, }{z}_1, 0\right)d{x}_{1}d{y}_1=\frac{c_0}{2}H\left(t-\tau -\frac{\left|z_p-z_1\right|}{c_0}\right)(21)$

is used, where G is given by Eq. 6 and H is the step function. This is the Green’s function in 1-D space. Eq. 20 means that plane wave propagates without attenuation:

${\left|\mathit{u}\left({\mathit{x}}_{\mathrm{p}}\mathrm{, t}\right)\right|}_{\mathrm{max t }}\mathrm{ =}{\left|\mathrm{ }\mathit{u}\left({\mathit{x}}_{\mathrm{1}}\mathrm{, t}\right)\mathrm{ }\right|}_{\mathrm{max t }},(22)$

where |·| _maxt indicates the maximum amplitude, such as PGA for accelerograms or PGV for velocity waveforms. Because plane waves form when a hypocenter is located infinitely far away, some attenuation is expected for hypocenters at finite distances,

${\left|\mathit{u}\left({\mathit{x}}_{\mathrm{p}}\mathrm{, }\mathit{t}\right)\right|}_{\mathrm{max t}}\mathrm{ }\le {\left|\mathrm{ }\mathit{u}\left({\mathit{x}}_{\mathrm{1}}\mathrm{, }\mathit{t}\right)\mathrm{ }\right|}_{\mathrm{max t}}\mathrm{ },(23)$

for waves arriving at x_p later than x₁, where PGA (or PGV) is expected to occur at x_p later than x₁. Plane waves correspond to the prediction for the most severe scenario. When several stations are available for monitoring the wavefield around the target site, the simple relation,

${\left|\mathit{u}\left({\mathit{x}}_{\mathrm{p}}\mathrm{, }\mathit{t}\right)\right|}_{\mathrm{max t}}\mathrm{ }\le Ma{x}_i{\left|\mathrm{ }\mathit{u}\left({\mathit{x}}_{\mathrm{i}}\mathrm{, }\mathit{t}\right)\mathrm{ }\right|}_{\mathrm{max t}}\mathrm{ },(24)$

may be valid, where i is the index of the monitoring site. Strictly speaking, this relation does not hold well for multiple simultaneous sources (i.e., multiple waves propagating towards x_p); nonetheless, it is an indicator of the possible strength of ground motions. Eq. 24 is the basis of the PLUM method, in which Max_i |u (x_i, t < t_c)| _maxt is the predicted strength of ground motions accounting for the site amplification (see later section for site amplification correction) and t_c is the current time. Because it assumes plane wave propagation and thus the most severe scenario, PLUM tends to overpredict ground motions. However, because the prediction is based on actual observations of ground motions, PLUM acts to reduce underpredictions and missed alarms.

Because PLUM assumes plane waves propagation, the distance between the monitoring and target sites must be much smaller than the hypocentral distance. The use of sites far from x_p as monitoring sites gives a long lead time, but is prone to overprediction. For this reason, long lead time predictions are not given by the PLUM method. In contrast, when monitoring sites around x_p are sparse, few sites are available for use in the PLUM method. Kodera et al. (2016) applied PLUM to the 2016 Kumamoto, Japan, earthquakes sequence (Mw6.2 and 7.1) and its foreshocks and aftershocks, and Kodera et al. (2018) tested PLUM using data from the 2011 Tohoku earthquake (Mw9.0) and its aftershocks, in which they used sites within 30 km of the target site, x_p, as monitoring sites, taking the stations interval within the observation network into account. Minson et al. (2020) reported a real-time application of PLUM to the 2019 Ridgecrest, California, earthquakes (Mw6.4 and 7.1). Cochran et al. (2019) and Kilb et al. (2021) applied PLUM to earthquakes in southern California and the west coast of USA, respectively. Meier et al. (2020) compared the performance of PLUM, point source algorithm and finite fault algorithm. Otake et al. (2020) investigated an approach similar to PLUM, but using machine-learning instead of the physics of wave propagation.

The PLUM method was implemented into the JMA’s operational EEW system in 2018, in addition to the point-source algorithms. Since then, PLUM has prevented underprediction caused by uncertainties in the GMPE, and sometimes issued earlier warnings than the point-source algorithm. Kodera et al. (2020) summarized its performance. For example, during the 2018 Eastern Iburi, Hokkaido, Japan, earthquake (Mw6.6, focal depth: 37 km), PLUM issued a public warning 13.35 s after the origin time, 3.1 s earlier than the point-source algorithms. For this earthquake, the GMPE significantly underpredicted PGA and PGV at near-source sites (Dhakal et al., 2019), meaning that the point-source algorithm underpredicted ground motions even when source parameters (hypocentral location and magnitude) were precisely estimated. In contrast, PLUM predicted them appropriately, reflecting the strong ground motion observed at neighboring sites.

Data Assimilation

The first step in obtaining a precise prediction using the wavefield-based method is to estimate the current wavefield. Data assimilation is a powerful technique for estimating current conditions that is widely used in numerical weather prediction, oceanography and rocket control (Kalnay, 2003; Awaji et al., 2009). Figure 4 illustrates the data assimilation procedure: the spatial distribution of the wavefield is estimated from not only actual observations but also the simulation of wave propagation based on wave propagation physics, leading to a precise estimation of the current wavefield. Therefore, data assimilation incorporates actual observations into the simulation of wave propagation. In this section, I will explain data assimilation technique, following Hoshiba and Aoki (2015).

FIGURE 4

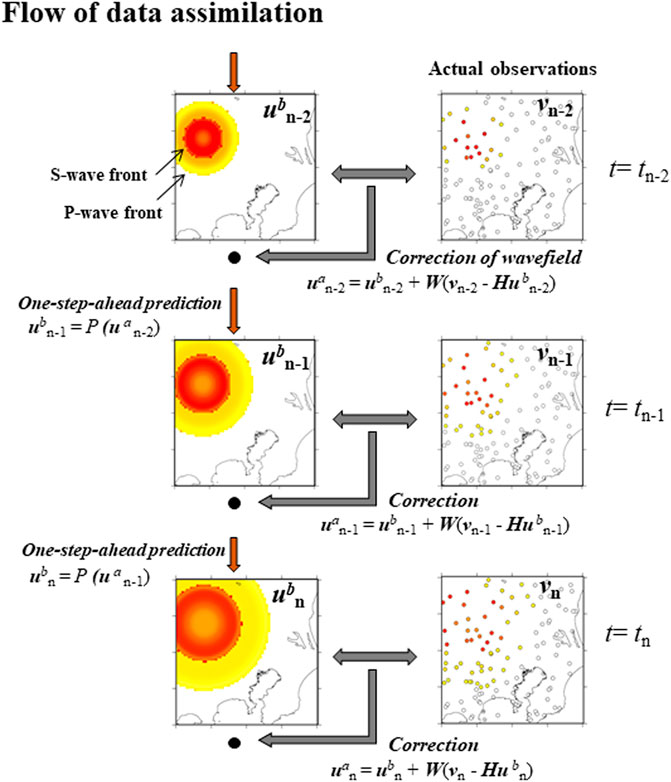
FIGURE 4. The flow of the data assimilation process. One-step-ahead prediction, u^b_n = P (u^a_n-1), is combined with actual observations, v_n, to correct the estimation of the current wavefield (after Hoshiba and Aoki, 2015). By repeating this process, the current wavefield, u^a_n, is estimated by using not only the current observation (v_n), but also all past observations (v_n-1, v_n-2, v_n-3, … ).

Let u_n indicate the wavefield in the model space at time t_n = nΔt, in which u_n = [u (x, nΔt), u (x (n-1)Δt) ] in the finite difference method, or u_n = [f (x, nΔt: q) ] in RTT. When the 3-D space is discretized as 0 to L_xΔx, 0 to L_yΔy and 0 to L_zΔz, the number of elements of u_n is I = 2·L_xL_y·L_z in the finite difference method, and when the azimuth is discretized as 0 to L_qΔq, the number is I = L_xL_y·L_zL_q in RTT. When u_n-1 is given, we can predict u_n by simulating the propagation of the wave; this prediction one time-step-ahead is expressed as u_n = P (u_n-1), where P is the operation of Eq. 2 or Eq. 17. To discriminate between u_n before and after being combined with the actual observations, the wavefields before and after are denoted u^b_n and u^a_n. P is applied to the wavefield after the combination at one time step before, i.e., t_n-1; thus, the one step-ahead prediction is expressed as:

${\mathit{u}}_n^b=P\left({\mathit{u}}_{n-1}^a\right).(25)$

Let v_n = (v_n1, v_n2, v_n3, … v_nj, … v_nJ)^T be the actual observation in observational space at time t_n, in which v_nj means the observed data at the jth element. Let the total number of observation elements be J. Usually I (the number of grids in model space) is much larger than J (number of observation elements). Data assimilation is expresses as

${\mathit{u}}_n^a={\mathit{u}}_n^b+\mathit{W}\left({\mathit{v}}_{\mathit{n}}-\mathit{H}{\mathit{u}}_n^b\right)(26)$

Here H is the J×I matrix called the observation matrix and it means the interpolation of grid points onto the location of the observation point, and then (v_n - Hu^b_n) is the difference between the one-step-ahead prediction and the actual observation at time t_n. W is the I×J matrix called weight matrix, and W (v_n - Hu^b_n) indicates the correction of the one-step-ahead prediction in the simulation of wave propagation. From u_n^a, u_n+1^b is obtained from Eq. 25. Iterative application of Eqs 25, 26 produces time-evolutional estimation of wavefield. The process of the left side in Figure 4 indicates repeated application of one-step-ahead prediction, that is, the simulation of wave propagation. In the data assimilation technique, actual observations are included in the simulation to correct the wavefield at each time step; that is, actual data are assimilated in the simulation process.

The parameter setting of W is important in data assimilation, and several techniques have been proposed. The simplest is the optimal interpolation method, in which W is constant irrespective of time n, though in the Kalman filter method it changes with increasing n. In the optimal interpolation method, Matrix W is expressed in relation to the errors in the one-step-ahead prediction (background error, σ_b), and in the observations (observational error, σ_o). When the correlation distance of the background error and the ratio σ_o/σ_b are assumed, matrix W is obtained (for detail, see Awaji et al., 2009; Kalnay, 2003; Hoshiba and Aoki, 2015).

When the correlation distance is large, the W (v_n - Hu^b_n) correction is applied to a wide area around each observation point, and when the distance is small, the correction is restricted to a small area around each observation point. The density of observation network, therefore, may influence the parameter setting of the correlation distance: large distance for sparse network and small distance for dense network. For sparse network, observation of each site needs to represent wavefield of wide area around the site, but small area for dense network. In general, dense network can reconstruct the complicated wavefield in data assimilation better than sparse network. When too large correlation distance is used, seismic wave propagates artificially faster than actual velocity in the process of W (v_n - Hu^b_n) correction, which reduces the accuracy of arrival time of strong shaking. The correlation distance at each observation point can be varied according to the network distribution: for example, small correlation distances where station interval is small around the site, and large correlation distances where station interval is large.

When the observational errors are assumed to be much larger than the background errors, σ_o/σ_b >>1, W≈0 and then u_n^a ≈ u_n^b. Iterative application of Eqs 25, 26, therefore, results in just the simulation of wave propagation, because the observation have no effect. In contrast, σ_o/σ_b ≈ 0 corresponds to the case where the contours of the actual observations are drawn independently at each time step, because the one-step-ahead prediction has little effect in Eq. 26. The ratio, σ_o/σ_b, at each observation point also can be varied according to quality condition. For example, large σ_o/σ_b for noisy stations in urban areas and small σ_o/σ_b for quiet stations in mountain areas.

Although the wavefield is observable at the ground surface when stations are densely deployed at the surface (i.e., 2-D space), the underground wavefield at depths of more than a few kilometers cannot be observed because many borehole observations deeper than a few kilometers are not realistic. Because actual seismic wavefields are expressed in 3-D space, assumptions are required to apply data assimilation to estimate the 3-D wavefield. Handling the difference between the 2- and 3-D spaces is an important subject for future advancement of the data assimilation technique.

Prediction

Once the present wavefield, u_n^a, has been estimated precisely by the data assimilation technique, the future wavefield, u^P, is predicted from the current wavefield, u^a_n,

${\mathit{u}}_{n+1}^P=P\left({\mathit{u}}_n^a\right)(27)$

and u^P_n+2 is forecast from u^P_n+1, that is u^P_n+2 = P (u^P_n+1) = P² (u^a_n). Repeating this process

${\mathit{u}}_{n+\mathrm{k}}^P=P\left({\mathit{u}}_{n+k-1}^P\right)=P^2\left({\mathit{u}}_{n+k-2}^P\right)=\dots =P^{k-1}\left({\mathit{u}}_{n+1}^P\right)=P^k\left({\mathit{u}}_n^a\right).(28)$

Future wavefield at any time can be predicted from the current wavefield.

Real-Time Correction of the Site Amplification Factor

Site amplification is an important factor to determine seismic-wave amplitude in addition to source and propagation factors, and it depends on frequency. In application of the wavefield-based method, the frequency-dependent site amplification should be removed from the observed amplitude when simulating wave propagation described in the previous section, and then include it to evaluate waveforms at target sites, especially those characterized by large amplification factors. Many previous studies have investigated frequency-dependent site amplification in the frequency domain by assuming a model,

$O_{kl}\left(f\right)=S_k\left(f\right)T_{kl}\left(f\right)A_l\left(f\right),(29)$

where O_kl(f), S_k(f), T_kl(f), and A_l(f) represent the observed seismic wave spectrum from event k at site l, the source spectrum characterizing event k, the propagation factor between event k and site l, and the site amplification factor at site l, respectively, and f is the frequency of the seismic waves. When borehole is available at the site, fine vertical structures of velocity and attenuation can be obtained, and A_l(f) is estimated theoretically. However, borehole observation at all sites is not realistic at present. Instead of the theoretical approach, many empirical approaches have been proposed to obtain the relative site amplification factors, {A₂(f)/A₁(f)}: spectral ratio (e.g., Ikeura and Kato, 2011); spectrum inversion of source, propagation, and site factors (e.g., Iwata and Irikura, 1988; Kato et al., 1992); coda normalization method (e.g., Phillips and Aki, 1986), and others. These approaches usually neglect phase characteristics, focusing on amplitude characteristics, |A₂(f)/A₁(f)|. For example, in the spectral ratio method, when sites 1 and 2 are adjacent, compared to the hypocentral distance, |T_k2(f)| ≈|T_k1(f)| is assumed, then

$\left|\frac{O_{k2}\left(f\right)}{O_{k1}\left(f\right)}\right|=\left|\frac{S_k\left(f\right)}{S_k\left(f\right)}\right|\cdot \left|\frac{T_{k2}\left(f\right)}{T_{k1}\left(f\right)}\right|\cdot \left|\frac{A_2\left(f\right)}{A_1\left(f\right)}\right|\approx \left|\frac{A_2\left(f\right)}{A_1\left(f\right)}\right|\cdot (30)$

The relative site amplification factor, |A₂(f)/A₁(f)|, can be estimated from spectral ratio of observed waveforms, |O_k2(f)/O_k1(f)|. When the site amplification factor at site 1 relative to site 1’ (different location from site 1) is known, that is |A₁(f)/A_1’(f)|, it is easy to estimate the amplification factor at site 2 relative to site 1′ from |A₂(f)/A_1’(f)| = |A₁(f)/A_1’(f)|·|A₂(f)/A₁(f)|. By repeating the process, it is possible to estimate relative site amplification factor even when the two sites are not adjacent. Here, |A₂(f)/A₁(f)| (and |A₂(f)/A_1’(f)|) is used to correct the difference of site-amplification condition.

In EEW, it is preferable to correct the frequency-dependent site amplification factor in real time. As |A₂(f)/A₁(f)| is expressed in the frequency domain, it may be possible to apply a fast Fourie transform (FFT) with a short time interval (i.e., every 1 s or less) to ongoing waveforms at site 1, multiply them by |A₂(f)/A₁(f)|, and then perform an inverse FFT to predict ongoing waveforms at site 2 (Figure 5). Instead of methods in the frequency domain, a method in the time domain was proposed (Hoshiba, 2013b; Pilz and Parolai, 2016), in which a causal recursive filter, which allows correction of site amplification factors in real time, is used. The time domain filter alleviates computational workload of the system, comparing with that of the frequency domain analysis, and makes it easy to estimate continuously site-corrected waveforms regardless of whether earthquakes are occurring or not. Trigger is not required in the continuous operation, which minimizes the fluctuation of the workload.

FIGURE 5

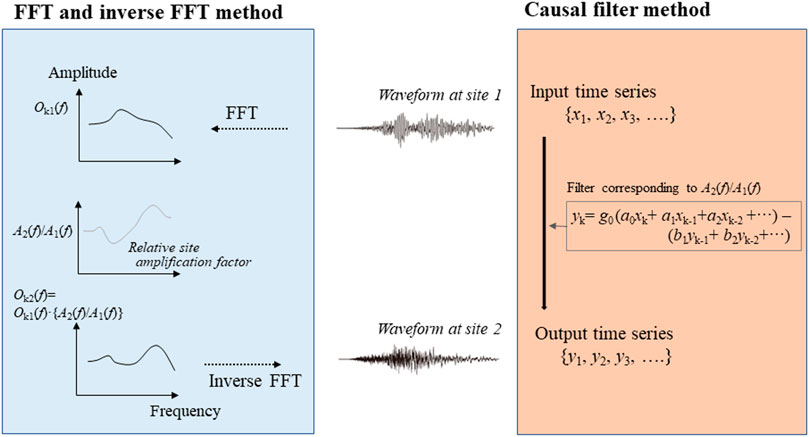
FIGURE 5. Comparison of the causal filter method with the FFT (and inverse FFT) method. In the FFT method, the frequency-dependent site amplification factor is corrected in the frequency domain. In the causal filter method, it is done in the time domain.

Hoshiba (2013b) proposed to model the frequency dependent site amplification using the form:

$F\left(s\right)=G_0{\displaystyle \prod _{n=1}^N\left(\frac{{\omega }_{2n}}{{\omega }_{1n}}\right)\cdot \frac{s+{\omega }_{1n}}{s+{\omega }_{2n}}}\cdot {\displaystyle \prod _{m=1}^M{\left(\frac{{\omega }_{2m}}{{\omega }_{1m}}\right)}^2\cdot \frac{s^2+2h_{1m}{\omega }_{1m}s+{\omega }_{1m}^2}{s^2+2h_{2m}{\omega }_{2m}s+{\omega }_{2m}^2}},(31)$

where N and M are the numbers of the first- and second-order filters, respectively, and s = i (2πf). Here ω_1n, ω_2n, ω_1m, and ω_2m are the angular frequencies and h_1m and h_2m are the damping factors that characterize the frequency dependence, respectively. Note that s²+2hω_ms +ω_m² represents a damping oscillation. Parameter ω_1n, ω_2n, ω_1m, ω_2m, h_1m and h_2m are positive numbers, and are estimated to satisfy |A₂(f)/A₁(f)|≈|F(s)|.

The filter is modeled as Eq. 31, where F(s) is represented by combination of first and second orders of s,

$F_{1n}\left(s\right)=\left(\frac{{\omega }_{2n}}{{\omega }_{1n}}\right)\cdot \frac{s+{\omega }_{1n}}{s+{\omega }_{2n}},F_{2m}\left(s\right)={\left(\frac{{\omega }_{2m}}{{\omega }_{1m}}\right)}^2\cdot \frac{s^2+2h_1{\omega }_{1m}s+{\omega }_{1m}^2}{s^2+2h_2{\omega }_{2m}s+{\omega }_{2m}^2}(32)$

By a mapping procedure called the bilinear transform,

$s=\frac{2}{\Delta T}\cdot \frac{1-z^{-1}}{1+z^{-1}},(33)$

and pre-warping for ω_1n, ω_2n, ω_1m, and ω_2m of the digital filtering technique,

$\omega \to \frac{2}{\Delta T}tan\left(\frac{\omega \Delta T}{2}\right),(34)$

the transfer function, F(z), is obtained (Scherbaum, 1996) in a form of infinite impulse response (IIR) filter, where ∆T is the sampling interval of the digital waveforms and z = exp (s∆T):

$F_{1n}\left(z\right)=g_0\cdot \frac{a_0+a_1{z}^{-1}}{1+b_1{z}^{-1}},F_{2m}\left(z\right)=g_0\cdot \frac{a_0+a_1{z}^{-1}+a_2{z}^{-2}}{1+b_1{z}^{-1}+b_2{z}^{-2}}.(35)$

The recursive filters are given by y_k = g₀ (a₀x_k + a₁x_k-1)-b₁y_k-1 for F_1n(z), and by y_k = g₀ (a₀x_k + a₁x_k-1+a₂x_k-2) - (b₁y_k-1+ b₂y_k-2) for F_2m(z), where x_k and y_k are the input and output of the time series of the digitized waveform, respectively.

Applying Eqs 33, 34, g_0,a₀, a_1, and b₁ for F_1n(z) are,

$\begin{array}{l}{g}_0=\frac{tan\left(\frac{{\omega }_{2n}\Delta T}{2}\right)}{tan\left(\frac{{\omega }_{1n}\Delta T}{2}\right)}\cdot \frac{1}{1+tan\left(\frac{{\omega }_2\Delta T}{2}\right)},a_0=1+tan\left(\frac{{\omega }_{1n}\Delta T}{2}\right),\\ a_1=tan\left(\frac{{\omega }_{1n}\Delta T}{2}\right)-1,b_1=\frac{tan\left(\frac{{\omega }_{2n}\Delta T}{2}\right)-1}{1+tan\left(\frac{{\omega }_{2n}\Delta T}{2}\right)}\end{array}(36)$

and, g_0,a₀, a_1,a_2,b₁, and b₂ for F_2m(z) are,

$\begin{array}{l}{g}_0={\left\{\frac{tan\left(\frac{{\omega }_{2m}\Delta T}{2}\right)}{tan\left(\frac{{\omega }_{1m}\Delta T}{2}\right)}\right\}}^2\cdot \frac{1}{1+2h_2 \tan \left(\frac{{\omega }_{2m}\Delta T}{2}\right)+ta{n}^2\left(\frac{{\omega }_{2m}\Delta T}{2}\right)},\\ a_0=1+2 h_1 tan\left(\frac{{\omega }_{1m}\Delta T}{2}\right)+ta{n}^2\left(\frac{{\omega }_{1m}\Delta T}{2}\right),a_1=2 {\mathit{tan}}^2\left(\frac{{\omega }_{1m}\Delta T}{2}\right)-2,\\ a_2=1-2h_1 \mathit{tan}\left(\frac{{\omega }_{1m}\Delta T}{2}\right)+ta{n}^2\left(\frac{{\omega }_{1m}\Delta T}{2}\right),\\ b_1=\frac{2{\mathit{tan}}^2\left(\frac{{\omega }_{2m}\Delta T}{2}\right)-2}{1+2 h_2 tan\left(\frac{{\omega }_{2m}\Delta T}{2}\right)+ta{n}^2\left(\frac{{\omega }_{2m}\Delta T}{2}\right)},\\ b_2=\frac{1-2h_2 \mathit{tan}\left(\frac{{\omega }_{2m}\Delta T}{2}\right)+{\tan }^2\left(\frac{{\omega }_{2m}\Delta T}{2}\right)}{1+2h_2 \mathit{tan}\left(\frac{{\omega }_{2m}\Delta T}{2}\right)+ta{n}^2\left(\frac{{\omega }_{2m}\Delta T}{2}\right)}.\end{array}(37)$

The causal filter, F(z), makes it possible to correct the relative site amplification factor in real time in the time domain. Ogiso et al. (2016) evaluated the relative site amplification factors of more than 2,200 stations in Japan and obtained their IIR filters, and Xie et al. (2019) also applied this technique. Pilz and Parolai (2016) extended this method to include phase characteristics.

In many researches of site amplification factors to estimate |A₂(f)/A₁(f)|, hard rock site is chosen for site 1 as a reference site. However, site 1 is not necessarily hard rock site here, because the purpose of the site factor correction is to make virtually the site conditions common to isolate seismic wave propagation. For the boundary equation method, for example, x₁ and x_p corresponds to site 1 and site 2, respectively. Many locations are assumed for site 1 (x₁), but site 2 (x_p) is single location. By applying F(z) to waveforms obtained at site 1, the waveforms are virtually converted to those having the site amplification of site 2. The integrals in Eqs 5, 7, 9 are carried out for waveforms of the common site amplification. In finite difference method and RTT, future wavefields are predicted by using the site-factor corrected waveforms. For prediction of amplitude at each location, it is necessary to convert inversely the waveforms to those having the site amplification factor at the individual location. For the inverse process, that is application of |A₁(f)/A₂(f)|, F⁻¹(s) can be used. Because denominator and numerator are the same order of s (Eq. 31), and h_1m and h_2m are positive numbers, both forward, F(s), and inverse, F⁻¹(s), filters are stable, where all poles and all zeros are distributed in the left half space in the s-plane (Scherbaum, 1996).

For the PLUM method (Eq. 24), the IIR filter F_pi(z) can be applied, which represents site amplification at the target site p relative to site i. Applying F_pi(z) to u (x_i, t) to obtain the corrected waveforms, u_c (x_i, t), and then

${\left|\mathit{u}\left(x_p,t\right)\right|}_{\max t}\le Ma{x}_i{\left|u_c\left(x_i,t\right)\right|}_{\max t},(38)$

can be used instead of Eq. 24. For the boundary integral equation method,

$\mathit{u}\left({\mathit{x}}_p,t\right)={\displaystyle {\int }_{-\infty }^{\infty }d\tau {\displaystyle \int \left({\mathit{u}}_c\left({\mathit{x}}_1,\tau \right)\frac{\partial G\left({\mathit{x}}_p,t-\tau ; {\mathit{x}}_1, 0\right)}{\partial n}-G\left({\mathit{x}}_p,t-\tau ;{\mathit{x}}_1, 0\right)\frac{\partial {\mathit{u}}_c\left({\mathit{x}}_1,\tau \right)}{\partial n}\right) dS}},(39)$

can be applied instead of Eq. 4.

Example of Application

Here, I provide an example of a real-time prediction by the wavefield-based approach.

Figure 6 shows the case of a Mw6.4 earthquake, the largest aftershock of the Mw6.7 Chuetsu, Niigata, Japan, earthquake (October 23, 2004) using radiative transfer theory. Small dots in the panels indicate the locations of observation points (many stations for site 1 in Eq. 30). Site amplification factors are corrected relative to that of the target site, Ohtemachi, Tokyo; i.e., Tokyo is the site 2. The distribution of observation of strong ground motions was complicated, differing from the concentric circles predicted by the source-based method. For example, relatively strong shaking was observed in Kanto, but weak shaking was observed in Tokai. Especially strong shaking was observed towards Tokyo. At t = 11s, strong ground motions were observed around the focal region, and the prediction from the observation indicates that the strong ground motion propagates like an expanding circle, with a final distribution similar to that predicted for a M7.0 event. At t = 50s, strong ground motions were observed toward Tokyo, and the prediction shows that the strong ground motion arrives at Tokyo 10 s later. The final eventual distribution is predicted to be the almost the same as the actual observation.

FIGURE 6

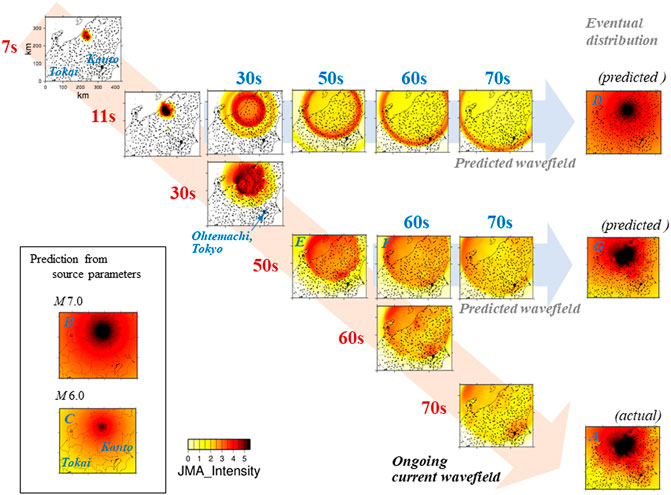
FIGURE 6. An example application of the wavefield based method using a Mw6.4 earthquake (the largest aftershock of the Mw6.7 Chuetsu, Niigata, Japan earthquake; October 23, 2004). Data from K-NET and KiK-net of the National Research Institute for Earth Science and Disaster Prevention (NIED) were used. The locations of observation points are shown by small dots. The actual eventual distribution of ground motion was complicated (A) relatively strong ground motion was observed at Kanto, and weak one at Tokai. This complicated distribution is not reproduced by the source-based method, as shown in (B,C) using M7.0 and M6.0, respectively. In the wavefield-based method, the predicted eventual distribution from the observation at t = 11s (D) is similar to the prediction using a M7.0 event (B). At t = 50s, strong ground motions were observed to be propagating toward Tokyo (E), and the updated prediction indicates the arrival of the strong ground motions at Tokyo at t = 60s (F) The predicted eventual distribution from t = 50s (G) reproduces well the actual distribution (A).

Prediction of distant future is normally less precise than that of near future. As shown in Figure 6, predicted wavefield at 70 s from 11 s does not forecast well the actual wavefield, but that from 50 s predicts it better. For improvement of distant-future prediction, introduction of velocity and attenuation structures is a key. Ogiso et al. (2018) introduced heterogeneous structures in the calculation of the radiative transfer theory. They estimated g_s(x) and h_s(x) at first, and then used Eq. 14 instead of Eq. 16 in the prediction. Estimation of detail velocity and attenuation structures contributes to the precise prediction, especially that of distant future.

Hoshiba and Aoki (2015) applied the technique to data of the 2011 Tohoku earthquake (Mw9.0) and the 2004 Chuetsu, Niigata, earthquake (mainshock, Mw6.7), and Ogiso et al. (2018) did it to data of the 2016 Kumamoto earthquake (Mw7.1) incorporating the heterogeneous attenuation structure. Wang et al. (2017a, b) also used the technique for real-time prediction of ground shaking. Furumura et al. (2019) and Oba et al. (2020) used the finite difference approach to predict long period ground motions (>3–10 s) for the 2007 Off Niigata earthquake (Mw6.6) and the 2004 Off Kii Peninsula earthquake (Mw7.4), respectively.

Summary

One of important key elements of EEW is the real-time prediction of ground motion, as well as the rapid transmission of monitored data and the wide dissemination of warnings. Because seismic motion is a wave propagation phenomenon, the physics of wave propagation, which have been well studied in many research fields, is the basis of real-time prediction of ground motion. In history of EEW research, in the source-based method many authors have focused on rapidly estimating source parameters (e.g., source location, magnitude, source extent), from which peak ground motions (PGA, PGV or seismic intensity) are estimated using a GMPE. Although GMPEs usually indicates empirical relations between the peak ground motion and the source parameters, they do not express the physics of wave propagation in detail; notably, the causality of the occurrence of peak ground motions is not included in it. In the near fault region, PGA and PGV occur before rupture completion, that is, before estimation of eventual magnitude, which essentially leads to late EEWs (Hoshiba, 2020). GMPEs are mainly aimed at explaining the peak ground motion of anticipated future earthquakes (or of past events at locations where seismometers were not deployed). Thus, GMPEs are not necessarily constructed for the purpose of real-time prediction, such as EEW. Instead of borrowing GMPEs, new technique based on the physics of wave propagation for the purpose of the real-time prediction of ground motion is a key to more precise and timely warning. The wavefield-based method described in this review follows this strategy.

To conclude, I compare the wavefield-based (ground-motion-based) method with the conventional method based on source parameters (Figure 7) (Hoshiba and Aoki, 2015). In the source-based method, using monitored data from past to present we look back to the “oldest past situation”. Not only is the future situation predicted, the past situation is post-dicted from the “oldest past situation”. The time needed for estimation of the source parameters can be regarded as blind time with respect to EEW. In contrast, all data up to the present are used in the wavefield-based method to estimate the “present situation” of wave propagation. Post-diction is not performed in the process.

FIGURE 7

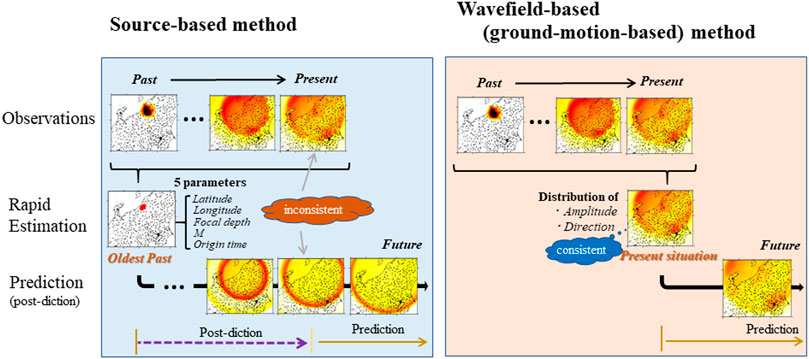
FIGURE 7. Comparison of the wavefield-based (ground-motion-based) method and the source-based method. This figure and comparison of the two methods are presented in detail in the Summary. In the source-based method, we look back to the “oldest past situation” to represent it by five parameters, and then expand again to reconstruct the spatial distribution from the oldest past situation. In the wavefield-based method, all data up to the present are used to estimate “present situation,” and then we predict future spatial distribution from the present situation.

In the source-based method, information about the very complicated space-time distribution of ground motion is first compressed in order to represent it with a limited number of parameters (such as latitude, longitude, focal depth, origin time, and M), and then it is expanded again to predict ground motion. It is difficult to completely reconstruct the spatial distribution of ground motion even for the present situation: inevitably there are discrepancies between the predicted present situation and the actual present observation. As a result, even if estimation of the source parameters is precise, the prediction of ground motion is not necessarily precise. In contrast, in the wavefield-based method the actual present observation is reflected as much as possible in the estimate of the present situation. Discrepancies are minimized between the estimated present situation and the actual present observation before proceeding to the prediction.

Author Contributions

MH designed the study, performed analyses, and drafted the article.

Funding

This research was partially supported by the JSPS KAKENHI Grant Number 17H0264.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

I appreciate reviewers’ careful reading of the article and constructive comments. Waveform data from K–NET and KiK-net (NIED) are used. I thank NIED for their efforts. Discussions with M. Ogiso, Y. Kodera, S. Aoki, N. and Hayashimoto were useful in this research. M. Kamachi, Y. Fujii, N. Usui, and T. Toyoda helped me to learn data assimilation technique. Figures are produced using Generic Mapping Tools (Wessel and Smith, 1995). Any opinions, findings and conclusions described in this paper are solely those of the author and do not necessarily reflect the view of JMA.

References

Awaji, T., Kamachi, M., Ikeda, M., and Ishikawa, Y. (2009). Data Assimilation: Innovation Combining Observation and Model (In Japanese), pp284. Kyoto: Kyoto University Press.

Böse, M., Smith, D. E., Felizardo, C., Meier, M.-A., Heaton, T. H., and Clinton, J. F. (2018). FinDer v.2: Improved Real-Time Ground-Motion Predictions for M2-M9 With Seismic Finite-Source Characterization. Geophys. J. Int. 212, 725–742. doi:10.1093/gji/ggx430

CrossRef Full Text | Google Scholar

Chen, D. Y., Hsiao, N. C., and Wu, Y. M. (2015). The Earthworm Based Earthquake Alarm Reporting System in Taiwan. Bull. Seismological Soc. America. 105, 568–579. doi:10.1785/0120140147

CrossRef Full Text | Google Scholar

Cochran, E. S., Bunn, J., Minson, S. E., Baltay, A. S., Kilb, D. L., Kodera, Y., et al. (2019). Event Detection Performance of the PLUM Earthquake Early Warning Algorithm in Southern California. Bull. Seismol. Soc. Am. 109, 1524–1541. doi:10.1785/0120180326

CrossRef Full Text | Google Scholar

Cochran, E. S., Kohler, M. D., Given, D. D., Guiwits, S., Andrews, J., Meier, M. A., et al. (2018). Earthquake Early Warning ShakeAlert System: Testing and Certification Platform. Seismol. Res. Lett. 89, 108–117. doi:10.1785/0220170138

CrossRef Full Text | Google Scholar

Cuéllar, A., Espinosa-Aranda, J. M., Suárez, R., Ibarrola, G., Uribe, A., Rodríguez, F. H., et al. (2014). The Mexican Seismic Alert System (SASMEX): Its Alert Signals, Broadcast Results and Performance During the M 7.4 Punta Maldonado Earthquake of March 20th, 2012, 2012, in Early Warning for Geological Disasters. Berlin, Germany: Springer, 71–87. doi:10.1007/978-3-642-12233-0_4

CrossRef Full Text

Dhakal, Y. P., Kunugi, T., Kimura, T., Suzuki, W., and Aoi, S. (2019). Peak Ground Motions and Characteristics of Nonlinear Site Response During the 2018 Mw 6.6 Hokkaido Eastern Iburi Earthquake. Earth Planets Space. 71, 56. doi:10.1186/s40623-019-1038-2

CrossRef Full Text | Google Scholar

Furumura, T., Maeda, T., and Oba, A. (2019). Early Forecast of Long‐Period Ground Motions via Data Assimilation of Observed Ground Motions and Wave Propagation Simulations. Geophys. Res. Lett. 46, 138–147. doi:10.1029/2018GL081163

CrossRef Full Text | Google Scholar

Gusev, A. A., and Abubakirov, I. R. (1987). Monte-Carlo Simulation of Record Envelope of a Near Earthquake. Phys. Earth Planet. Interiors. 49, 30–36. doi:10.1016/0031-9201(87)90130-0

CrossRef Full Text | Google Scholar

Hoshiba, M., and Aoki, S. (2015). Numerical Shake Prediction for Earthquake Early Warning: Data Assimilation, Real‐Time Shake Mapping, and Simulation of Wave Propagation. Bull. Seismological Soc. America. 105, 1324–1338. doi:10.1785/0120140280

CrossRef Full Text | Google Scholar

Hoshiba, M. (1995). Estimation of Nonisotropic Scattering in Western Japan Using Coda Wave Envelopes: Application of a Multiple Nonisotropic Scattering Model. J. Geophys. Res. 100, 645–657. doi:10.1029/94jb02064

CrossRef Full Text | Google Scholar

Hoshiba, M., Kamigaichi, O., Saito, M., Tsukada, S. Y., and Hamada, N. (2008). Earthquake Early Warning Starts Nationwide in Japan. Eos Trans. AGU. 89, 73–74. doi:10.1029/2008EO080001

CrossRef Full Text | Google Scholar

Hoshiba, M. (1997). Seismic Coda Wave Envelope in Depth-Dependent S Wave Velocity Structure. Phys. Earth Planet. Interiors. 104, 15–22. doi:10.1016/s0031-9201(97)00055-1

CrossRef Full Text | Google Scholar

Hoshiba, M. (1991). Simulation of Multiple-Scattered Coda Wave Excitation Based on the Energy Conservation Law. Phys. Earth Planet. Interiors. 67, 123–136. doi:10.1016/0031-9201(91)90066-q

CrossRef Full Text | Google Scholar

Hoshiba, M. (2013a). Real-Time Prediction of Ground Motion by Kirchhoff-Fresnel Boundary Integral Equation Method: Extended Front Detection Method for Earthquake Early Warning. J. Geophys. Res. Solid Earth. 118, 1038–1050. doi:10.1002/jgrb.50119

CrossRef Full Text | Google Scholar

Hoshiba, M. (2013b). Real-Time Correction of Frequency-Dependent Site Amplification Factors for Application to Earthquake Early Warning. Bull. Seismological Soc. America. 103, 3179–3188. doi:10.1785/0120130060

CrossRef Full Text | Google Scholar

Hoshiba, M. (2014). “Review of the Nationwide Earthquake Early Warning in Japan During its First Five Years,” in Earthquake Hazard, Risk, and Disasters. Editor M. Wyss (Elsevier), 505–529. doi:10.1016/b978-0-12-394848-9.00019-5

CrossRef Full Text | Google Scholar

Hoshiba, M. (2020). Too-Late Warnings by Estimating Mw: Earthquake Early Warning in the Near-Fault Region. Bull. Seismol. Soc. Am. 110, 1276–1288. doi:10.1785/0120190306

CrossRef Full Text | Google Scholar

Iervolino, I. (2014). “Engineering Earthquake Early Warning via Regional Networks,” in Early Warning for Geological Disasters—Scientific Methods and Current Practice. Editors J. Zschau, and F. Wenzel (Berlin, Heidelberg, New York: Springer), 333–351. doi:10.1007/978-3-642-12233-0_17

CrossRef Full Text | Google Scholar

Iervolino, I., Manfredi, G., and Cosenza, E. (2007). “Earthquake Early Warning and Engineering Application Prospects,” in Earthquake Early Warning Systems. Editors P. Gasparini, G. Manfredi, and J. Zschau (Berlin, Heidelberg: Springer), 233–247. doi:10.1007/978-3-540-72241-0_12

CrossRef Full Text | Google Scholar

Ikeura, T., and Kato, K. (2011). Evaluation of Relative Site Amplification Factors by Combining Average Spectral Ratios of Strong Ground Motions Simultaneously Observed at Adjacent Two Sites. J. JAEE. 11, 48–67. (in Japanese with English abstract). doi:10.5610/jaee.11.4_48

CrossRef Full Text | Google Scholar

Iwata, T., and Irikura, K. (1988). Source Parameters of the 1983 Japan Sea Earthquake Sequence. J,Phys,Earth. 36, 155–184. doi:10.4294/jpe1952.36.155

CrossRef Full Text | Google Scholar

Kalnay, E. (2003). Atmospheric Modeling, Data Assimilation and Predictability. New York, NY: Cambridge University Press, pp341.

Kato, K., Takemura, M., Ikeura, T., Urao, K., and Uetake, T. (1992). Preliminary Analysis for Evaluation of Local Site Effects From Strong Motion Spectra by an Inversion Method. J,Phys,Earth. 40, 175–191. doi:10.4294/jpe1952.40.175

CrossRef Full Text | Google Scholar

Kilb, D., Bunn, J., Saunders, J., Cochran, E., Minson, S., Baltay, A., et al. (2021). The PLUM Earthquake Early Warning Algorithm: A Retrospective Case Study of West Coast, USA, Data. J. Geophys. Res. Solid Earth. 126. doi:10.1029/2020jb021053

CrossRef Full Text | Google Scholar

Kodera, Y., Hayashimoto, N., Moriwaki, K., Noguchi, K., Saito, J., Akutagawa, J., et al. (2020). First-Year Performance of a Nationwide Earthquake Early Warning System Using a Wavefield-Based Ground-Motion Prediction Algorithm in Japan. Seismol. Res. Lett. 91, 826–834. doi:10.1785/0220190263

CrossRef Full Text | Google Scholar

Kodera, Y., Saitou, J., Hayashimoto, N., Adachi, S., Saitou, J., Hayashimoto, N., et al. (2016). Earthquake Early Warning for the 2016 Kumamoto Earthquake: Performance Evaluation of the Current System and the Next-Generation Methods of the Japan Meteorological Agency. Earth Planets Space. 68, 202. doi:10.1186/s40623-016-0567-1

CrossRef Full Text | Google Scholar

Kodera, Y., Yamada, Y., Hirano, K., Tamaribuchi, K., Adachi, S., Hayashimoto, N., et al. (2018). The Propagation of Local Undamped Motion (PLUM) Method: a Simple and Robust Seismic Wavefield Estimation Approach for Earthquake Early Warning. Bull. Seismol. Soc. Am. 108, 983–1003. doi:10.1785/0120170085

CrossRef Full Text | Google Scholar

Kuyuk, H. S., and Motosaka, M. (2009). Real-Time Ground Motion Forecasting Using Front-Site Waveform Data Based on Artificial Neural Network. J. Disaster Res. 4, 260–266. doi:10.20965/jdr.2009.p0260

CrossRef Full Text | Google Scholar

Meier, M.-A., Heaton, T., and Clinton, J. (2016). Evidence for Universal Earthquake Rupture Initiation Behavior. Geophys. Res. Lett. 43, 7991–7996. doi:10.1002/2016GL070081

CrossRef Full Text | Google Scholar

Meier, M. A., Kodera, Y., Böse, M., Chung, A., Hoshiba, M., Cochran, E., et al. (2020). How Often Can Earthquake Early Warning Systems Alert Sites With High‐Intensity Ground Motion? J. Geophys. Res. Solid Earth. 125, e2019JB017718. doi:10.1029/2019JB017718

CrossRef Full Text | Google Scholar

Melgar, D., and Hayes, G. P. (2019). Characterizing Large Earthquakes Before Rupture Is Complete. Sci. Adv. 5, eaav2032. doi:10.1126/sciadv.aav2032

PubMed Abstract | CrossRef Full Text | Google Scholar

Minson, S. E., Baltay, A. S., Cochran, E. S., Hanks, T. C., Page, M. T., McBride, S. K., et al. (2019). The Limits of Earthquake Early Warning Accuracy and Best Alerting Strategy. Sci. Rep. 9, 2478. doi:10.1038/s41598-019-39384-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Minson, S. E., Meier, M.-A., Baltay, A. S., Hanks, T. C., and Cochran, E. S. (2018). The Limits of Earthquake Early Warning: Timeliness of Ground Motion Estimates. Sci. Adv. 4, eaaq0504. doi:10.1126/sciadv.aaq0504

PubMed Abstract | CrossRef Full Text | Google Scholar

Minson, S. E., Saunders, J. K., Bunn, J. J., Cochran, E. S., Baltay, A. S., Kilb, D. L., et al. (2020). Real-Time Performance of the PLUM Earthquake Early Warning Method During the 2019 M 6.4 and 7.1 Ridgecrest, California, Earthquakes. Bull. Seism. Soc. Amer. 110, 1887–1903. doi:10.1785/0120200021

CrossRef Full Text | Google Scholar

Nagashima, I., Yoshimura, C., Uchiyama, Y., Maseki, R., and Itoi, T. (2008). “Real-time Prediction of Earthquake Ground Motion Using Empirical Transfer Function,” in Proceedings of 14th world conference on earthquake engineering, S02–S023.

Google Scholar

Noda, S., and Ellsworth, W. L. (2016). Scaling Relation Between Earthquake Magnitude and the Departure Time From Pwave Similar Growth. Geophys. Res. Lett. 43, 9053–9060. doi:10.1002/2016GL070069

CrossRef Full Text | Google Scholar

Oba, A., Furumura, T., and Maeda, T. (2020). Data Assimilation‐Based Early Forecasting of Long‐Period Ground Motions for Large Earthquakes along the Nankai Trough. J. Geophys. Res. Solid Earth. 125, e2019JB019047. doi:10.1029/2019JB019047

CrossRef Full Text | Google Scholar

Ogiso, M., Aoki, S., and Hoshiba, M. (2016). Real-Time Seismic Intensity Prediction Using Frequency-Dependent Site Amplification Factors. Earth Planet. Sp. 68, 83. doi:10.1186/s40623-016-0467-4

CrossRef Full Text | Google Scholar

Ogiso, M., Hoshiba, M., Shito, A., and Matsumoto, S. (2018). Numerical Shake Prediction for Earthquake Early Warning Incorporating Heterogeneous Attenuation Structure: The Case of the 2016 Kumamoto Earthquake. Bull. Seismol. Soc. Am. 108, 3457–3468. doi:10.1785/0120180063

CrossRef Full Text | Google Scholar

Okuda, T., and Ide, S. (2018). Hierarchical Rupture Growth Evidenced by the Initial Seismic Waveforms. Nat. Commun. 9, 3714. doi:10.1038/s41467-018-06168-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Olson, E. L., and Allen, R. M. (2005). The Deterministic Nature of Earthquake Rupture. Nature. 438, 212–215. doi:10.1038/nature04214

PubMed Abstract | CrossRef Full Text | Google Scholar

Otake, R., Kurima, J., Goto, H., and Sawada, S. (2020). Deep Learning Model for Spatial Interpolation of Real-Time Seismic Intensity. Seismol. Res. Lett. 91, 3433–3443. doi:10.1785/0220200006

CrossRef Full Text | Google Scholar

Phillips, W. S., and Aki, K. (1986). Site Amplification of Coda Waves From Local Earthquakes in Central California. Bull. Seism. Soc. Amer. 76, 627–648. doi:10.1785/bssa0760030627

CrossRef Full Text | Google Scholar

Pilz, M., and Parolai, S. (2016). Ground‐Motion Forecasting Using a Reference Station and Complex Site‐Response Functions Accounting for the Shallow Geology, Bull. Seismological Soc. America. 106, 1570–1583. doi:10.1785/0120150281

CrossRef Full Text | Google Scholar

Rydelek, P., and Horiuchi, S. (2006). Is Earthquake Rupture Deterministic? Nature 442, E5. doi:10.1038/nature04963

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, H., Fehler, M. C., and Maeda, T. (2012). Seismic Wave Propagation and Scattering in the Heterogeneous Earth. 2nd edition. Berlin, Heidelberg: Springer, pp494. doi:10.1007/978-3-642-23029-5

CrossRef Full Text

Scherbaum, F. (1996). Of Poles and Zeros: Fundamentals of Digital Seismology. Dordrecht, Netherlands: Kluwer Academic Publishers, 156.

Shearer, P. M. (1999). Introduction to Seismology. Cambridge, United Kingdom: Cambridge University Press, pp260.

Trugman, D. T., Page, M. T., Minson, S. E., and Cochran, E. S. (2019). Peak Ground Displacement Saturates Exactly When Expected: Implications for Earthquake Early Warning. J. Geophys. Res. Solid Earth. 124, 4642–4653. doi:10.1029/2018JB017093

CrossRef Full Text | Google Scholar

Wang, T., Jin, X., Wei, Y., and Huang, Y. (2017a). Real-Time Numerical Shake Prediction and Updating for Earthquake Early Warning. Earthq. Sci. 30, 251–267. doi:10.1007/s11589-017-0195-2

CrossRef Full Text | Google Scholar

Wang, T., Jin, X., Huang, Y., and Wei, Y. (2017b). Real-time 3-D Space Numerical Shake Prediction for Earthquake Early Warning. Earthq. Sci. 30, 269–281. doi:10.1007/s11589-017-0196-1

CrossRef Full Text | Google Scholar

Wessel, P., and Smith, W. H. F. (1995). New Version of the Generic Mapping Tools. Eos Trans. AGU. 76, 329. doi:10.1029/95eo00198

CrossRef Full Text | Google Scholar

Xie, Q., Ma, Q., Zhang, J., and Yu, H. (2019). Study on Real-Time Correction of Site Amplification Factor. Nat. Hazards Earth Syst. Sci. 19, 2827–2839. doi:10.5194/nhess-19-2827-2019

CrossRef Full Text | Google Scholar

Yamada, M. (2014). “Estimation of Fault Rupture Extent Using Near-Source Records for Earthquake Early Warning,” in Early Warning for Geological Disasters - Scientific Methods and Current Practice. Editors J. Zschau, and F. Wenzel (Berlin, Heidelberg, New York: Springer), 29–47. doi:10.1007/978-3-642-12233-0_2

CrossRef Full Text | Google Scholar

Yoshimoto, K. (2000). Monte Carlo Simulation of Seismogram Envelopes in Scattering Media. J. Geophys. Res. 105, 6153–6161. doi:10.1029/1999JB900437

CrossRef Full Text | Google Scholar

Zollo, A., Lancieri, M., and Nielsen, S. (2006). Earthquake Magnitude Estimation From Peak Amplitudes of Very Early Seismic Signals on Strong Motion Records. Geophys. Res. Lett. 33, L23312. doi:10.1029/2006GL027795

CrossRef Full Text | Google Scholar