Intelligent Interpretation of the Geometric Properties of Rock Mass Discontinuities Based on an Unmanned Aerial Vehicle

Introduction

Research indicates that discontinuities are an intrinsic characteristic of rock masses (Umili et al., 2013), and they have significant influences on rock mass deformation and stability (Kong et al., 2020). Therefore, the accurate and comprehensive extraction of rock mass discontinuity information is critical for the assessment of the safety of rock masses.

Traditional surveys are conducted via a window method or a line-scanning method (Gigli and Casagli, 2010; Zhang et al., 2018; Kong et al., 2020), and require physical contact with the rock surface (Gigli and Casagli, 2010; Umili et al., 2013); however, this is time-consuming (Zhang et al., 2018; Kong et al., 2020) and subject to the expertise of the operator (Kong et al., 2020). With the advancement of measurement techniques, new non-contact surveying methods have been developed to acquire three-dimensional (3D) rock mass data, and include the total station method (Feng et al., 2001), close-range photogrammetry (De et al., 2012; Kaufmann, 2012; Francioni et al., 2019), and 3D laser scanning (Deliormanli et al., 2014; Monsalve et al., 2019; Wichmann et al., 2019; Jiang et al., 2020). These techniques have been rapidly utilized in slope monitoring (Kromer et al., 2019; Giacomini et al., 2020), rock mechanics and stability analysis (Firpo et al., 2011; Assali et al., 2014), and geomorphology (Brodie et al., 2015; Boothroyd et al., 2016), as well as the geological and geotechnical research fields (Giordan et al., 2018). While 3D laser scanning and close-range photogrammetry have made great development progress, these two survey means are characterized by the following disadvantages: 1) under unique and complex terrain conditions, it is difficult to find a suitable observation point at which to set up instruments; 2) scanning devices are expensive, and the prices of mainstream scanners on the market are more than 1 million yuan; 3) some rock mass data will inevitably be missing due to the scanning direction. Due to the conspicuous cost reduction of vehicles and sensors, as well as the recent progress in data processing software over the past decade (Manfreda et al., 2018), the application of unmanned aerial vehicles (UAVs) in the collection of rock mass information has been ensured. UAV photogrammetry has many benefits, such as light and flexible equipment, strong adaptability to various terrains, and wide coverage (Wang et al., 2020). In addition, a multi-rotor UAV can take images from different positions and in different directions, thereby avoiding possible shadows or vertical deviations in high and inaccessible rock surfaces (Salvini et al., 2020). Therefore, the use of a light and small UAV to acquire rock mass information is superior to 3D laser scanning and close-range photogrammetry in terms of the equipment cost, portability, efficiency, and integrity of data collection.

The UAV technique has been applied in slope monitoring (Rodriguez et al., 2020; Wang et al., 2020), the failure mechanism analysis of landslides (Xu et al., 2017; Zhang et al., 2018), photogrammetric inspection (Zhang et al., 2020), and topographic reconstruction (Agüera-Vega et al., 2018). However, it is rarely utilized in the extraction of rock mass discontinuity information. Yathunanthan et al. (2014) conducted the imaging analysis of a data set generated from UAV photography to map geological structures, after which the 3D feature coordinates corresponding to the pixel coordinates of two-dimensional (2D) feature points were calculated from the digital elevation model (DEM), and the best-fit plane coefficients were computed. Finally, the discontinuity orientation was extracted (Yathunanthan et al., 2014). However, in this method, the geological analysis of the images requires the acute intuition and deductive and inductive reasoning of interpreters. Jia et al. (2018) manually selected the exposed discontinuities from a 3D point cloud generated from UAV images, and then extracted discontinuity information using the least-squares plane-fitting algorithm (Jia et al., 2018). It is evident that the degree of automation of these methods remains to be increased.

To overcome the low efficiency of the existing methods for rock mass data acquisition and the low degree of automation in discontinuity identification, a UAV-based approach for the automatic identification of rock mass discontinuities is proposed in this paper. Efficient and comprehensive image acquisition can be realized by employing a multi-rotor UAV, and images collected by the UAV can be converted to a point cloud model of the rock mass via 3D model reconstruction. Moreover, rock mass discontinuities can be automatically recognized based on an improved random sample consensus (RANSAC) algorithm. The proposed method includes the following steps: 1) 3D model reconstruction; 2) Normal vector calculation; 3) Discontinuity extraction; 4) Boundary delineation; 5) Discontinuity orientation calculation.

Unmanned Aerial Vehicles Measurement System and Workflow

The survey was conducted using a four-rotor DJI Phantom 3 Professional UAV (Figure 1), which is equipped with a 20-mm low-distortion wide-angle camera, a GPS/GLONASS dual-mode system, and an automatic return function. Moreover, the aircraft supports 4 K video capture at 30 frames per second, and the two photo formats of JPG and Raw. In addition, the aircraft has the ability to capture smooth and stable video pictures, and can actively record all the details of each flight, including the course, flight time, and other information. The specific parameters of the UAV are listed in Table 1.

FIGURE 1

FIGURE 1. The phantom 3 professional UAV.

TABLE 1

TABLE 1. The parameters of the Phantom 3 Professional UAV.

A scene survey is the foremost step of, and lays a solid foundation for, data acquisition. After surveying the site conditions, the measurement range was determined, and the easily measured discontinuities were selected and marked. The DJI GO App, a mobile route-planning software, was used to plan the route. The flight path should exceed the survey range to shoot the whole area. The flying height was selected to be beyond the highest obstacle in the flying area to avoid a collision. It should be noted that it is necessary to balance the flying height with the flight time, as the battery consumption caused by an excessive flying height will exceed the battery capacity. Ultimately, the slope was photographed from left to right and from top to bottom. The flight speed was selected as the maximum value, and the camera angle was set to 45°. To maintain the integrity of the measured data, some overlaps were maintained between the images. An overlap of 80% and a side-lap of 50% were respectively used. After the field investigation, a 3D point cloud was generated from the photos taken by the UAV.

Materials and Methods

The proposed method is divided into five steps, as illuminated in the flowchart in Figure 2.

FIGURE 2

FIGURE 2. The flowchart of the proposed method.

3-Dimensional Model Reconstruction

Feature Point Extraction

Due to the strong distortion of photos taken by UAVs, it is difficult to effectively apply the traditional extraction method based on geometric and texture features to extract feature points. The scale-invariant feature transform (SIFT) algorithm is characterized by the three properties of scaling, rotation, and affine invariance, via which it is capable of resisting certain illumination changes and viewpoint transformation. Hence, the SIFT algorithm is adopted for feature point extraction in the proposed method. The main concept of the SIFT algorithm is that the scale-space representation of UAV aerial images is established, after which the extreme points of images are searched in the scale space and extracted as feature points.

Image Matching

Image matching is conducted to reconstruct 3D information from multiple 2D images. However, the process of image matching using only SIFT feature points is slow. The location data of GPS coordinates in the images collected by the UAV and the attitude angle data provided by the inertial measurement unit (IMU) can assist in the construction of the topological structure between images. Next, the nearest-neighbor method is utilized to find the corresponding relationships between the feature points of images and establish a set of matching feature points that meet the geometric constraints. A large number of coordinate points constitutes a 3D point cloud of the target object in space.

Structure From Motion

The image points in the photo are projected into spatial coordinates according to the principle of camera imaging. The error function is defined as the sum of squares of the reprojection errors. The objective function is defined as follows:

$g\left(C_p,X\right)={\sum }_{i=1}^n{\sum }_{j=1}^m{v}_{ij}f{\left(P\left(C_i,X_j\right),q_{ij}\right)}^2(1)$

where $C_p=\left\{C_1,C_2,C_3,\mathrm{...}{C}_n\right\}$ are camera parameters, $X=\left\{X_1,X_2,X_3,\mathrm{...}{X}_m\right\}$ are the coordinates of space points, the variable $v_{ij}$ represents the visibility of space point $X_i$ in camera $C_i$, n is the number of images, m is the number of feature points obtained by precise matching, and the function $f{\left(P\left(C_i,X_j\right),q_{ij}\right)}^2$ represents the projection error of point $X_j$ in camera $C_i$.

Finally, sparse beam adjustment is used for step-by-step iteration to minimize the reprojection error between the projected points and the points on the observed images, thereby calculating coordinates of the 3D point cloud in an optimal camera pose and camera scene.

Normal Vector Calculation

Considering that normal vector calculation is a necessary process for the extraction of discontinuities, the next step after obtaining the point cloud is to calculate the normal vector.

The normal vector calculation method consists of two key steps, namely 1) finding the k-nearest neighbors of each point P_i and creating the point set Q_i (Figure 3), and 2) conducting plane-fitting for each point set Q_i and calculating the surface variation.

FIGURE 3

FIGURE 3. Q_i is the subset of $P_i$, and $\alpha$ is the normal vector of $P_i$.

Nearest-Neighbor Search

A point cloud model commonly includes massive target points in a 3D region, and lacks topological information. Therefore, the principal problem of processing point cloud data is to establish a topological relationship among discrete points and realize the fast search of the nearest adjacent points.

A k-d tree (referred to as a k-dimensional tree) is a data structure that represents spatial partitions, and is mainly applied to search key data in multidimensional space (such as range searches and nearest-neighbor searches). In this study, the k-nearest neighbors are searched by the k-dimensional tree.

Surface Variation Calculation

The problem of determining the normal of a point on a surface is similar to the problem of estimating a section of a normal of a surface. Therefore, the problem can be transformed into one concerned with least-squares plane-fitting estimation. In this study, the surface normal is evaluated by analyzing the eigenvectors and eigenvalues (or principal component analysis, PCA) (Riquelme et al., 2014; Robson et al., 2016; Guo et al., 2017) of the covariance matrix created from the nearest points. The covariance matrix C corresponding to each point $P_i$ can be defined as

$C=\frac{1}{k}{\sum }_{i=1}^k\left(P_i-\overline{P}\right).{\left(P_i-\overline{P}\right)}^T,C.\overrightarrow{V_j}={\lambda }_j.\overrightarrow{V_j},j\in \left\{\mathrm{0,1,2}\right\},(2)$

where $k$ is the number of the adjacent points of $P_i$, $\overline{P}$ represents the 3D centroid of point sets, and ${\lambda }_j$ and $\overrightarrow{V_j}$ are the eigenvalue and eigenvector of the covariance matrix, respectively. The normal vector can be determined by the eigenvector that corresponds to its minimum eigenvalue. After all the normal vectors are obtained, the subsequent step is to extract rock mass discontinuities.

Rock Mass Discontinuity Extraction Based on the Improved Random Sample Consensus Algorithm

The RANSAC algorithm is an iterative computational algorithm, which determines the parameters of a predefined mathematical model by randomly selecting a subset sample, and then calculates the distance from all points to the model. A point is defined as an inlier if the distance between a point and the model is less than the threshold; otherwise, the point is regarded as an outlier. The number of inliers in each iteration is recorded, and the model with the largest number of inliers is considered as the optimal model (Uhercík et al., 2010). Figure 4 presents the simple application of the RANSAC algorithm to 2D data. Figure 4A displays a set of points that includes inliers and outliers, and in Figure 4B, the blue line is the generated mathematical model, and the inliers are indicated in red.

FIGURE 4

FIGURE 4. (A) Inliers and outliers are included in the two-dimensional point set. (B) The line extracted by RANSAC.

For rock discontinuity extraction (the mathematical model is a plane), the RANSAC algorithm has two advantages: 1) it can be directly applied to raw point cloud data without triangulation gridding, and 2) it has strong robustness and can process more than 50% of the outliers. Based on these advantages, the RANSAC algorithm has been studied for the extraction of planes or discontinuities (Wang et al., 2019). However, due to the large number of points of a rock mass, most approaches are inefficient. Therefore, an improved RANSAC algorithm is proposed to greatly improve the accuracy and speed of the original algorithm.

Overview of the Improved Random Sample Consensus Algorithm

Given a point cloud set $P=\{P_1,\mathrm{...},P_N\}$ and the normal vector $N=\{n_1,\mathrm{...}{n}_N\}$ of all points, the output result is a series of parameters $\psi =\{{\psi }_1,\mathrm{...}{\psi }_N\}$ of the plane model. In this paper, local sampling is proposed to acquire new candidate planes in each iteration. The RANSAC algorithm is then applied to determine the parameters of the plane model with the highest score (i.e., the largest number of inliers). All the candidate planes are placed in the set $C$, and a new evaluation method is used to calculate the score m of the best plane. Moreover, $\left|m\right|$ is the number of points in a candidate plane, $\left|c\right|$ is the number of candidate planes, and $p\left(\left|m\right|,\left|c\right|\right)$ is the probability of ignoring the planes with a higher score. When $p\left(\left|m\right|,\left|c\right|\right)$ is large enough, the extracted plane is the best, and the remaining points will be used for the subsequent iteration. When $p\left(\tau ,\left|c\right|\right)$ is sufficiently large, the iteration process is terminated. Finally, $\tau$ (default) is the number of minimum points on a plane.

Probability Calculation

Consider a point cloud with $N$ points and a plane with n points, and $k$ is the number of points in the minimum point cloud set that determines a plane. Provided that any subset with $k$ points will generate a plane model, then the probability of detecting the plane model in one iteration is as follows.

$P\left(n\right)=\left(\begin{array}{c}n\\ k\end{array}\right)/\left(\begin{array}{c}N\\ k\end{array}\right)\approx {\left(\frac{n}{N}\right)}^k(3)$

When s candidate planes are detected, the probability of detecting the plane Ψ is as follows.

$P\left(n,s\right)=1-{\left(1-P\left(n\right)\right)}^s(4)$

The threshold value $p_t$ is artificially set. The number of planes $T$ that meet the requirement $P\left(n,T\right)\ge p_t$ can then be obtained by solving s, as follows.

$T\ge \frac{\ln \left(1-p_t\right)}{\ln \left(1-P\left(n\right)\right)}(5)$

Because the value of $P\left(n\right)$ is commonly small, its logarithm $\ln \left(P\left(n\right)\right)$ can be expanded by its Taylor series: $\ln \left(1-P\left(n\right)\right)=-P\left(n\right)+O\left(P{\left(n\right)}^2\right)$. The substitution of $\ln \left(P\left(n\right)\right)$ into Eq. 5 yields the following.

$T\approx \frac{-\ln \left(1-p_t\right)}{P\left(n\right)}(6)$

Sampling Method

The complexity of an algorithm is closely related to the sampling method. The sampling method used in this study is detailed as follows. Shape is a local phenomenon, and the closer two points are, the more likely they belong to the same plane. The sampling efficiency can be greatly improved by utilizing this characteristic. Research has revealed that it may be effective to increase the number of inliers within the model by utilizing the locality of the shape to the sample (Myatt et al., 2002). Generally, in random sampling, a circle with a given radius is used to randomly select sample points, but the radius needs to be determined in advance according to the density and distribution of the points. However, the density and distribution of outliers vary greatly for different models; even at different locations on the same model, the density of outliers can vary dramatically. Therefore, a method is presented in this paper to adapt to the density of outliers.

The octree structure is an effective method by which to establish spatial proximity between sampling points. First, the point $p_1$ is chosen without restriction to create the candidate plane, and then a set $C$ that includes $p_1$ is randomly selected from the structural layers of the octree structure. Finally, the remaining $K-1$ sample points are selected from the set $C$. The probability of finding the plane $\psi$ containing $n$ points in this manner can be calculated as follows:

$P_{local}\left(n\right)=P\left(p_1\in \Psi \right)P\left(p_2\mathrm{...}{p}_k\in C\right)(7)$

where $n/N$ is the first probability value, and the second probability value relies on the choice of the elements in the set $C$. The set $C$ is considered to be an optimization if abundant points on the plane $\psi$ are included in the$$set. Most points on a plane, excluding boundary points and edge points, have neighbors that belong to the plane. Generally speaking, although the adjacent points on a plane cannot be determined by the element set of the octree structure, the candidate plane model includes a large number of points to ensure that it is more representative of the actual data. Therefore, the number of these neighbors must be as large as the number of elements in the octree structure, excluding a few points. To facilitate the analysis, it is assumed that the set $C$ embodies all points $p_i$ on the plane $\psi$$\left(p_i\subset \psi \right)$, the number of all points on the plane $\psi$ is half of the number of points in the set $C$, and the other half of the points in the set $C$ contains outliers or noise points. The probability of choosing a large set $C$ is conservatively evaluated to be $1/d$, where $d$ refers to the depth of the octree structure. Therefore, the conditional probability of choosing points $p_2$ and $p_3 \left(p_2,p_3\subset \psi \right)$ from the set $C$ set can be calculated by Eq. 8. Then, by introducing Eq. 8 into Eq. 7 and Eq. 9 can be obtained.

$\frac{\left(\begin{array}{c}\left|C\right|/2\\ k-1\end{array}\right)}{\left(\begin{array}{c}\left|C\right|\\ k-1\end{array}\right)}\approx {\left(\frac{1}{2}\right)}^{k-1}(8)$

$P_{local}\left(n\right)=\frac{n}{Nd{2}^{k-1}}(9)$

Evaluation Method

The evaluation function ${\sigma }_p$ is utilized to evaluate the extracted candidate plane model. This evaluation function mainly includes the following three aspects. 1) After the selected plane is created, the points whose distance to the plane is less than the distance threshold value $\epsilon$ are regarded as the points on the candidate plane. 2) The points that meet the distance requirement will be further filtered. When the angles between the normal vectors of the detected points and the normal vectors of the candidate planes are less than the angle threshold value $\alpha$, these points will be selected as the points in the plane. 3) A new threshold value $\beta$, which represents continuity, is added to the proposed method. For the points that have met the first two requirements, only those satisfying the continuity requirement can be selected as inliers on the plane.

In short, for a plane $\psi$, its evaluation function ${\sigma }_p$ can be expressed as follows.

${\sigma }_p\left(\Psi \right)=\left|P_{\psi }\right|(10)$

For example, points $P_{\psi }$ on a plane model $\psi$ can be defined in two steps:

$P_{\Psi }=\{p|p\in P\cap d\left(\Psi ,p\right)<\epsilon \cap \arccos \left(\left|n\left(p\right).n\left(\Psi ,p\right)\right|\right)<\alpha \}(11)$

$P_{\psi }=\max component\left(\Psi ,P_{\psi }\right)(12)$

where $d\left(\psi ,p\right)$ is the Euclidean distance from point $p$ to plane $\psi$, $n\left(p\right)$ is the normal vector of point $p$, $n\left(\psi ,p\right)$ is the relationship between the normal vector of the plane model $\psi$ and the projection of the normal vector of point $p$ on the plane $\psi ,\text{ and }\max component\left(\psi ,p_{\psi }\right)$ refers to the point set where the projected points on the plane $\psi$ can form the largest connected part.

Modified Graham Scan Algorithm

Rock mass discontinuities are generally not standard, and even very irregular planes. Hence, a new approach is presented to accurately depict the boundary of the discontinuities. Feature points of discontinuities extracted by the method in this paper are normally distributed on two sides of the vertical direction of extracted discontinuities. Thus, this 3D issue can be transformed into a problem of searching the optimal contour of a 2D point cloud by projecting points onto the fitting plane.

The Graham scan algorithm is a straightforward and efficient convex hull algorithm (Ferrada et al., 2020), the general concept of which is to remove points that are not part of the convex hull. Given a point cloud set $S$, the point $p_0$ is obtained from $S$ with the minimum y-coordinate, and the points are then sorted counterclockwise. By scanning from $p_0$, if $p_0$, $p_1$, and $p_2$ are on the convex surfaces, they must meet the following property: $p_2$ is on the left of the vector $\langle p_1,p_2\rangle$; otherwise, $p_1$ should be removed.

However, the disadvantage of the Graham scan algorithm is that the first boundary obtained by the algorithm is convex. Therefore, optimization should be conducted to tackle this issue. Given the boundary points $M_k$ and non-boundary points $N_j$, and provided that there are the two new lines $M_1-N_1$ and $N_1-M_2$, $N_1$ will be regarded as a new boundary point if the triangle formed by the two new lines and $M_1-M_2$ does not include the new boundary point and the angle formed by $M_1-N_1$, and $N_1-M_2$ conforms to the tolerance requirement of a concave angle. In addition, the two new sides can be used to calculate the new boundary points by utilizing a recursive algorithm. The results of the Graham scan algorithm and the modified Graham scan algorithm are respectively presented in Figures 5A,B.

FIGURE 5

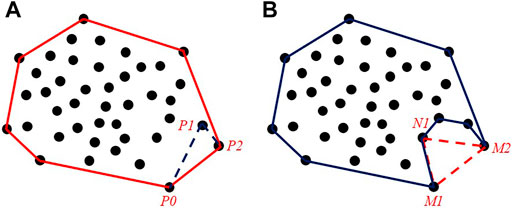
FIGURE 5. Boundary detection with the (A) Graham scan algorithm and (B) modified Graham scan algorithm.

After calculation, all the boundary points with concave-convex features are acquired. Figure 6 displays the extraction results of a set of points; Figure 6A presents the result of the fitting plane, and Figure 6B depicts the boundary of the fitting plane detected by the improved Graham scan algorithm.

FIGURE 6

FIGURE 6. (A) The fitting plane result; (B) the boundary delineation of the fitting plane.

Discontinuity Orientation Calculation

Orientation Calculation

The discontinuity of a plane can be represented as follows.

$Ax+By+Cz+D=0(13)$

The normal vector of the plane is as follows.

$N=(N_x,N_y,N_z)=(A,B,C)/\sqrt{A^2+B^2+C^2}(14)$

The orientation of the discontinuity can be calculated by the following equations.When $N_z>0$,

$\beta ={\cos }^{-1}\left(N_z\right)(15)$

If $N_x\ge 0$,

$\alpha ={\cos }^{-1}\frac{N_y}{\sqrt{N_z^2+N_y^2}}(16)$

If $N_x<0$,

$\alpha =2\pi -{\cos }^{-1}\frac{N_y}{\sqrt{N_z^2+N_y^2}}(17)$

When $N_z<0$,

$\beta ={\cos }^{-1}(-N_z)(18)$

If $-N_x\ge 0$,

$\alpha ={\cos }^{-1}\frac{-N_y}{\sqrt{N_z^2+N_y^2}}(19)$

If $-N_x<0$,

$\alpha =2\pi -{\cos }^{-1}\frac{N_y}{\sqrt{N_z^2+N_y^2}}(20)$

Case Study

Data Description

The study site was a rock mass slope located in Guishan Park in Wuhan City, China. The first task was to investigate the field conditions to determine the survey range and mark the easily measured discontinuities. The course was then planned, and the slope was photographed. Ultimately, twenty-six consecutive images were collected. Each image taken by the UAV was attached with geotags to provide a geographic reference for the point cloud, thereby producing highly detailed landform information (Rodriguez et al., 2020).

Subsequently, images from the survey were used to generate a point cloud. The 3D model (Figure 7) and point cloud data of the slope were automatically generated via 3D reconstruction with Smart3D software. There were 52,639,008 points in the point cloud data, which rendered it difficult to extract discontinuities in the later step. The point cloud model of the slope was acquired (Figure 8) by setting the point spacing of 16 mm in CloudCompare to down-sample the numerous point clouds.

FIGURE 7

FIGURE 7. The 3D model of the slope.

FIGURE 8

FIGURE 8. The point cloud model of the slope.

Discontinuity Information Results

A new extraction procedure called RANSAC Discontinuity Detection (RDD) was developed to automatically extract rock mass discontinuity information. The dialog box of RDD is presented in Figure 9, where $\epsilon$ is the distance from the point to the discontinuity, $\alpha$ is the angle between the normal vector of a point and the normal vector of the plane, and $\beta$ is the distance between the points that make up a continuous plane.

FIGURE 9

FIGURE 9. A dialog box for the parameters of the RDD plug-in.

The slope point cloud presented in Data description Section was employed to analyze the extraction effect of RDD. Figure 9 exhibits the parameter settings when RDD is used to extract discontinuities information of rock mass from the slope point cloud. As shown in Figure 10, most relatively smooth rock mass discontinuities were entirely detected by RDD, as were some small and fragmented discontinuities, even when the surface was rough or there were too many crushed pieces. It should be noted that the colors of these discontinuities were randomly assigned by the plug-in.

FIGURE 10

FIGURE 10. The extraction result of slope discontinuities.

The results of the three-point method were compared with those of the proposed RDD to quantitatively analyze the effect of RDD in identifying discontinuities. Thirteen planes from the slope model were marked (Figure 11). Similarly, these 13 planes were marked in the calculation results of RDD (Figure 12). Table 2 reports the comparative results of the orientations extracted by the three-point method and RDD. As shown in the table, when the discontinuities were flat enough, the difference between the two methods was less than 3°. Moreover, even for the rough discontinuities (such as plane 12), the difference in orientation was only 4.87°, which is within the reasonable error range in practical engineering applications.

FIGURE 11

FIGURE 11. The discontinuities extracted using the three-point method.

FIGURE 12

FIGURE 12. The discontinuities extracted with RDD.

TABLE 2

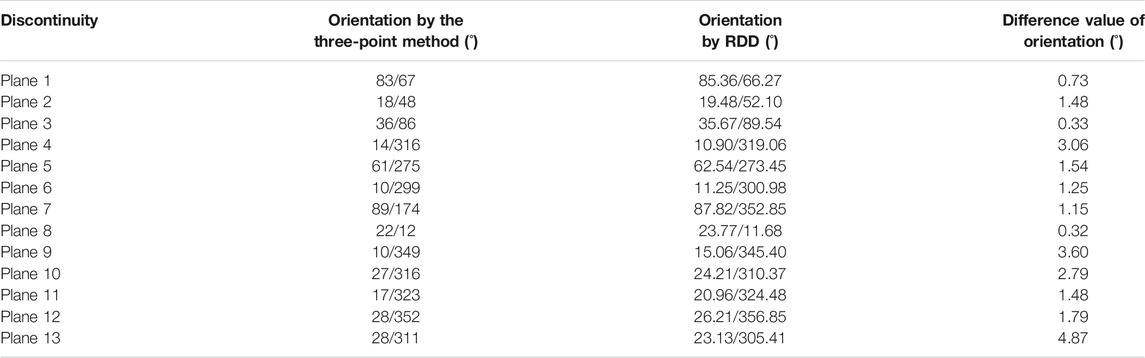
TABLE 2. Comparison between the discontinuity orientation results of the three-point method and RDD.

Conclusion

In this paper, a UAV-based approach was proposed for the data acquisition of rock masses and the automatic extraction of discontinuity information, which increases the automation level of discontinuity extraction and overcomes the disadvantages of close-range photogrammetry and 3D laser scanning, such as insufficient data.

Via the proposed method, discontinuity information can be extracted from the raw point cloud data, and the discontinuity boundary can be described with high precision.

A new procedure, RDD, was also developed to realize the automatic extraction of rock mass discontinuities. The orientations of the marked discontinuities calculated by the three-point method and the proposed RDD were compared, and the experimental results demonstrate the following: 1) RDD can completely detect most relatively smooth discontinuities, and therefore exhibits a good discontinuity detection effect; 2) the difference in the values of orientations calculated by the RDD and the manual three-point method was less than 3° when the discontinuity was smooth enough. Even for relatively rough discontinuities, the error was within an acceptable range for practical engineering applications. Therefore, the practicability of the proposed method was proven.

Nonetheless, this research was characterized by some disadvantages. For example, the extraction results of rock mass discontinuity information do not include the discontinuity spacing, roughness, degree of weathering, etc. Therefore, future research will be conducted to systematize the information extraction of rock mass discontinuities.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

NC proposed the algorithm and developed the RDD procedure. CD was responsible for data collection and curation, as well as wrote the manuscript and edited the charts. XD verified the experimental design, supervised and guided the process of data acquisition, as well as reviewed and revised the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52009038) and middle-aged Talents Project of Department of Education of Hubei Province (Q20201407).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agüera-Vega, F., Carvajal-Ramírez, F., Martínez-Carricondo, P., Sánchez-Hermosilla López, J., Mesas-Carrascosa, F. J., García-Ferrer, A., et al. (2018). Reconstruction of Extreme Topography from UAV Structure from Motion Photogrammetry. Measurement 121, 127–138. doi:10.1016/j.measurement.2018.02.062

CrossRef Full Text | Google Scholar

Assali, P., Grussenmeyer, P., Villemin, T., Pollet, N., and Viguier, F. (2014). Surveying and Modeling of Rock Discontinuities by Terrestrial Laser Scanning and Photogrammetry: Semi-automatic Approaches for Linear Outcrop Inspection. J. Struct. Geology. 66, 102–114. doi:10.1016/j.jsg.2014.05.014

CrossRef Full Text | Google Scholar

Boothroyd, R. J., Hardy, R. J., Warburton, J., and Marjoribanks, T. I. (2016). The Importance of Accurately Representing Submerged Vegetation Morphology in the Numerical Prediction of Complex River Flow. Earth Surf. Process. Landforms 41 (4), 567–576. doi:10.1002/esp.3871

CrossRef Full Text | Google Scholar

Brodie, K. L., Raubenheimer, B., Elgar, S., Slocum, R. K., and McNinch, J. E. (2015). Lidar and Pressure Measurements of Inner-Surfzone Waves and Setup. J. Atmos. Ocean Tech. 32 (10), 1945–1959. doi:10.1175/JTECH-D-14-00222.1

CrossRef Full Text | Google Scholar

De, V. P., Cevasco, A., and Cavallo, C. (2012). Detailed Rock Failure Susceptibility Mapping in Steep Rocky Coasts by Means of Non-contact Geostructural Surveys: the Case Study of the Tigullio Gulf (Eastern Liguria, Northern Italy). Nat. Hazard. Earth Sys 12 (153), 867–880. doi:10.5194/nhess-12-867-2012

CrossRef Full Text | Google Scholar

Deliormanli, A. H., Maerz, N. H., and Otoo, J. (2014). Using Terrestrial 3D Laser Scanning and Optical Methods to Determine Orientations of Discontinuities at a Granite Quarry. Int. J. Rock Mech. Mining Sci. 66, 41–48. doi:10.1016/j.ijrmms.2013.12.007

CrossRef Full Text | Google Scholar

Feng, Q., Sjögren, P., Stephansson, O., and Jing, L. (2001). Measuring Fracture Orientation at Exposed Rock Faces by Using a Non-reflector Total Station. Eng. Geology. 59 (1), 133–146. doi:10.1016/S0013-7952(00)00070-3

CrossRef Full Text | Google Scholar

Ferrada, H., Navarro, C. A., and Hitschfeld, N. (2020). A Filtering Technique for Fast Convex Hull Construction in R2. J. Comput. Appl. Math. 364, 112298. doi:10.1016/j.cam.2019.06.014

CrossRef Full Text | Google Scholar

Firpo, G., Salvini, R., Francioni, M., and Ranjith, P. G. (2011). Use of Digital Terrestrial Photogrammetry in Rocky Slope Stability Analysis by Distinct Elements Numerical Methods. Int. J. Rock Mech. Mining Sci. 48 (7), 1045–1054. doi:10.1016/j.ijrmms.2011.07.007

CrossRef Full Text | Google Scholar

Francioni, M., Simone, M., Stead, D., Sciarra, N., Mataloni, G., and Calamita, F. (2019). A New Fast and Low-Cost Photogrammetry Method for the Engineering Characterization of Rock Slopes. Remote Sensing 11 (11), 1267. doi:10.3390/rs11111267

CrossRef Full Text | Google Scholar

Giacomini, A., Thoeni, K., Santise, M., Diotri, F., Booth, S., Fityus, S., et al. (2020). Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System. Remote Sensing 12 (15), 2459. doi:10.3390/rs12152459

CrossRef Full Text | Google Scholar

Gigli, G., and Casagli, N. (2011). Semi-automatic Extraction of Rock Mass Structural Data from High Resolution LIDAR point Clouds. Int. J. Rock Mech. Mining Sci. 48 (2), 187–198. doi:10.1016/j.ijrmms.2010.11.009

CrossRef Full Text | Google Scholar

Giordan, D., Hayakawa, Y., Nex, F., Remondino, F., and Tarolli, P. (2018). Review Article: The Use of Remotely Piloted Aircraft Systems (RPASs) for Natural Hazards Monitoring and Management. Nat. Hazards Earth Syst. Sci. 18 (4), 1079–1096. doi:10.5194/nhess-18-1079-2018

CrossRef Full Text | Google Scholar

Guo, J. T., Liu, S. J., Zhang, P. N., Wu, L. X., Zhou, W. H., and Yu, Y. N. (2017). Towards Semi-automatic Rock Mass Discontinuity Orientation and Set Analysis from 3D point Clouds. Comput. Geosciences 103, 164–172. doi:10.1016/j.cageo.2017.03.017

CrossRef Full Text | Google Scholar

Jia, S. G., Jin, A. B., and Zhao, Y. Q. (2018). Application of UAV Oblique Photogrammetry in the Field of Geology Survey at the High and Steep Slope. Rock Soil Mech. 39 (3), 1130–1136. doi:10.16285/j.rsm.2017.1474

CrossRef Full Text | Google Scholar

Jiang, Q., Zhong, S., Pan, P.-Z., Shi, Y. N., Guo, H. G., and Kou, Y. Y. (2020). Observe the Temporal Evolution of Deep Tunnel's 3D Deformation by 3D Laser Scanning in the Jinchuan No. 2 mine. Tunnelling Underground Space Tech. 97 (C), 103237. doi:10.1016/j.tust.2019.103237

CrossRef Full Text | Google Scholar

Kaufmann, V. (2012). The Evolution of Rock Glacier Monitoring Using Terrestrial Photogrammetry: The Example of Ausseres Hochebenkar Rock Glacier (Austria). Aust. J. Earth Sci. 105 (2), 63–77.

Google Scholar

Kong, D. H., Wu, F. Q., and Saroglou, C. (2020). Automatic Identification and Characterization of Discontinuities in Rock Masses from 3D point Clouds. Eng. Geology. 265, 105442. doi:10.1016/j.enggeo.2019.105442

CrossRef Full Text | Google Scholar

Kromer, R., Walton, G., Gray, B., Lato, M., and Group, R. (2019). Development and Optimization of an Automated Fixed-Location Time Lapse Photogrammetric Rock Slope Monitoring System. Remote Sensing 11 (16), 1890. doi:10.3390/rs11161890

CrossRef Full Text | Google Scholar

Manfreda, S., McCabe, M., Miller, P., Lucas, R., Pajuelo Madrigal, V., Mallinis, G., et al. (2018). On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sensing 10 (4), 641. doi:10.3390/rs10040641

CrossRef Full Text | Google Scholar

Monsalve, J. J., Baggett, J., Bishop, R., and Ripepi, N. (2019). Application of Laser Scanning for Rock Mass Characterization and Discrete Fracture Network Generation in an Underground limestone Mine. Int. J. Mining Sci. Tech. 29 (1), 131–137. doi:10.1016/j.ijmst.2018.11.009

CrossRef Full Text | Google Scholar

Myatt, D., Torr, P., Nasuto, S., Bishop, J., and Craddock, R. (2002). “Napsac:High Dimensional Robust Estimation-It’s in the Bag,” in BMVC (Cardiff: Computer Vision Tools). doi:10.5244/c.16.44

CrossRef Full Text | Google Scholar

Riquelme, A. J., Abellán, A., Tomás, R., and Jaboyedoff, M. (2014). A New Approach for Semi-automatic Rock Mass Joints Recognition from 3D point Clouds. Comput. Geosciences 68, 38–52. doi:10.1016/j.cageo.2014.03.014

CrossRef Full Text | Google Scholar

Robson, K. G., Luiz, P. L. d. O., Luiz, G., Francisco, M. W. T., Mauricio, R. V., and Marcelo, K. d. S. (2016). An Algorithm for Automatic Detection and Orientation Estimation of Planar Structures in LiDAR-Scanned Outcrops. Comput. Geosci-uk 90, 170–178. doi:10.1016/j.cageo.2016.02.011

CrossRef Full Text | Google Scholar

Rodriguez, J., Macciotta, R., Hendry, M. T., Roustaei, M., Gräpel, C., and Skirrow, R. (2020). UAVs for Monitoring, Investigation, and Mitigation Design of a Rock Slope with Multiple Failure Mechanisms-A Case Study. Landslides 17, 2027–2040. doi:10.1007/s10346-020-01416-4

CrossRef Full Text | Google Scholar

Salvini, R., Vanneschi, C., Coggan, J. S., and Mastrorocco, G. (2020). Evaluation of the Use of UAV Photogrammetry for Rock Discontinuity Roughness Characterization. Rock Mech. Rock Eng. 53, 3699–3720. doi:10.1007/s00603-020-02130-2

CrossRef Full Text | Google Scholar

Uhercík, M., Kybic, J., Liebgott, H., and Cachard, C. (2010). Model Fitting Using RANSAC for Surgical Tool Localization in 3-D Ultrasound Images. IEEE Trans. Biomed. Eng. 57 (8), 1907–1916. doi:10.1109/TBME.2010.2046416

PubMed Abstract | CrossRef Full Text | Google Scholar

Umili, G., Ferrero, A., and Einstein, H. H. (2013). A New Method for Automatic Discontinuity Traces Sampling on Rock Mass 3D Model. Comput. Geosciences 51, 182–192. doi:10.1016/j.cageo.2012.07.026

CrossRef Full Text | Google Scholar

Wang, S. H., Ahmed, Z., Hashmi, M. Z., and Wang, P. Y. (2019). Cliff Face Rock Slope Stability Analysis Based on Unmanned Arial Vehicle (UAV) Photogrammetry. Geomech. Geophys. Geo-energ. Geo-resour. 5 (4), 333–344. doi:10.1007/s40948-019-00107-2

CrossRef Full Text | Google Scholar

Wang, S. H., Zhang, Z. S., Ren, Y. P., and Zhu, C. J. (2020). UAV Photogrammetry and AFSA-Elman Neural Network in Slopes Displacement Monitoring and Forecasting. Ksce J. Civ Eng. 24 (8), 19–29. doi:10.1007/s12205-020-1697-3

CrossRef Full Text | Google Scholar

Wang, Z. F., He, S. M., Liu, H. D., and Li, D. D. (2020). Formation Mechanism and Risk Assessment of Unstable Rock Mass at the Yumenkou Tunnel Entrance, Shanxi Province, China. Bull. Eng. Geol. Environ. 80 (2), 1433–1448. doi:10.1007/s10064-020-01953-1

CrossRef Full Text | Google Scholar

Wichmann, V., Strauhal, T., Fey, C., and Perzlmaier, S. (2019). Derivation of Space-Resolved normal Joint Spacing and In Situ Block Size Distribution Data from Terrestrial LIDAR point Clouds in a Rugged Alpine Relief (Kühtai, Austria). Bull. Eng. Geol. Environ. 78 (6), 4465–4478. doi:10.1007/s10064-018-1374-7

CrossRef Full Text | Google Scholar

Xu, Q., Li, W. l., Dong, X. J., Xiao, X. X., Fan, X. M., and Pei, X. J. (2017). The Xinmocun Landslide on June 24, 2017 in Maoxian, Sichuan: Characteristics and Failure Mechanism. Chin. J. Rock Mech. Eng. 36 (11), 2612–2628. doi:10.13722/j.cnki.jrme.2017.0855

CrossRef Full Text | Google Scholar

Yathunanthan, V., Eun-Jung, H., Peter, K., and Steven, M. (2014). Semi-automatic Mapping of Geological Structures Using UAV-Based Photogrammetric data:An Image Analysis Approach. Comput. Geosci-uk 69, 22–32. doi:10.1016/j.cageo.2014.04.012

CrossRef Full Text | Google Scholar

Zhang, D., Watson, R., Dobie, G., MacLeod, C., Khan, A., and Pierce, G. (2020). Quantifying Impacts on Remote Photogrammetric Inspection Using Unmanned Aerial Vehicles. Eng. Structures 209, 109940. doi:10.1016/j.engstruct.2019.109940

CrossRef Full Text | Google Scholar

Zhang, P., Du, K., Tannant, D. D., Zhu, H. H., and Zheng, W. B. (2018). Automated Method for Extracting and Analysing the Rock Discontinuities from point Clouds Based on Digital Surface Model of Rock Mass. Eng. Geology. 239, 109–118. doi:10.1016/j.enggeo.2018.03.020

CrossRef Full Text | Google Scholar

Zhang, Y. Y., Wen, H. J., Ma, C. C., Yang, Y., Fu, H. M., Huang, X. L., et al. (2018). Failure Mechanism and Stability Analysis of Huge Landslide of Caijiaba Based on Multi-Source Data. Chin. J. Rock Mech. Eng. 37 (9), 2048–2063. doi:10.13722/j.cnki.jrme.2018.0448

CrossRef Full Text | Google Scholar