- 1Alfred-Wegener-Institut Helmholtz-Zentrum für Polar- und Meeresforschung, Bremerhaven, Germany
- 2Institute of Environmental Physics, University of Bremen, Bremen, Germany
Radiation transmitted through sea ice and snow has an important impact on the energy partitioning at the atmosphere-ice-ocean interface. Snow depth and ice thickness are crucial in determining its temporal and spatial variations. Under-ice surveys using autonomous robotic vehicles to measure transmitted radiation often lack coincident snow depth and ice thickness measurements so that direct relationships cannot be investigated. Snow and ice imprint distinct features on the spectral shape of transmitted radiation. Here, we use those features to retrieve snow depth. Transmitted radiance was measured underneath landfast level first-year ice using a remotely operated vehicle in the Lincoln Sea in spring 2018. Colocated measurements of snow depth and ice thickness were acquired. Constant ice thickness, clear water conditions, and low in-ice biomass allowed us to separate the spectral features of snow. We successfully retrieved snow depth using two inverse methods based on under-ice optical spectra with 1) normalized difference indices and 2) an idealized two-layer radiative transfer model including spectral snow and sea ice extinction coefficients. The retrieved extinction coefficients were in agreement with previous studies. We then applied the methods to continuous time series of transmittance and snow depth from the landfast first-year ice and from drifting, melt-pond covered multiyear ice in the Central Arctic in autumn 2018. Both methods allow snow depth retrieval accuracies of approximately 5 cm. Our results show that atmospheric variations and absolute light levels have an influence on the snow depth retrieval.
1. Introduction
The Arctic sea ice is undergoing rapid and tremendous changes during the last decades (Meredith et al., 2019). The extent of sea ice is shrinking (Serreze et al., 2007; Stroeve et al., 2012). Old thick multiyear ice (MYI) is replaced by younger (e.g., Maslanik et al., 2007; Stroeve and Notz, 2018) and thinner first-year ice (FYI) (Haas et al., 2008; Kwok and Rothrock, 2009). Those changes are mainly driven by atmospheric (e.g., Graversen et al., 2008) and ocean warming (e.g., Steele et al., 2010). As the sea-ice cover shrinks, less area is available where snow can deposit. Due to its high reflectivity, snow plays a key role in the energy balance of the sea ice (Webster et al., 2018). It determines the amount of radiation transmitted through sea ice (e.g., Perovich, 2007; Nicolaus et al., 2013), and has a strong effect on the surface albedo (e.g., Perovich and Polashenski, 2012). Delays in sea-ice formation due to a prolonged melt season (e.g., Markus et al., 2009) reduce early snow accumulation. To further investigate and understand the solar partitioning and with that assess and monitor the changes in the Arctic sea ice, relationships between the under-ice solar radiation and snow depth must be established.
Under-ice radiation can be measured using remotely operated vehicles (ROVs, e.g., Nicolaus et al., 2012; Katlein et al., 2015; Arndt et al., 2017; Meiners et al., 2017; Katlein et al., 2019; Lange et al., 2019), towed platforms (Castellani et al., 2020), and autonomous underwater vehicles (AUVs, e.g., Wulff et al., 2016). Using such platforms minimizes the destruction of the sea-ice surface while measuring. Hardly or not at all accessible, undersampled, and heterogeneous ice-covered areas such as very thin, newly formed ice, and open and refreezing leads can be accessed and studied on large scales and in a reasonably short operation time. Time series of under-ice radiation at local fixed points and coincident snow depth and ice thickness can be collected by autonomous measuring system drifting with the sea ice (Richter-Menge et al., 2006; Nicolaus et al., 2010a; Nicolaus et al., 2021). However, for many ROVs and AUVs surveys coincident snow depth measurements are not available, especially when the vehicles are far away from their deployment site.
Solar radiation penetrating through sea ice is scattered or absorbed (Perovich, 1996). This attenuation depends strongly on snow, sea ice, water, and in-ice and water biomass and their physical properties (e.g., Smith and Baker, 1981; Arrigo et al., 1991; Katlein et al., 2015; Mundy et al., 2015). Those properties determine the magnitude and the spectral shape of the under-ice radiation and leave distinct features in the spectra at specific wavelengths (e.g., Mundy et al., 2007; McDonald et al., 2017). These distinct features can be used to retrieve snow and ice properties from under-ice radiation.
Normalized difference indices (NDIs) describe the spectral shape of under-ice radiation and can be correlated with the properties of snow, ice, water, and biomass. They have been successfully used to retrieve chlorophyll a concentration in the Arctic (Mundy et al., 2007; Campbell et al., 2014; Lange et al., 2016; Castellani et al., 2020) and Antarctic (Melbourne-Thomas et al., 2015; Meiners et al., 2017; Wongpan et al., 2018; Castellani et al., 2020; Cimoli et al., 2020). Relationships between the NDIs and snow depth have been established to investigate the potential to retrieve snow depth (Mundy et al., 2007; Melbourne-Thomas et al., 2015; Arndt et al., 2017; Wongpan et al., 2018). However, no attempts have been made yet to apply those findings and to retrieve snow depth as such. Inverse radiative transfer (RT) modelling can also be used to retrieve snow and ice properties through the dependency of under-ice radiation on the spectral extinction coefficients (e.g., McDonald et al., 2017; Arndt et al., 2017).
Recent remote sensing snow depth retrieval methods provide snow depth over large regions in the Arctic using space-borne passive microwave radiometry (e.g., Rostosky et al., 2018), dual-band satellite altimetry (e.g., Guerreiro et al., 2016; Lawrence et al., 2018), and airborne ultrawideband microwave radar (e.g., Jutila et al., 2021). However, the temporal and spatial scales of those space-borne retrievals are not applicable for colocation with small scale, localized under-ice radiation measurements. While it is easy to measure snow depth directly for small areas, e.g., using a magnaprobe (Sturm and Holmgren, 2018), simultaneous and repeated under-ice radiation measurements are not possible due to the destruction of the area through measuring snow depth.
Here, we utilize two non-destructive optical methods to inversely retrieve snow depth from under-ice radiation measurements. The methods are applied to landfast level FYI and to drifting, melt-pond covered MYI. We present colocated snow depth and ice thickness measurements along with under-ice hyperspectral radiation data from an ROV. Based on these data, we find the best wavelength pairs to retrieve snow depth from NDIs. We also retrieve snow depth by inverting an idealized two-layer RT model and snow and sea ice spectral extinction coefficients in the wavelength range between 400 and 700 nm. The discrepancies between directly measured and retrieved snow depth are the criteria to evaluate the performance of the two methods. We discuss how those methods could be applied to current sea ice research with a focus on technological advances.
2 Materials and Methods
2.1 Study Sites
The data presented in this study were collected during two field campaigns (Figure 1A). The Multidisciplinary Arctic Program—Last Ice Area (MAPLI18) campaign was conducted on landfast level FYI in the Lincoln Sea off the coast of Ellesmere Island near the Canadian Forces Station Alert, Canada, in spring 2018. The Arctic Ocean 2018 (AO18) MOCCHA—ACAS—ICE campaign was conducted with the Swedish Icebreaker Oden on drifting, melt-pond covered MYI close to the geographic North Pole in autumn 2018.
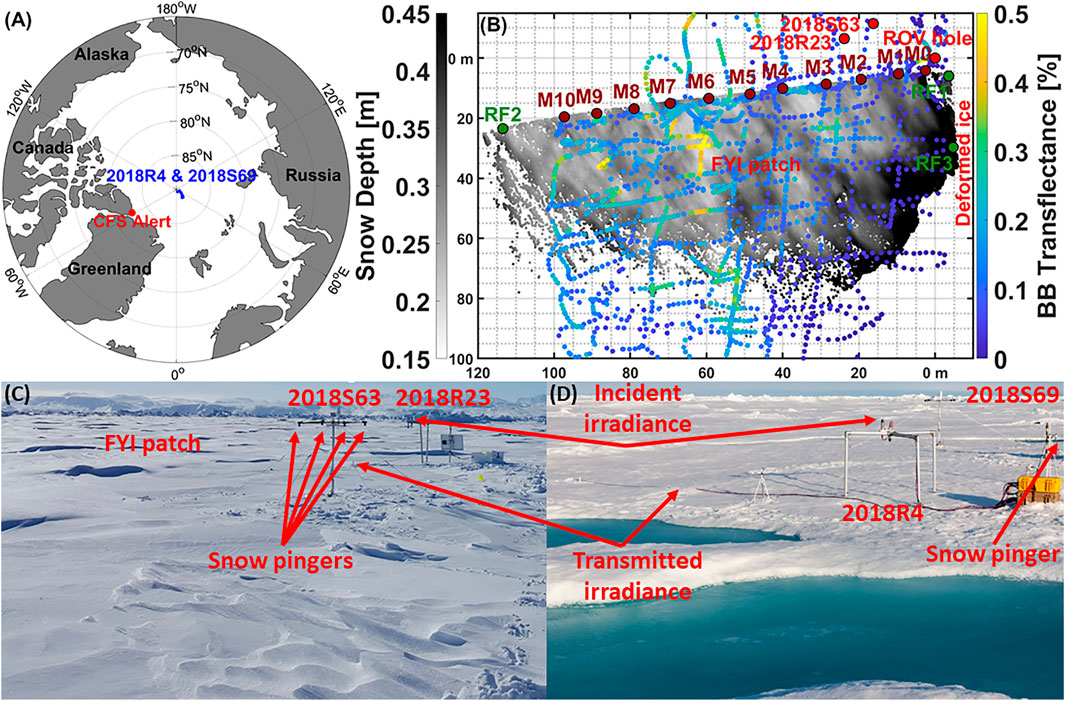
FIGURE 1. (A) Location of the MAPLI18 campaign close to the Canadian Forces Station (CFS) Alert in the Lincoln Sea and the drift of the radiation station 2018R4 and the snow buoy 2018S69 close to the geographic North Pole during the AO18 campaign. (B) Map of the FYI patch during MAPLI18 displaying snow depth in m derived from the terrestrial laser scanner as measured on 23 May (grey scale). Overlaid is the broadband (BB) transflectance in % (colour scale) measured by the ROV on 22 May. Circles indicate the marker locations M0 to M10 (dark red), the access hole of the ROV in the ice (red), and the locations of the radiation station 2018R23 and the Snow Buoy 2018S63 (red). RF1-3 (green circles) are the reflectors used to process the laser scanner data. (C) Radiation station 2018R23 and Snow Buoy 2018S63 as of May 5, 2018. (D) Radiation station 2018R4 and Snow Buoy 2018S69 as of August 20, 2018 (photo: Mario Hoppmann, AWI).
For the following description of data and results we refer only to MAPLI18 if not otherwise stated. Snow depth, total sea ice thickness (ice thickness plus snow depth), and transmitted radiance were measured on and under an approximately 120 m × 80 m landfast level FYI patch (Figure 1B). The measurements were performed along a 100 m transect and across the entire patch. At the marker locations M0–M10, plastic poles were put through drilled holes in the ice to ease under-ice navigation and ensure correct colocation of the data. Adjacent to the FYI patch was deformed MYI (Lange et al., 2019).
2.2 Snow Depth and Sea Ice Thickness
The surface topography of the FYI patch was measured with a terrestrial laser scanner (VZ-400i, RIEGL, Horn, Austria). The laser scanner was mounted on a tripod ∼2 m above the surface. Scan positions were distributed at the marker locations and along the transition to the deformed ice spaced 10–40 m apart (Figure 1B). The individual scans were each registered to a master scan position using three space-fixed cylindrical retro-reflectors (RF1-3) in the RiSCAN Pro software. Subsequently, a full point cloud was created with a mean horizontal resolution of 5 cm and a mean vertical accuracy of 2 cm caused by uncertainties in scanner orientation. The point clouds for three different days were each manually rotated for horizontal alignment with the marker locations. Snow depth was calculated from the surface topography by subtracting the height of the reflector center of RF2 above the ice surface (Table 1). The snow depth could be differentiated from the ice by assuring that neither the rod of the reflector nor the tripod penetrated deep into the surface scattering layer between ice and snow. Using the length of the reflector rod allowed the extraction of the snow depth for reference at this particular location within the RiSCAN Pro software. Snow depths exceeding 0.6 m close to the deformed ice area were removed as for higher snow loads the assumption of level sea ice was questionable. More details on the surface topography measurements and how snow depth was derived can be found in the data repository doi:10.1594/PANGAEA.932594.
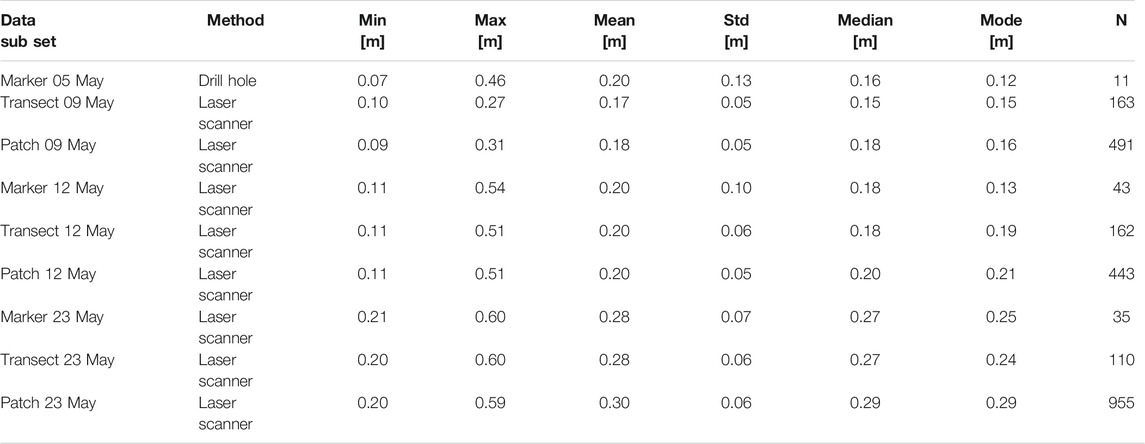
TABLE 1. Snow depth obtained in drill holes at the marker locations and with a laser scanner. Std is the first standard deviation of the mean snow depth and N the number of measurements. The modes were read from histograms with 1 cm bin width.
Snow depth point measurements with a horizontal resolution between 1 m and 3 m were obtained using a magnaprobe (Snow-Hydro, Fairbanks, AK, United States, Sturm and Holmgren, 2018) with an accuracy of 1 cm. The position of the measurements was recorded with an integrated GPS with an accuracy of ±2.5 m (Sturm and Holmgren, 2018). The magnaprobe measurements were used to validate the snow depths derived from the laser scanner. Laser scanner snow depths were averaged around magnaprobe measurements. Differences in modal snow depths between magnaprobe and laser scanner were with 0–2 cm within the laser scanner accuracy.
Total ice thickness was measured with a ground-based electromagnetic induction sounding device (EM31-SH, Geonics Limited, Mississauga, ON, Canada, Haas et al., 1997; Haas et al., 2017). The EM31-SH measurements were compared against measurements from other drill hole locations (not shown) for proper calibration on both FYI and MYI following the description from (Haas et al., 1997; Haas et al., 2017). The EM31-SH was placed on a sledge and dragged across the ice and has a vertical accuracy of 0.10 m. The ice thickness was then calculated by subtracting the laser scanner snow depth from the total ice thickness. The ice thickness was assumed to be level indicated by underwater images (Figure 2A), small standard deviations in ice thickness (Table 2), mean and modal thickness agreeing to within ±0.15 m which is close to ±0.10 m found by Rabenstein et al. (2010), multiple drillings and ice investigations in the area, and by the area extent of at least 100 m in length (Figure 1B). We further assumed the thickness to be constant during the study period because it did not vary by more than 0.10 m across the whole patch (Table 2). In-situ snow depth, ice thickness, draft, and freeboard were measured at drill holes at the marker locations using a tape measure.
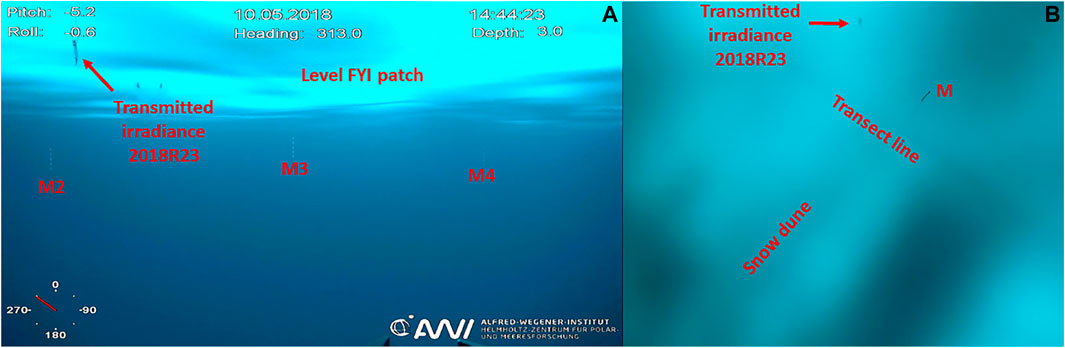
FIGURE 2. (A) Underwater image of the level FYI patch on 10 May as extracted from a video taken by the ROV HD camera. (B) Underwater upward looking still image at 55.6 m depth as taken by a 14.1-megapixel Tiger Shark camera (Imenco, Norway) attached to the ROV on 12 May.

TABLE 2. Drill hole ice thickness and draft (in brackets) at the marker locations and EM31-SH ice thickness. Std is the first standard deviation of the respective mean and N the number of measurements. The modes were read from histograms with 0.10 m bin width.
2.3 Under-ice Radiation
Horizontal profiles of under-ice spectral radiance were measured by a RAMSES-ARC hyper-spectral radiometer (320–950 nm, TriOS Mess-und Datentechnik GmbH, Rastede, Germany). The radiometer was mounted to an M500 ROV (Ocean Modules, Åtvidaberg, Sweden, Katlein et al., 2017). The ROV was lowered into the water through a 1.5 m × 1.5 m hole in the ice and operated horizontally along the ice bottom. The hole and the control system for the ROV were covered by a heated tent. To take into account atmospheric variability, the transmitted radiance was normalized by the incident downwelling planar irradiance recorded at the surface by a RAMSES-ACC radiometer. The ratio of transmitted radiance
For under-ice navigation of the ROV an acoustic long baseline positioning system (Pinpoint Linkquest, San Diego, CA, United States) was used. Manual post-processing of the position was required to remove distortion in positioning probably caused by local sound speed differences. To correct this distortion, the position of the ROV at the marker locations as recorded by the positioning system and as viewed by the ROV high definition zoom video camera (Surveyor WAHD, Bowtech, Figure 2A) was manually aligned with the marker locations measured by a handheld GPS at the surface to obtain scaling factors for correcting the position (Figure 1B).
The opening angle of the radiance radiometer β was about 7°. Based on this value, we determined 1.5 m as the approximate footprint radius R of the area from which the radiometer detected radiance through the surface based on
2.4 Continuous Radiation and Snow Depth Measurements
Continuous time series measurements of transmitted and incident irradiance were measured with RAMSES-ACC radiometers mounted on the radiation stations 2018R23 from 5 to 21 May during MAPLI18 and on 2018R4 from 27 August to 18 September during AO18 (Figure 1). The radiometer that measured the transmitted irradiance was hanging in the water at a distance to the ice bottom of 0.5 m. During the same periods time series of snow depth were measured by two Snow Buoys (Nicolaus et al., 2021), 2018S63 during MAPLI18 and 2018S69 during AO18 (Figure 1). Each snow buoy consisted of four ultrasonic snow pingers (Max Botix, Brainerd, MN, United States) with an accuracy of 1 cm. In addition, a single pinger was attached to the radiation station 2018R4 which was deployed 10–15 m away from the Snow Buoy 2018S69. The snow depth was calculated from the distance to the surface measured by the pingers and the initial in-situ snow depth. Data gaps from the 2018R4 pinger were replaced by data from previous time stamps. The temporal resolution for both radiation stations and snow buoys were 1 hour.
2.5 Normalized Difference Indices
The distinct features caused by the snow depth in the spectral shape of the transflectance was used as a non-invasive method to retrieve snow depth (Figure 3). We assumed that the effect of snow on the transflectance can be separated from the effect of the ice because the ice was level and the thickness did not vary by more than 0.10 m across the whole patch. Thus, in our dataset ice thickness does not influence retrieved snow depths, however our dataset only covers a small thickness variation to verify this. The absorption by water and phytoplankton was neglected because the visibility in the water was above 50 m (i.e., very clear water, Figure 2B) and Lange et al. (2019) reported low in-ice chlorophyll a biomass of 0.23 mg m−2 to 2.56 mg m−2 in the bottom and 1.42 ± 0.62 mg m−2 overall. Absorption by water close to the ice bottom was measured by a hyperspectral extinction sensor (VIPER-G2, TriOS, Rastede, Germany, Katlein et al., 2017) attached to the ROV. On average absorption was 0.06 m−1 at 436 nm and 0.03 m−1 at 620 nm on 12 May while on 22 May it was 0.07 m−1 at 436 nm and 0.03 m−1 at 620 nm. The maximum distance between radiometer and ice bottom based on the operational depth of the ROV and the mean sea-ice draft was 0.62 m (Section 2.3 and Table 2). Neglecting absorption by water resulted in relative errors ranging between 1.9% and 4.4% in transflectance measurements. Katlein et al. (2016) used a 3D model to investigate the effects of a spatially inhomogeneous sea-ice cover and of water absorption on under-ice radiation. They recommend to use radiance instead of irradiance for spatial variability studies and to rather discard measurements taken at greater distance to the ice bottom (e.g., >1.5 m, Lange et al., 2016) then correcting measurements for water absorption as this introduces unknown errors due to unknown geometry that cannot be quantified and thus, no gain in precision. We computed NDIs as described by Mundy et al. (2007) using ROV-based transflectance
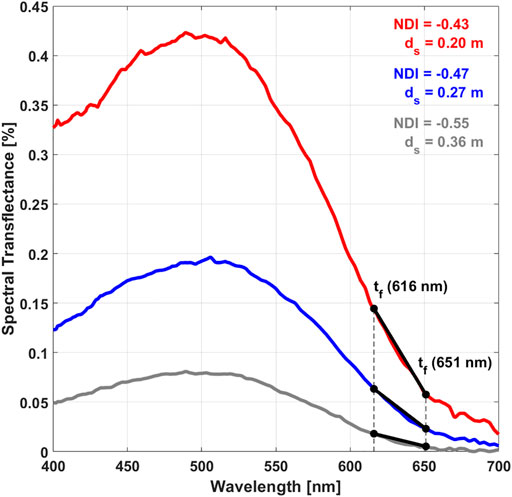
FIGURE 3. Spectral transflectance in % for three different snow depths
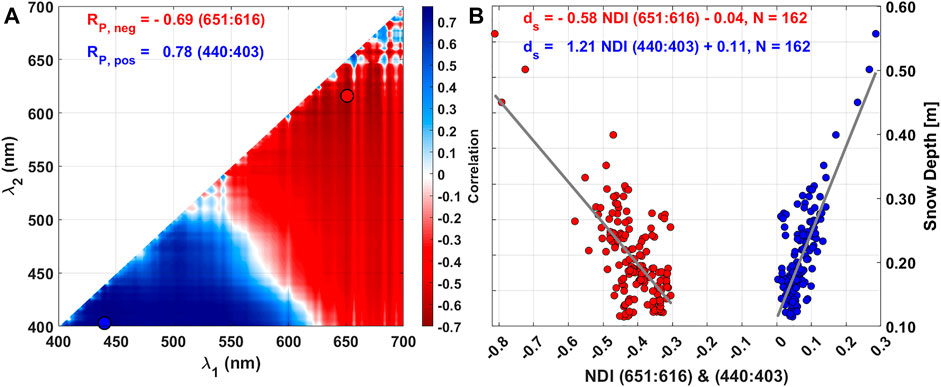
FIGURE 4. (A) Spectral correlation surface constructed from the Pearson correlation coefficients
2.6 Radiative Transfer Model
In addition to the NDI method, we applied a multiple exponential regression model from the MATLAB™ curve fitting toolbox with a non-linear least square Trust-Region algorithm (Sorensen, 1982) to approximate RT in sea ice. In this approach, the spectral transflectance transmitted through a two-layer system consisting of snow and sea ice decays exponentially with snow depth
The value
3 Results
3.1 Snow Depth and Sea Ice Thickness
We studied the snow stratigraphy close to the Snow Buoy 2018S63 and the radiation station 2018R23 on 12 May and at the end of the transect (close to M10) on 22 May (Figures 1B,C). We observed typical characteristics of snow on Arctic sea ice. Closest to the snow-ice interface was a poorly bonded layer of depth hoar underlying a wind slab layer of varying hardness. Between them, we found a thin layer of melt forms or even an ice lens. The topmost layer consisted of very soft, new snow. However, for further analysis we assumed the snow being one bulk layer.
Snow dunes were present across the FYI patch which caused spatial variability (Figure 1B). A wind-induced snow redistribution event took place between 9 and 10 May, also reported by Lange et al. (2019). This caused an increase in mean and modal snow depth along the transect and across the patch between 9 and 12 May (Table 1). Significant snow fall occurred on 16, 23, and 24 May. This caused further increases of mean and modal snow depth as evident on 23 May.
The mean standard deviation of the laser scanner snow depths within a radius of 1.5 m around every transflectance measurement was 5 cm. Hence, we used it as a tolerance value to evaluate the method performance that can be achieved using optical measurements in this study.
The difference between mean EM31-SH ice thicknesses along the transect measured on 10 and 24 May was within the measurement error of 0.10 m (Table 2). Modal ice thicknesses measured at the drill holes at the marker locations on 5 May and with the EM31-SH along the transect on 10 and 24 May and across the patch on 24 May were also within the error. Thus, we assume that the ice thickness did not change significantly during the observation period.
3.2 Normalized Difference Indices, Radiative Transfer Model, and Extinction Coefficients
Strong Pearson correlation coefficients (RP) between NDIs and snow depth displayed in the spectral correlation surface indicated that the snow depth explained the majority of the variability in the transflectance for the two wavelength pairs 651:616 nm and 440:403 nm (Figure 4A). The highest negative correlation was found for the wavelength pair 651:616 nm and the highest positive correlation for 440:403 nm. The snow depth explained 69 and 78% of the variability in the transflectance at those wavelengths along the transect, respectively (Figure 4A). We used both wavelength pairs to find the best snow depth retrieval using the NDI method. (Figure 4B).
The spectral snow extinction coefficients retrieved from inverse RT modeling decreased from 400 nm to their minimum at around 550 nm and then increased to a maximum at 661 nm (Figure 5A). The sea-ice extinction coefficients remained nearly constant between 400 nm and 520 nm at around 1.5 m−1, and increased above 550 nm to their maximum value of 3.5 m−1 at 700 nm (Figure 5B; Table 3).
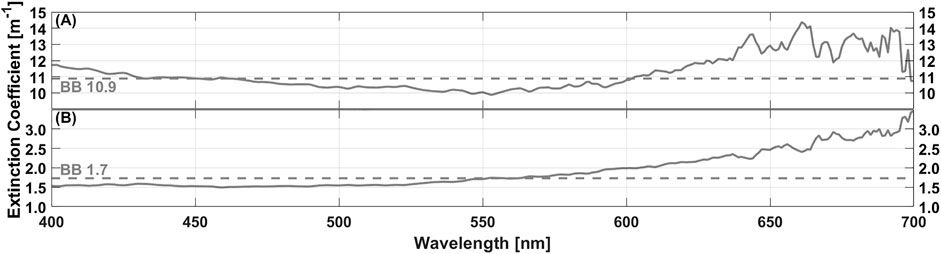
FIGURE 5. Spectral snow

TABLE 3. Statistics on the spectral snow
Snow influences and attenuates radiation most efficiently at longer wavelengths between 600 nm and 700 nm as expressed in high spectral snow extinction coefficients (Figure 5B). The extinction coefficients are also high between 400 nm and 450 nm indicating that snow also influences radiation at those wavelengths. As the transflectance increases with wavelength from 403 nm to 440 nm (Figure 3), correlation coefficients at those wavelengths are positive while between 616 nm and 651 nm the transflectance decreases with wavelength resulting in negative correlation coefficients.
3.3 Spatial Variability of Measured and Retrieved Snow Depths
The spatial variability in snow depth during MAPLI18 was well reproduced using the NDI method (Figure 6). The magnitude of the retrieved snow depths agreed with the direct snow depth measurements (Table 4). On 9 May, the NDI method achieved root mean square errors (RMSEs) between measured and retrieved snow depths below or slightly exceeding the tolerance of 5 cm (Table 4). The percentage of the direct snow depth measurements that were ±5 cm (tolerance) of the retrieved snow depths is referred to as agreement and was between 65 and 77% on 9 May. The snow depth was overestimated but with deviations between the modal snow depths, Δmode, within the tolerance. On 23 May, the achieved RMSEs were significantly above the tolerance. The agreements were between 17 and 58% and the snow depth was underestimated with Δmode of 3 and 8 cm.
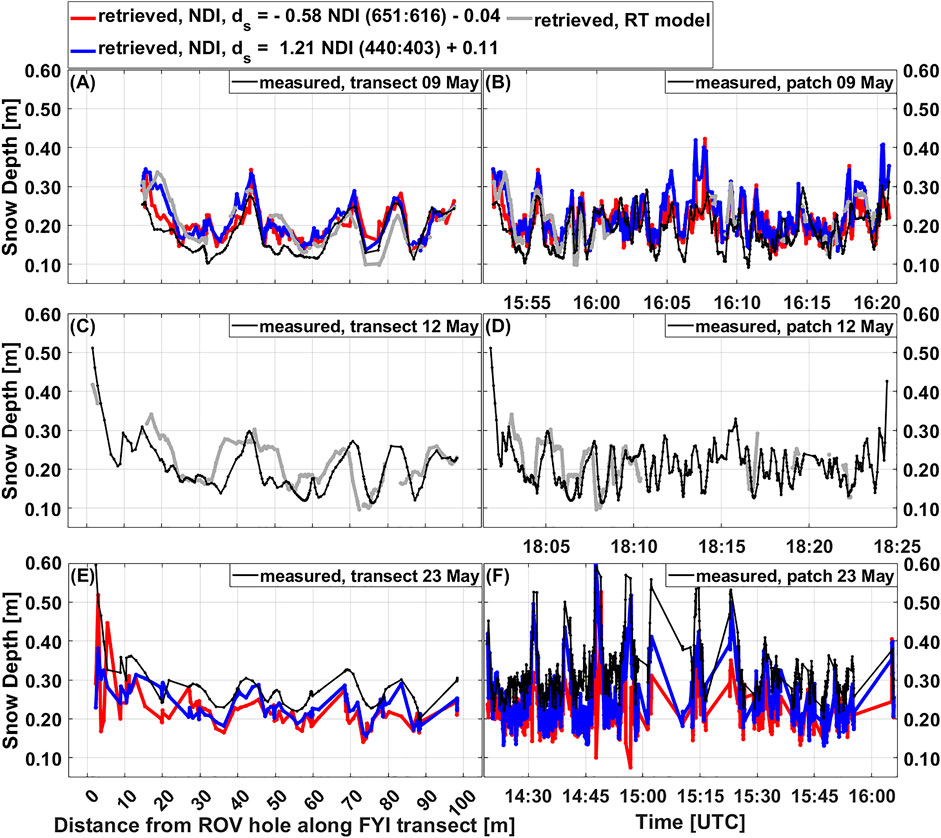
FIGURE 6. Measured snow depth (black) and retrieved snow depth using the NDI method (red, blue) and the RT model (grey) along the transect (A,C,E) and across the patch (B,D,F). Note that for the patches the x-axis is time.
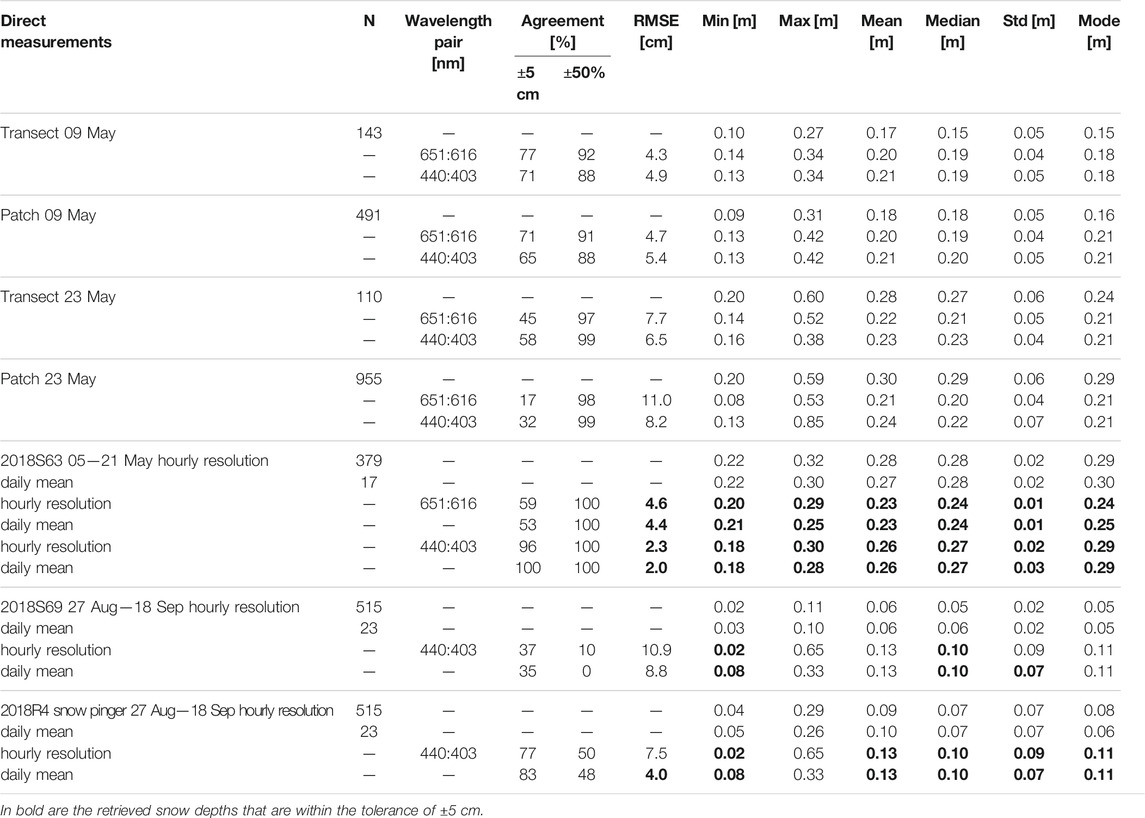
TABLE 4. Comparison of snow depth retrieval using the NDI method. The modes were read from histograms with 1 cm bin width. N is the number of measurements used.
To summarize, the NDI method with the wavelength pairs 651:616 nm and 440:403 nm performed well in reproducing the spatial variability and the magnitude of the measured snow depth with a combined mean RMSE of 6.6 cm.
The spectral snow and sea-ice extinction coefficients (Figure 5; Table 3) were implemented in the RT model (Eq. 2) together with measured transflectance to retrieve snow depth and ice thickness. The resulting magnitudes and the spatial variability of the retrieved snow depth agreed well with the direct measurements (Figure 6; Table 5). The mean RMSE was 5 cm (Table 5). Agreements were between 64 and 72%. Δmode ranged from 0 to 2 cm and were within the tolerance. Thus, the RT model performed better than the NDI method in reproducing the spatial variability of the measured snow depth.
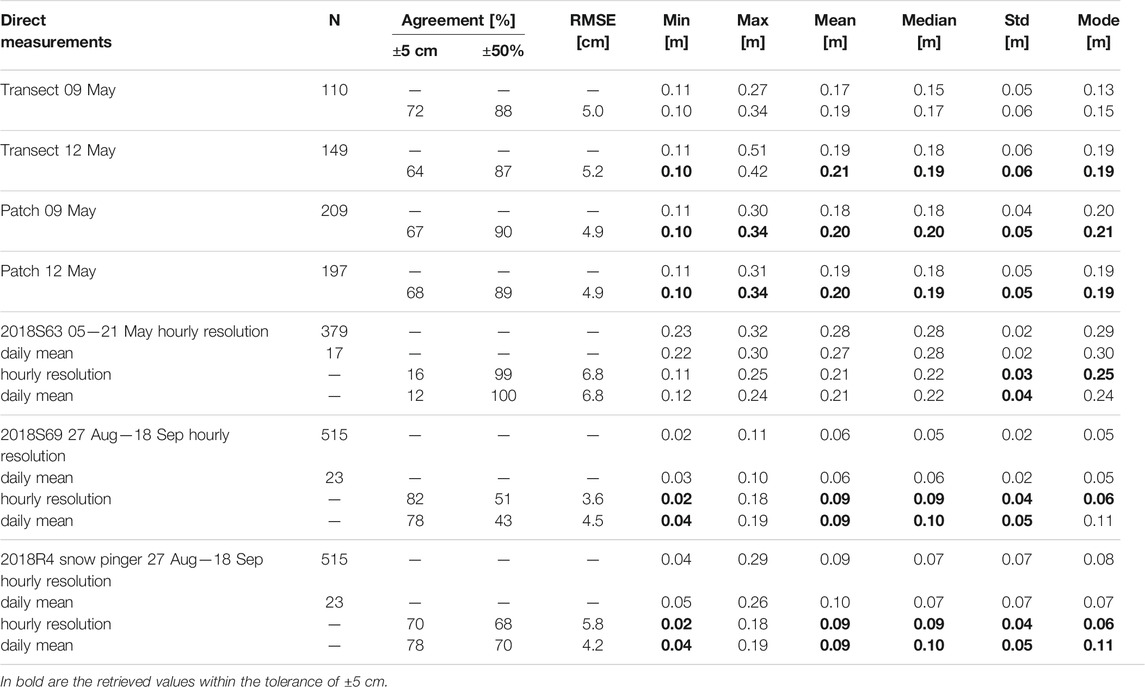
TABLE 5. Comparison of snow depth retrieval using the RT model and the snow and sea ice extinction coefficients from Table 3. The modes were read from histograms with 1 cm bin width. N is the number of measurements used.
3.4 Temporal Variability of Measured and Retrieved Snow Depths
Here, we applied the NDI method and the RT model to continuous time series measurements of snow depth and transmittance as obtained by Snow Buoys and radiation stations during MAPLI18 (Figure 7) and AO18 (Figure 8).
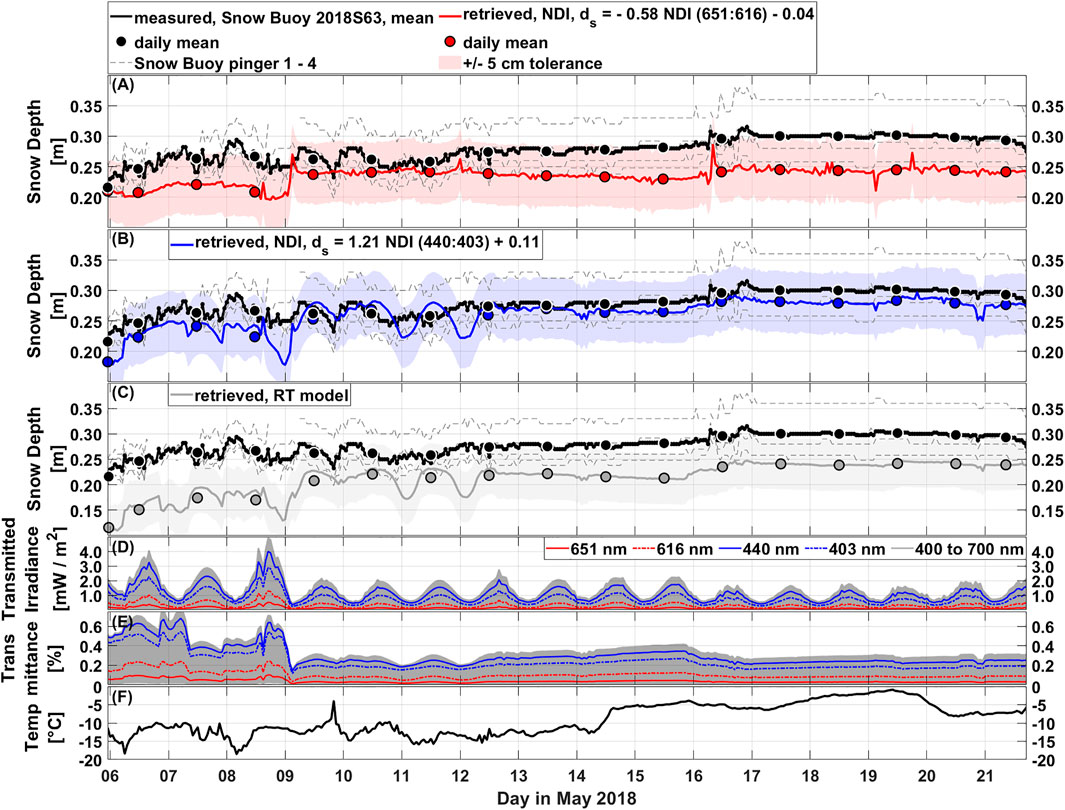
FIGURE 7. (A–C) Hourly mean snow depths measured by the Snow Buoy 2018S63 as obtained on FYI during MAPLI18 (solid black). Variations in the snow depth of the four individual ultrasonic snow pingers are indicated by the respective grey dashed lines. The snow depths retrieved using the NDI method with the wavelength pairs 651:616 nm [(A), red] and 440:403 nm [(B), blue] are overlaid. The NDIs were calculated from the 2018R23 transmittance. (C) Retrieved snow depths using the RT model with the extinction coefficients from Figure 5 (grey). Corresponding daily means (circles) are overlaid. The tolerance of ±5 cm is indicated by the respective coloured shadings. (D) Transmitted irradiance in
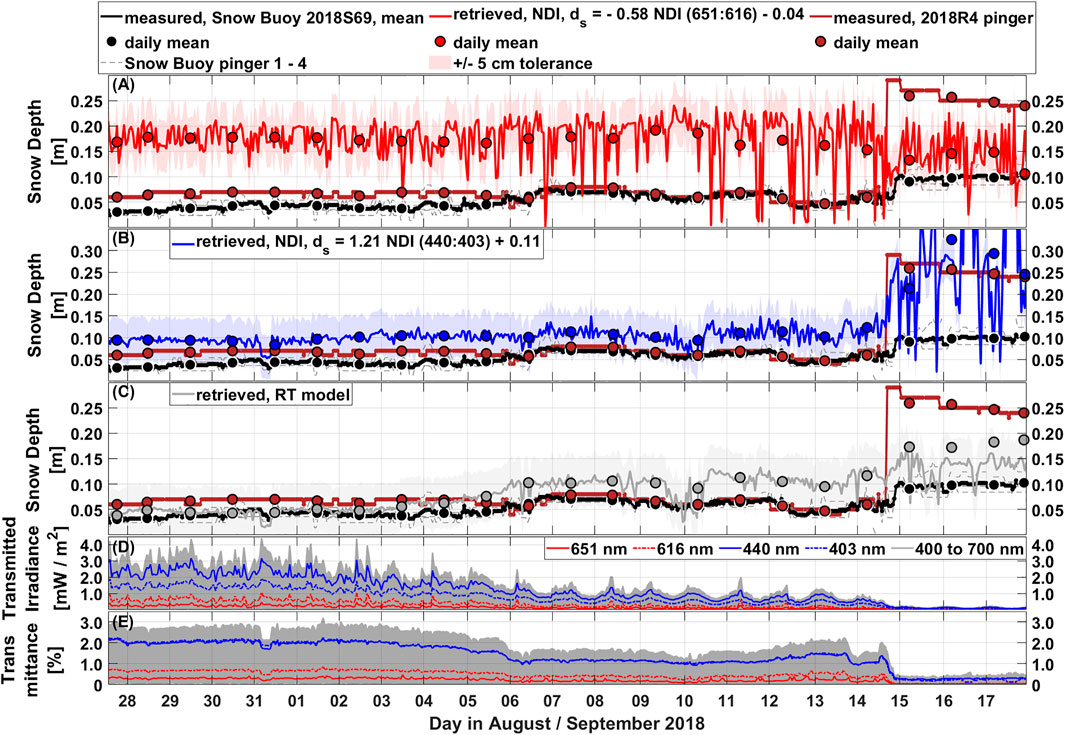
FIGURE 8. (A–C) Hourly mean snow depths measured by the Snow Buoy 2018S69 (solid black) as obtained on MYI during AO18. Variations in the snow depth due to the four individual ultrasonic snow pingers are indicated by the respective grey dashed lines. The snow depth measured by the snow pinger attached to the radiation station 2018R4 is indicated by the solid brown line. The snow depths retrieved using the NDI method with the wavelength pair 651:616 nm [(A), red] and 440:403 nm [(B), blue] are overlaid. The NDIs were calculated from the 2018R4 transmittance. (C) Retrieved snow depths using the RT model with the extinction coefficients from Figure 5 (grey). Corresponding daily means (circles) are overlaid. The tolerance of
Applying the NDI method with the wavelength pairs 651:616 nm and 440:403 nm to the MAPLI18 data set resulted in RMSEs of 4.6 and 2.3 cm, agreements of 59 and 96%, and Δmode of 5 and 0 cm, respectively (Figures 7A,B; Table 4). The NDI method with 440:403 nm was clearly better in reproducing the magnitude but also the results with 651:616 nm were within the tolerance.
Using the RT model resulted in a RMSE of 6.8 cm, an agreement of 16%, and a Δmode of 4 cm. Although the RMSE was above the tolerance and the agreement low, the temporal variability was well reproduced (Figure 7C).
Between 9 and 10 May a wind-induced snow-redistribution event took place. This caused an increase in measured snow depth early on 9 May, which was captured by the NDI method and the RT model (Figures 7B,C). The subsequent decrease was however not reproduced using the NDI method with 651:616 nm. The decrease was measured at the same time as an increase in air temperature from about −10°C to −4°C (Figure 7F).
The time series of snow depth retrieved using the NDI method with 440:403 nm and the RT model shows a diurnal cycle on 7 May and between 9 and 12 May (Figures 7B,C). This is attributed to the daily variations in the transmitted irradiance and transmittance at the wavelengths 440–500 nm which are part of the blue spectrum (Figures 7D,E). Those variations occur because radiation at blue wavelengths is scattered about 16 times more efficiently by air molecules in the atmosphere than radiation at red wavelengths. During sunset and sunrise, the solar zenith angle is highest and radiation travels a greater distance through the atmosphere while the radiation at blue wavelengths is scattered away. Thus, a diurnal cycle in solar radiation at blue wavelengths exists, here clearly affecting the snow depth retrieval using those wavelengths. The diurnal cycle in transmitted irradiance was present in the entire time series whereas diurnal variations in transmittance and retrieved snow depth occurred only on the specific days.
The diurnal cycle was removed by calculating daily means (Figures 7A–C). In general, comparing daily means resulted in lower RMSEs using the NDI method, whereas using the RT model it remained the same (Table 4 and Table 5). For the wavelengths in the red part of the spectrum as with 651:616 nm, the diurnal cycle was also present but less pronounced. Therefore, it was not present in the retrieved snow depth (Figure 7A).
During AO18, the snow depth measured by the Snow Buoy 2018S69 and the single pinger attached to the radiation station 2018R4 agreed until 14 September (Figure 8A). Then, the single pinger recorded a sharp increase, which was not measured by the buoy.
For most of the time series, the snow depth retrieved using the NDI method with 651:616 nm was significantly higher than the snow depth measured by the buoy (mean) and by the single pinger (Figure 8A). The NDI method was also unable to capture the increase recorded by the pinger. Due to transmitted irradiance below 1 mW m−2 for the wavelengths in the red part of the spectrum the retrieved snow depth was noisy (Figure 8A). The irradiance decreased further from 14 September onwards with the increase in snow depth. Similar results were achieved by using the NDI method with other wavelength pairs in the yellow/orange/red part of the spectrum (not shown). Because of this, the results using 651:616 nm were excluded from further analyses related to the temporal variability during AO18.
In contrast, the using 440:403 nm reproduced the increase and the retrieved snow depth agreed better to the measurements (Figure 8B). However, the retrieved snow depth was also noisy at the same time as the transmitted irradiance for the algorithms blue wavelengths became low (Figure 8D). RMSEs between retrieved and both buoy and pinger snow depths were above the tolerance (Table 4). The comparison to the pinger snow depth was better than to the buoy. While comparing daily means for the buoy led to similar results, the RMSE of 4 cm was within the tolerance when comparing to the pinger daily means.
On average, the snow depths retrieved inversely with the RT model agreed better than the snow depths from the NDI method (Figure 8C; Table 5). The overall temporal variability was reproduced and the RMSEs were 3.6 cm (buoy) and 5.8 cm (pinger). However, the sudden increase measured by the pinger was only partly captured and with a lower magnitude. Comparing daily means from the buoy led to worse results, while daily means from the pinger improved the RMSE.
To summarize, the magnitude of the mean snow depth measured by the Snow Buoy 2018S63 during MAPLI18 was well reproduced using the NDI method with both wavelength pairs and the RT model. However, the temporal variability using 440:403 nm in the NDI method and the RT model was influenced by the diurnal cycle in transmittance due the wavelengths in the blue part of the spectrum that were used to retrieve the snow depths. In contrast, the temporal variability during AO18 was well reproduced because no diurnal cycle was observed. The performance of the NDI method with the wavelengths in the red part of the spectrum, 651:616 nm, to this time series was limited due to the low transmitted irradiance. The overall performance of the NDI method and the RT model combined was with mean RMSEs of 5.6 and 5.3 cm, respectively, comparable.
4 Discussion
4.1 Accuracy of Snow Depth Retrieval
The total mean accuracy (RMSE) along spatial measurements and for time series from both methods and the two locations is 5.6 cm and with that slightly above the tolerance. The accuracies achieved using the RT model are better than using the NDI method for spatial scales but comparable for temporal scales (Table 4 and Table 5). The lateral resolution using the NDI method is on average less than 1 m owing the high-resolution ROV and laser scanner measurements while using the RT model it is 10 m attributed to the spacing between the marker locations (Figure 1B).
In this study, the range in snow depth retrieval is dictated by the range in measured snow depth which is between 0.02 and 0.60 m and, thus, covers a wide range (Table 4 and Table 5). Extreme snow depths and variability can occur in troughs between ridges, at ridge flanks, in form of sastrugi, and on newly formed, thin ice (cracked features). The transflectance under ridges is most likely quite low and noisy due to the thick ice which is expected to make snow depth retrieval difficult. However, this remains speculative as this was not investigated. On the same token, the difficulty in retrieving snow depth in form of sastrugi is explained by the extreme snow depth variability across 10th of centimetres in horizontal scales. As described in Section 2.3, the footprint radius of the radiance radiometer on the surface is 1.5–2.0 m which hints to the impossibility to retrieve snow depth of sastrugi correctly. We have not attempt to retrieve snow depth on thin ice but expect that the methods presented in this study are applicable and promising. However, little is known about radiative transfer in thin ice which might complicate the retrieval.
Compared to no snow depth information or vague visual observations from a ship´s bridge as for example during biological sampling with large nets towed behind a ship (e.g., Castellani et al., 2020), the accuracy achieved here appears satisfying.
Our total mean accuracy of 5.6 cm compares with retrieved snow depths using satellite and airborne products. Rostosky et al. (2018) present a RMSE of 3.7 cm using passive microwave on FYI in spring. Guerreiro et al. (2016) and Lawrence et al. (2018) use dual-band altimetry and retrieve mean RMSEs of 6.4 and 3.0 cm to 5.0 cm, respectively. However, these satellite products do not provide the same spatial resolution as our approach. Jutila et al. (2021) obtained a RMSE of 6.9 cm using an airborne microwave radar on level landfast FYI.
Once technology advances, autonomous platforms such as AUVs and submarines equipped with radiometers might travel many kilometers under the ice and measure transmitted radiation. Our methods might provide an option to remotely retrieve snow depth for regional or basin-wide scales covered during such surveys. For many research questions, it would then be sufficient to estimate whether an ice floe has a thin, intermediate, or thick snow cover within the accuracy achieved in this work. During those surveys, a wider range in sea ice types, snow covers, and seasonal differences and progressions in snow depth as well as in under-ice radiation could be investigated. Such measurements could serve to further develop and validate our methods and then provide a base for more targeted Arctic surveys over different spatial and temporal scales.
During MAPLI18, the fast snow depth variations measured by the buoy are probably unrealistic. The snow pack does not change so quickly except during strong wind events (Lange et al., 2019), which were not frequently observed. This might explain some discrepancies between then measured and the retrieved snow depths.
During AO18, we found a large discrepancy of 10.9 cm (daily mean 8.8 cm) between buoy measurements and the results from the NDI method with 440:403 nm. This can be explained by spatial variability in snow depth and the noise from 14 September onwards (Figures 8B,D). The buoy was deployed 10–15 m away from the under-ice irradiance radiometer which was closer to the pinger. In contrast, the RT model results agree better with the buoy than with the pinger snow depth because the RT model captures only partly the sharp increase measured by the pinger. Nonetheless, some discrepancies might also occur because we compare optical to geometrical snow depth.
4.2 NDI-Specific Comparison to Existing Studies
Our two wavelength pairs for the NDI method are similar to previous studies, reflecting their potential to retrieve snow depth. In the Antarctic, Melbourne-Thomas et al. (2015), Arndt et al. (2017), and Wongpan et al. (2018) found wavelength pairs in the orange/red and blue part of the spectrum. In the Arctic, Mundy et al. (2007) separated the influence of snow depth on the spectral magnitude and distribution. They found strongest correlation between their NDIs and snow depth at wavelengths less than 570 nm for the magnitude. However, they attribute snow depth little influence on the distribution between 400 and 550 nm. Nevertheless, our findings and the results from Wongpan et al. (2018) confirm that the snow depth influences the under-ice radiation also at wavelengths below 500 nm and supports the application of the NDI method with 440:403 nm.
We find that wavelength pairs with spectral ranges larger than 30 nm perform better than those with lower ranges. For example, we tested another wavelength pair with a spectral range lower than 20 nm that significantly overestimated the snow depth (not shown). Further, Melbourne-Thomas et al. (2015) provide wavelength pairs with spectral ranges of 3 and 4 nm. Those are likely too narrow to resolve the spectral influence of snow depth, given that the spectral resolution of the radiometer is only 3.3 nm.
4.3 Model-Specific Comparison to Existing Studies
The two-layer RT model (Eq. 2) is idealized and theoretically only valid in the absence of scattering and far away from boundaries (Mobley, 1994). Those simplified conditions are rarely met in sea ice (Light et al., 2004). However, this approximation is often used for modelling approaches within sea ice. It gives already useful information, as presented in this work, and is the easiest form of a RT model (Grenfell and Maykut, 1977). Further, Arndt et al. (2017) use this RT model in the Antarctic and find reliable estimates of spectral snow and sea ice extinction coefficients. This strengthens our confidence that this simple model is a justified tool for our application.
The values of our spectral snow extinction coefficients obtained during MAPLI18 agree with the lower ranges published by Warren (1982) and Perovich (2007). They are very close to values presented by McDonald et al. (2015) for landfast FYI near Resolute Passage, Canada, in spring. Their shape is in agreement with Grenfell and Maykut (1977) and McDonald et al. (2015). Our broadband coefficient matches with the values from Mundy et al. (2005) and McDonald et al. (2011) obtained also close to Resolute Passage during spring. The sea ice extinction coefficients seem too high compared to values stated by Grenfell and Maykut (1977), Perovich (1996), and Light et al. (2008). However, they compare well to results from Katlein et al. (2015, 2019). The overall agreement with literature values suggests that our snow and sea ice extinction coefficients are reliable estimates and justify their use to retrieve snow depth with the RT model.
During AO18, the spectral extinction coefficients and thus, the transmittance were likely influenced by a small melt pond in the vicinity (∼2 m) of where the radiometer was hanging underneath the bare ice (Figure 1D). This is supported by a footprint radius on the surface of the radiometer of about 3 m. Melt-pond covered MYI has clearly different optical properties than FYI. Assuming a scattering coefficient of the melt water of zero is likely justified as the ponds appear blue also after refreezing and thus, scattering can be neglected (Lu et al., 2018). A typical broadband absorption coefficient of 0.1 m−1 and the average melt pond depth of 0.3 m as measured during AO18 lead to a relative error of 3.1% in transmittance that arises when neglecting the absorption within the melt ponds. This small error and the well retrieved snow depth using the RT model (Figure 8C; Table 5) led conclude that besides the different optical properties of melt-pond covered MYI compared to FYI, the MAPLI18 extinction coefficients are suitable to apply also to the AO18 data set.
4.4 General Comparison to Existing Studies
The choice between radiance/transflectance and irradiance/transmittance likely affects the method calibration of snow depth retrieval. The opening angle of the radiometers influences the ability to resolve small spatial scales of snow depth and to capture outlier values. Transflectance is based on the much smaller opening angle of 7° of the radiance radiometer compared to the half sphere of the irradiance radiometer. Mundy et al. (2007), McDonald et al. (2015), Melbourne-Thomas et al. (2015), Arndt et al. (2017) and use transmitted irradiance. Wongpan et al. (2018) use transmitted radiance but do not account for atmospheric variations, which is more accounted forwhen using transflectance. For the spatial variability we use transflectance whereas for the temporal variability we use transmittance measurements from the buoys. This might be sufficient for the buoy measurements because we do not aim to resolve spatial scales but reproduce the temporal variability.
The methods calibrated with measurements collected at the marker locations are expected to yield better results compared to using non-marker measurements. The reasons for that assumption are a shallower water column between radiometer and ice bottom and with that less absorption by water and a stable well-known ROV position. However, the NDI method is based on all measurements along the transect, so also the non-marker measurements. Thus, we conclude that our assumption of neglecting absorption by water and water biomass during MAPLI18 is justified.
The performance seems to also depend on the variability of the measured snow depth used to calibrate the methods. On 9 May, the range in measured snow depths was in the mean 21 cm lower than on 12 and 23 May (Table 1). The methods calibrated with snow depths measured on 9 May did not perform as good as the methods presented here (not shown). This suggests that if the range in snow depth is limited in the calibration stage of the methods, their ability to retrieve a larger variety of snow depths will be modest.
4.5 Application to Sea Ice Research Including Technological Aspects
In general, it is easier to measure the snow depth directly, e.g., using a magnaprobe, than measuring under-ice radiation. However, when measuring under-ice radiation using an underwater platform coincident measurements of snow depth are often not practical because they can also destruct the surface which will impact subsequent under-ice radiation measurements, especially when time series under the same ice area need to be collected. Thus, the advantage of developing the two methods presented in this study is to enable snow depth retrieval remotely from under-ice radiation yielding co-localized, non-destructive data of under-ice radiation and snow depth.
Little is known about the spatiotemporal distribution of snow depth on sea ice on regional scales (Sturm and Massom, 2017). Hence, a future aim is to retrieve high spatial coverage snow depth for large regions of Arctic sea ice which is in particular necessary to improve the description of snow processes in climate models (Webster et al., 2018) and the validation of satellite products. A product derived from this study could be probability density functions of snow depth that could serve as input for, e.g., Icepack, the column physics package of the Los Alamos sea ice model CICE (e.g., Zampieri et al., 2021). However, for that to be feasible the gaps between local scale studies as presented here and larger scales studied in models need to be minimized. One step could be to apply the methods to all available under-ice surveys where radiation was measured and retrieve snow depths for the different ice types, and spatial and temporal scales covered therein. For example, Katlein et al. (2019) provide radiation data for many ROV surveys in the Arctic between 2011 and 2017. This would also help to further monitor and assess changes of under-ice radiation, snow depth, and their combined effects on the energy and mass balance of the sea ice in the focus of climate change. However, measuring snow depth in-situ for larger areas is neither practical nor appealing. This gap could be closed once extensive AUV surveys with a focus on measuring under-ice radiation from which snow depth can be retrieved can be conducted regularly. During an AUV survey presented by Wulff et al. (2016) measurements were collected along a short section of a few kilometers in a couple of hours at the marginal ice zone in Fram Strait. Possibilities for larger surveys will exist in the future, as technology in AUV operations advances.
In this study, we retrieve snow depth on two ice types, at two geographic locations, and during two seasons. FYI and melt-pond covered ice are predicted to prevail in the future Arctic (e.g., Maslanik et al., 2007; Perovich et al., 2009; Schröder et al., 2014). Therefore, information on the snow depth for those ice types is important to study the energy balance, especially prior to the melt season (MAPLI18) and before and during freezing (AO18).
Biological studies would benefit from using our methods by retrieving snow depth from the same data set used to estimate biogeochemical properties. With that, interpretation of data could be put in a broader context.
Chlorophyll a concentrations were successfully retrieved from ice core scanning using hyperspectral cameras (e.g., Cimoli et al., 2020). In this process, small sections of biomass containing ice cores are cut and illuminated with different light sources. Hyperspectral images of the through the ice section transmitted light result in light spectra from which, e.g., biomass absorption peaks can be investigated.
Such an optical set-up is in principal possible to perform on sections of snow-covered ice. However, it might be logistically challenging to retrieve an ice core with an undisturbed snow cover from the field. Instead, laboratory studies could be envisioned using in the freezer grown sea ice and artificial snow. Hyperspectral images could then be used to examine the spectral effect of snow on the transmitted light.
Another method used to retrieve chlorophyll a concentrations from under-ice radiation spectra is the principal component analysis (e.g., Lange et al., 2016; Cimoli et al., 2020). In this method, spectra are normalized to reduce the variability due to the magnitude and to focus on the spectral shape (Craig et al., 2012; Taylor et al., 2013). Several steps of statistical computations described by Lange et al. (2016) result in empirical orthogonal functions which modes characterize the variability in the spectra. Within linear functions, those modes act as predictor variables to retrieve chlorophyll a. In principle, this method could be used to retrieve snow depth.
The NDI method could benefit from a multilinear regression (e.g., Lange et al., 2016) or machine learning approach to use instead of one wavelength pair, several. This is expected to yield better results but the simplicity of the NDI method as presented here has its advantages. Radiometers with two wavelengths compared to hyperspectral radiometers (e.g., TriOS) are cheaper. For example, the Ocean Color Radiometer 504 or 507 manufactured by WET Labs, Inc. Thus, the application of the NDI method could also reduce costs and material for future deployments of autonomous stations.
4.6 Limitations
4.6.1 Atmospheric Influence
Optical measurements should be collected under overcast conditions and at around noon. Clear sky conditions and changing cloud cover and solar elevation lead to variations in the blue part of the spectrum. This also affects the direction from which photons originate and the distance they travel within the snow and sea ice.
The diurnal cycle during MAPLI18 is caused by variations of incident irradiance in the blue part of the spectrum which is reflected in the transmitted irradiance (Figure 7D). As evident in the transmittance, the influence of atmospheric absorption is not completely compensated for by normalizing the transmitted irradiance with the incident irradiance (Figure 7E). For some atmospheric conditions some variability persists under the ice which seems to have been the case during 7 and 9 to 12 May. In contrast, during AO18 a diurnal cycle is not present in the transmittance and thus not in the retrieved snow depths (Figure 8). Most likely, this is due to smaller daily solar variations owing the higher latitude and the season. The diurnal cycle is also not present in the retrieved snow depths when using wavelengths in the red part of the spectrum as the snow attenuates the incident irradiance very efficiently at those wavelengths (Figure 7, Perovich, 2007). Here, the retrieval depends more on the magnitude of the transmitted irradiance.
During AO18, substantial noise in the snow depth retrieved using red wavelengths is attributed to irradiances below 1.0 mWm−2 and transmittance below 1% (Figure 8, Katlein et al., 2021). From 14 September onwards noise is also evident in the snow depth retrieved using blue wavelengths (Figure 8B). This corresponds to transmitted irradiance and transmittance close to zero caused by the sharp increase in snow depth recorded by the pinger.
It seems that rapid and extensive variations in air temperature affect the measured snow depth from the ultrasonic pingers of Snow Buoy 2018S63 even though the measurements are temperature compensated (Figure 7, Nicolaus et al., 2021).
The limitations addressed here can be partly compensated for by using daily means of radiation to retrieve snow depth. For example, the period where the NDI method with the wavelength pairs 440:403 nm yields reasonable results can be prolonged but it is unclear for how long, e.g., towards winter (Figure 8B).
4.6.2 Influence of Other Constituents on the Extinction of Solar Radiation
Besides snow depth and ice thickness, the magnitude and spectral shape of the radiation are also determined by snow grain size, wetness, and density, snow and ice temperature, snow metamorphism (e.g., Warren, 1982; Perovich, 1996; Perovich et al., 1998), particulates in snow (Warren, 1982) and ice (Light et al., 2008), water (e.g., Baker and Smith, 1982) and in-ice biomass (e.g., Mundy et al., 2007). Especially the biomass has large effects during spring bloom (Perovich et al., 1998). The optical properties of snow can also be locally altered through flooding which changes the physical and optical snow properties, leads subsequently to refrozen snow ice and additional biomass introduced on the snow/ice interface (Perovich, 1990; Arndt et al., 2017).
During MAPLI18, we observed typical snow characteristics with metamorphic forms. Air temperatures were negative, thus, most likely no further melt processes were initiated (Figure 7F). Including information of the internal snow layers and their optical properties as well as scattering may improve the snow depth retrieval. However, we neglect the influences of the above mentioned effects and achieve satisfying accuracies for the snow depth retrieval by doing so. The calibration and results of the methods also benefit from clear water, low in-ice chlorophyll a (Lange et al., 2019), and level ice with constant thickness.
5 Conclusion
We apply two optical methods that successfully retrieve spatial and temporal variations in snow depth on different ice types, locations, and seasons with a combined mean RMSE of 5.6 cm. The spectral effect of snow on the transflectance can be separated from other components because the water was clear, in-ice biomass was low, and the ice was level and had a constant thickness. This makes it possible to establish relationships between transflectance and snow depth.
The spatial variability and magnitude in snow depth on landfast level FYI in the Lincoln Sea in spring 2018 (MAPLI18) can be reproduced 1) by NDIs with the wavelength pairs 651:616 nm and 440:403 nm and 2) by an idealized two-layer RT model with a nonlinear least square algorithm including inversely retrieved spectral snow and sea ice extinction coefficients.
Both methods are less reliable in retrieving the temporal variability of snow depth during MAPLI18 due to the influence of the diurnal cycle in solar radiation at wavelengths in the blue part of the spectrum. However, the magnitudes of the retrieved snow depths agree with the measured time series, especially when comparing daily means.
In contrast, the temporal variability on drifting, melt-pond covered MYI in the Central Arctic during autumn 2018 (AO18) can be reproduced by the methods using blue wavelengths. This is because atmospheric variations in the blue part of the spectrum are less pronounced here, likely owing the higher latitude and the different season. The NDI method with wavelengths close to the near-infrared produce noise in the retrieved snow depth because the extinction of radiation by snow at those wavelengths is strong. This can partly be compensated for when constraining to daily means.
In no regard is this work meant to replace in situ, airborne, or satellite snow depth measurements and retrievals. The methods can rather provide a step forward to retrieve snow depth from under-ice hyperspectral measurements and serve as a close-range sensing tool that can increase spatial and temporal coverage of local measurements that can be applied across different regions. This can be particularly useful in providing auxiliary data for remotely operated and autonomous under-ice missions, where surface data are unavailable.
Data Availability Statement
All data presented in this study are publicly available under the following DOIs: ROV: doi:10.1594/PANGAEA.930289. Terrestrial laser scanner, magnaprobe, EM31-SH: doi:10.1594/PANGAEA.932594. 2018S63: doi:10.1594/PANGAEA.905717. 2018R23: doi:10.1594/PANGAEA.936597 (dataset in review). 2018S69: doi:10.1594/PANGAEA.905723. 2018R4: doi:10.1594/PANGAEA.936930 (dataset in review).
Author Contributions
PA processed, analyzed, and interpreted the data, prepared the figures, and wrote the manuscript. PA, CK, and MN designed the research. SA provided input to calculate NDIs and perform RT model simulations. PA, CK, AJ, and CH collected data. AJ and CH partly processed EM31-SH ice thickness and magnaprobe snow depth data. All authors contributed to the improvement and discussing of text, figures, and methods.
Funding
This work was financed through the research programs PACES II and POF4 from the Alfred-Wegener-Institut Helmholtz-Zentrum für Polar-und Meeresforschung (AWI). This work represents a contribution to the Diatom-ARCTIC project (NE/R012849/1; 03F0810A), part of the Changing Arctic Ocean program, jointly funded by the UKRI Natural Environment Research Council (NERC) and the German Federal Ministry of Education and Research (BMBF). This work was supported by the German Research Council (DFG) in the framework of the priority program “Antarctic Research with comparative investigations in the Arctic ice areas” (grant nos. SPP1158 and AR1236/1). The deployment of the radiation station 2018R4 and the Snow Buoy 2018S69 as well as the ROV work were supported by the Helmholtz Infrastructure Initiative Frontiers in Arctic marine Monitoring (FRAM). We also acknowledge financial support by the Open Access Publication Funds of AWI.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Polar Continental Shelf Program (PCSP), Natural Resources Canada; Department of National Defense (DND) at CFS Alert, and Defense Research and Development Canada (DRDC), Environment and Climate Change Canada (ECCC), and the communities and Hunters and Trappers Associations of Resolute Bay and Grise Fjord. Special thanks to A. Platt (ECCC), C. Brown, J. Milne, J. Higgins and M. Simms at DRDC for all their efforts in logistics, and Major C. Stiles (CO), R. Hansen (SWO) and R. Lutz (Alta SWO) at CFS Alert. We also thank the MAP—Last Ice Program led by Christine Michel, funded by Fisheries and Oceans Canada (DFO) Science. Deployment of 2018R4 and participation in the AO18 expedition of the Swedish icebreaker Oden was facilitated by the Swedish Polar Research Secretariat (SPRS). We want to thank in particular Mario Hoppmann and Matthieu Labaste for field assistance, as well as Anja Nicolaus for administrative support around the buoy deployment.
References
Arndt, S., Meiners, K. M., Ricker, R., Krumpen, T., Katlein, C., and Nicolaus, M. (2017). Influence of Snow Depth and Surface Flooding on Light Transmission through Antarctic Pack Ice. J. Geophys. Res. Oceans 122 (3), 2108–2119. doi:10.1002/2016jc012325
Arrigo, K. R., Sullivan, C. W., and Kremer, J. N. (1991). A Bio-Optical Model of Antarctic Sea Ice. J. Geophys. Res. 96 (C6), 10581. doi:10.1029/91jc00455
Baker, K. S., and Smith, R. C. (1982). Bio-optical Classification and Model of Natural Waters. 21. Limnol. Oceanogr. 27 (3), 500–509. doi:10.4319/lo.1982.27.3.0500
Campbell, K., Mundy, C. J., Barber, D. G., and Gosselin, M. (2014). Remote Estimates of Ice Algae Biomass and Their Response to Environmental Conditions during Spring Melt. Arctic 67 (3), 375. doi:10.14430/arctic4409
Castellani, G., Schaafsma, F. L., Arndt, S., Lange, B. A., Peeken, I., Ehrlich, J., et al. (2020). Large-Scale Variability of Physical and Biological Sea-Ice Properties in Polar Oceans. Front. Mar. Sci. 7 (536), 1–22. doi:10.3389/fmars.2020.00536
Cimoli, E., Lucieer, V., Meiners, K. M., Chennu, A., Castrisios, K., Ryan, K. G., et al. (2020). Mapping the In Situ Microspatial Distribution of Ice Algal Biomass through Hyperspectral Imaging of Sea-Ice Cores. Sci. Rep. 10 (1), 1–18. doi:10.1038/s41598-020-79084-6
Craig, S. E., Jones, C. T., Li, W. K. W., Lazin, G., Horne, E., Caverhill, C., et al. (2012). Deriving Optical Metrics of Coastal Phytoplankton Biomass from Ocean Colour. Remote Sensing Environ. 119, 72–83. doi:10.1016/j.rse.2011.12.007
Graversen, R. G., Mauritsen, T., Tjernström, M., Källén, E., and Svensson, G. (2008). Vertical Structure of Recent Arctic Warming. Nature 451, 53–56. doi:10.1038/nature06502
Grenfell, T. C., and Maykut, G. A. (1977). The Optical Properties of Ice and Snow in the Arctic Basin. J. Glaciol. 18 (80), 445–463. doi:10.3189/S0022143000021122
Guerreiro, K., Fleury, S., Zakharova, E., Rémy, F., and Kouraev, A. (2016). Potential for Estimation of Snow Depth on Arctic Sea Ice from CryoSat-2 and SARAL/AltiKa Missions. Remote Sensing Environ. 186, 339-349. doi:10.1016/j.rse.2016.07.013
Haas, C., Beckers, J., King, J., Silis, A., Stroeve, J., Wilkinson, J., et al. (2017). Ice and Snow Thickness Variability and Change in the High Arctic Ocean Observed by In Situ Measurements. Geophys. Res. Lett. 44 (20), 10 462–10 469. doi:10.1002/2017gl075434
Haas, C., Gerland, S., Eicken, H., and Miller, H. (1997). Comparison of Sea‐ice Thickness Measurements under Summer and winter Conditions in the Arctic Using a Small Electromagnetic Induction Device. Geophysics 62 (3), 749–757. doi:10.1190/1.1444184
Haas, C., Pfaffling, A., Hendricks, S., Rabenstein, L., Etienne, J.-L., and Rigor, I. (2008). Reduced Ice Thickness in Arctic Transpolar Drift Favors Rapid Ice Retreat. Geophys. Res. Lett. 35 (17), 1–5. doi:10.1029/2008gl034457
Jutila, A., King, J., Paden, J., Ricker, R., Hendricks, S., Polashenski, C., et al. (2021). High-Resolution Snow Depth on Arctic Sea Ice from Low-Altitude Airborne Microwave Radar Data. IEEE Trans. Geosci. Remote Sensing, 1–16. doi:10.1109/tgrs.2021.3063756
Katlein, C., Arndt, S., Belter, H. J., Castellani, G., and Nicolaus, M. (2019). Seasonal Evolution of Light Transmission Distributions through Arctic Sea Ice. J. Geophys. Res. Oceans 124 (8), 5418–5435. doi:10.1029/2018jc014833
Katlein, C., Arndt, S., Nicolaus, M., Perovich, D. K., Jakuba, M. V., Suman, S., et al. (2015). Influence of Ice Thickness and Surface Properties on Light Transmission through A Rctic Sea Ice. J. Geophys. Res. Oceans 120 (9), 5932–5944. doi:10.1002/2015JC010914
Katlein, C., Perovich, D. K., and Nicolaus, M. (2016). Geometric Effects of an Inhomogeneous Sea Ice Cover on the under Ice Light Field. Front. Earth Sci. 4, 1–10. doi:10.3389/feart.2016.00006
Katlein, C. (2012). ROV basierte Untersuchung der räumlichen Variabilität der Lichttransmisson durch arktisches Meereis im Sommer. Diplomarbeit. Eberhard Karls Universität Tübingen. Available at: https://epic.awi.de/id/eprint/31748/.
Katlein, C., Schiller, M., Belter, H. J., Coppolaro, V., Wenslandt, D., and Nicolaus, M. (2017). A New Remotely Operated Sensor Platform for Interdisciplinary Observations under Sea Ice. Front. Mar. Sci. 4, 1–12. doi:10.3389/fmars.2017.00281
Katlein, C., Valcic, L., Lambert-Girard, S., and Hoppmann, M. (2021). New Insights into Radiative Transfer within Sea Ice Derived from Autonomous Optical Propagation Measurements. The Cryosphere 15 (1), 183–198. doi:10.5194/tc-15-183-2021
Kwok, R., and Rothrock, D. A. (2009). Decline in Arctic Sea Ice Thickness from Submarine and ICESat Records: 1958-2008. Geophys. Res. Lett. 36 (15), a–n. doi:10.1029/2009GL039035
Lange, B. A., Haas, C., Charette, J., Katlein, C., Campbell, K., Duerksen, S., et al. (2019). Contrasting Ice Algae and Snow‐Dependent Irradiance Relationships between First‐Year and Multiyear Sea Ice. Geophys. Res. Lett. 46 (19), 10834–10843. doi:10.1029/2019gl082873
Lange, B. A., Katlein, C., Nicolaus, M., Peeken, I., and Flores, H. (2016). Sea Ice Algae Chlorophyll a Concentrations Derived from Under-ice Spectral Radiation Profiling Platforms. J. Geophys. Res. Oceans 121 (12), 8511–8534. doi:10.1002/2016jc011991
Lawrence, I. R., Tsamados, M. C., Stroeve, J. C., Armitage, T. W. K., and Ridout, A. L. (2018). Estimating Snow Depth over Arctic Sea Ice from Calibrated Dual-Frequency Radar Freeboards. The Cryosphere 12 (11), 3551–3564. doi:10.5194/tc-12-3551-2018
Light, B., Grenfell, T. C., and Perovich, D. K. (2008). Transmission and Absorption of Solar Radiation by Arctic Sea Ice during the Melt Season. J. Geophys. Res. 113 (C3), 1–19. doi:10.1029/2006jc003977
Light, B., Maykut, G. A., and Grenfell, T. C. (2004). A Temperature-dependent, Structural-Optical Model of First-Year Sea Ice. J. Geophys. Res. 109 (C06013), 1–16. doi:10.1029/2003jc002164
Lu, P., Leppäranta, M., Cheng, B., Li, Z., Istomina, L., and Heygster, G. (2018). The Color of Melt Ponds on Arctic Sea Ice. The Cryosphere 12 (4), 1331–1345. doi:10.5194/tc-12-1331-2018
Markus, T., Stroeve, J. C., and Miller, J. (2009). Recent Changes in Arctic Sea Ice Melt Onset, Freezeup, and Melt Season Length. J. Geophys. Res. 114 (C12), 1–14. doi:10.1029/2009JC005436
Maslanik, J. A., Fowler, C., Stroeve, J., Drobot, S., Zwally, J., Yi, D., et al. (2007). A Younger, Thinner Arctic Ice Cover: Increased Potential for Rapid, Extensive Sea-Ice Loss. Geophys. Res. Lett. 34 (24), 1–5. doi:10.1029/2007gl032043
McDonald, S., Koulis, T., Ehn, J., Campbell, K., Gosselin, M., and Mundy, C. J. (2017). A Functional Regression Model for Predicting Optical Depth and Estimating Attenuation Coefficients in Sea-Ice Covers Near Resolute Passage, Canada. Ann. Glaciol. 56 (69), 147–154. doi:10.3189/2015AoG69A004
Meiners, K. M., Arndt, S., Bestley, S., Krumpen, T., Ricker, R., Milnes, M., et al. (2017). Antarctic Pack Ice Algal Distribution: Floe-Scale Spatial Variability and Predictability from Physical Parameters. Geophys. Res. Lett. 44 (14), 7382–7390. doi:10.1002/2017gl074346
Melbourne-Thomas, J., Meiners, K., Mundy, C., Schallenberg, C., Tattersall, K., and Dieckmann, G. (2015). Algorithms to Estimate Antarctic Sea Ice Algal Biomass from Under-ice Irradiance Spectra at Regional Scales. Mar. Ecol. Prog. Ser. 536, 107–121. doi:10.3354/meps11396
Meredith, M., Sommerkorn, M., Cassotta, S., Derksen, C., Ekaykin, A., Hollowed, A., et al. (2019). “Polar Regions,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. H. O. Pörtner, D. Roberts, V. Masson-Delmotte, P. Zhai, M. Tignor, E. Poloczanskaet al. Editors (Geneva, Switzerland: Intergovernmental Panel on Climate Change). URL https://www.ipcc.ch/srocc/chapter/chapter-3-2/.
Mobley, C. D. (1994). Light and Water: Radiative Transfer in Natural Waters. San Diego: Academic Press.
Mundy, C. J., Ehn, J. K., Barber, D. G., and Michel, C. (2007). Influence of Snow Cover and Algae on the Spectral Dependence of Transmitted Irradiance through Arctic Landfast First-Year Sea Ice. J. Geophys. Res. 112 (C3), 1–10. doi:10.1029/2006jc003683
Nicolaus, M., Gerland, S., Hudson, S. R., Hanson, S., Haapala, J., and Perovich, D. K. (2010a). Seasonality of Spectral Albedo and Transmittance as Observed in the Arctic Transpolar Drift in 2007. J. Geophys. Res. 115 (C11), 1–21. doi:10.1029/2009jc006074
Nicolaus, M., Hoppmann, M., Arndt, S., Hendricks, S., Katlein, C., Nicolaus, A., et al. (2021). Snow Depth and Air Temperature Seasonality on Sea Ice Derived from Snow Buoy Measurements. Front. Mar. Sci. 8, 1–21. doi:10.3389/fmars.2021.655446
Nicolaus, M., Hudson, S. R., Gerland, S., and Munderloh, K. (2010b). A Modern Concept for Autonomous and Continuous Measurements of Spectral Albedo and Transmittance of Sea Ice. Cold Regions Sci. Technology 62 (1), 14–28. doi:10.1016/j.coldregions.2010.03.001
Nicolaus, M., and Katlein, C. (2013). Mapping Radiation Transfer through Sea Ice Using a Remotely Operated Vehicle (ROV). The Cryosphere 7 (3), 763–777. doi:10.5194/tc-7-763-2013
Nicolaus, M., Katlein, C., Maslanik, J., and Hendricks, S. (2012). Changes in Arctic Sea Ice Result in Increasing Light Transmittance and Absorption. Geophys. Res. Lett. 39 (24). doi:10.1029/2012gl053738
Nicolaus, M., Petrich, C., Hudson, S. R., and Granskog, M. A. (2013). Variability of Light Transmission through Arctic Land-Fast Sea Ice during spring. The Cryosphere 7 (3), 977–986. doi:10.5194/tc-7-977-2013
Perovich, D. K., Grenfell, T. C., Light, B., Elder, B. C., Harbeck, J., Polashenski, C., et al. (2009). Transpolar Observations of the Morphological Properties of Arctic Sea Ice. J. Geophys. Res. 114 (C00A04), 1–17. doi:10.1029/2008jc004892
Perovich, D. K. (2007). Light Reflection and Transmission by a Temperate Snow Cover. J. Glaciol. 53 (181), 201–210. doi:10.3189/172756507782202919
Perovich, D. K., and Polashenski, C. (2012). Albedo Evolution of Seasonal Arctic Sea Ice. Geophys. Res. Lett. 39 (L08501), a–n. doi:10.1029/2012GL051432
Perovich, D. K., Roesler, C. S., and Pegau, W. S. (1998). Variability in Arctic Sea Ice Optical Properties. J. Geophys. Res. 103 (C1), 1193–1208. doi:10.1029/97jc01614
Perovich, D. K. (1996). “The Optical Properties of Sea Ice,” in Monogr N. H Hanover (US: U.S. Army Cold Regions Research and Engineering Laboratory), 96-1.
Perovich, D. K. (1990). Theoretical Estimates of Light Reflection and Transmission by Spatially Complex and Temporally Varying Sea Ice Covers. J. Geophys. Res. 95 (C6), 9557. doi:10.1029/JC095iC06p09557
Petrich, C., Nicolaus, M., and Gradinger, R. (2012). Sensitivity of the Light Field under Sea Ice to Spatially Inhomogeneous Optical Properties and Incident Light Assessed with Three-Dimensional Monte Carlo Radiative Transfer Simulations. Cold Regions Sci. Technology 73, 1–11. doi:10.1016/j.coldregions.2011.12.004
Rabenstein, L., Hendricks, S., Martin, T., Pfaffhuber, A., and Haas, C. (2010). Thickness and Surface-Properties of Different Sea-Ice Regimes within the Arctic Trans Polar Drift: Data from Summers 2001, 2004 and 2007. J. Geophys. Res. 115, 1–18. doi:10.1029/2009jc005846
Richter-Menge, J. A., Perovich, D. K., Elder, B. C., Claffey, K., Rigor, I., and Ortmeyer, M. (2006). Ice Mass-Balance Buoys: a Tool for Measuring and Attributing Changes in the Thickness of the Arctic Sea-Ice Cover. Ann. Glaciol. 44, 205–210. doi:10.3189/172756406781811727
Rostosky, P., Spreen, G., Farrell, S. L., Frost, T., Heygster, G., and Melsheimer, C. (2018). Snow Depth Retrieval on Arctic Sea Ice from Passive Microwave Radiometers-Improvements and Extensions to Multiyear Ice Using Lower Frequencies. J. Geophys. Res. Oceans 123 (10), 7120–7138. doi:10.1029/2018jc014028
Schröder, D., Feltham, D. L., Flocco, D., and Tsamados, M. (2014). September Arctic Sea-Ice Minimum Predicted by spring Melt-Pond Fraction. Nat. Clim Change 4 (5), 353–357. doi:10.1038/nclimate2203
Serreze, M. C., Holland, M. M., and Stroeve, J. (2007). Perspectives on the Arctic's Shrinking Sea-Ice Cover. Science 315, 1533–1536. doi:10.1126/science.1139426
Smith, R. C., and Baker, K. S. (1981). Optical Properties of the Clearest Natural Waters (200-800 Nm). Appl. Opt. 20 (2), 177. doi:10.1364/AO.20.000177
Sorensen, D. C. (1982). Newton's Method with a Model Trust Region Modification. SIAM J. Numer. Anal. 19 (2), 409–426. doi:10.1137/0719026
Steele, M., Zhang, J., and Ermold, W. (2010). Mechanisms of Summertime Upper Arctic Ocean Warming and the Effect on Sea Ice Melt. J. Geophys. Res. 115 (C11004). doi:10.1029/2009JC005849
Stroeve, J. C., Kattsov, V., Barrett, A., Serreze, M., Pavlova, T., Holland, M., et al. (2012). Trends in Arctic Sea Ice Extent from CMIP5, CMIP3 and Observations. Geophys. Res. Lett. 39 (16), a–n. doi:10.1029/2012gl052676
Stroeve, J., and Notz, D. (2018). Changing State of Arctic Sea Ice across All Seasons. Environ. Res. Lett. 13 (10), 103001. doi:10.1088/1748-9326/aade56
Sturm, M., and Holmgren, J. (2018). An Automatic Snow Depth Probe for Field Validation Campaigns. Water Resour. Res. 54 (11), 9695–9701. doi:10.1029/2018wr023559
Sturm, M., and Massom, R. A. (2017). Snow in the Sea Ice System: Friend or Foe? Sea Ice. Editor D. M. Thomas, Hoboken, New Jersey, United States: Wiley, 65–109. doi:10.1002/9781118778371.ch3
Taylor, B. B., Taylor, M. H., Dinter, T., and Bracher, A. (2013). Estimation of Relative Phycoerythrin Concentrations from Hyperspectral Underwater Radiance Measurements--A Statistical Approach. J. Geophys. Res. Oceans 118 (6), 2948–2960. doi:10.1002/jgrc.20201
Warren, S. G. (1982). Optical Properties of Snow. Rev. Geophys. 20 (1), 67. doi:10.1029/RG020i001p00067
Webster, M., Gerland, S., Holland, M., Hunke, E., Kwok, R., Lecomte, O., et al. (2018). Snow in the Changing Sea-Ice Systems. Nat. Clim Change 8 (11), 946–953. doi:10.1038/s41558-018-0286-7
Wongpan, P., Meiners, K. M., Langhorne, P. J., Heil, P., Smith, I. J., Leonard, G. H., et al. (2018). Estimation of Antarctic Land-Fast Sea Ice Algal Biomass and Snow Thickness from Under-ice Radiance Spectra in Two Contrasting Areas. J. Geophys. Res. Oceans 123 (3), 1907–1923. doi:10.1002/2017jc013711
Wulff, T., Bauerfeind, E., and von Appen, W.-J. (2016). Physical and Ecological Processes at a Moving Ice Edge in the Fram Strait as Observed with an AUV. Deep Sea Res. Oceanographic Res. Pap. 115, 253–264. doi:10.1016/j.dsr.2016.07.001
Zampieri, L., Kauker, F., Fröhle, J., Sumata, H., Hunke, E. C., and Goessling, H. F. (2021). Impact of Sea‐Ice Model Complexity on the Performance of an Unstructured‐Mesh Sea‐Ice/Ocean Model under Different Atmospheric Forcings. J. Adv. Model. Earth Syst. 13 (5), e2020MS002438. doi:10.1029/2020ms002438
Keywords: snow depth, retrieval, sea ice, under-ice optics, remotely operated vehicle
Citation: Anhaus P, Katlein C, Nicolaus M, Arndt S, Jutila A and Haas C (2021) Snow Depth Retrieval on Arctic Sea Ice Using Under-Ice Hyperspectral Radiation Measurements. Front. Earth Sci. 9:711306. doi: 10.3389/feart.2021.711306
Received: 18 May 2021; Accepted: 12 November 2021;
Published: 17 December 2021.
Edited by:
Hongjie Xie, University of Texas at San Antonio, United StatesReviewed by:
Emiliano Cimoli, University of Tasmania, AustraliaPeng Lu, Dalian University of Technology, China
Copyright © 2021 Anhaus, Katlein, Nicolaus, Arndt, Jutila and Haas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Philipp Anhaus, cGhpbGlwcC5hbmhhdXNAYXdpLmRl
 Philipp Anhaus
Philipp Anhaus Christian Katlein
Christian Katlein Marcel Nicolaus
Marcel Nicolaus Stefanie Arndt
Stefanie Arndt Arttu Jutila
Arttu Jutila Christian Haas1,2
Christian Haas1,2