Dynamic Process and Mechanism of the Catastrophic Taihongcun Landslide Triggered by the 2008 Wenchuan Earthquake Based on Field Investigations and Discrete Element Method Simulations

The Taihongcun landslide, which was a remarkable geological disaster triggered by the 2008 Wenchuan earthquake, had a volume of about 2 × 106 m³ and killed about 23 people. Through detailed field investigations, basic information of topography, geological structure and stratigraphy for the landslide were acquired and key kinetic characteristics of the landslide were identified. On the basis of filed investigations, 2D numerical models with discrete element method (DEM) were established to simulate the kinematics and failure process of the landslide. To ensure the validity of the dynamic calculations, the free-field boundary condition was developed and introduced intro the DEM models. According to filed investigations and DEM simulations, the dynamic processes of the Taihongcun landslide can be divided into four phases: fragmentation, projection motion, scraping, and granular debris flow and accumulation. In addition, the parameter analysis showed that the particle bond strength had a significant influence on the runout distance and landslide debris morphology. Finally, the possible mechanism of the Taihongcun landslide was determined: a rock mass of poor quality provided the lithological basis for this landslide formation; a joint set J₁ in the back scarp and a weak interlayer of carbonaceous slate and shale between the upper sliding mass and the bedrock formed the rupture boundaries of the upper source area; a strong seismic ground motion was the external excitation that triggered the destructive landslide event; additionally, hypermobility was caused by the high elevation and topographical conditions of the landslide.

Introduction

On May 12, 2008, a magnitude Mw 7.9 earthquake occurred in the Longmenshan Mountains tectonic zone of Sichuan Province, China. The earthquake’s epicenter was located at Yingxiu Town, Wenchuan County (31.0°N and 103.4°E), and the hypocenter was at a depth of approximately 19 km. Surface displacements produced by the fault rupture reached several meters, propagating from the epicenter for approximately 240 km along the mountain range (Fan et al., 2018). According to the statistical data provided by the Chinese government, this earthquake claimed the lives of more than 87,000 people and injured approximately 459,000 others (Qi et al., 2010). More than 60,000 rock avalanches and landslides were triggered by the 2008 Wenchuan earthquake (Gorum et al., 2011; Wang et al., 2014), and several hundred landslide dams were formed.

Landslides triggered by strong earthquakes have always been a popular topic of discussion. The dynamics and failure mechanisms of earthquake-induced landslides are critical to elucidate for improving hazard prevention and mitigation measures. Field investigations indicate that the kinematic processes of earthquake-induced landslides are characterized by high speeds, long runouts, and high mobilities (Wang et al., 2009; Yin et al., 2009; Chigira et al., 2010; Dai et al., 2011; Gorum et al., 2011; Tang et al., 2011; Huang et al., 2012; Zhang and Yin, 2013; Zhang et al., 2016). Considerable kinetic energy, high toe to rupture surface elevations, elastic energy release due to grain fragmentation, and high excessive pore water pressure generated by undrained loading were underscored as the principal controlling factors for the long travel distance, high speed, and high mobility (Wang et al., 2009; Chigira et al., 2010; Zhang and Yin, 2013; Wang et al., 2014). It was concluded that the occurrence of an earthquake-induced landslide is controlled mainly by seismic, terrain, and geological factors (Huang et al., 2012). Strong ground motion generated by the earthquake and topographic amplification of seismic waves due to features of the terrain were emphasized as the main triggers of rock avalanches and landslides (Havenith et al., 2003; Murphy, 2006; Bourdeau and Havenith, 2008; Yin et al., 2009; Huang et al., 2012; Zhou et al., 2013).

Field investigation and numerical simulation are two fundamental techniques for analyzing the dynamics and revealing the possible mechanism of individual landslides induced by strong earthquakes. Through field investigation, detailed information about a single landslide can be obtained, such as its geological and topographical features (Has and Nozaki 2014; Wang et al., 2014; Zhang et al., 2016; Zhuang et al., 2018). Furthermore, field investigation can provide evidence of the dynamic processes for landslides (Zhang et al., 2011, Zhang et al., 2016; Xu et al., 2013). Numerical simulation is an important approach for modelling the dynamic process of rock avalanches and exploring the formation mechanism of earthquake-triggered landslides. At present, numerical simulation methods for the seismic response analysis of rock or soil slopes are mainly divided into two categories. The first category is composed of traditional continuum methods, including the finite element method (FEM) (Charatpangoon et al., 2014; Che et al., 2016) and finite difference method (FDM) (Bouckovalas and Papadimitriou, 2005; Bourdeau and Havenith, 2008; Zhou et al., 2013). The continuous simulation methods are based on the assumption of small deformation and displacement; therefore, using this type of approach, it is difficult to describe large displacements along discontinuities and rotations of blocks in a jointed rock mass under seismic loading. The second category consists of discontinuum methods such as discontinuous deformation analysis (DDA) (Wu and Chen, 2011; Zhang et al., 2015; Huang et al., 2016; Fu et al., 2019) and the discrete element method (DEM). With an explicit scheme-based force balance solution, the DEM exhibits a high computational efficiency in the seismic analysis of large-scale rock mass engineering. In the DEM, blocks or particles resulting from different discretizations of the domain of interest can lead to different approaches. The most popular block-based DEMs are the commercialized UDEC and 3DEC for solving two- and three-dimensional (2D and 3D) problems; these programs have been extensively used in seismic response analyses for rock engineering (Kveldsvik et al., 2009; Cui et al., 2016; Song et al., 2018). The particle-based DEM method introduced by Cundall and Strack (1979) simulates the mechanical behavior of a material by representing it as an assemblage of discs (2D) and spheres (3D). The DEM was originally used to investigate granular materials such as soils/sands and was eventually implemented in a commercial code, i.e., Particle Flow Code (PFC) (Itasca Consulting Group Inc., 2008). To solve problems related to a rock mass, a bonded particle model (BPM), in which intact rocks are represented as assemblages of cemented rigid particles, was developed (Potyondy and Cundall, 2004), and a smooth joint contact model (SJCM) was proposed to model the joints (Ivars et al., 2011).

As previously documented, many earthquake-triggered landslides are characterized by flow-like movement, and the sliding material disintegrates into fragments during the high-speed movement, ultimately forming a granular deposit. The particle-based DEM method simulates the geomaterial as assemblies of rigid discs (in 2D) or spheres (in 3D) bonded at their contacts and allows finite displacements, rotations and separations of the discrete particles. The failure process in the synthetic material can be represented by the breakage of bonds and propagation and coalescence of these microcracks. Therefore, the particle-based DEM is more appropriate than DDA or the continuum methods for simulating the dynamic failure process and kinematic characteristics of landslides triggered by earthquakes. Huang et al. (2012), Tang et al. (2013), Zhou et al. (2013), Yuan et al. (2014), and Deng et al. (2017) developed 2D DEM models to simulate the dynamic process of landslides triggered by earthquakes and explore their seismic failure mechanism. In their simulations, the sliding surface and bedrock were represented by wall elements, and the seismic ground motion histories were applied to the wall boundaries. One drawback of this approach is that the wall boundaries cannot absorb the scattering waves from the upper sliding body, and the radiation of waves from the sliding mass into the bedrock cannot be modeled. Therefore, nonreflecting boundary conditions instead of wall boundaries are required to simulate the failure process of earthquake-induced landslides.

In this study, detailed geological and geomorphological surveys were conducted for the catastrophic Taihongcun landslide triggered by the 2008 Wenchuan earthquake; this landslide is located in Chenjiaba town, Beichuan County, Sichuan Province, China. From the detailed field investigation, the main characteristics of the Taihongcun landslide were identified. Subsequently, 2D DEM models were established to simulate the kinematic and failure processes of the Taihongcun landslide through the PFC2D code. To ensure the validity of the dynamic calculations, the free-field boundary condition was developed and introduced into the DEM models. The effects of the vertical and horizontal seismic forces on the dynamic failure process of this landslide were considered. Finally, based on field investigations and numerical simulations, we discussed the possible mechanism contributing to this landslide event.

Geomorphological and Geological Settings

The catastrophic Taihongcun landslide occurred on the east-facing slope of Shuijingyan Mountain (31°58′25.4″N, 104°35′55.6″E, see Figures 1, 2), which is located northeast of Taihong Village, Chenjiaba Town, Beichuan County in Sichuan Province, China. The landslide, triggered by the 2008 Wenchuan earthquake, killed approximately 23 people, destroyed one village, and blocked the Duba River. The Taihongcun landslide lies on the right bank of the Duba River, originating from the north-south trending ridge of the Shuijingyan mountain (Figure 2B). Due to the long-term river erosion, the west bank is concave, causing the slope near the bank to be unstable (Figure 2A). The geomorphology of the Taihongcun coseismic landslide is chair-shaped and can be divided into two parts by the existence of a notable cliff on the edge of the upper sliding bed (Figure 3A). The upper source area is between 960 and 1,300 m in elevation, with an estimated volume of 1.5 million m³, and the original slope was between 20° and 30° (Figure 3). The back scarp of the upper source area is 170 m wide, 200 m high and has an average slope of approximately 70°. The northern flank (Figure 4C) is approximately 79 m high and approximately 134 m long, with a strike of 90° and a slope of approximately 52°. The southern flank is approximately 42 m high and approximately 200 m long, with a strike of 120° and a slope of approximately 33°. A flat sliding bed can be seen in the middle of the landslide. This flat section is covered with landslide deposits with an average thickness of 40 m; the deposits are gray, with moderately weathered slate fragments present at the surface. The lower cliff induced by the secondary landslide is between 780 and 960 m in elevation and 400 m in width, with an average slope of approximately 50°. Field investigations show that the Yingxiu-Beicuan fault is located at the toe of the landslide (Figure 3). The floodplain of the Duba River is below the lower cliff, and the depth from the bottom of the river to the bank is 35–41 m. The main sliding direction along line I-I′ in Figure 3B is 110°.

FIGURE 1

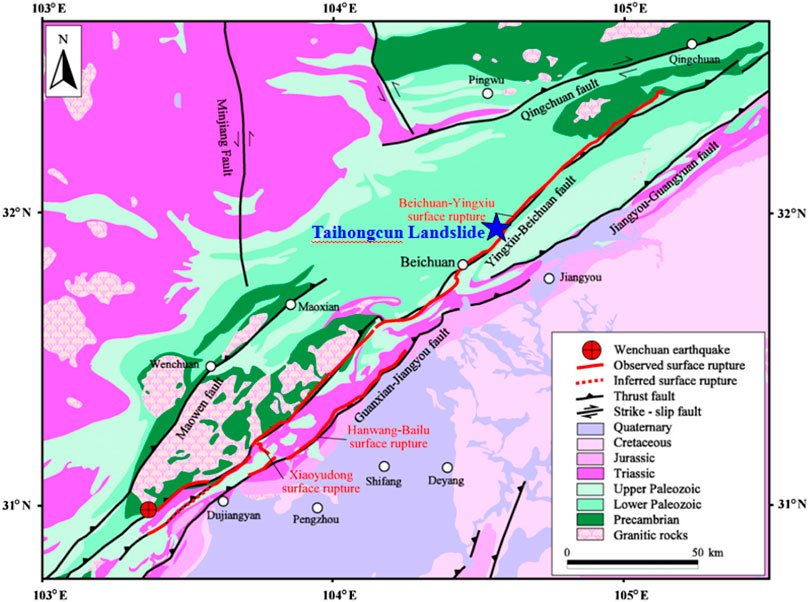
FIGURE 1. Location of the Taihongcun landslide in Beichuan County, Sichuan Province (modified from Dai et al., 2011).

FIGURE 2

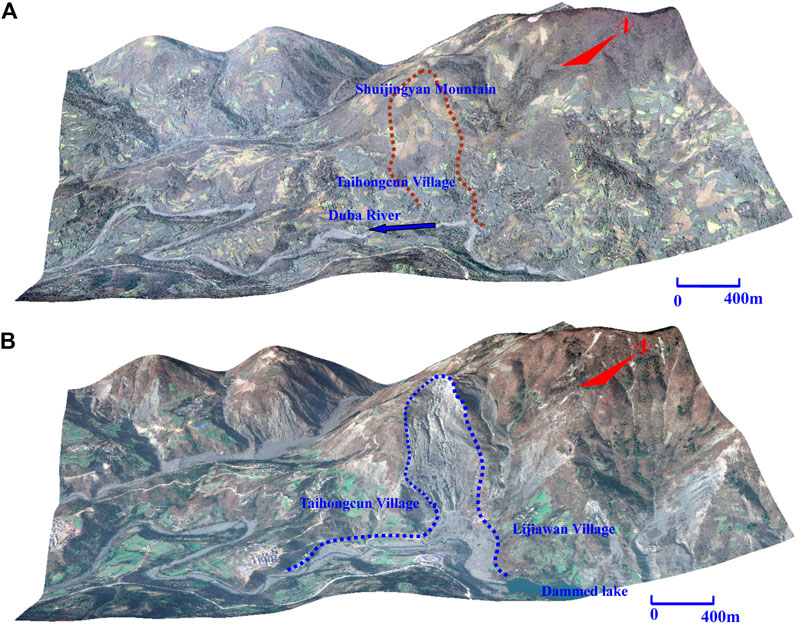
FIGURE 2. (A) Pre-sliding image from Google Earth taken on April 2, 2005; (B) Post-sliding image from Google Earth taken on January 22, 2011.

FIGURE 3

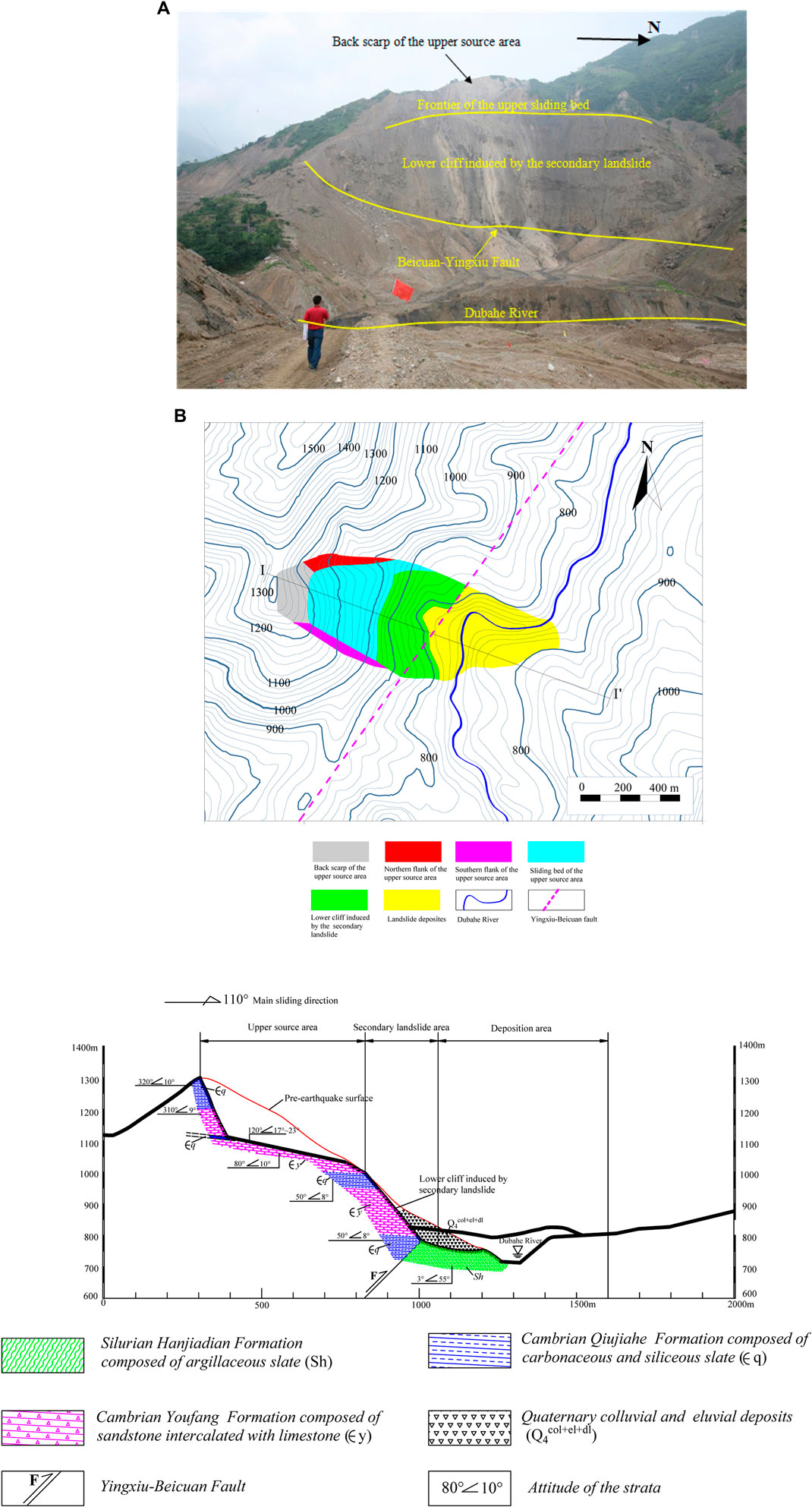
FIGURE 3. (A) Photograph of Taihongcun coseismic landslide, which was taken on July 3, 2008 and the landslide dam had already been breached artificially. (B) Plane view of the Taihongcun landslide. (C) Geological longitudinal section through the main slding direction I-I′ for the Taihongcun landslide.

FIGURE 4

FIGURE 4. Photographs of different parts of the upper source area, which are taken on December 3, 2012. (A) Back scarp. (B) Rock mass of the lower part of back scarp and the photo location are shown as the red circle A in Figure 4A. (C ) Northern flank of the upper source. (D) Sourthern flank of the upper source area.

Figure 3C displays the geological longitudinal section through the main slding direction I-I′ for the Taihongcun landslide. According to field investigations, the Taihongcun slope consists of the Cambrian Qiujiahe Formation (Єq), Cambrian Youfang Formation (Єy) and Silurian Hanjiadian Formation (Sh). The Cambrian Qiujiahe Formation is mainly composed of carbonaceous and siliceous slate (Figure 5D); the Cambrian Youfang Formation is composed of extensively jointed sandstone (Figure 5E); and the Silurian Hanjiadian Formation is composed of thin layers of argillaceous slate. The Cambrian Qiujiahe Formation outcrop, in which the slate is strongly weathered, is observed at the top of the back scarp, with a thickness of approximately 96 m. A 0.4 m wide tension crack is found at the top of the back scarp (Figure 4A). The lower part of the back scarp consists of the Cambrian Youfang Formation, in which the sandstone is intercalated with limestone (Figure 4B), with a thickness of approximately 80 m. Karst erosion has developed along the preexisting fissures in the limestone, weakening the stability of the back scarp. The bedding planes of the strata around the back scarp of the slope gently dip away from the slope surface at an angle of approximately 10°. Two dominant and steep joint sets (J₁, J₂) are widely developed in the back scarp (Figure 4B). Set J1 dips away from the back scarp surface at an angle of approximately 80° and controls the surface deformation of the back scarp.

FIGURE 5

FIGURE 5. Strata in the upper source area. (A) Sliding surface on the location spot B shown in Figure 4A. (B) Sliding surface on the location spot C shown in Figure 4D. (C) Sliding surface on the location spot D shown in Figure 4D. (D) Carbonaceous and siliceous slate of Cambrian Qiujiahe Formation. (E) Sandstone intercalated with limestone of Cambrian Youfang Formation.

The displaced material covering the sliding bed of the upper source area is mainly composed of gray slate blocks and fragments, as observed on the surface. The bedrock of the upper source is the extensively jointed sandstone of the Cambrian Youfang Formation (Figure 5E). Several gullies incised into the deposit by rainfall runoff enabled the internal structure of the deposit and sliding surface to be examined and sampled. As shown in Figures 5A–C, according to observations from a gully, a weak interlayer of carbonaceous slate and shale exists between the landslide deposits and the bedrock, with a dip angle ranging from 17° to 23°. The thickness of this layer is approximately 0.2–1.5 m. An obvious sliding surface can be seen between the displaced material and carbonaceous shale (Figures 5A–C). Therefore, the carbonaceous shale is the strata on top of which the sliding surface occurred. The lower cliff was determined to have formed after the Wenchuan earthquake by comparing Figures 2A,B; this area was subsequently covered by Quaternary colluvial and eluvial deposits with an average thickness of 70 m. The basement rock of the cliff consists of the carbonaceous and siliceous slate of the Cambrian Qiujiahe Formation and sandstone of the Cambrian Youfang Formation. Based on the field observations, the strata in the shallow part of the cliff are highly weathered. Due to the long-term strong tectonic activities of the Yingxiu-Beicuan fault, which lies across the foot of the cliff, the rock mass of the entire slope is fractured and is vulnerable to weathering. Thus, the strength of the slope rock mass is low. The Yingxiu-Beicuan fault is the interface between the Cambrian strata (in the hanging wall) and Silurian strata (in the footwall) (Figure 3).

Kinematic Characteristics of Taihongcun Landslide

As shown in Figure 3, the study area can be divided into three regions: the upper source area, the secondary landslide area, and the debris deposit area. The elevation difference between the toe and the crest of the slope in the upper source area is 260 m, and the corresponding horizontal distance is 460 m. The original slope of the upper source area failed due to the substantial seismic forces. After the landslide initiation in this area, the source mass detached from the parent rock mass and slid along the sliding surface at an increasing speed. High-temperature carbonization observed near the sliding surface indicates that a high-speed shearing effect between the sliding body and the sliding surface was produced during the high-speed movement of the displaced mass (Figures 5A–C). The initial velocity was obtained when the upper sliding body slid in front of the toe of the sliding surface and was projected into the air. After the failed rock mass was projected into the air from the toe of the upper sliding surface, this mass would exhibit a parabolic airborne course, and the gravitational potential energy would be converted into kinetic energy in the falling stage. The secondary landslide area is characterized by the cliff below the upper source area. A large elevation difference of 200 m between the toe of the sliding surface and the cliff base allowed the airborne rock mass from the upper source area to acquire considerable momentum and thus to scrape the preexisting deposit overlaying the cliff. The loose deposit material was entrained by the rock debris due to the impact and pushed downwards with it.

In the deposit area, the granular debris flow reached the valley bottom below the 180 m high cliff, blocked the Duba River, and climbed the opposite bank of the river (Figure 6A). The horizontal travel distance was approximately 1,200 m, and the vertical fall height was approximately 550 m. The thickness of landslide deposits is affected by terrain. The deposits in the gullies and rivers are thickest, and the average thickness is approximately 50 m. Specifically, the deposits are the thickest at the landslide dam, with a thickness of up to approximately 95 m. The thickness of the debris flow deposits along the river course is generally approximately 30 m, while the thickness at the edge of the accumulation area is only 2–5 m. Field investigations show that the deposits are composed mostly of highly fragmented sandstone and shale; the grain size is in the range of sand, gravel, and cobble, with some large boulder-sized blocks (Figure 6C). The main grain size is gravel and cobble, and the majority of the deposits are subangular to angular. As shown in Figure 6B, in the front of the deposits on the opposite bank, wheat stalks were pushed down and arranged in radial lines by the powerful air blast induced by the displaced material, indicating the high-speed movement of the granular debris flow.

FIGURE 6

FIGURE 6. Deposition area of the Taihongcun landslide. (A) Granular debris covered the Duba rive and the farmlands (the landslide dam had already been breached artificially). (B) Air wave blew down the wheat due to granular debris on the location shown as the red circle B in Figure 6A. (C) Compact landslide deposits composed of angular fragments on the location shown as the red circle A in Figure 6A.

Discrete Element Method Modeling

The dynamic processes of landslides under seismic loading conditions are very complicated. The DEM is well suited for simulating the cracks and subsequent large displacements of catastrophic landslides or rock avalanches and is therefore a useful tool for analyzing their complex kinematics and failure mechanisms. In this section, based on the two-dimensional code PFC2D, DEM models were used to investigate the kinematical process and failure mechanism of the Taihongcun landslide triggered by the 2008 Wenchuan earthquake.

Free-Field Boundary Condition for Discrete Element Method

In a numerical analysis of the seismic response of rock slopes, earthquake waves such as plane body waves are usually applied at the bottom of the model and propagate upward. The boundary conditions at the sides of the model should account for the free-field motion that would exist in the absence of a structure, such as a slope or a tunnel. The free-field boundary algorithm proposed by Zienkiewicz et al. (1989) is selected to “enforce” the free-field motion in such a way that the boundaries retain their nonreflecting properties (i.e., outward waves originating from the structure are properly absorbed). In this approach, the lateral boundaries of the main grid domain are coupled to the free-field domain by viscous dashpots to simulate an absorbing boundary, and the unbalanced forces from the free-field grid are applied to the main grid boundary. The free-field grid is solved in parallel with the main grid. For a lateral boundary of the main grid domain with its normal in the direction of the x-axis, the free-field boundary condition for 2D problems can be expressed as follows:

${\sigma }_{\mathit{x}}=-\rho c_p\left({\dot{u}}_x^m-{\dot{u}}_x^{ff}\right)+{\sigma }_x^{ff}(1)$

${\tau }_{xy}=-\rho c_s\left({\dot{u}}_y^m-{\dot{u}}_y^{ff}\right)+{\tau }_{xy}^{ff}(2)$

where ${\mathit{\sigma }}_{\mathrm{x}}$ and ${\tau }_{xy}$ are the normal and shear components of the traction applied to the lateral boundary, respectively; ${\dot{u}}_x^m$ and ${\dot{u}}_y^m$ are the x and y components of the main grid point velocity at the lateral boundary; ${\dot{u}}_x^{ff}$ and ${\dot{u}}_y^{ff}$ are the x and y components of the velocity of the grid point in the free-field domain; and ${\dot{u}}_x^{ff}$ and ${\dot{u}}_x^{ff}$ are the tractions contributed from the free-field grid in the x and y directions.

Eqs 1, 2 are defined based on the continuum condition. To apply the free-field boundary condition in the DEM models, Eqs 1, 2 need to be discretized. For regular packing geometries, it may be possible to develop analytical expressions of the equivalent discrete free-field boundary condition based on Eqs 1, 2. For a square array of disks (each particle has four neighbors) of unit thickness in 2D, the particles in the assemblies have a common diameter D_b. The regular square packing is subjected to an unconfined compression test. The axial stress, ${\mathit{k}}_{\mathrm{n,SJ}}$, is related to the axial force, ${\mathit{k}}_{\mathrm{s,SJ}}$, as follows:

${\sigma }_{\mathit{a}}=\frac{F_a}{D_b\times 1}(3)$

Substituting Eq. 3 into Eqs 1, 2, the free-field boundary condition for the DEM in 2D is obtained by

${\mathit{f}}_{\mathit{x}}=-{\beta }_{2p}\rho c_p{D}_b\left({\dot{u}}_x^m-{\dot{u}}_x^{ff}\right)+f_x^{ff}(4)$

${\mathit{f}}_{\mathit{y}}=-{\beta }_{2s}\rho c_s{D}_b\left({\dot{u}}_y^m-{\dot{u}}_y^{ff}\right)+f_y^{ff}(5)$

where ${\mathit{f}}_{\mathit{x}}$ and ${\mathit{f}}_{\mathit{y}}$ are the normal and shear components of the force applied to the particles at the lateral boundaries of the main grid domain; ${\mathit{f}}_{\mathit{x}}^{\mathit{ff}}$ and ${\mathit{f}}_{\mathit{y}}^{\mathit{ff}}$ are the forces of a particle in the free-field domain in the x and y directions; and ${\mathit{\beta }}_{\mathit{2p}}$ and ${\mathit{\beta }}_{\mathit{3s}}$ are the nondimensional calibration factors for optimum wave absorption.

Numerical Model

Figure 7A shows the 2D DEM model of the Taihongcun landslide, constructed based on the geological longitudinal section shown in Figure 3C. The sliding mass in the upper source area can be detailed in Figure 7B, and the secondary landslide area in the model is shown in Figure 7C. To capture the main features of the large rock avalanche, the following assumptions were made:

1. The sliding mass in the source area is cut by two sets of discontinuities, including joint set J₁ and the bedding planes.

2. Given the radius difference between the bedrock and the sliding mass, an 8 m thick transition layer is produced between the bedrock and sliding mass (see the enlarged view in the box in Figure 7B).

3. The rupture surface, including the back scarp and the sliding surface, is preset along the interface between the transition layer and sliding mass.

4. The bedrock below the sliding surface is considered homogeneous.

5. To avoid a large computational burden, the bedrock under the riverbed and east bank are simulated by wall elements. The seismic ground motion of the wall elements is in accordance with the movements of disk A (see Figure 7D).

FIGURE 7

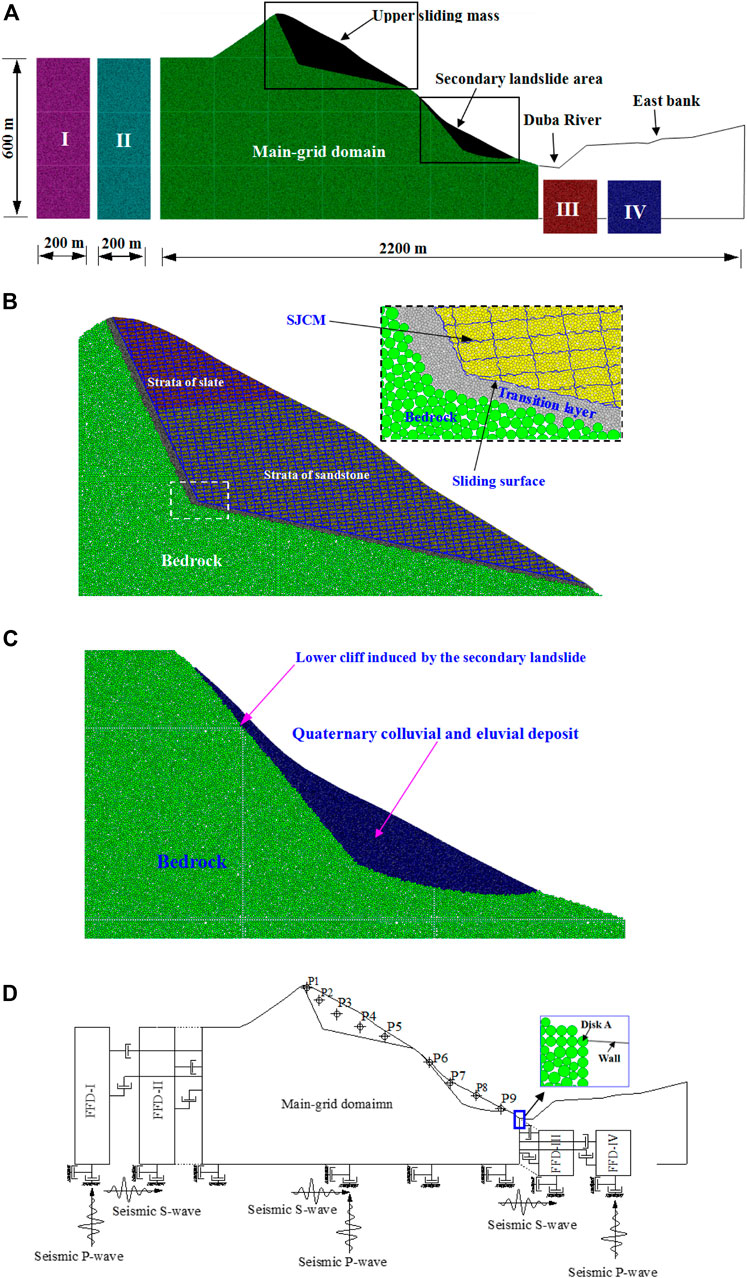
FIGURE 7. DEM model of the Taihongcun landslide. (A) Part I is the free-field domain I (FFD-I), part II is the free-field domain II (FFD-II), part III is the free-field domain III (FFD-III), and part IV is the free-field domain IV (FFD-IV). (B) Upper sliding mass and bedrock. (C) Secondary landslide area. (D) Dynamic boundary setting and locations of monitoring disks for the landslide.

The sliding mass in the upper source area is composed of slate and sandstone (see Figure 7B). In PFC2D, a joint is identified as a contact between particles lying on opposite sides of the joint plane. Joint plane contacts follow a contact model with properties that are different from those assigned to particle contacts elsewhere in the rock mass.

The most commonly used method for the generation of rock joints is to set the bond strengths of the joint plane contacts to low values (or zero for the lowest shear strength) (Kulatilake et al., 2001; Wang et al., 2003; Huang et al., 2015). The shortcomings of this method are that the surface of a generated joint has an inherent microscale roughness that is due to the circular shape and the nonuniform size and distribution of the particles (Bahaaddini et al., 2015). Therefore, it is difficult for the particles to slide along the discontinuities, especially along the sliding surface. To solve this problem, the smooth joint contact model (SJCM) was developed and introduced into PFC to simulate joints on a mesoscopic scale (Ivars et al., 2011). The SJCM simulates the behavior of an interface regardless of the local particle contact orientations along the interface. The behavior of a frictional or bonded joint can be modeled by assigning the SJCM to all contacts between particles that lie on opposite sides of a joint. With this approach, the shear behavior and mechanisms of rock joints under direct shear tests were studied in detail (Bahaaddini et al., 2013, 2015; Gutiérrez-Ch et al., 2018). In this study, the J₁ joint set, bedding planes, sliding surface and back scarp are modeled with the SJCM (Figure 7B). Thus, the sliding mass in the upper source area can slide or separate along the sliding surface and back scarp.

The dynamic boundary conditions and monitoring disks for the DEM model are shown in Figure 7D. To absorb outward propagating waves and avoid plane waves propagating upward from being distorted at the lateral boundaries of the model, the free-field boundary conditions described in Free-Field Boundary Condition for Discrete Element Method are applied to the model. To ensure that the free-field domain has the same elastic behavior as the main grid domain, the microscale properties of the free-field domains are the same as those of the bedrock. The free-field domain is composed of four soil columns. The soil columns FFD-I and FFD-II are located on the left of the main grid domain, and the soil columns FFD-III and FFD-IV are located on the right. Note that only a seismic P-wave is applied on the bottom boundaries of soil columns FFD-I and FFD-IV and that only a seismic S-wave is applied on the bottom boundaries of soil columns FFD-II and FFD-III, while seismic P- and S-waves are applied to the bottom boundary of the main grid domain. When only an S-wave (or a P-wave) is required as input for the model, the free-field domain is merely composed of soil columns FFD-II and FFD-III (or FFD-I and FFD-IV). Viscous boundary conditions are applied to the bottom boundary of the main grid and free-field domains.

Model Parameters and Seismic Input

PFC2D simulates the intact material as an assembly of circular particles bonded at their contacts with the contact bond model or parallel-bond model and is thus referred to as a bonded particle model (BPM) (Potyondy and Cundall, 2004). The macroscopic mechanical behavior of the synthetic material depends on the microscopic parameters of the particles and bonds between particles. However, the microscopic parameters cannot, in general, be related directly to a set of relevant material properties (Itasca Consulting Group Inc., 2008). In general, the microscopic parameters can be obtained by means of a calibration process in which a series of numerical tests are performed to reproduce the desired macroscopic properties measured in laboratory experiments. In this study, numerical uniaxial compressive strength tests are carried out on BPMs to calibrate microscopic parameters against the uniaxial compressive strength UCS, elastic modulus E and Poisson’s ratio v. The derived microscopic parameters of the BPMs for the landslide are listed in Table 1. A comparison of the macroscopic properties between the BPMs and laboratory experiments is conducted. The results from the BPMs are very close to those from the laboratory experiments.

TABLE 1

TABLE 1. Micro-parameters for different types of material used in the DEM models.

Numerical direct shear tests under constant normal stress are employed to determine the strength and stiffness parameters of the SJCM interfaces. The SJCM is applied to the contacts between particles that lie on opposite sides of the shear plane. To simulate the direct shear tests, the lower block is kept stationary during the tests, and a horizontal velocity V, which is low enough to ensure that the sample remains in quasistatic equilibrium, is applied to upper walls. The normal stress is applied vertically to the upper block, and this normal stress is kept constant during the tests by using a servo-control mechanism (Itasca Consulting Group Inc., 2008). The shear and normal displacements are obtained by tracing the horizontal and vertical displacements of the upper block, respectively, and the shear stress is calculated by dividing the average force reaction on the upper left and lower right walls by the joint length. The calibrated SJCM parameters for the sliding surface, bedding planes and joint set J₁ are listed in Table 2.

TABLE 2

TABLE 2. Calibrated parameters for smooth joint contact model (SJCM).

Because no strong motion station is present at the landslide site, records of the Wenchuan earthquake waves from the strong motion station Qingping, which is close to the seismogenic Yingxiu-Beicuan fault and is 40 km away from the landslide, are chosen as the seismic loading inputs. The peak ground accelerations (PGAs) of the original seismic records at the Qingping station are 824.12 cm/s² in the east-west direction, 802.7103 cm/s² in the north-south direction, and 622.91 cm/s² in the vertical direction. Because the 2D DEM models (Figure 7) are constructed based on a geological longitudinal section (Figure 3C), it is necessary to project the horizontal acceleration records in the east-west and north-south directions into the main sliding direction of the landslide using the following equation:

${\mathit{a}}_{\mathrm{H}}={\mathit{a}}_{\mathrm{E}-\mathrm{W}}\cdot \sin \left(\mathrm{110}°\right)+{\mathit{a}}_{\mathrm{N}-\mathrm{S}}\cdot \cos \left(\mathrm{110}°\right)(6)$

where ${\mathit{a}}_{\mathrm{H}}$ is the acceleration in the main sliding direction, ${\mathit{a}}_{\mathrm{E-W}}$ is the acceleration in the east-west direction, ${\mathit{a}}_{\mathrm{N-S}}$ is the acceleration in the north-south direction, and 110° is the azimuth of the main sliding direction.

The ultimate acceleration histories after filtering and baseline correction are shown in Figure 8. The velocity time-history records are transformed into force time-history records and applied to the bottom boundaries of the main grid and free-field domains.

FIGURE 8

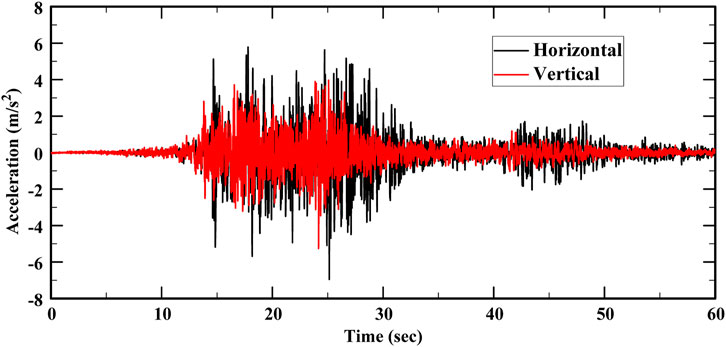
FIGURE 8. Input horizontal and vertical ground acceleration records after filtering and baseline correction.

To effectively dissipate the kinetic energy of the assembly system, numerical damping must be used in the simulations. Local damping and viscous damping are available in DEM models to dissipate kinetic energy. Local damping applies a damping force, with a magnitude proportional to the unbalanced force, to each particle, while viscous damping adds normal and shear dashpots at each contact. Local damping is not applicable for landslide simulation (Deng et al., 2017). Therefore, viscous damping is used in the simulations. The parameters of viscous damping can have a significant impact on the results, but they cannot be explicitly related to any physical mechanism. The parameters of viscous damping in DEM models can also influence the grain motion and reflect energy dissipation during collision. The damping parameters are correlated with the coefficients of restitution, which can be measured in the laboratory or field. The results of field restitution coefficient tests conducted by Giani (1992) are used to define the damping parameters. The values of the normal and shear damping coefficients are thus set to 0.4 and 0.2, respectively, (Deng et al., 2017).

Numerical Simulation Results and Analysis

The dynamic process of the Taihongcun rock avalanche can be classified into four stages: upper sliding mass fragmentation, projection of the upper displaced mass, scraping of the upper sliding mass toward the Quaternary colluvial and eluvial deposit, and granular debris flow and accumulation. Each of the stages is discussed in detail in Upper Sliding Mass Fragmentation–Granular Debris Flow and Accumulation. The numerical parameter of internal bonding strength is the most crucial factor influencing landslide transport and deposition in the DEM model (Zhang et al., 2017). Therefore, the influence of the parallel-bond strength on the runout distance and deposition patterns is investigated in Influence of the Bond Strength on the Runout Distance and Deposition Patterns.

Upper Sliding Mass Fragmentation

Figure 9 shows the progressive fragmentation of the upper sliding body under the combined horizontal and vertical seismic loadings; the cluster plots indicate fractured blocks (Itasca Consulting Group Inc., 2008). In the static gravity equilibrium situation (Figure 9A), damage can be observed in the rock mass near the scarp and sliding surface and on the top part of the slope. Cracks or fissures develop along the bedding planes and joint set J₁ in the damaged regions, and the rock mass is broken into small blocks. The entire model can be brought to equilibrium under gravity so that the slope is stable before the earthquake. After the seismic force is applied to the base of the model, the slope is not stable (Figures 9E–H). In the initial stage of the Taihongcun rock avalanche, a rock slide occurred, and an obvious settlement is observed near the top of the slope when the shear stress at the sliding surface reaches the shear strength (Figure 9B). The development of cracks or fissures in the rock mass, induced by the shaking and sliding, is observed (Figures 9E–H). The high-speed shearing effect between the sliding body and the sliding bed resulted in fragmentation of the rock blocks into small particles (Figures 9B,C). The jointed rock blocks in the slope begin falling and fragment into smaller sizes as a result of the internal forces exceeding the bonding strength (Figures 9E–H). Under strong seismic loadings, tensile cracks develop in the rear part of the sliding body, forming a tensile stress concentration zone (Figures 9E–D). Then, the cracks widened laterally and propagated vertically to the intersection between the scarp and the sliding surface, generating horizontal and vertical displacements. The large elevation difference between the slope and the slip plane facilitated the rockslide, triggered by the violent quaking.

FIGURE 9

FIGURE 9. Progressive fragmentation of the upper sliding mass during earthquake.

Projectile Motion of the Upper Displaced Mass

Under seismic and gravity forces, the upper sliding mass achieved a high initial speed of approximately 40 m/s over a short period as it slid away from the toe of the sliding surface (Figure 10A). There is sufficient open space in the movement direction of the landslide, allowing the upper sliding mass to run out from the top of the 180 m cliff at a high speed, along a parabolic path (Figures 9E–G, Figure 10A). After the upper sliding mass was projected into the air, the speed increased rapidly during the vertical drop from the toe of the sliding surface to the valley bottom. The high initial velocity, high elevation of the toe of the sliding surface and sufficient open space in the movement direction induced projectile motion.

FIGURE 10

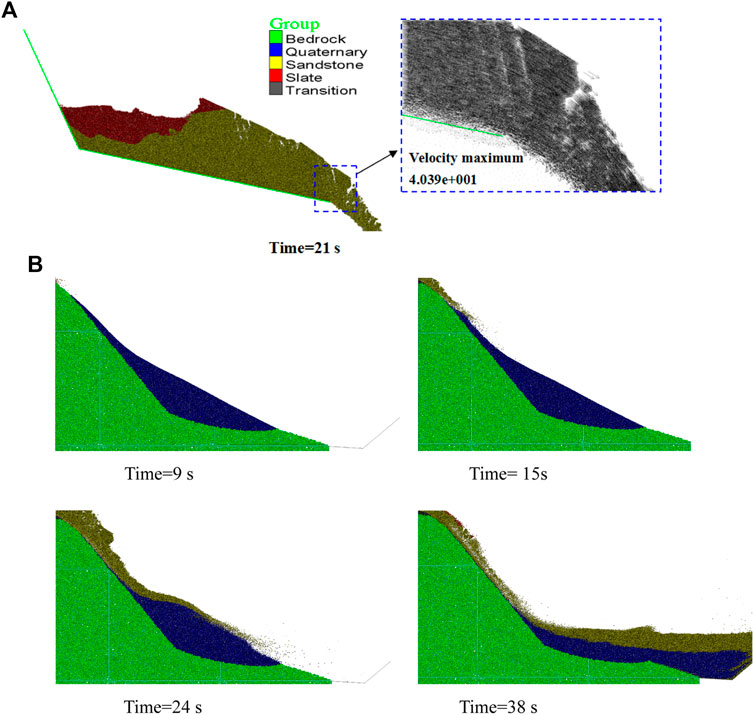
FIGURE 10. (A) Projectile motion: the toe of the sliding surface projects the upper sliding mass into the air. (B) Scraping action of the upper sliding mass toward the Quaternary colluvial and eluvial deposit covering the lower cliff.

Scraping of the Upper Sliding Mass

Figure 10B shows the scraping of the upper sliding mass into the Quaternary colluvial and eluvial deposit on the lower cliff. As the gravitational potential energy would be converted into kinetic energy in the falling stage, with a substantial kinetic energy, the thrown upper sliding mass collided with and intensely scraped off the Quaternary deposit, completely entraining and removing the deposits. The bedrock below the Quaternary deposits was completely exposed after the event, and the lower cliff formed. The lower part of the landslide was triggered into a secondary failure due to the earthquake activity and the effects from the upper part of the landslide.

Granular Debris Flow and Accumulation

Figure 11 shows the velocity histories of the monitoring particles at different locations in the upper sliding mass and the lower Quaternary deposit (shown in Figure 7D). As shown in Figure 11A, the maximum velocity of the monitoring particles is approximately 60 m/s, which was recorded at point 5, and the peaks of the recorded velocities decrease from the front of the upper sliding mass to the rear. Particles in the rear of the upper sliding mass (particles 1, 2, and 3) start moving slowly, and their movement continues for a short time. However, particles in the front of the upper sliding mass (particles 4 and 5) start moving quickly, and their movement continues for a longer period. The peaks in the recorded velocities in the front of the upper sliding mass (particles 4 and 5) appear later than those in the rear of the upper sliding mass (particles 1, 2, and 3). The seismic response of the upper sliding mass is most intensive at t = 6–50 s, and the direct cause of the landslide is the earthquake. As illustrated in Figure 11B, monitoring particle 6 in the top of the lower Quaternary deposit was displaced by the thrown upper sliding mass at approximately 13 s. The particles in the top of the lower Quaternary deposit were displaced earlier and farther than those in the bottom. Therefore, the velocity peaks of the monitoring particles decrease from the top of the lower Quaternary deposit to the bottom. The speeds of the monitoring particles in the lower Quaternary deposit peaked at approximately 30 s, then gradually decreased, and reached zero at approximately 43 s.

FIGURE 11

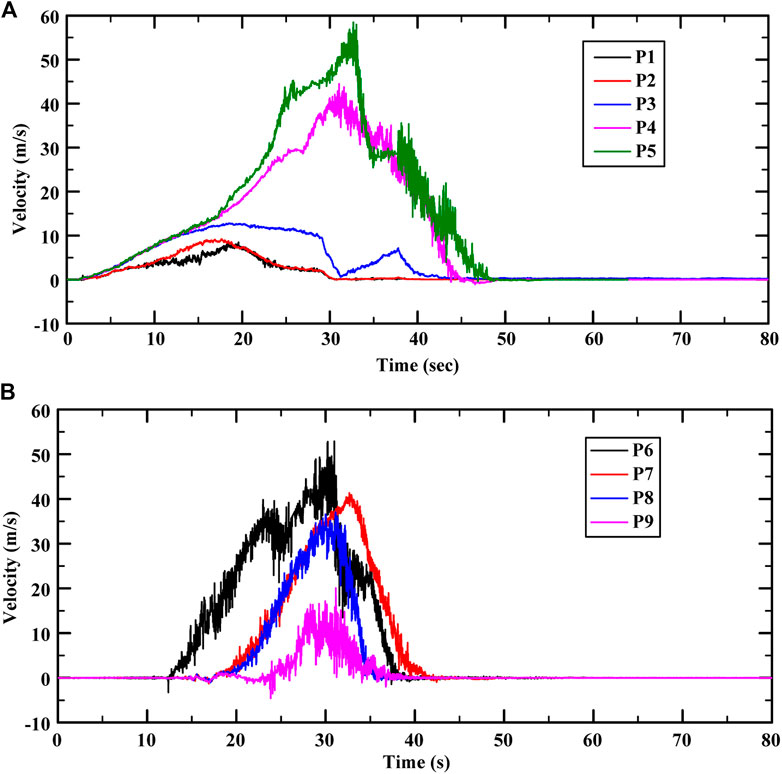
FIGURE 11. Time-history curves of horizontal velocity for monitoring points. (A) Velocities of monitoring points in the upper source area. (B) Velocities of monitoring points in the Quaternary colluvial and eluvial deposit.

The upper sliding mass was disintegrated into fragments due to the strong vibration, intensive collision, and violent scraping action. Then, the fragmented geomaterial transformed into granular debris with a rapid, flow-like motion. The lower Quaternary deposit was entrained due to the rock debris collision on the slope surface. The topography after sliding is shown in Figure 12A, which indicates that there are two deposition zones of the Taihongcun landslide: the first is in the upper source area, where fragmented rock debris accumulates on the sliding surface; the second is in the valley of the Duba River. In the first deposition zone (Figure 12B), the average thickness of the deposit is approximately 40 m, which is in accordance with the field observations, and the deposit can be divided into two layers: an upper layer of slate and a lower layer of sandstone. In the second deposition zone, the granular debris flow reached the valley bottom below the 180 m high cliff, blocked the Duba River, and climbed over the opposite bank of the river (Figure 12C). The second deposition zone has a maximum thickness of approximately 35 m on the opposite bank, and the greatest height of the landslide dam in the Duba River valley is approximately 95 m. The landslide deposit in the second deposition zone is mainly composed of sandstone and Quaternary deposits. The Quaternary deposits are covered by sandstone debris. The distance between the summit of the mountain before the earthquake and the edge of the deposit on the opposite bank is approximately 1,200 m in the horizontal direction, and the vertical height from the summit of the mountain to the bottom of the Duba River is approximately 600 m.

FIGURE 12

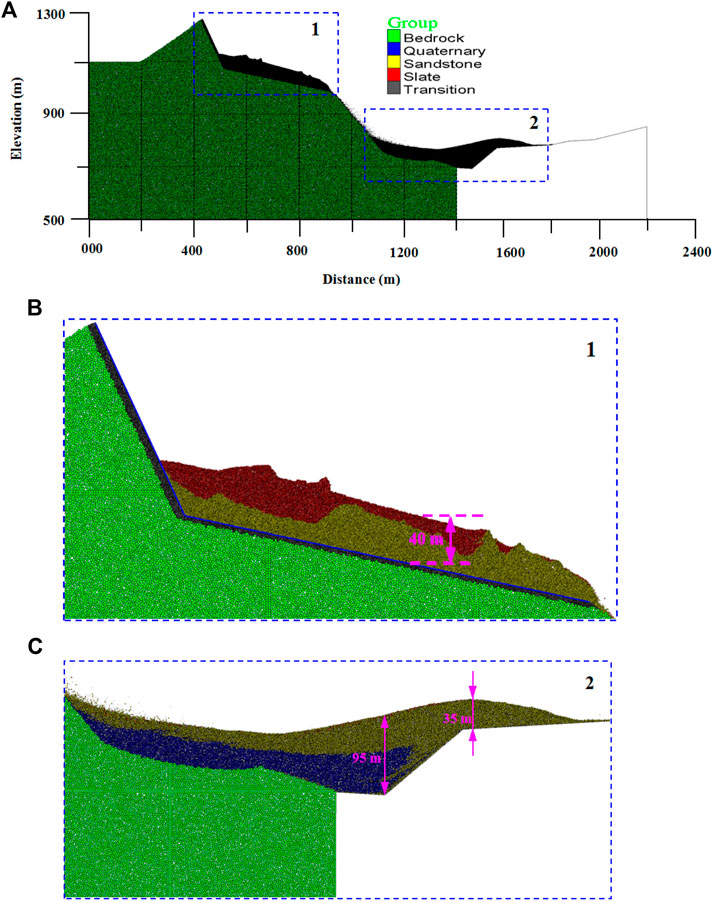
FIGURE 12. Ultimate landslide deposit accumulation. (A) Entire model. (B) Deposits in the upper source area. (C) Deposits in the valley of the Duba River.

Influence of the Bond Strength on the Runout Distance and Deposition Patterns

Some researchers noted that the basal friction coefficient and the internal bonding strength were the most crucial factors influencing landslide transport and deposition in PFC2D models (Tang et al., 2009; Deng et al., 2017; Zhang et al., 2017). The influence of the basal friction coefficient on the runout distance and deposition patterns can be understood easily. However, the influence of the internal bonding strength on the runout distance and deposition patterns is disputed and poorly understood. A series of numerical simulations that were performed to investigate the runout distance and deposition area of the Taihongcun landslide in relation to internal bond strength are presented in this section. Three cases for the parallel-bond normal strength of the particles are used in the numerical simulations:

Case 1. The parallel-bond normal strength for sandstone is 4 MPa, and the parallel-bond normal strength for slate is 1.6 MPa.

Case 2. The parallel-bond normal strength for sandstone is 12.5 MPa, and the parallel-bond normal strength for slate is 5 MPa.

Case 3. The parallel-bond normal strength for sandstone is 25 MPa, and the parallel-bond normal strength for slate is 10 MPa.

Figures 13A–C shows the final topography of the first deposition zone for the three cases, and Figures 13D–F shows the final topography of the second deposition zone for the three cases. As depicted in Figure 13, the final topography of the deposits in the simulations indicate that the internal bonding significantly influences the resultant runout distance and debris flow avalanche deposit. Figure 13 show that Case 1 results in the minimum thickness of the first deposition zone, the maximum thickness of the second deposition zone, and the longest runout distance, while Case 3 results in the maximum thickness of the first deposition zone, the minimum thickness of the second deposition zone and the shortest runout distance. Moreover, the deposits for Case 1 are the densest of the three cases. The series of simulation results indicates that a lower bond strength enables the upper sliding mass to more easily fragment (Figure 13A), while a high bond strength will cause the main body mass to behave as a rigid block, thus hindering fragmentation (Figure 13C). With respect to the back analysis of the runout distance and debris accumulation topography, Case 2 provides the best simulation results for the Taihongcun landslide dynamics process.

FIGURE 13

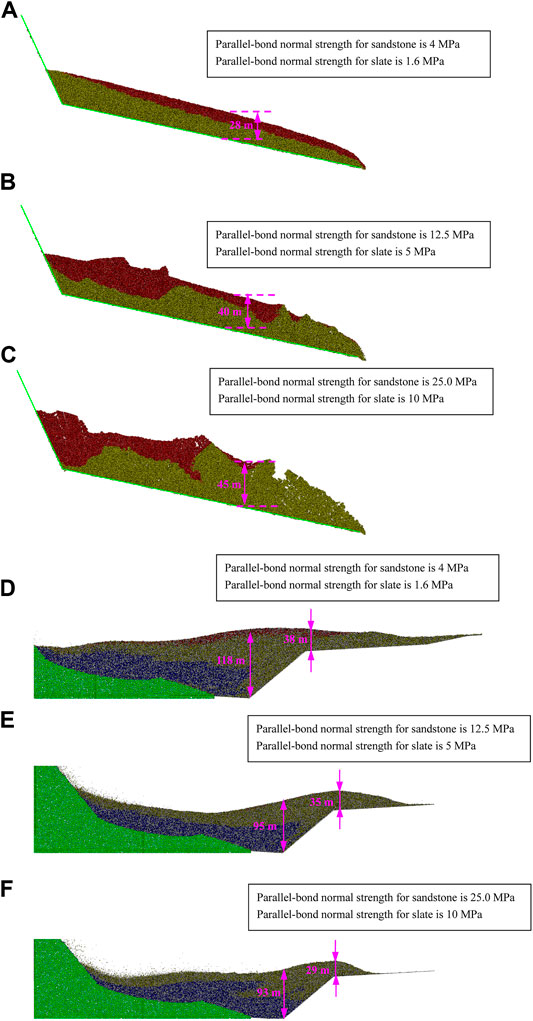
FIGURE 13. (A–C) Influence of bonding strength on the landslide deposit accumulation in the upper source area. (D–F) Influence of bonding strength on the landslide deposit accumulation in the valley of the Duba River.

Formation Mechanism Analysis

Based on field investigations and discrete element simulations, we conclude that the occurrence of the Taihongcun landslide is the result of a combination of seismic, terrain, and geological factors. The formation mechanism of the Taihongcun landslide will be discussed in this section.

Weak Rock in the Slope

Rock mass quality is the basis for the stability of rock slopes. The strength and deformation modulus of a rock mass with a good quality are high, which is beneficial to the slope stability, while that with a poor quality are low, which challenges slope stability. The rock mass in the study area was of poor quality due to the shearing and brecciation associated with past fault movement, rendering the rock slopes prone to failure and contributing to the high degree of disintegration of the failed rock mass. The strength of the Cambrian sandstone and slate in the upper source area is low, and the rocks are vulnerable to weathering, leading to fracturing of the upper sliding mass. The weak rock mass of the slope is the lithological basis for this landslide formation.

Unfavorable Geological Structure

Based on the field investigations, there exists a group of joints J₁, which steeply dip outward, in the residual slope of the upper source area, and the back scarp developed along this joint set. As observed in the outcrop (Figure 5), a weak interlayer composed of carbonaceous slate and shale is present. Under strong ground motion induced by earthquakes, the slope is easily shears along the weak interlayer, and a large-displacement slide can occur. The joint set J₁ and the weak interlayer formed the rupture surfaces of the upper source area.

Strong Seismic Ground Motion

The seismic intensity in the study area is more than X (Chinese seismic intensity) (Huang and Li 2009), and the seismogenic Yingxiu-Beicuan fault passes through the foot of the valley slope. The original PGA in the area is greater than 600 Gal, a seismic intensity greater than X (Li et al., 2008). Furthermore, the main source area is located in the hanging wall of the fault, and the hanging wall effect in the near-fault ground motion (Li et al., 2008; Huang and Li, 2009) may be obvious in the study area. The strong seismic ground motion is an external excitation that triggers the destructive landslide event.

High Elevation and Topographical Conditions

The vertical distance from the toe of the upper sliding surface to the valley bottom is approximately 300 m. Therefore, the upper sliding mass can gain substantial kinetic energy, transformed from the gravity potential energy, in the falling stage. There is enough transport space downslope to facilitate the projection of the upper sliding mass into the air. Three faces of the Shuijingyan mountain, where the landslide originated, are free, and the terrain is steep, high and convex. The topographic amplification effect on seismic waves is strong at or near ridge crests in this kind of topography, which favors slope failure. The high elevation and topographical conditions provided the basis for hypermobility.

Conclusion

This paper focuses on the dynamic process and formation mechanism of the catastrophic Taihongcun landslide triggered by the 2008 Wenchuan earthquake. Through detailed field surveys, basic information of the topography, geological structure and stratigraphy for the landslide was acquired, and key kinetic characteristics of the landslide were identified. Based on field investigations, 2D DEM models were established to simulate the kinematics and failure process of the landslide. To ensure the validity of the dynamic calculations, the free-field boundary condition was developed and introduced into the DEM models. The modeled scenario had a reasonably good fit to the actual topography, adding credibility to the modeling results.

Based on the field investigations and numerical simulations, the dynamic processes of the Taihongcun landslide was divided into four phases: upper sliding mass fragmentation, projection of the upper displaced mass, scraping of the upper sliding mass toward the Quaternary colluvial and eluvial deposit, and granular debris flow and accumulation. The progressive fragmentation and projectile motion of the upper sliding body under the combined horizontal and vertical seismic loadings were effectively simulated. The mechanism of the Quaternary deposit on the lower cliff scraped by the upper sliding mass was revealed through these simulations. In addition, a parameter analysis showed that the internal bond strength of the particles had a significant influence on the runout distance and landslide debris morphology.

According to field investigations and numerical simulations, a possible mechanism of the Taihongcun landslide was determined: the rock mass in the study area was of poor quality and was vulnerable to weathering, which provided the lithological basis for this landslide formation; the joint set J₁, which steeply dips outward in the residual slope, and the weak interlayer, which was comprised of carbonaceous slate and shale, formed the rupture boundary of the upper source area; the strong seismic ground motion was an external excitation that triggered the destructive landslide event; additionally, the high elevation and topographical conditions provided the bases for hypermobility.

Notably, the seismogenic Yingxiu-Beicuan fault that ruptured during the Wenchuan earthquake lay across the foot of the valley slope. The role of oblique-thrust faulting in the initiation of earthquake-induced landslides needs to be quantitatively assessed. However, it is difficult to account for oblique-thrust faulting in our simulations at present. Therefore, further research is needed to consider the effects of oblique thrusting on the initiation of near-fault landslides in such simulations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Ethics Statement

Written informed consent was obtained from the relevant individuals for the publication of any potentially identifiable images or data included in this article.

Author Contributions

XZ and XF were involved in the final development of the project and manuscript preparation. XZ and PW wrote the manuscript draft. LL and XX analyzed the data. All authors: corrections, modifications, and final acceptation.

Funding

The study was financially supported by the National Basic Research Program of China (no. 2015CB057905), the National Natural Science Foundation of China (nos. 51779253, 41672319), and the National Key R&D Program of China (no. 2016YFC0401803).

Conflict of Interest

Author XX was employed by the company China Shanxi Transportation Technology Research & Development Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge the reviewers and the editors for their comments and suggestions.

References

Bahaaddini, M., Hagan, P. C., Mitra, R., and Hebblewhite, B. K. (2015). Parametric Study of Smooth Joint Parameters on the Shear Behaviour of Rock Joints. Rock Mech. Rock Eng. 48 (3), 923–940. doi:10.1007/s00603-014-0641-6

CrossRef Full Text | Google Scholar

Bahaaddini, M., Sharrock, G., and Hebblewhite, B. K. (2013). Numerical Direct Shear Tests to Model the Shear Behaviour of Rock Joints. Comput. Geotechnics 51 (51), 101–115. doi:10.1016/j.compgeo.2013.02.003

CrossRef Full Text | Google Scholar

Bouckovalas, G. D., and Papadimitriou, A. G. (2005). Numerical Evaluation of Slope Topography Effects on Seismic Ground Motion. Soil Dyn. Earthquake Eng. 25, 547–558. doi:10.1016/j.soildyn.2004.11.008

CrossRef Full Text | Google Scholar

Bourdeau, C., and Havenith, H. B. (2008). Site Effects Modelling Applied to the Slope Affected by the Suusamyr Earthquake (Kyrgyzstan, 1992). Eng. Geology 97 (3), 126–145. doi:10.1016/j.enggeo.2007.12.009

CrossRef Full Text | Google Scholar

Charatpangoon, B., Kiyono, J., Furukawa, A., and Hansapinyo, C. (2014). Dynamic Analysis of Earth Dam Damaged by the 2011 off the Pacific Coast of Tohoku Earthquake. Soil Dyn. Earthquake Eng. 64 (3), 50–62. doi:10.1016/j.soildyn.2014.05.002

CrossRef Full Text | Google Scholar

Che, A., Yang, H., Wang, B., and Ge, X. (2016). Wave Propagations through Jointed Rock Masses and Their Effects on the Stability of Slopes. Eng. Geology 201, 45–56. doi:10.1016/j.enggeo.2015.12.018

CrossRef Full Text | Google Scholar

Chigira, M., Wu, X. Y., Inokuchi, T., and Wang, G. H. (2010). Landslides Induced by the 2008 Wenchuan Earthquake, Sichuan, China. Geomorphology 118 (3), 225–238. doi:10.1016/j.geomorph.2010.01.003

CrossRef Full Text | Google Scholar

Cui, Z., Sheng, Q., and Leng, X. (2016). Control Effect of a Large Geological Discontinuity on the Seismic Response and Stability of Underground Rock Caverns: a Case Study of the Baihetan #1 Surge Chamber. Rock Mech. Rock Eng. 49 (6), 2099–2114. doi:10.1007/s00603-015-0908-6

CrossRef Full Text | Google Scholar

Cundall, P. A., and Strack, O. D. L. (1979). A Discrete Numerical Model for Granular Assemblies. Geothechnique 29 (1), 47–65.

Dai, F. C., Tu, X. B., Xu, C., Gong, Q. M., and Yao, X. (2011). Rock Avalanches Triggered by Oblique-Thrusting during the 12 May 2008 Ms 8.0 Wenchuan Earthquake, China. Geomorphology 132 (3), 300–318. doi:10.1016/j.geomorph.2011.05.016

CrossRef Full Text | Google Scholar

Deng, Q., Gong, L., Zhang, L., Yuan, R., Xue, Y., Geng, X., et al. (2017). Simulating Dynamic Processes and Hypermobility Mechanisms of the Wenjiagou Rock Avalanche Triggered by the 2008 Wenchuan Earthquake Using Discrete Element Modelling. Bull. Eng. Geol. Environ. 76, 923–936. doi:10.1007/s10064-016-0914-2

CrossRef Full Text | Google Scholar

Fan, X., Juang, C. H., Wasowski, J., Huang, R., Xu, Q., Scaringi, G., et al. (2018). What We Have Learned from the 2008 Wenchuan Earthquake and its Aftermath: A Decade of Research and Challenges. Eng. Geology 241, 25–32. doi:10.1016/j.enggeo.2018.05.004

CrossRef Full Text | Google Scholar

Fu, X., Sheng, Q., Tang, H., Chen, J., Du, Y., Zhang, Z., et al. (2019). Seismic Stability Analysis of a Rock Block Using the Block Theory and Newmark Method. Int. J. Numer. Anal. Methods Geomech. 43, 1392–1409. doi:10.1002/nag.2903

CrossRef Full Text | Google Scholar

Giani, G. P. (1992). Rock Slope Stability Analysis. Rotterdam: Balkema.

Gorum, T., Fan, X. M., Westen, C. J., Huang, R. Q., Xu, Q., Tang, C. A., et al. (2011). Distribution Pattern of Earthquake-Induced Landslides Triggered by the 12 May 2008 Wenchuan Earthquake. Geomorphology 133 (3), 152–167. doi:10.1016/j.geomorph.2010.12.030

CrossRef Full Text | Google Scholar

Gutiérrez-Ch, J. G., Senent, S., Melentijevic, S., and Jimenez, R. (2018). Distinct Element Method Simulations of Rock-concrete Interfaces under Different Boundary Conditions. Eng. Geology 240, 123–139. doi:10.1016/j.enggeo.2018.04.017

CrossRef Full Text | Google Scholar

Has, B., and Nozaki, T. (2014). Role of Geological Structure in the Occurrence of Earthquake-Induced Landslides, the Case of the 2007 Mid-niigata Offshore Earthquake, Japan. Eng. Geology 182, 25–36. doi:10.1016/j.enggeo.2014.09.006

CrossRef Full Text | Google Scholar

Havenith, H.-B., Vanini, M., Jongmans, D., and Faccioli, E. (2003). Initiation of Earthquake-Induced Slope Failure: Influence of Topographical and Other Site Specific Amplification Effects. J. Seismology 7 (3), 397–412. doi:10.1023/a:1024534105559

CrossRef Full Text | Google Scholar

Huang, D., Song, Y. X., Cen, D. F., and Fu, G. Y. (2016). Numerical Modeling of the 2008 Wenchuan Earthquake-Triggered Daguangbao Landslide Using a Velocity and Displacement Dependent Friction Law. Eng. Geology 215, 50–68. doi:10.1016/j.enggeo.2016.11.003

CrossRef Full Text | Google Scholar

Huang, D., Cen, D., Ma, G., and Huang, R. (2015). Step-path Failure of Rock Slopes with Intermittent Joints. Landslides 12 (5), 911–926. doi:10.1007/s10346-014-0517-6

CrossRef Full Text | Google Scholar

Huang, R., Pei, X., Fan, X., Zhang, W., Li, S., and Li, B. (2012). The Characteristics and Failure Mechanism of the Largest Landslide Triggered by the Wenchuan Earthquake, May 12, 2008, China. Landslides 9 (1), 131–142. doi:10.1007/s10346-011-0276-6

CrossRef Full Text | Google Scholar

Huang, R. Q., and Li, W. L. (2009). Analysis of the Geo-Hazards Triggered by the 12 May 2008 Wenchuan Earthquake, China. Bull. Eng. Geol. Environ. 68 (3), 363–371. doi:10.1007/s10064-009-0207-0

CrossRef Full Text | Google Scholar

Itasca Consulting Group Inc (2008). Version 4.0. manual. PFC2D/3D. Minneapolis (USA).

Kulatilake, P. H. S. W., Malama, B., and Wang, J. (2001). Physical and Particle Flow Modeling of Jointed Rock Block Behavior under Uniaxial Loading. Int. J. Rock Mech. Mining Sci. 38 (5), 641–657. doi:10.1016/s1365-1609(01)00025-9

CrossRef Full Text | Google Scholar

Kveldsvik, V., Kaynia, A. M., Nadim, F., Bhasin, R., Nilsen, B., and Einstein, H. H. (2009). Dynamic Distinct-Element Analysis of the 800m High Åknes Rock Slope. Int. J. Rock Mech. Mining Sci. 46, 686–698. doi:10.1016/j.ijrmms.2008.10.007

CrossRef Full Text | Google Scholar

Li, X., Zhou, Z., Yu, H., Wen, R., Lu, D., Huang, M., et al. (2008). Strong Motion Observations and Recordings from the Great Wenchuan Earthquake. Earthq. Eng. Eng. Vib. 7 (3), 235–246. doi:10.1007/s11803-008-0892-x

CrossRef Full Text | Google Scholar

Mas Ivars, D., Pierce, M. E., Darcel, C., Reyes-Montes, J., Potyondy, D. O., Paul Young, R., et al. (2011). The Synthetic Rock Mass Approach for Jointed Rock Mass Modelling. Int. J. Rock Mech. Mining Sci. 48 (2), 219–244. doi:10.1016/j.ijrmms.2010.11.014

CrossRef Full Text | Google Scholar

Murphy, W. (2006). Landslides from Massive Rock Slope Failure. Netherlands: Springer. The Role of Topographic Amplification on the Initiation of Rock Slopes Failures during Earthquakes.

Google Scholar

Potyondy, D. O., and Cundall, P. A. (2004). A Bonded-Particle Model for Rock. Int. J. Rock Mech. Mining Sci. 41 (8), 1329–1364. doi:10.1016/j.ijrmms.2004.09.011

CrossRef Full Text | Google Scholar

Qi, S., Xu, Q., Lan, H. X., Zhang, B., and Liu, J. Y. (2010). Spatial Distribution Analysis of Landslides Triggered by 2008.5.12 Wenchuan Earthquake, China. Eng. Geology 116, 95–108. doi:10.1016/j.enggeo.2010.07.011

CrossRef Full Text | Google Scholar

Song, Z.-C., Zhao, L.-H., Li, L., Zhang, Y., and Tang, G. (2018). Distinct Element Modelling of a Landslide Triggered by the 5.12 Wenchuan Earthquake: A Case Study. Geotech Geol. Eng. 36 (4), 2533–2551. doi:10.1007/s10706-018-0481-3

CrossRef Full Text | Google Scholar

Tang, C., Zhu, J., Qi, X., and Ding, J. (2011). Landslides Induced by the Wenchuan Earthquake and the Subsequent strong Rainfall Event: A Case Study in the Beichuan Area of China. Eng. Geology 122 (1), 22–33. doi:10.1016/j.enggeo.2011.03.013

CrossRef Full Text | Google Scholar

Tang, C.-L., Hu, J.-C., Lin, M.-L., Angelier, J., Lu, C.-Y., Chan, Y.-C., et al. (2009). The Tsaoling Landslide Triggered by the Chi-Chi Earthquake, Taiwan: Insights from a Discrete Element Simulation. Eng. Geology 106, 1–19. doi:10.1016/j.enggeo.2009.02.011

CrossRef Full Text | Google Scholar

Tang, C.-L., Hu, J.-C., Lin, M.-L., Yuan, R.-M., and Cheng, C.-C. (2013). The Mechanism of the 1941 Tsaoling Landslide, Taiwan: Insight from a 2D Discrete Element Simulation. Environ. Earth Sci. 70 (3), 1005–1019. doi:10.1007/s12665-012-2190-1

CrossRef Full Text | Google Scholar

Wang, C., Tannant, D. D., and Lilly, P. A. (2003). Numerical Analysis of the Stability of Heavily Jointed Rock Slopes Using PFC2D. Int. J. Rock Mech. Mining Sci. 40 (3), 415–424. doi:10.1016/s1365-1609(03)00004-2

CrossRef Full Text | Google Scholar

Wang, F., Cheng, Q., Highland, L., Miyajima, M., Wang, H., and Yan, C. (2009). Preliminary Investigation of Some Large Landslides Triggered by the 2008 Wenchuan Earthquake, Sichuan Province, China. Landslides 6 (1), 47–54. doi:10.1007/s10346-009-0141-z

CrossRef Full Text | Google Scholar

Wang, G., Huang, R., Lourenço, S. D. N., and Kamai, T. (2014). A Large Landslide Triggered by the 2008 Wenchuan (M8.0) Earthquake in Donghekou Area: Phenomena and Mechanisms. Eng. Geology 182, 148–157. doi:10.1016/j.enggeo.2014.07.013

CrossRef Full Text | Google Scholar

Wu, J.-H., and Chen, C.-H. (2011). Application of DDA to Simulate Characteristics of the Tsaoling Landslide. Comput. Geotechnics 38, 741–750. doi:10.1016/j.compgeo.2011.04.003

CrossRef Full Text | Google Scholar

Xu, W.-J., Xu, Q., and Wang, Y.-J. (2013). The Mechanism of High-Speed Motion and Damming of the Tangjiashan Landslide. Eng. Geology 157 (6), 8–20. doi:10.1016/j.enggeo.2013.01.020

CrossRef Full Text | Google Scholar

Yin, Y., Wang, F., and Sun, P. (2009). Landslide Hazards Triggered by the 2008 Wenchuan Earthquake, Sichuan, China. Landslides 6 (2), 139–152. doi:10.1007/s10346-009-0148-5

CrossRef Full Text | Google Scholar

Yuan, R.-M., Tang, C.-L., Hu, J.-C., and Xu, X.-W. (2014). Mechanism of the Donghekou Landslide Triggered by the 2008 Wenchuan Earthquake Revealed by Discrete Element Modeling. Nat. Hazards Earth Syst. Sci. 14 (5), 1195–1205. doi:10.5194/nhess-14-1195-2014

CrossRef Full Text | Google Scholar

Zhang, M., and Yin, Y. (2013). Dynamics, Mobility-Controlling Factors and Transport Mechanisms of Rapid Long-Runout Rock Avalanches in China. Eng. Geology 167 (12), 37–58. doi:10.1016/j.enggeo.2013.10.010

CrossRef Full Text | Google Scholar

Zhang, M., Yin, Y., and Mcsaveney, M. (2016). Dynamics of the 2008 Earthquake-Triggered Wenjiagou Creek Rock Avalanche, Qingping, Sichuan, China. Eng. Geology 200, 75–87. doi:10.1016/j.enggeo.2015.12.008

CrossRef Full Text | Google Scholar

Zhang, M., Yin, Y., Wu, S., Zhang, Y., and Han, J. (2011). Dynamics of the Niumiangou Creek Rock Avalanche Triggered by 2008 Ms 8.0 Wenchuan Earthquake, Sichuan, China. Landslides 8 (3), 363–371. doi:10.1007/s10346-011-0265-9

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, J., Xu, Q., Chen, G., X Zhao, J., Zheng, L., et al. (2015). DDA Validation of the Mobility of Earthquake-Induced Landslides. Eng. Geology 194, 38–51. doi:10.1016/j.enggeo.2014.08.024

CrossRef Full Text | Google Scholar

Zhang, Z., Wang, T., Wu, S., Tang, H., and Liang, C. (2017). The Role of Seismic Triggering in a Deep-Seated Mudstone Landslide, China: Historical Reconstruction and Mechanism Analysis. Eng. Geology 226, 122–135. doi:10.1016/j.enggeo.2017.06.001

CrossRef Full Text | Google Scholar

Zhou, J.-w., Cui, P., and Yang, X.-g. (2013). Dynamic Process Analysis for the Initiation and Movement of the Donghekou Landslide-Debris Flow Triggered by the Wenchuan Earthquake. J. Asian Earth Sci. 76 (S1), 70–84. doi:10.1016/j.jseaes.2013.08.007

CrossRef Full Text | Google Scholar

Zhuang, J., Peng, J., Xu, C., Li, Z., Densmore, A., Milledge, D., et al. (2018). Distribution and Characteristics of Loess Landslides Triggered by the 1920 Haiyuan Earthquake, Northwest of China. Geomorphology 314, 1–12. doi:10.1016/j.geomorph.2018.04.012

CrossRef Full Text | Google Scholar

Zienkiewicz, O. C., Bicanic, N., and Shen, F. Q. (1989). Advances in Computational Nonlinear Mechanics. Vienna: Springer. doi:10.1007/978-3-7091-2828-2_3 Earthquake Input Definition and the Trasmitting Boundary Conditions.

CrossRef Full Text | Google Scholar