Determining the Geotechnical Slope Failure Factors via Ensemble and Individual Machine Learning Techniques: A Case Study in Mandi, India

Landslide disaster risk reduction necessitates the investigation of different geotechnical causal factors for slope failures. Machine learning (ML) techniques have been proposed to study causal factors across many application areas. However, the development of ensemble ML techniques for identifying the geotechnical causal factors for slope failures and their subsequent prediction has lacked in literature. The primary goal of this research is to develop and evaluate novel feature selection methods for identifying causal factors for slope failures and assess the potential of ensemble and individual ML techniques for slope failure prediction. Twenty-one geotechnical causal factors were obtained from 60 sites (both landslide and non-landslide) spread across a landslide-prone area in Mandi, India. Relevant causal factors were evaluated by developing a novel ensemble feature selection method that involved an average of different individual feature selection methods like correlation, information-gain, gain-ratio, OneR, and F-ratio. Furthermore, different ensemble ML techniques (Random Forest (RF), AdaBoost (AB), Bagging, Stacking, and Voting) and individual ML techniques (Bayesian network (BN), decision tree (DT), multilayer perceptron (MLP), and support vector machine (SVM)) were calibrated to 70% of the locations and tested on 30% of the sites. The ensemble feature selection method yielded six major contributing parameters to slope failures: relative compaction, porosity, saturated permeability, slope angle, angle of the internal friction, and in-situ moisture content. Furthermore, the ensemble RF and AB techniques performed the best compared to other ensemble and individual ML techniques on test data. The present study discusses the implications of different causal factors for slope failure prediction.

Introduction

Slope failures, the soil or debris movements along sloping surfaces, have significantly impacted the infrastructure and life in hilly areas (National Institute of Disaster Management, 2016; Parkash 2011). For example, according to Yilmaz (2009), in the 1990s, slope failures constituted about 9% of all disasters. In the Himalayan region, slope failures have occurred due to rainfall, earthquakes, and geological and anthropogenic factors, causing nearly 200 deaths per year and about $82 million in infrastructure-related damages (Chaturvedi and Dutt 2015; Chaturvedi et al., 2018). Slope failures and associated landslides have affected nearly 0.49 million square kilometres of area in India (National Institute of Disaster Management, 2016). Some attempts to monitor these slope failures have relied on a number of conventional and low-cost methods (Fell et al., 2005; Joyce et al., 2008; Guzzetti et al., 2012; Thiebes et al., 2012; Calvello et al., 2015; Dikshit et al., 2017; Kumar et al., 2019; Park et al., 2019; Ma et al., 2020). These methods have helped generate slope movement estimates at deployment sites (Kumar et al., 2021).

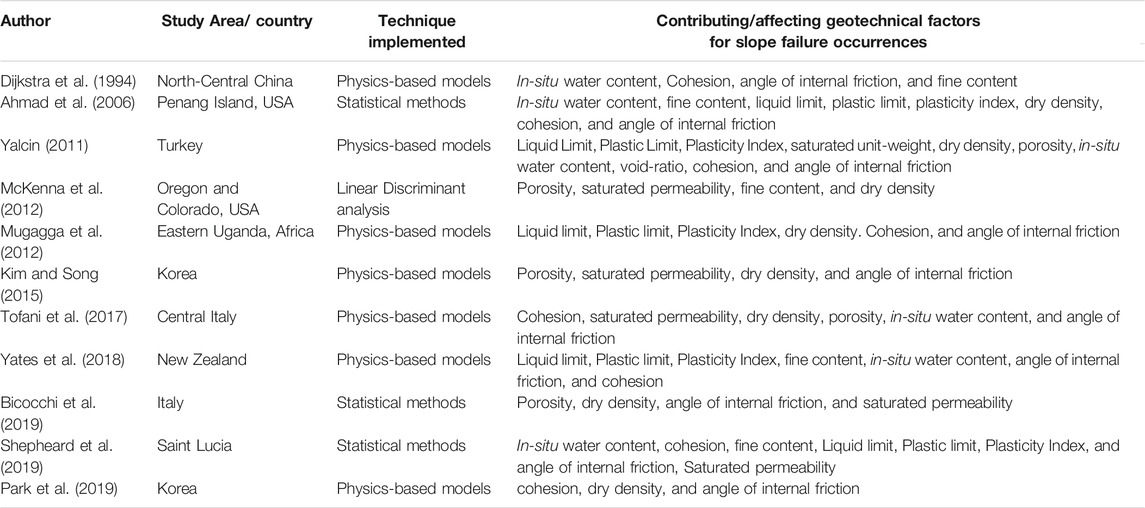
The relative probability of landslide occurrence in any specific area can be represented using susceptibility models, which help to produce hazard zonation maps. These zonation maps are subjective and prepared based on deterministic models. These models include the mathematical relationships between the driving and resisting forces, engineering characteristics of the rock and soils, slope geometry, and hydrological conditions (Yilmaz 2009; Ohlmacher and Davis, 2003; Alimohammadlou et al., 2014). A critical review of the literature reveals a set of regional, zonal, and local geotechnical factors as potential candidates for causing slope failures (see Table 1). As shown in Table 1, several factors may include: porosity, particle size distribution, dry density, saturated permeability, shear strength parameters, and fines content.

TABLE 1

TABLE 1. Contributing geotechnical factors reported in the literature.

As shown in Table 1, Dijkstra et al. (1994) determined the influencing factors for the slope instability. The results revealed that the in-situ moisture content played a vital role in slope failure occurring in North-Central China. Although Dijkstra et al. (1994) determined the geotechnical properties and their influence for slope instability considering the physics-based models; however, individual and ensemble machine learning techniques were not explored. Ahmad et al. (2006) determined the influencing factors for slope instability using the statistical approach in Penang Island, USA; however, individual and ensemble feature selection techniques were not explored.

Similarly, as shown in Table 1, Yalcin (2011) revealed the factors influencing the failures occurring in the Turkey area employing a physics-based approach. However, the individual and ensemble feature selection techniques were not explored. McKenna et al. (2012) performed a linear discriminant analysis to determine the slope failures in Oregon and Colorado, USA. However, individual and ensemble-based machine learning algorithms were not explored for determining the influencing factors for slope failures. Mugagga et al. (2012) performed a physics-based approach for determining the factor of the safety for the slopes and determined the influencing factors for slope failures in Eastern Uganda, Africa. Although Mugagga et al. (2012) utilized the physics-based models for obtaining the safety factor for the slopes, individual, predicting slope failures, and ensemble feature selection techniques were not explored.

Kim and Song (2015) determined the factors influencing the slope instability and employed a physics-based approach using GIS application. However, the individual and ensemble-based machine learning techniques were not explored. Tofani et al. (2017) developed physics-based models whereas, Bicocchi et al. (2019) performed a statistical approach for determining the factors influencing the slope failures in Italy. However, the application of individual and ensemble-based machine learning techniques was not explored. Yates et al. (2018) revealed the factors influencing the failures occurring in New Zealand employing a physics-based approach. However, the individual and ensemble feature selection techniques were not explored.

Shepheard et al. (2019) performed a statistical approach for determining the factors influencing the slope failures in Saint Lucia. However, the application of individual and ensemble-based machine learning techniques was not explored. Similarly, Park et al. (2019) revealed the factors influencing the failures occurring in New Zealand employing a physics-based approach. However, the individual and ensemble feature selection techniques were not explored. The geotechnical factors assessment has been confirmed mostly by physical-based models or statistical analysis. It was felt that less or no emphasis on the slope failures from the site has been given in the literature concerning the use of individual and ensemble techniques for slope failures.

The geotechnical factors are characterized by both uniform and continuous spatial distributions due to intrinsic inconsistency, and these factors may be prone to other uncertainties due to sampling errors and measurements (Aloetti and Chowdhury 1999; Phoon and Kulhawy 1999; Akbas and Kulhawy 2010). Physical models may involve different geotechnical factors, which may help these models generate forecasts about slope failures (Tofani et al., 2017; Bicocchi et al., 2019). However, physical models involving different geotechnical factors may be constraint by the underlying mechanics explaining slope failures (Yalcin 2011; Igwe, 2015; Tofani et al., 2017; Bicocchi et al., 2019; Shepheard et al., 2019). Amidst constraints in physical models, data-driven machine-learning (ML) techniques may provide an alternate approach for predicting slope failures (Aloetti and Chowdhury 1999; Kavzoglu et al., 2014; Huang et al., 2017; Park et al., 2019; Asheghi et al., 2020; Moayedi et al., 2021). These ML techniques may learn about the underlying relationships between geotechnical factors and their role in causing slope failures using statistical approaches (Phoon and Kulhawy 1999). Thus, the ML techniques may help predict slope failures and aid in determining the contributing geotechnical factors responsible for slope failures (Pham et al., 2017).

Among the ML techniques, Shahri et al. (2019) developed an artificial neural network (ANN) model for determining landslide susceptibility in Sweden due to 14 different causative factors extracted from geological, hydrological, hydrogeological, topographic, and geomorphological characteristics. However, only one ML technique (ANN) was proposed. Ma et al. (2020) provided a review of ML techniques that have been proposed for landslide detection based upon images, landslide susceptibility assessment, and the development of warning systems. Although Ma et al. (2020) provided a large set of ML and other approaches; however, a review of different factors and their influence on slope failures were not provided. Nhu et al. (2020) provided a case study for landslide susceptibility mapping using AdaBoost (AB) and decision tree (DT) techniques. These authors found that the AB technique performed better than the DT technique and an ensemble of AB and DT techniques. However, a comprehensive evaluation of a large class of geotechnical factors was not performed and only a small number of ML techniques were explored. Ahmad et al. (2006) proposed a number of ensemble techniques (random forests and gradient boosting trees) and individual techniques (linear regression and multi-layer perceptron (MLP)) for predicting landslides in southeast Bangladesh. However, these authors did not propose the investigation of factors important for landslides and relied on a small class of ML techniques. Shahri and Maghsoudi, (2021) proposed a hybrid block-based neural network model (HBNN) for producing landslide susceptibility mapping. The HBNN was compared against an MLP generalized feed-forward neural network (GFFN). However, these authors did not understand the relative importance of different factors. Pham et al. (2019) proposed hybrid machine learning techniques (bagging, random subspace, and random forest) with alternating decision trees for predicting landslides in Uttarakhand, India. Ten different conditioning factors were extracted from geomorphological characteristics. However, only the land cover was the most influencing factor. Madawala et al. (2019) developed an ensemble approach combining support vector machine and Naïve Bayes approach to predicting landslides in Sri Lanka. However, different considered factors had a relatively similar positive correlation with the slope failure.

Similarly, Bui et al. (2012) relied upon support vector machine (SVM), decision tree (DT), and Bayesian ML techniques for landslide susceptibility mapping in Hoa Binh province, Vietnam. Although Bui et al. (2012) proposed several ML techniques; however, a review of different geotechnical factors and their influence on the slope failures were not explored. Chen et al. (2018) proposed SVM, random forest (RF), and logistic model tree (LMT) techniques for landslide susceptibility mapping in the Long County area, China. Results showed that the RF algorithm outperformed the other two algorithms. However, the causal factors and their influence on the slope failures was not explored. Agrawal et al. (2017) compared logistic regression, DT, SVM, RF, and multilayer perceptron (MLP) techniques for landslide susceptibility mapping using the rainfall and previous landslide instances 2011 to 2015 on National Highway NH-21 between Mandi and Manali, India. The best performing technique included RF, followed by DT and logistic regression. Although Agrawal et al. (2017) proposed several ML approaches; however, geotechnical factors and their influence on slope failures was not explored. Kumar et al. (2019) compared ensemble and individual machine-learning algorithms to predict the weekly debris flow at Tangni (India) between 2013-17. However, different causal factors and their influence on slope failures was not explored.

Although some literature is available on adopting ML techniques for landslide susceptibility mapping and debris flow predictions; however, the development of novel ML techniques for identifying the causal factors for slope failures and the subsequent prediction of slope failures has lacked in literature. Also, to the authors’ best knowledge, ML techniques for slope failure assessment with emphasis on geotechnical factors have not been explored for the Indian part of the Himalayan mountains.

The current study overcomes these literature gaps by performing slope failure assessment in the Mandi, India, which falls in the mid-Himalayan range of the Indian Himalayas. The area has been selected based on the numerous failures found at the site. Although prior literature in ML has proposed some feature selection methods (Guyon and Elisseeff 2003; Guyon et al., 2006), this study offers a novel ensemble feature selection method that involves a weighted combination of some feature selection approaches. Another novelty of this study is that it compares state-of-the-art ensemble ML techniques with individual ML techniques for predicting slope failures. This study also proposes a new approach for identifying a combination of causal factors for slope failures.

One of the study objectives is to evaluate a set of geotechnical factors for causing slope failures via a novel ensemble feature selection method. Further, this study intends to develop ensemble and individual ML models for slope failure prediction by relying upon causal factors. Based on prior literature (Kumar et al., 2019; Pathania et al., 2020; Kaushik et al., 2020), the ensemble feature selection is expected to yield a combination of relevant geotechnical factors for slope failure assessment than the individual techniques.

In what follows, first, the methodologies involved in determining the geotechnical factors for the collected soil samples are detailed. Further, the working of different ensemble and individual ML techniques for predicting slope failures are discussed. Next, the ranking of different geotechnical factors involved in slope failure is performed via an ensemble feature selection method. Finally, the results obtained from the ensemble and individual ML techniques are presented, and the importance of a combination of geotechnical factors for slope failure studies is discussed.

Study Area Description

The study was performed in the Mandi, Himachal Pradesh, India. The township is situated in the mid-Himalayan region (see Figure 1). Specifically, the investigated area (along the road between Mandi to Kamand) is located between 31°42^'25^″N and 31°46^'26^″N latitudes and between 76°55^'54^″E and 76^º59^'42^″E longitudes. The elevation range of the study area is between 850 m and 1,250 m. A reason for choosing the Mandi township for this study is due to several slope failures in the past in this area (Kahlon et al., 2014). A triggering factor for these slope failures in the study area could be the rainfall, with an average annual precipitation of 1,380 mm (Gupta and Shukla 2018).

FIGURE 1

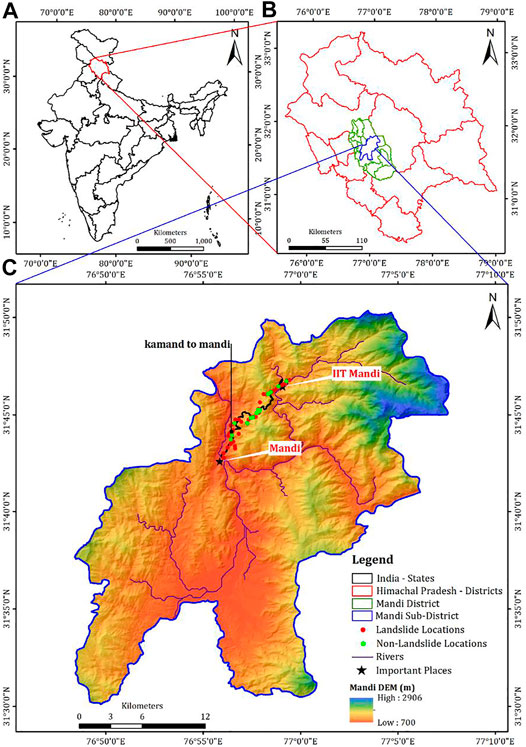
FIGURE 1. Locations of sites where data were collected for the study in India. (A) Map of India showing Himachal Pradesh state. (B) Map of Himachal Pradesh showing Mandi district. (C) The sites in Mandi district where soil samples were collected. Red dots show the soil samples were collected from the landslide locations, and green dots show the soil samples were collected from the no-landslides locations.

Materials and Methodology

Samples of soil were collected in the Mandi township over a 15 km road stretch across different slope failure sites. Soil samples were collected from sixty locations in the study area at depths of up to 0.5 m along the sloping surfaces. The soil samples were collected from both slope failures and no-slope failure locations. The samples included field inventory data, including in-situ moisture content (ASTM D 2216-19, 2019), location coordinates (in latitude-longitude and elevation), and whether slope failures had occurred recently at the investigated site. To obtain soil samples, stainless soil sampler (diameter = 10 cm, height = 13 cm, and area ratio <10%) was employed. Soils, 0.3–0.5 m deep, were removed by driving a soil sampler into the sloping surface using a plastic-coated hammer. The in-situ soil sampling helped determine the in-situ bulk density and in-situ water content (w_n) of the respective sample. Soil samples of about 40 kg were collected via a trowel at places with boulders and rocky strata. The soil samples collected were packed, marked carefully, and transported to the laboratory for further analyses.

Among the 60 sites in the study area, 43 sites had experienced slope failures, and 17 sites had not experienced slope failures. Computation of 21 geotechnical factors was done across the 60 sites. These data were then used for the identification of different geotechnical factors as well as for making slope failure predictions.

Methods

The geotechnical factors were analyzed using different test procedures. The specific gravity test (ASTM D 5550-00, 2000) was conducted using a gas pycnometer. The gradation analysis was carried out for the soil samples as per ASTM D 422-63, 1994. The liquid and plasticity limits along with the plasticity index were determined as per ASTM D 6913 (2009), ASTM D 4318 - 17e1 (2010). The standard proctor test (ASTM D 698 - 12e2, 2012) was conducted to determine the dry density and optimum moisture content. The saturated permeability was determined according to ASTM D2434-19, 2019. The relative compaction of soil was calculated by computing the ratio of the dry density (in-situ) and the dry density (laboratory). The porosity was calculated based on the in-situ density.

Machine Learning Techniques

Machine learning (ML) techniques deal with the development of algorithms that rely upon data to learn patterns present in data (Bishop 2006; Awad and Khanna 2015; Mali et al., 2019). ML techniques learn patterns present in data, and researchers can develop ML techniques for several applications, including those in the geotechnical areas. Thus, ML techniques could be developed for factor analyses (feature engineering) and predicting slope failures due to different geotechnical factors. Some of the ML techniques that have been developed in this paper are discussed next.

Individual Techniques

Support Vector Machines

Vapnik (1995) proposed the SVM technique. This technique uses a statistical approach to achieve an optimal hyperplane dividing two classes (Ballabio and Sterlacchini 2012). If $\times =\left({\times }_1,{\times }_2,\dots {\times }_n\right)$ represents the vectors corresponding to the slope-failure contributing factors and let Y_j is the vector classifying data into the slope failure and no-slope failure classes (Kavzoglu et al., 2014), then the optimal dividing hyperplane is established by:

$\mathrm{f}(\times )=\text{sign} \left[{\displaystyle \sum _{i=1}^n{\mathrm{\alpha }}_{\mathrm{i}}{\mathrm{Y}}_{\mathrm{j}}\mathrm{k}\left(\times ,{\times }_i\right)+\mathrm{a}}\right](1)$

where ‘a’ is the offset from hyperplane’s origin, ‘n’ is the number of geotechnical factors, α_i is the i^th positive constant, and $\text{k}\left(\times ,{\times }_i\right)$ is the kernel function. For binary classification (slope failure or no-slope failure), the conditions for solving the Eq. 1 become the following:

${\mathrm{Y}}_{\mathrm{j}}\left[{\mathrm{\omega }}^{\mathrm{T}}{\times }_{\mathrm{i}}+\mathrm{c}\right]\ge 1\iff \{\begin{array}{c}{\mathrm{\omega }}^{\mathrm{T}}{\times }_{\mathrm{i}}+\mathrm{c}\ge 1,\text{if}{Y}_j=+1\left(\text{slope}\text{failure}\right)\\ {\mathrm{\omega }}^{\mathrm{T}}{\times }_{\mathrm{i}}+\mathrm{c}\le 1,\text{if}{Y}_j=-1\left(\text{no}-\text{slope}\text{failure}\right)\end{array}(2)$

where, ‘k’ separates one space into a second space with more dimensions, and ‘ω’ is the weight vector.

Multilayer Perceptron

A MLP is an artificial neural network, which includes input, hidden, and output layers (Zare et al., 2013). The training processes in an MLP involves the following procedure: 1) feeding the input data into the hidden layers, where the resulting values are checked against the actual values to estimate the error; and 2) amending connection weights based upon the error propagated backwards (Bishop 2006; Tien et al., 2016). A MLP was developed where the affecting factors for slope failures were considered as inputs, and the class (slope failure or no-slope failure) was considered the output. The hidden layers helped transform inputs into outcomes.

If t = t_i and i = 1 to n are the corresponding vectors of affecting factors, and ϕ = ϕ_j for j ε {0, 1} represents the two classes, then,

$\varphi =g\left(t\right)(3)$

where, $\text{g}\left(\text{t}\right)$ represents an unknown function in the MLP, where the necessary weights are amended to train the technique.

Bayesian Network

The BN mostly employs algorithms adapted for complex systems modeling (Friedman et al., 1997; Pham et al., 2016a). In BN, the probability of slope failure and no-slope failure classes is analyzed given the value of geotechnical factors. The BN technique relies upon the Bayes’ theorem for a given set of factor values (Bishop 2006). Let $\text{X}={\text{x}}_{\text{i}}$ for i = 1 to n represent the vectors corresponding to the contributing factors. Using the BN technique, the unique joint probability of a slope failure (SF) event can be represented as (Pham et al., 2016b):

$\text{P }\left(\frac{{\text{C}}_{\text{k}}}{\text{A}}\right)=\frac{\text{P}\left(\frac{\text{A}}{{\text{C}}_{\text{K}}}\right)\text{*P}\left({\text{C}}_{\text{k}}\right)}{\text{P}\left(\text{A}\right)}(4)$

where, $\text{P}\left(\frac{{\text{C}}_{\text{k}}}{\text{A}}\right)$ represents the posterior, i.e., the conditional probability of a class C_k for the given factors A.

$\text{P}\left(\frac{\text{A}}{{\text{C}}_{\text{k}}}\right)$ is the likelihood, representing the probability of factors A given a class C_k. P(C_k) is the prior probability of the class C_k in the given data, and P(A) is the probability of the factors A.

Decision Tree

A DT is an entropy-based classification technique (Catani et al., 2013). In DT, a tree is developed based on binary classification (slope failure or no-slope failure), and the tree includes root, internal, and child nodes (Tien et al., 2012a). In DT, one of the several factors is considered on a tree edge emanating from a node. The DT technique involves: 1) building a tree based on information theory and 2) trimming the developed tree to reduce its height (Tien et al., 2016). Identification of different factors is performed at different nodes. The selection of a factor on edges emanating from a node is based on the highest information gain. Finally, a data point’s classification (slope failure or no-slope failure) is determined based upon the DT’s traversal.

Ensemble Techniques

Ensemble methods are specific techniques, which are usually created by a combination of multiple individual techniques. As ensemble methods combine several unique techniques, these methods are expected to possess better performance than individual techniques (Kavicky et al., 2017; Kumar et al., 2019). The ensemble models tried in this research are discussed in the following sections.

Random Forest (RF)

The RF technique was proposed by Breiman (2001), and it is an aggregate tree-based approach that relies upon a collection of decision trees created through bootstrapping. The RF technique assumes a combination of many trees in which a random subset of causal factors is considered for generating different trees (Breiman 2001; Pham et al., 2017). A single tree’s classification could be unstable, and different trees are developed to minimize classification errors. For this reason, the RF method makes use of an ensemble of trees (the so-called “forest”), thereby ensuring model stability (Agrawal et al., 2017). Furthermore, the developed trees are based upon a randomized subset of the contributing factors. Randomization helps to estimate the importance of contributing factors and their impacts on the classification (Catani et al., 2013).

AdaBoost (AB)

The AB technique was developed by Freund and Schapire (1997). It is a dominant boosting technique that involves enhancing the simpler techniques’ performance by combining them (Tattar 2018). Generally, AB uses short decision trees, each with a root node. In AB, a preliminary model is first constructed. Each data point is weighted, and weights are changed based on the model’s overall accuracy and whether a specific data point is classified correctly or not (Tattar 2018). Different decision tree models are weighted and added until no further improvements in the overall accuracy are possible (Tattar 2018). Furthermore, AB can assess the significance of factors by investigating how often the simpler/weak learning techniques are selected.

Bagging

Bagging (or bootstrap aggregation) is an ensemble method in which random samples are selected repeatedly with replacement (Breiman 1996a; Boehmke and Greenwell, 2019). Each time a random training data sample is selected, a machine-learning model is built (Boehmke and Greenwell, 2019). The algorithm builds some such machine-learning models and then averages these models’ predictions to generate its prediction (Boehmke and Greenwell, 2019). In this research, the random forest technique was employed as the machine-learning model in bagging. This made the bagging algorithm comparable to other chosen methods.

Voting

According to Bonaccorso (2018), voting is the simplest ensemble technique where a majority of the classifiers help estimate the final-predicted class of the target variable. The class obtained from the highest votes is to be the final prediction of the ensemble voting technique. To make it comparable to other individual techniques in the present study, individual algorithms reported in the section above were used in voting.

Stacking

Stacking (or stacked generalization; Wolpert 1992; Dangeti, 2017) is a modified voting technique. Unlike in voting, where an unpretentious majority may decide the ensemble’s prediction, in stacking, the predictions of the individual techniques are fed into another meta-model, which then determines the prediction of the ensemble. The RF classifier was implemented as a meta-model to compare with the individual techniques.

Ensemble Feature Selection Methods

Feature (factor) selection performs a selection of a subset of relevant features (factors) from all features present in data (Bishop 2006; Wang and Tang, 2009; Micheletti et al., 2014). A novel ensemble-based feature selection method was formulated, which combines some particular feature selection methods. The motivation behind ensembling different feature selection methods was to take the best of the different individual feature selection approaches. The average of the feature ranks from different individual methods in the ensemble feature selection method was assumed. The feature selection methods include the following: correlation-based feature selection (CFS), information–gain ratio (IGR) based feature selection, gain ratio (GR)-based feature selection, relief-F feature selection, and OneR selection. Next, the following feature selection methods were detailed.

Correlation-Based Feature Selection

The CFS is an efficient and popular technique for causal factor identification (Hall 1999; Bishop 2006; Pham et al., 2016a). The recognition of different factors is based on the Pearson correlation between various factors and the class variable (Nguyen et al., 2010).

Information Gain Ratio

Information gain (also known as entropy) is based on information theory, and it quantifies the amount of information possessed by factors. The information gain (or entropy) is computed as:

$\text{I}\left(\text{Y}\right)=-{\displaystyle \sum _{\text{i}=1}^2\frac{\text{n}\left({\text{L}}_{\text{i}},\text{Y}\right)}{\left[\text{Y}\right]}}{\text{log}}_2\frac{\text{n}\left({\text{L}}_{\text{i}},\text{Y}\right)}{\left[\text{Y}\right]}(5)$

where, for a given training data Y containing input samples n, n (L_i, Y) is the number of samples in training data Y that belong to the class L_i (slope failure or no-slope failure). The information amount that splits Y into (Y₁, Y₂, … , Y_m) regarding the slope failure affecting factor X is estimated as:

$\text{I }\left(\text{Y},\text{ X}\right)={\displaystyle \sum _{\text{j}=1}^{\text{m}}\frac{{\text{Y}}_{\text{j}}}{\left[\text{Y}\right]}\text{I}\left(\text{Y}\right)}(6)$

The IGR for a certain slope failure-influencing factor A is computed as:

$\text{IGR}\left(\text{Y},\text{X}\right)=\frac{\text{I}\left(\text{Y}\right)-\text{I}\left(\text{Y},\text{X}\right)}{\text{SpI}\left(\text{Y},\text{X}\right)}(7)$

where, $\text{SpI}\left(\text{Y},\text{X}\right)$ represents the potential information generated by dividing the training data Y into m subsets. It is deduced as:

$\text{SpI}\left(\text{Y},\text{X}\right)=-{\displaystyle \sum _{\text{j}=1}^{\text{m}}\frac{\left[{\text{Y}}_{\text{j}}\right]}{\left[\text{Y}\right]}}{\text{log}}_2\frac{\left[{\text{Y}}_{\text{j}}\right]}{\left[\text{Y}\right]}(8)$

Gain Ratio

The GR is a modified version of the info-gain ratio feature selection method (Han and Kamber 2001). The GR considers different branches in a tree, and it computes the information gain based upon the information of a split. The split information is based upon the instances’ entropy, where information’s value for an attribute decreases based on the increase in split information (Han and Kamber 2001). The GR is defined as:

$\text{GR}=\frac{\text{Gain}\left(\text{attribute}\right)}{\text{Split}\_\text{info}\left(\text{attribute}\right)}(9)$

where $\text{Gain}\left(\text{attribute}\right)$ is the information gain for an attribute, and $\text{Split}\_\text{info}\left(\text{attribute}\right)$ is the split information value for the same attribute.

Relief-F

The relief-F is a filter method that evaluates an attribute’s worth by sampling values repeatedly (Kira and Rendell 1992; Urbanowicz et al., 2018). Generally, it is desirable to apply this method in binary classification problems. According to Urbanowicz et al. (2018), the method determines the relief feature score for an individual feature and finally takes the high-scoring features. Generally, the feature differences between the nearest neighbouring instance pairs determine the score. The feature score is decreased or increased based upon the feature value difference being a hit or a miss.

OneR

The OneR feature-selection method uses the OneR classifier to determine the feature importance. For each feature in data, it generates one rule and then chooses the rule of the feature that produces the largest accuracy for the class variable (Holte 1993). The OneR algorithm is known to produce rules that compete well with other state-of-the-art algorithms in the literature.

Validation and Comparison Methods

The employed ML techniques’ performance in terms of sensitivity, specificity, accuracy, and kappa (k) statistics were computed (Tien et al., 2016). The formulae used and the description of different performance measures have been reported in Table 2. The area under the ROC curve (AUROC) was also used as an evaluation metric (Bradley 1997). The AUROC is formed by plotting false-positive rates (i.e., 1-specificity) against true-positive rates (i.e., sensitivity). The AUROC ranges between 0.5 (an inaccurate classification technique) and 1 (a perfect classification technique) (Pham et al., 2016a; Tien et al., 2016).

TABLE 2

TABLE 2. Description of performance measures for evaluating ML models.

Construction of the Slope-Failure Inventory for Model Training and Testing

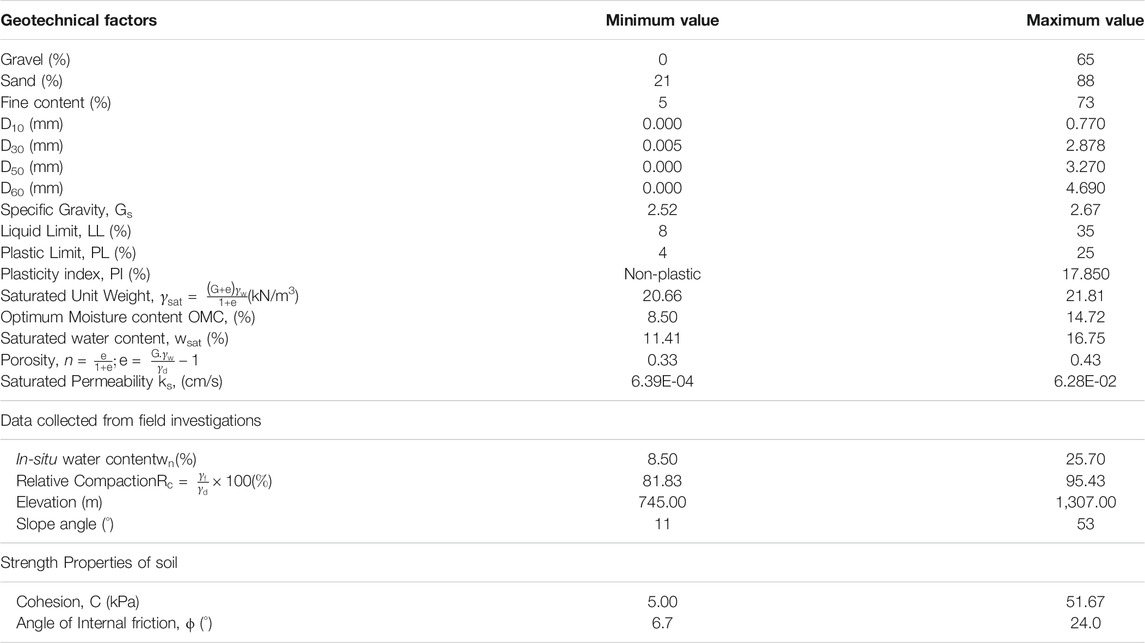
The results obtained from the field and laboratory investigations served as input data into different ML techniques. The inputs were kept at their original values and not scaled or normalized in analyses. All the identified geotechnical factors were considered as the affecting factors for the current study (see Table 3 for a list of affecting factors and their range of measured values). As shown in Table 3, the factors considered were gravel; sand; fines content; diameter corresponding to different particle sizes (D₁₀; D₃₀; D₅₀; D₆₀); liquid limit (LL); plastic limit (PL); plasticity index (PI); specific gravity; saturated unit weight; saturated water content; optimum moisture content; porosity; saturated permeability; in-situ water content; relative compaction; elevation; slope angle; cohesion; and angle of internal friction (ϕ).

TABLE 3

TABLE 3. Range of values of the geotechnical factors across 60 locations.

Out of the 60 data points (one from each site), 70% 42) randomly selected data points (slope failure = 31; No-slope failure = 11) were used for training different ML techniques and the remaining 30% 18) data points (slope failure = 12; No-slope failure = 06) were used for testing the ML techniques.

Machine Learning Techniques’ Configurations and Implementation

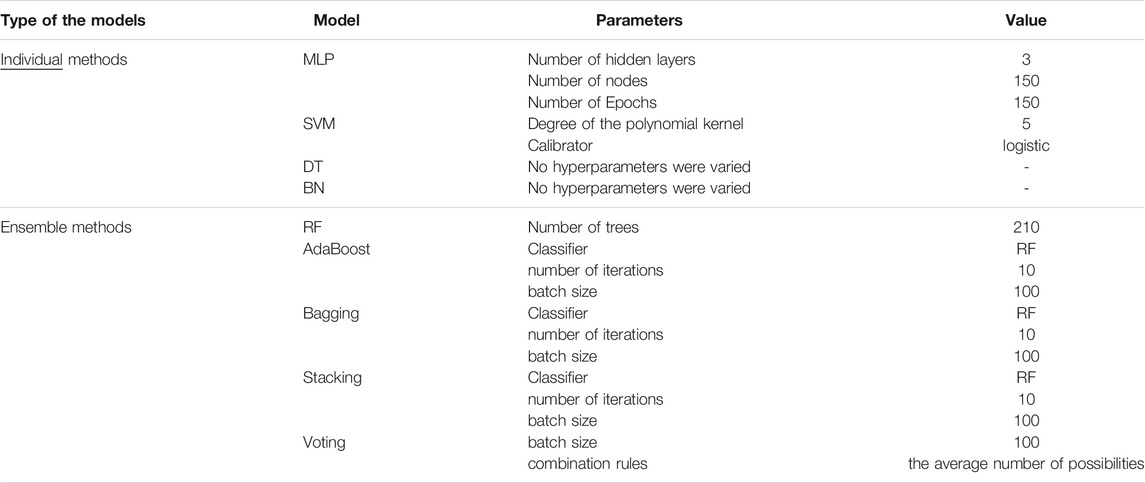
In the current study, both individual and ensemble ML techniques detailed above were evaluated for slope-failure prediction. Table 4 details different hyperparameters in different ML techniques and their range of variation. All hyperparameters were varied in a grid search, where the grid points were the values of different parameters in a model as specified in Table 4.

TABLE 4

TABLE 4. Hyperparameters across different models along with their values.

Individual Techniques

Multi-Layer Perceptron

The MLP possessed five different hyperparameters, which included: hidden layers (varied as 1, 3, 6); the number of the nodes in each hidden layers (varied as 50, 100, 150, 200); the number of the epochs (the number of times the weight change took place; varied as 50, 100, 150), and the activation functions present in the hidden layers (varied as rectified linear, linear, and sigmoid). Furthermore, the output layer possessed one node with a sigmoid activation function.

Bayesian Network

In this model, there was no hyperparameters present that needed to be varied.

Decision Tree

In this model, no hyperparameters present needed to be varied.

Support Vector Machines

In this model, the polynomial kernel degree was varied as 1, 3, 5, 8. The calibrator used was logistic.

Ensemble Techniques

Random Forest

The following were the hyperparameters varied for training the RF model: the number of trees (varied as 25, 50, 75, 100, 150, 200, 210).

AdaBoost

In the AB model, the base classifier selected was Random Forest. Furthermore, the different hyperparameters varied included: the batch size (varied as 1, 2, 5, 7, 10) and the iterations (varied as 1, 10, 25, 50, 75, 100).

Stacking

In this model, the base classifier selected was Random Forest. Furthermore, the following hyperparameters were varied: the batch size (varied as 1, 2, 5, 7, 10) and the number of the iterations (varied as 1, 10, 25, 50, 75, 100).

Bagging

In this model, the base classifier selected was Random Forest. Furthermore, the following hyperparameters were varied: the batch size (varied as 1, 2, 5, 7, 10) and the number of the iterations (varied as 1, 10, 25, 50, 75, 100).

Voting

In this model, the base classifier selected was the Random Forest technique, and only one hyperparameter varied for training the model: batch size (varied as 1, 2, 5, 7, 10).

Figure 2 depicts the sequence of steps to identify the influencing factors for slope failures. Initially, the geotechnical dataset was obtained by performing laboratory tests on data collected from the field investigation. Out of the collected dataset, 70% of data were used to train different ML techniques, and the remaining 30% of data were used to test different ML techniques. The influencing factors for slope failures were obtained using the ensemble feature selection method, which considered several individual feature selection methods. Next, the contributing factors were used in the ML techniques for predicting slope failures. For obtaining the best hyperparameters in the employed ML technique, the different hyperparameters were calibrated using training data. Furthermore, different ML techniques with calibrated parameters were validated using the test dataset. The ensemble feature selection and ML techniques were analysed using the WEKA 3.9.0 tool (Frank et al., 2016).

FIGURE 2

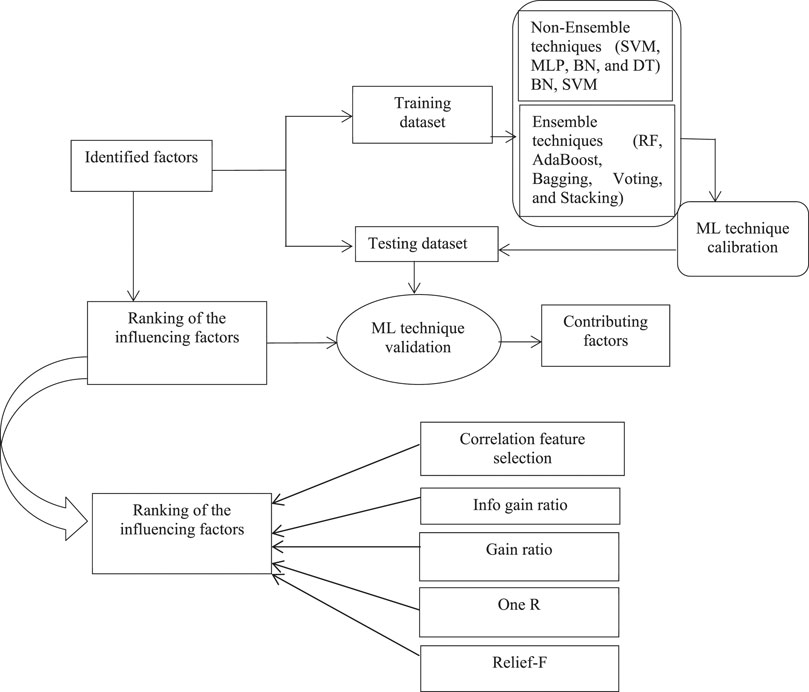
FIGURE 2. The methodology adopted in this study for ranking geotechnical factors and performing machine-learning for slope-failure predictions.

Results

Slope Failure Prediction

First, the ensemble and individual ML techniques with all 21 geotechnical factors were evaluated for their ability to predict slope failures across different sites. Table 5 represents different ensemble and individual ML techniques in the training dataset based upon the statistical indices such as sensitivity, specificity, accuracy, and the kappa statistic. These statistical indices were the highest for the RF, AB, and Bagging ensemble techniques and the MLP individual technique. The individual DT, SVM, and BN techniques and the ensemble stacking and voting techniques, respectively, followed these techniques’ performance.

TABLE 5

TABLE 5. ML technique evaluation in training dataset using different performance measures.

Overall, based upon accuracy, the RF, AB, and Bagging ensemble techniques and the individual MLP technique performed better than other ensemble and individual techniques. Also, results revealed that a larger number of ensemble techniques performed optimally compared to the individual techniques.

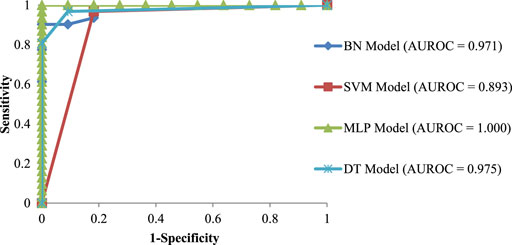
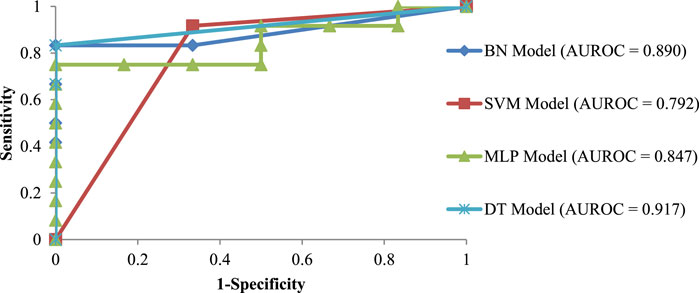
To explore the performance of ensemble and individual techniques, the ROC curves for these techniques were investigated. Figure 3 depicts the ROC curves for individual techniques in the training dataset. The highest AUROC value for the individual methods belonged to the MLP technique (AUROC = 1.00). The next highest AUROC values were as per the following sequence: The DT technique (AUROC = 0.975), the BN technique (AUROC = 0.971), and the SVM technique (AUROC = 0.893).

FIGURE 3

FIGURE 3. ROC curves for individual ML techniques in the training dataset.

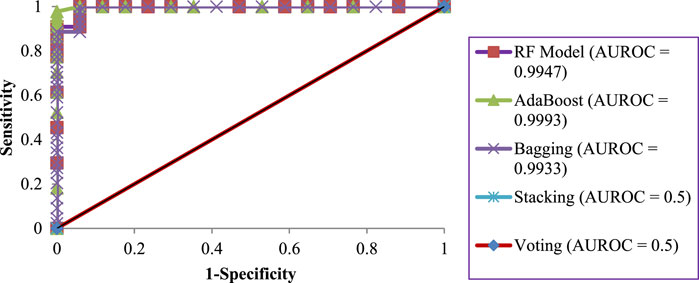
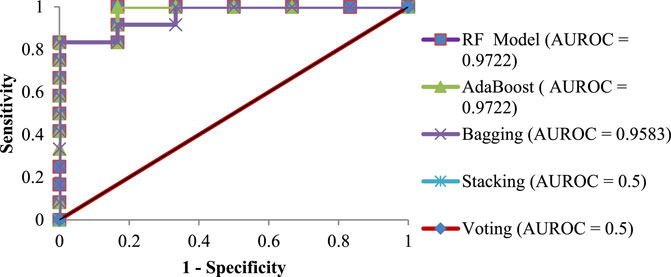
Figure 4 depicts the ROC curves for the ensemble ML techniques in the training dataset. The highest AUROC value among the ensemble techniques belonged to the AB technique (AUROC = 0.9993). The next highest AUROC was as per the following sequence: The RF technique (AUROC = 0.9947), the Bagging technique (AUROC = 0.9933), and the Stacking and Voting techniques (AUROC = 0.5).

FIGURE 4

FIGURE 4. ROC curves for ensemble ML techniques in the training dataset.

Table 6 shows the best set of hyperparameters obtained across different ML techniques in the training dataset. As shown in Table 6, among the individual techniques, the MLP possessed the following parameters: the number of nodes per hidden layer was 150, the hidden layers were 3, the number of epochs was 150, and the activation function was sigmoid. Furthermore, among the ensemble techniques, the RF technique possessed 210 as the optimal number of trees. Among other ensemble techniques (AB, Bagging, and Stacking), the desired batch size was 100, and the number of iterations was 10. However, in the ensemble voting technique, the desired batch size was 100.

TABLE 6

TABLE 6. The best set of hyperparameters obtained across different ML techniques in training data.

Table 7 shows the performance of different ensemble and individual ML techniques in the test dataset. Among different individual ML techniques, the sensitivity, specificity, accuracy, and kappa statistic were the highest for the DT technique, followed by SVM, BN, and MLP techniques.

TABLE 7

TABLE 7. The evaluation of different ML techniques in the test dataset using different performance measures.

Furthermore, among the different ensemble ML techniques, the sensitivity, specificity, accuracy, and kappa statistic were the highest for the RF, AB, and Bagging techniques, followed by the Stacking and Voting techniques.

Figure 5 presents the ROC curves for the individual techniques in the test dataset. The results revealed that the DT technique obtained the highest AUROC value compared to other individual techniques (SVM, BN, and MLP). Here, the DT technique performed the best with an AUROC of 0.917, and it was followed by the BN technique with an AUROC of 0.890.

FIGURE 5

FIGURE 5. ROC curves for individual ML techniques in the test dataset.

Figure 6 presents the ROC curves for the ensemble techniques in the test dataset. The results revealed that the RF, AB, and Bagging techniques showed the highest AUROCs than other ensemble ML techniques (Stacking and Voting). Here, the RF and AB techniques performed the best with an AUROC of 0.9722, and they were followed by the bagging technique with an AUROC of 0.9583. The AUROCs of Stacking and Voting were 0.5, showing no class separation capacity.

FIGURE 6

FIGURE 6. ROC curves for ensemble ML techniques in the test dataset.

Geotechnical Factors

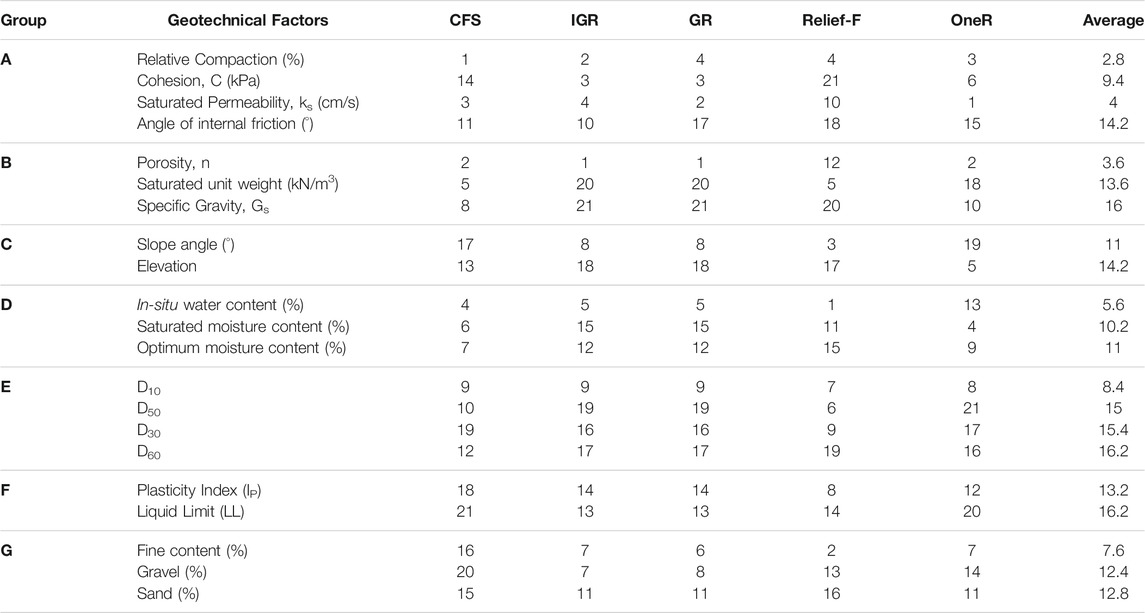
As the geotechnical analyses involving 21 factors can be tedious and exhaustive, it necessitates an iterative procedure to choose the best subset of the affecting factors as a combination. For the iterative process, different factors were divided into six groups based on the engineering properties of the soil, slope and terrain geometry, moisture indices, soil gradation parameters, Atterberg indices, and particle size constituents. Furthermore, individual factors causing slope failures across different groups were ranked by adopting different feature selection methods (Micheletti et al., 2014).

Table 8 shows the ranking of different factors by employing the different feature selection methods (i.e., correlation feature selection, IGR, GR, relief-F, and OneR) considering the two-class values (slope failure or no-slope failure). The ensemble (average) of the five feature selection methods was considered for the combined rank of each factor. The smaller the rank, the more important the individual factor for slope-failure prediction. The feature selection results revealed that the considered factors were found to be related (strongly or weakly) to the possibility of slope failures. Subsequently, the top-ranked factors obtained according to the ensemble feature selection technique from each group in Table 8 were considered as a combination in the RF and AB ensemble techniques iteratively. Table 9 shows the AUROC results from the RF and AB techniques in the iterative process.

TABLE 8

TABLE 8. Ranking of different geotechnical factors using different feature selection methods.

TABLE 9

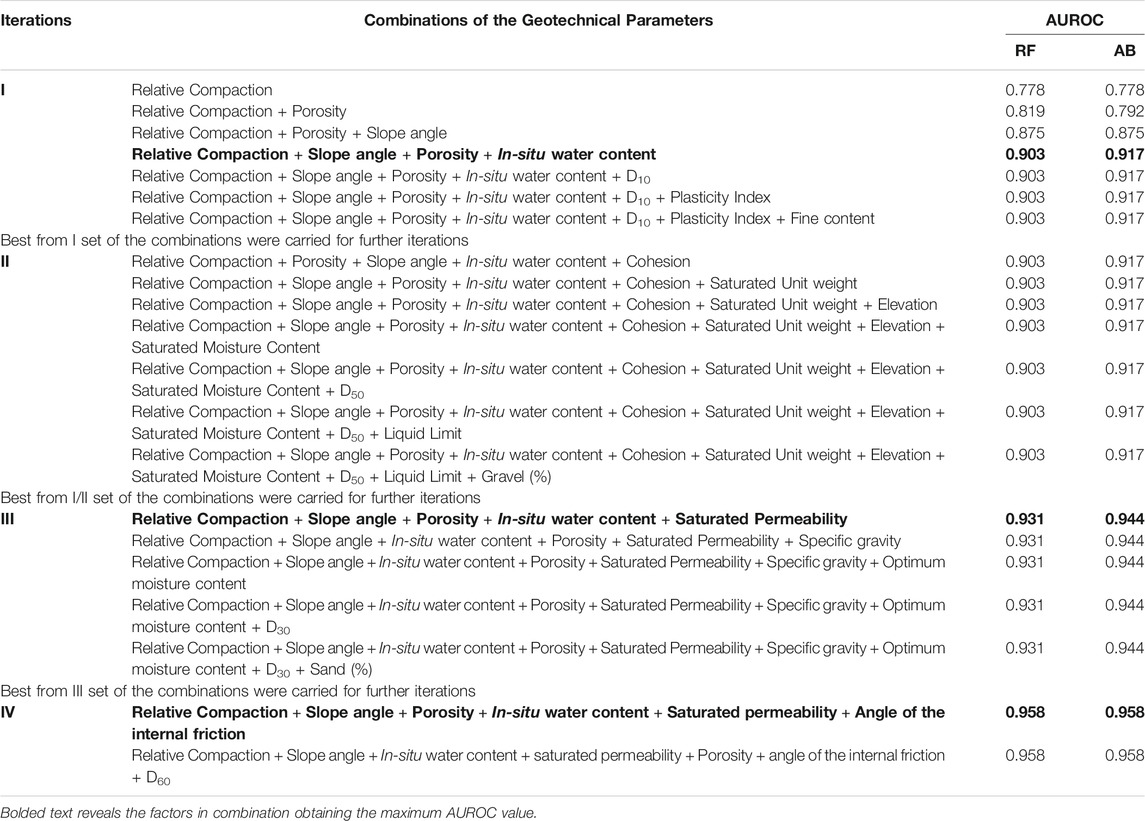
TABLE 9. AUROC values for selected factor combinations in different iterations involving the RF and AB techniques.

For instance, in the first iteration in Table 9, the AUROCs corresponding to the RF and AB techniques were computed for the top-ranked factors from each of the seven groups from Table 8. These factors were: relative compaction (group A), slope angle (group B), porosity (group C), in-situ water content (group D), D₁₀ (group E), plasticity index (group F), and fines content (group G). The second iteration was built upon the first iteration, where the best AUROC result from the first iteration was taken as a base, and the second-ranked factors from each of the seven groups were added. As there was no change in the AUROCs for RF and AB techniques in the second iteration, the best result from the first iteration was again revisited and taken into the third iteration. In the third iteration, the process is repeated by selecting the next available top-ranked factors from each group. As the AUROCs increased by did not change across the addition of factors in the third iteration, the minimal set of parameter combinations was taken from the third iteration into the fourth iteration. In the fourth iteration, the process ended when the remaining factors in the groups were consumed. Overall, the process ended in the fourth iteration with the minimal set of factors for which the AUROCs in the RF and AB techniques were minimized. The factors corresponding to the maximum values of AUROCs were considered the most contributing factors as a combination. These factors included the following six parameters: relative compaction, porosity, slope angle, saturated permeability, in-situ water content, and angle of the internal friction. The maximum AUROCs (95.80% in RF and 95.80% in AB) were obtained for these six factors.

Discussions

This paper’s primary objective was to develop novel ensemble feature selection methods to determine different geotechnical factors in isolation and as a combination, which may help indicate the possibility of slope failures at real-world landslide sites. Another objective of this paper was to develop ensemble and individual machine learning (ML) techniques to utilize the identified geotechnical factors and predict slope failures on real-world slopes. Overall, these investigations may help develop early warning systems based on real-time monitoring of the identified factors. Relevant data were collected for 21 geotechnical factors from in-situ and laboratory investigations across 60 different sites (prone to recurring landslide incidents due to rainfall) in the Mandi region, India. Several ensembles and individual ML techniques were employed to process data from both field and laboratory methods.

The results revealed that the Random Forest (RF) and AdaBoost (AB) ensemble techniques performed better than other individual techniques (Bayesian network, support vector machines, multilayer perceptron) and ensemble techniques (Stacking, Bagging, and Voting). A likely reason for this result could be that the RF and AB techniques involve an information-gain-based feature selection method as part of their algorithm. Each tree is developed to minimize classification errors using an information-gain approach; however, random selection influences the results. Overall, the ensemble RF and AB models created multiple tree classifiers on different subsets of the original data. The aggregate opinion of multiple classifiers was likely less noisy than one classifier, leading to better and more stable predictions (Agrawal et al., 2017; Pham et al., 2019). At the same time, other techniques (i.e., BN, MLP, SVM, Bagging, Voting, and Stacking) employed other classification ideas that may be different from the information gain approach.

Furthermore, an analysis of geotechnical factors based on different feature selection methods revealed that each of the 21 factors contributed to slope failures. As measuring all 21 factors may be a laborious and time-consuming exercise, one needs to identify a minimum combination of factors that would allow researchers to evaluate slope failures. In this paper, an iterative methodology was proposed to combine a minimal set of isolated factors with improving ML techniques’ classification accuracy. Referring to the iterative feature selection procedure, six factors, namely, relative compaction, porosity, saturated permeability, slope angle, angle of the internal friction, and in-situ water content, were strongly relevant to predicting the failure of slopes in the study area. Based on the field investigations, it has been understood that the in-situ water content of the soil was very close to the plastic limit of the soil because the soil sampling in the study area were collected in the rainy season (Dijkstra et al., 1994; Ahmad et al., 2006; Yalcin 2011; Kim and Song 2015). The high value of soil porosity (Kim and Song 2015) and void ratio permit the water to flow easily within the soil matrix and increase the infiltrating process. Further, denser soil (McKenna et al., 2012; Kim and Song 2015) with lesser pore size leads to obstruction of the water passing into the soil matrix and thus the risk of landslide decreases. During the wetting condition, it was understood that a reduction of the soil’s strength is pivotal responsible for slope failures in the present study area, especially in rainy seasons (Mugagga et al., 2012).

Geotechnical factors like the porosity, gradation factors, dry density, saturated permeability, and shear strength have been identified to contribute to the predictions of slope failures from the physical-based approach (McKenna et al., 2012; Park et al., 2019; Shepheard et al., 2019). Furthermore, prior research has proposed dry density, saturated permeability, and porosity as factors to understand different slope failure modes (slide or flow type; Iverson 1997; Yalcin 2011; McKenna et al., 2012; Mugagga et al., 2012). In the current study, relative compaction, porosity, saturated permeability, in-situ water content, slope angle, and angle of the internal friction have significantly influenced slope failures. These results agree with those of others, where the average soil porosity and soil-saturated permeability possessed higher values at slope failure sites than at no slope failure sites (Kim and Song 2015).

A review of the literature depicts that most of the slope failures occur immediately after the infiltration due to rainfall, which increases the in-situ water content of the soil close to the plastic limit of the soil (Yalcin 2011; Kim and Song 2015). The soils in slopes with higher permeability and porosity permit the water to permeate into the soil matrix, increasing the infiltration. Here, the increased moisture in soil significantly decreases the soil strength and leads to slope failures. In a different context, the infiltration leads to pore water pressures, which can trigger rainfall-induced landslides. Hence, as found in the present study, the in-situ moisture content does likely play a predominant role in influencing the slope failure at a given site. Overall, it is hypothesized that the in-situ moisture content could be employed as a factor for slope monitoring with an inverse relation with strength, imposing the condition: if more moisture, then more chances of slope failure. Threshold moisture values can be determined statistically based on prior slope failure data, if available, or in combination with soil movements (measured by deployed accelerometer sensors). This validation will likely reduce false alarms from early warning systems for monitoring slope failures.

Given the technical advancement in real-time monitoring (Kumar et al., 2019), various in-situ-based soil-moisture sensing techniques could be employed after appropriate calibration and sensitivity investigations (Mali et al., 2019). The varying soil moisture with seasons, precipitation, and ground conditions may indicate soil strength and failure susceptibility. Additionally, as other causal factors like the porosity, saturated permeability, slope angle, angle of the internal friction, and relative compaction are relatively constant over time (considering no external disturbances), these factors could be adopted for developing regional level susceptibility maps. These maps could help in identifying the locations or slopes for the installation of real-time monitoring systems. The present study results revealed that other significant factors like fines content and their constituents did not significantly contribute to slope failures in the study area. A likely reason for the absence of these factors may be their low ranges in the soils collected from the study area. As part of our future study, we plan to evaluate the ensemble and non-ensemble machine learning techniques for defining the rainfall thresholds for zonal susceptibility considering the daily and cumulative rainfall events prior to the landslide events. Furthermore, the use of deep learning techniques incorporating the above-mentioned parameters as well as soil movements obtained from sensing technologies may help improve the predictions of future failure events.

Limitation for the Present Study

The present study’s primary intent was to identify certain geotechnical factors acquired from field and laboratory investigations in causing slope failures in Mandi, India. Different individual and ensemble machine-learning (ML) techniques were employed for the analyses and a novel ensemble feature selection method. However, the present analysis outcome is limited to its study area, i.e., Mandi, India, and the 60 sites investigated. Thus, extensive future studies may be needed to collect more data from different regions to validate the reported findings ecologically. Although data from 60 sites resulted in impressive results from ML techniques in this paper, future studies may collect data from many sites for training ML techniques and their parameters.

The different ML techniques were employed among data-driven techniques to determine the major influencing factors for slope failures. However, numerous other ML techniques are available for performing machine learning, which could be tried as part of future research.

In the studies related to rainfall-triggered slope failure assessment, rainfall thresholds have been presented as indicators of early warning or predicting anticipated slope failures. Though the current study falls in a similar domain, rainfall intensity has not been considered in the analyses directly. Overall, considering rainfall as the triggering factor may be undertaken as part of future work in this area.

The slope height was not considered in the current study due to the equipment’s failure to work on inaccessible slopes in the study area, and this factor may be incorporated as a part of future work. Based on the data available and correlation with precipitation factors during slope failures, further studies could be undertaken to evaluate the rainfall thresholds and causal properties to identify the vulnerable zone in the current study area.

Conclusion

The current study’s primary objectives were to develop an understanding of the causal factors for slope failures via ML feature-selection methods and to develop different ensemble and individual classification techniques for predicting slope failures. For achieving these objectives, a detailed field survey (60 sites) was performed in Mandi, India, and soils were collected from slope failure and no-slope failure areas. The laboratory investigations were performed on the collected soil samples from the study region and other relevant field data. Seventy percent of the data were used for model training, and the remaining data were used for model testing. The results revealed that the ensemble RF and AB techniques performed the best with 0.9722 AUROC, 91.65% accuracy, and 0.77 kappa statistics compared to other employed ensemble individual ML techniques. Furthermore, relative compaction, porosity, saturated permeability, slope angle, angle of the internal friction, and in-situ water content were identified as the most relevant causal factors as a combination for slope failures. These factors are a subset of those reported in other slope failure studies, and this combination forms the study’s interesting outcome. Overall, the suggested ML techniques and feature selection methods may be utilized for developing a prediction tool for local-scale susceptibility zonation and slope-failure investigations.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

NM: Formulation of the study, field investigation, data curing, model implementation, manuscript preparation. VD: methodology, compilation, interpretation of the data for the present study, reviewing and revising the Manuscript. KVU: Validation and importance of the geotechnical parameters in the present study, Reviewing and Revising the Manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This project was partially supported by grants to KVU (NGP/TPN01/34245, DST/TDT/DDP-11/2021) and VD (IITM/DDMA-M/VD/325). Also we are thankful to the Indian Institute of Technology Mandi for providing computational resources on the project.

References

Abbaszadeh Shahri, A., and Maghsoudi Moud, F. (2021). Landslide Susceptibility Mapping Using Hybridized Block Modular Intelligence Model. Bull. Eng. Geol. Environ. 80, 267–284. doi:10.1007/s10064-020-01922-8

CrossRef Full Text | Google Scholar

Abbaszadeh Shahri, A., Spross, J., Johansson, F., and Larsson, S. (2019). Landslide Susceptibility hazard Map in Southwest Sweden Using Artificial Neural Network. CATENA 183, 104225. doi:10.1016/j.catena.2019.104225

CrossRef Full Text | Google Scholar

Agrawal, K., Baweja, Y., Dwivedi, D., Saha, R., Prasad, P., Agrawal, S., Kapoor, S., Chaturvedi, P., Mali, N., Kala, V. U., and Dutt, V. (2017). “A Comparison of Class Imbalance Techniques for Real-World Landslide Predictions,” in International Conference on Machine Learning and Data Science (New Delhi: IEEE). doi:10.1109/mlds.2017.21Available at: http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8320251

CrossRef Full Text | Google Scholar

Ahmad, F., Yahaya, A. S., and Farooqi, M. A. (2006). Characterization and Geotechnical Properties of Penang Residual Soils with Emphasis on Landslides. Am. J. Environ. Sci. 2 (4), 121–128. doi:10.3844/ajessp.2006.121.128

CrossRef Full Text | Google Scholar

Akbas, S. O., and Kulhawy, F. H. (2010). Characterization and Estimation of Geotechnical Variability in Ankara clay: a Case History. Geotech Geol. Eng. 28, 619–631. doi:10.1007/s10706-010-9320-x

CrossRef Full Text | Google Scholar

Aleotti, P., and Chowdhury, R. (1999). Landslide hazard Assessment: Summary Review and New Perspectives. Bull. Eng. Geol. Env 58, 21–44. doi:10.1007/s100640050066

CrossRef Full Text | Google Scholar

Alimohammadlou, Y., Najafi, A., and Gokceoglu, C. (2014). Estimation of Rainfall-Induced Landslides Using ANN and Fuzzy Clustering Methods: a Case Study in Saeen Slope, Azerbaijan Province, Iran. Catena 120, 149–162. doi:10.1016/j.catena.2014.04.009

CrossRef Full Text | Google Scholar

Asheghi, R., Hosseini, S. A., Saneie, M., and Shahri, A. A. (2020). Updating the Neural Network Sediment Load Models Using Different Sensitivity Analysis Methods: a Regional Application. J. Hydroinformatics 22 (3), 562–577. doi:10.2166/hydro.2020.098

CrossRef Full Text | Google Scholar

ASTM D 2216-19 (2019). Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass. West Conshohocken, PA: Annual Book of ASTM Standards ASTM International.

ASTM D 422-63 (1994). Standard Test Method for Particle Size Analysis of Soils. West Conshohocken, PA, USA: Annual Book of ASTM Standards 04(08) ASTM International.

ASTM D 4318 - 17e1 (2010). Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. Philadelphia, USA: Annual Book of ASTM Standards.

ASTM D 5550-00 (2000). Test Method for Specific Gravity of Soil Solids by Gas Pycnometer. West Conshohocken, PA, USA: Annual Book of ASTM Standards 04(08) ASTM International.

ASTM D 6913 (2009). Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. Philadelphia, USA: Annual Book of ASTM Standards.

ASTM D 698 - 12e2 (2012). Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12 400 Ft-Lb/ft³ (600 kN-M/m³)). Philadelphia, USA: Annual Book of ASTM Standards.

ASTM D2434-19 (2019). Standard Test Methods for Permeability of Granular Soils. West Conshohocken, PA: Annual Book of ASTM Standards ASTM International.

Awad, M., and Khanna, R. (2015). “Machine Learning,” in Efficient Learning Machines (Berkeley, CA: A press). doi:10.1007/978-1-4302-5990-9_1

CrossRef Full Text | Google Scholar

Ballabio, C., and Sterlacchini, S. (2012). Support Vector Machines for Landslide Susceptibility Mapping: the Staffora River basin Case Study, Italy. Math. Geosci. 44 (1), 47–70. doi:10.1007/s11004-011-9379-9

CrossRef Full Text | Google Scholar

Bennett, N. D., Croke, B. F. W., Guariso, G., Guillaume, J. H. A., Hamilton, S. H., Jakeman, A. J., et al. (2013). Characterising Performance of Environmental Models. Environ. Model. Softw. 40, 1–20. doi:10.1016/j.envsoft.2012.09.011

CrossRef Full Text | Google Scholar

Bicocchi, G., Tofani, V., D’Ambrosio, M., Tacconi-Stefanelli, C., Vannocci, P., Casagli, N., et al. (2019). Geotechnical and Hydrological Characterization of Hillslope Deposits for Regional Landslide Prediction Modelling. Bull. Eng. Geol. Environ. 78, 4875–4891. doi:10.1007/s10064-018-01449-z

CrossRef Full Text | Google Scholar

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. 1st Edition. New York: Information Science and Statistics, Springer Verlag.

Boehmke, B., and Greenwell, B. (2019). Hands-On Machine Learning with R. 1st Edn. Chapman and Hall/CRC. doi:10.1201/9780367816377

CrossRef Full Text

Bonaccorso, G. (2006). Machine Learning Algorithms. 2nd Edn. Packt Publishers.

Bradley, A. P. (1997). The Use of the Area under the ROC Curve in the Evaluation of Machine Learning Algorithms. Pattern Recognition 30 (7), 1145–1159. doi:10.1016/S0031-3203(96)00142-2

CrossRef Full Text | Google Scholar

Breiman, L. (1996a). Bagging Predictors. Mach. Learn., 123–140. doi:10.1007/bf00058655

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random Forests. Mach Learn. 45, 5–32. doi:10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

Bui, T. D., Pradhan, B., Lofman, O., and Revhaug, I. (2012). Landslide Susceptibility Assessment in Vietnam Using Support Vector Machines, Decision Tree, and Naïve Bayes Models. Math. Probl. Eng., 1–26. doi:10.1155/2012/974638

CrossRef Full Text | Google Scholar

Calvello, M., d'Orsi, R. N., Piciullo, L., Paes, N., Magalhaes, M., and Lacerda, W. A. (2015). The Rio de Janeiro early warning system for rainfall-induced landslides: analysis of performance for the years 2010–2013. Int. J. Disaster Risk Reduct. 12, 3–15. doi:10.1016/j.ijdrr.2014.10.005

CrossRef Full Text | Google Scholar

Catani, F., Lagomarsino, D., Segoni, S., and Tofani, V. (2013). Landslide Susceptibility Estimation by Random Forests Technique: Sensitivity and Scaling Issues. Nat. Hazards Earth Syst. Sci. 13, 2815–2831. doi:10.5194/nhess-13-2815-2013

CrossRef Full Text | Google Scholar

Chaturvedi, P., Arora, A., and Dutt, V. (2018). Learning in an Interactive Simulation Tool against Landslide Risks: The Role of Amount and Availability of Experiential Feedback. Nat. Hazards Earth Syst. Sci. 18, 1599–1616. doi:10.5194/nhess-18-1599-2018

CrossRef Full Text | Google Scholar

Chaturvedi, P., and Dutt, V. (2015). “Evaluating the Public Perceptions of Landslide Risks in the Himalayan Mandi Town,” in Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 26–30th October (Los Angeles, USA, 1491–1495. doi:10.1177/1541931215591323

CrossRef Full Text | Google Scholar

Chen, W., Pourghasemi, H. R., and Naghibi, S. A. (2018). Prioritization of Landslide Conditioning Factors and its Spatial Modelling in Shangnan Country, China Using GIS-Based Data Mining Algorithms. Bull. Eng. Geol. Environ. 77, 611–629. doi:10.1007/s10064-017-1004-9

CrossRef Full Text | Google Scholar

Dangeti, P. (2017). Statistics for Machine Learning: Techniques for Exploring Supervised, Unsupervised, and Reinforcement Learning Models with Python and R. Packt Publishers, 1788295757.

Dijkstra, T. A., Rogers, C. D. F., Smalley, I. J., Derbyshire, E., Jin, L. Y., and Min, M. X. (1994). The Loess of north-central china: Geotechnical Properties and Their Relation to Slope Stability. Eng. Geology. 36 (3-4), 153–171. doi:10.1016/0013-7952(94)90001-9

CrossRef Full Text | Google Scholar

Dikshit, A., Satyam, N., and Towhata, I. (2017). Application of FlaIR Model for an Early Warning System in Kalimpong, India for Rainfall-Induced Landslides. Nat. Hazards Earth Syst. Sci. doi:10.5194/nhess-2017-295

CrossRef Full Text | Google Scholar

Fell, R., Ho, K. K. S., Lacasse, S., and Leroi, E. (2005). “A Framework for Landslide Risk Assessment and Management,” in Landslide Risk Management. Editors O. Hungr, R. Fell, R. Couture, and E. Eberhardt (London: Taylor & Francis), 3–26. doi:10.1201/9781439833711-4

CrossRef Full Text | Google Scholar

Frank, E., Hall, M. A., and Witten, I. H. (2016). The WEKA Workbench. 4th Edition. Morgan Kaufmann: Online Appendix for Data Mining: Practical Machine Learning Tools and Techniques.

Freund, Y., and Schapire, R. E. (1997). A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 55, 119–139. doi:10.1006/jcss.1997.1504

CrossRef Full Text | Google Scholar

Friedman, N., Geiger, D., and Goldszmidt, M. (1997). Bayesian Network Classifiers. Mach Learn. 29, 131–163. doi:10.1023/A:1007465528199

CrossRef Full Text | Google Scholar

Gupta, S. K., and Shukla, D. P. (2018). Application of Drone for Landslide Mapping, Dimension Estimation and its 3D Reconstruction. J. Indian Soc. Remote Sensing 46, 903–914. doi:10.1007/s12524-017-0727-1

CrossRef Full Text | Google Scholar

Guyon, I., and Elisseeff, A. (2003). An Introduction to Variable and Feature Selection. J. Mach Learn. Res. 3, 1157–1182.

Google Scholar

Guyon, I., Gunn, S., Nikravesh, M., and Zadeh, L. (2006). Feature Extraction: Foundations and Applications. New York: Springer.

Guzzetti, F., Mondini, A. C., Cardinali, M., Fiorucci, F., Santangelo, M., and Chang, K. T. (2012). Landslide Inventory Maps: New Tools for an Old Problem. Earth-Science Rev. 112 (1-2), 42–66. doi:10.1016/j.earscirev.2012.02.001

CrossRef Full Text | Google Scholar

Hall, M. A. (1999). Correlation-based Feature Selection for Machine Learning. Waikato: The University of Waikato.

Han, J., and Kamber, M. (2001). Data Mining Concepts and Techniques. Burlington: Morgan Kaufmann.

Holte, R. C. (1993). Very Simple Classification Rules Perform Well on Most Commonly Used Datasets. Mach. Learn. 11 (1), 63–91. doi:10.1023/A:1022631118932

CrossRef Full Text | Google Scholar

Huang, F., Huang, J., Jiang, S., and Zhou, C. (2017). Landslide Displacement Prediction Based on the Multivariate Chaotic Model and Extreme Learning Machine. Eng. Geology. 218, 173–186. doi:10.1016/j.enggeo.2017.01.016

CrossRef Full Text | Google Scholar

Igwe, O. (2015). The Geotechnical Characteristics of Landslides on the Sedimentary and Metamorphic Terrains of South-East Nigeria, West Africa. Geoenviron. Disasters 2, 1. doi:10.1186/s40677-014-0008-z

CrossRef Full Text | Google Scholar

Iverson, R. M. (1997). The Physics of Debris Flows. Rev. Geophys. 35, 245–296. doi:10.1029/97RG00426

CrossRef Full Text | Google Scholar

Joyce, K. E., Dellow, G. D., and Glassey, P. J. (2008). “Assessing Image Processing Techniques for Mapping Landslides,” in Geoscience and Remote Sensing Symposium, IGARSS 2008, IEEE International, Boston, MA, United States, July 2008 (IEEE) 2, 7–11. doi:10.1109/IGARSS.2008.4779224

CrossRef Full Text | Google Scholar

Kahlon, S., Chandel, V. B. S., and Brar, K. K. (2014). Landslides in Himalayan Mountains: a Study of Himachal Pradesh, India. Int. J. IT Eng. Appl. Sci. Res. 3 (9), 2319–4413.

Google Scholar

Kaushik, S., Choudhury, A., Natarajan, S., Pickett, L. A., and Dutt, V. (2020). Medicine Expenditure Prediction via a Variance-Based Generative Adversarial Network. IEEE Access Press 8, 110947–110958. doi:10.1109/ACCESS.2020.3002346

CrossRef Full Text | Google Scholar

Kavicky, R., Jain, A., and Dixit, A. (2017). Ensemble Machine Learning: A Beginner's Guide that Combines Powerful Machine Learning Algorithms to Build Optimized Models. Birmingham: Packt Publishing, 438. 178829775X9781788297752.

Kavzoglu, T., Sahin, E. K., and Colkesen, I. (2014). Susceptibility Mapping Using GIS-Based Multi-Criteria Decision Analysis, Support Vector Machines, and Logistic Regression. Landslides 11, 425–439. doi:10.1007/s10346-013-0391-7

CrossRef Full Text | Google Scholar

Kim, K. S., and Song, Y. S. (2015). Geometrical and Geotechnical Characteristics of Landslides in Korean under Various Geological Considerations. J. Mountain Sci. 12 (5), 1267–1280. doi:10.1007/s11629-014-3108-z

CrossRef Full Text | Google Scholar

Kira, K., and Rendell, L. (1992). The Feature Selection Problem: Traditional Methods and a New Algorithm. AAAI-92 Proc.

Google Scholar

Kumar, P., Priyanka, , Pathania, A., Agarwal, S., Mali, N., Singh, R., Chaturvedi, P., Uday, K. V., and Dutt, V. (2019). “Predictions of Weekly Slope Movements Using Moving-Average and Neural-Network Methods: A Case-Study in Chamoli, India,” in 9th International Conference on Soft Computing for Problem Solving - SocProS 2019 (Liverpool, UK: Landslide Risk Assessment and Management).

Google Scholar

Kumar, P., Sihag, P., Sharma, A., Pathania, A., Singh, R., Chaturvedi, P., et al. (2021). Prediction of Real-World Slope Movements via Recurrent and Non-recurrent Neural Network Algorithms: A Case Study of the Tangni Landslide. Indian Geotech J. 51, 788. doi:10.1007/s40098-021-00529-4

CrossRef Full Text | Google Scholar

Ma, Z., Mei, G., and Piccialli, F. (2020). Machine Learning for Landslides Prevention: a Survey. Neural Comput. Applic 33, 10881. doi:10.1007/s00521-020-05529-8

CrossRef Full Text | Google Scholar

Madawala, C. N., Kumara, B. T. G. S., and Indrathilaka, L. (2019). “Novel Machine Learning Ensemble Approach for Landslide Prediction,” in International Research Conference on Smart Computing and Systems Engineering (Colombo, Sri Lanka: SCSE), 78–84. doi:10.23919/SCSE.2019.8842762

CrossRef Full Text | Google Scholar

Mali, N., Dutt, V., and Uday, K. V. (2019). The Potential of Machine Learning for Geotechnical Applications. IGS News A Bull. Indian Geotechnical Soc. 51 (2), 4. doi:10.13140/RG.2.2.22927.53925

CrossRef Full Text | Google Scholar

McKenna, J. P., Santi, P. M., Amblard, X., and Negri, J. (2012). Effects of Soil-Engineering Properties on the Failure Mode of Shallow Landslides. Landslides 9, 215–228. doi:10.1007/s10346-011-0295-3

CrossRef Full Text | Google Scholar

Micheletti, N., Foresti, L., Robert, S., Leuenberger, M., Pedrazzini, A., Jaboyedoff, M., et al. (2014). Machine Learning Feature Selection Methods for Landslide Susceptibility Mapping. Math. Geosci. 46, 33–57. doi:10.1007/s11004-013-9511-0

CrossRef Full Text | Google Scholar

Moayedi, H., Osouli, A., Nguyen, H., and Rashid, A. S. A. (2021). A Novel Harris Hawks’ Optimization and K-fold Cross-Validation Predicting Slope Stability. Eng. Comput. 37, 369–379. doi:10.1007/s00366-019-00828-8

CrossRef Full Text | Google Scholar

Mugagga, F., Kakembo, V., and Buyinza, M. (2012). A Characterisation of the Physical Properties of Soil and the Implications for Landslide Occurrence on the Slopes of Mount Elgon, Eastern Uganda. Nat. Hazards 60 (3), 1113–1131. doi:10.1007/s11069-011-9896-3

CrossRef Full Text | Google Scholar

National Institute of Disaster Management (2006). Annual Report for 2015-16New Delhi, India: National Institute of Disaster Management. Available at https://nidm.gov.in/PDF/pubs/areport_14.pdf

Google Scholar

Nguyen, H., Franke, K., and Petrovic, S. (2010). “Improving the Effectiveness of Intrusion Detection by Correlation Feature Selection,” in Availability, Reliability, and Security, 2010 (ARES' 10) International Conference on IEEE (Piscataway: IEEE), 17–24. doi:10.1109/ARES.2010.70

CrossRef Full Text | Google Scholar

Nhu, V. H., Mohammadi, A., Shahabi, H., Ahmad, B. B., Al-Ansari, N., Shirzadi, A., et al. (2020). Landslide Susceptibility Mapping Using Machine Learning Algorithms and Remote Sensing Data in a Tropical Environment. Int. J. Environ. Res. Public Health 17, 4933. doi:10.3390/ijerph17144933

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohlmacher, G. C., and Davis, J. C. (2003). Using Multiple Logistic Regression and GIS Technology to Predict Landslide hazard in Northeast Kansas, USA. Eng. Geol. 69, 331–343. doi:10.1016/S0013-7952(03)00069-3

CrossRef Full Text | Google Scholar

Park, J. Y., Lee, S. R., Lee, D. H., Kim, Y. T., and Lee, J. S. (2019). A Regional-Scale Landslide Early Warning Methodology Applying Statistical and Physically-Based Approaches in Sequence. Eng. Geology. 260, 1051936. doi:10.1016/j.enggeo.2019.105193

CrossRef Full Text | Google Scholar

Parkash, S. (2011). Historical Records of Socio-Economically Significant Landslides in India. J. South Asia Disaster Stud. 4 (2), 177–204. doi:10.1007/978-4-431-55242-0_12

CrossRef Full Text | Google Scholar

Pathania, A., Kumar, P., Priyanka, A. M., Kumar, M., Singh, R., Chaturvedi, P., et al. (2020). Predictions of Soil Movements Using Persistence, Auto-Regression, and Neural Network Models: A Case-Study in Mandi, India. Int. J. Swarm Intell. Res. [Epub ahead of print].

Google Scholar

Pham, B. T., Khosravi, K., and Prakash, I. (2017). Application and Comparison of Decision Tree-Based Machine Learning Methods in Landslide Susceptibility Assessment at Pauri Garhwal Area, Uttarakhand, India. Environ. Process. 4, 711–730. doi:10.1007/s40710-017-0248-5

CrossRef Full Text | Google Scholar

Pham, B. T., Pradhan, B., Bui, D. T., Prakash, I., and Dholakia, M. B. (2016b). A Comparative Study of Different Machine Learning Methods for Landslide Susceptibility Assessment: A Case Study of Uttarkhand Area (India). Environ. Model. Softw. 84, 240–250. doi:10.1016/j.envsoft.2016.07.005

CrossRef Full Text | Google Scholar

Pham, B. T., Shirzadi, A., Shahabi, H., Omidvar, E., Singh, S. K., Sahana, M., et al. (2019). Landslide Susceptibility Assessment by Novel Hybrid Machine Learning Algorithms. Sustainability 11, 4386. doi:10.3390/su11164386

CrossRef Full Text | Google Scholar

Pham, B. T., Tien, Bui. D., Prakash, I., and Dholakia, M. (2016a). Evaluation of Predictive Ability of Support Vector Machines and Naïve Bayes Methods for Spatial Prediction of Landslides in Uttarkhand State (India) Using GIS. J. Geomatics. 10 (1), 71–79.

Google Scholar

Phoon, K. K., and Kulhawy, F. H. (1999). Characterization of Geotechnical Variability. Can. Geotechnical J. 36, 612–624. doi:10.1139/t99-038

CrossRef Full Text | Google Scholar

Shepheard, C. J., Vardanega, P. J., Holcombe, E. A., Hen-Jones, R., and De Luca, F. (2019). Minding the Geotechnical Data gap: an Appraisal of the Variability of Key Soil Parameters for Slope Stability Modelling in Saint Lucia. Bull. Eng. Geology. Environ. 78 (1), 1–14. doi:10.1007/s10064-018-01451-5

CrossRef Full Text | Google Scholar

Tattar, P. N. (2018). Hands-On Ensemble Learning with R: A Beginner's Guide to Combining the Power of Machine Learning Algorithms Using Ensemble Techniques. Birmingham, USA: Packt Publishing Limited, 376. 978-1788624145.

Thiebes, B., Glade, T., and Bell, R. (2012). “Landslide Analysis and Integrative Early Warning Local and Regional Case Studies,” in Landslides and Engineered Slopes: Protecting Society through Improved Understanding. Editor E. Eberhardt (London: Taylor & Francis Group), 1915–1921.

Google Scholar

Tien, B. D., Pradhan, B., Lofman, O., and Revhaug, I. (2012a). Landslide Susceptibility Assessment in Vietnam Using Support Vector Machines, Decision Tree, and Naïve Bayes Models. Math. Probl. Eng, 1–26. doi:10.1155/2012/974638

CrossRef Full Text | Google Scholar

Tien, B. D., Tuan, T. A., Klempe, H., Pradhan, B., and Revhaug, I. (2016). Spatial Prediction Models for Shallow Landslides Hazards: a Comparative Assessment of the Efficacy of Support Vector Machines, Artificial Neural Networks, Kernel Logistic Regression and Logistic Model Tree. Landslides 13 (2), 361–378. doi:10.1007/s10346-015-0557-6

CrossRef Full Text | Google Scholar

Tofani, V., Bicocchi, G., Rossi, G., Segoni, S., D'Ambrosio, M., Casagli, N., et al. (2017). Soil Characterisation for Shallow Landslides Modelling: a Case Study in the Northern Apennines (Central Italy). Landslides 14, 755–770. doi:10.1007/s10346-017-0809-8

CrossRef Full Text | Google Scholar

Urbanowicz, R. J., Meeker, M., La Cava, W., Olson, R. S., and Moore, J. H. (2018). Relief-based Feature Selection: Introduction and Review. J. Biomed. Inform. 85, 189–203. doi:10.1016/j.jbi.2018.07.014

CrossRef Full Text | Google Scholar

Vapnik, V. N. (1995). The Nature of Statistical Learning Theory. New York: Springer-Verlag.

Wang, R., and Tang, K. E. (2009). “Feature Selection for Maximizing the Area under the ROC Curve,” in IEEE International Conference on Data Mining Workshop (Piscataway: IEEE), 400–405. doi:10.1109/ICDMW.2009.25

CrossRef Full Text | Google Scholar

Wolpert, D. H. (1992). Stacked Generalization. Neural Networks 5 (2), 241–259. doi:10.1016/S0893-6080(05)80023-1

CrossRef Full Text | Google Scholar

Yalcin, A. (2011). A Geotechnical Study on the Landslides in the Trabzon Province. NE, Turkey. Appl. Clay Sci. 52, 11–19. doi:10.1016/j.clay.2011.01.015

CrossRef Full Text | Google Scholar

Yates, K., Fenton, C. H., and Bell, D. H. (2018). A Review of Geotechnical Characteristics of Loess and Loess-Derived Soils from Canterbury, South Island, New Zealand. Eng. Geology. 236, 11–21. doi:10.1016/j.enggeo.2017.08.001

CrossRef Full Text | Google Scholar

Yilmaz, I. (2009). Landslide Susceptibility Mapping Using Frequency Ratio, Logistic Regression, Artificial Neural Networks and Their Comparison: A Case Study from Kat Landslides (Tokat-Turkey). Comput. Geosciences 35, 1125–1138. doi:10.1016/j.cageo.2008.08.007

CrossRef Full Text | Google Scholar

Zare, M., Pourghasemi, H. R., Vafakhah, M., and Pradhan, B. (2013). Landslide Susceptibility Mapping at Vaz Watershed (Iran) Using Artificial Neural Network Model: a Comparison between Multilayer Perceptron (MLP) and Radial Basis Function (RBF) Algorithms. Arab J. Geosci. 6 (8), 2873–2883. doi:10.1007/s12517-012-0610-x

CrossRef Full Text | Google Scholar