Rapid Terrain Assessment for Earthquake-Triggered Landslide Susceptibility With High-Resolution DEM and Critical Acceleration

Earthquake ground motion often triggers landslides in mountainous areas. A simple, robust method to quickly evaluate the terrain’s susceptibility of specific locations to earthquake-triggered landslides is important for planning field reconnaissance and rescues after earthquakes. Different approaches have been used to estimate coseismic landslide susceptibility using Newmark’s sliding block model. This model requires an estimate of the landslide depth or thickness, which is a difficult parameter to estimate. We illustrate the use of Newmark sliding block’s critical acceleration for a glaciated valley affected by the 2015 Gorkha earthquake in Nepal. The landslide data came from comparing high-resolution pre- and post-earthquake digital elevation models (DEMs) derived from Spot 6/7 images. The areas where changes were detected provided an inventory of all the landslides triggered by the earthquake. The landslide susceptibility was modeled in a GIS environment using as inputs the pre-earthquake terrain and slope angles, the peak ground acceleration from the 2015 Gorkha earthquake, and a geological map. We exploit the depth information for the landslides (obtained by DEM difference) to apply the critical acceleration model. The spatial distribution of the predicted earthquake-triggered landslides matched the actual landslides when the assumed landslide thickness in the model is close to the median value of the actual landslide thickness (2.6 m in this case). The landslide predictions generated a map of landslide locations close to those observed and demonstrated the applicability of critical acceleration for rapidly creating a map of earthquake-triggered landslides.

Introduction

Earthquake ground motion is one of the main triggering agents for catastrophic landslides worldwide. According to Keefer (1984), earthquake magnitudes greater than 6.0 Moment Magnitude (Mw) can trigger landslides over areas extending up to 500,000 square kilometers. The 1994 Northridge earthquake (Mw = 6.7) in California triggered more than 11,000 landslides over an area of ∼10,000 km² (Harp and Jibson, 1996). The 2002 Denali Fault earthquake (Mw = 7.8) in Alaska triggered more than 1,580 landslides in a glaciated area of 7,150 km² (Gorum et al., 2014). The 2008 Wenchuan earthquake (Mw = 7.9) in China caused 197,481 landslides in ∼110,000 km² (Xu et al., 2014). In Nepal, the 2015 Gorkha earthquake (Mw = 7.8) triggered more than 25,000 landslides covering 61.5 km² in an area of 20,500 km² (Gnyawali and Adhikari, 2017; Roback et al., 2018; Tian et al., 2020).

Rapid assessment of earthquake-triggered landslide hazards is vital for planning response and recovery operations, in the immediate aftermath of an earthquake. Such landslides are widespread, so usually, the reconnaissance is carried out by flying helicopters in pre-defined priority tracks to identify the landslide hotspots, valley blocking slides, and damaged infrastructure locations. E.g., In the 2016 central Italy earthquake sequence by Stewart et al. (2018) and Lanzo et al. (2018); in the 2015 Gorkha earthquake sequence by Collins and Jibson (2015); and in the 2016 Kaikoura earthquake by Jibson et al. (2018). To efficiently plan the reconnaissance operation, as well as pre-planning of the earthquake-triggered landslide (ETL) hazards, a model to predict widespread landslide locations is pivotal for disaster management.

Newmark (1965) proposed a method for analyzing the deformation of embankments and dams caused by earthquake shaking, assuming the dam moves as a single rigid block. Although Newmark (1965) first developed this method for embankments and dams, Wilson and Keefer (1983) applied it for assessing the stability of natural slopes under earthquake shaking. Permanent displacement of the landslide occurs when the seismic acceleration exceeds a critical value (Newmark, 1965). When the seismic acceleration exceeds the critical acceleration, the block moves relative to the slope and stops when the earthquake acceleration drops below the critical acceleration. Newmark’s method considers only rigid block movements with no internal deformations. Shear deformation is assumed at the base of the block (Newmark, 1965). The method has been found suitable for shallow landslides during earthquakes (Keefer, 1994; Keefer, 2002). The Newmark sliding block method has been used to assess earthquake-triggered landslides (ETL) in Los Angeles, California (Jibson et al., 2000), Greece (Chousianitis et al., 2014), Wenchuan, China (Chen et al., 2014), Longmenshan, China (Yuan et al., 2016) and Lushan, China (Jin et al., 2019).

The Newmark method has been tested for evaluating slope stability for several earthquakes. Two different approaches for using the Newmark method are popular: a) evaluate the yield displacement (Newmark’s displacement) of a sliding block or b) evaluate the critical acceleration required to move a sliding block. The displacement method uses a threshold displacement as a sliding block criterion. The landslide displacement is calculated by double integrating the recorded acceleration-time record of the earthquake (Newmark, 1965) or using empirical formulae (Jibson et al., 2000; Jibson, 2007). For the acceleration method or simplified Newmark block method, the critical acceleration needed to cause a block to slide is compared with the measured peak ground acceleration (PGA). When PGA exceeds the critical acceleration, the landslide is triggered. Both approaches have been implemented to study ETL susceptibility.

Newmark’s displacement method was used to study areas affected by the Chi-Chi earthquake in Taiwan and showed a good prediction of shallow landslides compared with the observed landslides (Wang and Lin, 2010). Similarly, Jin et al. (2019) used a modified Newmark’s method and found that the predicted landslide map agreed well with the actual distribution of the landslides triggered by the Lushan earthquake, China. Newmark’s displacement method was used to model ETL from the 2015 Gorkha earthquake (Gallen et al., 2016). Although the model results had similarities with the general landslide pattern, the detailed distribution of landslides was not captured by the Newmark model (Gallen et al., 2016). The model shortcomings were attributed to large cell sizes in the digital elevation model (90 m), aspects of the ground motion spectra that PGA does not capture, and lack of spatial variability in surface material strength. Other studies have used critical acceleration, instead of Newmark’s displacement, to analyze the terrain’s susceptibility to ETL (Chen et al., 2014; Xiaoli and Chunguo, 2019; Chen et al., 2020). Chen et al. (2014) compared the landslide distribution triggered by the 2008 Wenchuan earthquake with a critical acceleration map and found good correspondence with the actual landslide locations. An ETL susceptibility map can be easily prepared from a probable PGA map using the critical acceleration concept (Xiaoli and Chunguo, 2019). But to prepare a map using Newmark’s displacement method, earthquake acceleration-time records are needed, which are often not available at the location of landslide-affected areas, and even less so before an earthquake disaster. These studies indicate that the critical acceleration method can help predict ETL locations via comparison with an independent estimate of the peak ground acceleration. Furthermore, when earthquake data are limited, critical acceleration is a better approach than Newmark’s displacement for rapid assessment of the terrain’s susceptibility to ETL locations.

The evaluation of the method presented here to predict ETL locations method requires a detailed inventory of actual ETL locations and an estimate of the landslide depths, which can be converted into thicknesses. Erial photographs or satellite images are commonly used to delineate landslide areas (as polygons) after an earthquake. These polygons can be used to validate the prediction results from the critical acceleration model (Wang and Lin, 2010; Chen et al., 2014; Shinoda and Miyata, 2017). These landslide inventories capture the areal information but typically lack the landslide depth data. Researchers have adopted different approaches to estimate the landslide depth. Wang and Lin (2010) estimated the depth using an empirical slope-depth relationship. Shinoda and Miyata (2017) assumed a 2 m landslide depth for the Niigata earthquake, based on a field study conducted by Kieffer et al. (2006). Ma and Xu (2019) set the landslide depth as 3 m based on field observation and previous research (Jibson et al., 2000; Dreyfus et al., 2013). Landslide depths derived from these approaches may not provide a reasonable estimate of the actual depths because they are based on regional studies or estimates from a few local field observations. Here, we determine the landslide areas and depth information by subtracting a high-resolution post-earthquake digital elevation model (DEM) from a pre-earthquake DEM. The availability of landslide depth information from the DEMs enables the calibration of the critical acceleration model and allows exploration of the relationship between observed landslide thicknesses and the thickness used in the model.

Study Area

Here, we focus on the Langtang area in Nepal, affected by the 2015 Gorkha earthquake (Mw7.8), to evaluate the critical acceleration method for ETL susceptibility assessment. This area is a glaciated valley and a popular tourist destination. It also had the largest and most destructive landslide triggered by the 2015 Gorkha earthquake, a rock avalanche that killed more than 350 people and buried the Langtang village (Kargel et al., 2015). An air blast created by the rock avalanche uprooted trees and flattened the forest on the opposite valley wall (Kargel et al., 2015; Lacroix, 2016). Aside from this rock avalanche, three different studies mapped between 160 and 205 landslides in the study area (Lacroix 2016; Gnyawali and Adhikari, 2017; Roback et al., 2018). The landslides varied in size from rockfalls to very large landslides, and many landslides had long-runout zones because of the steep terrain.

The valley lies approximately 60 km north of Kathmandu (Figure 1A). Nearly half of the Langtang valley (46% or 166 km²) is covered by glaciers (Immerzeel et al., 2012). Langtang Khola is the main river draining the valley westwards to the Bhote Koshi River at Syabru Besi. The Langtang valley has a U-shape (Immerzeel et al., 2012) and is surrounded by high mountains with the highest peak, Langtang Lirung, 7,227 m above sea level (masl) (Lacroix, 2016). The study area is a part of the Langtang valley (91.4 km²) and has a length and width of approximately 15 and 6 km (Figure 1B). The valley has steep slopes prone to landslides (Lacroix, 2016).

FIGURE 1

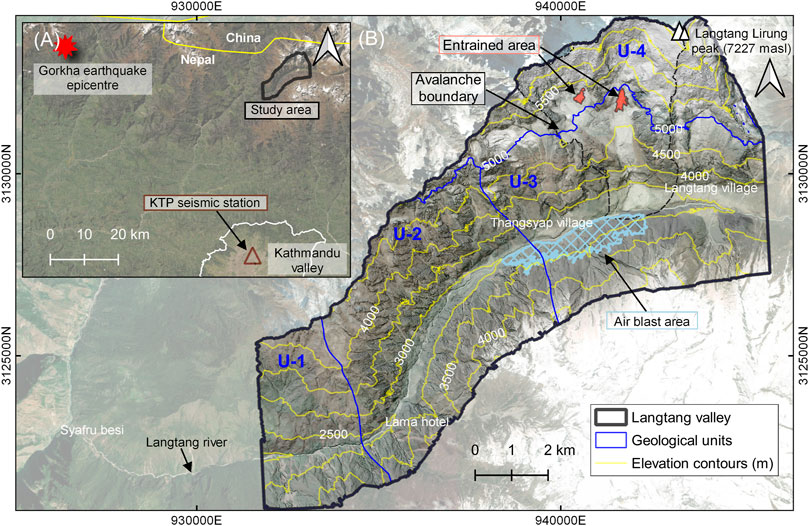
FIGURE 1. Map of Langtang valley. (A) Study area lies approximately 60 km north of Kathmandu. The red star shows the epicenter of the 2015 Gorkha earthquake. (B) Langtang valley topography indicated by yellow elevation contours. The blue lines are boundaries of geological units (Jones et al., 2020), U-1 (Syaprubesi formation), U-2 (Bamboo formation), and U-3 (Langtang formation). U-4 is above the permanent snowline at 5,000 masl and consists of glacier ice and snow. The black dashed line shows the catastrophic Langtang avalanche boundary that originated above 5,000 masl and descended onto Langtang village at ∼3,400 masl. The red polygons are the avalanche’s entrainment areas (Gnyawali et al., 2020). The blue hatched polygon is the air-blast impact area on the opposite slope of the valley.

The Gorkha earthquake epicenter was located approximately 70 km west of the study area. The 2015 Gorkha earthquake was followed by numerous aftershocks, including five greater than 6.0 Mw between April 25 and June 10, 2015 (Kargel et al., 2015). The peak ground acceleration measured at the closest seismic station (KTP) was 2.41 m/s² in the east-west direction. This station was near Kathmandu, approximately 60 km south of the study area (Takai et al., 2016). The 2015 Gorkha earthquake triggered more than 25,000 landslides in Central Nepal (Gnyawali and Adhikari, 2017; Roback et al., 2018; Tian et al., 2020).

Most landslides in the study area had shallow depths (<5 m), and many occurred in surficial glacial and post-glacial soils over the bedrock (Figure 2). The bedrock geology is dominated by gneiss in the valley, which likely resulted in glacial soils dominated by sand and gravel particle sizes. Figure 1 shows the bedrock units as U-1 to U-3, adapted from Jones et al. (2020). The Syaprubesi formation (U-1) consists of gneiss dominated by muscovite, biotite, and quartz, with subordinate plagioclase and garnet. Likewise, the Bamboo formation (U-2) is gneiss dominated by muscovite, biotite, and quartz, with subordinate tourmaline. The Langtang formation (U-3) consists of leucogranite, dominated by muscovite, tourmaline, epidote, and occasionally garnet. These previously glaciated areas are covered by various thicknesses of glacial materials such as glacial tills and glaciofluvial sediments, as well as more recent colluvium and debris flow deposits. Terraces of glacial soils exist near the valley bottom. Permanent snow occurs above the altitude of 5,000 masl in the valley (Fujita et al., 2017), and the U-4 area is covered by glacier ice and snow. During the 2015 Gorkha earthquake, the catastrophic Langtang avalanche originated from multiple high-altitude source areas in U-4 and involved snow, ice, and rock fragments (Lacroix, 2016; Gnyawali et al., 2020). As separate rock avalanches descended, they entrained debris before merging into one large rock avalanche that traveled to the valley bottom and burying the village of Langtang (Figure 1B).

FIGURE 2

FIGURE 2. Photos of earthquake-triggered landslides in the Langtang valley extracted from video recordings (Collins, 2015). The camera locations for each photograph (A–D) are shown in Figure 3. The yellow dot in panels (A) and (B) corresponds to the same landslide. US = upstream and DS = downstream.

Data and Methods

The critical acceleration method is used to map ETL susceptibility. This method compares the critical acceleration of a slope section with the expected PGA at this location to assess slope stability. The critical acceleration is calculated using topography and geology parameters. The slope angle is obtained from a high-resolution pre-earthquake DEM (Lacroix, 2016). The geotechnical parameters (cohesion, friction angle, and unit weight landslide materials) are estimated from a geology map of the Langtang valley (Jones et al., 2020). Table 1 summarizes the different types of data used in this study. In addition, an estimate of the landslide thickness is needed to calculate the factor of safety. The landslide thickness is unknown before an earthquake, but the model can be run using various landslide thicknesses. For the Langtang Valley case history, different thicknesses were used to create predicted landslide distribution maps. The map found to best match the actual landslide distribution map was used to determine the most suitable landslide thickness. This thickness was compared to actual landslide thicknesses found from analysis of the pre-and post-earthquake DEMs.

TABLE 1

TABLE 1. Different types of data used in this study.

The slope angle, geotechnical parameters, and landslide thickness were used to calculate the factor of safety and critical acceleration using Eqs 3, 4, respectively. The PGA values for the 2015 Gorkha earthquake came from the USGS ShakeMap for the Langtang valley (Figure 3). The calculated critical acceleration for each slope section (cell) was compared with the PGA from the Gorkha earthquake. If the PGA exceeds the critical acceleration, the cell is classified as unstable. The analysis yields an ETL susceptibility map using the critical acceleration of many slope cells. The entire model takes ∼10 min (7 min to produce six landslide susceptibility maps and 3 min to assess accuracy) on home desktop (Intel® Core™ i5-9300H; quad-core; 8 GB RAM) to calibrate landslide thickness. The detailed methodology is described in the following sections and summarized in Figure 4.

FIGURE 3

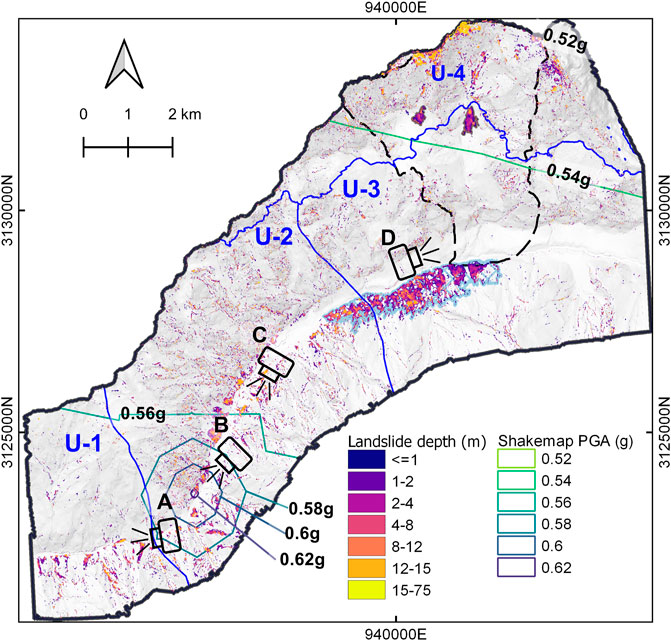
FIGURE 3. Landslide source area cells computed from pre- and post-earthquake DEM differences and adjusted for DEM elevation accuracies, modified after Lacroix (2016). (A–D) are camera locations corresponding to Figure 2. The difference between the 2 DEMs encompasses both the landslide depth and the removal of trees over the landslide. USGS Shakemap contours of the peak ground acceleration (PGA) ranging from 0.52 g (at U-4) to 0.62 g (at U-2) are shown in shades of green to blue.

FIGURE 4

FIGURE 4. Flowchart for creating ETL maps using DEM, critical acceleration, and earthquake PGA.

Digital Elevation Model Generation

A pre-earthquake (April 2014) and a post-earthquake (March 2015) DEM at a 4 m cell size were obtained from tri-stereo SPOT 6/7 images of the Langtang valley over 100 km² area. The DEMs were taken from Lacroix (2016). Some voids existed in the pre-earthquake (2014) DEM created from the Spot 6/7 stereo images. These voids were filled by interpolation from neighboring cells in QGIS. The DEMs were computed using the NASA open-source software Ames Stereo Pipeline (Broxton and Edwards, 2008). The reliability of the ground elevations in the DEM varies as a function of slope gradient. The ground elevation variability, calculated through the standard deviation of the difference of the 2014 and 2015 DEMs in stable areas, ranged from 0.5 m on flat terrain up to 12 m on slopes of 80° (Lacroix, 2016).

Preparation of the Landslide Map

An initial map of landslide locations was prepared by subtracting the post-earthquake (2015) DEM from the pre-earthquake (2014) DEM. However, the inherent uncertainty in the DEMs, created from errors in the stereo pair image processing, makes this step complicated. To increase confidence in the landslide map, a DEM error map was subtracted from the DEM difference map. Only cells with positive values in a range between 1 and 75 m were used as the map of landslide locations. The negative values indicated possible deposition areas and were eliminated from further analysis.

When the catastrophic Langtang avalanche descended into the Langtang village, it created an air blast that flattened the forest canopy on the opposite face of the valley wall. This phenomenon caused a positive elevation difference in DEM subtraction, thereby falsely classifying cells as a landslide. This air-blast zone (∼2 km²) was removed from the landslide map. Furthermore, some slope area materials were entrained during the avalanche descent, causing considerable depth variation (Gnyawali et al., 2020). These sites, which covered an area of approximately 0.25 km², were eliminated from the map. Figure 3 shows the resulting final map for the source areas of earthquake-triggered landslides. Landslide locations involved approximately 5.2 km² of the study area.

2015 Gorkha Earthquake Ground Motions

The measured ground motions caused by the Gorkha earthquake were important input for estimating ETL locations. The peak ground acceleration (PGA) closely correlates with landslide occurrence as a triggering factor (Keefer 1984; Kieffer et al., 2006; Qi et al., 2010; Dai et al., 2011; Tiwari and Ajmera, 2017). A benefit of using PGA is that probabilistic PGA maps are readily available for Nepal (Ram and Wang, 2013; Rahman and Bai, 2018). Jibson (2007) developed an empirical relationship to determine Newmark’s displacement using critical acceleration and Arias intensity (Arias, 1970). Arias intensity depends upon the recorded earthquake acceleration-time history. However, earthquake acceleration-time data are not available for the study area, which makes the use of PGA attractive given the availability of USGS ShakeMap estimates of PGA around the epicentre of the Gorkha earthquake. ShakeMap provides near-real-time maps of PGA and other ground motion parameters (peak ground velocity, pseudo-spectral acceleration, intensity) following significant earthquakes, and this source for PGA was used in the critical acceleration model. ShakeMap simulates PGA by combining information from individual stations, site amplification characteristics, and ground motion prediction equations (GMPEs) for the distance to the hypocentre (Worden et al., 2010; Worden et al., 2020). We adopted PGA values from ShakeMap for this model. The PGA ranges from 0.52 g (northern part, U-4) to 0.62 g (southern part, U-2) in the study area. The PGA contours from the USGS Shakemap for the Gorkha earthquake are shown in Figure 3.

Critical Acceleration Method

The ETL locations are assessed in the critical acceleration method by comparing each slope section’s critical acceleration and the PGA from an earthquake. If the earthquake ground acceleration surpasses a critical acceleration, the slope may fail during shaking (Chen et al., 2020). In the context of Newmark’s method, the dynamic stability of a slope is related to its static stability. Before an earthquake, a block’s stability is affected by its weight and the friction angle and cohesion acting along a potential sliding surface, as illustrated in Figure 5. The forces acting parallel to the slip surface from adjacent blocks above and below the block shown are assumed to cancel each other. The factor of safety F_S of the sliding block, as shown in Figure 5, can be expressed as:

$Fs=\frac{c\mathrm{A}+W\cos \alpha \cdot \tan \varphi }{W\sin \alpha }(1)$

Where W is the weight of the block, ϕ and c are the friction angle and cohesion along the sliding surface, α is the slope angle of the slip surface, which is assumed equal to the ground surface, and A is the area of the sliding surface. The groundwater table was likely below the landslide slip surface at most locations because the 2015 Gorkha earthquake occurred during the dry season and the typical landslide depths were less than 3 m (Gallen et al., 2016). Therefore, the groundwater pressures are not included in Eq. 1. The critical acceleration method was applied to each cell in the pre-earthquake DEM. Figure 5 shows a unit thick section of a block on the slope. The DEM cell size is based on a horizontal grid. Using the DEM cell size as the smallest block size in the critical acceleration analysis, Eq. 1 can be re-written as:

$F_S= \frac{c\mathrm{A}}{W\sin \alpha }+\frac{W\cos \alpha \cdot \tan \varphi }{W\sin \alpha }$

$F_S= \frac{c\mathrm{A}}{\gamma . A.T.\sin \alpha }+\frac{\tan \varphi }{tan \alpha }$

The above equation can be simplified as Eq. 2, which shows that the factor of safety is influenced by topographical, geological parameters, and landslide thickness and is independent of DEM cell size.

$F_S= \frac{c}{\gamma T\cdot \sin \alpha }+\frac{\tan \varphi }{\tan \alpha }(2)$

Where γ is the unit weight of the landslide material, and T is the thickness of the sliding block. The thickness of the sliding block is $D\cdot \cos \alpha$, where the landslide depth, D, is observed from differences in DEM elevations.

FIGURE 5

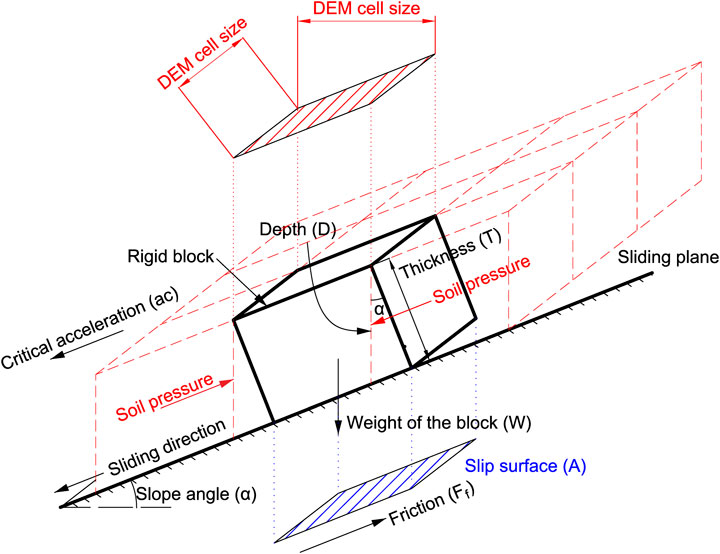
FIGURE 5. Schematic diagram illustrating the forces acting on a block resting on an inclined plane for static (pre-earthquake) conditions on a GIS environment.

In GIS implementation, cohesion raster, friction angle raster, and unit weight raster are obtained from the geology map. Similarly, slope raster is calculated from pre-earthquake DEM and block thickness is the assumed landslide thickness whose value varies in the model. Eq. 3. Demonstrates the use of Eq. 2 in a GIS environment.

$F_S=\frac{\left(cohesion raster\right)}{\left(Unit weight raster\right)\times block thickness\times \text{sin}\left(slope raster\right)}+\frac{\tan \left(friction angle raster\right)}{\text{tan} \left(slope raster\right)}(3)$

Newmark (1965) showed that the critical acceleration a_c for a potential landslide block is a simple function of the static factor of safety F_s and the slope angle.

$a_c=\left(F_s-1\right)\cdot \sin \alpha \cdot g(4)$

In Eq. 4, g is the gravitational acceleration.

Chen et al. (2014) investigated landslide areas associated with critical accelerations to determine PGA for the 2008 Wenchuan earthquake in China and showed that critical acceleration is a reliable criterion for assessing slope stability. Xiaoli and Chunguo (2019) analyzed the slope stability for the 2014 Ludian earthquake in China and showed that Newmark’s critical acceleration and PGA could be used to estimate accurate ETL locations. Similarly, Chen et al. (2020) concluded that it is possible to quickly evaluate ETL by comparing critical acceleration and PGA.

Predicting Landslide Source Areas Using Critical Acceleration Method

Input parameters for the landslide predictions include estimates of the shear strength and unit weight of the landslide materials or ice/snow, slope angles extracted from the pre-earthquake DEM (Lacroix, 2016), and PGA data obtained from USGS shakemap, Table 2. The values of cohesion, friction angle, and bulk density used in the analysis were adopted from published literature. Field observations of the ETLs indicated that these often occurred on steep slopes covered with a layer of colluvium. The sliding surface may have been within colluvium or slightly deeper within weathered and fractured bedrock. The assumed shear strength parameters for the sliding surface are listed in Table 2. The estimated friction angle and cohesion were based on published values for colluvium and increased to account for field evidence that most shallow landslides involved fractured bedrock, which likely has higher shear strength than colluvium. The bulk density for the sliding block was based on a combination of typical colluvium and fractured gneiss densities. For U-1 to U-3, the selected values were guided by values presented by Irfan and Tang (1992). The geotechnical properties for the glacier snow-ice (U-4) were obtained from Gnyawali et al. (2020).

TABLE 2

TABLE 2. Parameters used in the critical acceleration model and their uncertainty.

Critical acceleration values were calculated for each cell. The DEM was resampled to generate different cell sizes, and a range of landslide thicknesses was assumed to calculate the critical accelerations for each cell using Eq. 5. The calculated critical acceleration at each site was compared with the PGA at each site to determine if the cell was stable or could slide during the earthquake. All cells determined to be unstable (PGA > a_c) were used to produce a predicted distribution or map of earthquake-triggered landslides. Different maps were created for different assumed landslide thicknesses and cell sizes. Finally, the predicted landslide maps were compared to those observed from DEM differencing.

An estimate of the landslide thickness was required to calculate the static factor of safety. The landslide thickness was varied until the resulting prediction of landslide locations appeared to match the landslide map obtained from DEM subtraction.

Accuracy Assessment

A quantitative assessment of the match between predicted and observed landslide locations were obtained using a confusion matrix, which is a method for assessing the accuracy of a binary classification, in this case, for cells classified as either stable or unstable. The landslide map extracted from DEM subtraction was considered as the reference map, and the critical acceleration method provided prediction maps. A correctly predicted cell consists of two classes: i) an unstable cell occurs in both maps (true positive), TP, and ii) a stable cell occurs in both maps (true negative), TN. Similarly, incorrectly predicted cells include two classes: i) an unstable cell in the reference map but a stable cell in the predicted map (false negative), FN; and ii) a stable cell in the reference map but an unstable cell in the predicted map (false positive), FP.

The Matthews correlation coefficient (MCC) is used as a measure of the quality of the classification. MCC accounts for true and false positives and negatives and is generally regarded as a balanced measure that can be used even if the classes are of very different sizes (Chicco and Jurman, 2020; Chicco et al., 2021). The MCC is a correlation coefficient between the observed and predicted binary classifications; it returns a value between −1 and +1. The MCC is calculated as:

$MCC=\frac{TP\times TN-FP\times FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}(5)$

The value of MCC ranges from −1 to +1, where +1 represents a perfect prediction, 0 represents a random prediction, and −1 represents a total disagreement between prediction and observation. MCC was used to evaluate the cells in the ETL prediction maps relative to the reference landslide map.

Several studies (Rong et al., 2020; Wang et al., 2020; Meena et al., 2021) have adopted MCC to evaluate landslide susceptibility maps. Rong et al. (2020) obtained MCC = 0.44 for a hazard map of rainfall-induced landslides in Shuicheng, China. Wang and Lin, 2010 compared four different landslide susceptibility mapping methods and found that MCC varied from 0.4 to 0.5. In this study, the highest MCC value was 0.13, which indicates a modest positive relationship with the reference landslide map obtained from DEM differencing.

Cell Size

Previous DEM-based investigations of ETL were performed with relatively large DEM cell sizes (greater than 10–90 m) compared to that available for the Langtang Valley. For example, Chen et al. (2014), Gallen et al. (2016), and Allstadt et al. (2018) used 90 m cell sizes. Wang and Lin (2010) used 40 m cells, and Dreyfus et al. (2013), Shinoda and Miyata (2017), and Ma and Xu (2019) used 10 m cells. An assessment of cell size on the predicted spatial distribution of unstable and stable cells was performed to assess the influence of size. The DEM cells were resampled in QGIS from 4 to 40 m cell size, using bilinear interpolation. For each resampled DEM, a series of analyses were done with varying landslide thicknesses. The landslide thickness was varied from 2 to 4.2 m with a 0.2 m increment. The critical accelerations for the various assumed landslide thicknesses were obtained. The critical accelerations were then used to create maps of predicted ETL for each assumed landslide thickness. These maps were compared with the DEM-derived landslide map.

Results and Discussion

Spatial Distribution of Landslides - DEM-Derived Versus Satellite Imagery

Landslide inventories for the Langtang area were obtained from previously mapped landslide scars visually identified in satellite imagery (Gnyawali and Adhikari, 2017; Roback et al., 2018). As an alternative method for determining the landslide locations, the elevation differences between pre- and post-earthquake DEMs of the Langtang valley (Lacroix, 2016) were used. These maps provide a reference for comparison with predicted landslide locations obtained by applying the critical acceleration and PGA estimates.

The spatial distribution of landslide source areas obtained by DEM differencing in the Langtang valley is shown in Figure 3. The spatial distribution shows a cluster of landslides near the valley bottom and in the snow-covered region. As expected, the landslide map shows a high concentration of landslide source areas where the large Langtang avalanche occurred and in areas with steep slopes.

A visual comparison of the landslide sources detected using DEM differencing and existing landslide inventories (Lacroix, 2016; Gnyawali and Adhikari, 2017; Roback et al., 2018) shows some consistency. However, exceptions occurred in snow-covered regions and along the Langtang river banks, where landslides were captured in the DEM-derived map but were not found by visual interpretation of satellite imagery. Previously published maps of landslides in the Langtang Valley consisted of a relatively small number of locations compared to what was found by DEM differencing. In the snow-covered area (U-4), none of the visually prepared inventories had landslide source areas. However, the main Langtang avalanche originated from this area (Lacroix, 2016). Visual interpretation of satellite imagery for landslide mapping is a challenge if no contrast is seen between pre- and post-earthquake imagery (as in snow-covered areas) or terrain deformations do not result in long runout scars. The detection of landslide areas based on satellite image interpretation is sensitive to the image quality and the interpretation of those images. This results in landslide inventories that may miss landslides (Roback et al., 2018). However, it is important to note that DEM differencing derived landslide inventories are also subject to errors. For example, shadows, occlusions, and poor correlation can result in data gaps and residual artifacts in each of the cross-track stereo DEMs. Thus, interpretation requires caution and expert judgment. Ideally, visually prepared landslide inventories from satellite images and DEM differencing derived landslide cells should be used as complementary to each other.

The DEM differencing technique has been applied in numerous studies (Tsutsui et al., 2007; Martha et al., 2010; James et al., 2012) to study geomorphological changes, including detection of shallow landslides. Tsutsui et al. (2007) used this technique to detect landslides triggered by earthquakes in Japan and cyclones in Taiwan. They concluded that this technique delineated the large-scale landslides with an accuracy >70% for slopes under 40° and accuracy <40% for slopes over 40°. Kim et al. (2020) showed that DEM differencing could detect landslides in hilly and densely vegetated areas if the DEM uncertainty is constrained.

In this study, the DEM differencing technique was the desired approach for checking the result of the critical acceleration method because the ultimate goal is to use existing pre-earthquake DEMs and post-earthquake ShakeMap PGA to quickly generate maps of likely ETL locations to help plan field reconnaissance and rescues immediately after an earthquake. In an emergency situation, there may not be sufficient time to acquire and map many landslides using satellite imagery. Furthermore, to obtain a reliable estimate of the landslide depths for many landslides over a wide area, DEM differencing provided the best approach.

Landslide Thickness

The 2015 Gorkha earthquake triggered mostly shallow landslides. The landslide depth is measured vertically, while the landslide thickness is measured normal to the slope (Figure 5). The median landslide depth for all areas observed from DEM differencing was 4.8 m for cells that were 4 m in size. The median landslide depths were 3.8 m for U-1, 4.5 m for U-2, 3.6 m for U-3, and 6.7 m for U-4. U-4 was the source area of the largest rock-ice avalanche in the valley, which deposited 7 × 106 m³ on the valley floor (Lacroix, 2016). The calculated depths from DEMs in vegetated areas can be exaggerated by vegetation loss when a shallow landslide occurs (Lacroix, 2016). The thickness (measured perpendicular to the slope) of the material that failed was calculated using the slope at each cell. The median landslide thicknesses in each area were 2.4, 2.5, 1.9, and 3.3 m for U-1 to U-4, respectively.

The sliding block’s thickness is an important parameter when using the critical acceleration method with a sliding surface that has cohesion. Ma and Xu (2019) used an average landslide thickness of 3 m based on a field investigation for the 2013 Lushan earthquake in China. Shinoda and Miyata (2017) studied regional landslides using Newmark’s method and found that a 2 m landslide thickness worked well for the Mid Niigata earthquake. The thickness ranged from 0.8 to 4.6 m for landslides triggered by the 2016 Kumamoto earthquake (Mw 7.1) (Saito et al., 2018). Shinoda et al. (2019) used a 3 m landslide thickness based on a JSEG (2017) report of regional landslide susceptibility for the 2016 Kumamoto earthquake. The median landslide thicknesses in the Langtang region caused by the 2015 Gorkha earthquake are similar to these other studies, and most landslides are shallow, except for a few much larger landslides.

Cell Size and MCC

Figure 6 illustrates the influence of the DEM cell size on predicting stable and unstable cells. As the DEM cell size increases, the predictive accuracy as measured by MCC decreases. This suggests that a small (4 m) cell size is best when using the analysis approach presented here. Although doubling the cell size to 8 m gives a similar prediction accuracy while reducing the amount of data to be processed and stored in the GIS. The landslide thickness used in the critical acceleration model that best matches the spatial distribution of DEM-derived stable and unstable cell locations is approximately 2.6 m, as seen by the peak in the MCC curve for the 4 m cell size in Figure 6. When larger DEM cells are used, a thicker landslide gives the best match with the observed ETLs. Note that when the landslide thickness was less than 1 m, almost all cells were predicted to be stable (not shown in the figure).

FIGURE 6

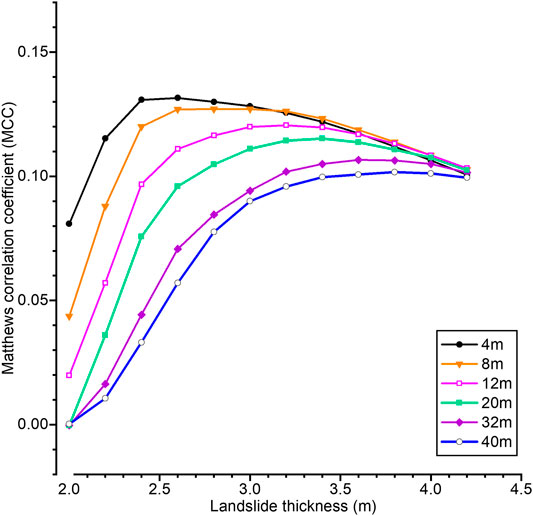
FIGURE 6. Matthews correlation coefficient for various DEM cell sizes (4–40 m) and assumed landslide thicknesses.

Wang et al. (2020) studied the influence of DEM cell size on ETL hazard assessment using Newmark’s sliding block method and found that a 30 m size gave a similar prediction to a 10 m cell size. In contrast, this study shows that a smaller cell size gives better results.

The influence of the landslide thickness on the predictions of landslide locations was explored. The results using a DEM cell size of 4 m with an assumption of a constant landslide thickness of 1, 2, 2.4, and 2.8 m are shown in Figure 7. Pixels with a brown color represent unstable cells predicted using the critical acceleration method. This figure clearly shows how sensitive the number and locations of predicted ETLs are to the assumed landslide thickness. When the thickness is less than 2.4 m, the critical acceleration model incorrectly classifies too many cells as stable, whereas when the thickness is 2.8 m, too many cells are predicted as unstable.

FIGURE 7

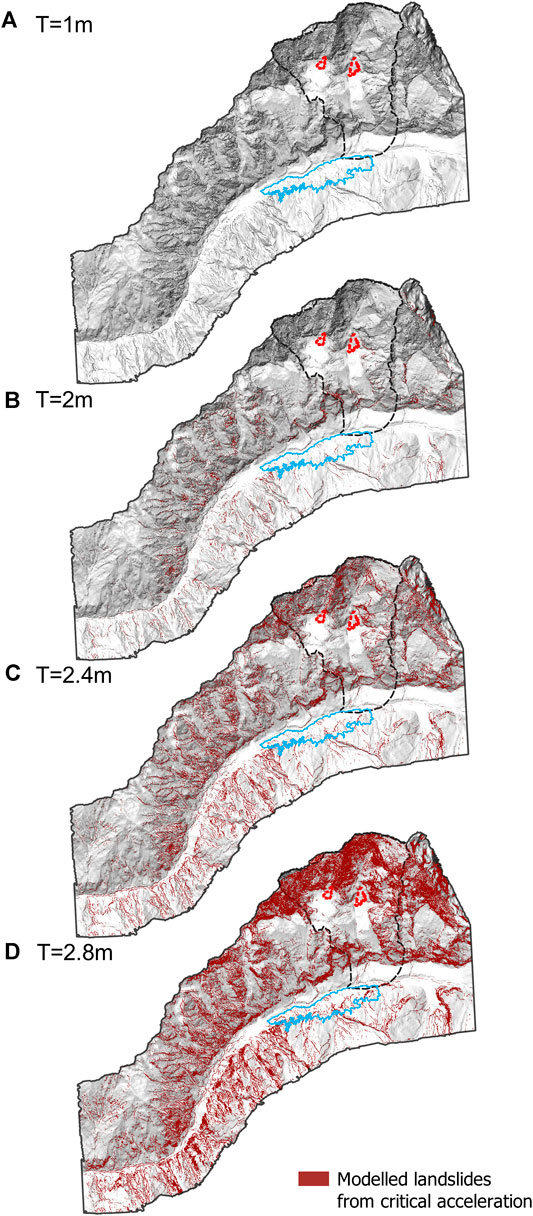
FIGURE 7. Predicted earthquake-triggered landslide maps for different assumed landslide thicknesses (A–D) with a DEM cell size of 4 m.

Critical Acceleration Model Predictions Versus DEM-Derived Map

An assumed landslide thickness of 2.6 m was used to determine the predicted ETL locations using the critical acceleration method. Figure 8 shows a comparison between the DEM-derived ETL locations and those predicted using the critical acceleration method. Cells predicted to be stable often correspond to locations where no elevation changes occurred in the DEM, which is a good match. However, cells predicted to be unstable in region U-4 are more scattered than those observed from DEM differencing.

FIGURE 8

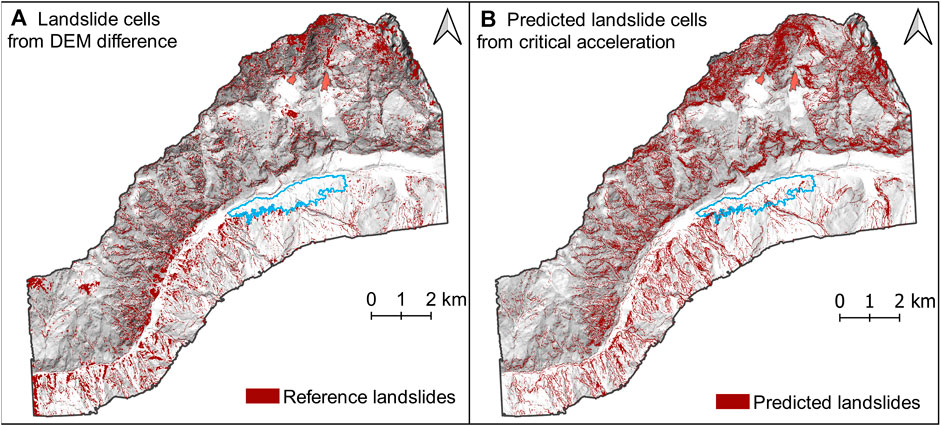
FIGURE 8. Comparison of ETL locations from (A) DEM subtraction and the (B) critical acceleration model with an assumed landslide thickness of 2.6 m and a 4 m cell size.

Immediately after an earthquake occurs, the resulting thickness for ETLs is typically unknown. Gallen et al. (2016) used an aggregate strength parameter to account for the unknown landslide thickness. The aggregate strength parameter is the ratio of soil cohesion and landslide thickness. They used a range of aggregate strength parameters varying from 5 to 15 kPa m⁻¹ and concluded that the lower and upper bound of the aggregate strength parameter is 10 kPa m⁻¹ and 15 kPa m⁻¹. This study took advantage of the post-earthquake DEM to measure the thickness for many landslides, which gave a median value of 2.6 m. Using this value gives an aggregate strength parameter equal to 10.4 and 18 kPa m⁻¹ in U-4 (glacier snow-ice) and U-1 to U-3, respectively. These values are similar to the values found by Gallen et al. (2016).

While the predicted landslide map has many similarities to the DEM-derived landslide distribution, there are differences. The prediction map is missing patches of landslides near the river in geological units U-1 and U-2. River erosion through colluvium and debris flow deposits near the valley bottom created over-steepened slopes prone to failure during the earthquake. Thus, many ETLs are observed along river banks (Tian et al., 2019). But the effect of slope undercutting or toe erosion by the river is often not captured in the DEM despite its small cell size. Thus, when running the critical acceleration model, it misses small steep slopes. Furthermore, these landslides often occur at the edges of terraces with top slopes <25°, which have a high factor of safety (Eq. 3). So, these cells were often classified as stable in the map showing predicted ETL. The critical acceleration method is a reliable technique for assessing earthquake-triggered landslides. However, cohesion plays an important role; thus, calibration of cohesion is critical to assessing slope stability.

Slopes

The predicted landslide distribution was examined in terms of slope angle, slope aspect, and bedrock geology. Most unstable cells (46.5%) in the study area faced southerly (SE to SW). 50 per cent of the cells in U-1 with a slope angle >78° were classified as unstable during the earthquake. Similarly, 42% of cells with a slope angle >79° and 36% of cells with a slope angle >80° were unstable in U-2 and U-3, respectively. While slopes with angles between 70 and 80° had a high proportion of unstable cells, more than 45% of the unstable cells occurred for slope angles between 40 and 60°. The median slope for unstable cells in U-1, U-2, U-3, and U-4 are 41, 50, 49, and 51°, respectively.

Uncertainty in Input Parameters

Primary input parameters for the critical acceleration method are topography data, geology data, and ground motion data. The topography is obtained from a pre-earthquake DEM (Lacroix, 2016). The reliability of the ground elevations in the DEM varies as a function of slope gradient (Figure 9). The ground elevation variability, calculated through the standard deviation of the difference of the 2014 and 2015 DEMs in stable areas, ranged from 0.5 m on flat terrain up to 12 m on slopes of 80° (Lacroix, 2016).

FIGURE 9

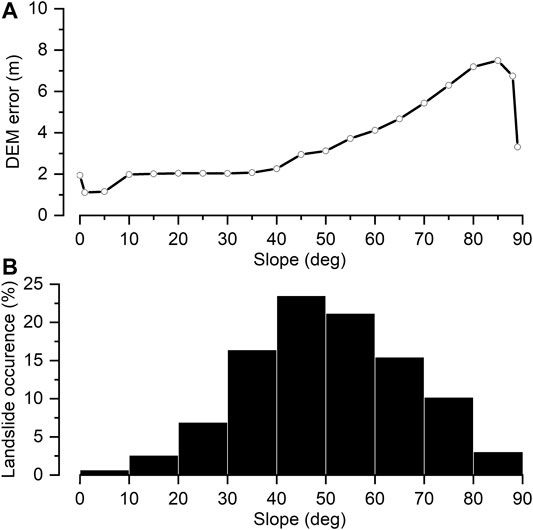
FIGURE 9. DEM uncertainty plot. (A) Mean DEM error as a function of slope angle, (B) Distribution of landslides in different slope ranges.

The landslide distribution is more continuous in the predicted map than in the landslide inventory derived from the DEM difference. This is perhaps due to the DEM error, uncertainty in geotechnical parameters, and PGA estimates from ShakeMap. The local variation in soil strength can affect the landslide distribution. The shear strength parameters were fixed over a large area due to no knowledge of their potential variations. This simplification affects the results from the critical acceleration model. Table 2 list the relative uncertainty in geotechnical parameters for the study area. Moreover, the absence of unstable cells near the river might be caused by ignoring potential groundwater pressures in the analysis.

USGS ShakeMap (map version 1, 2020-06-03) was used to generate an ETL susceptibility map in the Langtang valley. Two uncertainties linked with ShakeMap are (1) spatial variability of PGA near stations and (2) uncertainty in the ground-motion estimation relationships used to fill gaps between stations (Wald et al., 2008). The ShakeMap of the 2015 Gorkha earthquake has an uncertainty grade “C” (USGS, 2021a), which corresponds to a moderate quality ShakeMap (Wald et al., 2008). A middle range (“C”) grade corresponds to a moderate magnitude earthquake suitably represented with a point source location (Wald et al., 2008). A description of the USGS ShakeMap for the Gorkha earthquake is given in Table 3.

TABLE 3

TABLE 3. Metadata of USGS ShakeMap for the 2015 Gorkha earthquake.

Conclusion

The purpose of this paper was to demonstrate the use of a DEM and the critical acceleration method to quickly predict landslide locations after an earthquake as an aid to rapid landslide assessment and recovery after a devastating earthquake. The methodology was assessed by comparing predictions of unstable and stable cell locations with previously published ETL inventories, as well as a map of landslide locations obtained from the elevation difference between pre- and post-earthquake cells in the DEMs.

A DEM for most places on the earth is now available (e.g., Shuttle Radar Topography Mission), and DEMs are expected to improve quality over time with new satellite technologies. Thus, a critical input needed to predict the ETL locations is readily available.

Estimates of cohesion, friction angle, and unit weight of the landslide materials needed for the analysis can be inferred from geology maps (Hartmann and Moosdorf, 2012; USGS, 2021b) of the area of interest. For the case study presented here, the geological information was very limited, and the analysis only used two sets of values. However, in regions where better geological mapping is available, the shear strength parameters and bulk unit weight can vary according to the geological maps, which would help fine-tune the prediction of ETL locations.

For large earthquakes, PGA estimates are created by USGS ShakeMap soon after their occurrence. The landslide prediction method relies on comparing the critical acceleration within a GIS environment with estimates PGA for the raster cells over the area of interest. The PGA estimates from ShakeMap will likely improve as this tool becomes better calibrated, and this will contribute to better estimates of ETL locations.

The critical acceleration model is sensitive to the assumed landslide thickness when cohesion is present along the slip surface. Furthermore, it appears that the landslide thicknesses yielding the best match to observed stable and unstable cell locations can be influenced by the DEM cell size. Further research is needed to optimize the choice of a landslide thickness for conducting a regional analysis to predict ETL locations. This value will likely depend on the terrain and the soil and bedrock geology in the area of interest. However, as a starting point, evidence from past ETLs indicates that the typical landslide thickness is often in the range of 2–4 m.

ETL susceptibility mapping can be achieved in earthquake-prone mountainous regions because the basic input parameters needed for a Newmark model analysis (e.g., terrain, geology, and a probable PGA) are typically available. Therefore, applying a critical acceleration model in a GIS environment can assist with timely planning for disaster response after an earthquake. As expected, the results will be subject to error due to the simplifying assumptions used in the method. However, the results should still provide a fast way to prioritize the investigation of potential landslide areas after an earthquake. Furthermore, this approach has potential use in early planning for ETL by mapping the terrain susceptibility using readily available probabilistic PGA maps.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KG and SM conceived and designed the study. SM prepared and analyzed the data. DT guided the research through technical discussions. PL produced the DEMs. DT and PL provided crucial suggestions to improve the work. KG and SM wrote the first draft of the manuscript. DT, PL, and CX edited and reviewed the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge the support of Frontiers Fee Support program for covering the Article Processing Charge (APC) of this paper.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.689303/full#supplementary-material

References

Allstadt, K. E., Jibson, R. W., Thompson, E. M., Massey, C. I., Massey, C. I., Wald, D. J., Godt, J. W., et al. (2018). Improving Near–Real–Time Coseismic Landslide Models: Lessons Learned From the 2016 Kaikōura, New Zealand, Earthquake. Bull. Seismol. Soc. Am. 108 (3B), 1649–1664.

CrossRef Full Text | Google Scholar

Arias, A. (1970). Measure of Earthquake Intensity. Cambridge Santiago de Chile: Massachusetts Inst. of Tech. Univ. of Chile.

Broxton, M. J., and Edwards, L. J. (2008). “The Ames Stereo Pipeline: Automated 3D Surface Reconstruction from Orbital Imagery,” in Lunar and Planetary Science Conference. League City, TX, US: Meeting and Publication Services. 2419.

Google Scholar

Chen, X.-L., Liu, C.-G., Yu, L., and Lin, C.-X. (2014). Critical Acceleration as a Criterion in Seismic Landslide Susceptibility Assessment. Geomorphology 217, 15–22. doi:10.1016/j.geomorph.2014.04.011

CrossRef Full Text | Google Scholar

Chen, X.-L., Shan, X.-J., Wang, M.-M., Liu, C.-G., and Han, N.-N. (2020). Distribution Pattern of Coseismic Landslides Triggered by the 2017 Jiuzhaigou Ms 7.0 Earthquake of China: Control of Seismic Landslide Susceptibility. Ijgi 9 (4), 198. doi:10.3390/ijgi9040198

CrossRef Full Text | Google Scholar

Chicco, D., and Jurman, G. (2020). The Advantages of the Matthews Correlation Coefficient (MCC) over F1 Score and Accuracy in Binary Classification Evaluation. BMC Genomics 21 (1), 1–13. doi:10.1186/s12864-019-6413-7

CrossRef Full Text | Google Scholar

Chicco, D., Tötsch, N., and Jurman, G. (2021). The Matthews Correlation Coefficient (MCC) Is More Reliable Than Balanced Accuracy, Bookmaker Informedness, and Markedness in Two-Class Confusion Matrix Evaluation. BioData Mining 14 (1), 1–22. doi:10.1186/s13040-021-00244-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Chousianitis, K., Del Gaudio, V., Kalogeras, I., and Ganas, A. (2014). Predictive Model of Arias Intensity and Newmark Displacement for Regional Scale Evaluation of Earthquake-Induced Landslide hazard in Greece. Soil Dyn. Earthquake Eng. 65, 11–29. doi:10.1016/j.soildyn.2014.05.009

CrossRef Full Text | Google Scholar

Collins, B. D., and Jibson, R. W. (2015). Assessment of Existing and Potential Landslide Hazards Resulting from the April 25, 2015 Gorkha, Nepal Earthquake Sequence. Geol. Surv. Open-File Rep. 50. 1142 doi:10.3133/ofr20151142

CrossRef Full Text | Google Scholar

Collins, B. D. (2015).Video Data Files to Accompany USGS OFR 2015-1142--Assessment of Existing and Potential Landslide Hazards Resulting from the April 25, 2015 Gorkha, Nepal Earthquake Sequence. U.S. Geological Survey data release. doi:10.5066/F7X928BN10.3133/ofr20151142

CrossRef Full Text

Dai, F. C., Xu, C., Yao, X., Xu, L., Tu, X. B., and Gong, Q. M. (2011). Spatial Distribution of Landslides Triggered by the 2008 Ms 8.0 Wenchuan Earthquake, China. J. Asian Earth Sci. 40 (4), 883–895. doi:10.1016/j.jseaes.2010.04.010

CrossRef Full Text | Google Scholar

Dreyfus, D., Rathje, E. M., and Jibson, R. W. (2013). The Influence of Different Simplified Sliding-Block Models and Input Parameters on Regional Predictions of Seismic Landslides Triggered by the Northridge Earthquake. Eng. Geology 163, 41–54. doi:10.1016/j.enggeo.2013.05.015

CrossRef Full Text | Google Scholar

Fujita, K., Inoue, H., Izumi, T., Yamaguchi, S., Sadakane, A., Sunako, S., et al. (2017). Anomalous winter-snow-amplified Earthquake-Induced Disaster of the 2015 Langtang Avalanche in Nepal. Nat. Hazards Earth Syst. Sci. 17, 749–764. doi:10.5194/nhess-17-749-2017

CrossRef Full Text | Google Scholar

Gallen, S. F., Clark, M. K., Godt, J. W., Roback, K., and Niemi, N. A. (2016). Application and Evaluation of a Rapid Response Earthquake-Triggered Landslide Model to the April 25 2015 Mw 7.8 Gorkha Earthquake, Nepal. Tectonophysics 714, 173–187.

Google Scholar

Gnyawali, K. R., and Adhikari, B. R. (2017). “Spatial Relations of Earthquake Induced Landslides Triggered by 2015 Gorkha Earthquake Mw = 7.8Spatial Relations of Earthquake Induced Landslides Triggered by 2015 Gorkha Earthquake Mw= 7.8,” in Workshop on World Landslide Forum. Ljubljana, Slovenia: Springer, 85–93. doi:10.1007/978-3-319-53485-5_10

CrossRef Full Text | Google Scholar

Gnyawali, K. R., Xing, A., and Zhuang, Y. (2020). Dynamic Analysis of the Multi-Staged Ice-Rock Debris Avalanche in the Langtang valley Triggered by the 2015 Gorkha Earthquake, Nepal. Eng. Geology 265, 105440. doi:10.1016/j.enggeo.2019.105440

CrossRef Full Text | Google Scholar

Gorum, T., Korup, O., van Westen, C. J., van der Meijde, M., Xu, C., and van der Meer, F. D. (2014). Why So Few? Landslides Triggered by the 2002 Denali Earthquake, Alaska. Quat. Sci. Rev. 95, 80–94. doi:10.1016/j.quascirev.2014.04.032

CrossRef Full Text | Google Scholar

Harp, E. L., and Jibson, R. W. (1996). Landslides Triggered by the 1994 Northridge, California, Earthquake. Bull. Seismological Soc. America 86 (1B), S319–S332.

Google Scholar

Hartmann, J., and Moosdorf, N. (2012). The New Global Lithological Map Database GLiM: A Representation of Rock Properties at the Earth Surface. Geochem. Geophys. Geosyst. 13(12). doi:10.1029/2012gc004370

CrossRef Full Text | Google Scholar

Immerzeel, W. W., Van Beek, L. P. H., Konz, M., Shrestha, A. B., and Bierkens, M. F. P. (2012). Hydrological Response to Climate Change in a Glacierized Catchment in the Himalayas. Climatic Change 110 (3–4), 721–736. doi:10.1007/s10584-011-0143-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Irfan, T. Y., and Tang, K. Y. (1992). Effect of the Coarse Fraction on the Shear Strength of Colluvium. GEO Rep 23 GEO Special Project Report No. SPR 15/92.

James, L. A., Hodgson, M. E., Ghoshal, S., and Latiolais, M. M. (2012). Geomorphic Change Detection Using Historic Maps and DEM Differencing: The Temporal Dimension of Geospatial Analysis. Geomorphology 137 (1), 181–198. doi:10.1016/j.geomorph.2010.10.039

CrossRef Full Text | Google Scholar

JSEG (2017). Report of the 2016 Kumamoto, Oita Earthquake Disaster Research mission. Japan Society of Engineering Geology (Jseg) (in Japanese).

Jibson, R. W., Allstadt, K. E., Rengers, F. K., and Godt, J. W. (2018). Overview of the Geologic Effects of the November 14, 2016, Mw 7.8 Kaikoura, New Zealand, Earthquake. Geol. Surv. Scientific Invest. Rep. 2017–, 39.5146 doi:10.3133/sir20175146

CrossRef Full Text | Google Scholar

Jibson, R. W., Harp, E. L., and Michael, J. A. (2000). A Method for Producing Digital Probabilistic Seismic Landslide hazard Maps. Eng. Geology 58 (3–4), 271–289. doi:10.1016/s0013-7952(00)00039-9

CrossRef Full Text | Google Scholar

Jibson, R. W. (2007). Regression Models for Estimating Coseismic Landslide Displacement. Eng. Geology 91 (2-4), 209–218. doi:10.1016/j.enggeo.2007.01.013

CrossRef Full Text | Google Scholar

Jin, K. P., Yao, L. K., Cheng, Q. G., and Xing, A. G. (2019). Seismic Landslides hazard Zoning Based on the Modified Newmark Model: a Case Study from the Lushan Earthquake, China. Nat. Hazards 99 (1), 493–509. doi:10.1007/s11069-019-03754-6

CrossRef Full Text | Google Scholar

Jones, J. N., Stokes, M., Boulton, S. J., Bennett, G. L., and Whitworth, M. R. Z. (2020). Coseismic and Monsoon-Triggered Landslide Impacts on Remote Trekking Infrastructure, Langtang Valley, Nepal. Q. J. Eng. Geology Hydrogeology 53 (2), 159–166. doi:10.1144/qjegh2019-048

CrossRef Full Text | Google Scholar

Kargel, J. S., Leonard, G. J., Shugar, D. H., Haritashya, U. K., Bevington, A., Fielding, E. J., et al. (2015). Geomorphic and Geologic Controls of Geohazards Induced by Nepals 2015 Gorkha Earthquake. Science 351, aac8353. doi:10.1126/science.aac8353

PubMed Abstract | CrossRef Full Text | Google Scholar

Keefer, D. K. (2002). Investigating Landslides Caused by Earthquakes–A Historical Review. Surv. Geophys. 23 (6), 473–510. doi:10.1023/a:1021274710840

CrossRef Full Text | Google Scholar

Keefer, D. K. (1984). Landslides Caused by Earthquakes. Geol. Soc. America Bull. 95 (4), 406–421. doi:10.1130/0016-7606(1984)95<406:lcbe>2.0.co;2

CrossRef Full Text | Google Scholar

Keefer, D. K. (1994). “The Importance of Earthquake-Induced Landslides to Long-Term Slope Erosion and Slope-Failure Hazards in Seismically Active Regions,” in Geomorphology and Natural Hazards. Elsevier, 265–284. doi:10.1016/b978-0-444-82012-9.50022-0

CrossRef Full Text | Google Scholar

Kieffer, D. S., Jibson, R., Rathje, E. M., and Kelson, K. (2006). Landslides Triggered by the 2004 Niigata Ken Chuetsu, Japan, Earthquake. Earthquake Spectra 22 (1_Suppl. l), 47–73. doi:10.1193/1.2173021

CrossRef Full Text | Google Scholar

Kim, M.-K., Sohn, H.-G., and Kim, S. (2020). Incorporating the Effect of ALS-Derived DEM Uncertainty for Quantifying Changes Due to the Landslide in 2011, Mt. Umyeon, Seoul. GIScience & Remote Sensing 57 (3), 287–301. doi:10.1080/15481603.2019.1687133

CrossRef Full Text | Google Scholar

Lacroix, P. (2016). Landslides Triggered by the Gorkha Earthquake in the Langtang valley, Volumes and Initiation Processes. Earth, Planets and Space 68 (1), 46. doi:10.1186/s40623-016-0423-3

CrossRef Full Text | Google Scholar

Lanzo, G., Tommasi, P., Ausilio, E., Aversa, S., Bozzoni, F., Cairo, R., et al. (2018). Reconnaissance of Geotechnical Aspects of the 2016 Central Italy Earthquakes. Bull. Earthquake Eng. 17, 5495–5532. doi:10.1007/s10518-018-0350-8

CrossRef Full Text | Google Scholar

Ma, S., and Xu, C. (2019). Assessment of Co-seismic Landslide hazard Using the Newmark Model and Statistical Analyses: a Case Study of the 2013 Lushan, China, Mw6.6 Earthquake. Nat. Hazards 96 (1), 389–412. doi:10.1007/s11069-018-3548-9

CrossRef Full Text | Google Scholar

Martha, T. R., Kerle, N., Jetten, V., van Westen, C. J., and Vinod Kumar, K. (2010). Landslide Volumetric Analysis Using Cartosat-1-Derived DEMs. IEEE Geosci. Remote Sensing Lett. 7 (3), 582–586. doi:10.1109/lgrs.2010.2041895

CrossRef Full Text | Google Scholar

Meena, S. R., Ghorbanzadeh, O., van Westen, C. J., Nachappa, T. G., Blaschke, T., Singh, R. P., et al. (2021). Rapid Mapping of Landslides in the Western Ghats (India) Triggered by 2018 Extreme Monsoon Rainfall Using a Deep Learning Approach. Landslides, 18(5):1937-1950 doi:10.1007/s10346-020-01602-4

CrossRef Full Text | Google Scholar

Newmark, N. M. (1965). Effects of Earthquakes on Dams and Embankments. Géotechnique 15 (2), 139–160. doi:10.1680/geot.1965.15.2.139

CrossRef Full Text | Google Scholar

Qi, S., Xu, Q., Lan, H., Zhang, B., and Liu, J. (2010). Spatial Distribution Analysis of Landslides Triggered by 2008.5. 12 Wenchuan Earthquake, China. Eng. Geology 116 (1–2), 95–108. doi:10.1016/j.enggeo.2010.07.011

CrossRef Full Text | Google Scholar

Rahman, M. M., and Bai, L. (2018). Probabilistic Seismic hazard Assessment of Nepal Using Multiple Seismic Source Models. Earth Planet. Phys. 2 (4), 327–341.

Google Scholar

Ram, T. D., and Wang, G. (2013). Probabilistic Seismic hazard Analysis in Nepal. Earthq. Eng. Eng. Vib. 12 (4), 577–586. doi:10.1007/s11803-013-0191-z

CrossRef Full Text | Google Scholar

Roback, K., Clark, M. K., West, A. J., Zekkos, D., Li, G., Gallen, S. F., et al. (2018). The Size, Distribution, and Mobility of Landslides Caused by the 2015 Mw7.8 Gorkha Earthquake, Nepal. Geomorphology 301, 121–138. doi:10.1016/j.geomorph.2017.01.030

CrossRef Full Text | Google Scholar

Rong, G., Li, K., Han, L., Alu, S., Zhang, J., and Zhang, Y. (2020). Hazard Mapping of the Rainfall-Landslides Disaster Chain Based on GeoDetector and Bayesian Network Models in Shuicheng County, China. Water 12 (9), 2572. doi:10.3390/w12092572

CrossRef Full Text | Google Scholar

Saito, H., Uchiyama, S., Hayakawa, Y. S., and Obanawa, H. (2018). Landslides Triggered by an Earthquake and Heavy Rainfalls at Aso Volcano, Japan, Detected by UAS and SfM-MVS Photogrammetry. Prog. Earth Planet. Sci. 5 (1), 15. doi:10.1186/s40645-018-0169-6

CrossRef Full Text | Google Scholar

Shinoda, M., Miyata, Y., Kurokawa, U., and Kondo, K. (2019). Regional Landslide Susceptibility Following the 2016 Kumamoto Earthquake Using Back-Calculated Geomaterial Strength Parameters. Landslides 16 (8), 1497–1516. doi:10.1007/s10346-019-01171-1

CrossRef Full Text | Google Scholar

Shinoda, M., and Miyata, Y. (2017). Regional Landslide Susceptibility Following the Mid NIIGATA Prefecture Earthquake in 2004 with NEWMARK'S Sliding Block Analysis. Landslides 14 (6), 1887–1899. doi:10.1007/s10346-017-0833-8

CrossRef Full Text | Google Scholar

Stewart, J. P., Zimmaro, P., Lanzo, G., Mazzoni, S., Ausilio, E., Aversa, S., et al. (2018). Reconnaissance of 2016 Central Italy Earthquake Sequence. Earthquake Spectra 34, 1547–1555. doi:10.1193/080317eqs151m

CrossRef Full Text | Google Scholar

Takai, N., Shigefuji, M., Rajaure, S., Bijukchhen, S., Ichiyanagi, M., Dhital, M. R., et al. (2016). Strong Ground Motion in the Kathmandu Valley during the 2015 Gorkha, Nepal, Earthquake. Earth, Planets and Space 68 (1), 1–8. doi:10.1186/s40623-016-0383-7

CrossRef Full Text | Google Scholar

Tian, Y., Owen, L. A., Xu, C., Shen, L., Zhou, Q., and Figueiredo, P. M. (2020). Geomorphometry and Statistical Analyses of Landslides Triggered by the 2015 Mw 7.8 Gorkha Earthquake and the Mw 7.3 Aftershock, Nepal. Front. Earth Sci. 8, 407. doi:10.3389/feart.2020.572449

CrossRef Full Text | Google Scholar

Tian, Y., Xu, C., Hong, H., Zhou, Q., and Wang, D. (2019). Mapping Earthquake-Triggered Landslide Susceptibility by Use of Artificial Neural Network (ANN) Models: an Example of the 2013 minxian (China) Mw 5.9 Event. Geomatics, Nat. Hazards Risk 10 (1), 1–25. doi:10.1080/19475705.2018.1487471

CrossRef Full Text | Google Scholar

Tiwari, B., and Ajmera, B. (2017). “Landslides Triggered by Earthquakes from 1920 to 2015,” in Workshop on World Landslide Forum. Ljubljana, Slovenia: Springer, 5–15. doi:10.1007/978-3-319-53498-5_2

CrossRef Full Text | Google Scholar

Tsutsui, K., Rokugawa, S., Nakagawa, H., Miyazaki, S., Cheng, C.-T., Shiraishi, T., et al. (2007). Detection and Volume Estimation of Large-Scale Landslides Based on Elevation-Change Analysis Using DEMs Extracted from High-Resolution Satellite Stereo Imagery. IEEE Trans. Geosci. Remote Sensing 45 (6), 1681–1696. doi:10.1109/tgrs.2007.895209

CrossRef Full Text | Google Scholar

USGS (2021a). M 7.8 - 36km E of Khudi, Nepal. Available at: https://earthquake.usgs.gov/earthquakes/eventpage/us20002926/shakemap/metadata. (Accessed May 14, 2021).

Google Scholar

USGS (2021b). World Geologic Maps. (Accessed May 7, 2021).

Google Scholar

Wald, D. J., Lin, K. W., and Quitoriano, V. (2008). Quantifying and Qualifying USGS ShakeMap Uncertainty. US Geological Survey, Reston, Virginia, U.S. 26 .

Wang, K.-L., and Lin, M.-L. (2010). Development of Shallow Seismic Landslide Potential Map Based on Newmark's Displacement: the Case Study of Chi-Chi Earthquake, Taiwan. Environ. Earth Sci. 60 (4), 775–785. doi:10.1007/s12665-009-0215-1

CrossRef Full Text | Google Scholar

Wang, Y., Fang, Z., Wang, M., Peng, L., and Hong, H. (2020). Comparative Study of Landslide Susceptibility Mapping with Different Recurrent Neural Networks. Comput. Geosciences 138, 104445. doi:10.1016/j.cageo.2020.104445

CrossRef Full Text | Google Scholar

Wilson, R. C., and Keefer, D. K. (1983). Dynamic Analysis of a Slope Failure from the August 6 1979 Coyote Lake, California, Earthquake. Bull. Seismological Soc. America 73 (3), 863–877.

CrossRef Full Text | Google Scholar

Worden, C. B., Thompson, E. M., Hearne, M., and Wald, D. J. (2020). ShakeMap Manual Online: Technical Manual, User’s Guide, and Software Guide, U. S. Geological Survey. Reston, Virginia, U.S. doi:10.5066/F7D21VPQ

CrossRef Full Text

Worden, C. B., Wald, D. J., Allen, T. I., Lin, K., Garcia, D., and Cua, G. (2010). A Revised Ground-Motion and Intensity Interpolation Scheme for ShakeMap. Bull. Seismological Soc. America 100 (6), 3083–3096. doi:10.1785/0120100101

CrossRef Full Text | Google Scholar

Xiaoli, C., and Chunguo, L. (2019). “Assessment of Landslides Triggered by Earthquakes Based on the Combination of Peak Ground Motion and Critical Acceleration Analysis,” in IAEG/AEG Annual Meeting Proceedings, San Francisco, California Cham: Springer, 123–129. doi:10.1007/978-3-319-93136-4_15

CrossRef Full Text | Google Scholar

Xu, C., Xu, X., Yao, X., and Dai, F. (2014). Three (Nearly) Complete Inventories of Landslides Triggered by the May 12, 2008 Wenchuan Mw 7.9 Earthquake of China and Their Spatial Distribution Statistical Analysis. Landslides 11 (3), 441–461. doi:10.1007/s10346-013-0404-6

CrossRef Full Text | Google Scholar

Yuan, R., Deng, Q., Cunningham, D., Han, Z., Zhang, D., and Zhang, B. (2016). Newmark Displacement Model for Landslides Induced by the 2013 Ms 7.0 Lushan Earthquake, China. Front. Earth Sci. 10 (4), 740–750. doi:10.1007/s11707-015-0547-y

CrossRef Full Text | Google Scholar