- 1State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu, China
- 2College of Water Resources and Hydropower, Sichuan University, Chengdu, China
- 3Department of Dam Safety Management, Nanjing Hydraulic Research Institute, Nanjing, China
- 4State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing, China
Many of the existing reservoir dams are constructed in alpine and gorge regions, where the topography and geological conditions are complicated, bank slopes are steep, and landslides have a high potential to occur. Surges triggered by landslides in the reservoir are one of the major causes of dam overtopping failures. Many factors affect the slope stability of reservoir banks and the height of surges triggered by landslides, such as spatial variability of material properties, speed of landslides, etc. To reasonably evaluate dam overtopping risk caused by landslide-induced surges is a key technology in engineering that is urgent to be solved. Therefore, a novel risk analysis method for overtopping failures caused by waves triggered by landslides induced by bank instability considering the spatial variability of material parameters is proposed in this study. Based on the random field theory, the simulation method for the spatial variability of material parameters is proposed, and the most dangerous slip surface of the reservoir bank slope is determined with the minimum value of the safety factors. The proxy risk analysis models for both the slope instability and dam overtopping are constructed with the consideration of spatial variability of material parameters, and then the dam overtopping failure risk caused by landslide-induced surges is calculated using the Monte-Carlo sampling. The proposed models are applied to a practical engineering project. Results show that the spatial variability of material properties significantly affects the instability risk of slopes, without considering which the risks of slope instability and dam overtopping may be overestimated. This study gives a more reasonable and realistic risk assessment of dam overtopping failures, which can provide technical support for the safety evaluation and risk control of reservoir dams.
Introduction
Many dams have been constructed in alpine and gorge regions, where topography and geological conditions are complicated, the spatial variability of material properties is large, and the bank slopes are steep. Consequently, the instability risk of these slopes is high, which leads to landslide-triggered surges and subsequently induces dam overtopping failures. Therefore, the study on the reasonable evaluation of dam overtopping failure risks caused by landslide-induced surges considering spatial variability of material parameters is of great significance to ensure the long-term safety operation of dams.
The statistical analysis shows that overtopping is one of the main causes of dam breaks, and the break proportions of Earth dams, gravity dams, and landslide dams are 49.7, 29.3, and 91.8% (Zhang et al., 2016). Liu and Wu (2020) proposed a methodology for overtopping risk analysis of Earth dams considering the effects of failure duration of release structures based on the Bayesian networks. Zhang and Tan (2014) established a comprehensive risk assessment system of dam overtopping induced by flood, which considers the gate failure, randomness of the flood, initial water level, and time-varying effects (e.g., the height of dam crest is a function of time t). Sun et al. (2012) investigated a probability-based risk analysis methodology to evaluate Earth dam overtopping risk induced by concurrent flood and wind, and discussed the influence of initial water surface level, flood, wind velocity, and dam height.
In recent years, the risk assessment of landslides has been a research hotspot, and some new methods and achievements have been put forward (Hungr and McDougall, 2009; Zhang et al., 2019; Peng et al., 2020a; Peng et al., 2020b; Yu et al., 2021). The consequences of landslides are often very serious, the huge surge induced by the large-scale and high-speed landslide on the reservoir bank will not only destroy the hydraulic structures and block the river channel, but also cause overtopping, ship damage, casualties, and others (Jaeger, 1965; Ward and Day, 2011; Wang et al., 2020; Zheng et al., 2021), so it cannot be ignored. Lin et al. (2015) simulated the entire process of surge wave generation, propagation, and overtopping of a dam using a coupled incompressible smoothed particle hydrodynamics (ISPH) model. Liu, (2020) experimentally investigated whether landslide surge waves can influence a dam failure process caused by flood overtopping and found that the surge wave could lead to a large instantaneous peak discharge that exceeded the dam failure peak discharge of the experiments with no surge wave. Xiao and Lin (2016) studied the velocity and turbulence kinetic energy features during wave-generation and overtopping processes based on the coupled solid-fluid numerical model and an experiment of dam overtopping in an open channel. Tessema et al. (2019) studied the landslide-generated waves and the overtopping process over the dam crest in a three-dimensional (3D) physical model test and proposed dimensionless empirical relations between the overtopping volume and the governing parameters. In addition, some analysis methods about the height of surges are put forward, such as the Noda method (Noda, 1970), Pan method (Pan, 1980), the China Institute of Water Resources and Hydropower Research method (Cui and Zhu, 2011), etc. The above research mainly focuses on the height formulas, influence factors, and the process of the dam overtopping caused by the landside-induced surges, while there is not abundant research concerning the dam overtopping risk caused by the landside-induced surges. Moreover, the gradient of near-dam reservoir bank slopes is always large and the material parameters have high spatial variability (Cho, 2010; Jiang et al., 2018a; Qi and Li, 2018; Li et al., 2019), which has a direct effect on the overtopping risk caused by the landslide-induced surges, so the influence of the uncertainty of parameters in near-dam reservoir bank slopes on the overtopping caused by the landside surge should be paid more attention to.
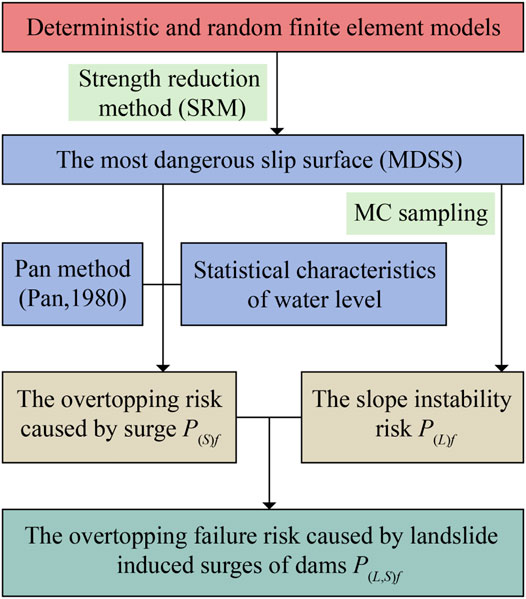
The objective of this paper is to study the dam overtopping failure risks caused by landslide-induced surges considering the spatial variability of material parameters. To achieve this research is arranged as follows: a) Studying the simulation technology of the spatial variability of soil materials in slopes based on the random field theory and the midpoint method; b) Determining the most dangerous slip surface and constructing the composite response surface equations of slope instability considering the spatial variation of parameters; c) Based on the Pan method, establishing the calculation formula of the landslide surge and putting forward the overtopping failure risk analysis method caused by landslide-induced surges; d) Taking the PB Earth rockfill dam as an example, to analyze and discuss the applicability and rationality of the proposed methodology.
Methodology
Dam overtopping failure risk caused by landslide-induced surges includes two aspects: the slope instability risk of reservoir banks and the overtopping risk caused by the surge, that is,
where
Instability Risk Analysis Method of the Near-Dam Reservoir Bank Slopes Considering the Spatial Variability of Material Parameters
Simulation Method for the Spatial Variability of Material Parameters
In the field of slope engineering, discrete random fields are commonly adopted to describe the spatial variability of soil parameters. A steady random field of parameters (e.g., elastic modulus, internal friction angle, cohesion, etc.) can be constructed by the corresponding mean value, the coefficient of variation, the autocorrelation function, and the autocorrelation distance. The discrete method commonly includes the midpoint method, the local average method, the spectral representation, and the Karhunen–Loève function (Montoya-Noguera et al., 2019). The midpoint method is widely applied because its dispersion is not affected by the shape of the element, and the calculation is simple (Lu et al., 2020; Li et al., 2021).
Based on the midpoint method, the two-dimensional slope model is divided into
where
When the material parameter obeys the log-normal distribution, the probability density function of the distribution is:
where
where
Based on the Cholesky decomposition method (Box and Muller, 1958), the steps to generate the random variable
Step 1: Generate the sampled sequence matrix
Step 2: Decompose the autocorrelation coefficient matrix
where
Step 3: Present the sampled sequence matrix
Failure Risk Analysis of Bank Slopes Considering the Spatial Variability of Parameters
At present, the rigid body limit equilibrium method and the finite element method are commonly used in the analysis of rock and soil slope stability (Liu et al., 2015). In this paper, the strength reduction method (SRM) is used to calculate the slope stability, and the convergence of the finite element calculation is taken as the criterion of the critical failure state (Liu et al. 2020; Ma et al., 2020).
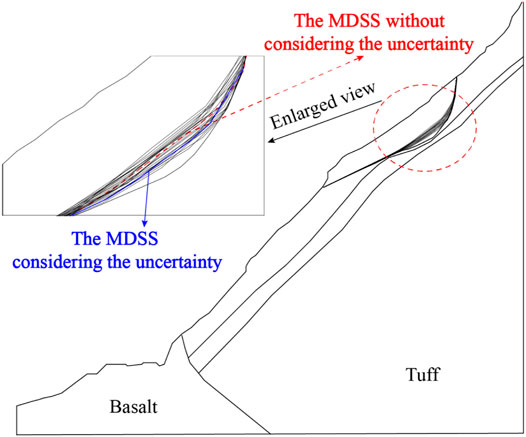
In the finite element analysis, the most dangerous slip surface (MDSS) is essentially a parallel system composed of several elements, and the Drucker-Prager criterion is commonly used in civil engineering analysis for determining the most dangerous slip surface. However, the location of the MDSS is closely related to the material properties of the slope, so the uncertainty of material parameters has a great influence on the MDSS. Aiming at this situation, the simulation method for the spatial variability of parameters is adopted to describe the uncertainty. In addition, a random field of parameters has a corresponding MDSS. In order to fully consider the influence of uncertainty of material parameters on the slip surfaces and determine the unique MDSS, the Monte-Carlo simulation method is used to generate enough random fields (
For the anti-sliding stability of a slope composed of joints, fissures, and faults, the stress algebra of elements in the sliding path is adopted to establish the performance function of the anti-sliding stability
where
However, the performance function (Eq. 7) cannot explicitly reflect the influence of random variables on the performance function, and cannot be directly applied in the engineering risk analysis. Therefore, the quadratic response surface method without considering the cross term is selected to construct the performance functions (Guo et al., 2016). In the traditional deterministic method, the parameters of soils in the same partition zone on the MDSS are the same, but the parameters of each element on the MDSS is different after considering the spatial variability of material properties, that is, the uncertainty of soil parameters is reflected in the elements on the MDSS, so the traditional functional response surface equation is difficult to describe the spatial variation of the element. Therefore, a composite response surface equation for the stability of slopes is proposed in this paper (Guo et al., 2016), that is
where
Based on the Eqs 8–10, by using the Monte-Carlo method (MC method), the failure risk of reservoir bank slope considering the spatial variability of material parameters can be obtained as follows:
where
Method for the Overtopping Failure Risk Caused by Landslide-Induced Surges
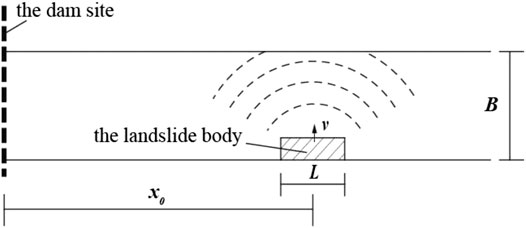
Whether the overtopping occurs depends on whether the sum of the surge height caused by the landslide due to conditions of instability of the near-dam reservoir bank slopes and the initial reservoir water level exceeds the elevation of the dam crest.
The Pan method (Pan, 1980) is used in this paper to calculate the surge height
where
where
where △L is the width of each slide block, it is noted that the landslide is equally divided into n vertical slide block;
Under the condition that the range of the landslide body is determined, the average water depth
where
Therefore, the overtopping failure risk
where
Finally, the flow chart of the procedure is shown in Figure 2.
Case Study
Project Specifications
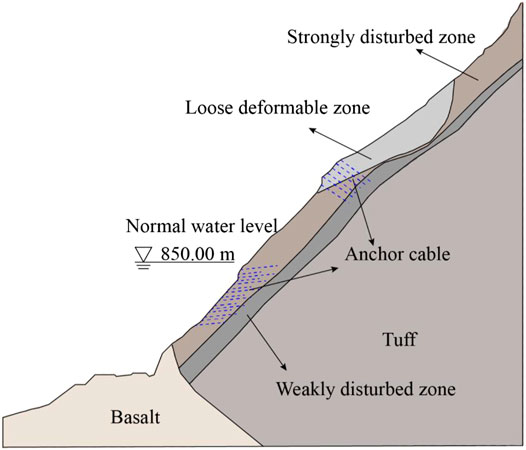
An Earth rockfill dam (named PB) is located on the Dadu River on the border between Hanyuan County and Ganluo County, Sichuan Province, China. The storage capacity is 5.39 billion m3, the maximum height of the dam is 186 m, and the normal water storage level is 850 m. A near-dam reservoir bank slope is located about 780 m upstream of the dam, with a relatively protruding topography, with an elevation of 730 m at the leading edge and 1,187 m at the trailing edge. The slope is about 400 m along the river and 360 m in the radial direction, and the height difference between the upper and lower edges is 450 m. The volume is about 123,000 m³, as shown in Figure 3. The exposed stratum of this slope is mainly composed of the pre-Sinian shallow metamorphic basalt (Anzβ) and the Lower Sinian Suxiong Formation (Zas). The Zas consists of the intermediate basic volcanic rocks and the intercalated with multi-layer tuffaceous glutenite. The bedrock is mainly composed of tuff. The rock mass is mainly weakly weathered. The depth of the strongly disturbed zone is generally 30–60 m, and the maximum value is about 70 m. The depth of the weakly disturbed zone is generally 65–90 m, and the maximum value is about 100 m. The typical profile of the slope is shown in Figure 4.
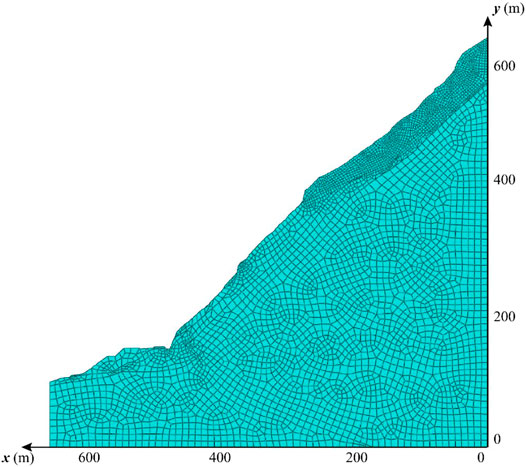
Finite Element Model and Material Parameters of the Near-Dam Reservoir Bank Slope
The finite element model of the slope was established with a vertical width of 620 m from the elevation of 600–1,220 m and a horizontal width of 660 m. The model was divided into 4,071 elements and 8,280 nodes, as shown in Figure 5. For the cross-river direction (X-axis), the direction pointing to the free surface is positive; for the vertical direction (Z-axis), the direction pointing vertically upward is positive. According to the model and actual geological conditions, the boundary conditions were determined as follows: horizontal constraints were imposed on the left and right boundaries of the model, the bottom fixed constraint, and no constraint at the top of the model. According to the slope reinforcement report (Powerchina Chengdu Engineering Corporation Limited, 2009), six anchor cables are set in the loose deformation zone at the upper part of the slope, and 15 anchor cables are set in the strong strongly disturbed zone at the lower part of the slope.
According to the design results of the PB Earth rock-fill dam and referring to the parameters of similar slope engineering (Powerchina Chengdu Engineering Corporation Limited, 2009), the physical and mechanical parameters of the slope are given in Table 2. It is well known that the shear strength parameters have a great influence on the slope reliability, so the cohesion and internal friction angle were selected as the random variables, and the specific parameters are shown in Table 3.
Slope Instability Risk Analysis
Performance Function of Slope Instability
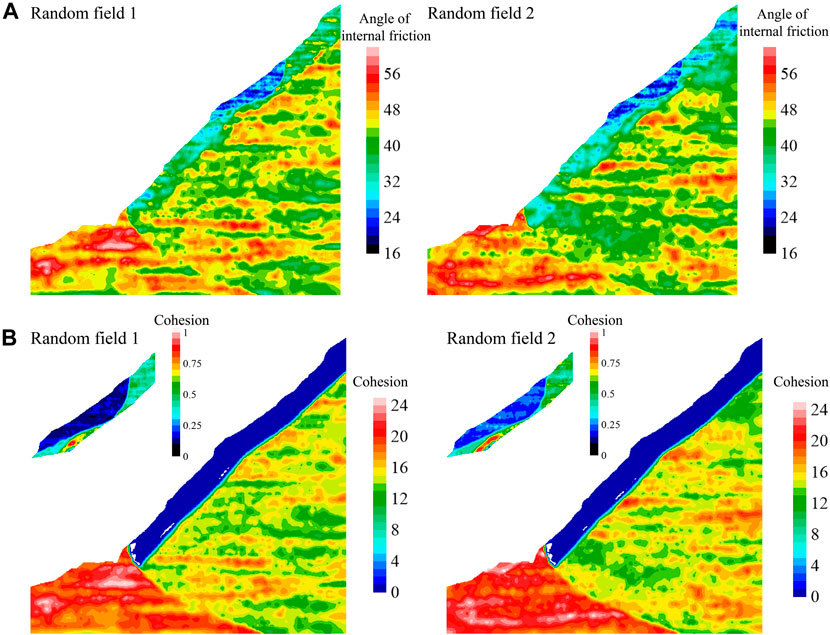
Based on the proposed method for the simulation of a random field, 100 groups of parameter random fields have been constructed, two of which are shown in Figure 6. As seen in Figure 6, the spatial variability and discretization of the parameters decrease gradually from top to bottom of the rock mass, which indicates that the random field samples are rational.
Based on the stability analysis results of 100 random fields of slope model and the model with deterministic parameters, the safety factor of the slope in the deterministic analysis is 1.355, and the safety factor of random field analysis ranged from 1.167 to 1.443. Figure 7 shows the MDSS of the slope for the random and deterministic analysis of slope stability analysis. As shown in Figure 7, the slip surfaces of the slope are compact. They are all located at the interface between the loose deformation zone and the lower strongly disturbed zone, and partial slip surfaces pass through the interior of the loose deformation zone.
Risk Analysis of Slope Instability
Combined with the MDSS and response surface equations of performance function, the orthogonal design of five factors five levels (
By using the proposed slope instability risk calculation method considering the spatial variability of material parameters, the failure probability of the slope with considering the spatial variability of materials is
Overtopping Failure Risk Analysis Caused by Landslide-induced Surges
Based on the MDSS in the random and deterministic analysis, the sliding range of the slope is determined to analyze the surge. According to the data of the Dadu River, the width of the river bed is 80 m and the riverbank slope angle is 40°. Due to the position of the landslide above the water surface, it is assumed that in the process of slope sliding, there is only friction
In this paper, the Pan method (Pan, 1980) is used to determine the height of the surge generated by a landslide. The landslide is divided into 18 horizontal strips, each with a width △L of 10 m. Based on Eqs 17–20, the maximum speed of landslide reached the
In the Pan method, the water depth of the reservoir is the main factor determining the final surge height. Combining the operation condition of the slope, the calculation water level in this paper is selected as 850 m (normal water level). Results show that the height of landslide surge into water is 11.49 m when considering the spatial variability of slope material parameters under the water level of 850 m, and the height of surge is 5.92 m in front of the dam. In view that the Pan method is an empirical estimate method, some scholars in the world have made experiments and numerical simulations to verify the applicability of the method. Results show that the average relative errors between the calculated values using the Pan method and the experiment or simulation values are about 10% (Huang et al., 2014; Ma et al., 2016), indicating that the uncertainty of the calculated values is low, and the results are relatively reliable.
In addition, the water level at the dam generally obeys normal distribution. For the PB dam, the reservoir water level satisfies the normal distribution with an average of 828.29 m and a standard deviation of 7.42 m. Combined with Eq. 12, the overtopping risk of the PB dam caused by the surge is
Finally, the overtopping risk caused by landslide-induced surges considering spatial variability of material parameters in the PB dam can be determined based on Eq. 1. Results show that the overtopping risk (
Ignoring the spatial variability of material parameters will overestimate the risk of slope instability and then overestimate the overtopping risk caused by landslide-induced surges. Therefore, the spatial variability of parameters in the slope near the dam in the upstream direction should be paid more attention to.
Conclusion
1) The landslide-induced surge is one of the main causes for the overtopping of dams, and its risk is susceptible to many factors, such as the spatial variability of material properties, speed of landslides, etc. To reasonably evaluate dam overtopping risk caused by landslide-induced surges is of great importance to ensure the long-term safe operation of dams.
2) A method to simulate spatial variability in the soil parameters of bank slopes was established based on the random field theory. A composite response surface equation of stability failure considering the spatial variability of parameters is proposed instead of the traditional performance functions which fail to describe the spatial variability of elements when the parameters field is discretized.
3) Based on the Pan method, the overtopping risk caused by landslide-induced surges is determined, and a novel risk analysis method for overtopping failures caused by waves triggered by landslides is proposed.
4) The application results of the PB Earth rock-fill dam show that the spatial variability of parameters has a great influence on the instability failure risk of slopes. Ignoring the spatial variability of parameters will overestimate the risk of slope instability and dam overtopping caused by the landslide-induced surges. The proposed method provides technical support for the safety evaluation and risk control of reservoir dams.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
KD: Methodology, Conceptualization, Writing—Original Draft, and Validation. ZL: Software and Data curation. XL and CC: Supervision, Revision, Review and Editing, and Validation. JS and JC: Supervision and Editing. ZW: Visualization and Funding acquisition.
Funding
This research was substantially supported by the National Key R&D Program of China (2019YFC1510705), the National Natural Science Foundation of China (Grant No. 51909181), and the Fundamental Research Funds for the Central Universities.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Box, G. E. P., and Muller, M. E. (1958). A Note on the Generation of Random normal Deviates. Ann. Math. Statist. 29 (2), 610–611. doi:10.1214/aoms/1177706645
Cho, S. E. (2010). Probabilistic Assessment of Slope Stability that Considers the Spatial Variability of Soil Properties. J. Geotech. Geoenviron. Eng. 136 (7), 975–984. doi:10.1061/(asce)gt.1943-5606.0000309
Cui, P., and Zhu, X. (2011). Surge Generation in Reservoirs by Landslides Triggered by the Wenchuan Earthquake. J. Earthquake Tsunami 05 (5), 461–474. doi:10.1142/s1793431111001194
El-Ramly, H., Morgenstern, N. R., and Cruden, D. M. (2011). Probabilistic Stability Analysis of a Tailings Dyke on Presheared clay-shale. Can. Geotechnical J. 40 (1), 192–208. doi:10.1139/t02-095
Feng, G., Lei, S., Guo, Y., Shi, D., and Shen, J. B. (2020). Optimisation of Air-Distributor Channel Structural Parameters Based on Taguchi Orthogonal Design. Case Stud. Therm. Eng. 21, 100685. doi:10.1016/j.csite.2020.100685
Guo, Q., Pei, L., Zhou, Z., Chen, J., and Yao, F. (2016). Response Surface and Genetic Method of Deformation Back Analysis for High Core Rockfill Dams. Comput. Geotechnics 74, 132–140. doi:10.1016/j.compgeo.2016.01.001
Huang, J. L., Zhang, T., and Li, J. L. (2014). Comparative Analysis of Empirical Estimate Methods of Reservoir Bank Landslide Surge. Rock Soil Mech. 35 (S1), 133–140. [in Chinese].
Hungr, O., and McDougall, S. (2009). Two Numerical Models for Landslide Dynamic Analysis. Comput. Geosciences 35 (5), 978–992. doi:10.1016/j.cageo.2007.12.003
Jiang, S.-H., Huang, J., Huang, F., Yang, J., Yao, C., and Zhou, C.-B. (2018a). Modelling of Spatial Variability of Soil Undrained Shear Strength by Conditional Random fields for Slope Reliability Analysis. Appl. Math. Model. 63, 374–389. doi:10.1016/j.apm.2018.06.030
Jiang, S. H., Yang, J. H., Yao, C., and Huang, J. S. (2018b). Quantitative Risk Assessment of Slope Failure Considering Spatial Variability of Soil Properties. Eng. Mech. 35 (1), 136–147. [in Chinese].
Li, D.-Q., Zheng, D., Cao, Z.-J., Tang, X.-S., and Qi, X.-H. (2019). Two-stage Dimension Reduction Method for Meta-Model Based Slope Reliability Analysis in Spatially Variable Soils. Struct. Saf. 81, 101872. doi:10.1016/j.strusafe.2019.101872
Li, K. S., and Lumb, P. (1987). Probabilistic Design of Slopes. Can. Geotech. J. 24 (4), 520–535. doi:10.1139/t87-068
Li, Z., Wu, Z., Chen, J., Lu, X., Pei, L., and Chen, C. (2021). Effect of Correlated Random fields on Nonlinear Dynamic Responses of Gravity Dam. Nat. Hazards 106 (1), 79–96. doi:10.1007/s11069-020-04451-5
Lin, P., Liu, X., and Zhang, J. (2015). The Simulation of a Landslide-Induced Surge Wave and its Overtopping of a Dam Using a Coupled ISPH Model. Eng. Appl. Comput. Fluid Mech. 9 (1), 432–444. doi:10.1080/19942060.2015.1048620
Liu, F. (2020). Stability Analysis of Geotechnical Slope Based on Strength Reduction Method. Geotech Geol. Eng. 38, 3653–3665. doi:10.1007/s10706-020-01243-3
Liu, J., Zhou, C., Guo, J., and Liu, J. (2020). Experimental Study of Landslide Surge Wave Overtopping an Earth Dam. Arab J. Sci. Eng. 46, 563–571. doi:10.1007/s13369-020-04933-5
Liu, L. J., and Wu, Z. Y. (2020). Overtopping Risk Analysis of Earth Dams Considering Effects of Failure Duration of Release Structures. Complexity 2020, 3528350. doi:10.1155/2020/3528350
Liu, S. Y., Shao, L. T., and Li, H. J. (2015). Slope Stability Analysis Using the Limit Equilibrium Method and Two Finite Element Methods. Comput. Geotechnics 63, 291–298. doi:10.1016/j.compgeo.2014.10.008
Lu, X., Pei, L., Chen, J. K., Wu, Z. Y., and Li, Z. F. (2020). Comparison of Homogenous and Random fields of Tensile Strength Effects on the Nonlinear Dynamical Response of Guandi concrete Gravity Dams under strong Earthquake Waves. Struct. Infrastructure Eng. [online]. doi:10.1080/15732479.2020.1832534
Ma, B., Zhang, T., and Li, H. W. (2016). Impacts of Landslide-Generated Waves of Yalong River basin on Reservoir Area. Hydro-Science Eng. 5, 47–53. [in Chinese].
Ma, Y. C., Su, P. D., and Li, Y. G. (2020). Three-dimensional Nonhomogeneous Slope Failure Analysis by the Strength Reduction Method and the Local Strength Reduction Method. Arabian J. Geosciences 13, 21. doi:10.1007/s12517-019-5000-1
Montoya-Noguera, S., Zhao, T., Hu, Y., Wang, Y., and Phoon, K.-K. (2019). Simulation of Non-stationary Non-gaussian Random fields from Sparse Measurements Using Bayesian Compressive Sampling and Karhunen-Loève Expansion. Struct. Saf. 79, 66–79. doi:10.1016/j.strusafe.2019.03.006
Noda, E. (1970). Water Waves Generated by Landslides. J. Wtrwy., Harb. Coast. Engrg. Div. 96 (4), 835–855. doi:10.1061/awhcar.0000045
Pan, J. (1980). Analysis of Stability against Sliding of Buildings and Landslides. Beijing, China: China Water Conservancy Press, 133–154. (in Chinese).
Peng, X., Yu, P., Chen, G., Xia, M., and Zhang, Y. (2020a). Development of a Coupled DDA-SPH Method and its Application to Dynamic Simulation of Landslides Involving Solid-Fluid Interaction. Rock Mech. Rock Eng. 53, 113–131. doi:10.1007/s00603-019-01900-x
Peng, X., Yu, P., Chen, G., Xia, M., and Zhang, Y. (2020b). CPU-accelerated Explicit Discontinuous Deformation Analysis and its Application to Landslide Analysis. Appl. Math. Model. 77 (1), 216–234. doi:10.1016/j.apm.2019.07.028
Powerchina Chengdu Engineering Corporation Limited (PCECL) (2009). Review Report on Stability Study of Tensile Deformation Body on Right Bank of Reservoir Head of PB Hydropower Station on Dadu River in Sichuan Province. Chengdu: PCECL, Sichuan. (in Chinese).
Qi, X.-H., and Li, D.-Q. (2018). Effect of Spatial Variability of Shear Strength Parameters on Critical Slip Surfaces of Slopes. Eng. Geology. 239, 41–49. doi:10.1016/j.enggeo.2018.03.007
Sun, Y., Chang, H., Miao, Z., and Zhong, D. (2012). Solution Method of Overtopping Risk Model for Earth Dams. Saf. Sci. 50 (9), 1906–1912. doi:10.1016/j.ssci.2012.05.006
Tessema, N. N., Sigtryggsdóttir, F. G., Lia, L., and Kemal Jabir, A. (2019). Case Study of Dam Overtopping from Waves Generated by Landslides Impinging Perpendicular to a Reservoir's Longitudinal Axis. Jmse 7 (7), 221. doi:10.3390/jmse7070221
Wang, M. L., Yang, S. F., Zhang, J., and Li, X. L. (2020). Risk Assessment of Landslide-Induced Surge Disaster of River Type Reservoir in Mountainous Area. Syst. Sci. Control. Eng. 8 (1), 454–461. doi:10.1080/21642583.2020.1788469
Ward, S. N., and Day, S. (2011). The 1963 Landslide and Flood at Vaiont Reservoir Italy. A Tsunami ball Simulation. Ital. J. Geosciences 130 (1), 16–26. doi:10.3301/IJG.2010.21
Xiao, H., and Lin, P. Z. (2016). Numerical Modeling and Experimentation of the Dam-Overtopping Process of Landslide-Generated Waves in an Idealized Mountainous Reservoir. J. Hydraulic Eng. 142 (12), 04016059. doi:10.1061/(asce)hy.1943-7900.0001203
Yu, P., Chen, G., Peng, X., Zhang, Y., Zhang, H., and Wang, W. (2021). Verification and Application of 2-D DDA-SPH Method in Solving Fluid-Structure Interaction Problems. J. Fluids Structures 102, 103252. doi:10.1016/j.jfluidstructs.2021.103252
Zhang, L. M., Peng, M., Chang, D. S., and Xu, Y. (2016). Dam Failure Mechanisms and Risk Assessment. Singapore: John Wiley & Sons Singapore Pte. Ltd. doi:10.1002/9781118558522
Zhang, S., and Tan, Y. (2014). Risk Assessment of Earth Dam Overtopping and its Application Research. Nat. Hazards 74, 717–736. doi:10.1007/s11069-014-1207-3
Zhang, W. G., Wang, Q., Liu, H. L., and Chen, F. Y. (2021). Influence of Rock Mass Spatial Variability on the Probability of Tunnel Roof Wedge Failure. Rock Soil Mech. 42 (05), 1462–1472. [in Chinese].
Zhang, Y., Wang, J., Zhao, J. X., Chen, G., Yu, P., and Yang, T. (2019). Multi-spring Edge-To-Edge Contact Model for Discontinuous Deformation Analysis and its Application to the Tensile Failure Behavior of Rock Joints. Rock Mech. Rock Eng. 53, 1243–1257. doi:10.1007/s00603-019-01973-8
Keywords: near-dam reservoir bank slope, spatial variability, surge, risk analysis, dam overtopping
Citation: Dong K, Li Z, Lu X, Chen C, Sheng J, Chen J and Wu Z (2021) Analysis of Dam Overtopping Failure Risks Caused by Landslide-Induced Surges Considering Spatial Variability of Material Parameters. Front. Earth Sci. 9:675900. doi: 10.3389/feart.2021.675900
Received: 04 March 2021; Accepted: 28 June 2021;
Published: 09 July 2021.
Edited by:
Tao Zhao, Brunel University London, United KingdomReviewed by:
Joern Lauterjung, German Research Centre for Geosciences, GermanyYingbin Zhang, Southwest Jiaotong University, China
Copyright © 2021 Dong, Li, Lu, Chen, Sheng, Chen and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chen Chen, bGF1cmFjaGVuQHNjdS5lZHUuY24=
 Kai Dong
Kai Dong Zefa Li1,2
Zefa Li1,2 Chen Chen
Chen Chen