Non-Arrhenian Temperature-Dependent Viscosity of Alkali(ne) Carbonate Melts at Mantle Pressures

The viscosity of carbonate melts is a fundamental parameter to constrain their migration and ascent rates through the mantle and ultimately, their role as carbon conveyors within the deep carbon cycle. Yet, data on the viscosity of carbonate melts have remained scarce due to experimental limitations and the lack of appropriate theoretical descriptions for molten carbonates. Here, we report the viscosity of K₂Mg(CO₃)₂ and K₂Ca(CO₃)₂ melts up to 13 GPa and 2,000 K by means of classical molecular dynamics (MD) simulations using optimized force fields and provide first evidence for non-Arrhenian temperature-dependent viscosity of molten carbonates at mantle pressures. The viscosity of K₂Mg(CO₃)₂ and K₂Ca(CO₃)₂ melts ranges respectively between 0.0056–0.0875 Pa s and 0.0046–0.0650 Pa s in the investigated pressure-temperature interval. Alkali(ne) carbonate melts, i.e. mixed alkali and alkaline earth carbonate melts -K₂Mg(CO₃)₂ and K₂Ca(CO₃)₂− display higher viscosity than alkaline earth carbonate melts -CaCO₃ and MgCO₃− at similar conditions, possibly reflecting the change in charge distribution upon addition of potassium. The non-Arrhenian temperature-dependence of the viscosity is accurately described by the Vogel-Fulcher-Tammann model with activation energies E_a for viscous flow that decrease with temperature at all investigated pressures, e.g. from ∼100 kJ/mol to ∼30 kJ/mol between 1,300 and 2,000 K at 3 GPa. Pressure is found to have a much more moderate effect on the viscosity of alkali(ne) carbonate melts, with activation volumes V_a that decrease from 4.5 to 1.9 cm³/mol between 1,300 and 2,000 K. The non-Arrhenian temperature-viscosity relationship reported here could be exhibited by other carbonate melt compositions as observed for a broad range of silicate melt compositions and it should be thus considered when modeling the mobility of carbonate melts in the upper mantle.

Introduction

Despite the rare occurrence of carbonate-rich volcanism in the present-day Earth (Woolley and Kjarsgaard, 2008; Jones et al., 2013), carbonate melts produced by incipient melting of carbonated lithologies play a critical role in subsurface magmatic processes and they are major phases for the storage and transport of carbon in the upper mantle (Dasgupta and Hirschmann, 2010; Dasgupta, 2013; Stagno, 2019). The percolation of carbonate-rich melts through the mantle, even at melt fractions as low as < 0.1 vol% (Gaillard et al., 2008; Massuyeau et al., 2021), has a large impact on the geochemical and geodynamic evolution of the Earth’s interior. Because of their excellent wetting properties, low density and low viscosity (e.g. Minarik and Watson, 1995; Dobson et al., 1996; Hammouda and Laporte, 2000; Kono et al., 2014; Ritter et al., 2020), carbonate melts are regarded as efficient metasomatic agents involved in the redistribution of incompatible trace elements and volatiles in the mantle (Green and Wallace, 1988; Yaxley et al., 1991; Rudnick et al., 1993; Dixon et al., 2008; Kiseeva et al., 2012; Poli, 2015; Keller et al., 2017), as well as in the generation of diamond-forming kimberlitic magmatism (Dalton and Presnall, 1998; Korsakov and Hermann, 2006; Russell et al., 2012; Sparks, 2013; Sun and Dasgupta, 2019). Besides, carbonate-rich melts are often proposed as an explanation for the low velocity zones (Dasgupta and Hirschmann, 2010; Fischer et al., 2010; Gardés et al., 2020) and electrical anomalies (Gaillard et al., 2008; Naif et al., 2013; Sifré et al., 2014; Massuyeau et al., 2021) observed at the Lithosphere-Asthenosphere-Boundary (LAB) beneath oceanic ridges and continents.

Although the chemistry and reactivity of carbonate-rich melts has been extensively investigated over the past decades (e.g., Wallace and Green, 1988; Veksler et al., 1998; Yaxley and Brey, 2004; Gudfinnsson and Presnall, 2005; Hammouda and Keshav, 2015 and references therein; Gervasoni et al., 2017), their physical properties (e.g. density and viscosity) remain poorly constrained to date despite their control on melt mobility through the mantle (Table 1). Particularly, the viscosity of melts governs the migration rates and the efficiency of melt transport across the mantle, hence affecting the carbon fluxes at depth and towards the surface (Keller et al., 2017). Data scarcity for mantle carbonate melts at relevant pressure-temperature conditions reflects the experimental challenges associated with direct viscosity measurements due to their high reactivity (Treiman and Schedl, 1983; Treiman, 1995), and the limitations of theoretical formalisms to predict the properties of complex chemical systems (Vuilleumier et al., 2014; Wilding et al., 2016; Wilson et al., 2018; Desmaele et al., 2019a, 2019b; Hurt and Wolf, 2019). Experimental studies of carbonate melt viscosity have thus been performed mostly at room pressure for endmember alkali (Li, K, Na) carbonate melts as well as their binary mixtures (e.g., Janz, 1988; Sato et al., 1999; Di Genova et al., 2016), with only three studies reporting carbonate melt viscosities at high pressure to date (Dobson et al., 1996; Kono et al., 2014; Stagno et al., 2018). Pioneering measurements by Dobson et al. (1996) using the falling sphere technique coupled with synchrotron X-ray imaging determined the viscosity of K₂Mg(CO₃)₂ and K₂Ca(CO₃)₂ melts up to 5.5 GPa. Reported viscosities for those compositions are however ca. one order of magnitude larger than more recent results for CaCO₃, CaMg(CO₃)₂ and Na₂CO₃ melts obtained by using an ultrafast X-ray imaging technique with improved accuracy on the viscosity determination (Kono et al., 2014; Stagno et al., 2018). Interestingly, these later studies report comparable viscosities for all investigated compositions and negligible pressure effects on the viscosity that are difficult to reconcile with computational studies (Desmaele et al., 2019a; 2019b). The scarcity of currently available data thus precludes the identification of pressure, temperature and compositional effects on the viscosity of carbonate melts and hence, the quantitative modelling of melt migration processes (Table 1).

TABLE 1

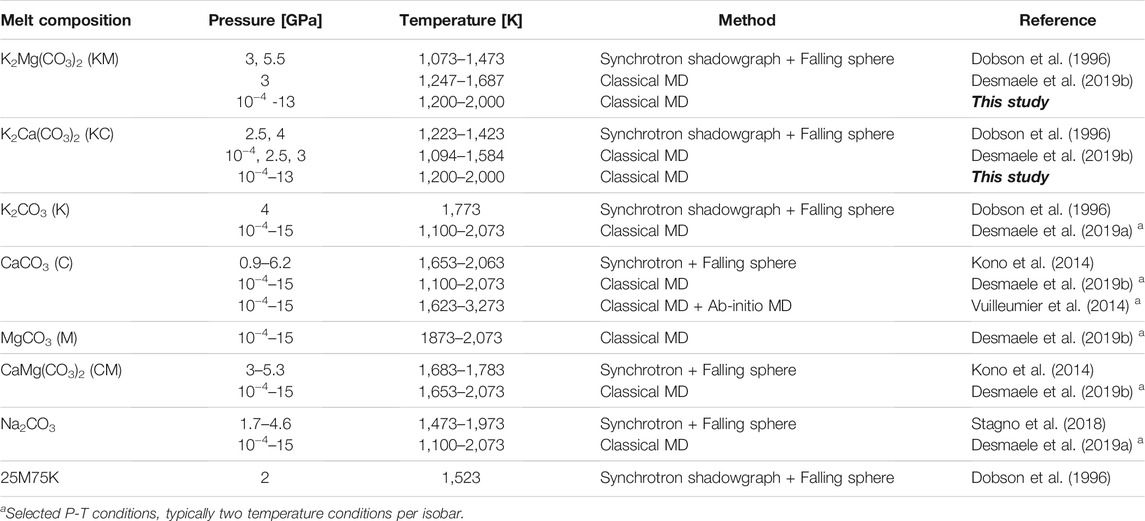
TABLE 1. Compilation of available high pressure viscosity data for alkali(ne) carbonate melts from experiments and classical/ab-initio MD simulations.

In the past decades, computational methods have emerged as a powerful tool to probe the chemical structure and physical properties, including the viscosity, of molten systems at high pressure-temperature conditions difficult to access experimentally (e.g. Kubicki and Lasaga, 1988; Rustad et al., 1990; Tissen et al., 1994; Genge et al., 1995; Guillot and Sator, 2007a, 2007b, 2011; Vuilleumier et al., 2014; Corradini et al., 2016; Wilding et al., 2016, 2019; Li et al., 2017; Dufils et al., 2017, 2018; Wilson et al., 2018; Desmaele et al., 2019b, 2019a; Hurt and Wolf, 2019). Molecular dynamics (MD) simulations based on ab initio and/or classical approaches have thus significantly contributed to expand the available viscosity datasets for carbonate melts at relevant pressure-temperature conditions (Table 1). Nevertheless, the theoretical studies remain largely limited to simple endmember compositions due to the high computational cost of the ab initio calculations and the lack of appropriate force-fields to describe the atomic/ionic interactions in classical simulations of complex multicomponent carbonate melts (Genge et al., 1995; Vuilleumier et al., 2014; Li et al., 2017; Desmaele et al., 2019a, 2019b; Hurt and Wolf, 2019). Recently, Desmaele et al., (2019a) developed optimized classical force-fields for molten carbonates in the system Li₂CO₃-Na₂CO₃-K₂CO₃-MgCO₃-CaCO₃ based on experimental data and melt structures issued from ab initio simulations of molten CaCO₃ (Vuilleumier et al., 2014), MgCO₃, CaMg(CO₃)₂ (Desmaele et al., 2019b), Na₂CO₃ and K₂CO₃ (Desmaele et al., 2019a). These force-fields accurately reproduce experimental data on the density (e.g. Liu and Lange, 2003; O’Leary et al., 2015), viscosity (e.g. Janz, 1988; Kono et al., 2014) and electrical conductivity (e.g. Gaillard et al., 2008; Kojima, 2009; Sifré et al., 2014) of simple and binary carbonate melts. These results open the possibility for studies of the viscosity of complex carbonate melts at pressure and temperature conditions previously unexplored (Table 1).

Here, classical molecular dynamics simulations using the optimized force-fields developed by Desmaele et al. (2019a) have been conducted to determine the viscosity of alkali(ne) melts, i.e. mixed alkali and alkaline-earth carbonate melts - K₂Mg(CO₃)₂ and K₂Ca(CO₃)₂ - up to 13 GPa between 1,000 and 2,000 K. These compositions mimic incipient melts of subducted continental potassium rich lithologies at high pressure (8–13 GPa; Grassi and Schmidt, 2011b, 2011a; Kiseeva et al., 2013) and allow a direct comparison of the results with previous high pressure experimental studies (Dobson et al., 1996). The results constrain pressure and temperature effects on the viscosity of alkali(ne) carbonate melts and reveal non-Arrhenian temperature-viscosity relations that could not be anticipated from the data available to date.

Materials and Methods

A total of 106 classical MD simulations were performed to determine the viscosity of K₂Mg(CO₃)₂ and K₂Ca(CO₃)₂ (hereafter referred to as KM and KC, respectively) melts from room pressure to 13 GPa and 1,000–2,000 K, with 1–3 GPa and 100 K increments. The MD simulations were conducted with the DL_POLY 2.0 code (Smith and Forester, 1996) in the microcanonical (NVE) ensemble, where the number of atoms (N), the volume (V) and the total energy (E) are fixed. The pressure (P) and temperature (T) conditions at equilibrium were determined in isothermal-isobaric (NPT ensemble) runs using a Nosé-Hoover thermostat. The thermodynamic parameters, P, T and E_Pot, are calculated from block averages of 500 k time steps after the system has reached equilibrium (Figure 1). The system was composed of N = 2002 atoms in a cubic box with periodic boundary conditions in 3D (Figure 1) as described in Desmaele et al. (2019b). The interionic interactions were described using empirical force fields recently developed for alkali and alkaline carbonate melts that take into account both the long-range Coulomb interactions and the short-range repulsion-dispersion interactions (Desmaele et al., 2019a). The force field is decomposed as a sum of pair potentials for the intramolecular (i.e. interactions within a carbonate CO₃²⁻ molecule) and intermolecular (i.e. between all ions) contributions, where the carbonate ion is featured as flexible and nondissociative (for further details see Desmaele et al., 2019a; 2019b). The interaction parameters employed in the simulations are those reported in Desmaele et al. (2019a, 2019b). The equations of motion for atoms were solved using the Verlet algorithm with a time step of 1 fs (10⁻¹⁵ s) and simulation runs lasted for 10⁷ steps (i.e. 10–20 ns). The run duration is thus sufficiently long compared to the characteristic time scale for viscous relaxation τ in carbonate melts, i.e. few ps to tens of ps as given by the Maxwell relation τ = η/G_∞, where the shear modulus at infinite high frequencies G_∞ is ∼10¹⁰ Pa (Dingwell and Webb, 1999) to achieve convergence of the simulations even at the lowest temperatures investigated here (Desmaele et al., 2019b). The convergence is confirmed by the attainment of a viscosity plateau region in the time-dependence of the simulated viscosity at all P-T conditions and thus ensures the robustness of the reported viscosity data (Figure 1D and Supplementary Figure S1).

FIGURE 1

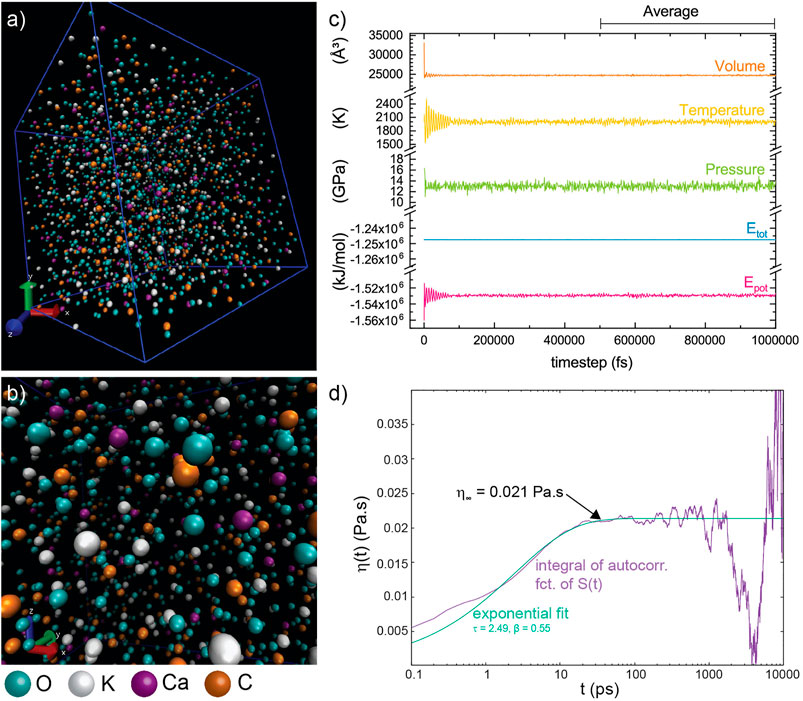
FIGURE 1. Classical MD simulation run in K₂Ca (CO₃)₂ melt (KC) at 13 GPa and 2,000 K. (A)–(B) Snapshots of the simulation box containing N = 2002 atoms. (C) Output of a classical MD simulation from the isothermal-isobaric (NPT) ensemble where the thermodynamic parameters (P, T, V) are calculated from block averages of 500 k time steps, after the system has reached equilibrium. All given uncertainties are the result from statistical fluctuations, i.e. standard deviation from the average. (D) Integral of the auto-correlation function of the stress tensor S(t) for K₂Ca(CO₃)₂ melt at 3.9 GPa and 1,472 K derived from the MD simulation run in the NVE ensemble (purple line), and corresponding fit (green line) to an exponential function [Eq.4] to determine the viscosity.

The shear viscosity of carbonate melts was then calculated by intergrating the auto-correlation function of the off-diagonal elements of the stress tensor S(t) using the Green-Kubo equation (Boon and Yip, 1980; Hess, 2002; Vuilleumier et al., 2014):

$\mathrm{\eta }=\frac{1}{{\mathrm{k}}_{\mathrm{B}}\mathrm{TV}}\underset{0}{\overset{\infty }{{\displaystyle \int }}}\mathrm{S}\left(\mathrm{t}\right)\mathrm{dt}(1)$

where k_B is the Boltzmann’s constant and S(t) is described as:

$\mathrm{S}\left(\mathrm{t}\right)={\displaystyle \sum }_{\mathrm{\alpha }\ne \mathrm{\beta }}<{\mathrm{P}}_{\mathrm{\alpha \beta }}\left(\mathrm{t}\right)\cdot {\mathrm{P}}_{\mathrm{\alpha \beta }}\left(0\right)>\left(\mathrm{\alpha },\mathrm{\beta }=\mathrm{x},\mathrm{y},\mathrm{z}\right)(2)$

${\mathrm{P}}_{\mathrm{\alpha \beta }}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{m}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}}^{\mathrm{\alpha }}{\mathrm{v}}_{\mathrm{i}}^{\mathrm{\beta }}+{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}{\displaystyle \sum }_{\mathrm{j}>\mathrm{i}}^{\mathrm{N}}{\mathrm{F}}_{\mathrm{ij}}^{\mathrm{\alpha }}{\mathrm{r}}_{\mathrm{ij}}^{\mathrm{\beta }}(3)$

where m_i is the mass of the ion i, $v_i^{\alpha }$ is the component α of its velocity, $r_{ij}^{\beta }$ and $v_i^{\beta }$ are the component β of the distance between ions i and j, and the velocity of the atom i, respectively, and $F_{ij}^{\alpha }$ is the component α of the force acting between ions i and j. The brackets refer to an average over the trajectories of all the ions in the simulation cell. Subsequently, the viscosity is derived by fitting the integral of the auto-correlation function of the stress tensor by an exponential function (Figure 1D):

$\eta \left(t\right)= {\eta }_{\infty }\left(1-e^{{\left(-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.\right)}^{\beta }}\right)(4)$

where ${\eta }_{\infty }$ is the desired viscosity, τ is the viscous relaxation time, and β is the stretching factor, which ranges between 0 (ultra-low viscosity melts) and 1 (highly viscous melts). A least-square minimization fit is performed in the short time shift region, where the statistics on the integrated auto-correlation function of S(t) is excellent (e.g. < 100 ps in Figure 1D), to retrieve the viscosity plateau independently of the fluctuations at long time shifts that could bias the results (Supplementary Figure.S1).

The accuracy of the auto-correlation function strongly depends on the number of time steps. Therefore, simulation runs were extended to 20 ns to keep the statistical uncertainties on the viscosity data around ±15% up to 1,700–1,800 K as estimated from the quality of the fit to the integrated auto-correlation function of the stress tensor S(t) (Figure 1D). Uncertainties further increase with temperature due to the larger fluctuations in temperature (and pressure), particularly during large simulation runs (Zhang et al., 2015), which hamper the unambiguous identification of the plateau region of the Green-Kubo integral to extract the viscosity (Figure 1D). We conservatively estimate that total uncertainties can reach ca. ± 40% at 2,000 K, the highest temperature of this study, although the overall precision is much better and typically yields viscosities within 10–15%. Statistical fluctuations on pressure and temperature were typically ΔP = ± 0.5 GPa and ΔT/T = ± 1%, respectively.

The stability of the melt phase at all investigate pressure-temperature conditions was verified by monitoring the atomic diffusion coefficients that, even at the highest pressures, display characteristic values for molten systems with e.g. $D_{C{O}_3^{2-}}$ ∼ 1 × 10⁻⁹ to 7 × 10⁻⁹ m²/s (Desmaele et al., 2019a). Furthermore, the investigated conditions up to 6 GPa fall above the experimental liquidus reported for the K₂CO₃-MgCO₃ and K₂CO₃-CaCO₃ systems (Ragone et al., 1966; Cooper et al., 1975; Shatskiy et al., 2015).

Results

The simulation conditions and the viscosity results are summarized in Table 2. The viscosity of KM and KC melts ranges respectively between 0.0056–0.0875 Pa s and 0.0046–0.0650 Pa s in the investigated pressure-temperature intervals. Figures 2, 3 display the temperature and pressure dependence of the viscosity of KM and KC melts at the investigated conditions. The viscosity of both melts follows a similar trend: it decreases with increasing temperature at constant pressure and increases linearly upon compression along an isotherm. Temperature appears as the primary control parameter on the viscosity of alkali(ne) carbonate melts whereas the effect of pressure is generally lower, although it is enhanced as temperature decreases (Figure 3). An interesting observation from the present results is that the viscosity of KM and KC melts only decreases linearly with temperature over a narrow (high) temperature interval (i.e. Arrhenian behavior), while a notable curvature in the logη vs 1/T data is apparent over the investigated temperature range at different pressures (Figure 3), thus indicating non-Arrhenian (i.e. fragile behavior, Angell, 1995) behavior. Yet, this behavior apperars to become less pronounces as pressure increases, even though the temperature span of the data is more limited above 9 GPa (Figure 3). The non-Arrhenian evolution of the viscosity implies a temperature-dependent activation energy E_a of viscous flow (Figure 4) that may reflect changes in atomic/molecular-scale interactions and configuration in the melt (e.g. clustering) with temperature as discussed below (Glasstone et al., 1941). To the best of our knowledge, this is the first observation of non-Arrhenian temperature-dependent viscosity in carbonate melts at high pressure, a feature that could not be anticipated from the limited P-T range covered by previous studies (Table 1).

TABLE 2

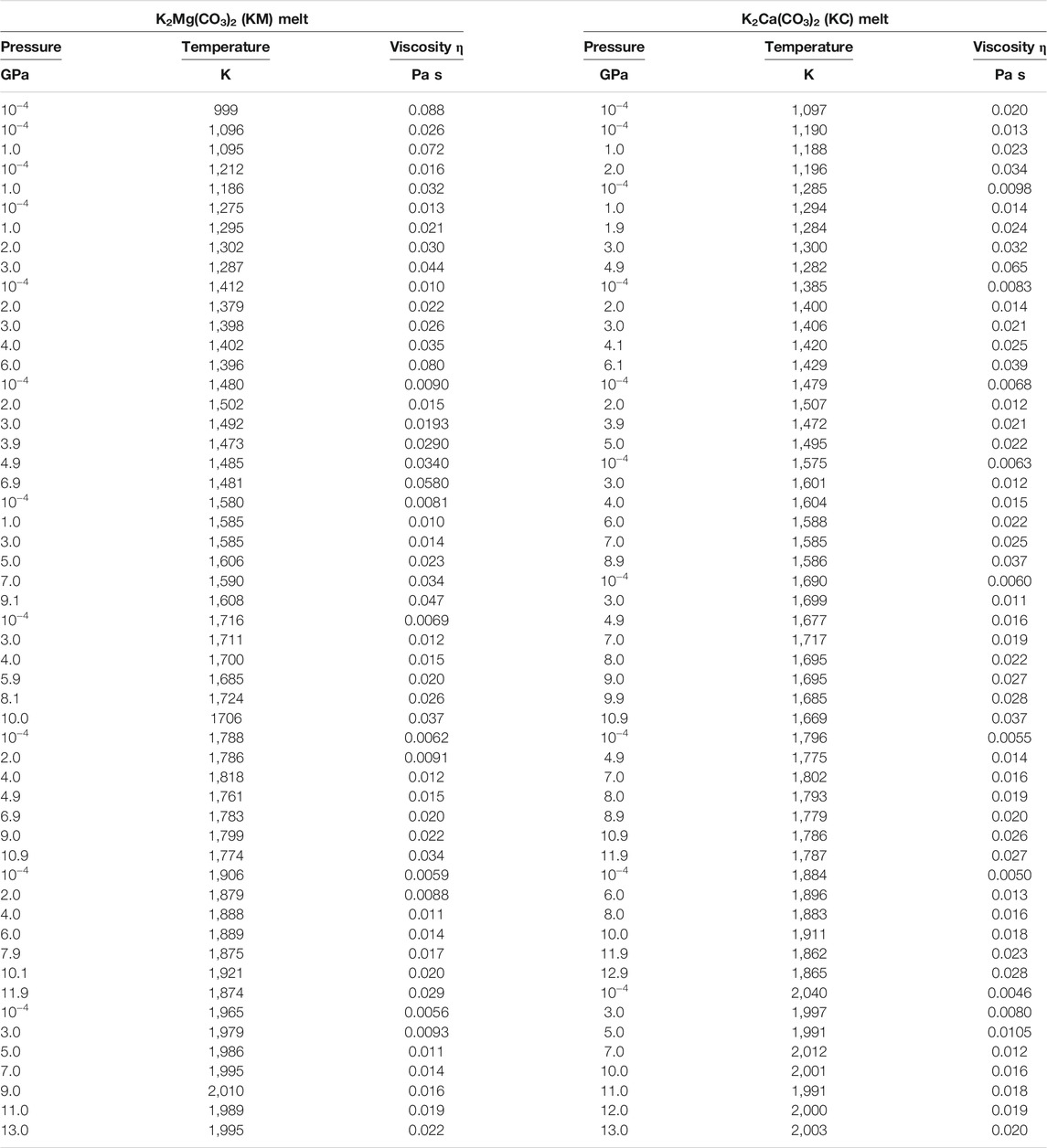
TABLE 2. Viscosities of K₂Mg(CO₃)₂ and K₂Ca(CO₃)₂ melts computed in the NVE ensemble as a function of pressure and temperature conditions. Uncertainty for pressure and temperature are ±0.5 GPa and 1%, repectively. Uncertainties in viscosity are typically ±15% up to 1,800 K and ca. ±40% at higher temperatures.

FIGURE 2

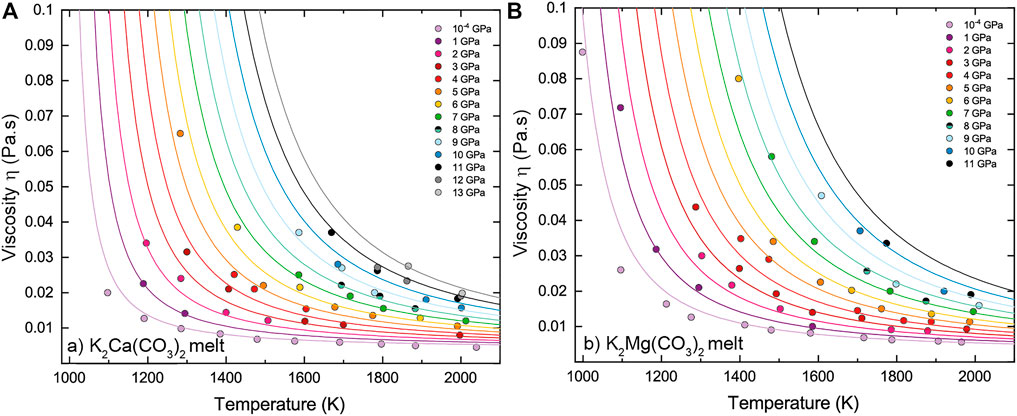
FIGURE 2. Effect of temperature on the viscosity of (A) K₂Ca(CO₃)₂ (KC) and (B) K₂Mg(CO₃)₂ (KM) melts along isobars from ambient pressure to 13 GPa. Symbols are MD calculated viscosities and lines represent fits to the data by the Vogel-Fulcher-Tammann (VFT [Eq. 6]) model. Colors have the same meaning in both figures.

FIGURE 3

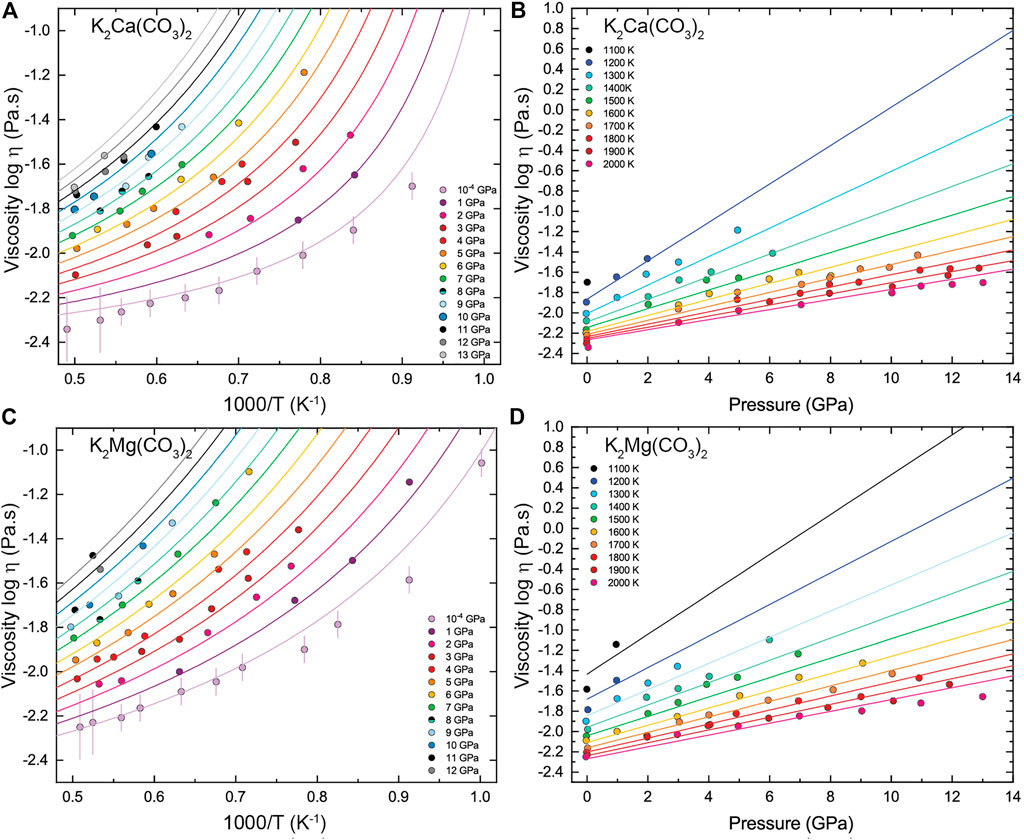
FIGURE 3. Temperature and pressure dependence of the viscosity of (A)–(C) K₂Ca(CO₃)₂ (KC) and (B)–(D) K₂Mg(CO₃)₂ (KM) melts. Symbols are MD calculated viscosities in this study. Solid lines represent fits to temperature- and pressure-dependence by the VFT model [Eq. 6]. Error bars in a) and b) correspond to ±15% up to 1,800 K (<0.55 K⁻¹) and ±40% at the higest temperatures. For the sake of clarity, error bars are only reported for the room pressure data but apply to all other isobars.

FIGURE 4

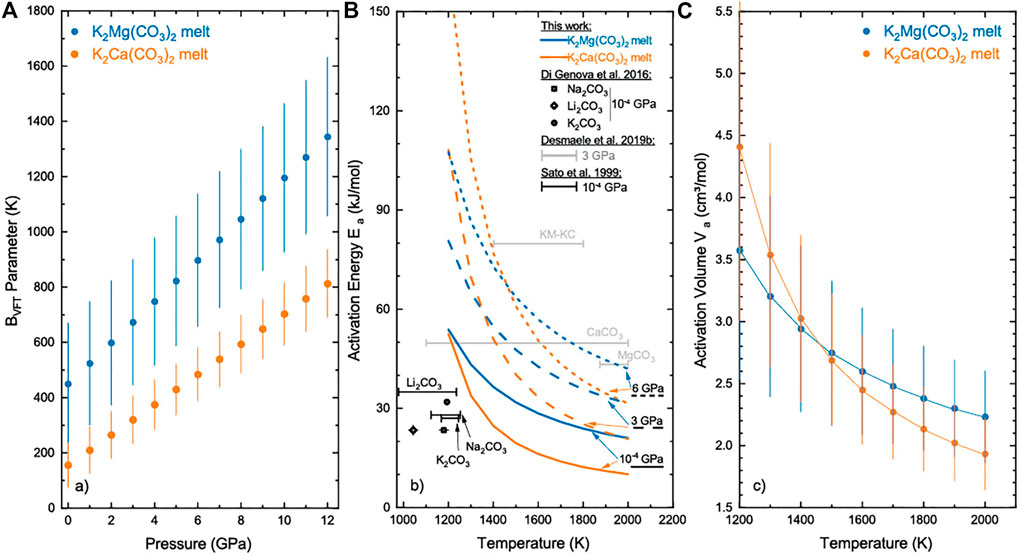
FIGURE 4. (A) Evolution with pressure of the best-fit B parameter in the VFT model for K₂Mg(CO₃)₂ (KM) and K₂Ca(CO₃)₂ (KC) melts; (B) Activation energy E_a for KM and KC melts as a function of temperature at selected pressures, 10⁻⁴, 3 and 6 GPa (this study) and comparison with literature data for alkali and alkaline earth carbonate melts. Symbols and black lines show respectively experimental data for alkali carbonate melts at ambient pressure by Di Genova et al. (2016) and Sato et al. (1999). Grey lines show the temperature-independent (Arrhenian) E_a at 3 GPa derived from classical MD simulations for CaCO₃, MgCO₃ and KM-KC melts by Desmaele et al. (2019b); (C) Temperature dependence of the activation volume V_a for KC and KM melts. The lines are guides for the eyes. Error bars were determined by propagation of undertainties [Eq.8] and correspond to ∼20% of the value.

Discussion

Effect of Temperature and Pressure on the Viscosity of Alkali(ne) Carbonate Melts

The viscosities of KM and KC melts reported here typically agree within errors with previous simulations by Desmaele et al. (2019b), with the exception of the highest temperature data where differences reach values of up to 40% (Figure 5). Differences may partially originate from larger uncertainties when fitting the auto-correleation functions to extract the viscosity due to larger fluctuations at high temperature (Figure 1D). In contrast, while the experimental data by Dobson et al. (1996) for KC melts are in strinkingly good aggrement with the MD results, those of KM melts are substantially lower than the theoretical predictions (Figure 5). Moreover, Dobson et al. (1996) reported negligible pressure effects on the viscosity of both compositions contrarily to the present results (Figure 3) and those of Desmaele et al. (2019b). The contrasting results for KM melt could be partially reconciled considering the large uncertainties (∼50%) estimated for the experimental results (Dobson et al., 1996), although possible experimental shortcoming cannot be excluded. We note for intance inconsistencies in the experimental viscosity dataset for high K-carbonate melts from the same study - KM and 25MgCO₃-75K₂CO₃ melts - (Figure 5) that could result from incomplete melting of the samples and/or convection in the high pressure cell as recognized by the authors (Dobson et al., 1996), as well as from limitations in the detection of the falling-sphere (Kono et al., 2014; Stagno et al., 2018) and/or possible sample decomposition/contamination. In particular, hydration of the highly hygroscopic KM samples and/or boron contamination from the assembly (Malfait et al., 2014) that would both decrease the viscosity of the melt cannot be ruled out because detailed analysis of the recovered samples are not reported by Dobson et al. (1996).

FIGURE 5

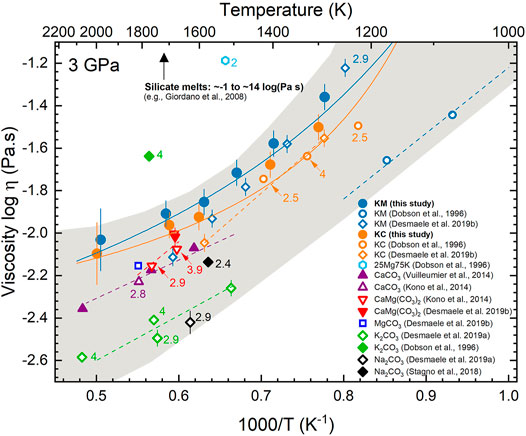
FIGURE 5. Effect of temperature on the viscosity of K₂Mg(CO₃)₂ (KM, blue) and K₂Ca(CO₃)₂ (KC, orange) melts from this MD study (full circles) and comparison with literature data for alkali and alkaline carbonate melts. All data are reported at 3 GPa unless indicated next to the symbols (in GPa). Solid lines represent fits to the temperature dependence of the viscosity data by the VFT model (present data) and dashed lines by an Arrhenian model (literature data). Errors bars on KM, KC and K₂CO₃ melts from Dobson et al. (1996) correspond to 50% (not shown for the sake of clarity). Viscosities of silicate melts are indicated for comparison (Giordano et al., 2008).

Further, we employ the data to implement a model for the pressure-temperature dependence of the viscosity of KM and KC melts at upper mantle conditions. Among the different equations commonly employed to describe the non-Arrhenian temperature dependence of the viscosity (e.g. Richet, 1984; Giordano and Dingwell, 2003; Russell et al., 2003), the Vogel-Fulcher-Tammann (VFT) equation (Vogel, 1921; Angell, 1995) was selected here owing to its ability to fit viscosity data over a wide range of temperature and to its empirical character:

$\log \mathit{\eta }={\mathit{A}}_{\mathit{VFT}}+\left(\frac{{\mathit{B}}_{\mathit{VFT}}}{\mathit{T}-{\mathit{T}}_{\mathit{VFT}}}\right)(5)$

where A_VFT is the pre-exponential factor and represents the viscosity at infinite temperature, i.e. the high temperature limit to viscosity, B_VFT is a fitting parameter (in K) related to the pseudo-activation energy for viscous flow, i.e. RB_VFT (in J/mol, with R the ideal gas contant, 8.314 J/mol.K), which represents the resistance to the structural rearrangement of the melt (Richet, 1984; Bottinga and Richet, 1995), and T_VFT is the temperature at which the viscosity becomes infinite (i.e. temperature of divergence).

The logη-(P,T) datasets for each melt composition (i.e. 53 viscosity data points each, Table 2) were thus fitted to the VFT equation including an expansion of the B_VFT term to parametrize the effects of pressure on melt viscosity as:

$\log \mathit{\eta }={\mathit{A}}_{\mathit{VFT}}+\left(\frac{{\mathit{B}}_1+{\mathit{B}}_2\mathit{P}}{\mathit{T}-{\mathit{T}}_{\mathit{VFT}}}\right)(6)$

where B₁ and B₂ are adjustable parameters and P is the pressure, in bar. The VFT coefficients were optimized by using a non-linear regression routine to minimize the differences between predicted viscosities, i.e. by [Eq. 6], and the original viscosity datasets (Table 2). Uncertainties associated with the fitting parameters were obtained by the bootstrap resampling method, where the original datasets were randomly resampled 100,000 + 1 times and the optimized VFT parameters processed to derive the 95% confidence intervals (Supplementary Note S1). The best-fit VFT parameters [Eq. 6] derived on the original datasets for each melt composition are reported in Table 3 along with their uncertainties. The VFT models reproduce the original databases (Table 2) with average residuals of ±0.05 and ±0.04 log units for KM and KC melts, respectively, and associated average relative errors of 3 and 2.2% and Root Mean Square Errors (RMSE) of 0.06 and 0.05, that support the goodness of the fits. Moreover, the random distribution of the residuals over the databases further indicates the lack of systematic errors with either pressure or temperature in the calibration (Supplementary Figure.S1). Attempts to fit the temperature-dependence of the KM and KC viscosity datasets by an Arrhenian model result in lower reproducibility of the datasets (Supplementary Figures S2−S4) as shown by the goodness of fit metrics (Supplementary Table S1). Additional details of the quantitative comparison between the VFT and Arrhenian fit models, which confirms the non-Arrhenian behaviour of alkali(ne) carbonate melts over the investigated P-T conditions, are provided in Supplementary Note 1.

TABLE 3

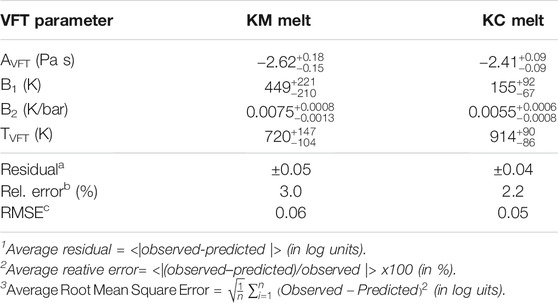
TABLE 3. Best-fit parameters for the Vogel-Fulcher-Tammann (VFT) model [Eq. 6] fitted to the pressure-temperature dependence of the viscosity of K₂Mg(CO₃)₂ (KM) and K₂Ca(CO₃)₂ (KC) melts.

The optimal value of A_VFT parameter for KM and KC melts in the preferred VFT model, $-{2.62}_{-0.15}^{+0.18}$ and $-{2.41}_{-0.09}^{+0.09}$ respectively, agree well within mutual uncertainties, and suggest a compositional independent infinite temperature viscosity for carbonate melts as observed for silicate melts (e.g. Giordano and Dingwell, 2003; Russell et al., 2003; Giordano et al., 2008). Nevertheless, additional viscosity data over a broader P-T-compositional range would be required to validate this observation. The linear increase of the B_VFT parameter with increasing pressure (Figure 4A), and hence of the pseudo-activation energy RB_VFT, suggests a progressive hindering of structural rearrangements in the melt at high pressure (Richet, 1984; Bottinga and Richet, 1995). At ambient pressure, the derived pseudo-activation energies for KM and KC melts, respectively ${\mathrm{3,740}}_{-1746}^{+1840}$ and ${\mathrm{1,290}}_{-557}^{+765}$ J/mol, are significantly lower than the range of values reported for silicate melts, 4,000–12,000 J/mol (Russell et al., 2003; Giordano et al., 2008; Li et al., 2021). The best-fit T_VFT values, ${720}_{-104}^{+147}$ and ${914}_{-86}^{+90}$ for KM and KC, respectively, fall below the corresponding liquidus temperatures at ambient pressure, 870–900 K for KM (Ragone et al., 1966) and ca. 1080 K for KC (Cooper et al., 1975).

The activation energy, E_a, which depends on both pressure and temperature, is further calculated from the slope of the curves in Figure 3, obtained by differentiating $\log \eta$ as provided by Eq. 6 with respect to 1/T following:

${\mathit{E}}_{\mathit{a}}=2.303\mathit{R}\frac{\partial \log \mathit{\eta }}{\partial \left(1/\mathit{T}\right)}=2.303\mathit{R}\left({\mathit{B}}_1+{\mathit{B}}_2.\mathit{P}\right){\left(\frac{\mathit{T}}{\left(\mathit{T}-{\mathit{T}}_{\mathit{VFT}}\right)}\right)}^2(7)$

where R is the gas constant, 8.314 J/mol.K, and the B₁, B₂ and T_VFT parameters for each melt composition are taken from Table 3. The activation energy E_a values for both KM and KC melts are reported in Figure 4 as a function of temperature at selected pressures, i.e. ambient, 3 and 6 GPa. The activation energy E_a decreases with temperature regardless of pressure and/or melt composition, in agreement with the decrease of the energy barrier for viscous flow at higher temperature (Bottinga and Richet, 1995). The effect of temperature on E_a is, however, more pronounced at higher pressures (Figure 4B). The ambient pressure activation energies derived here for KM and KC melts are higher than typical values for alkali carbonates melts, i.e. K₂CO₃, Na₂CO₃ and Li₂CO₃ (24–35 kJ/mol), as determined by experimental studies at 1,050–1,200 K (Sato et al., 1999; Di Genova et al., 2016) and classical MD simulations (Desmaele et al., 2019a) in the 1,100–1,900 K temperature range (Figure 4B). Our results at 3 GPa and low temperature compare well with the constant (i.e. Arrhenian) E_a of 80 kJ/mol reported for KM and KC melts at the same pressure in Desmaele et al. (2019b), although differences increase with temperature as the VFT model predicts a decrease of E_a down to ∼20–30 kJ/mol at 2,000 K. Moreover, the activation energies for KM and KC melts are generally larger than those calculated for the end-members CaCO₃ and MgCO₃ melts (43–49 kJ/mol) at similar P-T conditions (Desmaele et al., 2019b), consistent with the compositional effects discussed in detail below (Figure 5).

Pressure appears to have a non-negligible effect on the calculated viscosity of alkali(ne) carbonate melts (Figure 4) in contrast with the reports from experimental studies (Dobson et al., 1996; Kono et al., 2014; Stagno et al., 2018). We suggest that the large uncertainties in early viscosity measurements, 50% (Dobson et al., 1996), and the limited viscosity datasets reported in recent studies (Kono et al., 2014; Stagno et al., 2018), do not allow resolving pressure effects. Contrary to temperature, the pressure dependence of the viscosity is linear within the uncertainties (Figure 3). The activation volume of viscous flow, V_a, can be derived from the pressure effect on viscosity by differentiating Eq. 6 as:

${\mathit{V}}_{\mathit{a}}=2.303\mathit{RT}\frac{\partial \log \mathit{\eta }}{\partial \mathit{P}}=2.303\mathit{RT}\frac{{\mathit{B}}_2}{\left(\mathit{T}-{\mathit{T}}_{\mathit{VFT}}\right)}(8)$

where R is the gas constant, and the parameters T_VFT and B₂ are provided in Table 3 for each melt composition. The activation volumes V_a derived for both KM and KC melts are positive at all investigated temperatures, and range from 4.5–3.5 cm³/mol at 1,300 K to ∼2–1.9 cm³/mol at 2,000 K (Figure 4C). These V_a values are consistent with those reported in previous MD simulations for alkali and alkaline-earth carbonate melts, i.e. 2.2–4.7 cm³/mol (Desmaele et al., 2019a; 2019b). The results also compare well with the V_a values for CaCO₃-CaMg(CO₃)₂ melts retrieved using the experimental viscosity model of Kono et al. (2014) and Eq.8, i.e. 3.6 cm³/mol and 1.1 cm³/mol at 1,600 and 1,800 K, respectively. Conversely, Stagno et al. (2018) reported an activation volume from viscosity measurements on Na₂CO₃ melt, V_a = 54.52 cm³/mol, which is an order of magnitude larger than the results discussed above. We note however that this value does not represent the activation volume due to the non-Arrhenian fit model employed in the data analysis and therefore cannot be directly compared to the results obtained here. Additional inconsistencies in the Na₂CO₃ melt viscosity model, including for instance a temperature of divergence of the viscosity (i.e, T₀ in Stagno et al. (2018)) that is larger than the lowest temperature investigated and hence implies the divergence of the predicted viscosity on the calibration temperature interval, preclude the use of the fitting parameters to retrieve the V_a [Eq. 8] for comparison. These issues will be addressed in a Corrigendum that is currently in preparation (V. Stagno, pers. comm). The trend that emerges from the available data on the activation volume V_a of viscous flow of carbonate melts is that they are positive at mantle conditions and comparable with typical values reported for intermediate polymerized to depolymerized silicate melts, V_a ∼ 2–6 cm³/mol at 1,800–2,000 K (e.g. Liebske et al., 2005; Rai et al., 2019; Li et al., 2021).

Compositional Effects on the Viscosity of Alkali(ne) Carbonate Melts

The viscosities of KM and KC melts at 3 GPa and various temperatures are compared to available data at similar conditions for alkali and alkaline earth (and mixtures thereof) carbonate melts from experiments and MD simulations in Figure 5. Most carbonate melt viscosities reported to date fall between –2.6 and –1.2 on the logarithmic scale, which is generally several orders of magnitude lower compared to silicate melts (e.g. Giordano and Dingwell, 2003; Liebske et al., 2005; Giordano et al., 2008; Wang et al., 2014). The viscosities of K₂CO₃ melt at 4 GPa and 25MgCO₃-75K₂CO₃ melt at 2 GPa reported by Dobson et al. (1996) are significantly larger than those of the whole data sets and likely overestimated as discussed above.

Although specific compositional effects on the viscosity of carbonate melts are difficult to assess at this stage due to the limited datasets available and the inconsistencies between studies (Figure 5), some general trends can be identified. Molten CaCO₃, MgCO₃ and CaMg(CO₃)₂ show similar viscosities (Kono et al., 2014; Vuilleumier et al., 2014; Desmaele et al., 2019a, 2019b), which are larger than the viscosity of alkali carbonate melts, such as K₂CO₃ or Na₂CO₃, reported from MD studies by Desmaele et al. (2019a). Interestingly, the viscosity of KM and KC melts from this study and that of Desmaele et al., 2019b is larger than the viscosities of the corresponding alkali and alkaline earth end-members (Figure 5). Although this result may appear counter-intuitive, experimental studies show that the viscosity of binary ionic liquid mixtures can be higher or lower than the viscosity of the end-members, or close to their arithmetic mean (Fillon and Brennecke, 2017). The enhanced viscosity of KC and KM melts compared to the end-members likely results from the increase in Coulombic interactions between the metal cations (i.e. Ca, Mg, K) and/or carbonate groups upon mixing that will modify the charge distributions and enhance the dynamics in the system, hence increasing the viscosity (Wilson et al., 2018). Aditionally, we note that the experimental viscosities of Na₂CO₃ melt (Stagno et al., 2018) are substantially larger than the results from MD simulations (Desmaele et al., 2019a) but comparable to those of calcitic, magnesitic and dolomitic melts at similar pressures (Kono et al., 2014; Vuilleumier et al., 2014; Desmaele et al., 2019b). The origin of the discrepancies between simulated and experimental viscosities of Na₂CO₃ melt is, however, difficult to identify within the available data. With the exception of the results from Stagno et al., (2018), the data reported in Figure 5 suggest that alkali elements (i.e. Na and K) play a crucial role in modifying the viscosity of carbonate melt. This effect may result from the larger ionic radii of alkalis (Di Genova et al., 2016; Stagno et al., 2018) and/or enhanced interactions with alkaline elements upon substitution as discussed above. In contrast, the limited compositional effects on the viscosity of alkaline earth carbonate melts, CaCO₃-CaMg(CO₃)₂ (and likely MgCO₃) melts (Figure 5), upon Ca and Mg exchange reflect their structural similarities, with only minor differences in the interatomic distances as shown by X-ray diffraction studies (Kono et al., 2014). The effect of potassium on the viscosity of alkaline carbonate melts contrasts with its role in silicate melts, where the viscosity increases upon increasing the field strength of the network-stabilizing cation following the trend: η_K⁺ < η_Na⁺ < η_Sr⁺ < η_Ca²⁺ < η_Mg²⁺ (Dingwell, 2007). Contrary to previous reports (Kono et al., 2014; Stagno et al., 2018), the data reported in Figure 5 reveal compositional effects on the viscosity of alkali(ne) carbonate melts, despite the limitations to identify clear trends. Additional data on the viscosity of alkali(ne) carbonate melts, including a broad range of mixed compositions in the systems MgCO₃-CaCO₃-K₂CO₃-Na₂CO₃ would be required to draw further conclusions.

Non-Arrhenian Viscosity of Carbonate Melts in the Mantle

The non-Arrhenian temperature-dependent viscosity (fragile behavior) reported here for alkali(ne) carbonate melts is somehow not unexpected as the departure from an exponential activation law (i.e. Arrhenian behavior) is a common feature for most melt/liquid systems investigated to date, including for a broad range of silicate melt compositions over geologically relevant temperature intervals (Richet, 1984; Angell, 1995; Webb, 1997). Notable exceptions to this trend are highly polymerized silicate melts (i.e. strong melts, Angell, 1995) such as SiO₂ and granitic-albitic melts that display Arrhenian behavior at all investigated temperature conditions (e.g. Richet, 1984; Webb, 1997; Giordano and Dingwell, 2003). The strong/fragile pattern reflects the sensitivity of the liquid/melt structure to temperature changes, which is in turn controlled by the structural arrangements and nature of bonding in the system (Angell, 1995). For silicate melts, there is a clear correlation between the melt fragility and the degree of polymerization defined by the NBO/T parameter (Giordano et al., 2013; Malfait and Sanchez-Valle, 2013). The fragility exhibited by carbonate melts may thus arise from their ionic nature, characterized by simple Coulomb interactions, that readily permit for a variety of particle orientations and coordination states to reorganize the structure in response to thermal perturbations. Recent MD simulations performed in molten Na₂CO₃ provide indeed evidence for the formation of low-dimentional structures in the CO₃²⁻ network (e.g. chains, triangles and tetrahedra) that are temperature dependent and change the melt dynamics and hence, enhance melt fragility (Wilding et al., 2016; Wilson et al., 2018). Note that pressure also favors the formation of extended low-dimensional networks of CO₃²⁻ pairs and the rise of CO₃₊₁ local coordination environments in KM melt that result in an increase of melt viscosity with pressure (Wilding et al., 2019) consistent with the present observations (Figure 3).

The alkali(ne) carbonate melts investigated here are to date the only carbonate melt compositions displaying a non-Arrhenian temperature dependent viscosity (Figure 5), likely due to the limited temperature range investigated by previous studies (Table 1). Therefore, departures of the viscosity from theArrhenian behavior may not be ruled out for other carbonate melt compositions as observed for silicate melts (e.g. Richet, 1984; Webb, 1997; Giordano and Dingwell, 2003). The present results thus advice against the application of a simple Arrhenian model to extrapolate over a broad range of temperature the available data for the viscosity of other carbonate melt compositions (Figure 5). This will predict changes in viscosity with temperature that are larger than indicated by the non-Arrhenian behavior observed here and, in turn, would result in underestimations of carbonate melt mobility in the upper mantle. This point is particularly critical when modeling carbonate magmatic processes at crustal and shallow upper mantle conditions (< 7 GPa), e.g. carbonate magma chamber dynamics or carbonate melt mobility beneath mid-oceanic ridges, as they span the conditions where the strongest non-Arrhenian behavior of the viscosity has been observed (Figure 3).

Conclusion

The viscosity of alkali(ne) carbonate melts, KM and KC, has been determined over a broad range of pressure and temperature conditions, i.e. from ambient pressure to 13 GPa and 1,000–2,000 K, by means of classical MD simulations. Both melt compositions are more viscous than alkaline carbonate melts, i.e. CaCO₃, MgCO₃ and CaMg(CO₃)₂, likely due to the change in charge distribution upon potassium substitution. Temperature appears as the primary control parameter on the viscosity of alkali(ne) carbonate melts, even though pressure effects are not negligible in contrast with previous reports. Most interestingly, this study identifies for the first time non-Arrhenian temperature-dependent viscosities in carbonate melts at high pressure, while the viscosity increases linearly with pressure at all investigated conditions. The non-Arrhenian viscosity of KM and KC melts may arise from the formation of temperature-dependent low-dimensional structures in the melt that are more drastic in the carbonate network than in the cation network (Wilson et al., 2018). Therefore, the non-Arrhenian behaviour may be expected for other carbonate melt compositions regardless of the cation nature, although the experimental and/or theoretical confirmation is still awaiting. The present results might be taken into account when modeling the mobility of carbonate melts in the upper mantle.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. The repository containing the output files from the MD simulations are available at: https://uni-muenster.sciebo.de/s/N82lU5t1ejYFCq4. Further inquiries can be directed to the corresponding author.

Author Contributions

CS-V, BG and NS organized the project, XR performed the MD simulations in collaboration with BG and NS, ED implemented the force fields, CS-V, XR and MM processed the data and CS-V and XR wrote the manuscript with input from all the authors.

Funding

This research was funded through the German Science Foundation (DFG grant SA 2585/4-1 to CS-V), start-up funds from WWU Münster, a mobility grant from the DAAD (ref. no. 57381316 to XR) and the H2020-MSCA project MoVEMENT (grant No. 842339 to MM).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

XR acknowledges financial support from the DAAD for a 6 months stay at Sorbonne University Paris to perform the MD simulations (ref. no. 57381316). MM acknowledges support from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Actions (grant agreement No. 842339). We thank the two reviewers for their comments and the Associate Editor M. Mookherjee for editorial handling.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.674770/full#supplementary-material.

References

Angell, C. A. (1995). Formation of Glasses from Liquids and Biopolymers. Science 267, 1924–1935. doi:10.1126/science.267.5206.1924

PubMed Abstract | CrossRef Full Text | Google Scholar

Boon, J.-P., and Yip, S. (1980). Molecular Hydrodynamics. Toronto: McGraw-Hill.

Google Scholar

Bottinga, Y., and Richet, P. (1995). Silicate Melts: The “Anomalous” Pressure Dependence of the Viscosity. Geochimica et Cosmochimica Acta 59, 2725–2731. doi:10.1016/0016-7037(95)00168-Y

CrossRef Full Text | Google Scholar

Cooper, A. F., Gittins, J., and Tuttle, O. F. (1975). The System Na 2 CO 3 -K 2 CO 3 -CaCO 3 at 1 Kilobar and its Significance in Carbonatite Petrogenesis. Am. J. Sci. 275, 534–560. doi:10.2475/ajs.275.5.534

CrossRef Full Text | Google Scholar

Corradini, D., Coudert, F.-X., and Vuilleumier, R. (2016). Insight into the Li2CO3-K2CO3 Eutectic Mixture from Classical Molecular Dynamics: Thermodynamics, Structure, and Dynamics. J. Chem. Phys. 144, 104507. doi:10.1063/1.4943392

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalton, J. A., and Presnall, D. C. (1998). The Continuum of Primary Carbonatitic-Kimberlitic Melt Compositions in Equilibrium with Lherzolite: Data from the System CaO-MgO-Al2O3-SiO2-CO2 at 6 GPa. J. Petrol. 39, 1953–1964. doi:10.1093/petroj/39.11-12.1953

CrossRef Full Text | Google Scholar

Dasgupta, R., and Hirschmann, M. M. (2010). The Deep Carbon Cycle and Melting in Earth's interior. Earth Planet. Sci. Lett. 298, 1–13. doi:10.1016/j.epsl.2010.06.039

CrossRef Full Text | Google Scholar

Dasgupta, R. (2013). Ingassing, Storage, and Outgassing of Terrestrial Carbon through Geologic Time. Rev. Mineralogy Geochem. 75, 183–229. doi:10.2138/rmg.2013.75.7

CrossRef Full Text | Google Scholar

Desmaele, E., Sator, N., Vuilleumier, R., and Guillot, B. (2019a). Atomistic Simulations of Molten Carbonates: Thermodynamic and Transport Properties of the Li2CO3-Na2CO3-K2CO3 System. J. Chem. Phys. 150, 094504. doi:10.1063/1.5082731

PubMed Abstract | CrossRef Full Text | Google Scholar

Desmaele, E., Sator, N., Vuilleumier, R., and Guillot, B. (2019b). The MgCO3-CaCO3-Li2CO3-Na2CO3-K2CO3 Melts: Thermodynamics and Transport Properties by Atomistic Simulations. J. Chem. Phys. 150, 214503. doi:10.1063/1.5099015

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Genova, D., Cimarelli, C., Hess, K.-U., and Dingwell, D. B. (2016). An Advanced Rotational Rheometer System for Extremely Fluid Liquids up to 1273 K and Applications to Alkali Carbonate Meltsk. Am. Mineral. 101, 953–959. doi:10.2138/am-2016-5537CCBYNCND

CrossRef Full Text | Google Scholar

Dingwell, D. B. (2007). Properties of Rocks and Minerals - Diffusion, Viscosity, and Flow of Melts. Treatise Geophys. 2, 419–436. doi:10.1016/B978-044452748-6.00044-4

CrossRef Full Text | Google Scholar

Dingwell, D. B., and Webb, S. L. (1989). Structural Relaxation in Silicate Melts and Non-Newtonian Melt Rheology in Geologic Processes. Phys. Chem. Minerals 16, 508–516. doi:10.1007/bf00197020

CrossRef Full Text | Google Scholar

Dixon, J. E., Clague, D. A., Cousens, B., Monsalve, M. L., and Uhl, J. (2008). Carbonatite and Silicate Melt Metasomatism of the Mantle Surrounding the Hawaiian Plume: Evidence from Volatiles, Trace Elements, and Radiogrenic Isotopes in Rejuvenated-Stage Lavas from Niihau, Hawaii. Geochem. Geophys. Geosystems 9, 1–34. doi:10.1029/2008gc002076

CrossRef Full Text | Google Scholar

Dobson, D. P., Jones, A. P., Rabe, R., Sekine, T., Kurita, K., Taniguchi, T., et al. (1996). In-Situ Measurement of Viscosity and Density of Carbonate Melts at High Pressure. Earth Planet. Sci. Lett. 143, 207–215. doi:10.1016/0012-821X(96)00139-2

CrossRef Full Text | Google Scholar

Dufils, T., Folliet, N., Mantisi, B., Sator, N., and Guillot, B. (2017). Properties of Magmatic Liquids by Molecular Dynamics Simulation: The Example of a MORB Melt. Chem. Geology. 461, 34–46. doi:10.1016/j.chemgeo.2016.06.030

CrossRef Full Text | Google Scholar

Dufils, T., Sator, N., and Guillot, B. (2018). Properties of Planetary Silicate Melts by Molecular Dynamics Simulation. Chem. Geology. 493, 298–315. doi:10.1016/j.chemgeo.2018.06.003

CrossRef Full Text | Google Scholar

Fillon, J. J., and Brennecke, J. F. (2017). Viscosity of Ionic Liquid-Ionic Liquid Mixtures. J. Chem. Eng. Data 62, 1884–1901. doi:10.1021/acs.jced.7b00221

CrossRef Full Text | Google Scholar

Fischer, K. M., Ford, H. A., Abt, D. L., and Rychert, C. A. (2010). The Lithosphere-Asthenosphere Boundary. Annu. Rev. Earth Planet. Sci. 38, 551–575. doi:10.1146/annurev-earth-040809-152438

CrossRef Full Text | Google Scholar

Gaillard, F., Malki, M., Iacono-Marziano, G., Pichavant, M., and Scaillet, B. (2008). Carbonatite Melts and Electrical Conductivity in the Asthenosphere. Science 322, 1363–1365. doi:10.1126/science.1164446

PubMed Abstract | CrossRef Full Text | Google Scholar

Gardés, E., Laumonier, M., Massuyeau, M., and Gaillard, F. (2020). Unravelling Partial Melt Distribution in the Oceanic Low Velocity Zone. Earth Planet. Sci. Lett. 540, 116242. doi:10.1016/j.epsl.2020.116242

CrossRef Full Text | Google Scholar

Genge, M. J., Price, G. D., and Jones, A. P. (1995). Molecular Dynamics Simulations of CaCO3 Melts to Mantle Pressures and Temperatures: Implications for Carbonatite Magmas. Earth Planet. Sci. Lett. 131, 225–238. doi:10.1016/0012-821X(95)00020-D

CrossRef Full Text | Google Scholar

Gervasoni, F., Klemme, S., Rohrbach, A., Grützner, T., and Berndt, J. (2017). Experimental Constraints on Mantle Metasomatism Caused by Silicate and Carbonate Melts. Lithos 282-283, 173–186. doi:10.1016/j.lithos.2017.03.004

CrossRef Full Text | Google Scholar

Giordano, D., and Dingwell, D. B. (2003). Non-Arrhenian Multicomponent Melt Viscosity: A Model. Earth Planet. Sci. Lett. 208, 337–349. doi:10.1016/S0012-821X(03)00042-6

CrossRef Full Text | Google Scholar

Giordano, D., Russell, J. K., and Dingwell, D. B. (2008). Viscosity of Magmatic Liquids: A Model. Earth Planet. Sci. Lett. 271, 123–134. doi:10.1016/j.epsl.2008.03.038

CrossRef Full Text | Google Scholar

Glasstone, S., Laidler, K. J., and Eyring, H. (1941). The Theory of Rate Processes. New York: McGraw-Hill.

Google Scholar

Grassi, D., and Schmidt, M. W. (2011a). Melting of Carbonated Pelites at 8-13 GPa: Generating K-Rich Carbonatites for Mantle Metasomatism. Contrib. Mineral. Petrol. 162, 169–191. doi:10.1007/s00410-010-0589-9

CrossRef Full Text | Google Scholar

Grassi, D., and Schmidt, M. W. (2011b). The Melting of Carbonated Pelites from 70 to 700 Km Depth. J. Petrol. 52, 765–789. doi:10.1093/petrology/egr002

CrossRef Full Text | Google Scholar

Green, D. H., and Wallace, M. E. (1988). Mantle Metasomatism by Ephemeral Carbonatite Melts. Nature 336, 459–462. doi:10.1038/336459a0

CrossRef Full Text | Google Scholar

Gudfinnsson, G. H., and Presnall, D. C. (2005). Continuous Gradations Among Primary Carbonatitic, Kimberlitic, Melilititic, Basaltic, Picritic, and Komatiitic Melts in Equilibrium with Garnet Lherzolite at 3-8 GPa. J. Petrol. 46, 1645–1659. doi:10.1093/petrology/egi029

CrossRef Full Text | Google Scholar

Guillot, B., and Sator, N. (2007a). A Computer Simulation Study of Natural Silicate Melts. Part I: Low Pressure Properties. Geochimica et Cosmochimica Acta 71, 1249–1265. doi:10.1016/j.gca.2006.11.015

CrossRef Full Text | Google Scholar

Guillot, B., and Sator, N. (2007b). A Computer Simulation Study of Natural Silicate Melts. Part II: High Pressure Properties. Geochimica et Cosmochimica Acta 71, 4538–4556. doi:10.1016/j.gca.2007.05.029

CrossRef Full Text | Google Scholar

Guillot, B., and Sator, N. (2011). Carbon Dioxide in Silicate Melts: A Molecular Dynamics Simulation Study. Geochimica et Cosmochimica Acta 75, 1829–1857. doi:10.1016/j.gca.2011.01.004

CrossRef Full Text | Google Scholar

Hammouda, T., and Keshav, S. (2015). Melting in the Mantle in the Presence of Carbon: Review of Experiments and Discussion on the Origin of Carbonatites. Chem. Geology. 418, 171–188. doi:10.1016/j.chemgeo.2015.05.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammouda, T., and Laporte, D. (2000). Ultrafast Mantle Impregnation by Carbonatite Melts. Geology 28, 283–285. doi:10.1130/0091-7613(2000)028<0283:umibcm>2.3.co;2

CrossRef Full Text | Google Scholar

Hess, B. (2002). Determining the Shear Viscosity of Model Liquids from Molecular Dynamics Simulations. J. Chem. Phys. 116, 209. doi:10.1063/1.1421362

CrossRef Full Text | Google Scholar

Hurt, S. M., and Wolf, A. S. (2019). Thermodynamic Properties of CaCO3-SrCO3-BaCO3 Liquids: a Molecular Dynamics Study Using New Empirical Atomic Potentials for Alkaline Earth Carbonates. Phys. Chem. Minerals 46, 165–180. doi:10.1007/s00269-018-0995-5

CrossRef Full Text | Google Scholar

Janz, G. J. (1988). Thermodynamic and Transport Properties for Molten Salts: Correlation Equations for Critically Evaluated Density, Surface Tension, Electrical Conductance, and Viscosity Data. J. Phys. Chem. Ref. Data 17, 325.

Google Scholar

Jones, A. P., Genge, M., and Carmody, L. (2013). Carbonate Melts and Carbonatites. Rev. Mineralogy Geochem. 75, 289–322. doi:10.2138/rmg.2013.75.10

CrossRef Full Text | Google Scholar

Keller, T., Katz, R. F., and Hirschmann, M. M. (2017). Volatiles Beneath Mid-Ocean Ridges: Deep Melting, Channelised Transport, Focusing, and Metasomatism. Earth Planet. Sci. Lett. 464, 55–68. doi:10.1016/j.epsl.2017.02.006

CrossRef Full Text | Google Scholar

Kiseeva, E. S., Litasov, K. D., Yaxley, G. M., Ohtani, E., and Kamenetsky, V. S. (2013). Melting and Phase Relations of Carbonated Eclogite at 9-21 GPa and the Petrogenesis of Alkali-Rich Melts in the Deep Mantle. J. Petrol. 54, 1555–1583. doi:10.1093/petrology/egt023

CrossRef Full Text | Google Scholar

Kiseeva, E. S., Yaxley, G. M., Hermann, J., Litasov, K. D., Rosenthal, A., and Kamenetsky, V. S. (2012). An Experimental Study of Carbonated Eclogite at 3{middle Dot}5-5{middle Dot}5 GPa--Implications for Silicate and Carbonate Metasomatism in the Cratonic Mantle. J. Petrol. 53, 727–759. doi:10.1093/petrology/egr078

CrossRef Full Text | Google Scholar

Kojima, T. (2009). Physical and Chemical Properties of Molten Carbonates. PhD Thesis, Kobe University.

Google Scholar

Kono, Y., Kenney-Benson, C., Hummer, D., Ohfuji, H., Park, C., Shen, G., et al. (2014). Ultralow Viscosity of Carbonate Melts at High Pressures. Nat. Commun. 5, 5091. doi:10.1038/ncomms6091

PubMed Abstract | CrossRef Full Text | Google Scholar

Korsakov, A. V., and Hermann, J. (2006). Silicate and Carbonate Melt Inclusions Associated with Diamonds in Deeply Subducted Carbonate Rocks. Earth Planet. Sci. Lett. 241, 104–118. doi:10.1016/j.epsl.2005.10.037

CrossRef Full Text | Google Scholar

Kubicki, J. D., and Lasaga, A. C. (1988). Molecular Dynamics Simulations of SiO₂ Melt and Glass: Ionic and Covalent Models. Am. Mineral. 73, 941–955.

Google Scholar

Li, M., Russell, J. K., and Giordano, D. (2021). Temperature-Pressure-Composition Model for Melt Viscosity in the Di-an-ab System. Chem. Geology. 560, 119895. doi:10.1016/j.chemgeo.2020.119895

CrossRef Full Text | Google Scholar

Li, Z., Li, J., Lange, R., Liu, J., and Militzer, B. (2017). Determination of Calcium Carbonate and Sodium Carbonate Melting Curves up to Earth's Transition Zone Pressures with Implications for the Deep Carbon Cycle. Earth Planet. Sci. Lett. 457, 395–402. doi:10.1016/j.epsl.2016.10.027

CrossRef Full Text | Google Scholar

Liebske, C., Schmickler, B., Terasaki, H., Poe, B., Suzuki, A., Funakoshi, K., et al. (2005). Viscosity of Peridotite Liquid up to 13 GPa: Implications for Magma Ocean Viscosities. Earth Planet. Sci. Lett. 240, 589–604. doi:10.1016/j.epsl.2005.10.004

CrossRef Full Text | Google Scholar

Liu, Q., and Lange, R. A. (2003). New Density Measurements on Carbonate Liquids and the Partial Molar Volume of the CaCO 3 Component. Contrib. Mineralogy Petrol. 146, 370–381. doi:10.1007/s00410-003-0505-7

CrossRef Full Text | Google Scholar

Malfait, W. J., and Sanchez-Valle, C. (2013). Effect of Water and Network Connectivity on Glass Elasticity and Melt Fragility. Chem. Geology. 346, 72–80. doi:10.1016/j.chemgeo.2012.04.034

CrossRef Full Text | Google Scholar

Malfait, W. J., Seifert, R., Petitgirard, S., Mezouar, M., and Sanchez-Valle, C. (2014). The Density of Andesitic Melts and the Compressibility of Dissolved Water in Silicate Melts at Crustal and Upper Mantle Conditions. Earth Planet. Sci. Lett. 393, 31–38. doi:10.1016/j.epsl.2014.02.042

CrossRef Full Text | Google Scholar

Massuyeau, M., Gardés, E., Rogerie, G., Aulbach, S., Tappe, S., Le Trong, E., et al. (2021). MAGLAB: A Computing Platform Connecting Geophysical Signatures to Melting Processes in Earth's Mantle. Phys. Earth Planet. Interiors 314, 106638. doi:10.1016/j.pepi.2020.106638

CrossRef Full Text | Google Scholar

Minarik, W. G., and Watson, E. B. (1995). Interconnectivity of Carbonate Melt at Low Melt Fraction. Earth Planet. Sci. Lett. 133, 423–437. doi:10.1016/0012-821X(95)00085-Q

CrossRef Full Text | Google Scholar

Naif, S., Key, K., Constable, S., and Evans, R. L. (2013). Melt-Rich Channel Observed at the Lithosphere-Asthenosphere Boundary. Nature 495, 356–359. doi:10.1038/nature11939

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Leary, M. C., Lange, R. A., and Ai, Y. (2015). The Compressibility of CaCO3-Li2CO3-Na2CO3-K2CO3 Liquids: Application to Natrocarbonatite and CO2-Bearing Nephelinite Liquids from Oldoinyo Lengai. Contrib. Mineral. Petrol. 170, 3. doi:10.1007/s00410-015-1157-0

CrossRef Full Text | Google Scholar

Poli, S. (2015). Carbon Mobilized at Shallow Depths in Subduction Zones by Carbonatitic Liquids. Nat. Geosci. 8, 633–636. doi:10.1038/ngeo2464

CrossRef Full Text | Google Scholar

Ragone, S. E., Datta, R. K., Roy, D. M., and Tuttle, O. F. (1966). The System Potassium Carbonate-Magnesium Carbonate. J. Phys. Chem. 70, 3360–3361. doi:10.1021/j100882a515

CrossRef Full Text | Google Scholar

Rai, N., Perrillat, J.-P., Mezouar, M., Colin, A., Petitgirard, S., and van Westrenen, W. (2019). In Situ Viscometry of Primitive Lunar Magmas at High Pressure and High Temperature. Front. Earth Sci. 7 (1-12), 94. doi:10.3389/feart.2019.00094

CrossRef Full Text | Google Scholar

Richet, P. (1984). Viscosity and Configurational Entropy of Silicate Melts. Geochimica et Cosmochimica Acta 48, 471–483. doi:10.1016/0016-7037(84)90275-8

CrossRef Full Text | Google Scholar

Ritter, X., Sanchez-Valle, C., Sator, N., Desmaele, E., Guignot, N., King, A., et al. (2020). Density of Hydrous Carbonate Melts under Pressure, Compressibility of Volatiles and Implications for Carbonate Melt Mobility in the Upper Mantle. Earth Planet. Sci. Lett. 533, 116043. doi:10.1016/j.epsl.2019.116043

CrossRef Full Text | Google Scholar

Rudnick, R. L., McDonough, W. F., and Chappell, B. W. (1993). Carbonatite Metasomatism in the Northern Tanzanian Mantle: Petrographic and Geochemical Characteristics. Earth Planet. Sci. Lett. 114, 463–475. doi:10.1016/0012-821X(93)90076-L

CrossRef Full Text | Google Scholar

Russell, J. K., Giordano, D., and Dingwell, D. B. (2003). High-Temperature Limits on Viscosity of Non-Arrhenian Silicate Melts. Am. Mineral. 88, 1390–1394. doi:10.2138/am-2003-8-924

CrossRef Full Text | Google Scholar

Russell, J. K., Porritt, L. A., Lavallée, Y., and Dingwell, D. B. (2012). Kimberlite Ascent by Assimilation-Fuelled Buoyancy. Nature 481, 352–356. doi:10.1038/nature10740

PubMed Abstract | CrossRef Full Text | Google Scholar

Rustad, J. R., Yuen, D. A., and Spera, F. J. (1990). Molecular Dynamics of liquidSiO2under High Pressure. Phys. Rev. A. 42, 2081–2089. doi:10.1103/physreva.42.2081

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, Y., Yaegashi, S., Kijima, T., Takeuchi, E., Tamai, K., Hasebe, M., et al. (1999). Viscosities of Molten Alkali Carbonates. Jpn. J. Thermophys. Prop. 13, 156–161. doi:10.2963/jjtp.13.156

CrossRef Full Text | Google Scholar

Shatskiy, A. F., Litasov, K. D., and Palyanov, Y. N. (2015). Phase Relations in Carbonate Systems at Pressures and Temperatures of Lithospheric Mantle: Review of Experimental Data. Russ. Geol. Geophys. 56, 113–142. doi:10.1016/j.rgg.2015.01.007

CrossRef Full Text | Google Scholar

Sifré, D., Gardés, E., Massuyeau, M., Hashim, L., Hier-Majumder, S., and Gaillard, F. (2014). Electrical Conductivity during Incipient Melting in the Oceanic Low-Velocity Zone. Nature 509, 81–85. doi:10.1038/nature13245

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, W., and Forester, T. R. (1996). DL_POLY_2.0: A General-Purpose Parallel Molecular Dynamics Simulation Package. J. Mol. Graphics 14, 136–141. doi:10.1016/S0263-7855(96)00043-4

CrossRef Full Text | Google Scholar

Sparks, R. S. J. (2013). Kimberlite Volcanism. Annu. Rev. Earth Planet. Sci. 41, 497–528. doi:10.1146/annurev-earth-042711-105252

CrossRef Full Text | Google Scholar

Stagno, V. (2019). Carbon, Carbides, Carbonates and Carbonatitic Melts in the Earth's interior. J. Geol. Soc. 176, 375–387. doi:10.1144/jgs2018-095

CrossRef Full Text | Google Scholar

Stagno, V., Stopponi, V., Kono, Y., Manning, C. E., and Irifune, T. (2018). Experimental Determination of the Viscosity of Na2CO3 Melt between 1.7 and 4.6 GPa at 1,200-1700 °C: Implications for the Rheology of Carbonatite Magmas in the Earth's Upper Mantle. Chem. Geology. 501, 19–25. doi:10.1016/j.chemgeo.2018.09.036

CrossRef Full Text | Google Scholar

Sun, C., and Dasgupta, R. (2019). Slab-Mantle Interaction, Carbon Transport, and Kimberlite Generation in the Deep Upper Mantle. Earth Planet. Sci. Lett. 506, 38–52. doi:10.1016/j.epsl.2018.10.028

CrossRef Full Text | Google Scholar

Tissen, J. T. W. M., Janssen, G. J. M., and Eerden, P. V. D. (1994). Molecular Dynamics Simulation of Binary Mixtures of Molten Alkali Carbonates. Mol. Phys. 82, 101–111. doi:10.1080/00268979400100084

CrossRef Full Text | Google Scholar

Treiman, A. H. (1995). Ca-rich Carbonate Melts; a Regular-Solution Model, with Application to Carbonatite Magma + Vapor Equilibria and Carbonate Lavas on Venus. Am. Mineral. 80, 115–130. doi:10.2138/am-1995-1-212

CrossRef Full Text | Google Scholar

Treiman, A. H., and Schedl, A. (1983). Properties of Carbonatite Magma and Processes in Carbonatite Magma Chambers. J. Geology. 91, 437–447. doi:10.1086/628789

CrossRef Full Text | Google Scholar

Veksler, I. V., Petibon, C., Jenner, G. A., Dorfman, A. M., and Dingwell, D. B. (1998). Trace Element Partitioning in Immiscible Silicate-Carbonate Liquid Systems: an Initial Experimental Study Using a Centrifuge Autoclave. J. Petrol. 39, 2095–2104. doi:10.1093/petroj/39.11-12.2095

CrossRef Full Text | Google Scholar

Vogel, D. H. (1921). Das Temperaturabhaengigkeitsgesetz der Viskositaet von Fluessigkeiten. Phys. Z. 22, 645.

Google Scholar

Vuilleumier, R., Seitsonen, A., Sator, N., and Guillot, B. (2014). Structure, Equation of State and Transport Properties of Molten Calcium Carbonate (CaCO3) by Atomistic Simulations. Geochimica et Cosmochimica Acta 141, 547–566. doi:10.1016/j.gca.2014.06.037

CrossRef Full Text | Google Scholar

Wallace, M. E., and Green, D. H. (1988). An Experimental Determination of Primary Carbonatite Magma Composition. Nature 335, 343–346. doi:10.1038/335343a0

CrossRef Full Text | Google Scholar

Wang, Y., Sakamaki, T., Skinner, L. B., Jing, Z., Yu, T., Kono, Y., et al. (2014). Atomistic Insight into Viscosity and Density of Silicate Melts under Pressure. Nat. Commun. 5, 3241. doi:10.1038/ncomms4241

PubMed Abstract | CrossRef Full Text | Google Scholar

Webb, S. (1997). Silicate Melts: Relaxation, Rheology, and the Glass Transition. Rev. Geophys. 35 (2), 191–218. doi:10.1029/96rg03263

CrossRef Full Text | Google Scholar

Wilding, M., Bingham, P. A., Wilson, M., Kono, Y., Drewitt, J. W. E., Brooker, R. A., et al. (2019). CO3+1 Network Formation in Ultra-High Pressure Carbonate Liquids. Sci. Rep. 9, 2–5. doi:10.1038/s41598-019-51306-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilding, M. C., Wilson, M., Alderman, O. L. G., Benmore, C., Weber, J. K. R., Parise, J. B., et al. (2016). Low-Dimensional Network Formation in Molten Sodium Carbonate. Sci. Rep. 6, 24415. doi:10.1038/srep24415

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, M., Ribeiro, M. C. C., Wilding, M. C., Benmore, C., Weber, J. K. R., Alderman, O., et al. (2018). Structure and Liquid Fragility in Sodium Carbonate. J. Phys. Chem. A. 122, 1071–1076. doi:10.1021/acs.jpca.7b10712

PubMed Abstract | CrossRef Full Text | Google Scholar

Woolley, A. R., and Kjarsgaard, B. A. (2008). Carbonatite Occurrences of the World: Map and Database. Geological Survey of Canada, Open File Report 5796. doi:10.4095/225115

CrossRef Full Text | Google Scholar

Yaxley, G. M., and Brey, G. P. (2004). Phase Relations of Carbonate-Bearing Eclogite Assemblages from 2.5 to 5.5 GPa: Implications for Petrogenesis of Carbonatites. Contrib. Mineralogy Petrol. 146, 606–619. doi:10.1007/s00410-003-0517-3

CrossRef Full Text | Google Scholar

Yaxley, G. M., Crawford, A. J., and Green, D. H. (1991). Evidence for Carbonatite Metasomatism in Spinel Peridotite Xenoliths from Western Victoria, Australia. Earth Planet. Sci. Lett. 107, 305–317. doi:10.1016/0012-821X(91)90078-V

CrossRef Full Text | Google Scholar

Zhang, Y., Otani, A., and Maginn, E. J. (2015). Reliable Viscosity Calculation from Equilibrium Molecular Dynamics Simulations: A Time Decomposition Method. J. Chem. Theor. Comput. 11, 3537–3546. doi:10.1021/acs.jctc.5b00351

PubMed Abstract | CrossRef Full Text | Google Scholar