Systematic Triggering of Large Earthquakes by Karst Water Recharge: Statistical Evidence in Northeastern Italy

It is known that surface water accumulation by natural or anthropic causes like precipitation and reservoir impoundment can trigger earthquakes. The phenomenon is amplified and sped up in karst areas, where fracture systems can store large quantities of water and facilitate its percolation to seismogenic depths, increasing both elastic stress and pore pressure on pre-existent faults. The present work explored the possibility that this mechanism had systematically triggered major earthquakes in northeastern Italy, where seismicity is concentrated along the pre-Alpine thrust belt, characterized by the alignment of a series of karst massifs. The time occurrence of damaging and destructive earthquakes (moment magnitude Mw between 4.8 and 6.4) since 1901 was compared with the evolution of the Palmer Drought Severity Index (PDSI), an index of soil moisture that summarizes precipitation and, through temperature, water evaporation. Statistical analysis based on the bivariate Ripley’s K-function shows a significant time correlation between earthquakes and the peaks of PDSI since 1934, with the two strongest earthquakes (1936 Alpago-Cansiglio earthquake and 1976 Friuli earthquake, Mw 6.1 and 6.4, respectively) placed by the two PDSI maxima. The analysis was extended back in time to the last millennium, showing a time correlation between the occurrence of destructive earthquakes (Mw ≥ 6.2) and the peaks of ice extension in the European Alps, assumed as a proxy for groundwater accumulation in the study area. This evidence presented herein coupled with geological characteristics of the area and recent observations on large crustal deformations induced by heavy precipitation suggests that, if PDSI is a valid ground water indicator, karst water recharge may play a role in triggering major earthquakes in northeastern Italy, also relating their occurrence to the large scale climate changes affecting precipitation and evaporation.

Introduction

Seismic activity is mainly driven by plate tectonics, which induces strain in the crust and causes its rupture along faults. Observations and modeling suggest that various processes can interfere with the main mechanism and modulate seismicity in different ways, by either accelerating or delaying the occurrence of earthquakes, acting from the local to the global scale. These include, among the others, the mutual triggering between earthquakes by stress diffusion (Hough, 2005) or viscoelastic relaxation (Mantovani et al., 2010), sea-level changes (Luttrel and Sandwell., 2010), tidal and astronomic effects (Tolstoy et al., 2002; Scafetta and Mazzarella, 2015), impulses in the Earth’s rate of rotation and interaction of adjacent seismic regions (Liritzis et al., 1995). In particular, it is known that inland water accumulation in form of groundwater, lakes, ice, snow, reservoir impoundment as well as underground injection can enhance seismicity at time scales that range from days to millennia (Raleigh et al., 1976; Huang et al., 1979; Kafri and Shapira, 1990; Liritzis and Petropoulos, 1992; Liritzis and Petropoulos, 1994; Gupta, 2002; Heki, 2003; Saar and Manga, 2003; Kraft et al., 2006; Bettinelli et al., 2008; Hampel et al., 2010; Wang and Manga, 2010; D’Agostino et al., 2018). The basic mechanism is delineated in Figure 1 for the case of precipitation in a karst environment: the portion of the meteoric water which is not dispersed by evaporation, plant transpiration and surface runoff is stored as groundwater. The accumulation of water can trigger earthquakes, and the two main mechanisms (arrows in magenta in Figure 1) are explained by poroelastic models (Mulargia and Bizzarri, 2014): the addition to faults of further elastic stress caused by the groundwater load; the propagation through faults of pulses of fluid pore pressure that reduce their frictional strength. Elastic stress triggering is almost instantaneous and selective on the type of fault, as it depends on its geometry and its relative position in respect to the surface load (Johnson eta al., 2017). In general, according to the failure model illustrated by Saar and Manga (2003), an additive vertical load should enhance normal faulting, inhibit thrust faulting, and be neutral for strike-slip faults. The triggering mechanism based on pore-pressure propagation acts within days or years. It is less dependent on the fault geometry but requires hydraulic continuity from the surface to the seismogenic fault. According to Talwani et al. (2007) the pulse of fluid pressure can transmit even at long distances (up to 30 km) travelling along pre-existing narrow paths (fractures and joints) characterized by higher permeability than the confining medium. In the setting of karst aquifers, like those observed in northeastern Italy, where meteoric water resides at depth for long times (up to several thousand years as reported by Torresan et al., 2020), the new precipitation water can trigger seismicity without reaching the seismogenic depth. Its infiltration, in fact, generates the pulse of pressure that transmits by means of the pre-existing water. A further critical point concerns the features of the loading process most affecting seismicity. El Hariri et al. (2010) analyzed reservoir-induced seismicity in Brazil and concluded that both the absolute water level, the magnitude of the water-level rise and the time since a previous water-level peak contribute to trigger earthquakes. Bettinelli et al. (2008) suggested that in the Himalayan area seismicity is better controlled by the rate of the hydrological load rather than by the load itself. Huang et al. (1979) pointed out that also a severe drought period preceding an intense rainfall could contribute to the triggering of large earthquakes in Southern California.

FIGURE 1

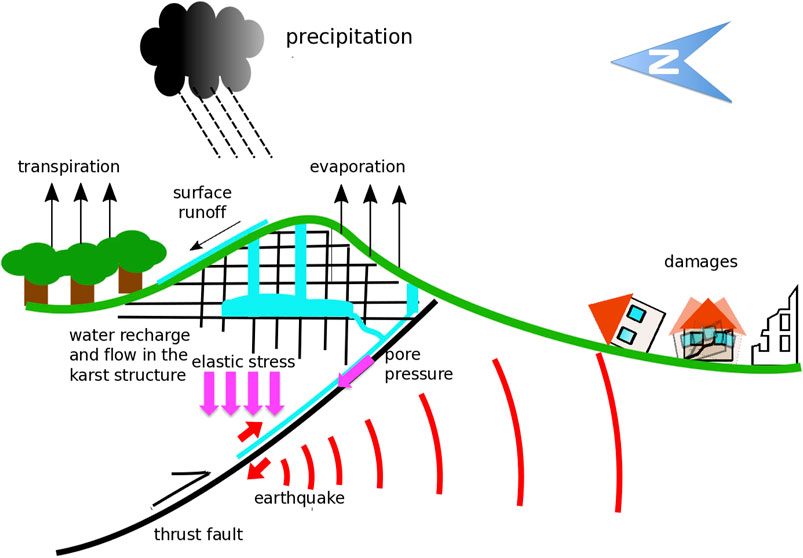
FIGURE 1. Cycle of water and earthquake triggering in a karst environment: precipitation water recharges the karst network increasing elastic stress and pore pressure on faults. The figure depicts the tectonic setting typical of north-eastern Italy, with thrust faults dipping northwards under the Alpine-Prealpine belt.

Karst environments (Figure 1) are particularly suitable for earthquake triggering (Miller, 2008). Their fracture systems can store large quantities of water and allow the necessary hydraulic continuity between the surface and the seismogenic structures. This role emerged for extreme precipitation episodes triggering minor seismicity within days (Hainzl et al., 2006; Kraft et al., 2006; Miller, 2008; Rigo et al., 2008). It is left open the question if karst water recharge can trigger large earthquakes in systematic way, even for mild variations of groundwater occurring at longer time scales. The question is of general interest, because important seismic districts affected by destructive earthquakes are characterized by surface karst geology. Liritzis and Petropoulos (1992), Liritzis and Petropoulos (1994) addressed the theme for the region of Athens in Greece. Other possibly affected karst areas include southern and central Italy (D’Agostino et al., 2018; Silverii et al., 2019), the entire Dinaric region (Figure 2) and various zones of China, including those hit by the 1976 Tangshan earthquake, Mw 7.6 (Hu et al., 2001), and by the 2008 Sichuan earthquake, Mw 7.9 (Lu et al., 2013). The tight connection between seismicity and the hydrogeology of karst environments works also in the opposite direction, with strong earthquakes that are able to affect and modify groundwater circulation (Amoruso et al., 2010).

FIGURE 2

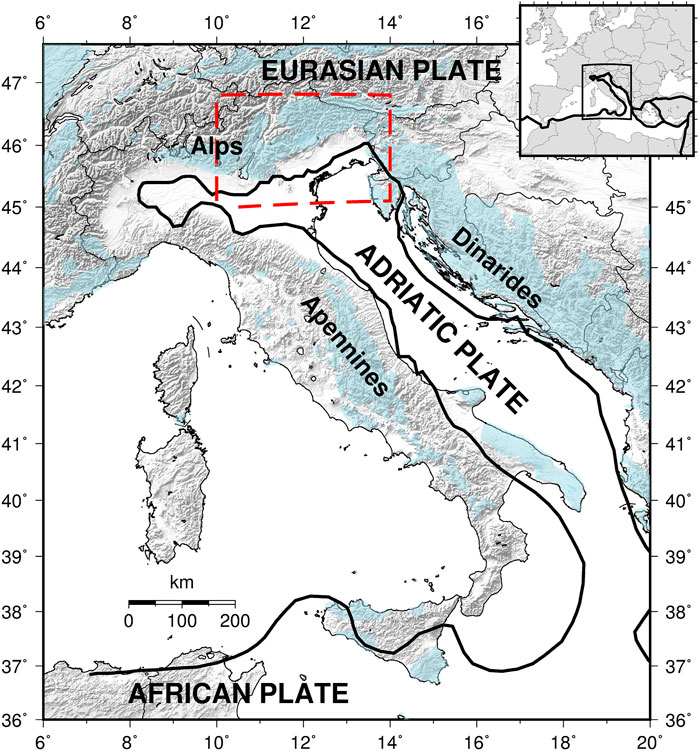
FIGURE 2. Tectonic setting of Italy with the indication of the study area (dashed red rectangle). In light blue the carbonate rock outcrops (https://www.fos.auckland.ac.nz/our_research/karst/).

Northeastern Italy has favorable conditions for investigating the effect of groundwater recharge on seismicity because it combines geological features (active tectonics and developed karst) with long time series of observed earthquakes and meteorological parameters. The optimal method of study should apply accurate hydrogeological and geophysical modeling, taking into account precise measures or, at least, realistic estimations of the variables that are involved. Due to the large number of details and the inherent complexity, such a deep investigation can be carried out for limited portions of the territory. Furthermore, important observations are available just for the last few decades (e.g., values of geodetic deformation from GNSS or gravity data from GRACE) and are still insufficient to investigate on the systematic connection between precipitation and the rare occurrence of serious earthquakes. Nevertheless Pintori et al. (2021) have carried out an important research of this type for the central sector of the study area, analyzing the relationship between precipitation and minor seismicity in the time period 2010–2019. The present study adopted a complementary approach and looked at major seismicity in a long time period using solely statistical methods (no physical modeling). The occurrence of damaging earthquakes (magnitude Mw ≥ 4.8) in the last 120 years was compared with the evolution of the Palmer Drought Severity Index (PDSI), a coarse index of soil moisture introduced for agriculture applications that takes into account the effect of precipitation and temperature cumulated through time. Despite its limitations (Alley, 1984) and the lack of a direct applicability to karst environments (it was devised for agricultural soils) PDSI has shown to correlate over most land areas with the water storage changes estimated from GRACE (Gravity Recovery and Climate Experiment) satellite observations (Dai, 2011). The hypothesis here investigated was that major groundwater increases at the regional level detected by means of PDSI could indicate favorable conditions for the occurrence of strong earthquakes and a situation of augmented seismic hazard in a broad area.

The relationship between groundwater and strong earthquakes was explored further in this work by extending the analysis to the last millennium: the series of historical destructive earthquakes with Mw ≥6.2 since 1000 AD was compared with the fluctuations of the ice cover in the Alps, which demonstrated to be an indicator of groundwater accumulation at the continental level (Holzhauser et al., 2005).

Study Area

The investigation was carried out in the area comprised between latitude 45.1–46.8°N and longitude 10.0–14.0°E, corresponding to northeastern Italy and a limited portion of southern Austria and western Slovenia (Figures 2, 3). The area is positioned at the collisional boundary between the Adria microplate and the Eurasia plate, characterized by a compressive regime (Sugan and Peruzza, 2011; Bressan et al., 2019). It includes a series of seismogenic structures along the margin of the eastern Southern Alps, shown as dotted areas in Figure 3 (DISS Working Group, 2018). According to the Italian seismic catalog (Rovida et al., 2019) they originated at least six destructive earthquakes in the last millennium (moment magnitude Mw between 6.2 and 6.5, stars in Figure 3) and 27 damaging-destructive earthquakes since 1901 (Mw between 4.8 and 6.4, red circles in Figure 3). Altogether these earthquakes delineate four spatial clusters: from east to west, the broad Friuli area roughly centered on Mt. Canin; the Cansiglio Plateau; the Mt. Grappa area and the lake Garda area, with approximate center on Mt. Baldo. The mountainous part of the investigated area is largely covered by calcareous rock (light blue shadow in Figure 3), mainly limestone with developed karst systems hosting large aquifers (Società Speleologica Italiana, 2002; Christian and Spötl, 2010; Turk et al., 2014). There are numerous karst massifs, often thicker than 2,000 m, located by the main seismic clusters (triangles in Figure 3).

FIGURE 3

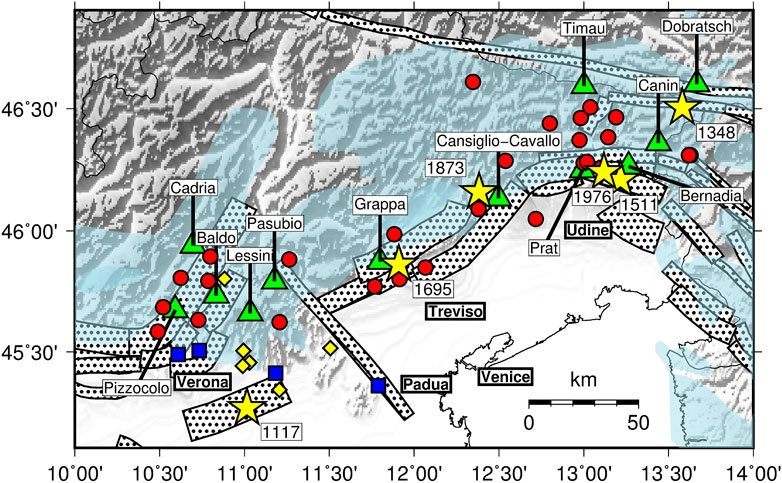
FIGURE 3. Epicenters of damaging and destructive earthquakes located in northeastern Italy (Rovida et al., 2019; Rovida et al., 2020): M ≥ 6.2 earthquakes since 1000 AD (yellow stars) and M ≥ 4.8 earthquakes since 1900 (red circles). The diamonds are alternative epicenters of the 1117 earthquake proposed by various authors, collected by Guidoboni et al. (2005). The dotted areas are the composite seismogenic sources from the DISS database (DISS Working Group, 2018). In light blue the carbonate rock outcrops (http://web.env.auckland.ac.nz/our_research/karst). The triangles are the karst massifs placed by the main clusters of earthquakes. The blue squares are geothermal fields fed by meteorological water from karst areas.

The study area is the rainiest in Italy, reaching an average yearly precipitation larger than 2,500 mm on east, by the Slovenian border (Auer et al., 2007), which is also the zone of maximum release of seismic energy (Figure 4). Due to the orography and general circulation patterns, the area of most intense precipitation (more than 1,200 mm/year, Figure 4) roughly follows the alignment of the seismogenic structures and the main clusters of earthquakes. By filling karst aquifers, precipitation causes significant transients of crustal deformation, an effect studied in detail based on recent GPS measurements (Devoti et al., 2015; Serpelloni et al., 2018).

FIGURE 4

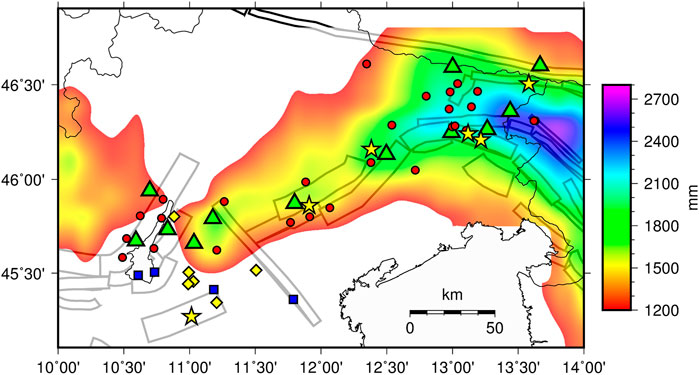
FIGURE 4. Cumulative yearly precipitation (average 1901–2012) in northeastern Italy (only areas with at least 1200 mm/year). The other elements are the same of Figure 3.

Data

Seismic data were drawn form the catalog CPTI15, version 2.0 (Rovida et al., 2019, 2020), considering earthquakes with moment magnitude Mw ≥4.8 occurred in the study area since 1901. The magnitude threshold corresponds, on average, to the lowest limit for damaging earthquakes (Gasperini, 2004) and, according to magnitude/frequency analysis (Bragato, 2014), it guarantees the completeness of the catalog. The investigation concentrated on the mainshocks, with aftershocks removed. The events were selected using the declustering algorithm by Gardner and Knopoff (1974) but preliminary tests showed that other algorithms (Reasenberg, 1985; Uhrhammer, 1986) give almost identical results. The final catalog includes 27 earthquakes with epicenters shown in Figures 3, 4 (red circles) and magnitude/time distribution shown in Figure 5 (red vertical bars). The largest event is the 1976 Friuli earthquake (Mw 6.45). Since 1901, two other earthquakes exceeded magnitude 6: the 1936, Alpago-Cansiglio earthquake and the 1928, Tolmezzo earthquake (Mw 6.06 and 6.02, respectively).

FIGURE 5

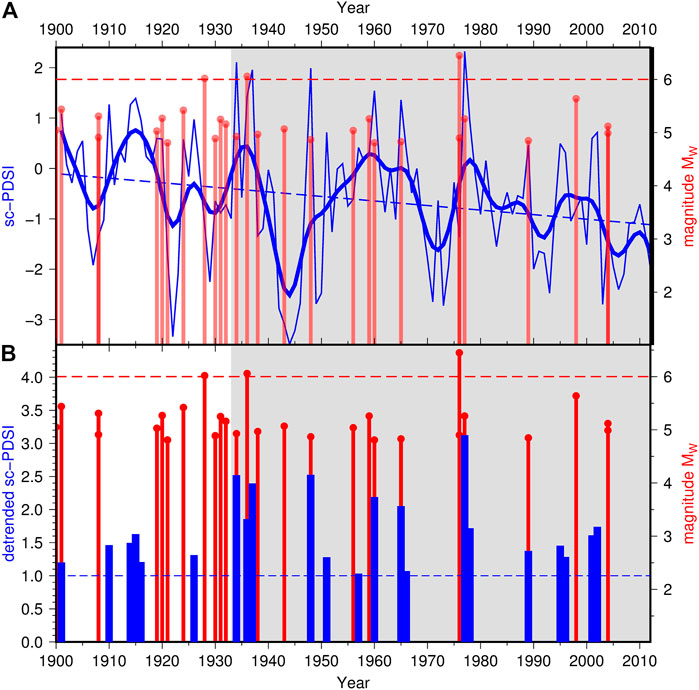
FIGURE 5. Relationship between the occurrence of M ≥ 4.8 earthquakes and the evolution of sc-PDSI in northeastern Italy in the time period 1901–2012 (in grey the time period 1934–2012): (A) earthquakes (red bars) and sc-PDSI time series (thin blue line) with the indication of its smoothed version obtained by kernel regression using a smoothing bandwidth ±2 years (thick blue line) and its trend estimated by linear regression (dashed blue line); (B) earthquakes (red bars) and detrended sc-PDSI (only values larger than 1, blue bars).

Earthquake data were compared with the time evolution of the Palmer Drought Severity Index (PDSI). The PDSI is a standardized measure of soil moisture used in agriculture (Palmer, 1965; Dai, 2011; Dai and National Center for Atmospheric Research Staff, 2019) computed from rainfall data and a model of evapotranspiration based on surface temperature and soil characteristics. It takes values between −10 and 10 going from extremely dry to extremely wet conditions. Its main application is for drought monitoring, with values below −3 representing severe to extreme drought. For example, referring to a well-documented recent case, in the years 2012–2016 California suffered one of the worst droughts of its history (Lund et al., 2018), with PDSI reaching values between −5 and −3 (data from the NOAA National Climatic Data Center available at https://www7.ncdc.noaa.gov/CDO/CDODivisionalSelect.jsp, Vose et al., 2014). PDSI has memory of the climate history (9–18 months in North America, Vicente-Serrano et al., 2010) and works at a resolution of about one year (i.e., it is insensitive to drought episodes shorter than one year). As mentioned in the Introduction, the adoption of PDSI for the present work is justified by the geophysical meaning pointed out by Dai (2011), according to which PDSI correlates well with groundwater recharges estimated using GRACE data. The data source was the Old-World Drought Atlas (OWDA) by Cook et al. (2015) restricted to the time interval 1901–2012 (the portion of the atlas entirely based on instrumental measurements). The OWDA reports values of the self-calibrated PDSI (sc-PDSI), a variant of the original PDSI proposed by Wells et al. (2004) to improve its spatial comparability. The time series of sc-PDSI are provided for a grid of points spaced 0.5° in latitude and longitude, covering Europe, North Africa, and the Middle East. This work refers to the spatial average computed over the study area, obtained directly from the web page of the OWDA (http://drought.memphis.edu/OWDA). At OWDA the values of sc-PDSI are available for a specific month of the year (e.g., every June) or as the average over consecutive months (maximum the entire year). The following analysis refers to the default (average over the summer months June-July-August). The time series of sc-PDSI is shown in Figure 5A (thin blue line). It is characterized by large oscillations, both annual and multi-annual (smoothed curve, thick blue line), with a marked drought period (sc-PDSI near to -3.5) around 1945 and a few maxima near to the value 2. Noticeably, it is characterized by a decreasing trend that reflects the ongoing climate change in the study area, towards higher temperature and less precipitation.

Preliminary Analysis

The present work aimed to assess the time correlation between seismicity and sc-PDSI using a statistical formal test. In order to choose the best statistical approach, some preliminary analysis was performed. Figure 5A shows the time evolutions of the sc-PDSI and the occurrence of Mw ≥4.8 mainshocks in the study area between 1901 and 2012 (thin blue line and red bars, respectively). Following the indications by El Hariri et al. (2010) mentioned in the Introduction, the comparison was performed by looking at both the absolute levels of the groundwater recharge and to the amplitude of the increase compared to a base level (in this case the sc-PDSI signal with the long-term trend removed). According to Figure 5A the two strongest earthquakes (1936 Alpago-Cansiglio earthquake, Mw 6.06, and 1976 Friuli earthquake, Mw 6.45) occurred near to the two largest peaks of sc-PDSI: the 1936 earthquake follows the peak by 2 years; the 1976 earthquake precedes the largest peak by 1 year, but within a multi-year increasing trend evidenced by the smoothed sc-PDSI curve (thick blue line). The third strongest earthquake (1928 Tolmezzo earthquake, Mw 6.02) also follows a minor peak by 2 years Figure 5B is more concise and allows a thorough assessment of the time correlation between peaks of sc-PDSI and earthquake occurrence. The best correlation was obtained by removing the long-term linear trend of sc-PDSI (dashed blue line in Figure 5A) and considering the values larger than 1 (blue bars in Figure 5B). In the figure it is possible to recognize two time periods, evidenced by different background colors: one before 1934 (white background), more chaotic, with three clusters of seismicity that are uncorrelated with sc-PDSI (before 1910, around 1920 and just after 1930, 9 earthquakes in total); a second period, after 1934 (grey background) more regular, where the earthquakes are almost in one-to-one relationship with the peaks of sc-PDSI. Here (see the histogram in Figure 6) 15 out of 16 earthquakes are within 2 years from a peak of soil moisture (in 4 cases preceding the peak by one year). On the other hand, just one peak of sc-PDSI (on 1951) has no corresponding earthquake. This apparent time correlation will be formally tested in the following section, in order to assess its statistical significance and the probability that a similar combination could emerge for a random distribution of the events.

FIGURE 6

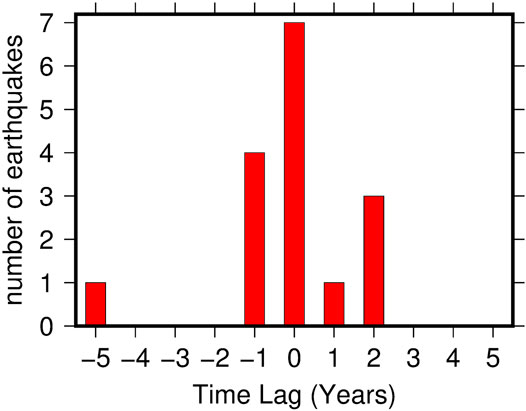
FIGURE 6. Earthquakes with M ≥ 4.8 occurred between 1934 and 2012 classified according to the time lag computed for the nearest sc-PDSI peak in Figure 5B.

Assessment of the Time Correlation

The time correlation between earthquakes and sc-PDSI was formally tested using the technique proposed by Doss (1989) and implemented in the software package K1D by Gavin et al. (2006). This technique is based on a simplification for one dimension of the bivariate Ripley’s K-function (Ripley, 1977): for two sets of arrival times P = {P₁,…,P_nP} and E = {E₁,..E_nE) (for peaks of sc-PDSI and earthquakes, respectively), the one-dimensional K-function is given by

${\mathrm{K}}_{\mathit{PE}}\left(\mathrm{t}\right)=\frac{\mathrm{T}}{{\mathrm{n}}_{\mathrm{P}}{\mathrm{n}}_{\mathrm{E}}}{\displaystyle \sum }_{\mathit{i}=1}^{{\mathrm{n}}_{\mathit{P}}}{\displaystyle \sum }_{\mathit{j}=1}^{{\mathrm{n}}_{\mathit{E}}}\mathrm{I}\left(\left|{\mathrm{P}}_{\mathit{i}}-{\mathrm{E}}_{\mathit{j}}\right|<\mathrm{t}\right),(1)$

where T is the overall observation period and I () is the identity function which gives 1 if the argument is true, 0 otherwise. The function K_PE(t) returns the number of couples (P_i,E_j) having a time lag shorter than t, normalized for the number of data and the time period of observation. From it derives the function

${\mathrm{L}}_{\mathit{PE}}\left(\mathrm{t}\right)=\frac{{\mathrm{K}}_{\mathit{PE}}\left(\mathrm{t}\right)}{2}-\mathrm{t}(2)$

Furthermore, the 95% confidence envelope for L_PE(t) in Equation 2 is computed using N randomizations of P and E (1,000 in the present case). If the function L_PE(t) obtained for the original data sets is above the confidence envelope, then the number of couples (P_i,E_j) with |P_i-E_j|<t is significantly larger than those awaited in a random distribution, which is an indication of significant synchrony within the time lag t.

The application of the test to peaks of sc-PDSI and earthquakes is illustrated by Figure 7. Between 1934 and 2012 the time correlation is significant within a time lag of both 2 and 3 years, in agreement with what suggested by the visual inspection. On the other hand, no significant correlation is found considering the time period 1901–1934.

FIGURE 7

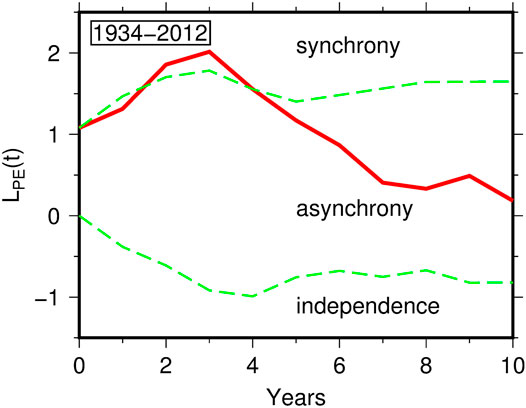
FIGURE 7. Test for synchronization between M ≥ 4.8 earthquakes in northeastern Italy and peaks of sc-PDSI of Figure 5B restricted to the time period 1934–2012. The three curves indicate the function L_PE (t) computed according to equation 2 (continuous line) and its 95% confidence envelope (dashed lines).

Extension to the Last Millennium

The Italian seismic catalog CPTI15 covers the last millennium. It is particularly reliable for the destructive earthquakes occurred in northeastern Italy since the late Middle Age, this because the earthquakes were clearly felt and able to produce damage in developed cities like Venice, Padua and Verona. Stucchi et al. (2011) estimated that, in the whole northern Italy (Alpine and Po Plain areas), the catalog is complete for Mw ≥6.14 earthquakes occurred since 1300. For northeastern Italy it reports five of these earthquakes, occurred on 1348, 1511, 1695, 1873, and 1976, whose epicenters are represented by yellow stars in Figures 3, 4. Another strong earthquake struck northeastern Italy on 1117, with major damages in the city of Verona. Although its existence is almost certain, the epicentral localization is still debated. CPTI15 assigns it to a seismogenic structure buried in the Po Plain (yellow star on the left of Figure 3), but various studies summarized by Guidoboni et al. (2005) placed it northerly (yellow diamonds in Figure 3), leaving open the possibility of a connection with the karst area of the Lessini Mountains.

As a long-term indicator of groundwater recharge, it was considered the reconstruction of the glacial evolution in the Alps. This because glacial expansion is mainly controlled by the same factors that improve water absorption in the soil: increased precipitation and low temperature (Bragato and Holzhauser, 2019 and references therein). A widely used glacial indicator is the length of the Great Aletsch Glacier (Alps of Valais, Switzerland, the largest glacier in the European Alps) reconstructed by Holzhauser (1997). Such a reconstruction was considered in many climate studies and was at the basis of the recognition of the Little Ice Age in Europe (Matthews and Briffa 2005). In particular, since 1000 AD (Figure 8) it evidences three main phases of expansion in the 14th, 18th and 19th centuries (termed Little Ice Age-Type Events by Wanner et al., 2000) and a minor expansion around 1100 AD. According to Holzhauser et al. (2005) the behavior of the Great Aletsch is time correlated with that of other glaciers and lakes in the western and central Europe, so that it is an index of water accumulation at the continental level. Under this hypothesis, Bragato and Holzhauser (2019) compared the glacial expansion with seismicity throughout Italy, finding a good correlation with variable earthquake rate of the last millennium. In Figure 8 the comparison is restricted to the earthquakes occurred in northeastern Italy between 1000 and 1900 AD: even in the long term it is confirmed an almost one-to-one match between seismicity and groundwater accumulation, with only one out of five major earthquakes occurred out of phase (the 1511 earthquake).

FIGURE 8

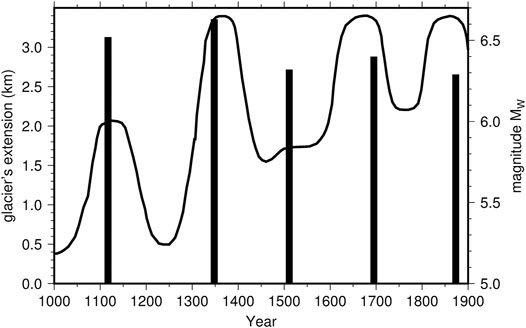
FIGURE 8. Relationship between the occurrence of M ≥ 6.2 earthquakes in northeastern Italy (vertical bars) and the glacial evolution in the Swiss Alps between 1000 and 1900 AD (continuous line).

Discussion and Conclusions

Statistical analysis for the time period 1901–2012 based on the one-dimensional Ripley function and graphical comparison extended back to the last millennium show a tight temporal connection between groundwater recharge and damaging earthquakes in northeastern Italy. The study area is positioned on an active plate boundary and subjected to compressive stress and faulting. It is therefore conceivable a triggering effect on pre-existing faults near to their critical state. The effect appears strong and systematic since 1934, with the two strongest earthquakes (1936 and 1976) placed by the two largest peaks of PDSI (Figure 5A) and almost all the damaging/destructive earthquake (15 out of 16 earthquakes with Mw ≥4.8) placed within two years from a relative maximum of PDSI (Figures 5B, 6). A similar proportion is observed for the destructive historical earthquakes, with four out of five major earthquakes (Mw ≥ 6.2) occurred between 1100 and 1900 AD that are synchronous with the main phases of glacial expansion and raising of lakes in the Alpine area (Figure 8). On the other hand, it is to recognize the groundwater contribution is not sufficient to explain the totality of earthquakes, as it is for a few clusters of earthquakes in the early part of the 20th century and the destructive earthquake of 1511 (Figures 5, 8, respectively).

Apparently contradictory with the triggering effect, in a few occasions (1956, 1959, and 1976) the earthquake preceded the peak of sc-PDSI by one year. In those cases the earthquake occurred during a multi-year increasing phase of the soil moisture parameter (most evident in the smoothed curve, thick blue line in Figure 5A), so that the time inversion might be explained by the long-term memory (9–18 months mentioned before) and consequent inertia of sc-PDSI, which records with delay significant changes of soil moisture. This delay evidences that sc-PDSI, although useful for a preliminary analysis of the triggering effect of groundwater, is not a valid seismic precursor. For this purpose more appropriate, reactive indexes must be devised, better if based on direct ground measurements. Furthermore, sc-PDSI does not take into account snow. Snow can accumulate large quantities of water and release it almost impulsively (in one month or so) by melting in spring. The relative contribution of snowmelt to groundwater recharge is quite variable, as it depends on local soil and climate characteristics (Hammond et al., 2019) and it is even more complex in heterogeneous karst areas (Chen et al., 2018). Nonetheless, in general, for the same amount of precipitation water, impulsive snowmelt is more effective than time-diffused rain to transfer moisture to soil, because it reduces the time for evapotranspiration. Snow may have contributed to triggering the earthquake of May 6, 1976. The event was preceded in the winter of 1974/1975 by significant snowfalls on Mt. Canin (the karst massif about 30 km northeast of the epicenter, Figure 3) that cumulated up to 7 m of snow (Pegani et al., 2002).

Previous considerations relate earthquake occurrence to the ongoing climate change. In agreement with other areas of the world, northeastern Italy is moving towards a dryer climate, mainly due to the increasing temperature, testified by the decreasing trend of sc-PDSI. In parallel to sc-PDSI, also the rate of damaging earthquakes has been reducing: there have been four earthquakes since 1980 (average 0.1 per year) compared to 12 between 1934 and 1980 (average 0.25 per year). Furthermore the current period without damaging earthquakes (16 years since November 2004) is the longest since 1901. A similar earthquake reduction involves the entire northern hemisphere (Bragato and Sugan, 2014), suggesting that meteoric groundwater plays a fundamental role on controlling seismicity at a large spatial scale.

In the last few years northeastern Italy has been hit by a series of extreme weather events characterized by heavy precipitation concentrated within a few days in autumn: the All Saints flood of 2010, the storm Vaia of October 2018; the flood of November 2019 with the exceptional “acqua alta” in Venice; the combined rainstorm and snowstorm of December 2020. These pulse-like events should have little effect on the sc-PDSI, which is most dependent on the yearly temperature/precipitation trend (see the minor rebound of the parameter after the flood of 2010 in Figure 5A). Nonetheless, similarly to what discussed for snow melting, the short time for evaporation could affect groundwater recharge in an anomalous way. The possible effect on seismicity might emerge in the next few years and should be monitored with attention. Even in this case, the need to follow rapidly changing groundwater conditions makes sc-PDSI inappropriate, so that alternative groundwater indexes must be devised.

The present analysis is not sufficient to clarify what is the most effective mechanism by which karst water recharge could trigger earthquakes in the study area. Both elastic stress transfer and diffusion of fluid pore pressure remain valid hypotheses. As a general criterion, the result of elastic stress transfer should be distinguished for the almost instantaneous response, compared to the slow advancement of pore pressure in a homogeneous media. Unfortunately this criterion is of no help in highly fractured areas. Based on observed phenomena, Talwani et al. (2007) have concluded that, in order to trigger earthquakes, fluid pulses must transmit along pre-existing fractures and joints with hydraulic diffusivity larger than that of the confining medium, with values in the range 0.1÷10 m²s⁻¹. Using the highest value of 10 m²s⁻¹, Mulargia and Bizzarri (2014) estimated that a fluid pulse takes about 150 days to reach a distance of 6 km from the source. Applied to northeastern Italy, where seismicity is mainly localized at depths between 5 and 15 km, it means that surface water can trigger earthquakes with a delay of the order of one year, which is compatible with what found in the present analysis. It is also to note that the seismic sources of the study area are mainly thrust faults, changing to strike-slip in the easternmost sector, by the Alpine-Dinaric junction (Saraò et al., 2020). According to the failure model mentioned in the Introduction (Saar and Manga, 2003) these types of fault should be blocked (for thrust) or insensitive (for strike-slip) to water recharge. This characteristic represents an element in favor of the alternative hypothesis of pore-pressure triggering. This type of triggering requires the hydraulic continuity between the Earth surface and deep seismogenic structures. Such a feature has not yet been proven for specific earthquakes sources. Nonetheless, the circulation of meteorological water originated in the pre-Alps and reaching depths up to 2.5–3.0 km has been demonstrated by studies on the geothermal fields localized south of the karst massifs in the western sector of the study area, shown as blue squares in Figures 3, 4 (Agostini, 2016; Torresan et al., 2020).

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: CPTI15 seismic catalog https://emidius.mi.ingv.it/CPTI15-DBMI15/index_en.htm; Old-World drought atlas http://drought.memphis.edu/OWDA/; Database of individual seismogenic sources http://diss.rm.ingv.it/diss.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This study was carried out with contributions from the programme POR-FESR Regione Veneto 2014–2020, Action 5.3.1.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Carla Barnaba and Fabiana Zandonai helped in the recognition of the karst massifs with large aquifers. All the figures were produced using the Generic Mapping Tools (Wessel et al., 2019).

References

National Center for Atmospheric Research Staff (Editor) (2019). The Climate Data Guide: Palmer Drought Severity Index (PDSI) Boulder, CO: National Center for Atmospheric ResearchAvailable at: https://climatedataguide.ucar.edu/climate-data/palmer-drought-severity-index-pdsi.

Agostini, L. (2016). Geological And Hydrogeochemical Characterization of Lake Garda-Lessini Mountains’ thermal Zone. PhD Thesis. Padua, (Italy): University of Padua.

Alley, W. M. (1984). The Palmer Drought Severity Index: Limitations and Assumptions. J. Clim. Appl. Meteorology 23, 1100–1109. doi:10.1175/1520-0450(1984)023<1100:TPDSIL>2.0.CO;2

CrossRef Full Text | Google Scholar

Amoruso, A., Crescentini, L., Petitta, M., Rusi, S., and Tallini, M. (2010). Impact of the 6 April 2009 L'Aquila Earthquake on Groundwater Flow in the Gran Sasso Carbonate Aquifer, Central Italyflow in the Gran Sasso Carbonate Aquifer. Hydrol. Process. 25, 1754–1764. doi:10.1002/hyp.7933

CrossRef Full Text | Google Scholar

Auer, I., Böhm, R., Jurkovic, A., Lipa, W., Orlik, A., Potzmann, R., et al. (2007). HISTALP-historical Instrumental Climatological Surface Time Series of the Greater Alpine Region. Int. J. Climatol. 27, 17–46. doi:10.1002/joc.1377

CrossRef Full Text | Google Scholar

Bettinelli, P., Avouac, J.-P., Flouzat, M., Bollinger, L., Ramillien, G., Rajaure, S., et al. (2008). Seasonal Variations of Seismicity and Geodetic Strain in the Himalaya Induced by Surface Hydrology. Earth Planet. Sci. Lett. 266, 332–344. doi:10.1016/j.epsl.2007.11.021

CrossRef Full Text | Google Scholar

Bragato, P. L., and Holzhauser, H. (2019). Observations on the Connection between Glacial Phases, Natural Catastrophes and Economic Trends of the Last Millennium in Italy. The Holocene 29, 1322–1334. doi:10.1177/0959683619846984

CrossRef Full Text | Google Scholar

Bragato, P. L. (2014). Rate Changes, Premonitory Quiescence, and Synchronization of Earthquakes in Northern Italy and its Surroundings. Seismological Res. Lett. 85, 639–648. doi:10.1785/0220130139

CrossRef Full Text | Google Scholar

Bragato, P. L., and Sugan, M. (2014). Decreasing Rate of M>=7 Earthquakes in the Northern Hemisphere since 1900. Seismological Res. Lett. 85, 1234–1242. doi:10.1785/0220140111

CrossRef Full Text | Google Scholar

Bressan, G., Barnaba, C., Bragato, P. L., Peresan, A., Rossi, G., and Urban, S. (2019). Distretti sismici del Friuli Venezia Giulia. Boll. Geof. Teor. Appl. 60, s1–s74. doi:10.4430/bgta0300

CrossRef Full Text | Google Scholar

Chen, Z., Hartmann, A., Wagener, T., and Goldscheider, N. (2018). Dynamics of Water Fluxes and Storages in an Alpine Karst Catchment under Current and Potential Future Climate Conditions. Hydrol. Earth Syst. Sci. 22, 3807–3823. doi:10.5194/hess-22-3807-2018

CrossRef Full Text | Google Scholar

Christian, E., and Spötl, C. (2010). Karst Geology and Cave Fauna of Austria: a Concise Review. Int. J. Speleogy. 39, 71–90. doi:10.5038/1827-806X.39.2.3

CrossRef Full Text | Google Scholar

Cook, E. R., Seager, R., Kushnir, Y., Briffa, K. R., Büntgen, U., Frank, D., et al. (2015). Old World Megadroughts and Pluvials during the Common Era. Sci. Adv. 1, e1500561. doi:10.1126/sciadv.1500561

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Agostino, N., Silverii, F., Amoroso, O., Convertito, V., Fiorillo, F., Ventafridda, G., et al. (2018). Crustal Deformation and Seismicity Modulated by Groundwater Recharge of Karst Aquifers. Geophys. Res. Lett. 45, 12. doi:10.1029/2018GL079794

CrossRef Full Text | Google Scholar

Dai, A. (2011). Characteristics and Trends in Various Forms of the Palmer Drought Severity Index during 1900-2008. J. Geophys. Res. 116, D12115. doi:10.1029/2010JD015541

CrossRef Full Text | Google Scholar

Devoti, R., Zuliani, D., Braitenberg, C., Fabris, P., and Grillo, B. (2015). Hydrologically Induced Slope Deformations Detected by GPS and Clinometric Surveys in the Cansiglio Plateau, Southern Alps. Earth Planet. Sci. Lett. 419, 134–142. doi:10.1016/j.epsl.2015.03.023

CrossRef Full Text | Google Scholar

DISS Working Group (2018). Database of Individual Seismogenic Sources (DISS), Version 3.2.1: A Compilation of Potential Sources for Earthquakes Larger Than M 5.5 in Italy and Surrounding Areas. Available at: http://diss.rm.ingv.it/diss/, Istituto Nazionale di Geofisica e Vulcanologia. doi:10.6092/INGV.IT-DISS3.2.1

CrossRef Full Text | Google Scholar

Doss, H. (1989). On Estimating the Dependence between Two point Processes. Ann. Stat. 17, 749–763. doi:10.1214/aos/1176347140

CrossRef Full Text | Google Scholar

El Hariri, M., Abercrombie, R. E., Rowe, C. A., and do Nascimento, A. F. (2010). The Role of Fluids in Triggering Earthquakes: Observations from Reservoir Induced Seismicity in Brazil. Geophys. J. Int. 181, 1566–1574. doi:10.1111/j.1365-246X.2010.04554.x

CrossRef Full Text | Google Scholar

Gardner, J. K., and Knopoff, L. (1974). Is the Sequence of Earthquakes in Southern California, with Aftershocks Removed, Poissonian?. Bull. Seismol. Soc. Am. 64, 1363–1367.

Google Scholar

Gavin, D. G., Hu, F. S., Lertzman, K., and Corbett, P. (2006). Weak Climatic Control of Stand-Scale Fire History during the Late Holocene in southeastern British Columbia. Ecology 87, 1722–1732. doi:10.1890/0012-9658(2006)87[1722:wccosf]2.0.co;

PubMed Abstract | CrossRef Full Text | Google Scholar

Guidoboni, E., Comastri, A., and Boschi, E. (2005). The "exceptional" Earthquake of 3 January 1117 in the Verona Area (Northern Italy): A Critical Time Review and Detection of Two Lost Earthquakes (Lower Germany and Tuscany. J. Geophys. Res. 110, B12309. doi:10.1029/2005JB003683

CrossRef Full Text | Google Scholar

Gupta, H. K. (2002). A Review of Recent Studies of Triggered Earthquakes by Artificial Water Reservoirs with Special Emphasis on Earthquakes in Koyna, India. Earth-Science Rev. 58, 279–310. doi:10.1016/S0012-8252(02)00063-6

CrossRef Full Text | Google Scholar

Hainzl, S., Kraft, T., Wassermann, J., Igel, H., and Schmedes, E. (2006). Evidence for Rainfall-Triggered Earthquake Activity. Geophys. Res. Lett. 33, L19303. doi:10.1029/2006GL027642

CrossRef Full Text | Google Scholar

Hammond, J. C., Harpold, A. A., Weiss, S., and Kampf, S. K. (2019). Partitioning Snowmelt and Rainfall in the Critical Zone: Effects of Climate Type and Soil Properties. Hydrol. Earth Syst. Sci. 23, 3553–3570. doi:10.5194/hess-23-3553-2019

CrossRef Full Text | Google Scholar

Hampel, A., Hetzel, R., and Maniatis, G. (2010). Response of Faults to Climate-Driven Changes in Ice and Water Volumes on Earth's Surface. Phil. Trans. R. Soc. A. 368, 2501–2517. doi:10.1098/rsta.2010.0031

PubMed Abstract | CrossRef Full Text | Google Scholar

Heki, K. (2003). Snow Load and Seasonal Variation of Earthquake Occurrence in Japan. Earth Planet. Sci. Lett. 207, 159–164. doi:10.1016/S0012-821X(02)01148-2

CrossRef Full Text | Google Scholar

Holzhauser, H. (1997). “Fluctuations of the Grosser Aletsch Glacier and the Gorner Glacier during the Last 3200 Years – New Results,” in Glacier Fluctuations during the Holocene (Paläoklimaforschung/Palaeäoclimate Research 24). Editor B. Frenzel (Stutgart, Germany: Gustav Fischer Verlag), 35–58.

Google Scholar

Holzhauser, H., Magny, M., and Zumbuühl, H. J. (2005). Glacier and lake-level Variations in West-central Europe over the Last 3500 Years. The Holocene 15, 789–801. doi:10.1191/0959683605hl853ra

CrossRef Full Text | Google Scholar

Hough, S. E. (2005). Remotely Triggered Earthquakes Following Moderate Mainshocks (Or, Why California Is Not Falling into the Ocean). Seismological Res. Lett. 76, 58–66. doi:10.1785/gssrl.76.1.58

CrossRef Full Text | Google Scholar

Hu, R., Yeung, M., Lee, C., and Jiang, J. X. (2001). Regional Risk Assessment of Karst Collapse in Tangshan. China. Env. Geol. 40, 1377–1389. doi:10.1007/s002540100319

CrossRef Full Text | Google Scholar

Huang, L.-S., McRaney, J., Teng, T.-L., and Prebish, M. (1979). A Preliminary Study on the Relationship between Precipitation and Large Earthquakes in Southern California. Pageoph 117, 1286–1300. doi:10.1007/bf00876220

CrossRef Full Text | Google Scholar

Johnson, C. W., Fu, Y., and Bürgmann, R. (2017). Seasonal Water Storage, Stress Modulation, and California Seismicity. Science 356, 1161–1164. doi:10.1126/science.aak9547

PubMed Abstract | CrossRef Full Text | Google Scholar

Kafri, U., and Shapira, A. (1990). A Correlation between Earthquake Occurrence, Rainfall and Water Level in Lake Kinnereth, Israel. Phys. Earth Planet. Interiors 62, 277–283. doi:10.1016/0031-9201(90)90172-t

CrossRef Full Text | Google Scholar

Kraft, T., Wassermann, J., Schmedes, E., and Igel, H. (2006). Meteorological Triggering of Earthquake Swarms at Mt. Hochstaufen, SE-Germany. Tectonophysics 424, 245–258. doi:10.1016/j.tecto.2006.03.044

CrossRef Full Text | Google Scholar

Liritzis, I., Diagourtas, D., and Makropoulos, C. (1995). A Statistical Reappraisal in the Relationship between Global and Greek Seismic Activity. Earth Moon Planet. 69, 69–86. doi:10.1007/bf00627771

CrossRef Full Text | Google Scholar

Liritzis, I., and Petropoulos, B. (1994). The Relationship between Precipitation and Shallow Earthquakes (M≥5 1/2) Revisited. Europ. Seism. Comm. XXIV. Gen. Assembly. Vol. 1. , 1973–1979.

Google Scholar

Liritzis, Y., and Petropoulos, B. (1992). A Preliminary Study of the Relationship between Large Earthquakes and Precipitation for the Region of Athens, Greece. Earth Moon Planet. 57, 13–21. doi:10.1007/bf00115412

CrossRef Full Text | Google Scholar

Lu, Y., Liu, Q., and Zhang, F. e. (2013). Environmental Characteristics of Karst in China and Their Effect on Engineering. Carbonates Evaporites 28, 251–258. doi:10.1007/s13146-013-0158-1

CrossRef Full Text | Google Scholar

Lund, J., Medellin-Azuara, J., Durand, J., and Stone, K. (2018). Lessons from California’s 2012–2016 Drought. J. Water Resour. Plann. Manage. 144, 04018067. doi:10.1061/(ASCE)WR.1943-5452.0000984

CrossRef Full Text | Google Scholar

Luttrell, K., and Sandwell, D. (2010). Ocean Loading Effects on Stress at Near Shore Plate Boundary Fault Systems. J. Geophys. Res. 115, B08411. doi:10.1029/2009JB006541

CrossRef Full Text | Google Scholar

Mantovani, E., Viti, M., Babbucci, D., Albarello, D., Cenni, N., and Vannucchi, A. (2010). Long-term Earthquake Triggering in the Southern and Northern Apennines. J. Seismol. 14, 53–65. doi:10.1007/s10950-008-9141-z

CrossRef Full Text | Google Scholar

Matthews, J. A., and Briffa, K. R. (2005). The ‘little Ice Age': Re‐evaluation of an Evolving Concept. Geografiska Annaler: Ser. A, Phys. Geogr. 87, 17–36. doi:10.1111/j.0435-3676.2005.00242.x

CrossRef Full Text | Google Scholar

Miller, S. A. (2008). Note on Rain-Triggered Earthquakes and Their Dependence on Karst Geology. Geophys. J. Int. 173, 334–338. doi:10.1111/j.1365-246X.2008.03735.x

CrossRef Full Text | Google Scholar

Mulargia, F., and Bizzarri, A. (2014). Anthropogenic Triggering of Large Earthquakes. Sci. Rep. 4, 6100. doi:10.1038/srep06100

PubMed Abstract | CrossRef Full Text | Google Scholar

Palmer, W. C. (1965). Meteorological Drought. Res. Paper No.45. Washington, D.C: Dept. of Commerce, 58.

Pegani, M., Filaferro, E., and Gregoris, C. (2002). Dieci Cannoni Per Una Rinascita?. Neve e Valanghe 46, 6–12.

Google Scholar

P. Gasperini Editor (2004). Catalogo dei terremoti CPTI2—App 1 Rapporto Conclusivo, Gruppo di Lavoro per la redazione della mappa di pericolosità sismica (Ordinanza PCM 20.03.03, n. 3274 (Istituto Nazionale di Geofisica e Vulcanologia), 29. Available at: http://zonesismiche.mi.ingv.it/documenti/App1.pdf.

Pintori, F., Serpelloni, E., Longuevergne, L., Garcia, A., Faenza, L., D'Alberto, L., et al. (2021). Mechanical Response of Shallow Crust to Groundwater Storage Variations: Inferences from Deformation and Seismic Observations in the Eastern Southern Alps, Italy. J. Geophys. Res. Solid Earth 126, e2020JB020586. doi:10.1029/2020JB020586

CrossRef Full Text | Google Scholar

Raleigh, C. B., Healy, J. H., and Bredehoeft, J. D. (1976). An experiment in Earthquake Control at Rangely, Colorado. Science 191, 1230–1237. doi:10.1126/science.191.4233.1230

PubMed Abstract | CrossRef Full Text | Google Scholar

Reasenberg, P. (1985). Second-order Moment of central California Seismicity, 1969-1982. J. Geophys. Res. 90, 5479–5495. doi:10.1029/jb090ib07p05479

CrossRef Full Text | Google Scholar

Rigo, A., Béthoux, N., Masson, F., and Ritz, J.-F. (2008). Seismicity Rate and Wave-Velocity Variations as Consequences of Rainfall: the Case of the Catastrophic Storm of September 2002 in the Nîmes Fault Region (Gard, France). Geophys. J. Int. 173, 473–482. doi:10.1111/j.1365-246X.2008.03718.x

CrossRef Full Text | Google Scholar

Ripley, B. D. (1977). Modelling Spatial Patterns. J. R. Stat. Soc. Ser. B (Methodological) 39, 172–192. doi:10.1111/j.2517-6161.1977.tb01615.x

CrossRef Full Text | Google Scholar

Rovida, A., Locati, M., Camassi, R., Lolli, B., and Gasperini, P. (2019). Catalogo Parametrico dei Terremoti Italiani (CPTI15), versione 2.0. Rome, Italy: Istituto Nazionale di Geofisica e Vulcanologia (INGV). doi:10.13127/CPTI/CPTI15.2

CrossRef Full Text

Rovida, A., Locati, M., Camassi, R., Lolli, B., and Gasperini, P. (2020). The Italian Earthquake Catalogue CPTI15. Bull. Earthquake Eng. 18, 2953–2984. doi:10.1007/s10518-020-00818-y

CrossRef Full Text | Google Scholar

Saar, M. O., and Manga, M. (2003). Seismicity Induced by Seasonal Groundwater Recharge at Mt. Hood, Oregon. Earth Planet. Sci. Lett. 214, 605–618. doi:10.1016/S0012-821X(03)00418-7

CrossRef Full Text | Google Scholar

Saraò, A., Sugan, M., Bressan, G., Renner, G., and Restivo, A. (2020). A Focal Mechanism Catalogue of Earthquakes that Occurred in the southeastern Alps and Surrounding Areas from 1928-2019. Earth Syst. Sci. Data 13, 2245–2258. doi:10.5194/essd-13-2245-2021

CrossRef Full Text | Google Scholar

Scafetta, N., and Mazzarella, A. (2015). Spectral Coherence between Climate Oscillations and the M ≥ 7 Earthquake Historical Worldwide Record. Nat. Hazards 76, 1807–1829. doi:10.1007/s11069-014-1571-z

CrossRef Full Text | Google Scholar

Serpelloni, E., Pintori, F., Gualandi, A., Scoccimarro, E., Cavaliere, A., Anderlini, L., et al. (2018). Hydrologically Induced Karst Deformation: Insights from GPS Measurements in the Adria‐Eurasia Plate Boundary Zone. J. Geophys. Res. Solid Earth 123, 4413–4430. doi:10.1002/2017JB015252

CrossRef Full Text | Google Scholar

Silverii, F., D'Agostino, N., Borsa, A. A., Calcaterra, S., Gambino, P., Giuliani, R., et al. (2019). Transient Crustal Deformation from Karst Aquifers Hydrology in the Apennines (Italy). Earth Planet. Sci. Lett. 506, 23–37. doi:10.1016/j.epsl.2018.10.019

CrossRef Full Text | Google Scholar

Società Speleologica Italiana (2002). Carta delle principali aree e sorgenti carsiche d'Italia. Genoa, Italy: ERGA Edizioni.

Stucchi, M., Meletti, C., Montaldo, V., Crowley, H., Calvi, G. M., and Boschi, E. (2011). Seismic Hazard Assessment (2003-2009) for the Italian Building Code. Bull. Seismological Soc. America 101, 1885–1911. doi:10.1785/0120100130

CrossRef Full Text | Google Scholar

Sugan, M., and Peruzza, L. (2011). Distretti sismici del Veneto. Boll. Geof. Teor. Appl. 52, s3–s90. doi:10.4430/bgta0057

CrossRef Full Text | Google Scholar

Talwani, P., Chen, L., and Gahalaut, K. (2007). Seismogenic Permeability,ks. J. Geophys. Res. 112, B07309. doi:10.1029/2006JB004665

CrossRef Full Text | Google Scholar

Tolstoy, M., Vernon, F. L., Orcutt, J. A., and Wyatt, F. K. (2002). Breathing of the Seafloor: Tidal Correlations of Seismicity at Axial Volcano. Geology 30, 503–506. doi:10.1130/0091-7613(2002)030<0503:BOTSTC>2.0.CO;2

CrossRef Full Text | Google Scholar

Torresan, F., Piccinini, L., Pola, M., Zampieri, D., and Fabbri, P. (2020). 3D Hydrogeological Reconstruction of the Fault-Controlled Euganean Geothermal System (NE Italy). Eng. Geology. 274, 105740. doi:10.1016/j.enggeo.2020.105740

CrossRef Full Text | Google Scholar

Turk, J., Malard, A., Jeannin, P.-Y., Petrič, M., Gabrovšek, F., Ravbar, N., et al. (2014). Hydrogeological Characterization of Groundwater Storage and Drainage in an alpine Karst Aquifer (The Kanin Massif, Julian Alps). Hydrol. Process. 29, 1986–1998. doi:10.1002/hyp.10313

CrossRef Full Text | Google Scholar

Uhrhammer, R. (1986). Characteristics of Northern and central California Seismicity, Earthq. Notes 57, 22–37.

Google Scholar

Vicente-Serrano, S. M., Beguería, S., López-Moreno, J. I., Angulo, M., and El Kenawy, A. (2010). A New Global 0.5° Gridded Dataset (1901-2006) of a Multiscalar Drought Index: Comparison with Current Drought Index Datasets Based on the Palmer Drought Severity Index. J. Hydrometeorol. 11, 1033–1043. doi:10.1175/2010JHM1224.1

CrossRef Full Text | Google Scholar

Vose, R. S., Applequist, S., Squires, M., Durre, I., Menne, M. J., Williams, C. N., et al. (2014). Improved Historical Temperature and Precipitation Time Series for U.S. Climate Divisions. J. Appl. Meteorol. Climatol. 53, 1232–1251. doi:10.1175/JAMC-D-13-0248.1

CrossRef Full Text | Google Scholar

Wang, C-Y., and Manga, M. (2010). Earthquakes and Water. Berlin and Heidelberg, Germany: Springer-Verlag. doi:10.1111/j.1468-8123.2009.00270.x

CrossRef Full Text

Wanner, H., Holzhauser, H., Pfister, C., and Zumbühl, H. (2000). Interannual To Century Scale Climate Variability In The European Alps. Erdkunde 54, 62–69. doi:10.3112/erdkunde.2000.01.05

Wells, N., Goddard, S., and Hayes, M. J. (2004). A Self-Calibrating Palmer Drought Severity Index. J. Clim., 17. CO, 2335–2351. doi:10.1175/1520-0442(2004)017<2335:ASPDSI>2.0

CrossRef Full Text | Google Scholar

Wessel, P., Luis, J. F., Uieda, L., Scharroo, R., Wobbe, F., Smith, W. H. F., et al. (2019). The Generic Mapping Tools Version 6. Geochem. Geophys. Geosyst. 20, 5556–5564. doi:10.1029/2019GC008515

CrossRef Full Text | Google Scholar