Performance Evaluation of GIS-Based Novel Ensemble Approaches for Land Subsidence Susceptibility Mapping

The optimal prediction of land subsidence (LS) is very much difficult because of limitations in proper monitoring techniques, field-base surveys and knowledge related to functioning and behavior of LS. Thus, due to the lack of LS susceptibility maps it is almost impossible to identify LS prone areas and as a result it influences severe economic and human losses. Hence, preparation of LS susceptibility mapping (LSSM) can help to prevent natural and human catastrophes and reduce the economic damages significantly. Machine learning (ML) techniques are becoming increasingly proficient in modeling purpose of such kinds of occurrences and they are increasing used for LSSM. This study compares the performances of single and hybrid ML models to preparation of LSSM for future prediction of performance analysis. In this study, the spatial prediction of LS was assessed using four ML models of maximum entropy (MaxEnt), general linear model (GLM), artificial neural network (ANN) and support vector machine (SVM). Alongside, the possible numbers of novel ensemble models were integrated through the aforementioned four ML models for optimal analysis of LSSM. An inventory LS map was prepared based on the previous occurrences of LS points and the dataset were divvied into 70:30 ratios for training and validating of the modeling process. To identify the robust and best LSSMs, receiver operating characteristic-area under curve (ROC-AUC) curve was employed. The ROC-AUC result indicated that ANN model gives the highest ROC-AUC (0.924) in training accuracy. The highest AUC (0.823) of the LSSMs was determined based on validation datasets identified by SVM followed by ANN-SVM (0.812).

Introduction

Land subsidence (LS) is a natural geo-hazard phenomenon that occurs around the globe and causes extensive deformation of the earth’s surface. More specifically, subsidence may causes lowering of the earth’s land surface by natural or human induced activities, most importantly mobilization of solid or fluid underground materials are the main causes (Herrera-García et al., 2021). In general, there is a downward motion of the rock and soil surface in an almost vertical direction or sometimes with a slight angle that is known as LS (Cigna and Tapete, 2021). This phenomenon occurs suddenly or sometimes gradually due to a number of natural as well as anthropogenic factors. The main factors for their occurrences are earthquakes, volcanic activity, floods, over-exploitation of groundwater and its decline, mining activities, tunnel construction, and so on (Erkens and Stouthamer, 2020; Lyu et al., 2020). Among all these possible factors, groundwater exploitation and structural weakness are the most important issues in this concern (Yu et al., 2020). Groundwater depletion is most responsible for LS and it is a slow and gradual process (Galloway and Burbey, 2011). The overdraft aquifer systems particularly in the agricultural and residential area are the most susceptible zone for the occurrences of LS (Shirzadi et al., 2018; Orhan et al., 2021). Like other natural geo-hazard phenomena, this incident also causes life loss and huge economic losses. Essentially, land loss causes devastating damage to property and infrastructure, such as construction, communication with transport networks, drainage systems, underground pipelines, and many more (Cigna and Tapete, 2021). LS not only affected environmental changes but also impacts on social and economic activities. Apart from all these direct effects, several indirect results such as minimizing groundwater storage capacity, water contamination, increases flood hazards (Wang et al., 2018; Nhu et al., 2020), dissolution of calcareous rocks and stem faulting and mining. The phenomenon of LS is not a recent activities rather it has a long history. A body of literature studies has been shown that during the past century LS occurred due to the depletion of groundwater over 200 places in 34 countries across the globe (Herrera-García et al., 2021). Land subsidence on a spatial and temporal scale is therefore causing significant environmental, socio-economic and financial damage across the globe.

Iran, its geographical location and associated conditions have favored a semi-arid and arid climatic region with frequency of drought in recent decades (Arabameri et al., 2021). Therefore, in order to overcome the drought, this country is faced with an increasing demand for water supply through over-extraction of groundwater due to the expansion of urban and agricultural uses (Babaee et al., 2020; Pourghasemi et al., 2020). In the upcoming decades, population growth and associated economic activities will continue to increase the demand of groundwater and groundwater depletion, and severe LS activities are found in different regions of the world (Famiglietti, 2014). Thus, the most important natural resources, i.e., water levels, are gradually declining due to over-extraction for agricultural, domestic and industrial uses (Abdollahi et al., 2019; Guzy and Malinowska, 2020). Apart from this, climate change and its associated phenomena have a major impact on LS in this region. The Phenomenon of climate change significantly increases the atmospheric temperature, as a result drought condition have been occurred and a large number of people greatly depends on groundwater, and gradually destruction of aquifers causes LS, particularly in the central and north-eastern parts of Iran (Rateb and Abotalib, 2020). Land use change is one of the most important factors for LS in arid and semi-arid climates (Tian et al., 2015; Pourghasemi et al., 2017). The pattern of land use land cover also impacted on groundwater availability and recharge capacity. Land use changes have been directly supported by land subsidence, particularly in the extreme semi-arid and arid climatic condition. As a result, the recovery of deformation surface after LS is costly and time consuming, it is therefore essential to predict land subsidence susceptibility mapping (LSSM) for proper management and optimal uses of land resources. The occurrences of LS subsequently causes land degradation and it is destroy infrastructure, agricultural land and other natural resources. Therefore, to control and manage the fertile agricultural land, infrastructure from LS it is necessary to optimal mapping of LS by which land use planners management the land resources in sustainable way (Ghorbanzadeh et al., 2018; Arabameri et al., 2021).

As a result, several geo-environmental conditioning factors, along with different prediction models, have been used to predict LSS. A number of hazard susceptibility maps have been developed worldwide, based on qualitative and quantitative methods (Oh et al., 2019; Mohammady et al., 2019). Advances in Remote Sensing and Geographic Information System (RS-GIS) technology, along with artificial intelligence, greatly help in the mapping of a number of natural hazards with proper management of environmental issues through land use planning. Recently, Interferometric Synthetic Aperture Radar (InSAR) observations satellite data have been used to monitor and detected LS areas (Karimzadeh and Matsuoka, 2020). The spatial and temporal land deformation is measured through InSAR observations and it is a microwave remote sensing system (Orhan et al., 2021). Several machine learning algorithm (MLA) has been used over time to predict LSSM, such as logistic regression (LR) (Tien Bui et al., 2018), artificial neural network (ANN) (Mohebbi Tafreshi et al., 2020), support vector machine (SVM) (Arabameri et al., 2021), logistic tree model (LTM) (Arabameri et al., 2021), decision tree (DT) (Lee and Park, 2013) and so on. However, the most recent ensemble model, i.e. a combination of several MLAs, has been widely used for better and meaningful results for this purpose. In another way, we can say that the Ensemble Model was used for the accurate presentation of single classifiers along with its higher accuracy (Pham et al., 2017). Beside this, the ensemble model also has the capacity to deal with the difficult relationship between different scales of influence and spatial data (Kanevski et al., 2004). Several research studies on LSS mapping using MLA and their ensemble by various researchers, such as Tien Bui et al. (2018); Abdollahi et al. (2019); and many more.

Thus, current research work on LSSM has been carried out in the arid and hyper-arid climate zone of the Kashan plain in the north of Esfahan Province to mitigate surface deformation and the proper management of surface structures. A body of literature survey (Arabameri et al., 2020d, 2021; Babaee et al., 2020; Rezaei et al., 2020) and based on the local topographical, hydrological, climatological, geological and environmental condition, here we have selected twelve appropriate LS conditioning factors. Therefore, we used twelve geo-environmental conditioning factors namely elevation, aspect, distance to road (DtR), groundwater drawdown, distance to fault (DtF), topographic wetness index (TWI), distance from stream (DtS), normalized differentiate vegetation index (NDVI), curvature, slope, land use and lithology to meet our objective. In this study, four popular MLAs namely the Maximum Entropy (MaxEnt), general linear model (GLM), artificial neural network (ANN) and support vector machine (SVM) were used for modeling and mapping of LS, based on the state-of-the-art skillful characteristics and literature study (Abdollahi et al., 2019). The selection behind these MLAs are based on their earlier involvement in different research work on natural hazard susceptibility studies and respective optimal prediction performance (Zamanirad et al., 2019; Mohebbi Tafreshi et al., 2020; Najafi et al., 2020). In the case of MaxEnt, it has the ability to choose the correct estimation of the uncertain probability distribution and to select the highest entropy of the given probabilistic constraints. The GLM algorithm is based on a logistic regression model and used for a fractional response to handle a binary value dataset. Structured code input and output nodes were determined by trial and error in ANN, and events and non-event phenomena were determined. SVM is mainly used for classification, error analysis; generalize the overall function and find out about the two-class hyperplane in the dataset. Finally, a total of 11 ensembles, in which six are two models ensemble and five are three-four models ensemble, have been developed for better predictive analysis of LSSM in this region. A body of literature survey and best of our knowledge it has been found that no research study on the 11 possible ensembles of aforementioned four ML algorithms were used in LS studies. The maximum ensemble methods were created using the aforementioned four popular ML algorithms to optimal estimation of LS prediction performance and this is the novelty in this research study. Thereafter, all of these output results were validated by area under curve (AUC) analysis. As a result, the LS susceptibility zones have been classified into five zones, i.e., very low, low, medium, high, and very high. Depending on the LS susceptibility zones, appropriate prevention strategies should be taken to control future occurrences and proper management strategies.

Materials and Methods

Description of the Study Area

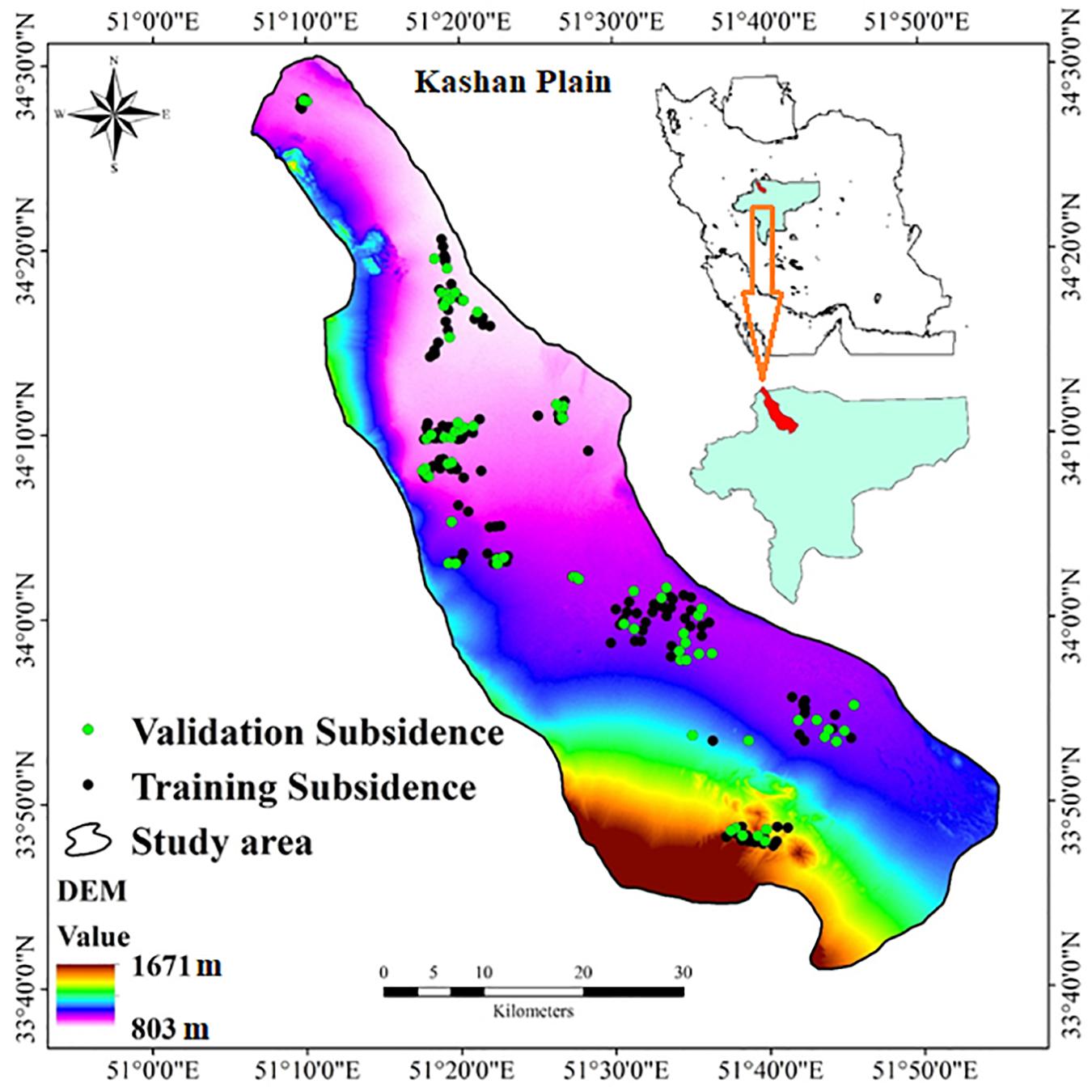
The Kashan plain is located in the North of the Esfahan Province in the Kashan city (between 33°40′00″ to 34°35′00″ N, and 51°05′00′ to 51°55′00″ E) and covers about 2,231 km² area (Figure 1). Elevation in the study area ranges between 803 m and 1,671 m above mean sea level. The average annual rainfall ranges between 75 and 185 mm and there is more rainfall in the west (Ghazifard et al., 2016). The climate of the study area has two classes of arid and hyper-arid. The minimum and maximum temperature in this area is 16 and 22°C, respectively, and also the minimum and maximum slopes in area are 0 and 129%, respectively (Ghazifard et al., 2016; Goorabi et al., 2020). Kashan plain is located in the foothills of the Karkas Mountains and on the margin of the central desert of Iran. Based on the land use map, poor rangeland the largest area (53.26%), and then by agricultural (21.5%), barren land (16.19%) and the remaining area is shared between afforest, sand dune, salt land and residential areas (Table 1). Based on the lithology map, diverse lithological have covered the area in which the largest area pertains to the low level piedmont fan and valley terrace deposits (68.33%), followed by unconsolidated windblown sand deposits including sand dunes (18.83%) and the remaining area is shared between other formations presented in detail in Table 1. Based on the land type (geomorphology) map, plates the largest area (32.09%), and then by flood plain (26.98%), low land (18.36%) and the remaining area is shared between mountains, scree and hill areas.

FIGURE 1

Figure 1. Location map of the study area.

TABLE 1

Table 1. Lithology of the study area.

Methodology

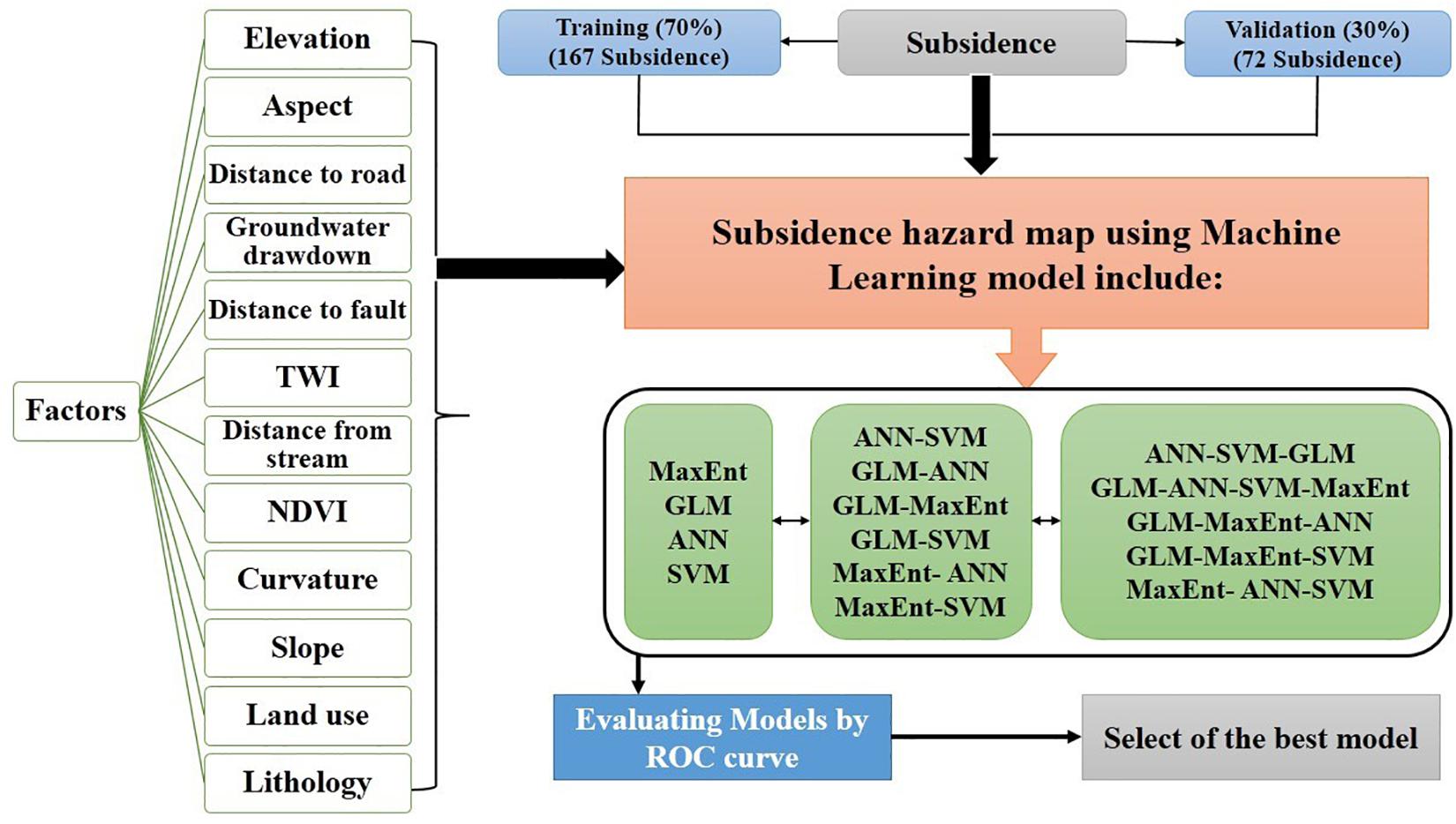
The research work of the LSSM has been carried out in four steps (Figure 2).

FIGURE 2

Figure 2. Flowchart of research in this study area.

• Preparing an LS inventory map using 239 LS points. Historical LS data were collected through field survey along with the help of Coppernnicus aerial view output and high resolution satellite images. A total of 12 geo-environmental control factors have been used to meet our research objective.

• Multi-collinearity testing was conducted among the conditioning factors used in this study using inflation factor variance (VIF) and tolerance (TOL) techniques (Band et al., 2020; Arabameri et al., 2021).

• To map the LS susceptibility of a number of MLAs, i.e., MaxEnt, GLM, ANN, and SVM have been used in this study together with a total of eleven ensemble methods.

• The performance of each model was validated by area under curve (AUC) analysis.

LS Inventory Map

The LS Inventory Map (LSIM) is the primary mapping tool for LSSM. LSIM shows the spatial distribution of a number of LS regions (Figure 1). It is well known that LS zones can be predicted on the basis of both the historical and the current spatial distribution of LS. The current inventory map in this area has been prepared using RS-GIS technology. As a result, LS areas have been identified from Coppernnicus aerial view output and extensive field surveys with the Global Positioning System (GPS) to locate the exact position in the field. In general, any type of inventory map can be used to assess the relationship between the distribution of a particular hazard location and the associated conditioning factors responsible for that hazard. A total of 239 LS points were used in this study, in which 70% (167) was used as a training dataset and 30% (72) was used for dataset validation. In this study, we have followed the influence of data Splitting performance (Nguyen et al., 2021) to divided the entire dataset was splitting into 70:30 ratio. Some of the field photographs in this study area are shown in Figure 3.

FIGURE 3

Figure 3. Some of mapped land subsidence in the study area.

Land Subsidence Conditioning Factors (LSCFs)

The quality of the predictive outcome of the LSSMs depends to a large extent on the selection of control factors. The evaluation of the relationship between the LS and their associated conditioning factors is therefore very necessary as it influences the modeling process. Twelve LSCFs have therefore been chosen to prepare the LSSM for this area. There is no universal criterion for the selection of these variables, although several literature studies have been conducted (Sahu et al., 2017). The types of LS and the availability of data are also taken into account for LSSM along with the geo-environmental conditions in this area. As already mentioned that in this study we have selected a total of 12 suitable LSCFs based on the literature survey and keeping in view the local geo-environmental conditions like topography, hydro-climatology and geological conditions. The 12 LSCFs used for this study are elevation, aspect, distance to road (DtR), groundwater drawdown, distance to fault (DtF), topographic wetness index (TWI), distance from stream (DtS), normalized differentiate vegetation index (NDVI), curvature, slope, land use and lithology (Figures 4A–L).

FIGURE 4

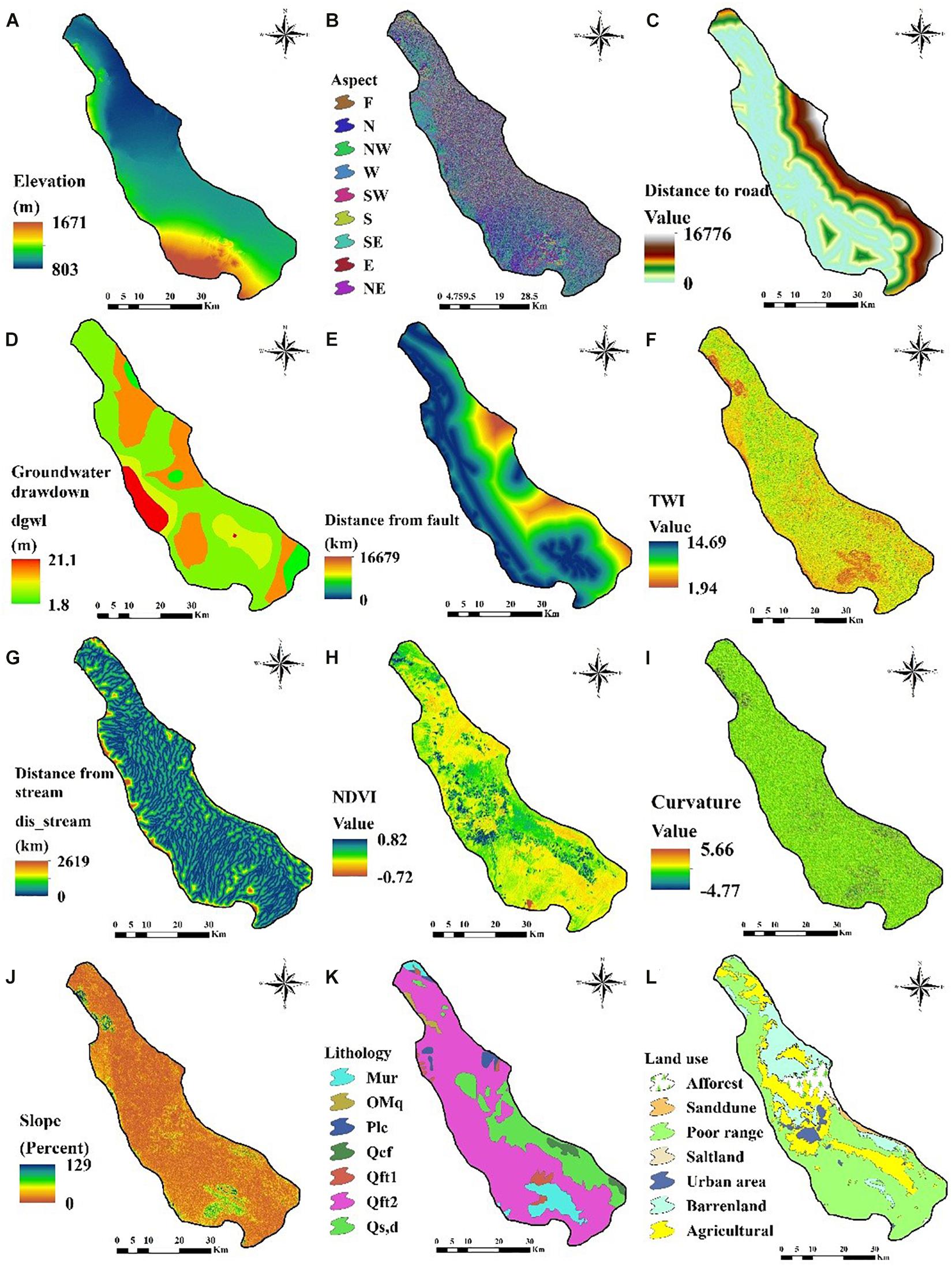
Figure 4. Land subsidence conditioning factors: (A) Elevation, (B) Aspect, (C) Distance to road, (D) Groundwater drawdown, (E) Distance from fault, (F) TWI, (G) Distance from stream, (H) NDVI, (I) Curvature, (J) Slope, (K) Lithology, and (L) Land use.

Therefore, several data sources were used to prepare these twelve conditioning factors. Different topographic and hydrological factors have been prepared from Advanced Land Observation satellite Phased Array type L-band Synthetic Aperture Radar digital elevation model (ALOSPALSAR DEM) with a 12.5 m resolution which is freely available on the Alaska Satellite Facility (ASF) website¹. Sentinel 2A satellite data with a resolution of 10 m was used to prepare land use and NDVI map. Beside this, the topographic map was collected from National Geographic Organization of Iran² at a scale of 1:1:50,000 to verify the land use map. The lithology map in this area was taken from the Geological Maps of Iran collected from the Geological Society of Iran (GSI)³ at a scale of 1:100,000.

As a result, the elevation map was derived from the DEM analysis of the ArcGIS 10.5 platform, with values ranging from 803 to 1671 m (Figure 4A). The second side of the slope is the derivative. Aspect is the altitude calculator and the slope direction of its eight neighbors. The aspect map of the present study area (Figure 4B) has been shown. DtR is an important factor in the occurrence of LS due to surface pressure and may cause LS in its surrounding area. The DtR range in this study ranges from 0 to 16,776 m (Figure 4C). Studies indicates that several types of factors such as climate-hydrological and physical factors significantly control soil moisture (Zhang et al., 2019).

Among the various factors, groundwater depletion is the most responsible conditioning factor for LS. The groundwater map shows values from 1.8 to 21.1 m (Figure 4D). DtF is also responsible for the deformation of the soil surface through the use of LS. The value of a DtF map is between 0 and 16,679 m (Figure 4E). The degree of water accumulation in the area depends on the TWI, which is a secondary topographic variable. The TWI map in this area was prepared using DEM on the ArcGIS 10.5 platform and the value ranges from 1.94 to 14.69 (Figure 4F). The following equation has been used to calculate the TWI.

$$TWI=lo{g}_e\left(\frac{A_s}{tan\mathrm{\beta }}\right)(1)$$

Where, A_s and β denotes cumulative catchment area (m²) and define slope angle, respectively.

The phenomenon of climate change and several human induced activities are considered the two major drivers flow pattern in a basin area and impacted on hydrological factors (Feng et al., 2020; Tian et al., 2020).

DtS is also a significant factor for LS. The probability of LS is increasing away from the river, and vice versa. The DtS map was shown in Figure 4G and ranged from 0 to 2,619 km. NDVI has the capacity to measure the growth and biomass of the vegetation (Yilmaz, 2009). This factor also plays an important role in the LSSM, as land use largely affects the occurrence of LS. The NDVI value ranged from −0.72 to 0.82, with a lower value indicating bare surface area and a higher value indicating forest cover (Figure 4H). The following equation was used to calculate the NDVI values using Sentinel 2A satellite data.

$$NDVI=\frac{Band8-Band4}{Band8+Band4}(2)$$

Where, Band8 is near-infrared and Band4 is red reflectance of the spectrum. Curvature represents the secondary geomorphic assets and shows the pattern of flow, sedimentation, erosion, etc. (Yesilnacar, 2005). The curvature map in this study was shown in Figure 4I and the values range from −4.77 to 5.66. The value of the slope map in this study area ranges from 0 to 129% (Figure 4J). LS is highly influenced by the slope of the area. Lithology is another key factor in the occurrence of LS as it affects the storage capacity of water. In this study, the lithological map (Figure 4K) was classified into seven types. Table 1 shows details of the lithological characteristics, such as their description, age of formation, percentage area, etc. Finally, the land use map has been prepared to understand the coverage of the surface area and its impact on the LS. The land use map (Figure 4L) for this area was classified into seven categories and their classes, along with their respective areas, are shown in Table 2.

TABLE 2

Table 2. Land use classes in the study area.

Multi-Collinearity (MC) Analysis

MC can be defined as the linear relationship between two or more variables in the dataset (Alin, 2010). Linear dependency is the top most priority given in this analysis and explained variables through correlation matrix (Saha et al., 2021b). Preparation of natural hazard related susceptibility mapping and their optimal prediction accuracy is based on suitable geo-environmental conditions (Arabameri et al., 2021). As a result, MC test has been carried out in this study to analysis the specific relationship among all of these variables and minimize the bias. Generally, MC occurs when there is a high correlation among the two or more variables (Arabameri et al., 2017). In other words, MC test is required to ensure the independent conditioning factors in a dataset (Chen et al., 2020). Tolerance (TOL) and variance inflation factors (VIF) techniques have been used by several researchers to test MC analyzes (Chowdhuri et al., 2020a). Therefore, in this study, we also used these two techniques and their respective equations were calculated as follows:

$$TOL=1-R_j^2(3)$$

$$VIF=\frac{1}{TOL}(4)$$

Where, $R_j^2$ is the regression value of j variables in a dataset. The MC occurred when the TOL value is < 0.10 or 0.20 and VIF value is > 5 or 10 of a respective variables in a given dataset.

Modeling of LSSMs

Maximum Entropy (MaxEnt)

The MaxEnt algorithm is based on the principle of maximum entropy and is one of the most popular predictive machine learning models (Woodbury et al., 1995). In general, MaxEnt estimates the probability distribution of the target based on the principle of maximum entropy and the probability distribution of LS occurrences in this study. MaxEnt has always chosen the highest entropy in a given probabilistic dataset. Apart from this, the presence features are used only by the MaxEnt model and have a significant impact on inaccessible areas with a reliable outcome (Reddy and Dávalos, 2003; Phillips et al., 2009). The relative influence of predictive variables (IPV) is estimated using jackknife re-sampling techniques within this model to generate response curves. Model performance was calculated by re-sampling the jackknife, excluding the predictor variables from the data set (Yang et al., 2013). Basically, this model identifies the true distribution (π) of LS, i.e. target occurrences over area X within a specific study area. Here, historical evidences of LS taken as a training dataset to define the true distribution (π). Let’s consider, the LS occurrence probability indicates the location of area X and the target probability distribution is π (X). Location X indicates the probability of LS occurring by P(y = 1|X) and the Bayes rule has been applied to express this algorithm as follows:

$$P(y=1|X)=\frac{P(y=1)P(X|y=1)}{P(X)}=\frac{P(y=1)\mathrm{\Phi }(\mathrm{X})}{1/|X|}(5)$$

Where, P(y = 1) indicates success of LS occurrences and (X) indicates total number of occurrences over the whole study area. π(X) is predicted through maximum entropy principle along with Gibbs probability distribution. Thus, Gibbs probability distribution may be expressed as follows:

$$q_{\mathrm{\lambda }}\left(X\right)=\frac{1}{Z_{\mathrm{\lambda }}(X)}\exp \left(\sum _{i=1}^n{\mathrm{\lambda }}_i{f}_i\left(X\right)\right)(6)$$

$$Z_{\mathrm{\lambda }}\left(X\right)=\sum _{y}exp\left(\sum _i{\mathrm{\lambda }}_i{f}_i(x,y)\right)(7)$$

Where, Z_λ(X) indicates normalization constant of a vector, λ_i indicates weights assigned of a vector. Furthermore, in the study area if m LS occurrences, variation between the regularization and log likelihood is expressed as follows (Phillips and Dudík, 2008):

$$\mathrm{\psi }\left(\mathrm{\lambda }\right)=\frac{1}{m}\sum _{i=1}^{m}In\left(q_{\mathrm{\lambda }}\left(X_i\right)\right)-\sum _{j=1}^n{\mathrm{\beta }}_j\left|{\mathrm{\lambda }}_j\right|(8)$$

Where, β_j represent the parameter of regularization for the j_th variables of predictor.

Generalized Linear Model (GLM)

The GLM was originally introduced and used by Nelder and Wedderburn (1972). In general, it is the probability of statistical method with a logit function and widely used in the field of natural hazards analysis (Lucà et al., 2011). The simple linear regression model was modified to form the GLM model. One major advantages of this model is that its simplicity, thus GLM extensively used in the wide fields of statistical analysis (Vorpahl et al., 2012). The basic function of this model is to develop multivariate regression between dependent and independent variables. Basically, the extensive form of a simple linear regression model is therefore GLM’s ability to build up a non-normal distribution between datasets (Payne et al., 2012). It also has the ability to develop binary datasets based on the presence and absence of data, using the logit link function for logistic regression. The GLM algorithm can easily handle the binary data set with the fractional response of the logit link function (Garosi et al., 2018). The basic function of this model fitting approaches includes finding out error distribution, determining the variables within this system and run the logit link function. According to Bernknopf et al. (1988) the function of GLM is as follows:

$$Y=\mathrm{Pr}\left(y=1\right)=\frac{e^{C_0+C_1+X_1+\mathrm{\cdots }+C_n{X}_n}}{1+e^{C_0+C_1{X}_1+\mathrm{\cdots }+C_n{X}_n}}(9)$$

Where, Y (logit-function) indicates the probability of an incident happening and it varies from 0 to 1; X₁…X_n represent the values of different controlling factors and C₁…C_n is their respective coefficient.

Artificial Neural Network (ANN)

One of the most popular MLAs, i.e., the ANN, is the most accurate and widely used forecasting model that has been effectively applied in various areas of forecasting analysis, such as social, economic, stock issues, natural hazard susceptibility mapping, etc. In general, ANN is a flexible statistical structure capable of identifying a non-linear relationship between input and output variables of a dataset (Hsu et al., 1995). In modern times, this model has been used with the utmost precision for forecasting, process control and pattern recognition in the broader perspective of science and technology fields (Sudheer et al., 2002). An ANN model has some unique features, and the result of this model’s output forecast is more attractive and accurate. The unique features of this model are based on data-driven, self-adapted methods, the ability to generalize, and the ability to manage complex non-linear relationships. Apart from that, among all non-linear classes, ANN is a universal approximator capable of approximating complex class functions with high accuracy (Zhang and Qi, 2005). Among the various algorithms used in the ANN model, Multilayer Perceptron (MLP) is the trendiest and widely used by a number of researchers (Kosko, 1992). Therefore, within this MLP algorithm ANN model consists of three layers, i.e., input layer, hidden layer and output layer (Mandal and Mondal, 2019). If the function of the input layer is not able to involve in a proper way than data structured of the model is measured by hidden layer nodes (Arabameri et al., 2020c). The hidden layer is determined through trial and error method within this model (Gong et al., 1996). Thus, the model structure systematically predicts by input as well as hidden layers and evaluates the output results. The output layer has been defined by Boolean value of 0 and 1. In this research study, 0 indicates no LS and 1 indicates LS. According to Hagan et al. (1995) the back propagation of an ANN model can be expressed as follows:

$$ne{t}_j^l\left(t\right)=\sum _{i=o}^p(y_i^{i-1}\left(t\right)w_{ji}^l(t))(10)$$

The net input of j^th neuron of layer l and I iteration

$$y_j^l\left(t\right)=f(ne{t}_j^{\left(l\right)}\left(t\right)(11)$$

$$f\left(net\right)=\frac{1}{1+e^{(-net)}}(12)$$

$$e_j\left(t\right)=c_j\left(t\right)-a_j\left(t\right)(13)$$

$${\mathrm{\delta }}_j^l\left(t\right)=e_j^l\left(t\right)a_j\left(t\right)\left[1-a_{j}x\left(t\right)\right](14)$$

δ factor for neuron j^th in the output layer i^th

$${\mathrm{\delta }}_j^l\left(t\right)=y_j^l\left(t\right)\left[1-y_j\left(t\right)\right]\sum {\mathrm{\delta }}_j^l\left(t\right)w_{kj}^{\left(l+1\right)}\left(t\right)(15)$$

δ factor for neuron j^th in the hidden layer i^th

$$w_{ji}^l\left(t+1\right)=w_{ji}^l\left(t\right)+\mathrm{\alpha }\left[w_{ji}^l\left(t\right)-w_{ji}^l\left(t-1\right)\right]+n{\mathrm{\delta }}_j^{\left(l\right)}\left(t\right)y_j^{\left(l-1\right)}\left(t\right)(16)$$

Where,αis the momentum rate and nis the learning rate within this model.

Support Vector Machine (SVM)

The SVM is a supervised machine learning method and broadly used in statistical test such as categorization and regression analysis (Chen et al., 2017). The algorithm of SVM is based on the principle of structural risk minimization and statistical learning (Vapnik, 2013). This model is binary classifiers and was introduced by Vapnik (2013) in 2013. In general, SVM has the capability of resolving the statistical dataset in the way of classification and regression analysis. In SVM model errors are recognized through several classification functions and finally generalize the overall function (Joachims, 1998). The main two principles of SVM are the optimal hyper-plane classification and the use of kernel function (Yao et al., 2008). Therefore, the principle of hyper-plane is used to differentiate into two classes, i.e., events and non-events, in this study it is LS and non-LS. The situation of closeness of optimal hyper-plane and training dataset is known as support vectors (Lee et al., 2017). The statistical induced problems in a SVM model can be employed in two ways: optimal separating hyper-plane from training dataset and conversion of non-linear data into linearly separable data through kernel function (Yao et al., 2008). In a SVM modeling, two classes have been created by hyper-plane, i.e., one is above the hyper-plane denoted by 1 and another is below the hyper-plane denoted by 0. The following equations have been used to calculate the hyper-plane in a SVM model.

$$Min\sum _{i=1}^n{\mathrm{\phi }}_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\mathrm{\phi }}_i{\mathrm{\phi }}_j{y}_i{y}_j(x_i,x_j)(17)$$

Subject to

$$Min\sum _{i=1}^n{\mathrm{\phi }}_i{y}_j=0and\mathrm{\hspace{0.33em}0}\le {\mathrm{\alpha }}_{\text{i}}\le \text{D}(18)$$

Where, x = x_i, i = 1, 2,… n represent the input variables of vector, y = y_i, j = 1, 2,…n represent the output variables of vector and φ_i is Lagrange multipliers.

The decision function of SVM can be expressed as follows:

$$f\left(x\right)=sgn\left(\sum _{i=j}^n{y}_i{\mathrm{\phi }}_{i}K(x_i,x_j)+a\right)(19)$$

Where, a is the bias which indicate linear distance of hyper plane from the origin, K(x_i,x_j)is kernel functions such as polynomial (POL) and radial basis function (RBF) and, these can be expressed as follow (Kavzoglu and Colkesen, 2009).

$$K_{POL}(x_i,x_j)={(\left(x*y\right)+1)}^d(20)$$

$$K_{RBF}(x_i,x_j)=e^{-y{||x-x_i||}^2}(21)$$

Validation and Accuracy Assessment

The Validation and evaluation of MLA and ensemble generated LSSMs were done by using area under receiver operating curve analysis (ROC-AUC) as it is a standard toll to do the same. ROC-AUC is a statistical analysis and has been widely used by a number of researchers to validate and assess the accuracy of several natural hazard susceptibility mappings (Moayedi et al., 2019; Nguyen et al., 2019; Yuan and Moayedi, 2019; Zhang and Wang, 2019). In general, it is a two-dimensional curve and consists of events and non-event phenomena (Frattini et al., 2010). It is a graphical construction on X-axis known as sensitivity and Y-axis known as 1-speficity. The X and Y axis are false positive (FP) and true positive (TP), respectively. The four indices, i.e., true positive (TP), true negative (TN), false positive (FP) and false negative (FN) have been used to assessment the ACC of ROC. In which, true and false positive indicates LS and non-LS points correctly, on the other side, true and false negative indicates LS and non-LS points incorrectly. In the ROC-AUC sensitivity identifies LS and 1-specificity identifies non-LS accurately. The ROC-AUC value ranges from 0.5 to 1. The lower value (0.5) indicates poor performance and higher value (1) indicates good performance by the model. The following equations were used to calculate the ROC-AUC value of a model.

$$Sensitivity=\frac{TP}{TP+FN}(22)$$

$$Specificity=\frac{TN}{FP+TN}(23)$$

$$AUC=\frac{(\sum TP+\sum TN)}{(P+N)}(24)$$

Where, P indicates presence of LS and N indicates absence of LS.

Results

Multi-Collinearity Analysis

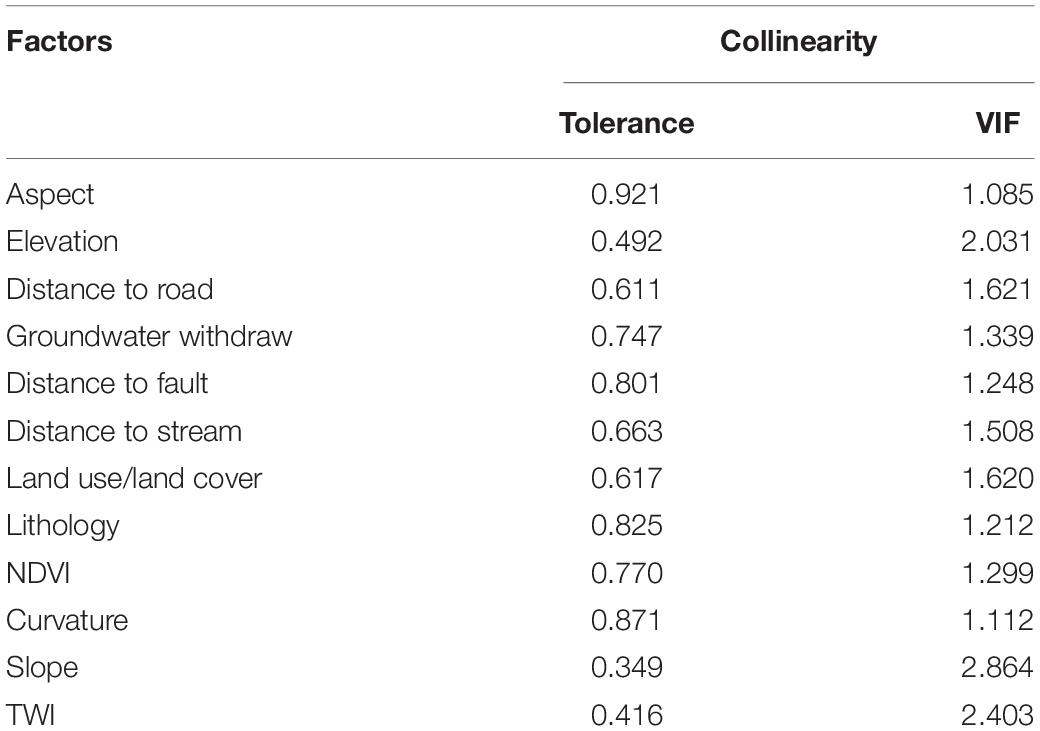
The multi-collinearity analysis is the significant factor selection method. It is the method where the land subsidence causative factors (LSCFs) have been filtered from high correlations among LSCF variables which have resulted in the erroneous output and uncertain predictions. In this study, the multi-collinearity analysis has been done through the Tolerance (TOL) and the Variance inflation factor (VIF) values of the LSCFs. When the TOL value is below 0.1 and the VIF is above 5, it has a problem with the multi-collinearity. Stream power index (SPI) and drainage density followed the above rules and we removed the variables. Rests of the 12 variables have been considered as LSCFs which have no multi-collinearity problems. The VIF of the 12 LSCFs ranges from 2.864 to 1.085 and the TOL value ranges from 0.349 to 0.921 (Table 3).

TABLE 3

Table 3. Multi-collinearity analysis of the subsidence factors.

Land Subsidence Susceptibility Maps (LSSMs)

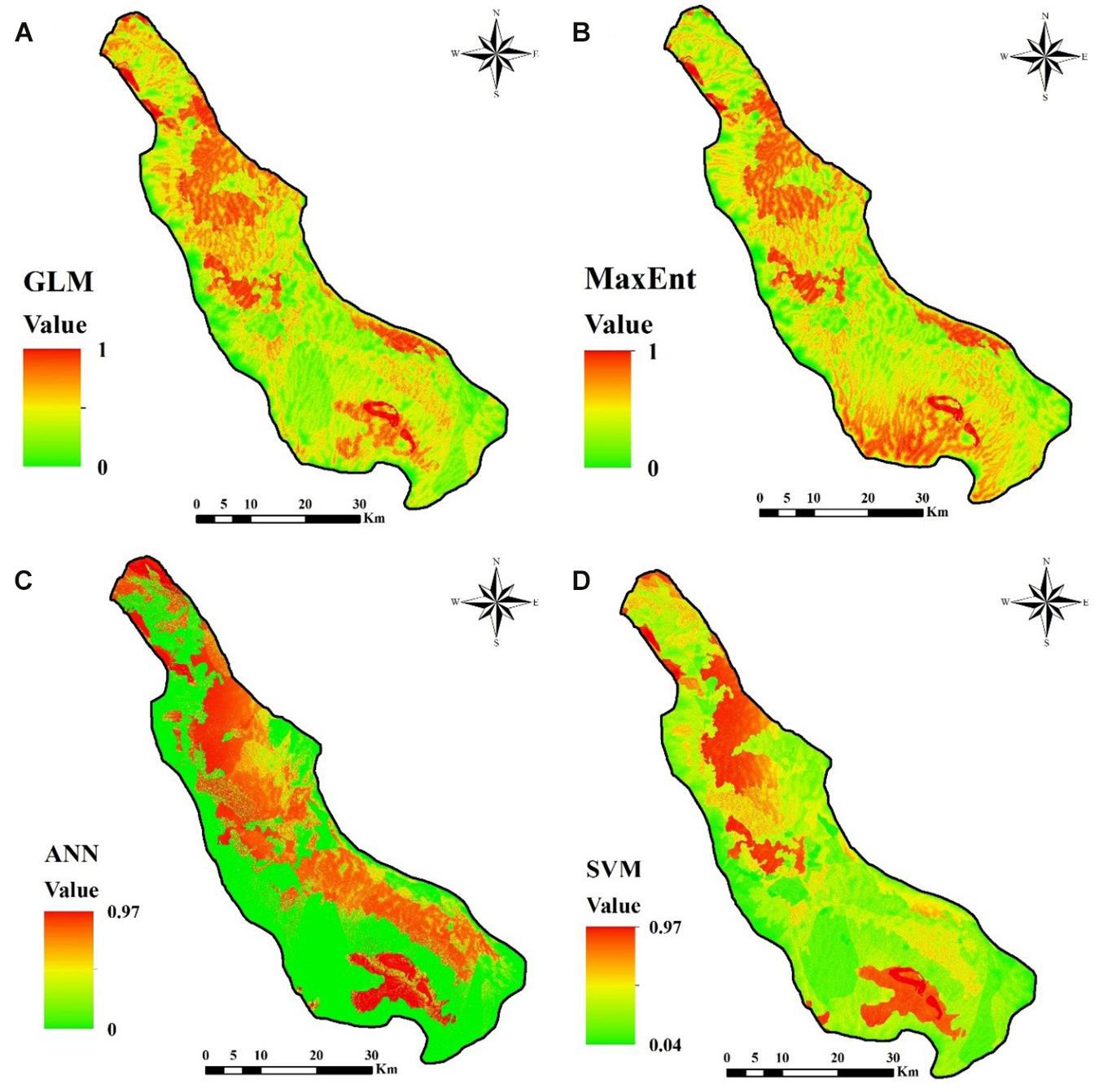
The land subsidence susceptibility maps of the Kashan plain have been created from the different single and ensemble classifier machine learning (ML) models. Here, four-stage of machine learning land subsidence susceptibility models were used. First, the four single or stand-alone ML; second, the two ensemble models were created by the integrated of two single models; third, again three ensemble models were created by the integrated of the three single ML models and last four ensemble models were created by the integrated of the four single ML model. Each of the models has presented an LSSM (Figures 5–7). The LSSMs were classified in five probability zones of very low, low, medium, high, and very high. There are many classification approaches to classify the land subsidence probability maps. These are natural break, quantile, equal interval, manual and standard deviation. In this study, all the mentioned classification methods have been applied and the natural break method gave the best classification result for all the maps. Where the spatial data have the big jump value, the natural break classification scheme is suitable for classification probability map (Ayalew and Yamagishi, 2005). The single ML and two, three, and four ensembles of LSSM have been analyzed in the next sections.

FIGURE 5

Figure 5. Land subsidence hazard mapping using: (A) GLM, (B) MaxEnt, (C) ANN, (D) SVM.

FIGURE 6

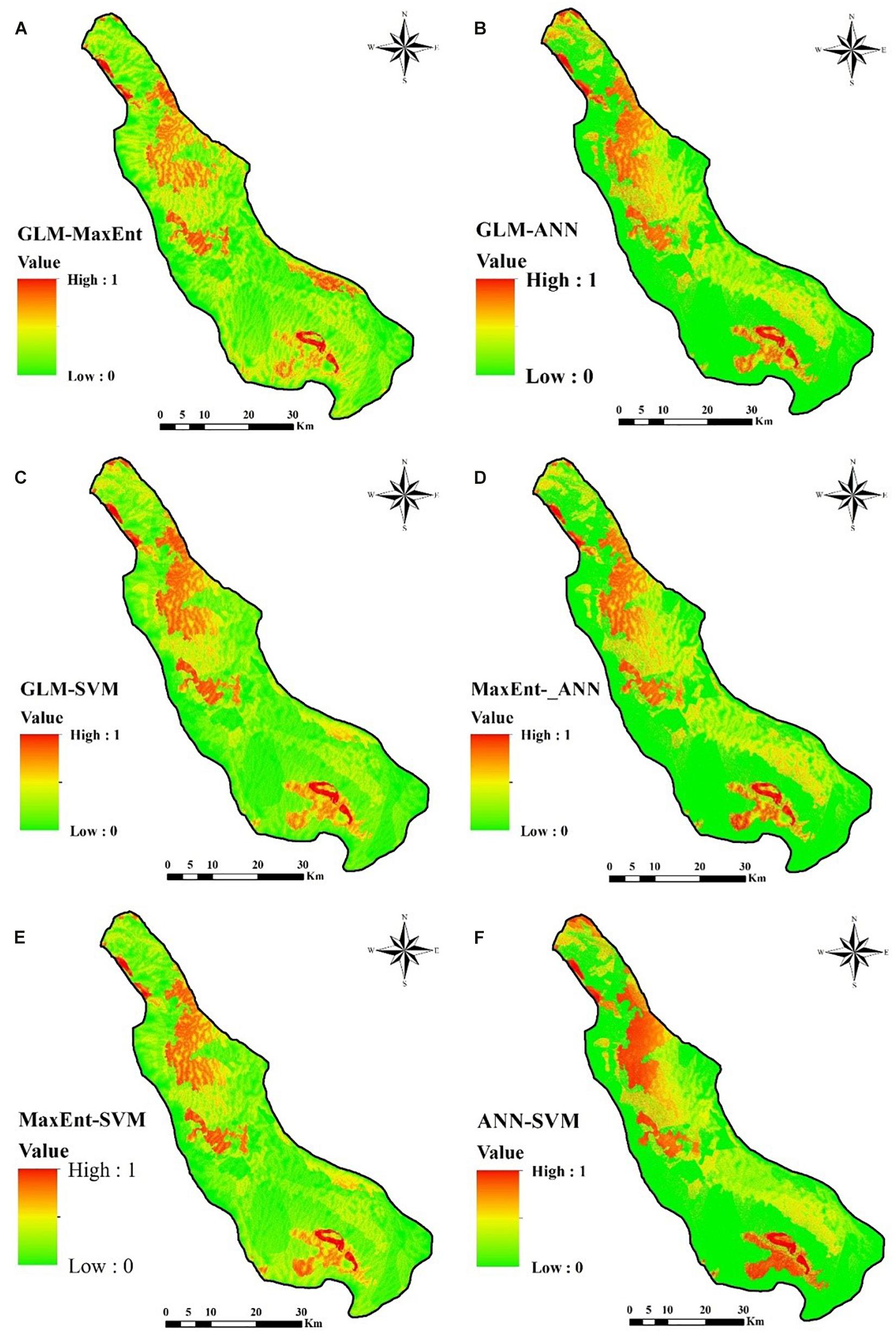
Figure 6. Land subsidence hazard mapping using: (A) GLM-MaxEnt, (B) GLM-ANN, (C) GLM-SVM, (D) MaxEnt-ANN, (E) MaxEnt-SVM, (F) ANN-SVM.

FIGURE 7

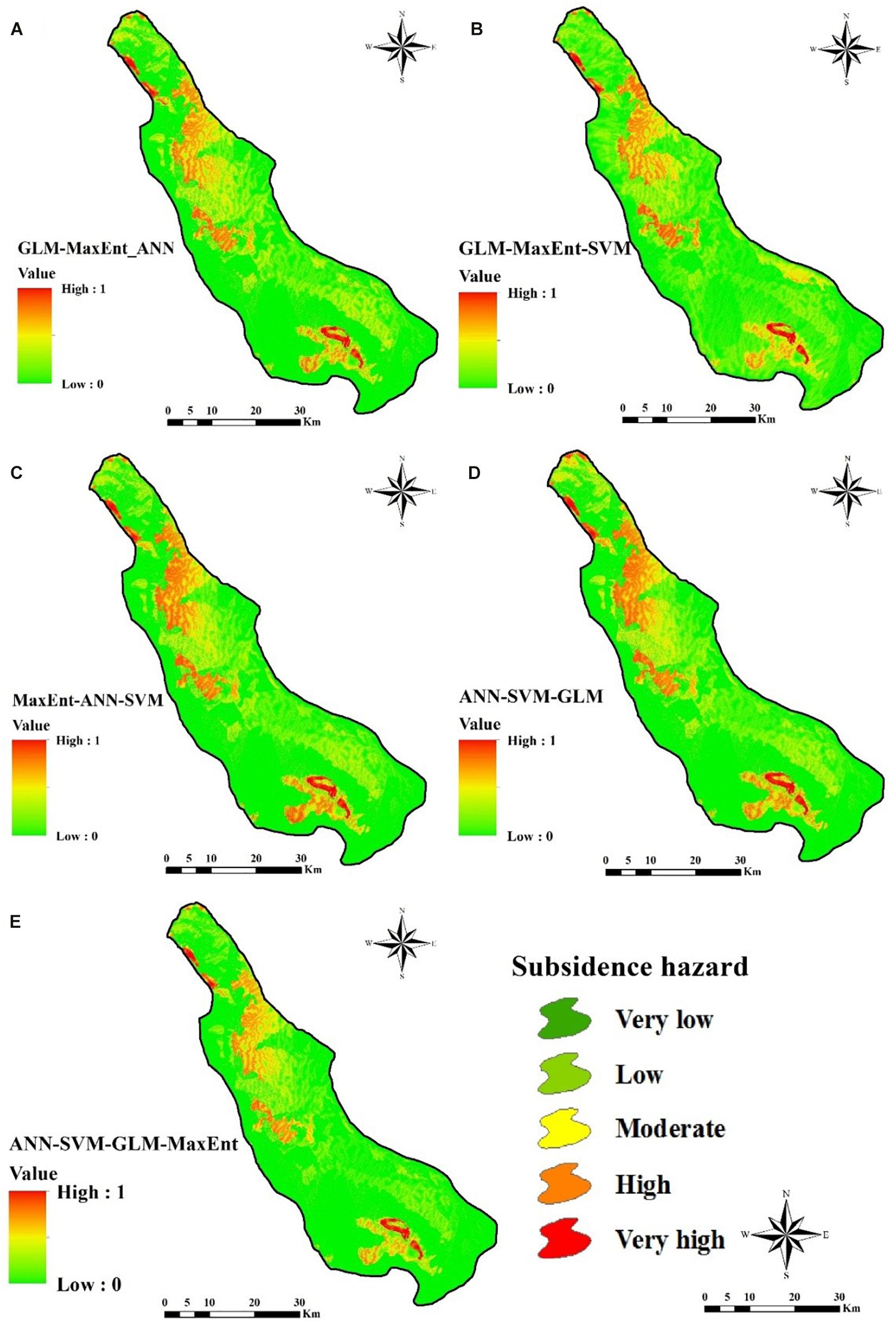
Figure 7. Land subsidence hazard mapping using: (A) GLM-MaxEnt-ANN, (B) GLM-MaxEnt-SVM, (C) MaxEnt-ANN-SVM, (D) ANN-SVM-GLM, (E) ANN-SVM-GLM-MaxEnt.

LSSMs From Single ML Models

There are four single ML models have been used for the LSSM. The LSSMs of the GLM, MaxEnt, ANN, and SVM models have been presented in Figure 5 and indicate the same symbol for each class. The areas of the very high, high, medium, low, and very low land subsidence susceptibility area in the GLM model are 15, 17, 24, 25, and 18% (Figure 8A). The percentage coverage of the very high, high, medium, low, and very low land subsidence susceptibility area in the MaxEnt model are 17, 19, 24, 24, and 16. The percent coverage of the very high, high, medium, low, and very low land subsidence susceptibility area in the ANN model are 25, 13, 6, 6, and 50%. And the areas of very high to very low land subsidence susceptibility area in the SVM model are 16, 10, 18, 29, and 27%. The areas of probability classes of land subsidence in the models of GLM, MaxEnt, and SVM are almost the same and they maintain consistency. The probability classes of LSSM in ANN model are slide difference from the other three models (Figure 8A).

FIGURE 8

Figure 8. Area percent classes in the different modeling: (A) one model, (B) two model, (C) three and four model.

LSSMs From First Stage Ensemble Models

After the single ML land subsidence susceptibility model, the first stage ensemble models were created by the integrated of two ML models. In this process, six ensemble models have been created. These are GLM-MaxEnt, GLM-ANN, GLM-SVM, MaxEnt-ANN, MaxEnt-SVM, and ANN-SVM (Figure 6). The very high probability of land subsidence areas varies from 9 to 10% in the above six ensemble models (Figure 8B). The percentage of the high probability of land subsidence areas ranges from 9 to 11. The percentage of medium probability of land subsidence areas ranges from 12 to 18. The low and very low probability area ranges from 13 to 27 and 37 to 54%, respectively (Figure 8B). So the very high and high probabilities of land subsidence classes have a good consistency in the six ensemble models.

LSSMs From Second and Third Stage Ensemble Models

In this stage, the possible ensemble models have been made by the integration of three and four single ML models. These ensemble models are GLM-MaxEnt-ANN, GLM-MaxEnt-SVM, MaxEnt-ANN-SVM, and ANN-SVM-GLM-MaxEnt. The LSSMs were prepared from these ensemble models presented in Figure 7. In this second stage ensemble model, the percentage of very high land subsidence susceptibility zone ranges from 5 to 6 (Figure 8C). The high land subsidence susceptibility probability zone varies from 7 to 8%. The percentage of medium land subsidence susceptibility probability zone ranges from 9 to 11. The low land subsidence probability zone varies from 15 to 21 and the very low land subsidence hazard probability zone ranges from 56 to 69%. So there are no such differences among the land subsidence hazard probability zone in second stage ensemble models. The final ensemble model or the third stage ensemble model was made through the integration of all four single models. The final ensemble model has 3, 7, 7, 14, and 69% of land subsidence susceptible areas for the very high, high, medium, low, and very low zone, respectively (Figure 8C).

Evaluation of Land Subsidence Model

Validation is an important task for modeling based output because of the accessibility of the model output determined by the model output validation. The goodness of fit and prediction accuracy of all ML ensemble models have been evaluated using training and validation land subsidence data applied the technique of area under curve (AUC) of the receiver operating characteristic (ROC) curve. The evaluation performance result of single ML and ensemble of two, three, and four ML models in training and validating stage have been shown in Figures 9, 10. All the single ML and ensemble two, three, and four ML methods showed the excellent goodness of fit and prediction accuracy of the models. The AUC-ROC of the single four ML model on the training stage showed in Figure 9A. The ANN model has the highest AUC value (0.924) followed by SVM and GLM. On the validation stage (Figure 10A), the SVM model got the highest (0.823) accuracy among the single ML model and followed by ANN (0.794). In case of the ensemble of two ML methods (Figures 9B, 10B), the ensemble of the ANN-SVM model has higher AUC-ROC in training (0.915) and validating (0.812) datasets and followed by the GLM-ANN (0.808) and ANN-MaxEnt (0.805). The ensemble of three and four ML algorithms showed the good accuracy of the model in both training and validating stage (Figures 9C, 10C). In the training stage, the highest AUC (0.89) value came from the ANN-SVM-GLM model followed by GLM-MaxEnt-ANN (0.884) and MaxEnt-SVM-ANN (0.884) model. On the validating stage, the high prediction rate of AUC has come from GLM-MaxEnt-ANN (0.788) and followed by MaxEnt-ANN-SVM (0.786). The AUC of the ensemble GLM-MaxEnt-ANN-SVM in training and validating stage are 0.838 and 0.755.

FIGURE 9

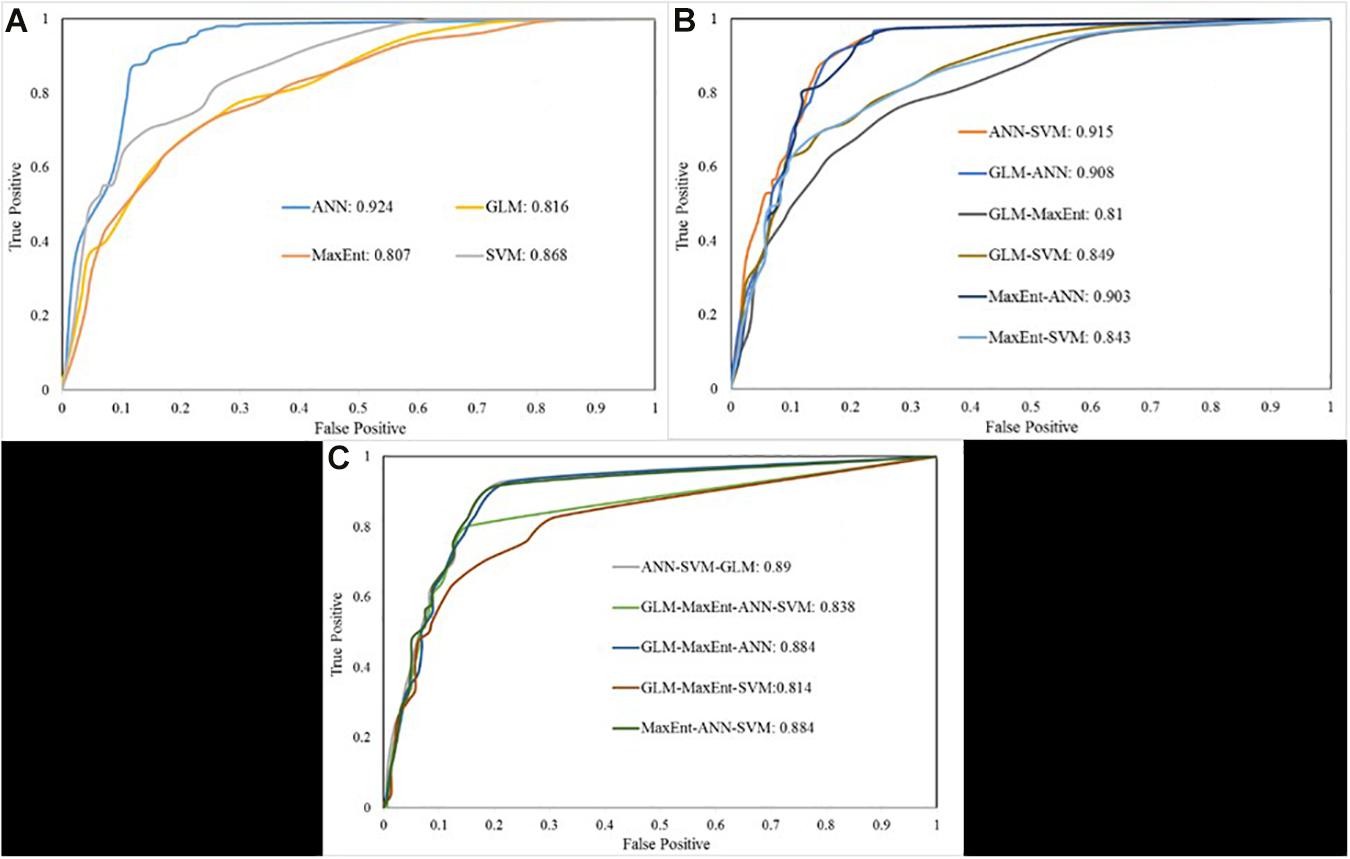
Figure 9. Area under the curves based on training datasets: (A) one model, (B) two model, (C) three and four model.

FIGURE 10

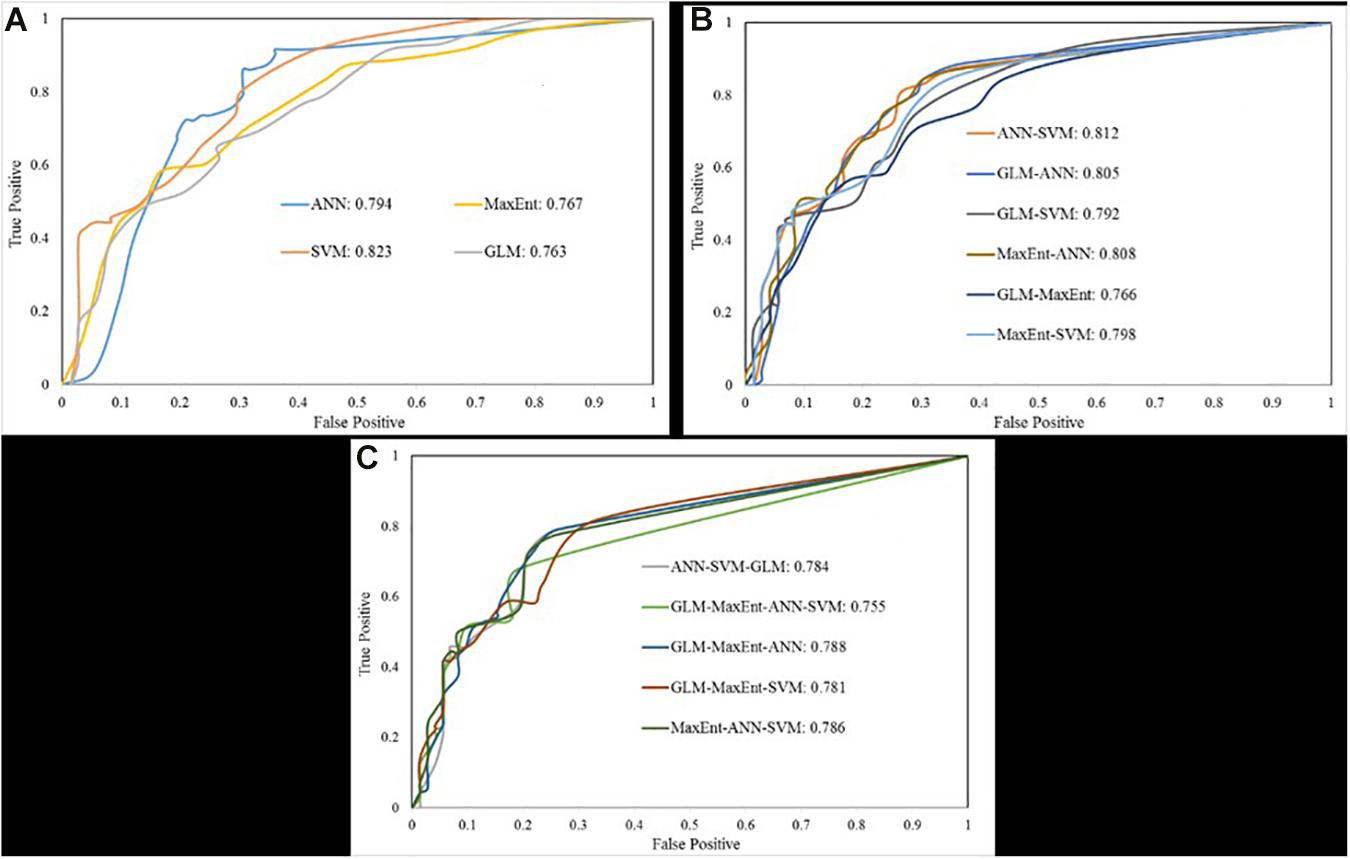
Figure 10. Area under the curves based on validation datasets: (A) one model, (B) two model, (C) three and four model.

Table 4 shows the comparison of AUC-ROC for all single ML and ensemble two, three, and four ML methods using training and validating datasets. The result of the reliability of ML algorithms based on training datasets has depicted that the ANN has the highest AUC (0.924) means this model is the best fit model for the land subsidence hazard mapping. And the second and third best fit models are the ANN-SVM (0.915) and GLM-ANN (0.908). The prediction accuracy of the ML algorithms based on validating datasets showed the SVM has the highest AUC (0.823) followed by ANN-SVM (0.812) and MaxEnt-ANN (0.808). The SVM model is the best model for the land subsidence susceptibility mapping because it has the finest prediction accuracy.

TABLE 4

Table 4. Area under the curve values of training and validation data in different models.

Discussion

Several kinds of natural hazards related environment problems has been solved by various research groups for sustainable management and utilization of natural resources (Pradhan and Kim, 2017; Jiang et al., 2018; Tsai et al., 2019; Wang et al., 2020; Xu et al., 2021) with the help of remote sensing (RS) technology (Han et al., 2019; Hu et al., 2020; Zhang et al., 2020c) and geographical information system (GIS) tool (Zuo et al., 2015; Xu et al., 2018; Zhu et al., 2019; Yang et al., 2020b) and widespread progress in the computational facilities (Chao et al., 2018; Zhang et al., 2018; 2020b; Cao et al., 2020; Xu et al., 2020; Feng et al., 2020). A noteworthy support from the combination of RS and GIS technology gives efficiently solution in the several types of natural hazards related problems (Yang et al., 2018, 2020a; Zhang et al., 2019; Sun et al., 2021). Therefore, the geospatial technology, i.e., remote sensing and GIS has been providing high resolution multispectral satellite data and their optimal processing which is immensely help to analysis and solves several types of natural hazards related risk. The optimal data processing without any kinds of bias is done through machine learning algorithms and their computation analysis has been presented through the help of GIS platform (Pourghasemi and Rossi, 2017; Yang et al., 2015; Chen et al., 2019a; Zhu et al., 2019). Thus, in the present time, RS-GIS techniques and machine learning algorithms has been widely helped for optimal evaluation of many scientific problems (Yang et al., 2015; Wu et al., 2020).

Preparing of LS hazard susceptibility mapping is an important and one of the key challenging tasks among the land use planners (Arabameri et al., 2021). Therefore, several researchers proposed various kinds of models to address this key challenges and there has been great interest in improving the prediction performance of the hazards related susceptibility mapping through ML models (Oh et al., 2019). It is also be mentioned here that no specific models can give an optimal result and have controversy among the researchers in this regards (Arabameri et al., 2020a). The reliability and accurate result is the most predominate condition for the LS hazard susceptibility mapping and researchers tried to form new novel ensemble models to produced good outcomes (Reichenbach et al., 2018). A lot of ML methods have been applied in the previous past few years for the spatial probability map of various kind of environmental hazards (Arabameri et al., 2020c). The spatial analysis of LS indicates that subsidence specifically occurred in the flat areas particularly in the alluvial deposited land and agricultural areas located in arid regions (Herrera-García et al., 2021). A present time, ML algorithms and their ensemble methods have been applied in various fields for the susceptibility mapping and it has been shown to be effective in terms of predictive performance (Nguyen et al., 2019; Arabameri et al., 2020c; Feng et al., 2020; Liu et al., 2020; Zhang et al., 2020a; Saha et al., 2021b). Particularly, ensemble models always enhanced the output result by integrated the several ML algorithms (Mojaddadi et al., 2017; Arabameri et al., 2020d; Saha et al., 2021a).

Thus, based on the literature survey and local geo-environmental conditions, different LSCFs have primarily selected to perform the LSSM in this present study area. After that multi-collinearity assessment studies was carried out and based on the result of multi-collinearity, a total of 12 geo-environmental variables were selected for the LS susceptibility modeling (Chen et al., 2019b; Arabameri et al., 2020d). Thereafter, ML algorithms of GLM, MaxEnt, SVM, and ANN were used and 11 possible ensemble models were developed to mapping LS susceptibility analysis. GLM or the logistic regression model is the most common statistical technique used for the prediction of landslide, flood, groundwater, gully erosion susceptibility. The most advantages of GLM is that assumes a linear relationship between a link function of the predictors and response. The presence-only feature can be considered as advantages of MaxEnt because the determination of non-land subsidence may result in uncertainty. SVM is a supervised based classification model and it is very capable of dealing with non-linear and high-dimensional grouping problems by use of the different SVM based function (Huang and Zhao, 2018). The ANN is an effective tool in a neural network, where the hidden and output layer nodes process their inputs (Lee et al., 2012) and successfully applied in this study. Ensemble models rapidly applied for the susceptibility modeling, but some author reported that ensemble models have better accuracy than the single models (Pham et al., 2019; Arabameri et al., 2020b; Chowdhuri et al., 2020b) consequently, some study reported that stand-alone ML models have better accuracy (Althuwaynee et al., 2014).

In this study, we used a total of 15 models for land subsidence modeling, but the ANN model was the best model by the success rate of accuracy (AUC = 0.924) and the success rate AUC obtained from the training datasets. On the other hand, the SVM land subsidence hazard susceptibility model was the best model by the prediction accuracy rate (AUC = 0.823) and the predictive accuracy rate obtained from the validating datasets. An ANN model is based on the non-linear statistical analysis of a given dataset and evaluation on the basis of observed coherence network dynamics. Thus, ANN gives the highest accuracy in the training dataset. On the other side, SVM model try to relocate the idea based on the kernel function using unsupervised function (Smits and Jordaan, 2002) and hence, gives the better performance in validation dataset. The accuracy of the models in success and prediction rate has been analyzed through the ROC- AUC curve. The ROC curve is a quantitative model evaluator successfully used for model performance evaluation in most of the studies (Su et al., 2017; Arabameri et al., 2020d). The graphical presentation of the ROC- AUC curve created its most suitable model evaluator. The ROC- AUC curve result demonstrated that the 15 models performed well, but the SVM and ANN-SVM models have made the best prediction of the gully erosion. Another study of LS in the Kashmar region, Iran based on MaxEnt models gives the result of ROC-AUC is 88.9% (Rahmati et al., 2019a,b) which is significantly higher than the present study. Similarly, LS susceptibility studies in the Semnan province of Iran using ANN models gives the result of ROC-AUC is 0.919 (Arabameri et al., 2020d) which is less than the our study result (AUC = 0.924). Therefore, studies indicate that the same ML models give different result in accuracy assessment from region to region, depending upon the local geo-environmental factors.

Thus, in this study, the combination of remote sensing and GIS techniques along with ML algorithms has given the optimal result for land subsidence susceptibility mapping. Among the four ML algorithms, SVM gives the most optimal prediction performance outcome than the others. Therefore, based on the output maps of LS resulting from hybrid ML algorithms will be very much helpful to the land use planners and policy makers for sustainable management and uses of land resources. The land degradation process through LS is also control through taken proper management strategies.

Conclusion

The phenomenon of LS is one of the economic threats among the global people through the land degradation processes usually induced by human misuse. Therefore, proper assessment and management of this kind of natural hazard is crucial for sustainable development of any region. Hence, for the purpose of land management it is necessary to identification, modeling, assessment and analysis, and in the present research study it has been carried out in the Kashan plain, Iran. Here, ML algorithms of GLM, ANN, MaxEnt, SVM and their 11 possible ensemble classifier models were used for LS susceptibility modeling and mapping. The final result indicates that the ANN model is the best in training phase among the 15 models. But in the prediction accuracy SVM model is the best among all models. Furthermore, the consistency between the LSSMs was mentioned properly and there are no such differences between the susceptibility zones. Additionally, maximum ensemble models from the four ML models were developed in this study and in near future several others ML models can be used to compare and evaluate the optimal result. Not only this, based on the optimal output of this study, these ensemble models can be used in further research studies such as several environmental hazards potentiality mapping and prediction. The best outcomes of the study are land subsidence susceptibility maps which will help in the local administrations and decision-makers in land use planning and proper management of land resources. As we know every research study have some limitations, therefore this study also carried some limitation in terms of using limited LS causative factors and lack of hydrological modeling. Another side, the strength of this research study is the quality of the ML modeling and their optimal prediction result.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

AA: conceptualization, methodology, software, validation, formal analysis, visualization, and resources. AA and SL investigation. OA: data curation. AA and SL: writing—original draft preparation. AA, SC, AS, IC, and HM: writing—review and editing. AA and SL: supervision. SL: funding. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Basic Research Project of the Korea Institute of Geoscience and Mineral Resources (KIGAM) and Project of Environmental Business Big Data Platform and Center Construction funded by the Ministry of Science and ICT.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^ https://asf.alaska.edu/
2. ^ www.ngo-org.ir
3. ^ http://www.gsi.ir/

References

Abdollahi, S., Pourghasemi, H. R., Ghanbarian, G. A., and Safaeian, R. (2019). Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 78, 4017–4034. doi: 10.1007/s10064-018-1403-6

CrossRef Full Text | Google Scholar

Alin, A. (2010). Multicollinearity. WIREs Comput. Stat. 2, 370–374. doi: 10.1002/wics.84

CrossRef Full Text | Google Scholar

Althuwaynee, O. F., Pradhan, B., Park, H.-J., and Lee, J. H. (2014). A novel ensemble bivariate statistical evidential belief function with knowledge-based analytical hierarchy process and multivariate statistical logistic regression for landslide susceptibility mapping. Catena 114, 21–36. doi: 10.1016/j.catena.2013.10.011

CrossRef Full Text | Google Scholar

Arabameri, A., Asadi Nalivan, O., Chandra Pal, S., Chakrabortty, R., Saha, A., Lee, S., et al. (2020a). Novel machine learning approaches for modelling the gully erosion susceptibility. Remote Sens. 12:2833. doi: 10.3390/rs12172833

CrossRef Full Text | Google Scholar

Arabameri, A., Asadi Nalivan, O., Saha, S., Roy, J., Pradhan, B., Tiefenbacher, J. P., et al. (2020b). Novel ensemble approaches of machine learning techniques in modeling the gully erosion susceptibility. Remote Sens. 12:1890. doi: 10.3390/rs12111890

CrossRef Full Text | Google Scholar

Arabameri, A., Pourghasemi, H. R., and Yamani, M. (2017). Applying different scenarios for landslide spatial modeling using computational intelligence methods. Environ. Earth Sci. 76:832.

Google Scholar

Arabameri, A., Saha, S., Roy, J., Chen, W., Blaschke, T., and Tien Bui, D. (2020c). Landslide susceptibility evaluation and management using different machine learning methods in The Gallicash River Watershed, Iran. Remote Sens. 12:475. doi: 10.3390/rs12030475

CrossRef Full Text | Google Scholar

Arabameri, A., Saha, S., Roy, J., Tiefenbacher, J. P., Cerda, A., Biggs, T., et al. (2020d). A novel ensemble computational intelligence approach for the spatial prediction of land subsidence susceptibility. Sci. Total Environ. 26:138595. doi: 10.1016/j.scitotenv.2020.138595

PubMed Abstract | CrossRef Full Text | Google Scholar

Arabameri, A., Yariyan, P., and Santosh, M. (2021). Land subsidence spatial modeling and assessment of the contribution of geo-environmental factors to land subsidence: comparison of different novel ensemble modeling approaches. Res. Sq. [Preprint]. doi: 10.21203/rs.3.rs-194202/v1

CrossRef Full Text | Google Scholar

Ayalew, L., and Yamagishi, H. (2005). The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 65, 15–31. doi: 10.1016/j.geomorph.2004.06.010

CrossRef Full Text | Google Scholar

Babaee, S., Mousavi, Z., Masoumi, Z., Malekshah, A. H., Roostaei, M., and Aflaki, M. (2020). Land subsidence from interferometric SAR and groundwater patterns in the Qazvin plain, Iran. Int. J. Remote Sens. 41, 4780–4798. doi: 10.1080/01431161.2020.1724345

CrossRef Full Text | Google Scholar

Band, S. S., Janizadeh, S., Chandra Pal, S., Saha, A., Chakrabortty, R., Shokri, M., et al. (2020). Novel ensemble approach of deep learning neural network (DLNN) model and particle swarm optimization (PSO) algorithm for prediction of gully erosion susceptibility. Sensors 20:5609. doi: 10.3390/s20195609

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernknopf, R. L., Campbell, R. H., Brookshire, D. S., and Shapiro, C. D. (1988). A probabilistic approach to landslide hazard mapping in Cincinnati, Ohio, with applications for economic evaluation. Bull. Assoc. Eng. Geol. 25, 39–56. doi: 10.2113/gseegeosci.xxv.1.39

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, B., Wang, X., Zhang, W., Song, H., and Lv, Z. (2020). A many-objective optimization model of industrial internet of things based on private blockchain. IEEE Netw. 34, 78–83. doi: 10.1109/mnet.011.1900536

CrossRef Full Text | Google Scholar

Chao, L., Zhang, K., Li, Z., Zhu, Y., Wang, J., and Yu, Z. (2018). Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 558, 275–289. doi: 10.1016/j.jhydrol.2018.01.042

CrossRef Full Text | Google Scholar

Chen, W., Fan, L., Li, C., and Pham, B. T. (2020). Spatial prediction of landslides using hybrid integration of artificial intelligence algorithms with frequency ratio and index of entropy in Nanzheng County, China. Appl. Sci. 10:29. doi: 10.3390/app10010029

CrossRef Full Text | Google Scholar

Chen, W., Panahi, M., Tsangaratos, P., Shahabi, H., Ilia, I., Panahi, S., et al. (2019a). Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. Catena 172, 212–231. doi: 10.1016/j.catena.2018.08.025

CrossRef Full Text | Google Scholar

Chen, W., Shahabi, H., Shirzadi, A., Hong, H., Akgun, A., Tian, Y., et al. (2019b). Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 78, 4397–4419. doi: 10.1007/s10064-018-1401-8

CrossRef Full Text | Google Scholar

Chen, W., Xie, X., Wang, J., Pradhan, B., Hong, H., Bui, D. T., et al. (2017). A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 151, 147–160. doi: 10.1016/j.catena.2016.11.032

CrossRef Full Text | Google Scholar

Chowdhuri, I., Pal, S., Arabameri, A., Ngo, P., Chakrabortty, R., Malik, S., et al. (2020a). Ensemble approach to develop landslide susceptibility map in landslide dominated Sikkim Himalayan region, India. Environ. Earth Sci. 79, 1–28. doi: 10.1007/s12665-020-09227-5

CrossRef Full Text | Google Scholar

Chowdhuri, I., Pal, S. C., and Chakrabortty, R. (2020b). Flood susceptibility mapping by ensemble evidential belief function and binomial logistic regression model on river basin of eastern India. Adv. Space Res. 65, 1466–1489. doi: 10.1016/j.asr.2019.12.003

CrossRef Full Text | Google Scholar

Cigna, F., and Tapete, D. (2021). Present-day land subsidence rates, surface faulting hazard and risk in Mexico City with 2014–2020 Sentinel-1 IW InSAR. Remote Sens. Environ. 253:112161. doi: 10.1016/j.rse.2020.112161

CrossRef Full Text | Google Scholar

Erkens, G., and Stouthamer, E. (2020). The 6M approach to land subsidence. Proc. Int. Assoc. Hydrol. Sci. 382, 733–740. doi: 10.5194/piahs-382-733-2020

CrossRef Full Text | Google Scholar

Famiglietti, J. S. (2014). The global groundwater crisis. Nat. Clim. Change 4, 945–948. doi: 10.1038/nclimate2425

CrossRef Full Text | Google Scholar

Feng, W., Lu, H., Yao, T., and Yu, Q. (2020). Drought characteristics and its elevation dependence in the Qinghai–Tibet plateau during the last half-century. Sci. Rep. 10, 1–11.

Google Scholar

Frattini, P., Crosta, G., and Carrara, A. (2010). Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 111, 62–72. doi: 10.1016/j.enggeo.2009.12.004

CrossRef Full Text | Google Scholar

Galloway, D. L., and Burbey, T. J. (2011). Review: regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 19, 1459–1486. doi: 10.1007/s10040-011-0775-5

CrossRef Full Text | Google Scholar

Garosi, Y., Sheklabadi, M., Pourghasemi, H. R., Besalatpour, A. A., Conoscenti, C., and Van Oost, K. (2018). Comparison of differences in resolution and sources of controlling factors for gully erosion susceptibility mapping. Geoderma 330, 65–78. doi: 10.1016/j.geoderma.2018.05.027

CrossRef Full Text | Google Scholar

Ghazifard, A., Moslehi, A., Safaei, H., and Roostaei, M. (2016). Effects of groundwater withdrawal on land subsidence in Kashan Plain, Iran. Bull. Eng. Geol. Environ. 75, 1157–1168. doi: 10.1007/s10064-016-0885-3

CrossRef Full Text | Google Scholar

Ghorbanzadeh, O., Rostamzadeh, H., Blaschke, T., Gholaminia, K., and Aryal, J. (2018). A new GIS-based data mining technique using an adaptive neuro-fuzzy inference system (ANFIS) and k-fold cross-validation approach for land subsidence susceptibility mapping. Nat. Hazards 94, 497–517. doi: 10.1007/s11069-018-3449-y

CrossRef Full Text | Google Scholar

Gong, P., Pu, R., and Chen, J. (1996). Elevation and forest-cover data using neural networks. Photogr. Eng. Remote Sens. 62, 1249–1260.

Google Scholar

Goorabi, A., Karimi, M., Yamani, M., and Perissin, D. (2020). Land subsidence in Isfahan metropolitatan and its relationship with geological and geomorphological settings revealed by Sentinel-1A InSAR observations. J. Arid Environ. 181:104238. doi: 10.1016/j.jaridenv.2020.104238

CrossRef Full Text | Google Scholar

Guzy, A., and Malinowska, A. A. (2020). State of the art and recent advancements in the modelling of land subsidence induced by groundwater withdrawal. Water 12:2051. doi: 10.3390/w12072051

CrossRef Full Text | Google Scholar

Hagan, M. T., Demuth, H. B., and Beale, M. H. (1995). Neural Network Design (Electrical Engineering). Belmont, CA: Thomson Learning.

Google Scholar

Han, C., Zhang, B., Chen, H., Wei, Z., and Liu, Y. (2019). Spatially distributed crop model based on remote sensing. Agric. Water Manag. 218, 165–173. doi: 10.1016/j.agwat.2019.03.035

CrossRef Full Text | Google Scholar

Herrera-García, G., Ezquerro, P., Tomás, R., Béjar-Pizarro, M., López-Vinielles, J., Rossi, M., et al. (2021). Mapping the global threat of land subsidence. Science 371, 34–36. doi: 10.1126/science.abb8549

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsu, K., Gupta, H. V., and Sorooshian, S. (1995). Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 31, 2517–2530.

Google Scholar

Hu, Y., Chen, Q., Feng, S., and Zuo, C. (2020). Microscopic fringe projection profilometry: a review. Opt. Las. Eng. 106192. doi: 10.1016/j.optlaseng.2020.106192

CrossRef Full Text | Google Scholar

Huang, Y., and Zhao, L. (2018). Review on landslide susceptibility mapping using support vector machines. Catena 165, 520–529. doi: 10.1016/j.catena.2018.03.003

CrossRef Full Text | Google Scholar

Jiang, Q., Shao, F., Lin, W., Gu, K., Jiang, Q., and Sun, H. (2018). Optimizing multistage discriminative dictionaries for blind image quality assessment. IEEE Transact. Multimed. 20, 2035–2048. doi: 10.1109/TMM.2017.2763321

CrossRef Full Text | Google Scholar

Joachims, T. (1998). “Text categorization with support vector machines: Learning with many relevant features,” in Proceedings of ECML-98, 10th European Conference on Machine Learning, 1398, Chemnitz, DE, (Heidelberg: Springer Verlag), 137–142. doi: 10.1007/bfb0026683

CrossRef Full Text | Google Scholar

Kanevski, M., Parkin, R., Pozdnukhov, A., Timonin, V., Maignan, M., Demyanov, V., et al. (2004). Environmental data mining and modeling based on machine learning algorithms and geostatistics. Environ. Model. Softw. 19, 845–855. doi: 10.1016/j.envsoft.2003.03.004

CrossRef Full Text | Google Scholar

Karimzadeh, S., and Matsuoka, M. (2020). Remote sensing X-Band SAR Data for land subsidence and pavement monitoring. Sensors 20:4751. doi: 10.3390/s20174751

PubMed Abstract | CrossRef Full Text | Google Scholar

Kavzoglu, T., and Colkesen, I. (2009). A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Observ. Geoinform. 11, 352–359. doi: 10.1016/j.jag.2009.06.002

CrossRef Full Text | Google Scholar

Kosko, B. (1992). Neural Networks and Fuzzy Systems: A Dynamical Systems Approach to Machine Intelligence. River, NJ: Prentice Hall.

Google Scholar

Lee, S., Hong, S.-M., and Jung, H.-S. (2017). A support vector machine for landslide susceptibility mapping in Gangwon Province, Korea. Sustainability 9:48. doi: 10.3390/su9010048

CrossRef Full Text | Google Scholar

Lee, S., and Park, I. (2013). Application of decision tree model for the ground subsidence hazard mapping near abandoned underground coal mines. J. Environ. Manag. 127, 166–176. doi: 10.1016/j.jenvman.2013.04.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S., Park, I., and Choi, J.-K. (2012). Spatial prediction of ground subsidence susceptibility using an artificial neural network. Environ. Manag. 49, 347–358. doi: 10.1007/s00267-011-9766-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Yu, W., Chan, F. T., and Niu, B. (2020). A variable weight-based hybrid approach for multi-attribute group decision making under interval-valued intuitionistic fuzzy sets. Int. J. Intell. Syst. 36, 1015–1052. doi: 10.1002/int.22329

CrossRef Full Text | Google Scholar

Lucà, F., Conforti, M., and Robustelli, G. (2011). Comparison of GIS-based gullying susceptibility mapping using bivariate and multivariate statistics: Northern Calabria, South Italy. Geomorphology 134, 297–308. doi: 10.1016/j.geomorph.2011.07.006

CrossRef Full Text | Google Scholar

Lyu, H.-M., Shen, S.-L., Zhou, A., and Yang, J. (2020). Risk assessment of mega-city infrastructures related to land subsidence using improved trapezoidal FAHP. Sci. Total Environ. 717:135310. doi: 10.1016/j.scitotenv.2019.135310

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandal, S., and Mondal, S. (2019). Statistical Approaches for Landslide Susceptibility Assessment and Prediction. Berlin: Springer.

Google Scholar

Moayedi, H., Tien Bui, D., Gör, M., Pradhan, B., and Jaafari, A. (2019). The feasibility of three prediction techniques of the artificial neural network, adaptive neuro-fuzzy inference system, and hybrid particle swarm optimization for assessing the safety factor of cohesive slopes. ISPRS Int. J. Geoinf. 8:391. doi: 10.3390/ijgi8090391

CrossRef Full Text | Google Scholar

Mohammady, M., Pourghasemi, H. R., and Amiri, M. (2019). Assessment of land subsidence susceptibility in Semnan plain (Iran): a comparison of support vector machine and weights of evidence data mining algorithms. Nat. Hazards 99, 951–971. doi: 10.1007/s11069-019-03785-z

CrossRef Full Text | Google Scholar

Mohebbi Tafreshi, G., Nakhaei, M., and Lak, R. (2020). A GIS-based comparative study of hybrid fuzzy-gene expression programming and hybrid fuzzy-artificial neural network for land subsidence susceptibility modeling. Stoch. Environ. Res. Risk Assess. 34, 1059–1087. doi: 10.1007/s00477-020-01810-3

CrossRef Full Text | Google Scholar

Mojaddadi, H., Pradhan, B., Nampak, H., Ahmad, N., and Ghazali, A. H. (2017). Ensemble machine-learning-based geospatial approach for flood risk assessment using multi-sensor remote-sensing data and GIS. Geomat. Nat. Hazards Risk 8, 1080–1102. doi: 10.1080/19475705.2017.1294113

CrossRef Full Text | Google Scholar

Najafi, Z., Pourghasemi, H. R., Ghanbarian, G., and Shamsi, S. R. F. (2020). Land-subsidence susceptibility zonation using remote sensing, GIS, and probability models in a Google Earth Engine platform. Environ. Earth Sci. 79:491.

Google Scholar

Nelder, J. A., and Wedderburn, R. W. (1972). Generalized linear models. J. R. Stat. Soc. Ser. A (General) 135, 370–384.

Google Scholar

Nguyen, H., Mehrabi, M., Kalantar, B., Moayedi, H., and Abdullahi, M. M. (2019). Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomat. Nat. Hazards Risk 10, 1667–1693. doi: 10.1080/19475705.2019.1607782

CrossRef Full Text | Google Scholar

Nguyen, Q. H., Ly, H.-B., Ho, L. S., Al-Ansari, N., Le, H. V., Tran, V. Q., et al. (2021). Influence of data splitting on performance of machine learning models in prediction of shear strength of soil. Math. Prob. Eng. 2021:e4832864. doi: 10.1155/2021/4832864

CrossRef Full Text | Google Scholar

Nhu, V.-H., Shirzadi, A., Shahabi, H., Singh, S. K., Al-Ansari, N., Clague, J. J., et al. (2020). Shallow landslide susceptibility mapping: a comparison between logistic model tree, logistic regression, naïve bayes tree, artificial neural network, and support vector machine algorithms. Int. J. Environ. Res. Public Health 17:2749. doi: 10.3390/ijerph17082749

PubMed Abstract | CrossRef Full Text | Google Scholar

Oh, H.-J., Syifa, M., Lee, C.-W., and Lee, S. (2019). Land subsidence susceptibility mapping using Bayesian, functional, and meta-ensemble machine learning models. Appl. Sci. 9:1248. doi: 10.3390/app9061248

CrossRef Full Text | Google Scholar

Orhan, O., Oliver-Cabrera, T., Wdowinski, S., Yalvac, S., and Yakar, M. (2021). Land subsidence and its relations with sinkhole activity in Karapınar region, Turkey: a multi-sensor InSAR time series study. Sensors 21:774. doi: 10.3390/s21030774

PubMed Abstract | CrossRef Full Text | Google Scholar

Payne, R., Harding, S. A., Murray, D. A., Soutar, D. M., Baird, D. B., Glaser, A. I., et al. (2012). A Guide to Regression, Nonlinear and Generalized Linear Models in GenStat. Hemel Hempstead: VSN International.

Google Scholar

Pham, B. T., Bui, D. T., Prakash, I., and Dholakia, M. B. (2017). Hybrid integration of multilayer perceptron neural networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 149, 52–63. doi: 10.1016/j.catena.2016.09.007

CrossRef Full Text | Google Scholar

Pham, B. T., Jaafari, A., Prakash, I., and Bui, D. T. (2019). A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 78, 2865–2886. doi: 10.1007/s10064-018-1281-y

CrossRef Full Text | Google Scholar

Phillips, S. J., and Dudík, M. (2008). Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. Ecography 31, 161–175. doi: 10.1111/j.0906-7590.2008.5203.x

CrossRef Full Text | Google Scholar

Phillips, S. J., Dudík, M., Elith, J., Graham, C. H., Lehmann, A., Leathwick, J., et al. (2009). Sample selection bias and presence-only distribution models: implications for background and pseudo-absence data. Ecol. Appl. 19, 181–197. doi: 10.1890/07-2153.1

CrossRef Full Text | Google Scholar

Pourghasemi, H. R., Kariminejad, N., Amiri, M., Edalat, M., Zarafshar, M., Blaschke, T., et al. (2020). Assessing and mapping multi-hazard risk susceptibility using a machine learning technique. Sci. Rep. 10:3203.

Google Scholar

Pourghasemi, H. R., and Rossi, M. (2017). Landslide susceptibility modeling in a landslide prone area in Mazandarn Province, north of Iran: a comparison between GLM, GAM, MARS, and M-AHP methods. Theor. Appl. Climatol. 130, 609–633. doi: 10.1007/s00704-016-1919-2

CrossRef Full Text | Google Scholar

Pourghasemi, H. R., Yousefi, S., Kornejady, A., and Cerdà, A. (2017). Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 609, 764–775. doi: 10.1016/j.scitotenv.2017.07.198

PubMed Abstract | CrossRef Full Text | Google Scholar

Pradhan, A. M. S., and Kim, Y.-T. (2017). Spatial data analysis and application of evidential belief functions to shallow landslide susceptibility mapping at Mt. Umyeon, Seoul, Korea. Bull. Eng. Geol. Environ. 76, 1263–1279. doi: 10.1007/s10064-016-0919-x

CrossRef Full Text | Google Scholar

Rahmati, O., Falah, F., Naghibi, S. A., Biggs, T., Soltani, M., Deo, R. C., et al. (2019a). Land subsidence modelling using tree-based machine learning algorithms. Sci. Total Environ. 672, 239–252. doi: 10.1016/j.scitotenv.2019.03.496

PubMed Abstract | CrossRef Full Text | Google Scholar

Rahmati, O., Golkarian, A., Biggs, T., Keesstra, S., Mohammadi, F., and Daliakopoulos, I. N. (2019b). Land subsidence hazard modeling: machine learning to identify predictors and the role of human activities. J. Environ. Manag. 236, 466–480. doi: 10.1016/j.jenvman.2019.02.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Rateb, A., and Abotalib, A. Z. (2020). Inferencing the land subsidence in the Nile Delta using Sentinel-1 satellites and GPS between 2015 and 2019. Sci. Total Environ. 729:138868. doi: 10.1016/j.scitotenv.2020.138868

PubMed Abstract | CrossRef Full Text | Google Scholar

Reddy, S., and Dávalos, L. M. (2003). Geographical sampling bias and its implications for conservation priorities in Africa. J. Biogeogr. 30, 1719–1727. doi: 10.1046/j.1365-2699.2003.00946.x

CrossRef Full Text | Google Scholar

Reichenbach, P., Rossi, M., Malamud, B. D., Mihir, M., and Guzzetti, F. (2018). A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 180, 60–91. doi: 10.1016/j.earscirev.2018.03.001

CrossRef Full Text | Google Scholar

Rezaei, M., Yazdani Noori, Z., and Dashti Barmaki, M. (2020). Land subsidence susceptibility mapping using analytical hierarchy process (AHP) and Certain Factor (CF) models at Neyshabur plain, Iran. Geocarto Int. 35, 1–17. doi: 10.1080/10106049.2020.1768596

CrossRef Full Text | Google Scholar

Saha, A., Pal, S. C., Arabameri, A., Blaschke, T., Panahi, S., Chowdhuri, I., et al. (2021a). Flood susceptibility assessment using novel ensemble of hyperpipes and support vector regression algorithms. Water 13:241. doi: 10.3390/w13020241

CrossRef Full Text | Google Scholar

Saha, A., Pal, S. C., Arabameri, A., Chowdhuri, I., Rezaie, F., Chakrabortty, R., et al. (2021b). Optimization modelling to establish false measures implemented with ex-situ plant species to control gully erosion in a monsoon-dominated region with novel in-situ measurements. J. Environ. Manag. 287:112284. doi: 10.1016/j.jenvman.2021.112284

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahu, S. P., Yadav, M., Das, A. J., Prakash, A., and Kumar, A. (2017). Multivariate statistical approach for assessment of subsidence in Jharia coalfields, India. Arab. J. Geosci. 10:191.

Google Scholar

Shirzadi, A., Soliamani, K., Habibnejhad, M., Kavian, A., Chapi, K., Shahabi, H., et al. (2018). Novel GIS based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 18:3777. doi: 10.3390/s18113777

PubMed Abstract | CrossRef Full Text | Google Scholar

Smits, G. F., and Jordaan, E. M. (2002). “Improved SVM regression using mixtures of kernels,” in Proceedings of the 2002 International Joint Conference on Neural Networks. IJCNN’02 (Cat. No. 02CH37290), (Honolulu, HI: IEEE), 2785–2790.

Google Scholar

Su, Q., Zhang, J., Zhao, S., Wang, L., Liu, J., and Guo, J. (2017). Comparative assessment of three nonlinear approaches for landslide susceptibility mapping in a coal mine area. ISPRS Int. J. Geoinf. 6:228. doi: 10.3390/ijgi6070228

CrossRef Full Text | Google Scholar

Sudheer, K. P., Gosain, A. K., Mohana Rangan, D., and Saheb, S. M. (2002). Modelling evaporation using an artificial neural network algorithm. Hydrol. Process. 16, 3189–3202. doi: 10.1002/hyp.1096

CrossRef Full Text | Google Scholar

Sun, G., Li, C., and Deng, L. (2021). An adaptive regeneration framework based on search space adjustment for differential evolution. Neural Comput. Appl. 1–17. doi: 10.1007/s00521-021-05708-1

CrossRef Full Text | Google Scholar

Tian, P., Lu, H., Feng, W., Guan, Y., and Xue, Y. (2020). Large decrease in streamflow and sediment load of Qinghai–Tibetan Plateau driven by future climate change: a case study in Lhasa River Basin. Catena 187:104340. doi: 10.1016/j.catena.2019.104340

CrossRef Full Text | Google Scholar

Tian, Y., Zheng, Y., Wu, B., Wu, X., Liu, J., and Zheng, C. (2015). Modeling surface water-groundwater interaction in arid and semi-arid regions with intensive agriculture. Environ. Modell. Softw. 63, 170–184. doi: 10.1016/j.envsoft.2014.10.011

CrossRef Full Text | Google Scholar

Tien Bui, D., Shahabi, H., Shirzadi, A., Chapi, K., Pradhan, B., Chen, W., et al. (2018). Land subsidence susceptibility mapping in South Korea using machine learning algorithms. Sensors 18:2464. doi: 10.3390/s18082464

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, Y.-H., Wang, J., Chien, W.-T., Wei, C.-Y., Wang, X., and Hsieh, S.-H. (2019). A BIM-based approach for predicting corrosion under insulation. Automat. Constr. 107:102923. doi: 10.1016/j.autcon.2019.102923

CrossRef Full Text | Google Scholar

Vapnik, V. (2013). The Nature of Statistical Learning Theory. Berlin: Springer science & business media.

Google Scholar

Vorpahl, P., Elsenbeer, H., Märker, M., and Schröder, B. (2012). How can statistical models help to determine driving factors of landslides? Ecol. Modell. 239, 27–39. doi: 10.1016/j.ecolmodel.2011.12.007

CrossRef Full Text | Google Scholar

Wang, J., Yi, S., Li, M., Wang, L., and Song, C. (2018). Effects of sea level rise, land subsidence, bathymetric change and typhoon tracks on storm flooding in the coastal areas of Shanghai. Sci. Total Environ. 621, 228–234. doi: 10.1016/j.scitotenv.2017.11.224

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Zhang, K., van Beek, L. P., Tian, X., and Bogaard, T. A. (2020). Physically-based landslide prediction over a large region: Scaling lowresolution hydrological model results for high-resolution slope stability assessment. Environ. Modell. Softw. 124:104607. doi: 10.1016/j.envsoft.2019.104607

CrossRef Full Text

Woodbury, A., Render, F., and Ulrych, T. (1995). Practical probabilistic ground-water modeling. Ground Water 33, 532–539. doi: 10.1111/j.1745-6584.1995.tb00307.x

CrossRef Full Text | Google Scholar

Wu, C., Wu, P., Wang, J., Jiang, R., Chen, M., and Wang, X. (2020). Critical review of data-driven decision-making in bridge operation and maintenance. Struct. Infrastruct. Eng. 7, 1–24. doi: 10.1080/15732479.2020.1833946

CrossRef Full Text | Google Scholar

Xu, M., Li, C., Chen, Z., Wang, Z., and Guan, Z. (2018). Assessing visual quality of omnidirectional videos. IEEE Transact. Circuit. Syst. Video Technol. 29, 3516–3530. doi: 10.1109/TCSVT.2018.2886277

CrossRef Full Text | Google Scholar

Xu, J., Li, Y., Ren, C., Wang, S., Vanapalli, S. K., and Chen, G. (2021). Influence of freeze-thaw cycles on microstructure and hydraulic conductivity of saline intact loess. Cold Reg. Sci. Technol. 181:103183.

Google Scholar

Xu, S., Wang, J., Shou, W., Ngo, T., Sadick, A.-M., and Wang, X. (2020). Computer vision techniques in construction: a critical review. Arch. Comput. Methods Eng. doi: 10.1007/s11831-020-09504-3

CrossRef Full Text | Google Scholar

Yang, Y., Hou, C., Lang, Y., Sakamoto, T., He, Y., and Xiang, W. (2020a). Omnidirectional motion classification with monostatic radar system using micro-doppler signatures. IEEE Transact. Geosci. Remote Sens. 1–14. doi: 10.1109/tgrs.2019.2958178

CrossRef Full Text | Google Scholar

Yang, X.-Q., Kushwaha, S. P. S., Saran, S., Xu, J., and Roy, P. S. (2013). Maxent modeling for predicting the potential distribution of medicinal plant, Justicia adhatoda L. in Lesser Himalayan foothills. Ecol. Eng. 51, 83–87. doi: 10.1016/j.ecoleng.2012.12.004

CrossRef Full Text | Google Scholar

Yang, Y., Tao, L., Yang, H., Iglauer, S., Wang, X., Askari, R., et al. (2020b). Stress sensitivity of fractured and vuggy carbonate: an X−ray computed tomography analysis. J. Geophys. Res. Solid Earth 125, e2019JB018759. doi: 10.1029/2019jb018759

CrossRef Full Text | Google Scholar

Yang, R., Xu, M., Liu, T., Wang, Z., and Guan, Z. (2018). Enhancing quality for HEVC Compressed videos. IEEE Transact. Circ. Syst. Video Technol. 1. doi: 10.1109/tcsvt.2018.2867568

CrossRef Full Text | Google Scholar

Yang, Y., Yao, J., Wang, C., Gao, Y., Zhang, Q., An, S., et al. (2015). New pore space characterization method of shale matrix formation by considering organic and inorganic pores. J. Nat. Gas. Sci. Eng. 27, 496–503.

Google Scholar

Yao, X., Tham, L. G., and Dai, F. C. (2008). Landslide susceptibility mapping based on support vector machine: a case study on natural slopes of Hong Kong, China. Geomorphology 101, 572–582. doi: 10.1016/j.geomorph.2008.02.011

CrossRef Full Text | Google Scholar

Yesilnacar, E. K. (2005). The Application of Computational Intelligence to Landslide Susceptibility Mapping in Turkey. Doctoral dissertation. Parkville VIC: University of Melbourne, Department, 200.

Google Scholar

Yilmaz, I. (2009). A case study from Koyulhisar (Sivas-Turkey) for landslide susceptibility mapping by artificial neural networks. Bull. Eng. Geol. Environ. 68, 297–306. doi: 10.1007/s10064-009-0185-2

CrossRef Full Text | Google Scholar

Yu, H., Gong, H., Chen, B., Liu, K., and Gao, M. (2020). Analysis of the influence of groundwater on land subsidence in Beijing based on the geographical weighted regression (GWR) model. Sci. Total Environ. 738, 139405. doi: 10.1016/j.scitotenv.2020.139405

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, C., and Moayedi, H. (2019). The performance of six neural-evolutionary classification techniques combined with multi-layer perception in two-layered cohesive slope stability analysis and failure recognition. Eng. Comput. 35, 1–10. doi: 10.1201/b20116-2

CrossRef Full Text | Google Scholar

Zamanirad, M., Sarraf, A., Sedghi, H., Saremi, A., and Rezaee, P. (2019). Modeling the influence of groundwater exploitation on land subsidence susceptibility using machine learning algorithms. Nat. Resour. Res. 29, 1127–1141. doi: 10.1007/s11053-019-09490-9

CrossRef Full Text | Google Scholar

Zhang, J., Chen, Q., Sun, J., Tian, L., and Zuo, C. (2020a). On a universal solution to the transport-of-intensity equation. Optics Let. 45, 3649–3652.

Google Scholar

Zhang, Z., Luo, C., and Zhao, Z. (2020b). Application of probabilistic method in maximum tsunami height prediction considering stochastic seabed topography. Nat. Hazards 104, 2511–2530. doi: 10.1007/s11069-020-04283-3

CrossRef Full Text | Google Scholar

Zhang, C., Sargent, I., Pan, X., Li, H., Gardiner, A., Hare, J., et al. (2018). An object-based convolutional neural network (OCNN) for urban land use classification. Remote Sens. Environ. 216, 57–70. doi: 10.1016/j.rse.2018.06.034

CrossRef Full Text | Google Scholar

Zhang, G. P., and Qi, M. (2005). Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 160, 501–514. doi: 10.1016/j.ejor.2003.08.037

CrossRef Full Text | Google Scholar

Zhang, J., Sun, J., Chen, Q., and Zuo, C. (2020c). Resolution analysis in a lens-free on-chip digital holographic microscope. IEEE Trans. Comput. Imag. 6, 697–710.

Google Scholar

Zhang, C., and Wang, H. (2019). Robustness of the active rotary inertia driver system for structural swing vibration control subjected to multi-type hazard excitations. Appl. Sci. 9:4391. doi: 10.3390/app9204391

CrossRef Full Text | Google Scholar

Zhang, K., Wang, Q., Chao, L., Ye, J., Li, Z., Yu, Z., et al. (2019). Ground observation-based analysis of soil moisture spatiotemporal variability across a humid to semi-humid transitional zone in China. J. Hydrol. 574, 903–914. doi: 10.1016/j.jhydrol.2019.04.087

CrossRef Full Text | Google Scholar

Zhu, J., Wang, X., Wang, P., Wu, Z., and Kim, M. J. (2019). Integration of BIM and GIS: geometry from IFC to shapefile using open-source technology. Automat. Construct. 102, 105–119. doi: 10.1016/j.autcon.2019.02.014

CrossRef Full Text | Google Scholar

Zuo, C., Chen, Q., Tian, L., Waller, L., and Asundi, A. (2015). Transport of intensity phase retrieval and computational imaging for partially coherent fields: the phase space perspective. Optics Lasers Eng. 71, 20–32. doi: 10.1016/j.optlaseng.2015.03.006

CrossRef Full Text | Google Scholar

Zuo, C., Sun, J., Li, J., Zhang, J., Asundi, A., and Chen, Q. (2017). High-resolution transport-of-intensity quantitative phase microscopy with annular illumination. Sci. Rep. 7, 1–22.

Google Scholar