
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
HYPOTHESIS AND THEORY article
Front. Earth Sci. , 21 December 2021
Sec. Cryospheric Sciences
Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.662695
This article is part of the Research Topic Debris-Covered Glaciers: Formation, Governing Processes, Present Status and Future Directions View all 20 articles
Ongoing changes in mountain glaciers affect local water resources, hazard potential and global sea level. An increasing proportion of remaining mountain glaciers are affected by the presence of a surface cover of rock debris, and the response of these debris-covered glaciers to climate forcing is different to that of glaciers without a debris cover. Here we take a back-to-basics look at the fundamental terms that control the processes of debris evolution at the glacier surface, to illustrate how the trajectory of debris cover development is partially decoupled from prevailing climate conditions, and that the development of a debris cover over time should prevent the glacier from achieving steady state. We discuss the approaches and limitations of how this has been treated in existing modeling efforts and propose that “surrogate world” numerical representations of debris-covered glaciers would facilitate the development of well-validated parameterizations of surface debris cover that can be used in regional and global glacier models. Finally, we highlight some key research targets that would need to be addressed in order to enable a full representation of debris-covered glacier system response to climate forcing.
Glaciers respond sensitively to climate variability with attendant impacts on melt water production, sea-level rise and geomorphic hazards (e.g. Watanabe et al., 1994; Kääb et al., 2005; Kaser et al., 2010; Bolch et al., 2011; Huss, 2011; Leclercq et al., 2011; Immerzeel et al., 2012; Marzeion et al., 2012). Therefore, understanding how glaciers worldwide will continue to respond to current and future climatic conditions is important for increasing our holistic understanding of glaciated mountain landsystems and the ecosystems and societies they impact. Understanding the glacier-climate relationship is also prerequisite to using geomorphic evidence of past glacier states as a proxy for former climate conditions (e.g. Osmaston, 2005).
All glacier systems contain sediment, but some mountain glaciers support a continuous cover of rock debris across a substantial part of the ablation zone, defining them as debris-covered glaciers (Kirkbride, 2011). The propensity for a glacier to become debris-covered is contingent on the relative proportions of snow/ice and debris in the system (Kirkbride, 1989). Hence, they are more likely to be prevalent 1) in tectonically active, high-relief orogenic belts, where denudation supplies abundant rock debris to the glacier surface, and 2) during periods of glacier recession, when inputs of snow and ice are reduced relative to the rock supply, and more ice mass is removed from the system. It has long been recognized that surface debris alters ice ablation rate (e.g. Østrem, 1959) and that debris-covered glaciers response to climate forcing is distinctly different to that of clean ice glaciers (e.g. Clark et al., 1994). Nevertheless, and despite of an upsurge of interest in the last decade, the details of the response of debris-covered glaciers to climate forcing, especially with respect to underlying glaciological theory, remain relatively little studied compared to that of clean ice glaciers.
Although regional model studies of glacier evolution and runoff show markedly different results if debris cover is accounted for or neglected (e.g. Shea et al., 2015; Ragettli et al., 2016; Rounce et al., 2020), global-scale projections of glacier change do not yet explicitly account for the role of surface debris in projections (e.g. Hock et al., 2019), and only one study has assessed the impact of the present distribution of surface debris at a global scale (Rounce et al., 2021). There are a number of reasons why neglecting debris cover in future projections of glacier behavior could be problematic. Firstly, in some regions a substantial proportion of the glacierized area is affected by surface debris cover, and this is projected to increase as glaciers continue to experience negative mass balance conditions. A recent global estimate based on automated mapping procedures suggests that about 4.4% ( 26,000 km2) of the global glacier area (excluding the Greenland and Antarctic ice sheets) is debris-covered (Scherler et al., 2018), while a study using detailed manual correction to the mapping datasets revised this upward to 7.3% (Herreid and Pellicciotti, 2020), highlighting that debris cover exceeding 1 km2 in area is found on 15% of global glaciers larger than 2 km2. Debris cover is found on more than 10% of the glacierized area in eight of the 18 Randolph Glacier Inventory (RGI) regions, and exceeds 15% of glacierized area in North Asia, Central Europe, Caucasus and Middle East, South Asia East and New Zealand (Herreid and Pellicciotti, 2020). The global distribution of mountain glaciers with regionally high concentrations of glaciers adds to the fact that more than half of all debris-covered ice is found in Alaska (38.6%), Southwest Asia (12.6%) and Greenland (12.0%). Individual studies highlight the prominence of debris cover in specific mountain ranges (e.g. Stokes et al., 2007; Hagg et al., 2008; Scherler et al., 2011a; Kääb et al., 2012), and globally the proportion of debris-covered ice is expected to increase as mountain glacier volumes diminish in coming decades (Stokes et al., 2007; Bolch et al., 2008a; Shukla et al., 2009; Lambrecht et al., 2011; Herreid and Pellicciotti, 2020; Tielidze et al., 2020). Secondly, satellite studies show glacier-wide ice mass loss from these debris-covered glaciers tongues over recent decades is substantial and increasing (e.g. Berthier et al., 2007; Bolch et al., 2008b, 2011). Together, these two points imply that understanding the role of surface debris on meltwater production will be prerequisite to correctly forcasting the volume and timing of glacier meltwater contributions to local hydrological resources and global sea level rise in the coming decades and centuries. Thirdly, mass loss of debris-covered glaciers is closely associated with the formation of ice-contact and moraine-dammed lakes that are likely to pose an increasing local hazard potential in the context of future climate projections (Benn et al., 2012).
In this paper we review the fundamentals of how supraglacial debris cover influences the climate response of mountain glaciers and identify some priorities for furthering our understanding of these systems. We provide a brief description of the principles and key metrics of glacier-climate interaction in section 2, and identify the salient features of debris-covered glacier systems and their observed response to climate forcing in section 3. In section 4 we use simple glacier models to examine the terms that control the extent and thickness of a supraglacial debris cover, and show the inherent non-stationarity of debris cover development and attendant consequences on traditional approaches to quantifying glacier response to climate. In section 5 we discuss how existing modeling approaches account for supraglacial debris and highlight the case for developing a complex system model of debris-covered glaciers capable of incorporating the time-evolving impact of the debris on the glacier system. In section 6 we identify some of the outstanding challenges of including the role of supraglacial debris in glacier system models. We conclude with summary comments on the nature of the problem and the potential ways forward.
Glacier mass balance is the key property linking the glacier system to climate, and is authoritatively described in Cuffey and Paterson (2010) and Cogley et al. (2011). Here we briefly cover some aspects and terminology of glacier response to climate forcing that we use within this paper.
The annual climatic glacier mass balance B is the sum of snow/ice accumulation and ice mass loss by ablation over the whole glacier surface A, usually expressed as the mass balance rate
The surface mass balance rate, typically increases systematically with elevation, which is referred to as the mass balance gradient. Mountain glaciers continuously redress this unequal mass distribution pattern via downstream transfer of ice by deformation and basal sliding. The driving stress for ice flow is a function of gravitational acceleration, slope, and ice thickness, with the local distribution of ice thickness being influenced by the mass balance gradient.
Conditions that favour more snowfall and less ice ablation result in B > 0, while conditions favouring less snowfall and more ice ablation result in B < 0. If B > 0 the glacier will tend to thicken and advance, while if B < 0, the glacier will tend to thin and retreat.
Ice flow and mass balance rate together determine the geometry of the glacier, following the continuity equation:
Where H is the ice thickness and q is the ice flux. If
The concept of a glacier achieving a steady state geometry underpins the method of quantifying glacier response to a prescribed climate forcing, and is widely used in glacier modeling. Analysing the length and/or volume change between two glacier steady states due to two different climate states reveals 1) the glacier change that will result from a defined step-change in climate, and conversely, 2) the equivalent step-change climate forcing signal that can be extracted from a known glacier geometry change. In reality, a glacier is expected to only rarely achieve a quasi steady state because stochastic variability even within statistically unchanging climate conditions cause glacier length fluctuations of up to several kilometers (Roe, 2011). Furthermore, although over sufficiently long timescales glacier models converge to a single geometry regardless of the initial state (Eis et al., 2019), over the shorter term, the cumulative climate history recorded in the glacier will also impact its response. Nevertheless, the concept of a steady state glacier remains a valuable idealization for quantifying and comparing system sensitivity, and is considered to be roughly achievable if climate changes are small and slow compared to the glacier response time (Cogley et al., 2011).
While the equilibrium response time of a glacier is valuable for quantifying system sensitivity and developing paleoclimatic proxies, studies for planning and policy purposes are generally more interested in the transient glacier response, specifically forward in time from the current state. Climate analysis based on, and projections of, the transient response of glaciers requires numerical modeling. The climate forcing is expressed through a regional mass balance condition, and is applied to an initial glacier geometry to force a coupled numerical model of mass exchange across the glacier boundaries, and mass redistribution within them, to quantify how the glacier system, as defined by the model constraints, is expected to evolve over time (e.g. Mackintosh et al., 2002; Jouvet et al., 2009, 2011; Clarke et al., 2015; Seguinot et al., 2018).
Historically, glacier-climate interactions have been viewed as relatively direct proxies of climate conditions because the mass change of a glacier is primarily governed directly by atmospheric conditions (the amount of solid precipitation, and the amount of atmospheric energy supplied to the glacier surface), and because the mass redistribution by ice flow and sliding is constrained by physical laws. However, glacier geometry can also be influenced by internal instability, such as surging behavior (e.g. Benn et al., 2019), or mass exchanges that are not solely governed by climate, such as iceberg calving (e.g. Benn et al., 2007) or modification of climatic ablation rate by surface debris (e.g. Vacco et al., 2010).
The foremost effect of supraglacial debris is to alter the ablation rate of underlying ice (e.g. Østrem, 1959). Thin debris cover enhances ablation by absorbing more solar radiation compared to “clean” ice and transmitting this additional energy efficiently to the ice beneath. However, energy absorbed by thicker debris in the daytime is re-emitted to the atmosphere at night rather than being transmitted to the ice beneath (Reznichenko et al., 2010). As a result, beyond a critical debris thickness, ablation is inhibited compared to that of exposed ice and beyond this thickness, ablation rate decreases with increasing debris thickness. This relationship, here termed the Østrem curve, has a shape that is relatively poorly understood within the ascending limb of the relationship (e.g. Adhikary et al., 2000; Evatt et al., 2015; Fyffe et al., 2020), but well-represented by a reciprocal function in the falling limb part of the curve (Anderson and Anderson, 2016). Field (e.g. Mattson et al., 1993; Nicholson and Benn, 2013; Rowan et al., 2021), laboratory (Reznichenko et al., 2010) and modeling (e.g. Nakawo and Young, 1981; Nicholson and Benn, 2006; Reid and Brock, 2010; Evatt et al., 2015) studies demonstrate that debris thickness is the primary determinant of how sub-debris ice ablation rate differs to that of clean ice, with other properties of the debris layer, such as lithology, porosity and moisture content playing only secondary roles (e.g. Reznichenko et al., 2010; Nicholson and Benn, 2013; Collier et al., 2014).
There is a systematic tendency for supraglacial debris cover thickness to increase downglacier (e.g. Zhang et al., 2011; Nicholson and Benn, 2013). This is because melt out of englacial material can only occur in the ablation zone of the glacier, and debris is continually conveyed downglacier with ice flow (Kirkbride, 2000), and is concentrated towards the glacier terminus by ice flow deceleration towards the glacier front (Anderson et al., 2018). Further to the impact of compressional flow towards the terminus, the spatial distribution of extensional or compressional flow across the glacier will also impact the debris thickness distribution, for example, thinning the debris cover over piedmont glacier terminus, and tending to thicken debris towards slow-flowing glacier margins. Due to the progressive downglacier increase in debris thickness, the downglacier pattern in ablation rate of a debris-covered glacier has a zone of enhanced ice ablation rate associated with the thin or patchy debris at the upper end of the supraglacial debris cover (Adhikary et al., 2000), and below this zone, ablation is progressively reduced towards the terminus as a function of increasing debris thickness (e.g. Benn and Lehmkuhl, 2000; Benn et al., 2012). This is in stark contrast to the monotonic increase in ablation rate with decreasing elevation towards the terminus of a clean ice glacier.
Superimposed on the systematic spatial variation of debris thickness, local debris thickness variability (e.g. Reid and Brock, 2014; Nicholson and Mertes, 2017) leads to strong small-scale inhomogeneity in ablation rate, which can form pronounced surface relief, which facilitates ice cliff exposure by debris slumping (Moore, 2018), and the formation of supraglacial meltwater ponds within closed surface basins (Watanabe et al., 1986). These features form “hotspots” of ablation (e.g. Sakai et al., 1998, 2000; Buri et al., 2016; Miles et al., 2016; Nicholson et al., 2018), that have been shown to contribute disproportionately to glacier-wide ablation (e.g. Sakai et al., 1998; Immerzeel et al., 2014; Juen et al., 2014; Thompson et al., 2016).
Numerous studies have shown a prevalence of debris-covered glaciers losing mass by thinning (e.g. Lundstrom et al., 1993; Bolch et al., 2008b; Deline et al., 2015; Ragettli et al., 2016; Purdie et al., 2018; King et al., 2020; Anderson et al., 2021), in contrast to the characteristic terminus retreat of clean ice glaciers. This can be explained by the ablation gradient of debris-covered glaciers, whereby 1) enhanced ablation at the upper limit of the debris cover, if not adequately compensated by ice influx from upglacier, results in a flattening of the surface along the flow direction (e.g. Benn et al., 2012; Rowan, 2017; Salerno et al., 2017) and 2) inhibition of ablation means that debris-covered glacier termini can survive at much lower elevations than neighbouring clean ice glaciers, and maintain stable terminus locations over long periods of volume loss (e.g. Mayer et al., 2006; Scherler et al., 2011b; Lambrecht et al., 2014). Declining surface gradient and mean ice thickness during negative mass balance phases both act to reduce the driving stress and ice flow within the debris-covered tongue, typically causing progressive stagnation (e.g. Bolch et al., 2008b; Quincey et al., 2009; Thompson et al., 2016).
Some debris-covered glaciers form large, impounding latero-terminal moraine complexes, as are prevalent in the eastern Nepalese Himalaya (e.g. Benn and Owen, 2002; Hambrey et al., 2008). Other present-day debris-covered glaciers terminate in outwash plains without substantial terminal moraines (e.g. Kirkbride, 1989; Mayer et al., 2006; Anderson et al., 2021), although in some cases aggradation of the outwash plain contributes to the terminus location being overdeepened with respect to the forefield (e.g. Bennett and Evans, 2012). If there are impounding glacier moraines, these affect the englacial water table, pinning it at the lowest exit point of the moraine. In negative mass balance conditions, as the glacier surface lowers towards the water table determined by the moraine, supraglacial ponds can coalesce to form large ice-contact lakes, triggering the onset of ablation by calving of ice into water (Benn et al., 2012). These hydrological states appear to be strongly tied to the surface slope angle (e.g. Reynolds, 2000) and the total amount of surface lowering that has occurred (Sakai and Fujita, 2010). If there are no impounding moraines, terminal lakes can only form by external geomorphic processes such as water being impounded by advances of neighbouring glaciers, or slope failures damming the valley downstream.
While some glaciers in the Karakoram have experienced slightly positive mass balance in recent decades (e.g. Gardelle et al., 2012), observations of glaciers under positive climatic mass balance conditions is scant and interpreting debris-covered glacier behavior in response to this is complicated by widespread surging behavior in the region (e.g. Quincey et al., 2011). Kirkbride (2000) offers a conceptual framework describing how alternating cycles of “ablation dominant” (negative mass balance) and “transport dominant” (positive mass balance) conditions serve to expand and contract the extent of the debris-covered area respectively, while also contributing to progressive downglacier thickening of the debris cover.
Individual glacier advances can be triggered by large rock avalanches onto glacier surfaces. For example, following a large rock avalanche in 1920, the Brenva glacier advanced 490 m between 1920 and 1941, whereas neighboring glaciers in the Mont Blanc massif (European Alps) retreated from the mid-1920s (Deline et al., 2015). In other cases the impacts of rockfall onto glaciers are more ambiguous (e.g. Shugar et al., 2012; Berthier and Brun, 2019), but large rockfall events have been proposed as mechanisms for forming anomalously distal moraine deposits (e.g. Tovar et al., 2008; Shulmeister et al., 2009).
While it is apparent that the modification of the surface mass balance drives a different glacier behavior, the conceptual understanding gleaned from these observations does not reveal the relevant process timescales or controls that dictate how debris-covered glaciers can be formed and evolve over time. To explore these aspects requires numerical modeling, but, before reviewing the existing modeling approaches, we describe the basic governing processes.
In this section we examine the first principles of how supraglacial debris cover filters the climate forcing, as a function of its extent and thickness, and how this effect develops over time. The fundamental glacier-scale processes controlling surface debris distribution are 1) melt out of englacial debris and 2) redistribution of debris with ice flow, by both passive advection and thinning/thickening of debris due to extensional/compressional flow of the underlying ice. We use a simple glacier geometry to study the individual effects of melt out and ice flow redistribution in turn, to isolate how these processes individually, and together, contribute to the spatio-temporal variations in the surface debris distribution.
In our analysis we specifically neglect the local-scale, site-specific processes related to avalanching, rockfall deposits, reworking of debris by gravity or meltwater, as well as the local ablation modification associated with exposed ice cliffs, supraglacial ponds or englacial conduits. This is justified insofar as the significance of all these components varies from glacier to glacier, and we wish to highlight generalized behaviors.
To describe how the fundamental processes govern the distribution of debris on the glacier surface we employ the following continuity equation along a glacier flowline:
Where us is the ice surface velocity, hd is the debris layer thickness and md represents any debris sources or sinks. Similar forms of this equation have been used previously to represent the transport of debris on the glacier surface (e.g. Anderson and Anderson, 2016), however often in a modified form (e.g. Vacco et al., 2010), where a diffusion term is added in order to account for gravitational mass movements. The first term represents the advection of thicker or thinner debris from upglacier; the second represents thickening or thinning of a debris layer due to compressional or extensional ice flow; and in our study the source term md represents melt out of englacial debris, and we do not treat direct surface deposition nor any processes of debris removal at the terminus. Surface deposition and debris evacuation processes are certainly important to the development of a debris-covered glacier system, and would be an essential component of a transient system model, but given that we 1) do not perform transient simulations, and 2) wish to highlight the known systematic effects of debris on the glacier, we neglect these processes as they are complex, site-specific, and lacking well constrained physical relationships (see Section 6 for further discussion). The melt out term will add debris mass to the glacier surface whenever there is ice ablation, at a rate determined by the prescribed englacial debris concentration, local climatic ablation rate and modification of ice ablation rate imposed by the existing debris cover at any point, whereas ice flow will cause a redistribution of surface debris.
First, we look at the vertical profile of surface mass balance and investigate how it is modified by the presence of supraglacial debris cover. For this, we consider a regional surface mass balance rate with a gradient of −15 kg m−2 km−1 and an equilibrium line altitude (ELA) of 3000 m a.s.l., and assume the glacier elevation range spans 2140–3600 m (see Figure 1A, where the annual mass balance is plotted in units of ice equivalent in order to be consistent with later glacier surface evolution calculations). In this illustrative study we have assumed that the reference (clean ice) mass balance gradient is linear. This is an unrealistic representation of the real world condition in which 1) the positive part of the mass balance profile frequently shows only slight variation with elevation as snowfall is more weakly related to elevation, and 2) the negative part of the mass balance profile is often non-linear due to the influence of the gradual rise of the snowline over the ablation season. Lower elevations have longer ice ablation seasons and, as ice albedo is lower than that of snow, ablation rates are enhanced towards the terminus. Nevertheless for our illustrations we use the linear reference mass balance gradient in order to simplify and generalize the visualisation of the effect of debris, as the non-linearity in mass balance for an individual glacier is strongly dependent on its specific climate. To this, we can apply two example debris cover distributions that affect the glacier ablation below 2750 m: 1) a debris cover of constant thickness of 0.5 m, and 2) a debris cover that increases linearly with elevation from 0 m at 2750–0.5 m at the lower limit of glaciation at 2140 m (see Figure 2A).
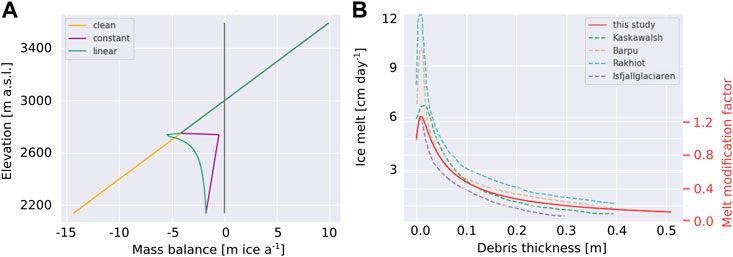
FIGURE 1. (A) The vertical mass balance profile for clean ice (orange), and how it is modified by a debris layer of constant 0.5 m thickness below 2750 m (purple) and by a debris layer that increases linearly in thickness from 0 m at 2750–0.5 m at the lower limit of glaciation at 2140 m (green). (B) Østrem curves from Mattson et al. (1993) compared to the one used in this study, for which we also show the melt modification factor (fdebris) that we apply to the clean ice ablation gradient.
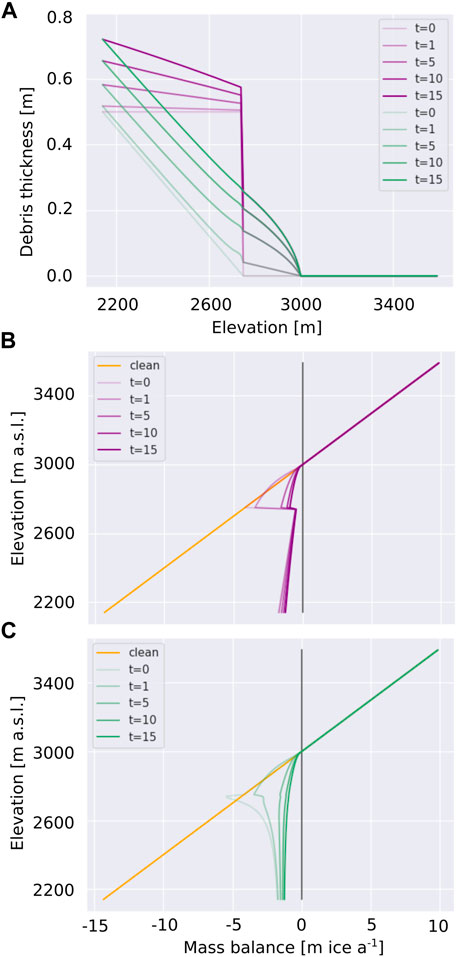
FIGURE 2. (A) The two prescribed initial debris distributions of constant (purple) or linearly increasing (green) debris thickness, and their changes over time (t in years), as a result of melt out alone (md in Eq. 4). The modification of the ablation gradient as a result of progressive debris accumulation by melt out alone, while neglecting all other processes, is shown over time (t in years) in (B,C) for an initially constant (purple) and linearly increasing (green) debris thickness respectively, alongside the vertical mass balance profile for clean ice (orange).
We generate an Østrem curve to describe the modification of ice melt beneath supraglacial debris cover as a function of its thickness, using the approach presented in Evatt et al. (2015). We selected a combination of meteorological parameters (incoming shortwave radiation (500 W m−2), incoming longwave radiation (100 W m−2), wind speed (1.5 m s−1), humidity (10%), and air temperature (275 K)) such that the resulting curve best mimics those measured in the field and presented in Mattson et al. (1993) (Figure 1A). This Østrem curve is converted into a melt modification factor (fdebris) expressing the sub-debris ablation as a function of clean ice ablation, shown on the secondary axis of Figure 1A, and we calculate sub-debris ablation by multiplying the clean ice ablation by this factor for the respective debris layer thickness. While the relationships in Figure 1A are based only on ablation season measurements, we apply the ablation modification factor to the reference mass balance gradient directly as the debris affects the whole snow-free ablation period. As such is independent of any inherent non-linearity of the real-world clean ice mass balance gradient inherited from the progressive decrease in the snow-free ablation season with elevation. Considering the mass balance profiles for the two different debris thickness distributions; in scenario 1) sub-debris ablation rate is always substantially less than the ablation rate of clean ice (see Figure 1B, purple), while in scenario 2) the upglacier part of the debris cover is thin enough to enhance the ablation compared to that of clean ice, and, with increasing debris thickness the ablation rate rapidly decreases and becomes significantly lower than that of clean ice (see Figure 1B, green).
Accumulation and thickening of debris by melt out at the surface progressively shifts the respective sub-debris ablation rate to values further along x-axis of the Østrem curve. We first consider this process of debris melt out alone, as if it were the only factor affecting the debris thickness distribution, in order to isolate how this process influences the ablation gradient over the course of time. Treating this process in isolation from the dynamic glacier system is a strong abstraction of reality, but it is useful for a first principles understanding of the feedback between ablation and debris melt out over time. We consider the simplest case with a constant climate and uniform englacial debris concentration of 1% by volume, so that the debris thickness accumulated at the surface is simply a function of the debris-thickness-dependent ablation rate. This englacial concentration is within the range of those found within the Khumbu glacier (0.1–6.5%, although in reality debris is not evenly distributed within the ice (Miles et al., 2021)). As a result of the mass balance gradient, over time the initially constant debris layer thickness develops into a layer that thickens downglacier (Figure 2A, purple). This highlights how ablation, and melt out of debris, contributes to the systematic downglacier thickening of debris over the glacier surface. For the case of an initial debris thickness distribution that increases linearly with distance downglacier, the maximum debris thickening over 15 years occurs at the upper limit of the initial debris cover extent (Figure 2A, green). In both of our prescribed scenarios, above the upper limit of the initial debris cover debris melt out forms a thin debris layer extending up to the ELA. The debris layer thickness in this newly debris-covered area varies with the linear ablation gradient in the first time step, and, as it is thin, causes enhanced ablation over a relatively wide elevation range. This debris accumulation is initially rapid but, slows down due to the negative feedback on ablation rate imposed by increasingly thick debris cover. As the Østrem curve is non-linear, the newly accumulated debris layer develops a convex-downglacier variation in thickness, even with the linear mass balance gradient as forcing. This example shows how, in the absence of other factors modifying debris thickness, continual exhumation of debris causes the ablation regime of the glacier to change over time even if the climate is constant, thereby revealing the fundamental manner in which the temporal evolution of the sub-debris ablation is partially decoupled from climate forcing.
We can also illustrate a second way in which supraglacial debris cover decouples the glacier ablation gradient from a prescribed climate forcing by considering how the perturbation by the existing debris cover. In this case, we perturb the regional clean ice surface mass balance condition in four example ways: By increasing and decreasing the ELA by 100 m while maintaining the same mass balance gradient (Figure 3B), and by retaining the ELA but modifying the mass balance gradient by ± 2 kg m−2 km−1 (Figure 3D).
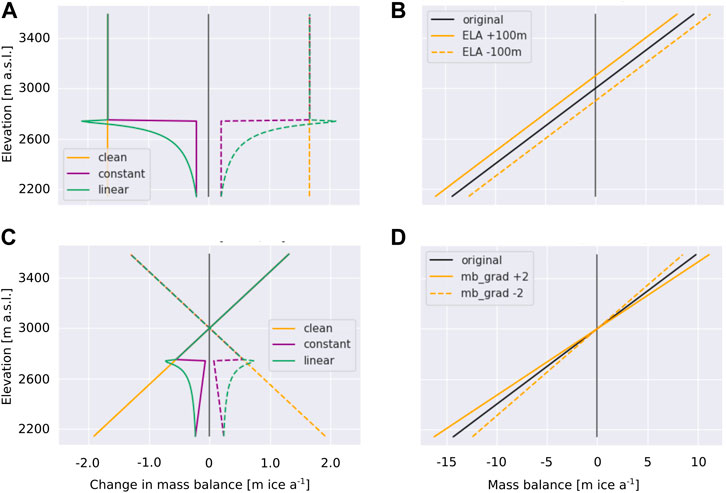
FIGURE 3. Illustrating how an existing debris cover modifies the glacier ablation response to a climate forcing, where the climate forcing is represented as an alteration to the clean ice mass balance gradient: (A) shows the change of the mass balance profile experienced by shifting the ELA of the regional clean ice mass balance gradient by ± 100 m (B), and how this affects the mass balance gradient for an initially constant (purple) and linearly increasing (green) debris thickness respectively; (C) shows the effect of altering the mass balance gradient by ± 2 kg m−2 km−1 (D). Positive perturbations to the ELA and mass balance gradient are shown in solid and negative changes in dashed lines. All actual and differences in mass balance gradients are shown converted into units of ice surface height change.
Upward/downward migration of the ELA for our linear clean ice mass balance gradient produces uniform negative/positive change in the mass balance profile for clean ice glaciers (orange lines in Figure 3A). However, the resulting change in mass balance is not uniform with elevation if a debris cover is present (purple and green lines in Figure 3A). Beneath a thick debris layer, the effect of a shift in ELA on the surface mass balance is greatly reduced. Beneath the 0.5 m thick debris cover the change in ablation associated with an upward shift in ELA is reduced to the order of 20% of that experienced by a clean ice glacier surface, while beneath the thin debris, the upward shift in ELA causes a local increase in ablation that is the order of 30% more than that experienced by clean ice in the same portion of the glacier (Figure 3A). As in the case of ELA migration, the effect of perturbing the linear mass balance gradient (orange lines in Figure 3C)), is strongly damped beneath the debris layer of constant thickness (purple lines in Figure 3C), and shows strong non-linearity beneath the debris cover that increases in thickness linearly with decreasing elevation (green lines in Figure 3C). These simple illustrations show how the surface mass balance forcing experienced by a glacier in response to changing climate conditions, varies depending on the existence and distribution of surface debris. The likely pattern of debris cover thickness on a glacier implies that over most of a debris-covered zone the expression of the climate shift on the surface mass balance rate is damped compared to that experienced by a clean ice glacier surface.
The effects of melt out as illustrated in the previous section are of course not the whole picture, as other factors affecting the surface debris distribution have been neglected; the most important of which is the effect of ice flow. To see how the fundamental processes of advection of upstream debris, and thickening or thinning of the overlying debris due to compressional or extensional ice flow play out in the case of a plausible glacier geometry, we compute a steady state geometry for a simple clean ice glacier long profile. This initial glacier geometry is constrained for a bed with a constant slope of 4.5° and ice flow is computed using an open-source flux-limited Shallow Ice Approximation (SIA) model (Jarosch et al. (2013), https://github.com/alexjarosch/sia-fluxlim). The same prescribed time-invariant mass balance gradient as used in the previous section (−15 kg m−2 km−1) and an ELA of 3000 m is applied until a steady state geometry is achieved (see Figure 4A). For this steady-state clean-ice glacier longitudinal profile, we compute a velocity field with an open-source full-Stokes ice flow model (icetools, Jarosch (2008), https://github.com/alexjarosch/icetools). These computations are performed with a no-slip condition at the glacier bed and zero velocity in the flow direction (x-direction) is imposed at the upper margin. We use a full-Stokes model here to resolve the vertical distribution of ice velocities, from which we extract the surface velocities required. By considering only the variation down a flowline, we neglect any cross-glacier effects due to compressional flow at the lateral margins of the glacier. The initial debris thickness conditions for Eq. 4, are defined so that the lower part of the glacier ablation area (
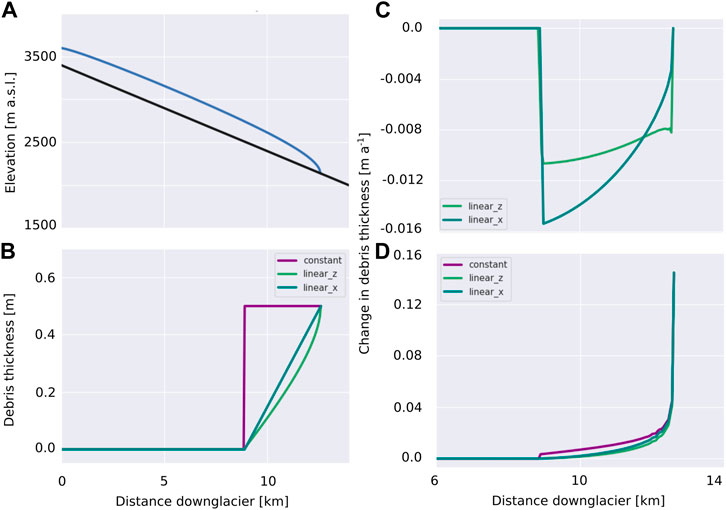
FIGURE 4. Configuration of the illustrative example discussed in the text. (A) the 2D longitudinal glacier profile generated using a SIA model on a constant slope, (B) the three initial debris covers prescribed below 2750 m with 1) constant thickness (purple), 2) linear increase in thickness with decreasing elevation (green) and 3) linear increase in thickness with downglacier distance (blue) debris thickness, (C) the downglacier pattern of debris advection with ice flow (first term in Eq. 4) and (D) the downglacier pattern of thickening or thinning of the debris layer due to compressional or extensional ice flow (second term in Eq. 4).
In the case of an initially constant debris thickness distribution 1), the advection term in Eq. 4 does not lead to a change of debris thickness, except that the upper margin of the debris layer will migrate downstream, which causes a change from debris to no debris cover at that location. Therefore the result for this debris distribution is not shown quantitatively in Figure 4C, as its magnitude is dependent on the model discretization. For the case of both variable debris thickness distributions, the advection term causes a local decrease of debris thickness throughout Figure 4C. For case 2) applied to our glacier geometry (blue line in Figure 4A), the steep elevation change at the glacier terminus creates strong gradients in debris thickness resulting in more pronounced advective thinning towards the glacier front.
For our simple glacier geometry, surface ice velocities within the ablation zone decrease monotonically towards the glacier terminus, causing convergence of the debris layer (see Figure 4D). This process causes compressional thickening of debris cover for all three initial debris thickness distributions over time, at a rate that increases downglacier and is especially pronounced close to the glacier terminus where ice velocities decelerate rapidly to zero. Thus, at any given point along the glacier long profile, the processes of advection is generally acting to thin the debris cover, while compressional ice flow is serving to thicken debris, although a more complex downglacier bedslope could lead to sections of extensional ice flow. In this analysis, it should be noted that though we examine the behavior of the terms in Eq. 4, we do not perform transient simulations.
In order to meet the conditions of steady state given by Eq. 3, the mass balance gradient, including the part influenced by debris cover, would need to be maintained constant in space and time, which in turn would require a solution for Eq. 4 that can sustain a specific debris thickness distribution that is constant in space and time.
If we revisit Eq. 2, in the case of debris-covered glaciers, this formulation changes to:
Where the clean ice mass balance rate
However, following Eq. 4, debris cover thickness is not constant in time, but a function of ice velocity and the melt out of englacial debris, which is determined by the mass balance rate and the englacial debris concentration. These interdependencies highlight that it is very unlikely that the divergence of ice flux can, over an extended period of time, balance the debris-dependent mass balance rate, as this itself is a function of ice velocity and mass balance rate, constantly evolving with time.
Posed another way, the question is whether ongoing melt out of englacial debris could be exactly offset by debris thickness redistribution by ice flow to sustain the initial debris distribution in the context of our plausible glacier mass balance and flow field conditions. The melt out and ice flow terms are plotted together in Figure 5 to examine the relative scale of their combined effects along the glacier longitudinal profile. We emphasise that the relationships shown in Figure 5 are not the result of transient simulations but show a representation of the processes at work for the given configuration of prescribed debris thickness distributions, glacier geometry and mass balance rate as a snapshot in time, and as such gives only a first order indication of the interplay between these processes. By plotting these together, we wish to highlight how the downglacier variation of the three processes of 1) debris meltout, 2) advection of debris with ice flow and 3) debris thickening/thinning due to compressional or extensional ice flow flow, result in a debris thickness change that cannot be easily offset by a glacier flowfield to maintain the constant surface geometry as specified by the steady state condition given in Eq. 3.
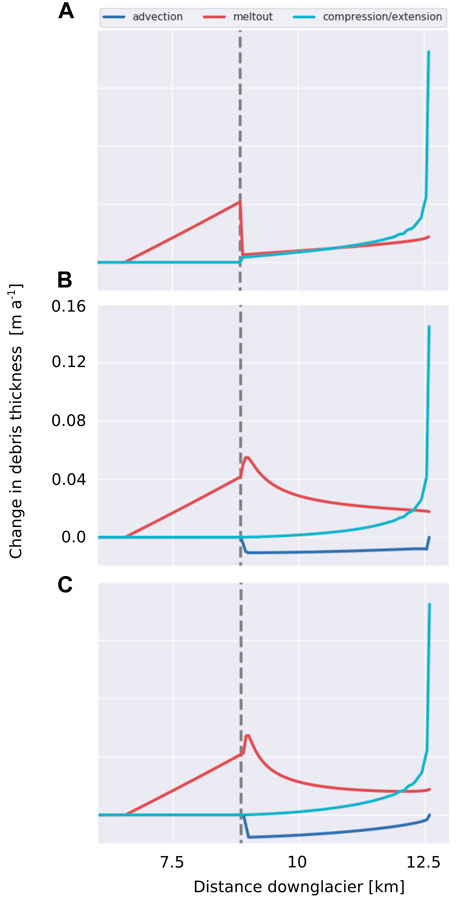
FIGURE 5. The effect of 1) meltout of englacial debris (red, (third term in Eq. 4)), 2) advection (dark blue, second term in Eq. 4) and 3) extensional/compressional ice flow (light blue, (second term in Eq. 4) as a result of three initial boundary conditions (A) constant, (B) linearly increasing with decreasing elevation and (C) linearly increasing with downglacier distance debris thickness distribution. Note that these are showing the instantaneous state for the initial boundary conditions, without time dependency. The grey dashed line indicates the upper limit of the initial debris cover distributions. In (A) we do not plot the advection term, which is zero everywhere except at the onset of the debris cover, where it is locally strongly negative and would cause the upper margin of the debris cover to shift downglacier.
For an initially constant debris thickness 1), the melt out of englacial debris is stronger further downglacier and the deceleration of ice flow causes convergence of the debris layer (Figure 5A). This leads to an increase of debris thickness along glacier that is stronger further downglacier and hence, the initially constant debris thickness will not be sustained. In the case of an initially varying debris thickness 2) and 3), there is an obvious incompatibility of monotonic downglacier variation of debris thickening with strongly non-linear melt out, so that these terms cannot cancel each other out to sustain a constant debris thickness distribution downglacier (see Figures 5B,C). These illustrative figures highlight that, as also indicated by considering Eqs 5, 6, that a constant debris thickness is unlikely to be sustained for a prescribed set of constant climate conditions even for the simplest glacier cases.
The simple illustrations of the fundamental properties of debris-covered glaciers presented in the previous sections, show that 1) the impact of supraglacial debris cover on the glacier mass balance is controlled by linked processes that are time-dependent, and themselves related to the temporal changes in supraglacial debris extent and thickness, 2) these time-dependent processes and the related thresholds and feedbacks between them together determine the climate response of debris-covered glaciers and 3) the conditions of steady state are unlikely to be achievable for a debris-covered glacier, even with idealized constant climate forcing. In short; even when considering only the fundamental governing processes in the simplest configuration, surface debris cover, and therefore the spatial pattern of surface ablation, is continually changing as a result of the dynamic coupled processes of debris melt out and alteration by ice flow. This pose challenges to understanding both the transient and equilibrium responses of debris-covered glaciers, even for highly idealized glacier cases. Numerical model representations of debris-covered glaciers in the literature differ in the level of detail they include, and the processes they represent, so in the following section we briefly describe how existing modeling approaches have dealt with these specific challenges, summarize the key lessons learned, and suggest a path forward.
Two decades ago, Konrad and Humphrey (2000) suggested that under steady state climate conditions, a debris-covered glacier terminus has to constantly advance. While a provocative concept, their model effectively forces this behavior by prescribing a constant surface supply of debris
Naito et al. (2000) present a more complete process-representation of an evolving debris-covered glacier tongue. To recreate the evolution of the Khumbu glacier tongue from 1978 to 1999 they used a reconstructed climate series based on local measurements, prescribed upstream ice influx based on a 1976 estimate. They then applied a debris-modified mass balance initially constructed on the basis of the residual lowering after accounting for ice flux divergence based on the continuity equation of Kadota et al. (2000) for a glacier longitudinal profile, accounting for lateral drag via a shape factors assuming the glacier tongue has a trapezoidal cross-section. This mass balance was allowed to evolve gradually over time as a function of debris thickening by melt out and underlying ice flow convergence. The inputs to this scheme were simple, and uncertain, but the observed surface lowering up to 1999 was quite well captured.
A number of subsequent published modeling studies tended to move away from the coupled, time-evolving debris flux and mass balance representations of Naito et al. (2000). Banerjee and Shankar (2013), for example, compared the response of idealized clean and debris-covered glaciers to climate forcing using a shallow ice approximation flowline model in conjunction with simplified, unchanging, linearized glacier mass balance gradient forcing. By applying a fixed mass balance condition, which can neither evolve with further debris meltout, nor with redistribution of debris by ice flow, the model can achieve steady state geometries. The first conclusion of this study is that debris-covered glaciers show a longer response time, but greater sensitivity, in terms of equilibrium length change, to a given climate forcing than clean ice glaciers. The second conclusion is that debris-covered glacier response comprises two stages with two different timescales: Firstly, a stagnation timescale related to the rate at which changes propagate downglacier, and secondly, a separation timescale related to the ice thickness at the upper margin of the debris cover that controls when the debris-covered terminus becomes detached from the active glacier upstream. The pattern of these responses differs in advance and retreat, indicating that hysteresis inherent in glacier response could be amplified in the case of debris-covered glaciers. The authors explicitly highlight the need to compare their results to those of a coupled debris/ice model in order to test the robustness of their simplified model, and to determine how the mass balance profile evolves with the development of a dynamically coupled debris cover.
Jouvet et al. (2011) incorporated simple representations of surface debris into a 3D full-Stokes ice flow model that solves for an evolving glacier surface using a volume of fluid approach. This study reported difficulties in constraining an empirical representation of the rate of debris cover expansion as a function of melt-rate and a parameterized spreading function for medial moraines (Anderson, 2000). Instead they present a sensitivity analysis in which the effect of debris cover on the glacier evolution was demonstrated by prescribing several estimates of a factor simulating spreading of supraglacial debris, and reducing the ablation rate by 40% wherever there is debris cover. These simulations for different spreading rates of supraglacial debris cover highlight that the debris will substantially alter the glacier length response compared to that of a clean ice glacier, while the difference in volume response was found to be smaller. The timing of the maximum difference in glacier geometry response between the clean and debris-covered cases was dependent on the parameterization of lateral debris spreading.
Rowan et al. (2015) studied the evolution of Khumbu glacier in Nepal including a representation of the feedbacks between ice dynamics, glacier mass balance, the effect of surface debris cover and debris transport in a return to more fully coupled model systems. In this study, the impact of debris on ice melt was represented by an exponentially decaying function for increasing debris thickness, neglecting the enhancing effect of thin debris layers. Debris is supplied constantly across the whole accumulation zone, and is subsequently modified by ice flow and ablation. Debris transport is treated as an advection problem, and a higher-order shallow ice model, ISOSIA (Egholm et al., 2011), is used to simulate ice flow. ISOSIA computes depth averaged velocity components, hence the required 3D velocity field for the debris transport is computed as a post-processing step based on several assumptions. Their optimized model could recreate debris accumulation at the glacier margins and terminus, and capture the general behavior of Khumbu glacier, but neighbouring glaciers were markedly less well reproduced. Their simulations are run to steady state, although the definition of steady state is not reported. The study highlighted the importance of coupling of the debris and glacier evolution as fixed ablation reduction could not represent the present-day glacier.
Anderson and Anderson (2016) also developed a debris-covered glacier model that accounts for debris transport and melt out. They examine the sensitivity of the modelled glacier to the specific location of debris input within the system. Their model represents a 2D vertical glacier flowline, by including parameters for the longitudinal stress gradient, lateral drag, and generating vertically-resolved velocity profile from the continuity equation. Debris is transported through the glacier by ice flow and, once it has emerged on the surface, is advected with the ice surface velocity and modified by the downglacier surface velocity gradients. Debris is evacuated at the terminus according to a parameterization linked to the terminus melt rate. In keeping with expectations based on theoretical glacier flowlines, their study highlights that the system is most sensitive to debris inputs near the equilibrium line. This is because deposits in the upper accumulation zone are buried and transported at greater depth within the glacier body and so are exhumed by ablation lower down in the ablation zone. They find a convex-to-concave curvature of downglacier debris thickness which is a result of the dominance of ablation (decelerating ice velocity) in the upper (lower) zones of the debris cover. This model can achieve a glacier steady state as debris inputs are in the form of constant supply at a single location, rather than debris distributed through the ice body, and debris removal at the terminus is stipulated at a rate that offsets the addition of debris to the surface, which together mean that a solution can be found to convey this stripe of debris through the glacier in a stable form.
More recently, a study used a shallow ice approximation flowline model to explore the impact of debris on the transient response of glaciers over centennial timescales (Ferguson and Vieli, 2021). This model neglects the possibility of enhanced ablation under thin debris, and evacuates debris from the system via a terminal ice cliff, whose position is a function of an ice thickness threshold. An interesting feature is the introduction of a parameterisation for ablation associated with thermokarst features into the surface mass balance forcing. The results suggest that the distinctive debris-covered glacier geometry is related to the fact that they “remember cold periods more than warm.”
Some general lessons can be drawn from reviewing the existing numerical modeling studies. Firstly, regardless of the climate conditions, increased debris influx to a glacier results in a longer glacier, with a flatter, and therefore, slower flowing terminus. Secondly, model outputs robustly demonstrate that the geometrical response of the debris-covered glacier system is sensitive to the location at which surface debris emerges (e.g. Anderson and Anderson, 2016), highlighting need to account for the location at which debris is delivered, or emerges. Thirdly, the response times of retreating debris-covered glaciers are generally shown to be longer than those for clean ice glaciers, and there may be a pronounced asymmetry in response and response rate between positive and negative mass balance phases (Banerjee and Shankar, 2013; Ferguson and Vieli, 2021).
However, there are also a number of distinct limitations of the existing numerical modeling studies of the response of debris-covered glaciers to climate forcing:
• A common feature of these numerical model studies with the exception of Naito et al. (2000) is that the existence of enhanced ablation caused by thin debris is overlooked. Instead, ablation reduction caused by debris has been prescribed as a fixed value (Jouvet et al., 2011), a linearly decreasing ablation gradient with elevation (Banerjee and Shankar, 2013) or an exponentially decreasing ablation rate (Anderson, 2000; Ferguson and Vieli, 2021), but no analysis of the impact of neglecting the role of enhanced ablation has been performed.
• The chosen model dimension also limits the processes that can be represented. For example, representing the glacier as a 1D flowline necessarily neglects the potentially important processes of debris accumulation in medial moraines and at lateral margins as well as neglecting the 2D pattern of ice surface velocities and how they redistribute debris laterally as well as longitudinally within the ablation zone.
• The time-dependent nature of the developing debris cover is often neglected, by applying time-invariant modifications to the surface mass balance forcing (e.g. Konrad and Humphrey, 2000; Banerjee and Shankar, 2013). A proposed simple model of debris expansion rates, could not be sufficiently well constrained to allow transient modeling of debris cover (Jouvet et al., 2011).
• Although steady state can be achieved in model simulations through specific formulations of the debris ablation modification, transport and evacuation problems (e.g. Banerjee and Shankar, 2013; Anderson and Anderson, 2016; Ferguson and Vieli, 2021), the underlying assumptions that allow this to be achieved have not been rigorously tested. Our analysis in this paper suggests that this warrants further investigation.
• Simple modeling suggests that debris cover alters both the response time and total volume response of a glacier (e.g. Banerjee and Shankar, 2013), and more physical modeling suggests that response times are related to the rate of debris removal (Anderson and Anderson, 2016). In both cases, untested simplifications in the models used means that it remains unclear to what extent the response times might reflects real-world short and long term glacier meltwater contribution to rising sea levels.
• In general, simplifications and assumptions used in these model formulations are not evaluated against reality, so the model study findings should be assessed critically in the light of the specific model capacities.
Conceptually, the individual components required to represent debris within a glacier system are known (Figure 6). However, the details of how to quantify the variation in space and time of these individual processes and their interactions remain elusive. Given that the long-term debris-covered glacier response is strongly influenced by the interaction between two time-dependent processes: dynamic debris evolution and climate variability, and as it seems improbable that the traditional conception of glacier equilibrium can apply in the case of distributed englacial debris melting out to form a surface debris cover, climate response investigations for these systems is reliant on transient system modeling. The main limitation to interpreting the results of numerical models presented in the previous section is that the models have not been, and maybe cannot be, validated at the centennial and upward timescales relevant for the development of debris-covered glaciers. Thus, it is questionable if existing model studies will improve the accuracy of projections or just offer a different way of indicating the model uncertainty associated with debris cover.
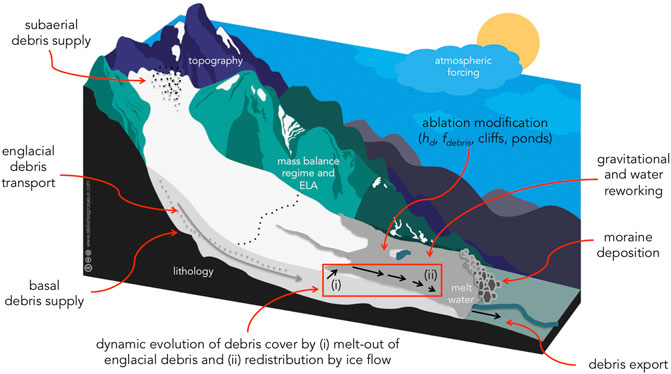
FIGURE 6. Illustration of the processes of debris flux through a mountain glacier, that ultimately govern the surface debris cover distribution and therefore the way that surface ablation is modified by the debris cover. CC-BY-SA Lindsey Nicholson, adapted from CC-BY-SA Anne Maussion, Atelier les Gros Yeux (http://atelierlesgrosyeux.com).
The numerical implementation deployed within a model can be verified using appropriate rigorous testing, for example comparison to exact solutions (Bueler et al., 2005). As an example, the implementation of englacial debris transport, computed as advection of a scalar quantity in an incompressible flow field in Wirbel et al. (2018), was tested by reproducing the results of a “rotating three body problem” (see e.g. de Frutos et al., 2014) where the initial shapes are recovered after flow displacement. However, what is further needed is model validation against a representation of reality (Bueler et al., 2005). Unfortunately, the decadal/centennial/millenial timescales involved in the development and evolution of debris-covered glaciers inhibit real-world validation as past behavior of debris-covered glaciers cannot yet be unambiguously reconstructed from the geomorphic record. Given this, a viable alternative solution could be the development of a “surrogate world” model sufficiently complex to capture the coupled, time-evolving, processes operating on debris-covered glaciers.
In addition to representing the total debris flux through the glacier system, a debris-covered glacier system model would need to represent the development of the surface debris cover over time and how it feeds back into other glacier processes, shown schematically in Figure 7. Specifically, in order to understand the systematic response of the glacier, even over relatively short timescales, it is crucial to accurately include the partial climate decoupling caused by how supraglacial debris modifies the spatial distribution of ice ablation, and furthermore, the knock-on effects this ablation modification has on 1) subsequent meltout rate of englacial debris, 2) the development of the glacier surface geometry and, consequently, 3) the large-scale debris redistribution by ice flow. Coupling these feedbacks is made difficult by the fact that there is embedded non-stationarity within stages of the development of surface debris cover. The effect and importance of processes linked to ablation (transition from enhancement to inhibition), dynamics (transition from flowing to stagnant) and hydrology (transition from drainage to storage), themselves change in space and time with the development of the whole glacier system. Treating these embedded, non-stationary processes, operating at multiple spatio-temporal scales, poses a substantial challenge for time-dependent modeling of debris-covered glaciers systems. Added to this it is not clear to what extent treatment of non-systematic impacts of site-specific features such as localized avalanche and rockfall inputs, variable bedforms, impounding terminal moraines, gravitational reworking of surface debris and additional ablation hotspots associated with cliffs and ponds, is required in order to satisfactorily reproduce glacier behavior.
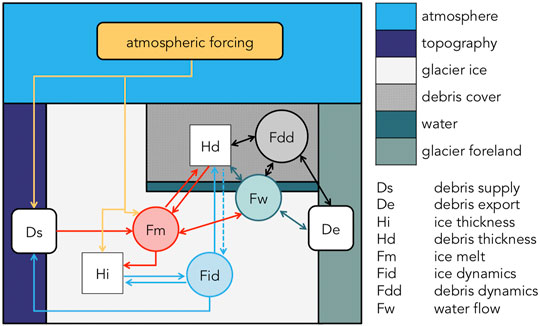
FIGURE 7. Schematic of the processes interacting (in circles) between forcing variables (rounded boxes) governing the state of a debris-covered glacier system given by the thickness distribution of ice and debris (square boxes), placed in the colour-coded domain of the glacier system where they operate (cf. Figure 6).
Clearly the complexity of such a proposed model renders it not applicable to regional and global problems due to restrictions related to computer power and suitable input data. Nevertheless, the development of a time-dependent system model for debris-covered glaciers would offer a crucial tool to evaluate simpler model representations that could then be incorporated into larger scale modeling efforts. Alternatively, sensitivity testing with a surrogate world model could form the basis of identifying robust statistical representations of the impact of surface debris so that it can be reliably incorporated as a parameterized term in regional and global models used to predict runoff supply, contributions to sea level rise and longer-term histories and projections of glacier-climate interaction (e.g. OGGM (Maussion et al., 2019) and PyGEM (Rounce et al., 2020)).
Developing a coupled, time-dependent, system model of debris-covered glaciers would require overcoming a number of significant obstacles, related to poorly constrained inputs, scale bridging, and dealing robustly with (differing) time-dependency in various components of the system. While some system processes have clear quantifiable process-representation developed through previous work, we highlight problematic components in the following sections, and indicate where they lie within a proposed structure of a coupled debris-covered glacier landsystem model in Figure 8. Regardless of the process-understanding for individual components, it remains a challenge to couple these at meaningful spatio-temporal scales, and to generate a model that offers quantifiable uncertainty and predictive power.
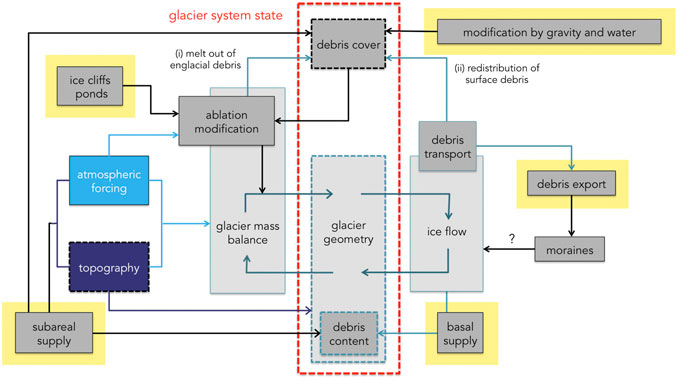
FIGURE 8. Flowchart of a suggested model structure for a transient, coupled “surrogate world” numerical model of a debris-covered glacier system in order to determine the glacier state (within the red dashed box) at any point in time. The processes represented in solid boxes all vary in space and time, and their interactions represented by the connecting arrows operate on different spatial and temporal scales, that must be handled by the model. We highlight in yellow the components that currently pose significant open challenges to quantify within a numerical model framework: rates and processes of debris supply (subareal and basal), integration of small-scale processes (e.g. cliffs, ponds, gravitational and water re-working) and rates and processes of debris evacuation and deposition.
Space- and time-variant supraglacial debris supply, both subaeral and basal (Figure 8), is difficult to constrain and implement realistically in a numerical modeling framework, which is problematic as previous studies suggest that the timing and location of debris inputs is critical to their ultimate impact on the glacier. Debris supply may consist of both semi-continuous small-scale inputs and episodic large deposits, necessitating some treatment of both. Applying debris continuously or episodically will influence the debris concentration distribution throughout the glacier at any point in time (Wirbel et al., 2018), and both this and the specific location and intensity of debris delivery determines location and pattern of subsequent debris emergence (e.g. Anderson and Anderson, 2016). Although it is understood that lithology and weathering rates will affect debris supply (Matsuoka and Sakai, 1999; Nagai et al., 2013; Scherler, 2014), debris source and deposition areas, volumes, frequency and rates remain poorly constrained (Benn and Evans, 2010). Estimates of denudation rates from headwall retreat (Heimsath and McGlynn, 2008; Seong et al., 2009), given in units per century or per millennium are difficult to integrate with a glacier system model that requires representation of episodic, discrete debris supply events (Scherler and Egholm, 2020). Measurements of rock volumes from individual events (e.g. Deline, 2009; Hewitt, 2009; Reznichenko et al., 2011) are relatively scarce and therefore not readily generalized. Gravitational movement of debris onto glaciers is expected to be at least partly a function of climate conditions, glacier debutressing and the changing expanse of exposed rockwall, though the nature of this relationship remains contentious. Thus, debris supply rate is also a non-stationary component of a climatically-forced glacier simulation, making it difficult to accurately know the englacial debris distribution at any specific point in time (Scherler and Egholm, 2020). Supply rate estimates based on more readily observable properties such as lithology or projected climate conditions would be helpful, but debris supply will likely continue to be associated with large uncertainties. Therefore it would be valuable to incorporate the findings of sensitivity studies as a means to bracket glacier response to a variety of possible debris supply regimes. In a subsequent step, the valuable experiments of glacier response to different debris supply regimes in Anderson and Anderson (2016), could be built upon by performing sensitivity studies using high resolution models, that can capture the specifics of englacial debris transport and emergence (Wirbel et al., 2018; Scherler and Egholm, 2020) in the required detail to predict the thickness at the point of emergence (Kirkbride and Deline, 2013). Quantifying rates of basal debris incorporation is dependent on detailed knowledge of the basal properties, which are usually unknown, and as a result prescribed by simple assumptions and parameterizations in glacier models.
In addition to the systematic downglacier thickening of surface debris, as soon as debris emerges at the surface, gravitational and meltwater reworking of the supraglacial debris (Figure 8), potentially conditioned by differential ablation rates, modifies the spatial distribution of debris thickness (Anderson, 2000; Kirkbride and Deline, 2013). The resultant local debris thickness variability and presence of bare ice cliffs and ponded water (Figure 8) can all create ablation hotspots that can significantly alter the ablation and runoff regime of debris-covered glaciers (Irvine-Fynn et al., 2017). Therefore, some treatment of these effects is required in a transient modeling framework. Numerous careful field and model studies at specific glaciers have assessed the impact of ice cliffs and ponds on local and glacier-wide ablation (e.g Reid and Brock, 2014; Steiner et al., 2015; Miles et al., 2016). Although some studies suggest governing relationships might be found, for example relating local variability of debris thickness to the time elapsed since the debris formation (e.g Nicholson et al., 2018); ice cliff formation to debris stability (e.g Moore, 2018); ice cliff persistence to aspect (e.g. Buri and Pellicciotti, 2018); pond formation to the glacier surface profile flattening and the degree of net downwasting (Reynolds, 2000; Sakai and Fujita, 2010), these relationships and their effect on net ablation over time is not yet routinely incorporated into glacier scale simulations. One potential way to include these aspects would be to first robustly evaluate these proposed relationships against either field observations or detailed physically-based numerical models, and then develop statistical relationships to represent their impact at the glacier scale (c.f. Ferguson and Vieli, 2021).
Both the process of debris removal from the system, the conditions under which large impounding moraines are formed and the impact of such moraines remain open questions (Figure 8). The rate of debris loss from the system will affect both timescale and length response of a glacier, yet a clear way of handling debris removal processes within numerical models of glacier evolution is still lacking. Relationships mimicking debris offloading have been implemented (Anderson and Anderson, 2016; Ferguson and Vieli, 2021), but these have not been rigorously validated, and in general the mechanism connecting the glacier debris load and marginal deposition is unclear. At unconstrained debris-covered glacier termini, debris can readily exit the glacier onto the forefield, but if impounding latero-terminal moraines are formed, debris cannot readily be exported to the proglacial area. Developing an understanding of how and why such large impounding moraines are formed is prerequisite to including their effects on glacial water storage, upstream ice dynamics and subsequent glacier geometry in both retreat and advance phases. Improved understanding of how debris cover affects glacier behavior and associated deposition will help clarify the paleoclimatic significance of former glacier geometries that may have been influenced by surface debris. At present, this remains complicated because: Debris-covered glaciers are difficult to identify unambiguously in the sedimentary record (e.g. Fernández-Fernández et al., 2017); the proxy climate interpretation of the moraine position is not well constrained (e.g. Clark et al., 1994; Jansson and Fredin, 2002).
As is the case with all glaciers, the transient response of a glacier to a prescribed climate forcing is in part dependent on its state when the forcing is applied. In the case of debris-covered glaciers this requires knowing, both initially and throughout time, whether (in the framework of the listed citations) the debris-covered glacier system state is 1) currently transport- or ablation-dominant (Kirkbride, 2000), 2) enhancing or inhibiting ablation relative to clean ice (Østrem, 1959), 3) close to the threshold between downwasting behaviour and the separation of the active glacier from the former glacier terminus (Banerjee and Shankar, 2013), 4) close to the hydrological thresholds of pond formation, coalescence, or onset of calving retreat (Benn et al., 2012). The onset of calving retreat is related to rapid terminus retreat, and more negative mass balances compared to similar glaciers without a terminus lake (e.g King et al., 2019), and model studies have highlighted that neglecting the transition from land to lake terminating glaciers will result in inaccurately simulated glacier recession and mass balance (e.g Sutherland et al., 2020). All the processes represented in Figure 8, vary in both space and time and furthermore, interactions represented by the connecting arrows operate on different spatial and temporal scales, that must be handled by the model. Some feedbacks are expected to be approximately instantaneous, such as the modification of debris cover by progressive melt out of englacial debris, while others, connected to the rate of ice throughput, such as debris transport by ice flow, and glacier geometry adjustments will involve time lags of decadal to centennial scales, and possibly longer. Finally, as evidence points towards longer response times for debris-covered glaciers it is increasingly likely that multiple timescales of forcing are involved in the observed response, including long inertial phases which might exceed the duration of a given climate perturbation, making it even more difficult to untangle a climate signal from these glaciers.
We have presented a back-to-basics approach to isolate and explore the fundamental processes by which supraglacial debris thickness is controlled by englacial melt out and redistribution by ice flow. In doing so, we demonstrated 1) the key ways in which surface debris decouples a glacier system from a climate forcing and 2) that if debris is distributed throughout the glacier, then steady state may be unattainable for a debris-covered glacier, because melt out and redistribution of debris by ice flow cannot offset each other even under constant climate forcing. As a result, classical analysis of equilibrium glacier response to climate is unlikely to be an appropriate approach for debris-covered glaciers, even with constant climate forcing. Added to which, the expected long (and possibly multiple) timescales of debris-covered glacier response to climate forcing increase the likelihood that response time exceeds the duration of the climate forcing. Recent progress in developing and applying numerical glacier system models that capture the co-evolution of debris, ice and landscape, still contain numerous untested assumptions and increasing understanding of individual components of the system, won through detailed field investigations and remote sensing investigations, remains difficult to ingest into a coupled understanding of the whole system. While it is not realistic to represent all local features correctly, we argue that understanding the response of these glaciers in a meaningful way is likely to require “surrogate world” numerical process modeling in order to validate simpler representations. The effort to include robust treatment of the full system complexity would furthermore offer the possibility to perform 1) the validation required for existing simplified model schemes, as well as 2) the sensitivity testing required to develop robust, yet tractable, simplified representations of debris cover that are needed to implement the long term effect of supraglacial debris in regional and global glacier modeling.
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
LN conceived the paper, and all authors brainstormed the scope and content of the paper together. LN prepared the manuscript and AW performed computations and prepared the figures. All authors contributed to the final version of the manuscript and the design of the schematic figures.
This work was supported by Austrian Science Fund (FWF) Grants V309 and P28521.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer AR declared a past co-authorship with one of the authors LN to the handling editor.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Thanks to Argha Banerjee and James Ferguson for stimulating discussions on a poster version of this paper, and Alexander H. Jarosch for giving input on how to frame the paper.
Adhikary, S., Nakawo, M., Seko, K., and Shakya, B. (2000). Dust Influence on the Melting Process of Glacier Ice: Experimental Results from Lirung Glacier, Nepal Himalayas. Debris-Covered Glaciers: Proceedings of an International Workshop. Seattle, WA: International Association of Hydrological Science, 43–52.
Anderson, L. S., and Anderson, R. S. (2016). Modeling Debris-Covered Glaciers: Response to Steady Debris Deposition. Cryosphere 10, 1105–1124. doi:10.5194/tc-10-1105-2016
Anderson, R. S., Anderson, L. S., Armstrong, W. H., Rossi, M. W., and Crump, S. E. (2018). Glaciation of Alpine Valleys: The Glacier - Debris-Covered Glacier - Rock Glacier Continuum. Geomorphology 311, 127–142. doi:10.1016/j.geomorph.2018.03.015
Anderson, L. S., Armstrong, W. H., Anderson, R. S., and Buri, P. (2021). Debris Cover and the Thinning of Kennicott Glacier, Alaska: In Situ Measurements, Automated Ice Cliff Delineation and Distributed Melt Estimates. Cryosphere 15, 265–282. doi:10.5194/tc-15-265-2021
Anderson, R. S. (2000). A Model of Ablation-Dominated Medial Moraines and the Generation of Debris-Mantled Glacier Snouts. J. Glaciol. 46, 459–469. doi:10.3189/172756500781833025
Banerjee, A., and Shankar, R. (2013). On the Response of Himalayan Glaciers to Climate Change. J. Glaciol. 59, 480–490. doi:10.3189/2013jog12j130
Benn, D. I., and Lehmkuhl, F. (2000). Mass Balance and Equilibrium-Line Altitudes of Glaciers in High-Mountain Environments. Quat. Int. 65-66, 15–29. doi:10.1016/s1040-6182(99)00034-8
Benn, D. I., and Owen, L. A. (2002). Himalayan Glacial Sedimentary Environments: A Framework for Reconstructing and Dating the Former Extent of Glaciers in High Mountains. Quat. Int. 97–98, 3–25. doi:10.1016/s1040-6182(02)00048-4
Benn, D. I., Warren, C. R., and Mottram, R. H. (2007). Calving Processes and the Dynamics of Calving Glaciers. Earth Sci. Rev. 82, 143–179. doi:10.1016/j.earscirev.2007.02.002
Benn, D. I., Bolch, T., Hands, K., Gulley, J., Luckman, A., Nicholson, L. I., et al. (2012). Response of Debris-Covered Glaciers in the Mount Everest Region to Recent Warming, and Implications for Outburst Flood Hazards. Earth Sci. Rev. 114, 156–174. doi:10.1016/j.earscirev.2012.03.008
Benn, D. I., Fowler, A. C., Hewitt, I., and Sevestre, H. (2019). A General Theory of Glacier Surges. J. Glaciol. 65, 701–716. doi:10.1017/jog.2019.62
Bennett, G. L., and Evans, D. J. A. (2012). Glacier Retreat and Landform Production on an Overdeepened Glacier Foreland: The Debris-Charged Glacial Landsystem at Kvíárjökull, Iceland. Earth Surf. Process. Landforms 37, 1584–1602. doi:10.1002/esp.3259
Berthier, E., and Brun, F. (2019). Karakoram Geodetic Glacier Mass Balances Between 2008 and 2016: Persistence of the Anomaly and Influence of a Large Rock Avalanche on Siachen Glacier. J. Glaciol. 65, 494–507. doi:10.1017/jog.2019.32
Berthier, E., Arnaud, Y., Kumar, R., Ahmad, S., Wagnon, P., and Chevallier, P. (2007). Remote Sensing Estimates of Glacier Mass Balances in the Himachal Pradesh (Western Himalaya, India). Remote Sensing Environ. 108, 327–338. doi:10.1016/j.rse.2006.11.017
Bolch, T., Buchroithner, M., Pieczonka, T., and Kunert, A. (2008a). Planimetric and Volumetric Glacier Changes in the Khumbu Himal, Nepal, Since 1962 Using Corona, Landsat Tm and Aster Data. J. Glaciol. 54, 592–600. doi:10.3189/002214308786570782
Bolch, T., Buchroithner, M. F., Peters, J., Baessler, M., and Bajracharya, S. (2008b). Identification of Glacier Motion and Potentially Dangerous Glacial Lakes in the Mt. Everest Region/Nepal Using Spaceborne Imagery. Nat. Hazards Earth Syst. Sci. 8, 1329–1340. doi:10.5194/nhess-8-1329-2008
Bolch, T., Pieczonka, T., and Benn, D. I. (2011). Multi-decadal Mass Loss of Glaciers in the Everest Area (Nepal Himalaya) Derived from Stereo Imagery. Cryosphere 5, 349–358. doi:10.5194/tc-5-349-2011
Bueler, E., Lingle, C. S., Kallen-Brown, J. A., Covey, D. N., and Bowman, L. N. (2005). Exact Solutions and Verification of Numerical Models for Isothermal Ice Sheets. J. Glaciol. 51, 291–306. doi:10.3189/172756505781829449
Buri, P., and Pellicciotti, F. (2018). Aspect Controls the Survival of Ice Cliffs on Debris-Covered Glaciers. Proc. Natl. Acad. Sci. USA 115, 4369–4374. doi:10.1073/pnas.1713892115
Buri, P., Miles, E. S., Steiner, J. F., Immerzeel, W. W., Wagnon, P., and Pellicciotti, F. (2016). A Physically Based 3‐D Model of Ice Cliff Evolution Over Debris‐covered Glaciers. J. Geophys. Res. Earth Surf. 121, 2471–2493. doi:10.1002/2016jf004039
Clark, D. H., Clark, M. M., and Gillespie, A. R. (1994). Debris-covered Glaciers in the Sierra Nevada, California, and Their Implications for Snowline Reconstructions. Quat. Res. 41, 139–153. doi:10.1006/qres.1994.1016
Clarke, G. K. C., Jarosch, A. H., Anslow, F. S., Radić, V., and Menounos, B. (2015). Projected Deglaciation of Western Canada in the Twenty-First Century. Nat. Geosci. 8, 372–377. doi:10.1038/ngeo2407
Cogley, J., Arendt, A., Bauder, A., Braithwaite, R., Hock, R., Jansson, P., et al. (2011). “Glossary of Glacier Mass Balance and Related Terms. IHP-VII Technical Documents in Hydrology No. 86, IACS Contribution No. 2. Paris: UNESCO-IHP.
Collier, E., Nicholson, L., Brock, B., Maussion, F., Essery, R., and Bush, A. (2014). Representing Moisture Fluxes and Phase Changes in Glacier Debris Cover Using a Single-Reservoir Approach. Cryosphere Discuss. 8, 1589–1629. doi:10.5194/tc-8-1429-2014
de Frutos, J., García-Archilla, B., John, V., and Novo, J. (2014). An Adaptive SUPG Method for Evolutionary Convection-Diffusion Equations. Comput. Methods Appl. Mech. Eng. 273, 219–237. doi:10.1016/j.cma.2014.01.022
Deline, P., Akçar, N., Ivy-Ochs, S., and Kubik, P. W. (2015). Repeated Holocene Rock Avalanches onto the Brenva Glacier, Mont Blanc Massif, Italy: A Chronology. Quat. Sci. Rev. 126, 186–200. doi:10.1016/j.quascirev.2015.09.004
Deline, P. (2009). Interactions Between Rock Avalanches and Glaciers in the Mont Blanc Massif During the Late Holocene. Quat. Sci. Rev. 28, 1070–1083. doi:10.1016/j.quascirev.2008.09.025
Egholm, D. L., Knudsen, M. F., Clark, C. D., and Lesemann, J. E. (2011). Modeling the Flow of Glaciers in Steep Terrains: The Integrated Second-Order Shallow Ice Approximation (iSOSIA). J. Geophys. Res. Earth Surf. 116, F02012. doi:10.1029/2010jf001900
Eis, J., Maussion, F., and Marzeion, B. (2019). Initialization of a Global Glacier Model Based on Present-Day Glacier Geometry and Past Climate Information: An Ensemble Approach. Cryosphere 13, 3317–3335. doi:10.5194/tc-13-3317-2019
Evatt, G. W., Abrahams, I. D., Heil, M., Mayer, C., Kingslake, J., Mitchell, S. L., et al. (2015). Glacial Melt Under a Porous Debris Layer. J. Glaciol. 61, 825–836. doi:10.3189/2015jog14j235
Ferguson, J. C., and Vieli, A. (2021). Modelling Steady States and the Transient Response of Debris-Covered Glaciers. Cryosphere 15, 3377–3399. doi:10.5194/tc-15-3377-2021
Fernández-Fernández, J. M., Palacios, D., García-Ruiz, J. M., Andrés, N., Schimmelpfennig, I., Gómez-Villar, A., et al. (2017). Chronological and Geomorphological Investigation of Fossil Debris-covered Glaciers in Relation to Deglaciation Processes: A Case Study in the Sierra de la Demanda, Northern Spain. Quat. Sci. Rev. 170, 232–249. doi:10.1016/j.quascirev.2017.06.034
Fyffe, C. L., Woodget, A. S., Kirkbride, M. P., Deline, P., Westoby, M. J., and Brock, B. W. (2020). Processes at the Margins of Supraglacial Debris Cover: Quantifying Dirty Ice Ablation and Debris Redistribution. Earth Surf. Process. Landforms 45, 2272–2290. doi:10.1002/esp.4879
Gardelle, J., Berthier, E., and Arnaud, Y. (2012). Slight Mass Gain of Karakoram Glaciers in the Early Twenty-First Century. Nat. Geosci. 5, 322–325. doi:10.1038/ngeo1450
Hagg, W., Mayer, C., Lambrecht, A., and Helm, A. (2008). Sub‐debris Melt Rates on Southern Inylchek Glacier, Central Tian Shan. Geografiska Annaler: Ser. A Phys. Geogr. 90, 55–63. doi:10.1111/j.1468-0459.2008.00333.x
Hambrey, M. J., Quincey, D. J., Glasser, N. F., Reynolds, J. M., Richardson, S. J., and Clemmens, S. (2008). Sedimentological, Geomorphological and Dynamic Context of Debris-Mantled Glaciers, Mount Everest (Sagarmatha) Region, Nepal. Quat. Sci. Rev. 27, 2361–2389. doi:10.1016/j.quascirev.2008.08.010
Heimsath, A. M., and McGlynn, R. (2008). Quantifying Periglacial Erosion in the Nepal High Himalaya. Geomorphology 97, 5–23. doi:10.1016/j.geomorph.2007.02.046
Herreid, S., and Pellicciotti, F. (2020). The State of Rock Debris Covering Earth's Glaciers. Nat. Geosci. 13, 621–627. doi:10.1038/s41561-020-0615-0
Hewitt, K. (2009). Rock Avalanches that Travel onto Glaciers and Related Developments, Karakoram Himalaya, Inner Asia. Geomorphology 103, 66–79. doi:10.1016/j.geomorph.2007.10.017
Hock, R., Bliss, A., Marzeion, B., Giesen, R. H., Hirabayashi, Y., Huss, M., et al. (2019). GlacierMIP - A Model Intercomparison of Global-Scale Glacier Mass-Balance Models and Projections. J. Glaciol. 65, 453–467. doi:10.1017/jog.2019.22
Huss, M. (2011). Present and Future Contribution of Glacier Storage Change to Runoff from Macroscale Drainage Basins in Europe. Water Resour. Res. 47, W07511. doi:10.1029/2010wr010299
Immerzeel, W. W., Van Beek, L. P. H., Konz, M., Shrestha, A. B., and Bierkens, M. F. P. (2012). Hydrological Response to Climate Change in a Glacierized Catchment in the Himalayas. Climatic change 110, 721–736. doi:10.1007/s10584-011-0143-4
Immerzeel, W. W., Kraaijenbrink, P. D. A., Shea, J. M., Shrestha, A. B., Pellicciotti, F., Bierkens, M. F. P., et al. (2014). High-resolution Monitoring of Himalayan Glacier Dynamics Using Unmanned Aerial Vehicles. Remote Sensing Environ. 150, 93–103. doi:10.1016/j.rse.2014.04.025
Irvine-Fynn, T. D., Porter, P. R., Rowan, A. V., Quincey, D. J., Gibson, M. J., Bridge, J. W., et al. (2017). Supraglacial Ponds Regulate Runoff from Himalayan Debris-Covered Glaciers. Geophys. Res. Lett. 44, 11–894. doi:10.1002/2017gl075398
Jansson, P., and Fredin, O. (2002). Ice Sheet Growth under Dirty Conditions: Implications of Debris Cover for Early Glaciation Advances. Quat. Int. 95-96, 35–42. doi:10.1016/s1040-6182(02)00025-3
Jarosch, A. H., Schoof, C. G., and Anslow, F. S. (2013). Restoring Mass Conservation to Shallow Ice Flow Models over Complex Terrain. Cryosphere 7, 229–240. doi:10.5194/tc-7-229-2013
Jarosch, A. H. (2008). Icetools: A Full Stokes Finite Element Model for Glaciers. Comput. Geosci. 34, 1005–1014. doi:10.1016/j.cageo.2007.06.012
Jouvet, G., Huss, M., Blatter, H., Picasso, M., and Rappaz, J. (2009). Numerical Simulation of Rhonegletscher from 1874 to 2100. J. Comput. Phys. 228, 6426–6439. doi:10.1016/j.jcp.2009.05.033
Jouvet, G., Huss, M., Funk, M., and Blatter, H. (2011). Modelling the Retreat of Grosser Aletschgletscher, Switzerland, in a Changing Climate. J. Glaciol. 57, 1033–1045. doi:10.3189/002214311798843359
Juen, M., Mayer, C., Lambrecht, A., Han, H., and Liu, S. (2014). Impact of Varying Debris Cover Thickness on Ablation: A Case Study for Koxkar Glacier in the Tien Shan. Cryosphere 8, 377–386. doi:10.5194/tc-8-377-2014
Kääb, A., Huggel, C., Fischer, L., Guex, S., Paul, F., Roer, I., et al. (2005). Remote Sensing of Glacier- and Permafrost-Related Hazards in High Mountains: An Overview. Nat. Hazards Earth Syst. Sci. 5, 527–554. doi:10.5194/nhess-5-527-2005
Kääb, A., Berthier, E., Nuth, C., Gardelle, J., and Arnaud, Y. (2012). Contrasting Patterns of Early Twenty-First-Century Glacier Mass Change in the Himalayas. Nature 488, 495–498. doi:10.1038/nature11324
Kadota, T., Seko, K., Aoki, T., Iwata, S., and Yamaguchi, S. (2000). Shrinkage of the Khumbu Glacier, East Nepal from 1978 to 1995. IAHS-AISH Publication, 235–243.
Kaser, G., Grosshauser, M., and Marzeion, B. (2010). Contribution Potential of Glaciers to Water Availability in Different Climate Regimes. Proc. Natl. Acad. Sci. 107, 20223–20227. doi:10.1073/pnas.1008162107
King, O., Bhattacharya, A., Bhambri, R., and Bolch, T. (2019). Glacial Lakes Exacerbate Himalayan Glacier Mass Loss. Sci. Rep. 9, 18145–18149. doi:10.1038/s41598-019-53733-x
King, O., Bhattacharya, A., Ghuffar, S., Tait, A., Guilford, S., Elmore, A. C., et al. (2020). Six Decades of Glacier Mass Changes Around Mt. Everest Are Revealed by Historical and Contemporary Images. One Earth 3, 608–620. doi:10.1016/j.oneear.2020.10.019
Kirkbride, M. P., and Deline, P. (2013). The Formation of Supraglacial Debris Covers by Primary Dispersal from Transverse Englacial Debris Bands. Earth Surf. Process. Landforms 38, 1779–1792. doi:10.1002/esp.3416
Kirkbride, M. (1989). About the Concepts of Continuum and Age. Boreas 18, 87–88. doi:10.1111/j.1502-3885.1989.tb00376.x
Kirkbride, M. P. (2000). “Ice-marginal Geomorphology and Holocene Expansion of Debris-Covered Tasman Glacier, New Zealand,” in Debris-covered Glaciers: Proceedings of an International Workshop Held at the University of Washington in Seattle, Seattle, Washington, USA, 13–15 September, 2000 (IAHS), 211–218.
Kirkbride, M. P. (2011). “Debris-covered Glaciers,” in Encyclopedia of Snow, Ice and Glaciers. Editors V. P. Singh, P. Singh, and U. K. Haritashya (Dordrecht: Springer Netherlands), 180–182. doi:10.1007/978-90-481-2642-2_622
Konrad, S. K., and Humphrey, N. F. (2000). “Steady-state Flow Model of Debris-Covered Glaciers (Rock Glaciers),” in Debris-covered Glaciers: Proceedings of an International Workshop Held at the University of Washington in Seattle, Seattle, Washington, USA, 13–15 September, 2000 (IAHS), 255–266.
Lambrecht, A., Mayer, C., Hagg, W., Popovnin, V., Rezepkin, A., Lomidze, N., et al. (2011). A Comparison of Glacier Melt on Debris-Covered Glaciers in the Northern and Southern Caucasus. Cryosphere 5, 525–538. doi:10.5194/tc-5-525-2011
Lambrecht, A., Mayer, C., Aizen, V., Floricioiu, D., and Surazakov, A. (2014). The Evolution of Fedchenko Glacier in the Pamir, Tajikistan, During the Past Eight Decades. J. Glaciol. 60, 233–244. doi:10.3189/2014jog13j110
Leclercq, P. W., Oerlemans, J., and Cogley, J. G. (2011). Estimating the Glacier Contribution to Sea-Level Rise for the Period 1800-2005. Surv. Geophys. 32, 519–535. doi:10.1007/s10712-011-9121-7
Lundstrom, S. C., McCafferty, A. E., and Coe, J. A. (1993). Photogrammetric Analysis of 1984-89 Surface Altitude Change of the Partially Debris-Covered Eliot Glacier, Mount Hood, Oregon, U.S.A. A. Glaciol. 17, 167–170. doi:10.1017/s0260305500012787
Mackintosh, A. N., Dugmore, A. J., and Hubbard, A. L. (2002). Holocene Climatic Changes in Iceland: Evidence from Modelling Glacier Length Fluctuations at Sólheimajökull. Quat. Int. 91, 39–52. doi:10.1016/s1040-6182(01)00101-x
Marzeion, B., Jarosch, A. H., and Hofer, M. (2012). Past and Future Sea-Level Change from the Surface Mass Balance of Glaciers. Cryosphere 6, 1295–1322. doi:10.5194/tc-6-1295-2012
Matsuoka, N., and Sakai, H. (1999). Rockfall Activity from an Alpine Cliff During Thawing Periods. Geomorphology 28, 309–328. doi:10.1016/s0169-555x(98)00116-0
Mattson, L., Gardner, J., and Young, G. (1993). “Ablation on Debris Covered Glaciers: An Example from the Rakhiot Glacier, Punjab, Himalaya,” in Snow and Glacier Hydrology: Proceedings of the Kathmandu Symposium (IAHS), 289–296.
Maussion, F., Butenko, A., Champollion, N., Dusch, M., Eis, J., Fourteau, K., et al. (2019). The Open Global Glacier Model (OGGM) v1.1. Geosci. Model. Dev. 12, 909–931. doi:10.5194/gmd-12-909-2019
Mayer, C., Lambrecht, A., Belò, M., Smiraglia, C., and Diolaiuti, G. (2006). Glaciological Characteristics of the Ablation Zone of Baltoro Glacier, Karakoram, Pakistan. Ann. Glaciol. 43, 123–131. doi:10.3189/172756406781812087
Menounos, B., Clague, J. J., Clarke, G. K. C., Marcott, S. A., Osborn, G., Clark, P. U., et al. (2013). Did Rock Avalanche Deposits Modulate the Late Holocene Advance of Tiedemann Glacier, Southern Coast Mountains, British Columbia, Canada? Earth Planet. Sci. Lett. 384, 154–164. doi:10.1016/j.epsl.2013.10.008
Miles, E. S., Pellicciotti, F., Willis, I. C., Steiner, J. F., Buri, P., and Arnold, N. S. (2016). Refined Energy-Balance Modelling of a Supraglacial Pond, Langtang Khola, Nepal. Ann. Glaciol. 57, 29–40. doi:10.3189/2016aog71a421
Miles, K. E., Hubbard, B., Miles, E. S., Quincey, D. J., Rowan, A. V., Kirkbride, M., et al. (2021). Continuous Borehole Optical Televiewing Reveals Variable Englacial Debris Concentrations at Khumbu Glacier, Nepal. Commun. Earth Environ. 2, 1–9. doi:10.1038/s43247-020-00070-x
Moore, P. L. (2018). Stability of Supraglacial Debris. Earth Surf. Process. Landforms 43, 285–297. doi:10.1002/esp.4244
Nagai, H., Fujita, K., Nuimura, T., and Sakai, A. (2013). Southwest-facing Slopes Control the Formation of Debris-Covered Glaciers in the Bhutan Himalaya. Cryosphere 7, 1303–1314. doi:10.5194/tc-7-1303-2013
Naito, M., Nakawo, M., Kadoata, T., and Raymond, C. (2000). “Numerical Simulation of Recent Shrinkage of Khumbu Glacier, Nepal Himalayas,” in Debris-covered Glaciers: Proceedings of an International Workshop Held at the University of Washington in Seattle, Seattle, Washington, USA, 13–15 September, 2000 (IAHS), 245–254.
Nakawo, M., and Young, G. J. (1981). Field Experiments to Determine the Effect of a Debris Layer on Ablation of Glacier Ice. Ann. Glaciol. 2, 85–91. doi:10.3189/172756481794352432
Nicholson, L., and Benn, D. I. (2006). Calculating Ice Melt beneath a Debris Layer Using Meteorological Data. J. Glaciol. 52, 463–470. doi:10.3189/172756506781828584
Nicholson, L., and Benn, D. I. (2013). Properties of Natural Supraglacial Debris in Relation to Modelling Sub-debris Ice Ablation. Earth Surf. Process. Landforms 38, 490–501. doi:10.1002/esp.3299
Nicholson, L., and Mertes, J. (2017). Thickness Estimation of Supraglacial Debris above Ice Cliff Exposures Using a High-Resolution Digital Surface Model Derived from Terrestrial Photography. J. Glaciol. 63, 989–998. doi:10.1017/jog.2017.68
Nicholson, L. I., McCarthy, M., Pritchard, H. D., and Willis, I. (2018). Supraglacial Debris Thickness Variability: Impact on Ablation and Relation to Terrain Properties. Cryosphere 12, 3719–3734. doi:10.5194/tc-12-3719-2018
Osmaston, H. (2005). Estimates of Glacier Equilibrium Line Altitudes by the Area×Altitude, the Area×Altitude Balance Ratio and the Area×Altitude Balance Index Methods and Their Validation. Quat. Int. 138-139, 22–31. doi:10.1016/j.quaint.2005.02.004
Østrem, G. (1959). Ice Melting Under a Thin Layer of Moraine, and the Existence of Ice Cores in Moraine Ridges. Geografiska Annaler 41, 228–230. doi:10.1080/20014422.1959.11907953
Purdie, H., Anderson, B., Mackintosh, A., and Lawson, W. (2018). Revisiting Glaciological Measurements on Haupapa/Tasman Glacier, New Zealand, in a Contemporary Context. Geografiska Annaler: Ser. A Phys. Geogr. 100, 351–369. doi:10.1080/04353676.2018.1522958
Quincey, D. J., Luckman, A., and Benn, D. (2009). Quantification of Everest Region Glacier Velocities Between 1992 and 2002, Using Satellite Radar Interferometry and Feature Tracking. J. Glaciol. 55, 596–606. doi:10.3189/002214309789470987
Quincey, D., Braun, M., Glasser, N. F., Bishop, M., Hewitt, K., and Luckman, A. (2011). Karakoram Glacier Surge Dynamics. Geophys. Res. Lett. 38, L18504. doi:10.1029/2011gl049004
Ragettli, S., Immerzeel, W. W., and Pellicciotti, F. (2016). Contrasting Climate Change Impact on River Flows from High-Altitude Catchments in the Himalayan and Andes Mountains. Proc. Natl. Acad. Sci. USA 113, 9222–9227. doi:10.1073/pnas.1606526113
Reid, T. D., and Brock, B. W. (2010). An Energy-Balance Model for Debris-Covered Glaciers Including Heat Conduction Through the Debris Layer. J. Glaciol. 56, 903–916. doi:10.3189/002214310794457218
Reid, T. D., and Brock, B. W. (2014). Assessing Ice-Cliff Backwasting and its Contribution to Total Ablation of Debris-Covered Miage Glacier, Mont Blanc Massif, Italy. J. Glaciol. 60, 3–13. doi:10.3189/2014jog13j045
Reznichenko, N., Davies, T., Shulmeister, J., and McSaveney, M. (2010). Effects of Debris on Ice-Surface Melting Rates: An Experimental Study. J. Glaciol. 56, 384–394. doi:10.3189/002214310792447725
Reznichenko, N. V., Davies, T. R. H., and Alexander, D. J. (2011). Effects of Rock Avalanches on Glacier Behaviour and Moraine Formation. Geomorphology 132, 327–338. doi:10.1016/j.geomorph.2011.05.019
Roe, G. H. (2011). What Do Glaciers Tell Us about Climate Variability and Climate Change? J. Glaciol. 57, 567–578. doi:10.3189/002214311796905640
Rounce, D. R., Hock, R., and Shean, D. E. (2020). Glacier Mass Change in High Mountain Asia through 2100 Using the Open-Source Python Glacier Evolution Model (PyGEM). Front. Earth Sci. 7, 331. doi:10.3389/feart.2019.00331
Rounce, D. R., Hock, R., McNabb, R. W., Millan, R., Sommer, C., Braun, M. H., et al. (2021). Distributed Global Debris Thickness Estimates Reveal Debris Significantly Impacts Glacier Mass Balance. Geophys. Res. Lett. 48, e2020GL091311. doi:10.1029/2020GL091311
Rowan, A. V., Egholm, D. L., Quincey, D. J., and Glasser, N. F. (2015). Modelling the Feedbacks Between Mass Balance, Ice Flow and Debris Transport to Predict the Response to Climate Change of Debris-Covered Glaciers in the Himalaya. Earth Planet. Sci. Lett. 430, 427–438. doi:10.1016/j.epsl.2015.09.004
Rowan, A. V., Nicholson, L. I., Quincey, D. J., Gibson, M. J., Irvine-Fynn, T. D. L., Watson, C. S., et al. (2021). Seasonally Stable Temperature Gradients Through Supraglacial Debris in the Everest Region of Nepal, Central Himalaya. J. Glaciol. 67, 170–181. doi:10.1017/jog.2020.100
Rowan, A. V. (2017). The 'Little Ice Age' in the Himalaya: A Review of Glacier advance Driven by Northern Hemisphere Temperature Change. Holocene 27, 292–308. doi:10.1177/0959683616658530
Sakai, A., and Fujita, K. (2010). Formation Conditions of Supraglacial Lakes on Debris-Covered Glaciers in the Himalaya. J. Glaciol. 56, 177–181. doi:10.3189/002214310791190785
Sakai, A., Nakawo, M., and Koji, F. (1998). Melt Rate of Ice Cliffs on the Lirung Glacier, Nepal Himalayas, 1996. Bull. Glacier Res. 16, 57–66.
Sakai, A., Takeuchi, N., Fujita, K., and Nakawo, M. (2000). “Role of Supraglacial Ponds in the Ablation Process of a Debris-Covered Glacier in the Nepal Himalayas,” in Debris-covered Glaciers: Proceedings of an International Workshop Held at the University of Washington in Seattle, Seattle, Washington, USA, 13–15 September, 2000 (IAHS), 119–132.
Salerno, F., Thakuri, S., Tartari, G., Nuimura, T., Sunako, S., Sakai, A., et al. (2017). Debris-covered Glacier Anomaly? Morphological Factors Controlling Changes in the Mass Balance, Surface Area, Terminus Position, and Snow Line Altitude of Himalayan Glaciers. Earth Planet. Sci. Lett. 471, 19–31. doi:10.1016/j.epsl.2017.04.039
Scherler, D., and Egholm, D. (2020). Production and Transport of Supraglacial Debris: Insights from Cosmogenic 10Be and Numerical Modeling, Chhota Shigri Glacier, Indian Himalaya. J. Geophys. Res. Earth Surf. 125, e2020JF005586. doi:10.1029/2020jf005586
Scherler, D., Bookhagen, B., and Strecker, M. R. (2011a). Hillslope-glacier Coupling: The Interplay of Topography and Glacial Dynamics in High Asia. J. Geophys. Res. Earth Surf. 116, F02019. doi:10.1029/2010jf001751
Scherler, D., Bookhagen, B., and Strecker, M. R. (2011b). Spatially Variable Response of Himalayan Glaciers to Climate Change Affected by Debris Cover. Nat. Geosci. 4, 156–159. doi:10.1038/ngeo1068
Scherler, D., Wulf, H., and Gorelick, N. (2018). Global Assessment of Supraglacial Debris-Cover Extents. Geophys. Res. Lett. 45, 11–798. doi:10.1029/2018gl080158
Scherler, D. (2014). Climatic Limits to Headwall Retreat in the Khumbu Himalaya, Eastern Nepal. Geology 42, 1019–1022. doi:10.1130/g35975.1
Seguinot, J., Ivy-Ochs, S., Jouvet, G., Huss, M., Funk, M., and Preusser, F. (2018). Modelling Last Glacial Cycle Ice Dynamics in the Alps. Cryosphere 12, 3265–3285. doi:10.5194/tc-12-3265-2018
Seong, Y. B., Owen, L. A., Caffee, M. W., Kamp, U., Bishop, M. P., Bush, A., et al. (2009). Rates of basin-wide rockwall Retreat in the K2 Region of the Central Karakoram Defined by Terrestrial Cosmogenic Nuclide 10Be. Geomorphology 107, 254–262. doi:10.1016/j.geomorph.2008.12.014
Shea, J. M., Immerzeel, W. W., Wagnon, P., Vincent, C., and Bajracharya, S. (2015). Modelling Glacier Change in the Everest Region, Nepal Himalaya. Cryosphere 9, 1105–1128. doi:10.5194/tc-9-1105-2015
Shugar, D. H., Rabus, B. T., Clague, J. J., and Capps, D. M. (2012). The Response of Black Rapids Glacier, Alaska, to the Denali Earthquake Rock Avalanches. J. Geophys. Res. Earth Surf. 117, F01006. doi:10.1029/2011jf002011
Shukla, A., Gupta, R. P., and Arora, M. K. (2009). Estimation of Debris Cover and its Temporal Variation Using Optical Satellite Sensor Data: A Case Study in Chenab Basin, Himalaya. J. Glaciol. 55, 444–452. doi:10.3189/002214309788816632
Shulmeister, J., Davies, T. R., Evans, D. J. A., Hyatt, O. M., and Tovar, D. S. (2009). Catastrophic Landslides, Glacier Behaviour and Moraine Formation - A View from an Active Plate Margin. Quat. Sci. Rev. 28, 1085–1096. doi:10.1016/j.quascirev.2008.11.015
Steiner, J. F., Pellicciotti, F., Buri, P., Miles, E. S., Immerzeel, W. W., and Reid, T. D. (2015). Modelling Ice-Cliff Backwasting on a Debris-Covered Glacier in the Nepalese Himalaya. J. Glaciol. 61, 889–907. doi:10.3189/2015jog14j194
Stokes, C. R., Popovnin, V., Aleynikov, A., Gurney, S. D., and Shahgedanova, M. (2007). Recent Glacier Retreat in the Caucasus Mountains, Russia, and Associated Increase in Supraglacial Debris Cover and Supra-/proglacial lake Development. Ann. Glaciol. 46, 195–203. doi:10.3189/172756407782871468
Sutherland, J., Carrivick, J., Gandy, N., Shulmeister, J., Quincey, D., and Cornford, S. (2020). Proglacial Lakes Control Glacier Geometry and Behavior during Recession. Geophys. Res. Lett. 47, e2020GL088865. doi:10.1029/2020gl088865
Thompson, S., Benn, D. I., Mertes, J., and Luckman, A. (2016). Stagnation and Mass Loss on a Himalayan Debris-Covered Glacier: Processes, Patterns and Rates. J. Glaciol. 62, 467–485. doi:10.1017/jog.2016.37
Tielidze, L. G., Bolch, T., Wheate, R. D., Kutuzov, S. S., Lavrentiev, I. I., and Zemp, M. (2020). Supra-glacial Debris Cover Changes in the Greater Caucasus from 1986 to 2014. Cryosphere 14, 585–598. doi:10.5194/tc-14-585-2020
Santamaria Tovar, D., Shulmeister, J., and Davies, T. R. (2008). Evidence for a Landslide Origin of New Zealand's Waiho Loop Moraine. Nat. Geosci 1, 524–526. doi:10.1038/ngeo249
Vacco, D. A., Alley, R. B., Pollard, D., and Reusch, D. B. (2010). Numerical Modeling of Valley Glacier Stagnation as a Paleoclimatic Indicator. Quat. Res. 73, 403–409. doi:10.1016/j.yqres.2009.09.006
Watanabe, O., Iwata, S., and Fushimi, H. (1986). Topographic Characteristics in the Ablation Area of the Khumbu Glacier, Nepal Himalaya. A. Glaciol. 8, 177–180. doi:10.1017/s0260305500001415
Watanabe, T., Ives, J. D., and Hammond, J. E. (1994). Rapid Growth of a Glacial lake in Khumbu Himal, Himalaya: Prospects for a Catastrophic Flood. Mountain Res. Develop. 14, 329–340. doi:10.2307/3673729
Wirbel, A., Jarosch, A. H., and Nicholson, L. (2018). Modelling Debris Transport Within Glaciers by Advection in a Full-Stokes Ice Flow Model. Cryosphere 12, 189–204. doi:10.5194/tc-12-189-2018
Keywords: debris-covered glacier, review, climate change, modelling, glacier system
Citation: Nicholson L, Wirbel A, Mayer C and Lambrecht A (2021) The Challenge of Non-Stationary Feedbacks in Modeling the Response of Debris-Covered Glaciers to Climate Forcing. Front. Earth Sci. 9:662695. doi: 10.3389/feart.2021.662695
Received: 01 February 2021; Accepted: 04 November 2021;
Published: 21 December 2021.
Edited by:
Shin Sugiyama, Hokkaido University, JapanReviewed by:
Ann V Rowan, The University of Sheffield, United KingdomCopyright © 2021 Nicholson, Wirbel, Mayer and Lambrecht. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lindsey Nicholson, TGluZHNleS5OaWNob2xzb25AdWliay5hYy5hdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.